Parametric Alpha- and Beta-Band Signatures of Supramodal Numerosity Information in Human Working Memory

Abstract

Numerosity can be assessed by analog estimation, similar to a continuous magnitude, or by discrete quantification of the individual items in a set. While the extent to which these two processes rely on common neural mechanisms remains debated, recent studies of sensory working memory (WM) have identified an oscillatory signature of continuous magnitude information, in terms of quantitative modulations of prefrontal upper beta activity (20–30 Hz). Here, we examined how such parametric oscillatory WM activity may also reflect the abstract assessment of the numerosity of discrete items. We recorded EEG while participants (n = 24) processed the number of stimulus pulses presented in the visual, auditory, or tactile modality, under otherwise identical experimental conditions. Behavioral response profiles showed varying degrees of analog estimation and of discretized quantification in the different modalities. During sustained processing in WM, the amplitude of posterior alpha oscillations (8–13 Hz) reflected the increased memory load associated with maintaining larger sets of discrete items. In contrast, earlier numerosity-dependent modulations of right prefrontal upper beta (20–30 Hz) specifically reflected the extent to which numerosity was assessed by analog estimation, both between and within presentation modalities. Together, the analog approximation—but not the discretized representation—of numerosity information exhibited a parametric oscillatory signature akin to a continuous sensory magnitude. The results suggest dissociable oscillatory mechanisms of abstract numerosity integration, at a supramodal processing stage in human WM.

Introduction

When the first raindrops announce a change in weather, an assessment of “how many” drops one has already noticed can be derived from tactile, visual, and/or auditory perception regardless of the particular sensory attributes of the individual drops. Humans may accomplish such abstract, supramodal quantification of numerosity for instance by counting, which requires the discrete items in a set to be individuated, serially indexed, and actively encoded into verbal/symbolic labels (Gelman and Gallistel, 1978; Nieder, 2005; Piazza et al., 2006; Piazza and Izard, 2009). Only for small sets of up to three or four items, discrete numerosity information appears to be available with little effort and almost immediately, a phenomenon also called “subitizing” (Kaufman and Lord, 1949). Whereas subitizing and counting rely on discretization, numerosity can also be approximated by analog estimation, which is often assumed to resemble the direct assessment of a continuous magnitude (Dehaene, 1997; Piazza et al., 2006; Nieder and Dehaene, 2009; Piazza, 2010). To what extent discretized and analog processing of quantity information may share common mechanisms, across different presentation modes, remains a subject of ongoing debate (Walsh, 2003; Cohen Kadosh and Walsh, 2009; Henik et al., 2011; Hyde, 2011; Van Opstal and Verguts, 2013).

Experiments in animals and humans have proceeded in deciphering neural codes that may underlie the processing of discrete and continuous quantity information. Upon presentation, number, numerosity, and other—mostly visual—quantities (but see Eger et al., 2003; Nieder, 2012) are encoded by overlapping populations of discretely tuned neurons in parietal cortex and prefrontal cortex (PFC; for review, see Nieder and Dehaene, 2009). On the other hand, the active, sustained processing of continuous sensory magnitudes in working memory (WM) was found to entail analog “parametric” changes of ongoing activity in PFC (Romo et al., 1999; Barak et al., 2010; Spitzer et al., 2010, 2013a), regardless of presentation modality (Spitzer and Blankenburg, 2012). A yet unresolved question is how these different types of abstract quantity processing in PFC might be empirically and theoretically reconciled (Nieder and Merten, 2007; Nieder and Dehaene, 2009). In particular, Electroencephalography (EEG) studies in humans have shown that the parametric prefrontal WM processing of analog continua entails modulations of large-scale oscillatory synchrony in the beta-frequency range (20–30 Hz; Spitzer et al., 2010, 2013a), a level of observation that, so far, has been left entirely unexplored in the domain of number and numerosity.

Here, we examine the oscillatory correlates of supramodal numerosity processing in WM. Based on behavioral response profiles, we identified varying degrees of analog estimation and of discretized quantification, respectively, of numerosity information presented in the tactile, visual, and auditory modalities. The central question was the extent to which the two types of numerosity processing may exhibit characteristic oscillatory WM signatures, across the different presentation modalities.

Materials and Methods

Subjects.

Twenty-six healthy volunteers (age range, 22–35 years; 17 female, 9 male) participated in the study after providing written informed consent. Two participants (1 female, 1 male) were excluded from analysis due to excessive ocular and movement artifacts. The study was approved by the ethics commission of the Free University Berlin and adhered to the Human Subjects Guidelines of the Declaration of Helsinki.

Overview of experimental protocol.

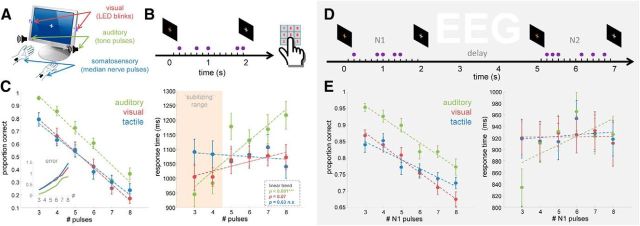
Discrete suprathreshold pulses were presented by visual, auditory, or tactile stimulation (Fig. 1A). In each modality condition, participants evaluated the numerosity of pulses delivered pseudo-randomly within a 2 s stimulation interval. Subjects' behavioral performance in explicitly naming the number of perceived pulses was assessed in a separate test (Fig. 1B,C). Identically designed pulse sequences were used in a delayed comparison task for examination of EEG activity during WM processing (Fig. 1D). In this task, subjects were asked to maintain the numerosity information in memory (N1; 3–8 pulses, randomly varied), and to indicate whether a comparison sequence (N2; N1 ± 1 pulse) contained more or fewer pulses.

Figure 1.

Experimental setup, tasks, and behavioral results. A, Pulsed stimulus sequences were presented either visually, auditorily, or by electrical stimulation of the median nerve. All stimuli were presented bilaterally. B, In a separate behavioral test, subjects were asked to explicitly name the number of pulses in each sequence. C, Left, Mean proportion of correct number judgments. Error bars show SEM. Dashed lines show linear fit. Inset plot shows the average deviation (error) from the true pulse count. Right, RTs indicate serial (i.e., discretized) processing in the auditory condition, and more direct analog estimation in the remaining modalities. Red shading indicates the subitizing range (#≤4, see text for details). D, Delayed numerosity comparison task for EEG analysis. On each trial, a pulse sequence (N1, 3–8 pulses) was presented for WM maintenance and subsequent comparison against a second sequence (N2, ±1 pulse) in the same modality. E, Behavioral results. Left, Mean proportion correct N1–N2 comparisons. Right, Mean RTs, see text for details.

Stimuli.

On visual trials, bilateral light pulses were delivered by two sets of white light-emitting diodes (LEDs) mounted to the left and the right of a 19 inch TFT screen. On each pulse, the LEDs were driven for 50 ms by an 8 kHz carrier signal (sampled at 48 kHz for an optimized 6-point elementary waveform; for details, see Allefeld et al., 2011) controlled via the right channel of the onboard soundcard of the stimulation PC, using a high-fidelity amplifier (model CS-PA1, Dynavox) and a custom-built circuit of resistors (6 Ω) and diodes to match the impedance and polarity of the LEDs.

On auditory trials, acoustic pulses were delivered by stereo loudspeakers located in front of the subject (model AX 510, Dell). Auditory stimuli consisted of 1 kHz sine tone pulses of 50 ms duration, including 2.5 ms linear fade-in/fade-out to avoid onset/offset artifacts. The sounds were generated at a 48 kHz sampling rate and were output via the left channel of the onboard soundcard of the stimulation PC.

On tactile trials, square-wave electric pulses (200 μs) were delivered bilaterally via two pairs of disposable, surface-adhesive electrodes attached to the wrists of both arms, using two simultaneously triggered constant current neurostimulators (DS3, Digitimer). Subjects reported bilateral tactile sensations radiating to the thumbs, index, and middle fingers, verifying stimulation of the median nerve. Individual sensory thresholds were determined using a staircase procedure (mean, 1.754 mA; SE, 0.08 mA). The stimulus intensity was then adjusted to a target value of 150% of the individual threshold. Minor individual adjustments (±0.2 mA) were optionally made to subjects' comfort. The resulting average intensity used in the experiment was 2.50 mA (SE, 0.09 mA).

In each modality, pulse sequences were identically devised by pseudo-randomly distributing two to nine single pulses over a visually cued stimulation interval of 2000 ms (Fig. 1B, D), with the restrictions that no pulses occurred within the first and the last 100 ms of the stimulation interval, and that successive pulse onsets were separated by at least 150 ms. This was achieved by randomly allocating each single pulse to one of 13 equidistant positions between 100 and 1900 ms of the stimulation interval (Fig. 1B). As a result, the temporal frequency spectrum of the pulse sequences, as a potential source of EEG entrainment, was physically bound to 6.67 Hz and/or its lower subharmonics (e.g., 3.33, 2.22, or 1.66 Hz) for all possible sequences.

Number naming test.

On each trial, a pulse sequence was presented, and subjects were asked to enter the number of pulses via the number pad on the PC keyboard (Fig. 1B). The test comprised 144 trials (6 trials for each numerosity and modality condition) with individual pulse sequences presented identically as in the delayed comparison experiment (see below). For comparability with the delay task, and because the range of potential error responses was limited to one-digit numbers, sequences with two or nine pulses were excluded from analysis. The number naming test was performed after the delayed comparison task, in order not to bias subjects toward explicitly numerical WM processing.

Delayed numerosity comparison.

A schematic of the WM/EEG protocol is illustrated in Figure 1D. Before each block of 20 trials, a brief visual instruction (“seeing,” “hearing,” or “touching”) indicated the modality in which the forthcoming stimuli would be presented. The experimental procedure (Fig. 1D) was identical for all stimulus modalities. Each trial began with the presentation of a small gray fixation cross centered on the TFT screen. After a variable pretrial interval (1500–2000 ms), the color of the cross changed to red and the first pulse sequence (N1, three to eight pulses, randomly varied) was delivered. The end of the N1 interval was indicated by the fixation cross turning back to gray, followed by a 3000 ms memory delay. After the delay, the N2 pulse sequence was presented, which always contained the number of pulses in N1 ± 1 pulse (randomly varied). Note that the temporal positions of the individual pulses in each sequence were randomly assigned, such that on any given trial, N2 could have a very different temporal structure (i.e., rhythm, sequence length, or pulse density) than N1 (Fig. 1D; for additional control analyses, see Fig. 6A–D). Responses were entered by pressing a right foot pedal to indicate that N2 contained more pulses than N1, and by pressing a left pedal otherwise. After a 2000 ms response time (RT), performance feedback was given. Participants were instructed to look at the fixation cross throughout the entire experiment. After a few practice trials, each subject performed five sessions of six blocks (two of each modality, in a counterbalanced serial order) of 20 trials, for a total of 200 trials in each modality.

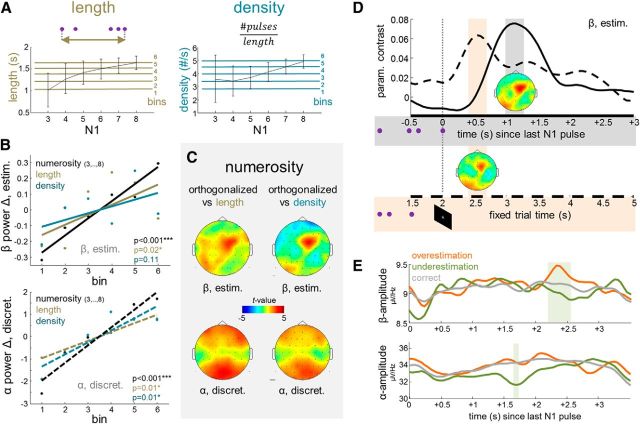
Figure 6.

A–C, Control analyses of modulations by task-irrelevant stimulus properties. A, Left, Sequence length, measured as the time interval between the first and the last pulse in each N1. Right, Temporal density, measured as the frequency of pulses within each N1 sequence. Line plots illustrate the relation to N1 numerosity; error bars indicate SD. Horizontal colored lines show the binning raster used for comparative analyses in B. B, Changes in normalized EEG power as functions of numerosity, length, or density. Top, Prefrontal upper beta, collapsed over all estimating subjects and conditions. Lower, Posterior alpha, collapsed over all discretizing subjects and conditions. C, Statistical topographical maps of parametric modulations by numerosity computed from single-trial GLM regressors that were orthogonalized against length (left) or density (right). D, Time course of prefrontal upper beta modulation, collapsed over all estimating subjects and conditions, computed from epochs time locked to the last pulse in N1 (solid line, gray shading; as in main analysis) or time locked invariantly to the end of the cued 2 s interval (dashed line, red shading; see time axis in Fig. 1D). Same color scale of statistical topographical maps as in C. E, Top, Time course of prefrontal upper beta amplitude on error trials in which N1 was overestimated (orange) or underestimated (green) in subsequent comparison against N2. The shaded area indicates the time window of significant differences. Gray line shows time course for correct comparison trials; see text for details. Bottom, Same as top, for posterior alpha amplitude.

EEG recording and analysis.

EEG was recorded using a 64-channel active electrode system (ActiveTwo, BioSemi), with electrodes placed in an elastic cap according to the extended 10–20 system. Individual electrode locations were registered using an electrode positioning system (Zebris Medical GmbH). Vertical and horizontal eye movements were recorded from four additional channels. Signals were digitized at a sampling rate of 2048 Hz, off-line bandpass filtered (1–100 Hz), downsampled to 512 Hz, and average referenced. All analyses were performed using SPM8 for MEG/EEG (Wellcome Department of Cognitive Neurology, London, UK; www.fil.ion.ucl.ac.uk/spm/) and custom MATLAB code (MathWorks). The EEG was corrected for eye blinks using calibration data to generate individual artifact coefficients and adaptive spatial filtering (for details, see Ille et al., 2002). Remaining artifacts were rejected by excluding all epochs containing amplitudes >80 μV from analysis. Time–frequency (TF) representations of spectral power were obtained by applying a Morlet Wavelet transform of 7 cycles per frequency. For analysis of task-induced power changes (Fig. 2A,B), the TF data were baseline corrected with respect to the average power in the pretrial interval (−1500 to 0 ms relative to N1 onset). No baseline correction was used for the remaining analyses (Spitzer and Blankenburg, 2011, 2012). Only correct comparison trials were included in the analyses.

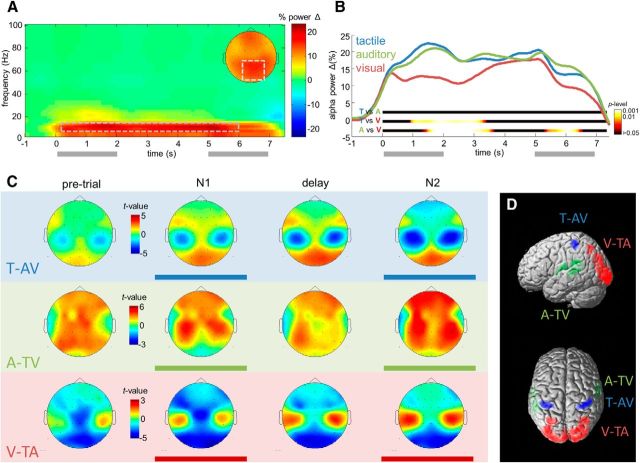
Figure 2.

Alpha-band oscillations (8–13 Hz) during WM processing reflect overall task demands and presentation modality. A, B, Task-induced changes of alpha power. A, TF map of power changes relative to pretrial baseline, collapsed across modality conditions. Inset shows posterior scalp topography of the power changes in the TF window outlined by dashed rectangle. B, Throughout the WM delay, alpha power over parieto-occipital channels increases in each modality condition. Colored ribbons indicate the significance of pairwise comparisons between modalities. The alpha increase in the visual condition is significantly reduced only during early retention. C, D, Modality-dependent alpha topographies. C, Statistical topographical maps of modality-specific alpha activity during the different task periods, without baseline correction. For each map, alpha activity in one modality (blue, tactile; green, auditory; red, visual) was contrasted against the two remaining modalities. D, 3D source reconstructions of the modality-specific alpha decreases during WM processing, see text for details.

Statistical analysis.

The statistical design was implemented in SPM8, using the general linear model (GLM) applied to each subject's single-trial TF data (for details, see Spitzer and Blankenburg, 2011; Spitzer et al., 2013a). To warrant conformity with the GLM under normal error assumptions, the TF data were square-root-transformed and convolved with a 3 Hz × 500 ms (full-width at half-maximum) Gaussian kernel (for details, see Kilner et al., 2005). The GLM design matrix consisted of three dummy variables specifying the trials' modality condition (visual, auditory, or tactile) and three parametric regressors coding the number of N1 pulses in the respective modality condition. The parametric regressors were zero-centered and normalized. The model was inverted using restricted maximum-likelihood estimation as implemented in SPM8, yielding beta parameter estimates for each model regressor at each TF bin. TF contrasts of interest were then computed by weighted summation of individual regressors' beta estimates.

The individual contrast spectra were subjected to mass-univariate analysis on the group level, using one-sample t tests as implemented in SPM8. This involved computing for each TF bin a t value that reflected the significance of the contrast. Family-wise errors (FWEs) in TF space were controlled using Random Field Theory (Worsley et al., 1996) to determine the FWE-corrected probability that at a given channel a cluster of adjacent significant TF bins may have been obtained by chance. A cluster was defined as a group of adjacent TF bins that all exceeded a threshold of p < 0.01 (uncorrected). To account for multiple comparisons across channels, only clusters exceeding a conservative FWE-corrected threshold of p_{cluster (FWE)} < 0.001 were considered significant.

Source reconstruction.

The sources of oscillatory EEG activity were reconstructed using distributed 3D source modeling based on multiple sparse priors (MSP) as implemented in SPM8 (Friston et al., 2006). For each participant, a forward model was constructed, using an 8196 vertex template cortical mesh coregistered to the individual electrode positions via three fiducial markers. The lead field of the forward model was computed using the three-shell boundary element method EEG head model available in SPM8. Source estimates were then computed on the canonical mesh using MSP under group constraints (Litvak and Friston, 2008). Trial-specific TF contrasts were used to summarize oscillatory source power for specific frequency bands and at specific times as 3D images, which were then analyzed using conventional statistical parametric mapping procedures. The SPM anatomy toolbox (Eickhoff et al., 2005) was used to establish a cytoarchitectonic reference where possible.

Results

Number naming

As expected from previous behavioral studies (Lechelt, 1975; Philippi et al., 2008; Tokita et al., 2013), explicitly identifying the count of the sequential pulses (Fig. 1B,C) was more accurate in the auditory condition (63.6% correct; SE, 0.024%) compared with the remaining modalities (visual: 47.4%, SE, 0.037%; tactile: 47.9%, SE, 0.033%; both p < 0.001; visual vs tactile: p > 0.85). Correct responses generally decreased with increasing numerosity (Fig. 1C, left; all p < 0.001, linear trend analysis), with similar slopes in all modalities (all pairwise p > 0.10). Judgments of the largest numerosity (eight pulses) showed mean deviations of 0.86 (auditory), 1.29 (visual), and 1.49 (tactile) from the true pulse count (Fig. 1C, left, inset), mostly by underestimation (in 87%, 96%, and 98% of inaccurate judgments; see also Lechelt, 1975; Philippi et al., 2008; Tokita et al., 2013).

Overall, mean RTs (Fig. 1C, right) did not differ between modalities (visual, 1049 ms; auditory, 1103; tactile, 1076; all pairwise p > 0.20). Importantly, however, RTs in the auditory condition increased markedly with increasing pulse count (p < 0.001, linear trend analysis, corrected) compared with the remaining conditions (both pairwise p < 0.05, corrected). This was characterized by subitizing-like responses (i.e., particularly speeded responses to small numerosities ≤4; Fig. 1C, right, red shading), and by relatively slow responses for larger numerosities, as expected for (attempts of) counting. Only a moderate trend for increasing RTs was evident in the visual modality (p = 0.07, uncorrected), and no systematic RT increase at all arose for the tactile stimulus sequences (p > 0.60; visual vs tactile, p = 0.08, uncorrected), as is expected for more direct, quasi-analog quantity estimation. Together, the response profiles indicate a relative predominance of discretized quantification (as reflected by subitizing and counting) in the auditory condition, and a stronger reliance on analog estimation in the remaining modalities, in particular in the tactile condition.

Note that with a sequential protocol demanded by multimodal presentation, we expectedly found overall shallower RT slopes than are typically seen with simultaneous (e.g., visuospatial) presentation (Kaufman and Lord, 1949). In particular, as individual pulses may have been quantified already “on-line” throughout the presentation interval (Nieder et al., 2006; Nieder, 2012), the response profiles may underrepresent the overall contribution of discretized quantification (i.e., subitizing and counting), and are to be interpreted only in terms of relative differences.

Delayed comparison: behavior

Comparison accuracy in the WM/EEG experiment (Fig. 1D) resembled the above results, with superior performance in the auditory condition (86.5%; SE, 0.012%), compared with the tactile (77.6%; SE, 0.015%; p < 0.001) and visual conditions (78.1%; SE, 0.013%; p < 0.001). As expected by the numerical magnitude effect (Moyer and Landauer, 1967) in analogy to the Weber–Fechner law, accuracy declined with increasing N1 numerosity in all modalities (Fig. 1E, left; all p < 0.001), with similar slopes (all pairwise p > 0.10). Overall mean RTs (Fig. 1E, right) were similar across modalities (922, 914, and 925 ms; all pairwise p > 0.40). However, in the auditory condition responses were markedly faster if N1 contained only three pulses (834 ms; p < 0.05, corrected), mirroring the above subitizing pattern for numerosities of 4 and smaller (Fig. 1C, right; note that in the delay task, N1 = 3 was to be compared against either N2 = 2 or N2 = 4; see Materials and Methods).

EEG results

Task-related changes in oscillatory activity

First, we identified overall changes of spectral activity (Fig. 2A) during the delayed comparison task, relative to a pretrial baseline (−1500 to 0 ms). Replicating previous findings during internally oriented WM processing (Spitzer and Blankenburg, 2012; for review, see Hanslmayr et al., 2012), a sustained and widespread increase in posterior alpha power (8–13 Hz) was evident throughout the trial period (Fig. 2A). In comparison between modalities (Fig. 2B), the increase was less pronounced during encoding and early retention in the visual condition (1200–3150 ms; all time bins, p < 0.05), likely due to relative suppression by visual perceptual processing. Later in the retention interval however, posterior alpha power increased to a similar level in all three modalities (3500–5200 ms; all time bins, p > 0.05).

Modality-specific alpha topographies

We next examined the effects of attentional orienting during WM processing (Spitzer and Blankenburg, 2011, 2012) by inspecting for each modality topographical statistical maps of the difference in alpha power compared with the two remaining modalities (Fig. 2C). A systematic pattern of modality-specific alpha topographies emerged, with relatively decreased power over bilateral central areas in the tactile contrast, temporal areas in the auditory contrast, and posterior areas in the visual contrast. By tendency, the modality-specific topographies appeared most prominent during the stimulation periods (0–2 s and 5–7 s), but were clearly evident also during the retention interval (2–5 s). In line with previous findings (Spitzer and Blankenburg, 2012), an indication of the modality-specific differences had already appeared in the pretrial interval (Fig. 2C, leftmost column). For comparison, note that the task-induced effects in Figure 2, A and B, reflect power changes relative to pretrial baseline (see Materials and Methods; for related analyses and discussion, see Spitzer and Blankenburg, 2011, 2012). 3D source reconstruction (Fig. 2D) localized the modality-specific decreases in the tactile and visual contrasts during retention to bilateral somatosensory cortex (areas 3b, 2, and 1) and visual cortex (area 17), respectively (Fig. 2D, blue and red; p < 0.001, uncorrected; all p_cluster < 0.05, FWE). Localization of the auditory alpha decrease, albeit statistically unreliable (p < 0.20, uncorrected), was consistent with a source in auditory sensory areas (Fig. 2D, green).

Numerosity-dependent modulations of posterior alpha power (8–13 Hz)

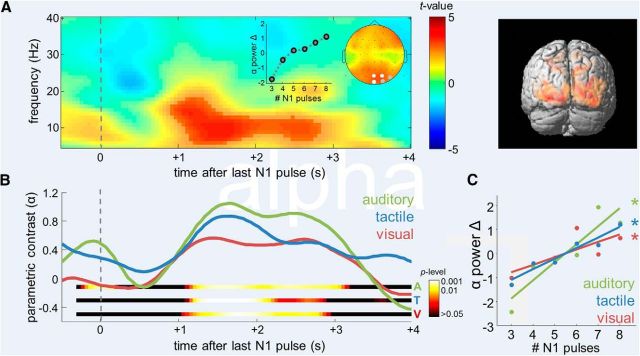
To identify modulations of EEG oscillations by the numerosity information maintained in WM, we analyzed parametric contrasts that reflect the strength of a linear relation between TF activity and the number of pulses in N1. To rule out stimulus confounds by the trial-specific temporal structure of N1, the data were epoched in a trial-specific manner such that time 0 is aligned with the presentation of the last pulse in each N1 sequence (for additional control analyses, see Fig. 6D).

Figure 3A illustrates the overall parametric modulation by N1 numerosity, collapsed across modality conditions, over posterior areas. A significant (p_cluster < 0.001, FWE) delayed modulation emerged in the alpha band (8–13 Hz) between 1000 and 3000 ms after presentation of the last N1 pulse, extending over several occipitoparietal channels (PO4, Oz, POz, both p_cluster < 0.001, FWE; O₂, PO8, both p_cluster < 0.005, FWE). The overall modulation was characterized by a monotonic alpha power increase, which appeared particularly pronounced in the subitizing range (N1 < 5; Fig. 3A, inset graph), suggesting an association with discretized processing. 3D source reconstruction localized the parametric effect to striate and extrastriate visual cortex (Fig. 3A, right, areas 17/18; p < 0.001, uncorrected; p_cluster < 0.05, FWE). The numerosity-dependent modulation was significantly evident in each individual modality condition (Fig. 3B), with similar time courses (1250–2150 ms; all time bins, p < 0.01) and overlapping sources in visual areas (Fig. 3A, right, red; p_conjunction < 0.05). The grand average changes of posterior alpha power as a function of N1 numerosity in each modality are illustrated in Figure 3C. Despite a tendency for the modulation to be strongest in the auditory condition, pairwise comparisons between modalities did not reach significance (all p > 0.05).

Figure 3.

Supramodal numerosity-dependent modulation of posterior alpha. A, Left, Statistical parametric TF map indicating the significance of the linear modulation of oscillatory activity by the number of pulses in N1, collapsed across modality conditions. Epochs were time locked to presentation of the last pulse in each N1 sequence. Saturated colors delineate significant TF cluster. Channels exhibiting a significant effect are marked white in inset scalp topographical map (p < 0.001, FWE; gray, p < 0.005, FWE). Inset graph shows grand average changes in normalized alpha power as a function of numerosity. Right, 3D source reconstruction of the parametric modulation identified in left (apricot color rendering, p < 0.001) and overlap of sources in the three modalities (red rendering, p_conjunction < 0.05). B, Time courses of the posterior alpha-power modulation by numerosity in the different modality conditions. Colored ribbons indicate the significance of modulation in each modality. C, Grand average changes in normalized alpha power as a function of numerosity, in the different modality conditions. Asterisks indicate the significance of linear modulation.

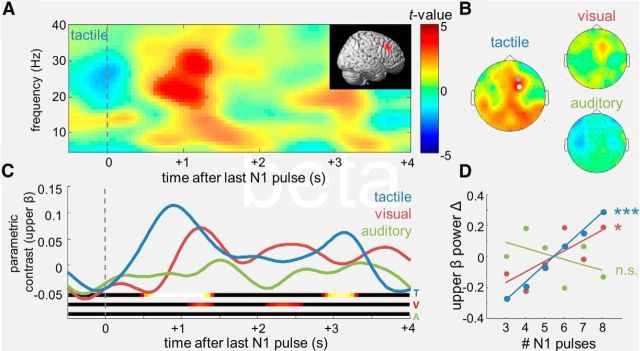
Numerosity-dependent modulations of prefrontal upper beta power (20–30 Hz) reflect analog estimation

Analyses of the individual parametric contrasts in the different modalities revealed a significant modulation of upper beta power (∼20–30 Hz; 0.65–1.4 s) in the tactile condition (Fig. 4A), with a maximum over right prefrontal channels (Fig. 4B, left; FC2, p_cluster < 0.001, FWE). The effect was spectrally and topographically very similar to the parametric WM modulations by continuous sensory magnitudes reported in previous EEG work (Spitzer et al., 2010, 2013a; Spitzer and Blankenburg, 2012, 2011), albeit source localized to a slightly more dorsal region of right lateral PFC (Fig. 4A, inset; p < 0.05, uncorrected; note potential precision limits of EEG source localization). Like in the previous studies of analog continua, the prefrontal upper beta modulation appeared evenly linear over the entire range of quantities (N1, three to eight pulses; Fig. 4D, blue). Targeted inspection of upper beta in the remaining modality conditions (Fig. 4B–D) showed a weak right prefrontal modulation also in the visual task, which, however, fell short of significance (p_cluster >0.05, FWE). No indication of such modulation was evident in the auditory condition (Fig. 4B, right, C,D, green).

Figure 4.

Numerosity-dependent modulations of prefrontal upper beta (20–30 Hz). A, Statistical parametric TF map of the numerosity-dependent modulation in the tactile condition, for right-prefrontal channel FC2. Saturated colors delineate significant TF cluster. Inset shows the reconstructed source in right lateral PFC. B, Statistical topographical maps of the upper-beta modulation identified in A, for the different modality conditions. Dots indicate channels showing significant effects (white, p < 0.001, FWE; gray, p < 0.05, FWE). C, D, Same layout as Figure 3, B and C, for the modulation of prefrontal upper beta.

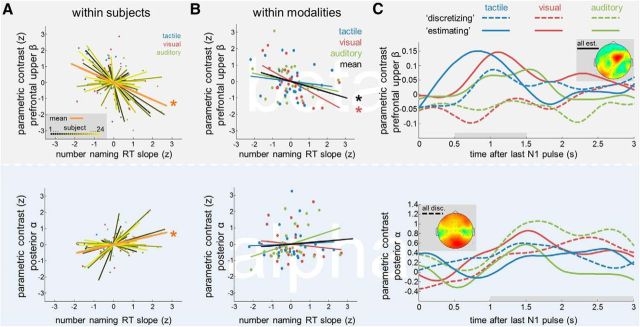
Across modalities, the pattern of numerosity-dependent modulations in the beta band (Fig. 4D) resembled the differences in analog/discretized numerosity processing, as inferred from the RT slopes during number naming (compare Figs. 1C, right, 4D; note inverse pattern). We performed two complementary types of analysis to scrutinize a potential link between these two measures. First, we examined in each participant the 3-point correlation between the number naming RT slope and the strength of the beta modulation across the three modality conditions (Fig. 5A, top). Before this analysis, both variables were z-normalized relative to the individual subject mean, thus retaining exclusively the within-subjects covariance across conditions. Indeed, a negative mean correlation between the prefrontal beta modulation and the number naming RT slope was found (r = −0.39; p < 0.001; Fig. 5A, top, orange), indicating that the descriptively related behavior of the two measures across modalities (compare Figs. 1C, right, 4D) was characterized by significant covariation within subjects.

Figure 5.

Relation between numerosity-dependent EEG modulations in the WM delay and analog versus discretized quantification in the number naming task. A, Top, Within-subjects normalized correlation between the linear slope of the RT increase in the number naming task (compare Fig. 1C, right) and the parametric modulation of prefrontal upper beta (compare Fig. 4). Shallower RT slopes (indicative of analog estimation) are associated with stronger prefrontal beta-band modulations. Bottom, Same as top, for the parametric modulation of posterior alpha (compare Fig. 3). Steeper RT slopes (indicative of discretized quantification) are associated with stronger posterior alpha modulations. B, Within-modalities normalized correlation between the same variables as in A. Also within modalities, in particular in the visual condition, analog estimation is associated with enhanced parametric modulations of prefrontal upper beta. See text for details. C, Median split illustration of the delayed EEG modulation patterns according to quantification strategy. For each modality, subjects were separated into discretizing (dashed lines) or estimating (solid lines) groups, according to their individual RT slopes in the number naming task. Top, Prefrontal upper beta modulation. Bottom, Posterior alpha modulation. Topographical maps show the aggregate parametric modulations after median splitting, collapsed over all estimating (top) and discretizing (bottom) subjects and conditions.

Next, we examined the complementary relation between the same two variables (i.e., RT slope and prefrontal beta modulation), within modality conditions, in the covariability across subjects (Fig. 5B, top). To this end, the individual RT slopes and the prefrontal beta modulations were each z-normalized relative to their respective modality condition means, retaining only the between-subjects variability. Again, a significantly negative correlation was found (r = −0.33; p = 0.005; Fig. 5B, top, black). Crucially, this finding indicates a negative relation between the two measures that cannot be explained by differences in presentation modality. In particular, a significantly negative correlation was evident within the visual modality (r = −0.60; p < 0.005; Fig. 5B, top, red), for which the grand mean RT profile indicated a relative balance of analog and discretized quantification (Fig. 1C, right, red). Within-modality correlations were by tendency negative also in the auditory (r = −0.24) and tactile (r = −0.14) conditions, although not significantly (both p > 0.10; Fig. 5B, top, green and blue). The relatively weaker correlations within these conditions may be explained by the overall relatively flat (tactile) and steep (auditory) grand mean RT slopes (Fig. 1C, right, blue and green), likely yielding less meaningful between-subjects RT variability in these two conditions (Fig. 1C, right). For illustration of the modulation pattern implied by the above analyses, we median split subjects with respect to their individual RT slopes in each modality (Fig. 5C, top). The median tercile of intermediate RT slopes was excluded to increase the contrast between “discretizing” and “estimating” participants. Notably, for the more estimating subjects, a similar early (<2 s) modulation of prefrontal upper beta power emerged in all modalities (Fig. 5C, top), including the visual and even the auditory conditions (compare Figs. 5C, top, 4C).

The bottom panels in Figure 5A–C show the results for identical analyses of the parametric modulation of posterior alpha power (Fig. 3C). Here, the within-subjects 3-point correlation revealed a significantly positive correlation with the RT slope in the number naming task (Fig. 5A, bottom; r = 0.35, p < 0.005), corroborating the trend observed in the grand average analysis (Fig. 3C). Note that the parametric 3-point analyses in Figure 5A can be more sensitive in that they capture the covariance of interest also in individuals whose data order the three modalities differently than the grand average. Complementary inspection of the correlation with the posterior alpha modulation within modalities yielded no additional effects (Fig. 5B, bottom; all p > 0.40), aside from a nonsignificant trend for a positive correlation in the auditory condition (r = 0.38, p = 0.066). Accordingly, when median splitting the subject sample (Fig. 5C, bottom), the numerosity-dependent modulation of posterior alpha power appeared enhanced for more discretizing subjects, in particular during later stages of the delay period.

Control analyses of modulations by task-irrelevant temporal factors

Central to any study of the neural representation of numerosity information is the role of potentially confounding modulations by low-level stimulus properties (Gebuis et al., 2014). In the present experimental setup, two such potential factors were the trial-specific sequence “length” (i.e., the time interval between the first and the last pulse in each sequence) and the temporal “density” of pulses $\left(\text{i}.\text{e}.,\frac{\text{number}\text{of}\text{pulses}}{\text{length}}\right)$, which were both correlated with the to-be-maintained numerosity information (for illustration of the detailed relation, see Fig. 6A). In an initial control analysis, we entered these two temporal parameters as single-trial regressors in separate GLMs, analogous to the numerosity regressors used in the main analysis (see Statistical analysis, Materials and Methods). Neither of the control regressions exceeded the FWE-corrected significance threshold (no TF clusters p < 0.001, FWE).

For targeted inspection and direct comparison with the numerosity effects, we binned the trial-specific lengths and densities into six discrete levels (Fig. 6A), and computed the modulation of changes in normalized prefrontal beta power (analogous to Fig. 4D). When collapsing across all estimating subjects and conditions for maximum sensitivity (Fig. 6B, top), as expected, moderate beta modulations by length (p = 0.02) and density (p = 0.11) arose, alongside the highly significant modulation by numerosity (p < 0.001). Analogous analysis of modulations of posterior alpha power, collapsed across all discretizing subjects and conditions, exhibited a similar pattern (Fig. 6B, bottom; length, p = 0.01; density, p = 0.01; numerosity, p < 0.001). To scrutinize the specificity of the modulations by numerosity, over and above the variance explained by length or density, respectively, we recomputed the main analysis results from numerosity regressors that were post hoc orthogonalized (using the SPM function spm_orth.m) relative to the trial-specific temporal parameters (for a similar approach, see Siegel et al., 2007). The resulting modified numerosity regressors model exclusively residual single-trial variance that is unaccounted for by length or density. Both modified GLM analyses (Fig. 6C) replicated the modulation pattern found in the main analysis, both for prefrontal upper beta power (Fig. 6C, top, estimating; both maxima at channel FC2; both p_cluster = 0.002, FWE) and for posterior alpha power (Fig. 6C, bottom, discretizing; channel POz; numerosity vs length: p_cluster = 0.002, FWE; numerosity vs density: p_cluster = 0.003, FWE), indicating that the primary source of the reported effects was indeed the to-be-maintained numerosity information, rather than task-irrelevant temporal properties of the individual pulse sequences.

A potential alternative explanation for the present prefrontal beta modulations might be that instead of actually estimating numerosity, subjects may have evaluated the overall temporal stimulus “rate,” in terms of a quasi-analog frequency integral over the entire 2 s time window. In this case, however, the prefrontal beta modulations should be temporally contingent to the end of the visually cued 2 s interval (Fig. 1D, white fixation cross at 2 s). Figure 6D illustrates the time course of the prefrontal parametric beta modulation, collapsed across all estimating subjects and conditions, for epochs time locked to the end of the 2 s interval (Fig. 6D, dashed line), compared with epochs time locked to the presentation of the last N1 pulse (Fig. 6D, solid line; as in main analysis). Indeed, the prefrontal upper beta modulation appeared enhanced and showed a clearer temporal peak when computed from the pulse-locked epochs, suggesting greater temporal contingency on the last N1 pulse than on the 2 s interval. Together, in line with the lack of a substantial modulation by density (Fig. 6B, top), the control analysis yielded no support for an interpretation of the present numerosity effects in terms of temporal frequency estimation.

Overestimation versus underestimation on error trials

In an additional analysis, we examined the extent to which the EEG signatures of quantity processing may also reflect the overestimation/underestimation of N1 on error trials. To this end, we contrasted trials in which N1 was incorrectly judged higher or lower in the subsequent comparison against N2. For this contrast to be unbiased with respect to N1, an equal number of overestimating and underestimating trials was randomly drawn, according to the respective minimum of available trials, for each N1 numerosity. This led to the exclusion of five subjects with <15 overestimating or underestimating trials when collapsing across modality conditions. For the remaining participants (on average 25.2 trials per error type), to avoid sampling bias, the drawing procedure was repeated 100 times, and the results were averaged before statistical analysis. The same sampling scheme was applied to also select a subsample of correct trials of equal size for comparison (Fig. 6E, gray). As illustrated in Figure 6E, top, the amplitude of prefrontal upper beta in fact reflected overestimation compared with underestimation on error trials (2.25–2.55 s after N1 offset; all time bins, p < 0.05), corroborating its role in quasi-analog approximate estimation. The relatively late timing of this effect seems to suggest that retrospective estimation errors may increase with the time passed since the presentation of N1.

A priori, specific types of quantification errors may also affect discretized WM representations of N1, for instance, if individual pulses were missed due to lapses of attention during encoding. However, in contrast to inaccurate analog estimation, discretizing is rather unlikely to represent a higher N1 numerosity than was actually presented. An error-trial analysis of posterior alpha amplitudes conformed to these predictions (Fig. 6E, bottom). Here, only a moderate difference between error types was evident (1.6–1.7 s after N1 offset; p < 0.05), which was exclusively characterized by underrepresenting N1 (Fig. 6E, bottom).

Discussion

We used EEG to examine the oscillatory signature of abstract numerosity information in human working memory, within and across sensory modalities. As expected from previous behavioral studies (Lechelt, 1975; Philippi et al., 2008; Tokita et al., 2013), temporal numerosity judgments were most accurate for auditory presentation, likely reflecting auditory superiority in processing temporal sequences and rhythms (Gault and Goodfellow, 1938). Furthermore, auditory performance data indicated a prevalence of discretized quantification in terms of subitizing and attempts at counting, whereas the assessment of visual and, particularly, of tactile numerosity exhibited characteristics of more direct, quasi-continuous estimation. The modality-dependent differences in quantification strategy enabled us to examine the WM signatures of abstract quantity processing over a nominally identical range of numerosities, under otherwise identical experimental parameters and task requirements.

During active WM processing, alpha-band oscillations showed a very similar pattern of task- and attention-related changes as had recently been observed during maintenance of continuous sensory magnitudes (Haegens et al., 2010; Spitzer and Blankenburg, 2012). However, unlike previous findings for analog continua, posterior alpha activity further increased with the to-be-maintained stimulus numerosity in all presentation modalities. These parametric modulations resembled previous findings of alpha power increases with WM “load,” that is, with the multitude of distinct items that are to be maintained simultaneously (Jensen et al., 2002). In the present study, the repetitions of physically identical stimuli constituted increased WM load only to the extent to which they were individuated and processed as the discrete, distinctly identifiable elements of a set. Consistently, in previous WM studies of continuous magnitudes, parametric alpha effects were generally absent (Spitzer and Blankenburg, 2011, 2012; Spitzer et al., 2013a) or were stimulus-driven and short lived (Spitzer et al., 2010). As such, we interpret the present alpha modulations as being mediated in particular by the discrete aspect of numerosity information, which—unless explicitly recoded into semantic labels (i.e., numbers)—entails load-like demands on sustained WM processing. In line with this view, the predominance of discretized processing during explicitly numerical judgments was associated with particularly strong and long-lasting alpha modulations during sustained WM maintenance.

The complementary contribution of analog, quasi-continuous quantification was systematically reflected by parametric modulations of upper beta oscillations over right lateral PFC. This effect explained not only the differences in explicitly numerical response behavior between modalities, but also accounted for intersubject variance within presentation conditions, corroborating a picture of prefrontal upper beta modulations as a supramodal correlate of analog quantification in human WM (Spitzer and Blankenburg, 2012). The present findings for the first time indicate that such parametric WM activity in lateral PFC, previously linked only to basic sensory stimulus properties (Romo et al., 1999; Nieder and Dehaene, 2009), may also monotonically encode abstract numerosity information derived from discretely presented items.

Ample evidence from monkey electrophysiology and human neuroimaging studies (for review, see Nieder and Dehaene, 2009) indicates that, upon presentation, discrete quantity information is encoded by numerosity-selective neurons in (intra-)parietal and prefrontal cortices. Whereas the precise nature of the early, potentially automatic representation of numerosity in parietal areas continues to be intensively discussed (Cohen Kadosh and Walsh, 2009; Harvey et al., 2013; Gebuis et al., 2014), the contribution of PFC is often ascribed more loosely to postrepresentational, associative, and mnemonic processing (Walsh, 2003). Indeed, quantity-selective responses in monkey PFC are temporally lagged behind parietal areas, and show remarkable similarities across different presentation formats and sensory modalities (Diester and Nieder, 2007; Tudusciuc and Nieder, 2009; Jacob et al., 2012; Nieder, 2012), which may suggest that PFC operates in particular on higher-level, potentially generic abstractions of quantity information.

While selective tuning to specific numerosity values as routinely found in single-cell electrophysiology may not be readily detectable in scalp EEG recordings, our analyses provide a complementary perspective on prefrontal quantity processing, in terms of parametric synchronization of large-scale oscillatory activity. Interestingly, in a recent analysis of monkey local field potentials (Haegens et al., 2011), parametric beta modulations coincided with monotonic modulations of single-cell firing recorded in the same cortical areas, during processing of vibrotactile frequency information. In this light, the present prefrontal modulations may suggest that numerosity information, first registered by peaked tuning functions in dedicated parieto-frontal circuits, may converge on a similar parametric WM representation as the quantitative assessment of low-level stimulus properties, which had already been parametrically encoded in the primary sensory cortices (for review, see Romo and de Lafuente, 2013).

On correct comparison trials, the prefrontal WM signature of analog quantification by tendency emerged sooner than the alpha-band indices of discretized processing. This observation agrees with the view that approximate estimation may represent a more basic type of assessment than the discretized elaboration required, for instance, for effortful counting (Nieder, 2005; Piazza and Izard, 2009). Further, as in previous studies of analog continua (Spitzer and Blankenburg, 2011, 2012; Spitzer et al., 2013a), the upper beta modulations were by tendency short lived. The nonstationary, irregular nature of parametric WM representations has already been documented on the level of single-cell firing (Romo et al., 1999; Barak et al., 2010) and has been attributed to the prevalence of recurrent network activity in PFC (Miller et al., 2003; Jun et al., 2010). Prefrontal parametric WM dynamics that arise on a larger-scale neural population level have in particular been linked to the active internal updating of WM with task-relevant analog quantity information (Spitzer and Blankenburg, 2011; Spitzer et al., 2013b). The present findings support this interpretation and additionally show how such analog-quantitative WM update may be traded off against a potentially more accurate discretized elaboration of the to-be-evaluated stimulus information.

We performed several control analyses to scrutinize the extent to which the present numerosity-dependent EEG modulations might have been affected by lower-level sensory stimulus attributes. The results yielded no evidence for a prominent contribution of other parameters than the numerosity of pulses in N1, in accordance with the explicit task instructions. Yet, it remains an open theoretical question how far cognition of numerosity per se may be separated from mechanisms of sensory magnitude processing (Dakin et al., 2011; Leibovich and Henik, 2013). The present approach of analyzing delay activity across different sensory modalities proved efficient in disentangling not only different modes of numerosity processing, but also a range of potential confounding factors and specific quantification errors. Indeed, the analysis framework used here is not limited to oscillatory EEG responses, and may in the future be similarly applied to functional imaging or invasive electrophysiology studies of numerical cognition.

To summarize, complementing ample research on the neural encoding of numerosity in parietal and prefrontal cortices upon stimulus presentation, the present study suggests a role of parametric oscillatory activity in integrating numerosity information at the stage of goal-directed quantitative processing in human WM. This level of investigation revealed differential oscillatory signatures for analog and discretized representations of numerosity, and delineates conditions under which the quantitative valuation of discrete item sets may engage similar prefrontal WM mechanisms as basic sensory continua.