Impaired Path Integration and Grid Cell Spatial Periodicity in Mice Lacking GluA1-Containing AMPA Receptors

Abstract

The hippocampus and the parahippocampal region have been proposed to contribute to path integration. Mice lacking GluA1-containing AMPA receptors (GluA1^−/− mice) were previously shown to exhibit impaired hippocampal place cell selectivity. Here we investigated whether path integration performance and the activity of grid cells of the medial entorhinal cortex (MEC) are affected in these mice. We first tested GluA1^−/− mice on a standard food-carrying homing task and found that they were impaired in processing idiothetic cues. To corroborate these findings, we developed an L-maze task that is less complex and is performed entirely in darkness, thereby reducing numerous confounding variables when testing path integration. Also in this task, the performance of GluA1^−/− mice was impaired. Next, we performed in vivo recordings in the MEC of GluA1^−/− mice. MEC neurons exhibited altered grid cell spatial periodicity and reduced spatial selectivity, whereas head direction tuning and speed modulation were not affected. The firing associations between pairs of neurons in GluA1^−/− mice were stable, both in time and space, indicating that attractor states were still present despite the lack of grid periodicity. Together, these results support the hypothesis that spatial representations in the hippocampal–entorhinal network contribute to path integration.

Introduction

Studies on mice lacking the GluA1 subunit of the AMPA receptor (GluA1^−/− mice) have contributed to the understanding of mechanisms underlying synaptic plasticity and revealed a dissociation between distinct spatial memory processes (Zamanillo et al., 1999; Reisel et al., 2002). Although GluA1^−/− mice lack the GluA1 subunit constitutively, they develop normally and their life expectancy is unchanged. In the hippocampus, the lack of GluA1 in mutant mice leads to a decreased number of functional AMPA receptors and deficits in forms of short-lasting synaptic plasticity (Zamanillo et al., 1999; Hoffman et al., 2002; Romberg et al., 2009; Erickson et al., 2010). Place cells in GluA1^−/− mice exhibit reduced spatial selectivity, supporting the notion that hippocampal spatial representations are altered in these mice (Resnik et al., 2012). At the behavioral level, GluA1^−/− mice show impaired spatial working memory but spared spatial reference memory (Zamanillo et al., 1999; Reisel et al., 2002; Schmitt et al., 2003).

Spatial memory tested in GluA1^−/− mice largely depends on the use of external (i.e., allothetic) cues. However, mammals also obtain spatial information from idiothetic cues derived from their own movements (Mittelstaedt and Mittelstaedt, 1980). Orientation based on idiothetic cues, also termed path integration, requires the animal to integrate its rotational and translational movements during an excursion to estimate its current position relative to a starting point. Ablation studies suggest that the hippocampus and the parahippocampal region are involved in path integration (Whishaw and Maaswinkel, 1998; Maaswinkel et al., 1999; Parron and Save, 2004; Van Cauter et al., 2013).

The firing properties of grid cells of the medial entorhinal cortex (MEC) strongly suggest that they are part of the neuronal network underlying path integration (Hafting et al., 2005; McNaughton et al., 2006; Boccara et al., 2010). First, the regular organization of the grid firing fields implies that grid cells integrate linear and angular movements, two essential components to perform path integration. Second, the grid arrangement persists when the animal is placed in the dark, indicating that grid cell firing can be updated via idiothetic cues (Hafting et al., 2005; McNaughton et al., 2006; Burgess et al., 2007; Burak and Fiete, 2009). Accordingly, computational models of grid cells (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Burgess et al., 2007; Hasselmo et al., 2007; Blair et al., 2008; Burak and Fiete, 2009) also suggest that idiothetic cues play a central role in updating the firing rate of grid cells during navigation. For these reasons, we characterized the activity of MEC neurons in GluA1^−/− mice along with the behavioral assessment of path integration. Our results indicate that path integration is impaired in GluA1^−/− mice. Consistent with the hypothesized role of grid cells in path integration, grid cell periodicity was altered in GluA1^−/− mice.

Materials and Methods

Homing task on a circular arena

Subjects.

The homing task was performed in 10 control and 9 GluA1^−/− male littermate mice (Zamanillo et al., 1999). Mice were between 3 and 6 months of age at the beginning of the experiment. They were singly housed in Plexiglas home cages (25 × 19 × 13 cm) containing a nest made of cardboard (5 × 5 × 8 cm) and were maintained at 80–85% of their normal body weight with free access to water. They were kept under a 12 h light/dark schedule. All procedures were performed during the light phase.

Apparatus.

Pretraining took place in a rectangular open field (50 × 30 × 20 cm). The rest of the experiment was performed on an elevated (79 cm) circular arena (120 cm diameter) with eight equidistant holes (5 cm diameter) centered 5 cm from the edge of the arena. The holes were separated by walls (32 cm long, 15 cm high) that delimited an octagonal perimeter. A home base made of black Plexiglas (15.5 × 9 × 6 cm) could be attached below any hole of the arena. The arena was located in a dark chamber (2 × 2 × 2.1 m). A video camera with infrared filter was located above the center of the arena and the arena was illuminated with infrared light. The arena was also illuminated with visible light during the pretraining and part of the training. Two loudspeakers producing white noise were located below the arena to mask potential directional auditory cues.

Pretraining.

Pretraining was performed under visible light and consisted of three phases. (1) Carrying food to the nest: a mouse was transported inside the nest to the rectangular open field. The nest was placed in one of the four corners of the open field and a food pellet (∼0.7 g, LASvendi, LAS QCdiets, Rod 18) was placed in the opposite corner. The mouse had to leave the nest, pick up the food pellet, and bring it to the nest. The trial ended when the mouse brought the food into the nest or when 10 min elapsed. Mice received two or three daily trials until they performed successfully 10 consecutive trials. (2) Habituation to the arena: a mouse was transported inside the nest to the circular arena. The nest was placed on the arena at 5 cm from the periphery and its location remained constant across trials. The food pellet was located at the center of the arena. The mouse had to leave the nest, pick up the food pellet, and bring it to the nest for consumption. The trial ended when the mouse brought the food into the nest or when 10 min elapsed. Mice received two or three daily trials until they performed successfully 5 consecutive trials. (3) Habituation to the home base: a mouse was placed into the Plexiglas home base, which was attached below one of the eight holes located at the periphery of the arena. The position of the home base was kept constant across trials. The food pellet was located at the center of the table in an opaque food cup (3.5 cm diameter and 1 cm high). The mouse had to climb onto the arena, find the food pellet, and carry it to the home base for consumption. A trial ended when the mouse entered the home base with the pellet or when 15 min elapsed. Mice received two or three daily trials until they performed successfully 5 consecutive trials. During the three pretraining phases, a 3 s auditory stimulus (Piezo: resonant frequency 3.3 0.5 kHz, 88 dB) was presented any time the mouse attempted to eat the food outside the nest or home base. Five seconds after the onset of the auditory stimulus, the food was taken away by the experimenter for 10 s and then placed back to its original position. If the trial was successful, the mouse was carried to its home cage to consume the retrieved food.

Training.

At the beginning of each trial, a mouse was placed into the home base. Next, the experimenter attached the home base under one of the eight holes of the arena. Five opaque cups were present at fixed locations on the arena and only one cup was baited. The position of the food pellet varied pseudo-randomly between the five cups from trial to trial. The mouse had to climb onto the arena, find the food and carry it to the home base for consumption. If a mouse started to eat the food outside the home base, the 3 s auditory stimulus was presented and the food was taken away by the experimenter. Likewise, if the mouse carried the food to a location other than the home base, the pellet was removed from the arena. In both cases, the pellet was relocated in the food cup only after the mouse entered the home base. This procedure was repeated until the mouse brought the pellet to its home base successfully or until 15 min elapsed. If the trial was successful, the mouse was carried to its home cage to consume the retrieved food. The arena was carefully cleaned between trials. The performance of the mice on this homing task was assessed in three conditions. (1) LF condition (light on/familiar position): the chamber containing the arena was illuminated with visible light and offered conspicuous visual cues. Moreover, the position of the home base was kept constant across trials. (2) LV condition (light on/variable position): the illumination and visual cues surrounding the arena remained identical as in the LF condition, but the home base location varied pseudo-randomly across trials. (3) D condition (dark): the visible light was turned off, the visual cues removed, and the position of the home base varied pseudo-randomly across trials. Each condition lasted 5 d in which mice performed three daily trials. Between conditions, there were 2 d in which the mice did not receive any trial on the table. We performed the experiment with two cohorts of mice. The first cohort contained 5 control and 5 GluA1^−/− mice and the second consisted of 5 control and 4 GluA1^−/− mice. The experimenter was blind to the genotype of the mice.

Data analysis.

All trials were video recorded at 12.5 frames/s and the x-y coordinates of the mice on the arena were obtained using a position tracking system (Ethovision XT, Noldus). Custom-built programs were used to extract different trajectory parameters from the raw positional data. Excursions on the table were broken down into outward and homing paths. Outward paths corresponded to the trajectory of the mouse from its exit of the home base until it took the food pellet. Homing paths corresponded to the trajectory covered by the mouse from the moment it took the food until it stopped to eat or dropped the pellet. Excursions that did not involve a food-carrying event were not considered. We measured the following: (1) The number of incorrect homing paths, defined as the number of excursions in which a mouse brought the food pellet to a place other than the home base during a given trial. (2) A straightness index for the outward path, calculated as the distance between the home base and the food pellet divided by the outward path length (i.e., the distance that was actually traveled to reach the pellet). This index ranged from 0 to 1 and was designed to be positively correlated with the straightness of the outward path (i.e., as this index further decreased, paths became progressively more circuitous). (3) The duration of the outward path, as the time elapsed between the time the mouse left the home base and the time it took the pellet. (4) The angular deviation of the homing path, computed as the angle formed between the lines connecting the center of the arena with the home base and the position at which the animal first reached the periphery of the arena. The periphery was defined as an imaginary circle with a radius of 47 cm centered on the arena. (5) The heading at periphery, defined as the difference between the angular deviation (calculated as in point 4) and a second angle formed between the lines connecting the center of the arena with the home base and the position of the mouse once it had run 10 cm after reaching the periphery. For this calculation, homing paths with an absolute angular deviation between 20° and 60° were selected. Statistical analysis was performed with R (http://www.r-project.org) and GraphPad Prism 6 (GraphPad Software).

Path integration on an L-maze task

Subjects.

We used a group of 9 control and 9 GluA1^−/− male littermate mice in this task. Mice were 14–16 months old at the beginning of the experiment. They were singly housed in Plexiglas home cages (25 × 19 × 13 cm) with free access to food and water and kept under a 12 h light/dark schedule. All procedures were performed during the light phase.

Apparatus. The experiment was performed in a circular tank (120 cm diameter and 60 cm high) filled with water (21 ± 1°C) to a depth of 22 cm. The water was made opaque by the addition of milk. The tank was located in a dark chamber (2 × 2 × 2.1 m). During training, an L-shaped maze was present inside the tank. The maze was made of Plexiglas and consisted of a corridor that had a long (82.5 × 10 × 35 cm) and a short segment (42.5 × 10 × 35 cm) joined at a 90° angle. A start-end box (13 × 10 × 35 cm) was attached at the end of each segment. At the beginning of each trial, the mouse was confined to the start box that contained a sliding door. The end box contained a circular platform (6.5 cm diameter) that remained submerged 1 cm below the water surface. The entire experiment was performed in darkness. The tank was illuminated with infrared light and a video camera with infrared filter was located above the center. The camera was connected to a position tracking system (Ethovision XT, Noldus). Two loudspeakers producing white noise were located below the tank to mask potential directional auditory cues.

Training and test.

The experiment consisted of six consecutive trials (five training trials and one test trial) with intertrial intervals of 15 min. At the beginning of each trial, a mouse was placed inside the start box for 10 s before the sliding door was removed. During training trials, the mouse had to swim along the corridor to find the hidden platform located in the end box. Mice were trained in three distinct corridors. (1) Straight (Str): the start box was connected to the long segment with the platform hidden at its end. Thus, mice had to swim in a straight line to find the platform. (2) Long-Short (L-S): the start box was connected to the long segment followed by the short segment. Thus, mice had to swim along the long segment first and then turn 90° and swim along the shorter segment to find the platform. (3) Short-Long (S-L): the start box was connected to the short segment followed by the long segment. In this case, mice had to swim first along the short segment and then turn 90° and swim along the long segment to find the platform. The position of the platform relative to the long axis of the start box was at 0°, 30°, and 60° in the Str, L-S, and S-L corridors, respectively. After the fifth training trial with the same corridor, the corridor was removed, leaving in place only the start box and the hidden platform. During the test trial, the mouse was placed inside the start box, but this time it had to swim in the open tank to find the hidden platform. Both training and test trials lasted until the mouse found the platform or 1 min elapsed. If the mouse failed to find the platform within 1 min, it was placed onto it by the experimenter. The mouse was left on the platform for 20 s before it was returned to its home cage. The experiment was repeated twice per day during 5 d in the following sequence: day 1, Str and Str; day 2, S-L and L-S; day 3, L-S and S-L; day 4, Str and Str; day 5, S-L and L-S. No difference was found between data collected on different days (data not shown); hence, data across days were pooled. We repeated the experiments with three cohorts of mice each containing 3 control and 3 GluA1^−/− mice. The experimenter was blind to the genotype of the mice.

Data analysis.

All trials were video recorded at 12.5 frames/s, and the trajectory was computed using Ethovision XT (Noldus). During the test, we measured the heading of the swimming path, computed as the angle formed between the long axis of the start box and a line connecting the center of the start box with the position of the animal. We plotted the heading as a function of the distance to the start box for each mouse. For the statistical analysis, we calculated the area under the curves for each mouse and compared the values between the three corridors. Observed heading was calculated as the average of the values obtained at increasing distances from the start box (20–90 cm). We also calculated the mean swimming speed during the test and the latency to reach the platform during training (as the time elapsed between the moment the mouse left the start box and the time when the mouse found the platform). Statistical analysis was performed using GraphPad Prism 6 (GraphPad Software).

Electrophysiological recordings from the MEC

Surgery.

Microdrives allowing independent movement of 4–8 tetrodes were implanted in wild-type (n = 17) and GluA1^−/− (n = 14) age-matched male mice. The mice were 4–12 months old at the time of implantation and were kept on a 12 h light/dark schedule, with all procedures performed during the light phase. Anesthesia was induced and maintained with isoflurane (1–2.5%), and a craniotomy was performed above the MEC (0.2 mm anterior from the transverse sinus and 3.1 mm lateral from bregma) of the right hemisphere. Tetrodes were inserted with a 6° angle in the sagittal plane, with the tips pointing in the posterior direction. Four anchor screws were attached to the skull, two of which were located above the cerebellum and served as ground and reference signals. The tetrodes were lowered 0.6 mm below the brain surface and the microdrive was fixed to the skull with dental acrylic. Mice were injected with buprenorphine (0.1 mg/kg s.c.) at the end of the surgery and twice on the following day.

Recording sessions.

One week after surgery, mice were put on a restricted diet to maintain them at 85% of their normal body weight. Water was available ad libitum. Mice were trained to forage for small food pellets in an open field (70 × 70 × 30 cm). The training phase lasted 2–4 weeks. The recording period started when mice readily ran, covering the whole environment within a 10 min trial. All recording sessions included at least one 20 min exploratory trial in the open field. Four control and 5 GluA1^−/− mice (out of the 17 control and 14 GluA1^−/− mice) were used to assess the effect of visual cues on the spatial firing of MEC neurons. These mice were trained in the open field with normal light as previously described. During recording sessions, they foraged for 15 min in the open field with normal illumination before the light was switched off. After 15 min of foraging in darkness, the light was switched back on for an additional 15 min. The mice were left in the open field for the entire recording session. There was no source of visible light in the room during trials performed in darkness.

Electrophysiological recording and position tracking.

Tetrodes were lowered to their recording position over a period of ∼2 weeks. Tetrodes were considered to be in the MEC when large theta oscillations together with strong theta modulation of cell activity were observed. After each recording session, the tetrodes were lowered ∼25–50 μm. Brain signals passed through operational amplifiers before being amplified (×1000) and sampled at 24 kHz (dacqUSB, Axona). Three LEDs of different colors were attached to the microdrive of the mouse. The position of the LEDs was monitored by a custom-made computer program, which saved the location and head direction of the mouse every 40 ms. The position and head direction were only calculated when at least 2 LEDs were detected by the tracking program. When no or only one LED was detected on <10 consecutive samples, the position of the mouse and its head direction were linearly interpolated. For mice in which recordings were performed in darkness, infrared LEDs were used and head direction was not calculated.

Spike detection and cluster analysis.

Spike detection was performed offline as previously described (Csicsvari et al., 1999). The first three principal components of spike waveforms on each tetrode wire were calculated and used as features for cluster analysis. Spikes were subjected to automatic clustering (https://github.com/klusta-team/klustakwik) before being manually refined. Only clusters with stable features and a clear refractory period in their spike-time autocorrelation were analyzed. Separation between clusters was estimated by the isolation distance (Schmitzer-Torbert et al., 2005). Putative excitatory cells were distinguished from putative interneurons based on their mean firing rate. Cells with a firing rate <5 Hz were considered putative excitatory cells, whereas cells with a firing rate >5 Hz were considered putative interneurons. Unless specified, interneurons were not included in the analysis presented.

Spatial properties of recorded cells.

The spatial properties of recorded neurons were analyzed during open-field exploration. Only cells that fired at least 300 spikes during the exploratory trial were considered. Firing rate maps were computed by dividing the recording environment into 2 × 2 cm bins and only considering data when the mouse ran faster than 3 cm/s. The time spent in each bin was calculated, and the resulting occupancy map was smoothed with a Gaussian kernel (SD = 3 cm). The number of spikes in each bin was then divided by the corresponding bin of the occupancy map. The resulting firing rate maps were smoothed with the Gaussian kernel. Spatial information score and spatial sparsity were used to quantify spatial selectivity of each cell (Skaggs et al., 1996). The spatial sparsity was defined as follows:

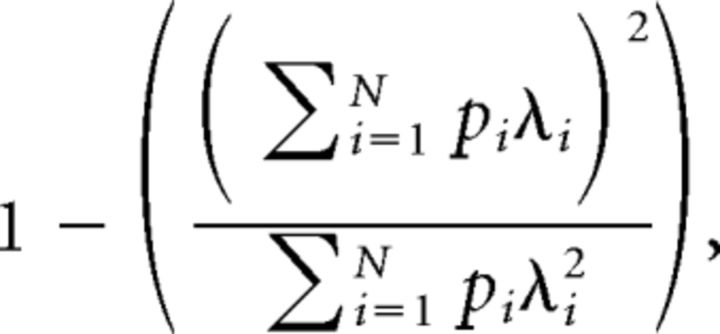where N is the number of bins in the firing rate map, p_i is the occupancy probability of bin i in the map, and λ_i is the mean firing rate in bin i. We estimated spatial coherence by calculating a correlation between the firing rate of each bin of the map and the averaged firing rate in the eight adjacent bins (Müller and Kubie, 1989). Unsmoothed firing rate maps were used for calculating spatial coherence. Firing fields consisted of at least one bin with a firing rate >5 Hz and a minimum of 10 adjacent bins (40 cm²) with a firing rate >20% of the highest firing rate in the field.

Spatial autocorrelation matrices were computed from the firing rate maps as described previously (Hafting et al., 2005). Each bin of a spatial autocorrelation matrix represented a Pearson correlation coefficient between all possible pairs of bins in a firing rate map with a given spatial lag. The spatial lag associated with a particular bin of the matrix was determined by the location of that bin relative to the matrix center. Pearson correlations at spatial lags for which <20 pairs of firing rates were available were not considered. A peak in the autocorrelation matrix was defined as >10 adjacent bins with a correlation coefficient higher than a peak detection threshold that was set to 0.1. The periodicity in the spatial autocorrelation matrix was estimated by the grid score (Sargolini et al., 2006). A circular region of the spatial autocorrelation matrix containing up to six peaks, but excluding the central peak, was defined. Pearson correlation coefficients (r) were calculated between that circular region of the matrix and a rotated version of it (by 30°, 60°, 90°, 120°, and 150°). The grid score was obtained using the following formula:

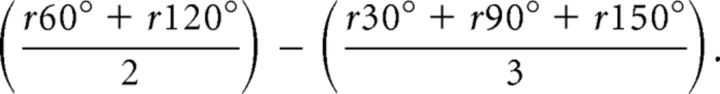A shuffling procedure in which the spike times of the cells were shifted by a minimum of 20 s before recalculating the firing rate map, and the grid score was used to establish the probability associated with different grid scores. This was repeated 500 times for each neuron. Cells with a grid score >99% of the grid scores obtained with the shuffling procedure were considered grid cells.

Dynamic firing rate maps were constructed by taking each spike of a neuron as a reference spike and considering only data occurring within time windows centered on reference spikes. The position data within each time window were shifted so that the reference spike was aligned to position 0,0. The space surrounding the reference spikes was divided into 2 × 2 cm bins, and both the occupancy maps and the resulting dynamic firing rate maps were smoothed with a Gaussian kernel (SD = 3 cm). The area covered by the dynamic firing rate maps varied according to the size of the time window and the running speed of the mouse. In addition, the amount of data entering the analysis for each neuron is proportional to the firing rate of the neuron. Grid scores were calculated from dynamic firing rate maps as for standard firing maps. Grid cells were identified using the shuffling procedure described above but applied to dynamic firing rate maps.

Modulation of the firing rate by the head direction of the mouse was computed for each cell. A polar histogram with the firing rate of the cell in 10° bins was constructed and the mean vector length of the firing rate distribution was calculated. The effect of running speed on firing rate was quantified by calculating the mean firing rate of neurons in three speed intervals (2.5–10, 10–20, and 20–30 cm/s). Normalization of the rate was done by dividing the mean firing rate in each speed interval by the firing rate of neurons at 0–2.5 cm/s.

Theta rhythmic activity of MEC neurons.

Modulation of the spiking activity by theta oscillations was measured from the spike trains. The spike-time autocorrelation of each neuron was computed using a time window of 2 s and bins of 2 ms, considering only periods when the mouse ran faster than 5 cm/s. This threshold was used to include only periods of movement-related theta oscillations. The power spectrum of each spike-time autocorrelation was calculated. The mean power at theta frequency (6–10 Hz) was compared with a baseline power defined as the mean power within two frequency intervals (3–5 and 11–13 Hz). A theta rhythmicity score was defined as follows: (θ − baseline)/(θ + baseline). A score >0 indicates more power at theta frequency than for adjacent frequencies. The peak theta frequency of neurons with a theta rhythmicity score >0.5 was the frequency between 6 and 10 Hz with the highest power.

Firing associations between spatially selective neurons of the MEC.

The instantaneous firing rate of each neuron with a firing rate <5 Hz, spatial sparsity >0.25, and more than one firing field was calculated within 250 ms time windows. These criteria were set to select mainly principal cells with several firing fields and clear spatial selectivity. Pearson correlations between the instantaneous firing rate vectors of simultaneously recorded cells were performed to estimate firing associations between pairs of cells. Chance levels for these correlations were obtained using a shuffling procedure in which instantaneous firing rate vectors were shifted by a random amount while imposing circular boundary conditions to the vectors. This process was repeated 100 times for each pair of vectors to generate a distribution of correlation coefficients that would be obtained by chance. Cell pairs for which the correlation coefficient was smaller or larger than 99% of the coefficients obtained during the shuffling procedure were considered significant.

Histological analysis.

Upon completion of the electrophysiological recordings, mice were deeply anesthetized (ketamine/xylazine) and perfused transcardially with PBS followed by 4% PFA. Their brains were removed and stored in 4% PFA for at least 24 h. The brains were then transferred to PBS and cut into sagittal sections (50 mm) on a vibrating blade microtome (Leica, VT100 S). The sections were stained with cresyl violet. The tetrode locations were estimated on digital pictures of the sagittal sections. The dorsoventral position of the tetrode tips was measured using AxioVision LE software and was defined as the distance between the dorsal border of the MEC and the tetrode tip. The mediolateral position was obtained from a stereotaxic atlas (Paxinos and Franklin, 2001). The mediolateral position of the atlas section that best matched the brain section in which a tetrode tip was observed was used.

Results

Impaired homing behavior in mice lacking GluA1-containing AMPA receptors

To home efficiently, rodents, like many other species including humans, use both idiothetic and allothetic cues. Animals compute their rotational and translational motion components iteratively, integrating them into global vectors that connect the present locations and the starting point of their journeys. The efficiency of this strategy, termed path integration, is dramatically improved by the use of allothetic (external) cues, as the subjects invariably act based on information available within their perceptual range (Mittelstaedt and Mittelstaedt, 1973; Gallistel, 1993; Healy, 1998). Because of the compound nature of this navigational strategy, we established a homing task in which both the reliability and availability of allothetic cues decreased as the experiment progressed, compelling the mice to use proportionally more idiothetic over allothetic cues. Thus, we tested the homing performance of GluA1^−/− and control mice in a setting with varying availability of navigational information.

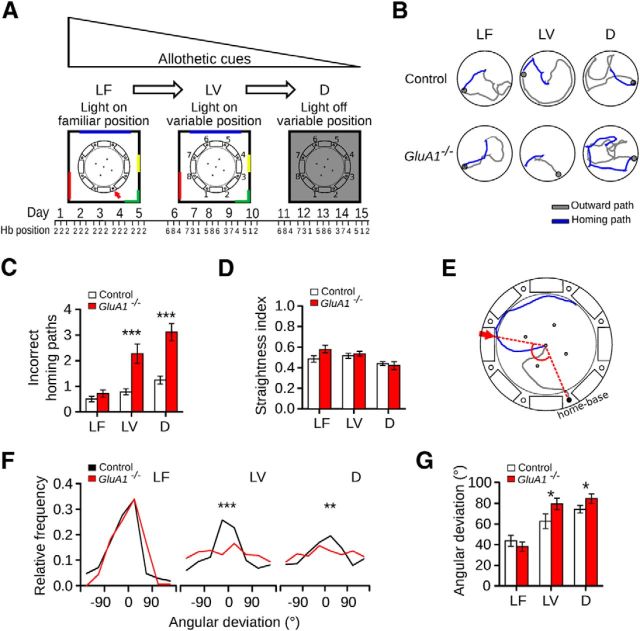
We adapted a food-carrying task previously used in rats (Whishaw and Tomie, 1997), training the mice to first leave a hidden home base placed at the periphery of a circular arena, search for a food pellet on the arena, and, finally, bring the food to the home base for consumption. The experiment consisted of a sequence of homing trials performed under three conditions (Fig. 1A). In the first condition (LF), the arena was illuminated and surrounded by conspicuous visual cues, and the position of the home base remained fixed across trials. Efficient homing could therefore be achieved by relying on allothetic cues, as the configuration of visual cues specified the position of the home base. In the second condition (LV), we kept illumination levels and visual cues as before but varied the location of the home base across trials. Consequently, although mice could still use visual cues for beaconing and rotational computations, they could not use them to specify the location of the home base over consecutive trials. In the third, final condition (D), mice had to forage in complete darkness while the position of the home base varied continuously across trials. In D, therefore, homing could only be performed based on idiothetic cues. Examples of homing paths observed under the above conditions are shown in Figure 1B.

Figure 1.

Homing with decreasing reliability and availability of allothetic cues. A, Schematics of the experimental design. The homing performance of mice in a food-carrying task was evaluated in a circular arena. At the beginning of each trial, a mouse was placed inside a home base below one of eight holes located at the rim of the arena. The mouse had to climb onto the arena to forage and bring a food pellet to its home base for consumption. The colored lines correspond to visual cues attached to a black curtain. The numbers around the arena indicate the identity of each hole. In the LF condition, the experimental room containing visual cues was illuminated and the position of the home base (Hb) was kept constant across trials (red arrow). In the LV condition, the room was illuminated and the home base position varied pseudo-randomly across trials. In the D condition, the light was turned off and the home base position varied pseudo-randomly across trials. Each condition lasted 5 d in which mice performed three daily trials. The position of the home base on individual trials is indicated below the diagrams. B, Examples of paths taken by control and GluA1^−/− mice in the three conditions. Excursions on the arena were broken down into an outward path (i.e., the trajectory of a mouse from the home base until it took the food; gray lines) and a homing path (i.e., the trajectory of a mouse from the moment it took the food until it reached the home base or stopped at another place of the arena; blue lines). C, Number of incorrect homing paths (mean ±SEM), as the number of occasions when the mice took the food to a place other than the home base, performed by control and GluA1^−/− mice in the three conditions. D, Straightness index for the outward paths (mean ±SEM) performed by control and GluA1^−/− mice in the three conditions. E, Illustration of the homing angular deviation. We measured the angle between the two dotted lines connecting the center of the arena with the home base and the position at which the animal first reached the periphery of the arena during the homing path (red arrow). In this example, the angular deviation was 125°. F, Distribution of the angular deviations of homing paths (control: n_LF = 210, n_LV = 233, n_D = 276; GluA1^−/−: n_LF = 202, n_LV = 362, n_D = 532) and (G) corresponding mean (±SEM) of control and GluA1^−/− mice in the three conditions (control n = 10, GluA1^−/− n = 9). *p < 0.05. **p < 0.005. ***p < 0.0001.

We hypothesized that task difficulty would increase, and homing efficiency decrease, throughout the experiment, from LF to D condition. We first explored how the number of incorrect homing paths, a measure of task difficulty, changed throughout the experiment. In both control and GluA1^−/− mice, the number of incorrect homing paths increased, being minimal in LF and maximal in D (Fig. 1C; Friedman test, control: Q = 8.36, p = 0.012; GluA1^−/−: Q = 14.89, p < 0.0001). Further, we observed a greater increase in the number of incorrect homing paths in GluA1^−/− than in control mice in both LV and D (Fig. 1C; Mann–Whitney U test, LF: U = 30, p = 0.23, LV: U = 5, p = 0.0004, D: U = 3, p = 0.0002). Such a difference could not be accounted for by the complexity of the foraging excursion, as the straightness of the outward path did not differ between genotypes (Fig. 1D; two-way ANOVA with repeated measures, genotype × condition interaction: F_(2,34) = 3.64, p = 0.040, simple main effects: effect of condition, one-way ANOVA with repeated measures and Tukey's multiple comparisons, control: F_(2,9) = 4.58, p = 0.03, LV vs D: p < 0.001, GluA1^−/−: F_(2,8) = 11.07, p = 0.012, LF vs D: p < 0.001, LV vs D: p < 0.001, effect of genotype, t test, LF: t₍₁₇₎ = 1.93, p = 0.074, LV: t₍₁₇₎ = 0.57, p = 0.64, D: t₍₁₇₎ = 0.49, p = 0.63). Similarly, the duration of the outward path did not differ between genotypes (two-way ANOVA with repeated measures, effect of genotype: F_(1,17) = 0.39, p = 0.54, effect of condition: F_(2,34) = 1.64, p = 0.21, genotype × condition interaction: F_(2,34) = 3.15, p = 0.55).

We subsequently investigated how the mean direction and accuracy of the homing path varied across conditions and between genotypes (Fig. 1E). In line with the view that task difficulty increased as the experiment progressed, control mice showed reduced homing accuracy from LF to D (i.e., the directions of their homing paths became less concentrated around the home base direction) (Fig. 1F,G; all trials: Equal Kappa test, LF vs LV: χ² = 19.85, p < 0.0001, LV vs D: χ² = 4.65, p = 0.031; subject means: Friedman test, Q = 9.8, p = 0.006, Dunn's multiple comparisons, LF vs D: p < 0.001, LF vs LV: p < 0.001). In GluA1^−/− mice, homing accuracy also decreased from LF to D (Fig. 1F,G; all trials: Equal Kappa test, LF vs LV: χ² = 13.62, p < 0.0001, LV vs D: χ² = 0.32, p = 0.56; subject means: Friedman test, Q = 14, p = 0.0002, Dunn's multiple comparisons, LF vs LV: p < 0.001, LF vs D: p < 0.001). Yet, we observed clear differences in performance between genotypes. Both groups of mice performed similarly in LF (Fig. 1F,G; all trials: Equal Kappa test, χ² = 3.44, p = 0.06; subject means: Mann–Whitney U test, U = 27, p = 0.15). This was not the case in LV, where the directions of homing paths in GluA1^−/− mice were less concentrated around the home base direction (Fig. 1F; Equal Kappa test, χ² = 19.02, p < 0.0001). They thus showed a significantly larger mean angular deviation (Fig. 1G; Mann–Whitney U test, U = 23, p = 0.039). Interestingly, in LV, GluA1^−/− mice showed a clear disposition to home toward the past location of the home base (i.e., that of LF) (Fig. 2A; all trials: Equal Kappa test, χ²= 30.82, p < 0.0001; subject means: Mann–Whitney U test, U = 2, p < 0.0001). In D finally, GluA1^−/− mice had homing directions that were much less concentrated around the home base direction compared with those of control mice (Fig. 1F; Equal Kappa test, χ² = 8.28, p = 0.0034), which led to significantly larger angular deviations (Fig. 1G; Mann–Whitney U test, U = 21, p = 0.026). This latter difference was not the result of the use of olfactory cues emanating from the home base, as seen from the fact that running toward or away from the home base was equally probable when the mice reached the periphery of the arena. Had olfactory cues been followed, mice would have proceeded toward the home base when reaching its proximity, and the median of the distribution of their headings at the periphery (Fig. 2B) would have been shifted toward positive values. This was not the case, as the median did not differ from zero in either genotype (Fig. 2B,C; one-sample Wilcoxon signed rank test, control: W = 1427, p = 0.67; GluA1^−/−: W = 3270, p = 0.23).

Figure 2.

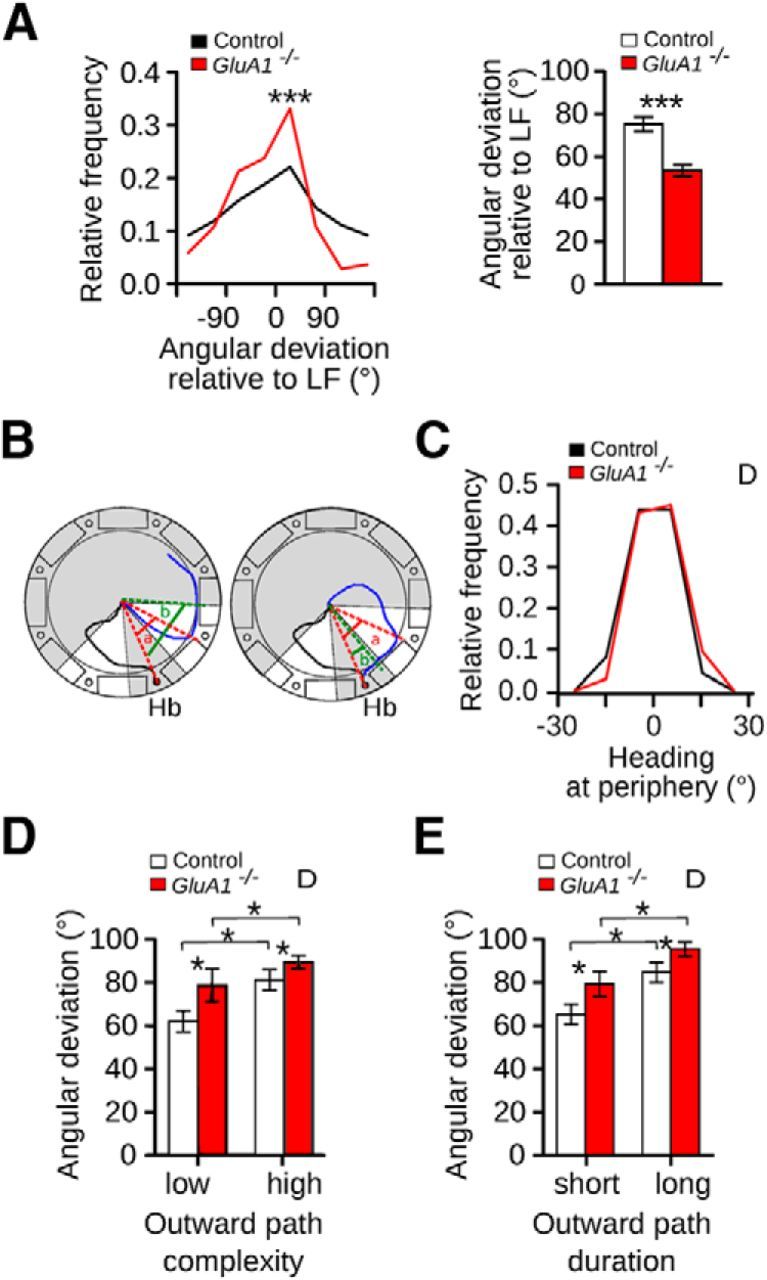
GluA1^−/− mice showed a deficit in coping with decreasing reliability and availability of allothetic cues on a homing task. A, Distribution of the angular deviations of the homing paths (control n = 233, GluA1^−/− n = 362) and corresponding mean (±SEM) of control and GluA1^−/− mice in the LV condition using as reference the home base location of the LF condition. B, Schematics illustrating the calculation of the heading at periphery. Black and blue lines correspond to the outward and homing paths, respectively. Red dashed lines indicate the angular deviation of the homing path (a). Homing paths that had an absolute angular deviation between 20° and 60° were selected. A second angular deviation was calculated once the mouse ran 10 cm after reaching the periphery (green dashed lines, b). Heading at periphery was calculated as a − b. If a mouse ran toward the home base, the heading at periphery was positive (right). If a mouse ran away from the home base after reaching the periphery, the heading at periphery was negative (left). C, Distribution of the heading at periphery for control and GluA1^−/− mice in the D condition (control n = 82, GluA1^−/− n = 123). Angular deviation (mean ±SEM) for outward paths with (D) low and high complexity and (E) short and long duration in the D condition for control and GluA1^−/− mice. Outward paths of low and high complexity corresponded to straightness index values higher and lower than 0.5, respectively. Outward paths with short and long duration correspond to duration values shorter and longer than 6.5 s, respectively (6.5 s was the median of the distribution of all outward paths). D, Dark. *p < 0.05. ***p < 0.0001.

In the absence of allothetic cues, the integration of idiothetic cues leads to an accumulation of errors. As a result, more complex outward paths lead to larger deviations of global vector directions (Mittelstaedt and Mittelstaedt, 1973; Müller and Wehner, 1988). In D, the angular deviation of the homing directions in both genotypes correlated well with the complexity and duration of the outward paths (Fig. 2D,E), in line with the view that both GluA1^−/− and control mice used idiothetic cues generated during the outward trip to specify the location of the home base. However, regardless of the level of complexity or duration of the outward path, GluA1^−/− mice showed higher angular deviations than controls (Fig. 2D,E; two-way ANOVA with repeated measures, Complexity: effect of genotype: F_(1,17) = 4.57, p = 0.040, effect of condition: F_(1,17) = 10.52, p = 0.0048, genotype × condition interaction: F_(1,17) = 0.83, p = 0.37; Duration: effect of genotype: F_(1,17) = 4.94, p = 0.040, effect of duration: F_(1,17) = 24.94, p = 0.0001, genotype × duration interaction: F_(1,17) = 0.19, p = 0.66). This indicated that the ability of GluA1^−/− mice to integrate idiothetic cues was impaired.

Impaired path integration in mice lacking GluA1-containing AMPA receptors

When testing mice on the food-carrying task in darkness without previous training in the presence of allothetic cues, control mice could not solve the task (data not shown). This is indicative that the performance of the mice reflects not just path integration but other abilities, perhaps including learning ability, motivation to feed, etc. To eliminate several confounding variables, we developed a simpler task to directly test computation of path integration coordinates in mice and asked whether the performance of GluA1^−/− mice differed from that of controls. First, we trained mice to swim and reach a submerged platform placed at the end of a corridor. Subsequently, we removed the corridor and tested their ability to find, in the open tank, the platform, whose position relative to the starting point of the path (start box) remained unchanged. We tested mice that were trained to swim in three distinct corridors, referred to as Str (straight), L-S (long-short), and S-L (short-long) (Fig. 3A). In the three corridors, the angle between the long axis of the start box and the straight line connecting the box and the platform was 0°, 30°, and 60°, respectively. The rationale of the experiment was as follows: mice performing path integration during training would use a reversed form of the ensuing global vector to quickly find the platform during testing. Accordingly, when tested in the open tank, their average heading relative to the long axis of the start box would approach 0°, 30°, and 60° following training with the Str, L-S, and S-L corridors, respectively. Figure 3B shows examples of swimming paths from mice trained in the three different corridors.

Figure 3.

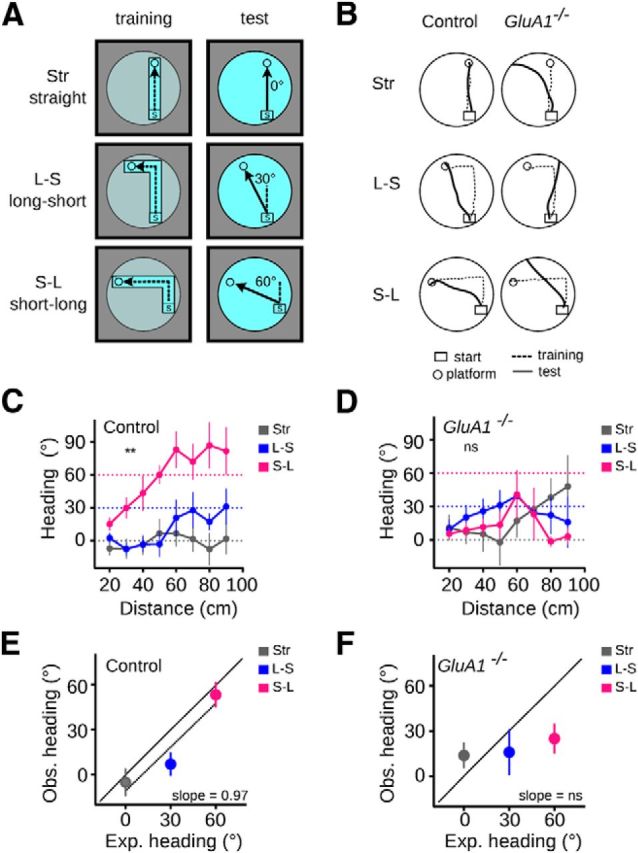
GluA1^−/− mice showed a deficit in path integration on an L-maze task. A, Schematics of the experimental design. Mice were trained to find a submerged platform at the end of three different corridors: Str (straight), L-S (long-short), and S-L (short-long), in which the platform was located at 0°, 30°, and 60° relative to the start box, respectively. During the test, the corridor was removed and the mice had to find the platform in the open tank. The experiment was performed in complete darkness. B, Examples of swimming paths by control and GluA1^−/− mice in the Str, L-S, and S-L corridors. C, D, Mean heading (±SEM) at different distances from the start box for the three corridors for control (C) and GluA1^−/− (D) mice. The area under the curve was compared within each genotype (see Materials and Methods). Dashed lines indicate the expected heading if mice computed path integration (i.e., swam in a straight line to the platform). E, F, Relationship between expected and observed heading (mean ±SEM) for control (E) and GluA1^−/− (F) mice. The black diagonal line indicates a regression line of slope = 1. Control n = 9; GluA1^−/− n = 9. **p = 0.007. ns, Not significant.

Control mice fitted these predictions well. Their heading at increasing distances from the start box differed significantly when trained in the different corridors (Fig. 3C; one-way ANOVA with repeated measures and Tukey's multiple comparisons, Control: F_(2,16) = 6.76, p = 0.0074, Str vs S-L p = 0.0079, L-S vs S-L p = 0.034, Str vs L-S p = 0.82). Further, the relationship between the expected and observed headings could be approximated by a linear regression whose slope did not differ from 1 (Fig. 3E; linear regression, slope = 0.97 ± 0.20, F_(1,25) = 21.81, p < 0.0001; Comparison of fits, H_0: slope = 1, F_(1,25) = 0.023, p = 0.9). By contrast, the behavior of GluA1^−/− mice did not match the above predictions (Fig. 3D,F). Their heading at increasing distances from the start box did not differ when trained in the different corridors (Fig. 3D; one-way ANOVA with repeated measures, F_(2,16) = 0.19, p = 0.88), and the relationship between the expected and observed headings could not be approximated by a linear regression (Fig. 3F; linear regression, slope = 0.18 ± 0.23, F_(1,25) = 0.48, p = 0.49). Therefore, control but not GluA1^−/− mice were able to use the global vector resulting from path integration. These results also showed that during testing neither control nor GluA1^−/− mice used memories arising from the repeated turns experienced during training (i.e., they did not repeat a learned motor pattern). If this were the case, sharp turns (90°) would have been observed at different distances from the start box (75 and 35 cm for mice trained in L-S and S-L corridors, respectively), corresponding to the virtual locations of the turning points experienced during training. Accordingly, the heading of the mice before and after the turning point would have been 0° and 90°, respectively. Clearly, that was not what we observed (Fig. 3C,D; one-sample Wilcoxon signed rank test, L-S_Control: H₀ = 0°, W = 7, p = 0.73, H₀ = 90°, W = −26, p = 0.031. S-L_Control: H₀ = 0°, W = 39, p = 0.019, H₀ = 90°, W = −12, p = 0.46. L-S_GluA1−/−: H₀ = 0°, W = 13, p = 0.49, H₀ = 90°, W = −11, p = 0.31. S-L_GluA1−/−: H₀ = 0°, W = 29, p = 0.98, H₀ = 90°, W = −23, p = 0.037). The differences between genotypes could not be accounted for by differences in swimming speed during testing or overall performance during training. Both genotypes swam at a similar speed during the test trials (two-way ANOVA with repeated measures, effect of genotype: F_(1,16) = 0.29, p = 0.59, effect of corridor: F_(2,32) = 3.25, p = 0.056, genotype × corridor interaction: F_(2,32) = 1.62, p = 0.21). Also, the latency to find the platform decreased significantly as training progressed and was similar between genotypes (two-way ANOVA with repeated measures, Str: effect of genotype: F_(1,16) = 0.25, p = 0.62, effect of trials: F_(4,64) = 4.55, p = 0.0027, genotype × trial interaction: F_(4,64) = 0.18, p = 0.94; L-S: effect of genotype: F_(1,16) = 0.27, p = 0.61, effect of trials: F_(4,64) = 4.91, p = 0.0016, genotype × trial interaction: F_(4,64) = 0.36, p = 0.85; L-S: effect of genotype: F_(1,16) = 0.91, p = 0.35, effect of trials: F_(4,64) = 6.37, p = 0.0002, genotype × trial interaction: F_(4,64) = 0.84, p = 0.50). Together, these results constitute the first account of path integration in mice. Furthermore, they allow us to conclude that GluA1^−/− mice exhibited a deficit in path integration.

Disruption of the grid spatial periodicity in the MEC of GluA1^−/− mice

To investigate the properties of grid cells in GluA1^−/− mice, we performed extracellular tetrode recordings from the MEC of 17 control and 14 GluA1^−/− mice. Histological examination showed that the tips of most tetrodes were located in the dorsal third of the MEC (Fig. 4A). A small fraction of the tetrodes was found in the parasubiculum, close to the border between the parasubiculum and the MEC (17.4% and 10.0% of the tetrodes in control and GluA1^−/− mice, respectively). To ensure that the location of the tetrodes within the MEC did not differ across the two groups of mice, we calculated a dorsoventral and mediolateral coordinate for each tetrode tip (Fig. 4B). There was no significant difference in tetrode location across genotypes (Mann–Whitney U test, dorsoventral: U = 59.5, p = 0.40, mediolateral: U = 78.5, p = 0.91). The distribution of the tetrode tips across the different layers of the MEC is shown in Figure 4C. The majority of tetrodes in both genotypes went through the superficial layers (II and III). No overt change was observed in the cytoarchitecture of the parahippocampal area in GluA1^−/− mice.

Figure 4.

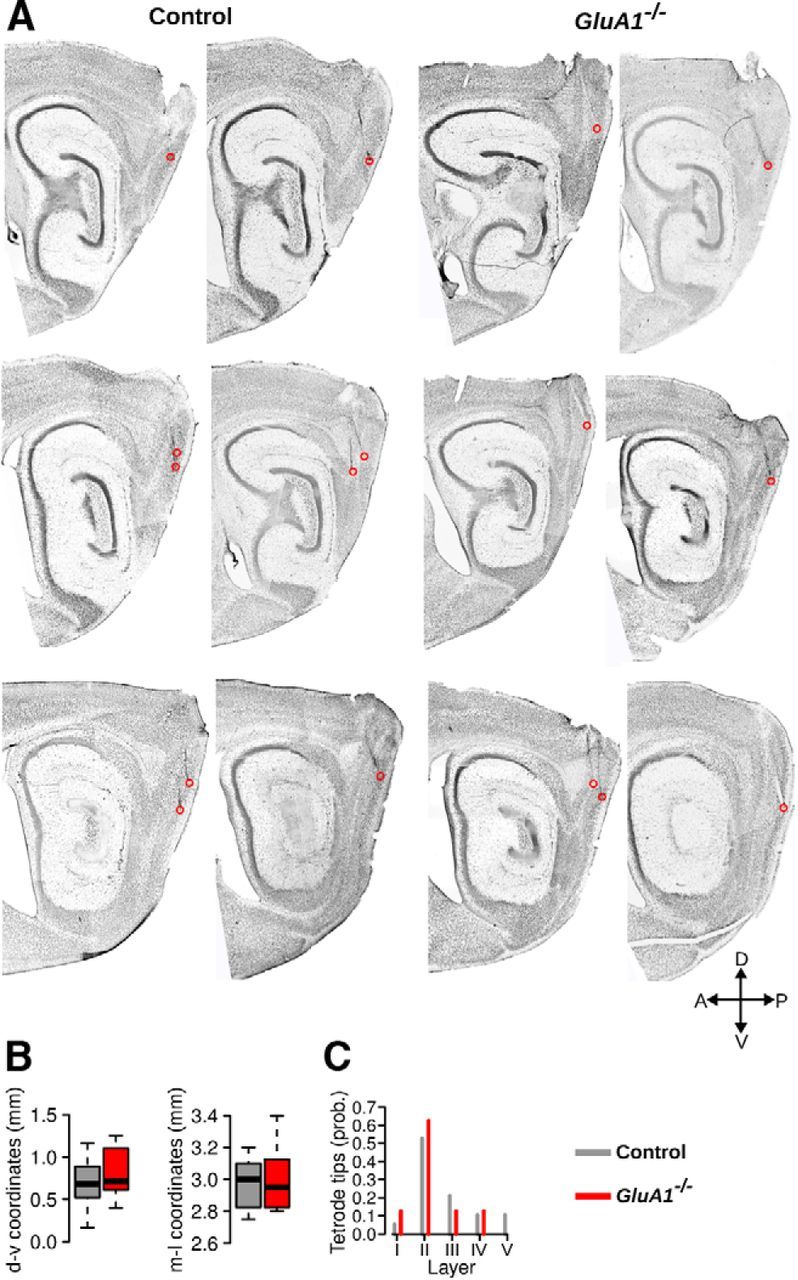
Histological examination of tetrode location in control and GluA1^−/− mice. A, Sagittal sections stained with cresyl violet showing tetrode tracks reaching the MEC. Red circles represent the tips of the tetrodes. B, Dorsoventral (d-v) and mediolateral (m-l) coordinates of the tetrode tips in the MEC of control and GluA1^−/− mice. The horizontal bar, the box, and the whiskers represent the median, the interquartile range, and the range, respectively. The location of the tetrode tips in control and GluA1^−/− mice did not differ. C, Distribution of tetrode tips across different layers of the MEC in control and GluA1^−/− mice.

Recording sessions took place in a 70 × 70 cm open field, where mice searched for food pellets delivered at random locations. The mean running speed of the mice was not statistically different across genotypes (median, control: 10.86 cm/s, GluA1^−/−: 9.025 cm/s, Mann–Whitney U test, U = 156, p = 0.15). A total of 902 neurons in control mice and 643 neurons in GluA1^−/− mice fired at least 300 spikes during open-field exploration. The isolation distance of neurons recorded in GluA1^−/− mice was slightly larger than that in control mice (median, control: 23.91, GluA1^−/−: 26.65, Mann–Whitney U test, U = 233288, p = 0.019), indicating that spike clusters in GluA1^−/− mice were well separated from each other.

Figure 5A shows firing rate maps of typical MEC neurons recorded in control and GluA1^−/− mice. GluA1^−/− mice had almost no neurons with a clear periodic firing pattern during exploration. The distribution of grid scores for neurons with a firing rate <5 Hz in both genotypes is shown in Figure 5B. Neurons in GluA1^−/− mice had lower grid scores than those in control mice (control n = 595, GluA1^−/− n = 427, median, control: 0.13, GluA1^−/−: −0.02, Mann–Whitney U test, U = 162762, p = 1.62⁻¹⁴). The mean grid score per mouse was lower in GluA1^−/− than in control mice, indicating that the grid pattern was disrupted in the majority of knock-out mice (Fig. 5C; Mann–Whitney U test, U = 219, p = 1.55⁻⁵). We also estimated the proportion of neurons with a grid score significantly above chance levels in both genotypes. This was done by comparing the grid scores of recorded neurons to a distribution of grid scores obtained after shifting spike times forward on the path of the animal by a minimum of 20 s (Langston et al., 2010). The proportion of grid cells in GluA1^−/− mice was significantly smaller than that in control mice (Fig. 5D,E; threshold control: 0.52, control: 23.87%, 142 grid cells of 595 neurons, threshold GluA1^−/−: 0.50, GluA1^−/−: 6.79%, 29 grid cells of 427 neurons, Pearson χ² test, χ² = 50.80, p = 1.02⁻¹²).

Figure 5.

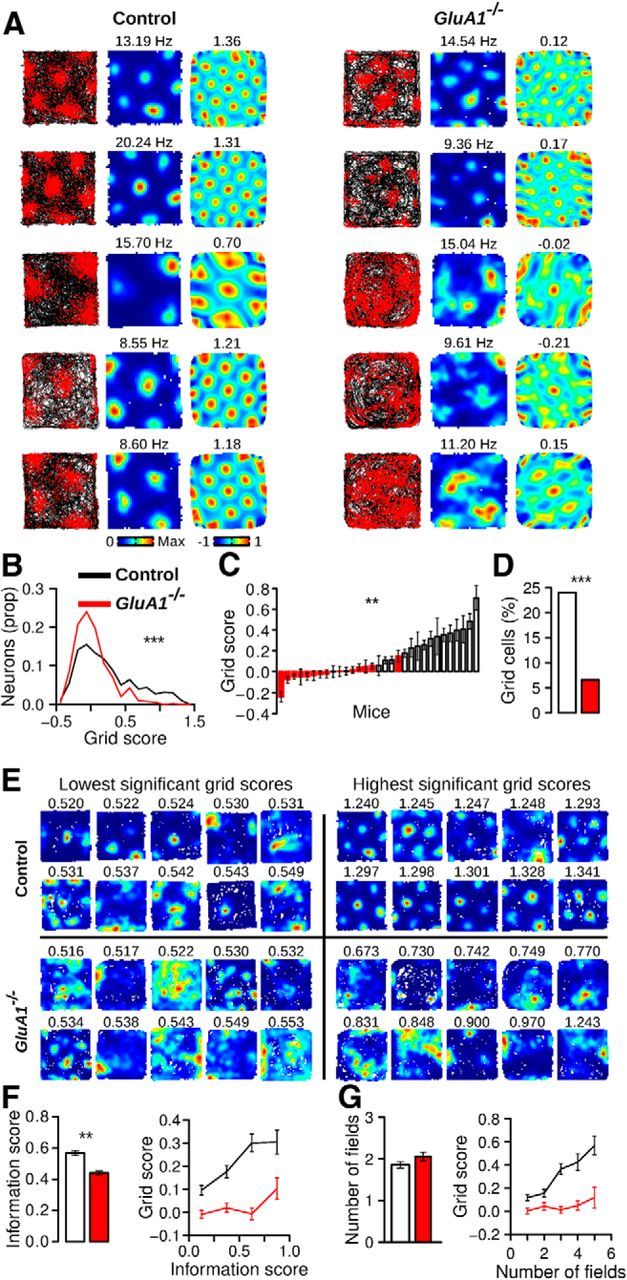
Disruption of the grid cell spatial periodicity in the MEC of GluA1^−/− mice. A, Trajectory with spike position, firing rate map, and spatial autocorrelation matrix of five grid cells recorded in control (left) and GluA1^−/− mice (right). The numbers above the firing rate maps and spatial autocorrelation matrices represent the maximum firing rate and grid score for each cell, respectively. The spatial autocorrelation matrices of cells in GluA1^−/− mice lack the periodic pattern of grid cells. B, Distribution of grid scores for principal cells in control and GluA1^−/− mice. C, Mean (±SEM) grid score per mouse. D, Percentage of grid cells recorded in control and GluA1^−/− mice. E, Firing rate maps of 10 neurons with the lowest and highest significant grid scores in both genotypes. Significance was tested using a shuffling procedure. The grid score of each neuron is indicated above its firing rate map. F, Mean (±SEM) information score (left) and grid score of neurons with different information scores (right). G, Mean (±SEM) number of firing fields per neuron in control and GluA1^−/− mice (left). Grid score of neurons with various numbers of firing fields (right). ***p < 10⁻¹⁰. **p < 10⁻⁵.

We next asked whether the reduced regularity of the grid pattern in GluA1^−/− mice could be explained by a loss in spatial selectivity. Indeed, neurons from the knock-out mice had lower spatial coherence (median, control: 0.51, GluA1^−/−: 0.49, Mann–Whitney U test, U = 144933, p = 0.00012) and lower spatial information scores (Fig. 5F; Mann–Whitney U test, U = 154379, p = 4.21⁻⁹) than those of control mice. The reduction of spatial selectivity in the mutant mice, however, could not explain the lack of spatial periodicity. When mean grid scores were calculated for cells with different levels of spatial information score, neurons from GluA1^−/− mice had lower grid scores than control mice, regardless of spatial selectivity (Fig. 5F). Hence, the difference in grid score between genotypes persisted when controlling for the effect of spatial information score on grid score (ANCOVA, effect of genotype: F_(1,1019) = 60.04, p = 2.25⁻¹⁴, effect of information score: F_(1,1019) = 80.54, p = 2.2⁻¹⁶). These findings demonstrated that the impairment in grid cell regularity in GluA1^−/− mice could not be accounted for by a loss in spatial selectivity. Moreover, they suggested that the network mechanisms responsible for the spatial selectivity of grid cells can be partially dissociated from the mechanisms giving rise to grid periodicity.

Neurons in GluA1^−/− mice had as many firing fields as neurons in control mice (Fig. 5G; Mann–Whitney U test, U = 120292, p = 0.14). In control mice, the number of firing fields per cell was positively correlated with grid scores (Fig. 5G; Pearson correlation, r₍₅₉₃₎ = 0.44, p = 2.2⁻¹⁶). This correlation was absent in knock-out mice (r₍₄₂₅₎ = 0.08, p = 0.12). The size of the firing fields and their peak firing rate were not significantly different across genotypes (control n = 1107, GluA1^−/− n = 865, median field area as a proportion of the open field area, control: 0.093, GluA1^−/−: 0.101, Mann–Whitney U test, U = 468512.5, p = 0.41, median peak firing rate, control: 8.78 Hz, GluA1^−/−: 8.76 Hz, U = 492306, p = 0.28). Therefore, although neurons in the mutant mice had a normal number of firing fields, the spatial arrangement of the fields did not follow that of a grid of equilateral triangles.

Grid cell periodicity in GluA1^−/− mice is not preserved over short time periods

The apparent lack of periodicity in firing rate maps of GluA1^−/− mice could originate from a disruption in the anchoring of the MEC spatial representation to the recording environment (Bonnevie et al., 2013). In such a scenario, the firing activity of neurons in GluA1^−/− mice would still be organized as a regular grid; but when firing rate maps are calculated by averaging several minutes of data, the periodicity is lost. To test for this, we computed dynamic firing rate maps in which each spike is used as a reference spike. The dynamic maps were constructed using time windows immediately preceding and following the reference spikes, with the positional data adjusted relative to the position of the animal when the reference spike occurred.

When the time windows were long enough to allow mice to run the distance separating grid fields, a hexagonal firing pattern emerged in the dynamic firing rate maps of control mice (Fig. 6A). Clear grid patterns were not observed in GluA1^−/− mice. Grid scores calculated from the dynamic firing rate maps were lower in GluA1^−/− mice than in control mice with time windows of 3–5 s (Fig. 6B; control n = 595, GluA1^−/− n = 427, Mann–Whitney U test, 3 s: U = 141186, p = 0.0024, 4 s: U = 148265, p = 5.06⁻⁶, 5 s: U = 140849, p = 0.003). In addition, we found significant correlations between grid scores calculated from the time-averaged and spike-triggered firing rate maps in control but not in GluA1^−/− mice (Fig. 6C; Pearson correlation, control, 1 s: p = 0.61, 2 s: p = 1.07⁻¹², 3 s: p < 2.2⁻¹⁶, 4 s: p < 2.2⁻¹⁶, 5 s: p < 2.2⁻¹⁶, GluA1^−/−,1 s: p = 0.17, 2 s: p = 0.81, 3 s: p = 0.04, 4 s: p = 0.81, 5 s: p = 0.08). The proportion of cells classified as grid cells based on their dynamic firing rate maps was lower in GluA1^−/− mice than in control mice with time windows of 3–5 s (Fig. 6D; Pearson χ² test, 3 s: χ² = 10.01, p = 0.0016, 4 s: χ² = 10.50, p = 0.0012, 5 s: χ² = 11.38, p = 0.00074). Similar results were obtained when smoothing kernels of different width were applied to the dynamic firing rate maps (SD of smoothing kernel varying from 0 to 4 cm; data not shown). These results indicate that neurons in GluA1^−/− mice did not express normal spatial periodicity over short time periods. Thus, the grid cell periodicity impairment in GluA1^−/− mice was not simply the result of a disruption of the anchoring of the MEC spatial representation to the recording environment.

Figure 6.

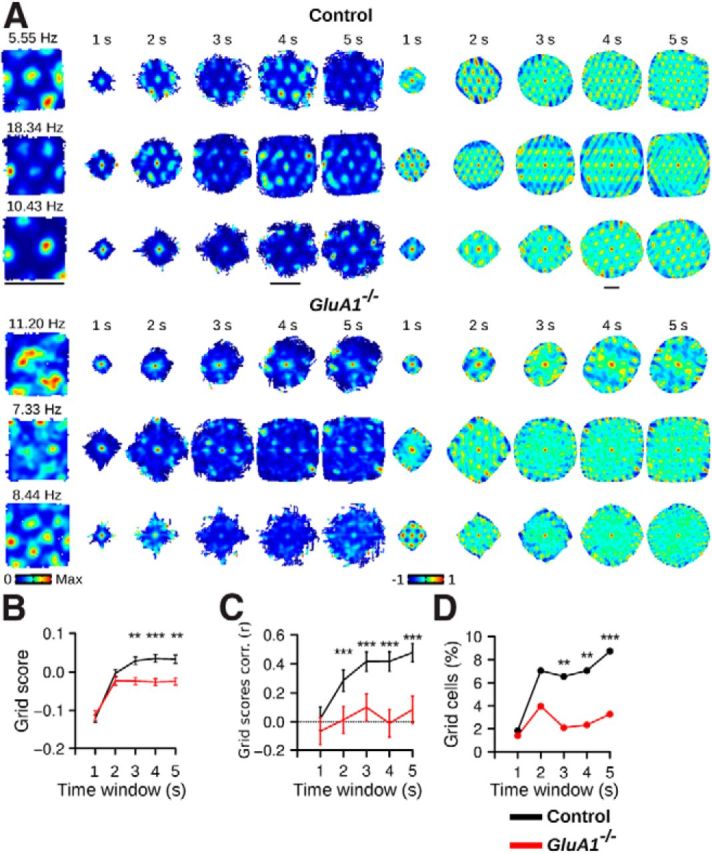
Grid cell periodicity in GluA1^−/− mice is not preserved over short time periods. A, Examples of three neurons in control and GluA1^−/− mice. Leftmost column, Firing rate maps calculated from 40 min of data recorded during open-field exploration. Next 5 columns on the right, Dynamic firing rate maps constructed using time windows of 1–5 s. There is an absence of periodic firing fields in the dynamic firing rate maps of GluA1^−/− mice. The corresponding spatial autocorrelations of the dynamic firing rate maps are presented in the last 5 columns on the right. Scale bars, 70 cm. B, Mean (±SEM) grid score in control and GluA1^−/− mice calculated from dynamic firing rate maps with different time windows. The dynamic firing rate maps of GluA1^−/− mice displayed less periodicity when time windows >2 s were used. C, Mean (±SEM) Pearson correlation coefficient between grid scores calculated from the time-averaged and dynamic firing rate maps. D, Percentage of grid cells found in control and GluA1^−/− mice. Grid cells were identified using a shuffling procedure in which spikes were shifted on the path of the mouse before recalculating the dynamic firing rate maps. Fewer grid cells were observed in GluA1^−/− mice with time windows of >2 s. ***p < 0.001. **p < 0.01. *p < 0.05.

Residual spatial selectivity of MEC neurons in GluA1^−/− mice

MEC neurons in GluA1^−/− mice displayed a reduction in spatial selectivity (Fig. 5F). However, when the spatial sparsity of GluA1^−/− neurons was compared with the shuffled data, a large proportion of neurons in GluA1^−/− mice showed significant spatial selectivity (neurons with p < 0.01, control mice: 44.37%, GluA1^−/−: 24.59%, Pearson χ² text, χ² = 41.31, p = 1.30⁻¹⁰). We therefore tested whether the residual spatial selectivity of neurons in GluA1^−/− and control mice depended to a similar extent on visual cues and whether it was maintained in darkness. The activity of MEC neurons in 4 control and 5 GluA1^−/− mice was recorded in the open field during normal lighting conditions and in darkness (Fig. 7A). We observed a reversible reduction in spatial sparsity in both genotypes when visual cues were transiently eliminated (Fig. 7B; Friedman test, control: n = 285, Q = 78.26, p < 2.2⁻¹⁶, post hoc tests, light1-dark: p = 8.75⁻¹², light2-dark: p = 1.44⁻¹⁵, light1-light2: p = 0.60, GluA1^−/−: n = 192, Q = 59.45, p = 1.24⁻¹³, post hoc tests, light1-dark: p = 5.41⁻¹¹, light2-dark: p = 2.80⁻¹⁰, light1-light2: p = 0.99). Thus, in both groups, visual cues contributed to the spatial selectivity of MEC neurons. The spatial sparsity was above chance levels in all conditions for both control and GluA1^−/− mice (all p values < 10.0⁻¹⁴). These results suggest that spatial selectivity in GluA1^−/− was not more dependent on visual cues than in control mice.

Figure 7.

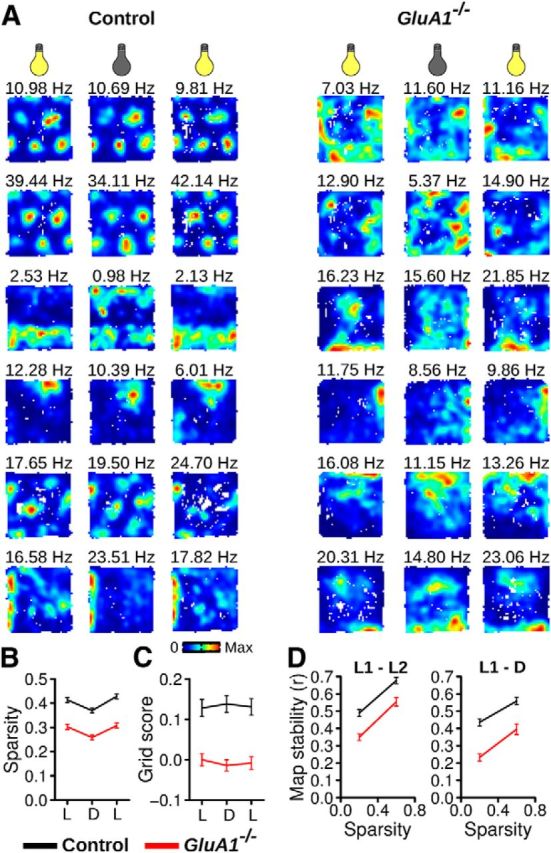
Residual spatial firing in GluA1^−/− mice is preserved in darkness. A, Examples of firing rate maps from six neurons in control and GluA1^−/− mice tested with normal light illumination (left and right columns) or in darkness (middle column). B, Mean (±SEM) spatial sparsity during trials in the light (L) or darkness (D). C, Mean (±SEM) grid score during trials in the light or darkness. D, Mean (±SEM) map stability between two trials in the light (L1–L2) or between a trial in the light and in darkness (L1-D). Data are shown for cells with different degrees of spatial sparsity. Neurons in GluA1^−/− mice were less spatially stable across trials.

In control mice, grid periodicity was not affected by eliminating visual cues (Fig. 7C; Friedman test, Q = 0.36, p = 0.83), indicating that in mice, as in rats, grid cell periodicity persists in darkness (Hafting et al., 2005). As expected, grid periodicity in GluA1^−/− mice was reduced compared with controls in all three conditions (Fig. 7C; Mann–Whitney U test, light1: U = 31868, p = 0.002, dark: U = 32182, p = 0.001, light2: U = 33589, p = 2.46⁻⁵).

We also assessed the stability of firing rate maps between two trials in the open field. We found that the firing rate maps of GluA1^−/− neurons were less stable than those of control mice (Fig. 7D). When comparing stability between two trials with normal illumination (intertrial interval = 15 min), firing rate maps of GluA1^−/− neurons were less stable than those of controls, even after controlling for the effect of spatial sparsity on map stability (ANCOVA, effect of genotype: F_(1,473) = 33.63, p = 1.22⁻⁸, effect of sparsity: F_(1,473) = 162.99, p < 2.2⁻¹⁶). This reduction in map stability of GluA1^−/− neurons was also observed when assessing stability between a trial with normal illumination and a trial performed in the dark (ANCOVA, effect of genotype: F_(1,473) = 60.06, p = 5.66⁻¹⁴, effect of sparsity: F_(1,473) = 75.21, p < 2.2⁻¹⁶).

Preserved head direction and running velocity signals in MEC neurons of GluA1^−/− mice

As expected, the firing rate of some MEC neurons in control mice was modulated by the head direction of the mouse (Sargolini et al., 2006). Figure 8A shows examples of neurons with different head direction selectivity. Head direction selectivity of a neuron was estimated by computing the length of the mean vector for the distribution of firing rates across all head directions. The vector length of recorded neurons was not different across genotypes (Fig. 8B; control n = 325, GluA1^−/− n = 242, Mann–Whitney U test, U = 39722, p = 0.84). A shuffling procedure was performed to estimate the number of cells with significant head direction selectivity. The proportion of head direction cells in GluA1^−/− mice was not significantly different from that in control mice (Fig. 8C; Pearson χ² test, χ² = 0.01, p = 0.92).

Figure 8.

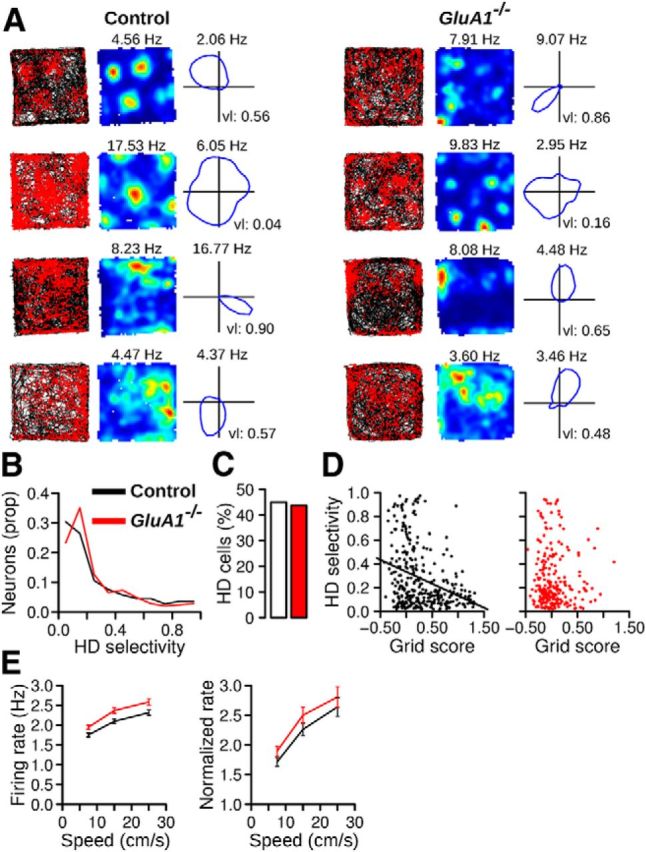
Preserved head direction and running velocity signals in MEC neurons of GluA1^−/− mice. A, Examples of four neurons in control and GluA1^−/− mice with different head direction selectivity. Left to right, Trajectory with spike position, firing rate map, and directional plot. The directional plot shows the firing rate of the neurons when the head of the mouse points in different directions. B, Distribution of head direction selectivity (mean vector length) for MEC neurons in control and GluA1^−/− mice. C, Percentage of cells for which the firing rate was significantly modulated by head direction. D, Relationship between the head direction selectivity and grid score. Most neurons with high grid scores in control mice had low head direction selectivity. E, Mean (±SEM) firing rate of neurons at different running speeds in control and GluA1^−/− mice. Right, The firing rate of the neurons was normalized by their firing rate when the animal was immobile (running speed < 2.5 cm/s).

In control mice, there was a negative correlation between grid score and head direction selectivity (Fig. 8D; Pearson correlation, r₍₃₂₃₎ = −0.33, p = 1.50⁻⁹). The majority of neurons with high grid scores had relatively low head direction selectivity. This negative correlation was not observed in GluA1^−/− mice (Fig. 8D; r₍₂₄₀₎ = 0.02, p = 0.79). The proportion of conjunctive cells (grid cells with significant head direction selectivity) was low in both genotypes (control: 7.38%, 24 of 325, GluA1^−/−: 2.89%, 7 of 242, Pearson χ² test, χ² = 4.58, p = 0.03).

The firing rate of MEC neurons also encodes information about running speed, with the firing rate being positively correlated with the velocity of the animal (Sargolini et al., 2006). We therefore tested whether the modulation of firing rate by running speed was present in GluA1^−/− mice. The mean firing rate of neurons was calculated for time windows in which the mice ran at different speed intervals (Fig. 8E). We found that neurons in GluA1^−/− mice had slightly higher firing rates than those of control mice for a given running speed (Fig. 8E; two-way ANOVA, effect of genotype: F_(1,1019) = 8.08, p = 0.005, effect of speed: F_(2,2038) = 302.27, p < 2⁻¹⁶, genotype × speed interaction: F_(2,2038) = 1.56, p = 0.21). The increase in firing rate associated with running speed was also similar in the two groups of mice if the firing rate of the neurons was normalized to their firing rate at running speed <2.5 cm/s (Fig. 8E; effect of genotype: F_(1,1019) = 1.30, p = 0.26, effect of speed: F_(2,2038) = 169.43, p < 2⁻¹⁶, genotype × speed interaction: F_(2,2038) = 0.27, p = 0.76). These results indicate that the modulation of firing rate by running speed was preserved in GluA1^−/− mice.

Theta rhythmic activity at lower frequency in GluA1^−/− mice

Recent studies have shown that inactivation of the medial septum leads to a strong reduction of grid spatial periodicity and theta oscillations in the MEC (Brandon et al., 2011; Koenig et al., 2011). We therefore tested whether the modulation of firing activity by theta oscillations was reduced in GluA1^−/− mice. We computed the spike-time autocorrelation using periods in which the mouse was running faster than 5 cm/s (Fig. 9A). The firing probability of neurons in GluA1^−/− and control mice showed a similar increase at theta frequency (∼125 ms, Fig. 9A,B). Theta rhythmicity scores were calculated from the power spectra of the spike-time autocorrelations (Fig. 9C). Positive scores, indicating a stronger rhythmicity at theta frequency than for adjacent frequencies, were observed for the majority of cells in both genotypes (Fig. 9C,D). There was no significant difference in theta rhythmicity scores between genotypes (Fig. 9D), either for principal cells (control n = 595, GluA1^−/− n = 427, Mann–Whitney U test, U = 122638, p = 0.35) or for interneurons (control n = 307, GluA1^−/− n = 215, U = 34749, p = 0.30). The peak theta frequency was also calculated for neurons with a theta rhythmicity score >0.5 (i.e., neurons for which this variable could be estimated precisely). The peak frequencies of principal cells and interneurons were lower in GluA1^−/− mice (Fig. 9E; Mann–Whitney U test, principal cells, U = 71898.5, p = 2.2⁻¹⁶, interneurons, U = 14620.5, p = 2.2⁻¹⁶). This lower theta frequency in GluA1^−/− mice was not the result of a lower running speed in GluA1^−/− mice, as the peak theta frequency was lower independently of running speed (Fig. 9F; two-way ANOVA, principal cells: effect of genotype: F_(1,1600) = 259.99, p < 2.2⁻¹⁶, effect of speed: F_(2,1600) = 153.88, p < 2.2⁻¹⁶, genotype × speed interaction: F_(2,1600) = 2.25, p = 0.11, interneurons: effect of genotype: F_(1,690) = 304.29, p < 2.2⁻¹⁶, effect of speed: F_(2,690) = 92.11, p < 2.2⁻¹⁶, genotype × speed interaction: F_(2,690) = 2.18, p = 0.11). These results indicate that rhythmic firing at theta frequency was still present in GluA1^−/− mice, but the frequency of theta oscillations was lower than in control mice. As also demonstrated by the ANOVAs presented above, theta frequency increased with running speed in both genotypes.

Figure 9.

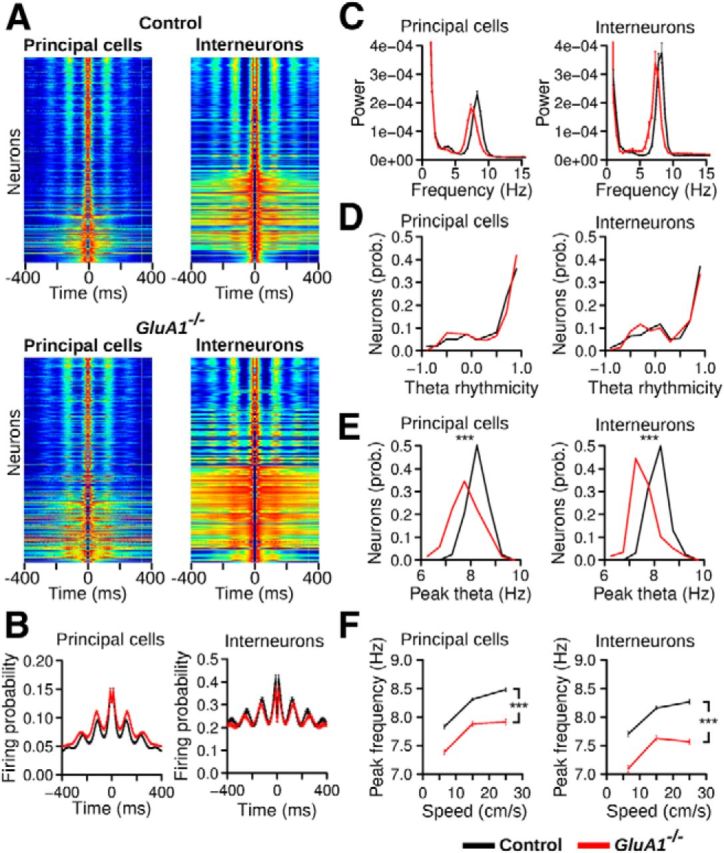
Theta rhythmicity in GluA1^−/− mice. A, Spike-time autocorrelation for principal cells and interneurons recorded in control and GluA1^−/− mice, ordered from the bottom to the top according to their theta rhythmicity index. Red and dark blue were assigned to the highest and lowest value, respectively, of each individual autocorrelation. Theta rhythmic activity was still present in mutant mice. B, Mean (±SEM) spike-time autocorrelation for principal cells and interneurons in control and GluA1^−/− mice. C, Mean power spectrum of spike-time autocorrelations for principal cells and interneurons in control and GluA1^−/− mice. Theta was the dominant rhythmic frequency in both control and GluA1^−/− mice. D, Theta rhythmicity index for neurons in control and GluA1^−/− mice. E, Peak theta frequency of neurons in control and GluA1^−/− mice. F, Mean (±SEM) peak theta frequencies calculated when mice ran at different speeds. Theta peak frequencies in GluA1^−/− mice were lower independently of running speed. ***p < 2.2⁻¹⁶.

Stable network state in GluA1^−/− mice despite absent periodicity

Several computational models suggest that grid cell spatial periodicity emerges from cellular interactions within a continuous attractor network (McNaughton et al., 2006; Burak and Fiete, 2009; Couey et al., 2013; Pastoll et al., 2013). This class of models makes explicit predictions regarding the firing associations between ensembles of grid cells (Burak and Fiete, 2009; Yoon et al., 2013). For example, only a very small subset of attractor states in the network is possible, and these states should be stable in time. In a normal grid cell network, each state is defined by strict firing associations between neurons, where only cell pairs with similar phases will be allowed to fire together. We therefore investigated whether stable states were also present in GluA1^−/− mice, despite the lack of spatial periodicity in these mice.

To estimate the firing associations of cell pairs, we first calculated the instantaneous firing rate of the cells during 250 ms time windows (Fig. 10A). Only cells with a spatial sparsity score >0.25, with a mean firing rate <5 Hz and with more than one firing field were selected. These cells were silent in most time windows (median, control: 79.09%, GluA1^−/−: 79.14%, Mann–Whitney U test, U = 127143, p = 0.65) and, when active, they fired bursts of spikes (Fig. 10A,B). The likelihood that a cell fired between 0 and 5 spikes per time window was not significantly different across genotypes (Fig. 10B; Mann–Whitney U tests, all p values > 0.01), suggesting that the selected cells in the two genotypes were recruited in a similar manner during exploratory behavior. As expected, the selected cells had lower grid periodicity and spatial sparsity in GluA1^−/− mice than in control mice (control n = 204, GluA1^−/− n = 154, median grid score, control: 0.33, GluA1^−/−: −0.01, Mann–Whitney U test, U = 22994, p = 5.69⁻¹⁴, median spatial sparsity, control: 0.52, GluA1^−/−: 0.44, U = 20250, p = 2.81⁻⁶).

Figure 10.

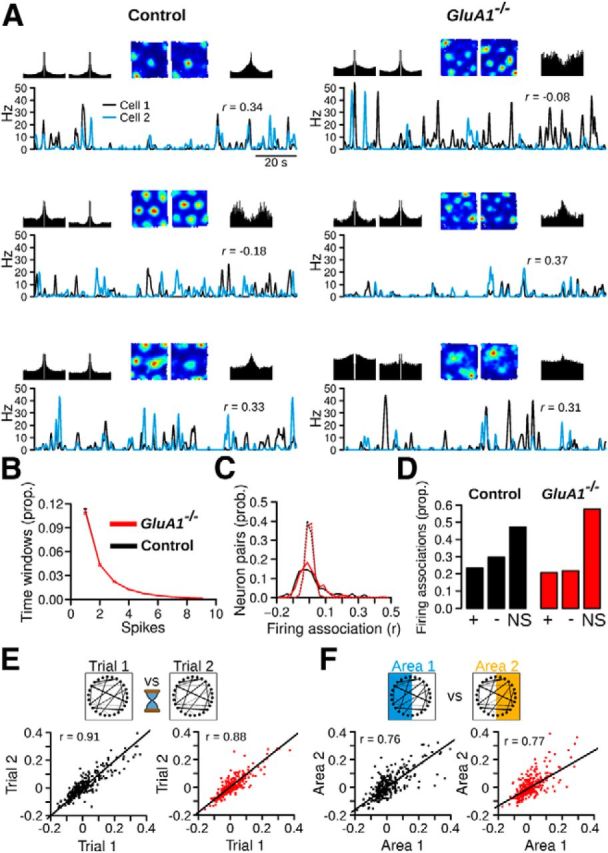
Stable network states in GluA1^−/− mice. A, Examples of three cell pairs recorded in control and GluA1^−/− mice. For each pair: top row left, spike-time autocorrelation (from −100 to 100 ms) of both cells; top row middle, firing rate map of both cells; top row right, spike-time cross correlation (from −100 to 100 ms) between the two cells; bottom, instantaneous firing rate of the two cells during 120 s of exploration in the open-field. The firing association between the two cells is the correlation coefficient (r value) between the two instantaneous firing rate vectors. B, Time windows with different number of spikes. The recruitment of principal neurons in GluA1^−/− mice was very similar to that of control mice. C, Distribution of firing associations between MEC neurons in control and GluA1^−/− mice. The data from the first open-field trials are shown. The dotted lines indicate chance levels for pairs of control and GluA1^−/− cells. In both genotypes, stronger negative and positive associations were observed compared with chance levels. D, Proportion of significantly negative and positive firing associations in control and GluA1^−/− mice. +, positive firing associations; −, negative firing associations; NS, nonsignificant firing associations. E, Stability of firing associations. Top, Schematic of the analysis. Firing associations between recorded cells are represented by lines between the circles. The firing associations between cells were compared during two trials in the open field. Bottom, Correlations of firing associations observed during the two trials. Firing associations in GluA1^−/− mice were as stable as those of control mice, despite a lack of grid cell periodicity and a reduction of spatial selectivity. F, Stability of firing associations as mice explored two nonoverlapping regions of the open field. In both genotypes, the firing associations were maintained across the two areas. Red and black dots represent cell pairs from GluA1^−/− and control mice, respectively.

Firing associations between pairs of simultaneously recorded cells were estimated by performing Pearson correlations between instantaneous firing rate vectors. The distribution of firing associations (r values) in GluA1^−/− mice was not significantly different from that of control mice (Fig. 10C; control n = 262, GluA1^−/− n = 261, Mann–Whitney U test, U = 32575, p = 0.35). In both groups, the distribution was much wider than that obtained after shifting the spike train of each cell member by a random amount (Fig. 10C). The proportion of cells with significant positive and negative associations was higher than predicted by chance in both genotypes (Fig. 10D; chance level: 0.01), although we found a significant difference between the two groups (Pearson χ² test, χ² = 5.38, p = 0.02). These results suggest that despite the lack of spatial periodicity of neurons in GluA1^−/− mice, stable attractor states were to a large extent preserved during open-field exploration. Similar results were obtained if time windows of 125 ms were used to calculate the instantaneous firing rate of the neurons or if cells with only one firing field were also included in the analysis. We also tested to which extent the firing associations between pairs of cells could be explained by firing rate map similarity. Pearson correlations between firing associations and map similarity showed that map similarity explained a large proportion of the variance in firing associations (control: r₍₂₆₀₎ = 0.84, p < 2.2⁻¹⁶, GluA1^−/−: r₍₂₅₉₎ = 0.78, p < 2.2⁻¹⁶). The correlation was not significantly different between genotypes (Fisher r-to-Z transformation, Z = 1.91, p = 0.056).

Attractor states within networks depend on anatomical connections between neurons and are assumed to be stable for hours. We therefore tested whether the firing relationships between pairs of neurons in GluA1^−/− mice were stable by calculating the similarity between the firing associations of cell pairs obtained during two recording trials in the open field (minimum and maximum intertrial interval of 15 and 60 min, respectively). The firing associations of pairs of neurons were highly stable in both control and GluA1^−/− mice (Fig. 10E; Pearson correlation, control: r₍₂₆₀₎ = 0.91, p < 2.2⁻¹⁶, GluA1^−/−: r₍₂₅₉₎ = 0.88, p < 2.2⁻¹⁶), and there was no significant difference between genotypes (Fisher r-to-Z transformation, Z = 1.59, p = 0.11). Thus, network states in the MEC of GluA1^−/− mice were as stable as those of control mice over periods of up to an hour.

A prediction of current attractor network models is that in an environment larger than the spacing of the grid, the same subset of attractor states is activated at different locations. Thus, firing associations between cell pairs should be maintained when comparing firing activity in two large areas explored by a mouse. If stable attractor states are still present in GluA1^−/− mice despite the loss of grid cell periodicity, the same firing associations between pairs of neurons should be observed in two sufficiently large areas. To test this, we compared the firing associations of cell pairs in two halves of the open field. We found that, in both control and GluA1^−/− mice, the firing associations of cell pairs were preserved across two nonoverlapping open-field areas (Fig. 10F; Pearson correlation, control: r₍₂₆₀₎ = 0.76, p < 2.2⁻¹⁶, GluA1^−/−: r₍₂₅₉₎ = 0.77, p < 2.2⁻¹⁶). The correlations between the firing associations in the two different areas were not significantly different between control and GluA1^−/− mice (Fisher r-to-Z transformation, Z = −0.25, p = 0.80). Firing rate map similarity for cell pairs in the two areas was also positively correlated (Pearson correlation, control: r₍₂₆₀₎ = 0.45, p = 1.16⁻¹⁴, GluA1^−/−: r₍₂₅₉₎ = 0.36, p = 1.50⁻⁹, difference between groups: Z = 1.23, p = 0.22). These results indicate that similar network states were activated in different locations in both genotypes.

Discussion

Here we show that mice lacking GluA1-containing AMPA receptors are impaired at homing efficiently when allothetic cues are either unreliable or absent. We further demonstrate that they are unable to compute path integration coordinates. Moreover, these mice exhibit selective alterations in the spatial activity patterns of MEC neurons. GluA1^−/− mice show a disruption of the periodic firing pattern of grid cells, whereas head direction selectivity, speed modulation, and theta rhythmic activity are largely unaffected.

We explored the ability of GluA1^−/− mice to use idiothetic cues for successful orientation by using two different behavioral tasks: a food-carrying homing task and an L-maze task in the dark. We found striking differences in the orientation abilities when comparing GluA1^−/− and control mice on both tasks. Using the homing task, we found that, whereas GluA1^−/− mice succeeded in relying on external visual cues for orientation, their homing performance was impaired as the demand on idiothetic-based orientation increased. Thus, GluA1^−/− mice failed to update the relationship between available visual cues and their position at the beginning of their outward path (LV condition). Furthermore, they showed a deficiency in keeping track of their location relative to a reference point when they used idiothetic cues only (D condition). Finally, using the L-maze task, we demonstrated that GluA1^−/− mice exhibit a deficit in the computation of path integration coordinates.

In the LV condition of the homing task, the mice could not rely on allothetic cues to identify the position of the home base over consecutive trials. Hence, successful orientation relied heavily on the integration of both allothetic and idiothetic cues. In such a situation, GluA1^−/− mice showed a reduced homing ability as well as an increased tendency to return to the location previously associated with the home base in the LF condition. This phenomenon is reminiscent of the performance of rats with fimbria-fornix lesions when tested under similar conditions (Whishaw and Maaswinkel, 1998). It could be that GluA1^−/− mice were unable to learn new associations between extra-maze visual cues and the home base, or that they were impaired in spatial reversal learning. The latter suggestion has been proposed already, based on the performance of GluA1^−/− mice on a plus-maze task (Bannerman et al., 2003).

In the D condition, the inverse relationship between the complexity of the outward path and the accuracy of homing suggests that the mice used idiothetic cues to home successfully in the absence of allothetic cues. Accordingly, the poorer performance of GluA1^−/− mice in this condition might be explained by a deficit in their ability to perform path integration efficiently. Using the L-maze task, we directly addressed this question and found that GluA1^−/− mice indeed are impaired at computing path integration coordinates.

The deficient spatial performance of GluA1^−/− mice did not result from sensorimotor or motivational deficits because their general swimming performance (L-maze task) and homing ability during the LF condition of the homing task did not differ from those of control mice. Their normal homing performance when allothetic cues were reliable (LF condition) is in line with studies reporting normal performance of GluA1^−/− mice on standard spatial reference memory tasks (Zamanillo et al., 1999; Reisel et al., 2002), a phenomenon that is surprising if one considers the reduced spatial selectivity of hippocampal place cells in these mice (Resnik et al., 2012). Together, these results indicate that neither normal spatial selectivity of hippocampal place cells (Korotkova et al., 2010; Allen et al., 2011) nor grid cell spatial periodicity in the MEC is required for learning the location of a goal in relation to familiar visual cues. Instead, normal spatial firing in the hippocampus and the MEC might be essential to encode and express spatial memory in which the recent spatial history of the animal plays a central part. This form of memory for retrospective spatial trajectories could be affected in GluA1^−/− mice, which would explain why they are impaired on spatial working memory tasks and on tasks requiring the processing of idiothetic cues to keep track of their position. This proposition is in line with the hypothesis that path integration and self-referenced memory share the same neuronal networks and algorithms (Whishaw et al., 1997; Buzsáki and Moser, 2013). It remains to be seen whether more local genetic manipulations will allow a clear-cut dissociation between these two processes.

Our in vivo assessment of MEC neuron activity demonstrates that grid cell spatial periodicity in GluA1^−/− mice is disrupted. Although the neurons showed a reduction in spatial selectivity, this could not account for the reduced periodicity in neurons of GluA1^−/− mice. This dissociation was perhaps best illustrated by the firing of some GluA1^−/− neurons having several well-defined firing fields. The organization of the firing fields failed to follow the hexagonal arrangement commonly observed in control mice.

The alterations seen in GluA1^−/− mice share some similarity with previous reports of loss of grid cell periodicity after inactivation of the medial septum or the hippocampus (Brandon et al., 2011; Koenig et al., 2011; Bonnevie et al., 2013). In these studies, head direction tuning in head direction and conjunctive cells of the MEC was retained despite a severe loss of grid periodicity. In the current study, we also report a dissociation between grid periodicity and head direction selectivity. In addition, we found that the speed modulation of the firing rate of MEC neurons was preserved in GluA1^−/− mice. Together, these observations demonstrate that head direction and running speed signals, which are thought to update the spatial representation within grid cell networks as the animal moves in space (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Burgess et al., 2007), can be dissociated from the periodic arrangement of grid cell firing.

One important distinction between the GluA1^−/− phenotype and that observed after pharmacological inactivation of the medial septum or the hippocampus is that the firing rate of MEC neurons was largely preserved in GluA1^−/− mice. In contrast, the pharmacological manipulations resulted in a reduction of 40–60% of the firing rate of MEC neurons (Koenig et al., 2011; Bonnevie et al., 2013). After hippocampal inactivation, the decrease of firing rate in grid cells was correlated with the reduction of grid periodicity, suggesting that the loss of grid periodicity depended on this decrease of firing rate (Bonnevie et al., 2013). In GluA1^−/− mice, the firing rate of principal cells was slightly higher than that of control mice for a given running speed, yet grid cell periodicity was disrupted. This suggests that mechanisms independent of the firing rate were at play in GluA1^−/− mice.

The periodic firing of grid cells can be explained by various models (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Burgess et al., 2007; Burak and Fiete, 2009; Zilli and Hasselmo, 2010; Couey et al., 2013; Pastoll et al., 2013). A major difference between these models is whether the path integrator is implemented at the single-cell level via oscillatory interference or within a neuronal attractor network. Our results support the presence of an attractor network within the MEC based on the following considerations. In GluA1^−/− mice, MEC neurons showed a loss of grid periodicity, a decrease in spatial selectivity, and a reduction in map stability, suggesting that MEC neurons were impaired in updating their firing rate based on the integration of velocity and head direction inputs. Despite this impairment, we found that the firing associations between MEC neurons in GluA1^−/− mice had a distribution similar to that in control mice. In a model in which no attractor network is present, one expects that the firing associations between pairs of MEC neurons in GluA1^−/− show a shift toward 0 because the error accumulating in the path integrator of different neurons would be independent from each other. This would thus lead to more variability in the firing associations over time. Our results suggest that, independently of the mechanisms generating grid periodicity, network interactions between grid cells are likely to play a significant role in determining the instantaneous firing rate of grid cells. The network interactions could operate via direct excitatory connections between grid cells in layer III (Dhillon and Jones, 2000) or via a recurrent network of inhibitory interneurons present in layer II of the MEC (Couey et al., 2013; Pastoll et al., 2013).

Previous experimental and modeling studies support the notion that the hippocampus and the MEC are involved in path integration. Therefore, we suggest that alterations in place and grid cell firing account for the impaired path integration in GluA1^−/− mice, although, given the constitutive nature of the GluA1 ablation, we cannot rule out that modifications outside of the hippocampal–entorhinal network contribute to the behavioral deficit reported here. Remaining questions concern the specific contribution of place and grid cells to path integration and whether the reduction in grid cell periodicity originates from the altered firing of place cells (Bonnevie et al., 2013), or vice versa (McNaughton et al., 2006; Solstad et al., 2006). GluA1^−/− mice, although not suitable to address these questions, provide evidence that the firing of spatially tuned cells in the hippocampal–entorhinal circuit sustains path integration. Moreover, our findings support the hypothesis that grid cells are embedded in a continuous attractor network.