Action Recognition by Motion Detection in Posture Space

Abstract

The visual recognition of action can be obtained from the change of body posture over time. Even for point-light stimuli in which the body posture is conveyed by only a few light points, biological motion can be perceived from posture sequence analysis. We present and analyze a formal model of how action recognition may be computed and represented in the brain. This model assumes that motion energy detectors similar to those well-established for the luminance-based motion of objects in space are applied to a cortical representation of body posture. Similar to the spatio-temporal receptive fields of regular motion detectors, these body motion detectors attain receptive fields in a posture–time space. We describe the properties of these receptive fields and compare them with properties of body-sensitive neurons found in the superior temporal sulcus of macaque monkeys. We consider tuning properties for 3D views of static and moving bodies. Our simulations show that key properties of action representation in the STS can directly be explained from the properties of natural action stimuli. Our model also suggests an explanation for the phenomenon of implied motion, the perceptual appearance, and neural activation of motion from static images.

Introduction

In biological motion stimuli, such as point-light displays (Johansson, 1973), information about the body posture is encoded in the location of the point-lights, which convey the positions of the limbs. The movements of the limbs with respect to each other signal body motion. The movement of each single point-light presents the local motion of a single joint. Many psychophysical experiments over the last years have shown that local motion information is not necessary to perceive the movement of the walker (Beintema and Lappe, 2002; Beintema et al., 2006; Lange and Lappe, 2007; Kuhlmann et al., 2009; McKay et al., 2009; Reid et al., 2009; Lu, 2010; Thirkettle et al., 2010; Theusner et al., 2011). Instead, biological motion perception can be performed by analyzing first body posture and then body motion (Beintema and Lappe, 2002; Giese and Poggio, 2003; Lee and Wong, 2004; Lange and Lappe, 2006). This approach, which is also quite popular in computer graphics and image analysis (recent surveys in Poppe, 2010; Weinland et al., 2011), uses templates of the human figure to obtain articulated movement, rather than motion signals from the joints as suggested by older literature (Johansson, 1973; Cutting, 1981; Webb and Aggarwal, 1982; Giese and Poggio, 2003). The present paper focuses on the neural processes that may support this approach.

In the human brain, visual information about body posture is represented in the fusiform body area (Michels et al., 2005; Peelen and Downing, 2005b; Schwarzlose et al., 2005), the occipital face area (Vaina et al., 2001; Grossman and Blake, 2002; Michels et al., 2005; Peelen and Downing, 2005a), and the extrastriate body area (Downing et al., 2001). Recent electrophysiological studies in macaque monkeys found single neurons in the lower bank of the superior temporal sulcus (STS) and the inferior temporal cortex that respond to static images of body postures (Vangeneugden et al., 2009, 2011; Singer and Sheinberg, 2010). In the upper bank of the STS, neurons were found that respond to body motion (Vangeneugden et al., 2011), consistent with the selectivity of the STS to biological motion (Oram and Perrett, 1994; Vaina et al., 2001; Grossman and Blake, 2002; Saygin, 2007).

In the present paper, we describe a model of body motion perception that uses (static) posture selectivity to derive body motion via generalized motion mechanisms operating on the posture representation. The model considers body postures in three dimensions by implemented 2D postures seen from different view points (profile, half-profile, or frontal view). This allows us to compare model and data and determine which aspects of the neural representation of action result from which static or dynamic features.

Materials and Methods

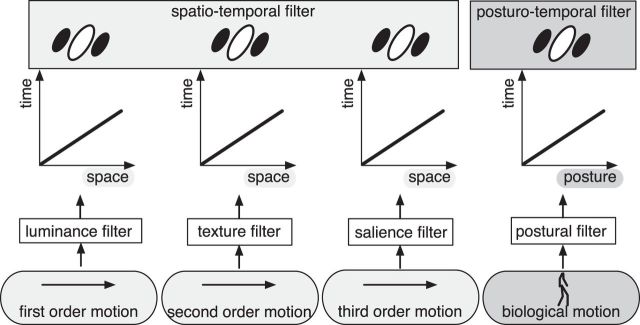
Following earlier proposals (Lange and Lappe, 2006; Lange et al., 2006) and consistent with recent experimental findings (Lu, 2010; Theusner et al., 2011), our model consists of two consecutive processing stages: a template matching stage for body posture analysis followed by a motion detection stage for body motion analysis. The model, however, deviates from previous models in two important aspects. First, it uses posture templates from different view points to allow recognition of actions in different 3D directions. Second, the motion stage is modeled as motion energy detection (a standard model in luminance-based motion perception) (Reichardt, 1957; van Santen and Sperling, 1984; Adelson and Bergen, 1985; Watson and Ahumada, 1985; Burr et al., 1986) applied to the posture representation. In analogy to the spatio-temporal receptive fields of object motion detectors, our model generates what we will call posturo-temporal receptive fields, the properties of which we will compare with known properties of action-selective neurons in the temporal cortex. In the following, we will describe both processing stages in detail. The model is depicted in Fig. 3 and described in detail below.

Figure 3.

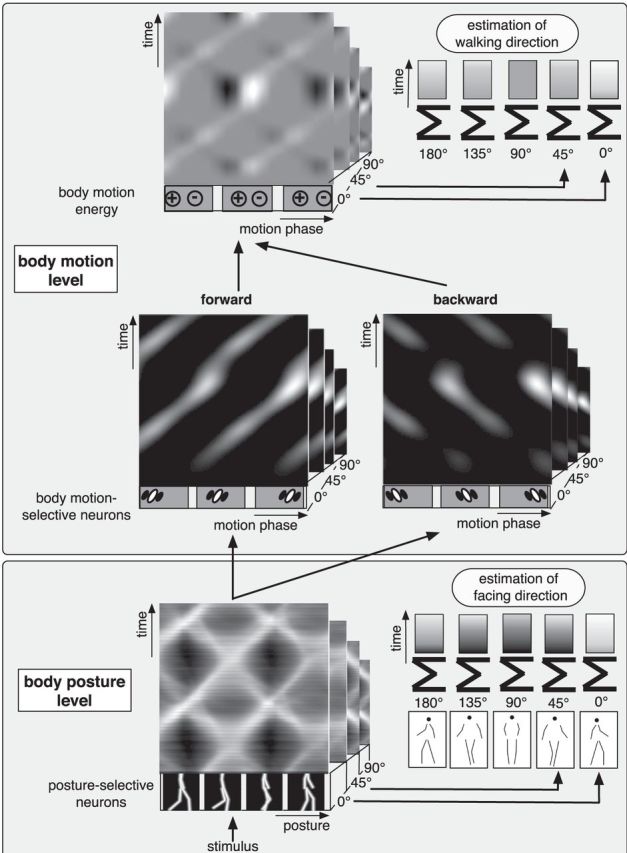
Schematic depiction of the posturo-temporal filter model. The model consists of a body posture level followed by a body motion level. At the body posture level, the posture of a stimulus is analyzed by posture-selective neurons. Each posture-selective neuron represents a particular posture. The population represents all postures of the action. At the body motion level, activity within the posture-selective representation over the course of time is analyzed by posturo-temporal filters. By combining these filters and calculating the difference between the half-squared response of the forward-oriented posturo-temporal filter and the backward-oriented posturo-temporal filter, the model computes body motion energy. An estimate of body motion energy is determined at every point in time. Maximum pooling and summation over the stimulus duration provide an estimate of the motion direction. Similarly, an estimate of the facing direction is obtained by maximum pooling and summing the activities in the body posture representation.

The representation of body posture

The body posture representation is formed by neurons that are selective to specific body postures. The distribution of activity in the body posture representation over time contains information about the change of the posture during the movement (i.e., the body motion). This will be the basis for the subsequent motion analysis.

The body posture selectivity of single neurons is modeled as a template matching process. We therefore describe how the templates were generated, how the template matching was implemented, and how the response of the template representation to a stimulus was simulated.

Generation of templates and test stimuli.

We collected motion-tracking data from nine individuals that walked along a short hallway (Beintema et al., 2006). We recorded the 3D coordinates of the 12 major joints (feet, knees, hips, hands, elbows, and shoulders) and interpolated between them to obtain coordinates for the whole limbs. From the 3D coordinates, five different 2D orthographic projections were created: leftward, rightward, frontal, and the two 45° intermediate facing directions. The orthographic projections for the facing directions 225°, 270°, or 315° are identical to those for 135°, 90°, and 45°, respectively, and were therefore not separately created. The datasets were normalized such that the midpoint between the hips was always in the same position and the height of the body (feet to shoulders) was the same for each walker. The walking cycle (two steps) was normalized to 1.39 s and was divided into 100 frames. These frames were used to construct the template representation.

The same dataset was used to construct the stimuli for the simulation of model responses. Using a jackknife procedure, one of the walkers was selected as stimulus, whereas the other eight served as templates. The simulations were run 9 times, once for each of the walkers as stimulus. The stimuli were constructed as point-light walkers with points either located on the joints (Johansson, 1973), or on a few randomly selected locations on the limbs (Beintema and Lappe, 2002), or densely covering the limbs (248 points) to simulate a stick figure walker. The locations of the joint positions at time points that fell between the 100 frames of the recording, were approximated by linear interpolation.

Posture-selective neurons through template matching.

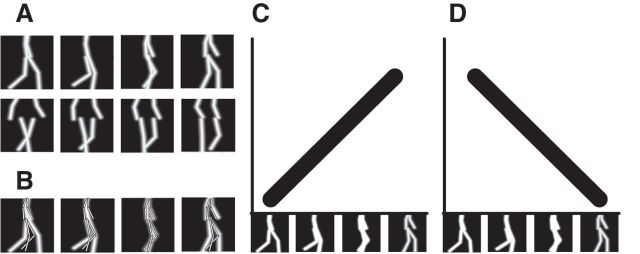
The posture-selective neurons were simulated as template detectors as described by Lange and Lappe (2006). Each neuron had a preferred static body posture that matched one of the frames of the walker data. Thus, there were 4000 posture-selective neurons (8 walkers × 100 frames × 5 facing directions). The limb configuration of the respective frame of the walker data was used as the template for the neuron's selectivity. Figure 1A shows four example templates for different walking postures. Illustrated are representations of a walker with the facing direction 0° and 45°. The body (arms and legs) is illustrated by white lines. These templates are considered as receptive fields for which the sensitivity falls off as a Gaussian function of the Euclidean distance between a stimulus point (x_i, y_i) presented at the time t and the corresponding nearest location on a limb (c_i, r_i) of the preferred posture ψ of the template. The neuron's response R to a stimulus consisting of N points is given by the sum of the responses to all the individual points of the stimulus as follows:

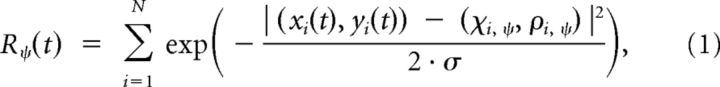where σ denotes the width of the limbs. This parameter was chosen to correspond to 10 cm for an average person of ∼180 cm height. Figure 1B illustrates the template matching procedure.

Figure 1.

A, Examples of posture representations in the model. Each posture-selective neuron represents a single posture (the stick figures) from a 2D view of an action, in this case walking. Top row, Examples of postures during the walking cycle seen in profile view (0° facing direction). Bottom row, Similar examples in half-profile view (45° facing direction). B, In the template-matching step, a stimulus posture is spatially compared with all templates, and the degree of overlap determines the activity of the respective template neuron. C, When a continuous walking stimulus is presented, it will excite each of the neurons from that particular facing direction in order. At each point in time, the walking stimulus has a slightly different posture for which one of the posture-selective neurons is most responsive. As the posture of the stimulus changes because of the movement, the highest posture-selective neuron response shifts from one posture-selective neuron to the next. This results in an oriented activation profile in the posture–time plot. D, When the stimulus is shown in reversed order (backwards walking), the posturo-temporal activation is oriented in the orthogonal direction.

Temporal evolution of the population activity in the posture representation during walking stimulation.

As the posture of the stimulus changes during the walking movement, the similarity between the stimulus and the preferred body posture of any posture-sensitive neuron also varies. In the course of the stimulus movement, different posture-sensitive neurons will be activated most strongly. Figure 1C illustrates this. Posture selectivities are arranged in the temporal order of the walking cycle along the horizontal axis of the graph. Time runs along the vertical axis. Over time, a sequence of best-matching postures is activated in order, leading to a diagonal trace of activation (black line) in this figure. For a stimulus that walks backward (i.e., in which the sequence of stimulus frames is presented in reversed order), the activation trace is oriented in the opposite direction (Fig. 1D).

The representation of body motion

In our model, body motion selectivity is generated by applying standard concepts of motion detection to the posture representation. We will describe the analogy between this computational step and standard motion detection, introduce the posturo-temporal filters, and describe model neurons selective to body motion.

Motion detection in posture space.

The estimation of motion in posture space is based on the temporal evolution of activity in the posture representation as shown in the graphs of Figure 1C, D. We will call these graphs “posture–time plots” in analogy to the space–time plots used to depict motion of objects over the retina (Adelson and Bergen, 1985). Space–time plots have been essential tools to illustrate the concept of spatio-temporal filters for motion detection (Fig. 2). The movement of a light point across the retina is plotted in a graph comprising a spatial dimension x and a temporal dimension t. For constant motion, the velocity of the stimulus is then given by the slope of the line in this plot. It can be analyzed by oriented spatio-temporal filters that extract motion energy (Reichardt, 1957; van Santen and Sperling, 1984; Adelson and Bergen, 1985; Watson and Ahumada, 1985; Burr et al., 1986). In a similar way, the motion of higher-order properties (e.g., texture, second-order motion; or salience, third-order motion), can be analyzed by first applying respective filters (e.g., texture grabbers or salience detectors) to the retinal image and then applying spatio-temporal filters to the resulting texture or salience representation (Lu and Sperling, 1995). In this model, the mechanisms of motion detection are always the same, namely, spatio-temporal filters, and the sensitivity results from applying these filters to different spatial representations, which are created by first applying luminance, texture, or salience filters to the retinal input (Fig. 2).

Figure 2.

The spatio-temporal filter model of first-, second-, and third-order motion extended to posturo-temporal filters for body motion perception. In first-, second-, and third-order motion, spatio-temporal filters are applied to spatial maps of different features: luminance, texture, and salience. The posturo-temporal filter model uses a similar principle on a representation of body postures arranged in a map-like structure according to the temporal evolution of body posture during an action.

Our model for biological motion detection is similar in spirit but replaces the spatial dimension of retinal position with the dimension of posture along the represented movement. The retinal input is first transformed into a representation of body postures through the template-matching process in the posture-sensitive neurons. In this posture–time plot, body motion is analyzed through posturo-temporal filters. These filters are oriented in the posture dimension and the time dimension. The process by which these filters estimate motion is analogous to that for first-order luminance motion and consists of (1) divisive normalization of the input representation, (2) posturo-temporal filtering, (3) half-squaring, and (4) calculation of motion energy as the difference between forward and backward walking.

Posturo-temporal filters.

First, the responses of the posture-selective neurons are normalized following Simoncelli and Heeger (1998):

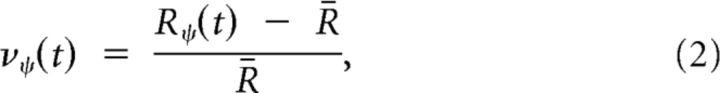where R_y(t) is the response of the neuron with preferred posture ψ at time t, R̄ is the mean response over all neurons at time t, and n_y(t) is the resulting normalized response. Next, posturo-temporal filters are defined for forward (g^f) and backward (g^b) walking. These posturo-temporal filters are implemented as Gabor functions in the postural (p) and the temporal (t) dimension as follows:

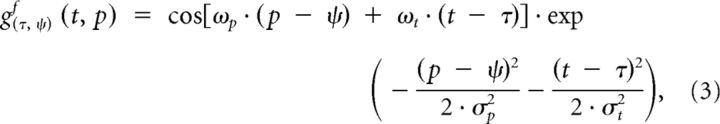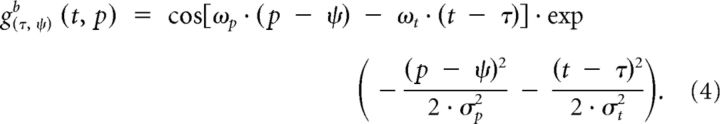where ψ is the posture on which the filter is centered and τ is the point in time at which the filter is calculated. The parameters of the cosine function determine the filter frequencies along the postural and temporal dimensions. The temporal and postural frequencies (ω_t and ω_p) should be matched to the walking movement. For one step, which corresponds to 50 templates and 0.69 s, the frequencies were chosen to be w_t = 2π/0.69 Hz and w_p = 2π/50. The parameters σ_p and σ_t of the Gaussian function determine the integration widths of the filter along the postural and temporal dimensions. The width along the postural dimension σ_p was set to 42 frames, corresponding to a weighting of 0.5 for the second local maxima along the postural dimension. We checked that a different value (σ_p = 250) did not lead to substantially different results. The temporal width σ_t was set to 250 ms such that the filter was biphasic in time, in analogy to motion energy models for luminance-based motion (e.g., Adelson and Bergen, 1985).

The response r of the posturo-temporal filter is determined by convolution with the normalized posture representation as follows:

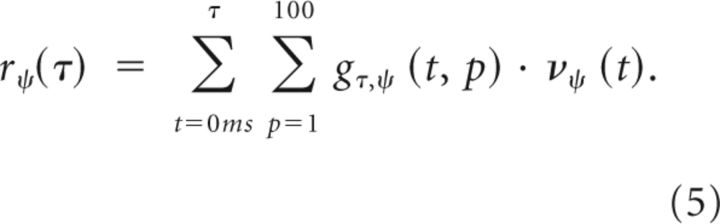To estimate the response r of the posturo-temporal filter at the time τ, only normalized responses of the posture-selective neurons are taken into account with t ≤ t.

Third, the response r of the posturo-temporal filter is rectified and normalized

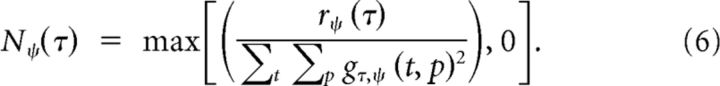The result describes the response of a neuron selective to body motion N. The neuron computes body motion for a particular range of postures and for a particular motion direction (forward or backward).

Finally, from these neurons, body motion energy (ε) can be calculated by taking the difference between the squared filter responses for forward and backward motion

Facing selectivity of body motion-selective neurons.

Our model consists of a set of neurons selective for body motion that are modeled as posturo-temporal filters tuned to one of two motion directions (forward or backward) and a particular range of preferred postures. These neurons process input from the representation of body posture in the posture-selective neurons.

We implemented the posturo-temporal filters separately for each facing direction, consistent with the observation that most body motion-selective cells in macaques are selective for a combination between motion and facing direction (Oram and Perrett, 1994, 1996; Singer and Sheinberg, 2010; Vangeneugden et al., 2011). Thus, posture-selective neurons provide information to the body motion-sensitive neurons specific to the facing direction of the body, and only posture-selective neurons from the same facing category contribute to a posturo-temporal filter.

The estimation of facing and walking direction

The main focus of our model is on the properties of the body motion-selective neurons and the posture-selective neurons, and comparing these to the properties of respective neurons in the brain. However, the model should also describe the perception of biological motion at the system level. Therefore, we have to test whether the model can explain and replicate the perception of biological motion in humans. Experimental studies of biological motion perception have often used discrimination tasks in which participants reported the facing direction or the walking direction of a point-light walker. To simulate such experiments, we need to implement mechanisms to read out the activity in the body posture representation and the body motion representation. We simply use maximum pooling of the responses in the respective stages of the model.

Estimation of facing direction.

For each facing direction, the maximum response is determined for each time step and the values are summed over the entire stimulus duration as follows:

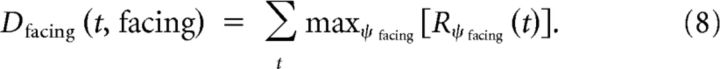The maximum operation was performed on all posture sensitive neurons of one facing direction (i.e., 100 postures × 8 walkers), excluding those of the currently presented walker.

Estimation of walking direction.

In the same way, for the estimation of walking direction the maximum values of body motion energy ε are summed over the stimulus duration as follows:

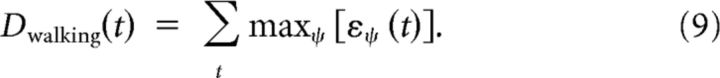Here the sign of the sum determines the perception of the walking direction. Positive values indicate forward walking, and negative values indicate backward walking. An alternative would be to compare the responses to the two motion directions with each other rather than using the body motion energy. We chose to use body motion energy mainly for consistency with the motion energy literature.

Results

Two types of neurons were implemented in our model: posture-selective neurons and body motion-selective neurons. The selectivity of the former was modeled as template matching for preferred postures. The selectivity of the latter was modeled as posturo-temporal filtering applied to the activities of the posture-selective neurons. We will now study the properties of those neurons and investigate how the model can replicate and explain the properties of corresponding neurons in the brain and the results of psychophysical experiments. Because the parameters of both sets of model neurons are derived from the temporal and spatial properties of the action stimuli, our investigations will demonstrate how much the action sensitivity of neurons in the brain is directly related to stimulus properties.

Properties of posture and facing selectivity

The posture selectivity in our model is similar to the template matching process in the model of Lange and Lappe (2006); hence, many properties of the posture-selective neurons are the same as those described in that paper. However, unlike previous models, our current model uses templates from different 3D view points. Therefore, our description of the properties of the posture-selective neurons will concentrate on their sensitivity to facing direction in 3D.

Sensitivity to facing direction in single neurons

We have assumed that the 3D body is represented by 2D, orthographic projections. Those 2D, orthographic projections are stored in posture-selective neurons representing different facing directions. The properties of those posture-selective neurons are determined by geometric features of the stimulus. We will compare the tuning of the view representation of the posture-selective neurons with corresponding facing direction-selective neurons in the macaques STS.

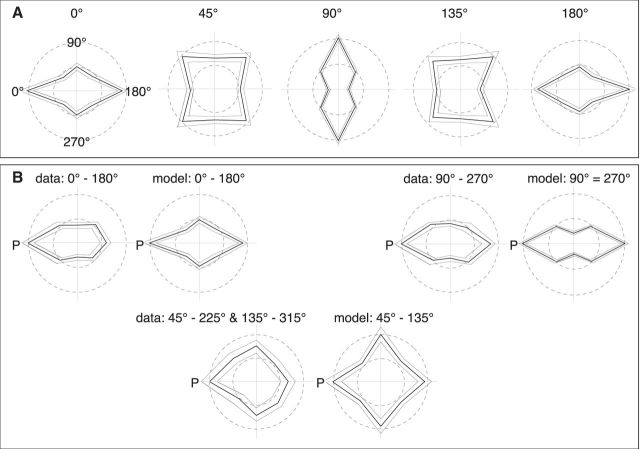
Our model contains representations of 0°, 45°, 90°, 135°, and 180° facing direction, with 0° facing rightward (Fig. 3). The 225°, 270°, and 315° facing directions are identical to the 135°, 90°, and 45° facing directions, respectively, because of the orthographic projection. For each of the five facing representations, we created average tuning curves of the neurons from the posture representation to stimuli of eight different facing directions. This was done in the following way. First, we calculated for each neuron the average activity over a full walking cycle to a stick-figure stimulus with the respective facing direction. Then, we averaged the activity over all neurons of a single facing population. This was repeated for all facing populations. Thus, we had a mean response for each facing population to a stimulus facing in one particular direction. This set of mean responses was determined for each stimulus facing direction separately.

Figure 4A shows the resulting tuning curves. These tuning curves show some characteristic features that have also been observed for action-selective neurons in macaque temporal cortex (Vangeneugden et al., 2011). First, the tuning is axial: high responses are observed for stimuli facing 180° away from the preferred facing indicated above each plot (see leftmost plot for the orientation of the coordinate system). This is uncommon for simple visual features, such as orientation or direction, which typically show Gaussian tuning, but is observed in temporal cortex neurons selective for body posture. The axial tuning is trivially expected for the 90° facing because it is geometrically identical to the opposite 270° in orthographic projection, but it occurs also for the other facing directions (e.g., 0° and 180°), which are not geometric ambiguous. Instead, the axial tuning points toward a similarity in shape between the opposing facing directions. Second, the tuning curves for the half-profile views (45° and 135°) show strong responses to stimuli facing in orthogonal directions (i.e., 90° rotated from the preferred facing). This is not the case for the left, right, or frontal facing directions, for which the orthogonal facing stimuli give lower responses than the preferred or opposite facing stimuli. This has also been found in monkey temporal neurons. To illustrate this, we have plotted the tuning curves of the model neurons along the data of Vangeneugden et al. (2011) (Figure 4B). Vangeneugden et al. (2011) measured the response of neurons preferring facing directions of 0°, 45°, 90°, 135°, 180°, 225°, 270°, or 315° to stimulus facing in different directions. They then combined the neurons with opposite facing preferences (e.g., 0° and 180°) into one plot by rotating the data such that the preferred direction always pointed to the left in the plot. We did the same for our simulation data. In addition, we combined their data for the 45°, 135°, 225°, and 315° facing preferences because in the model 45° and 225° are geometrically identical, as are 135° and 315°. The resulting plots are shown in Figure 4B. The axial tuning is clearly visible for the 0°/180° and the 90°/270° preferences. For the 45°/135° plots model, data show only a slight preference for a particular direction and strong responses along all four cardinal directions. This is more pronounced in the model than in the data (which is true also for the other comparisons). However, the model captures the essential differences between the 45°/135° facing representations on the one side and the 0°/180° and the 90°/270° facing representations on the other.

Figure 4.

A, Polar plots of average tuning curves for facing direction for each of the five facing representations (0°, 45°, 90°, 135°, and 180°). The thick lines indicate the mean; the thin lines indicate the SEM. The outer circles represent maximal response; the inner circles represent 50% of that. B, Comparison of the tuning curves of the posture-selective neurons of the model to the tuning curves of the facing direction-selective neurons found in STS (Vangeneugden et al., 2011) for the stimuli grouping used in that study.

Population activity in the posture representation

The properties of the responses to the different facing directions can be illustrated for the entire population of posture-selective neurons in posture–time plots. Figure 5 shows posture–time plots of the responses to the five stimulus facings for each of the five facing selectivities. These posture–time plots show the similarities between different facing directions seen in the average tuning curves in more detail in the unfolding of activity over time in the posture representation. For example, the posture representation for 0° facing responds in a very similar pattern for stimuli facing toward 0° and for stimuli facing toward 180°. Other facing directions result in activation patterns with less similarity. Likewise, the responses of the representation for 45° facing to its preferred 45° stimulus are similar to those of a stimulus facing toward 135°.

Figure 5.

Posture–time plots of population activity in the different facing representations. Neural activity is encoded in grayscale. In every row, the response of the posture-selective neurons representing a particular facing direction (e.g., 0° in the upper row) to a stimulus facing in one of the five possible facing directions is shown.

Specificities of the activation patterns can also be seen when comparing responses to the preferred facing stimuli in different facing representations (i.e., the plots along the diagonal). Between the 45° and the 0° representations, a frequency doubling can be observed that is related to the ambiguity between the left and right body halves in the profile view. In the half-profile or profile view, the ambiguity of the right and left half of the body is resolved and the spurious activation vanishes.

The temporal distribution of activity over the posture representation is the basis for body motion analysis in our model. The orientation and width of the streaks of activation in the posture–time plots determine the direction and precision of the motion estimate. The spread of activation for the preferred facing in the 90° representation is much broader and much weaker oriented than in the 0°, 45°, 135°, or 180° cases. This suggests that the frontal view provides less body motion energy than the other views. In the profile and half-profile facings, on the other hand, the posture–time plots show not only a strong oriented activation in the correct (forward) direction but feature prominent streaks of spurious activation in the opposite (backward) direction (i.e., tilted leftward in the plots along the diagonal). This suggests that there is considerable motion energy in the opposite direction in the stimulus sequences. We therefore tested the dependence of the motion discrimination performance of the model on the facing direction of the stimulus.

Facing dependence of motion discrimination: problems with frontal facing

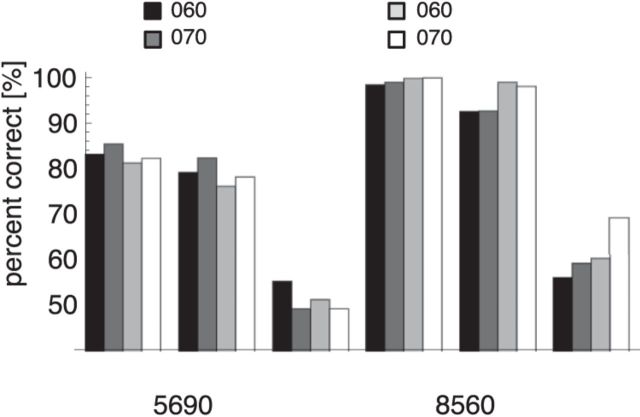
The illustrations in Figure 5 show that the activities in the posture representation are very different for the different facing directions. Because the subsequent body motion estimation is based on the posturo-temporal variation of these activities, one should expect differences in body motion estimation for different facing directions. An experimental quantification of the discrimination performance for a forward/backward decision was provided by Kuhlmann et al. (2009). We simulated their first experiment with the model and compared the model results with the psychophysical data. The stimulus was a limited-lifetime walker with a small number of dots placed on random location on the limbs. In different conditions, the stimulus was shown in profile view (0°), in half-profile view (45°), or in frontal view (90°) for one walking cycle, either walking forward or walking backward (reversed temporal order of the frames). Either 2 or 4 points were shown per frame. By varying the frame duration, the total number of points that were presented during the whole trial was either 128 or 512 (for both numbers of points per frame, 2 and 4). Kuhlmann et al. (2009) also tested different lifetimes of the dots; but because dot lifetime had no effect on performance, we simulated only a lifetime of one frame.

Figure 6 shows that the results of the model simulations closely match the experimental data. The performance of the model and the human subjects was higher for 512 in comparison with 128 points per trial. The profile view gave slightly better discrimination than the half-profile view. In contrast, discrimination was very poor in the frontal view. The poor discrimination ability in the frontal view relates to the smeared-out activation in the posture representation in Figure 5 (middle), which does not allow a distinction between the two walking directions.

Figure 6.

Simulation results of performance in the walking direction discrimination study of Kuhlmann et al. (2009). The stimulus was facing in profile (P), half-profile (HP), or frontal (F) view. Black and dark gray represent model simulations; light gray and white represent human data.

Facing dependence of motion discrimination: coupling between facing and walking direction

The walking direction estimate in the model is based on the posture representation that shows the highest activation. Usually, this is the facing representation that matches the true facing of the stimulus. However, the tuning properties and the activities in the posture–time plots showed that the 0° and the 180° activities are quite similar to each other, and so are the 45° and 135° activations. The similarity pertains not only to the activation in the correct motion direction (rightward orientation in Fig. 5) but also extends to the spurious backward motion signals (leftward orientation in Fig. 5). Indeed, a closer inspection of the activities showed that the similarity was even stronger along the backward orientation than along the forward orientation. To illustrate this, we presented stimuli facing toward 0°, 45°, 135°, or 180° and collected in each case a separate motion estimate from each posture representation (Fig. 7). For example, Figure 7A shows four motion direction estimates for a stimulus facing toward 0° obtained from each of the four posture representations (0°, 45°, 135°, or 180°). The posture representation that corresponds to the correct 0° facing provides a correct identification of the motion direction. However, the estimates taken from the other, nonmatching, facing representations are incorrect, falsely predicting the opposite direction of motion. Similar effects are seen for the other facing directions (Fig. 7B–D), showing that the model calculates the correct motion direction when the activities of the correct facing representation are used; but when the responses of other facing directions are used, the opposite motion direction would be indicated.

Figure 7.

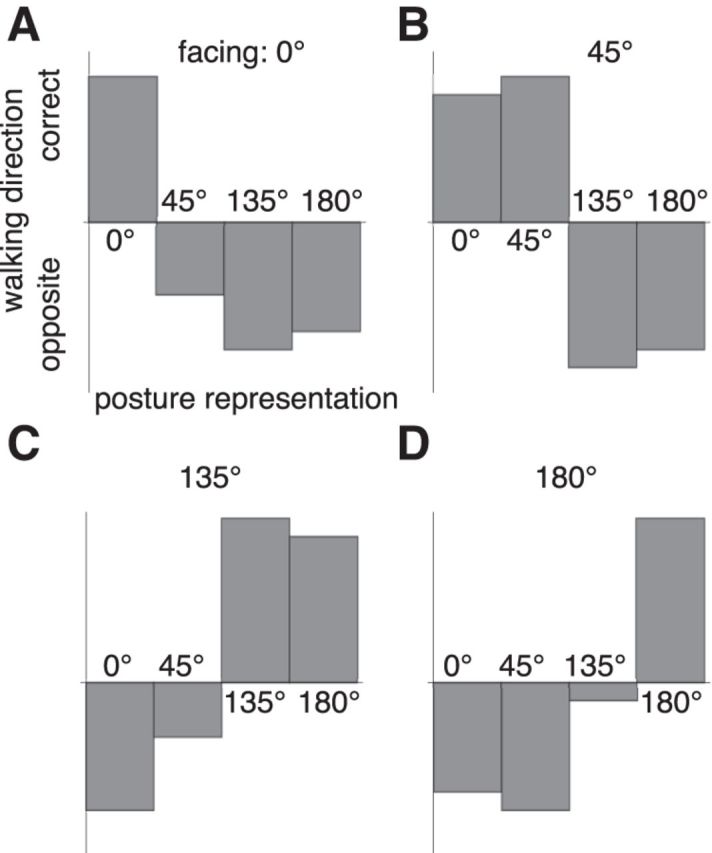
Interactions between facing and walking direction can lead to erroneous motion energy in the opposite direction when the stimulus facing differs from the preferred facing of the posture representation. A, Facing 0°. B, Facing 45°. C, Facing 135°. D, Facing 180°.

In particular, Figure 7 shows an inversion of the estimated motion direction when the 180° facing representation is used with a 0° facing stimulus and vice versa, and an inversion of walking direction when the 45° representation is used with a 135° stimulus. Because these representations are each rather similar to each other, they might easily be confused. Our model would predict that such a confusion of the facing direction should also lead to a confusion of the walking direction such that 45° stimuli that are erroneously perceived as facing toward 135° should be perceived as walking backward when they truly walk forward and vice versa. This may be tested in experiments in which subjects have to simultaneously judge facing and walking directions.

Properties of body motion selectivity

In our model, the estimation of body motion is performed by posturo-temporal oriented filters applied to the activities in the posture representation. Although the above simulations already showed that this procedure allows discrimination of walking direction similar to human observers, we next wanted to illustrate the temporal and postural properties of single-body motion-selective neurons in the model. We were interested in which way the model can replicate and explain the behavior and the features of body motion-selective neurons described in electrophysiological studies.

Temporal integration in body motion-selective neurons

The posturo-temporal filters, like their spatio-temporal counterparts in luminance motion detection, have a certain period of temporal integration that is determined by the Gaussian width σ_t. The temporal integration along with the temporal frequency ω_t determines the time course of activity in the body motion-selective neurons. The two parameters were chosen to match the frequency of the gait cycle (w_t = 2π/0.69) and to ensure a biphasic response profile of the filters (σ_t = 250 ms), which is a prerequisite for motion detection. The combination of these parameters generates a filter that is optimally matched to the walking action. We can then ask how the properties of the filter responses relate to the temporal properties of the action-selective neurons in monkey temporal cortex, to estimate whether these are adapted to the properties of the walking cycle. Figure 8A shows the mean filter responses for motion in the preferred and nonpreferred directions for a stick-figure stimulus in profile view averaged over all starting phases. Consistent with typical motion detector properties for simple luminance motion, the responses are initially the same for both direction. The response to the preferred motion separates from the response to nonpreferred motion after ∼200 ms. However, some response to nonpreferred motion remains throughout the stimulus presentation. This is different from motion detector responses to simple motion. It is a consequence of the distribution of activity in the posture representation, which features a considerable amount of spurious motion in the wrong direction (Fig. 5, leftward tilted streaks of activity). This response behavior is consistent with rather weak selectivity for forward versus backward stimuli in macaque temporal neurons that was noted in Vangeneugden et al. (2011). To directly compare the temporal properties of our model neurons to the data of Vangeneugden et al., 2011 (their supplemental Fig. 5), we plotted the difference between preferred and nonpreferred responses over time (Fig. 8). The comparison indicates similar temporal properties. The response difference between the two motion directions is small for the first 100 ms and then increases to the saturation level, which is reached after ∼400–600 ms.

Figure 8.

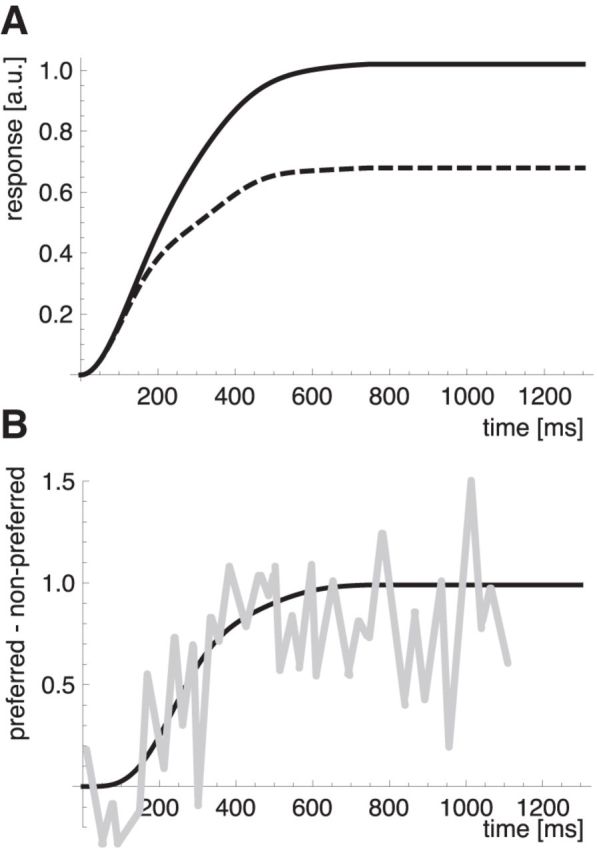
A, Time course of the posturo-temporal filter response to a stimulus walking in the preferred direction (solid line) and in the nonpreferred direction (dashed line). B, Time course of the difference between the posturo-temporal filter responses to the preferred and the nonpreferred walking direction. Black represents model results; gray represents comparison data from the monkey. Monkey data adapted from Vangeneugden et al. (2011, their supplemental Fig. 5).

Postural integration

Besides the temporal integration, there is also postural integration because the postural temporal filters combine signals from a range of postures around the posture ψ on which the filter is centered. These postures have to appear in the correct temporal arrangement of the preferred motion direction (forward or backward). Thus, the filter's selectivity combined motion direction and posture. The neuron responds only if both fit the filter's preference. The posturo-temporal filters therefore combine body motion with body form selectivity. Such combined selectivities have often been described in action-selective neurons in monkey temporal cortex (Oram and Perrett, 1994, 1996; Jellema et al., 2004; Vangeneugden et al., 2009, 2011; Singer and Sheinberg, 2010). However, the responses to moving stimuli (i.e., a sequence of postures) are much stronger than the responses to static postures. On average, the response to the preferred posture ψ alone reaches only 24% of the maximum response to that posture embedded in the walking cycle. Vangeneugden et al. (2011) used an action index (response to moving stimulus − response to static presentation)/(response to moving stimulus + response to static presentation), to categorize temporal neurons into action (“A,” action index >0.2) and static + action (“SA,” action index <0.2) neurons. The average action index for the posturo-temporal filters in our model is 0.68. Thus, the body motion-selective neurons of the model on average fit well to the action category introduced by Vangeneugden et al. (2011). However, the match between body motion-selective neurons and “A” neurons and between posture-selective neurons and “SA” neurons is somewhat difficult because the distinction between “SA” and “A” neurons in Vangeneugden et al. (2011) is based purely on the action index. If applied to our model, this criterion would classify a small number of body motion-selective neurons that have relatively weak direction selectivity, and hence an action index smaller than 0.2, as “SA” neurons. Vangeneugden et al. (2011) also reported that some of the neurons classified as “SA” had a significant forward–backward selectivity.

Ratio of posture-selective neurons and body motion-selective neurons

In monkeys, the ratio of posture to action-selective neurons was found to be ∼10:4 (Vangeneugden et al., 2011). Assuming that in essence these cells are analogous in function to the posture-selective neurons and the body motion-selective neurons of the model, one can ask whether there is an optimal ratio for these model neurons.

The model currently has 100 equally spaced posture-selective neurons for each represented walking cycle. Theoretically, the maximal total motion signals can be obtained with two body motion-selective neurons on each posture-selective neuron (one neuron representing forwards motion and one representing backwards motion for each represented posture). However, because the body motion-selective neurons integrate over a range of postures (represented by ω_p, Eqs. 3 and 4), it can be expected that the average responses of the body motion-selective neurons will hardly decrease for a smaller number of body motion-selective neurons.

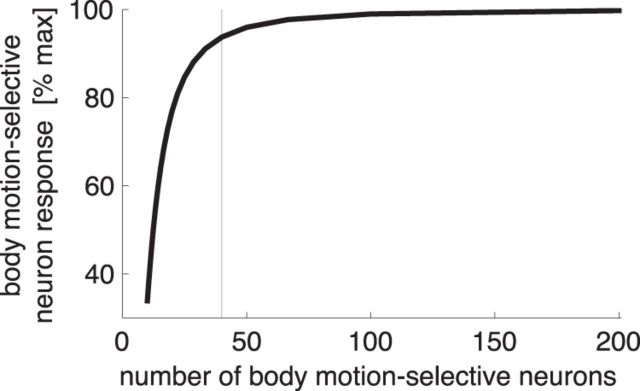
Figure 9 shows the average maximal response computed for different numbers of body motion-selective neurons while all other model parameters are kept constant. Indeed, the average response remains almost constant even with 50 neurons and only begins to drop steeply with fewer than ∼30 neurons. Thus, the model agrees with the data in predicting that the number of body motion-selective neurons can be considerably lower than the number of posture-selective neurons while maintaining an almost maximal motion signal.

Figure 9.

Average maximal response of the body motion-selective neurons, as a function of the number of body motion-selective neurons in the model. The maximum (100%) of the average maximal response is reached when two body motion-selective neurons (one forward and backward) sample each represented posture (i.e., at N = 200). The vertical line indicates 40 body motion-selective neurons.

Number of posture-selective neurons and body motion-selective neurons

A related question is how many posture and body motion-selective neurons are needed. For the simulations above, we have divided the gait cycle into 100 posture stimuli and used each one to construct a single posture-selective neuron. However, the broadness of tuning of these neurons suggests that a much smaller number may suffice. The posture-selective neurons in the model respond not only to their preferred posture but also to many other postures around their preferred posture. Indeed, similar to what has been reported in monkey neurons (Vangeneugden et al., 2011), most posture-selective neurons respond to some degree to all postures of the walking cycle. To show the average tuning width compared with the monkey data, we adopted the procedure that Vangeneugden et al. (2011) used for their supplemental Figure 4. For each neuron, we took the responses to each of the postures in the walking cycle and ranked them in the order of their strength. Then we averaged the ranked responses over all neurons. The result is shown in Figure 10A. Figure 10B shows the monkey data for comparison. In both cases, the posture-selective neurons clearly respond to a broad range of postures. The correspondence is an important point because the broadness of this tuning is not a parameter of the model but rather emerges from the template structure. It is thus a further aspect of the close fit of the physiological properties to the stimulus properties that the model is intended to show.

Figure 10.

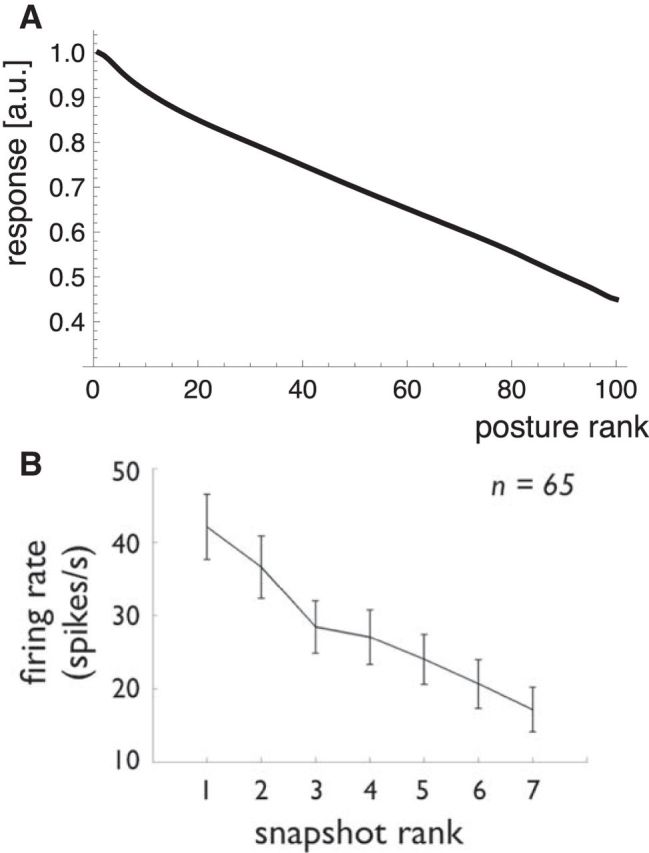
Selectivity of the posture-selective neurons. A, The average response of the posture cells to all posture of the walking cycle in the order of their strength. B, Same analysis for the monkey neurons from Vangeneugden et al. (2011, their supplemental Fig. 4).

The broad tuning in posture space implies that the model does not require a high resolution of postures along the walking cycle. Instead, it works well with a much smaller number of templates. We tested this in simulations in which we varied the number of posture-selective neurons and computed the performance in the walking direction task. These simulations showed that full accuracy (close to 100% correct discriminations) was achieved already with just 25 posture-selective neurons. Further simulations showed that performance was not limited by the number of posture selective-neurons but rather by the number of body motion-selective neurons. When we used a ratio of 1:1 for the posture and body motion-selective neurons rather than a ratio of 5:1, full accuracy was already observed with a mere 5 posture-selective neurons.

Responses to full- and half-body configurations

It is known from psychophysical (Mather et al., 1992; Troje and Westhoff, 2006; Chang and Troje, 2009; Hirai et al., 2011) and computational (Lange and Lappe, 2006) research that the motion of the lower body, especially the feet, is more important for some aspects of biological motion perception than the movements of the upper body. Likewise, Vangeneugden et al. (2011) described that neurons responded stronger to stimuli that showed only the lower body than to stimuli that showed only the upper body. However, this selectivity difference was more pronounced in the “A” than in the “SA” neurons. We were interested to determine whether such a sensitivity difference between the neuron types emerges in our model, even though the body motion-selective (“A”) neurons in our model derive their selectivity directly from the posture (“SA”) neurons.

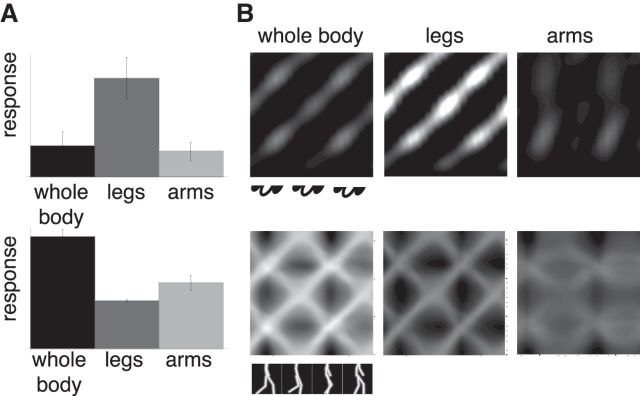
Therefore, we calculated responses to only the legs, only the arms, or both arms and legs, using stick-figures stimuli in each case. Figure 11 shows the results. Figure 11A shows average activities of the body motion-selective neurons (top) and the posture-selective neurons (bottom) for the three conditions. Like the “A” neurons of Vangeneugden et al. (2011), the body motion-selective neurons in our model respond strongly to stimuli showing only the legs and weakly to stimuli showing only the arms. Indeed, the response to the legs-only stimulus is even stronger than the response to the full body stimulus. This is different for the posture-selective neurons. They respond strongest to the full body stimulus and approximately half as strong to each of the half-body stimuli. This is similar to the response properties of the “SA” neurons in the monkey.

Figure 11.

Responses to full-body and half-body configurations. A, Sum of the posture-selective neuron responses and the forward-oriented filter neurons to a stick figure (whole body, legs-only, arms-only). B, Posture–time plots in the postural (lower row) and the body motion representation (response of the forward-oriented filter, upper row) for a stick figure stimulus (whole body, legs-only, arms-only).

Figure 11B shows posture–time plots of the activities in the posture and the body motion representation, and illustrates the reasons for the different average responses. The posture representation for the whole-body stimuli shows the diagonal pattern of activity that represents the veridical body motion as well as the spurious activity that corresponds to the opposite walking motion (Fig. 11B). In the legs-only condition, the same pattern is present, but the difference between the activity of the veridical body motion and the spurious activity of the wrong body motion becomes larger. In the arms-only condition, in contrast, the difference between the veridical and the wrong body motion becomes weak and the posture specificity becomes blurred. Consequently, the body motion representation shows crisp responses in the legs-only and whole-body conditions, but weak and unfocussed activity in the arms-only condition. Thus, although in our model body motion is derived from body form information over time, the responses to body motion do not depend on the total amount of form information but rather on the motion specificity of the form information, which is higher in the lower than in the upper body.

Implied motion

Pictures of certain static postures of humans and animals sometimes give the impression of motion. Such an impression may originate from spurious activation of body motion detectors from these postures (Jellema and Perrett, 2003; Barraclough et al., 2006; Lorteije et al., 2006).

The body motion-selective neurons in our model do respond to static postures, albeit only weakly. We wanted to characterize the properties of these responses and compare them with responses of neurons from the STS. To do this, we calculated for each body motion-selective neuron the responses over a full gait cycle of preferred motion and determined the single posture in that data that gave the strongest response. We then calculated the response of the neuron when this posture was presented as a static stimulus and normalized it to the maximum response during the walking stimulus. We did this for all neurons and averaged the resulting response time courses. Figure 12A (solid line) shows the result. The curve reaches a peak of ∼15% of the maximum motion response at 200 ms after stimulus onset. The response stays above zero throughout the stimulus presentation. Thus, the body motion energy is non-zero and may support an impression of motion.

Figure 12.

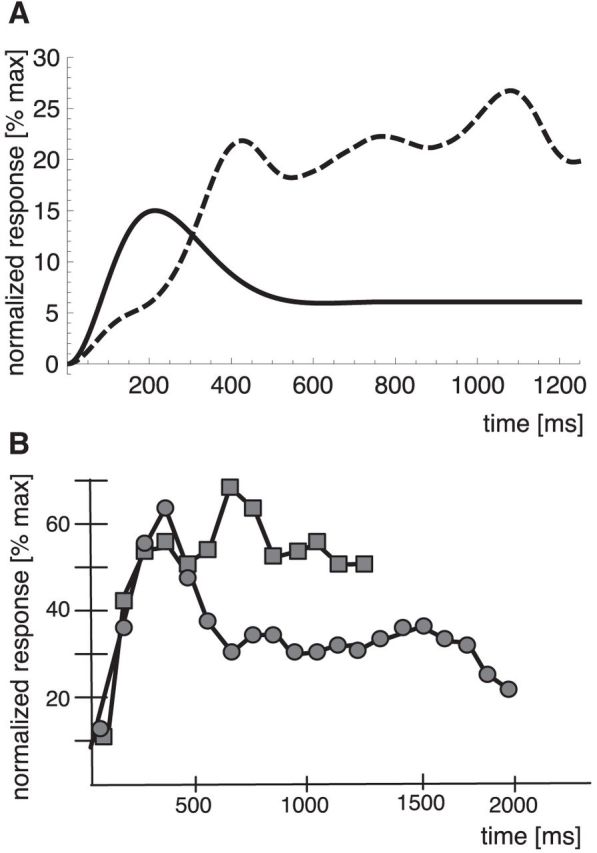
A, Normalized response of the forward-oriented filters of the model to a walking stimulus (dashed line) and to a static stimulus (solid line). B, Temporal development of the normalized population response in monkey STS to a moving stimulus (squares) and to a static stimulus (circles) replotted from the study of Jellema and Perrett (2003) (their Fig. 3).

Figure 12B shows comparison data from Jellema and Perrett (2003). They recorded neurons sensitive to articulated action with moving and static views of the head and body. Although this is not directly comparable with walking motion, we do think that the main features of implied motion responses can nevertheless be illustrated. As in our simulations, the plot for the static responses shows averaged normalized responses to the preferred static postures from the moving sequence. The time course of the implied motion signal is similar between the model and the data from the STS. In both cases, the signal reaches a maximum at ∼200 to 300 ms and declines afterward. After ∼700 ms, the signals asymptote to a level of approximately half of the maximum response. In the model, this time course results from the biphasic nature of the posturo-temporal filters, in which an excitatory response to an input is followed by an inhibition to that same input to generate motion selectivity. To investigate whether the time course of the implied motion signal is dependent on the biphasic nature of the posturo-temporal filters, we have repeated the simulations with different values of σ_t. We have used values of σ_t for which the posturo-temporal filters show a monophasic and a polyphasic behavior. Both values of σ_t led to a different time course of the implied motion signal. Thus, the biphasic shape of the temporal response profile forms the basis for the occurrence of an implied motion signal similar to the findings of Jellema and Perrett (2003).

Figure 12A (dashed line) shows the average response to a moving stimulus. This response was calculated similarly to the experimental paradigm of Jellema and Perrett (2003) by averaging the responses of all neurons to a walking stimulus starting from a single posture in which the limbs were wide extended. The comparison data from Jellema and Perrett (2003) are shown in Figure 12B. In both cases, the moving stimulus induces a stronger response than the static stimulus in later phases of the trial. Thus, the response to the static stimulus is weaker than to a moving stimulus, consistent with these neurons being sensitive for action sequences.

However, the response to the static stimulus could induce an overall (weak) percept of motion if the responses of filters for one motion direction (e.g., forward) are on average higher than the responses to the opposite motion (backward). This difference in activity (i.e., the difference in population activation) could be interpreted as an overall motion signal that is induced by a single static image (i.e., as implied motion). To show this, we calculated forward and backward filter responses to static stimuli from different phases of the walking cycle and determined which population gave the stronger response. We did this for all 9 template walkers and determined the ratio of forward/backward decisions in the model. Figure 13A shows that the implied motion direction varies over the postures of the walking cycle such that some postures imply forward motion in the model whereas other postures imply backward motion.

Figure 13.

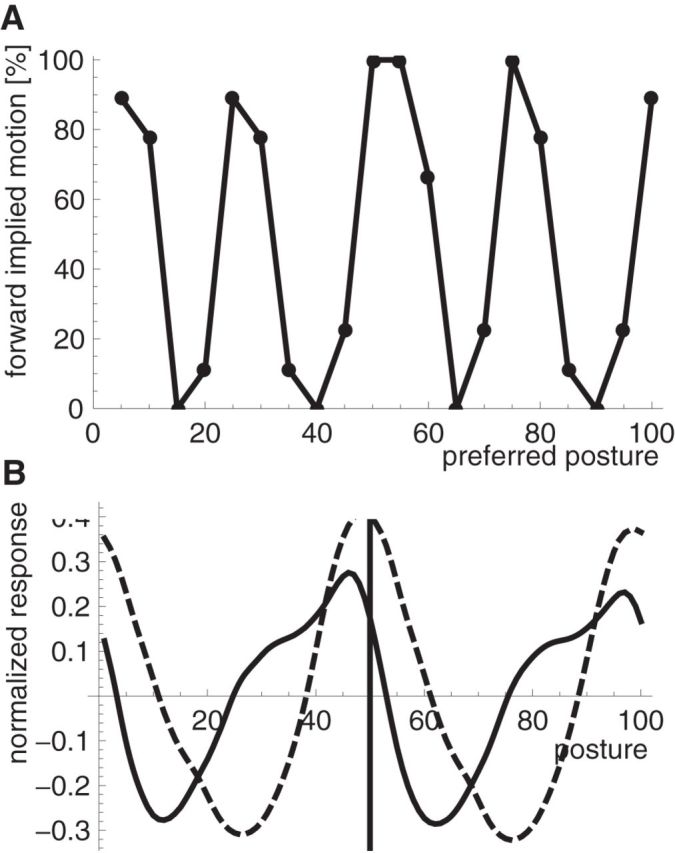
A, Ratio of forward implied motion for every posturo-temporal oriented filter position. B, Mean over the template walker and the filter positions of the normalized posture-selective neuron response for forward implied motion (solid line) or for backward implied motion (dashed line). The vertical line indicates the preferred filter position.

These simulations show that the responses of body motion-selective neurons to static stimuli can induce an overall bias for one motion direction over the other in the population. Such a bias does not occur in regular luminance-based motion, where opposite motion responses are balanced for static stimuli. We thus asked what determines the bias in motion defined from body posture. Analysis of the filter responses to the posture representation shows that the bias is related to asymmetric activation in posture space. Figure 13B compares the responses in the posture representation for static stimuli that implied forward (solid line) and backward (dashed line) motion, centered on the posture-selective neuron that gave the best response. The distribution of activity shows a clear asymmetry. For stimuli that imply forward motion, responses of posture-selective cells that precede this posture in the forward walking cycle are stronger than those of posture-selective cells that follow this posture in the forward walking cycle. For stimuli that imply backward motion, this asymmetry becomes very small but oppositely directed such that backward-oriented filter fits the responses of the posture representation better than the forward filter.

The asymmetry in the posture representation occurs because the postures that precede the central posture are more similar to this posture than the posture that follows. Thus, the similarity of the static posture to those postures that precede or follow it in the walking cycle determines whether the implied motion is forward or backward. This offers an explanation why implied biological motion occurs and why there is no implied motion for first-order luminance motion, even though our approach to analyze biological motion uses the same mechanism as the analysis of first-order motion. The luminance filters for first-order motion transform the stimulus (light point) to retinal coordinates. There is no asymmetry for the positions of the light point in the retinal coordinates. However, the posture-selective neurons (postural filter) transform the stimulus into postural configurations, which show a clear asymmetry along the walking cycle. This suggests that implied motion for static action stimuli occurs because of the typical development of body configuration around that static posture.

Discussion

We have introduced a model of visual action recognition through analysis of body posture. In this model, filters similar to standard motion energy detectors are applied in a representational space of body postures. We have termed these filters posturo-temporal filters in analogy to the term spatio-temporal filters in motion energy detection of spatio-temporal motion. Two types of neurons were implemented in our model: posture-selective neurons, which encode specific postures; and body motion-selective neurons, which encode bodily action through the sequence of body postures. The spatial and temporal parameters of those neurons are set to match the performed action. We determined those parameters and compared them with existing electrophysiological and psychophysical data. Our analysis was aimed to study how far the tuning properties of action-selective neurons in primate temporal cortex can be related directly to the spatial properties of the static postures and temporal properties of the action.

We found that, as in primate cortex Vangeneugden et al. (2011), the neurons in our model can be grouped into static-action neurons, which respond both to a static view of a body posture and to that same posture embedded in an action sequence, and action neurons that respond much stronger to an action than to any individual posture. The former correspond to the posture-selective neurons in our model and the latter to the body motion-selective neurons. The analysis of the tuning properties of the posture-selective neurons to 3D facing directions showed strong similarities to those of the primate cortical neurons, suggesting that their tuning properties can be explained from the spatial features of the static body view. These properties included the peculiar axial orientation tuning, which was found in primate cortical neurons, spurious responses for facing directions rotated by 90° in neurons that prefer half-profile views, and weak discriminability in the frontal view. These properties can be directly linked to the similarities in the respective posture stimuli because the model uses only simple template matching to generate the neural selectivities.

Based on the concept of posturo-temporal analysis, we have introduced posture–time plots of the temporal development of population activity in a posture representation. These posture–time plots provide a helpful tool to illustrate several features of the geometric basis for action recognition from posture analysis. For example, they visualize spatial similarity and geometric features of different facing direction. Through those posture–time plots, we were able to explain performance differences in a walking direction task for different stimulus views found in psychophysical data (Kuhlmann et al., 2009) and to predict that a confusion of the facing direction should lead to the percept of the wrong walking direction.

The posture–time plots, as well as the posturo-temporal filters that act upon them, rely on a sequential arrangement of body posture selectivities along the walking cycle (i.e., a 1D mapping of postures in temporal order). For other types of action, other body postures would be needed to be arranged in a similar temporal order specific for that action. To allow the analysis of many different actions, many such arrangements have to be assumed that trace the body posture representation in temporal cortex along different directions. It is conceivable that individual postures could be part of several such traces in a multidimensional postural action space.

Action analysis is performed in the model by posturo-temporal filters applied to the posture representation in analogy to spatio-temporal filters applied to spatial representations for object motion in space. The parameters of the posturo-temporal oriented filters are determined by postural and temporal features of the action and thus predict the temporal properties of the posturo-temporal oriented filter. As same temporal behavior was found in walking direction specific neurons in the macaques STS (Vangeneugden et al., 2011), we can conclude that the temporal behavior of the body motion-selective neurons is due to postural and temporal features of the action. Moreover, because each single posturo-temporal filter acts only upon a limited posture range, the posturo-temporal filters are not only sensitive to body motion but also to a certain range of body postures. Thus, they combine posture and motion analysis, like body motion-selective neurons in the primate brain (Oram and Perrett, 1994, 1996; Vangeneugden et al., 2009, 2011; Singer and Sheinberg, 2010). Yet, this combination creates novel dependencies on the spatial and temporal parameters of the stimulus. For example, a decrease in body posture information must not lead to a decrease in body motion response. Because body motion information is highest in the lower part of the body (legs), the response of the posturo-temporal oriented filters is stronger for a legs-only stimulus than for a or an arms-only stimulus. We therefore conclude that motion specificity is more important in these neurons than posture specificity, even though motion is directly derived from posture analysis.

A further feature that emerges from the spatio-temporal filter construction is the response to static postures in the body motion-selective neurons. These responses correspond to the sensitivity of some motion-selective neurons in primate STS (Jellema and Perrett, 2003; Lorteije et al., 2006, 2011) to static views of action and may be the basis for implied motion (i.e., the percept of motion from static images). We found that some body motion-selective neurons in the model have a preferred static image that activates them and that the time course of activation was comparable with that observed in body motion-selective neurons in macaques STS, even though different actions were used (Jellema and Perrett, 2003). In the model, the activation by specific static images can be explained by asymmetries in the spatial and temporal properties of the postures leading to and following the preferred posture. It is thus a consequence of the tuning of these neurons to an action, the combination of posture and motion in the posturo-temporal filtering, and the temporal characteristics of the action. Depending on the specific combination of these parameters, a static stimulus may imply forward (asymmetric response) or backward motion (symmetric response) at the population and perception level.

Our simple model uses standard mechanisms developed for other fields of visual perception but applies them in a novel way to obtain a high-level analysis of motion of the human body. This shows, on the one hand, how specific computational strategies can be reused by the brain for different tasks and, on the other hand, how different types of motion perception (e.g., object motion and body motion) can be based on very different cues (luminance vs body configuration) and pathways (dorsal vs ventral) but eventually use similar algorithms. Our model proposes a route to action recognition that relies on form extraction about the body supplied by shape-selective neurons. Although this is a useful path toward action recognition, similar computational procedures may be possible for more general types of nonrigid motion perception of deformable objects, provided their shapes are represented in sufficient detail in the inferotemporal cortex.

Limitations of our model relate to typical problems in motion and object perception. For example, as the parameters of the posture-temporal filters have to match the gait cycle to obtain the necessary biphasic response profile of the filters one would need different filters for each walking speed, much as luminance-based motion detection needs a battery of speed selectivities. However, the problem for body-motion selectivity is much less severe than for luminance-based motion mechanisms because actions typically have a more restrained speed range. Walking, for example, can be maintained only over a small speed range. If speed exceeds this range, the locomotor pattern changes to running, which is a different action and uses different postures (Giese and Lappe, 2002). The speed range for walking could easily be covered by a small set of detectors tuned for only a few speeds. On the other hand, as the parameters of the posture-selective neurons have to match the retinal size of the stimulus, one needs templates of different sizes or ways to establish size invariance, as for other types of object recognition. Indeed, body-shape-selective neurons have only limited size invariance (Ashbridge et al., 2000), suggesting that indeed posture-selective neurons for different sizes might be needed.

Action selectivity in our model depends on different posture-selective neurons being activated in sequence. Luminance-based retinal motion signals, such as the motion of individual points on the limbs, are ignored. These motion signals may be used in two ways. First, they can provide information about the kinematics of the movement, which in turn can also be used to estimate walking direction (Troje and Westhoff, 2006; Chang and Troje, 2008, 2009). However, many aspects of the kinematics of the movement are included in the model because the body-motion mechanisms in the model analyze the changes in posture of the body. Second, luminance-based retinal motion signals provide information about walking direction in the overall translation of the body in space. The simulations of the present paper and many studies on which they are based have used stimuli that displayed walking-in-place, as if on a treadmill. Real walking, in contrast, translates the body in space, and unless one tracks the walker with pursuit eye movements, also on the retina. This global translational motion of the stimulus in the walking direction is likely to be picked up by motion detectors sensitive for correlated motion (e.g., in area MT). Their signal could be combined with the motion obtained through articulation (Perrett et al., 1990a). Indeed, results from single-cell studies indicate that many cells will respond to one posture translated (without articulation) in the requisite direction or simply with the right relative motion against a background (Perrett et al., 1990a,b). Such a combination may also explain why response latencies to walking and translating human figures can be shorter than response latencies to static postures (Oram and Perrett, 1996). It could be interesting to extend our model in this direction.