Human Muscle Spindle Sensitivity Reflects the Balance of Activity between Antagonistic Muscles

Abstract

Muscle spindles are commonly considered as stretch receptors encoding movement, but the functional consequence of their efferent control has remained unclear. The “α–γ coactivation” hypothesis states that activity in a muscle is positively related to the output of its spindle afferents. However, in addition to the above, possible reciprocal inhibition of spindle controllers entails a negative relationship between contractile activity in one muscle and spindle afferent output from its antagonist. By recording spindle afferent responses from alert humans using microneurography, I show that spindle output does reflect antagonistic muscle balance. Specifically, regardless of identical kinematic profiles across active finger movements, stretch of the loaded antagonist muscle (i.e., extensor) was accompanied by increased afferent firing rates from this muscle compared with the baseline case of no constant external load. In contrast, spindle firing rates from the stretching antagonist were lowest when the agonist muscle powering movement (i.e., flexor) acted against an additional resistive load. Stepwise regressions confirmed that instantaneous velocity, extensor, and flexor muscle activity had a significant effect on spindle afferent responses, with flexor activity having a negative effect. Therefore, the results indicate that, as consequence of their efferent control, spindle sensitivity (gain) to muscle stretch reflects the balance of activity between antagonistic muscles rather than only the activity of the spindle-bearing muscle.

Introduction

Muscle spindle receptors are implicated in a variety of functions, ranging from reflex control (Houk, 1976; Sinkjaer et al., 1988) and proprioception (Goodwin et al., 1972; Roll and Vedel, 1982) to the acquisition and update of internal models of limb dynamics (Hwang and Shadmehr, 2005; Hwang et al., 2006). Beyond muscle stretch itself, spindle output can be powerfully influenced by efferent signals conveyed by motor neurons, termed “fusimotor” neurons (Matthews, 1972). However, the functional consequence of this fusimotor control has remained unclear (Prochazka and Hulliger, 1998; Proske, 2005; Windhorst, 2007; Matthews, 2008; Dimitriou and Edin, 2010; Prochazka and Ellaway, 2012), primarily because of the difficulty in documenting spindle activity from alert subjects during naturalistic active movement.

It is well established that, because of “α–γ coactivation” (Vallbo, 1970), skeletomotor activity in a muscle can be positively related to the output of its spindle afferents. Such an effect can also be achieved through “β” or “skeletofusimotor” neurons, which innervate both spindle and skeletomotor muscle (Scott et al., 1995; Kakuda et al., 1998). However, in addition to the above coactivation effect, activity in a muscle powering movement may be negatively related to spindle afferent responses from its stretching antagonist, if fusimotor neurons are subject to reciprocal inhibition (as are α motor neurons). Reciprocal inhibition of fusimotor drive has been demonstrated previously for γ motor neurons of intercostal muscles in the cat (Sears, 1964). Because the purpose of reciprocal inhibition is to prevent or otherwise curb contractile force production in the antagonist muscle, β motor neurons may also be reciprocally inhibited, because a proportion of these neurons in cat (Jami et al., 1982) and the overwhelming majority of these neurons in the primate (Murthy, 1983) innervate motor units of the fast-twitch fatigable type, capable of producing high forces.

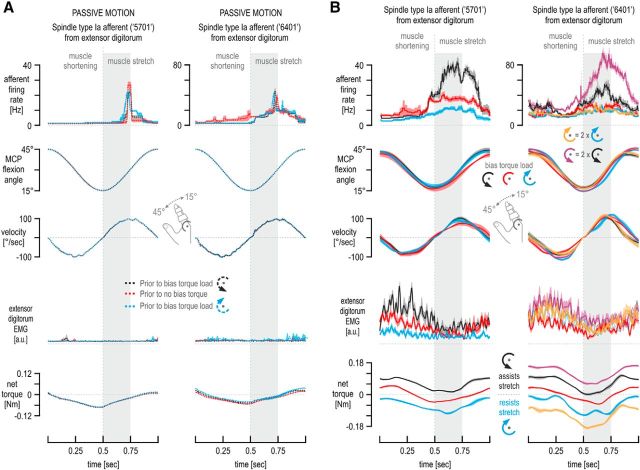
Together, the combination of α–γ coactivation (Vallbo, 1970) and possible concurrent reciprocal inhibition of fusimotor neurons suggests that muscle spindle responses should reflect the balance of activity between the agonist and antagonist muscle (i.e., reflect “antagonistic muscle balance”; Fig. 1A). To test this hypothesis, I used the technique of microneurography (Vallbo and Hagbarth, 1968) to record spindle afferent activity from the extensor digitorum muscle while alert human subjects performed continuous movements of a single finger under constant external loads (i.e., “bias” torque load). These loads were used primarily for inducing different levels of agonist/antagonist activity balance during muscle stretch by either resisting finger flexion or assisting finger flexion (Fig. 1B). To better isolate any effects of bias load on spindle output, a central feature of the current paradigm was maintaining kinematics as similar as possible across the experimental conditions while manipulating the experienced dynamics. Because the kinematic input to the spindles is the same across experimental conditions in the current paradigm (Fig. 1B), any systematic difference in spindle output across conditions was thought indicative of changes in spindle sensitivity (i.e., output “gain”). Both at the single afferent and afferent ensemble levels, I found that spindle sensitivity to muscle stretch does indeed reflect antagonistic muscle activity.

Figure 1.

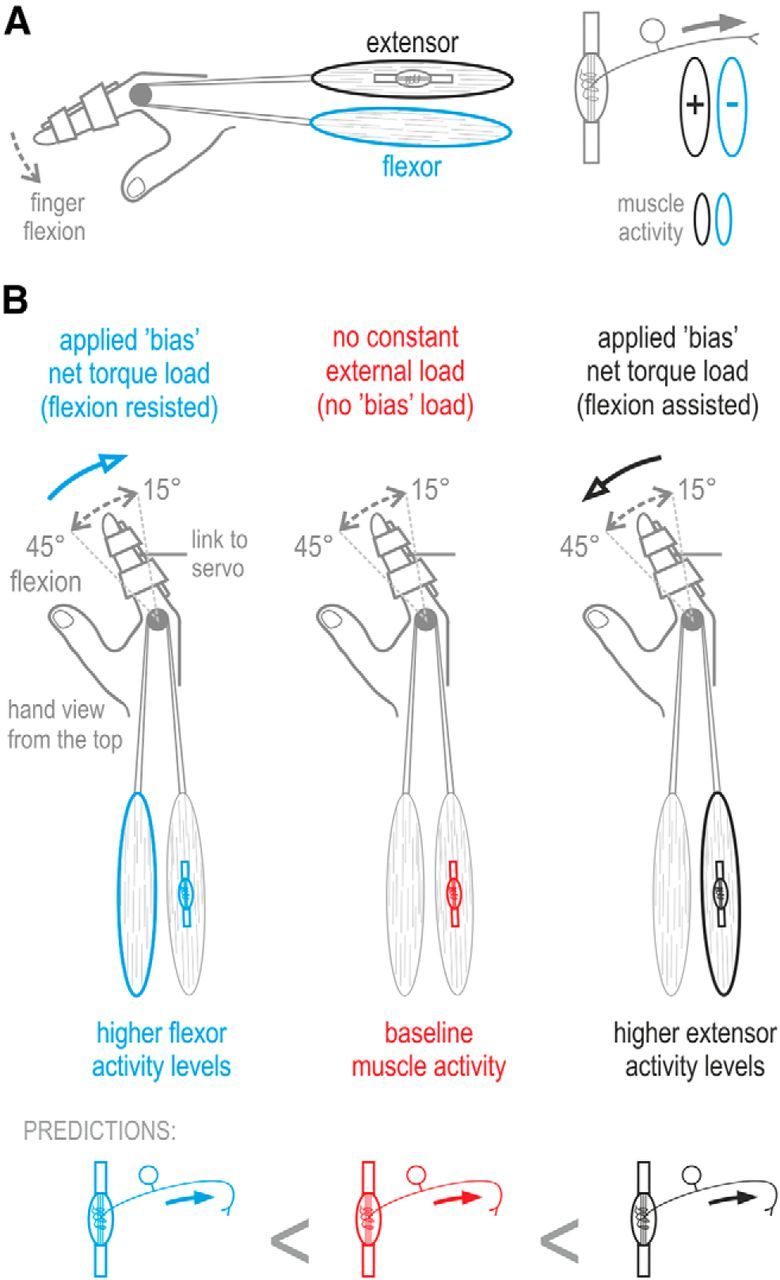
Hypothesis, experimental methodology, and predictions. A, Because of α–γ coactivation, skeletomotor activity in the stretching extensor muscle (black) should be positively related to the sensitivity (gain) of its muscle spindles to stretch. However, because of possible reciprocal inhibition of fusimotor neurons, activity in the flexor muscle (blue) should be negatively related to the sensitivity of spindles located in the extensor muscle. Therefore, it is hypothesized that spindle sensitivity should reflect the balance of instantaneous activity between antagonistic muscles. B, In the current study, subjects were asked to continuously move a single finger between 15° and 45° of MCP joint flexion at a 1 Hz pace. The main experimental manipulation involved moving the finger either under a servo-generated constant torque load (bias load) that continuously resisted finger flexion (blue condition: induced higher levels of flexor activity), moving under a bias torque load that assisted flexion (black condition: induced higher levels of extensor activity) or under no constant bias load (red condition: baseline muscle activity). In addition to any bias load, a relatively small viscous or inertial load was applied (common across all 3 bias load conditions) to promote identical kinematics across the experimental conditions (i.e., prevent finger tremor). The schematic at the bottom of the figure describes the predictions made by the antagonistic muscle balance hypothesis described in A. Because the kinematic input to the spindles is the same across the experimental conditions of the current paradigm, differences in spindle output across conditions reflect changes in spindle sensitivity (i.e., output gain).

Materials and Methods

Subjects.

Seven healthy right-handed subjects (four females) with a mean ± SD age of 22.4 ± 3.3 years participated in the experiments. All subjects gave their written consent before experimentation. The current study was part of a program that the local ethics committee (Ethics Committee of Umeå University, Umeå, Sweden) had approved and followed the Declaration of Helsinki regarding medical research with humans. The subjects were financially compensated for their participation. No complaints were reported as a result of taking part in this study.

Experimental setup.

Throughout, the subjects were seated in a comfortable adjustable chair with their semi-pronated right forearm resting on a mobile ramp and supported by a vacuum pillow. A cushioned clamp placed just proximal to the wrist and another clamp placed around the hand limited movements of the whole hand and upper arm that could otherwise cause electrode dislocations; in this setup, the subjects could move their fingers freely. A single finger (index, middle, or ring finger) of the right hand could be attached to the appendage of a custom servo machine (see below, Apparatus and generated loads) using strong double-sided tape, and the attachment to the finger was tightened further using two hook-and-loop straps (see the hand schematic in Fig. 1A). A computer monitor that was placed in front and above the subjects was used for presenting visual feedback (see below, Experimental paradigm). The monitor was suspended from the ceiling so that the subjects' right hand was not in view during the main experimental task. The subjects were also instructed to maintain their head straight looking at the screen, which also prevented view of the hand.

Apparatus and generated loads.

The used servo machine was created at the department of Integrative Medical Biology of Umeå University. The servo motor produces forces on a finger attachment through a thin metallic rod connected to the attachment though a flexible hinge joint. The forces at the attachment point are measured by four strain gauges (Tokyo Sokki Kenkyujo) that are located near the base of the rod. In addition to any constant (bias) torque loads at the metacarpophalangeal (MCP) joint of the moving finger, applied in either the finger flexion or finger extension direction regardless of ongoing kinematics (Fig. 1B), the servo was used to simultaneously produce a viscous or an inertial load (used for dampening movement/tremor and therefore promoting similar kinematics across the bias load conditions). The coefficients for the time-varying loads were such that peak force modulation would be 0.062 Nm (i.e., 1N) given the required kinematics of the behavioral task. For all subjects except one, bias torque loads of a 0.062 Nm magnitude were used (bias torque loads of 0.124 Nm were used for the additional single subject to ensure adequate stimulation given the subject's size). The chosen bias load magnitude of 0.062 Nm (equivalent to ∼100 g load against gravity, as the distance between point of rotation and point of force application was 6.2 cm) induced the desired effect on antagonistic muscle activity (see Fig. 6E,F) without being fatiguing or otherwise unconformable for subjects. With one subject, the afferent recording lasted long enough to apply both bias load magnitudes (see Fig. 4B, right column). The responses across all bias load magnitudes are congruent with the main findings of this study. The averaged data across all bias load magnitudes of the same direction were used for the statistical analyses examining the effect of bias load direction.

Figure 6.

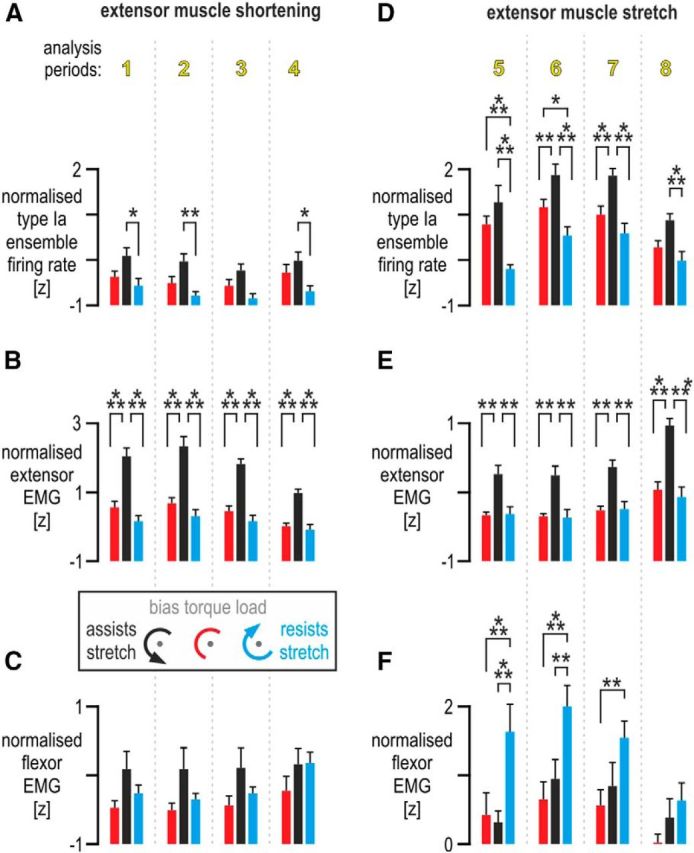
Analyses of afferent responses and muscle activity. A, The effect of bias load on standardized (i.e., z-transformed) firing rates across afferents (n = 9), during periods when the spindle-bearing muscle (extensor digitorum) was shortening (i.e., periods 1–4, as indicated in the middle of Fig. 5). Throughout, bars indicate mean values across afferents, and error bars represent 1 SEM. B, As in A but with regard to extensor muscle EMG. As expected, higher levels of extensor EMG were present throughout shortening when the bias load resisted extension (i.e., flexion was, overzealously, assisted; black bars). However, there were no significant differences in extensor EMG between the no bias load (red) and flexor bias load (blue) conditions throughout extensor shortening. C, As in B but pertaining to flexor EMG. No significant differences in flexor EMG were observed during extensor shortening. D, The effect of bias load on ensemble firing rates at each period during extensor muscle stretch (i.e., periods 5–8, as indicated in the middle of Fig. 5). E, As in D but pertaining to extensor digitorum EMG activity. The same differences were observed as in B. That is, higher levels of extensor EMG were present throughout extensor stretch when the extensor was loaded (i.e., flexion was assisted; black bars). However, there were no significant differences in extensor EMG between the no bias load (red) and flexor bias load conditions (blue) throughout extensor stretch. F, As in E but pertaining to flexor EMG. Throughout extensor stretch, there were no significant differences in flexor EMG between the no bias load (red) condition and the condition in which the bias load induced higher extensor activity levels (black bars). However, significantly higher flexor EMG was observed when the flexor muscle was loaded during extensor stretch (i.e., flexion resisted; blue bars), particularly during the initial two periods of extensor stretch (i.e., periods 5 and 6). *p < 0.05, **p < 0.01, ***p < 0.001.

Figure 4.

Single afferent responses from passive and active muscle. A, Cycle-averaged responses of two type Ia afferents (same as in Fig. 3) along with the simultaneously recorded kinematics of the moving finger, spindle-bearing muscle EMG, and net torque, when the passive middle finger was continuously moved about its MCP joint by the servo machine (n = 10 cycles). Although recorded at different times (i.e., before active movement in a particular bias load condition), the responses were very similar across conditions, indicating that the state of the muscle and that of the spindles were not substantially different at the different recording times so as to affect spindle behavior in a systematic way during the subsequent active movement. B, Cycle averages as in Figure 3, but here the subjects moved against an inertial load (rather than viscous) in addition to any bias loads experienced. Traces represent means across repetitions (n = 10), and shaded colored areas represent ±1 SEM. The same effects of bias load on afferent firing rates were seen as in Figure 3. In fact, discharges of afferent 5701 (left column) were higher during the initial 250 ms of stretch when no bias load was applied (red traces) compared with when a bias load opposed flexion (blue traces), although the former case (red) was characterized by noticeably lower stretch velocities and smaller joint angles overall. Recording from afferent 6401 (right column) lasted long enough to apply bias loads of two magnitudes, as well as of two directions. Although the 0.124 Nm bias load in the direction of muscle stretch was accompanied by even higher firing rates than the 0.062 Nm bias load of the equivalent direction (purple vs black trace, top right), firing rates were similarly low when either the flexion-resistive 0.124 Nm load (orange traces) or the equivalent 0.062 Nm bias load were applied (blue traces), regardless of even higher EMG activity levels when the 0.124 Nm load was experienced (yellow traces) compared with the EMG levels during the baseline no bias load condition (red traces). Some EMG traces in the right column are represented by thinner lines and are shown without the corresponding SEMs for visual clarity.

Custom sensors placed along the servo motor axis (an optical sensor and an electromagnetic induction sensor) provided the instantaneous joint angle and angular velocity estimates pertaining to the MCP joint of the moving finger, sampled at 2 kHz with a 16 bit resolution. The servo machine also produced an estimate of acceleration that was derived from angular velocity using a time constant of 16 ms.

Experimental paradigm.

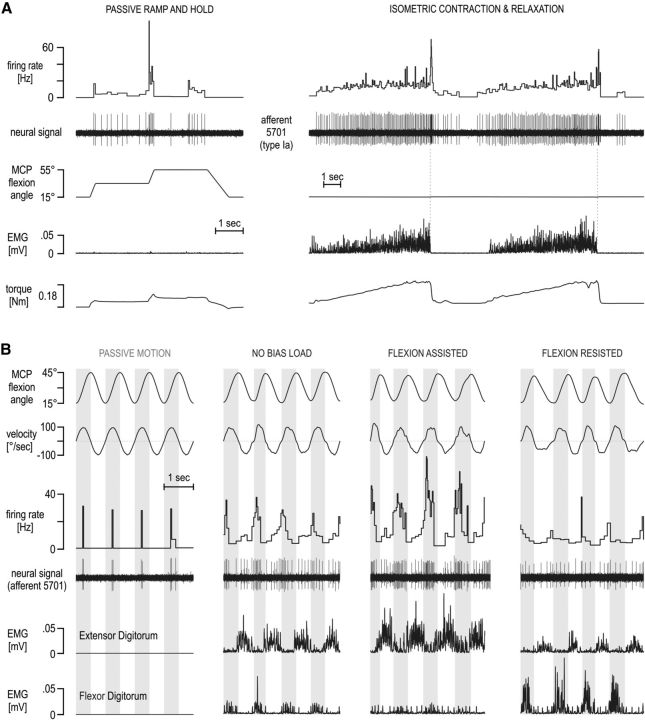
In the main task of this study, the activity of single muscle spindle afferents from the extensor digitorum muscle was recorded (see below, Spindle afferent recordings) along with surface EMG of relevant muscles, MCP joint torque, and kinematics, while fully alert human subjects continuously moved a finger to and from 15° and 45° of flexion at a required 1 Hz pace about the MCP joint (Fig. 1B). The particular finger used to conduct the task (i.e., finger chosen to attach to the servo) was the one that elicited the strongest responses in the isolated spindle afferent. Subjects received constant visual feedback on the location of their finger in the form of a vertical line moving horizontally across a monitor. The extremes of the required movement were also displayed in the form of vertical lines located at the lateral edges of the monitor. Movements were paced by an auditory metronome. Specifically, two clicks per cycle were heard, each coinciding with the time the finger ought to have been at one extreme of the required movement. A main feature of the experimental paradigm was maintaining the kinematic input to the spindles as similar as possible and varying only the experienced dynamics. Several measures contributed to keeping kinematics as similar as possible, such as requiring repetitive rhythmical movement, providing constant visual and auditory feedback, and using comparatively small viscous or inertial loads for movement damping (i.e., to limit potential tremor at the finger). Thus, the main experimental manipulation involved the application of an external bias torque during movement for differentially loading the extensor or flexor digitorum muscle (black and blue conditions in Fig. 1B, respectively), with a baseline condition in which no bias torque load was applied (Fig. 1B, red condition). Bias loads were not affected by ongoing kinematics.

Once the activity of a single afferent from the extensor digitorum was isolated in the radial nerve and the afferent was classified as a spindle type Ia (see below, Spindle afferent recordings), the subjects performed one block of trials without any bias torque load present. One trial “block” represented 10 passive (i.e., servo-led) movement cycles with the muscles relaxed, followed by 12 active movement cycles under no time-varying load, 12 cycles under an elastic load, 12 cycles under a viscous load, and then 12 cycles/trials under an inertial load. Because the “no time-varying load” and “elastic load” conditions were characterized by enhanced rather than dampened tremor at the finger, thus making kinematic profiles dissimilar, they were not used in the analyses or figures of this study. All time-varying loads were introduced gradually over two movement cycles. Because each block of trials involved continuous rhythmical movement of the same range and speed from start to finish, the data during the transitional loads (i.e., initial two cycles) were not included in this study. After the initial trial block in which no bias load was present, the subjects would then experience another trial block with an additional flexion-assistive (or flexion-resistive) bias torque load—present in all but the initial 10 passive movement cycles—and then another trial block with an additional flexion-resistive (or flexion-assistive) load. The presentation order of the bias load direction (i.e., flexion-resistive vs flexion-assistive) had no bearing on the reported results, because the two bias loads were experienced during practice, passive movements were performed for 10 s at the start of each block of trials, and the duration of each trial block was rather short (i.e., ∼40 s). For example, the reverse order of bias load presentation was used for the two afferents displayed in Figure 3 (obtained from two individual subjects), and the same main effects of bias load on afferent firing rate were observed. The subjects were allowed to take a small break between trial blocks if they wanted to (there was always a minimum delay of ∼10 s between trial blocks). The subjects practiced the main behavioral task before microneurography began for ∼10 min. Because of the simplicity and repetitive nature of the task, subjects attained proficiency quickly.

Figure 3.

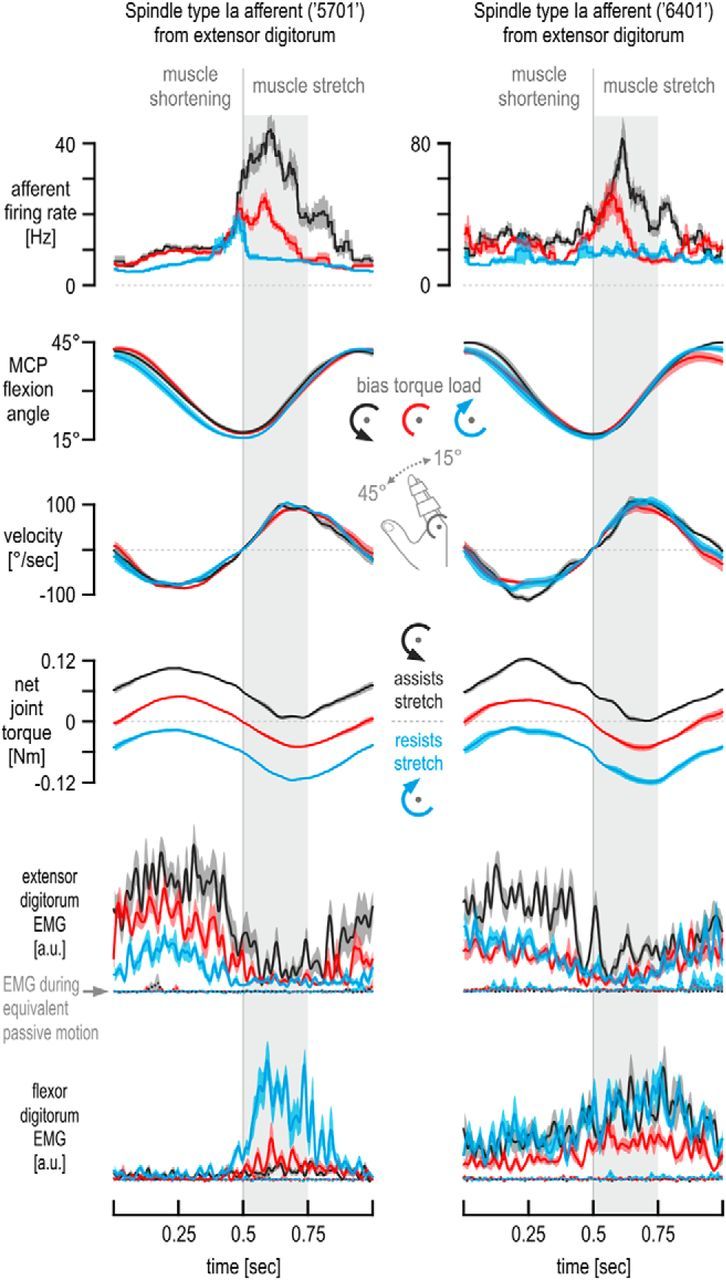
Exemplary spindle afferent responses across movement cycles. Responses of the afferent 5701 (also shown in Fig. 2) and of another type Ia afferent recorded from the extensor digitorum muscle of a different subject. Also shown are the simultaneously recorded EMG signals, MCP joint torque, and kinematics from the two individuals (left and right columns, respectively) from which each afferent was recorded. Each trace represents the average across 10 continuous movement cycles. Shaded colored areas represent ±1 SEM, and the coloring scheme is the same as in Figure 1B. In addition to any bias load, the same viscous load was experienced across all conditions for damping. Despite the very similar kinematics during the initial 250 ms of muscle stretch (gray background bars), large differences in afferent firing rate were observed as a function of bias load condition, with even no clear difference in extensor muscle EMG between the no bias load (red) and the bias load resisting flexion (blue) over most of this period. For comparison, extensor EMG during equivalent passive motion of the finger is also shown (dashed colored lines).

Spindle afferent recordings.

Single afferent spikes originating from muscle spindle receptors located in the common finger extensor muscle (extensor digitorum communis) were obtained using the technique of microneurography (Vallbo and Hagbarth, 1968) at the radial nerve of the right arm. Specifically, the radial nerve was impaled ∼5 cm proximal to the elbow joint using custom tungsten electrodes (200 μm shaft diameter, coated with a 25–30 μm layer of lacquer except for the distal 10–40 μm, with the distal 1 mm tapered to a 5–15 μm tip). The electrical impedance measured in situ at 1 kHz was normally 100–400 kΩ. Once inside the radial nerve, the position of the electrode was manipulated in small steps until single afferent spikes could be clearly isolated from background (mass) neural activity. By a combination of muscle palpation, ramp-and-hold stretches, passive muscle shortening, and isometric contraction–relaxation maneuvers (Fig. 2A), each recorded unit could be identified as an afferent originating from the extensor digitorum and distinguished from Golgi tendon organ and spindle type II afferents, as described in detail previously (Edin and Vallbo, 1990a,b). From the seven individual subjects participating in this study, nine type Ia spindle afferents were recorded (minimum of one type Ia afferent per subject, two subjects offered two afferents), with the activity of each afferent recorded over 100 movement cycles. Note that the amount of recorded afferents from a single muscle is typical for such type of study and that ensemble firing rates created using more than five spindle afferents are considered fair approximations of the underlying population responses (Prochazka, 1996, p 101). The context in which afferents were recorded in the current study (i.e., rhythmic movement) represents one of the fundamental behavioral paradigms in which spindle responses have been studied in the past (e.g., cat locomotion).

Figure 2.

Single afferent responses from a muscle spindle in the extensor digitorum. The neural activity in a single primary afferent (type Ia afferent 5701) from the common finger extensor muscle during afferent-type classification maneuvers (A) and sinusoidal movements of the middle finger (B) in different contexts. In A, the unit is classed as a primary (type Ia) afferent. It responded to stretch and was silent during muscle shortening (left). It also responded during isometric contractions and with a burst of spikes during sudden relaxation (right; 2 repetitions shown). In B, the signals include the angle and angular velocity at the MCP joint, flexor, and extensor digitorum electromyography (EMG). Vertical gray bars in the background indicate periods of flexion (i.e., extensor digitorum stretch). The same viscous load was experienced across all active movement for damping any potential tremor at the finger and so promoting similar kinematics across conditions. Despite similar kinematics across the four contexts above, higher discharge rates were seen when the bias load induced higher levels of activity in the spindle-bearing extensor muscle (flexion assisted) compared with the no bias load condition (i.e., red condition in Fig. 1B) and vice versa when higher flexor activity was induced during extensor stretch (flexion resisted; far right column). Note that the extensor (i.e., spindle-bearing) muscle EMG levels in both the no bias load and flexor bias load condition (flexion resisted) were similar during periods of extensor stretch, indicated by the vertical gray bars.

EMG recordings.

EMG was recorded from the common digit extensor and digit flexor muscles (extensor digitorum communis and flexor digitorum) from two compartments of each muscle, one pertaining to the index finger and one to the middle/ring finger. Isometric contraction/relaxation maneuvers and a hand-held muscle stimulator probe were used for identifying the optimal recording site for each compartment on each muscle. Two custom-built surface electrodes (2 mm diameter; 12 mm apart) were used for recording EMG activity from each muscle. The electrodes were coated with electrode jelly and attached to the skin at the optimal sites using double-sided adhesive tape. Although there was considerable overlap between the signals in each EMG electrode from compartments of the same muscle, the particular EMG channel/electrode used in the analyses/displays of each afferent was the one related to the moving finger, as designated before electrode placement. Because each experimental session normally lasted ∼5 h, the use of intramuscular EMG electrodes was not preferred.

Data sampling and processing.

The data were digitally sampled using SC/ZOOM. The neural signals were stored at 12.4 kHz after amplification close to the recording site (10,000×, 0.47–5.0 kHz bandwidth). Identification of single action potentials was made semiautomatically under visual control (Edin et al., 1988). Each EMG channel was root-mean-square processed with a rise time constant of 1.0 ms and a decay time constant of 3.0 ms and then digitally sampled at 1600 Hz. For display purposes alone, the EMG channels were low bandpass filtered with a fifth-order, zero-phase-lag Butterworth filter with a 40 Hz cutoff. Filtering did not change the nature of the EMG signals. Nevertheless, only unfiltered data were used for statistical analyses. To compare between EMG responses across subjects, the EMG signals were standardized (i.e., z-transformed) for each subject and each EMG channel separately, by using a single mean and a single SD value across all relevant single-trial data (i.e., across all data used for plotting and analyses) so that the differences in EMG across conditions were maintained (same technique used previously; Dimitriou and Edin, 2008a,b). The same standardization (z-transform) procedure was performed on spindle afferent discharge rates for contrasting spindle responses across afferents (see Figs. 5, 6). Because the normalized “ensemble” spindle responses emphasize the consistency of differences within single afferents across the bias load conditions, the z-transformation procedure was preferred for plotting and analyses (absolute discharge rates in single afferents may differ for relatively mundane reasons, such as the location of the spindle receptor within each muscle). Nevertheless, the effect of bias load can be clearly appreciated in terms of actual discharge rates, as well (Fig. 3). MATLAB (MathWorks) was used for creating data displays and performing data tabulations.

Figure 5.

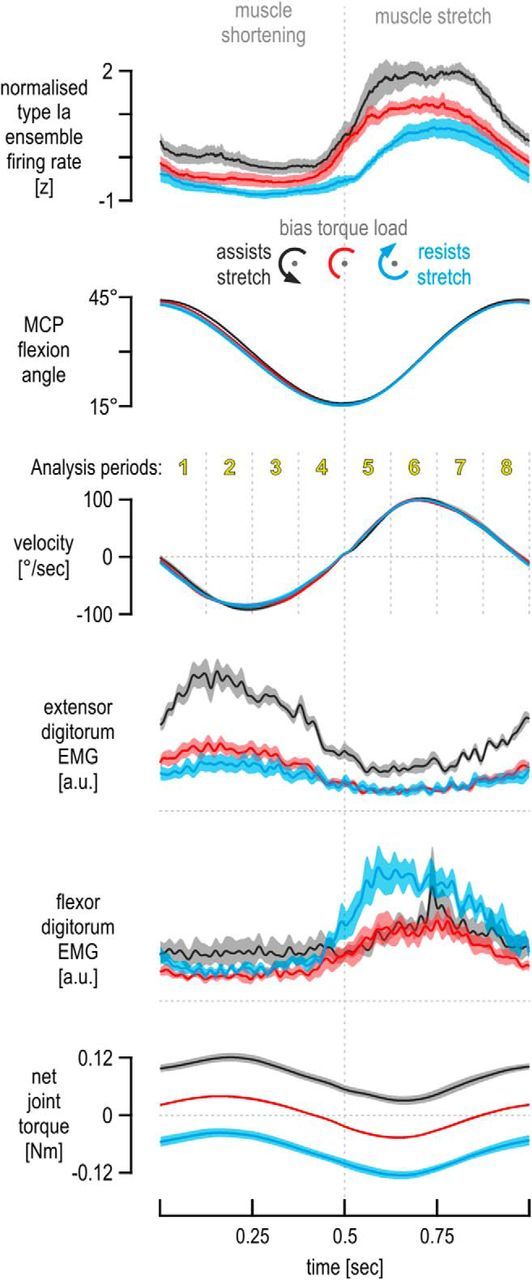
Responses across all spindle afferents. Responses across an ensemble of nine type Ia afferents from the extensor digitorum, recorded from seven individuals during repetitive finger movement. All traces represent means across afferents, and the shaded colored areas represent ±1 SEM. Despite identical kinematic profiles across bias load conditions, the same effects of bias load on the ensemble of standardized (i.e., z-transformed) firing rates were observed as in the single afferent case (Fig. 3). Note that the EMG levels of the spindle-bearing muscle (extensor digitorum) during its stretch were not noticeably different between the no bias load and flexion-resistive bias load conditions (red vs blue traces), despite the difference in their corresponding ensemble firing rate signals (top), which is particularly clear during the initial periods of stretch (i.e., periods 5 and 6). In contrast to the extensor EMG, there is a difference in flexor EMG between the two conditions, and this difference is particularly apparent over periods 5 and 6.

Statistics.

Cycle-averaged data (as shown in Fig. 3), after standardization (i.e., z-transform) at the level of the single afferent, were incorporated in a repeated-measures ANOVA under a 3 × 8 design (bias load condition × analysis period) on a per-afferent basis (i.e., n = 9). Each of the eight analysis periods corresponded to a time window of 125 ms. A separate ANOVA of the same 3 × 8 design was performed for each investigated variable with n = 9 in all cases, except flexor EMG (n = 7), because of noise in the relevant EMG channel of a single subject. In addition to the repeated-measures ANOVA tests, multi-linear regressions were conducted to reproduce firing rate responses of either the afferent ensemble (see Figs. 7, 8) or of single afferents (see Fig. 9). At the ensemble level, the regressions were forward stepwise (see Figs. 7, 8) to attempt to isolate the factors shaping ensemble responses, whereas simple multi-linear regressions were conducted at the single afferent level to ensure a coefficient for each predictor variable, the effect of which would then be averaged across afferents (see Fig. 9B). Equivalent results were obtained at the single afferent and afferent ensemble level. Across all regressions, the independent variables (i.e., predictors) included the kinematic signals (MCP joint angle, angular velocity, and acceleration) and extensor and flexor EMG, and, on identified occasions (see Fig. 7A,B, right columns), the recorded net torque around the MCP joint was also used as an additional predictor. The data used for each regression were cycle averages (i.e., mean traces as per Fig. 3) that were downsampled with 50 ms moving windows, that is, sampled at 20 Hz leading to 20 data points per representative cycle: 3 bias loads × 20 = 60 data points in total per variable. The 20 Hz sampling rate was found previously to allow a good representation of underlying kinetic and kinematic signals during voluntary movement at naturally occurring or “normal” everyday speeds, while avoiding inflated p values attributable to autocorrelations in the signals (Dimitriou and Edin, 2008a,b).

Figure 7.

Factors affecting afferent ensemble responses. A, Left column, β coefficients of the variables found to significantly contribute in reconstructing ensemble discharge rates after a forward stepwise regression (all variables shown in Fig. 5 and angular acceleration used as predictors, except net torque). Right column, as in the left column but the measured net torque was also used as an additional predictor variable. B, As in A, but only data during extensor muscle stretch was used, i.e., data over periods 5–8, as indicated in Figure 5. C, Correlation between flexor digitorum EMG evident during extensor stretch and extensor EMG present during stretch and at various periods in the past. There was a weak relationship between flexor EMG during extensor stretch and concurrent extensor EMG (r = 0.42). The relationship became progressively weaker as flexor EMG evident during stretch was correlated with lagged extensor EMG. Error bars in A and B represent 95% confidence intervals.

Figure 8.

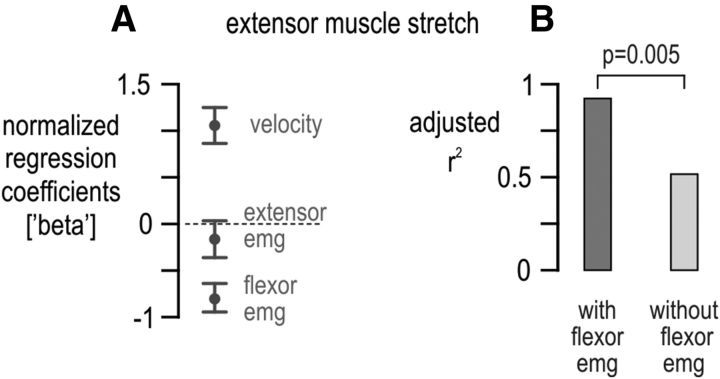
The effect of flexor activity on extensor spindle output. A, As in Figure 7B, but here only data across the no bias load and flexion-resistive bias load conditions were used (i.e., blue and red conditions indicated in Fig. 1B). Only angular velocity and flexor EMG had a significant effect on extensor spindle output, with flexor activity exerting a negative effect. B, The dark gray bar represents the accounted-for variance in afferent ensemble firing rate (i.e., adjusted r²) resulting from the regression in A, and the light gray bar is the equivalent of the dark gray bar but having not included flexor EMG as a predictor in the regression. The two bars in B differed significantly (p = 0.005). Error bars in A represent 95% confidence intervals.

Figure 9.

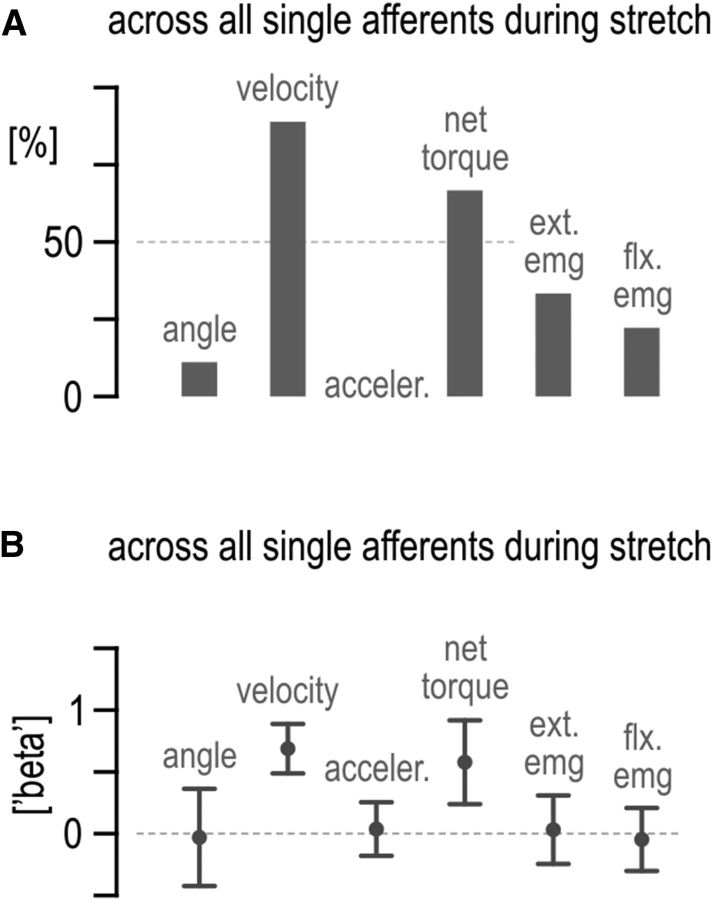
Factors affecting single afferent responses. A, Percentage of single afferents significantly affected by each predictor variable during extensor muscle stretch. One multi-linear regression per afferent was performed to reconstruct the observed afferent firing rates. B, Average of all (both significant and insignificant) β regression coefficients corresponding to A. Error bars in B represent 95% confidence intervals. acceler., Acceleration; ext., extensor; flx., flexor.

Holm–Bonferroni-corrected α values were used for designating each coefficient as significant within each regression equation (i.e., accounting for the number of multiple predictor variables used simultaneously). Only adjusted r² values are reported that compensate for the number of predictor variables used in a regression. To also account for the number of pairwise comparisons after each ANOVA test, Tukey's HSD test was used for all post hoc analyses. The statistical significance level used in the study was 0.05, before any correction for familywise error. All statistical tests were implemented in either MATLAB (MathWorks) or Statistica (StatSoft).

Results

To investigate the hypothesis that spindle sensitivity reflects the balance of activity between antagonistic muscles, I recorded spindle afferent responses from the common finger extensor muscle while fully alert human subjects performed continuous movements of a single finger under constant external loads (Fig. 1B). These constant (bias) loads were designed to preferentially load either the spindle-bearing extensor muscle or its antagonist. Because the kinematic input to the spindles was expected to be essentially the same across load conditions in the current paradigm (Fig. 1B), any systematic difference in spindle output across conditions captured changes in spindle sensitivity (i.e., output gain). Because fusimotor control was expected to reflect the balance in antagonistic muscle activity (Fig. 1A), it was predicted that flexing the finger against a resistive bias load will produce lower firing rates in spindle afferents of the stretching extensor compared with performing the same movement with no bias load and vice versa for finger flexion under an assistive bias load (Fig. 1B, bottom schematic).

Figure 2 shows exemplary responses of a muscle spindle primary afferent (type Ia afferent 5701) from the extensor digitorum muscle. Figure 2A shows some of the afferent classification maneuvers performed. As expected from a type Ia spindle afferent, there were prominent responses during stretch of the spindle-bearing muscle (i.e., during finger flexion), the afferent was silent during muscle shortening, and its firing showed no stable relationship with static muscle length (Fig. 2A, left). The afferent also responded during periods of isometric contraction of the spindle-bearing muscle, and a burst of spikes was evident during sudden muscle relaxation (Fig. 2A, right). The relaxation burst further indicates that the afferent is a spindle type Ia rather than type II or type Ib. Figure 2B shows responses of the same afferent when the finger was continuously moved about the MCP joint, as required by the main task of this study. This movement was performed passively when the subject was relaxed (the finger was moved by the servo; Fig. 2B, far left column) and actively against all bias load conditions. Despite the similar kinematics across experimental (i.e., bias load) conditions, clear differences in afferent discharge rates can be seen. Note that the levels of extensor muscle activity during extensor stretch are similar in the flexion-resisted and no bias load cases (periods of stretch indicated by vertical gray bars in Fig. 2B), whereas flexor activity clearly differs between the two conditions. Figure 3 shows the cycle-averaged responses of the same afferent (5701; left column) and of afferent 6401 (right column; recorded from a different subject) when the middle finger was continuously moved about the MCP joint (for cycle-averaged responses during passive movement, see Fig. 4A). Despite the very similar kinematics across the bias load conditions during the initial 250 ms of extensor stretch, clearly higher type Ia firing rates were observed when the external bias load induced higher levels of extensor muscle activity during muscle stretch (i.e., assisted flexion/stretch) compared with the baseline case of no bias load (Fig. 3, top, black vs red traces). The opposite effect was evident when the external bias load induced higher levels of flexor activity during stretch (i.e., flexion/stretch was resisted; Fig. 3, top, blue vs red traces). For the latter two conditions (red and blue), there was little difference in EMG activity of the spindle-bearing extensor muscle during the initial 250 ms of extensor stretch, particularly so for afferent 6401 (i.e., differences in spindle responses presumably not only attributable to the state of the spindle-bearing muscle alone). Similar effects of bias load on spindle firing rates were seen when the subjects encountered an inertial rather than a viscous background load for movement damping (Fig. 4B). Therefore, for all statistical analyses, responses of the same afferents were collapsed across viscous and inertial loads.

The same effects of bias load on spindle afferent responses were evident at the level of the afferent population (Fig. 5). The observed differences in afferent responses were confirmed as significant through a 3 × 8 repeated-measures ANOVA (i.e., bias load condition × analysis time period). Significant differences in spindle afferent output were observed primarily during muscle stretch (Fig. 6A,D). The same 3 × 8 ANOVA design was used to examine whether the bias load condition influenced joint angle, angular velocity, or acceleration. As expected by inspecting Figure 5, there was no significant effect of bias load condition on any of the kinematic signals during the muscle stretch periods 5–8 that could account for the differences in spindle firing rates evident during these periods (Fig. 6D). However, the same ANOVA design indicated significant differences in extensor and flexor EMG across bias load conditions, which in turn suggested a positive effect of extensor EMG and a negative effect of flexor EMG on spindle afferent responses from the extensor muscle during its stretch, as predicted by the antagonistic muscle balance hypothesis (Fig. 6E,F). The following two paragraphs describe all ANOVA results in detail.

The ANOVA of normalized (i.e., z-transformed) responses across afferents (Fig. 6A,D) indicated a significant main effect of bias load (F_(2,16) = 29.01, p < 10⁻⁵). Tukey's HSD post hoc test indicated significantly higher firing rates when finger flexion was assisted rather than resisted by the bias load (i.e., extensor stretch assisted rather than resisted, black vs blue bars, respectively, p = 0.00017) or when no bias load was applied (i.e., black vs red bars, p = 0.002). There was also an overall decrease in firing rates when flexion was resisted compared with the baseline case of no bias load (i.e., blue vs red bars, p = 0.009). The ANOVA also yielded a significant interaction effect between bias load condition and analysis period (F_(14,112) = 2.7, p = 0.002). As Figure 5 suggests, Tukey's HSD test indicated that significant differences in discharge rate occurred mainly during extensor muscle stretch rather than shortening (Fig. 6D,A, respectively). Specifically, during the initial 125 ms of extensor stretch (Fig. 6D, period 5), significantly lower spindle firing rates were observed when the bias load resisted extensor stretch (blue) compared with when the bias load assisted stretch (blue bar vs black bar, p = 0.0002) or when no bias load was applied (blue bar vs red bar, p = 0.0002). However, despite clearly higher extensor EMG when the extensor was loaded in period 5, there was no significant difference in discharge rates between the extensor load and the baseline case of no bias torque (Fig. 6D, period 5, black vs red bar, p = 0.36). In analysis period 6, there was a significant difference in afferent firing rates between the no bias load (red) and flexion-resistive bias load (blue), with red > blue (p = 0.047). There were no other significant differences in discharge rate between the above two conditions during periods 7 and 8. Discharge rates under the bias load inducing higher levels of extensor muscle activity (black) were significantly higher than both other load conditions in periods 6 and 7 (p < 0.001; Fig. 6D). During analysis period 8, discharge rates under extensor muscle loading were also significantly higher than those evident when the flexor was loaded (i.e., black > blue, p = 0.0003).

Applying the same ANOVA design on extensor EMG (Fig. 6B,E) yielded a significant main effect of bias load (F_(2,16) = 26.8, p < 10⁻⁴). As expected, Tukey's HSD indicated higher EMG activity under the bias load inducing extensor activity compared with the other two loads (p < 0.0003). However, there was no significant main difference in extensor EMG between the no bias load and flexor bias load conditions (blue vs red, p = 0.65); this was clearly the case across all analysis periods, during both extensor muscle shortening (Fig. 6B) and muscle stretch (Fig. 6E). In contrast, extensor muscle EMG was significantly higher in the flexion-assistive black condition compared with the other two conditions, across all eight analysis periods. The same ANOVA design gave no significant main effect of bias load on flexor EMG (F_(2,12) = 2.46, p = 0.18), but there was a significant interaction effect between bias load and analysis period (F_(14,84) = 4.99, p < 10⁻⁵). Tukey's HSD indicated no effect of bias load on flexor EMG across the extensor muscle-shortening periods 1–4 (Fig. 6C). However, significantly higher flexor EMG was observed when the flexor muscle was loaded during extensor stretch (blue condition) compared with both other bias load conditions, with particularly large differences seen during the initial two periods of extensor stretch (Fig. 6F, p < 0.0003 for period 5 and p < 0.003 for period 6).

The ANOVA results indicated that the direction of external bias loads (i.e., different categorical states of agonist/antagonist balance) influence spindle afferent output during movement, and this spindle behavior cannot be accounted for by differences in kinematics and/or spindle-bearing muscle EMG alone (see period 5 across Fig. 6D–F). To test whether spindle afferent responses reflect the instantaneous balance between antagonistic muscle activity, the kinematic signals shown in Figure 5 (in addition to angular acceleration) and extensor and flexor digitorum EMG were entered as predictor variables in a forward stepwise regression to reproduce ensemble afferent discharges (for more details, see Materials and Methods). A very good reproduction of ensemble afferent responses was achieved (Fig. 7A, left column, adjusted r² = 0.90, p < 10⁻⁵). As Figure 7A shows, angular velocity (i.e., representing the influence of the rate of change of muscle length on spindle afferents) was found to have a strong relative effect on spindle output (β regression coefficient = 1.53, p < 10⁻⁵). However, spindle-bearing (i.e., extensor) and flexor EMG were also found to exert a significant and substantial effect on afferent firing rate, with the latter exerting a negative influence (β = 0.55, p < 10⁻⁵ and β = −0.48, p < 10⁻⁵, respectively). There was also a small effect of acceleration on ensemble responses (β = 0.12, p = 0.007). Adding measured net torque (force) as a predictor in the above stepwise regression yielded velocity and net torque as the only variables with a significant effect on spindle discharge rates (Fig. 7A, right column, adjusted r² = 0.94, p < 10⁻⁵). This replacement of extensor and flexor EMG by the measured net torque validates the EMG measurements as fair approximations of levels of muscle activity during movement in this task.

Performing a forward stepwise regression using data during extensor stretch alone produced similarly good results when using kinematics and EMGs (adjusted r² = 0.90, p < 10⁻⁵), but the relative effect of velocity versus muscle activity was more equal in this case (Fig. 7B, left column; β = 1.1, β = 0.59, and β = −0.54 for velocity, extensor, and flexor EMG, respectively, all p < 10⁻⁵). There was also a significant but relatively small effect of acceleration on ensemble responses (β = 0.19, p = 0.007). Adding net torque as a predictor of ensemble firing rates again produced a good reconstruction ensemble responses (adjusted r² = 0.94, p < 10⁻⁵), but this time it revealed no significant difference in the effect of velocity (β = 0.74, p < 10⁻⁵) versus net torque (β = 0.9, p < 10⁻⁵) on spindle responses, with p = 0.12 (Fig. 7B, right column). The relatively strong effect of net joint torque on ensemble responses provides additional support for the antagonistic balance hypothesis and highlights that spindle sensitivity (gain) to stretch can be adjusted according to prevalent single joint dynamics rather than to the activation state of an individual muscle alone. Moreover, using only kinematic signals in the stepwise regression pertaining to extensor stretch led to a much weaker reproduction of afferent responses (adjusted r² = 0.34, p = 0.0005), with only velocity found to be a significant predictor of discharge rate (β = 0.60, p = 0.0005).

The antagonistic muscle balance hypothesis proposes that the strong effect of net joint torque on ensemble responses during muscle stretch is secondary to the effect of antagonistic muscle activity on spindle sensitivity. Indeed, in the current study, the results show a positive relationship between extensor muscle activity and extensor spindle sensitivity and a concurrent negative relationship between flexor muscle activity and extensor spindle sensitivity (Fig. 7A,B). Although contrary to a strict interpretation of α–γ coactivation (Vallbo, 1970), it is possible that, in the current study, extensor muscle activity levels evident during extensor shortening might systematically account for a substantial portion of the differences in spindle afferent responses during subsequent extensor stretches (but note that there was little and no significant difference in extensor EMG during extensor shortening between the blue and red conditions; Fig. 5). If the above conjecture is true, then the instantaneous variance displayed by the flexor EMG during extensor stretch (across all load conditions) should relate rather closely to the extensor EMG signal evident sometime in the past. Figure 7C shows that this does not hold. Specifically, the weak relationship between flexor and concurrent extensor EMG activity evident during stretch (r = 0.42, lag time = 0; Fig. 7C) becomes weaker (and approaches r = 0) as a more backward-lagged version of extensor EMG is used in the correlation. The above finding is an additional indication that the inhibitory effect of flexor activity on extensor spindle sensitivity is not simply an epiphenomenon secondary to either preceding or concurrent extensor muscle activity.

The effect of agonist muscle activity on antagonist spindle sensitivity becomes even clearer when preferential loading of the antagonist muscle is not included in the regression analyses. That is, if data relating to preferential extensor loading is excluded from the stepwise regression aiming to reconstruct ensemble firing rates during extensor stretch (i.e., if only baseline red and flexor-resist blue conditions are used in the regression; Fig. 1B), extensor muscle activity has a negligible (and insignificant) effect on extensor spindle output, whereas flexor activity accounts for ∼40% of the variance in the spindle responses (Fig. 8). Last, the same predictor variables used in the ensemble regressions (kinematics, EMGs, and net torque) were used to reconstruct single afferent firing rates evident across all bias loads (i.e., one simple multiple regression per afferent). For the majority of afferents, both angular velocity and net torque were found to exert a significant and sufficiently strong effect on spindle firing rate during muscle stretch (Fig. 9).

Discussion

The current study shows that muscle spindle sensitivity (gain) to stretch reflects the balance of activity between antagonistic muscles (i.e., “antagonistic muscle balance”). Specifically, activity in the stretching antagonist muscle was found to exert a positive effect on the sensitivity of its spindles, as predicted by the α–γ coactivation hypothesis (Vallbo, 1970; Kakuda and Nagaoka, 1998). However, in addition to the above effect, a negative relationship was found between agonist muscle activity and antagonist spindle sensitivity, presumably attributable to reciprocal inhibition of spindle controllers (i.e., reciprocal inhibition of fusimotor drive, concurrent to any positive effect of α–γ coactivation). The influence of antagonistic muscle balance on spindle output was also expressed in terms of a strong relationship between spindle responses and joint torque; this relationship was evident at both the single afferent and afferent ensemble levels (Figs. 7, 9). In what follows, I argue that existing alternative explanations of fusimotor function cannot account for the present findings and also discuss the implications of the current results in terms of the role of the spindle in reflex feedback control and proprioception.

The current study demonstrates clear differences in spindle firing rates across conditions characterized by identical repetitive kinematics (Fig. 5). Therefore, the current findings challenge the view that the primary spindle receptor in the antagonist muscle signals actual limb position or speed during movement (alternative sources of such kinematic information do exist; Proske and Gandevia, 2009). That is, to extract such kinematic information from primary spindles across contexts, the CNS must account for the combined effect of agonist and antagonist activity on spindle sensitivity to stretch. The demonstrated effects of antagonistic muscle balance on spindle sensitivity are presumed to primarily reflect changes in dynamic fusimotor drive. Existing hypotheses of spindle and fusimotor function cannot account for the differences in spindle firing rates demonstrated across identical kinematics and identical task goals in the current study (Fig. 5). Specifically, alternative explanations of fusimotor function (for review, see Prochazka and Ellaway, 2012) predict no difference in muscle spindle responses across bias load conditions, because the intended/executed movement profiles were essentially the same throughout (e.g., tonic and phasic γ activation hypothesis; Taylor et al., 2000) as were task goals and, presumably, alertness levels as well (e.g., fusimotor set hypothesis; Prochazka et al., 1985). Even the recent forward sensory model hypothesis (Dimitriou and Edin, 2010), which holds that spindles encode future kinematic states, cannot account for differences in spindle responses across conditions with known loads/dynamics and identical repetitive kinematics (i.e., future kinematic states were also the same across the bias load conditions). In fact, it is unclear how the above hypothesis can account for the negative relationship between skeletomotor activity in an agonist and spindle output from its stretching antagonist, because increasing agonist activity would normally entail an increased likelihood of faster antagonist stretch in the near future. Last, the antagonistic muscle balance hypothesis proposed in the current study ascribes a role for α–γ coactivation beyond maintaining the responsiveness of spindles to stretch and assumes that no active learning of independent fusimotor control is required, contrary to the forward sensory model hypothesis (Dimitriou and Edin, 2010).

In addition to the effects of agonist and antagonist activity on spindle afferent responses in the current study, angular velocity also had a strong effect on spindle output, with joint angle having essentially no effect and angular acceleration only a small effect (Fig. 7A,B). Previous studies have also shown that changes in joint angle (i.e., muscle length) have a negligible effect on spindle type Ia responses during active movement, although both velocity (i.e., first derivative of muscle length) and acceleration do affect spindle output substantially (Dimitriou and Edin, 2008a,b). However, the current study was not meant to tease out any effect of acceleration on spindle afferents. On the contrary, the current analyses concentrated on data in which high accelerations were actively prevented by applying a viscous or an inertial load during movement to maintain finger kinematics as similar as possible across the experimental conditions (i.e., prevent finger tremor). It should be noted that recent modeling efforts indicate that appropriate modulation of fusimotor activity may be capable of inducing a phase advance in the responses of spindles to velocity, thereby giving rise to a signal that reflects acceleration (Grandjean and Maier, 2014).

Muscle spindles have been characterized as “multifunctional” (Windhorst, 2007, 2008), and they have been proposed to play major roles in proprioception (Goodwin et al., 1972; Roll and Vedel, 1982) and reflex feedback control (Houk, 1976; Sinkjaer et al., 1988). A large body of recent work has emphasized the task-dependent sophistication of rapid motor (i.e., reflex) responses, revealing the highly flexible nature of long-latency feedback gains (for review, see Shemmell et al., 2010; Pruszynski and Scott, 2012). However, unlike the gains of the longer-latency stretch reflexes found to modulate according to dynamic interactions across multiple joints (Kurtzer et al., 2008; Pruszynski et al., 2011), the gain of the monosynaptic stretch reflex is proposed to vary only according to the pre-perturbation activity levels of the stretched muscle, a phenomenon termed “gain-scaling” (Marsden et al., 1976; Pruszynski et al., 2009). In addition to providing evidence that gain-scaling can partly depend on heightened spindle responses (in addition to any increases in excitability of α motor neurons), the current study suggests that the short-latency reflex gain may reflect the balance in activity across antagonistic muscle pairs; that is, it may reflect the prevalent dynamics around a single joint (i.e., net torque; Fig. 7A,B, right columns). If so, then the monosynaptic stretch reflex may represent the initial output in a progression of increasingly sophisticated motor responses tailored for acting in joint dynamic space.

It has been recognized long ago that the ability to distinguish between self-generated and externally generated sensory events is crucial for accurate perception and motor control (von Helmholtz, 1867; Sperry, 1950; von Holst and Mittelstaedt, 1973). The dominant account of how this distinction is made is provided by the “comparator model” (Frith et al., 2000; Carruthers, 2012), which is itself based on notions of internal predictive or “forward” models of the sensory consequences of its own actions (Wolpert et al., 1995; Wolpert and Ghahramani, 2000). According to the comparator model, if a movement is self-produced, internal predictive signals and incoming sensory signals should cancel out (i.e., “sensory cancellation” is performed), whereas any resulting discrepancy between the two information streams reveals the component of the sensory signal caused by an external source (i.e., “exafference”; von Holst and Mittelstaedt, 1973). Based on the above framework, it has been further suggested that a reduction of proprioceptive feedback or awareness during limb movement should indicate that it is the self who was the cause (or the “agent”) of movement (Frith, 2005). This is compatible with the findings of the current study; that is, the demonstrated inhibitory effect of agonist activity on antagonist spindle sensitivity may also contribute to the sensory cancellation of movement (i.e., antagonist stretch) that is powered by agonist activity. This sensory cancellation scheme of antagonist stretch does not require comparisons with the predictions of an internal model. Therefore, it might serve as a first line of “treatment” of the proprioceptive sensory signal that can occur even in novel or otherwise unpredictable environments (in which internal predictions are lacking or outdated). Interestingly, enhanced spindle afferent responses are expected if the same antagonist stretch occurs when the antagonist muscle itself is predominantly active (attributable to α–γ coactivation); predominant levels of antagonist activity during antagonist stretch means that muscle stretch must have occurred as a result of a force other than that produced by the agonist (i.e., antagonist stretch is imposed). The ability of the spindle to respond preferentially to imposed rather than agonist-generated muscle stretch should also facilitate their function in negative feedback control. That is, reflex feedback responses should scale in a functionally optimal way according to the cause (or agent) of stretch. Amplified spindle and monosynaptic reflex output is expected when antagonist stretch is imposed, whereas weaker stretch reflex output is expected during voluntary (i.e., agonist-generated) antagonist stretch.

In summary, the current study shows that, as a consequence of efferent control, muscle spindle sensitivity to stretch reflects the balance of activity between antagonistic muscles. Specifically, activity in the stretching antagonist muscle has a positive effect on the sensitivity of its spindles, whereas agonist muscle activity has a negative effect on antagonist spindle sensitivity. The sensitivity of the spindles to antagonistic muscle activity suggests that the monosynaptic reflex gain may in fact reflect the prevalent dynamics around a single joint rather than the activation state of the stretched muscle alone. In addition, the inhibitory effect of agonist activity on antagonist spindle sensitivity may facilitate online sensory cancellation of antagonist stretch, thereby also preventing or otherwise limiting counteractive stretch reflex output during voluntary movement.