A Contrast and Surface Code Explains Complex Responses to Black and White Stimuli in V1

Abstract

We investigated the cortical mechanisms underlying the visual perception of luminance-defined surfaces and the preference for black over white stimuli in the macaque primary visual cortex, V1. We measured V1 population responses with voltage-sensitive dye imaging in fixating monkeys that were presented with white or black squares of equal contrast around a mid-gray. Regions corresponding to the squares' edges exhibited higher activity than those corresponding to the center. Responses to black were higher than to white, surprisingly to a much greater extent in the representation of the square's center. Additionally, the square-evoked activation patterns exhibited spatial modulations along the edges and corners. A model comprised of neural mechanisms that compute local contrast, local luminance temporal modulations in the black and white directions, and cortical center-surround interactions, could explain the observed population activity patterns in detail. The model captured the weaker contribution of V1 neurons that respond to positive (white) and negative (black) luminance surfaces, and the stronger contribution of V1 neurons that respond to edge contrast. Also, the model demonstrated how the response preference for black could be explained in terms of stronger surface-related activation to negative luminance modulation. The spatial modulations along the edges were accounted for by surround suppression. Overall the results reveal the relative strength of edge contrast and surface signals in the V1 response to visual objects.

Introduction

A key feature of neurons in the primary visual cortex (V1) cortex is their response to spatial contrast (De Valois and De Valois, 1988; Friedman et al., 2003). Most neurons in V1 respond best to some intermediate spatial frequency and produce weaker responses to a spatially uniform field (De Valois and De Valois, 1988). However, there is also neurophysiological evidence for surface-responsive neurons in V1 that convey information about luminance modulation within regions of the visual field (Kinoshita and Komatsu, 2001; Peng and Van Essen, 2005; Roe et al., 2005; Dai and Wang, 2012).

Luminance surfaces can be black or white. Electrophysiological evidence has been accumulating indicating that many neurons in V1 are more sensitive to black stimuli (negative contrast) than to white stimuli (positive contrast). The black–white difference was found first in visually evoked human EEG responses (Zemon et al., 1988, 1995). More recent neurophysiological studies of single-cell activity in nonhuman primates (Yeh et al., 2009; Xing et al., 2010) found that layer 2/3 neurons responded better to small, localized black spots than to white spots, and also that neurons preferring black outnumbered neurons preferring white stimuli. Others also have observed larger black responses in V1 (Jin et al., 2008; Kremkow et al., 2014). The physiological data on black–white preferences are consistent with data from human perceptual experiments (Chubb and Nam, 2000; Chubb et al., 2004).

The relative contributions of edge-contrast processing and local surface processing to the cortical representations of black and white surfaces remain unresolved. Therefore, our motivation in the present study was to investigate V1 population responses to black and white square surfaces that include both stimulus components: edge-contrast and surface at squares' center. To do so, we measured the spatiotemporal activity pattern evoked in V1 by black and white squares with voltage-sensitive dye imaging (VSDI). Monkeys trained on a fixation task were presented with either a white square or a black square against a gray uniform background.

Black and white square surfaces both evoked a square-like spatial activity pattern in V1. The responses showed marked variation with location in the evoked pattern. The voltage-sensitive dye (VSD) response in regions corresponding to the edges was much larger than in regions corresponding to the center of the square. Edge responses were slightly higher for the black than for the white squares, but center responses evoked by black were substantially larger than for white stimuli. We developed a model that could explain the VSD data. The model was comprised of neural populations that computed local contrast at the edges, and that compute local temporal luminance modulation (LTLM) in the black and white directions. Such LTLM-responsive neuronal populations could perform surface processing in V1. In addition the model included cortical center-surround interactions that account for the greater responsiveness at the corners of the squares.

Materials and Methods

Visual stimulation and experimental setup

Visual stimuli were presented on a 21 inch Mitsubishi monitor at a refresh rate of 85 Hz. The monitor was located 100 cm from the monkey's eyes. Stimuli were centered at eccentricity 1.5–3.25° below the horizontal meridian and 1.2–2° from the vertical meridian. To generalize the results, the visual field positions of the stimuli varied across imaging sessions and across monkeys, covering most of the visual field area whose retinotopic projection falls within our imaging chamber. The variations of the visual field positions kept the informative features (square center or square edges) within the imaged area. Two linked personal computers managed visual stimulation, data acquisition, and controlled the monkey's behavior. We used a combination of imaging software (MiCAM ULTIMA) and the NIMH-CORTEX software package. The behavior PC was equipped with a PCI-DAS 1602/12 card to control the behavioral task and data acquisition. The protocol of data acquisition in VSDI has been described previously (Slovin et al., 2002). To remove the heartbeat artifact, we triggered the VSDI data acquisition on the animal's heartbeat signal (see below, VSD data analysis and in Slovin et al., 2002).

Behavioral task and visual stimuli

Two adult male Macaca fascicularis (13 and 12 kg) were trained on a simple fixation task. Monkeys fixated before and during stimulus presentation. Prestimulus duration was varied randomly between 3 and 4 s, at the end of which, while monkeys maintained fixation, the stimulus was turned on for 300 ms. The monkey was required to maintain tight fixation throughout the whole trial and was rewarded with a drop of juice for each correct trial. During the stimulus presentation fixation was within ±1° around the fixation point. Stimulated trials were interleaved with blank trials, in which the monkeys fixated but no visual stimulus appeared.

Visual stimuli for the black and white squares experiments were black and white squares sized 2 × 2° presented against a gray background. The luminance of the white and black squares was adjusted to generate the same contrast magnitude. Background luminance was 33–37 cd m⁻² for most sessions (in a few sessions background luminance values were 9–15 cd m⁻²). Squares' luminance values were varied to generate Weber contrast values of 4, 8, 16, 64, 74, and 78% for the white square and −4, −8, −16, −64, −74, and −78% for the black square. On each trial, only one square (either black or white) was shown (Fig. 1A). Visual stimuli for model validation were a high-contrast square contour (2 × 2°, −100% contrast), a high-contrast square surface (2 × 2°, −80% contrast), and a large square surface (8 × 8°, −80% contrast). For a detailed description of the experimental setup see Ayzenshtat et al. (2012) and see above, Visual stimulation and experimental setup.

Figure 1.

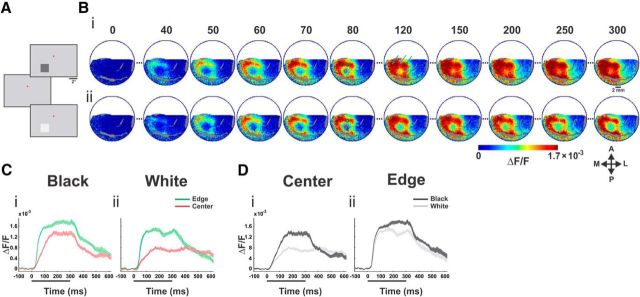
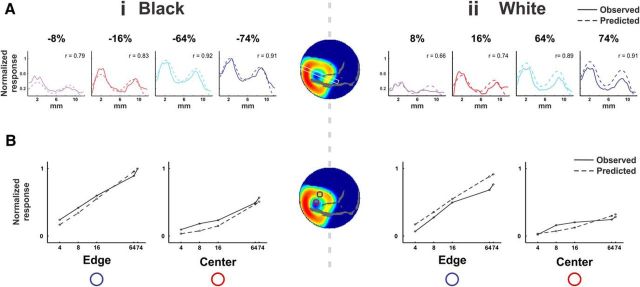
Spatiotemporal response of VSD signal evoked by black/white stimuli. Population responses to black and white square stimuli from one example imaging session. A, Following fixation on a uniform gray screen, a 2 × 2° square appeared. In the current example, the stimuli were centered at 1.75° left of the fixation point (red dot) and 3.0° below. The squares had either negative contrast (“Black,” −64%) or positive contrast (“White,” +64%) with respect to the background luminance. B, Average VSD activation maps evoked by a 300 ms presentation of black stimulus (Bi) and white stimulus (Bii); n = 12 trials. Big blood vessels are colored in gray (here and in all other figures). Numbers correspond to milliseconds after stimulus onset. The arrows (map at t = 120) point to the spatial modulation in the upper and right edges. The three green arrows point to the evoked neural response at the corners and the two cyan arrows point to the evoked response at the edge middles of the square stimulus. A, anterior; P, posterior; M, medial; L, lateral. C, Time courses of the evoked population response for the black (Ci) and white (Cii) stimulus. Time courses are computed for ROIs (depicted in B, on the map at t = 80, red and green circles) located at the center and at the edge of the evoked pattern. Trace width denotes ±1 SEM over trials. Stimulus duration is denoted by a black bar below the x-axis. D, Same as in C but grouped by center ROI (Di) and edge ROI (Dii) for comparison between the black and the white responses.

Surgical procedures and voltage-sensitive dye imaging

The surgical, staining and imaging procedure have been reported in detail previously (Arieli et al., 2002; Slovin et al., 2002). All experimental procedures were approved by the Animal Care and Use Guidelines Committee of Bar-Ilan University, supervised by the Israeli authorities for animal experiments, and conformed to the NIH guidelines. Briefly, the monkeys were anesthetized, ventilated, and an intravenous catheter was inserted. A head holder and two cranial windows (25 mm inner diameter) were bilaterally placed over the primary visual cortices and cemented to the cranium with dental acrylic cement. After craniotomy, the dura mater was removed, exposing the visual cortex. A thin, transparent artificial dura of silicone was implanted over the visual cortex. Appropriate analgesics and antibiotics were given during surgery and postoperatively. The anterior border of the exposed area was 3–6 mm anterior to the lunate sulcus. The size of the exposed imaged area covered approximately 3–4 × 4–5° of the visual field, at the reported eccentricities. We used the Oxonol VSDs, RH-1691 or RH-1838 (Optical Imaging) to stain the cortical surface. The procedure for applying VSDs to macaque cortex is described in detail in Slovin et al. (2002). For imaging we used the MiCAM ULTIMA system based on a sensitive, fast camera providing a resolution of 10⁴ pixels at up to a 10 kHz sampling rate. The actual pixel size was 170 × 170 μm², every pixel summing the neural activity mostly from the upper 400 μm of the cortex. This yielded an optical signal representing the population activity of ∼500 neurons per pixel (0.17 × 0.17 × 0.4 × 40,000 cells/mm³). Sampling rate was 100 Hz (10 ms/frame). The exposed cortex was illuminated by an epi-illumination stage with appropriate excitation filter (peak transmission 630 nm, width at half-height 10 nm) and a dichroic mirror (DRLP 650), both from Omega Filters. To collect the fluorescence and reject stray excitation light, a barrier post-filter was placed above the dichroic mirror (RG 665; Schott).

Retinotopic mapping of V1

Retinotopic mapping of V1 and the V1/V2 border was obtained in a separate set of imaging sessions using VSD and optical imaging of intrinsic signals and has been described previously (Ayzenshtat et al., 2012). Briefly, during a simple fixation task, we presented to the monkey small squares (0.1–0.2°), Gabors (σ = 0.125°), or high-contrast square contours (2 × 2°) at various eccentricities and imaged the evoked responses. Orientation maps were obtained by presenting full-field square moving gratings of horizontal and vertical orientations and then by computing differential maps. The orientation domains' size and organization are different in V1 and V2 thus enabling us to detect the V1/V2 border.

Eye movements

Eye position was monitored by a monocular infrared eye tracker (Dr. Bouis, Karlsruhe, Germany), sampled at 1 kHz and recorded at 250 Hz. Only trials where the animals maintained a tight fixation were analyzed.

VSD data analysis

VSDI data were obtained from a total of 23 imaging sessions in two hemispheres of two adult monkeys: nine sessions of the square stimuli (high-contrast) paradigm from monkeys T (six sessions) and H (three sessions), four sessions of the square stimuli (low-medium contrast) paradigm from monkey T, and 10 retinotopic and model validation sessions from monkeys T (seven sessions) and H (three sessions). Typically we analyzed ∼12–30 correct trials for each visual stimulus condition in a recording session. MATLAB software was used for statistical analyses and calculations. The basic VSDI analysis consisted of the following: (1) defining region of interest (only pixels with fluorescence level ≥15% of maximal fluorescence were analyzed), (2) normalizing to background fluorescence, (3) average blank subtraction (see schematic illustration of the basic VSDI analysis in Ayzenshtat et al., 2012 supplemental Figure S12), and (4) removal of pixels located on blood vessels. For each recording session the VSDI signal was averaged over all the correct trials and the averaged signal used for further analysis.

Throughout this study we focused on the average population response during the rising phase of activation (60–100 ms for the high-contrast conditions, 64–78%). This approach was used for all contrast conditions. As the latency of response onset decreased with increasing stimulus contrast (Albrecht, 1995; Meirovithz et al., 2010; data not shown), the rising phase of the response appeared earlier. For this reason, the VSD response was averaged and analyzed in the following time windows: 16% contrast 70–110 ms; 8% contrast, 90–130 ms; 4% contrast, 110–150 ms. Data for the variable contrast analysis (4–74%) were obtained from eight imaging sessions. One advantage for our choice of the early time frame (in addition to avoiding late neural influences) was related specifically to the avoidance of signals evoked by eye movements. It is well established that following stimulus onset, a microsaccadic/saccade suppression is initiated (in fixating monkeys and humans) that lasts for ∼200–250 ms (Reingold and Stampe, 2002; Engbert and Kliegl, 2003; Graupner et al., 2007; Rolfs et al., 2008). Therefore, during the very early phase of the response, eye movements are suppressed, and this holds also for time interval of 600–100 ms post stimulus—the time period we analyzed.

Time course onset latency was calculated by fitting a linear approximation to the rising phase of activation and calculating its intersection with the baseline.

Analysis of spatial profiles and ROIs

To analyze and compare maps of population response and model predictions we measured response profiles along spatial paths through the images (rectangular with a length of 52–94 pixels, ∼9–16 mm) spanning the entire activation patterns from side to side, in various orientations (Figs. 3B, 6A). For each rectangular path we averaged VSD responses along the width (the narrow dimension of the rectangle, 5–10 pixels, ∼0.85–1.7 mm). The colocalization of the cortical spatial paths with the edges, corners, and center of the square in the visual field was validated using both independent retinotopic experiments as well as a theoretical simulation using the retinotopic model (see below, Retinotopic transformation from the visual field to the cortical surface). For visualization purposes only, we smoothed the resulting 1D curve by convolution with a Gaussian window (σ = 0.26 mm/1.5 pixels) or with a rectangular window (6 pixels/∼1 mm). All reported correlations for the spatial profiles were calculated before smoothing.

Figure 3.

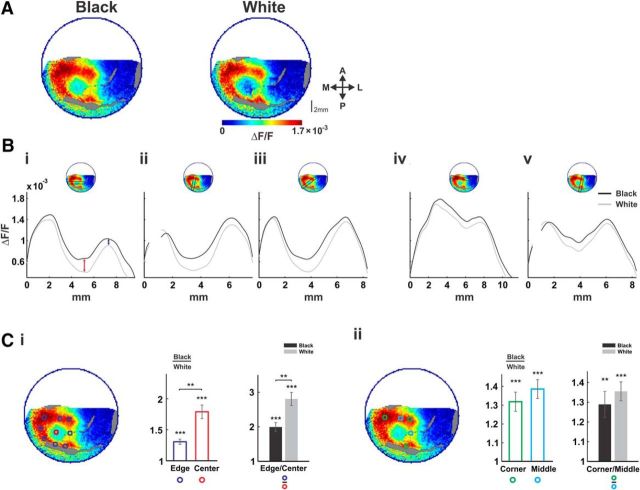
Spatial differences between black and white neural responses. Population responses to black and white stimuli. A, B, Same data as in Figure 1. A, Maps of population response (averaged over 60–100 ms post-stimulus onset) from one example session, evoked by black (left) and white (right) squares. Bi–Bv Spatial profiles of the black and white population responses (see Materials and Methods). The location of the spatial profiles on the maps is shown on the top insets. Black and gray curves depict the responses to the black and white stimuli, respectively. C, Grand average of response ratios averaged >9 imaging sessions. Ci, Edges versus center. Left, Location of ROIs on the example map from A. Blue ROIs correspond to the square edges and the red ROI to the center. Middle, Black/white ratios for the edges (blue) and center (red) ROIs. Error bars are ±1 SEM over sessions, asterisks across bars indicate significance of differences between ratios. Asterisks over individual bars indicate significance of difference from a ratio of 1 (*p < 0.05, **p < 0.01, ***p < 0.001). Right, The edges/center ratio for the black and white responses. Cii, Corners versus edges middles. Same as Ci, only for the corners (marked in green) and the middles of the edges (cyan) ROIs.

Figure 6.

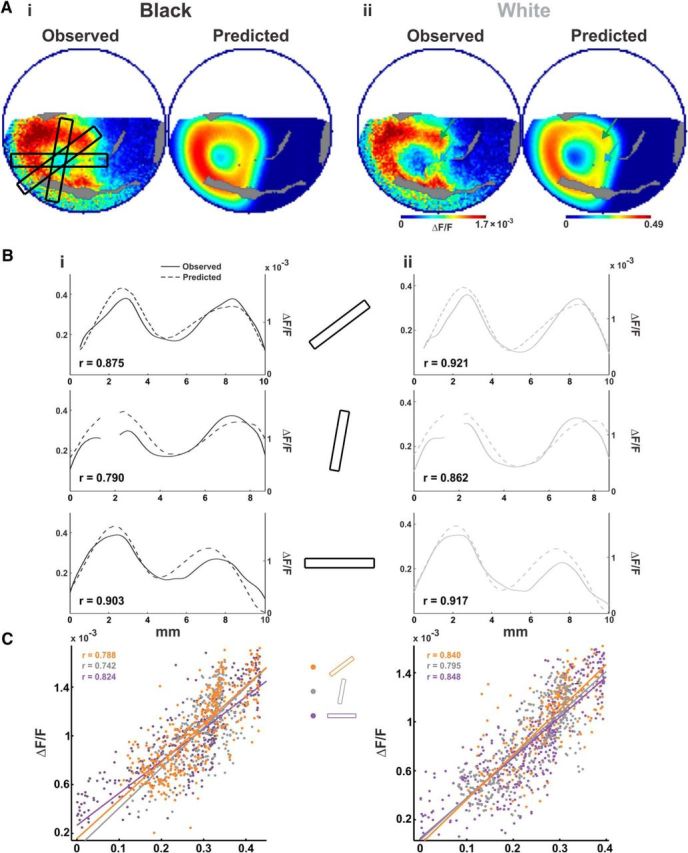
Model performance—observed versus predicted. Evaluation of model performance on the example session from Figure 1. A, Spatial maps of the observed VSD signal from one imaging session (maps averaged over 60–100 ms post-stimulus onset) and the predicted maps. Ai, Black stimulus. Aii, White stimulus. B, Spatial paths over the maps in A, showing three spatial profiles (marked over the left map in Ai) that pass through the center, corners, and edges of the black (Bi) and white (Bii) patterns. Solid curves show the observed response, and dashed curves show the predicted response (gaps in the curves correspond to blood vessels). Left y-axis is for the predicted response; right y-axis is for the observed response. Ordinate ranges are set between 0 and mean + 2 SD for each curve individually. C, Scatter plots of the expected versus the observed response of all the pixels in the three spatial profiles for black (Ci, left) and white (Cii, right), along with regression lines for each section and r values.

To analyze and compare responses at specific locations over the evoked response, we set ROIs (16–64 pixels/0.46–1.85 mm²) over specific cortical sites in the evoked pattern. The analysis was performed over the average response of all pixels within each ROI. SNR for each defined area (ROI or spatial profile) was defined as the difference in SD units between the mean activity (averaged across pixels of the defined area) before stimulus onset and after stimulus onset. Areas with SNR values below 8 SDs were discarded from the analysis.

Computation of contrast curves

Contrast curves were computed by defining ROIs positioned on the edges and at the center of the responses and predicted responses to squares of variable contrast. For each response map the average activation was calculated for each ROI type (edge or center, see above). All activation values were normalized to the activation at the edges for the 74% black condition (for data and predictions separately, resulting in an activation value of 1 for the black/edge ROI for both the data and the predictions). Observed and predicted contrast curves were then constructed for each ROI/contrast-sign combination separately, plotting observed/predicted activation as a function of stimulus contrast.

Statistical tests

Significance of ratio measures compared with a ratio of 1 (as the null hypothesis) was tested using Wilcoxon rank sum. Significance of RMSE values for contrast curves was calculated as follows: for each curve, a “shuffle” distribution was constructed from all possible permutations of the observed contrast curve. In each shuffle curve, contrast labels for each data point in the curve were ordered differently. RMSE values were calculated for each permutation to form a distribution. P values were then extracted as the percentile under which the original RMSE falls in the shuffle distribution. Wilcoxon signed rank was used for all other tests.

Encoding model

The encoding model (Fig. 5) transformed the 2D stimulus image, from the stimulus pixel level (Fig. 5A), to a predicted population response map (Fig. 5F) in cortical coordinates (the predicted map of the VSD signal in V1). To evaluate the model fit, we compared between the predicted and observed maps (Figs. 5F, 6Ai,ii).

Figure 5.

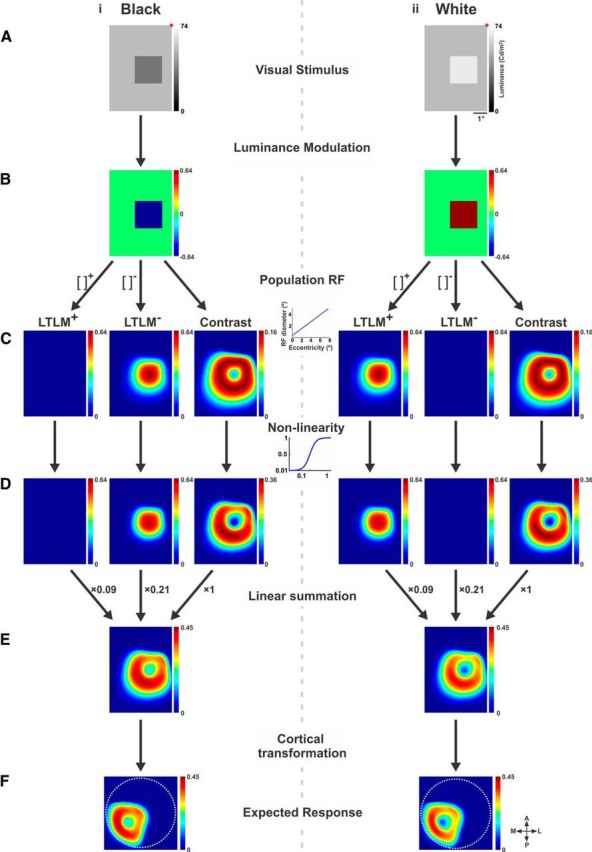
Computing the expected response using a model. A, Visual stimuli. Left, Black stimulus. Right, White stimulus (lower left quadrants). B, Relative luminance values of each stimulus from A. Each pixel with respect to the luminance value present at the same location before stimulus onset (see Materials and Methods and Eq. 1). C, Values from B diverged into three pathways of processing: positive LTLM, negative LTLM (both obtained by rectification, Eqs. 5 and 6), and contrast (Eqs. 7 and 8). All three pathways are calculated using a weighted sum of a circular PRF (Eqs. 2 and 3) with a size that increases linearly as a function of eccentricity (Eq. 4). D, The three pathways from C, operated on by a nonlinearity function (Naka—Rushton; Eq. 9). Half-saturation values (C₅₀, L₅₀⁺, and L₅₀⁻) for the Naka–Rushton equation are calculated from response statistics in a surround field that is larger than the PRF, resulting in spatially specific divisive surround (Eqs. 10–12). E, The expected response obtained by linear summation of the three pathways from D (Eq. 13). F, The expected response after spatial transformation to cortical coordinates (V1) of the imaged eccentricities (see Materials and Methods for further details).

The model was comprised of three key pathways: positive temporal luminance modulations, negative temporal luminance modulations, and contrast. These processes were previously demonstrated to take place in V1. For each pathway we computed the relevant neural transformation of the image separately using a population receptive field (PRF; RF for a neuronal population signal, i.e., the VSD signal, rather than for single neurons) and nonlinearity. The PRF was the same for all three pathways: positive and negative luminance modulation and contrast. The next step of the model was linear summation of all three pathways. The model includes the hypothesis that the three pathways occur, to some extent, in separate neuronal populations of V1. It is well established that the VSD signal reflects the sum of membrane potential of all neuronal elements within an imaged cortical pixel/area (Shoham et al., 1999). Therefore, the VSD signal from an imaged pixel/area in V1 represented the sum of membrane potential from neurons in all three pathways.

The imaged pixel size we used in V1 for the current study was relatively large (170 × 170 μm²), and thus was influenced by several functional columns (e.g., orientations, spatial frequencies, etc.). Therefore, the VSD signal from each V1 pixel represented the underlying responses of many neurons with a wide range of tuning properties. Accordingly, in the model each pixel in the stimulus image was treated as a population signal. Thus each pixel's response was modeled as a sum of all underlying neuronal activity. In the last step, we transformed the predicted response from visual field coordinates into cortical coordinates and compared the map of the predicted response (computed on the stimulus pixels) with the map of the observed response in V1 (imaged pixels in V1). The model steps are detailed below.

First, LTLM was computed from stimulus luminance values (Fig. 5Ai,ii) as a normalized measure, comparing for each stimulus pixel the luminance level during presentation with the prestimulus luminance (Fig. 5Bi,ii):

where for each pixel i in the stimulus image, I_i is the luminance value during stimulus presentation and I_0i the screen luminance for the same pixel before stimulus onset.

PRF.

The PRF (Fig. 5C, inset between i and ii) represents the contribution from all neurons whose RF centers fall within a single pixel in the stimulus image. The PRF weighting function was calculated using a raised cosine, for each PRF center (x_i, y_i) as follows:

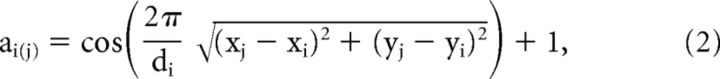where a_i(j) is the jth pixel in the PRF window centered at visual field coordinates (x_i, y_i), d_i is the diameter, and (x_j, y_j) the visual field coordinates of the jth pixel in the window. The weights w_i(j) within each window were normalized to a sum of 1:

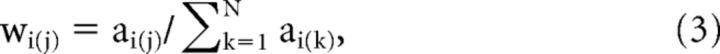where w_i(j) is the weight of the jth pixel in the PRF window centered at (x_i, y_i). Since our imaging area spanned eccentricities ranging between ∼1–5 degrees of visual angle, PRF sizes were adapted accordingly. Sizes of RFs in the primary visual cortex have been shown to depend linearly on eccentricity (Angelucci et al., 2002). We calculated PRF diameter as a linear function of the eccentricity of the PRF's center in the visual field (x_i, y_i), using the following formula:

where ecc_i is the eccentricity of pixel i in the visual field and m and n the slope and intercept parameters, respectively (note the linear curve in Fig. 5C, inset between i and ii). In our model, m,n values were found empirically using an iterative fitting process performed on one imaging session per monkey (m = 0.59 and n = 0.36 for monkey T and m = 0.59 and n = 0.6 for monkey H; fixed for all sessions), and resulted in a PRF size versus eccentricity curve that fell within ranges previously reported for summation fields in macaque V1 (data not shown; Angelucci et al., 2002).

Pixels with positive relative luminance levels and pixels with negative relative luminance levels were treated in parallel pathways, separated by positive and negative half-wave rectification: the LTLM⁺ channel (L⁺, Eq. 5) and LTLM⁻ channel (L⁻, Eq. 6). The final LTLM value was calculated for each pixel in the visual field using a circular, weighted PRF window, taking into account LTLM⁺ or LTLM⁻ inputs from neighboring pixels in the visual field:

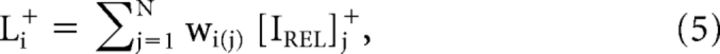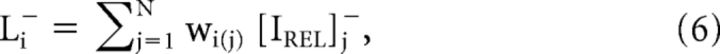where w_i(j) is the weight of the jth pixel of the PRF weighting function centered at pixel i, and [I_REL]_j⁺ and [I_REL]_j⁻ are the relative luminances of the corresponding jth pixel of the positive and negative half-wave rectifications of I_REL, respectively. The resulting 2D LTLM maps are depicted in Figure 5Ci,ii: LTLM⁺ and LTLM⁻.

Local contrast.

Local contrast (Fig. 5Ci,ii; contrast) was computed for each pixel in the stimulus image separately, using the PRF (see above) and a modified version of RMS contrast (Peli, 1990; Mante et al., 2005). In our model, the local contrast computation was defined as a weighted SD:

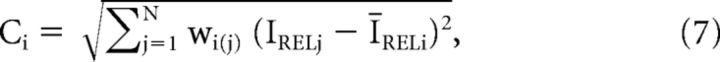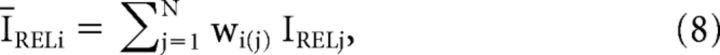where C_i is the contrast of the ith pixel in the image in the visual field; Ī_RELi the mean weighted relative luminance of all pixels in the visual field that are located within the PRF centered at the ith pixel; and w_i(j) the jth pixel of the PRF weighting function centered at pixel i, the same PRF as used for the local luminance calculation (Eq. 3). Different from Mante et al. (2005), the above formula for local contrast (Eq. 7) does not include normalization by the mean luminance, since all input values for each pixel in the contrast calculation (I_REL) are already normalized by prestimulus luminance, as a result of the LTLM computed in Equation 1.

Finally, the next stage of the model handles nonlinearity of the overall local activation and spatial interactions within the cortex (Eq. 9; Fig. 5D; Cavanaugh et al., 2002). A known property of V1 neurons is gain-controlled responses that are of a nonlinear nature. In our model, we represent gain control by using a simple nonlinearity function (Naka and Rushton, 1966; Eq. 9) to describe a divisive gain control that varies with eccentricity. This nonlinear step was applied separately for each of the two LTLM channels and contrast channel (note the three parts of Fig. 5Di,ii). Calculation for LTLM⁻ luminance is demonstrated below:

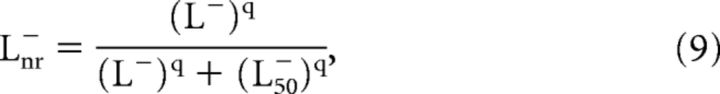where parameter q was fixed at 2 for all pathways, in agreement with previous reports for nonlinearity in the visual system of macaques for spiking and VSDI (Albrecht, 1995; Contreras and Palmer, 2003; Meirovithz et al., 2010; Reynaud et al., 2012). The nonlinear step was applied to each channel at the pixel level.

Semisaturation values (L₅₀⁺, L₅₀⁻, C₅₀) were key parameters in the local gain control. These values were channel dependent and surround dependent (Eqs. 10 and 11). For each stimulus pixel, each of the three parameters was influenced by pathway-specific properties (LTLM, contrast) and by the pooled activity of a large, “surround” field (a field centered at the same location as the PRF but with a larger radius, extending beyond the classical RF, see Eq.12; Cavanaugh et al., 2002).

Each semisaturation value was constructed from (1) a sensitivity baseline for the pathway type (LTLM or contrast, parameters P_L, P_C in Eqs. 10 and 11); (2) in the contrast pathway, a representation of stimulus contrast (within a large surround field, expressed in our model as a “max” operation, Eq. 11), capturing the known effect of stimulus contrast on the modulation depth and extent of V1 responses (Sceniak et al., 1999; Angelucci et al., 2002); and (3) the median of the distribution of values in the large surround field for each pixel in the visual field (defined below), determining the final degree of local gain:

where p_L and p_C are the minimal values for the LTLM channels and the contrast channel, fixed at 0.5 and 0.05, respectively (converged to by an iterative fitting process) reflecting a lower baseline (higher sensitivity) for contrast than for LTLM; K is a factor that determines the strength of surround-dependent suppression. K values were 1 and 2.5 (for monkeys T and H), resulting in suppression indices of 0.59 and 0.84 (see Materials and Methods; Sceniak et al., 1999; Shushruth et al., 2009). The additional term in the contrast pathway [max(C*Y_i), the maximum contrast value present in the large field Y_i] represents the dependence of the sensitivity on stimulus contrast, the latter affecting the degree to which activation within the PRF is modulated, corresponding to previous accounts of measured RF sizes that depend on stimulus contrast (Sceniak et al., 1999; Angelucci et al., 2002; Nauhaus et al., 2009). The surround field (Y_i) used for calculating the above parameters was defined as a flat circular field centered at pixel i in the visual field:

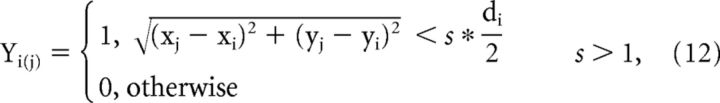where Y_i(j) is the jth pixel in the surround field window centered at visual field coordinates (x_i, y_i), (x_j, y_j) is the visual field location of the jth pixel in the window, and s the ratio between diameter of the surround field and the smaller diameter d_c of the PRF at the same visual field location (Eq. 4). s was found empirically using an iterative fitting process that converged to a value of 2.4(1.8) for monkey T(H). These values fall well within previous reports: 1.3–5 (Sceniak et al., 1999; Cavanaugh et al., 2002; Shushruth et al., 2009). s was fixed across all analyzed sessions. The nonlinearity step also provides a mechanism of divisive surround that is spatially specific and depends on the stimulus properties of the surround field for each pixel.

The combined model.

This model (Fig. 5E) was a linear combination of all three processing pathways:

The optimal parameters t and u were obtained from an iterative fitting process described below (see below, Encoding model parameters and iterative fitting process). In other words, the relative weights of the three pathways were determined by the data. The best-fit values for the relative weights were 1 for contrast and 0.09 and 0.21 for positive and negative luminance modulation, respectively. These values reflect higher weighting to the contrast signal than to the surface-related LTLM signals and a high ratio of negative to positive surface responses (LTLM), and relate well to the literature. The model's weights were used for the analysis of all data sessions.

Calculation of suppression index

To quantify the effect of scaling factor K on the divisive surround in the contrast pathway, the suppression index was calculated on a stimulus with identical contrast contents in the PRF and surround, namely a uniform distribution, of high contrast (64–78%). Naka–Rushton (NR) was then applied to a typical pixel of the stimulus, with a C₅₀ value that accounts for the stimulus surround distribution and K (see Eq. 11). Suppression index was calculated as the ratio of activation value after NR to that of before (the pixel's contrast), using the following formula:

where C′ is the calculated contrast of the pixel before NR (Eq. 7) and C′_nr the value after NR is applied.

Retinotopic transformation from the visual field to the cortical surface

To map model predictions from the visual field to the cortical surface we implemented the monopole version of the model of Schira et al., 2010 with a polar compression factor as previously described (Ayzenshtat et al., 2012). The model's three free parameters (k, a, α) were determined for each imaged V1 hemisphere using a set of 7–11 control points obtained in an independent experiment (see above, Retinotopic mapping of V1; Ayzenshtat et al., 2012), and were a = 0.74, k = 2.95, and α = 1.54 for monkey T, and a = 3.8, k = 1.2, and α = 0.59 for monkey H.

Encoding model parameters and iterative fitting process

In our model, we attempt to arrive at one fixed parameter set that would explain all data. However, some parameters inevitably vary between subjects, specifically retinotopy and PRF sizes. Accordingly, optimal values for the general parameters, reflecting the weighting of each pathway (t, u) were found using a training set of one imaging session from one animal (monkey T, values converged via an iterative optimization process), and remained fixed throughout the analysis for all sessions and monkeys. Optimal values for parameters reflecting PRF sizes, the PRF/surround ratio, and the surround strength (m, n, s. and K), were obtained using a training set of one imaging session per monkey, and remained fixed throughout the analysis for all sessions per each monkey. Finally, parameters handling processing of various luminance and contrast levels (P_L, P_C, and q) were found using a training set of one imaging session per contrast from one monkey (T), and remained fixed throughout the analysis for all sessions and monkeys.

Results

Two monkeys were trained on a fixation task. During each fixation trial the monkey was presented with either a white or a black square (Fig. 1A; see Materials and Methods). Using VSDI, we measured the evoked population responses in the striate cortex (V1). The dye signal measures the sum of membrane potential changes of all neuronal elements (dendrites, axons, and somata) within each 170 × 170 μm² pixel in the imaged area (Shoham et al., 1999; Slovin et al., 2002) and therefore measures population responses rather than responses of single neurons. Data were analyzed from 23 imaging sessions for all experimental conditions and retinotopic mapping in two hemispheres of two adult monkeys (see Materials and Methods).

General characteristics of population response to black and white squares

To investigate the neuronal processing of luminance surfaces in V1, monkeys fixated for 3–4 s and were then presented with 2 × 2° squares of positive (“White”) and negative (“Black”) high-contrast equal in magnitude with respect to the background luminance (Fig. 1A). Figure 1B shows the spatiotemporal population response from an example recording session, evoked by the black (Fig. 1Bi) and white (Fig. 1Bii) squares presented for 300 ms. Shortly after stimulus onset (40–50 ms) the map had a square-like pattern in the V1 imaged area, as expected from the known retinotopic organization of V1. The early evoked response was activated mainly along the contour of the square: edges/corners. At later times there were further increased responses at the edges/corners regions along with a slow increased population response at the center of the square (compare maps in Figs. 1B, t = 80, 120, 300; C, 2A for grand average across sessions). The “hole” at the center of activation is striking, especially when compared with our perception of a uniform surface (Huang and Paradiso, 2008). More subtle spatial modulations occurred for the upper and right edge. For example, the response to the rightmost edge was weaker than responses at other edges (Fig 1Bi,ii, t = 80). Finally, the corners of the right and upper edge evoked more neuronal activity (Fig 1Bi, t = 120, green arrows) than the middle part of the same edges (cyan arrows).

Figure 2.

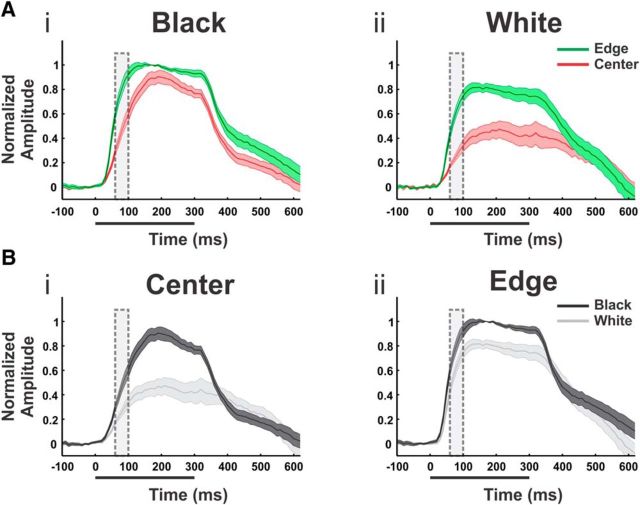
Response time courses—grand averages. Responses to black and white square stimuli averaged over n = 9 sessions from both monkeys. A, Time courses of the evoked population response for the black (Ai) and white (Aii) stimulus. Time course are computed for ROIs located at the center and at the edges of the evoked pattern (red and blue ROIs in Fig. 3Ci, left). Trace width denotes ±1 SEM over sessions. B, Same as in A but time courses grouped by center ROI (Bi) and edge ROI (Bii) for comparison between the black and the white responses. In each session, the time courses were normalized to the response amplitude of the black, edge condition at t = 170 ms. Dashed rectangles in A and B mark the time frames of averaging for spatial analysis and model evaluation (60–100 ms).

Although the spatial patterns of population responses to the black and white stimuli were similar (Fig. 1B), the response amplitude to black was higher (compare the maps for black and white stimuli in Fig. 1B, t = 80, 120, or 300). To quantify the black–white difference we set two ROIs: one on the upper edge and one on the hole at the center (Fig. 1Bi,ii, t = 80; green and red ROIs). For both ROIs the black squares evoked larger responses (Fig. 1C,D), but evidently the difference between black and white responses was greatest at the cortical region representing the center of the square (Fig. 1D), as analyzed below on data obtained from multiple sessions.

The single session results of Figure 1 were replicated across many recording sessions. The average across sessions (Fig. 2; normalized response) yielded significant black/white differences (n = 9, p < 0.01 for both ROIs, measured at 60–100 ms; Fig. 2, dashed rectangle). In addition, the rising phase of the response to black was faster than to white (average slopes were 8.89 ± 0.66 × 10⁻⁵ and 5.85 ± 1.03 × 10⁻⁵ ΔF/F/10 ms at the center ROI for black and white, respectively, and 11.1 ± 1.06 × 10⁻⁵ and 9.56 ± 1.11 × 10⁻⁵ at the edge; mean ± SEM, n = 9, p < 0.01 for both edge and center).

Quantification and comparison of the spatial cortical response to black and white squares

In this paper, we analyzed the response for early times (60–100 ms) after stimulus onset, avoiding later complex neural influences. Another advantage for our choice of the early time frame was the avoidance of response modulation evoked by eye movements, due to early saccadic suppression (see Materials and Methods for more details).

To quantify and compare the evoked spatial pattern of the black and white squares, we first computed the average (60–100 ms post-stimulus onset; Fig. 2, dashed rectangle area) response map (Fig. 3A) on the same data from Figure 1B. Then we analyzed spatial profiles, comparing the evoked patterns on paths through the corners, the center, and the edges (Fig. 3Bi–v; see Materials and Methods). The black and gray curves in Figure 3B correspond to the spatial profiles of the population response for the black and white stimuli, respectively.

The spatial profiles passing through the center (Fig. 3Bi–iii) suggest that the black–white difference is more prominent at the center of the square (Fig. 3Bi, red arrow) than at the corners and edges (Fig. 3Bi, blue arrow). To quantify this further, we set ROIs along the edges and center of the evoked pattern (blue and red ROIs in Fig. 3Ci, left map; see Materials and Methods). Figure 3Ci (middle) shows the grand average across sessions of the black/white response ratio at the edges (blue) versus the center (red) for the black and white squares (n = 9 sessions, error bars are SEM). The ratios were significantly greater than 1, confirming higher response to black for both edges and center ROIs (p < 0.001 for both). However, the black/white ratio was clearly higher at the center (p < 0.01). The edge/center response ratio for the black and white squares separately is shown in Figure 3Ci, right (n = 9 sessions). It was significantly greater than 1 for both (p < 0.001), indicating higher activation at the edges than the center for both black and white; however, the ratio was larger for the white square (p < 0.01), due to the increased response at the center for the black.

We next turned to examine the finer spatial relationships among responses for both black and white. Interestingly, profiles along the upper and right edges (Fig. 3Biv,v) displayed a double-peaked shape, indicating higher activation at the corners compared with the middle of the edge. This effect appeared in both black and white responses, but was specific to the two more foveal edges (top and right) of the square. The other two more peripheral edges did not exhibit such modulation (Fig. 3A, left edge). This eccentricity dependence was confirmed by presenting the stimuli more foveally (Fig. 4) and is addressed in the Discussion. To quantify the corner-edge modulation, we calculated ratios between population responses of ROIs centered on the corners (green ROIs) versus the middle of the edge (cyan ROIs; Fig. 3Cii, left map). Figure 3Cii (right) shows the grand average of corner/edge-middle response ratios for the black and white (n = 9 sessions). The response at the corners was larger than the edge middles for both black (p < 0.01) and white (p < 0.001). In addition, the black/white ratios were significantly greater than 1 for both regions (Fig. 3Cii, middle; p < 0.001, n = 9). Finally, we examined whether the corner-edge modulation can be explained by slow neuronal filling in from the corners toward edge middles. We compared the response profiles at both regions and found very similar dynamics, with no difference in onset latency (p = 0.36, 0.73 for black and white, respectively, n = 9) or time to peak (p = 0.65 and 0.1; see Materials and Methods for more details). We therefore conclude that neuronal filling in does not explain this modulation.

Figure 4.

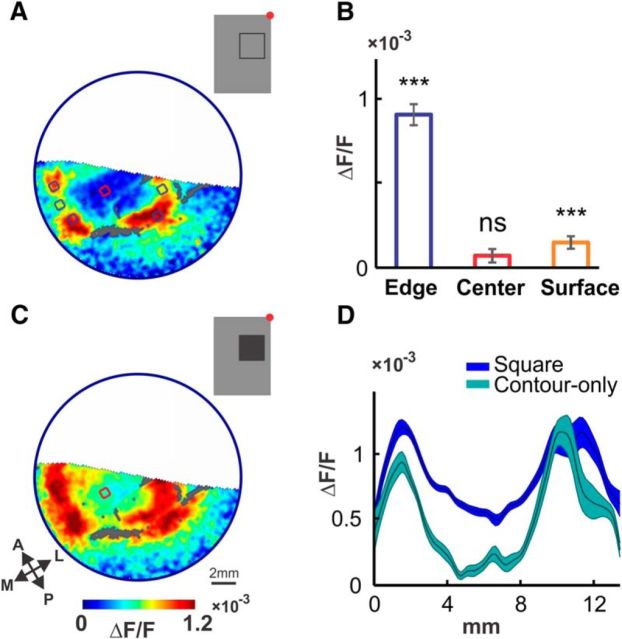
Different contributions of contrast responses and surface responses. A, VSD activation pattern evoked by a 2 × 2° square contour stimulus (inset, red dot marks the fixation point), presented 1.5 left of the fixation point and 2.5° below for 300 ms, averaged 60–100 ms (n = 11 trials, large blood vessels are colored gray). Blue and red regions (area 0.46 mm²) depict the ROIs used to measure edge and center activation, respectively. B, Average activation evoked by the stimulus in A at the edges (blue) and center (red) ROIs, and at the center region of the response evoked by a large surface stimulus (orange), centered at the same location as A (size 8 × 8°, n = 21 trials). Significance of >0 activation measured by Wilcoxon signed rank test (***p < 0.001). C, VSD pattern evoked by a 2 × 2° square surface stimulus (inset) presented at (−1.5 and −2.5°) for 300 ms, averaged 60–100 ms (n = 20 trials, large blood vessels are colored gray). Red region depicts ROI used to measure center activation, same one as in A. D, Comparison of spatial profiles of the responses shown in A (cyan curve) and C (blue curve, shading marks ±1 SEM). Paths spanned the top-left corner, center, and bottom-right corner of both responses (1.2 × 13.6 mm). Curves smoothed with a Gaussian (σ = 0.17 mm) for visualization purposes. Center activation in response to the filled square is clearly present and much higher than that evoked by the square contour.

To summarize, our analyses demonstrate edge/center, black versus white, and corners/edge-middle modulations of the evoked responses. We next wanted to present a model that can account for the observed behavior of the V1 neuronal population in these experiments. As first step, we set out to evaluate the separate contributions of neuronal mechanism that can give rise to the large response difference between edge and center.

Separate edge and surface processing in responses evoked by square surfaces

The square stimuli we use are comprised of mainly contrast content at the edges and surface content at the center. Correspondingly, our results also demonstrated qualitatively different responses at the edge and center regions. To evaluate the separate contributions of edge-responsive and surface-responsive populations, we presented stimuli comprising either mainly contrast content (a 2 × 2° square contour; Fig. 4A, inset) or surface content (a large 8 × 8° square surface), separately. A contrast–response component was confirmed by the pattern evoked by the square contour stimulus (Fig. 4A). As expected, activation was substantial at the edge regions. Additionally, there was no significant response at the center (p = 0.15), where local contrast was absent (Fig. 4B, blue and red bars). We further confirmed the absence of the center activation by spatial comparison to a response evoked by a filled-square surface presented at the same location (Fig. 4C), where center activation was substantial (cyan color at the center; compare to Fig. 4A, same area). Analysis of spatial paths through the corners and center of both responses confirmed the large difference at the center (Fig. 4D, blue and cyan curves). The separate origin of the center activation was verified by the response to the large, black surface stimulus, which evoked significant activation at the center (Fig. 4B, orange bar), despite the absence of local contrast (edges were 4° away in each direction). The surface-evoked activation measured at the center was substantially lower than contrast-evoked activation (blue bar) at the edges (ratio of 1:6, p < 0.00001). Combined, these data suggest separate mechanisms for edge/contrast processing and for surface processing. Finally, we note that the corner versus edge-middle modulation along the edges is accounted for by the contrast-processing component, as clearly seen in Figure 4A. We next present a model that is based on separate contrast- and surface-processing components that accounts for the observed V1 population responses.

A combined model of luminance and contrast for computing the predicted population response

To compute the predicted early (60–100 ms) population response to black and white stimuli, we constructed a model of the V1 population (Fig. 5; see Materials and Methods). Based on the above observations the model was comprised of separate elements, well known to be present in V1: neuronal populations sensitive to contrast (Hubel and Wiesel, 1959; De Valois et al., 1982) and to luminance surfaces (MacEvoy et al., 1998; Kinoshita and Komatsu, 2001; Roe et al., 2005; Dai and Wang, 2012). The model was computed on the stimulus image [Fig. 5Ai (black), Aii (white)] and resulted in predicted VSD maps (Fig. 5F). All model parameters were obtained via an iterative fitting process (for more details see Materials and Methods).

The first step in the model was to compute, for each stimulus pixel, the relative temporal luminance change (Fig. 5A,B; Eq. 1; see Materials and Methods). Next, the model computed the responses using three distinct channels (Fig. 5C): positive luminance modulation (LTLM⁺), negative luminance modulation (LTLM⁻), and local contrast. The PRF for each pixel was described by a raised cosine (Mante et al., 2005; Ayzenshtat et al., 2012; see Materials and Methods). PRF diameter varied linearly with retinal eccentricity (Angelucci et al., 2002; Eqs. 2–4), resulting in PRF sizes in agreement with previous studies (Angelucci et al., 2002; Sceniak et al., 1999; see Materials and Methods), for the imaged eccentricity. The input to LTLM⁺ was computed by summing positive luminance changes (scaled by the prestimulus luminance) within the PRF and correspondingly LTLM⁻ was computed by summing negative luminance modulations [Eqs. 5 and 6; Fig. 5Ci (black), Cii (white)].

Local contrast was handled as a separate third, contrast sign-insensitive channel and was computed using a modification of RMS contrast (Mante et al., 2005), calculated on the relative luminance change (Eqs. 7 and 8; Fig. 5C; see Materials and Methods). Local contrast was computed for a PRF (Fig. 5C, right in black and white), similar to that of the LTLM⁺ and LTLM⁻ pathways (Fig. 5C, left and middle in black and white). The choice of a single contrast mechanism that was contrast sign insensitive was motivated by our VSDI data, which indicated that the black/white difference was much smaller at edges than in the center of the squares.

Next, the model had a stage to account for spatial interactions within the cortex and for the known nonlinearity of V1 neurons. To perform this stage of processing, the NR function was applied to each pixel in the stimulus image (Eq. 9; Fig. 5D; see Materials and Methods). The L₅₀/C₅₀ parameters of the NR were influenced by responses evoked by surrounding stimulus pixels via a divisive mechanism (Eqs. 10 and 11; Cavanaugh et al., 2002; Webb et al., 2003). Surround pixels were taken from a circular field centered at the PRF's center (Eq. 12), whose size was larger than the corresponding PRF by a fixed ratio for each monkey (average 2.15), as determined by the fitting process and in correspondence with previous literature (see Materials and Methods for more details). The L₅₀/C₅₀ values were calculated individually for each pixel in the stimulus and were determined independently for the different channels. Effectively, this step resulted in a divisive surround mechanism varying in space as a function of the PRF size (maps of the C₅₀/L₅₀ parameters show marked variation in visual space, data not shown). The effect of spatial interactions at this stage in the model can be seen by comparing the LTLM and contrast responses before and after NR was applied in Figure 5C and D. This part of the model explains a key spatial property of our data, the elevated activation at the corners compared with the edges middles in the response (see below, Comparing model predictions with VSDI measurements). A model with a subtractive (rather than divisive) surround performed similarly for our data (data not shown).

The next step of the model was linear summation of all three pathways (Eq. 13; Fig. 5E) using weighting coefficients specific for each channel: 0.09, 0.21, and 1 for the LTLM⁺, LTLM⁻, and local contrast, respectively (coefficients obtained by an iterative fitting process described in Materials and Methods). The assignment of different weights to the positive and negative LTLM pathways enabled the model to account for the amplitude differences between responses to black and white (see below). It is important to note the relative weights of each of the three pathways; fitting the model to the data required assigning a substantially higher weight to the contrast signal (∼77%) than to the surface-related LTLM signals, and a 2.33 ratio of negative to positive surface responses (LTLM). The model's weights of contrast-responsive versus surface-responsive neurons relate well to our observations (Fig. 4B) and to the literature. Previous accounts of the balance between contrast-responsive and surface-responsive neurons in macaque V1 reported that a minority, between 20 and 40%, of neurons respond to uniform surfaces (Peng and Van Essen, 2005; Huang and Paradiso, 2008; Dai and Wang, 2012). Electrophysiological studies of black versus white asymmetry report ratios of ∼2–3 (Yeh et al., 2009; Xing et al., 2010) and 1.9–2.1 (Kremkow et al., 2014). The correspondence between our model's parameters and known attributes of V1 from the literature is an indication of the validity of the proposed model.

In the final step of the modeling, we used a retinotopic model (Schira et al., 2010; Ayzenshtat et al., 2012) to transform the resulting prediction from visual space to the cortical space (See Materials and Methods). This enabled us to compare directly between the predicted (Fig. 5F) and observed (Fig. 3A) response maps.

Comparing model predictions with VSDI measurements

The model accounted for key properties of the evoked spatial pattern and for the differences between the early responses to black and white stimuli. Figure 6, Ai and Aii, shows the predicted cortical response (right columns) alongside the observed data (left columns; same data as in Figs. 1, 3) for black and white. First, both model and data demonstrate higher activation along the edges and lower activation at the center, an area corresponding retinotopically to the squares' center. Second, while the overall predicted activation and corresponding peak values (i.e., square's contour) for the black condition are only slightly higher than those of white, predicted activation at the center is notably higher for black than for white, also a characteristic of the data (compare Fig. 6Ai right, Aii right). This difference between the responses to black and white is expressed in the model by the different coefficients assigned to the LTLM⁺ and LTLM⁻ pathways. Finally, higher activation at the corners compared with the edge middles appears for both the predicted and the observed data (compare activation of corners and edge middles in the predictions with those of the observed data, for example, green and cyan arrows in Fig. 6Aii, right and left). This effect, clear in both data and model predictions, is captured by the surround mechanism in the NR stage in the model. The “corner” and “middle” pixels have different surround field input because of their different spatial locations over the stimulus (that result in different C₅₀ values at these regions), resulting in different spatial modulation. This is addressed further in the Discussion.

To quantify the model's fit to the observed data, we computed spatial profiles along identical paths on the predicted and evoked patterns (see Materials and Methods) and then computed the Pearson correlation coefficient (r) between the profiles. Schematic illustration of the spatial profiles sampling the edges, center, and corners of the square are depicted in Figure 6Ai. The spatial profile curves are plotted in Figure 6, Bi and Bii, and show high similarity between the observed (continuous line; right y-axis) and the predicted response (dashed line; left y-axis), and consequently high correlation values (r values for the example shown in Fig. 6 are given within each panel of 6Bi,ii). The analysis was repeated with pixel-by-pixel correlations within each profile and resulted in similar r values, as shown in Figure 6, Ci and Cii, for the data shown in Figure 6A. Figure 6, Bi and Bii, top row, demonstrates the spatial profiles located over the corners and center. Note that the activation level at the trough is higher for black than white for both observed data and prediction. The grand average correlations between spatial profiles of the observed data and prediction are high: 0.72 ± 0.04 and 0.74 ± 0.03 for black and white, respectively (mean ± SEM over n = 9 sessions, average p values were p̄ <1 × 10⁻⁵ and 1 × 10⁻⁷ for black and white, respectively). The middle row in Figure 6, Bi and Bii, depicts the spatial profile extending from the top edge and through the center. The locations of both peaks and of the center region are relatively well predicted, as is the relative activation amplitude. Corresponding grand average correlation values were also high, with r = 0.74 ± 0.04 and 0.69 ± 0.09 for black and white, respectively (n = 5 sessions, p̄ < 1 × 10⁻⁶ and 1 × 10⁻⁴; profiles with poor SNR were excluded from the average, see Materials and Methods). Figure 6, Bi and Bii, bottom row, depicts the spatial profile extending from the right edge and through the center. The location of the right peak is predicted with reasonable accuracy. Moreover, the difference in relative activation levels between the right and left peaks (corresponding to right and left edges in the data, and to the top and bottom edge of the stimulus in the visual field) is also predicted, with the left peak showing higher amplitude than the right. This effect, caused by the varying size of the PRFs as function of eccentricity, provides a good example for the importance of employing eccentricity-dependent PRF sizes. For the profiles in the bottom row of Figure 6, Bi and Bii, the grand average correlations were also high, with r = 0.74 ± 0.07 and 0.75 ± 0.05 (mean ± SEM; n = 9 sessions, p̄ < 1 × 10⁻⁴ and 1 × 10⁻⁷) for black and white squares, respectively. Overall, spatial profiles were well predicted, resulting in a grand average r value of 0.73 ± 0.02 (mean ± SEM, p̄ < 1 × 10⁻⁴) over n = 46 profiles, spanning all locations and conditions.

To further evaluate the model's performance, we tested predictions of specific ROIs (labeled in Fig. 7C) and their response ratios. Figure 7A summarizes, over all sessions, the observed (solid bars) and predicted (textured bars) ratios between edges and center and the ratio between corners and edge middles for the black and white stimuli (mean ± SEM over n = 9 sessions). Predicted edge versus center ratios were comparable to the corresponding observed ratios, and were greater than one for both white and black squares. Similar to the observed response, the edge versus center ratio was greater for the white square (note the different scales in Fig. 7Aii, left and Ai, left). Predicted ratios for corner versus edge-middles were also both greater than one, comparable to the slightly higher observed ratios. The dependence of surround sizes on eccentricity enabled the model to capture the presence (or absence) of the corner versus edge-middle effects in the individual edges of the square pattern, a point we elaborate on in the Discussion. Overall, we note comparable values above one for all ratios for both conditions, reflecting the similarity between the data and model images, seen in Figure 6A.

Figure 7.

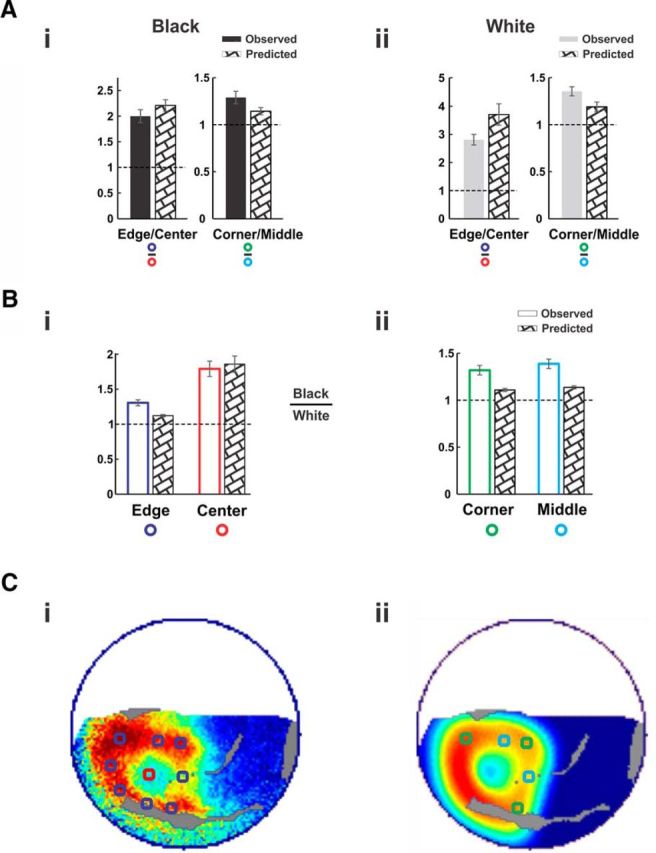
Model performance—average over all sessions. Quantification of model prediction performance for spatial and black/white ratios, averaged over all n = 9 sessions. A, Observed and predicted responses in the ROIs. Locations of ROIs are depicted in Ci and Cii for Ai, Bi, and Aii, Bii, respectively (see Materials and Methods). Ai, Left, Depicts the ratio between the edges and the center for black; right depicts the ratio between the corners and the edge middles for black. Error bars are ±1 SEM over sessions. Aii, Same as Ai but for the responses to the white square. B, The ratios between the black and white responses in all four ROI types: edges and center (Bi) and corners and edge middles (Bii). C, Illustration of ROIs on an example map and corresponding predicted map from session shown in Figure 1. Ci, ROIs corresponding to square edges (blue) and to the center (red), superposed on a response map. Cii, ROIs corresponding to square corners (green) and to the edge middles (cyan), superposed on the corresponding predicted map.

Black/white predicted ratios also corresponded well to the observations. Figure 7, Bi and Bii, shows the observed ratios (unfilled bars) and predicted ratios (textured bars) for all four ROI groups (mean ± SEM over n = 9 sessions). Similar to the observed response ratios, all black/white predicted ratios lie above the baseline of one, meaning higher predicted values for black than white across all regions. Predicted and observed black/white response ratios at the center region had similar values (Fig. 7Bi, “center” bar, 1.86 ± 0.12 and 1.79 ± 0.11 for predicted and observed, respectively). Predicted ratios at the edges, corners, and middle ROIs were all above one, indicating the higher activation for black over all regions was captured by the model (Fig. 7B, Edge, Corner, and Middle bars). There were, however, several small deviations of the model's predicted ratios and curves from the observed data. Such deviations may arise from inaccuracies of the retinotopic model, or from other factors that are addressed in the Discussion.

Population responses to varying the contrast of black and white squares

Next, we measured the population responses to 2 × 2° black and white squares, with five contrasts ranging from high (64 and 74%) to medium and low (4, 8, and 16%; see Materials and Methods). This new dataset was used to test whether or not the model could also explain the effect of stimulus contrast on the evoked VSD pattern. Using the model with exactly the same parameters, we generated prediction maps for each contrast (see Materials and Methods) and examined as in Figure 6 the model's ability to capture the spatial properties of responses using spatial profiles (Fig. 8A, middle map; see Materials and Methods). Figure 8, Ai and Aii, shows the observed and predicted spatial profiles and their correlation in an example recording day. The correlations were high for most contrast conditions with mean r (n = 15 spatial profiles, seven sessions; see Materials and Methods) of 0.73 ± 0.04 and 0.71 ± 0.04 (p̄ < 1 × 10⁻⁵, p̄ < 0.001) for black and white squares (the spatial profiles for the lowest contrast ±4% are not shown due to poor SNR of the spatial profile, see Materials and Methods).

Figure 8.

Contrast– response curves—observed versus predicted. A, Observed versus predicted responses in a rectangular spatial profile for different contrast levels. Negative contrasts represent the black squares (Ai) and positive contrasts represent the white squares (Aii). The path of the spatial profile is marked as a white rectangle over the map in the middle. Solid curves show the observed response, normalized to the maximal response across all curves. Dashed curves show the predicted response, normalized to the maximal predicted response across all curves. Correlation values (r) between the observed and predicted curves, computed before normalization, are marked on each graph. B, Contrast curves for the black (Bi, left) and white (Bii, right) stimuli compared between the observed and the predicted in two ROIs: The center of the square (red) and the mean over the square edges (blue), as depicted in the map. All activation values normalized to the activation at the edges for the 74% black condition for data and predictions separately, resulting in an activation value of 1 for the black/edge ROI for both the data and model.

The contrast–response curve for the edge and center responses was well predicted by the model (Fig. 8B; see Materials and Methods). In the observed data, the slope of the contrast–response curve for the edges was larger than for the center and the contrast–response curve of the black response at the center was steeper than that of white (Fig. 8B). The model predicted these main features of the data. RMSE values between the data and model contrast–response curves (calculated over n = 8 contrast sessions; see Materials and Methods) were as follows: 0.06 (for the black edges, p < 0.01), 0.14 (white edges, p < 0.01), 0.07 (black center, p < 0.01), and 0.07 (white center, p < 0.01).

Also, we examined whether or not the black versus white differences and their spatial relationships, observed for high contrast (shown in Fig. 3), persisted at lower contrast levels (4–16%). The preference for black was smaller at lower contrasts, specifically in the center of the cortical representation of the squares (compare the Black Center curve in Fig. 8Bi with the White Center curve in Fig. 8Bii, both plotted as solid curves). Predicted contrast curves for the center also demonstrated this difference (compare center curves in Fig. 8Bi and Bii, dashed curves). In addition, in the observed data we found that edge/center ratios were notably higher for white (2.76 ± 0.03, mean ratio ± 1 SEM) than black (1.77 ± 0.05) only at high contrasts (64–74%). Almost no difference was observed for the low and medium contrasts (4–16%, 2.47 ± 0.55 for white vs 2.46 ± 0.1 for black). This qualitative change in edge/center ratio for black versus white was also predicted by the model. Mean edge/center ratios for high contrasts are different for white versus black (2.90 ± 0.05 vs 2.0 ± 0.03), whereas for low contrast the ratios are more similar for white versus black (4.83 ± 0.3 vs 4.38 ± 0.44). This transition to a more balanced response for black and white at lower contrasts was also found in the time courses of activation (data not shown). The mechanism by which the model captures how the black versus white differences vary with contrast is considered in the Discussion.

Discussion

We measured population response in V1 of fixating monkeys presented with black and white squares. The evoked pattern showed enhanced responses at the edges, significant differences between responses to the black and white squares that were more emphasized at the center, and higher responses at corners than at edge middles. We modeled the population response at early times as the sum of neural mechanisms that responded to local contrast and to local temporal modulation of luminance. Our model predicted the early time evolution of evoked cortical VSD patterns to the black and white square stimuli with high accuracy and fine spatial detail.

Local contrast versus local temporal luminance modulation

In the VSD responses to squares, the strongest response was to local contrast. This was observed empirically and indicated quantitatively in the model fits where the coefficient for the contrast mechanism was bigger than the coefficients for local luminance modulation. This is in accordance with contrast encoding that has been studied extensively in V1 (Hubel and Wiesel, 1959; De Valois et al., 1982).

To represent cortical responses to surfaces in the model, we used positive and negative luminance change pathways (LTLM), representing temporal changes in illumination levels falling on the retina. The smaller weighting coefficients for the LTLM pathways captured the weaker responsiveness for luminance versus contrast. Consequently, the predicted maps computed from the weighted sums of surface and contrast pathways resembled the observed maps, showing higher activation along the squares' edges and lower activation at the center. Although the suppressive effects of the LTLM surround mechanism also acted more strongly on the squares' center than at the edges, its contribution to the edge versus center difference was minor and accounted for only a small fraction of the difference.

In a previous study (Ayzenshtat et al., 2012) we found that the VSD signal was positively correlated with an unsigned local luminance quantity. However, that study involved complex stimuli (natural color images of faces and their scrambled versions), which had a complex contrast-luminance interaction: negative interdependency. This is very different from the present study, where we used only simple square stimuli that enabled us to isolate edge/contrast content from surface content and to avoid possible complex interactions of higher order stimulus attributes (e.g., chromaticity and high-frequency features).

Filling in as a contributing mechanism for edge versus center modulation

Contrast and surface processing were modeled as separate subpopulations. Another candidate model for explaining modulation at the square's center is filling in from the edges, as proposed in Lamme et al. (1999). In the latter, orientation-defined squares evoked a delayed figure-ground (center-outside) difference at the square's center, and filling in was proposed as the underlying mechanism, which was attributed to attention-mediated, top-down processing (Roelfsema et al., 2002; Poort et al., 2012). The present study is essentially different: the times at which the main effects were found are qualitatively different (rising phase vs post-peak responses), as are the neuronal measures (differences in raw amplitude vs a more complex differential figure background). Attention as a facilitating mechanism is also unlikely due to the fixation-only paradigm and the early time frames of analysis. Therefore, filling in is unlikely as a good explanation for our observations. However, we do not rule out some overlap between the findings and corresponding models. For example, there may be some contribution of an early figure-ground signal to the observed differences. Additionally, late filling in and the early edge versus center difference may interact, especially in the presence of high-level processing.

Black versus white

Recent accumulated evidence indicates that neurons in V1 are more sensitive to black than to white stimuli (Jin et al., 2008; Yeh et al., 2009; Xing et al., 2010; Kremkow et al., 2014). Our data support these findings and further show the spatial characteristics of the black/white differences: a strong difference at the squares' center and a weaker difference at the edges. These effects are well explained by our model that includes individually weighted positive and negative LTLM (surface) pathways. The weight for negative surfaces had to be higher to fit the data. The response at the edges of the squares was mainly accounted for by a contrast (edge)-coding pathway with weighting that is independent of contrast sign.

Our data also indicate that the differences between black and white, and specifically the edge/center ratio, behave differently at high contrasts and at lower contrasts. This contrast dependence is captured by the encoding model despite black and white LTLM coefficients that remained fixed at 0.21 and 0.09 for all contrasts. The contrast dependence emerges from the model as follows: in low-contrast conditions, contributions from the LTLM pathways at the center are very small (due to LTLM values that are much lower than the L₅₀s, which are 0.5 or higher). In parallel, residual contributions from the contrast pathway (the outer regions of the PRF blur of the edges toward the center region) add a constant, equalizing baseline to both black and white. This equal contribution results in nearly equal black/white ratios for low contrasts at the center because the observed response is coming from the contrast mechanism that has equal black/white responses. At higher stimulus contrasts, contributions of the contrast signal to the center are minor relative to the LTLM signal and therefore do not have a notable effect on the observed black/white ratio.

Alternative explanations for black versus white asymmetry

The preference for black stimuli was modeled via different linear weighting of black-preferring and white-preferring cortical subpopulations. In a recent study, Kremkow et al. (2014) showed ON/OFF asymmetry in the LGN and V1, which was accounted for by nonlinear processing that was qualitatively different for the two pathways. Our cortical data did not exhibit a clear difference in nonlinearity for all regions (Fig. 8B; contrast curves). As a result, nonlinear processing was modeled symmetrically (with identical parameters) for the LTLM pathways, and the resulting predicted contrast curves are well fit to the data. However, we do not rule out such a contribution that was not explicitly modeled. As shown in Figure 7B, the black/white asymmetry was qualitatively captured (by >1 ratios), but some of the asymmetry remained quantitatively unexplained. The abovementioned account of feedforward (thalamic), nonlinear differences may be a complementary mechanism in accounting for the additional asymmetry.

Another possible mechanism for explaining the black preference could be that of sign-sensitive contrast responses, in which responses to negative contrast are higher than to positive contrast. While such a model could not account for the black–white difference being greatest at the center (where contrast is minimal), it may provide a plausible complementary neural mechanism that accounts for the portion of black versus white preference that remains unexplained by the model.

Divisive surround modulation explains the “corner” effect

An important finding in our data is the higher activation at regions corresponding to the square stimulus' corners, compared with regions corresponding to the middle of the edges. The proposed model captures this spatial effect qualitatively by introducing a surround calculation (Eq. 11). In this mechanism, the difference between what drives the surrounds of corner pixels and edge-middle pixels leads to different C₅₀ values for the two locations, despite similar contrast, consequently resulting in different predicted activation values. Moreover, since the model's account of the corner effect depends on PRF sizes (that vary with eccentricity), predictions will be influenced by stimulus eccentricity. Corners and edge middles with a large PRF and surround size would show similar activation due to the relative uniformity of their surround fields. Indeed, looking at the data and corresponding predictions shown in Figure 6A, we note a lesser corner effect for the peripheral (top left and bottom left) corners for both data and predictions. The same stimulus presented more foveally does demonstrate a corner effect for the more peripheral corners (Fig. 4C).

The corner versus edge-middle effects reported above are caused in the model by untuned surround suppression, pooled over all the neurons in the population sampled by VSDI. This approach does not account for orientation-tuned suppression, which has been shown to drive a higher degree of suppression in individual V1 neurons for colinear orientations compared with orthogonal orientations (Nelson and Frost, 1978; Levitt and Lund, 1997; Cavanaugh et al., 2002; Ringach et al., 2003; Shushruth et al., 2012; Henry et al., 2013). However, it was also shown that V1 neurons are suppressed for all surround orientations (Levitt and Lund, 1997; Cavanaugh et al., 2002; Ringach et al., 2003; Shushruth et al., 2012; Henry et al., 2013), implying a global, untuned suppression component. Furthermore, untuned global suppression has been shown to operate earlier than tuned suppression, shortly after stimulus onset and during the rising phase of response (Ringach et al., 2003), the time frame analyzed in this paper. The approach taken here, of early untuned suppression, is sufficient in reproducing our observations qualitatively. However, we do not rule out additional contribution of a tuned suppression component to the observed spatial modulations.

Notes

Supplemental material for this article is available at neuroimag.ls.biu.ac.il/Zurawel2014/Zurawel et al 2014 supplemental Information.pdf. The supplemental material contains Figures S1–S8. This material has not been peer reviewed.