Linking Macroscale Graph Analytical Organization to Microscale Neuroarchitectonics in the Macaque Connectome

Abstract

Macroscale connectivity of the mammalian brain has been shown to display several characteristics of an efficient communication network architecture. In parallel, at the microscopic scale, histological studies have extensively revealed large interregional variation in cortical neural architectonics. However, how these two “scales” of cerebrum organization are linked remains an open question. Collating and combining data across multiple studies on the cortical cytoarchitecture of the macaque cortex with information on macroscale anatomical wiring derived from tract tracing studies, this study focuses on examining the interplay between macroscale organization of the macaque connectome and microscale cortical neuronal architecture. Our findings show that both macroscale degree as well as the topological role in the overall network are related to the level of neuronal complexity of cortical regions at the microscale, showing (among several effects) a positive overall association between macroscale degree and metrics of microscale pyramidal complexity. Macroscale hub regions, together forming a densely interconnected “rich club,” are noted to display a high level of neuronal complexity, findings supportive of a high level of integrative neuronal processes to occur in these regions. Together, we report on cross-scale observations that jointly suggest that a region's microscale neuronal architecture is tuned to its role in the global brain network.

Introduction

A fundamental characteristic of the architecture of neural systems is their combined ability to process specialized information and to efficiently integrate information across segregated domains. Embracing network science as a theoretical framework to examine the topological organization of neural systems, studies have consistently shown features of an efficient communication architecture of macroscale brain networks, showing high local clustering of connections, pronounced community structure, short communication pathways (Bullmore and Sporns, 2009), and the formation of densely connected and centrally embedded hub regions (Sporns et al., 2007; van den Heuvel and Sporns, 2011, 2013a).

For the mammalian brain, network organizational features have mostly been studied at the macroscopic scale, describing and examining neural systems in terms of large-scale brain regions interconnected by bundles of long-distance white matter axonal projections (Goldman-Rakic, 1988; Hagmann et al., 2008; Iturria-Medina et al., 2008; van den Heuvel et al., 2012). In parallel, decades of pioneering histological studies have provided a wealth of evidence about the neuroarchitectonic organization of cortical regions at the microscopic scale, illustrating that cortical regions can differ widely in variety of receptor binding sites, cell types, neuronal count, synaptic connectivity, etc. (Brodmann, 1909; Schüz and Miller, 2002; Garey, 2006; Amunts and Zilles, 2012). However, how the macroscale network topological architecture of the brain network is linked to the neuroarchitectonic organization of cortical regions at the microscale remains an open question.

To start addressing this question, the present report focuses on the relationship between network organizational features of the large-scale anatomical wiring of the primate brain and cellular and neuronal properties of the interconnected cortical regions. At the macroscale, a connectome map describing the organization of corticocortical wiring of the macaque cortex was reconstructed on the basis of metadata from anatomical tracer studies (Stephan et al., 2001), which was combined with information on the functional role of these edges as collated from metadata of strychnine connectivity studies (Stephan et al., 2000). At the microscale, information on the cytoarchitectonics of cortical regions was collated from a series of studies examining the neuronal architecture of cortical regions of the macaque cerebral cortex, including information on cortical cell and neuronal count (Collins et al., 2010), dendritic branching of cortical layer III pyramidal neurons (Elston, 2000), and glucose metabolism and neurotransmitter binding levels (Kötter et al., 2001), aspects that have all been suggested to relate to the processing and integration capacity of neurons. Examining the neuroarchitectonic embedding of macroscopic topological network attributes can provide new insights into the workings of the mammalian connectome.

Materials and Methods

In what follows, we first describe the parcellation atlas and connectivity matrices used in our analyses, followed by the methods used for the macroscale graph analysis and collation of the microscale neuroarchitectonic information.

Parcellation atlas

Connectivity and cytoarchitectonic data were analyzed using the combined Walker-von Bonin and Bailey (WBB47) parcellation atlas, dividing the macaque cortical surface into 39 nonoverlapping cortical regions, as introduced by Stephan et al. (2000). The WBB47 atlas forms a conjunction of the cortical parcellation of the 1947 von Bonin and Bailey atlas (von Bonin and Bailey, 1947) for parietal, occipital, and temporal regions and the 1940 Walker atlas for prefrontal brain areas (areas 8A, 8B, 9, 10, 11, 12, 13, 14, 45, and 46) (Walker, 1940) (see Fig. 1 and Table 1 for regions).

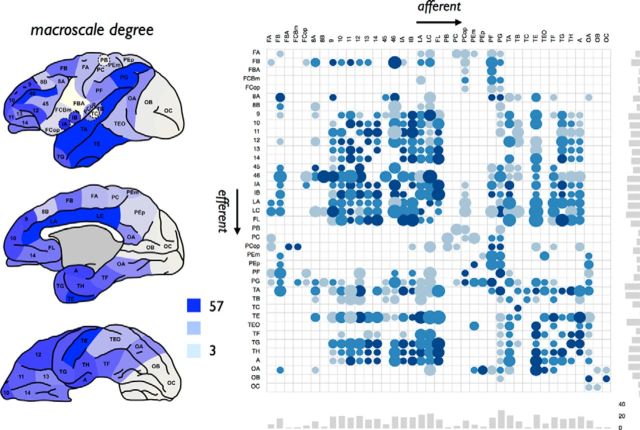
Figure 1.

Anatomical connectivity matrix. Left, Degree (i.e., total number of efferent and afferent connections) of cortical regions. The figure represents a lateral, medial, and ventral view, as originally presented by Stephan et al. (2000). Right, Matching directed weighted connectivity matrix derived from the CoCoMac database (Stephan et al., 2001). Rows represent the efferent anatomical connections of regions; columns represent afferent connections of regions. Dots represent anatomical projections; size reflects estimated projection distance (small to large), color (light blue to dark blue), the averaged reported connectivity strength. Bottom and side bar plots represent, respectively, the in-degree and out-degree of the 39 cortical regions.

Table 1.

Overview of the mapping of all neuronal measures included in the meta-analysis to the WBB47 parcellation^a

WBB47 atlas	Pyramidal complexity	Cell and neuronal count	PET glucose metabolism	Receptor densities	Visual hierarchy
FA	4 (ER02)	30, 36 (CA10)	Precentral/postcentral gyrus (CR00)	F1 (KO01)	—
FB	6 (ER02)	33, 34, 36, 38 (CA10)	—	F2v, F2d, F3, F6, F7 (KO01)	—
FBA	—	29, 30, 35, 38 (CA10)	—	F4v, F4d (KO01)	—
FCBm	—	26, 35 (CA10)	—	F5 (KO01)	—
FCop	—	26 (CA10)	—	—	—
8A	—	40 (CA10)	Lateral frontal (CR00)	—	FEF (HI00)
8B	—	37, 38 (CA10)	—	—	—
9	9d (EB11)	37, 40 (CA10)	—	—	—
10	10 (E00, EB11)	41 (CA10)	Principal sulcus (CR00)	—	—
11	11 (E00)	40 (CA10)	—	—	—
12	12 (E00, EB11)	26, 35, 40 (CA10)	—	—	—
13	13 (EB11)	26 (CA10)	—	—	—
14	—	26, 40 (CA10)	—	—	—
45	—	40, 41 (CA10)	—	—	—
46	46 (EB11)	41 (CA10)	—	—	reg46 (HI00)
IA	—	26 (CA10)	—	—	—
IB	—	24, 26, 35 (CA10)	—	—	—
LA	Ant cing (EBD05)	39, 41 (CA10)	Anterior cingulate (CR00)	—	—
LC	Post cing (EBD05)	39 (CA10)	Posterior cingulate (CR00)	—	—
FL	—	41 (CA10)	—	—	—
PB	3b (ER02)	29 (CA10)	—	—	—
PC	—	29 (CA10)	Precentral/postcentral gyrus (CR00)	—	—
PCop	—	32, 35 (CA10)	—	—	—
PEm	5 (ER02)	31, 32 (CA10)	—	VIP (KO01)	PIP, VIP (HI00)
PEp	7m (EO1)	15, 31 (CA10)	—	PO, MIP, PEP (KO01)
PF	7b (ER02)	32 (CA10)	Lateral parietal, supramarginal gyrus (CR00)	—	7a (HI00)
PG	MT, LIPv, 7a (ER97)	19, 20, 28, 32 (CA10)	Lateral parietal, supramarginal gyrus (CR00)	LIP, PG, MT, MTp, MST (KO01)	7a, LIP (HI00)
TA	STP (ETR99, E01)	23, 27, 28 (CA10)	—	FST (KO01)	MSTl, FST, STPa, STPp, MSTd (HI00)
TB	—	25 (CA10)	—	—	—
TC	A1 (EO10)	24 (CA10)	—	—	—
TE	TE (E99, EO11), IT (EBD05)	18, 22, 23 (CA10)	—	—	PITd, PITv, CITv, AITv, AITd, CITd (HI00)
TEO	TEO (ER98)	17, 18, 20, 21, 22 (CA10)	Lateral temporal (CR00)	—	VP, V3, V3A, V4, PO, DP, VOT, V4t (HI00)
TF	—	22 (CA10)	—	—	TF (HI00)
TG	—	23 (CA10)	—	—	—
TH	—	22 (CA10)	—	—	TH (HI00)
A	—	22 (CA10)	—	—	—
OA	MT (ER97), V4 (ER98)	14, 15, 16, 17, 19, 20, 21, 22 (CA10)	Lateral occipital (CR00)	V3v, V3d, V3A, V4v, V4d, V6A, V4t, MT (KO01)	V2, VP, V3, V3A, V4, PO, DP, VOT, MT (HI00)
OB	V2 (ER97, ER98)	1, 2, 3, 4, 5, 8, 19, 20, 21 (CA10)	—	V2v, V2d (KO01)	V2 (HI00)
OC	V1 (ER97, ER98, ETR99)	6, 7, 9, 10, 11, 12, 13 (CA10)	Cuneus/lingual gyrus (CR00)	V1 (KO01)	V1 (HI00)

^aThe first column lists all cortical areas included in the WBB47 parcellation, to which the areas listed in the subsequent columns were mapped. Pyramidal complexity information was mapped from a series of studies by Elston and colleagues: E00 (Elston, 2000), E01 (Elston et al., 2001), EB11 (Elston et al., 2011b), EBD05 (Elston et al., 2005), EO10 (Elston et al., 2010), EO11 (Elston et al., 2011a), ER02 (Elston and Rockland, 2002), ER97 (Elston and Rosa, 1997), ER98 (Elston and Rosa, 1998), and ETR99 (Elston et al., 1999); cell and neuronal count was mapped from a study by Collins and colleagues: CA10 (Collins et al., 2010); PET glucose metabolism from work by Cross and colleagues: CR00 (Cross et al., 2000); receptor fingerprint from Kötter and colleagues: KO01 (Kötter et al., 2001); and visual hierarchy from Hilgetag and colleagues: HI00 (Hilgetag et al., 2000).

Macroscale structural connectivity (SC) data

Information on the presence (and absence) of macroscale corticocortical white matter axonal projections between WBB47 regions was obtained from the open source CoCoMac neuroinformatics database of published macaque anatomical tracer studies (Stephan et al., 2001) (CoCoMac, RRID: nif-0000–00022). This database includes information on cortical parcellation schemes of the macaque cortical surface, including the combined von Bonin and Bailey (1947) and Walker (1940) atlas. The CoCoMac database contains information on studies making report of the specific presence (i.e., an examined and observed anatomical tract between brain regions) as well as the specific absence (i.e., an examined, but not found tract) of anatomical projections between brain regions. The database was queried for the existence of tracer studies reporting on the presence (or absence) of anatomical projections between each pair of regions in the WBB47 atlas. An anatomical tract between region i and region j was included in the SC matrix if at least ≥5 reports were made on this potential tract in the CoCoMac database, and if the number of positive reports (i.e., reports of the presence of an anatomical connection of any strength) or “prevalence” across these ≥5 studies was at least two-thirds (66%) (de Reus and van den Heuvel, 2013). Testing other settings (e.g., number of reports being ≥4 or ≥6 and the prevalence set to 60% or 70%) revealed consistent findings. Based on these query results, a 39 × 39 SC matrix was constructed between the 39 cortical WBB47 regions. As the CoCoMac database provides information on the source and target site of each tracer injection, the connectivity matrix included a directed SC matrix. No clear information on the sex or age of the macaque monkeys was available from the CoCoMac database; the included dataset therefore most likely consists of combined information on connectivity in both male and female macaque cortex. Spatial coordinates of the included WBB47 regions were taken from information provided by the CARET software package (Van Essen et al., 2001), and from which the Euclidean distance between region pairs was computed as a proxy of the projection distance of anatomical pathways.

Macroscale functional connectivity data

Information on corticocortical functional connectivity (stryFC) was obtained from a meta-study by Stephan et al. (2000a). Using the WBB47 parcellation scheme, the macaque functional connectivity (stryFC) dataset, as presented by Stephan et al. (2000a), contains information on directed unihemispheric corticocortical functional connections between the 39 WBB47 regions of the macaque cortex collated from strychnine neuronography studies (Stephan et al., 2000). The technique of strychninization as developed by Dusser de Barenne (1924) and Dusser de Barenne and Mcculloch (1938) involves the application of the GABA_A and glycine receptor antagonist strychnine on the cortical surface, leading to local disinhibition, thereby facilitating glutamatergic transmission of action potentials, causing multisynaptic spread of the signal across long-distance axonal projections (Dusser de Barenne, 1924; Dusser de Barenne and Mcculloch, 1938). Early studies have shown that strychnine induced patterns of cortical activation are highly reproducible within a single animal, stable for any given area across individuals, and highly similar to those found after electrical stimulation (Dusser de Barenne and Mcculloch, 1938). This method has thus been suggested as an approach to map functional connections between brain regions (Dusser de Barenne and Mcculloch, 1938). Interestingly, literature does not just describe anatomically connected areas to become activated after strychninization, but regular reports have been made on anatomical projections to have no net excitatory effect on target regions or even to consistently induce deactivation in target areas (Dusser de Barenne et al., 1941). The application of strychninization techniques thus provides the unique opportunity to map net excitatory as well as net inhibitory influence of brain regions on each other, information that is not directly accessible by means of modern functional neuroimaging techniques, such as EEG or fMRI.

Macroscale graph analytical analysis

Network science was used to elucidate aspects of topological organization of the SC network, including the assessment of nodal and edge-centric metrics (Rubinov and Sporns, 2010) (Brain Connectivity Toolbox, RRID nlx_143925). The following commonly used nodal metrics were computed from the SC matrix:

1. Nodal total degree and in-degree and out-degree, being the number of afferent and efferent connections of a node;

2. Clustering coefficient, describing the level of local connectedness of a node, computed as the proportion of connected triangles around a node;

3. Shortest path length, describing the number of binary steps needed to travel from source node i to target node j in the network, averaged over all j;

4. Eigenvalue centrality, describing the largest eigenvector of the eigenvalue decomposition of the connectivity matrix, providing an estimate of the centrality of each node in the overall network (Rubinov and Sporns, 2010; Zuo et al., 2012; de Lange et al., 2014).

Community structure

Functional domains of the macaque brain were extracted from the stryFC matrix by means of Newman's modularity algorithm as present in the Brain Connectivity Toolbox (Rubinov and Sporns, 2010) (1000 runs, taking the highest modularity value Q) (Kofuji and Newman, 2004). Similar to the community analysis performed by Stephan et al. (2000a) on the stryFC matrix, community detection resulted in three communities (see Results). In addition, performing a two-step approach in which each of these main communities was again examined individually for the existence of subclusters using Newman's modularity algorithm revealed a total of 8 smaller subnetworks (see Results). These communities were taken as a functional modular partitioning of the macaque cortex. A similar two-step approach was used to detect possible community structure in the anatomical SC matrix.

Testing robustness of community structure.

Robustness of community structure was examined by means of a random rewiring procedure (Karrer et al., 2008). This procedure involves the random rewiring of p% edges (randomly selected) of the matrix across a set of iterations, followed by a subsequent comparison of the community structure of each of the randomized matrices with the community structure of the original matrix. Here, 1000 random matrices were computed with p = 10%, and the overlap in community structure between the original and randomized situations was computed using the Rand index (Rand, 1971), which involves the pairwise count of the number of node pairs that are classified in the same or different modules across the module assignments of the two compared matrices (Karrer et al., 2008) (a Rand index of 0 indicates no overlap, 1 indicates complete overlap). To assess a null distribution of Rand-indices that might occur at chance level (Bassett et al., 2008; van den Heuvel et al., 2010), module assignment of the original matrix was randomized (10,000 runs) and the Rand index with the original module assignment was computed. A p value was then assigned to the original observed Rand-indices (i.e., between original module assignment and module assignments of the 10% randomized matrices) by testing for statistical difference between the two distributions.

Comparison of the community structure of anatomical and functional data.

The Rand index was also used to directly compare the modularity structure of the SC and stryFC matrix. The Rand index between the two-step community structure of the SC and stryFC was computed, and statistical significance was assessed by permutation testing using a similar approach as described above: The modular assignments of the nodes of both the SC and stryFC were randomized (thus keeping the number and size of the modules intact) across 10,000 permutations, and the Rand index in the random situations was computed. This resulted in a null distribution of effects occurring at chance level. Using this null distribution, the original Rand index of overlapping community structure of the SC and stryFC matrix was assigned a p value as the percentage of observations in the random condition exceeding the original value.

Intramodular and intermodular connectivity profile of nodes

Within-module degree z-score.

With the functional modules describing a modular decomposition of the network, the level of intramodular involvement of each node i was examined by means of the within-module degree z-score z_i, describing the extent to which node i is structurally connected to the other nodes in its module (Rubinov and Sporns, 2010), with a high z_i-score reflecting a relatively high involvement of a node within its own community.

Participation coefficient.

The intermodular character of a node in the network was assessed by computing the participation coefficient P_i of each node i, formally given by the following:

with k_iS being the number of structural links from node i to nodes in functional module S, m the number of modules, and k_i the total degree of node i. A high P_i indicates a strong intermodular character of node i, showing that its connections are relatively equally distributed over the modules in the network.

Rich club organization

A rich club organization of a network reflects the existence of a series of sets of nodes with increasing degree k that display a level of interconnectivity exceeding the level of connectivity that can be expected on basis of chance alone. Formally, the unweighted rich club coefficient Φ(k) is computed as the fraction of the number of connections present within the subnetwork S of nodes with a degree >k (van den Heuvel and Sporns, 2011) and the total number of possible connections in S (Colizza et al., 2006):

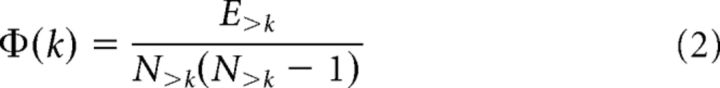Φ(k) is typically normalized by Φrandom(k), being the average rich club coefficient for each k of a set of randomized graphs (acquired by randomizing the adjacency matrix, while preserving the degree sequence of the network), resulting in a normalized rich club coefficient Φnorm(k). Φrandom(k) was computed for a set of a 1000 random networks (van den Heuvel and Sporns, 2011). A network is said to display rich club organization if Φ(k) > Φrandom(k) (or, equivalently, Φnorm(k) >1) for a range of increasing k. Taking Φrandom(k) as a null distribution of the level of connectivity between nodes of degree >k, the level Φ(k) (and thus the ratio Φnorm(k)) was assigned a p value as the percentage of observations in Φrandom(k) exceeding Φ(k). Previous studies have described consistent structural rich club organization of the mammalian brain: human (van den Heuvel and Sporns, 2011; van den Heuvel et al., 2012; van den Heuvel and Sporns, 2013b), cat (Zamora-López et al., 2009; Zamora-López et al., 2011; de Reus and van den Heuvel, 2013), and macaque (Harriger et al., 2012) brain, for different resolutions and for different parcellation schemes.

Rich club selection.

In this study, the cortical rich club was taken as the set of nodes showing a total degree k >38 (van den Heuvel and Sporns, 2011; Harriger et al., 2012). Nodes participating in the rich club were classified as “rich club hub nodes”; other nodes were categorized as “peripheral nodes” (van den Heuvel et al., 2012; Towlson et al., 2013).

Classification of edges

This classification of network nodes into rich club hub nodes and peripheral nonhub nodes allowed for the categorization of edges into the following: (1) rich club connections, edges between two rich club nodes; (2) feeder connections, edges linking peripheral nodes to hub nodes (feeder-in connections) and vice versa (feeder-out connections); and (3) local connections, edges interlinking peripheral nodes (van den Heuvel et al., 2012).

In addition, edges were classified according to their role with respect to module formation in the network. Edges were labeled as intramodular when they connected nodes within the same functional module, and intermodular when they linked two nodes in two different modules (de Reus and van den Heuvel, 2013; van den Heuvel and Sporns, 2013b).

Microscale regional measures of layer III pyramidal neurons: soma size, spine count, spine density, and dendritic tree size

At the cellular level, basal dendrites are the largest target site for synaptic input onto cortical pyramidal neurons (Larkman, 1991; Lübke and Feldmeyer, 2007). To examine regional variation in neuronal morphology, Elston and colleagues performed a series of studies (e.g., Elston et al., 2010) investigating layer III pyramidal neurons across multiple sites of the macaque cortex. Combining information from their studies (for a list of all included papers, see Table 1), we collated morphological data from cortical layer III pyramidal neurons of 25 distinct regions. These regions were manually mapped by two anatomy experts to the cortical regions defined in the WBB47 atlas, obtaining pyramidal information of 22 of the 39 cortical regions of the WBB47 parcellation atlas. Table 1 provides detailed information on the performed regional mapping, including information on the original source of each metric value. Collated data on the morphology of layer III pyramidal cells included information on the following: (1) size of the pyramidal dendritic tree, (2) estimated total count of spines per cortical area of an average pyramidal neuron, (3) dendritic spine density, and (4) soma size of the layer III pyramidal neurons.

Microscale regional measures of cell count, cell density, and neural cell density of cortical regions

Information on the total cell count of regions of the macaque cortex was taken from the recent study of Collins et al. (2010), quantifying cell count and cell density of the entire cortex of a single macaque. In their study, Collins et al. (2010) divided the cortical mantle of the right hemisphere into 41 distinct blocks and acquired detailed information on the following: (1) total cell count (including glial cells and neurons), (2) neural cell count, (3) ratio of neurons to non-neuron cells, (4) total cell density (including non-neuron cells) (millions/g), and (5) neuronal cell density (millions/g) and neuronal cell percentage of each tissue block. The spatial locations of the 41 cortical blocks, as reported by Collins et al. (2010), were manually allocated to the regions in the WBB47 parcellation atlas (Table 1 provides a description of the mapping). The average neuronal characteristics of the brain pieces contained in each of the WBB47 cortical regions were computed (Table 1), obtaining cellular information of all regions of the WBB47 parcellation atlas.

Hierarchical organization of the visual system

In addition to information on the neuronal organization of cortical regions, information on the hierarchical ordering of regions of the visual system, as published by Hilgetag et al. (2000), was included in our network analysis. Hilgetag et al. (2000) defined the hierarchical ordering of visual regions based on interlaminar differences in cortical source and target layers, using the classification as proposed by Felleman and Van Essen (1991), classifying the interareal connections as ascending, descending, or lateral. Based on these classifications, Hilgetag et al. (2000) defined a hierarchical arrangement of 30 cortical areas of the visual system of a single hemisphere of the macaque cortex, assigning to each area a peak frequency of its location in the hierarchical arrangement, ranging from 1 (low hierarchy with predominantly feedforward (ascending) efferent connections and feedbackward (descending) afferent connections) to 16 (high in hierarchy with predominantly feed-backward efferent connections and feedforward afferent connections). The spatial location of all regions and their hierarchical scores were mapped to the WBB47 atlas (for the mapping, see Table 1), providing information on visual hierarchy of 13 of the 39 cortical areas of the WBB47 atlas.

Regional measures of metabolic activity

Cortical regional variation in cerebral glucose metabolism was obtained from a glucose metabolic PET imaging study by Cross et al. (2000), examining 6 young macaques (mean ± SD: 6.2 ± 2 years of age). After intravenous injection of the glucose uptake tracer fludeoxyglucose, tomographic (PET) images were acquired and overlaid with an anatomical T1 image, yielding quantitative reports of the rate of glucose metabolism of cortical regions. In addition to whole-brain levels, Cross et al. (2000) reported levels of glucose metabolism for 11 cortical structures (and 4 subcortical structures). These cortical structures were mapped to 11 regions in the WBB47 atlas. Table 1 summarizes the assignments across the used parcellation schemes.

Receptor fingerprint

Interregional variation in neurotransmitter receptor densities in the macaque cortex was taken from the study by Kötter et al. (2001), providing a “receptor fingerprint” (Zilles et al., 2002) of the chemoarchitecture of the unihemispheric cortical visual and motor system. For the motor and visual regions, ligand binding densities for five receptor types were reported, including the glutamatergic AMPA receptor, γ-aminobutyric acid receptor A (GABA_A), serotoninergic receptor 5-HT₂, and the muscarinergic acetylcholine receptors M₁ and M₂. All 29 reported areas were mapped to 11 areas in the WBB47 parcellation atlas, of which Table 1 provides a detailed description.

Statistical analyses

Overlap between macroscale structural and functional connectivity data.

Potential overlap between the anatomical SC connectivity matrix and strychnine derived stryFC connectivity matrix was assessed by means of the Mantel test for comparison of matrices (Mantel, 1967; van den Heuvel et al., 2014). A distance matrix was computed between the binary SC and stryFC expressing which cell entries displayed a 1 or 0 in both matrices, with the level of overlap O computed as the density of distance matrix. Permutation testing was used to obtain a null distribution of overlap scores that are present under the null-hypothesis of no overlap between the two matrices, randomizing the entries of the SC and stryFC matrix for 10,000 iterations (using the Maslov and Sneppen algorithm; Maslov and Sneppen, 2002; Rubinov and Sporns, 2010) with the overlap computed for each iteration. Based on this null distribution, the original observed overlap O between the SC and stryFC matrix was given a p value as the fraction of the null distribution that exceeded O (e.g., Bassett et al., 2008; van den Heuvel and Sporns, 2011; van den Heuvel and Sporns, 2013b).

Associations between macroscale network and microscale architectonic metrics.

Assessment of potential associations between graph topological metrics at the macroscale (in total 13 metrics, e.g., degree metrics, clustering, path length, participation coefficient) and architectonic metrics at the microscale (in total 18 metrics, e.g., metrics of pyramidal complexity, neuronal count, metabolism, receptor densities) was performed by computing Pearson's correlations. Between the two scales, the evaluation of a total of 234 tests would be possible, yielding the need for a proper correction to the α level. In situations of multiple testing, a correction method that balances Type I and Type II errors is needed, that is, a correction method that controls for the occurrence of false discoveries, without jeopardizing sensitivity (i.e., including too many false negatives). Classical Bonferroni correction is known to provide good control for family-wise error, but in case of existence of strong dependencies between the examined metrics, most often at the cost of Type II errors. In our study, and as commonly reported, the examined macroscale graph metrics showed an average correlation of 0.375 (SD: 0.28) (Lynall et al., 2010; van den Heuvel and Sporns, 2011), and the microscale metrics showed an average correlation of 0.37 (SD: 0.32). Several correction methods in such situations of correlated variables have been proposed. The false discovery rate (FDR) is designed to control for the expected proportion of incorrectly rejected null hypotheses (i.e., Type I errors) and can also incorporate information on the correlation between the examined variables (Benjamini and Yekutieli, 2001). Across the set of microscale–macroscale correlations, the FDR corrected α level q = 0.05 yielded 0.0121.

FDR methods provide a less stringent control compared with methods that control for family-wise error rate (e.g., Bonferroni), which are designed to reduce the probability of even one false discovery. To control for Type I error in a more conservative way while still keeping enough sensitivity, methods to estimate the effective number of tests from which a “partial Bonferroni”-corrected α can be computed have been designed (Li and Ji, 2005; Gao et al., 2008; Shriner et al., 2008). To this end, we applied a method based on principal component analysis (PCA) (Gao et al., 2008). A PCA analysis involves the transformation of a dataset of related variables to a set of linearly uncorrelated variables, named “principal components,” with the extracted components ordered according to the amount of explained variance. The procedure involved the following steps (Gao et al., 2008): First, at the macrolevel, a PCA was performed on the data matrix of the macroscale metrics, and the number of largest components together explaining 95% of the total variance in the data was selected. Following the same approach, also a PCA was performed on the data matrix of the microscale metrics, and the number of components together explaining 95% of the total variance of the microscale data were selected. For the macroscale graph theoretical data, the first three largest components were found to explain >95% of the variance; for the microscale data, the first two largest components were found to explain >95% of the variance. Finally, based on these PCA results, a partial Bonferroni correction factor was computed as the number of tests performed between the 3 and 2 PCA components, resulting in an adjusted α of 0.05/(3 × 2) = 0.0083.

Based on these two statistical thresholds (with FDR controlling for FDR and partial Bonferroni for family-wise error), evaluated macroscale–microscale correlations reaching FDR correction were taken as trend-level effects, and effects reaching the more conservative partial Bonferroni correction were taken as significant. All other correlations were labeled as statistically nonsignificant effects.

Statistical analysis of differences in microscale metrics between hub and nonhub regions.

Nonparametric permutation testing was used to examine potential differences of microscale metrics between hub and nonhub regions. For the microscale metric of interest, the group difference between the mean values of rich club regions and peripheral regions was computed. A null distribution was computed by randomizing group assignment (i.e., hub vs peripheral), and the difference between the group means of the random groups was computed for 10,000 permutations. A p value was then assigned to the original difference (i.e., rich club vs peripheral nodes) as the fraction of observations of the null distribution exceeding the observed group difference. Based on the PCA results of the microscale metrics (see above), effects reaching a partial Bonferroni corrected α of 0.05/2 were interpreted as statistically significant.

Statistical analysis of differences on edge metrics.

Potential differences between rich club, feeder, and local edges on edge properties were tested using permutation testing by random group assignment, using a similar approach as described above. In total, across 3 edge metrics (edge directionality, edge projection length, stryFC) and across 4 classes (i.e., rich club, feeder-in, feeder-out and local), a total of 3 × 4 = 12 tests were performed. Tests reaching a strict Bonferroni corrected α level of 0.05/12 = 0.004 were interpreted as statistically significant.

FE91 atlas

The WBB47 atlas was taken as the primary parcellation approach in our study. Across the literature, several parcellation atlases of the macaque cortex have been presented. To verify that observed microscale–macroscale correlations in our study were independent of the selected WBB47 atlas, we validated our findings in the context of a second parcellation atlas. Another commonly used parcellation atlas of the macaque cortex is the Felleman and Van Essen 91 (FE91) atlas (Felleman and Van Essen, 1991). The FE91 atlas also describes a single hemisphere and includes a parcellation of the cerebral cortex into 78 nonoverlapping regions. Similar to the approach used for the WBB47 atlas, data on the anatomical connectivity between the FE91 regions were extracted from the CoCoMac database. To obtain good coverage of all region-to-region combinations of the more fine-grained FE91 atlas, information on all node-pairs was included without requiring a minimum number of reports, with a “1” included in the SC matrix when at least 66% (two-thirds) of the reports on a node-pair were positive; otherwise, a “0” was included in the matrix. This resulted in an SC connectivity matrix of 18.4% density. Next, using a similar approach as described for the main WBB47 analysis, the collated microscale data (i.e., metrics of pyramidal complexity, neuronal count, receptor levels, etc.) was manually mapped to the FE91 regions. Macroscale–microscale associations observed in the WBB47 dataset were validated with the FE91 dataset. Mapping resulted in pyramidal complexity data of 25 cortical regions (32% of total FE91 regions), neuronal and total cell count data of 78 regions (100%), visual hierarchy of 32 regions (41%), receptor levels of 20 regions (26%), and metabolism data of 11 regions (14%). Remapping of the stryFC data to the FE91 parcellation was not feasible because of the nature of the stryFC dataset, so we limited the FE91 analysis to anatomical SC effects.

Results

We will first describe the results of the graph analytical analysis of the macaque cortical network, followed by the cross-resolution analysis of the graph analytical findings in relation to collated microscale information of the cortical regions, associating macroscale network attributes with information on regional variation in dendritic complexity of layer III pyramidal cells, total cell and neuronal count, receptor binding levels, hierarchical ordering, and glucose metabolic activity.

Macroscale graph analytical findings

Anatomical connectivity

The macaque cortical brain network, represented by a 39 × 39 unweighted directed anatomical connectivity matrix (SC) (Fig. 1), was found to be 35.0% dense, to show a high level of clustering (0.73, normalized clustering: 1.14, p < 0.001, 10,000 permutations) and to have a short path length close to that of random networks (1.75, normalized shortest path length: 1.04), together indicating a small-world organization (small-world index: 1.09). Consistent with previous observations (Harriger et al., 2012; Goulas et al., 2014), the macaque anatomical network displayed an overall rich club organization, showing a Φnorm >1 for 11<k<41 (p < 0.001, surviving Bonferroni correction for 42 performed tests of different k levels). Community detection (Fig. 2, left) showed the existence of two main structural modules (Rand index at 10% random rewiring: 0.72, p < 0.001, 10,000 permutations), overlapping visual–somatosensory and frontal–temporal regions. Two-step community detection revealed 2 and 3 submodules, respectively, resulting in a total of 5 anatomical (sub)clusters (Rand index at 10% random rewiring: 0.86, p < 0.001, 10,000 permutations).

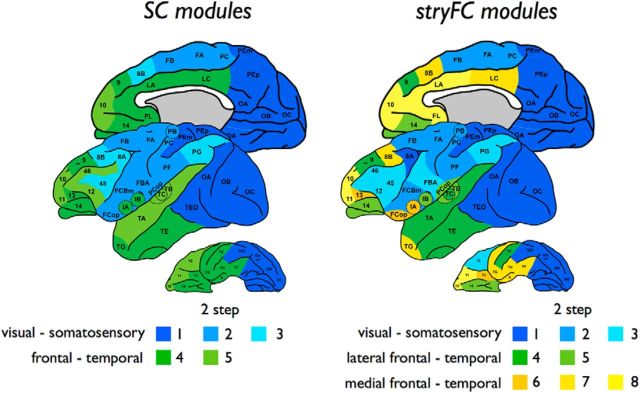
Figure 2.

Anatomical and functional community structure. Figure represents a side-to-side presentation of the community structure of the anatomical and strychnine functional macaque brain network. Left, Community structure of the anatomical SC network. Community detection revealed two main communities, including a community overlapping somatosensory and visual regions (blue) and a community overlapping frontal and temporal cortical regions (green). Using a two-step community detection approach (in which the main first-level communities were subject to community detection themselves; see Materials and Methods) revealed the existence of, respectively, three subclusters (light, medium, and dark blue) and two subclusters (light and dark green). Right, Community structure of the stryFC network. First-level community detection revealed three main communities, including a visual–somatosensory community (blue), a lateral frontal–temporal cluster (green), and a medial frontal–temporal cluster (yellow). Two-step community detection revealed three functional subclusters of the visual–somatosensory network, overlapping a visual (dark blue), motor and sensory network (medium and light). In addition, two-step community detection of the lateral frontal–temporal network revealed two subclusters (light and dark green) and three subclusters in the medial frontal–temporal network (light, medium, and dark yellow). Formal statistical testing of the anatomical and functional community structure revealed significant overlap between the two-step community structures (p < 0.001; see Results).

stryFC

Cross-reference of the stryFC with the anatomical SC matrix revealed a significant overlap (1.55 times more overlap than in the random condition, p < 0.001, Mantel test, 10,000 permutations). Overlapping the analysis of Stephan et al. (2000), community detection revealed the existence of 3 main functional communities, including a visual–somatosensory cluster (consisting of 18 regions), a lateral frontal–temporal cluster (8 regions), and a medial frontal–temporal cluster (13 regions) (Rand index at 10% random rewiring: 0.82, p < 0.001, 10,000 permutations) (Fig. 2, right). Two-step community detection revealed further subclustering (Rand index at 10% random rewiring: 0.84, p < 0.001, 1000 permutations). The visual–somatosensory community revealed 3 subclusters, consisting of 6, 7, and 5 regions, respectively, including visual (dark blue) and motor and sensory regions (medium and light blue shades). The medial temporal–frontal cluster included 3 subclusters, describing a frontal subcluster of 4 regions, including 10/11/FL and cingulate region LA (light yellow), a subcluster of 6 regions, including cingulate cortex LC, frontal region 8B and temporal regions (e.g., TH, TF, A) (medium yellow) and a subcluster of 3 regions including insular region IA and frontal regions 13 and FCoP (dark yellow). Community structure of the lateral frontal–temporal community involved 2 subclusters, including a subcluster overlapping auditory regions and frontal region 14 (4 regions, light green) and a subcluster overlapping superior/inferior temporal cortex (3 regions, dark green) and frontal area 9.

Figure 2 shows a side-by-side comparison of the two-step structural and functional community structure, demonstrating a relatively high level of overlap between the anatomical and functional community structure. Formal statistical testing of this overlap (see Materials and Methods) revealed a significant level of consistency between functional and structural module structure (Rand index: 0.81, p < 0.001, 10,000 permutations). Furthermore, the stryFC (sub)clusters, despite the relatively coarse parcellation of the cortex, tend to show overlap with functional networks as reported from resting-state fMRI recordings in the macaque (Hutchison et al., 2011; Hutchison and Everling, 2012). Examining this potential overlap in detail is out of the scope of our paper, but future studies examining the consistency (and differences) between stryFC and resting-state fMRI derived functional networks would be of interest.

Macroscale network–microscale metric associations

Figure 3 reports the correlations between all possible microscale–macroscale metrics and indicates which effects survived statistical evaluation. In what follows, we describe the most prominent findings, focusing on effects reaching FDR (labeled as trend-level effects) and partial Bonferroni corrected α levels (for the computation of these corrected α levels, see Materials and Methods).

Figure 3.

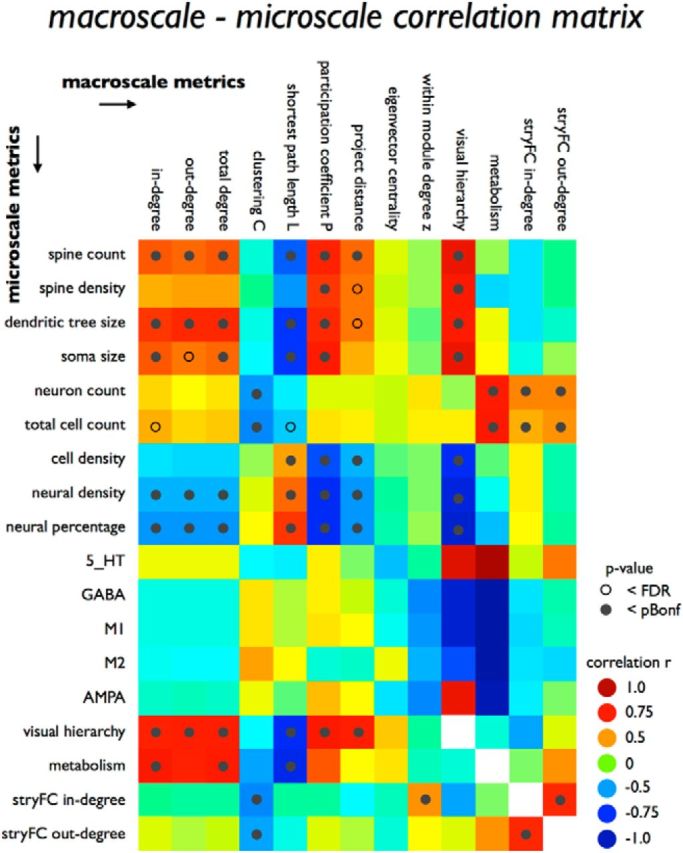
Macroscale–microscale metrics correlations. Figure plots all correlations between macroscale metrics (columns) and microscale metrics (rows). Green to blue represent negative associations; yellow to red represent positive correlations. Open circle represents effects reaching FDR correction for multiple testing; filled circle represents effects reaching the stricter partial Bonferroni correction. Metrics of stryFC, visual hierarchy, and metabolism were compared both to microscale metrics as well as to the class of macroscale metrics and are thus included in both categories.

Relationship between macroscale connectome organization and cytoarchitectural and dendritic architectural properties of layer III pyramidal neurons

Association with macroscale degree

Basal dendrites are the largest target site for synaptic input of cortical pyramidal neurons (Larkman, 1991; Lübke and Feldmeyer, 2007). Microscale data on regional variation in pyramidal cell complexity, as obtained from a series of studies by Elston et al. (2010), included information on the length of dendritic tree, estimated total count of spines per cortical area of an average pyramidal neuron, dendritic spine density, and soma size of layer III pyramidal neurons. Cross-correlating these microscale cellular metrics with macroscale network properties revealed several associations:

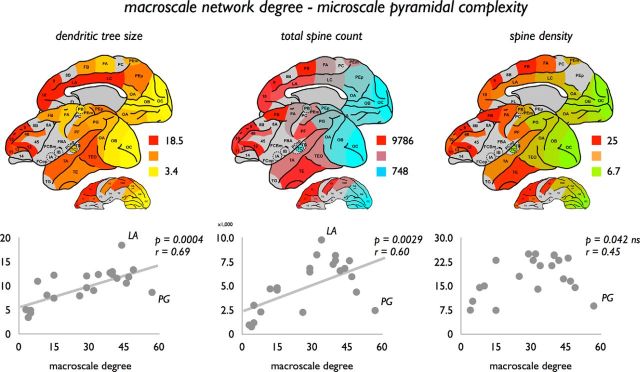
Pyramidal dendritic tree size positively correlated to macroscale anatomical degree (in-degree, p = 0.0005, r = 0.68; and out-degree, p = 0.0004, r = 0.69), indicating that pyramidal cells with the largest dendritic tree are found in those regions with the highest total number of efferent and afferent macroscale connections (Fig. 4). In addition, total spine count, reflecting the total amount of (possible) synaptic terminals on the dendritic tree of a neuron, positively correlated with regional variation in the number of macroscale efferent (p = 0.0027, r = 0.60) and afferent connections (p = 0.0039, r = 0.59) (effects reaching partial Bonferroni corrected α). However, no significant effects were found between degree and spine density (i.e., the number of spines per section of the dendritic tree; Elston, 2000) (in-degree, p = 0.0502, not significant, r = 0.43; out-degree, p = 0.0374, not significant, r = 0.47). A positive relationship between soma size of layer III pyramidal neurons and macroscale in-degree was observed (in-degree, p = 0.0049 r = 0.60; out-degree: p = 0.0101 FDR; r = 0.56).

Figure 4.

Association between macroscale degree and microscale layer III pyramidal complexity. Top, Dendritic tree size, total spine count, and spine density as derived for 22 cortical regions on basis of the studies of Elston and colleagues (Table 1). Bottom, Associations between macroscale degree and pyramidal complexity, showing a positive significant relationship between macroscale total degree (i.e., sum of in-degree and out-degree) and dendritic tree size (left, effect reaching partial Bonferroni correction) and total spine count (middle, effect reaching partial Bonferroni correction). Spine density did not show a significant correlation with macroscale degree (right, effect not reaching correction for multiple testing). Exploratory exclusion of region PG as a potential data outlier from the correlation analysis did reveal a potential relationship with total degree (p = 0.0026, r = 0.64).

An exception to the positive association between macroscale degree and layer III pyramidal neuron characteristics was region PG (Fig. 4). Cortical region PG, well recognized as a key region in the so-called visual where pathway (Felleman and Van Essen, 1991; Ungerleider and Haxby, 1994) of the macaque visual system, was found to display a relatively high macroscale degree, but a (relative to the fitted linear relationship) small dendritic tree (Fig. 4, region PG), low spine count, and low spine density. Excluding region PG from the correlation analysis revealed stronger correlations for all pyramidal metrics, now showing a potential positive association between macroscale degree and spine density (in-degree, p = 0.0022, r = 0.60; out-degree, p = 0.0037, r = 0.62). Interestingly, in contrast to region PG, region LA (anterior cingulate cortex) and LC (posterior cingulate cortex) formed a positive exception scoring above the fitted linear relationship (Fig. 4), with layer III pyramidal neurons in region LA showing the most elaborate dendritic trees of all reported regions, with region LC in second place. These findings led to the hypothesis of high-degree region PG being mostly involved in local neuronal processes, potentially the processing of mostly unimodal information, whereas regions LA and LC have a more globally orientated profile involved in the processing and integration of multimodal information across the whole network.

Association with macroscale projection distance

A possible local versus global connectivity profile of cortical regions was further examined by looking at a region's projection distance of afferent macroscale connections in relationship to microscale neuronal architecture. The white matter projections of outlier region PG were found to have a relatively short average projection distance (mean ± SD: 4.53 ± 3.06 a.u., averaged over 31 afferent connections; 26 efferent connections: 4.52/3.11), consistent with a potential local connectivity profile of this region. The connections of high-degree region LA (afferent/efferent 7.97, 23 connections) and LC (11.37, 25 connections) were found to display on average the longest white matter projections of the macaque macroscale connectome, thus on average receiving projections from more distant regions in the cortex (efferent connections, respectively, 4.98, 21 connections; and 5.61, 24 connections). These findings are consistent with the observation of LA and LC to have a high dendritic complexity.

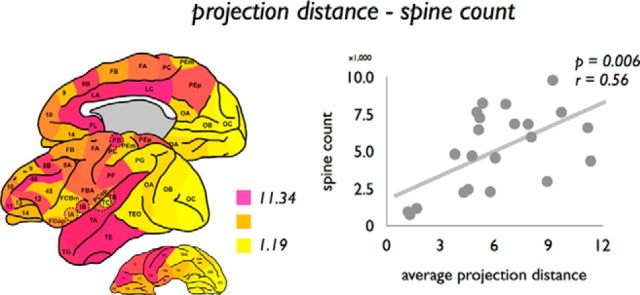
Next, we examined this association across the entire cortex. Projection distance of afferent connections was significantly correlated to spine count (p = 0.0060, r = 0.56; Fig. 5). Trend-level (FDR) effects were observed between projection distance and dendritic tree size (p = 0.0091, r = 0.54) and spine density (p = 0.0084, r = 0.57) (Fig. 3). Figure 3 summarizes the results of all examined correlations with projection distance.

Figure 5.

Association between average projection distance of cortical regions and microscale layer III spine count. Left, Mean projection distance of all connections (efferent and afferent combined) of each cortical region. Right, Association between mean projection length of connections of cortical regions (afferent and efferent connections) and spine count.

Association with macroscale visual hierarchy

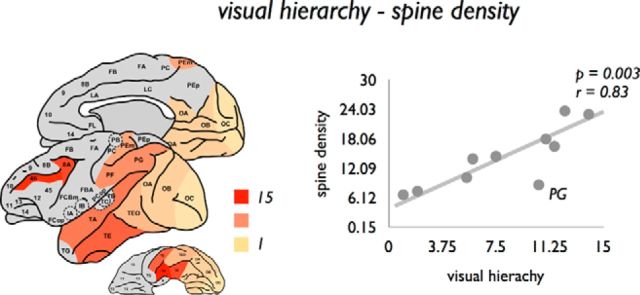
Information on the hierarchical ordering of cortical regions of the macaque visual system, as obtained by the study of Hilgetag et al. (2000) (see Materials and Methods), revealed further insight into a potential association between the topological organization of macroscale connectivity and the microstructural organization of cortical regions. Hierarchical ordering of visual regions, based on interlaminar differences in cortical source and target layers of afferent and efferent projections (Felleman and Van Essen, 1991) (see Materials and Methods), showed a positive correlation with dendritic tree size (p = 0.0058, r = 0.80), spine count (p = 0.0021, r = 0.85), and spine density (p = 0.0030, r = 0.83) (Fig. 6), with regions ranking higher in hierarchy showing the most complex pyramidal neuronal organization.

Figure 6.

Association between macroscale visual hierarchy and microscale layer III spine density. Left, Scored hierarchical ordering of regions of the visual system (based on the laminar projection patterns of a region's efferent and afferent projections), as translated from Hilgetag et al. (2000) plotted on the cortical surface. Right, Positive relationship between visual hierarchy and spine density.

Association with topological graph metrics

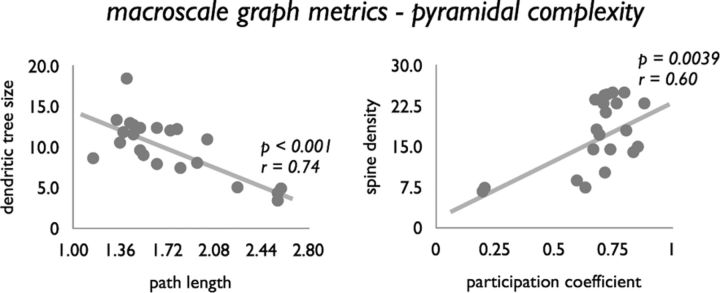
No significant relationships between network clustering Ci and pyramidal complexity metrics were observed (all p > 0.05; see also Fig. 3). In contrast, global shortest path length Li significantly negatively correlated to dendritic tree size (p < 0.001, r = 0.74; Fig. 7), spine count (p = 0.0011, r = 0.64), and soma size (p = 0.0064, r = 0.59). These findings tend to suggest that regions with a shorter path length show a more complex architecture, a relationship influenced by the positive association between dendritic complexity and degree (see above). Indeed, correcting for this interaction (by regressing out the effect of degree) revealed only a remaining effect for soma size (p = 0.0028).

Figure 7.

Relationship between macroscale graph organizational features and microscale complexity. Both nodal intermodular participation coefficient Pi and normalized path length Li were found to be significantly correlated with pyramidal complexity. Relationship between Li and dendritic tree size (left) and Pi (degree corrected) and spine density (right) are shown.

A potential link between topological architecture and microarchitecture is further supported by an observed positive association between the intermodular participation coefficient Pi and dendritic complexity, with regions with a more extensive intermodular connectivity profile showing a larger dendritic tree size (p = 0.0003, r = 0.70), higher spine count (p = 0.0002, r = 0.71), higher spine density (p = 0.0009, r = 0.67), and larger layer III pyramidal soma size (p = 0.0001, r = 0.77). Correcting Pi for nodal degree revealed a remaining effect for spine density (p = 0.0039, r = 0.60; Fig. 7).

Regional covariation in microarchitectural organization

Next, we examined the level of similarity in dendritic organization across the included cortical regions, computed as 1/distance (Euclidean) between the pyramidal metric values of each pair of cortical regions. Covariation in microstructural organization was found to be significantly higher for regions interconnected by a macroscale projection, compared with region pairs not directly connected (p < 0.001, 10,000 permutations), suggesting that anatomically connected regions tend to show overlap in their neuronal architecture.

Macroscale connectome organization and regional variation in total cell count, cell density, and neural cell density

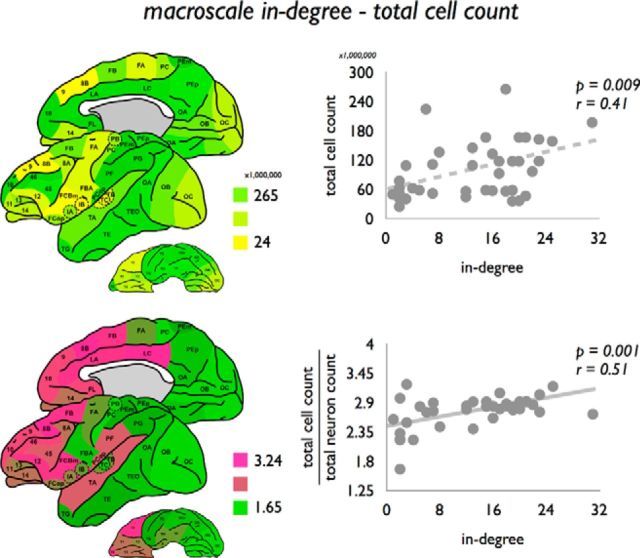
Information on regional variation in total cell and neuronal count across all cortical laminae was obtained from a recent study by Collins et al. (2010), in which the cortical mantle of a single macaque was divided into distinct blocks and examined for total cell count, total cell density, neuronal cell count, percentage of neurons, and neuronal cell density. Macroscale in-degree revealed a trend-level positive relationship with total cell count (p = 0.0091 FDR, r = 0.41; Fig. 8).

Figure 8.

Association between macroscale in-degree and neuronal count. Left, Total cell count and ratio total cell count/neuronal count. Cell count and neuronal count were translated from the study by Collins et al. (2010). Interestingly, a correlation was present not only between macroscale degree and total cell count (top right, effect reaching FDR correction), but also between macroscale degree and the ratio total cell count/neuronal count (bottom right), suggesting that macroscale degree is also related to regional variation in non-neuronal tissue at the microscale.

Correcting total cell count for the positive relationship with neuronal count (taking the ratio between total cell count and neuronal count) revealed a positive correlation with macroscale degree (in-degree: p = 0.0010, r = 0.51; Fig. 8; out-degree: p = 0.0006, r = 0.53). Indeed, macroscale in-degree and out-degree were found to correlate negatively with neural cell density (p = 0.0048, r = 0.44; p = 0.0024, r = 0.47) and neuronal percentage (p = 0.0008, r = 0.51; p = 0.0059, r = 0.53, reaching partial Bonferroni correction).

Relationship between macroscale connectivity and regional variation of glucose metabolism

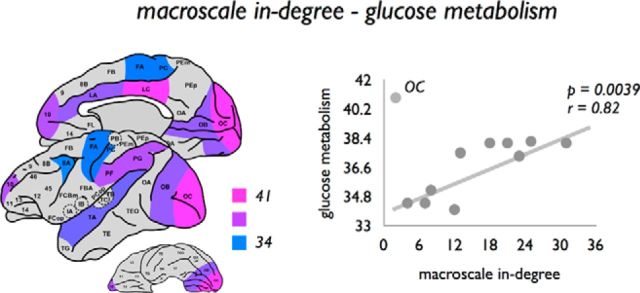
Examining graph organizational properties in relation to the level of glucose metabolism of cortical regions as reported by the study of Cross et al. (2000) (see also Materials and Methods) revealed a positive correlation between glucose metabolism and macroscale in-degree (p = 0.0039, r = 0.82, primary visual OC taken as outlier; Fig. 9). A positive relationship was also found between glucose metabolism and total cell (p = 0.0030, r = 0.83, region OC taken as outlier) and total neuronal count (p = 0.0071, r = 0.78, region OC taken as outlier).

Figure 9.

Association between macroscale in-degree and glucose metabolism. Left, Regional variation of glucose metabolism across the macaque cortex, with metabolic rates obtained from the study by Cross et al. (2000). Regional in-degree was found to be positively correlated with regional variation in glucose metabolism, suggesting that regions with a higher macroscale degree show a higher level of glucose metabolism. Region OC was interpreted as an outlier, and not taken into account in the statistical analysis.

Receptor fingerprints

Information on the chemoarchitecture of cortical regions of the macaque cortex was collated from the study of Kötter et al. (2001), summarizing levels of quantitative receptor binding in the motor and visual system of the macaque brain (see Materials and Methods), which were mapped to the WBB47 atlas. No direct correlations were found between macroscale anatomical degree and binding levels (all p > 0.05), indicating that our findings provide no evidence for the notion of receptor metrics to be associated with the network topological profile of regions (for the correlations, see Fig. 3). No clear difference between similarity in receptor binding levels (computed as 1/distance (Euclidean) between the metric values of each pair of cortical regions) of anatomically connected and nonconnected regions was observed (p = 0.0212, not significant, 10,000 permutations).

Microscale architectonics of macroscale rich club

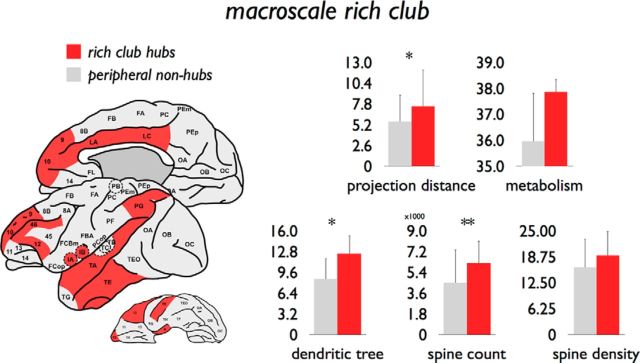
The rich club was selected as the set of nodes showing a combined in-degree and out-degree k > 38, including a set of in total 12 cortical regions (region 9, 10, 12, 46, IA, IB, LA, LC, PG, TA, TE, and A) (Fig. 10). Similar to previous observations (Harriger et al., 2012; de Reus and van den Heuvel, 2013), different rich club levels (e.g., k > 36 or k > 40) revealed consistent findings. Consistent with an overall rich club organization, these hub regions showed a dense level of mutual connectivity (98%), significantly higher than in a set of randomly connected networks (1.12× higher, p < 0.001, 1000 random networks preserving degree sequence) (van den Heuvel and Sporns, 2011).

Figure 10.

Microscale properties of graph analytically derived hub regions. Left, Red represents the 12 hub regions (k > 38). Gray represents all other peripheral nonhub nodes. Right, Differences between hub and peripheral nonhub nodes on several macroscale and microscale metrics. *p < 0.025 (reaching partial Bonferroni correction). **p = 0.0208 excluding outlier region PG (reaching partial Bonferroni correction).

stryFC

Efferent anatomical rich club edges (i.e., connections spanning between rich club nodes) were found to have significantly less often a net excitatory strychnine effect (15% of edges) on their target regions compared with the class of local connections (i.e., connections spanning between local nodes, 86%, p < 0.001, 10,000 permutations, surviving Bonferroni correction; feeder: 47%). In addition, examining the neuronal architecture of rich club regions, rich club hubs were found to be present in 3 of the 3 functional communities (100%) and 6 of the 8 (75%) functional subnetworks (as revealed by two-step community detection). Rich club and feeder edges were found to be well represented among intermodular connections (88% and 87% of connections, respectively), more than local connections (69% of connections), as computed on the basis of the two-step community approach. For the first-level stryFC communities, a similar pattern was observed, with rich club edges involving 72% intermodular connections, feeder connections 57%, and local connections 39%.

Figure 10 summarizes mean values of macroscale and microscale metrics of rich club and non-rich club regions. Rich club edges were found to be predominantly bidirectional (98%), more frequently than feeder (86%) and local connections (76%). Rich club edges were found to span significantly longer physical distances compared with local connections (i.e., edges connecting peripheral nodes, p < 0.001, 10,000 permutations, surviving Bonferroni correction). Rich club hub regions showed a significantly larger dendritic tree compared with non-rich club regions (p = 0.0024, 10,000 permutations; Fig. 10). No significant effects were found for spine count (p = 0.0788), spine density (p = 0.0958), soma size (p = 0.11), or metabolism (p = 0.0584). Excluding region PG (see text above; Fig. 4) revealed a difference in spine count between hub and nonhub peripheral nodes (p = 0.0208, 10,000 permutations; Fig. 10).

FE91 validation

Associations found to be significant in the main analysis were validated using the FE91 parcellation dataset, now involving CoCoMac extraction of macroscale anatomical connectivity on basis of the FE91 atlas, and mapping of the collated microscale pyramidal complexity data to the FE91 regions. The FE91 analysis results revealed high consistency with the associations reported for the WBB47 datasets. A summary of these findings include the following, with the computed FDR correction for the FE91 atlas set yielding a corrected α of 0.0175 and a partial Bonferroni corrected α of 0.05/(2 × 2) = 0.0125 (based on PCA analysis as described in Materials and Methods).

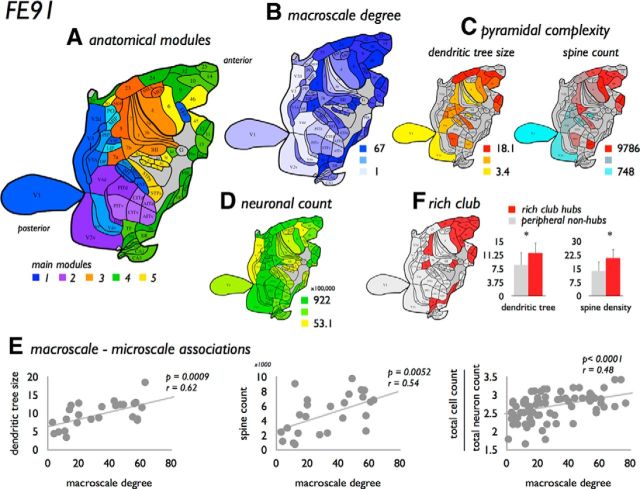
The FE91 network revealed a significant community structure (mean Rand index: 0.93, 10% rewiring, p < 0.001, 1000 iterations, two-step communities), including 5 main communities and in total 12 subcommunities (Fig. 11A), together with a significant rich club formation (12<k<62, p < 0.001, reaching Bonferroni correction). Confirming the WBB47 analysis, macroscale nodal degree (taken as the total sum of in-degree and out-degree) was found to show significant associations to pyramidal complexity (dendritic tree size, p = 0.0009, r = 0.62; spine count, p = 0.0052, r = 0.54; soma size, p = 0.0046, r = 0.57), the ratio of neuronal count and cell count (p < 0.0001, r = 0.48), neural percentage (p = 0.0033, r = 0.45), and an effect with neural cell density (p = 0.0051, r = 0.44) (Fig. 11). Pyramidal complexity also showed a positive correlation with visual hierarchy (e.g., dendritic tree size, p = 0.0013, r = 0.84; spine count, p = 0.0030, r = 0.80). No significant correlation was observed between degree and spine density (p = 0.0296, not significant, r = 0.44). Pyramidal complexity correlated negatively with network path length (e.g., dendritic tree, p = 0.0009, r = 0.62; spine count, p = 0.0052, r = 0.54). No significant relationship was observed between macroscale degree and regional metabolism (p = 0.30, not significant, r = 0.36) or between macroscale projection distance and pyramidal complexity (e.g., dendritic tree size, p = 0.29, not significant, r = 0.29; spine count, p = 0.51, not significant, r = 0.183). The latter may have been influenced by the notion that, of only 45 FE91 regions (58% of total), information on spatial coordinates was available.

Figure 11.

FE91 validation analysis. Figure summarizes findings of the validation analysis using the Felleman and Van Essen (1991) FE91 atlas. A, The 78 regions of the FE91 atlas (Felleman and Van Essen, 1991), color coded according to their anatomical modular structure (five main modules, color coded in blue, purple, orange, yellow, and green; and subclusters of the two-step module depicted in color shades). B, Map of the degree distribution across the FE91 regions. C, Two distribution maps of pyramidal complexity values as collated from the Elston papers, showing a map of dendritic tree size (left) and spine count (right). D, Distribution map of neuronal count as mapped by Collins et al. (2010). Consistent with the main analysis based on the WBB47 atlas (e.g., Fig. 4), analysis of the FE91 dataset revealed several associations between macroscale network organization and microscale neuroarchitectonics. E, Summary of three of these associations, showing a significant positive relationship between macroscale degree and dendritic tree size, spine count, and the ratio between total cell count and total neuronal count (surviving partial Bonferroni correction). F, Distribution of high-degree rich club nodes across the cortex as observed in the FE91 dataset (left). Consistent with the main analysis (Fig. 10), rich club nodes were observed to show a significantly larger dendritic tree size and higher spine count compared with the class of peripheral nodes. *p < 0.05 (surviving partial Bonferroni correction).

Consistent with the results of the WBB47 analysis and recent reports (Harriger et al., 2012; Goulas et al., 2014), the FE91 dataset revealed the existence of hub regions and a densely connected rich club (selected as regions with a combined degree >43, including 20 regions [25.6% of total], density 87%, 1.22 times more than random, p < 0.001, permutation testing) (selecting other rich club levels, e.g., k>41 or k>45, revealed consistent findings). Rich club and feeder edges were found to be strongly present among intermodular edges (rich club: 72%, feeder-in: 68%, feeder-out 75%, local: 53%, based on the revealed two-step communities), to mostly involve bidirectional connections (92% and significantly more than local edges, p < 0.001, with feeder-in: 59%, feeder-out 63%, local: 62%) and to project over longer distances than local edges (p < 0.001, 10,000 permutations); effects all reaching Bonferroni correction. Validating rich club observations of the WBB47 results, rich club nodes showed higher levels of pyramidal complexity (dendritic tree size, p = 0.0164 reaching FDR; spine count, p = 0.0042 partial Bonferroni; spine density, p = 0.0108 partial Bonferroni; soma size, p = 0.0142 FDR; Fig. 11). Figure 11 shows a summarized overview of the results of the FE91 dataset.

Discussion

Combining information on the topological organization of the macroscale macaque connectome with collated data on the neuroarchitectonic organization of cortical regions, our findings show several potential links between between macroscale network organization and microscale neuronal architecture. The number of macroscale white matter anatomical connections (i.e., network degree) was found to be associated with cortical variation in metrics of complexity of layer III pyramidal neurons, with higher connected regions showing more elaborate dendritic branching, larger soma size, and higher total spine count compared with macroscale low-degree regions. In addition, macroscale degree also significantly correlated to the ratio between regional variation in total cell and neuronal count and thus negatively with neural density, suggesting that macroscale wiring may also be potentially related to the relative density of other non-neural cortical tissue, for example, glial cells and capillaries (Collins et al., 2010). Furthermore, hierarchical position in the visual system was associated with dendritic organization (Fig. 6), with regions higher in the visual hierarchy showing both a higher pyramidal complexity as well as a more central role in the overall network. These observations point to the direction of regions low in hierarchy, processing predominantly unimodal information and having a low number of connections, to show a relatively low degree and low pyramidal complexity, whereas more richer connected regions positioned higher in the hierarchy, assumed to process more transmodal and multimodal information, display a more complex pyramidal architecture.

Our findings are in line with previous observations of macroscale and microscale organization of the mammalian brain. Across their experiments, Elston et al. (2009, 2010) noted a systematic trend for an increasing complexity of dendritic trees of functionally ordered regions, with pyramidal neurons becoming progressively larger, more branched, and more spinous when traveling in anterior direction through the visual system. Elston et al. (2010) already hypothesized that such a specialization of pyramidal cells could have an impact on the functioning of cortical regions at both the cellular and whole-brain levels. Our cross-resolution findings now indeed tend to suggest that a putative gradient of increasing microscale pyramidal organization goes hand in hand with a more and more central role of cortical regions at the macroscale network level. Furthermore, human and animal studies have noted that macroscale high-degree regions tend to predominantly overlap with functional multimodal areas of the cortex (Goldman-Rakic, 1988; Tomasi and Volkow, 2011; Power et al., 2013; de Reus and van den Heuvel, 2013), and neuroimaging studies have indeed already suggested that these high-degree regions belong to the most metabolically active regions of the cortex (Collins et al., 2010; Vaishnavi et al., 2010; Liang et al., 2013), with high levels of energy usage hypothesized to be potentially related to high synaptic turnover and synaptic plasticity (Lim and Isaac, 2005) and maintenance of elaborate dendritic trees of cortical neurons (Vaishnavi et al., 2010).

In addition to the total number of pathways, our study also provides indications of a possible link between the macroscale topological role of cortical regions and microscale architectonics. The average projection distance of a region's connections was observed to be positively related to pyramidal spine count (Figs. 3 and 5), with regions with a broad connectivity profile showing the most elaborate dendritic trees. Furthermore, network metrics, such as topological connection distance (shortest path length) and participation coefficient (reflecting the intermodular connectivity profile of a network node), were found to be associated with microscale dendritic tree length and spine count, suggesting a potential relationship between topological position of cortical regions in the macroscale brain network and microscale neuronal architecture.

Consistent with other recent studies, the anatomical macaque connectome showed the formation of macroscale neural hubs (Harriger et al., 2012; Markov et al., 2013). Because of their central embedding in the macroscale network, rich club hubs have been proposed to form a topologically central structure for global communication and information integration (van den Heuvel et al., 2012; Crossley et al., 2013; Park and Friston, 2013; van den Heuvel and Sporns, 2013a). Extending these findings, our study now suggests that on both the macroscale as well as on the microscale, high-degree hub regions display an architecture potentially suited for facilitating functional neural integration processes (Elston, 2000; Elston et al., 2001; Jacobs et al., 2001; Schüz and Miller, 2002; van den Heuvel and Sporns, 2013a).

Although tract tracing data are often seen as a “gold standard” of white matter pathway reconstruction, it is important to realize that animal connectome reconstructions (as also performed here) are often based on a collation of data across a wide range of experiments, experiments that have not always reported consistent results. For a robust reconstruction, pathways were included on which CoCoMac contained information from ≥5 studies and of which the majority of these studies (≥66%) involved a positive report, but there is no clear consensus on these settings. Sparse sampling of other settings (e.g., >4; 60% or >5 and 50%) resulted in consistent results, but it is important to note that recent studies have suggested much denser wiring diagrams of the macaque cortex (Markov et al., 2013) than resulting from our CoCoMac extraction. In addition, in the main analysis of this study, the WBB47 atlas was used to parcellate the cortex, providing complete coverage of the macaque cortex and allowing for the analysis of functional strychnine data, but many other parcellation atlases (as, e.g., the FE91 replication atlas) are available, with most of these atlases containing a more fine-grained parcellation. Last, the examined microscale data involved a collation of data across studies from the literature, thus also including information across multiple experiments, and moreover including only a relatively coarse sampling of the cortex with missing data on microscale metrics for several cortical regions (Table 1). These effects limit the sensitivity of our study.

Our study should only be seen as a first attempt to examine a potential microscale–macroscale relationship. Many open questions of course remain. For example, microscale–macroscale associations were assessed by means of a series of simple correlations. As shown by the correlation and PCA analysis, both microscale and macroscale metrics show strong intraclass correlations, suggesting that most presented macroscale–microscale associations are driven by global underlying organizational effects. Interestingly, although the strong dependency of network metrics on degree is well reported (Lynall et al., 2010; van den Heuvel and Sporns, 2011), PCA results also revealed strong correlations between several microscale metrics, effects that are potentially nontrivial. Future studies examining these microscale relationships, together with how they relate to global underlying macroscale network descriptors, would be of particular interest. Furthermore, the important question of “what is driving what” remains unanswered. Is the neuroarchitectonic organization of cortical regions tuned to accommodate large-scale macroscale projections, or does a high complexity of cortical regions allow for the existence of a large number of macroscale efferent and afferent white matter projections? Earlier studies have hypothesized differences in global connectivity patterns to have consequences for the structural and histological organization of cortical regions, with macroscale connectivity patterns potentially including an important factor for architectonic differentiation of cortical regions, bringing to attention the need for studies examining the link between macroscale connectional patterns and microscale architectonics (Kaas, 2002; Schüz and Miller, 2002). More experimental studies are needed to provide insight into a potential causal relationship between neuroarchitectural organization of cortical regions and macroscale connectivity patterns, as well as their interaction to the formation of large-scale hierarchies, community structure, and neural hubs (Elston et al., 2009; Buckner and Krienen, 2013). In addition, in this study we have primarily been focusing on the examination of anatomical architectonic features, but examination of the potential influence and interplay of microscale architectonics and macroscale connectome formation on the emergence of functional dynamics and functional hierarchical systems (Breakspear and Stam, 2005; Zhou et al., 2006; Kiebel et al., 2008; Meunier et al., 2010) would be of particular interest. Pioneering cross-species studies have noted that resting-state networks in the macaque as derived from resting-state fMRI data resemble those observed in the human (Hutchison et al., 2011, 2013), and similar cross-species observations have been made regarding anatomical connectivity (Goulas et al., 2014; Miranda-Dominguez et al., 2014). Because of the inherent nature of the method, the stryFC data as analyzed in this study are different from FC estimates based on resting-state fMRI; nevertheless, the stryFC subclusters have been noted to show overlap with known functional domains of the macaque cortex, identifying visual, somatosensory, and frontal networks (Stephan et al., 2000). A formal comparison between resting-state fMRI-derived functional communities and stryFC-defined community structure would be of interest and might provide new information on the underlying biological foundation of resting-state network formation in the mammalian cortex.

This study provides evidence for a potential relationship between the properties of macroscale and microscale connectivity of the mammalian cortex. Our findings converge on the notion of an interplay between the neuroarchitectonic organization of cortical regions and their connectional pattern on the macroscale connectome level.

Notes

Supplemental material for this article is available at www.dutchconnectomelab.org. This material has not been peer reviewed.