Context-Dependent Urgency Influences Speed–Accuracy Trade-Offs in Decision-Making and Movement Execution

Abstract

Speed–accuracy tradeoffs (SATs) exist in both decision-making and movement control, and are generally studied separately. However, in natural behavior animals are free to adjust the time invested in deciding and moving so as to maximize their reward rate. Here, we investigate whether shared mechanisms exist for SAT adjustment in both decisions and actions. Two monkeys performed a reach decision task in which they watched 15 tokens jump, one every 200 ms, from a central circle to one of two peripheral targets, and had to guess which target would ultimately receive the majority of tokens. The monkeys could decide at any time, and once a target was reached, the remaining token movements accelerated to either 50 ms (“fast” block) or 150 ms (“slow” block). Decisions were generally earlier and less accurate in fast than slow blocks, and in both blocks, the criterion of accuracy decreased over time within each trial. This could be explained by a simple model in which sensory information is combined with a linearly growing urgency signal. Remarkably, the duration of the reaching movements produced after the decision decreased over time in a similar block-dependent manner as the criterion of accuracy estimated by the model. This suggests that SATs for deciding and acting are influenced by a shared urgency/vigor signal. Consistent with this, we observed that the vigor of saccades performed during the decision process was higher in fast than in slow blocks, suggesting the influence of a context-dependent global arousal.

Introduction

To obtain rewards, animals must both choose the right action and perform it correctly. Although taking more time to decide improves choice accuracy (Pachella, 1974; Wickelgren, 1977), it also reduces the reward rate, facing animals with a speed–accuracy trade-off (SAT; Myerson and Green, 1995). A similar trade-off exists in movement control because moving fast tends to be less accurate (Fitts, 1954). The mechanisms of SAT adjustment in decision-making (Chittka et al., 2009; Balci et al., 2011; Hayden et al., 2011; Heitz and Schall, 2012) have generally been studied separately from those in movement control. However, because animals are often free to adjust the time they invest in deciding versus moving, they can also trade decision time for movement time to maximize their total reward rate. It is therefore possible that SAT mechanisms in decision-making and movement control are integrated, and perhaps involve similar neural substrates.

The predominant model of SAT in decision-making is the “drift-diffusion model,” which suggests that decisions involve a slow accumulation of sensory information until a fixed accuracy criterion is reached (Gold and Shadlen, 2007; Ratcliff and McKoon, 2008; Churchland et al., 2011). With a high boundary, decisions are accurate but slow, and with a lower boundary, they are faster but less accurate. Thus, it has been proposed that to adjust the SAT, the brain controls the boundary of the accumulation process (Bogacz et al., 2010). Neurally, this may involve a variety of mechanisms, including shifting the starting point, the threshold, or the gain of accumulation (Heitz and Schall, 2012; Hanks et al., 2014).

Recently, several studies have proposed that decision-making incorporates an “urgency” signal that grows over time to bring neural activity closer to the initiation threshold (Ditterich, 2006; Churchland et al., 2008; Cisek et al., 2009; Thura et al., 2012), effectively implementing an accuracy criterion that decreases over time. Importantly, to explain existing data, models that incorporate urgency need not assume a slow accumulation of evidence (Ditterich, 2006; Cisek et al., 2009; Thura et al., 2012). Instead, sensory information can be computed quickly using a low-pass filter with a short time constant (Ludwig et al., 2005; Ghose, 2006; Stanford et al., 2010), and then modulated by the urgency signal. The advantage of such “urgency-gating models” is that they respond more quickly to changes in the environment, and yield a higher reward rate than any constant criterion model (Thura et al., 2012; Miller and Katz, 2013). Recordings in the premotor and primary motor cortex of monkeys making decisions in dynamically changing situations have shown that neural activity combines rapid estimates of evidence with a growing urgency signal (Thura and Cisek, 2014).

Here, we investigate the hypothesis that the brain adapts its SAT by adjusting the urgency signal as a function of the task context. Furthermore, we explore the conjecture that a similar mechanism, perhaps sharing a common neural substrate, controls the vigor of movements after the choice is made. Some of these results have previously appeared in abstract form (Thura and Cisek, 2010, 2011, 2012).

Materials and Methods

Subjects and apparatus.

Two male macaque monkeys (Macaca mulatta; Monkey S: 6 years old, 6 kg; Monkey Z: 4 years old, 4 kg) participated in this study. The monkeys sat in a custom primate chair, with their heads fixed, and were trained to perform two planar reaching tasks. Their nonacting hand was maintained on an armrest with Velcro bands. Arm movements were performed using a vertically oriented cordless stylus whose position was recorded by a digitizing tablet (CalComp, 125 Hz). Target stimuli and continuous cursor feedback were projected onto a mirror suspended between the monkey's gaze and the tablet, creating the illusion that they were in the plane of the tablet. Unconstrained eye movements were recorded using an infrared camera (ASL, sampling rate of 120 Hz). In some sessions, neural recording was performed in the cerebral cortex (Thura and Cisek, 2014). All surgery, testing procedures, and animal care were approved by the local animal ethics committee.

Behavioral tasks.

In the “tokens” task (Fig. 1A) the monkey is presented with one central starting circle (1.75 cm radius) and two peripheral target circles (1.75 cm radius, arranged at 180° around a 5-cm-radius circle). The monkey begins each trial by placing the cursor in the central circle in which 15 small tokens are randomly arranged. The tokens then begin to jump, one-by-one every 200 ms (“predecision interval”), from the center to one of the two peripheral targets. The monkey's task is to move the cursor to the target that he believes will ultimately receive the majority of tokens. The monkey is allowed to make the decision as soon as he feels sufficiently confident, and has 500 ms to bring the cursor into a target after leaving the center. Crucially, when the monkey reaches a target, the remaining tokens move more quickly to their final targets (“postdecision interval,” which was either 50 ms or 150 ms between each token jump in separate fast and slow blocks of trials, respectively). After all tokens have jumped, visual feedback is provided to the monkey (the chosen target turns green for correct choices or red for error trials) and a drop of fruit juice is delivered for choosing the correct target. A 1500 ms intertrial interval precedes the following trial. In both fast and slow blocks, the monkey is thus presented with a trade-off: either wait until the decision can be made with confidence, or guess ahead of time, which may not be as reliable but could yield potential successes more quickly (because of the acceleration of the remaining tokens). Consequently, hasty decisions in the fast blocks are more advantageous in terms of reward rate because guessing quickly allows the monkey to save a larger amount of time than in the slow block.

Figure 1.

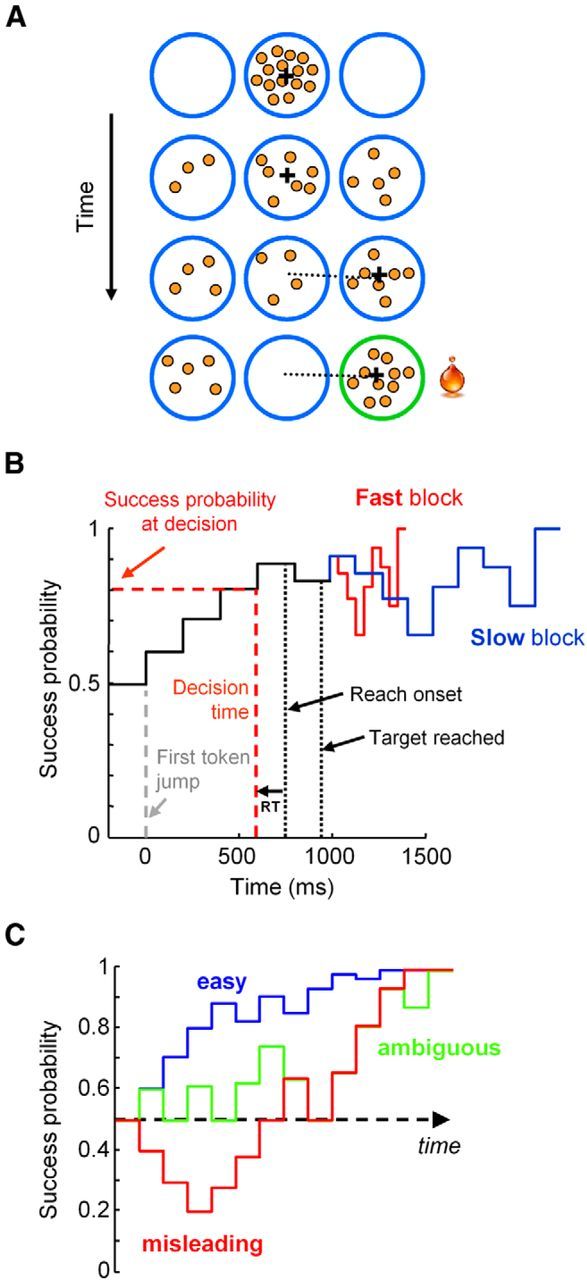
A, Schematic of the tokens task. B, Temporal profile of success probability in an example trial. The estimated time of the decision is computed by subtracting the monkey's mean reaction time (RT) in the delayed reach task from movement onset time, allowing computation of the success probability at that moment. C, Example success probability profiles of easy, ambiguous, and misleading trials. A trial is classified as “easy” if success probability (SP) exceeds 0.6 after two token jumps and 0.75 after five. A trial is ambiguous if the SP is 0.5 after two jumps, between 0.4 and 0.65 after three, and then between 0.55 and 0.66 after five and seven jumps. A trial is misleading if SP is <0.4 after three token jumps.

In the delayed reach (DR) task (usually 30–48 trials per session), the monkey again begins by placing the cursor in the central circle containing the 15 tokens. Next, one of six peripheral targets is presented (1.75 cm radius, spaced at 60° intervals around a 5-cm-radius circle) and after a variable delay (500 ± 100 ms), the 15 tokens simultaneously jump into that target. This “GO signal” instructs the monkey to move the handle to the target to receive a drop of juice. This task is used to determine the monkey's mean reaction time (RT) as an estimate of the total delays attributable to sensory processing of the stimulus and to response initiation.

Monkey training procedure.

Training animals in the tokens task involved three distinct stages: (1) Monkeys first learned the main logic of the task; i.e., to move the handle to the target that contains the majority of tokens. During that stage, the predecision and postdecision intervals were both 0 ms. (2) Next, we progressively and simultaneously increased both predecision and postdecision intervals across sessions. Until the predecision interval reached ∼50 ms, monkeys tended to move the handle after all tokens had jumped. As the predecision interval increased further, they began to make earlier decisions, and we began to set the postdecision interval to be shorter than the predecision interval. Both monkeys naturally learned to progressively adjust their SAT policy according to the timing parameters. Our goal then was to bring the predecision interval to 200 ms to compare our observations with human data (Cisek et al., 2009). The inherent challenge associated with choosing a postdecision interval was to prevent monkeys from either guessing too quickly or waiting too long. Indeed, if the postdecision interval is close to the predecision interval (i.e., 200 ms), the best strategy is to wait until all tokens have jumped. In contrast, if it is close to zero, then it is optimal to guess as soon as the first token jumps. During training, we gradually adjusted the parameters so as to keep the monkeys' behavior between these extremes. Ultimately, both monkeys achieved a policy that fell between hasty guessing and waiting to the end, with the same set of parameters for the predecision interval (200 ms per token jump) and postdecision interval (150 ms per token in slow blocks and 50 ms per token in fast blocks). (3) The last stage of training involved providing monkeys with alternating blocks of slow and fast trials (∼100–150 trials in a block). Because the main goal of the present study is to explore monkeys' SAT adjustment between the blocks, data presented in this report only includes trials performed during this final stage of training. Based on behavioral data (see Results), we defined two periods during this last stage: first, when behavior was comparable between the two blocks; and second, when the monkeys began to behave differently in the two blocks, in terms of decision duration and success probability.

Data analysis.

The tokens task allows us to calculate, at each moment in time, the “success probability” p_i(t) associated with choosing each target i. For instance, if at a particular moment in time the right target contains N_R tokens, whereas the left contains N_L tokens, and there are N_C tokens remaining in the center, then the probability that the target on the right will ultimately be the correct one (i.e., the success probability of guessing right) is as follows:

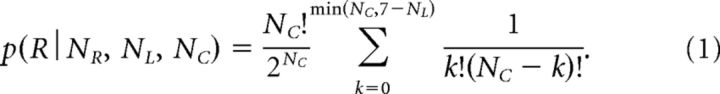To characterize the success probability profile for each trial, we calculated this quantity (with respect to the target ultimately chosen by the monkey) for each token jump (Fig. 1B). Although each token jump and each trial was completely random, we could classify a posteriori some specific classes of trials embedded in the fully random sequence (e.g., “easy,” “ambiguous,” and “misleading” trials; Fig. 1C). In easy trials, the initial token jumps consistently favor one of the targets, quickly driving the success probability for that target to 1. In ambiguous trials, the initial jumps are more balanced between the two targets, keeping success probability close to 0.5 until late in the trial. In misleading trials, the first tokens jump to the incorrect target and the following ones jump to the correct target.

To estimate the decision time (DT) on each trial in the tokens task, we detect the time of movement onset (based on kinematics) and subtract the monkey's mean RT from the DR task performed on the same day. We then use Equation 1 to compute for each trial the success probability at the time of the decision (SPD; Fig. 1B).

To quantify performance, we use a local definition of reward rate (Haith et al., 2012; Thura et al., 2012), which can be thought of as the time-discounted expected value of the choice made on each trial. This is computed as follows:

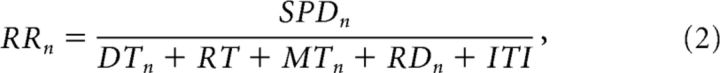where SPD_n is the probability that the choice made on trial n was correct, DT_n is the time taken to make the decision, RT is the average reaction time, MT_n is the movement time, RD_n is the duration of the remaining token jumps after the target is reached, and ITI is the intertrial interval (fixed at 1500 ms).

Calculation of the monkey's accuracy criterion (or “confidence”) at DT relies on the available sensory evidence at that time. Because we considered it very unlikely that monkeys can calculate Equation 1, we computed a simple “first order” approximation of sensory evidence as the sum of log-likelihood ratios (SumLogLR) of individual token movements as follows:

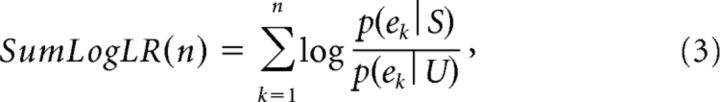where p(e_k | S) is the likelihood of a token event e_k (a token jumping into either the selected or unselected target) during trials in which the selected target S is correct, and p(e_k | U) is its likelihood during trials in which the unselected target U is correct. The SumLogLR is proportional to the difference in the number of tokens which have moved in each direction before the moment of decision (Cisek et al., 2009, provides more details on this analysis). To characterize the decision policy of a given monkey in a given block of trials, we binned trials as a function of the total number of tokens that moved before the decision, and calculated the average SumLogLR for each bin.

All arm and eye movement data were analyzed off-line using MATLAB (MathWorks). Reaching characteristics were assessed using monkeys' movement kinematics. Horizontal and vertical position data were first differentiated to obtain a velocity profile and then filtered using a sixth-order low-pass filter with a frequency cutoff of 15 Hz. Onset and offset of movements were determined using a 3 cm/s velocity threshold. Peak velocity was determined as the maximum value between these two events.

During both the tokens task and the DR task, monkeys' eye movements were unconstrained. After each session, eye data were first differentiated and then filtered using a sixth-order low-pass filter with a frequency cutoff of 50 Hz. The beginning and end of saccades were identified using an adaptive velocity threshold algorithm (varying as a function of signal–noise ratio). For analysis, we only used trials performed during the second period of Stage 3 of training and in which the horizontal targets were presented (because our oculometer accuracy was better for horizontal saccades). Moreover, to be included, saccades had to have amplitude between 10 and 15° (saccades between the two targets), duration <100 ms, and be executed before our estimate of the monkey's decision time.

Computational modeling.

To simulate the decision data, we used a minimal implementation of the urgency gating model (Cisek et al., 2009; Thura et al., 2012), in which evidence is multiplied by a linearly increasing urgency signal, and then compared with a threshold. In general, the urgency-gating model includes a low-pass filter, which is indispensable for dealing with intratrial stimulus noise when calculating evidence. However, in the present task there is no stimulus noise so we can simplify the model and calculate evidence simply as the difference in the number of tokens in each target. The result can be expressed as follows:

where y_i is the “neural activity” for choices to target i, N_i is the number of tokens in target i, t is the number of seconds elapsed since the start of the trial, m and b are the slope and y-intercept of the urgency signal, and [ ]⁺ denotes half-wave rectification (which sets all negative values to zero). When y_i for any target crosses the threshold T, that target is chosen. Two sources of internal variability were introduced into the model. Intertrial variability was simulated by multiplying the urgency signal by a factor that was normally distributed with mean 1 and SD 0.1. Intratrial variability was simulated by jittering the decision time by a term that was normally distributed with mean zero and SD of 0.2 s.

This simple model has only two parameters: m and b (the threshold T is just a scaling factor). To fit the data, we set T = 1 and then performed an exhaustive grid search for all combinations of m and b where m ranged from 0 to 1.75, and b ranged from −1.2 to 0.48. This was performed separately for each monkey and each block type, and the quality of fit was assessed using the mean-squared-error between the decision criterion as a function of time (Eq. 3) generated by the model and data for all decision times in the interval between 0.4 and 2.4 s (which accounted for 90% of the data). After finding the best pair of parameters for each dataset using the grid search, we fine-tuned the fit using constrained minimization procedures (fmincon function in MATLAB) starting with the best pair, as well as neighboring pairs to avoid local minima. The pair of m and b parameters that gave the lowest mean-squared-error among all of these minimizations was regarded as the best-fit solution, and errors on the fitted parameters were calculated using the diagonal elements of the square root of the inverse Hessian matrix around that best fit solution.

Results

Decision-making behavior

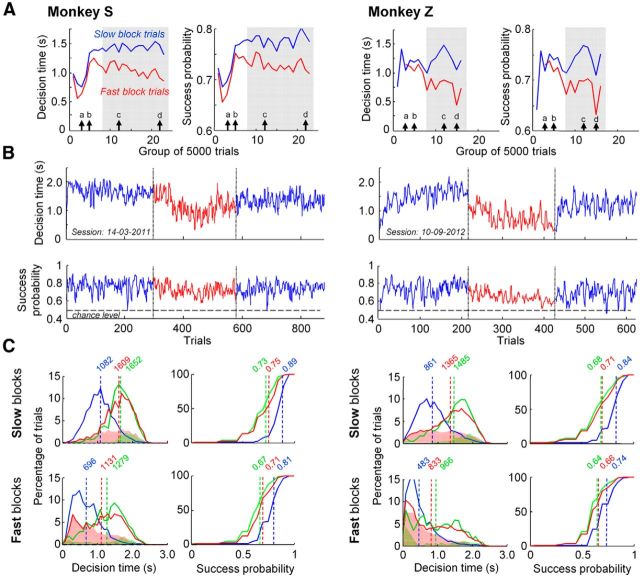
We focus here on the third stage of the monkeys' experience in the task, with the predecision interval (between token jumps) fixed at 200 ms, and postdecision interval (between token jumps) of 150 ms in slow blocks and 50 ms in fast blocks. This includes over 2 years of data for Monkey S, and 1.5 years for Monkey Z. Monkeys' behavior in the tokens task through this last stage exhibited two periods (Fig. 2A). The first months were characterized by comparable DTs and SPDs in both blocks. Later, monkeys adapted their behavior as a function of the postdecision interval. In this report, we will first describe behavior after the monkeys established clear and consistently different strategies in the two blocks (Fig. 2A, gray shaded areas). This amounts to 75,185 trials (both correct and error) from Monkey S (46,303 in slow blocks) and 43,506 trials from Monkey Z (30,669 in slow blocks). Subsequently, we will report how this SAT adjustment developed over the course of training, considering all trials performed during the entire third stage of experience in the task (n = 109,668 for Monkey S; n = 78,033 for Monkey Z).

Figure 2.

A, The evolution of mean decision times (and mean SPD), in slow (blue) and fast (red) blocks, over the course of training for Monkey S (left) and Monkey Z (right). Each bin represents the average decision time (and success probability) calculated across 5000 trials performed in either the fast or the slow blocks. The gray shaded area illustrates the period in training when each monkey's behavior is clearly and consistently different in the two blocks. Thin solid arrows indicate four specific times over the course of training, which will be examined in more detail later. B, Example sessions for each monkey, showing the decision times and success probability at decision for sequential trials in a slow block (blue), a subsequent fast block (red), and another slow block (blue). C, Distributions of decision times, and cumulative distributions of success probability at decision time for easy (blue), ambiguous (green) and misleading (red) trials in the slow (top) and fast (bottom) blocks for Monkey S (left) and Monkey Z (right). The vertical dotted lines mark mean values and shaded distributions of decision time illustrate error trials.

After extensive training, Monkey S was on average 397 ms faster in the fast blocks compared with the slow blocks, and the difference was 496 ms for monkey Z [Wilcoxon–Mann–Whitney (WMW) test, p < 0.001 for both monkeys]. Example sessions are shown in Figure 2B. Both monkeys also made decisions with a significantly lower level of success probability in the fast blocks compared with the slow blocks (0.73 vs 0.78 for Monkey S, 0.68 vs 0.74 for Monkey Z; WMW test, p < 0.001). This adjustment of behavior as a function of block was highly robust across weeks and months of training, as shown in Figure 2A.

Furthermore, the specific pattern of token movements within a trial had a significant effect on behavior, in both fast and slow blocks (Fig. 2C). As expected, monkeys made decisions significantly earlier in easy trials than in ambiguous and misleading trials (WMW test, p < 0.001 for all comparisons: slow easy vs slow ambiguous trials, slow easy vs slow misleading trials, fast easy vs fast ambiguous and fast easy vs fast misleading trials, in both monkeys). In addition, the initial bias in misleading trials clearly induced more errors compared with ambiguous or easy trials, especially in fast blocks. We also found that monkeys made decisions at a significantly lower level of success probability in ambiguous and misleading trials compared with easy trials (WMW test, p < 0.001 for the same eight comparisons stated above). This is consistent with human behavior (Cisek et al., 2009), and with the idea that to solve this task, monkeys lower their standards of accuracy as time is elapsing (i.e., they have a growing urgency signal). The rationale here is that spending time to collect more sensory evidence usually improves a subject's accuracy. However, as time is passing, the loss in terms of reward rate may exceed the benefit of potentially gaining accuracy, especially in a dynamic task in which one does not know whether better evidence will ever come.

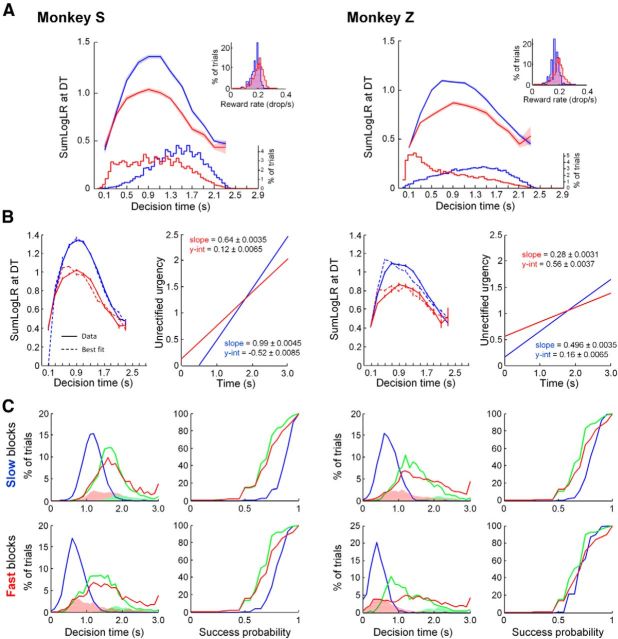
To further investigate this possibility, we estimated the “accuracy criterion” for committing to a choice by computing the available sensory evidence for the chosen target at the time of the decision as a function of decision duration (see Materials and Methods). Figure 3A shows that for both monkeys, the accuracy criterion (denoted as the SumLogLR) is significantly higher during slow blocks than fast blocks for decisions made between the third and the 10^th token jump (the majority of decisions: 76% and 78% of slow and fast decisions in Monkey S, respectively; 75% and 58% of slow and fast decisions in Monkey Z). This suggests that the monkeys are more willing to guess in the fast blocks and wait longer to decide in the slow blocks. We also found that except for very fast decisions (<1 s), the level of sensory evidence that monkeys require before committing to a target decreases as a function of decision duration, in both blocks. This means that if sensory information is strong (e.g., in easy trials), monkeys usually decide quickly. If information is ambiguous, they wait to see if it improves. Finally, if too much time has passed, the monkeys make a guess. We propose that this analysis reveals how animals voluntarily establish (in a given block) and adjust (between blocks) their “trade-off” between time and accuracy to solve the tokens task.

Figure 3.

A, Top, y-axis: mean (±SE) of our estimate of the monkey's accuracy criterion (calculated as the SumLogLR) at DT as a function of DT (in 200 ms bins) during slow (blue) and fast (red) blocks. Bottom, y-axis: distributions of decision time in the slow (blue) and the fast (red) blocks of trials. Insets, Distributions of the reward rate in each block (Eq. 2). B, In the left panels, the data (solid line ±SE) shown in A is compared, separately for each monkey and each block type, with the SumLogLR computed using the best-fit urgency-gating model (dotted line ±SE) with a simple linearly increasing urgency function, shown on the right. Note that the urgency signal that actually scales evidence in the model is a half-wave rectified version of these linear functions. That is, all negative values are set to zero. C, The distributions of decision time and cumulative distributions of success probability at decision time for each of the three trial types, produced by simulating the urgency-gating model using the functions shown in B (compare these results to Fig. 2C).

There are different ways in which such a process can occur in the brain and be implemented in a decision model. The decreasing accuracy criterion can be implemented either through a decreasing value of a neural firing threshold or through an increasing gain of neural activity and a fixed firing threshold. Our recent neural results (Thura and Cisek, 2014) favor the latter interpretation: during deliberation, neural activity in premotor and motor cortices is related to both the sensory evidence and elapsed time before reaching a fixed level of activity at the moment of commitment. Thus, our interpretation of the curves depicted in Figure 3A is the following: the decrease of the average SumLogLR function (our estimate of monkey's accuracy criterion) after ∼1 s can be easily explained by a (half-wave rectified) growing urgency signal, as in our simple model (Eq. 4). We believe this signal is a motor initiation-related buildup, unrelated to the sensory events, that reflects the growing urge to make a response. The initial rise of the average SumLogLR function may at first appear to require additional assumptions, but that is in fact not the case. It can simply be explained by noise: Because both urgency and evidence are low early in the trial, the only way for neural activity to reach the threshold is due to noise, which will obviously generate many errors. Consequently, the average SumLogLR across those trials will be close to zero and gradually increase as the influence of sensory information grows. Later in the trial decisions are less and less dominated by noise, and thus the average SumLogLR becomes a more veridical estimate of the level of sensory information that a monkey requires before committing to the decision.

To demonstrate this, we used our model to find, separately for each monkey and each block, the slope and intercept of urgency that produced the best estimate of the SumLogLR curve (in the least-mean-squared error sense). The best fitting parameters are shown in Figure 3B (right), along with errors on the parameter estimates. Although our goal was not to provide a perfect fit to the data, the simple assumption of a rectified linear urgency signal can capture the shape of the SumLogLR curve remarkably well, as shown in Figure 3B (left). For both monkeys, the urgency functions that best reproduce the data show a similar pattern: In the slow block, the urgency has a lower y-intercept but a higher slope than in the fast block. Consequently, although the urgency signal is initially lower in the slow block, the two functions eventually converge ∼1790 ms after the start of token movements. This makes sense because the difference in the amount of time potentially saved in the fast blocks versus slow blocks decreases as the number of remaining tokens decreases. Thus, later in the trial there is less of an advantage to behave differently in the two blocks. If time was the only factor taken into account by the monkeys and if they could estimate it perfectly, then the two urgency signals should ideally converge at exactly 3 s. However, real behaving animals do not usually behave in an idealized manner. Furthermore, because 90% of all decisions in the slow block are made before 2 s (98% before 2.2 s; Fig. 3A, see distribution of DTs), and in the fast block, 90% of decisions are made before 1.7 s (98% before 2 s), the results of our fits are unlikely to extrapolate beyond ∼2 s.

Overall, both monkeys adopted this qualitative pattern of decision policies in the two blocks, allowing them to improve their reward rate (Fig. 3A, insets). For both monkeys and both blocks, the errors on the fitted parameters were small (<2% for slope and <6% for intercept), suggesting that the fits were quite robust. Using the urgency functions derived from fitting the SumLogLR curves (Fig. 3B), we were able to simulate the qualitative patterns of behavior in the three trial types (easy, ambiguous, and misleading) for both monkeys and both block types (Fig. 3C). Although the model did not make very early decisions as often as the monkeys (especially in fast blocks), it did remarkably well for such a simple model. In particular, it qualitatively reproduced the shape of the SumLogLR curve, as well as the major trends in both decision time and success probability distributions in all three trial types. Thus, capturing the complex shape of the SumLogLR curves (rising until 1 s, and then falling) does not require one to posit multiple mechanisms or complex polynomial urgency functions, but can be well approximated with a minimal model that includes a rectified linear urgency signal that varies from trial to trial.

Arm reaching behavior

The results above show how monkeys exert control over three variables relevant to their reward rate (Eq. 2): the success probability of each choice, the time taken to decide, and the time of remaining token jumps. However, there is a fourth variable under their control, the time taken to complete the movement. It is important to note that in our task, the tokens remaining in the center start to accelerate only after the cursor enters the chosen target. This further increases the effect of movement duration on the reward rate (Eq. 2; Shadmehr, 2010). It is thus possible that the decision policy and in particular, the time at which decisions are made, influence the duration of the movements executed to report them. Intuitively, one might expect that the more time is spent deciding, the less is spent moving, and that this tradeoff may also be adjusted differently across the slow and fast blocks of trials. This prediction would be in agreement with results of Shadmehr et al. (2010), who showed that increasing the ITI (or delaying the reward) reduces the velocity of saccades. This is because the cost of movement duration is not as penalizing when reward is delayed as when it is not. In our task, monkeys are faced with the same temporal discounting problem: After long deliberation there are only a few tokens remaining and thus the reward and next trial come quickly (which is similar to a short ITI), so movement duration is shorter (higher speed and/or shorter amplitude). When comparing the two blocks, decisions in the slow blocks are usually longer than in the fast blocks, but the remaining tokens do not accelerate as much as in the fast blocks. The delay to reward is thus shorter in the fast blocks compared with the slow blocks, leading to shorter duration movements in the fast blocks, especially for decisions shorter than 1.8 s. Again, this makes sense because the difference in the amount of time potentially saved in the fast blocks versus slow blocks decreases as the number of remaining tokens decreases.

Therefore, a simple hypothesis is that the same urgency signal that drives the monkeys to make a decision also influences their movements, and especially their duration. This trivially predicts that if we group trials by decision time within a given block, we will see shorter movement durations (by means of higher speed and/or shorter amplitude) after longer decisions because the urgency signal increases monotonically as a function of time after it goes above zero. Furthermore, we expect shorter movement durations in the fast blocks because the urgency level is higher in fast blocks, and the difference between the two blocks to converge, as observed in the SumLogLR curves and the urgency signals derived using the model fits (Fig. 3A,B).

Analysis of arm movement properties supported these predictions. Similar to the decision variables, we only focus here on data collected when monkeys applied a block-dependent strategy to solve the task (i.e., period 2 of Stage 3 in Materials and Methods). As shown in Figure 4A (left), for Monkey S the peak velocity of movement increased for longer decisions and clearly differed between the two blocks (ANCOVA, velocity, block × time interaction, F_(1,1) = 202.63, p < 0.001), converging ∼2100 ms. Allowing for a significant baseline velocity, this trend strongly resembled the urgency functions estimated on the basis on Monkey S's decision policies (Fig. 3B, left). In Monkey Z, movement velocity also increased as a function of decision duration (velocity, time, F_(1,1) = 522.6, p < 0.001) in both speed conditions (velocity, block × time interaction, F_(1,1) = 3.3, p = 0.07), but here, velocity was generally higher in the slow condition (Fig. 4A, right). Nevertheless, if one also takes into account the amplitude of the movement, which for Monkey Z was larger in the slow block (Fig. 4B, right, block; F_(1,1) = 126.29, p < 0.001), then the total movement duration patterns in both monkeys were consistent with our hypothesis (Fig. 4C): First, for both animals, movement durations decreased as decision durations increased, regardless of the block condition (Monkey S: movement duration, time, F_(1,1) = 1391.8, p < 0.001; Monkey Z: F_(1,1) = 654.7, p < 0.001). Second, movement durations were shorter in fast blocks than slow blocks and the effect of time was block-dependent (ANCOVA, block × time, Monkey S: F_(1,1) = 83.5, p < 0.001; Monkey Z: F_(1,1) = 62.9, p < 0.001). As suggested by the urgency hypothesis, the range of movement duration reduction was larger in the slow blocks compared with the fast blocks, in both monkeys (Monkey S: from 393 ms to 312 ms, a 21% decrease in the slow blocks and from 358 ms to 308 ms, a 14% decrease, in the fast blocks; Monkey Z: from 361 ms to 316 ms, a 12% decrease in the slow blocks and from 343 ms to 309 ms, a 10% decrease, in the fast blocks; Fig. 4C). Thus, the difference of movement durations between blocks vanishes for long decisions. That both monkeys appeared to find a policy that adjusts movement duration makes sense in light of the fact that it is movement duration that is most relevant to reward rates. It is worth noting that the weaker effect of time on movement duration between blocks in Monkey Z is consistent with the weaker effect of time in that monkey's decision data: the difference of the SumLogLR curves is smaller in Monkey Z compared with Monkey S (Fig. 3B). This provides further support for the hypothesis that decision urgency is related to movement vigor. To assess to what degree urgency predicts movement durations, we performed a Pearson correlation analysis between the two variables, independently in each monkey in each block. For each trial, we estimated the urgency level at decision time using the urgency function derived for each monkey (Fig. 3B), and correlated this against movement duration. Although highly significant (p < 0.001 in all conditions), correlations were quite low in terms of r values (Monkey S, slow block: −0.15; Monkey S, fast block: −0.12; Monkey Z, slow block: −0.14; Monkey Z, fast block: −0.07). This means that although movement duration is significantly influenced by urgency, it is also strongly influenced by many other factors (starting point, biomechanics, changes in attention, etc.) that vary from trial to trial.

Figure 4.

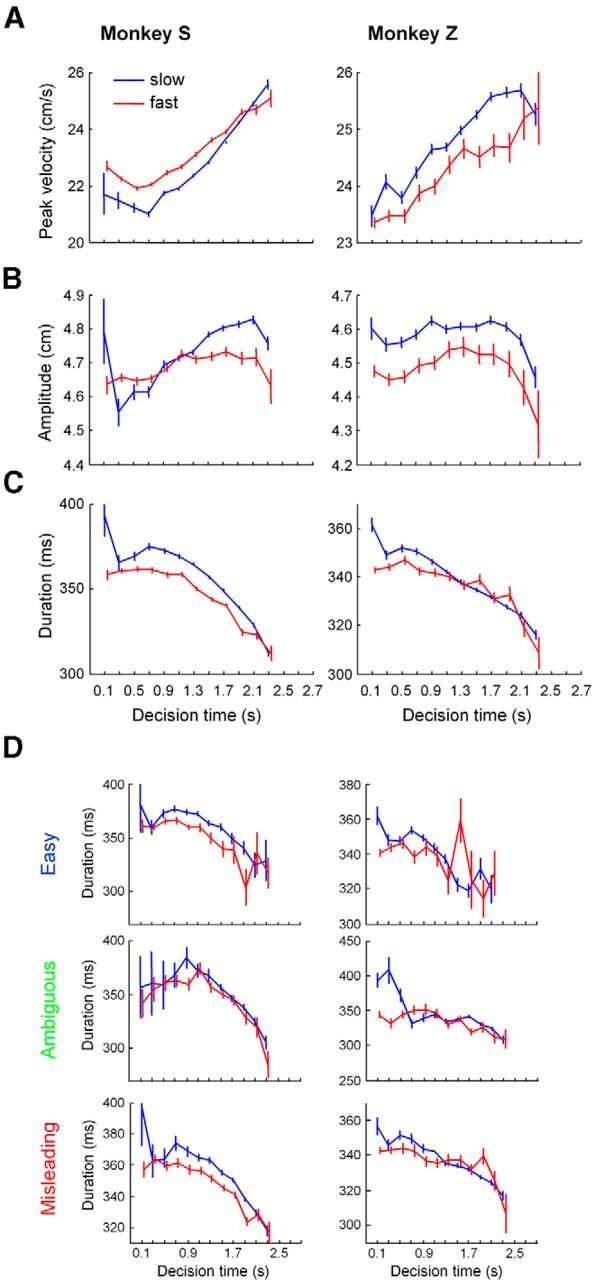
A, Mean (±SE) of the peak velocity of arm movement across trials binned according to DT in 200 ms bins, in the slow (blue) and fast (red) block for Monkey S (left) and for Monkey Z (right). B, Mean (±SE) of the movement amplitude in the same trials. C, Mean (±SE) of the total movement duration in the same trials. D, Mean (±SE) of the total movement duration in easy (top), ambiguous (middle) and misleading trials (bottom).

To control for a potential effect of trial difficulty or success probability on the results described above, we performed the same analysis on each trial type separately (Fig. 4D). For each of them, we observed the same phenomenon as those described above. In Monkey S, all ANCOVAs performed on the movement duration parameter (effect of block, effect of time, interaction of time and block) confirm significance of the results, except for the interaction of block ×time in easy trials (p = 0.08). In Monkey Z, all ANCOVAs performed on the movement duration parameter confirm significance.

Could the increase in movement velocity over time (Fig. 4A) be related to an increase in confidence as the tokens accumulate in the targets? We believe that cannot be the case. Recall that on average, decisions made later in time are made with less sensory evidence (Fig. 3A). The reason is that monkeys wait for an extended time only in trials in which the token movements were highly ambiguous. In easier trials, they tended to decide more quickly. A relationship between confidence (or uncertainty) and movement speed may exist (but see Georgopoulos et al., 1981), but it should have an effect that is the inverse of what we observed.

The findings summarized in Figure 4 are particularly noteworthy in our task because of the fairly large size of the targets (3.5 cm in diameter). Such targets are easy to hit, and the monkeys made very few aiming errors (Monkey S: 0.23%; Monkey Z: 0.14%). Thus, one might have expected the monkeys to make very fast movements in all conditions (e.g., 300–320 ms), exploiting the ease of the task to reduce the movement duration and increase reward rate. However, that was not the case. Instead, there appears to be a relationship between the duration of decisions and the duration of movements, which is controlled in a unified manner. It is plausible that this control involves the same context-dependent urgency signal that invigorates both the decisions that are made and the actions that are performed. This led us to hypothesize that the urgency signal may play a more general arousal role for all motor systems, even those that are not involved in yielding rewards.

Saccade behavior

In our task, eye movements were unconstrained and had no influence on reward rate. Nevertheless, if a general arousal signal exists then that signal may also invigorate the saccades made during the course of the decision process. To test this prediction, we focused our analysis on saccades made before the decision, using only trials performed by monkeys during the last period of training (Fig. 2A, gray shaded areas). Moreover, due to strict target selection (only horizontal targets) and technical reasons, only 8428 trials from Monkey S (5354 in slow blocks) and 7819 trials from Monkey Z (5624 in slow blocks) were included for the analysis, yielding a dataset consisting of 19,072 saccades from Monkey S (12,632 in slow blocks) and 15,634 from Monkey Z (11,626 in slow blocks).

Monkeys usually executed several saccades per trial, looking primarily at the center and the two targets, and usually (74–79% of trials) were already looking at the selected target at the moment of the decision. Figure 5A shows the instantaneous eye velocity for one trial, in which the decision was made at 1847 ms after six saccades were performed. By inspection, it appears that the velocity of the saccades is generally increasing before the decision.

Figure 5.

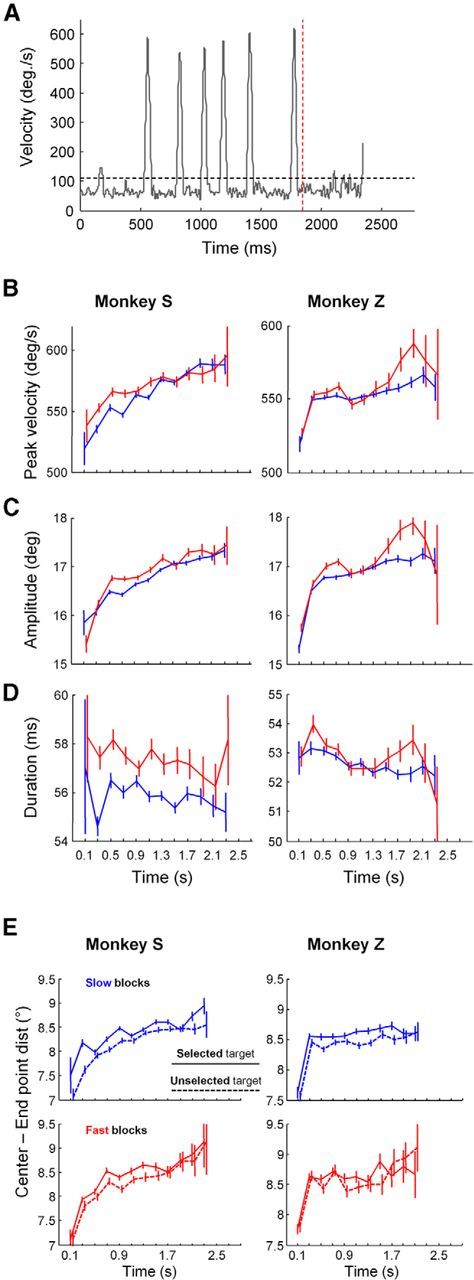
A, An example of the instantaneous eye movement velocity for an example trial. The vertical red dashed line indicates the decision time, and the horizontal dashed line indicates the adaptively set threshold for identifying saccades. B, Mean (±SE) of the peak velocity of saccades made before decision time, binned as a function of time in 200 ms bins, in the slow (blue) and the fast (red) block for Monkey S (left) and Monkey Z (right). C, Mean (±SE) of the amplitude of corresponding saccades. D, Mean (±SE) of the total duration of corresponding saccades. E, Effect of time on the mean (±SE) saccade amplitude (calculated from the center of the central circle to the saccade end point), separately for the target that was selected (solid) or not selected (dotted). In B–E, only saccades executed between the two horizontal targets (see Materials and Methods) and before our estimation of decision commitment are included for analysis.

Indeed, when we grouped all saccades made before the decision as a function of their latency with respect to the start of token movements, we saw in both blocks and in both monkeys a highly significant trend for increasing velocity and amplitude over the course of the trials (Fig. 5B,C), ranging between 520 and 580 deg/s (a 12% increase) for peak velocity and between 15.5° and 18° for amplitude. For both monkeys, time significantly affects saccade velocity (ANCOVA, time, Monkey S: F_(1,1) = 276.4, p < 0.001; Monkey Z: F_(1,1) = 68.7, p < 0.001) and amplitude (ANCOVA, time, Monkey S: F_(1,1) = 566.8, p < 0.001; Monkey Z: F_(1,1) = 334.8, p < 0.001).

Moreover, in Monkey S, saccade velocity was also higher in fast blocks compared with slow blocks (velocity, block, F_(1,1) = 23.6, p < 0.001). It is again interesting to note that in Monkey S, the velocity of saccades as a function of time resembles the context-dependent urgency functions derived from the model (Fig. 3B), including a convergence late in the trial (block × time interaction, F_(1,1) = 10.5, p = 0.001). A similar pattern is also seen in the amplitude of saccades, consistent with the well known correlation between saccade amplitude and velocity (Bahill et al., 1975). Consequently, Monkey S's saccade durations were longer in fast blocks compared with slow blocks (duration, block, F_(1,1) = 80.16, p < 0.001) and remain relatively stable across decision time (time, F_(1,1) = 3.65, p = 0.06), in both blocks (block × time interaction, F_(1,1) = 0.61, p = 0.43; Fig. 4D).

In Monkey Z, we observe similar trends overall. Again, velocity increases with time in both speed conditions, and this increase is block-dependent (velocity, block × time interaction, F_(1,1) = 5.48, p = 0.019; amplitude, block × time interaction, F_(1,1) = 11.80, p = 0.0006). Contrary to Monkey S, however, the effect of block appears to have a stronger effect on saccades executed late in the trial.

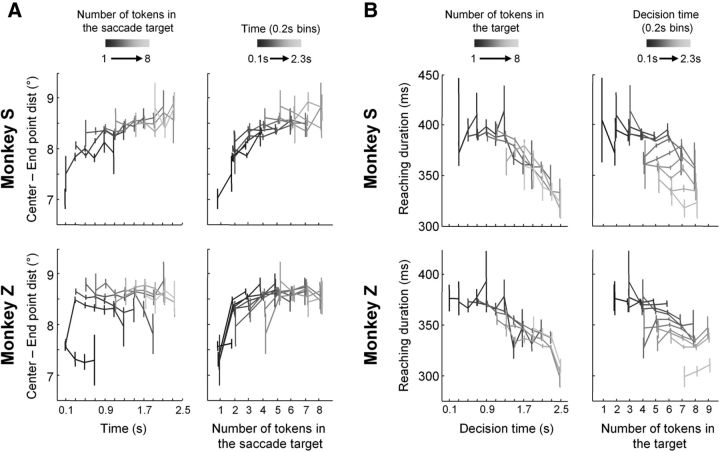
We considered several possible explanations for these effects. One is that saccade amplitudes are increasing over time because the tokens accumulating in the targets cover a larger area, presenting more targets for the eye that are further from the center. However, because the placement of each token was completely random, when averaged across a large number of trials the expected value of the center of the token distribution was always the center of the target, regardless of elapsed time. Another possibility is that the monkey's attention is increasingly driven toward the target that is ultimately selected by the monkey (and perhaps more likely to be rewarded), shifting saccade endpoints over time. However, despite the fact that we found that saccade amplitudes were slightly larger to the selected target compared with the unselected target, both exhibited the same trend for larger amplitudes over time (Fig. 5E).

Still another possibility is that attention is drawn toward sites in visual space with the larger number of tokens, and thus the effects shown on Figure 5 are due to the weakening pull exerted by the depleting tokens in the central circle and the increasing salience of targets receiving more tokens with time. To assess this possibility, we examined the effect of time on the amplitude of saccades made to a target with a given number of tokens. This showed that in Monkey Z, saccade amplitudes are only weakly affected by passing time but tend to increase with the increasing number of tokens in the target (Fig. 6A, bottom left). In Monkey S, we observed a mixed effect of both elapsing time and the number of tokens in the saccade target (Fig. 6A, top left). According to this analysis, time does not explain, at least for Monkey Z, the effects depicted in Figure 5. Thus, to better estimate the role of the number of tokens in the fixated target (i.e., the salience effect), we then performed the opposite analysis, looking at the effect of the number of tokens in the fixated target on saccade amplitude made within given time epochs (in 200 ms bins from the first token jump). This analysis clarified that saccade amplitude tends to increase with the number of tokens in the fixated target, regardless of the timing of the saccade (Fig. 6A, right). Thus, at least for Monkey Z, the apparent effect of elapsing time in the data in Figure 5 can be explained by the increasing number of tokens in the fixated target. The difference between the blocks, however, cannot be explained in this manner.

Figure 6.

Control analyses. A, Effects on saccade amplitude (calculated from the center of the central circle to the saccade end point). Left, Effect of time on mean (±SE) saccade end point for a given number of tokens in the target. Each shaded line corresponds to a different number of tokens. Data are shown for Monkey S (top) and Monkey Z (bottom) performing slow blocks of trials. Right, Effect of the number of tokens in the target on mean (±SE) saccade end points for a given time. Each shaded line corresponds to a different 200 ms time bin. Data are shown for Monkey S (top) and Monkey Z (bottom) in slow blocks of trials. B, Effects on reaching duration. Left, Effect of time on mean (±SE) reaching duration for a given number of tokens in the target. Right, Effect of the number of tokens in the target on mean (±SE) reaching duration for a given time. Same convention as in A.

We performed the same two control analyses on reaching durations to determine whether the effects depicted in Figure 4 were due to passing time, as we proposed via the increasing urgency signal, or if a salience effect (i.e., number of tokens in the selected target) was also responsible for these results. As illustrated in Figure 6B for both monkeys, the number of tokens in the selected target has very small effects on reach duration, whatever the timing of these movements (right). In contrast, in both monkeys most of the effect on movement durations can be attributed to elapsing time, regardless of how many tokens were in the selected target at the time of the reach (Fig. 6B, left).

Co-occurrence of the effects through practice

The hypothesis that a common vigor signal influences the decision policy as well as movement execution predicts that the effects we report should develop in parallel over the course of the monkeys' training in the task. To test this, we selected four epochs of time (Fig. 2A, vertical arrows) during the third stage of training, two before and two after a significant difference was observed in the decision policy. Each epoch consisted of 5000 trials performed either in the slow or in the fast blocks, and for each we performed the SumLogLR analysis (as a metric of the monkey's decision policy) as well as analyses probing the effect of decision duration on arm movement duration. This is illustrated in Figure 7 for both monkeys. In Monkey S, the specific decision policy between blocks progressively emerges with experience. The effects of decision duration and speed condition appear to emerge around the same time. In Monkey Z, this coemergence of effects on decision policy and movement properties through the time course of training appears less clear and consistent. Nevertheless, we still see that during the last tested epoch (trials 70,001–75,000), the monkey's decision policy is clearly different in the two blocks and his reaching movements also exhibit differences between the two blocks, especially in terms of duration. In contrast, these differences of decision policy and movement properties between blocks are not as large when we consider trials performed earlier in training.

Figure 7.

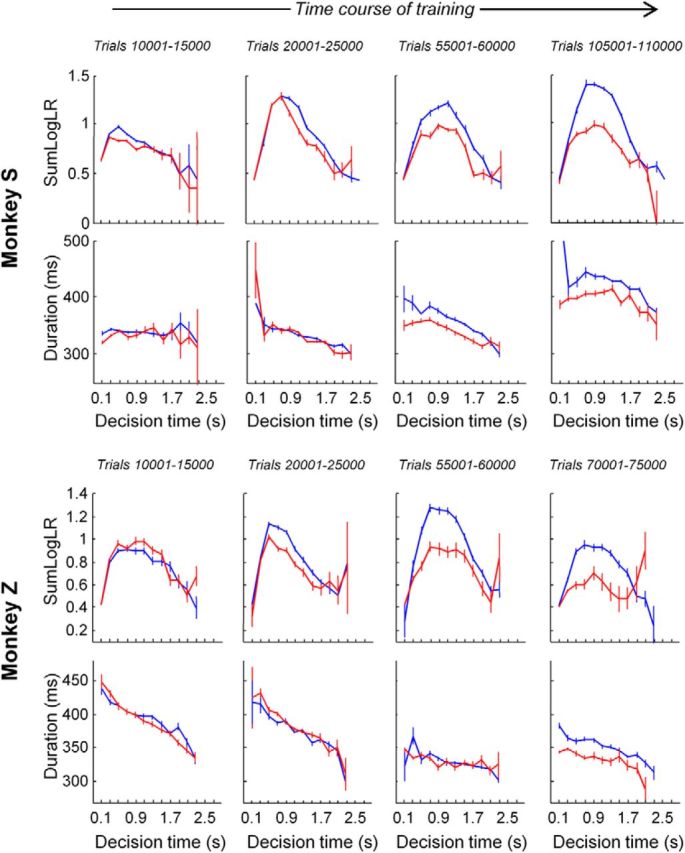
Top row, Mean SumLogLR (±SE) of Monkey S as a function of decision duration in the slow (blue) and the fast (red) blocks during the four periods of training indicated by arrows in Figure 2A (left). Each period consists of 5000 trials performed in either block. Second row, Mean (±SE) arm movement duration of Monkey S as a function of decision duration in the two blocks during the same four periods of training. Third row, SumLogLR for Monkey Z in the four periods of training indicated in Figure 2A (right). Fourth row, Mean movement duration for Monkey Z in the same four periods of training.

Figure 7 also illustrates idiosyncratic aspects of each monkey's personality. Monkey S has always been patient and conservative when performing the tokens task. As a consequence, during phase 2 of training (see Materials and Methods), we set the timing parameters to motivate him to decide more quickly. That is why at the beginning of phase 3 (data shown in Fig. 7), Monkey S both decided and moved relatively quickly. During phase 3, timing parameters were only varied between the two values corresponding to the fast and the slow blocks, so the conservative nature of Monkey S returned and he slowed down both his decisions and his reaches over the course of training. Note the link between decisions and actions during the evolution of the monkey's strategy: more conservative behavior during decision-making is accompanied by slower movements. This is highly consistent with the recent study of Choi et al. (2014), showing a link between human subjects' personality and the vigor of their movements.

Monkey Z has a different personality. He has always been impatient and hasty. During phase 2 of training, we thus set the postdecision interval to motivate him to slow down his decision times. This was successful and Monkey Z became conservative enough to start phase 3. However, as time was passing his impulsive nature reappeared and his movements became more and more vigorous. Note that in parallel, his decision policy did not become as conservative as the one reached by Monkey S. This demonstrates again the link between decision-making and movement execution, both processes reflecting the monkey's impulsivity.

Discussion

In the present study, we demonstrate a context-dependent correlation between two phenomena traditionally considered separate: the accuracy criterion for decisions (Fig. 3A) and the duration of movements used to report them (Fig. 4C). A simple way to explain our results is to suppose that the vigor of movements is in part influenced by the level of the urgency signal at decision time. Such a shared mechanism may allow animals to adjust the SAT of both decisions and movements to ultimately increase their reward rate.

Reward rate is a major motivating factor in decision-making. For instance, during foraging in a patchy environment, the food intake rate governs the stay-switch policy adopted by animals, including humans, both in nature and in the laboratory (Stephens and Krebs, 1986; Smith and Winterhalder, 1992; Hayden et al., 2011). Likewise, human subjects in a decision task adjust their SAT to maximize reward rate rather than performance per se (Balci et al., 2011). Reward rate, however, is influenced not only by the time spent in deciding but also by the time spent moving, and here too there are SATs. For arm movements, these are historically described by Fitts's law (Fitts, 1954), which relates how movement speed increases with movement amplitude and decreases with required accuracy. In the oculomotor system, saccades usually follow a “main sequence”, where larger movements typically have longer durations and velocities (Bahill et al., 1975; Harris and Wolpert, 2006), and can also depend on reward (Takikawa et al., 2002).

In general, SATs in decision-making have been studied separately from those in motor control. A recent exception is the work of Shadmehr and colleagues, who showed that delaying the reward reduces the velocity of saccades, as if their subjective cost is elevated (Shadmehr et al., 2010). Moreover, saccade peak velocities and durations can be predicted by a model in which the objective is to maximize reward rate (Haith et al., 2012). More recently, it has been shown that people who exhibit greater vigor in their movements tend to exhibit steeper temporal discounting (Choi et al., 2014). This suggests a link between decision-making and movement control, both of which ultimately influence reward rate.

Our work provides a complementary link, comparing the mechanisms involved in controlling the duration of decisions with those controlling the duration of the subsequent movements. Importantly, unlike previous studies of SATs (Reddi and Carpenter, 2000; Palmer et al., 2005; Heitz and Schall, 2012), here we do not explicitly instruct subjects to emphasize speed or accuracy, but simply change the timing parameters of the task so as to motivate a voluntary SAT modification. We deliberately make no attempt at instructing movement speed and place no constraints at all on saccadic behavior. This allows us to observe the decision and movement policies to which animals naturally converge in our task, presumably revealing principles of SAT adjustment in general.

We found that like humans (Cisek et al., 2009), monkeys gradually decrease over time the apparent criterion of evidence required for committing to a decision (Fig. 3A). The rationale for this is that if too much time has been invested in gathering evidence to increase accuracy, then it is better (in terms of reward rate) to make a best guess, especially if it is not known whether more evidence will appear. Moreover, both monkeys learned to modify their decision policy as the timing parameters of the task were varied, making hastier decisions in fast blocks and more conservative ones in slow blocks (Figs. 2, 3), but overall yielding a higher reward rate in the fast blocks. These results can be simulated by a simple version of the urgency gating model (Cisek et al., 2009; Thura et al., 2012), which suggests that neural activity combines an estimate of evidence that is computed rapidly (using a low-pass filter with a short time constant) with an urgency signal that grows linearly over time in a context-dependent manner (Fig. 3B,C). Our recent neural recordings in the premotor and primary motor cortex of Monkeys S and Z (Thura and Cisek, 2014) provide strong support for this model. Neural activity in both regions reflects the temporal profile of sensory evidence provided by the token movements, along with a tendency for activity to grow until the moment of commitment. We interpret the buildup of neural activity as a motor initiation-related signal that pushes the monkeys to decide and act. Remarkably, the urgency signal estimated from each monkey's decision policy for each block type resembled kinematic features of the corresponding arm movements, resulting in an inverse relationship between decision and movement duration within each block (Fig. 4). These results support the hypothesis that the vigor of movements is influenced by the level of urgency attained at the time the monkeys commit to their choice.

Is this influence specific to the arm motor system, or does it generalize to other systems, including ones that have no bearing on reward rate? When examining the unconstrained saccades made before the decision, we observed only a weak relationship between urgency and vigor of saccades. Nevertheless, although the effect of elapsing time is not significant in both monkeys, the difference between blocks is consistent with a higher urgency for the fast block. We thus suggest that part of the mechanism for SAT adjustment involves a global, context-dependent arousal that influences the oculomotor as well as the arm motor system. While our data cannot prove that the same signal governs all of these systems, it does suggest that they share similar principles.

According to the “drift diffusion” model (Ratcliff, 1978; Mazurek et al., 2003; Ratcliff and McKoon, 2008; Churchland et al., 2011), decisions are made when temporally integrated sensory information reaches a threshold, whose setting controls both the speed and the accuracy of decisions (Gold and Shadlen, 2002; Bogacz et al., 2006; Ditterich, 2006; Simen et al., 2006). Although this model can account for behavior in tasks where the pertinent sensory information pertinent is static, it fails in situations where the information is changing (Cisek et al., 2009; Thura et al., 2012), because slow integration is too sluggish to respond to sudden changes. Instead, we and others have proposed that sensory information is processed quickly (e.g., using a low-pass filter with a short time constant) and that what brings neural activity to the threshold is an urgency signal (Ditterich, 2006; Cisek et al., 2009; Stanford et al., 2010; Thura et al., 2012; Thura and Cisek, 2014). The urgency signal effectively implements an accuracy criterion that decreases over time within each trial, which yields higher reward rates than any setting of a constant criterion (Drugowitsch et al., 2012; Thura and Cisek, 2012). It remains to be established whether the urgency signal is multiplied, as we propose here, or simply added to the evidence.

Our work is in agreement with the conclusions of recent studies by Salinas et al. (2014) showing perceptual and motor adjustments during SAT in a compelled-saccade task. In particular, their results are well explained by their accelerated race-to-threshold model, which is very compatible with our urgency-gating model because it includes an increasing signal that represents the evolving motor plans during the decision process.

The hypothesis that decisions are influenced by a growing urgency signal suggests that this signal, not the threshold, controls the trade-off between decision speed and accuracy (Hanks et al., 2014). It also suggests that the same or related signal may also influence the action performed after commitment is made, as our data proposes. However, what is the origin of this signal? Buildup activity has been observed in many structures, including the supplementary motor areas (Mita et al., 2009; Casini and Vidal, 2011), dorsal premotor cortex (Renoult et al., 2006; Lebedev et al., 2008), and the lateral intraparietal cortex (Leon and Shadlen, 2003; Janssen and Shadlen, 2005; Maimon and Assad, 2006; Churchland et al., 2008; Hanks et al., 2011). Although any one or more of these regions may contribute, we believe the most promising candidate hypothesis is that urgency is controlled by the basal ganglia. In particular, the basal ganglia are intimately involved in the control of learned behaviors (Graybiel et al., 1994, 1998), are essential for modification of behavior through reinforcement (Barto, 1995; Doya, 2000; Daw and Doya, 2006), and have been implicated in the adjustment of the speed and accuracy of decisions (Bogacz and Gurney, 2007; Nagano-Saito et al., 2012). Moreover, the basal ganglia also play a critical role in motor control and appear to regulate the speed and size (the “vigor”) of movement (Niv et al., 2007; Turner and Desmurget, 2010). In monkeys, inactivation of the internal segment of the globus pallidus reduces movement velocity and acceleration (Horak and Anderson, 1984; Desmurget and Turner, 2010), and a major deficit of Parkinson's disease is the inability to move rapidly (Mazzoni et al., 2007). Thus, several converging lines of evidence suggest that the basal ganglia may be the central source of a general signal that energizes both the urgency of decisions and the vigor of the selected action.