Abstract
The middle temporal (MT) and medial superior temporal (MST) areas are successive stations of the visual motion-processing stream and project in parallel to the pontine nucleus, which is closely associated with rapid stabilization of gaze. We recorded the neural activities of MT and MST neurons of monkeys during short-latency ocular following responses (OFRs) elicited by large-field sinusoidal gratings with different spatial frequencies drifting at different temporal frequencies, and examined the dependence on spatiotemporal frequency. The results indicate that most MT/MST neurons were tuned almost separately for spatial and temporal frequencies of motion stimuli. The difference between MT and MST neurons was particularly striking for the optimal spatial frequency (higher for MT and lower for MST). The spatiotemporal frequency dependence of the OFRs could be reproduced by a weighted sum of the population activities of the MT and MST neurons. We conclude that MT and MST neurons work as spatiotemporal frequency sensors that extract motions of finer and coarser visual features and that both areas contribute to generation of OFRs.
Introduction
Extraction of motion from dynamic visual images is essential in humans and nonhuman primates for recognition of the surroundings and appropriate control of the eyes and body. Visually guided stabilization of gaze is a good example of behavior that uses rapid extraction of visual motion. We examined the neural activities of motion-processing areas of the monkey cerebral cortex during rapid stabilization of gaze to explore representations of different motion-processing stages associated with behavior.
In the primate visual system, the middle temporal (MT) and medial superior temporal (MST) areas are identified functionally as regions with a high proportion of directionally selective neurons (Zeki, 1974; Maunsell and Van Essen, 1983a; Desimone and Ungerleider, 1986; Tanaka et al., 1986; Komatsu and Wurtz, 1988a, b; Tanaka and Saito, 1989; Duffy and Wurtz, 1991). These motion-sensitive areas are closely related to ocular following responses (OFRs) that are elicited by sudden movements of the visual scene, which assists in rapid stabilization of gaze with respect to the stationary surroundings together with short-latency ocular vergence responses when our heads move in our daily life (Miles et al., 1986; Gellman et al., 1990; Kawano et al., 1994; Miles, 1998; Kawano, 1999; Sheliga et al., 2005; Miura et al., 2006; Takemura et al., 2007). Experimental lesions of area MT and MST resulted in significant impairments of short-latency ocular responses involving OFRs in monkeys, and it is expected that the vision would then be impaired after the lesions (Takemura et al., 2007).
The representation of visual motion in area MT has been extensively studied (Movshon et al., 1985; Simoncelli and Heeger, 1998; Perrone and Thiele, 2001; Priebe et al., 2003, 2006; Rust et al., 2006; Lui et al., 2007). Observing spatiotemporal frequency tuning of neurons is useful for understanding the representation of visual motion, and to date the MT area and the primary visual cortex (V1) have been studied in this way (Perrone and Thiele, 2001; Priebe et al., 2003, 2006; Lui et al., 2007). However, the relationship of frequency tuning with OFRs remains unclear. The activities of MST neurons during OFRs and their relationship with behavior have been examined (Kawano et al., 1994; Takemura et al., 2001), but the findings did not reveal the characteristics of visual motion because only moving random-dot stimuli were used. There are no results available for spatiotemporal frequency tuning of MST neurons.
In this study, we demonstrate spatiotemporal frequency tuning of directionally selective neurons in cortical areas MT and MST during OFRs. The present findings reveal differences in visual motion information represented as two successive hierarchies of sensory processing during a single behavior, providing an important example of hierarchical information processing in the cortex.
Materials and Methods
Animal preparation.
Three male rhesus monkeys (monkeys S, K, and T; Macaca mulatta) weighing 7–9 kg were used in this study. Before surgery, all animals were trained to fixate on a small target spot and anatomical images were obtained using MRI (General Electric). Surgeries were performed under general anesthesia with pentobarbital sodium. Under sterile conditions, scleral search coils for measuring eye position were chronically implanted (Judge et al., 1980) and a head holder and recording chambers were embedded in a dental acrylic cap that covered the top of the skull. The recording chambers were stereotaxically placed to allow for a dorsal approach to the parietal cortex in a vertical orientation (stereotaxic coordinates: anteroposterior, −2 to −4 mm; mediolateral, ±16–18 mm). All protocols were approved by the Animal Care and Use Committee of Kyoto University.
Recording technique and histology.
Initial mapping penetrations of the cortex in the dorsal part of the superior temporal sulcus (STS) were made with hand-made glass-coated tungsten electrodes. MRI was used to confirm the location of the STS. Within the STS, neurons were identified as MT or MST neurons based on published reports of their location relative to the STS and their receptive field characteristics (Gattass and Gross, 1981; Komatsu and Wurtz, 1988a). Single units were recorded with tungsten microelectrodes (Microprobe, FHC, or Nano Biosensors). Vertical microelectrode penetrations were made via transdural guide tubes inserted in the grid hole using a guide-tube grid system (Crist Instruments).
Histological sections through the STS of two monkeys (S and K) were obtained as previously described (Kawano et al., 1994; Inaba et al., 2011). Histological verification of the recording sites indicated that these neurons were located in area MT or MST (Maunsell and Van Essen, 1983a; Komatsu and Wurtz, 1988a; Kawano et al., 1994; see also Kawano et al., 1994, their Fig. 1, and Inaba et al., 2011, their supplemental Fig. 1). In the other animal (monkey T), histological verification of the recording sites has not yet been performed because recordings are still underway.
Figure 1.
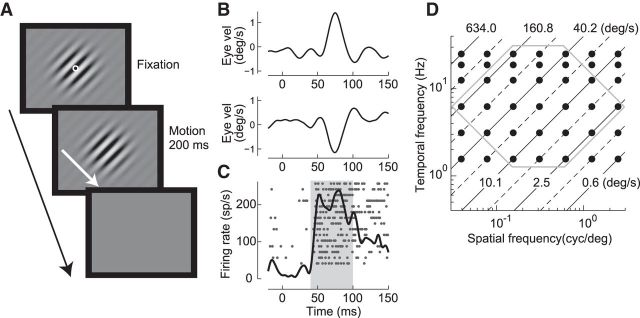
Schematic representation of the visual stimuli. A, The sinusoidal grating appeared at the beginning of each trial. After the monkey fixated on a central target spot, the spot disappeared and the pattern started to move in the preferred direction of the neuron for 200 ms. The orientation of the grating was orthogonal to this preferred direction. B, Mean horizontal (top) and vertical (bottom) eye velocity of the initial OFR elicited by the motion of a sinusoidal grating (0.16 cycles/° and 25 Hz). When the background moved, the eye followed the motion with a latency of ∼60 ms. C, Responses of a MST neuron to movement of the sinusoidal grating in the preferred direction of the neuron (down-rightward). The neuron started to respond ∼20 ms before the onset of eye movement. The raster and spike density functions are superimposed. Neuronal responses were measured as the average of the spike density from 40 to 100 ms after the onset of stimulus motion (shaded area). D, Spatiotemporal frequencies of moving sinusoidal grating stimuli used in this study (black dots). Diagonal lines indicate speeds of the visual stimuli. Note logarithmic abscissa and ordinate. The dataset inside the hexagon was used for later analysis.
Behavioral paradigms and visual stimuli.
The animal was seated in a primate chair in a dark room with its head fixed by a head holder and facing a 19-inch cathode ray tube monitor (FlexScan T766, Nanao), which was located 30 cm in front of the eyes. Visual stimuli were presented on the monitor [resolution, 1280 × 1024 pixels (59° × 48°); vertical refresh rate, 100 Hz]. RGB signals from the video card were converted to black and white images through an attenuator (Pelli and Zhang, 1991). The converted signal was fed into three channels of the display. A luminance look-up table with 32 equally spaced luminance levels ranging from 0.0 to 76.2 cd/m2 was created from direct luminance measurements (LS-100 photometer, [Konica-Minolta]) under software control. This table was then expanded to 2048 equally spaced levels by interpolation (Sheliga et al., 2005; Miura et al., 2006). The visual stimuli used in the study were created and presented using Matlab PsychoToolbox (Brainard, 1997; Pelli, 1997).
After isolating a single unit, we observed the responses to motion of a large-field random-dot pattern (45 × 45°) while the animal fixated on a stationary target at the center of the monitor screen. To determine the preferred direction of motion of the neuron for the random-dot pattern, the stimulus was moved at a constant velocity (40°/s) in eight directions spaced at 45° intervals (horizontal, vertical, and diagonal). If the neuron responded to motion of the large-field random-dot pattern with directional preference, experiments were performed on the neuron. For measuring and mapping the visual receptive field, a target (0.3°) and a random-dot pattern (1 × 1°, 5 × 5°, or 15 × 15°) were displayed. Visual receptive-field mapping was conducted while the animal looked at the central fixation target as the random-dot pattern moved at a constant velocity (40°/s) in the preferred direction.
The visual stimuli were one-dimensional vertical sine-wave gratings moving in the preferred direction of the neuron. The orientation of the visual image was orthogonal to this preferred direction. The contrast of the gratings was 32% at the center of the Gaussian window (the center of the monitor) and was gradually reduced with a Gaussian envelope (σ = 8.5°). In 50 neurons (20 MT and 30 MST) obtained from monkeys S and K, 25 visual motion stimuli were used to examine the spatiotemporal frequency dependence (five spatial frequency entries of 0.04–0.62 cycles/° and five temporal frequency entries of 3.12–25 Hz). In 185 neurons (112 MT and 73 MST) obtained from monkeys K and T, 42 stimuli were used (seven spatial frequency entries of 0.04–2.48 cycles/° and six temporal frequency entries of 1.56–25 Hz; Fig. 1D). In any given trial, one of the spatiotemporal frequencies was selected randomly from the look-up table.
At the beginning of each trial, a grating pattern appeared together with a central target spot (diameter, 0.4°; Fig. 1A). After the monkey's eye had been positioned within 2° of the fixation target for a randomized period of 300 to 500 ms, the fixation target disappeared and the stimulus motion began. If the eye went outside the window during this period or any saccade was detected in the last 250 ms of the period, the screen became uniform gray and the same trial was repeated. The stimulus motion lasted for 200 ms, at which point the screen became a uniform gray of the mean luminance. The animal was then rewarded with a drop of juice, signaling the end of the trial. After an intertrial interval of ∼1 s, a new grating pattern appeared together with a fixation point, to start a new trial. For each spatiotemporal frequency, data were collected over several sessions.
Data collection and analysis.
Stimulus presentation and data collection were controlled by a personal computer (PC) using the REX system (Hays et al., 1982). Eye movements were measured with the electromagnetic search-coil technique (Fuchs and Robinson, 1966). Voltage signals encoding the horizontal and vertical components of the eye position were low-pass filtered with resistor–capacitor circuitry (−3 dB at 170 Hz) and digitized to a resolution of 12 bits at 1 kHz. All data were transferred to a PC for analysis using an interactive computer program based on Matlab (Mathworks). Eye-position data were smoothed with a four-pole digital Butterworth filter (−3 dB at 25 Hz) and eye-velocity traces were derived from the two-point backward difference. Eye-acceleration profiles were derived from the two-point backward difference of the eye-velocity traces and were used to detect small saccades that went undetected during the experiment. Only data free of saccades were analyzed. The initial OFRs were quantified by measuring the changes in eye position over a 60 ms period starting 60 ms after the onset of motion stimuli. The latency of onset was ∼60 ms so that these measurements were made for initial open-loop responses restricted to the period before the closure of the visual feedback loop (i.e., twice the reaction time).
A time–amplitude window discriminator was used to identify spikes with a time resolution of 1 ms. Spike-density histograms were calculated by convolving the spike trains with a Gaussian curve (σ = 10 ms; Richmond et al., 1987). Neuronal responses to motion of stimuli were measured as the average spike density from 40 to 100 ms after onset of the stimulus motion. This temporal window was selected so that the responses were restricted to those caused by visual motion presented while the eyes were stationary. To characterize the properties of the spatiotemporal frequency tuning, neuronal responses to moving grating stimuli were fitted to a two-dimensional Gaussian function given by the following Equations 1 and 2:
 |
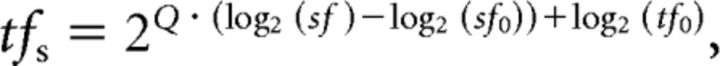 |
where A, b, sf0, tf0, σs, and σt are the maximal activity, spontaneous activity, optimal spatial frequency, optimal temporal frequency, SD of spatial frequency tuning, and SD of temporal frequency tuning, respectively. The value of Q in Equation 2 shows the dependence of the temporal frequency tuning on spatial frequencies (Priebe et al., 2003, 2006). When Q equals 1, the optimal speed is constant over the spatial frequency. In this case, the neuron is tuned for the stimulus speed independent of the spatial frequency of the motion stimulus. When Q is 0, the optimal temporal frequency is constant over the spatial frequency, and thus the optimal speed changes with the stimulus spatial frequency. These constants were optimized for each neuron.
The size and eccentricity of the receptive field of each neuron was estimated by fitting with a 2D Gaussian function of the following standard form, Equation 3:
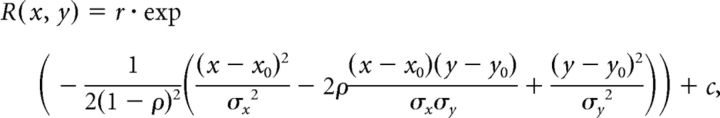 |
where r, c, x0, y0, σx, σy, and ρ were optimized for each neuron. The size was defined by the sum of times the SD along the long and short axes, each of which gives a half-width at half maximum along each axis of the 2D Gaussian function. Most of the MST neurons had receptive fields whose borders were outside of the monitor screen. Therefore, this analysis was applied for the MT neurons and MST neurons whose receptive field borders could be determined.
Also, using two analyses, we examined whether the population activities of areas MT and MST can explain the spatiotemporal tuning of the initial OFRs. A linear relationship between the population activities of MT and MST neurons and the initial OFRs was assumed, as in the following expression, Equation 4:
where ROFR (sf, tf), RMT (sf, tf), RMST (sf, tf) are the initial OFRs and the population activities of MT and MST neurons, and a1, a2, and a3 are coefficients. Regression analyses were carried out using this equation. In the first analysis, the population activity of area X (RX) was defined as follows in Equation 5:
 |
where ri (sf, tf), Ai, and n are the activity of neuron i in area X, the A value for the best-fit Gaussian, and the number of neurons, respectively; that is, the average of normalized activities over the neurons in each area. In the second analysis, population activities were defined simply as the average activity of all neurons in each area. The 95% confidence intervals of the coefficients and the coefficient of determination (R2) were calculated.
Results
We recorded the activities of 235 neurons (101 in the MST area and 132 in the MT area) in the STS during OFRs in three hemispheres of three monkeys. All of these neurons responded to visual motion and most showed clear directional selectivity, with average firing rates in the preferred directions that were ≥1.5 times those in the opposite direction.
Spatiotemporal frequency tuning of MT and MST neurons
Spatiotemporal frequency tuning reveals the information carried by neuronal activities. We first examined the dependence of the neurons on the spatiotemporal frequency when the monkeys were exposed to large-field sinusoidal grating stimuli with different spatial frequencies moving at different temporal frequencies. Figure 1 shows an example of the responses of a neuron to brief motion of the sinusoidal grating in the preferred direction (in this case, an MST neuron with a preferred down-rightward direction; Fig. 1A). Motion of such a large-field pattern elicits ocular responses with short latency in the direction of stimulus motion. In this case, the OFR was induced in a down-rightward direction with a latency of ∼60 ms (Fig. 1B; 0.16 cycle/°, 25 Hz, 32%). The neuron increased its firing rate in response to motion of the grating with a latency of ∼40 ms (Fig. 1C); that is, preceding the onset of eye movement responses for ∼20 ms. Mean firing rates in the 60 ms interval starting from 40 ms after onset of stimulus motion (shaded area) were quantified as the activities underlying the initial OFRs.
The responses of the MST neuron depended on the spatiotemporal frequency of the sinusoidal gratings (Fig. 2; the same MST neuron as in Fig. 1). The mean firing rate of the initial activities of this MST neuron showed the largest responses at 0.16 cycles/° (spatial frequency) and 18.75 Hz (temporal frequency). To estimate the optimal spatiotemporal frequency, a 2D Gaussian function (Eqs. 1, 2) was fitted to the mean firing rate data. For this MST neuron, the optimal spatial frequency (sfo) and optimal temporal frequency (tfo) were 0.13 cycles/° and 19.6 Hz, respectively (R2 = 0.87). Activities of other MST neurons also depended on the spatiotemporal frequency and 78 of these neurons were successfully characterized by the 2D Gaussian function. The initial activities of many MT neurons also tuned for the spatiotemporal frequency of the drifting sinusoidal gratings and these tunings were also characterized by the 2D Gaussian function (N = 88). Figure 3 shows the response field of an MT neuron in Fourier space. The response field was well characterized by the 2D Gaussian function; and the optimal spatial (sfo) and temporal frequency (tfo) were estimated to be 0.56 cycles/° and 21.4 Hz, respectively (R2 = 0.91).
Figure 2.
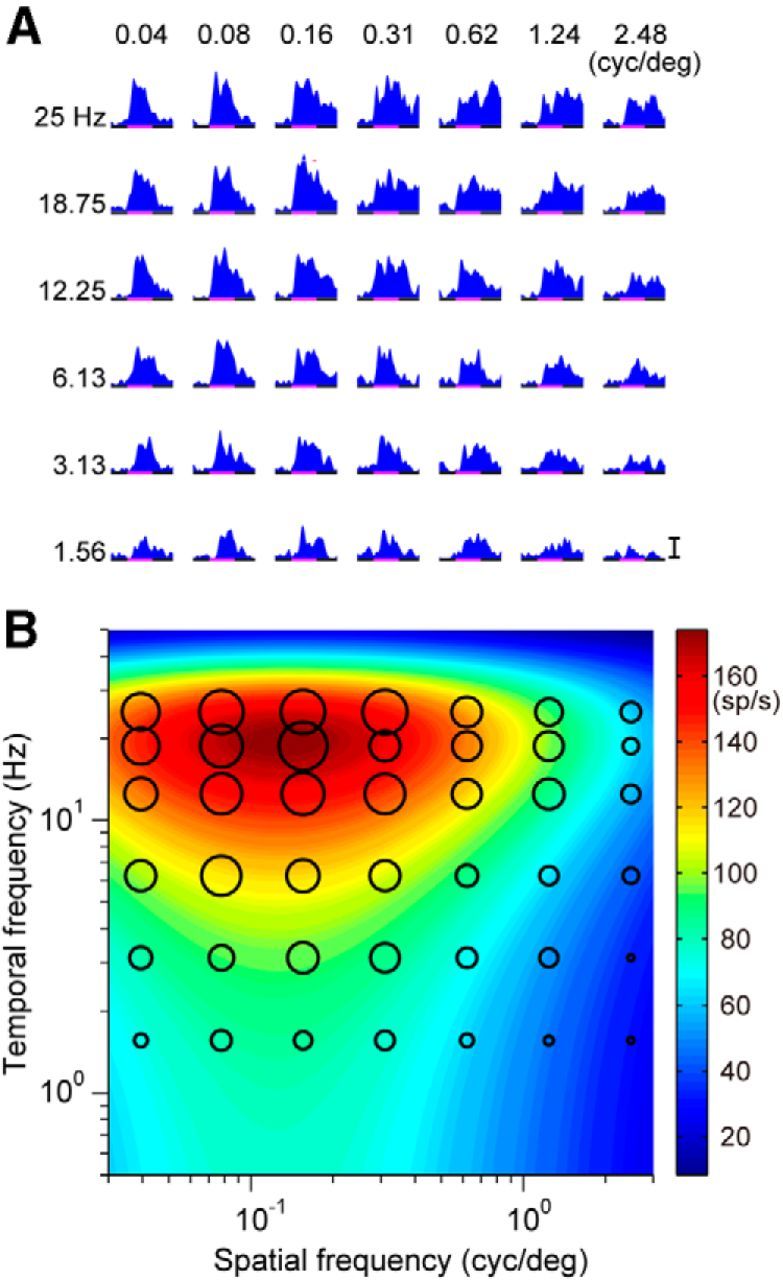
Spatiotemporal response tuning of a neuron in area MST. A, Neuronal responses of a single cell to drifting gratings with various spatiotemporal frequencies (25, 18.75, 12.25, 6.13, 3.13, and 1.56 Hz from top to bottom; 0.04, 0.08, 0.16, 0.31, 0.62, 1.24, and 2.48 cycles/° from left to right). The bar indicates 100 spikes/s. B, Contour plots of the best-fit 2D Gaussian functions in Fourier space. Magnitudes of the values are indicated by colors (blue, lower; red, higher). The diameters of the filled circles indicate the average of the spike density from 40 to 100 ms after onset of motion for each stimulus.
Figure 3.
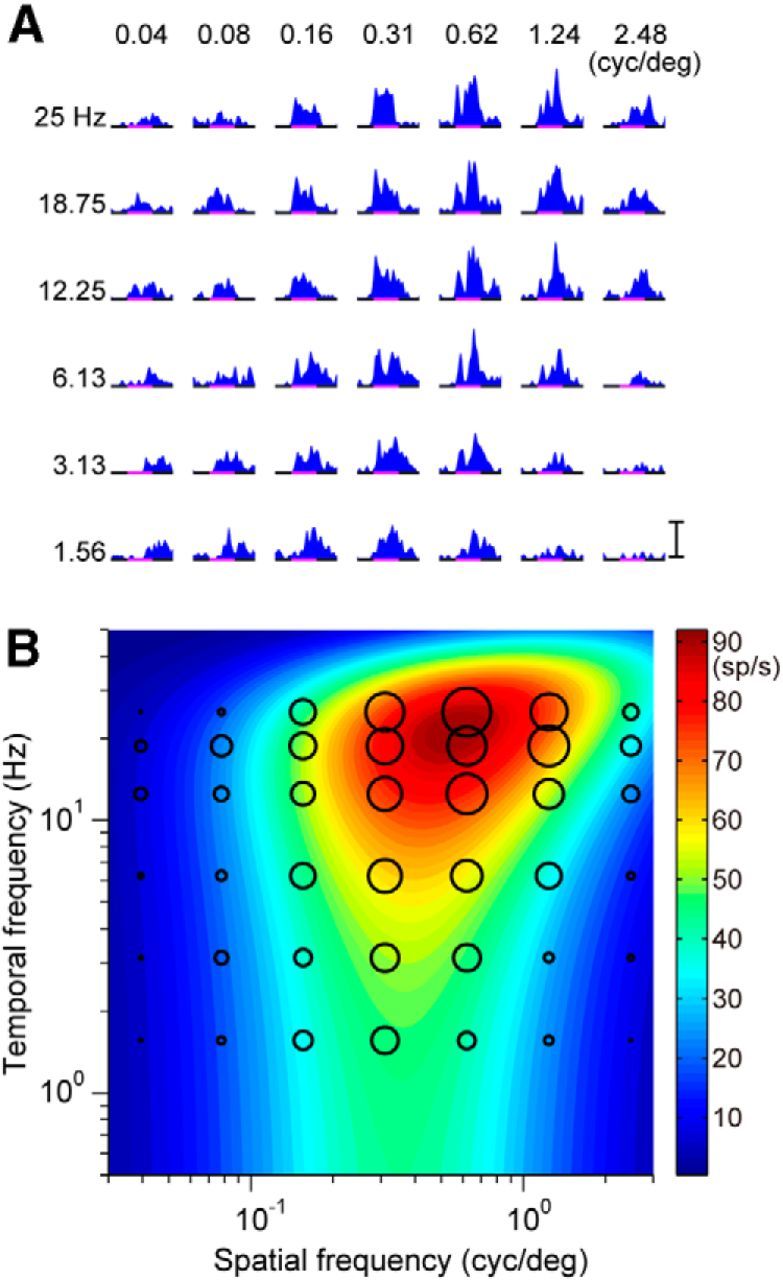
Spatiotemporal response tuning of a neuron in area MT. A, Neuronal responses of a single cell to drifting gratings with various spatiotemporal frequencies. B, Contour plots of the best-fit 2D Gaussian functions in Fourier space. Conventions are the same as in Figure 2.
The optimal spatiotemporal frequencies estimated from the best-fit Gaussian functions distributed widely in Fourier space and showed a difference between the two areas (Fig. 4A,B). Compared with the MT neurons (Fig. 4B; N = 88), the sfo of the MST neurons (Fig. 4A; N = 78) was distributed in a lower frequency range and the difference in distributions was significant (Kolmogorov–Smirnov test, p < 0.05). The tfo of the MST neurons was distributed in a slightly higher frequency range compared with the MT neurons, but this difference was not significant (p > 0.05).
Figure 4.
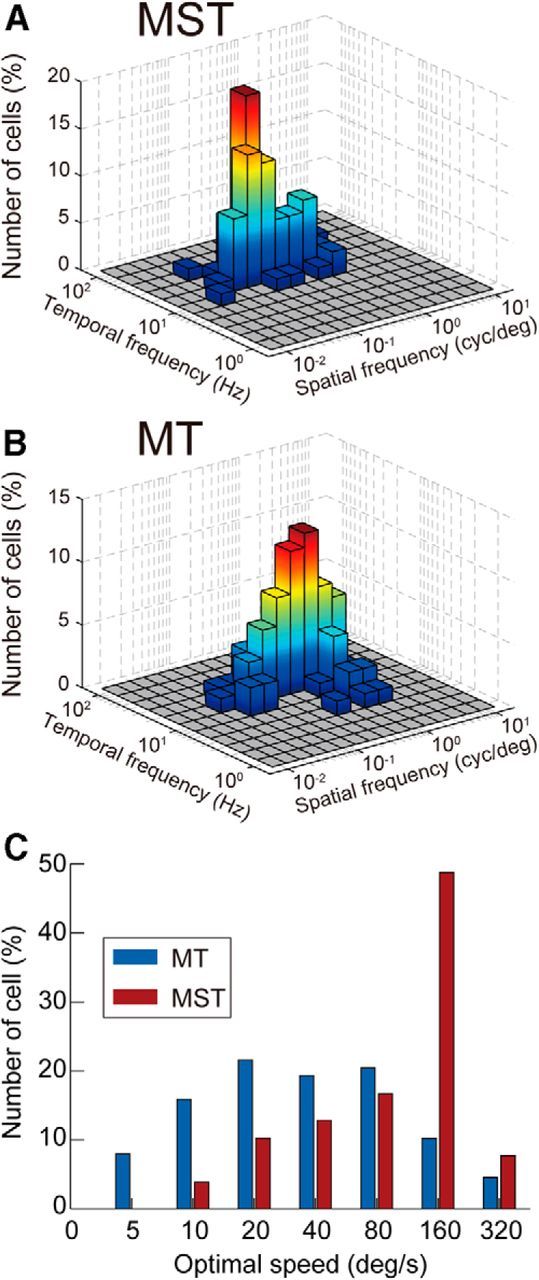
Spatiotemporal response tuning of individual neurons in areas MT and MST. A, B, Distributions of optimal spatiotemporal frequencies in MT (A) and MST (B). C, Distribution of speeds of the optimal gratings. Blue and red bars indicate the distributions of MT neurons and MST neurons, respectively. Note the logarithmic abscissa.
Our data suggest a speed preference mechanism in areas MT and MST. The speeds of the optimal stimuli of the MT neurons fell in a slower range, whereas those of the MST neurons tended to be faster (Fig. 4C). The medians for the MT and MST neurons were 34.8 and 132.7°/s, respectively, and were significantly different (rank-sum test, p < 0.05). The distributions were also significantly different (Kolmogorov–Smirnov test, p < 0.05). These results may be due to differences in the optimal spatial and temporal frequencies. However, the difference in the optimal spatial frequency may be more important, given that the median optimal spatial frequency of the MT neurons was >3 times that of the MST neurons (0.52 vs 0.15 cycles/°), while the median optimal temporal frequencies of the MT and MST neurons were similar (16.7 vs 18.2 Hz; Fig. 4).
Relationship between frequency tuning and receptive field properties
MT neurons have smaller receptive fields than MST neurons and the size increases with the distance from the fixation point (Desimone and Ungerleider, 1986; Tanaka et al., 1986; Albright and Desimone, 1987; Komatsu and Wurtz, 1988a; Tanaka and Saito, 1989). Consistent with these previous findings, the MT neurons examined in this study had limited receptive field sizes that were highly correlated with eccentricities. In contrast, the receptive fields of MST neurons often extended to >25° and involved the ipsilateral hemifield, and the edges of their receptive fields could not be determined.
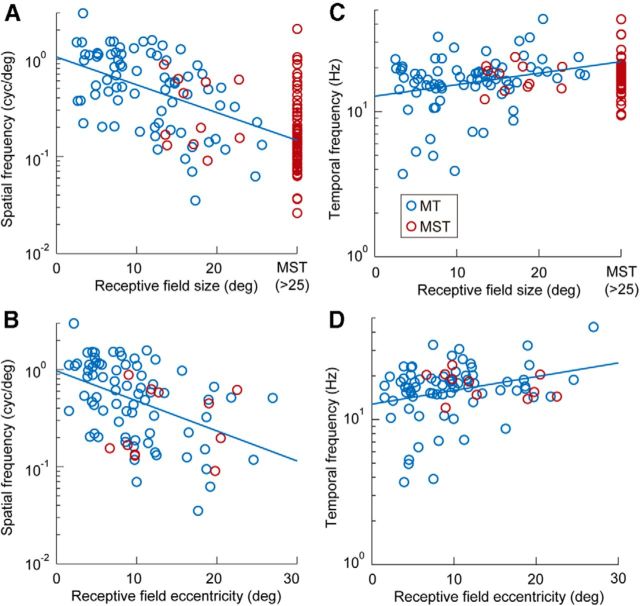
The significant correlation (Spearman rank correlation, r = −0.51, p < 0.05) between the size of receptive fields and the optimal spatial frequency of the MT neurons (blue circles, N = 75) is shown in Figure 5A. The logarithm of optimal spatial frequencies was almost linearly related to the size of the receptive field (Fig. 5A, blue line). In contrast, MST neurons with receptive field sizes <25° (N = 11, red circles) showed no significant correlation (r = −0.25, p > 0.05). The optimal spatial frequencies of the remaining MST neurons (N = 67) were distributed across almost the entire range of the optimal spatial frequencies of the MT neurons (Fig. 5A, red circles at right edge), although the MST neurons tended to be tuned for a lower spatial frequency, as described earlier. The optimal spatial frequencies of the MT neurons were also correlated with the eccentricity of the center location of the receptive field (Fig. 5B, blue circles; r = −0.48, p < 0.05), whereas MST neurons with receptive field sizes of <25° (N = 11, red circles) showed no correlation (r = 0.12, p > 0.05). These results indicate that, at least in area MT, the spatial frequency tuning of the neurons is related to the size and eccentricity of the receptive field.
Figure 5.
A, B, Relationship between optimal spatial frequency and receptive field size (A) and eccentricity (B; blue, MT neurons; red, MST neurons). The regression lines for data from MT neurons are also indicated as blue lines. Data from most of the MST neurons with receptive field sizes >25° are plotted on the rightmost side of the panel. Note the logarithmic ordinate for the optimal spatial frequency. C, D, Relationship between optimal temporal frequency and receptive field size (C) and eccentricity (D; blue, MT neurons; red, MST neurons). Conventions are the same as in A and B.
The optimal temporal frequency was related to receptive field properties in the MT neurons, although it was weaker compared with spatial frequency (Spearman rank correlation, r = −0.28, p < 0.05 for size; Fig. 5C; r = −0.25, p < 0.05 for eccentricity; Fig. 5D). No relationship was found in the MST neurons. The strengths of direction selectivity of the MT and MST neurons were calculated as the width at half-maximum of the best-fit von Mises functions [Inaba et al., 2011; MT (mean + SD): 125.5 + 33.2°; MST (mean + SD): 126.1 + 24.6°]. Neither was related to the optimal spatiotemporal frequency tuning.
Separable spatial and temporal frequency tuning in MT and MST neurons
The response field in Fourier space reveals information carried by neuronal activities. The Q value of the 2D Gaussian function (Eq. 2) quantifies the degree to which temporal frequency tuning depends on the spatial frequency of the stimulus. If Q = 0, the spatial and temporal frequency tunings are separable; if Q = 1, the neuron is tuned for a particular speed independent of the spatial frequency. The Q values of the MT and MST neurons in Figures 3 and 2, respectively, were 0.23 and 0.01, respectively. Q values were distributed between 0 and 1 with a bias toward 0 for both MT and MST neurons, but the distributions differed significantly between the MT and MST neurons (Fig. 6A; Kolmogorov–Smirnov test, p < 0.05). The median values for the MT and MST neurons were 0.25 and 0.07, respectively, which were also significantly different (rank-sum test, p < 0.05). That is, compared with the MT neurons, the MST neurons were tuned for the temporal frequency, rather than the speed of visual motion. We also repeated the same analysis using the dataset resampled from a tilted stimulus matrix (Fig. 1D, the dataset in the hexagon, similar to Simoncini et al., 2012, their Fig. 6b). to examine whether stimulus sampling influence of the MST neurons, but found no significant effect of stimulus sampling in Q values (Wilcoxon rank-sum test, p > 0.25).
Figure 6.

Separation of spatial and temporal frequency tunings. A, Distributions of Q values for the initial responses of MT (blue bars) and MST neurons (red bars). B, C, Relationships of Q values with the optimal spatial frequency (B) and the optimal temporal frequency (C). Blue and red circles indicate data for MT and MST neurons, respectively. The regression lines for data from MT and MST neurons are also indicated as blue and red lines, respectively.
The Q values were correlated with the optimal spatial frequency in the MT neurons (Fig. 6B, blue circles; Spearman rank correlation, r = 0.49, p < 0.05). When the optimal spatial frequency of the neuron was lower, the Q values tended to be closer to 0. The distribution of Q values tended to be intermediate between 0 and 1 as the optimal spatial frequency increased. Most of the MST neurons were tuned for a lower spatial frequency and had Q values close to 0. The Q values of the MST neurons showed no significant correlation with the optimal spatial frequency (Fig. 6B, red circles; r = 0.10, p > 0.05). Note that, for both MT and MST neurons, the Q values were correlated negatively with the optimal temporal frequency [Fig. 6C, blue (MT) and red (MST) circles; MT: r = −0.23, p < 0.05; MST: r = −0.23, p < 0.05]. The Q values were also correlated with the size and center eccentricity of the receptive field in the MT neurons (size: r = −0.29, p < 0.05; eccentricity: r = −0.23, p < 0.05). For the 11 MST neurons with receptive fields <25°, the correlations between Q values and the size and eccentricity of the receptive field were not significant (size: r = −0.33, p > 0.05; center: r = −0.41, p > 0.05).
Population activities of MT and MST neurons and properties of the OFRs
The optimal spatiotemporal frequencies of the MT and MST neurons (Fig. 4A,B) were distributed in a spatial frequency range over which the OFRs are operative. The optimal temporal frequencies were in general high and distributed in a narrow range, which is consistent with the temporal frequency tuning of the initial OFR. Here, the population activities of the MT and MST neurons were compared with the properties of the OFRs of monkeys (Fig. 7A). The initial integrative measures of OFRs showed a bandpass tuning for the sinusoidal grating stimuli, and that was well characterized by a 2D Gaussian function (R2 > 0.9) with optimal spatiotemporal frequencies at 0.37 cycles/° and 19.38 Hz (Q = 0.00). Similar patterns of spatiotemporal frequency tunings were observed for population activities in both areas (Fig. 7B,C). The population activities were defined as the average over the responses after dividing by the amplitude for the best-fit Gaussian for individual neurons (Eq. 5). The response field of the population activities showed that the MT population was tuned for relatively higher spatial frequency (0.48 cycles/° and 14.97 Hz, Q = 0.12), whereas that of the MST population tuned for lower spatial frequency (0.18 cycles/° and 18.79 Hz, Q = 0.00). The optimal spatial frequency of the initial OFRs lies intermediate between those of the MT and MST population activities.
Figure 7.
Reconstructions of the initial OFRs from population responses of MT and MST neurons. A, Contour plot of spatiotemporal frequency tuning of the initial OFRs. B, C, Spatiotemporal frequency tuning of the population activities of MT (B) and MST neurons (C). D, Reconstructed spatiotemporal frequency tuning of OFRs from the population activities of MT and MST neurons. The color column on the right of each panel indicates the initial change in eye position (A, D), and the population activity of the MT (B) and MST (C) neurons.
Regression analysis was performed to examine how strongly the activities of the MT and MST populations are related to the initial OFRs. A regression analysis with the population activities of the MT and MST neurons gave a good reconstruction of the initial OFRs with a coefficient of determination (R2) of 0.87 and an associated p value of <0.05. The spatiotemporal frequency tuning of the reconstructed responses is shown in Figure 7D (0.32 cycles/° and 17.83 Hz, Q = 0.03). The coefficients for MT and MST neurons were 0.041 ± 0.004 (p < 0.05) and 0.032 ± 0.004 (p < 0.05), respectively [0.003 ± 0.002 (p > 0.1) for the offset], indicating that both the MT and MST activities contribute to the reconstruction. Note that Akaike's information criterion also supported the need to include both the population activities of the MT and MST neurons. The same analysis was also performed with the population activities defined as simple averages of the responses of individual neurons, and gave slightly worse, but still good, reconstruction of the initial OFRs with R2 of 0.84 and the associated p value of <0.05. The p values associated with the coefficients of both MT and MST neurons were <0.05 [0.002 ± 0.004 (p > 0.1) for the offset].
Discussion
In this study, we found (1) that most MT/MST neurons have nearly separable spatiotemporal frequency tuning, (2) that MST neurons were tuned for a lower spatial frequency compared with MT neurons, and (3) that the spatiotemporal frequency tuning of OFRs could be reproduced by a weighted sum of the population activities of the MT and MST neurons. Below, we will discuss the representations of visual motion by the MT/MST neurons and their contributions to behavior.
Neurons code for spatiotemporal frequency
There is uncertainty regarding the visual motion information encoded by neuronal responses (Perrone and Thiele, 2001; Priebe et al., 2003, 2006; Lui et al., 2007). Perrone and Thiele (2001) examined spatiotemporal frequency tuning of MT neurons in awake macaque monkeys and suggested that most MT neurons were tuned for stimulus speed independent of spatial frequency. In contrast, Priebe et al. (2003) examined MT neurons in anesthetized, paralyzed macaque monkeys and showed that only a minority of the MT neurons (25%) were tuned for speed independent of spatial frequency, and that other neurons were tuned for temporal frequency independent of spatial frequency or showed intermediate properties. Lui et al. (2007) examined MT neurons in anesthetized common marmosets and found that the majority of these neurons had bandpass spatial and temporal frequency tuning, that the selectivity for these parameters was largely separable, and that only 10% of the neurons showed a spatial frequency-invariant representation of speed. However, these data come from different laboratories using different experimental conditions (e.g., awake or anesthetized) and species (macaques or marmosets), and these differences may account for the different conclusions.
In this study, we recorded the neural activities of awake macaques and used a similar method to characterize spatiotemporal frequency tuning to those of Priebe et al. (2003) and Lui et al. (2007). We found that the MT population had a similar distribution of Q values to those found by Priebe et al. (2003) and Lui et al. (2007). We therefore suggest that only a minority of MT neurons code for speed independent of spatial frequency, even in an awake condition. Closer observation revealed that Q values were correlated with the optimal spatial and temporal frequencies in the MT neurons, suggesting a functional difference among neurons in MT, depending on their optimal spatiotemporal frequencies. The Q value was closer to 1 as the optimal spatial frequency of the neuron increased and as the optimal temporal frequency decreased. Thus, representation of motion might differ in MT depending on the properties of visual stimuli; finer and slower visual stimuli may tend to be coded by speed, whereas coarser and faster visual stimuli by spatiotemporal frequency.
We also examined the properties of the MST neurons and found that a large proportion showed separable tuning for spatial and temporal frequency. Surprisingly, the distribution of Q values was shifted toward 0 compared with the MT neurons. The median Q value (0.07) was similar to the value for simple cells in the primary visual cortex (0.08) reported by Priebe et al. (2006). These results suggest that most MST neurons rather selectively receive signals from MT neurons with separable tuning for spatial and temporal frequencies. We thus conclude that the MST neurons represent the spatiotemporal frequency of the motion stimuli at least in their initial responses. It is possible that speed tuning might appear after the open-loop period, but that should be tested in a future study.
Mechanism of speed dependence
The activities of MT/MST neurons are known to depend on stimulus speed (Maunsell and Van Essen, 1983a; Kawano et al., 1994). Using a large-field random-dot pattern, Inaba and Kawano (2010) found that the optimal speeds of MT neurons tend to be slower than those of MST neurons (means of 49.0 and 93.0°/s for MT and MST, respectively). In the present study, by using sinusoidal gratings, we obtained a consistent finding that speeds estimated from optimal spatiotemporal frequencies of MT neurons were slower than those of MST neurons (medians of 34.2 and 131.5°/s for MT and MST, respectively). Our data also provide an insight into the mechanism of the difference in their speed-tunings. The speed of a sinusoidal grating (degrees per second) is given by its temporal frequency (hertz) divided by the spatial frequency (cycles per degree). The temporal frequency tunings of the MT and MST neurons were similar, but the spatial frequency tunings were different, with the median optimal spatial frequency of the MST neurons being ∼3 times that of the MT neurons. The results suggest that the difference in speed tuning is due to the difference in spatial frequency tuning between the two areas.
Representations of visual motion in areas MT and MST
Previous studies have shown that the size of the receptive field of MT neurons is correlated with eccentricity, with a larger size with increased eccentricity (Desimone and Ungerleider, 1986; Tanaka et al., 1986; Albright and Desimone, 1987; Komatsu and Wurtz, 1988a; Tanaka and Saito, 1989). We confirmed this relationship and also found that both the size and eccentricity were significantly correlated with the optimal spatial frequency. These results suggest that neurons with different receptive-field eccentricities (and also size) represent different aspects of visual motion stimuli, with larger (smaller) eccentricity representing motion of lower (higher) spatial frequency components of the visual stimuli.
We demonstrated that the optimal spatial frequencies of the MST neurons were distributed such that they covered almost the entire range of the optimal spatial frequencies of the MT neurons, suggesting that visual response properties of MST neurons are formed by inputs from a population of MT neurons, which is consistent with the anatomical evidence (Maunsell and Van Essen, 1983a; Ungerleider and Desimone, 1986). We further suggest that the majority of the neurons receive dominant signals from MT populations that are tuned for lower spatial frequencies and whose receptive field centers tend to be located in the peripheral visual field. MST neurons with smaller receptive fields (<25°) do not show a significant correlation of the optimal spatial frequency with the receptive field size or eccentricity, in contrast to MT neurons. This might be due to spatial integration of inputs from MT neurons with a range of eccentricity and size of receptive fields. We also note the diversity of the optimal spatial frequency of the MST neurons, which suggests that each MST neuron integrates signals from a different population of MT neurons.
Roles of MT and MST neurons in OFRs
Area MST is thought to be the central cortical area for OFRs (Kawano et al., 1994; Kawano, 1999; Takemura et al., 2007). Area MT is also thought to be important as the major source of visual information for MST neurons because area MST receives strong projections from area MT (Maunsell and Van Essen, 1983a; Ungerleider and Desimone, 1986). However, areas MT and MST project to the dorsolateral pontine nuclei (DLPN) (Brodal, 1978; Glickstein et al., 1980, 1985; Maunsell and van Essen, 1983b; Ungerleider et al., 1984; May and Andersen, 1986; Tusa and Ungerleider, 1988; Boussaoud et al., 1992). Thus, these two areas constitute a dual pathway system with a detour through area MST.
These anatomical findings suggest that areas MT and MST both contribute to generate OFRs. Our data support this suggestion and add new insights into the mechanisms. In the present study, we demonstrated that the optimal spatiotemporal frequency of the initial OFR was intermediate between the population activities of the MT and MST neurons. Regression analyses revealed that a weighted sum of the population activities of the MT and MST neurons gave a good reconstruction of the spatiotemporal frequency dependence of the OFRs, which is consistent with the idea that both areas mediate visual motion information. Furthermore, OFRs depend on the spatial frequency of the motion stimuli (Miles et al., 1986; Gellman et al., 1990; Sheliga et al., 2005; Miura et al., 2006, 2009), and the optimal spatial frequency shifts lower as the size or eccentricity of the visual stimulus increases (Aoki et al., 2012; Quaia et al., 2012). These properties may be explained by increased incorporation of MT neurons that have receptive fields at the peripheral visual field because they are tuned for lower spatial frequencies.
We conclude that in rapid extraction of visual motion, both MT and MST neurons work as spatiotemporal frequency sensors that extract motion of finer and coarser visual features and contribute to generation of OFRs. It seems practically that the existence of the projection from area MT to the DLPN is sufficient to generate the OFRs. However, there is a benefit of adding a secondary MST-DLPN pathway because MST neurons are tuned for lower spatial frequency and the secondary pathway boosts the signals from coarse visual features. Thus, MST neurons may regulate the operating range of the OFR system, allowing the system to work more robustly in everyday situations. Takemura et al. (2007) found that lesions of the STS affected OFRs. However, these lesions also spread into areas MT and MST. Thus, future studies with lesions exclusive to area MST are needed to test our hypothesis.
Footnotes
This work was supported by Ministry of Education, Culture, Sports, Science, and Technology (MEXT) Kakenhi Grant 23500467 to K.M. and by MEXT Kakenhi Grant 21240037 to K.K.
The authors declare no competing financial interests.
References
- Albright TD, Desimone R. Local precision of visuotopic organization in the middle temporal area (MT) of the macaque. Exp Brain Res. 1987;65:582–592. doi: 10.1007/BF00235981. [DOI] [PubMed] [Google Scholar]
- Aoki Y, Kawano K, Miura K. Facilitative integration of local motion signals in the peripheral visual field observed in monkey ocular following responses. Neurosci Res. 2012;74:48–58. doi: 10.1016/j.neures.2012.06.003. [DOI] [PubMed] [Google Scholar]
- Boussaoud D, Desimone R, Ungerleider LG. Subcortical connections of visual areas MST and FST in macaques. Vis Neurosci. 1992;9:291–302. doi: 10.1017/S0952523800010701. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10:433–436. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- Brodal P. The corticopontine projection in the rhesus monkey. Origin and principles of organization. Brain. 1978;101:251–283. doi: 10.1093/brain/101.2.251. [DOI] [PubMed] [Google Scholar]
- Desimone R, Ungerleider LG. Multiple visual areas in the caudal superior temporal sulcus of the macaque. J Comp Neurol. 1986;248:164–189. doi: 10.1002/cne.902480203. [DOI] [PubMed] [Google Scholar]
- Duffy CJ, Wurtz RH. Sensitivity of MST neurons to optic flow stimuli. I. A continuum of response selectivity to large-field stimuli. J Neurophysiol. 1991;65:1329–1345. doi: 10.1152/jn.1991.65.6.1329. [DOI] [PubMed] [Google Scholar]
- Fuchs AF, Robinson DA. A method for measuring horizontal and vertical eye movement chronically in the monkey. J Appl Physiol. 1966;21:1068–1070. doi: 10.1152/jappl.1966.21.3.1068. [DOI] [PubMed] [Google Scholar]
- Gattass R, Gross CG. Visual topography of striate projection zone (MT) in posterior superior temporal sulcus of the macaque. J Neurophysiol. 1981;46:621–638. doi: 10.1152/jn.1981.46.3.621. [DOI] [PubMed] [Google Scholar]
- Gellman RS, Carl JR, Miles FA. Short latency ocular-following responses in man. Vis Neurosci. 1990;5:107–122. doi: 10.1017/S0952523800000158. [DOI] [PubMed] [Google Scholar]
- Glickstein M, Cohen JL, Dixon B, Gibson A, Hollins M, Labossiere E, Robinson F. Corticopontine visual projections in macaque monkeys. J Comp Neurol. 1980;190:209–229. doi: 10.1002/cne.901900202. [DOI] [PubMed] [Google Scholar]
- Glickstein M, May JG, 3rd, Mercier BE. Corticopontine projection in the macaque: the distribution of labelled cortical cells after large injections of horseradish peroxidase in the pontine nuclei. J Comp Neurol. 1985;235:343–359. doi: 10.1002/cne.902350306. [DOI] [PubMed] [Google Scholar]
- Hays AV, Richmond BJ, Optican LM. A UNIX-based multiple process system for real-time data acquisition and control. WESCON Conf Proc. 1982;2:1–10. [Google Scholar]
- Inaba N, Kawano K. Responses of MSTd and MT neurons during smooth pursuit exhibit similar temporal frequency dependence on retinal image motion. Cereb Cortex. 2010;20:1708–1718. doi: 10.1093/cercor/bhp235. [DOI] [PubMed] [Google Scholar]
- Inaba N, Miura K, Kawano K. Direction and speed tuning to visual motion in cortical areas MT and MSTd during smooth pursuit eye movements. J Neurophysiol. 2011;105:1531–1545. doi: 10.1152/jn.00511.2010. [DOI] [PubMed] [Google Scholar]
- Judge SJ, Richmond BJ, Chu FC. Implantation of magnetic search coils for measurement of eye position: an improved method. Vision Res. 1980;20:535–538. doi: 10.1016/0042-6989(80)90128-5. [DOI] [PubMed] [Google Scholar]
- Kawano K. Ocular tracking: behavior and neurophysiology. Curr Opin Neurobiol. 1999;9:467–473. doi: 10.1016/S0959-4388(99)80070-1. [DOI] [PubMed] [Google Scholar]
- Kawano K, Shidara M, Watanabe Y, Yamane S. Neural activity in cortical area MST of alert monkey during ocular following responses. J Neurophysiol. 1994;71:2305–2324. doi: 10.1152/jn.1994.71.6.2305. [DOI] [PubMed] [Google Scholar]
- Komatsu H, Wurtz RH. Relation of cortical areas MT and MST to pursuit eye movements. I. Localization and visual properties of neurons. J Neurophysiol. 1988a;60:580–603. doi: 10.1152/jn.1988.60.2.580. [DOI] [PubMed] [Google Scholar]
- Komatsu H, Wurtz RH. Relation of cortical areas MT and MST to pursuit eye movements. III. Interaction with full-field visual stimulation. J Neurophysiol. 1988b;60:621–644. doi: 10.1152/jn.1988.60.2.621. [DOI] [PubMed] [Google Scholar]
- Lui LL, Bourne JA, Rosa MG. Spatial and temporal frequency selectivity of neurons in the middle temporal visual area of new world monkeys (Callithrix jacchus) Eur J Neurosci. 2007;25:1780–1792. doi: 10.1111/j.1460-9568.2007.05453.x. [DOI] [PubMed] [Google Scholar]
- Maunsell JH, Van Essen DC. Functional properties of neurons in middle temporal visual area of the macaque monkey. II. Binocular interactions and sensitivity to binocular disparity. J Neurophysiol. 1983a;49:1148–1167. doi: 10.1152/jn.1983.49.5.1148. [DOI] [PubMed] [Google Scholar]
- Maunsell JH, van Essen DC. The connections of the middle temporal visual area (MT) and their relationship to a cortical hierarchy in the macaque monkey. J Neurosci. 1983b;3:2563–2586. doi: 10.1523/JNEUROSCI.03-12-02563.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May JG, Andersen RA. Different patterns of corticopontine projections from separate cortical fields within the inferior parietal lobule and dorsal prelunate gyrus of the macaque. Exp Brain Res. 1986;63:265–278. doi: 10.1007/BF00236844. [DOI] [PubMed] [Google Scholar]
- Miles FA. The neural processing of 3-D visual information: evidence from eye movements. Eur J Neurosci. 1998;10:811–822. doi: 10.1046/j.1460-9568.1998.00112.x. [DOI] [PubMed] [Google Scholar]
- Miles FA, Kawano K, Optican LM. Short-latency ocular following responses of monkey. I. Dependence on temporospatial properties of visual input. J Neurophysiol. 1986;56:1321–1354. doi: 10.1152/jn.1986.56.5.1321. [DOI] [PubMed] [Google Scholar]
- Miura K, Matsuura K, Taki M, Tabata H, Inaba N, Kawano K, Miles FA. The visual motion detectors underlying ocular following responses in monkeys. Vision Res. 2006;46:869–878. doi: 10.1016/j.visres.2005.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miura K, Kobayashi Y, Kawano K. Ocular responses to brief motion of textured backgrounds during smooth pursuit in humans. J Neurophysiol. 2009;102:1736–1747. doi: 10.1152/jn.00430.2009. [DOI] [PubMed] [Google Scholar]
- Movshon JA, Adelson EH, Gizzi MS, Newsome WT. The analysis of moving visual patterns. In: Chagas C, Gattass R, Gross C, editors. Pattern recognition mechanisms (pontificiae academiae scientiarum scripta varia) Rome: Vatican; 1985. pp. 117–151. [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis. 1997;10:437–442. doi: 10.1163/156856897X00366. [DOI] [PubMed] [Google Scholar]
- Pelli DG, Zhang L. Accurate control of contrast on microcomputer displays. Vision Res. 1991;31:1337–1350. doi: 10.1016/0042-6989(91)90055-A. [DOI] [PubMed] [Google Scholar]
- Perrone JA, Thiele A. Speed skills: measuring the visual speed analyzing properties of primate MT neurons. Nat Neurosci. 2001;4:526–532. doi: 10.1038/87480. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Cassanello CR, Lisberger SG. The neural representation of speed in macaque area MT/V5. J Neurosci. 2003;23:5650–5661. doi: 10.1523/JNEUROSCI.23-13-05650.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Lisberger SG, Movshon JA. Tuning for spatiotemporal frequency and speed in directionally selective neurons of macaque striate cortex. J Neurosci. 2006;26:2941–2950. doi: 10.1523/JNEUROSCI.3936-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quaia C, Sheliga BM, Fitzgibbon EJ, Optican LM. Ocular following in humans: spatial properties. J Vis. 2012;12(4):13. doi: 10.1167/12.4.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richmond BJ, Optican LM, Podell M, Spitzer H. Temporal encoding of two-dimensional patterns by single units in primate inferior temporal cortex. I. Response characteristics. J Neurophysiol. 1987;57:132–146. doi: 10.1152/jn.1987.57.1.132. [DOI] [PubMed] [Google Scholar]
- Rust NC, Mante V, Simoncelli EP, Movshon JA. How MT cells analyze the motion of visual patterns. Nat Neurosci. 2006;9:1421–1431. doi: 10.1038/nn1786. [DOI] [PubMed] [Google Scholar]
- Sheliga BM, Chen KJ, Fitzgibbon EJ, Miles FA. Initial ocular following in humans: a response to first-order motion energy. Vision Res. 2005;45:3307–3321. doi: 10.1016/j.visres.2005.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simoncelli EP, Heeger DJ. A model of neuronal responses in visual area MT. Vision Res. 1998;38:743–761. doi: 10.1016/S0042-6989(97)00183-1. [DOI] [PubMed] [Google Scholar]
- Simoncini C, Perrinet LU, Montagnini A, Mamassian P, Masson GS. More is not always better: adaptive gain control explains dissociation between perception and action. Nat Neurosci. 2012;15:1596–1603. doi: 10.1038/nn.3229. [DOI] [PubMed] [Google Scholar]
- Takemura A, Inoue Y, Gomi H, Kawato M, Kawano K. Change in neuronal firing patterns in the process of motor command generation for the ocular following response. J Neurophysiol. 2001;86:1750–1763. doi: 10.1152/jn.2001.86.4.1750. [DOI] [PubMed] [Google Scholar]
- Takemura A, Murata Y, Kawano K, Miles FA. Deficits in short-latency tracking eye movements after chemical lesions in monkey cortical areas MT and MST. J Neurosci. 2007;27:529–541. doi: 10.1523/JNEUROSCI.3455-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka K, Saito H. Analysis of motion of the visual field by direction, expansion/contraction, and rotation cells clustered in the dorsal part of the medial superior temporal area of the macaque monkey. J Neurophysiol. 1989;62:626–641. doi: 10.1152/jn.1989.62.3.626. [DOI] [PubMed] [Google Scholar]
- Tanaka K, Hikosaka K, Saito H, Yukie M, Fukada Y, Iwai E. Analysis of local and wide-field movements in the superior temporal visual areas of the macaque monkey. J Neurosci. 1986;6:134–144. doi: 10.1523/JNEUROSCI.06-01-00134.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tusa RJ, Ungerleider LG. Fiber pathways of cortical areas mediating smooth pursuit eye movements in monkeys. Ann Neurol. 1988;23:174–183. doi: 10.1002/ana.410230211. [DOI] [PubMed] [Google Scholar]
- Ungerleider LG, Desimone R. Cortical connections of visual area MT in the macaque. J Comp Neurol. 1986;248:190–222. doi: 10.1002/cne.902480204. [DOI] [PubMed] [Google Scholar]
- Ungerleider LG, Desimone R, Galkin TW, Mishkin M. Subcortical projections of area MT in the macaque. J Comp Neurol. 1984;223:368–386. doi: 10.1002/cne.902230304. [DOI] [PubMed] [Google Scholar]
- Zeki SM. Functional organization of a visual area in the posterior bank of the superior temporal sulcus of the rhesus monkey. J Physiol. 1974;236:549–573. doi: 10.1113/jphysiol.1974.sp010452. [DOI] [PMC free article] [PubMed] [Google Scholar]