Performance evaluation of propensity score methods for estimating average treatment effects with multi-level treatments

Abstract

The propensity score (PS) method is widely used to estimate the average treatment effect (TE) in observational studies. However, it is generally confined to the binary treatment assignment. In an extension to the settings of a multi-level treatment, Imbens proposed a generalized propensity score which is the conditional probability of receiving a particular level of the treatment given pre-treatment variables. The average TE can then be estimated by conditioning solely on the generalized PS under the assumption of weak unconfounded-ness. In the present work, we adopted this approach and conducted extensive simulations to evaluate the performance of several methods using the generalized PS, including subclassification, matching, inverse probability of treatment weighting (IPTW), and covariate adjustment. Compared with other methods, IPTW had the preferred overall performance. We then applied these methods to a retrospective cohort study of 228,876 pregnant women. The impact of the exposure to different types of the antidepressant medications (no exposure, selective serotonin reuptake inhibitor (SSRI) only, non-SSRI only, and both) during pregnancy on several important infant outcomes (birth weight, gestation age, preterm labor, and respiratory distress) were assessed.

1. Introduction

Although randomized clinical trials (RCTs) are the widely accepted gold standard to estimate the causal effects of treatments and interventions, RCTs are not feasible in situations when it is unethical or impractical to randomize subjects into treatment groups [32]. Observational studies, on the other hand, allow studying the real-world impact of various clinical interventions and treatments [26]. It is challenging, however, to derive causal inferences from observational studies as there are often systematic differences between treatment groups [13]. Therefore, proper statistical methods to remove or minimize such confounding bias are necessary before valid inferences of TE can be drawn from observational studies [29].

Propensity score (PS) methods are a popular methodology used in observational studies to address limitations of confounding bias, classification bias, and failure to abide by the intention to treat principle [29]. The PS is the conditional probability of subjects receiving a particular treatment given all measured potential confounders. It is an effective summary score that incorporates multiple variables that may influence the treatment decision. There are four ways of applying PS to reduce confounding: covariate adjustment with the PS, stratification on the PS, matching on the PS, and inverse probability of treatment weighting (IPTW) using the PS [5,14,28–30].

Until recently, the PS methods have been mostly used in studies of two treatment groups. Treatment with more than two groups, however, is often of interest in the medical research. Rubin proposed to create separate PS models for each paired treatment comparison [22,31]. However, the sum of the probabilities of choosing all treatment arms can be greater than 1 as these models are not constrained [39]. Imbens developed the generalized propensity score (GPS) by extending Rosenbaum and Rubin’s work, in which the GPS was defined as the conditional probability of receiving a particular treatment given the pretreatment covariates and was estimated using a multinomial logistic regression model [11]. Similar application methods, covariate adjustment, subclassification, matching and IPTW that are designed for binary treatments, have been developed for GPS to accommodate treatment with more than two groups [7,8,10,18–21,38].

Despite its utility, evaluation of the performance of GPS derived from a multinomial regression model is limited [7,24,38,40]. Using multi-level treatment clinical trial data, Feng et al. 7] applied and compared GPS covariate adjustment and IPTW in assessing the relative effectiveness of individual treatments. When the sample size is moderate or large, GPS covariate adjustment and GPS IPTW show satisfactory performance in estimating the individual TE. In a separate study, Yang et al. [ 38] demonstrated and applied GPS matching and subclassification in a multi-level treatments case. To the best of our knowledge, there is no literature currently evaluating and comparing the performance of all four commonly used GPS methods simultaneously.

The objective of this study was to apply, evaluate and compare the performance of GPS methods, covariate adjustment, subclassification, matching and IPTW in bias reduction when treatment was multi-level with no particular ordering using the multinomial logistic regression to estimate GPS. We examined and applied the four GPS methods using both Monte Carlo simulations and a motivating study comparing different types of the antidepressant use during pregnancy on related outcomes.

The paper is organized as follows. In Section 2, we provide a detailed description of the motivating study. In Section 3, we review the GPS approach and describe the four methods using GPS to estimate TEs. In Section 4, we present an extensive simulation study to examine the performance of the four GPS methods. In Section 5, we re-visit the motivating study and report the results, followed by the discussion and conclusion in Section 6.

2. Motivating study

Our study of the application and evaluation of GPS in situations when treatment has more than two levels was motivated by comparison of different types of the antidepressant use during pregnancy and their effects on pregnancy-related outcomes. Antidepressants are widely prescribed to pregnant women with major depression and other psychiatric disorders [1,4,6,9,27,36]. Up to 13% of all pregnant women filled at least one antidepressant prescription during pregnancy [9,27].

Since their introduction in clinical practice in 1988, selective serotonin reuptake inhibitors (SSRIs) have become the most commonly prescribed antidepressants [9,16]. SSRIs purportedly ameliorate depressive symptoms by selectively blocking the reabsorption (reuptake) of the neurotransmitter serotonin and changing the balance of serotonin levels in the brain. Compared with other non-SSRI antidepressants, which in general affect more than one type of neurotransmitters, SSRIs primarily affect serotonin levels. However, studies have reported that SSRI use in the third trimester of pregnancy, but not non-SSRIs, is associated with infant convulsions representing a severe neurologic withdrawal syndrome [9,23,33]. It is unclear whether choice of antidepressants, SSRIs or non-SSRIs, affects other pregnancy-related outcomes.

Comparison of the effects of SSRIs and non-SSRIs on pregnancy-related outcomes is complicated. Choice of SSRIs or non-SSRIs is confounded by physicians and patients preference, as well as disease severity. SSRIs are the most commonly prescribed class of the antidepressant medication [3], likely because of their strong empirical base and tolerabil-ity, and are widely considered first-line pharmacotherapies [15,17]. In addition, depression itself may affect pregnancy-related outcomes. Therefore, direct comparison among the antidepressant treatment groups is confounded and may result in biased conclusions. PS methods, with their ability to summarize all measured confounders into one score, are valuable in assessing the effect of different type of the antidepressant exposure during pregnancy and pregnancy-related outcomes. This real-world study motivated us to compare multiple, unordered treatment groups in GPS calculation and TE estimation.

3. Methods

3.1. Notation

Imbens [11] developed the GPS methodology to estimate the average causal effects of multiple treatments. Below we closely follow his notation.

Let τ = {0,1,2,..., K} be K + 1 different mutually exclusive treatments. Following the potential outcome framework for causal inference, every subject in the population has K + 1 potential outcomes after receiving each of the K + 1 treatments. For individual i, we denote the potential outcome as Y_i(T = t) or simply Y_i(t), where T is the random variable indicating a treatment this subject might have received.

For each individual, the TE of interest is defined as the difference between the potential outcomes from the same individual. TE(j, k) = Y_i(j) − Y_i(k), for all j ≠ k. There exist K(K + 1)/2 individual pairwise TEs. Since Y_i(j) and Y_i(k) cannot be observed at the same time, TEs at the individual level cannot be estimated. Instead, the average treatment effect (ATE) in the population is considered. E{Y(j)} is the ATE that would have been observed if the entire population had received treatment j. The ATE of treatment j versus treatment k is the difference in mean outcomes for these treatments and is denoted ${\text{ATE}}_{j,k}=E\left\{Y_i(j)\right\}-E\left\{Y_i(k)\right\}.$ Notethatthe expectationinthisdefinitionisoverthe entire population regardless of the treatment that was actually received. In our case study with four treatment groups, there exist six ATEs, one for each pairwise comparison.

3.2. Estimation of ATE

To estimate ATEs, we first need to estimate $E\{Y(t)\}(t=0,1,2,\dots ,K)$. Since

$$E\{Y(t)\}=E\{Y(t)|T=t\}Pr(T=t)+E\{Y(t)|T\ne t\}Pr(T\ne t),$$

and the first part on the right side of the equation can be directly estimated in large samples using respective sample analogs, so the problem boils down to properly estimating $E\{Y(t)|T\ne t\}.$ In a completely randomized experiment where treatment assignment is independent of potential outcomes, we have $E\{Y(t)|T\ne t\}=E\{Y(t)|T=t\}.$ However, this equation usually does not hold in non-randomized studies due to the fact that the baseline covariates may have large differences among the treatment groups and the treatment assignment likely affects potential outcomes. Rosenbaum and Rubin proposed the PS approach to make use of baseline covariate information to obtain an unbiased estimate of $E\{Y(t)|T\ne t\}$ when there are only two levels of treatments. Imbens [11] extends their work to multiple treatments and proposed GPS to estimate this quantity.

The GPS, r(t, X), is defined as the conditional probability of receiving a particular level of treatment t given a set of pretreatment variables X,

$$r(t,X)\equiv Pr(T=t|X=X)=E\{D(t)|X=X\},$$

where D(t) is the indicator function that denotes the receipt of treatment t.

By construction, GPS satisfies a balancing property,

$$D(t)\perp X|r(t,X).$$

In combination with weak unconfoundedness of treatment assignment given the pretreatment covariates X

$$D(t)\perp Y(t)|X,$$

Imbens [11] proved that the assignment to treatment is also weakly unconfounded given the GPS,

$$D(t)\perp Y(t)|r(t,X).$$

Then, it follows that

$$E\{Y(t)|r(t,X)=r\}=E\{Y(t)|T=t,r(t,X)=r\}=E\{Y(t)|T\ne t,r(t,X)=r\}.$$

Therefore, GPS can be used to consistently estimate the potential outcome E{Y(t)} for the whole population (both the subjects who receive treatment t and those who do not).

The implementation follows three steps. The first step is to estimate r(t, X). In our study, we fitted a multinomial logistic regression model, with t = 0 as the reference level. The model is as follows.

$$ln\left(\frac{r(k,X)}{r(0,X)}\right)=ln\left(\frac{Pr(T=k|X)}{Pr(T=0|X)}\right)={\mathit{\beta }}_{0k}+{\mathit{\beta }}_{1k}^{\prime }X,k=1,2,\dots ,K.$$ (1)

Each subject has K linear predictors and K + 1 PSs. Second, we estimate the conditional expectation of the potential outcome at treatment level t asa function of a scalar variable r(t, X),

$$\beta (t,r)=E\{Y|T=t,r(t,X)=r\}.$$ (2)

Finally, we estimate the average outcome at treatment level t by averaging the estimated conditional expectation, $\widehat{\beta }(t,r(t,X)),$ over the distribution of r(t, X). That is,

$$E\{Y(t)\}=E\{\beta (t,r(t,X))\}.$$ (3)

3.3. Four GPS methods

With estimated r(t, X), we then applied matching, subclassification, IPTW and covariate adjustment to estimate $\beta (t,r(t,X))$ and E{Y(t)}s, and subsequently the ATEs.

3.3.1. Subclassification on GPS

Subclassification is a nonparametric estimating technique in which conditional expectation of the potential outcome $\beta (t,r(t,X))$ is estimated based on quantiles of r(t, X). To evaluate the average potential outcome E{Y(k)} at treatment level k, we first rank all subjects based on their estimated GPS at this treatment level, $\widehat{r}(k,X);$ subjects are then subclassified into five strata based on GPS quintiles $q_s^{r(k,X)}$ for s = 1,2,...,5. We assume each subgroup is a homogeneous subpopulation regarding $r(k,X),$ giving $E\left\{Y^s(k)\right\}=E\{Y^s(k)|T=k\}.$ Although such assumptions only hold in an ideal situation where each subgroup should contain a single value of r(k, X), evidence suggests that such quintile-based subclassification generally reduces 90% of the bias induced by baseline covariates [30]. Within each subgroup, we estimate the average potential outcome $E\left\{Y^S(k)\right\}$ by the mean outcome of the subjects who actually received treatment k in this subgroup.

$$\widehat{E}\left\{Y^s(k)\right\}=\frac{1}{N_{sk}}\sum _{i:q_{s-1}^{r(k,X)}<r(k,X)\le q_s^{r(k,X)}}{Y}_i(T=k),$$

where N_sk is the number of subjects in subgroup s who actually receive treatment k. The overall value of $\widehat{E}\{Y(k)\}$ is a weighted average of the within-strata estimates with the weight for each subgroup equaling the fraction of the sample within that subgroup. That is

$$\widehat{E}\{Y(k)\}=\sum _{s=1}^5\frac{N_s}{N}\widehat{E}\{Y^s(k)\}.$$

This procedure is repeated for each of the treatment level to obtain all of the values of $\widehat{E}\{Y(k)\}.$ The pairwise $\widehat{\text{ATE}}$ s are calculated accordingly.

3.3.2. Matching on GPS

Matching is another nonparametric estimating method, and what we have proposed here is similar to one-to-one nearest neighbor matching with replacement. All the subjects are subgrouped into K+1 subsamples based on the treatment each individual actually receives. In subsample k, each individual has an observed outcome Y_i(k). For each of the subjects not in subsample k, we select a single subject from subsample k who has the closest value in terms of r(k, X). In this process, the subjects in subsample k are used with replacement, so that a closest match (caliper not defined) can be found for every single subject not in subsample k and their potential outcome Y_i(k) are directly estimated by Y_i (k) of their matched subjects in the subsample k. Therefore, we have Y(k) (observed for those in subsample k or estimated through the matched for those not in subsample k) for all the subjects in the study sample, which represents the entire population. The average outcome E{Y(k)} and pairwise ATEs are then estimated by the sample average and the corresponding difference between the sample averages, respectively.

3.3.3. IPTW using GPS

As an alternative to the implementation using (2) and (3), Imbens [11] proposed using GPS to weight observations because of the equality $E\{YD(t\text{)/}r(T,X)\}=E\{Y(t)\}.$ The idea isto create potential sample (pseudo-population) for each treatment level t that are intended to represent the samples we would have observed if everyone had been received treatment t. To implement, we normalize the weights so that they add up to one in each treatment group [7]. The weighted outcome for treatment t is given by

$$\widehat{E}\{Y(t)\}=\left[\sum _{i=1}^N\frac{Y_i{D}_i(t)}{r\left(t,X_i\right)}\right]{\left[\sum _{i=1}^N\frac{D_i(t)}{r\left(t,X_i\right)}\right]}^{-1}.$$

3.3.4. Covariate adjustment using GPS

When using the covariate adjustment method to estimate E{Y(t)} and ATEs, we explored two different approaches. The first is a direct parametric implementation of (2) (covariate adjustment A). A generalized linear model was fitted for the outcome on the estimated GPS at each treatment level t. We used linear and logistic regression models for continuous and dichotomous outcomes, respectively.

$$E\{Y|T=t,r(t,X)=r\}=\beta (t,r(t,X))={\alpha }_{0t}+{\alpha }_{1t}r(t,X).$$

With K + 1 sets of ${\widehat{\alpha }}_{0t}$ and ${\widehat{\alpha }}_{1t},$ the potential outcome of each individual subject at treatment level t is estimated as

$$\widehat{E}\{Y(t)\}=\frac{1}{N}\sum _{i=1}^N\widehat{\beta }\left(t,r\left(t,X_i\right)\right)=\frac{1}{N}\sum _{i=1}^N{\widehat{\alpha }}_{0t}+{\widehat{\alpha }}_{1t}r\left(t,X_i\right).$$

In contrast to other GPS methods, covariate adjustment is relatively flexible in that we can adjust multiple GPS at the same time. For example,

$$\beta (t,r(t,X))={\alpha }_{0t}+{\alpha }_{1t}g\left(r\left(1,X_i\right)\right)+{\alpha }_{2t}g\left(r\left(2,X_i\right)\right)+\cdots +{\alpha }_{Kt}g\left(r\left(K,X_i\right)\right),$$

$$\widehat{E}\{Y(t)\}=\frac{1}{N}\sum _{i=1}^N{\widehat{\alpha }}_{0t}+{\widehat{\alpha }}_{1t}g\left(r\left(1,X_i\right)\right)+{\widehat{\alpha }}_{2t}g\left(r\left(2,X_i\right)\right)+\cdots +{\widehat{\alpha }}_{Kt}g\left(r\left(K,X_i\right)\right).$$

where we chose $g(r(t,X))=ln(r(t,X)/r(0,X)),$ which are the linear predictors based on the GPS model (1) (covariate adjustment B).

4. Simulation studies

We performed extensive Monte Carlo simulations to examine the performance of the different methods proposed in Section 3.

4.1. Data-generating process

First, we randomly simulated eight variables X₁, X₂,...,X₈ for each of the N subjects. X₁, X₂ and X₃ were Bernoulli with the probability of success equal to 0.3, 0.5, and 0.7, respectively; X₄, X₅, and X₆ were multivariate normal with means (0,1,0), variances of (1,2,3) and covariances of $(1,0.1,-1);X_{\text{7}}~U[-3,3];X_8~{\chi }_1^2.$

Second, we generated a treatment status for each of the N subjects as follows: we first determined the subject-specific probabilities of treatment assignment as

$$\begin{gathered} ln\left(\frac{p_{i,k}}{p_{i,0}}\right)={\gamma }_{k,0}+{\gamma }_{k,1}{X}_{1i}+{\gamma }_{k,2}{X}_{2i}+{\gamma }_{k,3}{X}_{3i}+{\gamma }_{k,4}{X}_{4i}+{\gamma }_{k,5}{X}_{5i}+{\gamma }_{k,6}{X}_{6i} \\ +{\gamma }_{k,7}{X}_{7i}+{\gamma }_{k,8}{X}_{8i},k=1,2,\dots ,K. \end{gathered}$$ (4)

We then randomly generated a treatment status for each of the N subjects from a multinomial distribution with subject-specific probabilities of the treatment assignment:

$$T_i~\text{Multinomial}\left(p_{i,0},p_{i,1},p_{i,2},\dots ,p_{i,K}\right)$$

Third, for each of the N subjects, we randomly generated K + 1 potential outcomes conditional on the eight variables

$$\begin{gathered} g\left(E\left\{Y_i(k)\right\}\right)={\beta }_{k,0}+{\beta }_{k,1}{X}_{1i}+{\beta }_{k,2}{X}_{2i}+{\beta }_{k,3}{X}_{3i}+{\beta }_{k,4}{X}_{4i}+{\beta }_{k,5}{X}_{5i} \\ +{\beta }_{k,6}{X}_{6i}+{\beta }_{k,7}{X}_{7i}+{\beta }_{k,8}{X}_{8i}, \end{gathered}$$ (5)

where g() was the identify link function for continuous outcomes and logit link function for binary outcomes.

The values assigned to the regression coefficients in Equations (4) and (5) were listed in Tables A1 and A2. The data-generating process thus randomly generated treatment status, covariates, and potential outcomes for each of the N subjects.

All the eight covariates are confounders. The absolute values of γ s in the treatment assignment model (4) were the same for all the covariates so that they had the same impact on the treatment assignment. The values of βs in the outcome model (5) were set in such a way that the effects of covariates on the outcome were largely comparable and the expected average potential outcomes were 1 or 2 for continuous outcomes and 0.4 or 0.6 for binary outcomes. Accordingly, the expected ATE is 1 or 0 for continuous outcomes and 0.2 or 0 for binary outcomes. The overall confounding effect of the covariates can be measured by the bias when using the observed sample means in each treatment group as estimates of the average potential outcomes, which was about 0.4 for continuous outcomes and was about 0.008 for binary outcomes.

4.2. Factors considered

We varied the values of the following factors to investigate the performance of the proposed methods in different situations.

• Outcome type: We generated both continuous and binary outcomes by using an identity or logit link function of g() in (5).

• Treatment levels: τ = {0,1}, {0,1,2}, {0,1,2,3}, {0,1,2,3,4} and {0,1,2,3,4,5} were considered, i.e. K = 1,2,3,4 or 5.

• Sample size: We used n = 50,100,200,500,1000 for continuous outcomes, and n = 100, 200, 500, 1000, 2000 for binary variables, where n is the sample size at each treatment level.

4.3. Evaluation criteria

For each of the scenarios described in Section 4.2, we simulated 1000 datasets and the proposed methods were applied to each of the datasets to obtain the estimate of E{Y (t) }s and ATEs. 95% confidence intervals (CI) for the point estimates were constructed using the nonparametric bootstrap percentile method, and in each bootstrap sample, GPS was re-estimated. We used four evaluation criteria, including absolute bias, variance, square root of mean square error (RMSE) and empirical coverage probability (CP) of 95% CI. To simplify the comparisons between different methods, we calculated an average statistics over the multiple treatment levels (Table 1).

Table 1.

Evaluation criteria.

Criteria	E{Y(t)}	E{ATE}
Average absolute bias	$\frac{1}{K+1}{\sum }_{t=0}^K{\varphi }_b(\widehat{\mathbf{E}}\{Y(t)\},E\{Y(t)\};m)$	$\frac{1}{K(K+1)/2}{\sum }_{j=0}^{K-1}{\sum }_{k=j+1}^K{\varphi }_b\left({\widehat{\mathbf{A}TE}}_{jk},E\left\{{\text{ATE}}_{jk}\right\};m\right)$
Average variance	$\frac{1}{K+1}{\sum }_{t=0}^K{\varphi }_v(\widehat{\mathbf{E}}\{Y(t)\};m)$	$\frac{1}{K(K+1)/2}{\sum }_{j=0}^{K-1}{\sum }_{k=j+1}^K{\varphi }_b\left({\widehat{\mathbf{ATE}}}_{jk};m\right)$
Average RMSE	$\frac{1}{K+1}{\sum }_{t=0}^K{\varphi }_r(\widehat{\mathbf{E}}\{Y(t)\},E\{Y(t)\};m)$	$\frac{1}{K(K+1)/2}{\sum }_{j=0}^{K-1}{\sum }_{k=j+1}^K{\varphi }_r\left({\widehat{\mathbf{A}TE}}_{jk},E\left\{{\text{ATE}}_{jk}\right\};m\right)$
Average 95% CI coverage	$\frac{1}{K+1}{\sum }_{t=0}^K{\varphi }_c(E\{Y(t)\};m)$	$\frac{1}{K(K+1)/2}{\sum }_{j=0}^{K-1}{\sum }_{k=j+1}^K{\varphi }_v\left(E\left\{{\text{ATE}}_{jk}\right\};m\right)$

We repeat the estimation procedure m = 1000 times. Denote ${\widehat{E}}^W\{Y(t)\}$ and ${\widehat{\text{ATE}}}_{ij}^w$ as the estimators obtained in the $w^{th}$ time for w = 1,2,...,1000. Let $\mathbf{z}=\left(z_1,\dots ,z_m\right).$ Define the following functions: ${\varphi }_b\left(\mathbf{z},z_0;m\right)=|(1/m){\sum }_{w=1}^m\left(z_w-z_0\right)|,{\varphi }_v(\mathbf{z};m)=(1/m){\sum }_{w=1}^m{(z_w-(1/m){\sum }_{w=1}^m{z}_w)}^2,{\varphi }_r\left(\mathbf{z},z_0;m\right)=\sqrt{(1/m){\sum }_{w=1}^m{\left(z_w-z_0\right)}^2,}\text{and}{\varphi }_c\left(z_0;m\right)=(1/m){\sum }_{w=1}^{m}l\left(q_{0.025}^w<z_0<q_{0.975}^W\right).$

4.4. Simulation results

The results of simulation studies were summarized by average absolute bias, variance, RMSE and 95% CI coverage defined in Section 3, and displayed in Figures 1–2 and Figures A1 and A2.

Figure 1.

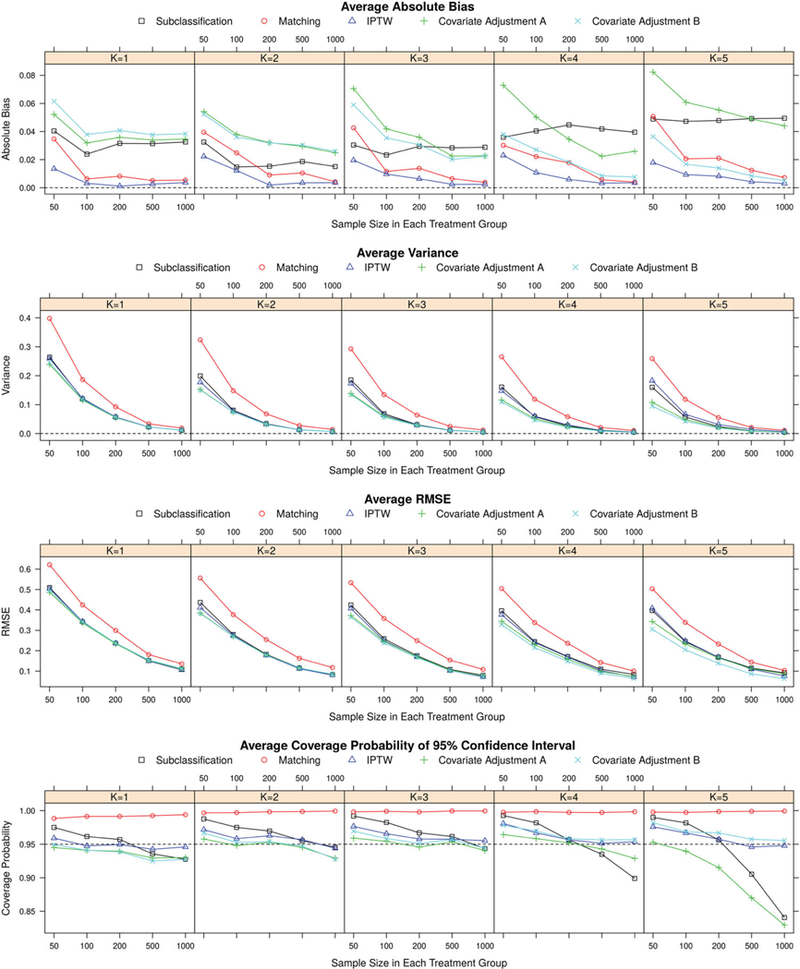
Results of simulation studies regarding potential outcome estimates for continuous outcomes.

Figure 2.

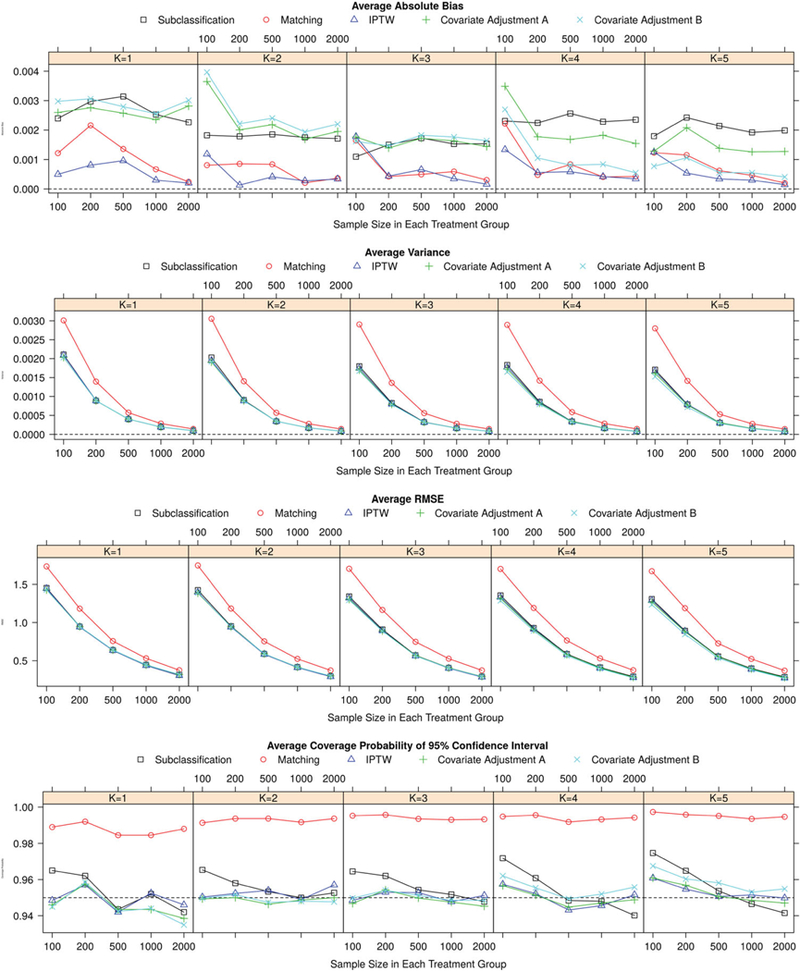
Results of simulation studies regarding potential outcome estimates for binary outcomes.

In all the methods studied, IPTW provided the most unbiased estimators overall. The bias of IPTW estimators was quite comparable for different numbers of treatment groups, and monotonically reduced with increasing sample size. The number of subjects needed in each treatment group for the IPTW method to reach negligible bias was smaller when the number of treatment groups was reduced. This was especially true when the outcome was continuous. The matching method also had small bias, for both continuous and binary outcomes. It performed consistently across different scenarios with varying numbers of treatment groups, and the bias decreased with increasing sample size. Compared with IPTW and matching methods, subclassification resulted in noticeably larger bias, especially with large sample size. The performance of subclassification was relatively invariant to the number of treatment groups and the sample size within each group.

The performance of the two covariate adjustment methods varied with the number of treatment groups. In general, the bias of estimators using covariate adjustment B (adjusting for all the linear predictors from the GPS model) decreased when the number of treatment groups increased. When there were only two treatment groups (K = 1), method of covariate adjustment B generated the estimators with largest bias among all the methods studied; while when there were six treatment groups (K = 5), this method performed better than all the other methods except IPTW. The bias of estimators based on the method of covariate adjustment A (adjusting for single PS separately), on the other hand, increased with increasing number of treatment groups. This trend was more profound for continuous outcome than for binary outcome where the bias using covariate adjustment A remained relatively stable with varying number of treatment groups. Yet for both types of outcomes, the method of covariate adjustment A outperformed covariate adjustment B when there were two treatment groups but underperformed B when there were five or six treatment levels. Increasing sample size decreased bias of estimators in both adjustment methods Such bias decrease was more noticeable when the outcome was a continuous variable.

In general, the variance of all the estimators declined with increasing sample size. Compared with other GPS methods, matching had the largest variance across all the scenarios. The covariate adjustment methods had the smallest variance, and IPTW and subclassification gave a slightly bigger variance. For all methods, increasing treatment groups and/or decreasing sample size increased the variance of estimators.

The patterns of RMSE for different methods were similarto the patterns ofvariance, and the matching method stood out from all the other methods with the largest RMSE. Compared with continuous outcome scenario, the differences in the performances of the IPTW, subclassification, and covariate adjustment methods were less significant with regard to variance and RMSE when the outcome was a binary variable.

The expected value of empirical CP for 95% confidence interval is 0.95. The confidence intervals of matching method were over-covered in all scenarios we studied. The CPs of the other methods fluctuated, or slightly decreased with increasing sample size around the nominal level of 0.95. In the scenario of six treatment levels and a continuous outcome, subclassification and covariate adjustment B had confidence intervals notably under-covered when the sample size was large.

5. Antidepressants and pregnancy outcome data analysis

5.1. Data source and statistical analysis

Data of 228,876 singleton pregnancies of women aged 15–44 years old were obtained from the linked Tennessee Medicaid program (TennCare) administrative database. All women were continuously enrolled in TennCare during 1995–2007 and from 180 days prior to their last menstrual period to 90 days after delivery [9]. We studied the antidepressant exposure during pregnancy and the risk of adverse pregnancy outcomes. Based on the type of antidepressants women received during pregnancy, pregnant women were categorized into four groups: no exposure, SSRI only, non-SSRI only, and both groups. The outcomes of interest included continuous outcomes: birth weight in grams, gestation age in days, and binary outcomes: respiratory distress and preterm labor (Table 3). We separated those women with both types of antidepressants as we hypothesized that women with both types of antidepressants had more severe illness. To minimize the confounding effect of depressive illness, we performed all analyses separately among women with or without an ICD-9 unipolar depressive disorder diagnosis (296.2, 296.3, 300.4, and/or 311) 180 days prior to pregnancy. Table 2 displays the baseline characteristics of the study subjects stratified by the types of the antidepressant exposure for the two subpopulations. The study was reviewed and deemed as an exempt study by the Vanderbilt University Institutional Review Board.

Table 3.

Adverse pregnancy outcomes by the antidepressant exposure.

	Without prior depression (N = 200,722)				With prior depression (N = 28,154)
	None N = 19,4587	SSRI only N = 3562	Non-SSRI only N = 2135	Both N = 438	None N = 13,532	SSRI only N= 7359	Non-SSRI only N = 4571	Both N = 2692
Birthweight (g)	3166±588	3133±572	3112±569	3026±602	3152±577	3164±582	3156±602	3138±609
Gestation age (days)	271±18	270±16	271±16	269±19	271±17	270±16	271±16	270±16
Respiratory distress	8342 (4.3)	159(4.5)	103(4.8)	28 (6.4)	626 (4.6)	350 (4.8)	208 (4.6)	165(6.1)
Preterm labor	50,040 (26.3)	990 (28.2)	546(26.1)	109 (25.3)	3816(28.6)	2129 (29.4)	1203 (26.7)	773 (29.2)

Data are given as mean ± SD for continuous variables and frequency (%) for categorical variables.

Table 2.

Baseline characteristics by the anidepressant exposure.

	Without prior depression (N = 200,722)					With prior depression (N = 28,154)
	None N = 194,587	SSRI only N = 3562	Non-SSRI only N = 2135	Both N = 438	P-value	None N = 13,532	SSRI only N = 7359	Non-SSRI only N = 4571	Both N = 2692	P-value
Age	22.9±5.1	23.9±4.9	24.6±5.4	24.8±5.5	< .001	23.6±5.3	25.1 ±5.7	25.6±5.8	26.4±6.0	< .001
Race					< .001					< .001
White	99,943 (51.4)	2775 (77.9)	1630 (76.4)	356 (81.3)		10,509 (77.7)	6267 (85.2)	3816(8305)	2296 (85.3)
Black	89,727 (46.1)	737 (20.7)	459 (21.5)	71 (16.2)		2674(19.8)	911 (12.4)	612 (13.4)	312(11.6)
Other	4917(2.5)	50 (1.4)	46 (2.2)	11 (2.5)		349 (2.6)	181 (2.5)	143 (3.1)	84(3.1)
Residence					< .001					< .001
Urban	101,599(52.3)	1433(40.4)	792 (37.1)	185(42.2)		4914(36.4)	2463 (33.5)	1526 (33.5)	978 (36.4)
Suburban	41,492 (21.4)	920 (25.9)	593 (27.8)	117 (26.7)		3780 (28.0)	2236 (30.4)	1386 (30.4)	792 (29.5)
Rural	51,090 (26.3)	1196(33.7)	749(35.1)	136(31.1)		4810(35.6)	2646 (36.0)	1646(36.1)	916(34.1)
Education					< .001					< .001
<12	82,403 (42.4)	1365 (38.4)	868 (40.8)	189 (43.2)		5929 (44.0)	2665 (36.3)	1767 (38.8)	984 (36.6)
12	83,683 (43.1)	1531 (43.1)	925 (43.4)	177 (40.4)		5572 (41.3)	3222 (43.9)	1960(43.0)	1154(43.0)
>12	28,069 (14.5)	656(18.5)	337 (15.8)	72(16.4)		1987(14.7)	1454(19.8)	833 (18.3)	548 (20.4)
Smoking in pregnancy	52,254 (26.9)	1658(46.6)	1066 (50.0)	245 (56.2)	< .001	5968 (44.2)	3367 (45.8)	2264 (49.6)	1426 (53.0)	< .001
Parity					< .001					< .001
Primiparous	58,008 (29.9)	800 (22.5)	463 (21.8)	95 (21.8)		4169(30.9)	1930 (26.3)	1167(25.6)	633 (23.6)
1	67,970 (35.0)	1282 (36.1)	791 (37.2)	149(34.2)		4589 (34.0)	2520 (34.4)	1574(34.5)	867 (32.3)
2	38,206(19.7)	830 (23.4)	487 (22.9)	111 (25.5)		2764 (20.5)	1694(23.1)	1083 (23.7)	638(23.7)
3+	29,984(15.4)	640(18.0)	387 (18.2)	81 (18.6)		1973(14.6)	1192(16.2)	739(16.2)	549 (20.4)
Married	60,712(31.2)	1356 (38.1)	847 (39.7)	171 (39.0)	< .001	5280 (39.0)	3248 (44.2)	2020 (44.2)	1171 (43.5)	< .001
Any comorbidity	19,829(10.2)	5620(17.4)	425(19.9)	99 (22.6)	< .001	2800(20.7)	1810(24.6)	1160 (25.4)	769 (28.6)	< .001
Substance abuse	23,473 (12.1)	1061 (29.8)	610(28.6)	177(40.4)	< .001	3916(28.9)	2448 (33.3)	1504(32.9)	1164(43.2)	< .001
Anxiety disorder	6979 (3.6)	826 (23.2)	390(18.3)	148(33.8)	< .001	3836 (28.3)	2908 (39.5)	1575 (34.5)	1296 (48.1)	< .001
Co-existing psychiatric diagnosis	3403 (1.8)	171 (4.8)	82 (3.8)	33 (7.5)	< .001	1054(7.8)	882 (12.0)	523 (11.4)	491 (18.2)	< .001
Adequacy of prenatal care					< .001					< .001
Adequate plus	54,032 (29.1)	1375(40.6)	692 (34.0)	156 (37.6)		4700 (36.4)	2756 (39.4)	1646(37.6)	1040(40.9)
Adequate	67,944 (36.6)	1129 (33.3)	718 (35.3)	127 (30.6)		4787(37.1)	2518(36.0)	1609 (36.8)	818(32.1)
Intermediate	24,082 (13.0)	316 (9.3)	247(12.2)	48 (11.6)		1507(11.7)	729(10.4)	513(11.7)	306(12.0)
Inadequate	39,543 (21.3)	570(16.8)	376(18.5)	84 (20.2)		1904(14.8)	998 (14.3)	606(13.9)	381 (15.0)
C-section	43,784 (22.5)	967 (27.1)	550 (25.8)	139 (31.7)	< .001	3527 (26.1)	2212 (30.1)	1351 (29.6)	877 (32.6)	< .001
Infant gender: boy	99,612(51.2)	1818(51.0)	1085 (50.8)	223 (50.9)	.984	6935 (51.2)	3811 (51.8)	2315 (50.6)	1362 (50.6)	.577
Birth year	2000.9±3.7	2003.5±2.6	2001.8±3.7	2003.0±3.2	< .001	2001.8±3.4	2003.0±2.8	2001.7±3.6	2002.8±2.9	< .001

Data are given as mean ± SD for continuous variables and frequency (%) for categorical variables.

P-values are based on the ANOVA test for continuous variables and χ² test for categorical variables.

We first fitted a multinomial logistic regression model with types of pregnancy antidepressant exposure as outcomes of interest to estimate GPS. Because the aim of the GPS model is to obtain the best estimate of the probability of treatment assignment, we were not concerned with over-parameterization; all the baseline covariates related to type of the antidepressant exposure or pregnancy outcomes were included in the model. Restricted cubic splines of the continuous covariates were included to model the potential nonlinear relationship between covariates and type of the antidepressant exposure.

For each subject, we obtained four GPS, $\widehat{r}\left(0,X_i\right),\widehat{r}\left(1,X_i\right),\widehat{r}\left(2,X_i\right),\text{and}\widehat{r}\left(3,X_i\right),$ which corresponded to no exposure, SSRI-only, non-SSRI only, and both treatment groups, respectively. Before applying GPS to the outcome analysis, we inspected the extent to which the distribution of $\widehat{r}\left(t,X_i\right)$ overlapped among subjects who received treatment t and those who did not. We further examined the covariate balance between treatment groups before and after GPS adjustment. The degree of imbalance was quantified by the absolute difference in the means of a covariate between the subjects in the treatment group t and the subjects not in the treatment group t divided by a pooled standard deviation within the sample matched on $\widehat{r}(t),$ stratified by $\widehat{r}(t)$ or between $\widehat{r}(t)$ weighted samples.

The methods described in Section 3 were then applied to estimate the ATEs between treatment groups for each of the outcomes.

5.2. Results

Among 228,876 pregnancies, 28,154 (12.3%) were from women carrying a depression diagnosis before pregnancy and 200,722 (87.7%) were from women without a depression diagnosis. Among the women with a depression diagnosis prior to pregnancy, 13,532 (48.0%) did not fill any prescription for an antidepressant during pregnancy, none: 7359 (26.1%) filled an SSRI only, 4571 (16.2%) filled a non-SSRI only, and 2.692 (9.6%) filled both SSRI and non-SSRI prescriptions. For the women who were not diagnosed with depression before pregnancy, the majority, 194,587 (96.9%), did not fill any antidepressant prescriptions during pregnancy, and the numbers of subjects who filled SSRI, non-SSRI or both SSRI and non-SSRI prescriptions were 3562(1.8%), 2135(1.1%), and 438(0.2%), respectively. In both subpopulations, there were significant differences in all the baseline characteristics except infant gender among the four antidepressant exposure groups (Table 3). We estimated the probabilities of the subjects having each of the four antidepressant exposure types during pregnancy, i.e. GPS, based on these baseline characteristics. Figure A3 shows the distributions of the GPS of the treatment groups. There was considerable overlap of GPS among the four treatment groups, indicating that the TEs we estimated using GPS would be applicable for the whole population. In addition, the estimated GPS had dramatically improved the covariate balancing between treatment groups by all the three methods evaluated (Figure A4). One rule of thumb for assessing the covariate balance is that an absolute standardized mean difference of 0.2 or greater maybe of concern[25,35]. Except that comorbidity and anxiety disorder had standardized difference of about 0.25 by the subclassification method for the subpopulation without prior depression, the standardized difference of all the covariates by all the three methods evaluated were smaller than 0.2. The IPTW method yielded the smallest standardized difference.

Figure 3 and 4 show the estimated ATEs for various pregnancy outcomes comparing patients receiving SSRI only, non-SSRI only, and both treatments with women receiving no treatment. These results are graphed for each GPS method. For the women without a depression diagnosis prior to pregnancy, children exposed to SSRI in utero had lower birth weights relative to those who were not exposed to any antidepressant in pregnancy. The effect of each type of antidepressants on birth weight was consistent across different GPS methods. Compared with no exposure, SSRI only had no significant decrease in birth weight, while exposure to non-SSRI only decreased birth weight by 43 g (96% CI: 7–76 g), 35 g (95% CI : 1–93 g), 41 g (95% CI : 8–76 g), 25 g (95% CI: −4 to 53 g) and 35 g (95% CI: —3 to 65 g) using subclassification, matching, IPTW, and covariate adjustments A and B, respectively. Across all GPS methods, exposure to both types of antidepressants during pregnancy was associated with the greatest reduction in birth weight with estimates ranging from 71 to 134 grams, although this reduction was not statistically significant. The type of antidepressant exposure did not show a consistent significant effect on either gestation age, the risk of respiratory disease or the risk of preterm labor across all of the GPS methods.

Figure 3.

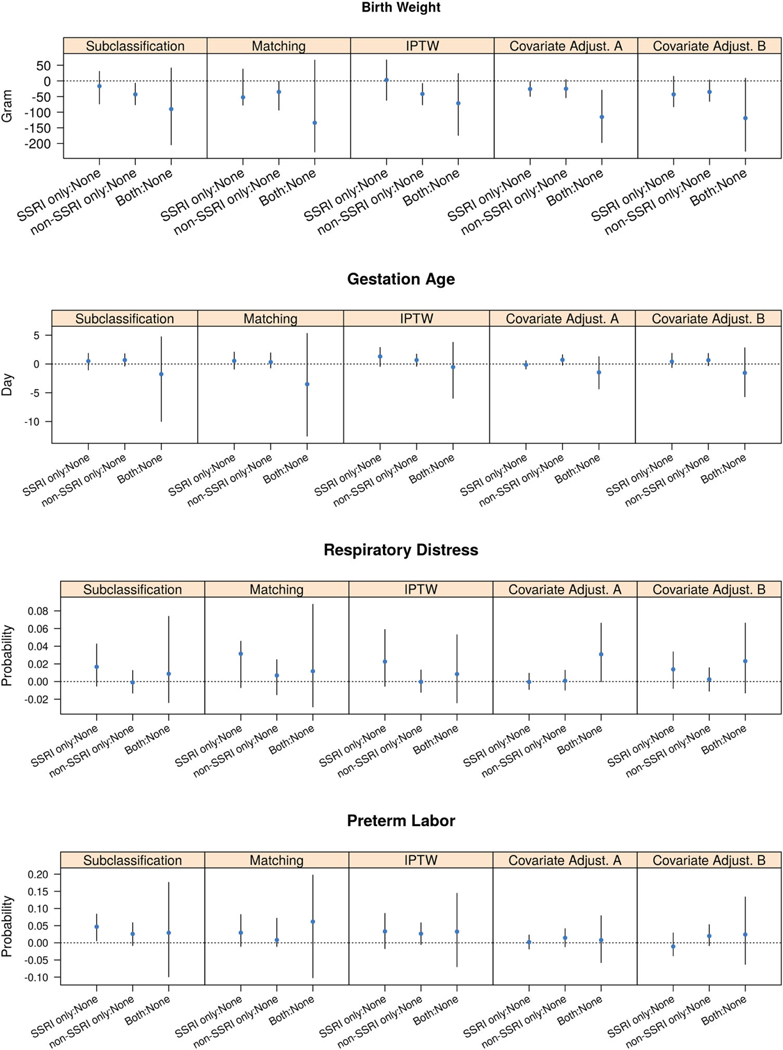
Estimates and 95% CIs of ATEs of the antidepressant exposure during pregnancy for subjects without prior depression.

Figure 4.

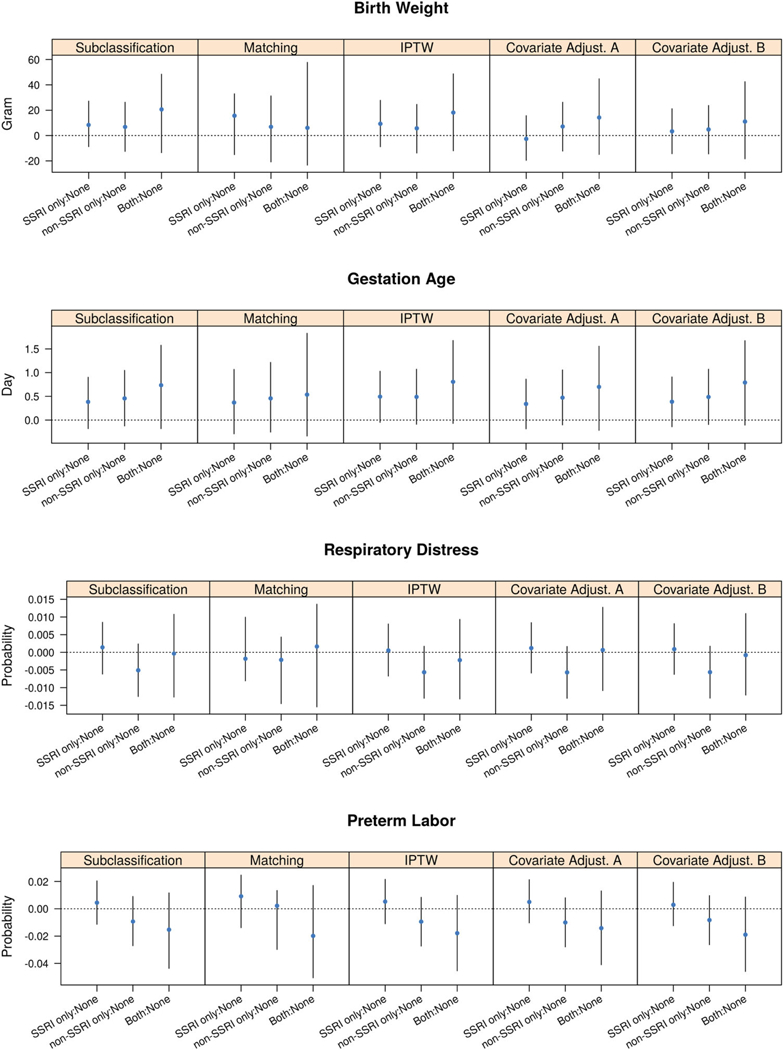
Estimates and 95% CIs of ATEs of the antidepressant exposure during pregnancy for subjects with prior depression.

Among women who were already diagnosed with depression prior to pregnancy, the effect of different types of antidepressant exposure on birth weight, gestational age, respiratory distress, and preterm labor was consistent across all GPS methods. Types of antidepressant exposure had no significant effect on birth weight and respiratory distress. Although the effect was not significant, exposure to SSRI only, non-SSRI only, and both treatments tended to increase the gestational age by half to one day compared with women with no exposure to any antidepressant during pregnancy; women exposed to both treatments had the longest gestational age, followed by women exposed to non-SSRI only and women exposed to SSRI only. These results relating the gestational age to the type of antidepressant was consistent with the results for the antidepressant exposure and the risk of preterm labor. Women receiving both treatments and non-SSRIs had a decreased risk of preterm labor.

6. Discussion

Subclassification, matching, IPTW, and covariate adjustment are four PS methods commonly used to draw causal inferences. These methods have been extensively studied in situations in which only two treatments are being considered. Although the concept of GPS was proposed years ago and is used occasionally, there is little research systematically investigating the performance of these four methods when more than two treatments are being evaluated. Further, there is no study comparing the performance of GPS with binary and with multi-level treatments. Our paper attempts to fill this research gap and provides some guidance in employing GPS in multi-level treatment settings.

The idea of GPS for multi-level treatments is relatively new, but it is a natural extension of PS methods The weak unconfoundedness assumption of GPS is that assignment to a certain treatment level is independent of the potential outcome at this treatment level given the GPS. It automatically turns into strong unconfoundedness assumption that the treatment assignment is independent of all the potential outcomes when the number of treatment levels reduces to two. In this paper, we did not distinguish the methods applied to two treatments from those applied to more than two treatments because they share the same procedures and formulas, and the change from K > 1to K = 1 is trivial and intuitive. For example, in matching and IPTW, we created four pseudo-populations for four-level treatments but two for binary treatments. In subclassification, we stratified the population four times in total based on each of the four r( t, X) swhen K = 3, while we did this twice for binary treatments. Note that because in binary treatments r(t = 1,X) = 1 − r(t = 0,X), the two stratifications lead to exactly the same set of subgroups, this is equivalent to ‘single’ subclassification on r(t = 1, X).

Our simulation studies showed all four GPS application methods perform quite consistently in binary treatments and, for the most part, in multiple treatments as well. IPTW consistently gives the smallest bias that diminishes with increasing sample size. The bias of the estimators based on the matching method is smaller than that of the subclassification method especially when the sample size is large. This is not surprising considering that the accuracy of these nonparametric estimators heavily depends on the fineness of the grid used, and one-to-one matching with replacement is analogous to the subclassification on each unique GPS value. The estimator of subclassification is probably inherently inconsistent, as the bias remained relatively unchanged with increasing sample size beyond a certain point. On the other hand, the bias for matching decreases as sample size increases to at least N = 2000 where the bias is almost negligible. In both binary and multiple treatments, IPT W and the matching method have relatively small bias. However, compared with matching, the IPTW method has consistently smaller RMSE estimators when the sample size is small to moderate. Due to the large variance, the matching method always has overcovered 95% confidence intervals. Previous simulation studies with binary treatments [2] also showed that IPTW had superior performance compared with all the other PS methods In some sense, these similarities in the performances of these methods between binary treatments and multi-level treatments demonstrate the natural extension of PS methods for two treatments to GPS methods for multiple treatments.

The only method whose performance varies with the number of treatments is covariate adjustment. Compared with other PS methods, covariate adjustment is probably the most convenient one with regard to implementation. For binary treatments, we can only include one PS as a covariate in the model, while for multiple treatments, we must choose either one or multiple GPSs. Spreeuwenberg et al. [34] proposed including all the K — 1 PSs in the model. Their rationale is based on the strong unconfoundedness assumption that the potential outcome is independent of treatment assignment given all the GPSs. In this paper, we followed the spirit of Imbens’ implementation that is based on the weak unconfound-edness assumption. We used one single relevant GPS to estimate the potential outcome at each of the treatment levels separately, which makes this method comparable to other PS methods As a comparison, we also examined Spreeuwenbery’s method and included all the GPSs in the form oflogit linear predictors as covariates in the model. With two treatment groups, the difference between these two covariate adjustment methods actually lies in whether the PS is included in the model in the form of probability or log odds. Our simulation studies indicate that including GPS on its original probability scale performs slightly better than including it on the logit scale for binary treatment. However, when the number of treatment groups increases, adjustment with multiple GPS on the logit scale gives much smaller bias than the case with a single GPS adjustment. The variances of these two methods were similar though multiple GPS adjustment tended to be slightly more precise when the sample size was small and the number of treatment groups was large. In general, including all the GPSs should reach better balance in multiple treatment settings.

We applied all four GPS methods in a dataset assessing the types of antidepressant use during pregnancy and their effects on pregnancy-related outcomes. Compared with the subclassification and matching methods, IPTW and covariate adjustment methods gave more precise estimates. Among women who had no depression diagnosis prior to pregnancy, the use of non-SSRI only and both type of antidepressants tended to lower their children’s birth weight, while the effect of SSRI only use was less clear, varying from no effect in the IPTW method to a significant decrease in the method involving covariate adjustment A. Types of antidepressant use during pregnancy had no significant effect on birth weight among women who had depression prior to pregnancy. The differential effect of types of antidepressant use during pregnancy on birth weight in women with and without depression prior to pregnancy is understandable. While antidepressants, particularly non-SSRIs, might increase the risk of low birth weight, it improves women’s depression symptoms and improves maternal function, and thus may improve the chances of a normal birth weight. Types of antidepressant use during pregnancy may affect gestational age. Among women with depression prior to pregnancy, exposure to any type of antidepressants tended to increase the infants gestational age and decrease the risk of preterm labor. Such effects of antidepressant use during pregnancy were more pronounced among women with both types of antidepressants, although women exposed to SSRI only or non-SSRI were also affected. Previous study focuses on timing (1st, 2nd, and 3rd trimester) and course (1, 2, and 3+) of antidepressant use, and treats the type of antidepressants in an equal manner (SSRI vs. non-SSRI) on pregnancy-related outcomes[9]. Application of different GPS methods presented in this study provides additional insights to the literature on types of antidepressant use and their risk on pregnancy outcomes. It is reassuring that results show no difference in birth weight, gestational age, respiratory distress, and preterm labor among women with a diagnosis of depression who take SSRI only, non-SSRI only, or both comparing with women who do not take medications.

One limitation of PS methodology that it only controls for observed covariates also applies to GPS. This is always a limitation of non-randomized studies, which makes assessment of unconfoundedness assumption difficult if not completely impossible[12,37]. So in practice, one should make every effort to collect data on the variables that might even potentially affect the outcome and the treatment assignment. In addition, in this study we estimated ATE instead of ATT, ATE among treated. ATE is clinically meaningful and relevant when the population at risk ought to be treated, and comparative TE size needs to be estimated. This is particularly important when treatment tend to be underutilized. In our application study, it is clinically relevant and important to know the potential impact of anti-depressant treatment on pregnancy outcomes among pregnant women with depression for whom treatment is indicated. It would be of interest to estimate ATT using the four GPS methods if all pregnant women regardless of depression are included in the study sample[24].

In conclusion, we evaluated the performance of four GPS methods when treatments have 2 or more than 2 levels. We showed that IPTW provides preferred performance compared with matching, sub classification, and covariate adjustmentwith single/multiple GPS. These methods provide a reasonable approach to assess the effects of multi-level treatments on patient outcomes.