Abstract
Anticipatory postural adjustments (APAs) precede gait initiation and function to accelerate the center of mass forward and towards the initial stance leg. Impairments in APA generation, such as those seen in people with Parkinson’s disease (PD), can impact the quality of the first step. An initial burst of activity in the dorsiflexor muscle (tibialis anterior) of the stepping leg is an important contributor to the posterior excursion of the center of pressure that accelerates the center of mass forward during an APA. Tibialis anterior activation can be diminished or absent in people with PD; however, the neuromechanical consequence of this diminished dorsiflexor torque on APA generation is not fully understood. Computational models of gait initiation that include components of the neuromuscular system may provide additional insight. In this study, an inverted pendulum model of the body generated from healthy young adult data was used to simulate reduced dorsiflexor torque during an APA for gait initiation. Forward body lean angle and center of pressure were assessed over various settings of decreased dorsiflexor torque and compared to experimental data from a person with PD. Results from the model demonstrate that reducing the peak dorsiflexor torque by as little as 8 Nm may alter forward body lean and the center of pressure from their nominal trajectories. These results can help inform how much torque is needed from an external device to effectively modulate APAs for gait initiation, as well as provide insight into compensation strategies for reduced dorsiflexor torque in pathology.
Index Terms—: computational modeling, anticipatory postural adjustments, Parkinson’s disease
I. Introduction
GAIT initiation is preceded and accompanied by a sequence of anticipatory postural adjustments (APAs) that function to accelerate the body forward and laterally toward the initial stance leg prior to the first step [1–3]. An APA starts with a reciprocal increase and decrease in the vertical ground reaction forces underneath the stepping and stance legs respectively, and excursion of the center of pressure backwards and laterally towards the stepping limb. The stereotypical sequence of muscle activations that accompany this phase includes an initial deactivation of plantarflexor muscles (gastrocnemius and soleus) and activation of the dorsiflexor muscle (tibialis anterior) of both the stepping and stance legs [1–3]. The magnitude of the initial tibialis anterior (TA) burst of the stepping leg and posterior center of pressure excursion have been shown to be highly correlated with gait initiation velocity [2, 4]. After this initial phase of an APA, forces are generated by the plantarflexor muscles of the stepping leg to accelerate the center of mass towards the stance foot and forward. Lastly, the dorsiflexor muscle (tibialis anterior) of the stepping leg is activated to lift the stepping leg off the ground for the first step [1–3]. Alteration in the timing or magnitude of this sequence can have detrimental effects on postural stability and the execution of the first step.
Impaired capacity to generate APAs during gait initiation has been reported in a variety of neurological disorders. One of the best characterized examples of APA impairment is in people with Parkinson’s disease (PD). A variety of studies have shown that ground reaction forces and center of pressure shifts during self-initiated forward stepping are diminished in magnitude and prolonged in duration when participants are in the off-medication state [5–8]. The initial TA burst of the stepping leg can often be diminished or absent, resulting in a decreased excursion of the center of pressure in the sagittal plane, reduced dorsiflexor torque, and slower gait initiation velocity [5–7]. However, the neuromechanical significance of this behavior has yet to be fully understood. Some have proposed that the decreased center of pressure excursion may be a way of maintaining stability by reducing the forward acceleration of the center of mass relative to the base of support [9]. On the other hand, diminished TA activation could also be due to impairment in muscle recruitment caused by dysfunction of the basal ganglia in PD [10, 11]. For instance, the inability to appropriately scale muscle activation to intended movement amplitude has been observed in PD [11]. A model of diminished TA activation during gait initiation could be utilized to better understand its neuromechanical significance and guide the development of modulation strategies for gait initiation in persons with PD (e.g., cues or externally applied mechanical assistance).
Currently, no computational models exist for how deficits in dorsiflexion might affect gait initiation. Inverted pendulum models have been widely used for studying upright standing postural control [12–14], including for persons with PD [15]. These models contain terms that effectively model the physiology of the human body, including the neuromuscular system (e.g., sensory feedback, neural controller). Inverted pendulum models have also been used to calculate the mechanics of gait initiation in healthy individuals [16, 17]. However, these gait initiation models do not include elements specifically related to the neuromuscular system. In this study, we aimed to utilize the neuromuscular components of postural control inverted pendulum models to effectively model an APA for gait initiation in persons with PD using healthy young adult data. We also aimed to investigate the neuromechanical consequences of reduced dorsiflexor torque on overall forward body progression and anterior-posterior excursion of the body’s total center of pressure. The model was then compared to experimental data from a person with PD.
II. Methods
A. Experimental Data
The model was defined using ten self-initiated (uncued) trials from a healthy young adult participant (male, age 30, ht 180 cm, wt 86 kg). These data were compared to seven self-initiated trials of an individual with PD (male, age 65, ht. 168 cm, wt. 77 kg). The individual with PD was tested after a 12-hr. withdrawal from Parkinson’s medication (i.e., levodopa). Participants stood on two force platforms (AMTI, Watertown, MA at UIUC and Kistler Instrument Corporation, Novi, MI, at UMN) and were instructed to initiate gait. To ensure that the participants did not step in response to the ready tone the young healthy participant was asked to initiate gait starting with the right foot approximately 3–5 seconds after hearing the tone (80 dB, 1 kHz). Similar instructions were given to the individual with PD except for he was asked to initiate gait with his left foot 3–8 seconds after hearing the verbal command “anytime.” If the person did not wait enough time after the ready tone (or verbal command), the trial was redone. Ground reaction forces and moments were collected at 1000 Hz in both cases and full body kinematic data were collected using motion capture systems (Qualisys North America, Inc., Buffalo Grove, Illinois, USA, Simi Motion Systems, GmBH, Unterschleissheim, Germany) at 200 Hz (healthy individual) and 120 Hz (individual with PD). All data collection and procedures were approved by the University of Illinois at Urbana-Champaign and the University of Minnesota Institutional Review Boards (IRBs).
B. Model Definition
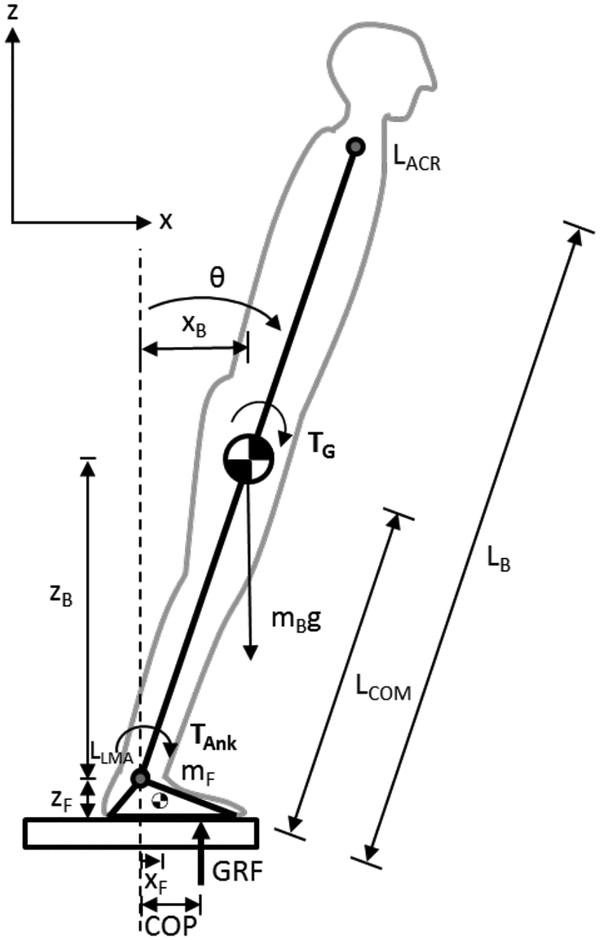
To study the effects of reduced dorsiflexor torque, the upright body during gait initiation was modeled as a single-link inverted pendulum in the sagittal plane (Fig. 1). It was assumed that both ankles pivoted around the same point and the feet were anchored to the ground [4]. The equations of motion for the body segment pivoting around the ankles were:
| (1) |
| (2) |
| (3) |
where Rx and Rz were the reaction forces at the ankle joint, mB was the body mass (excluding the feet), aBx was the acceleration of the body segment in the horizontal direction, aBz was the acceleration of the body in the vertical direction, g was acceleration due to gravity, was the moment of inertia about the ankles (under the assumption of the body being a uniform rod), and LB was the body length. LB was defined as the Euclidian distance between motion capture markers placed on the left acromion (shoulder, LACR) and lateral malleolus (ankle, LLMA) of the healthy young adult participant. TAnk was the torque applied at the ankle by the person (plantarflexor defined as positive), and TG was the torque due to gravity of the body. Body lean angle (θ) and torque due to gravity (TG) were calculated using equations 4 and 5:
| (4) |
| (5) |
where LACRx, LLMAx, LACRz, LLMAz were the horizontal and vertical positions of the motion capture markers placed on the left acromium and lateral malleolus, and LCOM was the position of the center of mass (assumed to be half of LB because the pendulum was assumed to be a uniform rod). Small angle approximation was used for equation 5. The transfer function from applied ankle torque (TAnk) to body lean angle (θModel) in the Laplace domain was derived from equation 3:
| (6) |
Fig 1:
Inverted pendulum model. List of terms: LACR left acromion marker, LLMA left lateral malleolus marker, θ forward body lean angle, xB horizontal position of the body center of mass, mB the mass of the body without the feet, LB length of the body, LCOM length of the body up to the center of mass, zB vertical position of the body center of mass, mF mass of the foot, zF height of the ankle joint, xF horizontal position of the center of mass of the foot, COP position of center of pressure, GRF vertical ground reaction force, TAnk applied ankle torque generated by the neuromuscular system, and TG torque due to gravity of body segment. The reaction forces at the ankle joint (Rx and Rz) are not pictured.
C. Neuromuscular Terms
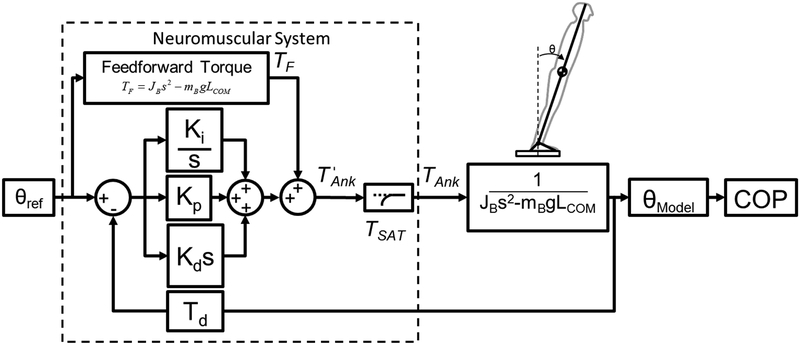
Multiple terms related to the neuromuscular system were included in the model in order to calculate TAnk (Fig 2). First a feed-forward ankle torque (TF) was calculated based on solving equation 3 for TAnk and setting it equal to TF:
| (7) |
The nominal trajectory (θRef) was generated using equation 4 from the average behavior of 10 self-initiated gait initiation trials (right foot steps) from the healthy test participant. Several experimental studies and computational models have demonstrated that the nervous system develops a predictive feedforward model for movements that can make online corrections with delayed sensory feedback within a neural circuit that involves the cerebellum [18, 19].
Fig. 2:
Block diagram of inverted pendulum model of gait initiation.
Similar to postural control inverted pendulum models [13, 15], sensory feedback detecting body lean angle (e.g., vestibular, proprioceptive) was modeled using position feedback (Fig 2). Stiffness (Kp), integrative (Ki), and damping (Kd) feedback gains were included to model corrective torques generated by the neuromuscular system based on sensory feedback. The delay of sensory transmission in the central nervous system was modeled with a time delay block (Td) of 0.171s [13, 15]. The feedback gains were heuristically tuned to reduce the sum of squared error between experimental (θRef) and simulated (θModel) body lean angle data. The sum of four neuromuscular terms equals:
| (8) |
Lastly, the maximum amount of dorsiflexor torque available for TAnk was limited using a saturation value (Tsat) defined in equation 9. At each time step, the value of was compared to (TDFmax - TSAT), where TDFmax was an integer value slightly greater than the maximum experimentally-observed dorsiflexor torque and the value of TSAT was incrementally increased by 2 Nm (starting at 0 Nm). For example, from the experimental data of the pilot test participant, the maximum dorsiflexor torque was −22.3 Nm, then TDFmax could be set to −22 Nm. The resultant value based on equation 9 (TAnk) was fed into the transfer function for the body (equation 6). This saturation procedure effectively modeled the diminished or absent TA activation by the central nervous system in people with PD.
All simulations were performed using Simulink software (MathWorks Inc. Natick, MA).
| (9) |
D. Center of Pressure
Along with body lean angle (θModel), another biomechanical measurement that has been calculated in other postural control models is the center of pressure (COP), or the point at which the total resultant ground reaction force (GRF) is acting on the feet, in the sagittal plane [13, 15]. The position of the COP was calculated using the following equation derived from the equations of motion for the feet and body:
| (10) |
where mF mass of the feet, zF height of the ankle joint, xF horizontal distance between ankle joint and foot center of mass. The last three terms (mF,zF,xF) were based on values for an average adult male used by Maurer and Peterka (2005).
III. Results
Prior to presenting the results, a clarification about the convention used to create the presented plots of TAnk is needed. Dorsiflexor torque was defined as positive within the model for TAnk (equation 8) in accordance with positive theta; however, TAnk was plotted (Figs 3 and 4) with plantarflexor positive to follow the typical biomechanics convention (i.e., extensor moments are presented as positive values).
Fig. 3:
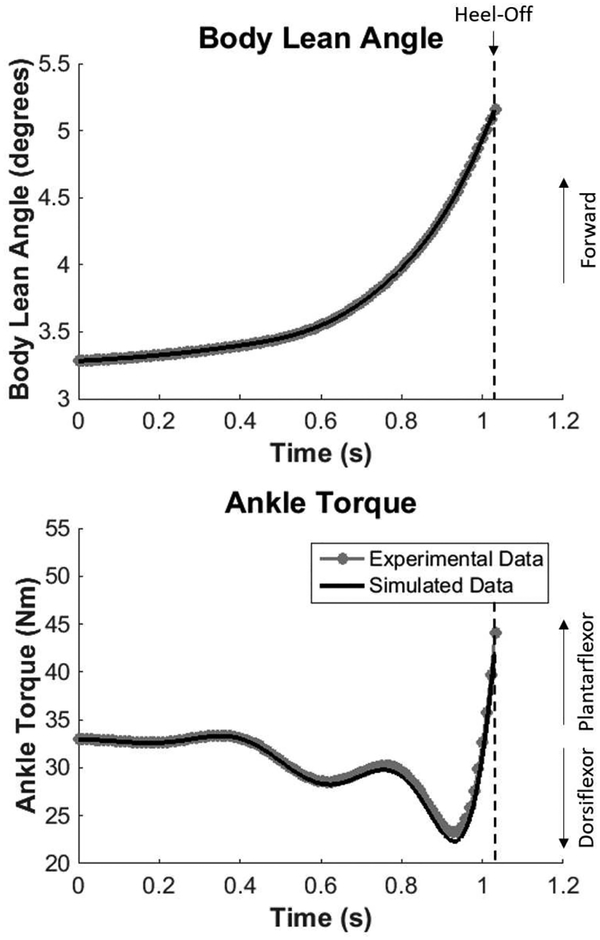
Body lean angle and ankle torque for simulated and experimental data from the healthy adult participant. Note the simulated data are based on the no-saturation condition (TSAT = 0).
Fig. 4:
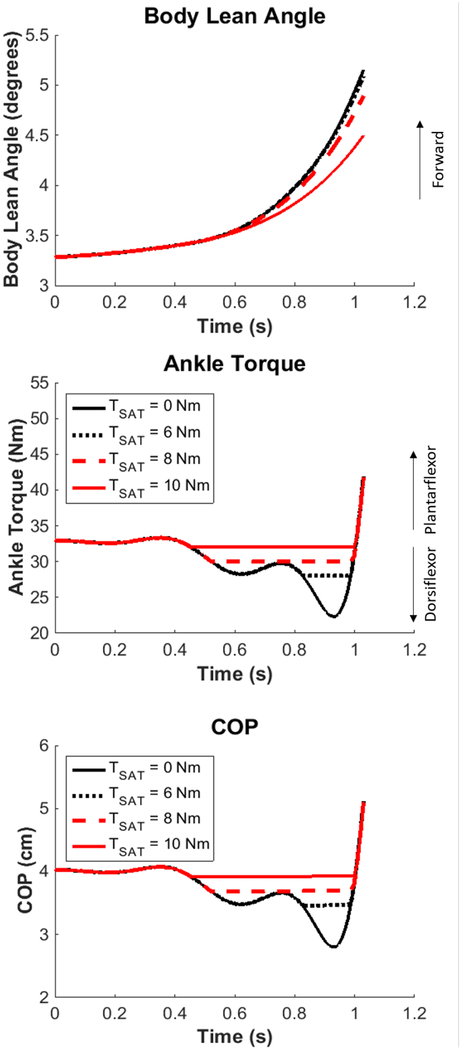
Simulated body lean angle, ankle torque, and center of pressure (COP) at different dorsiflexor torque saturation values.
A. Model Results
With TSAT = 0 (no limit on dorsiflexor torque), the model simulation for body lean angle and ankle torque matched the experimental data for the healthy young adult participant (Fig 3). Heuristic tuning of the feedback gains (to minimize the difference between experimental and simulated data) resulted in gain values of Kp = 1 Nm rad−1, Ki = 194 Nm s−1 rad−1, and Kd = 10 Nm s rad−1. Using these gain values, the general behavior for body lean angle was almost identical in the simulation, starting from a slight forward lean of 3.3 degrees progressing to 5.2 degrees at heel-off (Fig 3). Due to a slightly forward lean at the beginning, 33 Nm (of plantarflexor torque) was the initial ankle torque value. As the APA was generated, the model achieved the lowest torque (most dorsiflexor directed) at 22.3 Nm. Finally, the model went into increasing plantarflexor torque before heel-off (Fig 3). The only subtle differences in the simulated ankle torque existed after 0.4 seconds, but the general behavior was the same as the experimental data. Overall, the model was able to accurately simulate the experimental data for body lean angle and ankle torque.
Application of the saturation block (TSAT ≠ 0) revealed a possible threshold for decreased body lean angle and center of pressure excursion (Fig 4). Limiting the dorsiflexor torque up to 6 Nm (TSAT ≤ 6 Nm) did not result in large differences in body lean angle or ankle torque. However, when the dorsiflexor torque was limited by 8 Nm, a decrease of body lean angle (0.3°) became apparent and the posterior excursion of center of pressure was decreased by 0.9 cm. When dorsiflexor torque was almost fully limited with a saturation of 10 Nm (33 Nm (starting ankle torque) − 22.3 Nm (max dorsiflexor torque) = 10.7 Nm), the body lean angle was nearly a degree less (0.7°) than the no saturation condition, and the center of pressure excursion was diminished by 1.1 cm. Consequently, reduced dorsiflexor torque resulted in diminished forward progression and decreased posterior excursion of center of pressure.
B. PD Experimental Data Results
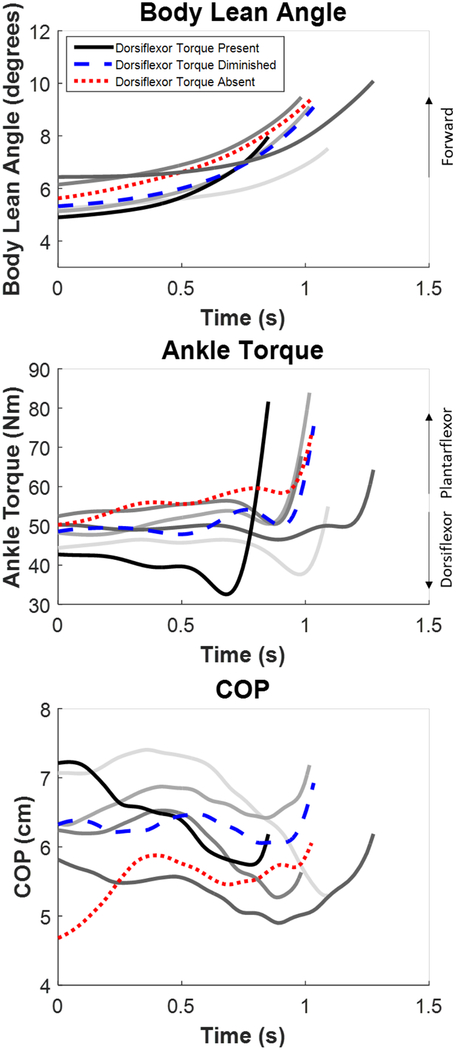
The experimental data from the PD participant demonstrated a range of different APA (ankle torque, lean angle, and COP) behaviors across the seven trials (Fig 5). These varied results matched well with the behaviors observed in the model predictions. In general, diminished or absent dorsiflexor torque before heel-off, which can be observed by the lack of a downward deflection in the net ankle torque (as demonstrated by the trials highlighted with dashed blue and dotted red lines, respectively), resulted in slower forward progression of the center of mass, increased duration to heel-off, and decreased posterior COP excursion. When a dorsiflexor torque was generated (as demonstrated by the solid black line trial), the rate of forward progression was faster, and the COP demonstrated a posterior excursion. Note that trials with an increased forward lean at the onset of the APA (as demonstrated by the darker grey lines) were associated with higher initial ankle torques, due to an increased contribution of the gravitation torque about the ankle, and either a markedly diminished or absent dorsiflexor torque during the APA.
Fig. 5:
Experimental data for body lean angle, ankle torque, and COP across all trials for the PD participant ending at heel-off. The sample trials with dorsiflexor torque present (black), diminished (blue), and absent (red) are highlighted. All grey lines are the remaining trials.
IV. Discussion
In this study, an inverted pendulum model of an APA for gait initiation was developed. Furthermore, simulations of reduced dorsiflexor torque during an APA were performed. The findings highlight the possible consequences of dorsiflexor torque limitations, including diminished forward progression and posterior excursion of the center of pressure (Fig 4). Specifically, limiting the dorsiflexor torque up to 6 Nm did not result in large differences in forward body lean angle or center of pressure excursion. However, limiting the dorsiflexor torque by 10 Nm resulted in a reduced forward body lean angle and center of pressure excursion similar to the APA profile observed in an individual with PD (Fig 5). Furthermore, the PD experimental data demonstrated that changes in the initial body lean angle may alter the magnitude and profile of the ankle torque. Ultimately, this APA model provides an initial basis for understanding the neuromechanical factors that may be important for gait initiation modulation paradigms and potential strategies that people with PD use to compensate for reduced dorsiflexor torque.
Without any limitation of dorsiflexor directed torque (TSAT = 0), the model was able to simulate the experimental body lean angle of the healthy young adult participant. The combination of feedback gains (Kp = 1 Nm rad−1, Ki = 194 Nm s−1 rad−1, Kd = 10 Nm s rad−1) and the addition of a feedforward torque (TF) resulted in a low amount of error between experimental and simulated body lean angle and ankle torque profiles. Physiologically, a similar online modification of the feedforward movement command through delayed sensory feedback has been demonstrated in several experimental studies [20]. By comparison to postural control models, our proportional (Kp) and derivative (Kd) gains were smaller and the integrative gain (Ki) was larger. For example, the same three gains in a healthy postural control model were Kp = 957 Nm rad−1, Ki = 34 Nm s−1rad−1, and Kd = 277 Nm s rad−1 [13]. Another study that only used proportional (Kp) and derivative (Kd) gains were Kp = 773 Nm rad−1 and Kd = 286 Nm s rad−1 for healthy individuals and Kp = 667 Nm rad−1 and Kd = 286 Nm s rad−1 for people with PD [15]. A key difference between these previous postural control models and the model of this study is the desired movement. For postural control, the reference trajectory is set to zero (no body lean angle) because the goal is to maintain standing posture. Consequently, per the feedforward torque equation for TF (equation 7), the feedforward torque would also be zero and the movement would be controlled with larger proportional (Kp) and derivative (Kd) gains. In our model, the feedforward torque was able to generate the desired forward body lean (θRef) with a small amount of error that accumulated due to the sensory time delay. Thus, a higher amount of integrative gain (Ki) was needed to eliminate the error. The difference in gains between these types of models may suggest that feedback gains are different for postural versus volitional movement. Overall, the APA model of this study was able to track the nominal trajectory with a minimal amount of error due to the inclusion of a feedforward torque.
The simulations of the reduced dorsiflexor torque were also able to reproduce the range of APA behaviors observed in an individual with PD. Trials with reduced dorsiflexor torque were associated with decreased posterior excursion of center of pressure and prolonged time to heel-off. Interestingly, the simulations suggest that there might be a threshold for decreased dorsiflexor torque before the body lean angle was considerably reduced. Between a 0–6 Nm reduction of dorsiflexor torque, body lean angle at the time of heel-off remained nearly the same as the nominal trajectory. However, when the dorsiflexor torque was limited by 8 Nm, forward body lean angle at heel-off was slightly decreased and the posterior center of pressure excursion was diminished. At 10 Nm of limitation, forward body lean was almost one degree less than the nominal trajectory and the posterior center of pressure excursion was diminished. Furthermore, the behavior of ankle torque remained relatively constant across different values of saturation aside from the dorsiflexor torque limitation (Fig 4). These results suggest that a certain amount of reduced dorsiflexor torque is allowable before it has a considerable effect on forward progression. Moreover, these findings give insight into the amount of external assistance that might be needed during an APA from an ankle torque device (e.g., a powered ankle-foot orthosis) to maintain a desired nominal trajectory for body lean angle and posterior center of pressure excursion.
The implications of a reduced capacity to generate a dorsiflexor torque during the APA were demonstrated in the experimental data obtained in an individual with PD. Trials with a diminished or absent dorsiflexor torque were associated with a relatively large forward lean and more anterior positioning of the center of mass relative to the ankle joint center prior to the APA. This behavior likely reflects a strategy whereby, in the absence of a sufficient dorsiflexor torque, the individual leverages the torque created by the gravitational force to generate the anterior acceleration of the body. The consequence of this strategy is a delayed heel-off, which may require a shortened first step in order to arrest the forward angular momentum of the body. Due to the assumptions of our model, we could not investigate what would happen after heel-off of the stepping foot. Future models would require more degrees of freedom (i.e., hip, knee, and ankle joints) and separated feet. This type of model could further predict the consequences of leaning further forward before the APA on step execution.
Future studies could further utilize the model to design and predict the effects of interventions that restore dorsiflexor torque via increases in strength (e.g., with medications) or by external assistance, such as a powered ankle foot orthosis [21]. For example, oral dopamine replacement therapy and deep brain stimulation have been shown to increase dorsiflexor strength in people with PD [22]. Similarly, medication has been shown to significantly improve the magnitude and timing of APA generation [5]. Accordingly, the model may provide estimates of the amount of dorsiflexor strength increase required to improve gait initiation.
Several limitations of our model should be considered for interpreting the results and developing models of gait initiation in the future. First, only the ankle joint was modeled, so alternative strategies for producing forward body lean through other joints (e.g., the hip joint) were not investigated. For example, a common symptom of PD is a forward body lean around the hip joint. Furthermore, we assumed that all motion was produced around the ankle joint and the feet did not move through the APA up to heel-off. It is possible that as the model approached heel-off that the model lost approximation of the true behavior of both limbs [4]. Finally, future models could investigate different values of sensory time delay. The time that was used in our model was based on previous postural control models (0.171 s) [13, 15]; however, it is possible that the sensory time delay during gait initiation would be different, especially in response to external assistance. Previous mechanical perturbation studies have demonstrated that adaptations could occur as fast as 88 ms depending on when the perturbation is provided in the APA [23]. Overall, our model provides an initial basis for future studies, but several factors should be considered in the development of APA models.
V. Conclusions
In conclusion, an inverted pendulum model of an APA was created using neuromuscular components. Moreover, the consequence of reduced dorsiflexor torque in people with PD was simulated. The results suggest that there may be a threshold of diminished dorsiflexor torque that results in diminished forward progression and posterior center of pressure excursion. Future models could investigate the consequences of these diminished APA behaviors to the subsequent step execution phase.
Acknowledgments
This paragraph of the first footnote will contain the date on which you submitted your paper for review. This material is based upon work supported by the National Science Foundation Neuroengineering IGERT under Grant No. 0903622 (MP) and NIH RO1 NS070264 (CM).
Biographies

Matthew N. Petrucci, PhD (M’ 13) received his B.S and B.A. in mechanical engineering from the University of San Diego, San Diego, CA, USA in 2003. He went on to obtain a M.S. in mechanical engineering and a Ph.D. in neuroscience from the University of Illinois at Urbana-Champaign, Urbana, IL, USA in 2016.
From 2011–2016, he was a Research Assistant in the Human Dynamics and Controls Lab. He received a Neuroengineering IGERT fellowship from 2013–2015. Most recently, he was awarded a MnDRIVE Neuromodulation Postdoctoral Fellowship in 2016 and the Parkinson’s Study Group Mentored Clinical Research Award in 2017 at the University of Minnesota. Currently, he is a Postdoctoral Fellow in the Department of Neurology and Neurological Sciences at Stanford University. His research interests include areas pertaining to modulation strategies for motor impairments of people with movement disorders.

Louis A. DiBerardino, III, PhD received his combined B.S. and M.S. degrees in mechanical engineering from the University of Illinois at Urbana-Champaign, Urbana, IL, USA in 2008. He then received his Ph.D. degree in mechanical engineering at the same institution in 2014.
From 2006–2014 he was a Research Assistant in the Human Dynamics and Controls Lab, and from 2009–2014 he was a Research Assistant in the Applied Dynamics Lab. He received the Eugine and Lina Abraham Endowed PhD Fellowship in 2009, and the Departmental Teaching Fellowship in 2012. Currently, he is an Assistant Professor of Mechanical Engineering at Ohio Northern University, Ada, OH, USA. His research interests include the dynamics and control of human movement biomechanics.

Colum D. MacKinnon, PhD received his B.Sc. and M.Sc. in Kinesiology from the University of Waterloo and Ph.D. in Physiology from the University of Toronto. He is the director of the Movement Disorders Laboratory and an Associate Professor in the Department of Neurology and Institute of Translational Neuroscience at the University of Minnesota. His research program uses biomechanical and neurophysiological approaches to better understand the mechanisms of impaired movement control in people with Parkinson’s disease and other movement disorders as well as develop novel interventions to facilitate movement production.

Elizabeth T. Hsiao-Wecksler, PhD (M’ll) received the B.S. degree from Cornell University, Ithaca, NY, the M.S. degree from Rochester Institute of Technology, Henrietta, NY, and the Ph.D. degree from the University of California, Berkeley, all in mechanical engineering.
She was a Postdoctoral Fellow in the Integrated Rehabilitation Engineering Program at Boston University and Harvard Medical School. She is currently a Professor, Willett Faculty Scholar and the Associate Head for Undergraduate Programs in the Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign. She directs the Human Dynamics and Controls Laboratory. Her research group uses methods from design, control theory, mechatronics, fluid power, soft robotics, and musculoskeletal biomechanics to investigate and improve movement control and function with relation to locomotion biomechanics and assistive device design.
Dr. Hsiao-Wecksler is a Fellow of the American Society of Mechanical Engineers and the American Society of Biomechanics, and an Associate Editor for the ASME Journal of Medical Devices.
Contributor Information
Matthew N. Petrucci, M.N. Petrucci was with the University of Illinois at Urbana-Champaign, Urbana, IL, 61801 USA. He is now a Postdoctoral Fellow at Stanford University, Stanford, CA, 94305 USA.
Louis A. DiBerardino, L.A. DiBerardino is an Assistant Professor in the Department of Mechanical Engineering at Ohio Northern University, Ada, OH, 45810 USA
Colum D. MacKinnon, C.D. MacKinnon is an Associate Professor in the Department of Neurology at the University of Minnesota, Minneapolis, MN, 55455, USA
Elizabeth T. Hsiao-Wecksler, E.T. Hsiao-Wecksler is a Professor in the Department of Mechanical Engineering at the University of Illinois at Urbana-Champaign, Urbana, IL, 61801 USA.
VI References
- [1].Carlsoo S, “The initiation of walking,” Acta Anat (Basel), vol. 65, pp. 1–9, 1966. [DOI] [PubMed] [Google Scholar]
- [2].Crenna P and Frigo C, “A motor programme for the initiation of forward-oriented movements in humans,” J Physiol, vol. 437, pp. 635–53, June 1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Elble RJ, Moody C, Leffler K, and Sinha R, “The initiation of normal walking,” Mov Disord, vol. 9, pp. 139–46, March 1994. [DOI] [PubMed] [Google Scholar]
- [4].Lepers R and Breniere Y, “The role of anticipatory postural adjustments and gravity in gait initiation,” Exp Brain Res, vol. 107, pp. 118–24, 1995. [DOI] [PubMed] [Google Scholar]
- [5].Burleigh-Jacobs A, Horak FB, Nutt JG, and Obeso JA, “Step initiation in Parkinson’s disease: influence of levodopa and external sensory triggers,” Mov Disord, vol. 12, pp. 206–15, March 1997. [DOI] [PubMed] [Google Scholar]
- [6].Rogers MW, Kennedy R, Palmer S, Pawar M, Reising M, Martinez KM, et al. , “Postural preparation prior to stepping in patients with Parkinson’s disease,” J Neurophysiol, vol. 106, pp. 915–24, August 2011. [DOI] [PubMed] [Google Scholar]
- [7].Halliday SE, Winter DA, Frank JS, Patla AE, and Prince F, “The initiation of gait in young, elderly, and Parkinson’s disease subjects,” Gait Posture, vol. 8, pp. 8–14, August 1 1998. [DOI] [PubMed] [Google Scholar]
- [8].Elble RJ, Cousins R, Leffler K, and Hughes L, “Gait initiation by patients with lower-half parkinsonism,” Brain, vol. 119 (Pt 5), pp. 1705–16, October 1996. [DOI] [PubMed] [Google Scholar]
- [9].Martin M, Shinberg M, Kuchibhatla M, Ray L, Carollo JJ, and Schenkman ML, “Gait initiation in community-dwelling adults with Parkinson disease: comparison with older and younger adults without the disease,” Phys Ther, vol. 82, pp. 566–77, June 2002. [PubMed] [Google Scholar]
- [10].Hallett M and Khoshbin S, “A physiological mechanism of bradykinesia,” Brain, vol. 103, pp. 301–14, June 1980. [DOI] [PubMed] [Google Scholar]
- [11].Pfann KD, Buchman AS, Comella CL, and Corcos DM, “Control of movement distance in Parkinson’s disease,” Mov Disord, vol. 16, pp. 1048–65, November 2001. [DOI] [PubMed] [Google Scholar]
- [12].Johansson R, Magnusson M, and Akesson M, “Identification of Human Postural Dynamics,” IEEE Transactions on Biomedical Engineering, vol. 35, pp. 858–869, October 1988. [DOI] [PubMed] [Google Scholar]
- [13].Maurer C and Peterka RJ, “A new interpretation of spontaneous sway measures based on a simple model of human postural control,” Journal of Neurophysiology, vol. 93, pp. 189–200, January 2005. [DOI] [PubMed] [Google Scholar]
- [14].Peterka RJ, “Postural control model interpretation of stabilogram diffusion analysis,” Biological Cybernetics, vol. 82, pp. 335–343, April 2000. [DOI] [PubMed] [Google Scholar]
- [15].Nogueira S, Ferreira E, Geisinger D, San Roman C, and Suarez H, “Model of Postural Control System applied in Parkinson’s disease patients,” 32nd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), pp. 5452–5455, 2010. [DOI] [PubMed] [Google Scholar]
- [16].Breniere Y, Cuong Do M, and Bouisset S, “Are dynamic phenomena prior to stepping essential to walking?,” Journal of Motor Behavior, vol. 19, pp. 62–76, March 1987. [DOI] [PubMed] [Google Scholar]
- [17].Lepers R and Breniere Y, “The role of anticipatory postural adjustments and gravity in gait initiation,” Experimental Brain Research, vol. 107, pp. 118–24, 1995. [DOI] [PubMed] [Google Scholar]
- [18].Kawato M, “Internal models for motor control and trajectory planning,” Current Opinion in Neurobiology, vol. 9, pp. 718–727, December 1999. [DOI] [PubMed] [Google Scholar]
- [19].Wolpert DM, Miall RC, and Kawato M, “Internal models in the cerebellum,” Trends in Cognitive Sciences, vol. 2, pp. 338–347, September 1998. [DOI] [PubMed] [Google Scholar]
- [20].Shadmehr R, Smith MA, and Krakauer JW, “Error Correction, Sensory Prediction, and Adaptation in Motor Control,” Annual Review of Neuroscience, vol. 33, pp. 89–108, 2010. [DOI] [PubMed] [Google Scholar]
- [21].Petrucci MN, MacKinnon CD, and Hsiao-Wecksler ET, “Modulation of anticipatory postural adjustments of gait using a portable powered ankle-foot orthosis,” IEEE Int Conf Rehabil Robot, vol. 2013, p. 6650450, June 2013. [DOI] [PubMed] [Google Scholar]
- [22].Vaillancourt DE, Prodoehl J, Sturman MM, Bakay RA, Metman LV, and Corcos DM, “Effects of deep brain stimulation and medication on strength, bradykinesia, and electromyographic patterns of the ankle joint in Parkinson’s disease,” Mov Disord, vol. 21, pp. 50–8, January 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Mouchnino L, Robert G, Ruget H, Blouin J, and Simoneau M, “Online control of anticipated postural adjustments in step initiation: evidence from behavioral and computational approaches,” Gait Posture, vol. 35, pp. 616–20, April 2012. [DOI] [PubMed] [Google Scholar]