Abstract
Data are reported for solutions of sea salt at concentrations up to 161 ppm (2.5 equivalent ppm chlorine) over the temperature range 5 to 120 °C. Analysis is made in terms of equivalent conductance and the limiting law, , with evaluation of Λo and α in terms of the temperature. As a result, the conductivity due to sea salt in water is calculable over these ranges of temperature and concentration with an estimated error of ± 0.3 percent or less.
1. Introduction
The conductivity-temperature relationship of dilute solutions of “sea-salt” in water is used as a base for rapid instrumental analysis of the salinity of such solutions. Furthermore, the degree of contamination of distilled water and steam condensate by sea water due to condenser leakage or entrainment of boiler water can be determined with suitable conductivity equipment. The relationship between conductivity and temperature can also be used conveniently as a rough measure of ionic contamination of nearly neutral salt solutions and as a partial correction in the analysis of acidic or basic salt solutions. Pertinent information both with regard to salinity indicator systems and the specific problems involved in utilization of conductivity methods and data for analysis is available in the literature [1 to 23].1
Empirically the present investigation paralleled that of previous determinations of this relationship [1, 2], with the exception that conductivities were determined on solutions above their normal boiling-points and considerable emphasis was placed upon determination of the solvent conductivity, so that the contribution due to the salt was more precisely determinable. It was therefore necessary to employ suitable pressurized equipment to avoid ebullition during the course of the measurements and to refine further the techniques of measurement in order to avoid significant residual contamination of the solutions and concomitant vitiation of the results.
2. Experimental Procedure
Solutions:
The synthetic ocean water used as a reference solution was prepared by dissolving the salts listed in table 1 in an air-equilibrated grade of conductivity water. Its composition was practically identical with that of the proposed “Synthetic Ocean Water” composition for Class II work listed in table XII of NRL report P-2909 [3]. Commercially available reagent-grade materials were used in the preparation of this solution, except where the formula called for MgCl2·6H2O. In this case, since the degree of hydration of magnesium chloride is difficult to determine, the required amount of the salt was prepared in solution by neutralization of constant boiling hydrochloric acid with magnesium oxide.
Table 1.
Composition of synthetic ocean water at 20 °C
| NRL Report P-2909 | |||
|---|---|---|---|
| Salt | Class II designationa g. 1−1 |
Anhydrous state g. 1−1 |
Equivalents 1−1 b |
| NaCl | 24.540 | 24.540 | 0.41989 |
| MgCl2·6H2O | 11.110 | 5.20 3 | .10926 |
| Na2SO4 | 4.094 | 4.094 | .05764 |
| CaCl2 | 1.159 | 1.159 | .02088 |
| KCl | 0.695 | 0.695 | .00932 |
| NaHCO3 | .201 | .201 | .00239 |
| KBr | .101 | .101 | .00084 |
| H3BO3 | .027 | .027 | .00043 |
| SrCl2·6H2O | .042 | .025 | .00032 |
| NaF | .003 | .003 | .00007 |
| Total salt | 41.972 | 36.048 | 0.62014 |
Class II designation (test purposes) differs from Class I designation (fundamental research purposes) by 1.3 mg/liter of total solutes.
1961 atomic weights.
From this primary reference solution a secondary reference solution containing 2.5050 equivalent ppm of chlorine was prepared on a weight basis. Volumetric glassware was then employed in diluting this solution to obtain the other solutions with the concentrations listed in table 2. A common source of ammonia-free distilled water at equilibrium with the carbon dioxide of the atmosphere (pH about 5.7 at 25 °C) was used throughout the course of the work.
Table 2.
Dilutions of synthetic sea water
| Chlorine and salt content | ||||||
|---|---|---|---|---|---|---|
| Concentration chlorine | Content chlorine | Content anhydrous salt | ||||
| eq. ppm | ppm | g/liter 20 °C | CC1 eq. C1/kg | ppm | g/liter 20 °C | CS eq. “Sea Salt”/kg |
| 2.505 | 88.81 | 0.08867 | 2.505 ×10−3 | 161.35 | 0.16109 | 2.7797 ×10−3 |
| 1.503 | 53.29 | .05320 | 1.5031 ×10−3 | 96.81 | .09665 | 1.6678 ×10−3 |
| 1.002 | 35.52 | .03546 | 1.0019 ×10−3 | 64.54 | .06442 | 1.1117 ×10−3 |
| .5009 | 17.76 | .01773 | .5009 ×10−3 | 32.27 | .03221 | .5558 ×10−3 |
| .3007 | 10.66 | .01064 | .3007 ×10−3 | 19.36 | .01933 | .3337 ×10−3 |
| .1503 | 5.329 | .005319 | .1503 ×10−3 | 9.680 | .009663 | .1668 ×10−3 |
| .1002 | 3.552 | .003546 | .1002 ×10−3 | 6.454 | .006442 | .1112 ×10−3 |
| .06014 | 2.132 | .002128 | .06014 ×10−3 | 3.873 | .003866 | .06673 ×10−3 |
| .02004 | .7105 | .0007092 | .02004 ×10−3 | 1.290 | .001288 | .02224 ×10−3 |
Apparatus:
Suitable equal ratio capacitance conductance bridges supplied with a Wagner earth were used to determine the resistance of the cells in the frequency range 1 to 12 kc/s.
Oil-filled thermostats were employed to control temperature which was determined by resistance thermometers in some of the measurements and by calibrated mercury thermometers in others.
Five conductivity cells were employed during the course of the measurements. They were constructed of Pyrex glass and had electrodes of platinum or platinum-iridium alloy. Of these only one, which was specially constructed for the purpose, was suitable both from the standpoint of its dimensions and its cell constant (ca. 0.2 cm−1) for use over the entire range of temperature and concentration. The other four cells, pipet and dilution types with constants in the range 4.4 to 0.06 cm−1, were used as needed over a temperature range from 5 to 60 °C.
A manostat suitable for use up to 2½ atmospheres absolute was fashioned from a one-gallon can and, with supporting framework, was used to contain the special cell for the measurements in the temperature range between 75 and 120 °C. Pressure within the manostat was maintained at the desired level by application of gas from a nitrogen tank through a reducing valve. In use, the manostat was partially filled with oil to the extent that the cell was nearly immersed and the manostat itself was completely immersed in the oil bath at the temperature of measurement. Equilibrium of the resistance of the cell was usually achieved in one hour or less.
Procedure:
Conductivities of the solutions were determined in two series of measurements. One series was made at 35, 5, 20, 50, 60, and again 35 °C and the other at 35, 75, 90, 105, 120, and again 35 °C. By bracketing the measurements at other temperatures between those at 35 °C, it was possible to determine the magnitude of any changes which had taken place in the resistance of a cell during the course of a series, and this served as a partial check upon the precision of the measurements. Ordinarily the resistance of the cell was read directly in terms of the adjacent arm of the bridge, but in some cases, at low concentrations in the special cell and for the companion measurements on equilibrium water, a shunt method with a 10,000 or 100,000 ohm standard resistor was used.
The variation of resistance of the cells with frequency was determined at 1, 3, and 12 kc/s so that the magnitude of electrode polarization and other frequency-dependent phenomena present could be evaluated and corrections applied where necessary.
3. Results
Discussion:
The data obtained were converted to values of specific conductance by means of the relation γ = S×106/R where γ is the specific conductance in micromhos/cm, S the cell constant in cm,−1 and R the observed resistance of the cell. The values so calculated for the sea water data are listed in table 3.
Table 3.
Observed values of γ in micromhos/cm
| Chlorine eq. ppm temperature | 0.02004 | 0.06014 | 0.1002 | 0.1503 | 0.3007 | 0.5009 | 1.0019 | 1.5031 | 2.5050 | |
|---|---|---|---|---|---|---|---|---|---|---|
| °F | °C | |||||||||
| 41.0 | 5.0 | 2.31 | 5. 78 | 9.14 | 13.33 | 26.02 | 42.60 | 84.11 | 124.8 | 205.4 |
| 68.0 | 20.0 | 3.43 | 8.56 | 13.40 | 19.46 | 38.09 | 62.20 | 122.8 | 182.1 | 299.8 |
| 95.0 | 35.0 | 4.65 | 11.35 | 18.04 | 26. 46 | 51.49 | 84.04 | 165.6 | 245.8 | 404.2 |
| 122.0 | 50.0 | 5.91 | 14.43 | 23.15 | 33.52 | 65.44 | 107.2 | 212.1 | 314.4 | 516.8 |
| 140.0 | 60.0 | 6.76 | 16.42 | 26.59 | 38.43 | 75.15 | 123.4 | 244.1 | 362.0 | 594.6 |
| 167.5 | 75.3 | 7.98 | 19.95 | 31.88 | 47.09 | 91.42 | 149.5 | 293.4 | 435.7 | 712.7 |
| 194.9 | 90.5 | 9.20 | 23.34 | 37.35 | 55.22 | 107.3 | 175.4 | 344.4 | 511.0 | 838.3 |
| 221.7 | 105.4 | 10.40 | 26.58 | 42.62 | 63.07 | 122.9 | 200.5 | 393.8 | 584.8 | 959.6 |
| 249.1 | 120.6 | 11.82 | 29.79 | 47.94 | 70.75 | 138.7 | 226.3 | 443.3 | 656.8 | 1,075.0 |
The conductivity of these solutions may be considered to be the sum of the specific conductance of the salt present and of the water used. Since the conductivity of otherwise pure distilled water is rather widely variable, due to the presence of volatile impurities such as carbon dioxide and ammonia, it is desirable that the specific conductance due to the salt alone be known. For nearly neutral solutions this may be obtained from the relation γ′ = γ—γw where γ′ is the specific conductance due to the salt and γw is that due to the water. Values of γ′ so calculated are listed in table 4.
Table 4.
Values of γ′ in micromhos/cm γ′ = γ — γw
| Chlorine eq. ppm temperature | 0.02004 | 0.06014 | 0.1002 | 0.1503 | 0.3007 | 0.5009 | 1.0019 | 1.5031 | 2.5050 | |
|---|---|---|---|---|---|---|---|---|---|---|
| °F | °C | |||||||||
| 41.0 | 5.0 | 1.71 | 5.12 | 8.48 | 12.67 | 25.36 | 41.94 | 83.45 | 124.19 | 204.73 |
| 68.0 | 20.0 | 2.51 | 7. 47 | 12.31 | 18.37 | 37.00 | 61.11 | 121.75 | 181.03 | 298.67 |
| 95.0 | 35.0 | 3.36 | 10.06 | 16.75 | 25.17 | 50.20 | 82.75 | 164.31 | 244.51 | 402.91 |
| 122.0 | 50.0 | 4.29 | 12.81 | 21.53 | 31.90 | 63.82 | 105.60 | 210.48 | 312.77 | 515.22 |
| 140.0 | 60.0 | 5.02 | 14.68 | 24.85 | 36. 69 | 73.41 | 121.66 | 242.38 | 360.23 | 592.81 |
| 167.5 | 75.3 | 6.03 | 18.00 | 29.93 | 45.14 | 89.47 | 147.56 | 291.43 | 433.77 | 710.71 |
| 194.9 | 90.5 | 7.05 | 21.19 | 35.2 | 53.07 | 105.16 | 173.27 | 342.30 | 508.88 | 836.15 |
| 221.7 | 105.4 | 8.08 | 24.26 | 40.3 | 60.75 | 120.59 | 198.21 | 391.47 | 582.48 | 957.23 |
| 249.1 | 120.6 | 9.15 | 27.12 | 45.27 | 68.08 | 135.99 | 223.59 | 440.66 | 654.13 | 1,072.33 |
The procedure adopted for determining the values of γw used in computing γ′ was based upon the fact that the observed values of γ when plotted with respect to the concentration C gave nearly straight lines at any one temperature and the data for such a temperature could be expressed by an equation of the type γ = γw + MC–NC2. For low concentrations (0.02–0.15 eq. ppm Cl) the NC2 term is of negligible proportions and γ = γw + MC.
The constants M and γw were evaluated for each temperature by the use of simultaneous equations, and the values of γw were used to calculate the values of γ′ in all except two cases. In these, experimental considerations made it preferable to use directly determined values of γe. The values of γw so calculated are given in table 5. Included are values of γx obtained by graphical extrapolation of γ to zero concentration. The conductivity, γe, of the distilled water used for preparation of the solutions was determined over the temperature range. Corrections of these values for the observed drift, assumed to be entirely due to loss of carbon dioxide, gives the listed values of γc which compare favorably with those of γw and γx.
Table 5.
Solvent water conductivity as derived and measured
| (Micromho/cm) | ||||
|---|---|---|---|---|
| Temp. | γw | γx | γe | γc |
| °C | ||||
| 20 | 0.92 | |||
| 5 | 0.66 | 0.63 | .61 | 0.61 |
| 20 | 1.09 | .93 | .92 | .92 |
| 35 | 1.29 | 1.25 | 1.193 | 1.193 |
| 50 | 1.62 | 1.52 | 1.468 | 1.51 |
| 60 | 1.74 | 1.71 | 1.623 | 1.69 |
| 75.28 | 1.95 | 1.86 | 1.779 | 1.88 |
| 90. 51 | 2.15 | 2.12 | 1.927 | 2.04 |
| 105.41 | 2.32 | 2.31 | 2.049 | 2.17 |
| 120.56 | 2.67 | 2.72 | 2.536 | 2.68 |
| 35 | 1.129 | 1.193 | ||
γw, values calculated from sea water data.
γx, values obtained by graphical extrapolation of data.
γe, values obtained by direct measurement.
γc, values obtained by correction of γe for drift observed between measured values at 35 °C. Drift assumed to be due to a partial loss of carbon dioxide assumed to be complete at 75 °C. No such significant drift could be established in the solution measurements.
Evaluation:
The magnitudes of the errors known to be associated with these results are estimated to be as follows.
Measurement of the resistance of the cells; less than ±0.04 percent.
Preparation of the solutions by adding the known weights of salts to the water; not greater than ±0.1 percent.
The temperatures of measurement were controlled to better than 0.01 °C in the range between 5 and 60 °C and to ±0.02 °C in the range 75 to 120 °C In all cases they were probably accurate within 0.1 °C, which would lead to an error not greater than ±0.1 percent in measured values of conductance.
The cell constants were known to 0.05 percent or better at 35 °C. Although no corrections were applied for their change with temperature, it is probable that any error due to such change is no greater than 0.1 percent at the most extreme temperature of measurement with respect to that at 35 °C.
Of the recognized errors, that due to variation of the conductivity of the water used is of greater magnitude at the lower concentrations than all the others. This error is difficult to evaluate precisely, since it can vary both with the carbon dioxide content of the atmosphere and the variation of its solubility and ionization in the solution with partial pressure and temperature.
In the present work, this latter effect became significant when cells of the dilution type were used to obtain some of the data for 50 and 60 °C at lower concentrations, with the result that these data at 60° are the least dependable (uncertain to ± 1 percent) of all the sea water data.
From an analysis of the data obtained and the derived values of γ′, it is estimated that the limits of the accuracy of the individual values of γ′ listed in table 4 vary with increasing concentration from ±1 percent to ±0.2 percent, which may be considered to be an overall measure of the empirical validity of the results.
4. Discussion
The values of γ listed in table 3 are representative of actual dilutions of “sea water” using a better than average grade of distilled water as solvent. The solvent conductivity is almost entirely due to its air equilibrium content of carbon dioxide combined with the ionization of the water. The values as such can be used directly as a base for scaling and calibration of salinity indicators or for the determination of salinity where equilibrium conditions exist or can be assumed to exist. When such assumptions cannot be made, the values of γ′ from table 4 can be used with a “water correction” applied as appropriate.
Comparison of the values listed in table 5 will indicate the order of uncertainty involved in assigning a water correction even when considerable effort is made to use a reasonably stable reference condition and to minimize contamination.
In this regard it may be pertinent to state briefly certain characteristics of distilled water. According to Kohlrausch and others [24, 25, 26, 31] the specific conductance of pure water is about 0.055 micromho/cm at 25 °C and has a temperature coefficient of about 5 percent per deg C. On the other hand, ordinary distilled water, in which the content of total solids (i.e., both salt and nonconducting material) is extremely low, has a conductivity of 1 to 3 micromhos/cm or more at 25 °C and a temperature coefficient of about 2 percent per deg C. In the main this conductivity is due to variable quantities of dissolved carbon dioxide and ammonia. These quantities are subject to variation with the temperature of condensation and the constitution of the boiler water as well as exposure to the atmosphere as a source of contamination.
It is usual to represent conductivity data in terms of an equivalent conductance
| (1) |
where C is the electrolyte concentration in equivalents per liter, and in very dilute solution to represent the variation of Λ with concentration by
| (2) |
where Λ0 and α are constants for a given electrolyte and temperature.
Theory [27, 28, 29, 30] permits computation of the values of α for single electrolytes but is not generally applicable to mixtures. Given the variation of Λ0 and α with temperature then either γ′ or C can be derived in terms of the other over the appropriate range of temperature and concentration. When the concentration is in equivalents of sea salt per liter up to 3 × 10−3 and the temperature is between 5 and 120 °C
| (3a) |
and
| (3b) |
where t is the temperature in degrees Celsius.
Since on this scale the concentration of a particular solution is temperature dependent, it is convenient, for purposes of analysis, to express concentration in equivalents per kilogram. For these concentrations in terms of chlorine, Cc1 (a scale commonly used for sea water)
| (4a) |
and
| (4b) |
Correspondingly for sea salt in equivalents per kilogram Cs,
| (5a) |
and
| (5b) |
A comparison of the locus of calculated from these relationships with the best apparent graphical locus obtained from plots of Λ versus shows a deviation as great as 0.41 percent only at one end of the 60 °C plot and an average maximum deviation of 0.29 percent over the range. As a result, it is likely that appropriate values of Λ so calculated within the applicable range of temperature and concentration are accurate to ±0.3 percent or better.
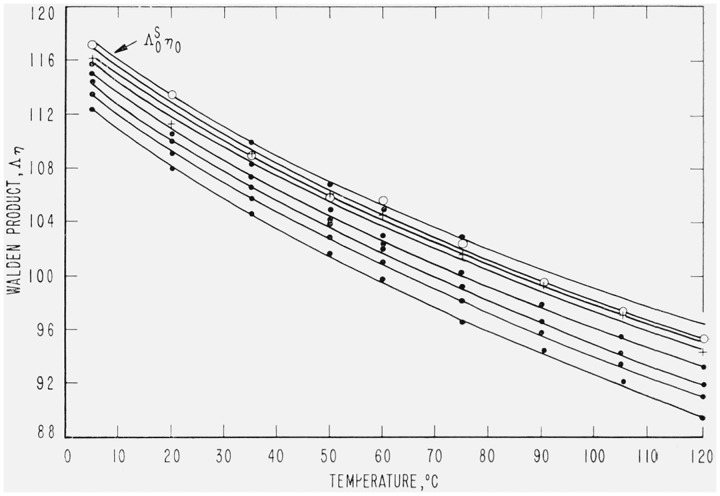
Additional evaluation of the data was accomplished using large plots of the Walden product, Λη, versus the temperature, where η is the solvent or solution viscosity. This gives a family of curves for solutions of different concentrations, as shown in figure 1. From these it is easy to detect any appreciable inconsistency of the data. Interpolation in terms of viscosity allows a reasonable evaluation of Λ at other concentrations and temperatures. To a degree this procedure is an extension of that used with limiting ion conductances [29, 30] and deserves more extensive use as an aid in evaluation of conductance data. The results obtained support the estimation of accuracy made regarding the individual values of γ′ in table 4 and that ascribed to the use of eq (2) combined with eq (3, 4, or 5).
Figure 1. The variation of the Walden product for sea salt with temperature and concentration.
Curves in descending order represent concentrations of 0.0, 2.2×10−5, 1.1×10−4, 3.3×−4, 5.6×10−4, 1.1×10−3, 1.7×10−3, and 2.8×10−3 in equivalents/kg.
It is interesting to compare the values of Λ0 for sea salt with those for sodium chloride calculated from acceptable values of limiting ion conductances [29] and also the observed values of α with those calculated, α′, assuming sea salt to be a 1:1 electrolyte. Comparative values are given in table 6. Included are values of limiting equivalent conductances of sea salt, Λ0x, calculated using appropriate limiting ion conductances weighted in proportion to the ionic composition of the sea salt (see table 1).
Table 6.
Comparison of the derived and measured constants of eq (2) for NaCl and sea salt
| Temp. °C |
NaCl Λ0 |
Sea salt Λ0 |
α | 1:1 electrolyte α′ |
Λ0x | Λ0x/Λ0 salt |
|---|---|---|---|---|---|---|
| 0 | 67.5a | 66.1b | 57b | 44c | 68.4d | 1.035 |
| 5 | 77.81 | 77.2 | 67 | 53 | ||
| 15 | 101.18 | 100.8 | 89 | 70 | ||
| 18 | 108.8 | 108.2 | 96 | 76 | 110.1 | 1.016 |
| 20 | 113.2 | 101 | 80 | |||
| 25 | 126.45 | 126.2 | 114 | 90 | 128.09 | 1.015 |
| 35 | 153.75 | 153.4 | 141 | 111 | ||
| 45 | 182.65 | 182.2 | 172 | 135 | ||
| 50 | 197.1 | 190 | 148 | |||
| 55 | 213.28 | 212.5 | 207 | 161 | ||
| 60 | 228.1 | 227 | 175 | |||
| 75.28 | 279.6 | 299 | 219 | |||
| 90.51 | 331.0 | 381 | 268 | |||
| 100 | 357 | 365.3 | 444 | 302 | 367 | 1.004 |
| 105.41 | 385.1 | 484 | 322 | |||
| 120.56 | 442.1 | 608 | 388 |
NaCl values Λ0 calculated. Appendix 6.1 (Robinson and Stokes) [29].
α′ values calculated for sea salt as a 1:1 electrolyte. Appendix 7.1 Electrolyte solutions (Robinson and Stokes) [29].
Λ0x = value of Λ0 for sea salt calculated through proportional use of equivalent ion conductances. Appendix 6.2 (Robinson and Stokes) [29].
The values of Λ0 for sodium chloride and the sea salt show a good and parallel agreement (not particularily to be expected) between 5 and 55 °C where the sodium chloride data are exceptionally good. On the other hand, the agreement between Λ0 and Λ0x for the sea salt is not as good as might be expected from a simple application of Kohlrausch’s law of independent migration of ions, a relationship which is well established for one solute solutions of electrolytes. Assuming that the absolute error in calculating Λ0 is not greater than that estimated, it would appear that a simple application of Kohlrausch’s law is only roughly valid for mixtures of this type [30A].
The observed differences in α and α′ are such that their misuse within the effective range of temperature and concentration would lead to a maximum error of 2.5 percent in γ′ or C. In terms of 2:1 and 2:2 electrolytes the error would be considerably larger.
The use of the conductance method in analysis of dilute solutions of unknown composition is admittedly subject to considerable uncertainty. Mixture effects as they influence both Λ0 and α. are not well understood, and in addition limiting ionic conductances show wide variation with ionic species. At the same time the method is particularly useful for rapid determinations and for comparative purposes. Since the present data are representative of dilute solutions of a common mixture of electrolytes they can be useful as reference data. From this base it is likely that conductometric analysis of nearly neutral natural waters can be made within 10 percent if an adequate water correction is made. On the other hand, conductometric analysis of dilute sea water solutions should be possible to 100.0±0.3 percent through appropriate use of equation 2 and correct values of Λ0 and α.
Footnotes
Figures in brackets indicate the literature references at the end of this paper
5. References
- [1].Huey C., J. Am. Soc. Naval Engineers 39, 658 (1927). [Google Scholar]
- [2].Lunn E. G. and Whybrew W., Navy Dept., Office of Naval Research, Resistance—Temperature Curves of Salinity Solutions, NRL Report No. P-1381 (July 1937) [Google Scholar]
- [3].May T. P. and Black C. E., Synthetic Ocean Water, Navy Dept., Office of Naval Research, NRL Report No. P-2909 (August 1946). [Google Scholar]
- [4].Sverdrup, Johnson, and Fleming, The Oceans (Prentice Hall, New York, N.Y., 1942). [Google Scholar]
- [5].Data of Geochemistry, Clarke F. W., Bull No. 770 U.S. Geological Survey.
- [6].Barnes A., Analyst 80/573 (1955).
- [7].Symposium on Problems and Practice in Determining Steam Purity by Conductivity Methods, Proc. ASTM 41, 1261–1340 (1941). [Google Scholar]
- [8].Symposium on Continuous Analysis of Industrial Water and Waste Water 1952, ASTM Special Tech. Pub. No. 130, (1953). [Google Scholar]
- [9].Symposium on Steam Quality, ASTM Special Tech. Publ. No. 192 (1956). [Google Scholar]
- [10].Symposium on Impurities in Steam, Proc. ASTM 61, 1369–1423 (1961). [Google Scholar]
- [11].Standard Methods for Examination of Water, Sewage and Industrial Wastes. 10th ed., pages 19 and 89. (Am. Public Health Assoc. Inc., New York, N.Y. 1955). [Google Scholar]
- [12].Lane R. W., Neff C. H. and Larson T. E., Am. Power Conference XXIII, 550 (1961). [Google Scholar]
- [13].Betz John D., Power Generation No. 12, 60–62 (1948). [Google Scholar]
- [14].Wilcox L. V., Am J.. Water Works Assoc. 42, 775 (1950). [Google Scholar]
- [15].Polsky J. W., Analytical Chemistry 19 657 (1947). [Google Scholar]
- [16].Gustafson H. and Behrman A. S., Ind. and Eng. Chem., Anal. ed. 11, 355 (1939). [Google Scholar]
- [17].Howard C. S., Ind. and Eng. Chem. 5, 5 (1933). [Google Scholar]
- [18].Oehme F., Gles-Instrument Tech. 4, 119 (1960). [Google Scholar]
- [19].Martin Madeleine, Rev. inst. franc. petrole et ann. Combustible Liquides 13, 985 (1958). [Google Scholar]
- [20].Whitehead G., J. Applied Chem. London 11, 136 (1961). [Google Scholar]
- [21].Deubner Alex and Heise Ruth, Ann. Physik. 9, 213–24 (1951). [Google Scholar]
- [22].Franco de Francisco Bull. Lab. chim provencialle, Bologna 4, 79 (1953). [Google Scholar]
- [23].Rossum J. R., Analytical Chem. 21, 631 (1949). [Google Scholar]
- [24].Kohlrausch F. and Heydweiller A., Weid. ann. 53, 209 (1894); [Google Scholar]; Zeit physik. chem. 14, 317 (1894). [Google Scholar]
- [25].Dorsey N. E., Properties of Ordinary Water Substance, A.C.S. monograph No. 81 (Reinhold Publishing Corp., New York, N.Y., 1940). [Google Scholar]
- [26].Haller W. and Duecker H. C., J. Research NBS 64A, 527 (1960). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Onsager L., Physik Z. 28, 277 (1927); [Google Scholar]; 27, 388 (1926). [Google Scholar]
- [28].MacInnes D. A., The Principles of Electrochemistry (Reinhold Publishing Corp., New York, N.Y., 1939). [Google Scholar]
- [29].Robinson R. A. and Stokes R. H., Electrolyte Solutions 2d ed. (Butterworths Sci. Pub., London, 1959). [Google Scholar]
- [30].Harned H. S. and Owen B. B., The Physical Chemistry of Electrolyte Solutions, 2d ed. (Reinhold Publishing Corp., New York, N.Y., 1950). [Google Scholar]
- [30A].Ibid., pp. 142–146.
- [31].Iverson A., J. Phys. Chem. 68, 515 (1964). [Google Scholar]