Wall Stress and Geometry Measures in Electively Repaired Abdominal Aortic Aneurysms

Abstract

Abdominal aortic aneurysm (AAA) is a vascular disease characterized by the enlargement of the infrarenal segment of the aorta. A ruptured AAA can cause internal bleeding and carries a high mortality rate, which is why the clinical management of the disease is focused on preventing aneurysm rupture. AAA rupture risk is estimated by the change in maximum diameter over time (i.e., growth rate) or if the diameter reaches a prescribed threshold. The latter is typically 5.5 cm in most clinical centers, at which time surgical intervention is recommended. While a size-based criterion is suitable for most patients who are diagnosed at an early stage of the disease, it is well known that some small AAA rupture or patients become symptomatic prior to a maximum diameter of 5.5 cm. Consequently, the mechanical stress in the aortic wall can also be used as an integral component of a biomechanics-based rupture risk assessment strategy. In this work, we seek to identify geometric characteristics that correlate strongly with wall stress using a sample space of 100 asymptomatic, unruptured, electively repaired AAA models. The segmentation of the clinical images, volume meshing, and quantification of up to 45 geometric measures of each AAA were done using in-house Matlab scripts. Finite element analysis was performed to compute the first principal stress distributions from which three global biomechanical parameters were calculated: peak wall stress, 99^th-percentile wall stress and spatially averaged wall stress. Following a feature reduction approach consisting of Pearson’s correlation matrices with Bonferroni correction and linear regressions, a multivariate stepwise regression analysis was conducted to find the geometric measures most highly correlated with each of the biomechanical parameters. Our findings indicate that wall stress can be predicted by geometric indices with an accuracy of up to 94% when AAA models are generated with uniform wall thickness and up to 67% for patient specific, non-uniform wall thickness AAA. These geometric predictors of wall stress could be used in lieu of complex finite element models as part of a geometry-based protocol for rupture risk assessment.

3. INTRODUCTION

An abdominal aortic aneurysm (AAA) is a focal dilation of the infrarenal aorta that causes loss of vessel wall structural integrity typically upstream of the aorto-iliac bifurcation. The current clinical practice for assessing rupture risk is to monitor the aneurysm’s growth until it reaches a maximum diameter of 5.5 cm or a rate of growth equivalent to 0.5 cm within the last 6 months.¹ Based on these clinical standards of care, intervention is recommended in the form of endovascular repair or open surgery if significant contraindications exist for an endovascular graft. As the standards for assessing the need for treatment are governed by a single measure (the maximum transverse diameter), there is evidence that small aneurysms also rupture while large, previously undiagnosed aneurysms are detected opportunistically in asymptomatic patients. In an autopsy analysis performed by Darling et al.,⁶ it was found that 60% of aneurysms with a diameter greater than 5.5 cm never ruptured and 13% of aneurysms with a diameter less than 5.5 cm ruptured. Brown and colleagues³ found that the risk of rupture for AAA with maximum diameters in the range 5.0 – 5.9 cm was low and four times greater in females compared to males, thus questioning the usefulness of maximum diameter as the sole predictor of risk of rupture. AAA rupture accounted for 9,863 deaths in the U.S. in 2014,⁴ which underscores the need for a more accurate metric for assessing AAA rupture risk.

Biomechanical analysis of AAA suggests that aneurysm rupture is a localized event occurring when wall stress exceeds the strength of the diseased aortic tissue. To this end, biomechanical measures such as peak wall stress (PWS) have been postulated as alternatives to the maximum diameter criterion. Fillinger et al.⁷ found that PWS in ruptured aneurysms was higher than that of unruptured aneurysms and differentiated the two AAA groups better than maximum diameter, concluding that PWS was a more accurate measure of rupture risk than the clinical standard. A meta-analysis performed on 348 patients by Khosla et al.¹² concluded that PWS is lower in symptomatic ruptured AAA than in asymptomatic intact AAA, after accounting for systolic blood pressure. Polzer and Gasser,²⁰ accounting for uncertainty in AAA wall thickness and wall strength, provided support to a probabilistic approach to rupture risk assessment combined with biomechanical analysis. PWS is strongly correlated with maximum diameter, hence it should not be the sole criterion for rupture risk prediction; other factors such as wall strength and aneurysm size are also contributors.⁸ As PWS is most commonly estimated using finite element analysis (FEA), the disadvantage of a biomechanical approach for rupture risk assessment is the lack of knowledge of the AAA wall material properties on an individual basis. An alternative approach, which eliminates the need for patient specific material properties while using standard of care computed tomography images and optional non-standard of care magnetic resonance images, is described by Joldes and colleagues.^{10, 11}

Geometry measures such as AAA shape and wall thickness can be used as part of a geometric modeling approach to rupture risk assessment. This can be justified, in part, by the strong dependence of wall stress on AAA shape.² Biquintic finite element modeling, as proposed by Sacks et al.,²⁴ is used to compute the first principal curvatures in arbitrary shapes such as individual AAA. These and other geometric indices can differentiate ruptured from unruptured aneurysms, by means of linear logistic regression.³¹ In addition, there is evidence of a strong correlation between PWS and the mean and maximum curvatures of the AAA centerline, as reported by Giannoglou and colleagues.⁹ According to Lijeqvist et al.,¹⁶ the infrarenal aortic volume strongly correlates with an FEA-derived rupture risk and helps predict AAA growth rate. Georgakarakos et al.⁸ reported a significant correlation between tortuosity of an aneurysm and PWS, where tortuosity is measured along the centerline of the abdominal aorta. To this end, using geometric indices that significantly correlate with biomechanical measures of rupture risk can result in the derivation of geometric surrogates of these measures and improved criteria for recommending repair compared to maximum diameter alone.

The objective of the present work is to perform a geometric analysis of patient specific, asymptomatic, unruptured AAA to interrogate the potential relationship between specific geometric indices and global measures of wall stress. Patients with these aneurysms received an elective repair within six months of the clinical images collected for this study. Therefore, the primary goal of the study is to derive a statistical model of geometric predictors of AAA wall stress for a clinically relevant group of aneurysms that were repaired due to their size and/or growth rate.

4. MATERIALS AND METHODS

4.1. 3D Image Reconstruction

The abdominal computed tomography angiography (CTA) scans of 100 patients who were diagnosed with AAA were obtained from an existing database in the Department of Radiology at Allegheny General Hospital (Pittsburgh, PA), after approval of the human subject’s research protocol by the corresponding Institutional Review Committee. The scans had the following imaging parameters: i) Scan matrix size = 512×512; ii) Pixel size = 0.64 to 0.79 mm; iii) Pixel intensity = 0–2000 Hounsfield units; iv) Slice thickness = 1.5 to 3.5 mm. These images were taken during routine visit to monitor AAA growth. Using custom in-house scripts written in MATLAB (Mathworks, Inc., Natick, MA), collectively known as AAAVasc (v1.03, The University of Texas at San Antonio, San Antonio, TX),²⁶ the lumen and wall of the abdominal aorta were segmented. The standard of care images in Digital Imaging and Communications in Medicine (DICOM) are the input for AAAVasc. Due to the significant difference in contrast between the lumen and the surrounding soft tissues, the lumen can be easily identified by region-growing.²⁶ To initiate the segmentation process, the user selects a seed point inside the lumen and the algorithm identifies the lumen boundary by analyzing the contrast gradient for each image.²⁶ The outer wall segmentation is automated in that the algorithm generates different possible contours from which the best fitted outer wall boundary is selected by the user.²⁷ The inner wall segmentation is performed by training a neural network, which is trained by manually extracting samples of the background, thrombus and lumen regions to build the feature vectors necessary for the network. The neural network is a single layer with eight nodes, which are texture and intensity based features.²⁶ The number of elements in the input vector r depends on the number of points the user manually enters during the training. Training stops when the maximum number of epochs is met, which in the present application is equal to one thousand.¹⁸ Finally, a point cloud is generated with the three segmented boundaries along with volumetric binary masks representing the three regions of interest in the aneurysm (lumen, wall, and thrombus). We have previously implemented this image segmentation protocol for generating patient specific AAA geometry.^{15, 28, 29}

4.2. Biomechanical Characterization Using FEA

The binary masks are imported into AAAMesh, another in-house MATLAB script, to generate volume and surface meshes.²³ We generated two different volume meshes for each AAA; one with a uniform wall thickness of 1.5 mm and the other with a patient specific wall thickness distribution (measured from the segmented images). The uniform wall thickness of 1.5 mm was chosen based on the work of Raghavan and colleagues,²¹ who performed uniaxial tensile testing on specimens from four post-mortem AAA, reporting wall thicknesses ranging from 0.23 to 4.26 mm with a median of 1.48 mm. The volume mesh file is output in a Nastran format, which is processed using the FEA solver ADINA (Adina R&D, Inc., Watertown, MA). The boundary conditions and material properties used for the uniform and non-uniform wall thickness models are identical. The volume meshes consist of approximately 48,000 to 90,000 quadratic hexahedral elements. Two elements across the thickness of the wall with an aspect ratio of nearly 1.0 was sufficient to achieve convergence of the first principal stress when the AAA was subject to peak systolic pressure.²³ The AAA were subject to an intraluminal pressure of 120 mmHg in at least 24 time steps. To simulate anatomical conditions and prevent unwanted displacements and rotation, the proximal and distal ends of the AAA were fixed for all degrees of freedom. A Mooney-Rivlin constitutive model was used to represent the AAA wall material properties, as described by Raghavan and Vorp.²² For such a model, the strain energy density is directly proportional to the first invariant of the left Cauchy-Green deformation tensor, described by Eq. (1),

$$W=c_1\left(I_1-3\right)+c_3{\left(I_1-3\right)}^2$$ (1)

where W represents the strain energy density, I₁ the first invariant of the Cauchy – Green tensor, and c₁ and c₃ are material constants derived from tensile testing of AAA wall specimens.²² With c₁ = 17.4 N/cm², c₃ = 188.1 N/cm², and a Poisson’s ratio of 0.499, the second order Mooney-Rivlin material was implemented for all FEA models. The results of the simulations were post processed and visualized using Ansys EnSight (Ansys Inc., Canonsburg, PA) to generate the first principal stress distributions, from which the three biomechanical parameters (PWS, 99^th percentile wall stress: 99^thWS, and spatially averaged wall stress: SAWS) were computed. Intraluminal thrombus (ILT) was neglected in the biomechanical analysis. While inclusion of ILT in an FEA model can yield a significantly lower PWS,^{24, 27, 31} we chose to calculate the biomechanical parameters based solely on the effect of wall mechanics. This is justified by the fact that all geometry measures are obtained using the coordinates of the AAA wall or the lumen, but not the ILT, as described in section 4.3 and the Supplementary Material.

4.3. AAA Geometry Quantification

Using previously developed in-house MATLAB scripts by Shum et al.,²⁶ we calculated patient specific geometric indices that best assess the shape, size, curvature, and wall thickness of each AAA. The mathematical formulation of these indices is included in the Supplementary Material. Point clouds generated from the segmentation were used to calculate the 1D and 2D indices, while the 3D indices were calculated using the volume and surface meshes. The Biquintic Hermite Finite Element (BQFE) method was employed to compute the curvature based indices, as described in Lee et al.¹⁵ In this method, local curvature distributions are used to evaluate the global curvature indices using a high order interpolation scheme. In contrast to the widely used method of biquadratic surface patching, BQFE discretizes the aneurysm wall into 12 elements. Local principal curvatures k₁ and k₂ are calculated at approximately 1600 nodes within each element using Eqs. (2) and (3),

$$k_1=a+c+\sqrt{{\left(a-c\right)}^2+4b^2}$$ (2)

$$k_2=a+c+\sqrt{{\left(a-c\right)}^2+4b^2}$$ (3)

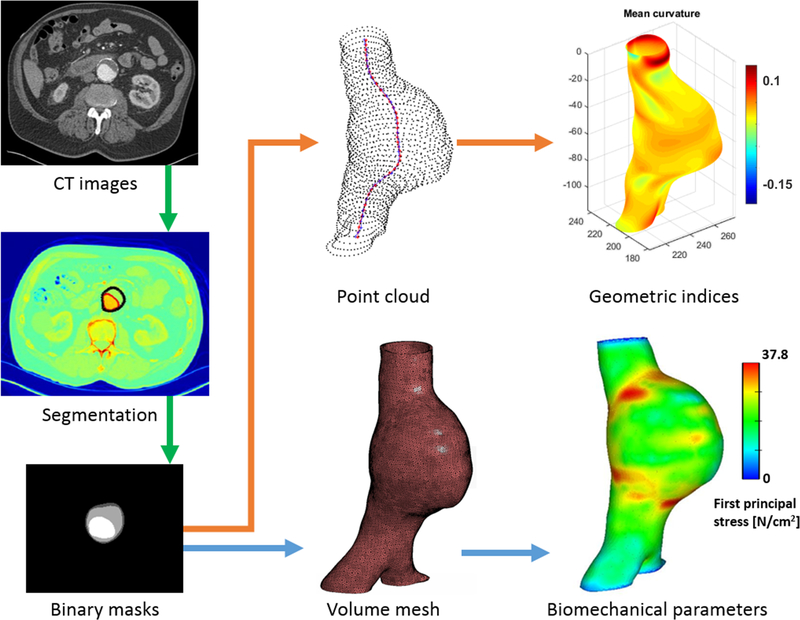
where a, b, and c are constants that best fit the equations for every surface node. The spatial distributions of k₁ and k₂ are used to compute the four global curvature indices using the mathematical formulation described in the Supplementary Material. These are the area averaged Gaussian and Mean curvatures (GAA, MAA), and the L2-norm of the Gaussian and Mean curvatures (GLN, MLN). Figure 1 shows a graphical representation of the work flow followed for image segmentation, volume mesh generation, FEA, and geometry quantification. Noteworthy is that 45 geometric indices were computed for the non-uniform wall thickness models while 32 indices were computed for the uniform wall thickness models. The discrepancy in the number of indices is due to the 13 wall thickness related indices that are valid only when there is a spatially varying wall thickness distribution.

Figure 1:

Schematic of the protocol for segmentation, meshing, and evaluation of the geometric indices and biomechanical parameters.

4.4. Data Analysis

To identify the geometric indices that most correlate with wall stress, a series of tests of hypothesis was carried out. For each j = 1, …, m (where m = 45 or 32) the null hypothesis $H_0^{(j)}:p_j=0$ was tested against the alternative hypothesis $H_a^{(j)}:p_j\ne 0$, where p_j is the population correlation coefficient between the j^th geometric index and wall stress. For each j, the test rejects $H_0^{(j)}$ for large values of T_j, where $T_j=\frac{r_j\sqrt{n-2}}{\sqrt{1-r_j^2}}$, n is the sample size, and r_j as given by Eq. (4),

$$r_j=\frac{{\sum }_{i=1}^n\left(x_{ij}-{\overline{x}}_j\right)\left(y_i-\overline{y}\right)}{{\left({{\sum }_{i=1}^n\left(x_{ij}-{\overline{x}}_j\right).{\sum }_{i=1}^n\left(y_i-\overline{y}\right)}^2\right)}^{\frac{1}{2}}}$$ (4)

which is the sample (Pearson’s) correlation coefficient between the j^th geometric index and wall stress, x_ij describes the j^th geometric index from the i^th patient, ${\overline{x}}_j=\frac{1}{n}{\sum }_{i=1}^n{x}_{ij}$, y_i describes the wall stress parameter (PWS, SAWS, or 99^thWS) for the i^th patient, and $\overline{y}=\frac{1}{n}{\sum }_{i=1}^n{y}_i$. The p-values of these tests are computed from the fact that T_j has a t-distribution with n-2 degrees of freedom when $H_0^{(j)}$ is true.³² When a p-value is lower than a chosen level of significance then the corresponding geometric index is said to have substantially high correlation with the wall stress parameter.

Testing each individual hypothesis using a traditional level of significance α = 0.05 would be inadequate due to a so-called multiple testing problem. If this were done, the type-I error of the overall (combined) test will be substantially larger than the intended significance level.²⁵ Using the Bonferroni correction, this complication can be corrected. Bonferroni correction involves performing the individual tests with a significance level of α^c = α / (number of tests), where α represents the desired overall test significance level. In this study, α^c = 0.05/45 = 0.00111 was used for the non-uniform wall thickness models while α^c = 0.05/32 = 0.00156 was used for the uniform wall thickness models. Therefore, the correlation between a geometric index and a wall stress parameter (PWS, SAWS, or 99^thWS) is considered significant when the corresponding p-value is less than 0.00111 (for non-uniform wall thickness) or 0.00156 (for uniform wall thickness).

The aforementioned protocol allows us to identify the geometric indices that most correlate with wall stress; however, it does not assess the degree of association that may be present between geometric indices. A stepwise regression analysis³² was conducted to eliminate multicollinearity among geometric indices and identify a reduced set of indices that are most strongly correlated with wall stress.

5. RESULTS

5.1. Wall Mechanics

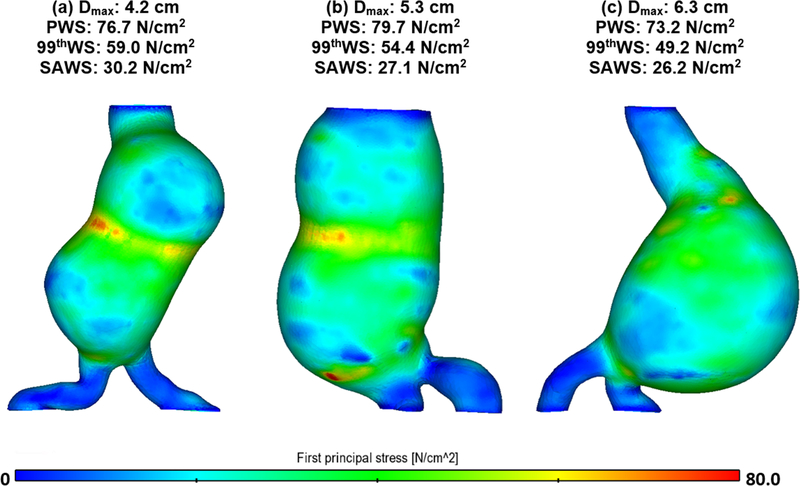
The first principal stress distributions for three exemplary AAA models with non-uniform wall thickness are shown in Fig. 2. The three biomechanical parameters (PWS, 99^thWS and SAWS) are also indicated for each model. The three models have maximum diameters (D_max) that are near the lower and upper limits and mean, respectively, of the range of maximum diameters of the population sample, i.e. 53.0 ± 12.1 mm. It can be seen that the AAA with the smallest D_max (4.2 cm) has the highest 99^thWS and SAWS, and second highest PWS.

Figure 2:

First principal stress map for three exemplary AAA models (non-uniform wall thickness) with (a) small, (b) average, and (c) large maximum diameter. The PWS, 99^thWS and SAWS of each model are also indicated.

The mean PWS for the non-uniform wall thickness models is 76.9 ± 27.7 N/cm² (with a maximum of 183.0 N/cm²), while the AAA models with uniform wall thickness have a mean PWS of 54.5 ± 19.6 N/cm² (with a maximum of 143.0 N/cm²). The mean and maximum 99^thWS for the non-uniform wall thickness AAA are 49.0 ± 16.6 N/cm² and 112.0 N/cm², respectively, while for the uniform wall thickness AAA the mean 99^thWS is 39.5 ± 9.7 N/cm² and the maximum 99^thWS is 69.4 N/cm². The mean and maximum SAWS are 23.2 ± 8.2 N/cm² and 46.3 N/cm², respectively, for the non-uniform wall thickness AAA, and 23.0 ± 5.8 N/cm² and 46.1 N/cm², respectively, for the uniform wall thickness AAA. Table 1 provides a complete summary of all biomechanical parameters and geometric indices.

Table 1:

The mean value, standard error, maximum, and minimum values of all geometric indices and biomechanical parameters (PWS, 99^thWS and SAWS are for the non-uniform wall thickness AAA models while PWS’, 99^thWS’ and SAWS’ are for the uniform wall thickness AAA models). The 13 indices about wall thickness are indicated by “*” and will not be considered in the AAA model with uniform wall thickness.

Geometric Index or Biomechanical Parameter	Mean	SD	Max	Min
Dmax (mm)	53.01	12.06	98.06	24.48
Dave (mm)	42.64	11.18	87.71	20.37
Dmin (mm)	28.54	8.3	51.46	17.22
Dneck,p (mm)	31.24	10.44	85.47	17.71
Dneck,d (mm)	34.65	21.28	103.12	0
H (mm)	99.84	15.24	138	61.5
L (mm)	112.96	19.37	175.12	68.12
Hneck (mm)	28.35	21.96	78	0
Lneck (mm)	34.32	24.65	95.58	0
Hsac (mm)	71.5	21.78	135	27
Lsac (mm)	78.65	25.04	144.63	29.33
Hb (mm)	56.70	19.14	105	20.30
dc (mm)	6.12	5.45	23.71	0.153
Dc,max (mm)	7.62	5.17	23.83	0.771
THmin (mm)*	0.630	0.397	1.67	1.77e-4
THmax (mm)*	4.16	2.85	20.49	1.56
THave (mm)*	1.89	0.917	9.01	0.86
THDmax (mm)*	1.97	1.13	11.01	0.847
THmode (mm)*	1.80	0.661	3.76	0.870
THmedian (mm)*	1.86	0.834	7.83	0.865
THminvar (mm)*	0.029	0.042	0.247	1.32e-3
THmaxvar (mm)*	1.51	3.55	33.95	0.01
THmedianvar (mm)*	0.177	0.485	4.63	5.66e-3
THmodevar (mm)*	0.042	0.061	0.405	1.3e-3
THmeanvar (mm)*	0.31	0.74	7.1	0.011
Pbelow*	50.48	6.31	74.96	35.93
Pabove*	49.52	6.31	64.07	25.04
DHr	0.538	0.139	1.14	0.247
DDr	1.79	0.482	3.55	1.01
Hr	0.277	0.211	0.742	0
BL	0.563	0.160	1	0.232
β	0.890	0.084	0.999	0.665
βmin	0.851	0.079	0.987	0.665
T	1.10	0.062	1.27	101
Cave	1.02	0.02	1.09	1.00
Cmax	1.09	0.07	1.35	1.01
Cmin	1.05	0.05	1.01	1.00
V (cm3)	166.79	103.09	745.39	28.66
S (cm2)	152.61	51.72	366.91	54.59
IPR	5.28	0.43	6.37	3.99
NFI	1.06	0.041	1.17	0.966
GAA (mm−1)	5.51e–05	1.67e–4	5.86e–4	−3.84e–4
MAA (mm−2)	0.028	0.006	0.048	0.015
GLN	2.69	1.08	7.66	0.951
MLN	0.331	0.043	0.548	0.242
PWS (N/cm2)	72.86	27.67	183	23.06
99thWS (N/cm2)	49.04	16.56	112	15.94
SAWS (N/cm2)	23.71	8.23	46.33	8.06
PWS’ (N/cm2)	54.53	19.59	143	18.09
99thWS’ (N/cm2)	39.45	9.65	69.44	16.34
SAWS’ (N/cm2)	22.97	5.76	46.08	10.83

The definition and mathematical formulation of the geometric indices are included in the Supplementary Material, while the biomechanical parameters are defined in section 4.2. The following are the most commonly used acronyms from this table: D_max (maximum transverse diameter); D_neck,p (proximal neck diameter); H_b (bulge height); d_c (distance between the lumen centroid and the centroid of the cross section where D_max is located); TH_Dmax (average wall thickness where D_max is located); TH_minvar (minimum variance of the wall thickness); DHr (diameter-height ratio); β (asymmetry factor); T (tortuosity); C_ave (average lumen compactness); IPR (isoperimetric ratio); NFI (non-fusiform index); GAA (area averaged Gaussian curvature).

5.2. Association between Biomechanical Parameters and Geometric Indices

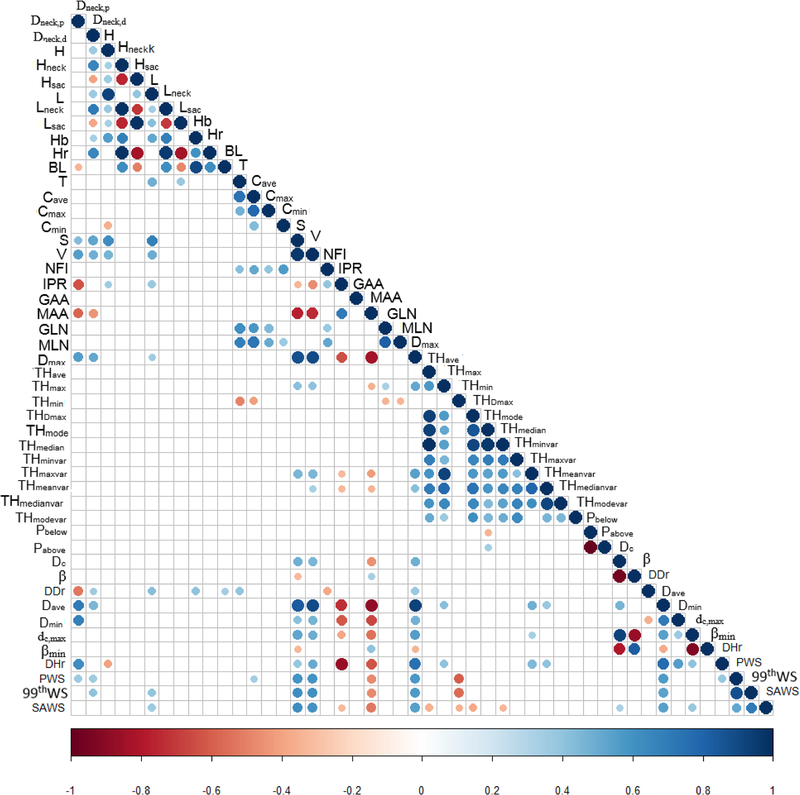
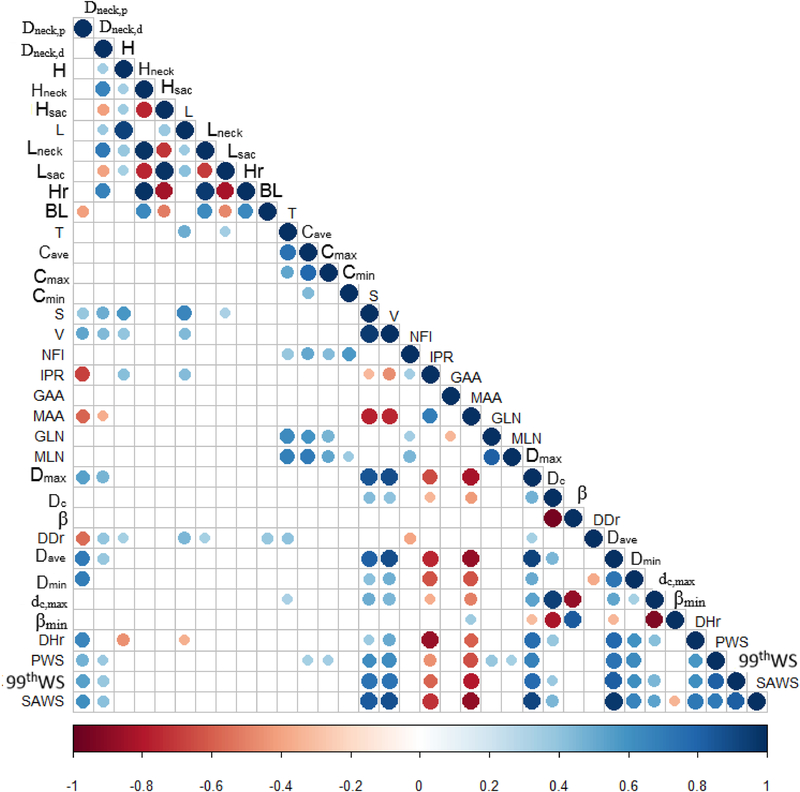
Correlation matrices were used to illustrate the calculated Pearson’s correlation coefficients for all possible pairs of geometric indices and biomechanical parameters, as Figs. 3 and 4 show. The correlation coefficients between any two variables are judged by the size and color of the circular dot in the matrices. For the non-uniform wall thickness models (Fig. 3), indices with p-values greater than 0.00111 were considered non-significant and the corresponding dots in the matrix entries are absent. Similarly, for the uniform wall thickness models (Fig. 4), matrix entries with absent dots correspond to p-values greater than 0.00156. Based on the remaining dots in the matrices, the geometric indices significantly correlated with PWS, 99^thWS, and SAWS are summarized in Table 2 (non-uniform wall thickness models) and Table 3 (uniform wall thickness models). In Table 2, 10 indices (D_neck,p, D_neck,d, C_ave, S, V, MAA, D_max, D_ave, TH_min, and DHr) were found to have a significant correlation with PWS; whereas for 99^thWS, 8 indices (D_neck,d, L, S, V, MAA, D_max, D_ave, and TH_min) were found to have a significant correlation. Similarly, SAWS is significantly correlated with 13 indices (L, S, V, IPR, MAA, D_max, D_ave, TH_ave, TH_min, TH_Dmax, TH_median, d_c, and d_c,max). In Table 3, 14 indices (D_neck,p, D_neck,d, C_ave, C_max, S, V, IPR, MAA, GLN, MLN, D_max, D_ave, D_min, and DHr) were found to be significantly correlated with PWS. Likewise, 12 indices (D_neck,p, D_neckd, S, V, IPR, MAA, D_max, d_c, D_ave, D_min, d_c,max, and DHr) are strongly correlated with 99^thWS while 13 indices (D_neck,p, D_neckd, S, V, IPR, MAA, D_max, d_c, D_ave, D_min, d_c,max, DHr, and β_min) are strongly correlated with SAWS.

Figure 3:

Correlation matrices for all pairs of geometric indices / biomechanical parameters for the non-uniform wall thickness AAA models. The size and color of the circles indicate the value of the correlation coefficients in the interval [−1, 1]. The correlation between two indices / parameters is more significant when the color is closer to the warm or cold ends of the scale with a large circle. Non-significant correlations are excluded when p > 0.00111 (as indicated by the absence of circles in the empty cells of the matrix). The test for significance follows the application of the Bonferroni correction given the large number of covariates measured for each AAA. The geometric indices that are significantly correlated with PWS, 99^thWS, and SAWS, are included in Table 2.

Figure 4:

Correlation matrices for all pairs of geometric indices / biomechanical parameters for the uniform wall thickness AAA models. Non-significant correlations are excluded when p > 0.00156 (as indicated by the absence of circles in the empty cells of the matrix). The test for significance follows the application of the Bonferroni correction given the large number of covariates measured for each AAA. The geometric indices that are significantly correlated with PWS, 99^thWS, and SAWS, are included in Table 3.

Table 2:

Pearson’s correlation coefficients and p-values for the relationships of PWS, 99^thWS, SAWS with the corresponding significantly correlated geometric indices for the non-uniform wall thickness AAA models. The superscripts ^a, ^b, ^c, ^d and ^e indicate geometric indices that were excluded following the analysis illustrated in Figure 5 in accordance to index pairs that were highly correlated.

Geometric index	PWS		99thWS		SAWS
	Correlation coefficient	p-value	Correlation coefficient	p-value	Correlation coefficient	p-value
Dneck,p	0.366	0.00021	−	−	−	−
Dneck,d	0.359	0.00028	0.383	0.00010	−	−
Cave	0.349	0.00043	−	−	−	−
L	−	−	0.392	<< 0.00111	0.365	0.00022
S	0.591a	<< 0.00111	0.615a	<< 0.00111	0.610	<< 0.00111
V	0.597	<< 0.00111	0.607	<< 0.00111	0.600a	<< 0.00111
IPR	−	−	−	−	−0.326	0.00106
MAA	−0.475	<< 0.00111	−0.474	<< 0.00111	−0.526	<< 0.00111
Dmax	0.577	<< 0.00111	0.563	<< 0.00111	0.548b	<< 0.00111
Dave	0.567b	<< 0.00111	0.530b	<< 0.00111	0.549	<< 0.00111
THave	−	−	−	−	−0.359c	0.00028
THmin	−0.603	<< 0.00111	−0.570	<< 0.00111	−0.351	0.00039
THmax	−	−	−	−	−0.383	0.00010
THmedian	−	−	−	−	−0.331d	0.00087
dc	−	−	−	−	0.329e	0.00095
dc,max	−	−	−	−	0.383	0.00010
DHr	0.383	<< 0.00111	−	−	−	−

Table 3:

Pearson’s correlation coefficients and p-values for the relationships of PWS, 99^thWS, SAWS with the corresponding significantly correlated geometric indices for the uniform wall thickness AAA models. The superscripts ^a, ^b, ^e and ^f indicate geometric indices that were excluded following the analysis illustrated in Figure 5 in accordance to index pairs that were highly correlated.

Geometric index	PWS		99thWS		SAWS
	Correlation coefficient	p-value	Correlation coefficient	p-value	Correlation coefficient	p-value
Dneck,p	0.477	<< 0.00156	0.545	<< 0.00156	0.617	<< 0.00156
Dneck,d	0.375	0.000119	0.405	<< 0.00156	0.416	0.0000167
Cave	0.331	0.000763	−		−	−
Cmax	0.347	0.000398	−		−	−
S	0.620a	<< 0.00156	0.765a	<< 0.00156	0.830a	<< 0.00156
V	0.628	<< 0.00156	0.769	<< 0.00156	0.874	<< 0.00156
IPR	0.457	<< 0.00156	−0.610	<< 0.00156	−0.727	<< 0.00156
MAA	−0.647	<< 0.00156	−0.825	<< 0.00156	−0.885	<< 0.00156
GLN	0.384	<< 0.00156	−	−	−	−
MLN	0.339	0.000559	−	−	−	−
Dmax	0.672b	<< 0.00156	0.830 b	<< 0.00156	0.910b	<< 0.00156
dc	−	−	0.365 c	<< 0.00156	0.458e	<< 0.00156
Dave	0.730	<< 0.00156	0.872	<< 0.00156	0.960	<< 0.00156
Dmin	0.633	<< 0.00156	0.602	<< 0.00156	0.665	<< 0.00156
Dc,max	−	−	0.479	<< 0.00156	0.531	<< 0.00156
βmin	−	−	−	−	−0.346f	0.000415
DHr	0.582	<< 0.00156	0.656	<< 0.00156	0.719	<< 0.00156

5.3. Filtering out Strongly Correlated Geometric Indices

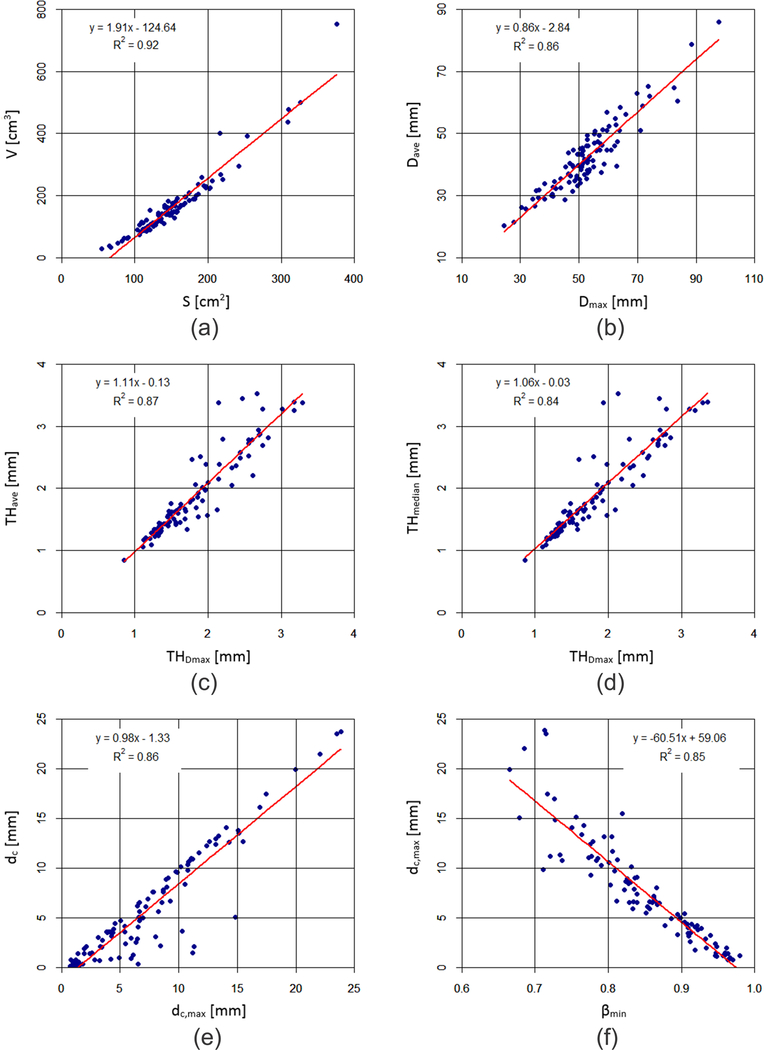
The correlation matrices also show that some geometric indices, which are significantly correlated to the same biomechanical parameter, exhibit strong correlations between themselves (defined by having a correlation coefficient |r| > 0.9). These pairs of indices were used for linear regression analyses, as shown in Fig. 5. It can be seen that the coefficients of determination (R²) between the following pairs: V and S, D_ave and D_max, TH_Dmax and TH_ave, TH_Dmax and TH_median, d_c and d_c,max, and d_c,max and β_min, are all greater than 0.84. Therefore, the geometric index from each pair exhibiting the smaller |r| in the correlation with each biomechanical parameter was removed before performing the subsequent stepwise regression analysis.

Figure 5:

Correlations between (a) V and S, (b) D_ave and D_max, (c) TH_Dmax and TH_ave, (d) TH_Dmax and TH_median, (e) d_c and d_{c_max}, and (f) β_min and d_c,max. For each pair, the correlation coefficient is high (|r| > 0.9 or R² > 0.81), such that one of the two indices can be ignored in the regression analyses described in Tables 2 and 3 with the superscripts ^a, ^b, ^c, ^d, ^e and ^f.

5.4. Stepwise Regression Analysis

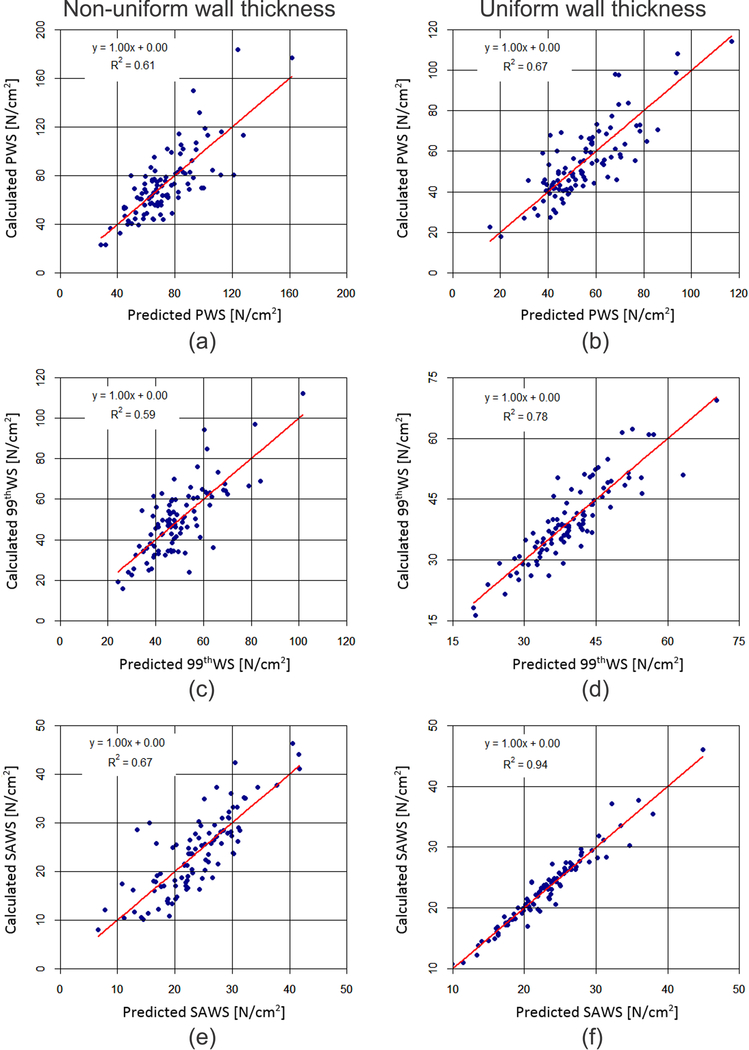
Stepwise regression analyses³² were performed with the filtered geometric indices listed in Tables 2 and 3 and each of the biomechanical parameters. The outcome of these analyses is shown in Table 4, along with the corresponding regression coefficients and standard errors of the regression residuals. The stepwise regressions were used to create biomechanical parameters “predicted” by the statistically significant geometric indices shown in Table 4, which were then compared to the “calculated” biomechanical parameters (obtained from FEA) to test the prediction accuracy. Figure 6 illustrates this comparison; for the non-uniform wall thickness models, TH_min, V, D_neck,d, and D_neck,p were the most significant predictors of PWS, while TH_min, V, and D_neck,d were the predictors of 99^thWS, and TH_Dmax, IPR, L, and TH_min the predictors of SAWS. The stepwise regression for SAWS had the highest coefficient of determination (0.67) with a standard deviation of 4.8 N/cm². For the uniform wall thickness models, five indices predicted PWS accurately (D_ave, MLN, D_min, MAA, and C_max), three indices were predictors of 99^thWS (D_ave, MAA and IPR), and five indices were found to be good predictors of SAWS (D_ave, MAA, V, D_neck,p, and IPR). SAWS also had the highest coefficient of determination (0.94) with a standard deviation of 1.4 N/cm².

Table 4:

The significantly correlated geometric indices with PWS, 99^thWS, and SAWS obtained by stepwise regression for the non-uniform and uniform wall thickness AAA models. The regression coefficients and standard errors of the regression residual are also indicated.

Biomechanical parameter	Non-uniform wall thickness		Uniform wall thickness
	Geometric index and its regression coefficient	Standard error of regression residual [N/cm2]	Geometric index and its regression coefficient	Standard error of regression residual [N/cm2]
PWS	THmin (−37.23) V (0.0752) Dneck.d (0.2645) Dneck,p (0.4655)	17.6	Dave (0.6217) MLN (133.94) Dmin (0.5798) MAA (−640.32) Cmax (29.44)	11.5
99thWS	THmin (−20.19) V (0.064) Dneckd (0.1518)	10.8	Dave (0.6267) MAA (−452.30) IPR (2.865)	4.5
SAWS	THDmax (−6.2716) IPR (−13.66) L (0.2448) THmin (−3.0379)	4.8	Dave (0.3086) MAA (−172.9) V (0.0120) Dneck,p (−0.0580) IPR (−1.682)	1.4

Figure 6:

Calculated (a, b) PWS, (c, d) 99^thWS, and (e, f) SAWS as a function of their predicted counterparts for the non-uniform wall thickness AAA models (left column) and uniform wall thickness AAA models (right column). The calculated biomechanical parameters are obtained from FEA while the predicted ones are obtained from the stepwise regression analyses using the regression coefficients of Table 4.

6. DISCUSSION

In the present study, three global metrics of wall stress (PWS, 99^thWS, and SAWS) derived from two types of patient specific AAA models (with spatially uniform and non-uniform wall thickness) were calculated to interrogate the relationship between geometric and biomechanical measures in electively repaired AAA. To the best of our knowledge, this is the first comprehensive study of its kind in a population group deemed clinically “at risk” for rupture due to its size or growth rate. With the finding of a relationship between geometry and biomechanics, the highly correlated geometric indices can be envisioned as surrogates for wall stress, which could then be used for subsequent rupture risk assessment following a purely geometric modeling approach.

It was observed that the variation of PWS amongst the individual AAA (23.1 – 183.0 N/cm² for non-uniform wall thickness and 18.1 – 143.0 N/cm² for uniform wall thickness), was greater compared to 99^thWS (15.9 – 112.0 N/cm² for non-uniform wall thickness and 16.3 – 69.4 N/cm² for uniform wall thickness) and SAWS (8.1 – 46.3 N/cm² for non-uniform wall thickness and 10.8 – 46.1 N/cm² for uniform wall thickness). The unusually high values of PWS (> 100 N/cm²) likely originated from isolated regions of the volume mesh exhibiting elements with high aspect ratios. The other biomechanical parameters are not influenced by these regions, since 99^thWS neglects the top 1% of wall stresses and SAWS represents a mean stress averaged over the surface area of each element in the mesh. This observation is in agreement with the rationale for calculating 99^thWS for rupture risk assessment, as originally proposed by Speelman and colleagues.³⁰

The outcome of the stepwise regression analyses for the non-uniform wall thickness models revealed that the minimum wall thickness (TH_min) was a strong predictor of all three biomechanical parameters. PWS, 99^thWS, and SAWS were negatively correlated with TH_min, which can be explained by the fact that rupture (likely where the highest wall stress to strength ratio exists) occurs where the wall is thinnest, as Raghavan and co-workers found in an autopsy study.²¹ AAA size also plays a role in predicting wall stress; 1D and 3D size indices D_neck,p, D_neck,d, and V were positively correlated with PWS and 99^thWS. Lederle et al.¹⁴ conducted a prospective, observational study in patients refusing or unfit for elective repair and observed that larger AAA are at higher risk of rupture. In a previous study performed with ruptured AAA, D_max was found to be one of the predictors of wall stress.⁵ However, in the present work, the significant predictors of wall stress (by stepwise regression analysis) are not inclusive of D_max for any of the biomechanical parameters. We infer from this that D_max appears to have a lesser influence on wall stress for asymptomatic, unruptured AAA compared to symptomatic, ruptured AAA. This could be explained by the relatively smaller variation of maximum diameters characterizing electively repaired AAA in contrast with the wide range of aneurysm sizes found in emergently repaired AAA.⁵ SAWS was found to be sensitive to size, shape, and wall thickness indices. The strongest predictor of SAWS was IPR, which is a 3D shape index that quantifies the degree of folding of the surface area. TH_Dmax was also strongly and negatively correlated with SAWS, while the 1D size index L completed the SAWS stepwise regression model for non-uniform wall thickness AAA. L and TH_Dmax were also strong predictors of SAWS for emergently repaired AAA, as reported by Chauan et al.⁵ Therefore, wall thickness, shape and size indices play a major role in predicting SAWS for electively repaired AAA when spatially distributed wall thicknesses are used for the geometric model.

The outcome of the stepwise regression analyses for the uniform wall thickness models revealed that the average diameter (D_ave) and the area averaged mean curvature (MAA) were strong predictors of all three biomechanical parameters. Since wall thickness in these models is assumed to be a uniform 1.5 mm, size and shape indices play major roles as predictors of wall stress. PWS, 99^thWS, and SAWS were negatively correlated with MAA, which was also the strongest predictor in the regression models. The mean curvature is the arithmetic mean of the principal curvatures (k₁ and k₂) evaluated at each mesh node. MAA is a global index calculated as the area-weighted sum of the mean curvatures at each outer wall face of the mesh elements. Therefore, higher wall stresses are predicted by non-zero, low values of MAA; non-zero mean curvatures indicate the AAA wall has curvature (concave or convex) in at least one of the principal directions. Shape related indices are better predictors of the three biomechanical parameters than size related indices. This is evident by the larger regression coefficients obtained for MAA, MLN, IPR, and C_max, in contrast to D_ave, D_min, V, and D_neck,p. Such finding is in agreement with the observations by Giannoglou et al.,⁹ who reported shape and curvature based indices as metrics for rupture risk assessment.

The higher coefficients of determination of the stepwise regression models for the uniform wall thickness AAA should not be interpreted as these models having a higher accuracy than those for the non-uniform wall thickness AAA. They are not directly comparable to each other as 13 additional geometric indices (all wall thickness related) were used as potential surrogates of wall stress when AAA were modeled with their patient specific wall stress distributions. For example, TH_min, V, D_neck,d, and D_neck,p can predict PWS for non-uniform wall thickness models while explaining 61% of the variance in the data collected from the 100 AAA. Likewise, D_ave, MLN, D_min, MAA, and C_max predict PWS for uniform wall thickness models while explaining 67% of the variance in the data. Similar statements can be made for 99^thWS and SAWS. As previous studies estimate rupture risk by calculating PWS or some other equivalent measure of wall stress,^{7, 13, 17, 33} it becomes important to have prior knowledge of the patient specific material properties and access to complex FEA tools. Geometric indices highly correlated to stress measures such as PWS, 99^thWS, and SAWS, could be used for rupture risk assessment without the need for complex FEA software or knowledge of patient specific material properties. To this end, prediction of wall stresses using geometric indices resulted in R² values of 60% and 74% for idealized¹⁹ and emergently⁵ repaired AAA, respectively. In the present work, the SAWS regression model for uniform wall thickness AAA explains 94% of the variance in the data when D_ave, MAA, V, D_neck,p, and IPR are used as surrogates of this biomechanical parameter.

This study is subject to several important limitations. There is suspected intra-observer variability in the segmentation of the clinical images, although its effect on the geometric indices was not quantified. There is also variability in the pixel size of the images. In this regard, the wall thickness calculation is limited by the pixel size and the intensity gradient across the vascular wall; the larger the pixels, the less precise is the wall thickness prediction. The exclusion of ILT in the FEA models is another limitation, which bounds the results of the study to stresses predicted only by wall mechanics. This likely yields an over-prediction of PWS, 99^thWS, and SAWS as ILT tends to act as a buffer from the normal forces caused by blood pressure. In addition, the zero-pressure state of stress and residual stresses of the AAA models were not calculated as part of the FEA modeling approach. The justification for this is that obtaining modified AAA finite element meshes as a result of estimating the zero-pressure geometries would have led to aneurysm shapes different than those from which the geometric indices were calculated. The use of mathematical formulations for the quantification of 45 geometric indices a priori is another limiting aspect of our geometry quantification approach. There could be shape measures important for differentiation amongst individual AAA that are not taken into account by our methodology and could be predicted by using other techniques that quantify, for example, cylindrical harmonics. Moreover, the regression analyses were limited to the use of measures of geometry and wall mechanics. These can be improved in a future study by including additional measures such as tissue composition metrics (such as those obtained from immunohistochemistry), which would be subject to the availability of AAA wall specimens for subsequent histological analysis. Finally, the Bonferroni correction applied to the 45 (for non-uniform wall thickness) and 32 (for uniform wall thickness) possible correlations of geometry and wall stress could be over-conservative, thus possibly leading to some correlations being excluded.

Based on a comprehensive quantification of geometric indices and biomechanical parameters for 100 asymptomatic, electively repaired AAA, three measures of wall stress, namely PWS, 99thWS and SAWS, were found to be strongly correlated with up to five geometric indices depending on the choice of uniform or non-uniform wall thickness distributions. The most promising outcome was the multiple regression model for SAWS for AAA uniform wall thickness, which yielded an accuracy of 94% with a residual error of 1.4 N/cm². Stepwise regression models can be useful tools to provide estimates of wall stress based on patient specific geometry measures.