Synaptic Mechanisms for Bandwidth Tuning in Awake Mouse Primary Auditory Cortex

Abstract

Spatial size tuning in the visual cortex has been considered as an important neuronal functional property for sensory perception. However, an analogous mechanism in the auditory system has remained controversial. In the present study, cell-attached recordings in the primary auditory cortex (A1) of awake mice revealed that excitatory neurons can be categorized into three types according to their bandwidth tuning profiles in response to band-passed noise (BPN) stimuli: nonmonotonic (NM), flat, and monotonic, with the latter two considered as non-tuned for bandwidth. The prevalence of bandwidth-tuned (i.e., NM) neurons increases significantly from layer 4 to layer 2/3. With sequential cell-attached and whole-cell voltage-clamp recordings from the same neurons, we found that the bandwidth preference of excitatory neurons is largely determined by the excitatory synaptic input they receive, and that the bandwidth selectivity is further enhanced by flatly tuned inhibition observed in all cells. The latter can be attributed at least partially to the flat tuning of parvalbumin inhibitory neurons. The tuning of auditory cortical neurons for bandwidth of BPN may contribute to the processing of complex sounds.

Introduction

In the mammalian auditory system, complex sound signals are first decomposed by narrow frequency filters, a process similar to that performed by a frequency analyzer (Kiang 1968). At a certain neuronal processing stage, signals from these lower-order frequency filters need to be integrated by higher-order neurons for auditory object recognition (Suga 1988, 1992; Doupe 1997; Rauschecker 1998b; Griffiths et al. 2004; Nelken 2008). Frequency integration can be effectively assessed with band-passed noise (BPN) stimuli, which can be well defined by a center frequency (CF) and bandwidth. BPN bursts are fundamental elements of many natural sounds, including those used for animal communications (Hauser 1996; Rauschecker and Tian 2000; Wang 2000; Wang and Kadia 2001; Akimov et al. 2017).

Previously, neuronal responses to BPN have been reported in the auditory cortex of anesthetized rhesus monkeys (Rauschecker et al. 1995; Rauschecker and Tian 2004). It has been found that neurons in the core areas (e.g., primary auditory cortex) in general have stronger responses to pure tones than BPN bursts, whereas those in lateral belt areas have more robust responses to BPN bursts than pure tones (Rauschecker and Tian 2004). In addition, the latter neurons usually exhibit a preference to certain bandwidths of BPN bursts. In other words, they are tuned for bandwidth. These neurons are thought to be analogous to size-tuned cells in the visual cortex (Hubel and Wiesel 1965; Desimone and Schein 1987; DeAngelis et al. 1994; Gilbert et al. 1996; Nolt et al. 2004; Angelucci and Bressloff 2006; Adesnik et al. 2012), and may form an important stage in the preprocessing of communication sounds (Rauschecker et al. 1995). However, due to the use of anesthetized animals and concerns over the design of testing BPN stimuli in those previous studies, it remains unclear whether bandwidth-tuned neurons are present in awake auditory cortex including the primary auditory cortex.

In this study, we examined bandwidth tuning in the primary auditory cortex (A1) of awake mice, using in vivo cell-attached recording. We found that bandwidth-tuned neurons are present in A1 and are more prevalent in layer 2/3 than layer 4. Using sequential cell-attached and whole-cell voltage-clamp recordings, we further revealed the synaptic mechanisms underlying bandwidth tuning. By dissecting excitatory and inhibitory inputs to layer 2/3 neurons, we found that excitation exhibits variable tuning profiles, including nonmonotonic (NM), flat, and monotonic (M), whereas inhibition ubiquitously displays flat tuning. The tuning property of the cell is thus inherited from the excitatory input it receives, while the universally flat inhibition plays an important role in enhancing bandwidth selectivity. Our study has, for the first time to our knowledge, elucidated the synaptic mechanisms for bandwidth tuning of auditory cortical neurons.

Materials and Methods

Experiments were carried out in the University of Southern California. Experimental procedures used in this study were approved by the Animal Care and Use Committee at the University of Southern California.

Animal Preparation

C57BL/6 J mice of both genders aged 2–3 months were used. Animals for awake recordings were prepared in a similar way as we previously described (Zhou et al. 2014; Xiong et al. 2015). Mice were housed with a 12-h light/dark cycle. A few days before the recording, the mouse was anesthetized with isoflurane (1.5%, vol/vol) and a screw for head fixation was mounted on top of the skull with dental cement. Skull over the A1 was cleaned and protected from being covered by dental cement. During the recovery period, the mouse was trained to get accustomed to the head fixation on the recording setup. To fix the head, the screw was tightly clamped by a custom-made post holder. The head-fixed animal was able to run freely on a rotatable flat plate mounted on an optical shaft encoder (US Digital). For recording carried out in a sound-attenuation booth (Acoustic Systems), the mouse was briefly anesthetized with isoflurane as to perform a craniotomy over the A1. The animal was then left to recover from isoflurane for at least 2 h. Recording experiments were started after the animal exhibited normal running. Each recording session lasted for ~4 h. The animal was given drops of 5% sucrose (wt/vol) through a pipette every hour. Between sessions, animals were returned to the home cage for a break of at least 2 h.

For recording auditory responses, sound stimuli were delivered through a calibrated open field speaker (Denmark D2905/97000) positioned 10 cm from mouse head and facing the left ear. Multiunit recordings were first made with a tungsten electrode (2 MΩ, FHC, Inc.) to determine the best frequency for an array of recording sites. The A1 was identified based on response properties and the tonotopic gradient of best frequencies, as described in previous studies (Zhang et al. 2001, 2002; Chang and Merzenich 2003; Sun et al. 2010; Li et al. 2014, 2015; Zhou et al. 2014). The animal head was tilted so that the electrode could penetrate the A1 surface at an angle of 80°.

In Vivo Blind Loose-Patch and Whole-Cell Recordings

Loose-patch and cell-attached followed by whole-cell recordings were made with an Axopatch 200B amplifier (Molecular Devices) as previously described (Poo and Isaacson 2009; Xiong et al. 2013; Zhou et al. 2014; Li et al. 2015). The patch pipette, controlled by a micromanipulator (Siskiyou), was lowered into the A1 at the same angle as in multiunit recordings. The cortical surface was covered with 3.5% agar prepared in warm artificial cerebrospinal fluid (ACSF; 124 mM NaCl, 1.2 mM NaH₂PO4, 2.5 mM KCl, 25 mM NaHCO₃, 20 mM glucose, 2 mM CaCl₂, 1 mM MgCl₂). Loose-patch recording (with 100–500 MΩ seal) was performed with a patch pipette (impedance of 5–7 MΩ) filled with ACSF. Pipette capacitance was fully compensated. Signals were recorded in voltage-clamp mode at 20 kHz, with a command voltage applied to adjust the baseline current to be 0. If a cell did not exhibit spontaneous spikes within 10 min, it was not further recorded.

For whole-cell voltage-clamp recordings, patch pipette (impedance of 4–5 MΩ) contained a cesium-based solution: 125 mM cesium gluconate, 5 mM TEA-Cl, 4 mM MgATP, 0.3 mM GTP, 10 mM phosphocreatine, 10 mM HEPES, 10 mM EGTA, 2 mM CsCl, 1.5 mM QX-314, 1% biocytin (wt/vol), or 0.25 mM fluorescent dextrans, pH = 7.3. Signals were low-pass filtered at 2 kHz and sampled at 10 kHz. Sequential cell-attached and whole-cell recordings were applied as previously described (Poo and Isaacson 2009; Sun et al. 2010). The sound-evoked and spontaneous spikes of the patched neuron were first recorded before breaking in the membrane to determine its spike response properties. A cell was not further recorded if it did not exhibit spontaneous spikes within 10 min. After forming a whole cell, whole-cell capacitance was fully compensated and the initial series resistance (Rs, 15–50 MΩ) was compensated for 40–50% to achieve an effective Rs of 10–30 MΩ. A −10-mV junction potential was corrected. Excitatory and inhibitory synaptic currents were recorded by clamping the cell at −70 mV and 0 mV, respectively. As demonstrated previously (Li et al. 2014; Liu et al. 2010; Sun et al. 2010), the blind whole-cell recording method with relatively large pipette openings resulted in almost exclusive sampling from excitatory cortical neurons.

The recording sites in relation to the tonotopic gradient of A1 were marked. The laminar locations of the recorded neurons were determined based on the micromanipulator reading, and in some cases confirmed by histology of the track of pipette penetration and/or fluorescence-dextran or biocytin labeled cell bodies. We found a relatively good correspondence between the traveling depth of the recording pipette from the pia and the reconstructed laminar location of the recorded neuron (Li et al. 2014; Zhou et al. 2014). The L2/3 neurons were sampled at a cortical depth of 175–325 μm from the pial surface, L4 neurons at a depth of 350–500 μm, following previous studies (Li et al. 2014; Zhou et al. 2014).

Optogenetically Guided Loose-Patch Recordings from PV Neurons

We expressed ChR2 in PV neurons through delivery of viral vectors (Li et al. 2013a, 2014). Adult PV-Cre (Jackson Laboratory) mice were anesthetized with 1.5% isoflurane. A small cut was made on the skin covering the right A1 and the muscles were removed. Two ~0.2-mm craniotomies were made in the A1 region (temporal lobe, 2.7 and 3.2 mm caudal to Bregma). Adeno-associated viruses (AAVs) encoding Cre-dependent ChR2 were purchased from the University of Pennsylvania Viral Vector Core: AAV2/9.EF1α.DIO.hChR2(H134R)-EYFP.WPRE.hGH (Addgene 20298). The virus was delivered using a beveled glass micropipette (tip diameter, ~40 μm) attached to a microsyringe pump (World Precision Instruments). Injections were performed at two locations and two depths (300 and 600 μm), at a volume of 100 nl per injection and at a rate of 20 nl min⁻¹. Right after each injection, the pipette was allowed to rest for 4 min before withdrawal. We then sutured the scalp, injected buprenorphine at 0.1 mg per kg and returned the mouse to its home cage. Mice were allowed to recover for 3–4 weeks.

On the day of recording, loose-patch recordings using pipettes of smaller tip openings (pipette impedance, ~10 MΩ) (Li et al. 2013a; Zhou et al. 2014) were performed. An optic fiber connecting to a blue LED source (470 nm, Thorlabs) was positioned close to the cortical surface of the recording site. We actively searched for neurons exhibiting LED-evoked spikes with the loose-patch recording paradigm, which were identified as PV neurons. After each experiment, that brain was sectioned and imaged to further confirm the expression of ChR2-EYFP.

Sound Generation

Software for sound stimulation was custom-developed in LabVIEW (National Instruments). For determining the CF of each cell, pure tones (2–64 kHz spaced at 0.1 octave, 50-ms duration, 3-ms ramp, 10–70 dB sound pressure level (SPL), three repetitions) were delivered in a pseudo-random sequence at 0.5-s inter-stimulus interval. For BPN stimulation, white noise (100 ms duration, 5 ms rise/fall time, 200 kHz sampling rate) was first generated by a Noise function in LabView. It was then band-pass filtered with different cutoff frequencies, which were determined by different center frequencies and bandwidths, to generate BPN bursts. All BPN bursts with different center frequencies (2–32 kHz spaced at 0.1 octave) and bandwidths (0.1–1.9 octave spaced at 0.2 octave) were pre-calibrated to 60 dB SPL, and the calibration indices for all bursts were saved as a LabView array for further BPN sound level calculation. After the CF of the cell was determined, the BPN bursts with the same CF were automatically calibrated based on the calibration indices array and were then delivered in a random sequence at 2-s inter-stimulus interval. Such calibration was not performed for stimuli in which the spectral intensity was kept the same. Since the CF of a cell was determined first before applying BPN, our stimulation strategy might lead to underrepresentation of neurons that did not respond robustly to pure tones while still responding strongly to BPN bursts.

Data Analysis

We performed data analysis with custom-developed software (MATLAB, MathWorks). Data from all the recorded neurons were first pooled together for a randomized batch processing without categorizing the neurons according to their specific identity (e.g., age, condition, laminar location, etc.).

Spike Responses

In cell-attached recordings, spikes could be detected without ambiguity because their amplitudes were normally higher than 50 pA, whereas the baseline fluctuation was <5 pA. BPN-evoked spikes were counted within a 0–100-ms time window after the onset of stimuli. Evoked firing rate (FR) was calculated after subtracting the average baseline FR.

Synaptic Responses

Synaptic response traces evoked by the same stimulus were averaged. Synaptic onset latency was determined at the time point where the evoked current exceeded the average baseline by two standard deviations. Peak amplitude was determined by averaging within a 5-ms window centered at the response peak after subtracting the baseline current. Excitatory and inhibitory synaptic conductances were derived according to ΔI = Ge (V − Ee) + Gi (V − Ei) (Borg-Graham et al. 1998; Sun et al. 2010; Xiong et al. 2013; Li et al. 2013a, 2014; Zhou et al. 2014). ΔI is the amplitude of the synaptic current at any time point after subtracting the average baseline current; Ge and Gi are the excitatory and inhibitory synaptic conductance; V is the holding voltage, and Ee (0 mV) and Ei (−70 mV) are the reversal potentials. The clamping voltage V was corrected from the applied holding voltage (Vh): V = Vh – Rs ∗ I, where Rs is the effective series resistance. By holding the recorded cell at two different voltages (the reversal potentials for excitatory and inhibitory current respectively), Ge and Gi could be resolved from the equation. Resting conductance was calculated based on the average baseline currents within a 50-ms window before the onset of evoked currents recorded under two different voltages (−70 mV and 0 mV).

Modeling

The synaptic responses in layer 2/3 excitatory neurons were simulated by the following function (Zhang et al. 2003; Zhou et al. 2010, 2012):

$$G(t)=a\cdot H(t-t_0)\cdot \left(1-{\mathrm{e}}^{-(t-t_0)/{\tau }_{rise}}\right)\cdot {\mathrm{e}}^{-(t-t_0)/{\tau }_{decay}}$$

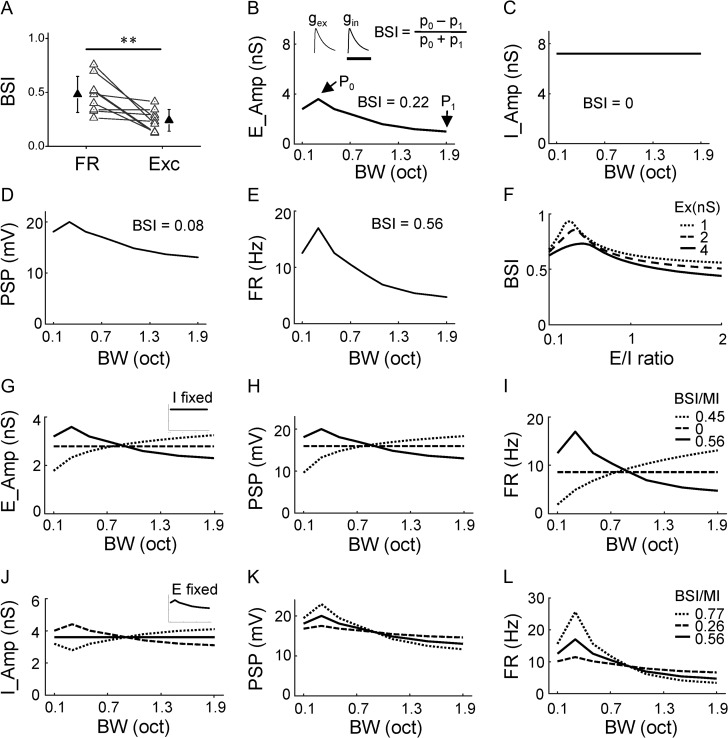
G(t) is the modeled synaptic conductance; a is the amplitude factor; H(t) is the Heaviside step function; t₀ is the onset delay of excitatory or inhibitory input. τ_rise and τ_decay define the shape of the rising phase and the decay of the synaptic current. The τ_rise (excitation: 2 ms; inhibition: 2 ms) and τ_decay (excitation: 40 ms; inhibition: 40 ms) were chosen by fitting the average shape of recorded synaptic responses with the above function. The t₀ (excitation: 0 ms; inhibition: 2 ms) and a were chosen based on our experimental data. The actual conductance amplitude was varied based on the simulation condition. The baseline condition is shown in Fig. 5B: excitation peaks at 3.6 nS (at 0.3 octave) and then becomes reduced with bandwidth increases (down to 2.3 nS at 1.9 octave), while inhibition is fixed at 3.6 nS across different bandwidths.

Figure 5.

Impacts of different tuning shapes of synaptic inputs. (A) Comparison of BSI between spike response (FR) and excitatory input (Exc) of the same cell. Data points for the same cell are connected with a line. ***P < 0.001, paired t-test, n = 9. (B) Tuning curve for the simulated excitation. P₀ points to the maximum response. P₁ points to the response at the broadest bandwidth. The BSI value is marked. Top inset, temporal profiles of simulated synaptic excitation (g_ex), inhibition (g_in) evoked by a stimulus. Scale: 100 ms. (C) Tuning curve for the simulated inhibition. (D) Tuning of peak PSP response resulting from integrating the excitation and inhibition shown in (B, C). (E) Tuning of firing rate derived from PSP using a power-law algorithm. (F) Dependence of BSI on the absolute amplitude of excitation (represented by different types of lines) and E/I ratio (as measured at P₀). (G–I) Varying the tuning shape of excitation while fixing the tuning of inhibition (inset), and derived tuning of resulting PSP response (H) and tuning of resulting firing rate response (I). Corresponding BSI (or MI) values are marked. (J–L) Varying the tuning shape of inhibition while fixing the tuning of excitation (inset), and derived tuning of resulting PSP response (K) and tuning of resulting firing rate response (L).

Membrane potential responses were derived from the simulated excitatory and inhibitory conductances based on an integrate-and-fire neuron model (Sun et al. 2010; Zhou et al. 2010):

$$\begin{array}{c}{V}_m(t+dt)=-\frac{dt}{C}[G_e(t)\ast (V_m(t)-E_e)+G_i(t)\ast (V_m(t)-E_i)\hfill \\ +G_r(V_m(t)-E_r)]+V_m(t)\hfill \end{array}$$

where V_m(t) is the membrane potential at time t, C the whole-cell capacitance (50 pF), E_r the resting membrane potential (−60 mV), E_e the reversal potential for excitatory current (0 mV), E_i the reversal potential for inhibitory current (−70 mV), G_r the resting leaky conductance. G_r was calculated based on the equation G_r = C ∗ G_m/C_m, where G_m, the specific membrane conductance is 2 e⁻⁵ S/cm² (Stuart and Spruston 1998), and C_m, the specific membrane capacitance is 1 e⁻⁶ F/cm² (Hines 1993; Hauser 1996). To simulate spike responses, the peak FR was derived from the peak membrane potential depolarization using the power-law (Miller and Troyer 2002; Liu et al. 2010), as FR = k ∗ (V_max − V_r)^p. We used p = 3 based on our previous experience (varying p between 2 and 4 did not affect the main conclusions) (Liu et al. 2010) and obtained k by fitting the experimental data for which both FR and membrane potential were known (k = 2.1 ∗ 10⁶ mv⁻³). It should be noted that while power-law has been widely applied because it is a good approximation to the noisy membrane (Miller and Troyer 2002), other accurate spike thresholding models should also lead to an increase in neuronal selectivity (Priebe and Ferster 2008).

Statistical test

Shapiro–Wilk test were first applied to exam whether samples had a normal distribution. In the case of a normal distribution, t test or ANOVA test was applied. Otherwise, a nonparametric test (Wilcoxon signed-rank test or Wilcoxon rank-sum test) was applied. Data were presented as mean ± SD if not otherwise specified.

Results

Bandwidth Tuning Properties of Excitatory Neurons in Awake Mouse A1

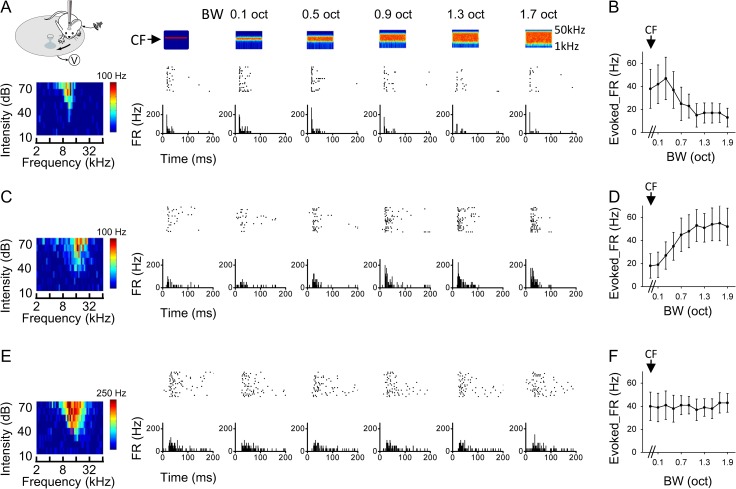
We examined neuronal responses to BPN of different bandwidths with in vivo cell-attached loose-patch recording in awake mouse A1 (see Materials and Methods). The selection of patch pipette parameters biased our sampling strongly towards excitatory neurons (see Materials and Methods). For each recorded neuron, we first determined its center frequency (CF) by applying pure tones of different frequencies and intensities (Fig. 1A, bottom left color map). The CF was defined as the tone frequency that evoked the maximum spike response at the lowest intensity. We then applied BPN bursts centering on the CF with varying bandwidths (0.1–1.9 octave, with the latter encompassing the complete frequency response range of most neurons, see Supplementary Fig. 1) at a selected intensity (60 dB SPL) in a pseudo-randomized order. The CF itself could be considered as BPN with the narrowest bandwidth. Based on the way the spike responses to different BPN bandwidths were modulated, we found that A1 neurons could be categorized into three types. A representative type-one neuron is shown in Fig. 1A. The CF of the cell was 10.56 kHz. Among different bandwidths, the strongest spike response was evoked by a relatively narrow bandwidth (0.3 octave). At broader bandwidths, the response was reduced progressively (Fig. 1B). This type of bandwidth tuning was described as “nonmonotonic” or “tuned” since a preferred bandwidth (0.3 octave for this cell) could be identified. For type-two neurons, we observed a different trend: the evoked spike rate was lowest at the narrowest bandwidth and increased with increasing bandwidths before reaching a plateau (Fig. 1C,D). This type of bandwidth tuning was described as “monotonic” or “integrative”, since the cell monotonically integrates information from increasing frequency channels. For type-three neurons, the evoked spike rate was not significantly changed across different testing bandwidths (Fig. 1E,F). This type of bandwidth tuning was described as “flat”. Both the type-two and type-three neurons were considered as non-tuned or unselective for bandwidth.

Figure 1.

Three types of bandwidth tuning in awake mouse A1. (A) An example, type-one neuron. Left most, illustration of awake recording setup and color map for the tonal receptive field (characteristic frequency is 10.56 kHz). Top, color graphs depict time-dependent spectrograms for the applied band-passed noise (BPN) sounds (100-ms duration), with the bandwidth marked on top. Arrow points to the center frequency (CF, 10.56 kHz for the cell). Middle, raster plot of spike responses (20 trials) to the corresponding stimulus. Bottom, post-stimulus spike time histogram (PSTH) for each testing bandwidth. FR, firing rate. (B) Average evoked firing rate (FR) at each bandwidth for the same cell as shown in (A). Bar = SD. The first data point represents the response to the center frequency alone. (C, D) An example, type-two neuron (CF = 14.93 kHz). Data are displayed in the same manner as in (A, B). (E, F) An example, type-three neuron (CF = 16.00 kHz).

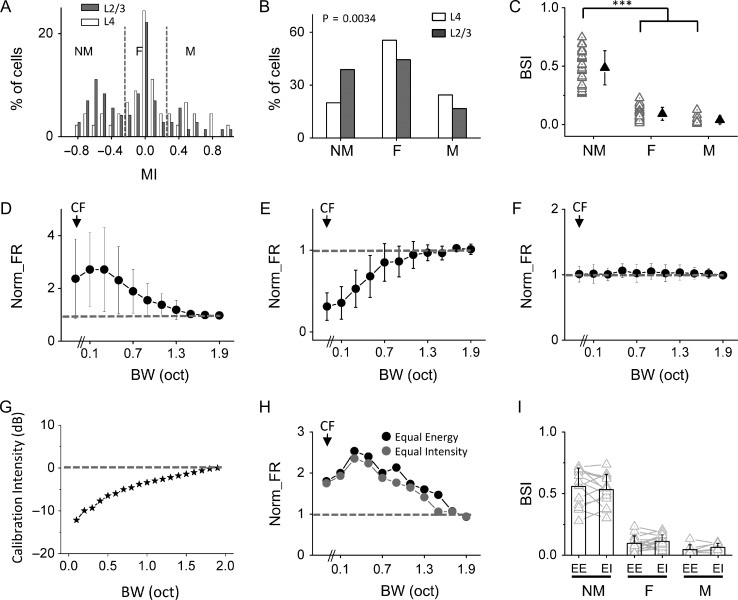
To quantify the shape of bandwidth tuning of A1 neurons, we used a monotonicity index (MI), which was defined as (R_high – R_low)/(R_high + R_low). R_high was the average spike rate evoked by the two broadest bandwidths (1.7 and 1.9 octave), and R_low was the average spike rate evoked by the two narrowest bandwidths (0.1 and 0.3 octave). MI varies from −1 to 1, with negative and positive values indicating a NM and M trend of tuning, respectively. Figure 2A shows the distribution of MIs for a total of 117 neurons we recorded from layers 2–4 of A1. Neurons with MI <−0.25 and >0.25 were defined as those with NM and M tuning, respectively. Neurons with 0.25 ≥ MI ≥ −0.25 were defined as those with flat tuning (F). Notably, there were relatively more NM neurons in layer 2/3 than layer 4 (Fig. 2B). In the layer 2/3 cell population, 39% (28/72) were NM, 17% (12/72) were M and 44% were flat tuning cells, while in the layer 4 population, 20% (9/45) were NM, 24% (11/45) were M and 56% were flat tuning cells. The average normalized bandwidth tuning curves are plotted for these three groups separately (Fig. 2D–F). For the NM cells, the maximum response was usually evoked at 0.1 or 0.3 octave bandwidth (Fig. 2D). For the M neurons, the maximum response was usually evoked at 1.7 or 1.9 octave bandwidth (Fig. 2E). For the flat tuning cells, the response was essentially unchanged across different bandwidths (Fig. 2F). Overall, frequency tuning of NM cells was narrower than flat tuning and M cells, as shown by the quantification of frequency tuning bandwidth of tonal receptive fields (Supplementary Fig. 2A). Additionally, in the population of NM cells, a negative correlation between bandwidth selectivity and frequency tuning bandwidth was observed (r = −0.55, P < 0.01, Supplementary Fig. 2B).

Figure 2.

Layer 2/3 contains more bandwidth-selective neurons than layer 4. (A) Distribution of monotonicity indices (MI) in layer 2/3 (gray, n = 72 cells in total) and layer 4 (white, n = 45 cells in total) populations. Two dotted lines mark MI = −0.25 and 0.25, respectively. (B) Percentage of nonmonotonic (NM) bandwidth tuning, flat tuning (F), and monotonic (M) neurons, respectively. There is a significant difference between layer 2/3 and layer 4 (P < 0.01, Cochran–Armitage test). (C) Comparison of bandwidth selectivity index (BSI) between three types of neurons in layer 2/3 (n = 28, 12, and 32, respectively). Solid symbol represents mean ± SD. ***P < 0.001, one-way ANOVA and post hoc test. (D) Average normalized firing rates for layer 2/3 nonmonotonic bandwidth tuning cells (n = 28). Dash line marks normalized FR = 1. Bar = SD. (E) Average normalized firing rates for layer 2/3 monotonic cells (n = 12). (F) Average normalized firing rates for layer 2/3 flat tuning cells (n = 32). (G) Comparison of the total sound intensity (relative) for BPN stimuli which had the same intensity of the CF component. (H) Comparison of evoked firing rates by stimuli of different designs in an example cell. (I) Comparison of BSI under two stimulation conditions in nonmonotonic (n = 14), flat (n = 17), and monotonic (n = 7) tuning groups, respectively. EE, equal energy; EI, equal intensity.

The NM neurons (Fig. 2D) are of particular interest in this study since they may represent neurons with significant bandwidth selectivity. We used a bandwidth selectivity index (BSI) to quantify the tuning selectivity. BSI was defined as (R_max – R_high)/(R_max + R_high). R_max was the maximally evoked spike rate (i.e., by the preferred bandwidth), and R_high was the spike rate evoked by the broadest bandwidth tested (1.9 octave). BSI varies from 0 to 1, with higher values indicating higher selectivity. As summarized in Fig. 2C, the NM neurons had an average BSI of 0.49 ± 0.15, whereas M and flat tuning neurons had an average BSI close to 0 (0.09 ± 0.06 and 0.04 ± 0.03, respectively). The larger proportion of NM neurons in layer 2/3 than layer 4 (Fig. 2B) thus indicates an enhancement of bandwidth selectivity in layer 2/3 circuits. The bandwidth-selective neurons appeared more or less uniformly distributed across different frequency bands in A1 (Supplementary Fig. 3). The BSI for individual bandwidth-tuned neurons was also comparable between two different intensity levels tested (Supplementary Fig. 4).

In the above experiments, the total energy of different auditory stimuli was kept the same as bandwidth was increased. The reduced response at broader bandwidths in NM cells might be attributed to the fact that the actual intensity of the CF component was reduced with increasing bandwidths. To address this issue, we examined how the total energy would change if the intensity of the CF component was kept the same across different bandwidths. Notably, the total energy increased only by about 10 dB from the narrowest to broadest bandwidths (Fig. 2G). We further compared responses in the same cell in the condition of keeping the total energy of stimuli the same (equal energy) or keeping the intensity of the CF component the same (equal intensity) (Fig. 2H). We found that these two stimulation conditions produced comparable tuning profiles (Fig. 2I). Therefore, the responses of NM cells could not be simply explained by the reduced CF intensity with increasing bandwidths. In the following experiments, we thus used stimuli with constant total energy.

Synaptic Mechanisms Underlying Bandwidth Tuning

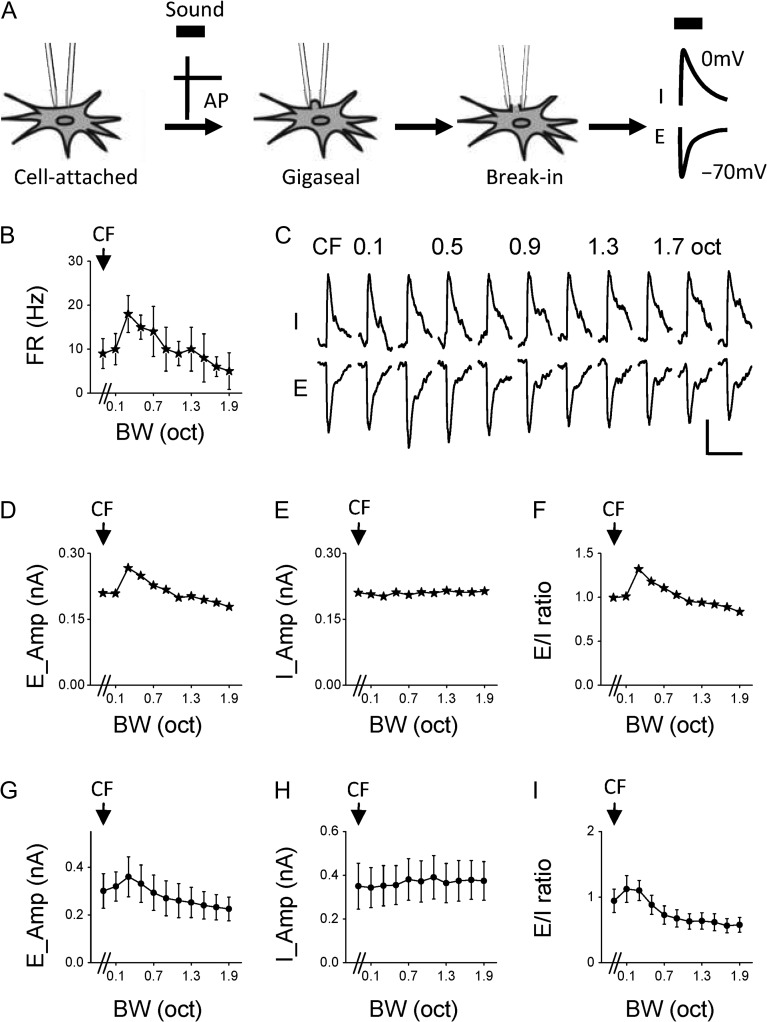
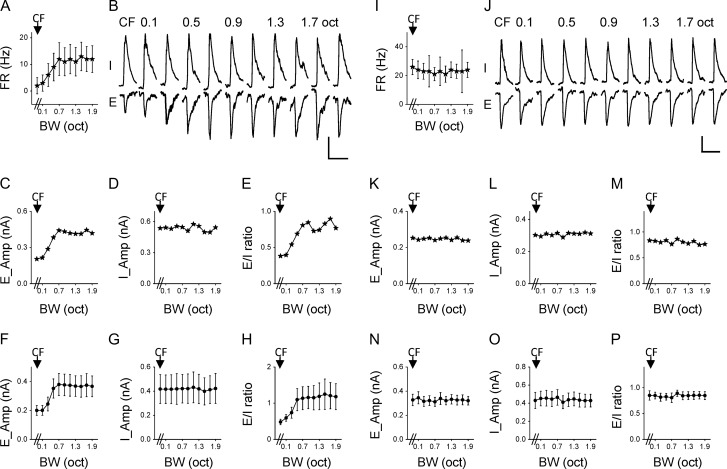
We next examined synaptic input patterns underlying differential bandwidth tuning properties with sequential cell-attached and voltage-clamp recordings. In the cell-attached mode, spike responses of the cell to BPN bursts of different bandwidths were first recorded. The seal was then broken, and excitatory and inhibitory synaptic currents were recorded by clamping the cell’s membrane potential at −70 mV and 0 mV, respectively (Fig. 3A). Because layer 2/3 contains more NM (i.e., bandwidth-tuned) neurons than layer 4, we focused our whole-cell recordings in layer 2/3. Figure 3B shows a representative NM cell. It exhibited the strongest spike response at 0.3 octave bandwidth. Figure 3C plots the cell’s average excitatory (E) and inhibitory (I) responses to different bandwidths. We found that the excitatory input to the cell exhibited a similar trend of modulation as its spike response: the strongest excitation was evoked at 0.3 octave bandwidth, and at broader bandwidths the peak amplitude was progressively reduced (Fig. 3D). In contrast, the amplitude of inhibition remained largely unchanged across different bandwidths (Fig. 3E). As a result, the excitation/inhibition (E/I) ratio showed a similar pattern of bandwidth tuning as excitation and spike responses (Fig. 3F). We identified nine NM cells in a similar manner. The average excitatory and inhibitory input amplitudes as well as the E/I ratio are summarized in Fig. 3G–I.

Figure 3.

Synaptic mechanisms for bandwidth selectivity. (A) Schematic illustration of sequential cell-attached and whole-cell voltage-clamp recordings from the same neuron. Thick black bar marks sound presentation. AP, action potential; E, excitation; I, inhibition. (B) Firing rates of an example nonmonotonic cell in response to BPN of different bandwidths. (C) Average excitatory (E) and inhibitory (I) synaptic currents of the same cell in response to BPN of different bandwidths. Scale: 100 pA, 100 ms. (D) Peak amplitudes of excitation at different bandwidths plotted for the same cell. (E) Peak amplitudes of inhibition for the same cell. (F) Bandwidth tuning of E/I ratio for the same cell. (G) Average peak amplitudes of excitation at different bandwidths for the group of nonmonotonic cells (n = 9). Bar = SD. (H) Average peak amplitudes of inhibition for the same group. (I) Average E/I ratios for the same group.

For five identified M cells, we observed that their excitatory inputs exhibited M bandwidth tuning, their inhibitory inputs exhibited flat tuning, and thus the E/I ratio had M tuning (Fig. 4A–H). For eight identified flat tuning cells, the excitation, inhibition, and the E/I ratio all exhibited flat tuning (Fig. 4I–P). As the inhibitory tuning in all recorded neurons was found to be flat, the tuning property of the cell is essentially inherited from the excitatory input it receives. In other words, excitation dictates the bandwidth tuning property of the cell.

Figure 4.

Synaptic mechanisms for monotonic and flat tuning. (A) Average firing rates of an example monotonic neuron. (B) Average excitatory and inhibitory currents of the same cell at different bandwidths. Scale: 200 pA, 100 ms. (C) Peak amplitudes of excitation for the same cell. (D) Peak amplitudes of inhibition for the same cell. (E) Tuning of E/I ratio for the same cell. (F) Average peak amplitudes of excitation for the group of monotonic neurons (n = 5). Bar = SD. (G) Average peak amplitudes of inhibition for the same group. (H) Average E/I ratios for the same group. (I–P) Bandwidth tuning of synaptic inputs for the group of flat tuning cells (n = 8). Data are presented in the way as in (A–H). Scale: 100 pA, 100 ms.

Consistent Enhancement of Bandwidth Selectivity by Flat Inhibition

Although the bandwidth tuning property is inherited from excitation, a comparison of BSI between spike responses and excitation of the same NM cell indicated that the selectivity of bandwidth tuning was greatly enhanced at the spike response level (Fig. 5A). We postulated that the flat inhibition, in addition to spike thresholding, might play a role in the enhancement of selectivity. To test this possibility, we performed neural modeling using parameters obtained from our experimental data. We simulated BPN-evoked excitatory and inhibitory synaptic inputs (Fig. 5B, top inset), and fed these inputs into a conductance-based neuron model to derive the expected postsynaptic membrane potential (PSP) response (see Materials and Methods). For simplicity, the temporal patterns of these inputs were fixed (see Supplementary Fig. 5), while the amplitudes were varied according to the bandwidth tuning profiles we selected. We simulated a NM tuning profile for excitation, with the maximum response (P₀) assigned at 0.3 octave bandwidth and BSI assigned at 0.22 (Fig. 5B), while the inhibitory input tuning was flat (Fig. 5C). For this model neuron, the derived PSP response exhibited NM tuning similar to excitation, but the selectivity level was reduced as compared with excitation (BSI = 0.08, Fig. 5D). Such reduction of selectivity at the output level is consistent with our previous report of nonlinearity of the input-output transfer function of neurons (Liu et al. 2011). After applying a power-law spike thresholding mechanism to derive the spike rate (FR) response from the PSP (Miller and Troyer 2002; Priebe and Ferster 2008; Liu et al. 2011), the selectivity level was greatly enhanced (BSI = 0.56, Fig. 5E), indicating a powerful effect of spike thresholding on enhancing neuronal selectivity (Priebe and Ferster 2008; Liu et al. 2011). We then varied the absolute amplitude of synaptic inputs as well as the E/I ratio (as defined at P₀), while keeping the tuning shape for both excitation and inhibition unchanged. As shown in Fig. 5F, the value of the E/I ratio could strongly affect bandwidth selectivity. In general, the selectivity was higher at lower E/I ratios, consistent with the notion that relatively stronger inhibition helps to improve selectivity (Liu et al. 2011; Zhou et al. 2012; Li et al. 2014). On the other hand, the absolute amplitude had a minor effect on BSI (Fig. 5F).

We next fixed flat inhibition and changed the tuning shape of excitation (Fig. 5G). NM, flat, and M tuning curves were simulated for excitation, with its mean amplitude across bandwidths kept the same (Fig. 5G). The PSP response essentially preserved the corresponding tuning shape (Fig. 5H), while the spike response enhanced the tuning selectivity in the case of NM tuning, and the monotonicity in the case of M tuning (Fig. 5I). These modeling results further demonstrate that with flat inhibition, the tuning shape of output responses would be inherited from excitation, and that the tuning selectivity would be enhanced at the spike response level.

Finally, we fixed the NM tuning of excitation, and varied the tuning shape of inhibition within a small range while keeping its mean amplitude the same (Fig. 5J). When inhibition had the same trend of bandwidth-dependent variation as excitation (Fig. 5J, dashed), the bandwidth selectivity of output responses (Fig. 5K–L, dashed) was largely reduced as compared to when inhibition was flat (Fig. 5K–L, solid). In contrast, when inhibition had an opposite trend of bandwidth-dependent variation to excitation (Fig. 5J, dotted), the tuning selectivity of output responses was further increased as compared to when inhibition was flat (Fig. 5K–L, dotted). Considering that there could be variations in synaptic amplitude, keeping inhibition more or less constant (i.e., inhibitory tuning flat) would be beneficial for maintaining relatively sharp bandwidth selectivity on a global scale. In other words, flat inhibition plays a role in consistently enhancing bandwidth selectivity in the cortical circuits.

Bandwidth Tuning of Parvalbumin Inhibitory Neurons

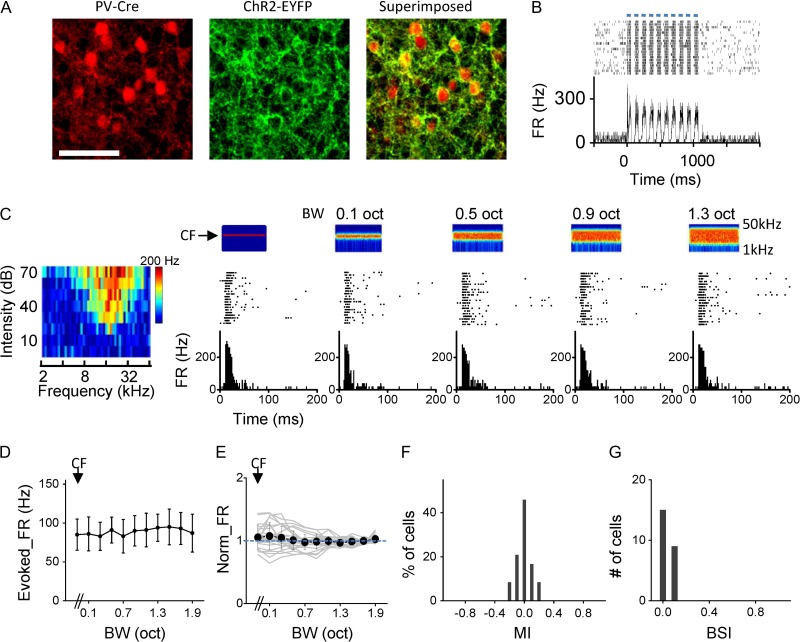
The flat tuning of inhibition might be explained by two scenarios. First, spike responses of inhibitory neurons might have flat tuning. Second, unselective pooling of inhibitory inputs with a variety of tuning shapes could result in flat tuning of the summed inhibition (Fino and Yuste 2011; Karnani et al. 2014). To test these possibilities, we examined responses of parvalbumin (PV) inhibitory neurons by employing optogenetic techniques. We expressed channelrhodopsin2 (ChR2) in PV neurons by injecting AAV encoding Cre-dependent ChR2 into A1 of PV-Cre mice (Fig. 6A). In loose-patch recordings, we identified PV neurons by their time-locked spike responses to pulses of blue LED light (473 nm) applied to the A1 surface (Fig. 6B). Similar to excitatory neurons, we identified the CF of the recorded PV cell and applied the same set of BPN bursts centering on the CF (Fig. 6C). Different from excitatory neurons, PV cells mostly exhibited flat bandwidth tuning (Fig. 6D–E). The MIs of these neurons were mostly distributed within a narrow range of −0.25 to 0.25 (Fig. 6F). The average BSI of these neurons was close to 0 (0.06 ± 0.05, Fig. 6G). Therefore, PV neurons do not exhibit bandwidth selectivity. They are essentially flat tuning cells and in a suitable position to provide flat inhibition to excitatory neurons.

Figure 6.

PV inhibitory neurons are essentially flat tuning cells. (A) Images of tdTomato-labeled PV cells (left), ChR2-EYFP expression (middle) in a slice of A1 and the superimposed image (right). Scale bar: 100 μm. (B) Top, raster plot of spike responses of an example PV neuron to pulses of blue LED light stimulation (marked by blue bars, 50 ms for each pulse). Bottom, corresponding PSTH. (C) Spike responses of the PV cell to BPN of different bandwidths (CF = 18.34 kHz). (D) Bandwidth tuning curve for the same cell as shown in (C). Data are presented as mean ± SD. (E) Average tuning curve for the group of PV cells recorded (n = 25). Light gray curves are for individual cells. Bar = SD. (F) Distribution of MIs for the group of PV cells. (E) Distribution of BSIs for the PV cells.

Discussion

In this study, we have identified three types of neurons in awake mouse A1 in terms of their tuning for bandwidth of BPN. NM neurons are bandwidth-selective cells. They respond best to narrow bandwidths, and thus act more like band-pass filters. M neurons progressively increase their responses as they integrate more and more frequency-specific inputs, and thus act more like integrators. Flat tuning cells respond equally to all bandwidths, and thus are insensitive to bandwidth variations. These tuning profiles represent intrinsic properties of the neurons, since they were not sensitive to the way auditory stimuli were designed (keeping the overall sound level or the intensity of the CF component constant). We found that the proportion of NM neurons is larger in layer 2/3 than layer 4, suggesting that as auditory information flows from the input to output layers, cortical neurons gain better selectivity for bandwidth. This is consistent with the idea that layer 2/3 is involved in more advanced auditory processing than the thalamorecipient layer 4 (Li et al. 2014).

Previously in anesthetized monkeys, bandwidth-selective neurons have only been found in higher auditory cortical regions such as lateral belt areas (Rauschecker et al. 1995; Rauschecker and Tian 2004). It remains unknown how higher cortical neurons gain the bandwidth selectivity as auditory information flows from lower to higher cortical regions. It is speculated that a neuron’s preference to certain bandwidths is the result of complex excitatory or inhibitory interactions (Rauschecker et al. 1995). However, the exact nature of these interactions has yet to be explored. In this study, we found in awake mice that even in the primary auditory cortical region bandwidth-selective neurons are present. There is a small fraction of bandwidth-selective neurons in the input layer, layer 4, raising the possibility that a subset of neurons in the auditory thalamus may already exhibit bandwidth selectivity. Therefore, our data suggest that bandwidth selectivity emerges prior to the stage of A1. At which stage along the ascending auditory pathway does the selectivity for bandwidth first appear remains to be investigated in the future. Nevertheless, since there is a great enhancement of bandwidth selectivity from layer 4 to layer 2/3, examining the excitatory and inhibitory interaction underlying bandwidth tuning in layer 2/3 may provide some important clues of how this selectivity feature emerges in neural circuits.

We find in layer 2/3 excitatory neurons that the tuning profile of excitatory input a cell receives determines the tuning property of its output responses, since inhibition in all types of neurons has flat tuning. The NM tuning of excitation in bandwidth-selective neurons suggests that selectivity can be inherited from layer 4 and thalamus to some extent, since thalamic axons also directly innervate pyramidal neurons in supragranular layers (Ji et al. 2016). The enhancement of selectivity could be attributed, at least partially, to the amplification of tuned excitatory input by intracortical circuits (Lien and Scanziani 2013; Li et al. 2013a, 2013b). The bandwidth tuning has been thought to be analogous to size tuning in the visual cortex (Hubel and Wiesel 1965; Desimone and Schein 1987; DeAngelis et al. 1994; Gilbert et al. 1996; Nolt et al. 2004; Angelucci and Bressloff 2006). For size tuning, intracortical inhibition, in particular that mediated by somatostatin-positive (SOM) inhibitory neurons, plays an important role in suppressing spike responses to large stimulus sizes (Adesnik et al. 2012). The SOM neurons exhibit M size tuning curves (Adesnik et al. 2012), therefore inhibition is expected to increase with increasing stimulus sizes (Adesnik 2017). In this study, we find a different role of inhibition. Instead of increasing with increasing bandwidths, inhibition stays constant. Nevertheless, the flat inhibition helps to sharpen bandwidth selectivity inherited from excitation alone. And by being flatly tuned in all cells, inhibition reliably and consistently enhances bandwidth selectivity in the entire population.

The flat inhibitory tuning can be explained, at least partially, by the tuning property of PV inhibitory neurons themselves, which are insensitive to bandwidth variations. It is interesting that all PV neurons exhibit flat tuning, which is reminiscent of broad orientation and frequency tuning of these neurons observed in the visual and auditory cortex, respectively (Kerlin et al. 2010; Ma et al. 2010; Hofer et al. 2011; Li et al. 2015; Mesik et al. 2015, but see Runyan et al. 2010; Moore and Wehr 2013). Possibly, this is due to a similar circuit mechanism that contributes to the broad orientation tuning in the visual cortex, that is, unselective pooling of inputs from nearby excitatory neurons no matter what their tuning properties are (Fino and Yuste 2011; Harris and Mrsic-Flogel 2013). In the current study, we only focused on PV cells to examine inhibitory neuron properties, based on our understanding of temporal properties of PV cell versus pyramidal cell responses. In our previous reports of tone-evoked responses (Li et al. 2014, 2015), we have shown that PV neurons spike 1–3 ms earlier than pyramidal cells while SOM neurons spike much later (8–9 ms later than pyramidal cells). Due to their delayed responses, SOM neurons are not thought to be able to impact the transient onset responses of pyramidal cells as much as PV neurons (Li et al. 2014, 2015). In the present study, we found that BPN stimuli also evoked mostly transient onset responses in excitatory neurons (Supplementary Fig. 6A). In addition, the evoked spiking of PV neurons started earlier than pyramidal cells, and their peak evoked FRs nearly coincided with pyramidal cells (Supplementary Fig. 6A). Furthermore, the evoked FR of NM cells was most strongly modulated by BPN bandwidth within a ~10-ms time window following the response onset (Supplementary Fig. 6B). All these observations suggest that the feedforward inhibition (see Supplementary Fig. 5) that most strongly modulates the onset responses of pyramidical cells to BPN stimuli is likely from PV neurons. Our data do not exclude the possibility of SOM neurons contributing to certain aspects of auditory response properties (Seybold et al. 2015; Kato et al. 2017), which awaits to be further studied extensively.

BPN bursts are essential elements of many natural sounds, including those used for communication by many species (Rauschecker and Tian 2000; Wang 2000; Wang and Kadia 2001; Akimov et al. 2017). For processing these complex sounds, bandwidth-selective neurons with different center frequencies may play important roles at the first step of processing. It is possible that by combining the outputs of bandwidth-selective neurons, for example, through their simultaneous activation of higher-order neurons acting as coincidence detectors (Rauschecker 1998a), neural networks may be built to be increasingly selective to increasingly more complex sounds. Understanding the neural circuit mechanisms underlying selectivity to bandwidth of BPN, the type of auditory stimuli with intermediate complexity, will provide insights into how brain circuits are constructed to gain capabilities to process complex sensory stimuli. In the present study, we have only tested a limited range of sound frequencies which are mostly lower than those used for mouse vocal communications (Holy and Guo 2005). It remains to be tested whether bandwidth selectivity is exhibited by neurons preferring ultrasonic frequencies (Linden et al. 2003). In short, our study has revealed important excitatory and inhibitory interactions underlying bandwidth selectivity in one output layer of A1. It will be of great interest to apply similar analyses to the neural structure where the selectivity first emerges in the ascending central auditory pathway.

Funding

This work was supported by grants from the US National Institutes of Health (NIH R01DC008983 to L.I.Z and NIH R01EY019049 to H.W.T). Z.X. was supported by a National Basic Research Program of China (973 Program) (2014CB943002) and grants from the National Science Foundation of China (31529003 and 31671083). F.L was supported by grants from the National Natural Science Foundation of China (31671084), and the Science and Technology Planning Project of Guangzhou (201804010443).