Polarizable Embedding for Simulating Redox Potentials of Biomolecules

Abstract

Redox reactions play a key role in various biological processes, including photosynthesis and respiration. Quantitative and predictive computational characterization of redox events is therefore highly desirable for enriching our knowledge on mechanistic features of biological redox-active macromolecules. Here, we present a computational protocol exploiting polarizable embedding hybrid quantum-classical approach and resulting in accurate estimates of redox potentials of biological macromolecules. A special attention is paid to fundamental aspects of the theoretical description such as the effects of environment polarization and of the long-range electrostatic interactions on the computed energetic parameters. Environment (protein and the solvent) polarization is shown to be crucial for accurate estimates of the redox potential: hybrid quantum-classical results with and without account for environment polarization differ by 1.4 V. Long-range electrostatic interactions are shown to contribute significantly to the computed redox potential value even at the distances far beyond the protein outer surface. The approach is tested on simulating reduction potential of cryptochrome 1 protein from Arabidopsis thaliana. The theoretical estimate (0.07 V) of the midpoint reduction potential is in good agreement with available experimental data (−0.15 V).

I. Introduction

Redox processes are ubiquitous in nature and industry. They play a crucial role in energy storage, photovoltaic devices, biological processes, including photosynthesis, respiration, DNA repair, magnetoreception, and many more.^1–10 A thorough discussion of different models for evaluating redox potentials for half-reactions can be found in a review by Marenich et al.¹¹ One can distinguish two classes of approaches for computation of redox potentials and relevant energies based on whether implicit^12–16 or explicit^17–26 solvent models are used.

Both classes of methods have been successfully used for calculating redox potentials for half-reactions and ionization energetics in homogeneous solvents.^12–25 In case of redox reactions in proteins or heterogeneous environment in general, the explicit solvent models, which can account for specific interactions, are needed.²⁷ Electronic embedding quantum mechanics/molecular mechanics (QM/MM) schemes combined with linear response approximation (LRA)^28–30 have been shown to reproduce the differences in redox potentials with a good accuracy,^29,31 yet computing the absolute values remains challenging. Similar strategy has been recently used to describe electron transfer and hemes’ redox potentials in bacterial decaheme cytochromes. ³² Electronic embedding QM/MM has been also exploited in the framework of free energy perturbation simulations to evaluate the reduction potential of FAD in cholesterol oxidase:³³ the obtained accuracy with respect to the experimental reference was 0.8 V.

While the importance of polarization in determination of redox energetics in biomolecules has been recognized (see for example work by Zhang et al.³⁴ with implicit account for environment polarization through molecular fractionalization with conjugate caps (MFCC) charge scheme³⁵), to our knowledge polarizable embedding models have not been used for calculating redox free energies and absolute redox potentials of proteins. Thus, the role of polarization on predictive computation of absolute values of redox potentials for biological macromolecules is yet to be explored.

The effects of environment polarization on excitation energies of chromophores in protein matrix have been previously investigated by Beerepoot et al. ³⁶ The authors showed that the excitation energies of chromophores in green fluorescent protein (GFP) and rhodopsin converge with respect to the size of the polarizable shell at ≈ 20 Å. Note that the quantum part’s charge density redistribution is less dramatic upon excitation in comparison to ionization or electron attachment, which are accompanied with the overall change of the charged state of the system, and one can therefore expect the redox potential values to be more sensitive to the environment polarization. Moreover, the excitation energies for the chromophores in homogeneous aqueous solutions converge faster with respect to the environment polarization than the excitation energies for the same chromophores in heterogeneous protein environment.³⁶ Thus, the effects of polarization on the computed values of redox potentials are expected to be even more pronounced in proteins than in homogeneous solutions,^21,23,24,26 where the differences in computed redox potentials in case of electronic (purely electrostatic) and polarizable embedding can be as large as 0.5 V.²⁶

Another important aspect of theoretical description of redox potentials is the treatment of system size effects. QM/MM calculations of redox potentials are often performed on truncated systems of finite size.^29,31,34 This poses a question on the magnitude of the effects of neglected long-range electrostatic interactions. For example, our previous computational studies of redox potentials of small molecules in aqueous solutions indicate that the convergence of the redox potentials with respect to the solvent shell radius is not reached even at the radius of 30 Å.²⁶ The slow convergence was attributed to the long-range electrostatic interactions between the redox-active site and bulk environment.^26,38,39 Therefore, for protein-solvent media, the long-range static electrostatic interactions are expected to contribute to the computed quantities as well, and are needed to be properly taken into account.

Here, we explore the role of long-range electrostatic interactions and of the environment polarization by considering FAD cofactor reduction in cryptochrome 1 from Arabidopsis thaliana (CrylAt, Fig. 1), for which the reference experimental value of the corresponding midpoint potential is available,^40–42 using hybrid QM/MM methods within LRA framework. Cryptochromes belong to the class of flavoprotein photoreceptors that are involved in growth and development, regulate entrainment of plant and animal circadian rhythms, and are proposed as primary magnetoreceptors in migratory birds.⁹ Effective Fragment Potential method for biomolecules (BioEFP)⁴³ is used to represent polarizable environment within a QM/MM scheme. The structure of the manuscript is as follows. The QM/MM protocol along with BioEFP approach are described in Sec. II. Computational details are provided in Sec. III. The computed energetic parameters and redox potentials of FAD in Cry1At are presented in Sec. IV. The conclusions are given in Sec. V.

Fig. 1.

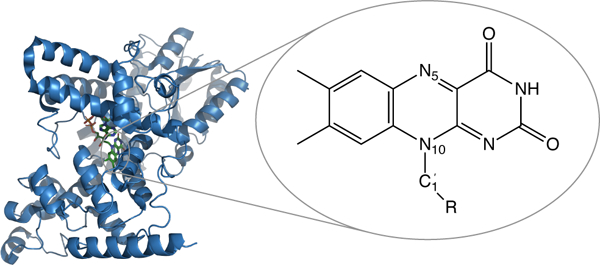
A structure of Cry1At (PDB: 1U3D³⁷) and chemical structure of flavin chromophore, part of FAD cofactor located inside the protein.

II. Theory and Methods

Redox potentials within linear response approximation

LRA^{17,20,21,24,26,28–32} was shown to be a powerful tool for computing reaction free energies and redox potentials and was previously validated for multiple systems, including both solvated organic molecules and biological macromolecules. In LRA,^17,28,30 oxidation free energy${\Delta }_r{G}^{\text{LRA}}$ and reorganization energy${\lambda }^{\text{LRA}}$ can be obtained from two quantities (Eq. 1 and 2): the ensemble-averaged vertical electron affinity $\left({\langle \text{VEA}\rangle }_{\text{Ox}}\right)$ of the oxidized form and the ensemble-averaged vertical ionization energy $\left({\langle \text{VIE}\rangle }_{\text{Red}}\right)$ of the reduced form.

$${\Delta }_r{G}^{\text{LRA}}=\frac{1}{2}\left({\langle \text{VEA}\rangle }_{\text{Ox}}+{\langle \text{VIE}\rangle }_{\text{Red}}\right)$$ (1)

$${\lambda }^{\text{LRA}}=\frac{1}{2}\left({\langle \text{VEA}\rangle }_{\text{Ox}}-{\langle \text{VIE}\rangle }_{\text{Red}}\right)$$ (2)

Where ${\langle \text{VEA}\rangle }_{\text{Ox}}={\langle E(\text{Ox})-E(\text{Red})\rangle }_{\text{Ox}}$ is computed for the ensemble of the oxidized form, ${\langle \text{VIE}\rangle }_{\text{Red}}={\langle E(\text{Ox})-E(\text{Red})\rangle }_{\text{Red}}$is computed for the ensemble of the reduced form. E(Ox) and E(Red) are electronic energies of the oxidized and reduced forms, respectively.

While Eq. 1 and 2 yield formal expressions for${\Delta }_r{G}^{\text{LRA}}$ and ${\lambda }^{\text{LRA}}$ , in practice, QM/MM energy calculations are performed on finite systems. Therefore, the finite system${\Delta }_r{G}^{\text{LRA},f}$ and ${\lambda }^{\text{LRA},f}$ are the quantities that are obtained directly from QM/MM calculations:

$${\Delta }_r{G}^{\text{LRA},f}=\frac{1}{2}\left({\langle \text{VEA}\rangle }_{\text{Ox}}^f+{\langle \text{VIE}\rangle }_{\text{Red}}^f\right)$$ (3)

$${\lambda }^{\text{LRA},f}=\frac{1}{2}\left({\langle \text{VEA}\rangle }_{\text{Ox}}^f-{\langle \text{VIE}\rangle }_{\text{Red}}^f\right)$$ (4)

Superscript ^f indicates that the calculations are performed on finite systems.

The missing long-range electrostatic interactions were shown to be crucial for quantitative estimates of vertical energy gaps (VEGs) such as VEA and VIE, and free energies,^26,38,39 and can be further accounted for following thermodynamic cycle shown in Fig. 2. The thermodynamic cycle relates the bulk reaction free energy$\left({\Delta }_r{G}^{\text{LRA}}\right)$ with the reaction free energy for the finite system $\left({\Delta }_r{G}^{\text{LRA},f}\right)$ and the solvation free energies for the finite systems representing the oxidized$\left(\Delta G_{\text{solv}}^f(\text{Ox})\right)$ and reduced forms $\left(\Delta G_{\text{solv}}^f(\text{Red})\right)$ . The final expression for ${\Delta }_r{G}^{\text{IRA}}$ therefore, will have the following form:

$${\Delta }_r{G}^{\text{LRA}}={\Delta }_r{G}^{\text{LRA},f}+\Delta \Delta G_{\text{solv}}^f$$ (5)

Fig. 2.

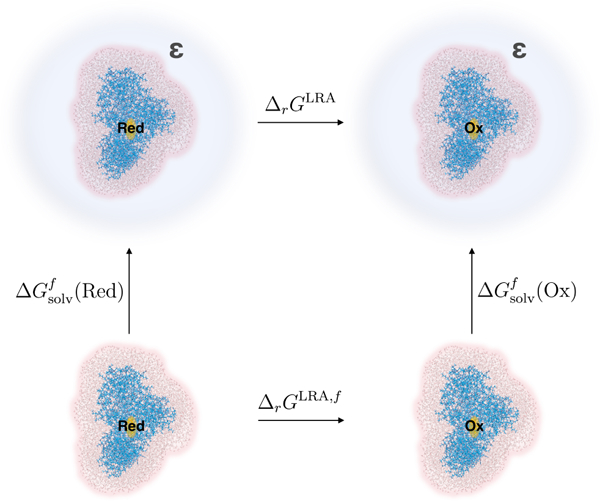
Thermodynamic cycle for calculation of bulk oxidation free energy $\left({\Delta }_r{G}^{\text{LRA}}\right)$ as shown in Eq. 5. FAD in oxidized and reduced states is embedded in the explicit protein-solvent environment. The entire model system is immersed in the solvent (blue) with the static dielectric constant ε.

Where $\Delta \Delta G_{\text{solv}}^f=\Delta G_{\text{solv}}^f(\text{Ox})-\Delta G_{\text{solv}}^f(\text{Red})$ is differential solvation free energy (see Fig. 2).

To mitigate artifacts caused by inconsistencies in the number of particles for the structures representing ensembles of oxidized and reduced forms, $\Delta \Delta G_{\text{solv}}^f$is further approximated by the av-erage between the corresponding quantities for oxidized and reduced ensembles:

$$\Delta \Delta G_{\text{solv}}^f\simeq \frac{1}{2}\left({\langle \Delta \Delta G_{\text{solv}}\rangle }_{\text{Ox}}^f+{\langle \Delta \Delta G_{\text{solv}}\rangle }_{\text{Red}}^f\right)$$

Where${\langle \Delta \Delta G_{\text{solv}}\rangle }_{\text{Ox}}^f$ is an ensemble-averaged difference in solvation free energy between oxidized and reduced forms for the oxidized form ensemble, and ${\langle \Delta \Delta G_{\text{solv}}\rangle }_{\text{Red}}^f$ is the similar quantity, computed for the reduced form ensemble (see Sec. III for more details).

Once the free energy of one-electron oxidation process is computed $\left({\Delta }_r{G}^{\text{LRA}}\right)$ ,the standard reduction potential can be evaluated as follows:

$$E^{°}=\frac{{\Delta }_r{G}^{\text{LRA}}+{\Delta }_r{G}^{°}\left({\text{H}}^{+}\to \frac{1}{2}{\text{H}}_2\right)+\text{EC}-\text{FD}}{F}$$ (6)

Where${\Delta }_r{G}^{°}\left({\text{H}}^{+}\to \frac{1}{2}{\text{H}}_2\right)$ is the standard Gibbs free energy for H⁺ reduction. EC-FD originates from the integrated heat capacity and the entropic contribution for electron, assuming the electron convention and Fermi-Dirac statistics (−0.038 eV),^11,44,45 and F is Faraday constant. The value of −4.281 eV is used in this work for the reference free energy of H⁺ reduction $\left({\Delta }_r{G}^{°}\left({\text{H}}^{+}\to \frac{1}{2}{\text{H}}_2\right)\right)$ , which was obtained omitting the gas-liquid interface surface potential.⁴⁵

The reduction potential relative to normal hydrogen electrode (NHE) can be further obtained as:

$$E^{{°}^{\prime }}=E^{°}+\Delta E(\text{SHE}\to \text{NHE})$$ (7)

Where$\Delta E(\text{SHE}\to \text{NHE})$ corresponds to switching from the standard hydrogen electrode (SHE) to NHE reference (+0.006 V).⁴⁵

Biomolecular/Macromolecular Effective Fragment Potential Method for Proteins (BioEFP)

The Effective Fragment Potential (EFP) method is an ab initio force field (FF) that describes the interactions between solute and solvent molecules in a complex environment.^46–50 The Biomolecular Effective Fragment Potential, or BioEFP, is an extension of the EFP method for modeling the interactions in proteins and macro-molecules.⁴³ In this work, the chromophore lumiflavin was modeled using density functional theory (QM region), while BioEFP was employed to model the protein environment and surrounding water (EFP region). The interactions between the QM and EFP regions are represented via electrostatic and polarization terms, corresponding to the polarizable embedding:

$$\widehat{H}={\widehat{H}}_0+\sum _{pq}\langle p\left|{\widehat{V}}^{\text{Coul}}+{\widehat{V}}^{\text{pol}}\right|q\rangle {\widehat{p}}^{†}\widehat{q},$$ (8)

where Ĥ is the Hamiltonian of the combined QM/EFP system, ${\widehat{H}}_0$is an unperturbed Hamiltonian of the QM part, ${\widehat{V}}^{\text{Coul}}$and${\widehat{V}}^{\text{pol}}$ are electrostatic and polarization perturbations due to effective fragments, and$|p\rangle$ ,$|q\rangle$ are the atomic orbitals of the QM region.

The electrostatic term in EFP is modeled using a multipolar expansion truncated at octupoles; multipoles are centered at all the atoms and bond midpoints. Polarization term is described via induced dipoles that are computed at the expansion points of the static anisotropic polarizability tensors located at the localized molecular orbital centroids of the effective fragments. Induced dipoles are iterated until self-consistency with induced dipoles of other fragments and a wave function of the QM region is reached.

The electrostatic and polarization terms are considered the most significant ones, as far as the effect of the EFP environment on the electronic properties of the QM solute are concerned,^51–54 even though this question requires further investigation.^55,56 The electrostatic and polarization EFP terms contribute to the QM Hamiltonian via one-electron integrals (Eq. 8), altering the quantum Hamiltonian and molecular wave function of the QM region.

In the BioEFP method, the FF parameters corresponding to the protein are obtained in preparatory first-principles calculations as follows. The polypetide chain is fragmented along C_α — C bonds. The resulting fragments, each containing a peptide group and an amino acid residue, are capped with hydrogen atoms along all the fragmented bonds. EFP parameters for the capped fragments are computed at HF/6–31G(d) level using the MAKEFP module in the GAMESS electronic structure package.⁵⁷ Following this, the parameters corresponding to the capping hydrogen atoms and bond midpoints are removed. The resulting excess charge is redistributed to the closest carbon atom, to ensure an integer charge in all the fragments. A detailed summary of this procedure is available in ref. 43.

The EFP parameters for ions were obtained using a mixed basis set simulation (6–31G(d) for electrostatics and 6–311++G(3df,2p) for polarization). Similarly, EFP parameters for water were prepared with 6–31+G(d) basis for electrostatics and 6–311++G(3df,2p) basis for polarization. Water molecules were described with simplified potentials, in which multipoles were truncated at the quadrupole level and distributed to atoms only (no bond midpoints), and polarizability was described with a single polarizability tensor located at the center of mass.

To account for charge penetration effects, electrostatic and polarization terms were augmented by short-range screening functions. The fragment-fragment electrostatic interactions were damped using an exponential screening function, while the QM-fragment interactions were damped with a gaussian-type screening, as discussed in ref. 43, 58.

Further, to avoid overpolarization of neighboring amino acid residues, a gaussian-type damping was applied to screen the fragment-fragment polarization at short distances.⁵⁸ A damping parameter a = 0.3 was used for the amino acid residues and water fragments, while a more rigorous screening a = 0.1 was used for ions.

III. Computational details

As evaluation of redox potentials relies on the ensemble-averaged VEGs, the first step of simulations is sampling of the configurational space for the ensembles of oxidized and reduced states. The sampling was performed with molecular mechanics molecular dynamics (MM MD) techniques. The initial structure was obtained from Protein Data Bank (PDB: 1U3D³⁷). Non-hydrolyzable analog of adenosine triphospate (ATP), adenylylimidodiphosphate (AMP-PNP), was replaced by ATP following the work by Cailliez et al.⁵⁹ The positions of crystallographic water molecules and magnesium ion were not altered. The protonation states of amino acid side chains were assigned following PropKa analysis,⁶⁰ pKa calculations with Poisson-Boltzmann equation (PBEQ) solvers in CHARMM-GUI,^61–63 and following discussion by Solov’yov et al.⁶⁴ Specifically, E350 and D396 were protonated, H253 was doubly protonated (positively charged), and H255 was singly protonated at the N_ε position. CHARMM36 FF for the protein,^65–67 general FF bonding and van der Waals parameters (excluding charges for lumiflavin) for the non-protein residues,⁶⁸ and TIP3P model for water were used.⁶⁹ The MM FF point charges for the oxidized form of FAD were adapted from the work by Solov’yov et al. ⁶⁴ The charges of the semireduced form of FAD $\left(q_i^{\text{SR}}\right)$ were adjusted in the following way:

$$q_i^{\text{SR}}=q_i^{\text{OX}}(\text{FF})+\left(q_i^{\text{SR}}(\text{NBO})-q_i^{\text{OX}}(\text{NBO})\right)$$

Where$q_i^{\text{OX}}(\text{FF})$ are point charges from ref. 64,$q_i^{0X}(\text{NBO})$ and $q_i^{\text{SR}}(\text{NBO})$ are natural bond orbital (NBO)^70,71 charges for oxidized and semireduced forms of lumiflavin, respectively. The NBO charges were obtained for lumiflavin in the gas phase for DFT charge density evaluated with ωB97X-D functional^72,73 and 6–31+G(d,p) basis. The point charge on H-atom capping $C_1^{\prime }$ of CH₂ group (Fig. 1) in DFT calculations was uniformly redistributed among all lumiflavin atoms. The total charge of the entire model system with the oxidized form of lumiflavin prior solvation was −9.

Protonated crystal structure was immersed in water dodecahedron box. 9 Na⁺ counterions were added for neutralization of total system charge followed by MM energy minimization. Equilibration was performed in two steps: NVT-equilibration (T = 300 K, t = 500 ps, velocity rescale thermostat⁷⁴), followed by NPT-equilibration (T = 300 K, p = 1 bar, t = 500 ps, velocity rescale thermostat⁷⁴ and Parinello-Rahman barostat⁷⁵) with 1 ns total equilibration time. 10 ns NPT MD simulation was then performed to obtain the production run trajectory. During MM minimization, equilibration and production MD simulations, periodic boundary conditions were enforced, bonds with the H-atoms were constrained using LINCS algorithm.⁷⁶ 2 fs time step was used. All classical MD simulations were performed with GROMACS package.⁷⁷

The first 5 ns of the production run trajectory were discarded, and 50 snapshots were selected with the equal 100 ps interval within the next 5 ns. For each MM MD snapshot, the geometry of lumiflavin was locally optimized within the fixed MM environment, eliminating possible artifacts coming from the MM MD geometries.⁷⁸ The local QM/MM optimization was performed at ωB97X-D/6–31G(d) level.

Two sets of energy calculations have been performed using the selected snapshots. In one, the role of long-range electrostatic interactions on the computed$\langle {\text{VEA}}^f\rangle$, ${\langle \text{VEA}\rangle }^f$ and${\Delta }_r{G}^{\text{LRA},f}$ was explored. In this case, the model systems for the following energy calculations were obtained from MM MD snapshots by including the entire protein molecule, all water molecules inside the protein, all counterions, and the water molecules located within the certain distance (R) from the protein outer surface (Fig. 3). R values have been varied from 3 to 15 Å. The vertical energy gaps were computed at ωB97X-D/6–31G(d) level for 50 configurations for eachR value, utilizing both hybrid approaches: QM/BioEFP⁴³ and electronic embedding QM/MM with the environment being represented by static multipoles (non-polarizable QM/BioEFP scheme referred to from here on as QM/NP-BioEFP). Quantum part included lumiflavin moiety of FAD cofactor capped at$C_1^{\prime }$ with H-atom. 1–4 electrostatic interactions were turned off. The rest of the FAD cofactor belonged to MM subsystem. All electronic structure calculations were performed in Q-Chem. ⁷⁹

Fig. 3.

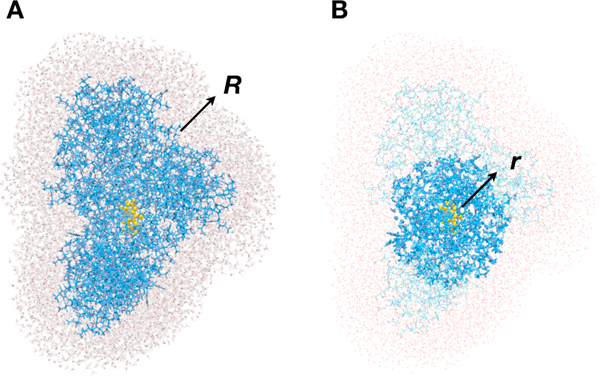
(A) Water shell from the protein, defined by radius R. (B) Polarizable shell, defined by the distance r from the center of mass of the QM part (lumiflavin).

The model system with water molecules within 10 Å from the protein outer surface (R = 10 Å) was chosen for another set of calculations, in which the convergence of computed quantities ($\langle \text{VEA}\rangle$and$\langle \text{VIE}\rangle$) with respect to the size of the polarizable shell has been explored. The polarizable shell (Fig. 3) was defined by the amino acid residues and water molecules located within certain distance (r) from lumiflavin center of mass. The size of the shell (r) was varied from 10 to 50 Å. The part of the FAD cofactor that belonged to the MM subsystem and ATP were always kept polarizable. If C_α-atom or oxygen atom were within r distance from the lumiflavin center of mass, the residue or water molecule, respectively, were treated as polarizable. Otherwise only static electrostatic interactions were accounted for. For each r, the ensemble-averaged value over 50 configurations was computed.

The bulk oxidation free energy $\left({\Delta }_r{G}^{\text{LRA}}\right)$ was obtained from${\Delta }_r{G}^{\text{LRA},f}$ by adding the precomputed difference in solvation energies ($\Delta \Delta G_{\text{solv}}^f$Fig. 2, Eq. 5). The latter was evaluated by numerically solving the PBEQ with Adaptive Poisson-Boltzmann Solver (APBS) program.⁸⁰ The cavity, specifying the boundary between solute system and continuous solvent, was defined as the outer boundary of the composite system, including protein, FAD, ATP, water (R = 10 Å), and counterions. Scaled Bondi radii^81,82 (with the factor f = 1.2^83,84) with adjusted radius for hydrogen to 1.1 Å⁸⁵ were chosen to form the solvation cavity, as it is commonly used in polarizable continuum models (PCM).⁸⁶ The point charges on all atoms of the finite system except the lumiflavin chromophore for both oxidized (Flv_OX) and semireduced form $\left({\text{Flv}}_{\text{SR}}^{\cdot -}\right)$ were zeroed out. The total charge of lumiflavin was either 0 for the oxidized form or −1 for the semireduced one. The scheme was validated for phenoxyl radical and phenolate anion embedded in spherical water clusters by comparing the numerical PBEQ results with the analytical Born solvation free energies (see Sec. S6 of ESI^†). The additive basis set correction (6–31G(d) to aug-cc-pVTZ) was applied to the resulting final bulk free energies (see Sec. S2 of ESI^†).

Once ${\Delta }_r{G}^{\text{LRA}}$ is available, the standard reduction potential can be obtained from Eq. 6. Note, however, that the computed reduction potential corresponds to${\text{Flv}}_{\text{OX}}\stackrel{{\text{e}}^{-}}{\to }{\text{Flv}}_{\text{SR}}^{\cdot -}$ half-reaction in Cry1At. Yet, the quantity measured experimentally by spectroelectrochemical titration is the midpoint potential for${\text{Flv}}_{\text{OX}}\stackrel{{\text{H}}^{+},{\text{e}}^{-}}{\to }{\text{FlvH}}_{\text{SR}}^{·}$ half-reaction^40–42 at pH 7.4. At this pH both protonated${\text{FlvH}}_{\text{SR}}^{·}$ and unprotonated ${\text{Flv}}_{\text{SR}}^{\cdot -}$semireduced forms of lumiflavin coexist, with the protonated form${\text{FlvH}}_{\text{SR}}^{·}$being the dominant one.^40,41 The direct comparison between the computational and experimental quantities is possible using Nernst equation based on available estimates of pK_a of N5-atom of flavin (Fig. 1) and pH value corresponding to the experimental conditions (see Sec. S7 of ESI^†).

IV. Results and Discussion

Below we present the computed ensemble-averaged vertical energy gaps, free energies, and redox potential, and discuss the effects of environment polarization and long-range electrostatic interactions on the energetics of FAD reduction in Cry1At.

Polarization convergence

Fig. 5 shows computed $\langle \text{VEA}\rangle$and$\langle \text{VIE}\rangle$ for different sizes of the environment polarizable shell (r, Fig. 3). One can see that$\langle \text{VEA}\rangle$ and$\langle \text{VIE}\rangle$ converge at$r\approx 40\text{Å}$ . Expanding the polarizable shell from 10 Å to 40 Å results in 0.83 and 0.66 eV shifts in $\langle \text{VEA}\rangle$ and$\langle \text{VIE}\rangle$, respectively. Slow convergence with respect to the environment polarization is in line with the previous studies of excitation energies of photoactive proteins (GFP and rhodopsin) by Kongsted and co-workers.³⁶ It was shown that the excitation energies converge with respect to the size of polarizable shell at ≈ 20 Å.³⁶ Ionization and electron attachment are accompanied by the change of the charge state of the chromophore, and, therefore, one would expect even more pronounced dependence of the corresponding energy gaps on the environment polarization and their slower convergence. The trends in$\langle \text{VEA}\rangle$and$\langle \text{VIE}\rangle$ dependency on r are similar: both monotonically rise with the increase of r and exhibit steps at 18–20 Å and 28–30 Å. Cryptochrome is a globular protein of a non-spherical shape (Fig. 1). Therefore, with the polarizable shell increasing, multiple protein-solvent boundaries are crossed and the nature of polarization interactions with the QM part changes: interactions with the protein vs. interactions with the protein-solvent environment. Thus, the steps are attributed to encountering protein-solvent interfaces accompanied by major changes in polarization interactions at the particular values of r.

Fig. 5.

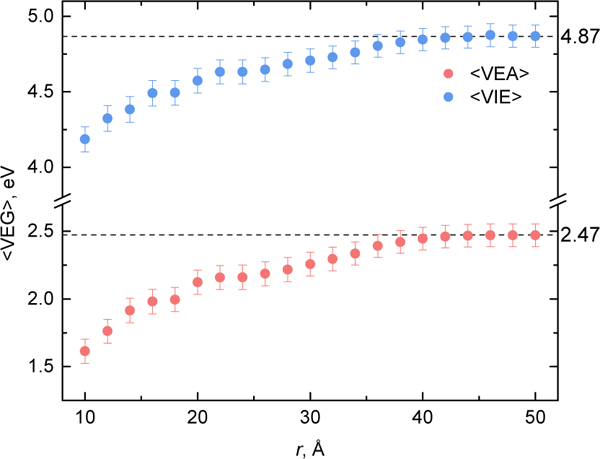
Ensemble-averaged vertical electron affinity $(\langle \text{VEA}\rangle )$ and vertical ionization energy $(\langle \text{VIE}\rangle )$ computed for different size of the polarizable shell r. The dashed lines represent the values obtained by QM/BioEFP (fully polarizable environment). The dots represent the values obtained from QM/BioEFP/NP-BioEFP calculations with the fragments beyond radius r desribed by NP-BioEFP.

QM/NP-BioEFP$\langle \text{VEA}\rangle$ and$\langle \text{VIE}\rangle$ computed without account for environment polarization are 0.80 and 3.74 eV, respectively, being shifted by −1.67 and −1.13 eV from the corresponding QM/BioEFP (fully polarizable environment) values. Thus, proper account for environment polarization is critical for accurate estimates of ionization and electron attachment energies in heterogeneous protein environment. The shifts in VEAs or VIEs for molecules in homogeneous environment were previously shown to be as large as several tenths of eV.^21,23,24,26

System size effects

While the target quantities are ${\Delta }_r{G}^{\text{LRA}}$ and $E^{{°}^{\prime }}(\text{NHE})$ , the computed QM/MM values of $\langle \text{VEA}\rangle$ and $\langle \text{VIE}\rangle$are obtained for the finite systems. Therefore, the dependence on the system size has to be explored. Computed${\langle \text{VEA}\rangle }^f$,${\langle \text{VIE}\rangle }^f$ and${\Delta }_r{G}^{\text{LR}}{}^{\text{A},f}$ as a function of system size (R, Fig. 3) are shown in Fig. 6 and 7. The shifts in computed QM/NP-BioEFP $\langle \text{VEG}\rangle$ between 3 Å and 15 Å water shells are significant: 0.70 eV and 0.99 eV for $\langle \text{VEA}\rangle$ and$\langle \text{VIE}\rangle$, respectively. Same shifts become 0.88 eV and 1.09 eV once the polarization is taken into account. QM/NP-BioEFP and QM/BioEFP $\langle \text{VEG}\rangle$ dependences on R exhibit the same trends, indicating that the long-range effects are the ones of static electrostatic origin.

Fig. 6.

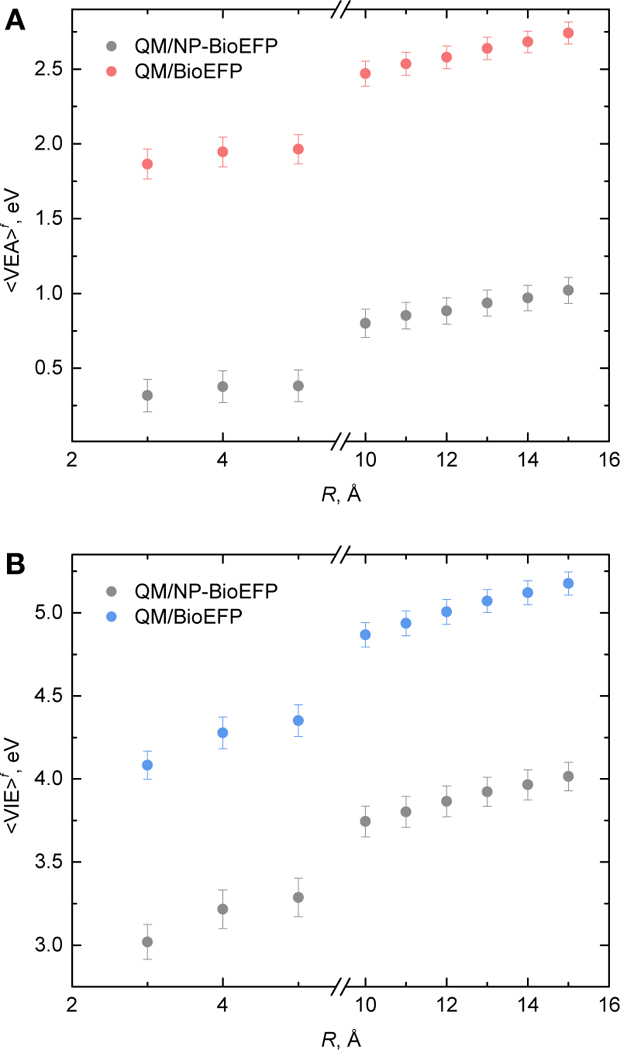
Ensemble-averaged vertical electron affinities$(\langle \text{VEA}\rangle )$, A) and vertical ionization energies$(\langle \text{VIE}\rangle )$, B) computed for different number of water molecules defined by the distance from protein atoms R.

Fig. 7.

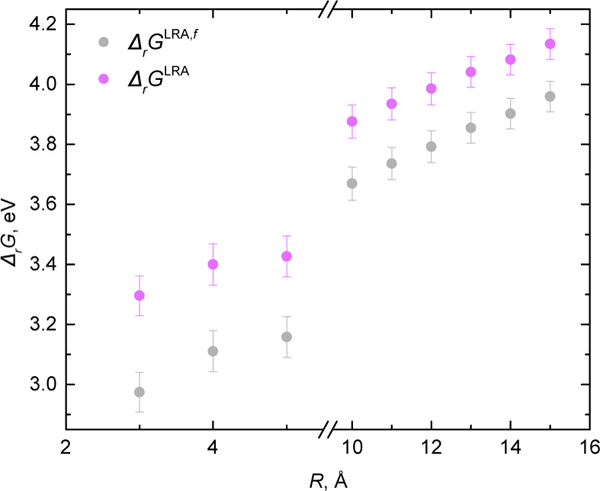
QM/BioEFP $\left({\Delta }_r{G}^{\text{LRA}}\right)$ dependence on the number of water molecules defined by the distance from protein atoms R without and with bulk solvation correction$\left(\Delta \Delta G_{\text{solv}}^f\right)$.

As follows from Fig. 6, $\langle \text{VEG}\rangle$s have not reached converegence with respect to the system size even for 15 Å water shell around the protein. Therefore, further account for long-electrostatic interactions is necessary (see Sec. II and III). Our previous studies ²⁶ showed that sampling of the configurational space using TIP3P water model (also used here) leads to overestimated pre-factor in Born corrections to vertical energy gaps, which in turn corresponds to higher effective charge of the solute. As the slope is overestimated, the effect on absolute values becomes more pronounced, when more explicit water molecules are present in the model system. The model system should be therefore large enough to account for important polarization effects, yet, small enough not to exhibit artifacts due to configurational sampling with employed MM FFs. Here, we chose R = 10 Å to satisfy the above criteria.

Redox potential in heterogeneous protein environment

Once the $\langle \text{VEG}\rangle$s are computed, the free energy of oxidation and reduction potential can be evaluated within LRA (Eq. 3, 6, and 7). As discussed above, the environment, including the protein, has a significant effect on the VEGs.^{21,23,24,26,36} Computed ensemble-averaged ${\langle \text{VEA}\rangle }^f$and ${\langle \text{VIE}\rangle }^f$ as well as linear response free energy${\Delta }_r{G}^{\text{LRA},f}$ for the gas phase (configurations of lumiflavin from MM MD without protein-solvent environment), QM/NP-BioEFP and QM/BioEFP are listed in Table 1. All values are averaged over 50 configurations, and provided for 10 Å water shell configurations (R = 10 Å).

Table 1.

Ensemble-averaged vertical electron affinity $({\langle \text{VEA}\rangle }^f)$ , vertical ionization energy$({\langle \text{VIE}\rangle }^f)$, and linear response reaction free energy $\left({\Delta }_r{G}^{LRA,f}\right)$ calculated for lumiflavin chromophore at ωB97X-D/6–31G(d) level. Protein, the rest of FAD, ATP, counterions, and water molecules within 10 Å from the protein (R = 10 Å) are present in the model system. All values are averaged over 50 configurations and given in eV

	gas-phase	QM/NP-BioEFP	QM/BioEFP
${\langle \text{VEA}\rangle }^f$	1.20 ±0.01	0.80 ±0.10	2.47 ±0.08
${\langle \text{VIE}\rangle }^f$	1.77 ±0.01	3.74 ±0.09	4.87 ±0.07
${\Delta }_r{G}^{LRA,f}$	1.48 ±0.01	2.27 ±0.07	3.67 ±0.06

Interaction with the protein-solvent environment significantly alters $\langle \text{VEG}\rangle$s of lumiflavin as can be seen from Table 1. Taking into account only static electrostatic interactions (gas phase vs. QM/NP-BioEFP) results in the shifts of −0.40, 1.97, and 0.79 eV In${\langle \text{VEA}\rangle }^f$,${\langle \text{VIE}\rangle }^f$ and${\Delta }_r{G}^{\text{LR}}{}^{\text{A},f}$, respectively. Further account of environment polarization (QM/NP-BioEFP vs. QM/BioEFP) also causes large shifts in computed energetic parameters: 1.67, 1.13, and 1.40 eV for${\langle \text{VEA}\rangle }^f$,${\langle \text{VIE}\rangle }^f$ and${\Delta }_r{G}^{\text{LR}}{}^{\text{A},f}$, respectively. Importantly, the effects of polarization on${\langle \text{VEA}\rangle }^f$ and ${\langle \text{VIE}\rangle }^f$are even more dramatic for the heterogeneous protein environment than for the previously reported values on small solutes in homogeneous aqueous solutions.²⁶

The bulk free energy $\left({\Delta }_r{G}^{\text{LR}}{}^{\text{A}}\right)$and the redox potential $\left(E^{{°}^{\prime }}(\text{NHE})\right)$ were evaluated following Eq. 6, 7, and 9. Note that as the geometry of the lumiflavin was locally optimized for each snapshot in the corresponding frozen environment, the lumiflavin nuclear degrees of freedom do not contribute to the final reaction Gibbs free energy. Therefore, the difference in zeropoint vibrational energy (ΔZPVE) and thermochemical correction$\left({\Delta }_r{G}^{\text{thermo}}\right)$ for lumiflavin approximated by their gas-phase values were added. Finally, since the $\langle \text{VEG}\rangle \text{s}\left({\langle \text{VEA}\rangle }^{f,\text{SB}}\text{and}{\langle \text{VIE}\rangle }^{f,\text{SB}}\right)$ were computed with the relatively small basis set without diffuse basis functions, 6–31G(d), the additive basis set corrections to aug-cc-pVTZ have been added $\left({\langle \Delta \text{VEA}\rangle }^{\text{BSC}}\text{and}{\langle \Delta \text{VIE}\rangle }^{\text{BSC}}\right)$ . The results based on the final expression for ${\Delta }_r{G}^{\text{LRA}}$ (Eq. 9) are provided in Table 2 with more details reported in Sec. S1, S2, S5 of ESI.^†

$$\begin{gathered} {\Delta }_r{G}^{\text{LRA}}=\frac{1}{2}\left({\langle \text{VEA}\rangle }^{f,\text{SB}}+{\langle \text{VIE}\rangle }^{f,\text{SB}}\right)+\frac{1}{2}\left({\langle \Delta \text{VEA}\rangle }^{\text{BSC}}+{\langle \Delta \text{VIE}\rangle }^{\text{BSC}}\right) \\ +\Delta \Delta G_{\text{solv}}^f \\ +\Delta \text{ZPVE}+{\Delta }_r{G}^{\text{thermo}} \end{gathered}$$ 9

Table 2.

Free energy$\left({\Delta }_r{G}^{LRA}\right)$ and midpoint potential of FAD in Cry1At w.r.t. normal hydrogen electrode $\left(E^{o^{\prime }}(\text{NHE})\right)$ . Protein, the rest of FAD, ATP, counterions, and only water molecules within 10 Å from the protein (R = 10 Å) were included in QM/NP-BioEFP and QM/BioEFP calculations, reflecting the magnitudes of electrostatic and polarization contributions w.r.t. to the gas-phase value${\Delta }_r{G}^{\text{LRA}}\text{and}{E}^{{°}^{\prime }}(\text{NHE})$ values are given in eV and V, respectively

	gas-phase	QM/NP-BioEFP	QM/BioEFP	experiment
${\Delta }_r{G}^{\text{LRA}}$	2.00 ±0.01	2.99 ±0.07	4.39 ±0.06	-
$E^{{°}^{\prime }}(\text{NHE})$	−2.32 ±0.01	−1.32 ±0.07	0.07 ±0.06	−0.15 ±0.0240

Presence of the environment as well as accounting for environment polarization is crucial for the quantitative estimates of redox potentials (Table 2). The differences in final values of redox potentials between the gas-phase and QM/NP-BioEFP, and between the gas-phase and QM/BioEFP values are 0.99 V and 2.39 V, respectively. Our best estimate of the midpoint potential of FAD in CrylAt (0.07 V) is in good agreement with the available experimental data.^40–42 Nevertheless, further improvements in the computational protocol are desirable with the main challenges being proper description of long-range electrostatic interactions and reliable configurational sampling. The former challenge could be addressed in a three-layered QM/polarizable MM/nonequilibrium PCM schemes. To our knowledge, there is no existing production level code enabling this type of calculations for vertical ionization and electron attachment energies. The role of solvent models on configurational sampling, in particular the possibility of using polarizable forcefileds or many-body potentials, is the subject of the ongoing work.

V. Conclusions

Here, we have presented the results of computational studies of redox potential of FAD in Cry1At and explored the effects of long-range electrostatic interactions and environment polarization on the relevant energetic parameters. We demonstrate that the account of environment polarization is crucial for accurate estimates of redox potentials of biomolecules: the shift in the value of reduction potential between non-polarizable and polarizable QM/MM schemes is 1.4 V. We also show that proper care should be taken of long-range electrostatic interactions if absolute values of the redox potentials are the target: computed VEGs are not converged with respect to the system size even for 15 Å water shell around the protein. The theoretical estimate of the midpoint potential of FAD in Cry1At, 0.07 V, is reported for the first time and is in excellent agreement with available experimental data.^40–42

Fig. 4.

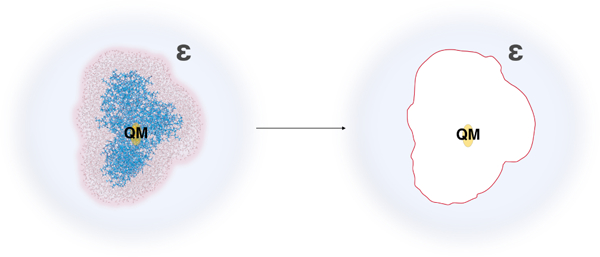
Solvation of model system by polarizable continuum (blue) representing the aqueous solution with the static dielectric constant ε. The charges of lumiflavin were preserved (yellow), and the charges of the MM part were zeroed-out (white).