Skip to main content
PMC home page
Science Advances logoLink to Science Advances
. 2019 Jul 5;5(7):eaaw0409. doi: 10.1126/sciadv.aaw0409

Antisymmetric magnetoresistance in van der Waals Fe3GeTe2/graphite/Fe3GeTe2 trilayer heterostructures

Sultan Albarakati 1,*, Cheng Tan 1,*, Zhong-Jia Chen 2,*, James G Partridge 1, Guolin Zheng 1, Lawrence Farrar 1, Edwin L H Mayes 1, Matthew R Field 1, Changgu Lee 3, Yihao Wang 4, Yiming Xiong 4, Mingliang Tian 4, Feixiang Xiang 5, Alex R Hamilton 5, Oleg A Tretiakov 5,6, Dimitrie Culcer 5,†, Yu-Jun Zhao 2,†, Lan Wang 1,†
PMCID: PMC6611684  PMID: 31281884

The observation of an antisymmetric magnetoresistance in a trilayer van der Waals heterostructure Fe3GeTe2/graphite/Fe3GeTe2.

Abstract

With no requirements for lattice matching, van der Waals (vdW) ferromagnetic materials are rapidly establishing themselves as effective building blocks for next-generation spintronic devices. We report a hitherto rarely seen antisymmetric magnetoresistance (MR) effect in vdW heterostructured Fe3GeTe2 (FGT)/graphite/FGT devices. Unlike conventional giant MR (GMR), which is characterized by two resistance states, the MR in these vdW heterostructures features distinct high-, intermediate-, and low-resistance states. This unique characteristic is suggestive of underlying physical mechanisms that differ from those observed before. After theoretical calculations, the three-resistance behavior was attributed to a spin momentum locking induced spin-polarized current at the graphite/FGT interface. Our work reveals that ferromagnetic heterostructures assembled from vdW materials can exhibit substantially different properties to those exhibited by similar heterostructures grown in vacuum. Hence, it highlights the potential for new physics and new spintronic applications to be discovered using vdW heterostructures.

INTRODUCTION

Microelectronic devices, such as diodes and transistors, can be incorporated into large integrated structures capable of performing diverse tasks, including logical operations (i.e., computing devices) and high-density information storage. Despite a vast range of architectures and applications, the fundamental principle of operation for all devices relies on the manipulation of a single quantity—the charge of the electron. The concept of using spin in addition to charge in microelectronics is termed spintronics. Giant magnetoresistance (GMR), which progressed from discovery to applications (modern disk storage) within a decade, illustrates the impact of spintronics. By manipulating the electron charge and spin simultaneously, ultrahigh-speed and low-power electronic devices with enhanced functionality can be realized. As a result, spintronics is now one of the most important technological research fields, encompassing electronics, materials science, and condensed matter physics (1, 2).

With the emergence of two-dimensional (2D) materials, van der Waals (vdW) ferromagnetic materials have attracted great interest. 2D ferromagnetism has been confirmed in three monolayer vdW materials: CrI3 (insulator), Cr2Ge2Te6 (insulator), and Fe3GeTe2 (FGT; metal) (3–6). So far, various spintronic devices have been fabricated on the basis of these materials (7–15). vdW ferromagnetic metal FGT has been studied for many years (16–30). Only very recently, it was realized that nanoflake vdW FGT is a promising vdW ferromagnetic metal for spintronics with a near-square–shaped hysteresis loop, large coercivity, and perpendicular magnetic anisotropy (16), making it a perfect vdW ferromagnetic metal for spintronic devices (9) and fundamental spintronic research. Furthermore, materials with very different crystal structures and lattice constants can be layered in vdW heterostructures without the deleterious effects seen in conventional thin-film heterostructures. Hence, a major design restriction is removed to provide near limitless possibilities for novel spintronic device architectures.

The discovery of GMR (31, 32) was honored with the Nobel Prize in 2007 and introduced the second fundamental property of the electron—its spin—into microelectronics. A standard GMR device has a trilayer structure with two ferromagnetic metals separated by a nonferromagnetic metal. To date, most GMR devices have been fabricated from metallic thin films grown in a high-vacuum chamber. The nonferromagnetic layers in these GMR devices are typically metals, such as Cr (32), Cu (33), or Pd (34), but interest is turning to nonferromagnetic conductive materials with desirable properties, such as multilayer graphene (35,36). Incompatibility with magnetic sputtering (commonly used for growth of GMR structures) is a concern with multilayer graphene, but once again, this is not a limitation in vdW heterostructure devices. Nonmagnetic conductors such as graphene can be sandwiched between vdW ferromagnets with atomically flat and ultraclean interfaces.

We have fabricated FGT/graphite/FGT devices using a pick-up transfer technique (37,38) and investigated their MR behavior, with surprising results. The thickness of graphite (multilayer graphene) within the structure varied from 3 to 11 nm. In a standard GMR experiment, a trilayer device shows a symmetric MR effect. When the magnetic moments in the two ferromagnetic layers point in opposite directions, the trilayer structure adopts a high-resistance state. When the magnetic moments point in the same direction, the trilayer GMR device adopts a low-resistance state. The FGT/graphite/FGT devices studied here display an intermediate resistance state when the magnetic moments are parallel. When the magnetic moments in the two FGT layers are antiparallel, the devices exhibit high resistance for positive magnetic fields and low resistance for negative magnetic fields (at times inversely). We propose that the interfaces between the graphite flake and the FGT flakes, and the strong spin orbit coupling (SOC) in FGT, discussed below, are responsible for the observed three-state MR behavior.

RESULTS AND DISCUSSION

In our experiment, 11 FGT/graphite/FGT devices with differing thicknesses of graphite layers were fabricated. The labels and dimensions are shown in the Supplementary Materials. Figure 1A shows the optical and atomic force microscopy (AFM) image of a trilayer heterostructure (sample FPC3) with a graphite layer sandwiched by two FGT layers. In the AFM image, the blue section defines the top FGT layer, the red section defines the graphite layer, and the yellow section defines the lower FGT layer. The device current flowed in plane from the source to the drain, and the longitudinal resistance, Rxx, and the anomalous Hall resistance, Rxy, were measured. As FGT shows strong perpendicular anisotropy (16), the magnetic field applied perpendicular to the device surface was swept from 1 to −1 T and then from −1 to 1 T. The diagram in Fig. 1B illustrates the normal (two-state) GMR effect, which is symmetric with respect to the applied magnetic field. In contrast, the FGT/graphite/FGT device (sample FPC3) displays an antisymmetric MR effect, as shown in Fig. 1C. The anomalous Hall measurements of the FGT/graphite/FGT device show very sharp magnetic transitions, in agreement with our previous work (16). Namely, an individual FGT nanoflake shows a near-square–shaped magnetic loop and has a single domain structure in the regime away from coercivity. At the positive value of the saturation magnetic field, the magnetic moments of both FGT layers point along the positive direction. When the magnetic field reaches a certain regime of negative values, the magnetic moments of the two FGT layers point in opposite directions due to the different coercivities of these layers. The MR exhibits a plateau with a sharp transition, while the anomalous Hall resistance exhibits step-like behavior. When the magnetic field reaches its negative saturation value, the moments in both FGT layers point along the negative direction. Rxx in this configuration is equal to Rxx when the moments in both layers point in the positive direction. When the field is swept back from the saturation value to a certain regime of positive values, the magnetic moments in the two FGT layers point in opposite directions. Again, Rxx exhibits a plateau and Rxy is stepped. However, unlike conventional GMR with two resistance states, the FGT/graphite/FGT device shows three resistance states, namely, high resistance (antiparallel magnetic moments), intermediate resistance (parallel magnetic moments), and low resistance (antiparallel magnetic moments). The magnitudes of the MR effect at 50 K in all 11 devices (with differing graphite layer thicknesses) are shown in Fig. 1D. These results show that the antisymmetric MR effect is independent of the thickness of the graphite layer. It is well known that graphene and nanoflake graphite display very large MR. However, the FGT/graphite/FGT devices show very small MR at 1 and − 1 T, which demonstrates the clean FGT/graphite interface. If the FGT/graphite interface is not clean (organic residues or bubbles), then Rxx is characterized by a large quasi-linear MR (fig. S3, C and D). This is because the current mainly flows in the graphite layer and, consequently, charge carriers are not scattered by the magnetic moments in the FGT layers.

Fig. 1. Overview of the MR effect in FGT/graphite/FGT heterostructures.

Fig. 1

Open in a new tab

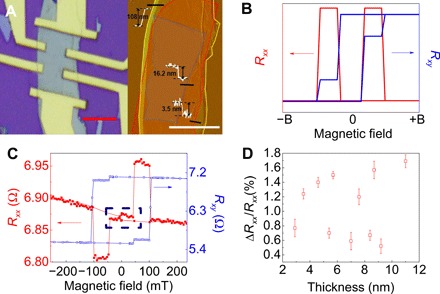
(A) Optical and AFM images of an FGT/graphite/FGT heterostructure. The device number is FPC3. Scale bars, 5 μm. The regions surrounded by the blue line, red line, and yellow line represent the top FGT layer, graphite layer, and bottom FGT layer, respectively. (B) Schematic diagram for the transport behavior of a typical GMR effect. (C) Field-dependent Rxx and Rxy measurements of an FGT/graphite/FGT heterostructure (sample FPC3) at 50 K. A loop surrounded by a dark blue dashed line is shown in the Rxx(B) curve. (D) ΔRxx/Rxx values for samples with various thicknesses of graphite layer. All the data are calculated for measurements at 50 K. The error bars come from the noise of the measurement.

Additional experimental work was performed to establish whether the observed phenomena were intrinsically generated from the heterostructure. First, it was a concern that the asymmetric nanoflakes within the devices could cause the antisymmetric Rxx due to the anomalous Hall effect. Second, the number of states in FGT/graphite/FGT heterostructure has not been confirmed. In Fig. 1C, a small “loop” (surrounded by a dark blue dashed line, open in vertical direction) between the two peaks can be observed, which may originate from the Hall resistance or indicate a four-state MR effect.

To address the two issues, three symmetric devices were prepared using focused ion beam (FIB) etching. Figure S4A shows the image of one etched device (sample FPC5). Alongside the device in fig. S4 are the Rxx and Rxy curves measured at 50 K. To elucidate the effects of device symmetry, we performed the FIB etching in two steps. In the first step, the parts identified by the orange dashed line were etched. Compared with the original Rxx (fig. S4B), the loop (surrounded by a green dashed line) in Rxx(B) between the two peaks decreases after this first etch step (fig. S4C). In the second FIB etch step, the parts identified by the red dashed line were etched and, afterward, only the parts surrounded by the blue dashed line remained. Figure S4D shows the Rxx and Rxy curves of the sample at 50 K after the second etch. The Rxy curve indicates that the completed device is symmetric, while the Rxx curve still shows the antisymmetric MR effect and the loops between the peaks disappear. These observations prove that the phenomenon is not an artifact caused by asymmetry in the devices and/or contacts but a genuine three-resistance state system originating from the FGT/graphite/FGT heterostructures. During this study, we found that despite precautionary measures, FIB etching could cause damage to the top FGT layer and affect its sharp magnetic transition. We therefore chose to remove FIB from the fabrication scheme to ensure that the MR effect was observed in devices composed of pristine FGT layers.

Figure 2 shows the temperature dependence of the antisymmetric MR, with the magnetic field applied perpendicular to a device (sample FPC1) plane. The magnitude of the antisymmetric MR decreases with increasing temperature and disappears when T > 140 K. As shown in our previous work, the magnetic properties of FGT nanoflakes undergo a sharp transition near 150 K. Below 150 K, they exhibit a near-square–shaped loop, while the magnetic remanence and coercivity decrease sharply to near zero when T > 150 K, although the Curie temperature is near 200 K. Together, the aforementioned results indicate that a magnetic hysteresis loop with nonzero remanence is essential for the antisymmetric MR observed in our FGT/graphite/FGT devices.

Fig. 2. Temperature-dependent transport measurement for sample FPC1.

Fig. 2

Open in a new tab

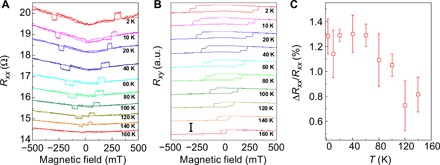
(A) Rxx curves in an FGT/graphite/FGT device at different temperatures. (B) Corresponding Rxy(B) curves at different temperatures. Scale bar, 3 Ω. (C) Temperature dependence of ΔRxx/Rxx values. The error bars are defined by the noise level. a.u., arbitrary units.

Figure 3 shows the angular dependence of the antisymmetric MR effect at 20 K. The angles shown in the figure represent the angles between the magnetic field and the direction perpendicular to the plane of the device. As shown in Fig. 3A, the magnitude of the MR effect does not change as the angle is varied. However, the two antisymmetric MR plateaus flip in the region between θ = 70° and 72°. From θ = 0 to 70°, the high-resistance state appears at positive fields and the low-resistance state appears at negative fields. The width of the resistance plateau decreases with increasing angle θ. When θ exceeds 72°, the resistance plateaus flip: The high-resistance state appears at negative fields, and the low-resistance state appears at positive fields. With a further increase in θ, the resistance plateaus increase in width. At θ = 85°, the resistance plateau shows several smaller plateaus. To understand this behavior, we compared the Rxx(B) and Rxy(B) curves (Fig. 3, A and B). As the thickness of the top and bottom FGT layers are 21.7 and 42 nm, respectively, the decrease in Rxy is less if a flip occurs in the top FGT layer than if a flip occurs in the bottom FGT layer. Hence, the layer that flips is distinguishable. From 0° to 70°, the Rxy curve (Fig. 3B) shows a smaller decrease first and a larger decrease after the resistance plateau when the magnetic field sweeps from 1 to −1 T, showing that the thinner top FGT layer is first to flip. At the location of the plateau in Rxx, the moments in both layers point into the graphite layer—this will be referred to as the “IN” configuration. When the magnetic field is scanned back from −1 to 1 T, the first layer to flip is again the top layer with a smaller decrease in Rxy. However, the magnetic moments are now in the “OUT” configuration. Namely, the magnetic moments in both layers point out of the trilayer structure. Therefore, from θ = 0° to θ = 70°, the IN configuration (at negative field) shows the low-resistance state, while the OUT configuration (at positive field) shows the high-resistance state. When θ > 70°, the states flip and the high-resistance state appears at negative field, while the low-resistance state appears at positive field. Further investigation of the Rxy indicates that the magnetic moment of the bottom layer flips first when θ > 70°, which is opposite to the condition when θ < 70°. Hence, the low-resistance state still corresponds to the IN state, and the high-resistance state still corresponds to the OUT state. Hence, from the analysis of the angular-dependent Rxx and Rxy measurements, we conclude that the magnetic configuration determines the resistance states. When the magnetic moments in the two FGT layers are parallel, the FGT/graphite/FGT device is in the intermediate-resistance state, and when they are antiparallel, the IN state causes low resistance and the OUT state causes high resistance.

Fig. 3. Angular-dependent transport measurements for sample FPC1 at 20 K.

Fig. 3

Open in a new tab

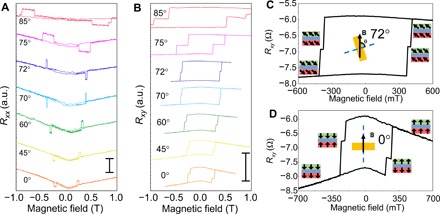
(A) Rxx(B) curves of an FGT/graphite/FGT device at different tilt angles at 20 K. 0° means the magnetic field perpendicular to the sample surface. Scale bar, 1.5 Ω. (B) Corresponding Rxy(B) curves at different tilt angles at 20 K. Scale bar, 4.5 Ω. (C) Rxy(B) curve at 72° (the magnetic moments in the bottom layer flip first with increasing magnetic field). (D) Rxy(B) curve at 0° (the magnetic moments in the top layer flip first with increasing magnetic field).

To further understand the three-state MR effect, we performed a series of measurements with opposing current directions and flipped device orientation. In the current direction–dependent MR measurements, the applied magnetic field is perpendicular to the sample surface (θ = 0°). As shown in Fig. 4A, the IN state shows the low- and high-resistance state with the positive and negative currents, respectively, while the OUT state shows the low- and high-resistance state with the negative and positive currents, respectively. In the device orientation–dependent MR experiments, the MR was first measured, with the FGT top layer facing upward. Thereafter, the device was inverted (with the original top FGT at the bottom of the device) and the MR was remeasured. As shown in Fig. 4B, the corresponding high- and low-resistance states reverse as well. We also measured the current density–dependent plateau resistance. As shown in Fig. 4C, the antisymmetric MR effect is independent of the current density.

Fig. 4. Current-dependent transport measurements on FPC3 at 100 K.

Fig. 4

Open in a new tab

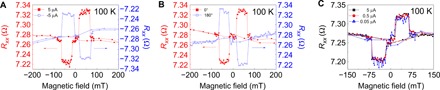
(A) Rxx(B) with different current directions. (B) Rxx measured when the top FGT layer faces upward (0°) and downward (180°). (C) Rxx(B) with different magnitudes of current.

Antisymmetric MR is uncommon, but it has been reported to have occurred in two different systems. The first was composed of single-layer magnetic thin films with perpendicular anisotropy (39,40). In a magnetic thin film with perpendicular anisotropy, two single magnetic domains separated by a 180° domain wall are formed. The magnetic moments in the two single domains point up and down, respectively. When a current is passed perpendicularly through the domain wall, a perpendicular electric field can form in the vicinity of the domain wall due to the anomalous Hall effect. An antisymmetric MR can then be observed if the magnetic domain wall is driven by an applied perpendicular magnetic field. The second system that reportedly produced antisymmetric MR was a novel topological materials–based magnetic heterostructure composed of CrSb/(Bi,Sb)2Te3/CrSb layers grown by molecular beam epitaxy (41). In this very recent report, the antisymmetric MR is proposed to be related to quantum anomalous Hall effect. As shown in Fig. 4 (A and B), the high- and low-resistance states switch to the low- and high-resistance states, respectively, when the direction of current flow is reversed. This phenomenon indicates the strong correlation between the electron spin and momentum, namely, spin momentum locking. There are two possible origins of spin momentum locking: topological surface states on topological materials (42) and an SOC-induced Rashba-split 2D electron gas (43). Recent work has identified FGT as a ferromagnetic topological nodal line semimetal (24), which is expected to have a strong spin-orbit interaction. To investigate the origin of spin momentum locking in the FGT/graphite/FGT devices, we performed a series of density functional theory calculations. The results of these calculations demonstrate that the spin of the surface state of FGT (the Fermi arc) points in the same direction as the magnetization (details in section S8). Therefore, the Fermi arc does not show spin momentum locking. Thus, the spin momentum locking can only originate from the SOC-induced Rashba-split 2D electron gas. In agreement with a recent report (24), our calculation also shows SOC-induced band splitting in FGT. This substantiates the assertion that an SOC-induced Rashba-split 2D electron gas causes spin momentum locking. Reversal of the current direction then flips the spins of the transported electrons.

On the basis of the current-dependent spin orientation at the FGT surface, we propose a tentative model that elucidates the appearance of a three-state MR in an FGT/graphite/FGT heterostructure. In an external electric field, the SOC-induced spin momentum locking will generate a sizable spin current transverse to the original electric current on the FGT surface [note that this is not a spin Hall current (44)]. Although the resistivity of graphite is 104 orders smaller than that of FGT, these spin currents will still be flowing through the two FGT/graphite interfaces. Because the thicknesses of our graphite layers, which are 2 to 11 nm, are much smaller than the electron mean free path in graphite (45), the electrons transported through the graphite can enter the FGT layers and scatter within them. This picture is well supported by the Rxy measurements. If the electrons only flowed in the graphite layer, then Rxy would not display any anomalous Hall effect. This is in contradiction to the experimental results. In this scenario, the electron spin polarization (determined by the current direction) of the spin current may coincide with or be opposite to the direction of the magnetization in one FGT layer. If the two directions are antiparallel, then this will lead to larger scattering and consequently higher resistance than observed when the polarizations of the spin current and the magnetization are parallel. With this in mind, one can distinguish three situations: (i) at both interfaces, the spin polarization and magnetization are parallel, which leads to the lowest observed resistance; (ii) at both interfaces, the spin polarization and magnetization are antiparallel, which leads to largest observed resistance; and (iii) at one of the interfaces, the spin polarization and magnetization are parallel, but at the other, they are antiparallel, which leads to an intermediate resistance.

The above theoretical description explains all the experimental results, as shown in fig. S9. Figure S9A illustrates the SOC-induced spin momentum locking in the Rashba spin-splitting surface states. When the current flows on the surface, spin current is generated because of spin momentum locking. As mentioned above, the current mainly flows in the graphite layer and at the interfaces. For the top and bottom FGT layers, the current flows at their bottom and top surface, respectively. Hence, the spin momentum locking induced current shows opposite spin orientations at the two interfaces. In this case, when the magnetizations of the two FGT layers point in the same direction, situation (iii) (intermediate-resistance state), as mentioned above, occurs, which is shown in fig. S9 (B and C). When the magnetizations of the two FGT layers point in opposite directions, situation (i) (low-resistance state) and situation (ii) (high-resistance state) occur, which are plotted in fig. S9 (D and E). If the direction of current flow is reversed, then the spin polarization of the electrons at the interface will be switched but the magnetization in the FGT layers is maintained; hence, the intermediate state remains, while the low- and high-resistance states switch. If, on the other hand, the direction of current flow is maintained and the device is flipped upside down, then the magnetization configuration switches, while the electron spin directions at the interface are maintained. Hence, again, the intermediate state remains unchanged, while the low- and high-resistance states switch. Last, as shown in Fig. 3 and fig. S5A, the magnetization configuration changes with the tilt angle and temperature, which determines whether the high- and low-resistance states appear at negative or positive field. As the magnetic dynamics of FGT layers are different for different devices, the evolution of the antisymmetric MR with tilt angle and temperature also varies with devices (section S9).

CONCLUSION

In summary, we have observed a previously unreported three-state MR effect in FGT/graphite/FGT vdW heterostructure devices. This unexpected result is contrary to previously held beliefs regarding GMR and its mechanisms. Band structure calculations performed on FGT have enabled us to propose that this three-state MR arises because of spin momentum locking at the FGT/graphite interface. This work highlights the potential to discover entirely new phenomena and applications in vdW heterostructure–based spintronic devices.

MATERIALS AND METHODS

Single-crystal growth

The FGT single crystals for the top and bottom device layers were grown by different methods to achieve different coercive fields. The FGT single crystals from C.L.’s group were grown by the chemical vapor transport (CVT) method. Iodine (5 mg/cm2), which served as a transport agent, was mixed with the Fe, Ge, and Te powder (3:1:5). The mixed powder was sealed into an evacuated quartz glass ampoule, which was then placed in a tubular furnace. The temperature of the furnace was ramped to 700°C at a rate of 1°C/min and maintained at the set point for 96 hours. The ampoule was subsequently cooled to 450°C for 250 hours. This slow cooling promotes high crystallinity. FGT single crystals from Y.X.’s group were also grown by the CVT method, but the transport agent I2 was replaced by TeCl4 to achieve larger single crystals suitable for transport measurements.

Device fabrication

The FGT and few-layer graphite flakes were mechanically exfoliated onto SiO2/Si wafers in a glove box with oxygen and water levels below 0.1 parts per million. The nanoflakes were examined by optical microscopy. Atomically smooth flakes were identified with thicknesses of 5 to 20 nm for the top FGT, 40 to 80 nm for the bottom FGT, and 2 to 15 nm for the graphene. All three layers were manipulated using a polymer-based dry transfer technique. The polymer was dissolved in chloroform outside of the glove box for approximately 1 min, and the sample was spin-coated immediately after the dissolution to minimize the exposure to ambient conditions. Cr/Au (5/120 nm) metal electrodes were deposited onto the overlap area by electron beam evaporation following a standard electron beam lithography technique using polymethyl methacrylate (PMMA) 950 7A as the electron beam resist (lift-off) layer.

FIB etch

The FIB etching of the heterostructure device was performed using an FEI Scios DualBeam system. The Ga ion energy was 30 keV, and the beam current was 1.5 pA. The duration of FIB etching was limited to 10 s and with a beam-blocked interval of at least 10 s to minimize heating of the sample. The FIB was not scanned over the device region, which is the part surrounded by the blue dashed line in fig. S4A.

Electrical measurement

The transport measurements were performed in the Physical Property Measurement System (Ever Cool ІІ, Quantum Design, San Diego, CA, USA) with a base temperature of 1.8 K and a magnetic field of up to 9 T. The devices were mounted on a Horizontal Rotator probe, which allows device rotations around an axis perpendicular to the magnetic field.

Supplementary Material

http://advances.sciencemag.org/cgi/content/full/5/7/eaaw0409/DC1
supp_5_7_eaaw0409__index.html (2.4KB, html)
Download PDF
aaw0409_SM.pdf (1.4MB, pdf)

Acknowledgments

Funding: This research was supported by the Australian Research Council Centre of Excellence in Future Low-Energy Electronics Technologies (CE170100039), the Natural Science Foundation of China (11574088), the National Key Research and Development Program of China (2016YFA0300404), and the Institute for Information and Communications Technology Promotion (IITP) (grant B0117-16-1003, Fundamental technologies of 2D materials and devices for the platform of new-functional smart devices). Author contributions: L.W. conceived and designed the research. C.L., Y.W., Y.X., and M.T. synthesized the material. S.A. and C.T. fabricated the heterostructures. S.A., C.T., and G.Z. did the device fabrication. S.A., C.T., F.X., A.R.H., and L.W. performed the electron transport measurements. S.A., C.T., A.R.H., O.A.T., D.C., and L.W. did the data analysis and modeling. Z.-J.C. and Y.-J.Z. did the band structure calculation. L.F., E.L.H.M., and M.R.F. performed the TEM scan for the cross-section of heterostructures. S.A., C.T., Z.-J.C., Y.-J.Z., J.G.P., D.C., and L.W. wrote the paper with the help from all of the other co-authors. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/7/eaaw0409/DC1

Section S1. Ohmic contacts

Section S2. Dimensions of all FGT/graphite/FGT devices

Section S3. Transmission electron microscopy (TEM) on the heterostructures

Section S4. The effect of graphite layer etch and samples with weak interlayer coupling

Section S5. Fabrication of a symmetric Hall bar device based on FIB milling

Section S6. Transport measurement for other samples

Section S7. Tentative resistor model

Section S8. Band structure calculation

Section S9. Discussion about the angle-dependent results in Fig. 3

Fig. S1. Ohmic contact confirmation.

Fig. S2. TEM on FGT/graphite/FGT heterostructure.

Fig. S3. The effect of graphite layer etch and samples with weak interlayer coupling.

Fig. S4. Rxx and Rxy of an FIB-etched FGT/graphite/FGT device at 50 K.

Fig. S5. Measurements for FPC1 and FPC9.

Fig. S6. Measurement for an asymmetric sample FPC2 (the anomalous Hall signal is large).

Fig. S7. Angle-dependent curves at 50 K for sample FPC11, with top and bottom FGT touching each other.

Fig. S8. Rxx(B) and Rxy(B) curves for two samples with relatively larger ΔRxx/Rxx value at 50 K.

Fig. S9. Tentative resistor model.

Fig. S10. Surface states and surface spin texture of FGT.

Table S1. Dimensions of all FGT/graphite/FGT devices.

REFERENCES AND NOTES

  • 1.Wolf S. A., Awschalom D. D., Buhrman R. A., Daughton J. M., von Molnár S., Roukes M. L., Chtchelkanova A. Y., Treger D. M., Spintronics: A spin-based electronics vision for the future. Science 294, 1488–1495 (2001). [DOI] [PubMed] [Google Scholar]
  • 2.Žutić I., Fabian J., Sarma S. D., Spintronics: Fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004). [Google Scholar]
  • 3.Gong C., Li L., Li Z., Ji H., Stern A., Xia Y., Cao T., Bao W., Wang C., Wang Y., Qiu Z. Q., Cava R. J., Louie S. G., Xia J., Zhang X., Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017). [DOI] [PubMed] [Google Scholar]
  • 4.Huang B., Clark G., Navarro-Moratalla E., Klein D. R., Cheng R., Seyler K. L., Zhong D., Schmidgall E., McGuire M. A., Cobden D. H., Yao W., Xiao D., Jarillo-Herrero P., Xu X., Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017). [DOI] [PubMed] [Google Scholar]
  • 5.Deng Y., Yu Y., Song Y., Zhang J., Wang N. Z., Sun Z., Yi Y., Zheng Wu Y., Wu S., Zhu J., Wang J., Chen X. H., Zhang Y., Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 563, 94–99 (2018). [DOI] [PubMed] [Google Scholar]
  • 6.Fei Z., Huang B., Malinowski P., Wang W., Song T., Sanchez J., Yao W., Xiao D., Zhu X., May A. F., Wu W., Cobden D. H., Chu J.-H., Xu X., Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 17, 778–782 (2018). [DOI] [PubMed] [Google Scholar]
  • 7.Song T., Cai X., Tu M. W.-Y., Zhang X., Huang B., Wilson N. P., Seyler K. L., Zhu L., Taniguchi T., Watanabe K., McGuire M. A., Cobden D. H., Xiao D., Yao W., Xu X., Giant tunneling magnetoresistance in spin-filter van der Waals heterostructures. Science 360, 1214–1218 (2018). [DOI] [PubMed] [Google Scholar]
  • 8.Wang Z., Gutiérrez-Lezama I., Ubrig N., Kroner M., Gibertini M., Taniguchi T., Watanabe K., Imamoğlu A., Giannini E., Morpurgo A. F., Very large tunneling magnetoresistance in layered magnetic semiconductor CrI3. Nat. Commun. 9, 2516 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Wang Z., Sapkota D., Taniguchi T., Watanabe K., Mandrus D., Morpurgo A. F., Tunneling spin valves based on Fe3GeTe2/hBN/Fe3GeTe2 van der Waals heterostructures. Nano Lett. 18, 4303–4308 (2018). [DOI] [PubMed] [Google Scholar]
  • 10.Jiang S., Shan J., Mak K. F., Electric-field switching of two-dimensional van der Waals magnets. Nat. Mater. 17, 406–410 (2018). [DOI] [PubMed] [Google Scholar]
  • 11.Wang Z., Zhang T., Ding M., Dong B., Li Y., Chen M., Li X., Huang J., Wang H., Zhao X., Li Y., Li D., Jia C., Sun L., Guo H., Ye Y., Sun D., Chen Y., Yang T., Zhang J., Ono S., Han Z., Zhang Z., Electric-field control of magnetism in a few-layered van der Waals ferromagnetic semiconductor. Nat. Nanotechnol. 13, 554–559 (2018). [DOI] [PubMed] [Google Scholar]
  • 12.Ghazaryan D., Greenaway M. T., Wang Z., Guarochico-Moreira V. H., Vera-Marun I. J., Yin J., Liao Y., Morozov S. V., Kristanovski O., Lichtenstein A. I., Katsnelson M. I., Withers F., Mishchenko A., Eaves L., Geim A. K., Novoselov K. S., Misra A., Magnon-assisted tunnelling in van der Waals heterostructures based on CrBr3. Nat. Electron. 1, 344–349 (2018). [Google Scholar]
  • 13.Si M., Liao P.-Y., Qiu G., Duan Y., Ye P. D., Ferroelectric field-effect transistors based on MoS2 and CuInP2S6 two-dimensional van der Waals heterostructure. ACS Nano 12, 6700–6705 (2018). [DOI] [PubMed] [Google Scholar]
  • 14.Huang B., Clark G., Klein D. R., MacNeill D., Navarro-Moratalla E., Seyler K. L., Wilson N., McGuire M. A., Cobden D. H., Xiao D., Yao W., Jarillo-Herrero P., Xu X., Electrical control of 2D magnetism in bilayer CrI3. Nat. Nanotechnol. 13, 544–548 (2018). [DOI] [PubMed] [Google Scholar]
  • 15.Klein D. R., MacNeill D., Lado J. L., Soriano D., Navarro-Moratalla E., Watanabe K., Taniguchi T., Manni S., Canfield P., Fernández-Rossier J., Jarillo-Herrero P., Probing magnetism in 2D van der Waals crystalline insulators via electron tunneling. Science 360, 1218–1222 (2018). [DOI] [PubMed] [Google Scholar]
  • 16.Tan C., Lee J., Jung S.-G., Park T., Albarakati S., Partridge J., Field M. R., McCulloch D. G., Wang L., Lee C., Hard magnetic properties in nanoflake van der Waals Fe3GeTe2. Nat. Commun. 9, 1554 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Wang Y., Xian C., Wang J., Liu B., Ling L., Zhang L., Cao L., Qu Z., Xiong Y., Anisotropic anomalous Hall effect in triangular itinerant ferromagnet Fe3GeTe2. Phys. Rev. B 96, 134428 (2017). [Google Scholar]
  • 18.Yi J., Zhuang H., Zou Q., Wu Z., Cao G., Tang S., Calder S. A., Kent P. R. C., Mandrus D., Gai Z., Competing antiferromagnetism in a quasi-2D itinerant ferromagnet: Fe3GeTe2. 2D Mater. 4, 011005 (2017). [Google Scholar]
  • 19.Liu B., Zou Y., Zhou S., Zhang L., Wang Z., Li H., Qu Z., Zhang Y., Critical behavior of the van der Waals bonded high TC ferromagnet Fe3GeTe2. Sci. Rep. 7, 6184 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Zhu J.-X., Janoschek M., Chaves D. S., Cezar J. C., Durakiewicz T., Ronning F., Sassa Y., Mansson M., Scott B. L., Wakeham N., Bauer E. D., Thompson J. D., Electronic correlation and magnetism in the ferromagnetic metal Fe3GeTe2. Phys. Rev. B 93, 144404 (2016). [Google Scholar]
  • 21.Zhang Y., Lu H., Zhu X., Tan S., Feng W., Liu Q., Zhang W., Chen Q., Liu Y., Luo X., Xie D., Luo L., Zhang Z., Lai X., Emergence of Kondo lattice behavior in a van der Waals itinerant ferromagnet, Fe3GeTe2. Sci. Adv. 4, eaao6791 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Deiseroth H.-J., Aleksandrov K., Reiner C., Kienle L., Kremer R. K., Fe3GeTe2 and Ni3GeTe2-Two new layered transition-metal compounds: Crystal structures, HRTEM investigations, and magnetic and electrical properties. Eur. J. Inorg. Chem. 2006, 1561–1567 (2006). [Google Scholar]
  • 23.Li Q., Yang M., Gong C., Chopdekar R. V., N’Diaye A. T., Turner J., Chen G., Scholl A., Shafer P., Arenholz E., Schmid A. K., Wang S., Liu K., Gao N., Admasu A. S., Cheong S.-W., Hwang C., Li J., Wang F., Zhang X., Qiu Z., Patterning-induced ferromagnetism of Fe3GeTe2 van der Waals materials beyond room temperature. Nano Lett. 18, 5974–5980 (2018). [DOI] [PubMed] [Google Scholar]
  • 24.Kim K., Seo J., Lee E., Ko K.-T., Kim B. S., Jang B. G., Ok J. M., Lee J., Jo Y. J., Kang W., Shim J. H., Kim C., Yeom H. W., Min B., Yang B.-J., Kim J. S., Large anomalous Hall current induced by topological nodal lines in a ferromagnetic van der Waals semimetal. Nat. Mater. 17, 794–799 (2018). [DOI] [PubMed] [Google Scholar]
  • 25.León-Brito N., Bauer E. D., Ronning F., Thompson J. D., Movshovich R., Magnetic microstructure and magnetic properties of uniaxial itinerant ferromagnet Fe3GeTe2. J. Appl. Phys. 120, 083903 (2016). [Google Scholar]
  • 26.May A. F., Calder S., Cantoni C., Cao H., McGuire M. A., Magnetic structure and phase stability of the van der Waals bonded ferromagnet Fe3-xGeTe2. Phys. Rev. B 93, 014411 (2016). [Google Scholar]
  • 27.Liu Y., Stavitski E., Attenkofer K., Petrovic C., Anomalous Hall effect in the van der Waals bonded ferromagnet Fe3−xGeTe2. Phys. Rev. B 97, 165415 (2018). [Google Scholar]
  • 28.Zhuang H. L., Kent P. R. C., Hennig R. G., Strong anisotropy and magnetostriction in the two-dimensional Stoner ferromagnet Fe3GeTe2. Phys. Rev. B 93, 134407 (2016). [Google Scholar]
  • 29.Liu S., Yuan X., Zou Y., Sheng Y., Huang C., Zhang E., Ling J., Liu Y., Wang W., Zhang C., Zou J., Wang K., Xiu F., Wafer-scale two-dimensional ferromagnetic Fe3GeTe2 thin films grown by molecular beam epitaxy. NPJ 2D Mater. Appl. 1, 30 (2017). [Google Scholar]
  • 30.Nguyen G. D., Lee J., Berlijn T., Zou Q., Hus S. M., Park J., Gai Z., Lee C., Li A.-P., Visualization and manipulation of magnetic domains in the quasi-two-dimensional material Fe3GeTe2. Phys. Rev. B 97, 014425 (2018). [Google Scholar]
  • 31.Binasch G., Grünberg P., Saurenbach F., Zinn W., Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 39, 4828–4830 (1989). [DOI] [PubMed] [Google Scholar]
  • 32.Baibich M. N., Broto J. M., Fert A., Van Dau F. N., Petroff F., Etienne P., Creuzet G., Friederich A., Chazelas J., Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices. Phys. Rev. Lett. 61, 2472–2475 (1988). [DOI] [PubMed] [Google Scholar]
  • 33.Berkowitz A. E., Mitchell J. R., Carey M. J., Young A. P., Zhang S., Spada F. E., Parker F. T., Hutten A., Thomas G., Giant magnetoresistance in heterogeneous Cu-Co alloys. Phys. Rev. Lett. 68, 3745–3748 (1992). [DOI] [PubMed] [Google Scholar]
  • 34.Law R., Sbiaa R., Liew T., Chong T. C., Effects of Ta seed layer and annealing on magnetoresistance in Co Fe/Pd-based pseudo-spin-valves with perpendicular anisotropy. Appl. Phys. Lett. 91, 242504 (2007). [Google Scholar]
  • 35.Karpan V. M., Giovannetti G., Khomyakov P. A., Talanana M., Starikov A. A., Zwierzycki M., van den Brink J., Brocks G., Kelly P. J., Graphite and graphene as perfect spin filters. Phys. Rev. Lett. 99, 176602 (2007). [DOI] [PubMed] [Google Scholar]
  • 36.Huerkamp F., Krüger P., Pollmann J., Investigation of electron transmission through Co/C/Co magnetic tunnel junctions. Phys. Rev. B 89, 125302 (2014). [Google Scholar]
  • 37.Zomer P. J., Guimarães M. H. D., Brant J. C., Tombros N., Van Wees B. J., Fast pick up technique for high quality heterostructures of bilayer graphene and hexagonal boron nitride. Appl. Phys. Lett. 105, 013101 (2014). [Google Scholar]
  • 38.Wang L., Meric I., Huang P. Y., Gao Q., Gao Y., Tran H., Taniguchi T., Watanabe K., Campos L. M., Muller D. A., Guo J., Kim P., Hone J., Shepard K. L., Dean C. R., One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013). [DOI] [PubMed] [Google Scholar]
  • 39.Eid K., Ocola L., Liu X., Furdyna J. K., Large antisymmetric magnetoresistance across chemically etched GaMnAs nanoconstrictions. Appl. Phys. Lett. 102, 242407 (2013). [Google Scholar]
  • 40.Desrat W., Kamara S., Terki F., Charar S., Sadowski J., Maude D. K., Antisymmetric magnetoresistance anomalies and magnetic domain structure in GaMnAs/InGaAs layers. Semicond. Sci. Technol. 24, 065011 (2009). [Google Scholar]
  • 41.He Q. L., Yin G., Yu L., Grutter A. J., Pan L., Kou X., Che X., Yu G., Nie T., Zhang B., Shao Q., Murata K., Zhu X., Fan Y., Han X., Kirby B. J., Wang K. L., Topological transitions induced by antiferromagnetism in a thin-film topological insulator. Phys. Rev. Lett. 121, 096802 (2018). [DOI] [PubMed] [Google Scholar]
  • 42.Xu S.-Y., Liu C., Kushwaha S. K., Sankar R., Krizan J. W., Belopolski I., Neupane M., Bian G., Alidoust N., Chang T.-R., Jeng H.-T., Huang C.-Y., Tsai W.-F., Lin H., Shibayev P. P., Chou F.-C., Cava R. J., Hasan M. Z., Observation of Fermi arc surface states in a topological metal. Science 347, 294–298 (2015). [DOI] [PubMed] [Google Scholar]
  • 43.King P. D. C., Hatch R. C., Bianchi M., Ovsyannikov R., Lupulescu C., Landolt G., Slomski B., Dil J. H., Guan D., Mi J. L., Rienks E. D. L., Fink J., Lindblad A., Svensson S., Bao S., Balakrishnan G., Iversen B. B., Osterwalder J., Eberhardt W., Baumberger F., Hofmann Ph., Large tunable Rashba spin splitting of a two-dimensional electron gas in Bi2Se3. Phys. Rev. Lett. 107, 096802 (2011). [DOI] [PubMed] [Google Scholar]
  • 44.Culcer D., Winkler R., Generation of spin currents and spin densities in systems with reduced symmetry. Phys. Rev. Lett. 99, 226601 (2007). [DOI] [PubMed] [Google Scholar]
  • 45.Kinchin G. H., Cockcroft J. D., The electrical properties of graphite. Proc. R. Soc. Lond. A 217, 9–26 (1953). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

http://advances.sciencemag.org/cgi/content/full/5/7/eaaw0409/DC1
supp_5_7_eaaw0409__index.html (2.4KB, html)
Download PDF
aaw0409_SM.pdf (1.4MB, pdf)

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/7/eaaw0409/DC1

Section S1. Ohmic contacts

Section S2. Dimensions of all FGT/graphite/FGT devices

Section S3. Transmission electron microscopy (TEM) on the heterostructures

Section S4. The effect of graphite layer etch and samples with weak interlayer coupling

Section S5. Fabrication of a symmetric Hall bar device based on FIB milling

Section S6. Transport measurement for other samples

Section S7. Tentative resistor model

Section S8. Band structure calculation

Section S9. Discussion about the angle-dependent results in Fig. 3

Fig. S1. Ohmic contact confirmation.

Fig. S2. TEM on FGT/graphite/FGT heterostructure.

Fig. S3. The effect of graphite layer etch and samples with weak interlayer coupling.

Fig. S4. Rxx and Rxy of an FIB-etched FGT/graphite/FGT device at 50 K.

Fig. S5. Measurements for FPC1 and FPC9.

Fig. S6. Measurement for an asymmetric sample FPC2 (the anomalous Hall signal is large).

Fig. S7. Angle-dependent curves at 50 K for sample FPC11, with top and bottom FGT touching each other.

Fig. S8. Rxx(B) and Rxy(B) curves for two samples with relatively larger ΔRxx/Rxx value at 50 K.

Fig. S9. Tentative resistor model.

Fig. S10. Surface states and surface spin texture of FGT.

Table S1. Dimensions of all FGT/graphite/FGT devices.

Articles from Science Advances are provided here courtesy of American Association for the Advancement of Science

RESOURCES