Elastic Statistical Shape Analysis of Biological Structures with Case Studies: A Tutorial

Abstract

We describe a recent framework for statistical shape analysis of curves, and show its applicability to various biological datasets. The presented methods are based on a functional representation of shape called the square-root velocity function and a closely related elastic metric. The main benefit of this approach is its invariance to re-parameterization (in addition to the standard shape preserving transformations of translation, rotation and scale), and ability to compute optimal registrations (point correspondences) across objects. Building upon the defined distance between shapes, we additionally describe tools for computing sample statistics including the mean and covariance. Based on the covariance structure, one can also explore variability in shape samples via principal component analysis. Finally, the estimated mean and covariance can be used to define Wrapped Gaussian models on the shape space, which are easy to sample from. We present multiple case studies on various biological datasets including (1) leaf outlines, (2) internal carotid arteries, (3) Diffusion Tensor Magnetic Resonance Imaging fiber tracts, (4) Glioblastoma Multiforme tumors, and (5) vertebrae in mice. We additionally provide a Matlab package that can be used to produce the results given in this manuscript.

1. Introduction

1.1. Motivation

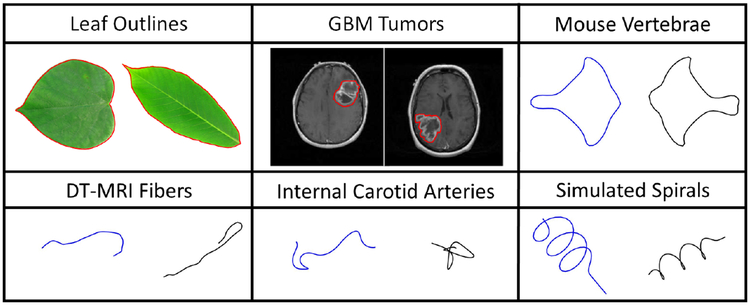
Shape is one of the most fundamental properties of biological structures, and it provides a unique characterization of their overall appearance. For example, the shape of a leaf outline as well as the internal vein structure are highly indicative of the tree species that the leaf came from [9,25]. In another context, the shape/structure of a protein is often closely related to its function [20,14,30]. Thus, shape analysis provides an important set of data analytic tools for multiple biological applications including botany, bioinformatics, medical imaging, etc. Shape analysis methods develop appropriate mathematical representations of shape, metrics on the corresponding shape spaces, and efficient computational tools that can be used to quantify shape differences. Statistical shape analysis treats shape as a random object and provides tools for computing summary statistics of a sample of shapes, characterization of variability in shape classes via principal component analysis (PCA), classification and clustering of shapes, definition and fitting of statistical models on shape spaces as well as associated inferential tools such as hypothesis testing [24], Figure 1 shows several examples of biological data that can benefit from statistical shape analysis: this includes leaf outlines, Glioblastoma Multiforme (GBM) tumors, mouse vertebrae, Diffusion Tensor Magnetic Resonance Imaging (DT-MRI) fiber tracts and internal carotid arteries. For the leaf and GBM tumor examples, we show the outlines in red overlayed on the original images from which the data was extracted. We additionally include two simulated spiral curves that are helpful in understanding the shape of α-helices in protein structures [29]. It is also important to note that while this paper focuses on applications in biology (in the most general meaning of the word), statistical shape analysis plays an important role in many other applications, including computer vision, graphics, anthropology, geology, and more [42].

Fig. 1:

Several examples of biological structures where shape plays an important role in the characterization of their appearance: leaf outlines extracted from photo images, GBM tumor outlines extracted from MRIs, mouse vertebrae, fiber curves extracted from DT-MRIs, internal carotid arteries and simulated spirals.

1.2. Landmark-based Shape Analysis

In 1984, D.G. Kendall [17] defined shape as a geometric property of an object that remains after rigid motion (translation and rotation) and scaling variabilities are filtered out. Kendall, and many others, represented shapes via a finite collection of points called landmarks. The landmarks can either be provided by an expert in the application area of interest or automatically identified through simple mathematical features of the objects such as high absolute curvature. The former type of landmarks are called anatomical due to their semantic meaning in the context of the objects being studied. The latter are simply called mathematical landmarks. Statistical shape analysis using the landmark-based representation is very well-developed, especially for two-dimensional objects; there are many books on this topic including [38,4] and [12], These methods have also reached deep into biological applications; for some examples, see [31,34,10,3,5]. However, in many modem “big data” scenarios, the need for landmark selection becomes impractical and sometimes even impossible. In medical imaging, radiologists and doctors are usually the experts who annotate landmarks for shape analysis. However, when the sample size reaches hundreds or thousands of images, this process becomes expensive and extremely tedious. At the same time, in the context of tumor shape analysis, anatomical landmarks often do not exist. Another drawback of landmark-based shape representations is loss of information, i.e., once the landmarks are chosen, the rest of the object’s outline is discarded.

1.3. Contour-based Shape Analysis

In the past two decades, there has been a steady push in the shape analysis community to define new tools based on functional representations of the objects’ outlines. These methods bypass the need for landmark selection, and use the entire outline as a shape representation for statistical analysis. The main challenge in such approaches is the need for an additional form of invariance in the analysis: re-parameterizations of the functions representing the objects’ contours do not change their shape. There are two ways to deal with this issue. Earlier works fixed the parameterization of all objects to arc-length and proceeded with shape analysis under this normalized setting [47,19,40]. The main drawback of these approaches is that fixed parameterizations are often suboptimal in terms of the matching of geometric features across objects, i.e., the same part of a leaf outline may not be well-matched across two leaves under fixed, arc-length parameterization. Allowing arbitrary parameterizations of objects in the representation of shape allows one to achieve invariance to this nuisance variability through the process of registration. Informally, registration achieves point-to-point correspondence across objects based on their geometric features. More formally, this process requires a metric on the representation space that is preserved under common re-parameterizations. One can then compute optimal registrations, under this metric, by minimizing the distance between two shapes with respect to re-parameterization (this process is described formally in Section 2.3).

Figure 2 confirms that a translation, scale, rotation and re-parameterization of the outline of a biological object do not change its shape. The translation, scale and rotation nuisance variables only change the two-dimensional coordinates traced by the outline of the object; in addition, a re-parameterization (a special function made precise later) changes the speed at which the outline is traversed (shown in the figure using color and spacing between neighboring points along the outline). Thus, any statistical shape analysis framework must respect the invariance to these four transformations.

Fig. 2:

Translation, scale, rotation and re-parameterization represent nuisance transformations in shape analysis (left). We generally observe curve data under random such transformations (right). Different parameterizations are displayed using a change in color as one traverses the outline from the start (blue) to the end point (yellow), and as points on the outline sampled according to the rate of traversal (compared to arc length, points are more (less) spread out when the curve is traversed faster (slower).

This paper describes a particular recent framework for shape analysis of 2D and 3D curves that allows elastic registration. The methods described here are based on an elastic metric (hence, elastic registration) [32,46], which provides a natural and intuitive interpretation of shape deformations, and their contribution to comparisons and statistics of shapes. An important ingredient is a simplification of the elastic metric through a convenient transformation called the square-root velocity function (SRVF) [16,41,22,42]; this, in turn, allows efficient computation on the shape space, thus facilitating statistical analysis of potentially large shape datasets. Some aspects of the mathematical properties of the SRVF framework are discussed in [7,26]. As seen in detail in subsequent sections, the SRVF chooses a particular instance within the general family of elastic metrics by fixing two parameters related to penalties on stretching and bending of curves. Recent efforts within the community have focused on extending the SRVF approach to accommodate the entire family of elastic metrics [21,1], Other extensions of the original SRVF framework consider landmark-constrained elastic shape analysis, which is often of interest in biological applications [43].

1.4. Organization of Manuscript

The intent of this paper is to provide a light introduction to elastic shape analysis of curves under the SRVF framework, with many biological examples and a ready-to-use, documented Matlab package to reproduce some of the analyses. To achieve these goals, the rest of this paper is organized as follows. Section 2 provides the necessary mathematical background to define the elastic shape analysis framework. In particular, we provide a detailed description of the elastic metric and it’s relation to the SRVF. We also show how one can achieve invariance to all shape preserving transformations under this metric and representation. Section 3 builds on this by defining sample statistics of shapes including the mean and covariance, and for summarizing variability in shape data via PCA. It also provides tools for random sampling from the so-called Wrapped Gaussian distribution, which is extremely useful for model validation. In Section 4, we begin by describing the multiple datasets used throughout this paper. Then, to clearly show the benefits of the elastic shape analysis approach, we first apply it to a simulated spiral dataset. We then showcase the method on multiple biological datasets. We close the paper with a short discussion in Section 5.

2. Mathematical Framework

In this section, we first provide several preliminary definitions that will be helpful throughout the rest of the paper. For a more comprehensive review of these concepts, werefer the interested reader to texts on differential and Riemannian geometry including [6,27,39]. We then shift our attention to the description of elastic shape analysis under the SRVF framework.

2.1. Definitions and Preliminaries

In differential geometry, a nonlinear manifold M is a space that is not a vector space, i.e., ax + by ∉ M even if x,y ∉ M for $a,b\in ℝ$. However, manifolds have an important property of being locally Euclidean, i.e., a small neighborhood of any point on the manifold can be represented as a linear Euclidean space. The tangent space at a point p ∈ M is a vector space; it contains all possible tangential perturbations of p and is denoted by T_p(M). A Riemannian manifold is a smooth manifold M equipped with a smoothly varying inner-product ≪·,·≫_p defined on the linear tangent spaces. This inner-product is called a Riemannian metric. In this paper, we denote elements of a tangent space at a point p by δp ∈ T_P(M), and refer to them as tangent vectors.

The Riemannian structure on M provides many important geometric tools. First, using the Riemannian metric, one can define the length of a path between two points p, q ∈ M as $L[\alpha ]={\int }_0^1\sqrt{{\langle \langle \dot{\alpha }(\tau ),\dot{\alpha }(\tau )\rangle \rangle }_{\alpha (\tau )}}d\tau$, where α is a parameterized path between p and q on M, and $\dot{\alpha }$ denotes its time derivative. The shortest path between two points p and q on the manifold is called a (locally distance minimizing) geodesic: $\widehat{\alpha }=\text{arg}{\text{min}}_{\alpha :[0,1]\to M|\alpha (0)=p,\alpha (1)=q}L[\alpha ]$. One can think of geodesics as paths of minimal deformation, under the defined Riemannian metric, between points p and q on M. Then, the geodesic distance between p and q on M is defined as $d\left(p,q\right)=L[\widehat{\alpha }]$. For any point p ∈ M, the exponential map exp_p: T_P(M) → M maps points in the tangent space, δp ∈ T_P(M), to the manifold M, such that starting from p with velocity δp one reaches exp_p(δp) along the geodesic path in unit time. Thus, we also sometimes refer to the tangent vector δp as a velocity or shooting vector. The inverse of this operation, called the inverse-exponential map ${\text{exp}}_p^{-1}:M\to T_p(M)$, projects a point q ∈ M to a corresponding tangent vector δp ∈ T_P(M) using $\delta p={\text{exp}}_p^{-1}(q)$; the length of this vector (as measured via the Riemannian metric) is exactly the same as the length of the geodesic path between p and q on M. The exponential map and its inverse allow us to seamlessly transfer points between the nonlinear manifold M and the linear tangent space T_P(M).

A highly relevant Riemannian manifold for shape analysis is the infinite-dimensional sphere in ${\mathbb{L}}^2\left([0,1],{ℝ}^d\right)=\left\{f:[0,1]\to {ℝ}^2|{\int }_0^1{\left|f\left(t\right)\right|}^{2}dt<\infty \right\}$, defined as ${\mathbb{S}}_{\infty }=\left\{f\in {\mathbb{L}}^2\left([0,1],{ℝ}^d\right)|{\int }_0^1{\left|f\left(t\right)\right|}^{2}dt=1\right\}$, endowed with the standard ${\mathbb{L}}^2$ Riemannian metric given by (for two tangent vectors $\delta f_1,\delta f_2\in T_f\left({\mathbb{S}}_{\infty }\right)$)

$$\langle \langle \delta f_1,\delta f_2\rangle \rangle ={\int }_0^1\langle \delta f_1(t),\delta f_2(t)\rangle dt,$$ (1)

where the inner-product inside the integral, 〈·,·〉, is the standard Euclidean product in ${ℝ}^d$. The relevant tangent space is defined as $T_f\left({\mathbb{S}}_{\infty }\right)=\left\{\delta f:[0,1]\to {ℝ}^d|\langle \langle \delta f,f\rangle \rangle =0\right\}$. The resulting ${\mathbb{L}}^2$ norm is given by $\Vert \delta f\Vert ={\left({\int }_0^1|\delta f(t){|}^{2}dt\right)}^{1/2}$, where |·| denotes the standard Euclidean norm in ${ℝ}^d$. Under this setup, the geodesic distance and path between any two functions $f_1,f_2\in {\mathbb{S}}_{\infty }$ can be computed analytically using the following two formulas:

$$d\left(f_1,f_2\right)={\text{cos}}^{-1}\left(\langle \langle f_1,f_2\rangle \rangle \right)=\nu ,$$ (2)

$$\widehat{\alpha }(\tau )=\frac{1}{\text{sin}(\nu )}\left(\text{sin}(\nu (1-\tau ))f_1+\text{sin}(\nu \tau )f_2\right),\tau \in [0,1].$$ (3)

Finally, one can also compute the exponential and inverse-exponential maps analytically using the following two formulas $\left(f_1,f_2\in {\mathbb{S}}_{\infty }\text{ and }\delta f\in T_{f_1}\left({\mathbb{S}}_{\infty }\right)\right)$:

$${\text{exp}}_{f_1}(\delta f)=\text{cos}(\Vert \delta f\Vert )f_1+\text{sin}(\Vert \delta f\Vert )\frac{\delta f}{\Vert \delta f\Vert },$$ (4)

$${\text{exp}}_{f_1}^{-1}\left(f_2\right)=\frac{\nu }{\text{sin}(\nu )}\left(f_2-\text{cos}(\nu )f_1\right).$$ (5)

As will becomes obvious in subsequent sections, the availability of analytical expressions for these geometric tools greatly simplifies the computation needed for statistical shape analysis.

2.2. Elastic Riemannian Metric, Square-Root Velocity Function and Pre-Shape Space

Although shapes seem to be trivial for human beings to understand, mathematically defining the notion of shape is a daunting task. As noted earlier, we define shape as a property of an object’s outline that is invariant to the shape preserving transformations of translation, rotation, scale and re-parameterization. To treat the topic formally, we need to define a parameterization of an object’s outline. While the methods and concepts presented in this paper can be easily generalized to any dimension, to keep the presentation simple, we focus on two-dimensional, i.e., planar, curves. In this case, an object’s outline is given by a parameterized curve $\beta :D\to {ℝ}^2$, where D = [0,1] for open curves and $D={\mathbb{S}}^1$ for closed curves (there is no natural start/end point on a closed curve). We use D where a distinction between these two cases is not necessary. In the framework presented next, we consider the space of all absolutely continuous planar curves and denote it by $\mathcal{F}$.

A re-parameterization of a curve β is given by a function γ: D → D, which is smooth with a smooth inverse, and preserves the direction of parameterization. We denote the space of such functions by Γ (the set of orientation-preserving diffeomorphisms). Figure 3 illustrates several examples of such re-parameterization functions for D = [0,1], with the identity element (no re-parameterization) in red. Given a $\beta \in \mathcal{F}$ and a γ ∈ Γ, the re-parameterized curve is given by composing β with γ: β ◦ γ. Intuitively, a re-parameterization preserves the shape of a curve and only changes the speed at which the points along the curve are traversed. Figure 2 shows three examples of different parameterizations of the same curve. The parameterization in each case is displayed in two different ways: (1) as a change in color as one traverses the outline from the start to the end point, and (2) as a set of points sampled on the outline according to the rate of traversal, i.e., compared to arc length, points are more spread out when the curve is traversed faster and less spread out when the curve is traversed slower.

Fig. 3:

Several examples of re-parameterization functions of D = [0, 1], The identity, i.e., no re-parameterization, is given in red.

To build a statistical shape analysis framework, we are interested in answering the following basic questions:

1. What is the distance between two given shapes?

2. Having a proper distance function, how can we define and find the mean of a sample of shapes?

3. What are the principal modes of variation in a sample of shapes?

4. Can we define simple probability models on shapes and generate random samples from them?

As reflected in the order of the statistical queries above, the most critical notion that must be formalized is the definition of a distance between two shapes. The simplest solution that comes to mind is the standard ${\mathbb{L}}^2$ distance: $\Vert {\beta }_1-{\beta }_2\Vert ={\left({\int }_0^1{\left|{\beta }_1(t)-{\beta }_2(t)\right|}^{2}dt\right)}^{1/2}$. However, it is easy to show that the ${\mathbb{L}}^2$ metric is not invariant to re-parameterization, i.e., ‖β₁–β₂‖ ≠ ‖β₁ ◦ γ–β₂ ◦ γ ‖ in general; this makes the ${\mathbb{L}}^2$ metric inappropriate for shape analysis of parameterized curves [41, 46].

To this end, we begin by introducing a Riemannian metric, which provides an interpretable measure of dissimilarity between two curves. First, we represent the curve β using the pair (r, θ) where $r=|\dot{\beta }|$ (the speed function) and $\theta =\frac{\dot{\beta }}{|\dot{\beta }|}$ (the direction or angle function), where $\dot{\beta }$ denotes the time derivative of β. Note that the representation of β using the pair (r, θ) is unique up to translations. However, this does not pose problems for shape analysis since shape is defined to be translation invariant. Under this new representation, we define the so-called Elastic Riemannian Metric (ERM) as follows (for two tangent vectors (δr₁, δθ₁) and (δr₂, δθ₂)) [32]:

$$\begin{gathered} {\langle \langle \langle \left(\delta r_1,\delta {\theta }_1\right),\left(\delta r_2,\delta {\theta }_2\right)\rangle \rangle \rangle }_{(r,\theta )}= \\ =a{\int }_D\delta r_1(t)\delta r_2(t)\frac{1}{r(t)}dt+b{\int }_D\langle \delta {\theta }_1(t),\delta {\theta }_2(t)\rangle r(t)dt. \end{gathered}$$ (6)

The ERM has an intuitive interpretation: the first term measures stretching of the curve because the δr_i s are variations of the speed function, while the second term measures bending of the curve since the δr_is are variations of the direction function. Finally, and importantly, it can be shown that the ERM is invariant to re-parameterizations of curves: d_Erm(β₁, β₂) = d_Erm(β₁ ◦ γ, β₂ ◦ γ)·These properties make the ERM well-suited for shape analysis of parameterized curves.

Unfortunately, the ERM, as given in Equation 6, is difficult to use in practice. In fact, even computing distances under this Riemannian metric turns out to be a difficult numerical task. To circumvent this issue, Srivastava et al. [41] defined the square-root velocity function (SRVF) as $q=\sqrt{r}\theta =\frac{\dot{\beta }}{\sqrt{|\dot{\beta }|}}$ to represent the curve β. Note that since the SRVF is defined using $\dot{\beta }$ only, it is automatically invariant to translations. One can also show that if the curve β is absolutely continuous, its SRVF is an element of the space ${\mathbb{L}}^2\left(D,{ℝ}^2\right)$ [36]. Finally, the inverse mapping from an SRVF q to the corresponding curve β is given by the simple formula: $\beta (t)={\int }_0^{t}q(s)|q(s)|ds$ for all t. The natural metric on the SRVF space is then given by the ${\mathbb{L}}^2$ metric.

The next question is: How is the SRVF related to the ERM? To establish this connection, we first need to express tangent vectors δq in terms of the corresponding tangent vector pairs (δr, δθ). To do this, we compute the variation on both sides of the equation $q=\sqrt{r}\theta$ and get the following relationship $\delta q=\frac{1}{2\sqrt{r}}\delta r\theta +\sqrt{r}\delta \theta$. Plugging this expression into the standard ${\mathbb{L}}^2$ inner-product we get the following:

$$\langle \langle \delta q_1,\delta q_2\rangle \rangle =\frac{1}{4}{\int }_D\delta r_1(t)\delta r_2(t)\frac{1}{r(t)}dt+{\int }_D\langle \delta {\theta }_1(t)\delta {\theta }_2(t)\rangle r(t)dt,$$ (7)

which is exactly the ERM defined in Equation 6 with $(a,b)=\left(\frac{1}{4},1\right)$. This result is striking! Instead of working with the complicated ERM, one can simply transform all curves to their SRVF representations and use the simple ${\mathbb{L}}^2$ metric; the two approaches are equivalent. The only thing that is sacrificed is the flexibility of working with general values for (a, b). However, this is a small price to pay for the tremendous computational simplification.

In addition to translation invariance, we also want to remove variability due to scaling, rotation and re-parameterization. To remove scaling, we simply rescale all curves to unit length, i.e., ${\int }_D|\dot{\beta }|dt={\int }_D|q(t){|}^{2}dt=\Vert q{\Vert }^2=1$. Thus, the SRVFs of unit length curves have ${\mathbb{L}}^2$ norm equal to one and are thus elements of S_∞ (we have already defined many important tools for analyzing elements of S_∞ in Section 2.1). For closed curves $\left(D={\mathbb{S}}^1\right)$, we have an additional nonlinear closure constraint given by ${\int }_{{\mathbb{S}}^1}q(t)|q(t)|dt=0$. This leads to two representation spaces that are relevant for shape analysis: $\mathcal{C}=\left\{q:[0,1]\to {ℝ}^2\Vert q{\Vert }^2=1\right\}={\mathbb{S}}_{\infty }$ (SRVF space of unit length, open curves) and ${\mathcal{C}}^c=\left\{q:{\mathbb{S}}^1\to {ℝ}^2\Vert q{\Vert }^2=1,{\int }_{{\mathbb{S}}^1}q(t)|q(t)|dt=0\right\}\subset {\mathbb{S}}_{\infty }$ (SRVF space of unit length, closed curves). These two spaces are termed pre-shape spaces since we have not yet accounted for the variability due to rotations and reparameterizations.

Figure 4(a) illustrates the geodesic path and distance between two SRVFs q₁ and q₂·, in the pre-shape space $\mathcal{C}$. Since $\mathcal{C}$ is a sphere, the geodesic path $\widehat{\alpha }$ is a great circle connecting q₁ and q₂; the expression for this path is given in Equation 3. The corresponding geodesic distance between q₁ and q₂ is simply the length of this great circle geodesic path. Figure 4(b) illustrates the mapping of points from the tangent space $T_{q_1}(\mathcal{C})$ to the pre-shape space $\mathcal{C}$, and vice versa, using the exponential and inverse-exponential maps, respectively. The mathematical expressions for these mappings are given in Equations 4 and 5.

Fig. 4:

(a) Geodesic path and distance between two SRVFs on the pre-shape space C. (b) Exponential and inverse-exponential maps on the SRVF pre-shape space C.

2.3. Shape Space and Distance

We use the notion of equivalence classes, also called orbits, to reconcile the remaining two nuisance variabilities: rotation and re-parameterization. First, the SRVF of a rotated curve Oβ, where $O\in SO(2)(SO(2)=\left\{O\in {ℝ}^{2\times 2}|O^{T}O=I,det(O)=1\right\}$ is the special orthogonal group, which contains all rotation matrices), is simply given by Oq. Second, the SRVF of a re-parameterized curve β ◦ γ, where γ ∈ Γ, is given by $(q,\gamma )=(q\circ \gamma )\sqrt{\dot{\gamma }}$. Thus, rotations act in the same way on SRVFs as they do on the original curves. However, re-parameterizations do not; there is an extra term of $\sqrt{\dot{\gamma }}$ in the action on SRVFs. Using this new action, one can show that the ${\mathbb{L}}^2$ metric on the SRVF space is invariant to re-parameterizations: ∥q₁–q₂∥ = ∥(q₁, γ) – (q₁, γ)∥ (we already knew this since the ${\mathbb{L}}^2$ metric on the SRVF space is equivalent to the parameterization-invariant ERM on the space of curves). We define an equivalence class of an SRVF as [q] = {O(q, γ)|O ∈ SO(2), γ ∈ Γ }, i.e., all possible rotations and re-parameterizations of q. The equivalence class [q] represents a shape uniquely, and the set of all such equivalence classes defines the shape space S = {[q]} = C/(SO(2) × Γ) (i.e., a quotient space of the pre-shape space under the action of the rotation and re-parameterization groups).

We begin by defining the shape distance for open curves. Due to parameterization invariance of the metric on the pre-shape space, this distance is defined as:

$$d_s\left(\left[q_1\right],\left[q_2\right]\right)=\underset{(O,\gamma )\in SO(2)\times \Gamma }{\text{inf}}{\text{cos}}^{-1}\left(\langle \langle q_1,O\left(q_2,\gamma \right)\rangle \rangle \right).$$ (8)

Denoting the minimizers of Equation 8 by O* and y*, we can compute $q_2^{*}=O^{*}\left(q_2,{\gamma }^{*}\right)\in \left[q_2\right]$, and construct the corresponding geodesic path from q₁ to $q_2^{*}$ for visualizing shape deformations (this geodesic is a path of minimal deformation between the two shapes); it is given by the great circle arc connecting q₁ and $q_2^{*}$ on the pre­ shape space $\mathcal{C}$. The minimizer O* ∈ SO(2) can be computed using Procrustes analysis (essentially a singular value decomposition problem). The minimizer γ* ∈ Γ can be computed using the Dynamic Programming algorithm [36] or a gradient descent approach [42], For closed curves, ${\mathcal{C}}^c\subset {\mathbb{S}}_{\infty }$, and therefore geodesic paths and distances between shapes are no longer available in closed form. However, one can use efficient numerical techniques, such as the path straightening algorithm [18], to perform these computations. We omit the description of these methods for brevity and refer the interested reader to [41] for further details. In the remainder of the paper, we abuse notation slightly and simply use d_s to refer to the shape distance between open and closed curves.

Figure 5 explains the process of computing the geodesic distance between two shapes. The orbits of two SRVFs q₁ and q₂ represent their shapes, and contain all of their possible rotations and re-parameterizations. Thus, we are tasked with computing the distance between the two orbits. To do this, we fix q₁ in [q₁] (corresponding to the left camel) and search for an optimal rotation O* e SO(2) and optimal re­ parameterization γ* ∈ Γ that moves q₂ (corresponding to the bottom-right camel) along its orbit to a point q₁ (corresponding to the top-right camel) that is closest to the orbit of q₁. Then, the distance between these two elements is the same as the distance between the two orbits in the shape space S. The change in rotation and parameterization between the bottom-right and top-right camels is clear, and allows for better matching of geometric features for the camel on the left and the camel on the right.

Fig. 5:

Computation of the geodesic distance between shapes involves the search for an optimal rotation and re-parameterization of one of the curves to best match it to the other. Initially, both curves are sampled using arc-length parameterization (left and bottom-right camels). The top-right camel has the same shape as the bottom-right camel, and has been optimally rotated and re-parameterized to match the left camel (note the different spacing of points and colors on the two front legs). Different parameterizations are displayed using a change in color as one traverses the outline from the start to the end point, and as points on the outline sampled according to the rate of traversal.

To further motivate the use of elastic shape analysis in real applications, we compare non-elastic deformations to their elastic counterparts for two examples taken from the MPEG-7 dataset¹, which consists of 1400 different shapes evenly split into 70 classes. This dataset is commonly used as a benchmark for various types of computer vision algorithms. Figure 6 presents these results. Elastic refers to a shape deformation computed under the SRVF representation in the shape space S; non-elastic refers to a shape deformation where the parameterization of both curves is fixed to arc-length. Visually, the elastic deformations are much more natural, where important features of the objects, such as legs, are preserved along the path. Elasticity becomes even more important during statistical analysis as any shape distortions become amplified. As an example, without formally defining an average shape, the midpoints of the presented paths are averages of the two endpoints. It is clear that elastic averages are better representatives than non-elastic ones.

Fig. 6:

Comparison of elastic versus non-elastic shape deformations. The two given shapes are shown in blue (start of path) and red (end of path). Each geodesic path of shapes is sampled using five equally spaced points in black.

3. Statistics on the SRVF Shape Space

After defining a meaningful distance between shapes, we can now also define various sample shape statistics. In the following, we define the mean, covariance, PCA, and a simple Wrapped Gaussian model that is easy to sample from.

3.1. KarcherMean Shape

The most basic summary statistic of interest is the sample mean shape. The main challenge in defining this mean is that the shape space S is not a vector space, but rather a quotient space of a nonlinear manifold. This points in the direction of computing an extrinsic or intrinsic mean on S. Extrinsic statistics require an embedding of the shape space in a larger linear space; it is not clear how this can be done for the shape space S. Thus, we proceed with the intrinsic shape mean defined through the Karcher mean.

Suppose {β₁, …, β_n} is a random sample of parameterized curves, and their corresponding SRVFs are given by {q₁, …, q_n}. Then, the Karcher mean shape is given by:

$$[\widehat{\mu }]=\text{arg}\underset{[q]\in \mathcal{S}}{\text{min}}\sum _{i=1}^n{d}_s{\left([q],\left[q_i\right]\right)}^2.$$ (9)

The Karcher mean $[\widehat{\mu }]$ is actually an entire equivalence class. However, for further analysis and visualization, we simply choose a single element within this class $\widehat{\mu }\in [\widehat{\mu }]$. The optimization problem in Equation 9 must be solved numerically via a gradient-based algorithm [35,28]. The detailed algorithm for computing the Karcher mean shape is given in [23] and uses the analytical expressions for the exponential and inverse-exponential maps provided in Equations 4 and 5. Note that the solution obtained via this algorithm may only be a local minimum. In some cases, one may be interested in computing a more robust measure of center such as the median. To do this, one minimizes the sum of shape distances rather than the sum of squared shape distances [13]. A detailed gradient-based algorithm for this optimization is also given in [23].

3.2. Karcher Covariance and Principal Component Analysis

Principal component analysis (PCA) is a statistical technique often used to (1) reduce the dimensionality of a dataset while retaining as much variation as possible, and (2) explore the main directions of variability in data. This is achieved through linear transformations of the original variables to new, uncorrelated variables called principal components (PCs). In general, PCA is performed via an eigendecomposition of the sample covariance matrix estimated from a set of given data. See [15] for a comprehensive introduction to PCA.

In the setting of elastic shape analysis, we estimate the sample covariance matrix and perform PCA in the tangent space at the estimated Karcher mean, $\widehat{\mu }$, as follows. We first project all of the data to this tangent space using the inverse-exponential map: $\delta q_i^{*}={\text{exp}}_{\widehat{\mu }}^{-1}\left(q_i^{*}\right)\in T_{\widehat{\mu }}(\mathcal{S}),i=1,\dots ,n$, where $q_i^{*}$ denotes the optimally rotated and re-parametereized SRVF q_i with respect to the mean $\widehat{\mu }$. Using this representation, the covariance kernel is defined as a function $K:D\times D\to ℝ$ given by $K(\omega ,\tau )=(1/(n-1)){\sum }_{i=1}^n\langle \delta q_i^{*}(\omega ),\delta q_i^{*}(\tau )\rangle$. Computationally, since the curves have to be sampled with a finite number of points, say N, the resulting covariance matrix is finite-dimensional and can be computed as follows. Let $X\in {ℝ}^{2N\times n}$ be the observed tangent data matrix with n observations and N discretization points in ${ℝ}^2$ on each tangent vector (where each $\delta q_i^{*}$ is reshaped to a vector of size 2N). Then, the Karcher covariance matrix $K_{2N}\in {ℝ}^{2N\times 2N}$ is computed using $K_{2N}=(1/(n-1)){\sum }_{i=1}^{n}X{X}^T$, since the Karcher mean has been identified with the origin of the tangent space $T_{\widehat{\mu }}(\mathcal{S})$.

Using the covariance matrix K_2N, one can perform PCA in the tangent space using standard singular value decomposition: K_2N = UΣU^T. The orthonormal matrix U contains the principal directions of variability in the observed data (orthonormal PCA basis). The diagonal matrix Σ contains the singular values of K_2N, ordered from largest to smallest, which correspond to the PC variances. Since the number of observations in real data analysis problems is typically smaller than the dimensionality of each tangent vector, i.e., n < 2N, there are at most n − 1 positive singular values in Σ. Then, the submatrix formed by the first r columns of U, call it U_r, spans the principal subspace of the observed data and provides the n observations of the principal coefficients in ${ℝ}^r$ as $C=U_r^{T}X$. An important tool in statistical shape analysis is the ability to visually assess the principal directions of variation by following geodesic paths in the directions given by columns of the matrix U. For a particular direction U_j, this is done by computing ${\text{exp}}_{\widehat{\mu }}\left(t\sqrt{{\Sigma }_{jj}}{U}_j\right)$, where Σ_jj is the jth singular value and the constant t is varied from t = −k to t = k (this will trace the geodesic path from −k standard deviations to +k standard deviations around the mean). We provide visualizations of this type in a later section to validate our PCA models.

3.3. Wrapped Gaussian Model and Random Sampling

Another useful statistical tool in shape analysis is the ability to generate random shapes from some model on the shape space; we use a simple one called the Wrapped Gaussian model. After dimension reduction through PCA, one can use a multivariate Gaussian distribution to model a tangent vector (rearranged as a long vector of size 2N). Then, to generate a random sample from this model, one computes $\delta q_{\text{rand}}={\sum }_{i=1}^k{z}_i\sqrt{{\Sigma }_{ii}}{U}_i$, where $z_i\stackrel{iid}{~}N(0,1)$ and k < n − 1. One can then rearrange the elements of δq_rand to form a matrix of size 2 × N and obtain a random shape in SRVF form by applying the exponential map $q_{\text{rand }}={\text{exp}}_{\widehat{\mu }}\left(\delta q_{\text{rand }}\right)$. The Wrapped Gaussian model, and its truncated version, are described in detail in [22].

4. Case Studies on Biological Data

In this section, we provide multiple examples of applications of the elastic shape analysis framework based on the SRVF representation to real biological datasets; we also consider a simulated dataset of spiral curves wherein the results are easily interpretable. Two examples from each dataset are displayed in Figure 1. This section considers two different data types: (1) three-dimensional open curves, and (2) two-dimensional closed curves. Each part contains three different datasets, each of which is described in more detail in the subsequent section. For each dataset, we show (1) geodesic paths and distances between pairs of shapes, (2) sample mean shapes, (3) principal modes of variability from PCA, and (4) a few random sample shapes from an estimated Wrapped Gaussian model.

4.1. Data Description

Simulated Data:

We begin with a simulated dataset of 3D open curves. Each curve in the dataset has a straight segment and three helices. The main sources of variability in this data come from the length of the straight segment and the width of the helices. This data was generated and used for illustrative purposes in [22].

AneuRisk65 Data:

This dataset of three-dimensional open curves represents the structure of internal carotid arteries. The curves were extracted from three-dimensional angiographic images taken from 65 subjects, hospitalized at Niguarda Ca’ Granda Hospital (Milan). The subjects were suspected of being affected by cerebral aneurysms. For a detailed description of this data and associated processing steps, see [37,45].

DT-MRI Fibers:

DT-MRI fiber tracts are typically represented as 3D curves; they are usually extracted via tractography from 3D DT-MRI scans. In short, tractography searches for the principal diffusion directions coinciding with the local tangent directions of fibrous tissues in the brain. The fiber tracts are then delineated by integration of the principal diffusion directions. The dataset used here was extracted from the human language circuit in the left hemisphere (see [33,22] for more details).

Flavia Plant Leaf Data:

The first dataset of two-dimensional closed curves is called the Flavia Plant Leaf data [44]. The leaf outlines were acquired from images of plants captured using a digital camera. The main task associated with this dataset is to classify leaves based on their shapes [25]. The entire dataset contains 32 classes of leaves with more than 50 observations per class.

Brain Tumor Contours:

Glioblastoma Multiforme (GBM) is a morphologically heterogeneous disease; it is known as one of the most common malignant brain tumors found in adults [2]. The dataset we use here corresponds to the outline of the GBM tumor in the axial MRI slice with largest tumor area. The original data from pre-surgical T1-weighted post-contrast and T2-weighted FLAIR MRIs were obtained from The Cancer Imaging Archive.

Mouse Vertebra:

The last dataset consists of the second thoracic (T2) vertebrae in mice. It has been analyzed in many previous papers including [11,8], and most recently [43]. The dataset contains three different groups of mice (30 control, 23 large, and 23 small). The large and small groups consist of mice that were genetically selected for large and small body weights; the control group was not genetically selected. This dataset is available in R as part of the “shapes” package².

4.2. Geodesic Paths and Distances Between Biological Shapes

We begin with several examples of elastic geodesic paths between shapes of various biological structures. Figure 7 presents the geodesic path and corresponding distance (number under the path) for each example. First, we note that the geodesic paths represent natural deformations between the considered shapes. In particular, it is noticeable that important geometric features are well-preserved along each path. For instance, in the case of the simulated spiral example, the first shape (start point of the geodesic) has a longer straight segment and a more contracted set of spirals. The second shape (endpoint of the geodesic) has a shorter straight segment and a stretched set of spirals. The corresponding shape deformation naturally preserves the three spirals and simply stretches them out while also contracting the straight segment. In the case of closed curves, we first focus on the geodesic path between the first pair of leaves. Here, the first thinner leaf deforms into a wider one, while preserving the structure of the sharp tip. In the second example for leaves, the first maple leaf has seven distinct peaks while the second one has only five peaks. Along the geodesic path, five of the peaks are nicely preserved while two are destroyed. The other examples, while more difficult to interpret, also show interesting shape deformations. Finally, it is clear that the associated distances are larger for shapes that visually differ more.

Fig. 7:

Several examples of elastic geodesic paths and corresponding distances (numbers under each path) between various types of biological shapes. The two given shapes are shown in blue (start of path) and red (end of path). Each geodesic path of shapes is sampled using five equally spaced points in black.

4.3. Karcher Means of Biological Shapes

As seen before, we can use the metric on the elastic shape space to define an average shape as a summary of given data. We show several examples for different types of data in Figure 8. To calculate the average shape, we first randomly select five objects from each original dataset. We show the selected samples in the left column of the figure. The corresponding Karcher mean shape for each sample is given in the right column of the figure. As one can see from the first example where we used the simulated spirals, the five shapes in the sample differ in two main ways: (1) the straight segments have very different lengths, and (2) the spirals have very different widths. The corresponding mean shape looks natural for this data, and nicely preserves the structure of the three spirals. For the two leaf outline examples, the computed average is also a nice representative of the given data, i.e., it is of very similar structure as the given sample. In the case of the GBM tumors, the given sample shapes are very heterogeneous. The resulting average is a bit smoother than the given data, but still contains some interesting geometric features.

Fig. 8:

Several examples of mean shapes for different types of biological data: the given samples are displayed in the left panel while the corresponding averages are shown in the right panel.

4.4. Principal Modes of Variation in Biological Shapes

Given a mean shape, one can project all of the sample shapes to the corresponding tangent space, estimate the covariance structure and perform PCA. It is then often useful to explore the principal modes of variability in shape data; this is done by following the PCA-based directions of variability within a certain amount of standard deviation around the mean for each direction. Figure 9 displays the shape paths for the first two principal directions of variability based on the data presented in Figure 8. For each direction, we traverse the path from −1.5 standard deviations to +1.5 standard deviations around the Karcher mean shape (displayed in red) (with a spacing of 0.5 standard deviations). We note that, overall, the displayed principal directions have a nice interpretation in terms of the variability present in the given data. For example, the first principal direction for the simulated spirals captures the variability in the length of the straight segment and the width of the spirals. The second direction reflects the amount of spread between the spirals; there appears to be much less variability in the second direction compared to the first one. Interestingly, the first principal direction for the maple leaf data captures the different shapes of the five peaks on the leaves. The second direction, on the other hand, captures the variability due to different numbers of peaks on the leaves: the path evolves from a maple leaf with seven peaks to a maple leaf with five peaks. The case of the GBM tumors is also interesting. Here, we note that the first principal direction of variability evolves from a relatively smooth, circular tumor to one with protruding parts, especially toward the top of the shape. This reflects natural variability in tumors; doctors often consider rounded tumors as milder than protruding ones. Finally, in the case of the internal carotid arteries, both directions of variability reflect the differing placements and magnitudes of high absolute curvature areas on the curves in the given data.

Fig. 9:

Several examples of the first two principal directions of variability (PD 1 and PD 2) in the data displayed in Figure 8. The displayed paths start at −1.5 standard deviations from the mean and deform to +1.5 standard deviations from the mean, with a spacing of 0.5 standard deviations between consecutive shapes.

4.5. Randomly Generated Biological Shapes Based on Wrapped Gaussian Model

We close this section with several examples of randomly generated biological shapes. We use the Karcher mean and PC directions to define the Wrapped Gaussian model based on each set of sample shapes displayed in Figure 8. Then, we randomly sample six different shapes for each case and display them in Figure 10. In all examples, the randomly sampled shapes have similar structure to the given data, i.e., they are natural in the context of each application. The six sample shapes of spirals differ in a natural way: they all have three spirals with different width and a straight segment with different length. The leaf random samples also vary in a natural way: some of the maple leaves have five peaks while others have six or seven. Thus, we conclude that the estimated model naturally reflects the variability in given data.

Fig. 10:

Several examples of random biological shapes generated from an estimated Wrapped Gaussian model.

5. Summary and Supplementary Materials

In this manuscript, we have described a framework for elastic statistical shape analysis of open and closed curves. This framework is based on an elastic Riemannian metric and a corresponding simplification via the SRVF transformation. This enables the definition of computationally efficient data analysis tools including (1) geodesic paths and distances, (2) Karcher means, (3) Karcher covariances and PCA, and (4) Wrapped Gaussian models. We demonstrate each of these ideas using multiple examples, and note that the resulting statistics are intuitive and naturally reflect variability in given data. In particular, we consider various biological applications including statistical shape analysis of (1) leaf outlines, (2) DT-MRI brain fibers, (3) internal carotid arteries, (4) GBM tumors, and (5) mouse vertebrae.

Most of the examples explored in this manuscript consider relatively smooth outlines of objects. A natural question arises regarding the robustness of these approaches to observation noise. In particular, it is important to understand the effect of noise on the estimation of the optimal re-parameterization during pairwise comparisons. In the small noise setting, this estimation is quite robust. However, in the presence of substantial noise, the described approach may be susceptible to registering geometric features created by the noise rather than the true underlying shape. Thus, in those cases, it is recommended to smooth or denoise the outlines prior to statistical analysis. For more details on the performance of these approaches in the presence of noise, we refer the interested reader to Section 4.8.3 in Srivastava and Klassen [42].

In addition to this manuscript, we have provided a package of Matlab functions that were used to produce all of the presented results. The functions include comments that help the user understand the different tasks being performed. Additionally, we have provided a ReadMe file with overall documentation for the package. The package can be downloaded using the following link: https://tinyurl.com/y8slvry7.