An Extended Dual Graph Library and Partitioning Algorithm Applicable to Pseudoknotted RNA Structures

Abstract

Exploring novel RNA topologies is imperative for understanding RNA structure and pursuing its design. Our RNA-As-Graphs (RAG) approach exploits graph theory tools and uses coarse-grained tree and dual graphs to represent RNA helices and loops by vertices and edges. Only dual graphs represent pseudoknotted RNAs fully. Here we develop a dual graph enumeration algorithm to generate an expanded library of dual graph topologies for 2 to 9 vertices, and extend our dual graph partitioning algorithm to identify all possible RNA subgraphs. Our enumeration algorithm connects smaller-vertex graphs, using all possible edge combinations, to build larger-vertex graphs and retain all non-isomorphic graph topologies, thereby more than doubling the size of our prior library to a total of 110,667 dual graph topologies. We apply our dual graph partitioning algorithm, which keeps pseudoknots and junctions intact, to all existing RNA structures to identify all possible substructures up to 9 vertices. In addition, our expanded dual graph library assigns graph topologies to all RNA graphs and subgraphs, rectifying prior inconsistencies. We update our RAG-3Dual database of RNA atomic fragments with all newly identified substructures and their graph IDs, increasing its size by more than 50 times. The enlarged dual graph library and RAG-3Dual database provide a comprehensive repertoire of graph topologies and atomic fragments to study yet undiscovered RNA molecules and design RNA sequences with novel topologies, including a variety of pseudoknotted RNAs.

1. Introduction

New RNA molecules with novel functions in cellular and biological processes are continuously being discovered. From a historical perspective, the traditional roles of RNA molecules in deciphering the genetic code and protein synthesis [1] were followed more recently by the discovery of a myriad of RNA molecules involved in regulation of gene expression (riboswitches, miRNAs, siRNAs, etc.) [2, 3] and catalysis [4, 5, 6]. Apart from naturally-occurring RNAs, new RNA molecules are also being created, using experimental methods like SELEX [7, 8, 9] and various computational RNA design algorithms [10, 11, 12, 13, 14, 15, 16, 17], with new structures and/or functions for various therapeutic and industrial applications [18, 19]. Because this trend indicates that our current pool of known RNAs and their structures will continue to increase [20], the development of computational and modeling tools to study and explore novel RNA topologies is thus a top priority [21, 22, 23].

One of the approaches to study RNA structures is to represent them using graph theory. Graphs were first used in the 1970s and 1980s to represent RNA secondary (2D) structures as a simplified method to study their interactions, similarities, and differences [24, 25, 26, 27]. Graph objects can be viewed as a coarse-grained approach to study RNA structures. Instead of representing nucleotides or atoms explicitly, multiple residues and base pairs are represented by simple edges and vertices. Such simplification allows us to use graph theoretical methods for the study of RNA structures and functions [28, 29, 30].

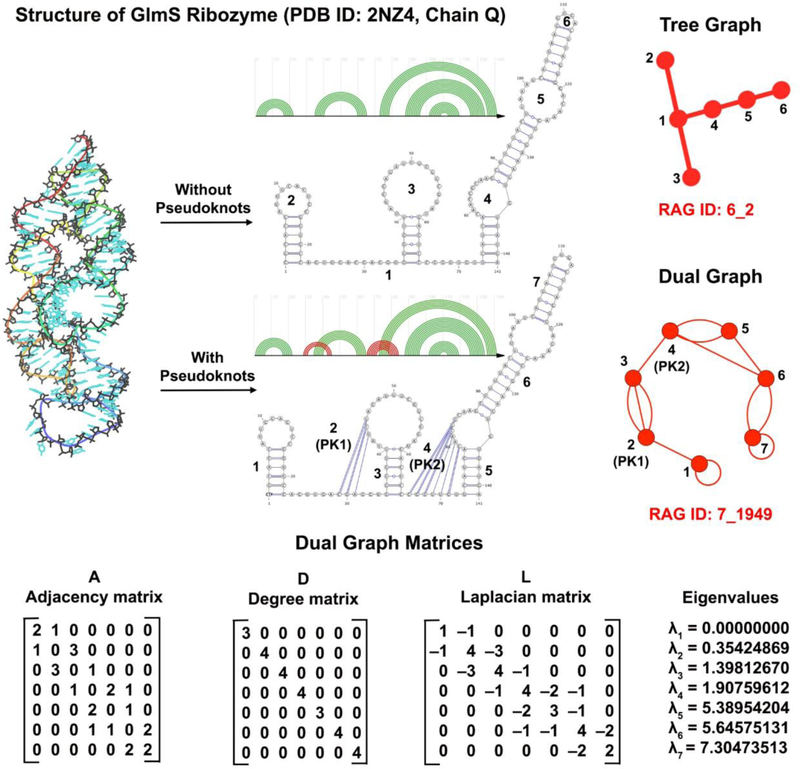
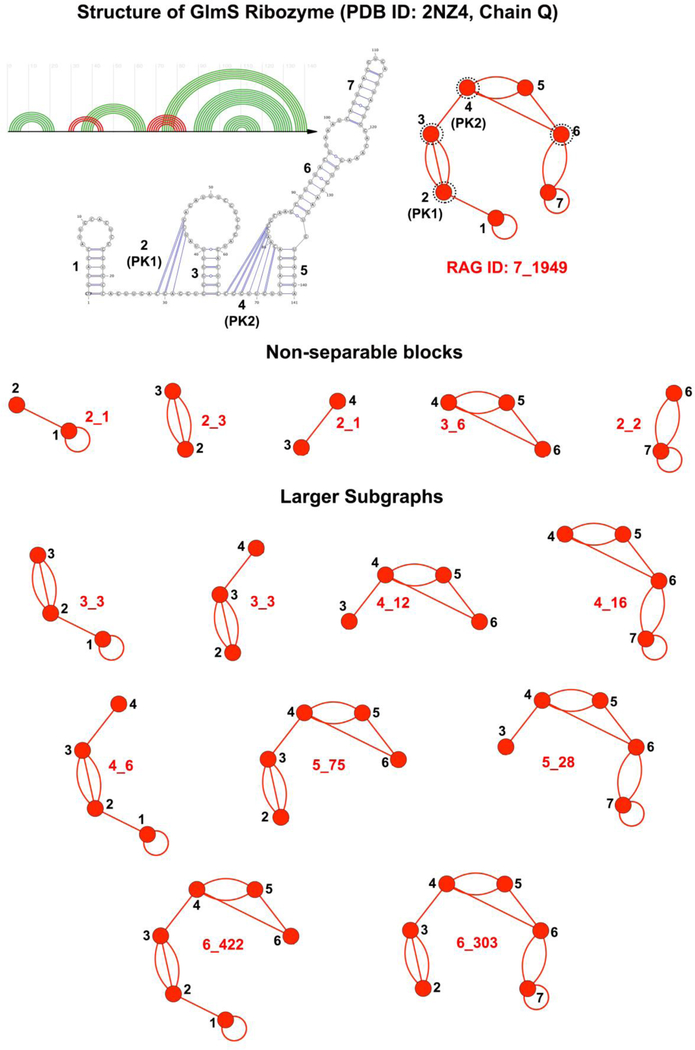
Specifically, our RNA-As-Graphs (RAG) approach represents RNA 2D structures as undirected and planar tree and dual graphs. Tree graphs represent unpaired loops in RNA structures as vertices and double-stranded helical regions connecting the loops as edges, whereas dual graphs represent helices as vertices and loop strands as edges [31]. Tree graphs are a type of simple graphs (i.e, one edge allowed between two vertices, with no self-edges) and make for a more intuitive representation of RNA 2D structure. Dual graphs, on the other hand, fall into the category of multigraphs that can have multiple edges between two vertices and also contain self-edges. These additional features make them capable of representing more complex RNA features like non-nested base pairs called pseudoknots which occur frequently in many important RNA molecules [32, 33]. Figure 1 shows the tree and dual graphs corresponding to the pseudoknot-free and pseudoknotted GlmS ribozyme structure (PDB ID: 2NZ4), respectively.

Figure 1:

Tree graph with 6 vertices and dual graph with 7 vertices for the GlmS ribozyme (PDB ID: 2NZ4), along with the adjacency matrix (A), degree matrix (D), and Laplacian (L = D − A) corresponding to the dual graph. The dual graph vertices corresponding to the pseudoknots are labelled as PK1 and PK2. The eigenvalue spectrum of the Laplacian is also given.

We have previously used graph representations in many contexts, such as to: create a library of graph topologies up to 13 vertices for tree graphs (that correspond to RNA molecules of ≈ 260 residues) [34] and 9 vertices for dual graphs [35]; partition tree graphs [36] to create a database of RNA atomic fragments (RAG-3D [37]); predict junction topologies for RNA [38, 39]; sample RNA tree graphs for the prediction of RNA topologies (RAGTOP) [40, 41]; build atomic models from tree graphs by fragment assembly (F-RAG) [42]; and design novel RNA topologies [43]. We have also partitioned dual graphs into non-separable subgraph blocks, i.e., subgraphs that cannot be partitioned further without breaking junctions and pseudoknots [44, 45], to identify commonly occurring subgraph motifs in RNA structures and create a database of corresponding RNA atomic fragments called RAG-3Dual [46].

RNA design applications rely on our concept of “RNA-like” topologies. Namely, we use clustering techniques to classify tree and dual graph topologies into three groups: “existing” (topologies corresponding to known RNA structures), “RNA-like” (topologies that are more likely to correspond to RNA structures yet to be discovered), or “non RNA-like” [34, 35, 47]. Such classification is useful not only to study known RNA structures and substructures, but also to pinpoint new candidates for RNA design. More recently, we have automated such a design protocol by piecing together RNA subgraphs and their corresponding atomic fragments (from the RAG-3D database mentioned above) using fragment assembly to create sequences that fold onto novel RNA-like tree graph topologies [43]. For dual graphs, we had early on designed sequences for 8 RNA-like topologies (with 3 to 4 vertices) by manually combining sequences of small existing RNA structures [47]. Similar to the tree graph design pipeline, automating this procedure for a larger scale dual graph design will require a comprehensive dual graph library with accompanying database of RNA atomic fragments.

Here we present two methodological developments to advance our dual graph approach to predict and design RNA structures. First, we develop a dual graph enumeration algorithm based on an inductive approach to connect smaller-vertex graphs to generate larger-vertex graphs and construct an expanded dual graph library. Unlike our previous graph-growing method [47], our algorithm generates graphs using all possible edge combinations to connect two smaller graphs and retains all non-isomorphic topologies. Second, we extend our dual graph partitioning algorithm [44, 45] to generate all possible subgraphs (rather than only the non-separable building blocks) by recursively combining adjacent subgraph blocks.

We apply the enumeration algorithm to generate dual graph topologies between 2 and 9 vertices (partly shown in Figure 6 and available at http://www.biomath.nyu.edu/?q=rag/dual_vertices.php). The expanded dual graph library, containing 110,667 graphs, is more than double the size of the prior one, giving us access to a larger number of possible dual graph topologies. We also apply our extended partitioning algorithm on 3853 existing RNA structures (see Subsection 2.4) to identify more than 300,000 RNA subgraphs up to 9 vertices. Using our expanded dual graph library, we assign graph IDs to all RNA graphs and subgraphs, rectifying incorrect and missed assignments by the prior library.

Figure 6:

Complete dual graph library for 2 to 5 vertices. All graphs were generated by the dual graph enumeration algorithm described in this paper. Red graphs correspond to existing RNA structures. The complete library for 2 to 9 vertices is available at http://www.biomath.nyu.edu/?q=rag/dual_vertices.php.

With the newly generated and correctly classified subgraphs, we extend our RAG-3Dual database (available at https://github.com/Schlicklab/RAG-3Dual) to include atomic fragments for all possible subgraphs (not only for basic building blocks) between 2 and 9 vertices and update our previous list [46] of RNA topologies for existing RNA graphs and subgraphs. The enlarged dual graph library, combined with the extended partitioning algorithm and the RAG-3Dual database, makes available a more comprehensive repertoire of graph topologies and fragments to study yet undiscovered pseudoknot-containing RNA molecules and design RNA sequences with novel topologies.

2. Materials and Methods

2.1. Dual graph representation rules

RNA molecules are composed of chains of four bases - adenine (A), guanine (G), cytosine (C), and uracil (U). These bases can pair with each other to form double-stranded regions called helices or stems, interspersed with single-stranded regions called loops. The composition of loops and helices and their connectivity forms the secondary (2D) structure of the RNA molecule. Our RNA-As-Graphs (RAG) approach uses dual graphs to represent RNA 2D structures as follows [48, 49] (see Figure 1):

1. All residues are considered as a single chain.

2. Vertices denote all double stranded helices/stems with at least two canonical base pairs (AU and GC Watson-Crick, and GU wobble).

3. Edges represent single-stranded loop strands (for bulges, internal loops, and junctions) that connect helices. Single-residue bulges and internal loops with only one residue in each strand are ignored.

4. Self-edges denote hairpin loops (and helical ends).

5. Helical ends and unpaired residues at the 5′ and/or 3′ ends of the RNA chain are not represented.

A dual graph can be represented mathematically using three matrices, the adjacency matrix A, the degree matrix D, and the Laplacian matrix L. The matrix A specifies the number of edges between vertices in the dual graph. Thus, the element a_ij is the number of edges between vertices i and j if they are connected, 0 otherwise; the diagonal element a_ii = 2 if a self-edge exists at vertex i, 0 otherwise. Note that this is the main difference between tree and dual graph adjacency matrices. In tree graphs, there are no self-edges and the maximum number of edges between two vertices is 1. The matrix D describes the degree of each vertex; that is, the diagonal element d_i contains the number of edges incident on vertex i, or the sum of elements of row i in matrix A; all offdiagonal elements of matrix D are zero. The Laplacian L = D − A. Self-edges are ignored while calculating the Laplacian.

The eigenvalues and eigenvectors of the Laplacian provide information about the topology of the corresponding dual graph. Figure 1 shows the dual graph, its corresponding matrices, and Laplacian eigenvalue spectrum for the GlmS ribozyme (PDB ID: 2NZ4). Since the Laplacian is symmetric and the sum of every row and column of L is zero, the matrix is positive semi-definite. The smallest eigenvalue λ₁ = 0, and the second smallest eigenvalue λ₂ > 0 (as the dual graph is a connected graph). This second eigenvalue defines the algebraic connectivity (or Fiedler value) of the dual graph [50], and is a measure of the connectivity or compactness of the dual graph topology [48, 49]. Isomorphic dual graphs (ignoring self-edges) have identical eigenvalue spectra for L, but dual graphs with identical eigenvalue spectra are not necessarily isomorphic.

2.2. Dual graph enumeration algorithm

Based on the definitions in Subsection 2.1 and properties of RNA molecules, we define the following rules for dual graphs that correspond to RNA 2D structures:

1. Dual graphs representing RNA 2D structure are connected graphs, i.e., a path exists between every vertex pair.

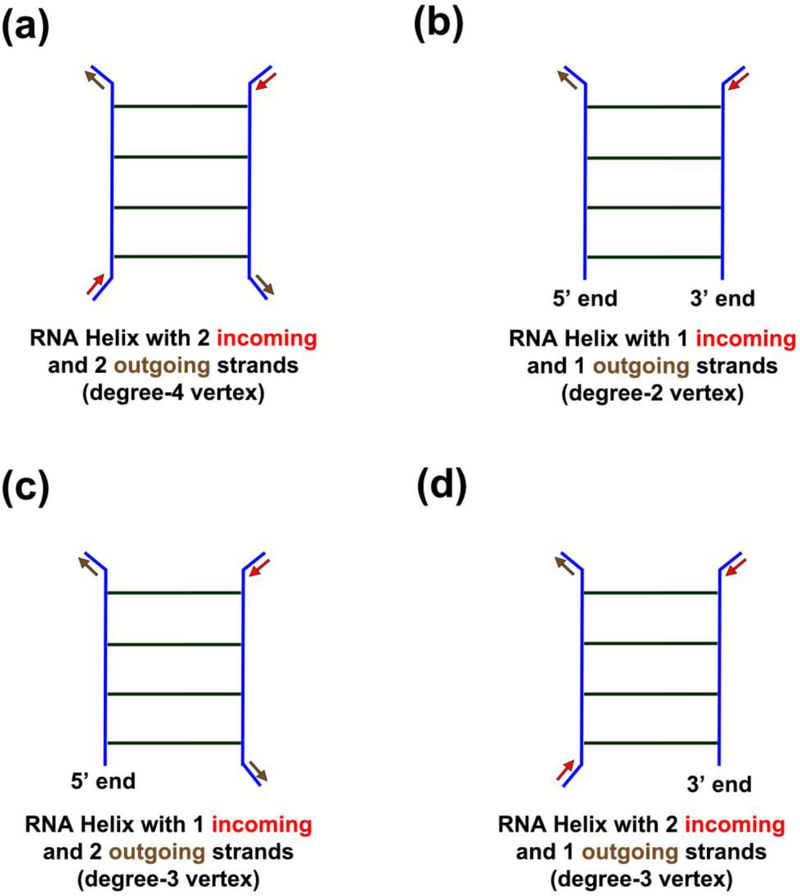
2. All RNA helices (except those with 5′ and/or 3′ ends) have two incoming strands and two outgoing strands. Therefore, the corresponding dual graph vertices have exactly four incident edges, i.e., they are “degree-4” vertices (see Figure 2(a)).

3. A dual graph must contain one of these features:

   1. exactly one degree-2 vertex, if both 5′ and 3′ ends are on the same helix (i.e., one incoming strand and one outgoing strand, Figure 2(b)),
   2. or exactly two degree-3 vertices, if 5′ and 3′ ends are on di erent helices (as they have three incoming and/or outgoing strands, Figure 2(c) and (d)).

   Therefore the degree sequence of a dual graph must be either (4,4,…,2) or (4,4,…,3,3).

4. A self-edge is counted twice, as it occupies one incoming and one outgoing strand on a helix.

Figure 2:

Types of RNA helices that correspond to di erent types of vertices in dual graphs. Incoming strands are indicated by red arrows and outgoing strands by brown arrows. (a) RNA helix with 2 incoming and 2 outgoing strands corresponds to a degree-4 vertex in the dual graph. (b) RNA helix containing both the 5′ and 3′ ends with 1 incoming and 1 outgoing strands corresponds to a degree-2 vertex in the dual graph. (c) RNA helix containing the 5′ end with 1 incoming and 2 outgoing strands corresponds to a degree-3 vertex in the dual graph. (d) RNA helix containing the 3′ end with 2 incoming and 1 outgoing strands corresponds to a degree-3 vertex in the dual graph.

2.2.1. Prior dual graph library

To study RNA molecules using dual graphs, we previously generated dual graph topologies that follow the above rules using a probabilistic graph-growing method [47, 48]. To generate a V -vertex graph, two vertices selected from the of V vertices were connected by a randomly selected number of edges (1, 2, or 3). This procedure was followed until all V vertices formed a connected graph. For every step (except the first), one of the two vertices was selected the set of previously connected vertices; thus the new graphs were inherently connected. This graph-growing process was performed multiple times to generate an ensemble of dual graph topologies. Since this method results in isomorphic graphs, dual graphs with identical eigenvalue spectra for the Laplacian were removed. The number of non-isomorphic graphs with identical eigenvalue spectra was used as a convergence criteria during the enumeration.

This method was used to generate dual graphs between 2 and 9 vertices. For vertex numbers V = 2, 3, 4, 5, 6, 7, 8, and 9, this resulted in 3, 8, 30, 108, 494, 2388, 12184, and 38595 dual graphs, respectively [47], defining our dual graph library. For comparative purposes here, we refer to the list of previously generated dual graphs as the Prior dual graph library. Each dual graph in the library was given a graph ID with the form V_n, where V denoted the number of vertices and n distinguished dual graphs with the same number of vertices. As every graph had a different Laplacian eigenvalue spectrum, each spectrum was assigned a unique integer n that uniquely identified its corresponding dual graph.

To assign a dual graph ID to a query RNA molecule, the RNA 2D structure was converted to a dual graph based on the rules mentioned in Subsection 2.1, and its Laplacian and eigenvalue spectrum were calculated. The eigenvalue spectrum of the query graph was compared to the spectra of the dual graphs in the prior library, and the RNA molecule was assigned the ID of the dual graph with the same eigenvalue spectrum [48].

2.2.2. New enumeration algorithm

The prior dual graph library eliminated dual graphs with identical Laplacian eigenvalue spectra to avoid including isomorphic graphs. However, this led to the exclusion of non-isomorphic dual graphs with identical eigenvalue spectra. The prior dual graph library also missed some dual graph topologies that corresponded to known RNA molecules, as we found recently [46].

To build a more complete library of dual graph topologies for RNA structures, we revised our graph-growing algorithm. Our new dual graph enumeration algorithm generates V -vertex dual graphs by connecting i-vertex graphs to V − i-vertex graphs (already computed on previous runs of the enumeration algorithm). The graphs are connected using all possible edge combinations and the resulting graphs of V vertices that do not follow all the dual graph rules listed above are discarded. All non-isomorphic graphs (ignoring self-edges) are retained among the remaining ones, even if they have identical eigenvalue spectra. Specifically, the steps are as follows:

Dual Graph Growing Algorithm

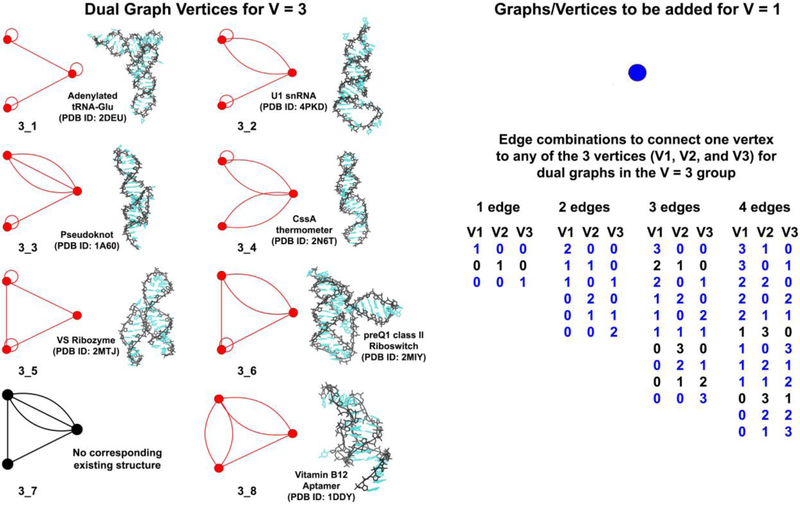
1. For each non-separable graph (graphs that do not have an articulation point and cannot be partitioned further, see Subsection 2.3 for details) with i vertices, remove all self-edges and generate all possible edge combinations by which this graph can be connected to any graph with V − i vertices. Depending on the number of edges already incident on them, each of the i vertices are allowed a maximum of 0, 1, 2, 3, or 4 additional edges (as the maximum degree of a vertex is 4). The additional edges can be used to connect this vertex to any of the V − i vertices of the second graph. All such possible connections for each of the i vertices constitute the possible edge combinations for this i-vertex graph.

   Figure 3 shows one vertex in blue (i = 1) that can be connected to the library of 8 graphs with 3 vertices shown in red and black (V − i = 3) to generate graphs with 4 vertices (V = 4). As this new vertex has no incident edges, it can be connected to any of the 3 previous vertices using 1, 2, 3, or 4 edges, resulting in 3, 6, 10, and 12 edge combinations, respectively. The figure lists the total of 31 edge combinations for connecting the new vertex to each of the 8 prior graphs.

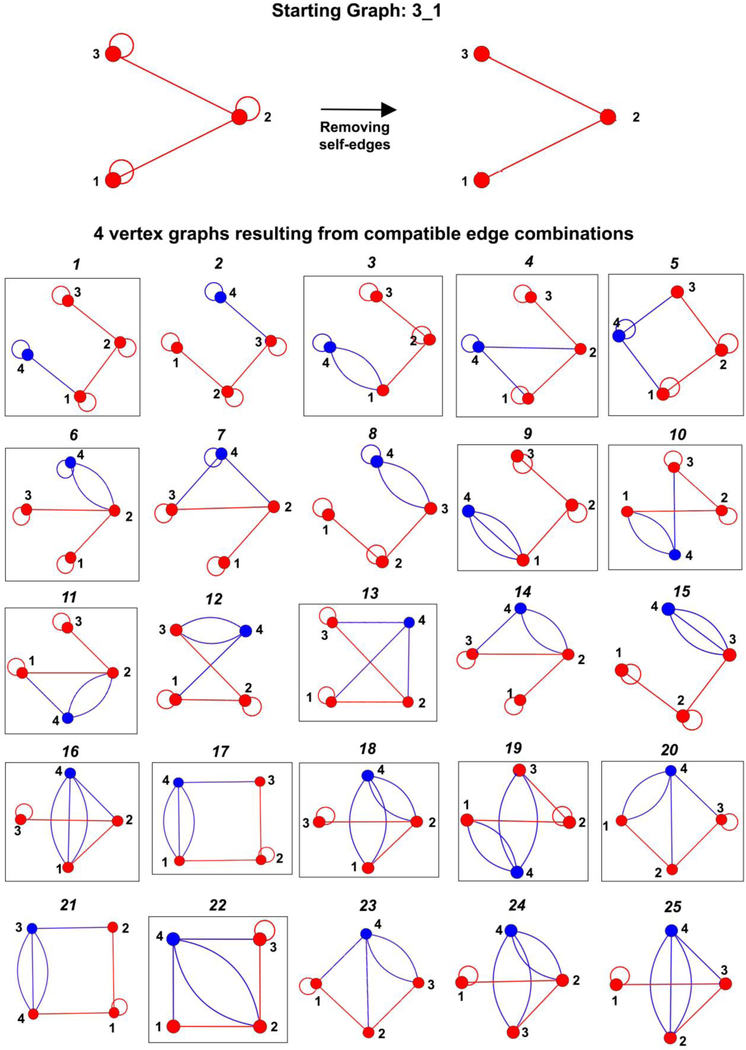
2. Next, connect the selected graph with i vertices to each graph with V − i vertices using every edge combination generated in Step 1. All self-edges are removed before the two graphs are connected. If the resulting graph of V vertex follows all the rules for dual graphs above (after adding back self-edges as required), it is retained for Step 3. Otherwise, the graph is discarded. Figure 4 illustrates the 25 of the 31 graphs generated by adding one vertex to the starting graph 3_1 using the 31 edge combinations listed in Figure 3. These 25 graphs follow all dual graph rules and are retained in this step. The remaining 6 graphs (shown in Supplementary Figure S1) are discarded.

   The number of graphs retained in this step depends on the starting graph. For example, 25 graphs illustrated in Figure 4 are retained for the starting graph 3_1, whereas this number is 17 and 7 for dual graphs 3_2 and 3_4, respectively (see Supplementary Figures S2 and S3).

3. Like the method used to generate the prior dual graph library (Subsection 2.2.1), Step 2 also results in isomorphic graphs. To ensure we retain only non-isomorphic graphs, the eigenvalue spectrum of the newly generated graph is compared to those of graphs already added to the dual graph library; if the eigenvalue spectrum is not found, then the new graph is added. If a graph or graphs with the same eigenvalue spectrum already exist, the new graph is added to the library only if it is non-isomorphic to the already added graphs (determined by generating permutations of rows and columns of the adjacency matrix of the new graph and comparing it to the already added ones). This ensures that non-isomorphic graphs with identical eigenvalue spectra are not discarded. For example, only the 15 non-isomorphic graphs boxed in black in Figure 4 are selected to be part of the dual graph library with 4 vertices.

Figure 3:

Dual graphs with 3 vertices (in red or black, along with one example of a corresponding existing RNA structure) used to generate dual graphs with 4 vertices by connecting one additional vertex (in blue). A total of 31 edge combinations (generated as described in Subsection 2.2.2) used to connect the new vertex to any of the 3 previous vertices with 1, 2, 3, or 4 edges are also listed. The numbers under columns V1, V2, and V3 in each edge combination are equal to the number of edges connecting the new and previous vertex numbers 1, 2, and 3 respectively. These 31 edge combinations are used to generate 31 4-vertex graphs, 25 of which (edge combinations highlighted in blue) follow all dual graph rules (shown in Figure 4). The remaining 6 edge combinations (in black) generate graphs that are discarded (shown in Supplementary Figure S1).

Figure 4:

Compatible dual graphs generated by our enumeration algorithm by connecting the new vertex (blue segment) to the starting graph 3 1 (red). Of the 31 graphs generated using the edge combinations listed in Figure 3, 25 graphs shown here follow all dual graph rules (see Supplementary Figure S1 for the remaining 6 graphs that do not follow our RNA dual graph rules). The 15 non-isomorphic graphs selected to be part of the dual graph library are shown in black boxes. The other 10 graphs, 2, 7, 8, 12, 14, 15, 21, 23, 24, and 25, are isomorphic to graphs 1, 4, 3, 10, 11, 9, 17, 20, 18, and 16, respectively.

The same form of graph ID is retained for graphs in the expanded dual graph library (see Subsection 2.2.1), but the integer n is now unique for each adjacency matrix, as non-isomorphic graphs in the new library can have identical eigenvalue spectra. As a result, an additional step is needed to assign graph IDs to query RNA graphs. After the eigenvalue spectrum of the query graph is matched to one or a set of the graphs in the expanded graph library, the query graph is assigned the ID of the graph that is isomorphic to it.

2.2.3. Implementation and performance

We implemented our dual graph enumeration algorithm in the Python programming language, and used the Linear Algebra package in the NumPy library for scientific computing for eigenvalue calculation and the inbuilt python dictionary for search. The algorithm takes the value of V, i, and V − i as input, along with the already computed eigenvalue spectra and adjacency matrices for i−vertex and V − i-vertex graphs. The output is the eigenvalue spectra and adjacency matrices for all non-isomorphic V-vertex graphs generated by the algorithm. Table 1 lists the di erent combinations of i and V − i used to generate new graphs with V vertices, for V = 2 to 9. We ran the graph-growing algorithm separately for each combination, collected all generated graphs, and retained all unique (or non-isomorphic) graphs to form the expanded dual graph library.

Table 1:

Vertex pairs used to generate dual graphs of 2 to 9 vertices from graphs with fewer vertices.

No. of Vertices	Vertex Combinations
2	1 and 1
3	1 and 2
4	1 and 3, 2 and 2
5	1 and 4, 2 and 3
6	1 and 5, 2 and 4, 3 and 3
7	1 and 6, 2 and 5, 3 and 4
8	1 and 7, 2 and 6, 3 and 5, 4 and 4
9	1 and 8, 2 and 7, 3 and 6, 4 and 5

The enumeration code was run on a linux cluster of 25 nodes with 888 Intel Xeon processors, with each node having 12 to 20 cores (2.2 − 2.4 GHz) and 128 − 198GB RAM. For V = 2 to 7, the computation time ranged from a few milliseconds to couple of hours. For V = 8 and 9, the computation was further divided into different graphs and run in parallel, and took several days to complete. The number of edge combinations to connect any two graphs grows exponentially with V, and most of the CPU time is spent on checking for graph isomorphism (each graph isomorphism check is O(V!)), as this problem has no known polynomial-time solution. However, since we only need to do the computation once, we did not expand any special optimization efforts. The details of the expanded dual graph library are provided in Section 3.

2.3. Extended dual graph partitioning algorithm

Our dual graph partitioning algorithm partitions dual graphs into distinct subgraphs while keeping pseudoknots and junctions intact [44, 45]. The algorithm partitions a dual graph into subgraphs by identifying articulation points. An articulation point is defined as a vertex v such that removing it and its incident edges from the graph results in a disconnected graph. If a graph or a subgraph does not contain any articulation point, it is called a non-separable subgraph or a block. Figure 5 shows the 5 non-separable blocks identified by the partitioning algorithm for a 7-vertex dual graph corresponding to the GlmS ribozyme. The articulation points identified by the algorithm are circled in black dotted lines.

Figure 5:

Non-separable blocks and larger subgraphs for the 7-vertex dual graph for the GlmS ribozyme (PDB ID: 2NZ4). The dual graph vertices corresponding to the pseudoknots are labelled as PK1 and PK2. Articulation points are denoted by black dotted circles. All larger subgraphs are generated by our extended partitioning algorithm by combining the non-separable blocks.

We have recently applied this partitioning algorithm to study most common subgraph blocks with and without pseudoknots in RNA structures, and identify possible ancestry relationships between ribosomal RNAs in different species [46]. However, the above algorithm only identifies non-separable blocks for dual graphs. We implemented an extension of the algorithm that recursively combines the non-separable blocks at the articulation points to identify all possible subgraphs. The steps below are followed to identify all subgraphs up to n vertices:

1. For each subgraph/block, identify all articulation points and associated adjacent blocks (blocks that share an articulation point).

2. Add the vertices and edges of adjacent blocks to the subgraphs, one adjacent block at a time, to identify new subgraphs. Duplicate subgraphs are discarded.

3. Follow Step 1 if the new subgraph has less than n vertices; otherwise terminate the recursive loop.

The above algorithm is run starting with each non-separabale block to identify all possible unique subgraphs. Figure 5 shows the 14 subgraphs (including the non-separable blocks) identified by the extended algorithm for the GlmS ribozyme dual graph.

2.4. RNA structure files

To build an RNA structure dataset to test our expanded dual graph library and extended partitioning algorithm, all RNA containing three-dimensional (3D) structures released on the Protein Data Bank (PDB) on or before August 31, 2018 were downloaded (total of 4042 PDB IDs), including multiple PDB files corresponding to parts of large structures (in mmCIF format). The 4042 downloaded RNA structures were separated into 9019 structure files or “Integrated Functional Elements” (i.e., single chains or multiple strongly base-paired chains) and grouped into “equivalence classes” (based on RNA molecule type, its sequence, structure, and species) as listed in the RNA dataset (version 3.37, August 31, 2018) available on the Bowling Green State University (BGSU) RNA site (http://rna.bgsu.edu/rna3dhub)[51]. Same rules were used to separate chains in RNA structures missing from the BGSU RNA dataset but present in the list download from the PDB. Equivalence classes were combined manually if necessary. Standard RNA residues (A, U, G, C) and modified RNA residues listed as “RNA linking” on the PDB were retained. All ligand and water molecules were removed, along with any protein or DNA residues. Residues in structures with insertion codes (residue numbers with letters) were renumbered. To avoid counting duplicate chains/models within the same PDB file that belong to the same equivalence class, we only retain one with the highest number of residues.

For the retained 6148 of the 9019 structure files, base pairs were identified using three different 2D structure annotation programs: RNAView [52], MC-Annotate [53], and DSSR [54]. Canonical base pairs (AU WC Saenger class XX, GC WC Saenger class XIX, and GC wobble Saenger class XXVIII, [55]) reported by at least two annotation programs were considered to create a consensus RNA 2D structure. Files with no base pairs, isolated single base pairs, or a single stem were removed, as they correspond to dual graphs with at most one vertex (with no associated adjacency matrix or dual graph ID). The remaining 3853 structure files were retained for assigning dual graph IDs and dual graph partitioning.

3. Results

3.1. Expanded dual graph library

Our enumeration algorithm of Subsection 2.2.2 was applied to generate dual graph topologies between 2 and 9 vertices. The dual graphs generated for a smaller vertex number were used to generate graphs for larger vertex number (see Subsection 2.2.3 for details). Figure 6 shows the dual graph library for V = 2 to 5 vertices. The full library is available on http://www.biomath.nyu.edu/?q=rag/dual_vertices.php. The graphs colored red correspond to existing RNA structures (see Subsection 3.2). Table 2 lists the number of dual graphs in the expanded library generated by our revised enumeration algorithm.

Table 2:

Number of dual graph topologies added (or removed) by the revised enumeration algorithm to form the current dual graph library. The 9 graphs that were manually assigned graph IDs recently [46] were not included in the prior library.

Number of Vertices	Number of dual graphs (Prior)	Prior graphs removed†	New graphs added	Number of dual graphs (Current)
2	3	0	0	3
3	8	0	0	8
4	30	1*	0	29
5	108	0	2	110
6	494	0	14	508
7	2388	1*	164	2551
8	12184	0	2486	14670
9	38595	0	54193	92788
Total	53810	2	56859	110667

^†The asterisk symbol denotes removal of a duplicate graph.

For V = 2, 3, and 4, no new graphs were added to the expanded library. For V = 5, 6, and 7, the enumeration algorithm adds 2, 14, and 164 new graphs, respectively, including the dual graph corresponding to a 7-way junction (7_2389) that was manually assigned a dual graph ID in our recent study [46]. We also removed two dual graphs labeled 4_15 and 7_174 as they were isomorphic (and hence duplicates) to 4_16 and 7_74, respectively. For consistency, graph 4_30 was re-labeled as 4_15, and one of the 164 newly added 7-vertex graphs was identified as 7_174.

The most significant changes to the library came for V = 8 and 9, where many more graphs were added, 20% and 140% of the prior library, respectively. Similar to 7_2389, the 8 9-vertex graphs corresponding to known RNA structures and non-separable blocks that were manually assigned graph IDs recently [46] were also generated automatically. The expanded dual graph library now contains 110,667 dual graphs, more than double the size of our prior library.

Of the new dual graph topologies added by the enumeration algorithm, the number of non-isomorphic graphs with identical eigenvalue spectra is significant (see Supplementary Table S1). The non-trivial number of graphs with at least one non-isomorphic graph sharing the same eigenvalue spectrum indicates the importance of including such topologies to avoid erroneous graph ID assignment of RNA graphs and subgraphs, as shown in Supplementary Section S1.

3.2. Dual graph IDs for existing RNA structures

In our recent study, we had identified 94 dual graph topologies between 2 and 9 vertices that corresponded to a non-redundant dataset of RNA structures [46]. This included the 4 9-vertex topologies (9_38596, 9_38597, 9_38598, and 9_38599) that were manually assigned a graph ID but are now automatically generated. To test our expanded dual graph library and generate a more comprehensive list of existing dual graph topologies, we updated our dataset of RNA structures to include all experimentally determined RNA 3D structures available in the PDB (see Subsection 2.4 for details). We then assigned dual graph IDs to 2495 RNA 2D structure files with RNA graphs between 2 and 9 vertices using the expanded dual graph library.

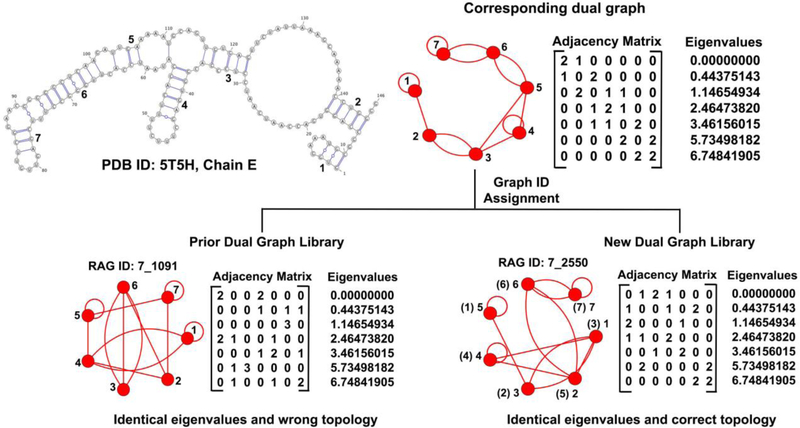
Table 3 shows the distribution of RNA dual graphs and their unique dual graph IDs. There are now a total of 121 existing dual graph topologies for V = 2 to 9. The added topologies include: 3_1 corresponding to tRNA-Glu pre-reaction state (PDB ID: 2DET), 5_27 corresponding to tRNA aminoacylation ribozyme (PDB ID: 3CUN), 5_71 corresponding to bound guanine riboswitch (PDB ID: 5C7W), and 5_97 corresponding to the poliovirus elongation complex (PDB ID: 3OL6) among others (shown in red in Figure 6). The added topologies also include 5 topologies that are present only in the expanded dual graph library: 7_2550 corresponding to short ribosomal RNA 1 (srRNA 1) of the 60S ribosomal subunit for Trypanosoma cruzi (PDB ID: 5T5H chain E), 8_12185 corresponding to bacteriophage MS2 genome fragments (PDB ID: 5TC1 chain R), 8_14143 corresponding to srRNA 1 of the large ribosomal subunit of Trypanosoma brucei (PDB ID: 4V8M, chain BE), 9_49214 corresponding to Taura syndrome virus IRES (PDB ID: 5JUU, chain EC), and 9_86359 corresponding to activated spliceosome from Saccharomyces cerevisiae (PDB ID: 5GM6, chain ELMN).

Table 3:

Number of dual graphs and subgraphs between 2–9 vertices for RNA 2D structure files and unique dual graph topologies corresponding to existing RNA graphs and subgraphs.

Number of Vertices	Existing RNAs		Subgraphs of Existing RNAs
	Total Graphs	Unique Graph Topologies	Total Subgraphs	Unique Subgraph Topologies
2	433	3	52506	3
3	309	7	34033	8
4	828	17	33021	24
5	189	20	35546	54
6	476	22	34951	113
7	201	21	36271	249
8	28	14	39124	564
9	31	17	45842	1257
Total	2495	121	311294	2272

The addition of graph ID 7_2550 to the set of existing RNA topologies is interesting. The RNA mentioned above was assigned the graph ID of 7_1091 previously [46]. Graph 7_1091 is non-isomorphic but has identical eigenvalue spectra as 7_2550, as shown in Figure 7. Since the prior library contained only one dual graph topology per spectrum (Subsection 2.2.1), this RNA was previously misclassified. With the correct graph ID assignment of 7_2550, 7_1091 is removed from the list of existing RNA topologies. In addition, 7 of the 94 topologies classified as existing previously are now removed because of re-labeled IDs (see Subsection 3.1), separate RNA chains now combined, or differences in base pair annotations (only one program, RNAView [52], previously, compared to consensus of three programs now, see Subsection 2.4).

Figure 7:

Changes in dual graph assignment for the short ribosomal RNA 1 of the 60S ribosomal subunit for Trypanosome cruzi (PDB ID: 5T5H chain E). The RNA was incorrectly assigned graph ID 7_1091 before, and is now 7_2550. The numbers in parenthesis show the vertex number of the RNA graph on top mapped onto the 7_2550 graph from the current library on right as they are isomorphic, and hence 7_2550 is the correct ID.

Further differences between the dual graph ID assignment for existing RNA structures can be found in Supplementary Subsection S1.1 and Table S2.

3.3. Dual graph IDs for RNA subgraphs

We now apply our dual graph partitioning algorithm (Subsection 2.3) to all existing 3853 RNA 2D structure files with more than 1 vertex. Each subgraph between 2 and 9 vertices is then assigned a graph ID using the expanded dual graph library, and the same procedure as for full RNA dual graphs is followed, except that now the query Laplacian corresponds to the vertices and edges in the subgraph. Our extended partitioning algorithm identifies 313,789 subgraphs (including the full graphs corresponding to 2495 RNA 2D structure files) between 2 and 9 vertices, as shown in Table 3. Using our expanded dual graph library, we assigned 2272 unique graph IDs to the 313,789 subgraphs.

Of the 2272 dual graph topologies, 73 dual graph topologies correspond to 74,995 non-separable subgraph blocks. Of the 56 dual graph topologies identified for subgraph blocks recently [46], 52 are included in the set of 73 topologies; the remaining 4 were removed because of difference in base pairs annotations (similar to removing some existing dual graph topologies in Subsection 3.2). The 21 newly added topologies include three topologies only present in the expanded dual graph library: namely 7_2416 corresponding to the pseudoknot containing fragment of group I intron (PDB ID: 2RKJ), 9_48753 corresponding to the 2-pseudoknot fragment of ribonuclease P (PDB ID: 2A2E), and 9_65778 corresponding to the large pseudoknot fragment in the assembly intermediate 16S rRNA (PDB ID: 3J2D).

More than 75% of the 313,789 subgraphs mentioned above are larger subgraphs (combination of non-separable blocks) identified by our extended partitioning algorithm. These subgraphs correspond to 2199 dual graph topologies, 882 of which are present only in our expanded dual graph library. Further updates to the prior dual graph library for RNA subgraphs are detailed in Supplementary Subsection S1.2 and Table S2.

Using these new subgraphs and their corresponding topologies, we have now updated our RAG-3Dual database (that previously consisted of 5332 atomic fragments corresponding to 56 dual graph topologies [46]) to include atomic fragments for all 313,789 RNA subgraphs cataloged based on 2272 dual graph topologies. Compared to our prior database, our updated RAG-3Dual database now contains more than 50 times the number of atomic fragments. Our updated RAG-3Dual database is available online at https://github.com/Schlicklab/RAG-3Dual.

4. Conclusion and Discussion

We have developed a dual graph enumeration algorithm that uses an inductive approach to connect smaller graphs, using all possible edge combinations, to construct larger dual graph topologies. We retain all non-isomorphic dual graph topologies that satisfy dual graph requirements for RNA structures, updating our prior approach [47, 48]. Our dual graph library for 2 to 9 vertices now has 110,667 graph topologies, more than double the size of our prior library. We have also extended our dual graph partitioning algorithm to identify all possible RNA subgraphs (and not just the basic non-separable blocks) and applied it to all existing RNA structures to obtain RNA substructures between 2 and 9 vertices. As a result, our updated RAG-3Dual database now contains 313,789 atomic fragments corresponding to 2272 dual graph topologies, more than 50 times its previous size. The current dual graph library is available at http://www.biomath.nyu.edu/?q=rag/dual_vertices.php, and the updated RAG-3Dual database is available at https://github.com/Schlicklab/RAG-3Dual.

Because the number of possible dual graph topologies increases exponentially with the number of vertices, the enumeration algorithm spends increasingly more time in checking all possible edge combinations to connect two dual graphs. Checking for isomorphic graphs requires generating all permutations of rows and columns of the adjacency matrices (see Subsection 2.2.3). Eliminating the edge combinations that produce isomorphic graphs (for example, by checking for graph symmetry) will reduce the run time, making the generation of dual graph libraries for greater than 9 vertices more feasible. Other algorithmic improvements can also be envisioned. Nevertheless, the number of topologies already available can be used for many exciting RNA structure analysis as well as design experiments.

Our recently developed pipeline to design sequences for RNA-like tree graphs [43] utilized our comprehensive library of tree graph topologies and RNA-like motifs we identified by clustering [34]. We also required a partitioning algorithm to identify different combinations of subgraphs and an extensive database of atomic fragments (to assemble the subgraph building blocks). The advances presented here will serve the same purpose for our future work on dual graph design for RNA with pseudoknots. With access to a much larger repertoire of possible dual graph topologies, we are currently working on clustering applications to classify them into RNA-like and non RNA-like, as done previously for both tree and dual graphs [34, 35, 47]. The expanded set of dual graph topologies we have identified as “existing” can help test the accuracy of different clustering methods. The RNA-like topologies we will identify will thus represent good candidates for RNA design [34]. Note, however, that although non RNA-like topologies are less likely to correspond to existing or new RNA structures compared to our RNA-like group, the classification is not perfect. Based on past assessments, we get “false negatives” in the non RNA-like group, but these are fewer than existing graph topologies that are correctly classified as RNA-like (as shown in our recent study with tree graphs [34]). In addition, both the extended partitioning algorithm and the updated RAG-3Dual database provide us with greater number of subgraphs (and corresponding atomic fragments) to generate novel combinations. These subgraph combinations and atomic fragments will also be useful in predicting RNA 3D structures, as we have previously done for tree graphs [42], from predicted graph topologies by our RAGTOP approach [40, 41].

Our partitioning algorithm and RAG-3Dual database can also be used to search and study similar substructures in RNA molecules, as done with RAG-3D search and database for tree graphs [37]. Classifying evolutionary relationships among ribosomal RNAs of different species and other large RNAs will also be possible by partitioning and motif search for dual graphs. Such analysis may shed insight into how different RNA molecules are related structurally, functionally, or evolutionarily (as we recently demonstrated [46]), and what features of RNA structures and corresponding graphs/subgraphs are more conserved. It will also be interesting to study the different sequences and tertiary interactions that eventually lead to the same overall fold. Such relationships might help explain why only a small proportion of all theoretically possible dual graph topologies are observed as graphs and subgraphs in existing RNA structures. Overall, the methodological developments presented here will advance our capability of using dual graphs to study, predict, and design RNA structures with more complex structural features.

Highlights:

1. Dual graph enumeration algorithm that retains all non-isomorphic dual graph topologies

2. Extended dual graph partitioning algorithm that keeps junctions and pseudoknots intact and identifies all possible RNA subgraphs

3. A more complete and comprehensive dual graph library and database of atomic fragments to study, predict, and design structurally complex RNA molecules

List of Abbreviations

RNA

Ribonucleic acid

DNA

Deoxy Ribonucleic acid

RAG

RNA-As-Graphs

PDB

Protein Data Bank

2D

secondary/two dimensional structure

3D

tertiary/three-dimensional structure

RAGTOP

RNA-As-Graphs Topology Prediction

F-RAG

Fragment Assembly for RNA-As-Graphs

sr-RNA

short ribosomal RNA

miRNA

micro RNA

siRNA

small interfering RNA