Characteristic, completion or matching timescales? An analysis of temporary boundaries in enzyme kinetics

Abstract

Scaling analysis exploiting timescale separation has been one of the most important techniques in the quantitative analysis of nonlinear dynamical systems in mathematical and theoretical biology. In the case of enzyme catalyzed reactions, it is often overlooked that the characteristic timescales used for the scaling the rate equations are not ideal for determining when concentrations and reaction rates reach their maximum values. In this work, we first illustrate this point by considering the classic example of the singleenzyme, single-substrate Michaelis–Menten reaction mechanism. We then extend this analysis to a more complicated reaction mechanism, the auxiliary enzyme reaction, in which a substrate is converted to product in two sequential enzyme-catalyzed reactions. In this case, depending on the ordering of the relevant timescales, several dynamic regimes can emerge. In addition to the characteristic timescales for these regimes, we derive matching timescales that determine (approximately) when the transitions from initial fast transient to steady-state kinetics occurs. The approach presented here is applicable to a wide range of singular perturbation problems in nonlinear dynamical systems.

1. Introduction

Nonlinear differential equations are used to model the dynamical behavior of natural phenomena in science. As the natural phenomena become more complex, the dynamics are influenced by multiple timescales, which create technical problems in the mathematical analysis and numerical computation of models (Lin and Segel, 1988).

The 21st century has been dominated by advances in the biological and biomedical sciences. As a result, examples of complex dynamical systems have become ubiquitous in theoretical and mathematical biology. Despite their complexity, all major levels of biological organization have one common dynamical denominator: chemical reactions are continuously taking place in living systems. Most of these reactions involve enzymes. Arguably, if biology is to be understood as a dynamical process, enzyme catalyzed reactions need to be investigated quantitatively (Gallagher, 2004).

The quantitative description of any enzyme catalyzed chemical reaction is often decomposed into two categories: thermodynamics and kinetics. The former tells us if a particular reaction is favorable, while latter describes the timescales over which reactions occur. From the point of view of the experimental scientist, chemical kinetics focuses on the measurement of concentrations as a function of time with the goal of characterizing reaction properties (Espenson, 1995). Regardless of whether a kinetic model is linear or nonlinear, stochastic or deterministic, the effectiveness of the model is only as good as the timescales it predicts (Shoffner and Schnell, 2017): timescales provide not only an estimation of the effective duration of the reaction, but are also critical in characterizing reaction mechanisms. This topic is not unfamiliar to Philip K. Maini, who has worked in a number of diverse areas of mathematical biology, including enzyme kinetics (Frenzen and Maini, 1988; Burke et al., 1990, 1993; Schnell and Maini, 2000, 2002, 2003).

Philip K. Maini mentored one of us, Santiago Schnell, through the rigorous theory of timescale analysis in chemical kinetics that lies at the intersection of chemistry and geometric singular perturbation theory (GSPT). In fact, GSPT is widely applicable not only to chemical kinetics, but to a plethora of important biological models (Bertram and Rubin, 2017). Largely, GSPT is the study of dynamical systems of the form

$$\stackrel{.}{x}=f(x,y),$$ (1a)

$$\epsilon \stackrel{.}{y}=g(x,y),$$ (1b)

where . denotes differentiation with respect to to time, and epsilon ≪ 1. These systems are often referred to as slow/fast systems, since changes in the variable x occur over timescales that are large compared to the timescales over which the variable y changes. For example, if time is rescaled as t_ε = t/ε, then the evolution of (1) becomes

$$x^{\prime }=\epsilon f(x,y),$$ (2a)

$$y^{\prime }=g(x,y),$$ (2b)

with ′ denoting differentiation with respect to t_ε. Over the t_ε-timescale, the variable x barely changes, while the variable y can change significantly. In contrast, the change in variable x is nontrivial over the t-timescale and, due to the presence of slow manifolds (Roussel and Fraser, 1990), the change in the variable y can be shown to be explicitly dependent on change in x. Thus, the dynamics of (1) is dependent on two different timescales: the fast timescale, t_ε, and the slow timescale, t. Each timescale defines a unique dynamical regime: the initial, “t_ε-regime”, over which x is essentially constant and y changes rapidly, and the “t-regime”, in which x changes significantly and the change in y is dependent on the change in x.

GSPT has a rich relationship with chemical kinetics, particularly regarding the application of matched asymptotics. Matched asymptotics is a common mathematical approach aimed at finding an accurate approximation to the solution of an equation, or system of equations (see Kuehn, 2015, for an excellent discussion on matched asymptotics). Usually, the study of matched asymptotics is linked to singular perturbation problems that arise as a consequence of underlying disparate spatial layers, such as boundary layers that form in pattern formation during embryonic development (see Maini et al., 2012). The specific aim of matched asymptotics is to generate a composite solution, which is constructed by gluing together local solutions (solutions that are asymptotically valid on different regimes) to comprise a solution that is uniformly valid (Holmes, 2013). Of principal interest in chemical kinetics, for which there typically exist multiple disparate timescales, is to determine the timescales that contribute to the composite solution.

In this work, we begin by introducing the characteristic timescale, which is a well-defined timescale from dynamical systems theory. We show that the established “fast timescale” of the single-enzyme, single-substrate, Michaelis–Menten (MM) reaction mechanism is in fact a characteristic timescale, and we demonstrate that characteristic timescales do provide a correct “partitioning” of time into the different slow and fast sub-domains from which the composite solution should be constructed. However, we also show that characteristic timescales are not suitable for determining when a transition from one dynamical regime to another dynamical regime occurs. This means that characteristic timescales cannot tell us when concentrations of certain chemical species reach their peak values, or when the rate of product generation reaches its maximum value. Thus, there is a need for an additional timescale, which we refer to as a matching timescale, that provides a temporal boundary between specific dynamic (kinetic) regimes. Its derivation follows directly from the theory of GSPT and matched asymptotics, and we demonstrate that appropriate matching timescales can be constructed from physical knowledge of the characteristic timescales. Specifically, through the application of Tikhonov–Fenichel Theory (Tikhonov, 1952; Fenichel, 1971), we derive the correct matching timescale for the MM reaction mechanism, and show that it can be explicitly obtained from the fast and slow characteristic timescales. We also categorize the corresponding slow timescale of the MM reaction mechanism as either a characteristic, depletion, or completion timescale.

Most chemical reactions that consist of two disparate timescales are well-understood. However, much of the modern GSPT analyzes problems comprising more than two timescales (Vo et al., 2013; Nan et al., 2015; Letson et al., 2017), and it is time to push enzyme kinetics in this direction. Thus, in this work, we analyze the kinetics of the auxiliary enzyme reaction mechanism (Eilertsen and Schnell, 2018)

$$\begin{gathered} S_1+E_1\underset{{}_{k_{-1}}}{\overset{{}^{k_1}}{\rightleftharpoons }}{C}_1\stackrel{{}^{{}^{k_2}}}{\to }{E}_1+S_2, \\ {S}_2+E_2\underset{{}_{k_{-3}}}{\overset{{}^{k_3}}{\rightleftharpoons }}{C}_2\stackrel{{}^{{}^{k_4}}}{\to }{E}_2+P, \end{gathered}$$

under the assumption that the auxiliary enzyme, E₂, is in excess with respect to E₁. We show that there are four timescales in a certain parameter regime of this reaction, and we illustrate that different orderings of the timescales must be considered in order to establish a complete description of the kinetics. The relevant characteristic timescales that approximate the duration of each regime are derived through geometric analysis of the phase-plane. Lastly, composite solutions and matching timescales are obtained.

2. The characteristic timescale

Consider a general, autonomous dynamical system of the form

$$\stackrel{.}{x}=f(x),$$ (3)

and suppose f(x) has a fixed point, x*, such that f(x*) = 0. The characteristic timescale is the reciprocal of the exponential growth/decay rate of the linearized equation in a small neighborhood surrounding x*. That is, if δ is a small perturbation, then

$${\phantom{\mid }f(x^{\ast }+\delta )\simeq \delta \frac{df}{dx}\mid }_{x=x^{\ast }}\equiv \delta f^{\prime }(x^{\ast })$$ (4)

and therefore

$$\stackrel{.}{\delta }\simeq f^{\prime }(x^{\ast })\delta .$$ (5)

Since linearized evolution of the perturbation grows or decays according to

$$\delta =\delta (0)\text{exp}[f^{\prime }(x^{\ast })t]$$ (6)

the characteristic timescale, t_χ, is the time required for the perturbation to significantly grow or decay:

$$t_{\chi }=\frac{1}{\mid f^{\prime }(x^{\ast })\mid }.$$ (7)

For a linear, exponential decay differential equation of the form

$$\stackrel{.}{x}=-\gamma x,x(0)=x_0,$$ (8)

the characteristic timescale is 1/γ, and corresponds to the exact amount of time it takes the initial condition to decay to

$$x(t_{\chi })=(1-\ell )x_0,\ell =\frac{\text{exp}(1)-1}{\text{exp}(1)},$$ (9)

which is roughly 0.37x₀. In addition, for a linear equation of the form

$$\stackrel{.}{x}=-\gamma x+A,x(0)=0,$$ (10)

where A is a constant, the characteristic timescale, 1/γ, is the exact amount of time it takes x to grow to

$$x(t_{\chi })=\ell \frac{A}{\gamma }\equiv \ell x^{\max },$$ (11)

or roughly 0.63x^max.

3. The slow and fast timescales of the Michaelis–Menten reaction mechanism: An exercise in the power and limitations of characteristic timescales

We continue by reviewing the pertinent characteristic timescales for the well-studied single-enzyme, single-substrate reaction mechanism (12), in which an enzyme, E₁, binds to a substrate, S₁ (forming an intermediate enzyme-substrate complex, C₁), and catalyzes the conversion of S₁ into product, P:

$$S_1+E_1\underset{{}_{k_{-1}}}{\overset{{}^{k_1}}{\rightleftharpoons }}{C}_1\stackrel{{}^{{}^{k_2}}}{\to }{E}_1+P.$$ (12)

The kinetics of the reaction depend not only in the rate constants, k₁ and k₋₁, and the catalytic constant k₂, but also on the initial concentrations of S₁ and E₁. Specifically, the reduced mass action equations that govern the kinetics of (12) are

$${\stackrel{.}{s}}_1=-k_1(e_1^0-c_1)s_1+k_{-1}{c}_1,$$ (13a)

$${\stackrel{.}{c}}_1=k_1(e_1^0-c_1)s_1-(k_{-1}+k_2)c_1.$$ (13b)

In this system, s₁ denotes the concentration of S₁, c₁ denotes the concentration of C₁, and $s_1^0$ and $e_1^0$ are, respectively, the initial substrate and enzyme concentrations. The mass action equations (13a)–(13b) can be approximated with the differential-algebraic equation,

$$\stackrel{.}{s}=-\frac{k_2{e}_2^0{k}_1}{k_{-1}+k_2+k_1{s}_1}{s}_1$$ (14a)

$$c_1=\frac{k_1{e}_1^0}{k_{-1}+k_2+k_1{s}_1}{s}_1,$$ (14b)

by assuming the quasi-steady-state approximation (QSSA).

Despite a significant body of literature dedicated to the development of methods and techniques for estimating timescales in chemical kinetics (Rice, 1960; Palsson and Lightfoot, 1984; Palsson et al., 1985; Palsson, 1987; Segel, 1988; Segel and Slemrod, 1989; Shoffner and Schnell, 2017), timescale estimation remains ad hoc in most applications, and we will later see that this work is no exception. We will study and review (12) in regimes where the QSSA is valid. Historically, the most common method employed to study the validity of the QSSA is scaling combined with singular perturbation analysis. Early studies (Heineken et al., 1967) of the validity of the QSSA suggested that the initial enzyme concentration must be small in comparison to the initial substrate concentration: $\stackrel{‒}{\epsilon }\equiv e_1^0∕s_1^0\ll 1$. One of the first authors to recognize that $\stackrel{‒}{\epsilon }\ll 1$ was an incomplete condition for the validity of the QSSA was Bernhard Palsson (Palsson and Lightfoot, 1984; Palsson, 1987). Palsson made two important discoveries: (1) he recognized that the QSSA was still applicable when $e_1^0\approx s_1^0$ as long as $e_1^0\ll (k_{-1}+k_2)∕k_1$; (2) he noted that the QSSA is still valid when $e_1^0\approx s_1^0\approx (k_{-1}+k_2)∕k_1$ as long as κ₁ ≡ k₋₁/k₂ ≫ 1. About a year later, Segel (1988), who understood that there was subtle difference between non-dimensionalization and scaling, correctly estimated the disparate timescales of complex formation and substrate depletion. In short, the earlier studies failed to determine necessary conditions for the validity of the QSSA because, although time had been properly non-dimensionalized in previous analyses, it had not been appropriately scaled. Thus, history tells us that it is difficult, if not impossible, to determine necessary conditions for the validity of reduction techniques (like the QSSA) when slow and fast timescales are unknown. We will review Segel’s analysis in the forthcoming subsections. In addition, we will show that the timescales derived by Segel can be used to approximate the matching timescale, which gives a better estimation of the time it takes for the reaction to reach quasi-steady-state (QSS).

3.1. The characteristic initial fast transient of the reaction

It is well-established that, under the reactant stationary assumption (RSA, Hanson and Schnell, 2008; Schnell, 2014), the dynamics of (12) initialize with a brief initial transient during which the intermediate complex concentration, c₁, accumulates rapidly towards its maximum while the substrate s₁ remains effectively unchanged from the initial substrate concentration $s_1^0$. The RSA ensures $s_1\approx s_1^0$ during the initial transient of the reaction. Under the RSA, equation (13b) is approximately

$${\stackrel{.}{c}}_1\simeq k_1(e_1^0-c_1)s_1^0-(k_{-1}+k_2)c_1,$$ (15)

which admits the solution

$$c_1\simeq c_1^{\max }\left[1-\text{exp}\left(-k_1\left(K_{M_1}+s_1^0\right)t\right)\right],c_1^{\max }=\frac{e_1^0{s}_1^0}{K_{M_1}+s_1^0}.$$ (16)

In the above equation, K_M1 = (k₋₁ + k₂)/k₁ is the Michaelis constant. The characteristic timescale of the intermediate complex that arises from (16) is t_c1

$$t_{c_1}=\frac{1}{k_1(K_{M_1}+s_1^0)}.$$ (17)

Technical justification for t_c1 was originally obtained by Segel (1988) and Segel and Slemrod (1989). Through scaling analysis, they introduced the dimensionless parameters

$${\sigma }_1\equiv \frac{s_1^0}{K_{M_1}},{\kappa }_1\equiv k_{-1}∕k_2,{\beta }_1\equiv \frac{1}{1+{\sigma }_1}<1,{\alpha }_1\equiv \frac{{\kappa }_1}{1+{\kappa }_1}<1,$$ (18)

allowing equations (13a)–(13b) to be rescaled into their dimensionless form

$$\begin{gathered} \frac{d{\widehat{s}}_1}{d\tau }={\epsilon }_1[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],{\epsilon }_1=\frac{e_1^0}{K_{M_1}+s_1^0} \\ \frac{d{\widehat{c}}_1}{d\tau }={\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1, \end{gathered}$$ (19)

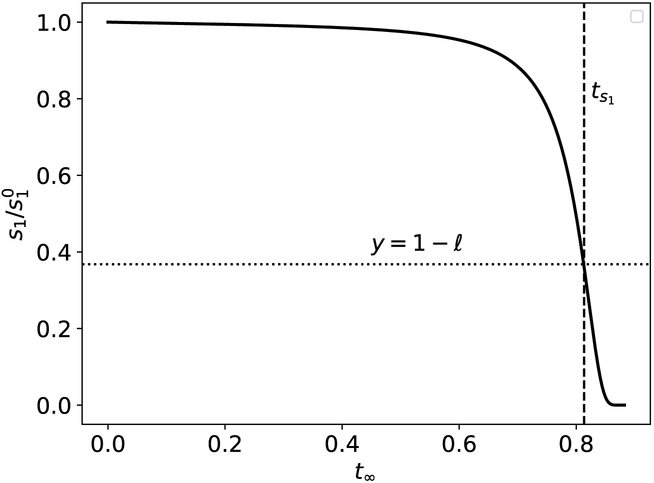
where τ = t/t_c1, ${\widehat{s}}_1=s_1∕s_1^0$ and ${\widehat{c}}_1=c_1∕c_1^{\max }$. It is clear from (19) that if ε₁ ≪ 1, then $s_1\simeq s_1^0$ when t ≤ t_c1. Formally, the qualifier ε₁ ≪ 1 is the condition for the RSA, and t_c1 is the characteristic timescale of the initial fast transient (see Figure 1).

Figure 1: The validity of t_c1 for the Michaelis-Menten reaction mechanism (12).

The solid black curve is the numerically-computed solution to (13a)–(13b). The dashed vertical curve is corresponds to $t_{c_1}=[k_1(K_{M_1}+s_1^0){]}^{-1}$. The dotted horizontal line corresponds to $\ell c_1∕c_1^{\max }=\ell$. The initial concentrations and rate constants used in the numerical simulation are: k₁ = 0.1, k₂ = 10, k₋₁ = 1, $e_1^0=1$ and $s_1^0=100$ (units have been omitted). Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)].

3.2. The slow timescale of the MM reaction: from characteristic to completion

In contrast to the brief timescale over which c₁ accumulates (i.e, t_c1), s₁ changes over a much longer timescale. The timescale over which there is appreciable change in s₁ is the slow timescale of the reaction or the substrate depletion timescale. As a direct result of singular perturbation theory, the depletion of s₁ is approximately

$${\stackrel{.}{s}}_1\simeq -\frac{V_1}{K_{M_1}+s_1}{s}_1$$ (20)

after the initial fast transient (i.e. for t > t_c1). The above expression, obtained from the QSSA, is known as the MM equation (see, Schnell and Maini, 2003; Schnell, 2014, for reviews), and $V_1=k_2{e}_1^0$ is the limiting rate of the reaction. The slow timescale, t_s1, is given by

$$t_{s_1}=\frac{s_1^0}{\max \mid {\stackrel{.}{s}}_1\mid }=\frac{K_{M_1}+s_1^0}{V_1}.$$ (21)

The technical justification of (21) is acquired through scaling analysis. By writing the dimensionless form (13a)–(13b) with respect to T = t/t_s1 yields

$$\begin{gathered} \frac{d{\widehat{s}}_1}{dT}=(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1], \\ {\epsilon }_2\frac{d{\widehat{c}}_1}{dT}={\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1. \end{gathered}$$ (22)

The dimensionless parameter, ε₂, is the ratio of fast and slow timescales: ε₂ = t_c1/t_s1.

While mathematicians typically refer to t_s1 as the slow timescale, the chemical interpretation of t_s1 depends on the initial specific concentration, σ₁. First, the MM equation (20) admits a closed-form solution with $s_1(t=0)=s_1^0$

$$s_1=K_{M_1}W[{\sigma }_1\text{exp}({\sigma }_1-{\eta }_{1}t)],{\eta }_1=\frac{V_1}{K_{M_1}},$$ (23)

where W[·] is the Lambert-W function (Corless et al., 1996; Schnell and Mendoza, 1997), and the closed-form solution is known as the Schnell–Mendoza equation (Clark et al., 2011; Feng et al., 2014; Son et al., 2015; Murugan, 2018). If σ₁ ≪ 1, then (23) is asymptotic to

$$s_1\simeq s_1^0({\eta }_{1}t)$$ (24)

from which we obtain:

$$s_1(t_{s_1})\simeq (1-\ell )s_1^0.$$ (25)

Thus, if the initial substrate concentration is much less than the Michaelis constant, K_M1, then the slow timescale, t_s1, is a characteristic timescale for the substrate species (see Figure 2).

Figure 2: The graphical illustration of the characteristic timescale for the Michaelis–Menten reaction mechanism (12).

When σ₁ ≪ 1, the timescale t_s1 is the characteristic time of the substrate species. The solid black curve is the numerical solution to the mass action equations (13a)–(13b) and the vertical dashed/dotted line corresponds to t = t_s1. The dotted horizontal line corresponds to the scaled characteristic value $(1-\ell )s_1^0$. The constants (without units) used in the numerical simulation are: $e_1^0=1$, k₁ = 0.01, k₂ = 10, k₋₁ = 1 and $s_1^0=100$. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)].

The calculus of the Lambert-W function determines the relevant chemical interpretation of t_s1 as σ₁ increases. When t = t_s1, the substrate concentration is, based on the RSA, K_M1W [(1 – ℓ)σ₁]. Furthermore,

$$W[u]\ll u,\text{when}1\ll u,$$ (26)

and we see from (26) that as the argument “u” gets large, the distance from u to W[u] gets greater. Since

$$s_1(t_{s_1})=K_{M_1}W[(1-\ell ){\sigma }_1)],$$ (27)

it follows from (26) that

$$W[(1-\ell ){\sigma }_1]\ll (1-\ell ){\sigma }_1$$ (28)

as σ₁ gets large. Thus, for large σ₁, it holds that

$$s_1(t_{s_1})\ll (1-\ell )s_1^0,$$ (29)

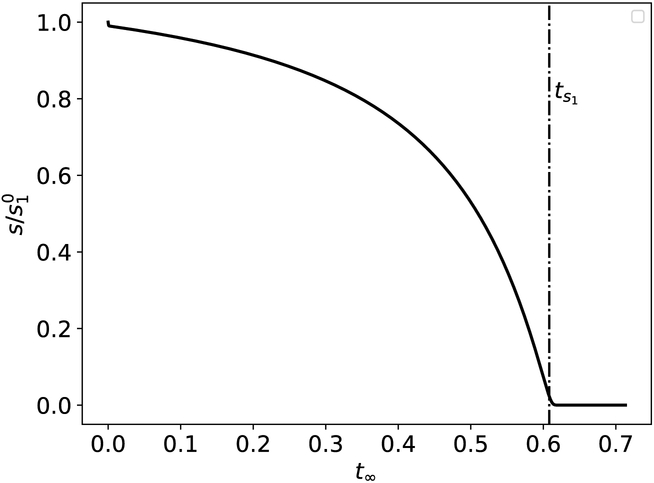
in which case we categorize t_s1 as a completion timescale, since it is proportional to the total length of the reaction (see Figure 3).

Figure 3: The graphical illustrations of the completion timescale for the Michaelis–Menten reaction mechanism (12).

When σ₁ ≫ 1, the reaction is essentially complete when t = t_s1. The solid black curve is the numerical solution to the mass action equations (13a)–(13b) and the vertical dashed/dotted line corresponds to t = t_s1. The constants (without units) used in the numerical simulation are: $e_1^0=1$, k₁ = 10, k₂ = 10, k₋₁ = 1 and $s_1^0=100$. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)].

In the intermediate range, when neither σ₁ ≪ 1 or σ₁ ≫ 1 holds, t_s1 is still the appropriate timescale over which a significant reduction in substrate concentration occurs, and in this case we refer to the slow timescale as the depletion timescale, since it is too long to be a characteristic timescale, but too short to be a completion timescale.

3.3. The QSSA versus the RSA

How did Segel’s work reconcile the work of Heineken et al. (1967) with the observations made by Palsson (1987)? In a nutshell, Segel and Slemrod (1989) found that over the fast timescale the mass action equations scale as

$${\dot{\widehat{s}}}_1={\epsilon }_{1}f({\widehat{s}}_1,{\widehat{c}}_1),$$ (30a)

$${\dot{\widehat{c}}}_1=g({\widehat{s}}_1,{\widehat{c}}_1),$$ (30b)

and on the slow timescale as

$${\widehat{s}}_1^{\prime }=\tilde{f}({\widehat{s}}_1,{\widehat{c}}_1),$$ (31a)

$${\epsilon }_2{\widehat{c}}_1^{\prime }=\tilde{g}({\widehat{s}}_1,{\widehat{c}}_1),$$ (31b)

where f, g denote the right hand sides of (19), and $\tilde{f}$, $\tilde{g}$ denotes the right hand sides of (22). If ε₁ ≪ 1, then the depletion of substrate over the fast timescale is negligible. However, if ε₁ ≈ 1, but ε₂ ≪ 1, then the QSSA is still valid after a brief transient. The distinguishing feature in the case when ε₂ ≪ ε₁ ~ 1 is that the depletion of s₁ over the initial transient is noticeable (Segel and Slemrod, 1989).

It is straightforward to the show that ε₂ < ε₁. Consequently, the condition for the validity of the RSA, ε₁ ≪ 1, ensures the validity of the QSSA on the slow timescale. Moreover, since ε₁ ≪ 1 guarantees that the depletion of s₁ minimal over t_c1, the qualifier ε₁ ≪ 1 ensures the validity of the QSSA for the entire dynamics of the reaction (12) (Hanson and Schnell, 2008).

3.4. Matched asymptotics: The composite solution for the time course of the reaction

Expressing the asymptotic solution to (13a)–(13b) as,

$$\{\begin{array}{cc}{s}_1\simeq s_1^0,\hfill & \hfill \\ \hfill & t\le t_{c_1}\hfill \\ c_1\simeq c_1^{\max }[1-\text{exp}(-t∕t_{c_1})],\hfill & \hfill \end{array}\phantom{\}}$$ (32a)

$$\{\begin{array}{cc}{s}_1\simeq K_{M_1}W[{\sigma }_1\text{exp}({\sigma }_1-{\eta }_{1}t)],\hfill & \hfill \\ \hfill & t>t_{c_1}\hfill \\ c_1\simeq \frac{e_1^0}{K_{M_1}+s_1}{s}_1,\hfill & \hfill \end{array}\phantom{\}}$$ (32b)

serves well to convey the fact that the dynamics of the reaction changes depending on where a particular time point falls in relation to t_c1, and these equations provide us with the correct inner and outer solutions that approximate the kinetics under the RSA. However, it is well-understood that equations (32a)–(32b) are misleading: there is a large transition regime surrounding t_c1 and, within this transition regime, the outer solution (32b) does not accurately approximate the solution. Note that the presence of a transition regime does not suggest that t_c1 is an inappropriate timescale. In fact, the timescales derived in the previous section are the appropriate timescales that categorize the fast and slow regimes of the reaction. To see why, and to mitigate the effect of the transition region, we construct the composite solution for the intermediate complex, $c_1^{io}$:

$$c_1^{io}=\frac{e_1^0}{K_{M_1}+s_1}{s}_1-c_1^{\max }\text{exp}(-t∕t_{c_1}).$$ (33)

The composite solution provides a uniform asymptotic solution that is valid for all time. Furthermore, the accuracy of (33) indicates that t_c1 and t_s1 quantify the appropriate temporal length scales of the initial fast transient and quasi-steady-state regime (see Figure 4).

Figure 4: A graphical comparison of the composite and numerical solutions for the time course of the Michaelis–Menten reaction (12).

The solid black curve is the numerical solution to (13a)–(13b). The unfilled circles mark the composite solution (33). The initial concentrations and rate constants used in the numerical simulation are: k₁ = 1, k₂ = 1, k₋₁ = 1, $e_1^0=1$ and $s_1^0=100$ (units have been omitted). All approximations have been scaled by their numerically-obtained maximum values, and time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)].

3.5. The characteristic timescale is not a matching timescale

From a theoretical point of view, the composite solution has little advantage over the numerical solution in terms of estimating when the transition to the quasi-steady-state phase occurs. We will refer to the time at which the transition to QSS occurs as a matching timescale, and a rough candidate for a matching timescale is t_c1. The caveat with utilizing t_c1 as a matching timescale is that t_c1 is a characteristic timescale, and hence will only provide characteristic (as opposed to limiting) values of the concentrations within a given regime. To clearly illustrate why t_c1 fails to be an adequate matching timescale requires a phase–plane analysis of the mass action equations (13a)–(13b). After the initial buildup of the intermediate, c₁, the phase–plane trajectory is asymptotic to a slow manifold, ${\mathcal{M}}_{\epsilon }$. The slow manifold is invariant, and is at a $\mathcal{O}({\epsilon }_2)$-distance from the c₁-nullcline, ${\mathcal{M}}_0$:

$${\mathcal{M}}_0=\left\{(s_1,c_1):c_1-\frac{e_1^0}{K_{M_1}+s_1}{s}_1=0\right\}.$$ (34)

The outer solution, (32a), is valid once the trajectory is extremely close to the slow manifold, which implies c₁ should be near its maximum value at the onset of the outer solution validity. The complex reaches its maximum value once the trajectory reaches ${\mathcal{M}}_0$. However, when t = t_c1, the concentration of the complex is far enough away from its maximum value to render the outer solution invalid:

$$c_1(t_{c_1})\approx \ell c_1^{\max }<c_1^{\max }.$$ (35)

Thus, $c_1(t_{c_1})\notin {\mathcal{M}}_0$, and therefore the trajectory is not quite close enough to ${\mathcal{M}}_{\epsilon }$ to justify (32a) as an asymptotic solution (see Figure 2).

A more accurate estimate of the actual time it takes c₁ to reach its maximum concentration (we will denote this timescale as $t_{c_1}^{\ast }$) can be obtained by either: (i) solving the mass action equations exactly or, (ii) by means of an asymptotic approximation. Employing strategy (i) is difficult due to the nonlinearity of the equations; strategy (ii) tends to be more straightforward to implement. If utilize (ii), we immediately meet with an obvious conundrum if we try to estimate $t_{c_1}^{\ast }$ directly from (32a) or (32b): (32a) predicts that it will take an infinite amount of time for c₁ to reach $c_1^{\max }$, while (32b) predicts $t_{c_1}^{\ast }=0$. To work around this, we look for an asymptotic estimate to $t_{c_1}^{\ast }$. Starting with the inner solution,

$$c_1(\tau )=c_1^{\max }[1-\text{exp}(-\tau )]$$ (36)

we rewrite (36) in terms of the slow variable, T = t/t_s1:

$$c_1(T)=c_1^{\max }[1-\text{exp}(-T∕{\epsilon }_2)].$$ (37)

By inspection of (37), we see that c₁ should be in an $\mathcal{O}({\epsilon }_2)$-neighborhood of the slow manifold when

$$T={\epsilon }_2\mid \text{ln}{\epsilon }_2\mid .$$ (38)

Next, since T = t/t_s1, we solve for t in (38) to obtain an asymptotic estimate on $t_{c_1}^{\ast }$:

$$t_{c_1}^{\ast }\simeq -t_{c_1}\text{ln}{\epsilon }_2.$$ (39)

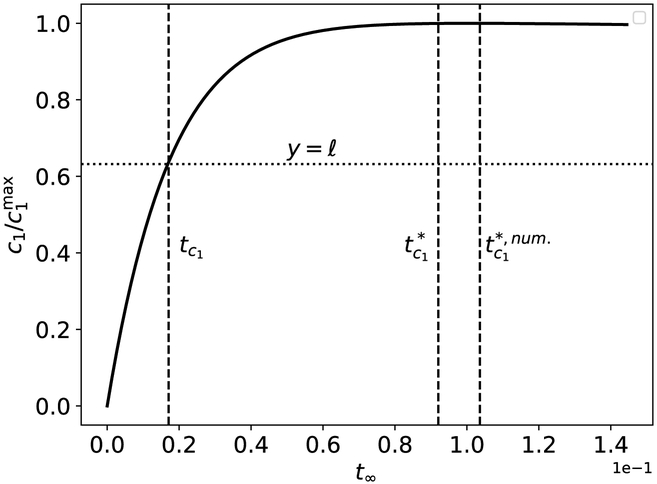
The timescale (39) is the matching timescale, although various authors refer to any timescale of order ε∣ lnε∣ as simply a slow time (Kuehn, 2015). While not exact, the approximation (39) provides a useful estimate of the time to transition from transient to quasi-steady-state kinetics for the single-enzyme, single-substrate MM reaction mechanism (see Figure 5).

Figure 5: The validity of $t_{c_1}^{\ast }$ and a graphical representation of its comparison with t_c1 for the Michaelis–Menten reaction mechanism (12).

The solid black curve is the numerically-computed solution to (13a)–(13b). The left-most dashed vertical curve is corresponds to t_c1, and the middle dashed vertical curve corresponds to the estimated value $t_{c_1}^{\ast }=-t_{c_1}\text{ln}{\epsilon }_2$. The dashed vertical line corresponds to the numerically-computed $t_{c_2}^{\ast }$, which is labeled as $t_{c_1}^{\ast ,num}$ in the figure. Notice that $t_{c_1}^{\ast }$ provides a much better estimate of the time it takes c₁ to reach its maximum than t_c1. The initial concentrations and rate constants used in the numerical simulation are: k₁ = 0.1, k₂ = 10, k₋₁ = 1, $e_1^0=1$ and $s_1^0=100$ (units have been omitted). Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ ln[t+exp(1)]. Note that the mass action equations have only been integrated from t = 0 to $t\approx t_{c_1}^{\ast }$ for clarity.

As a final remark, we note that the asymptotic approximation (39) is not without a more rigorous justification. So far, we have been able to estimate matching timescales by directly calculating them from the “inner” or transient solution; the direct method is possible because we have closed-form solutions comprised of exponential functions. However, for a generic fast/slow dynamical system of the form

$$\stackrel{.}{x}=f(x,y),$$ (40a)

$$\epsilon \stackrel{.}{y}=g(x,y),$$ (40b)

the equation ẏ = g(x₀, y) may not be linear, and a closed-form solution may not be possible. However, it is a well-known fact, stated in both textbooks (Kuehn, 2015) and literature (Klonowski, 1983), that the time necessary for the fast-variable to reach QSS is generally $\mathcal{O}(\epsilon \mid \text{ln}\epsilon \mid )$. This result is due to the work of Tikhonov (1952), who studied the convergence of the solution to the perturbed system (40a)–(40b) to the solution of the degenerate system, (41a)–(41b):

$$\stackrel{.}{x}=f(x,y),$$ (41a)

$$0=g(x,y).$$ (41b)

The work of Tikhonov is summarized as follows: First, (41b) defines a corresponding slow manifold of the form y = h(x), where g(x, h(x)) = 0. Next, let D be the domain over which $h:D\to {\mathbb{R}}^n$ is continuous. If g and f are sufficiently smooth, then the following theorem provides a more general technical justification for (39):

Theorem 1. Convergence towards the slow manifold: Suppose the system (40a)–(40b) has an associated slow manifold, ${\mathcal{M}}_0=\{(x,y):y=h(x)\&x\in D\}$, that is uniformly asymptotically stable. If f, g and their first two derivatives are uniformly bounded in a neighborhood “N” of ${\mathcal{M}}_0$, then there are positive constants ε₀, b₀, b₁, Λ, and M such that for any initial condition (x₀, y₀) ∈ N such that ∥y₀ – h(x₀)∥ ≤ b₀, and any ε such that 0 < ε < ε₀, the bound

$$\Vert y(t)-h(x(t))\Vert \le M\Vert y_0-h(x_0)\Vert \text{exp}[-\Lambda t∕\epsilon ]+b_1\epsilon ,$$ (42)

holds provided x(t) ∈ D.

Notice the slow manifold utilized in the theorem is not defined to be invariant. In fact, ${\mathcal{M}}_0$ is the nullcline associated with the fast variable, y, and is formally referred to as the critical manifold. The non-invariant slow manifold employed in Theorem (1) arises from the original form of the theorem introduced by Tikhonov (1952). The specific form of Theorem (1) is taken directly from Berglund and Gentz (2006), but originally introduced by Gradšteĭn (1953). Fenichel (1979) later extended slow/fast theory by demonstrating that there exists an invariant slow manifold that is present in the phase-space of the system when ε is sufficiently small but non-zero.

What the bound specifically tells us is that if t = ε∣ ln ε∣, then

$$\Vert y(t)-h(x(t))\Vert \le M\Vert y_0-h(x_0)\Vert {\epsilon }^{\Lambda }+b_1\epsilon ,$$ (43)

and thus the phase-plane trajectory should be at a distance that is $\mathcal{O}(\epsilon )$ from ${\mathcal{M}}_0$ once t = ε∣ lnε∣ (see Berglund and Gentz, 2006, for details). In a fast/slow system of the form (40a)–(40b), the small parameter ε is proportional to the ratio of the fast and slow timescales. Moreover, the system (40a)–(40b) is assumed to be dimensionless. Thus, if we apply Theorem (1) to

$$\begin{gathered} \frac{d{\widehat{s}}_1}{dT}=(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1], \\ {\epsilon }_2\frac{d{\widehat{c}}_1}{dT}={\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1, \end{gathered}$$ (44)

then the phase–plane trajectory should be $\mathcal{O}({\epsilon }_2)$ from the c₁-nullcline when T = ε₂∣ ln ε₂∣. Consequently, since T = t/t_s1, we obtain

$$t=t_{s_1}\cdot {\epsilon }_2\mid \text{ln}{\epsilon }_2\mid =-t_{c_1}\text{ln}{\epsilon }_2\approx t_{c_1}^{\ast }$$ (45)

as the asymptotic time required for c₁ to reach its maximum value.

The calculation of the matching timescale is more than just an exercise: there is chemical utility in computing $t_{c_1}^{\ast }$. Specifically, it indicates approximately when the rate of product formation reaches its maximum quasisteady-state production:

$$\max \stackrel{.}{p}\simeq \stackrel{.}{p}(t_{c_1}^{\ast }).$$ (46)

Thus, the matching timescale is a very good indication of how long it takes before the product formation rate reaches its maximum value, and when the reaction can be assumed to be in a quasi-steady-state phase.

4. The auxiliary enzyme reaction mechanism

We now consider the more complicated case of the auxiliary enzyme reaction mechanism (Eilertsen and Schnell, 2018). The mechanism is composed of two reactions: a primary reaction (47) that produces a substrate, S₂, that is synthesized in a catalytic step:

$$E_1+S_1\underset{{}_{k_{-1}}}{\overset{{}^{{}^{k_1}}}{\rightleftharpoons }}{C}_1\stackrel{{}^{{}^{k_2}}}{\to }{E}_1+S_2,$$ (47)

and a secondary reaction, (48), where S₂ binds with the auxiliary enzyme “E₂” and releases the final product, P:

$$E_2+S_2\underset{{}_{k_{-3}}}{\overset{{}^{{}^{k_3}}}{\rightleftharpoons }}{C}_2\stackrel{{}^{{}^{k_4}}}{\to }{E}_2+P.$$ (48)

The complete set of mass action equations that model the kinetics of the complete reaction mechanism (47)–(48) are

$${\stackrel{.}{s}}_1=-k_1(e_1^0-c_1)s_1+k_{-1}{c}_1,$$ (49a)

$${\stackrel{.}{c}}_1=k_1(e_1^0-c_1)s_1-(k_{-1}+k_2)c_1,$$ (49b)

$${\stackrel{.}{s}}_2=-k_3(e_2^0-c_2)s_2+k_{-3}{c}_2+k_2{c}_1,$$ (49c)

$${\stackrel{.}{c}}_2=k_3(e_2^0-c_2)s_2-(k_{-3}+k_4)c_2,$$ (49d)

where s₁ and s₂ denote the respective concentrations of the substrates S₁ and S₂, c₁ and c₂ denote the concentrations of the complexes C₁ and C₂, and $e_1^0$ and $e_2^0$ denote the initial concentrations of the primary and auxiliary enzymes, E₁ and E₂. k₃ and k₋₃ are rate constants, and k₄ is the catalytic constant of the secondary reaction. We define the initial conditions for the secondary reaction as (s₂, c₂)(t = 0) = (0, 0).

In forthcoming analysis, we will assume that the primary reaction obeys the RSA (i.e., ε₁ ≪ 1). Additionally, we will make the assumption that k₂ ≲ k₄, and that the initial auxiliary enzyme concentration is larger than $e_1^0$ (i.e., $e_1^0=1$, $e_2^0\gg 1$). We also compute matching timescales that yield a reliable estimate of the time it takes s₂ and c₂ to reach QSS. Moreover, a new timescale called the lag time will be introduced. The lag time corresponds to the time it takes ṗ to reach its maximum value, and we will show that it corresponds to a specific matching timescale. Thus, not only do matching timescales provide estimates for the time it takes a specific species to reach QSS, they also, in the context of auxiliary reactions, provide an approximation of the time it takes before the complete reaction begins generating product at a maximal rate.

4.1. The study of phase–plane geometry of the auxiliary enzyme reaction mechanisms permit a heuristic estimation of characteristic timescales

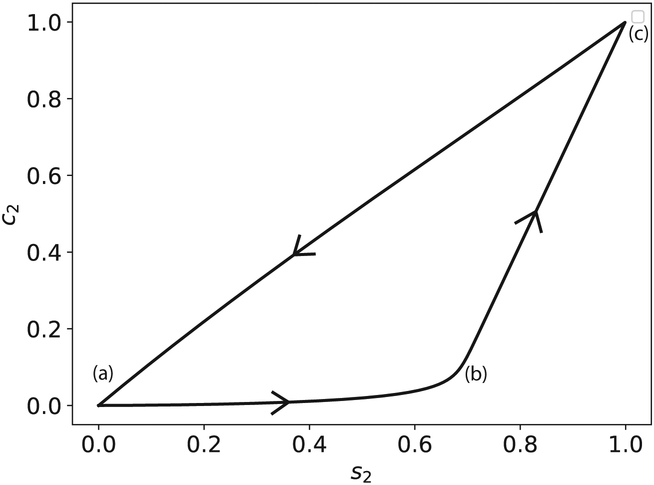
Perhaps the most intuitive way to derive the relevant characteristic timescales of (47)–(48) is to get a qualitative understanding of what a typical phase-plane trajectory looks like in the c₂–s₂ plane. Numerical simulations suggest that the phase–plane trajectory is almost “triangular” in certai parameter ranges (see Figure 6) and, based on the appearance of the phase–plane trajectory, there seems to be at least three distinct timescales:

Figure 6: The phase–plane portrait of the mass action trajectory for the auxiliary reaction mechanism (47)–(48).

The solid black curve is the numerically-computed solution to (49a)–(49d). The initial concentrations and rate constants used in the numerical simulation are: k₁ = 1, k₂ = 1, k₋₁ = 1, $e_1^0=1$, $e_2^0=100$, k₋₃ = 1, k₃ = 1, k₄ = 2 and $s_1^0=100$ (units have been omitted). s₂ and c₂ have been scaled by their numerically–obtained maximum values.

• The scale on which the trajectory travels from (a) to (b). We will denote this timescale as t_s2.

• The scale on which the trajectory travels from (b) to (c). We will denote this timescale as t_c2.

• The scale on which the trajectory travels from (c) back to (a). We will denote this timescale as t_p.

The logical step that follows will be to make some initial a priori assumptions about the ordering of all the timescales involved in the reaction. For the sake of simplicity, let us initially assume that t_c1 ≪ t_s2, t_c2 ≪ t_s1, and that the completion timescale for the secondary reaction is identically t_s1. This implies that the secondary reaction completes at roughly the same time as the primary reaction, and that t_p ≈ t_s1. Thus, we have eliminated one timescale (t_p) by imposing the assumption that the secondary reaction is as fast as the primary reaction.

The next step will be to exploit the presence and geometry of any manifolds (not necessarily invariant) that exist within the phase-plane of the secondary reaction. Notice that the intersection of the s₂-nullcline and c₂- nullcline is time-dependent since the s₂-nullcline moves as c₁ varies in time. Geometrically, the intersection of the nullclines is described by a moving fixed point, x*,

$$N_{s_2}\cap N_{c_2}\equiv x^{\ast },$$ (50)

where N_s2 denotes the s₂-nullcline and N_c2 denotes the c₂-nullcline. Algebraically, the coordinates of x*, ($s_2^{\ast }$, $c_2^{\ast }$), are

$$s_2^{\ast }=\frac{K_{M_2}{k}_2{c}_1(t)}{V_2-k_2{c}_1(t)},c_2^{\ast }=\frac{k_2{c}_1(t)}{k_4},$$ (51)

where K_M2 denotes the Michaelis constant of the secondary reaction

$$K_{M_2}\equiv \frac{k_{-3}+k_4}{k_3},$$ (52)

and V₂ denotes the limiting rate of the secondary reaction: $V_2\equiv k_4{e}_2^0$. Moreover, if the second reaction is as fast as the primary reaction, then the phase-plane geometry suggests that the trajectory should not only catch the fixed point x*, but will also approximately adhere to x* as it descends to the origin. If the trajectory adheres to x*, then

$$\stackrel{.}{p}=\frac{V_2\frac{K_{M_2}{k}_2{c}_1}{V_2-k_2{c}_1}}{K_{M_2}+\frac{K_{M_2}{k}_2{c}_1}{V_2-k_2{c}_1}}=k_2{c}_1,$$ (53)

and the product formation rate of the secondary reaction has reached its limiting value. Notice that by assuming that the secondary reaction is fast enough to virtually adhere to x* implies $V_2>k_2{c}_1^{\max }$. Thus, this assumption admits an automatic partition of parameter space, and we will only consider regions of parameter space within which $V_2>k_2{c}_1^{\max }=k_2{\epsilon }_1{s}_1^0$ holds.

Since the position of the s₂-nullcline depends on the concentration c₁, we want to estimate how c₁ varies over the course of the reaction. As we are assuming that the primary reaction follows the RSA, the phase plane trajectory will follow a slow manifold when $t\ge t_{c_1}^{\ast }$. If we know the shape of the slow manifold, then we can get a rough idea of how c₁ varies throughout the reaction. To do this, we will look at the dimensionless equations

$$\begin{gathered} \frac{d{\widehat{s}}_1}{dT}=(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1], \\ {\epsilon }_2\frac{d{\widehat{c}}_1}{dT}={\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1. \end{gathered}$$ (54)

The zeroth order asymptotic approximation to the slow manifold is the ${\widehat{c}}_1$-nullcline:

$${\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{2}}_1-{\beta }_1{\widehat{c}}_1=0$$ (55)

Notice that β₁ → 0 as σ₁ → ∞; thus, as σ₁ → ∞, the trajectory that follows the slow manifold will be asymptotic to the curve ${\widehat{c}}_1=1$ for most of the reaction. Hence, when σ₁ ≫ 1, the concentration of the intermediate complex remains near its maximum value, $c_1^{\max }$, for the majority of the reaction, and the s₂-nullcline will be effectively stationary after the initial buildup of c₁. Under the assumption that t_c1 is the shortest timescale, the initial transient behavior of c₂ will occur while the s₂-nullcline remains fixed. Thus, we look at the phase–plane trajectory with the s₂-nullcline (with fixed c₁) at its stationary value (see Figure 7). Let us denote this manifold as $N_{s_2}^{\max }$:

$$N_{s_2}^{\max }\equiv \left\{(s_2,c_2)\in {\mathbb{R}}^2:c_2-\frac{k_3{e}_2^0{s}_2-k_2{c}_1^{\max }}{k_3{s}_2+k_{-3}}=0\right\}.$$ (56)

Figure 7: The s₂–c₂ phase-plane trajectory (with nullclines) for the auxiliary reaction mechanism (47)–(48).

The thick black curve is the numerically-integrated solutions to the mass action equations (49a)–(49d). The broken red curve is the c₂-nullcline, and the broken blue curve is the fixed s₂-nullcline ($N_{s_2}^{\max }$, given by (56)). The phase–plane trajectory initially moves towards $N_{s_2}^{\max }$, then moves up $N_{s_2}^{\max }$ before moving back down the c₂-nullcline. The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1000$, k₁ = 1, k₂ = 1, k₃ = 1, k₋₃ = 1, k₄ = 2, $e_2^0=100$ and k₋₁ = 1. Curves were scaled by their numerically obtained maximum values.

Next, we want to exploit the phase-plane geometry in order to estimate critical timescales. We will first estimate t_s2 by noting that the phase–plane trajectory essentially lies along the s₂-axis for t ≤ t_s2. This suggests that

$${\stackrel{.}{s}}_2\approx -k_3{s}_2+k_2{c}_1,t\le t_{s_2}$$ (57)

is a reasonable approximation to (49c). If the initial fast transient of the primary reaction is negligibly short, i.e., t_c1 ≪ t_s2, then it is reasonable to assume

$${\stackrel{.}{s}}_2\approx -k_3{s}_2+k_2{c}_1^{\max },t\le t_{s_2}.$$ (58)

Since (58) is linear, its exact solution

$$s_2\approx s_2^{\lambda }[1-\text{exp}(-t∕t_{s_2})]$$ (59)

provides two critical estimates: characteristic timescale, t_s2, and an approximate maximum value of s₂ on the t_s2 timescale:

$$t_{s_2}\equiv \frac{1}{k_3{e}_2^0},s_2\le s_2^{\lambda }\equiv \frac{k_2{c}_1^{\max }}{k_3{e}_2^0}.$$ (60)

The prediction that $s_2<s_2^{\max }$ for t ≤ t_s2 (obtained from the linear equation) is in qualitative agreement with the phase-plane trajectory of the numerically-integrated equations (Figure 7).

Next, to estimate t_c2, we note that since the phase–plane trajectory lies close to $N_{s_2}^{\max }$ along its ascension to $c_2^{\max }$, the growth of the intermediate complex is approximately

$${\stackrel{.}{c}}_2\approx -k_4{c}_2+k_2{c}_1^{\max },t_{s_2}\le t\le t_{c_2},$$ (61)

which admits an analytical solution:

$$c_2\approx c_2^{\max }[1-\text{exp}(-k_{4}t)].$$ (62)

Trajectories that follow the s₂-nullcline closely are said to be in rapid equilibrium (Nguyen and Fraser, 1989; Roussel and Fraser, 1991) or a reverse quasi-steady-state (Schnell and Maini, 2000). This is in contrast to trajectories that follow the c₂-nullcline, which are said to be in a quasi-steady-state phase (Eilertsen and Schnell, 2018). From (62), we have two observations: (i) $k_4^{-1}$ is a reasonable estimate of t_c2, and (ii) this linearized solution predicts c₂ will approach $c_2^{\max }$, which is in qualitative agreement with the phase–plane trajectory.

As a concluding remark of this subsection, we note that there are four timescales, t_c1, t_s2, t_c2 and t_s1, that influence the overall dynamics of the coupled reaction. Only two timescales are needed to characterize the dynamics of the single-enzyme, single-substrate MM reaction mechanism. Thus, only the ordering of two timescales, t_c1 and t_s1, needs to be considered. In the case of the coupled reaction, there are multiple orderings that need to be considered in order to fully comprehend the dynamics. In the immediate subsections that follow, we will analyze the dynamics with respect to the orderings: t_c1 ≪ t_s2 ≪ t_c2 ≪ t_s1 and t_s2, t_c2 ≪ t_c1 ≪ t_s1. Both analyses of these orderings will be made under the assumption that $e_2^0$ is large with respect to $e_1^0$.

4.2. Scaling analysis: t_c1 ≪ t_s2 ≪ t_c2 ≪ t_s2

Although we now have estimates for the timescales t_s2 and t_c2, it is important to remember that these timescales were obtained under the assumption that c₁ is the fastest variable (i.e., c₁ reaches its maximum before any other variable). We must now: (i) determine the appropriate conditions under which approximate adhesion to x* is possible, and (ii) determine the onset of validity for (53). We begin by scaling the mass action equations. Introducing the additional scaled concentrations

$${\widehat{s}}_2=s_2∕s_2^{\max },{\widehat{c}}_2=c_2∕c_2^{\max }$$ (63)

into equations (49c)–(49d) admits the dimensionless form:

$$\frac{d{\widehat{s}}_1}{dT}=(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],$$ (64a)

$${\epsilon }_2\frac{d{\widehat{c}}_1}{dT}={\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1$$ (64b)

$${\mu }_1\frac{d{\widehat{s}}_2}{dT}=-{\widehat{s}}_2+(1-{\beta }_2){\widehat{s}}_2{\widehat{s}}_2+{\beta }_2{\alpha }_2{\widehat{c}}_2+r_S{\mu }_1{\widehat{c}}_1,$$ (64c)

$${\mu }_2\frac{d{\widehat{c}}_2}{dT}=(1+{\kappa }_2)(1+{\sigma }_2)[({\widehat{s}}_2-(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2-{\beta }_2{\widehat{c}}_2].$$ (64d)

The dimensionless parameters κ₂, σ₂, and r_S, introduced in (64a)–(64d), are

$${\alpha }_2\equiv \frac{{\kappa }_2}{1+{\kappa }_2},{\beta }_2\equiv \frac{1}{1+{\sigma }_2},{\kappa }_2\equiv \frac{k_{-3}}{k_4},{\sigma }_2\equiv \frac{s_2^{\max }}{K_{M_2}},r_S\equiv \frac{s_1^0}{s_2^{\max }}.$$ (65)

The remaining parameters, μ₁ and μ₂, are the ratios of the secondary reaction timescales to the primary reaction substrate timescale:

$${\mu }_1\equiv \frac{t_{s_2}}{t_{s_1}},{\mu }_2\equiv \frac{t_{c_2}}{t_{s_1}}.$$ (66)

It follows from (66) that if {ε₂, μ₁, μ₂} ≪ 1, then the dynamics of (49a)–(49d) consist of one slow variable, s₁, and three fast variables: c₁, s₂ and c₂. The designation of s₁ as a slow variable and c₁, s₂ and c₂ as fast variables implies that after an initial fast transient, the phase–plane trajectory is asymptotic to the intersecting nullclines:

$$s_2\simeq \frac{K_{M_1}}{V_2-k_2{c}_1}{k}_2{c}_1,$$ (67a)

$$c_2\simeq \frac{k_2{c}_1}{k_4}.$$ (67b)

After the initial fast transient of the primary reaction, k₂c₁ is asymptotic to

$$k_2{c}_1\simeq \frac{V_1}{K_{M_1}+s_1}{s}_1\equiv -{\stackrel{.}{s}}_1^{\epsilon },$$ (68)

and thus c₁, s₂ and c₂ are, in the asymptotic limit, explicitly dependent on s₁ only.

The above approximations, (67a)–(67b), confirm the hypothesis that the phase-plane trajectory follows the intersection of the s₂- and c₂-nullclines as long as the secondary reaction is fast (i.e., μ₁, μ₂ ≪ 1). The additional assumption made in the derivation of t_s2 and t_c2 was that t_c1 is the shortest timescale, and that there is no significant formation of s₂ or c₂ for 0 ≤ t ≤ t_c1. To assess the validity of this assumption, we rescale (49c)–(49d) with respect to τ = t/t_c1:

$$\frac{d{\widehat{s}}_1}{d\tau }={\epsilon }_1[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],$$ (69a)

$$\frac{d{\widehat{c}}_1}{d\tau }=[{\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1]$$ (69b)

$$\frac{d{\widehat{s}}_2}{d\tau }={\lambda }_1[-{\widehat{s}}_2+(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2+{\beta }_2{\alpha }_2{\widehat{c}}_2]+r_S{\epsilon }_2{\widehat{c}}_1,$$ (69c)

$$\frac{d{\widehat{c}}_2}{d\tau }={\lambda }_2(1+{\kappa }_2)(1+{\sigma }_2)[{\widehat{s}}_2-(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2-{\beta }_2{\widehat{c}}_2].$$ (69d)

The parameters that emerge from scaling, λ₁ and λ₂, are the ratios we need in order to calculate the time that transpires before (67a)–(67b) become valid approximations:

$${\lambda }_1=\frac{t_{c_1}}{t_{s_2}},{\lambda }_2=\frac{t_{c_1}}{t_{c_2}}.$$ (70)

It is straightforward to show that the term “r_Sε₂” in (69c) is bounded above,

$$r_S{\epsilon }_2<{\lambda }_1,$$ (71)

and therefore s₂ is slow on t_c1 when λ₁ ≪ 1. In addition, (69d) implies that λ₂(1 + κ₂)(1 + σ₂) ≪ 1 if c₂ is to be slow over t_c1. While it is certainly true that λ₂(1 + κ₂)(1 + σ₂) ≪ 1 is sufficient for c₂ to be slow, it is not necessary, given that s₂ ≃ 0 for t ≤ t_c1.

Piecing together the results obtained from the scaling analysis, we obtain

$$s_1\simeq s_1^0,$$ (72a)

$$c_1\simeq c_1^{\max }[1-\text{exp}(-t∕t_{c_1})],$$ (72b)

$$s_2\simeq 0,$$ (72c)

$$c_2\simeq 0,$$ (72d)

for t ≲ t_c1.

Moving forward, the next “fastest” timescale in our imposed ordering is t_s2. We note that in addition to c₂ scaling as a slow variable over t_c1, the phase-plane trajectory indicates that c₂ will also be slow over t_s2. Thus, we rescale the complete set of mass action equations with respect to $\stackrel{‒}{T}=t∕t_{s_2}$, ${\tilde{s}}_2=s_2∕s_2^{\lambda }$ and ${\tilde{c}}_2=c_2∕e_2^0{s}_2^{\lambda }∕(K_{M_2}+s_2^{\lambda })$:

$$\frac{d{\widehat{s}}_1}{d\stackrel{‒}{T}}={\mu }_1(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],$$ (73a)

$${\epsilon }_1\frac{d{\widehat{c}}_1}{d\stackrel{‒}{T}}={\mu }_1(1+{\kappa }_1)(1+{\sigma }_1)[{\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1]$$ (73b)

$$\frac{d{\tilde{s}}_2}{d\stackrel{‒}{T}}=-{\tilde{s}}_2+(1-{\tilde{\beta }}_2){\tilde{c}}_2{\tilde{s}}_2+{\tilde{\beta }}_2{\alpha }_2{\tilde{c}}_2+{\widehat{c}}_1,$$ (73c)

$$\frac{d{\tilde{c}}_2}{d\stackrel{‒}{T}}=\nu (1+{\kappa }_2)(1+{\tilde{\sigma }}_2)\left[{\tilde{s}}_2-(1-{\tilde{\beta }}_2){\tilde{c}}_2{\tilde{s}}_2-{\tilde{\beta }}_2{\tilde{c}}_2\right].$$ (73d)

In (73c), the dimensionless parameters ${\tilde{\sigma }}_2$ and ${\tilde{\beta }}_2$ are given by:

$${\tilde{\sigma }}_2\equiv \frac{s_2^{\lambda }}{K_{M_2}},{\tilde{\beta }}_2=\frac{1}{1+{\tilde{\sigma }}_2}$$ (74)

Consequently, the production of s₂ will be significant on t_s2. From (73d), we see that if ν(1 + κ₂)(1 + σ₂) ≪ 1, then c₂ will be a slow variable with respect to the t_c1 timescale. In fact, it is worth pointing out that

$$[\nu (1+{\kappa }_2)(1+{\sigma }_2){]}^{-1}=\frac{e_2^0}{K_{M_2}+s_2^{\max }}\equiv ϵ,$$ (75)

which is the analogue of ε₁ for the secondary reaction. Thus, the scaling analysis indicates that c₂ will be a slow variable over t_s2 if ϵ ≫ 1, which suggests $e_2^0$ should be large in comparison to $K_{M_2}+s_2^{\max }$.

Next, we see from (73b) that

$$\frac{{\epsilon }_1{\mu }_1^{-1}}{(1+{\kappa }_1)(1+{\sigma }_1)}=\frac{t_{c_1}}{t_{s_2}},$$ (76)

and thus c₁ will be in QSS on the t_s2 timescale as long as t_c1 ≪ t_s2.

From equation (73a), it is clear that if μ₁(1 + κ₁)(1 + σ₁) ≪ 1, then s₁ will be a slow variable over the t_s2 timescale. However, this condition is sufficient but not necessary; since c₁ is in QSS, we have:

$${\stackrel{.}{s}}_1\simeq -\frac{V_1}{K_{M_1}+s_1}{s}_1.$$ (77)

If we then rescale (77) with respect to $\stackrel{‒}{T}$, we obtain:

$$\frac{d{\widehat{s}}_1}{d\stackrel{‒}{T}}\simeq -{\mu }_1\frac{{\widehat{s}}_1(1+{\sigma }_1)}{1+{\sigma }_1{\widehat{s}}_1}\ge -{\mu }_1.$$ (78)

Thus, given (78), we see that μ₁ ≪ 1 is both necessary and sufficient for s₁ to be a slow variable with respect t_s2 when c₁ is in QSS. Assuming this condition is met, and the RSA holds, we obtain

$$s_1\simeq s_1^0,$$ (79a)

$$c_1\simeq c_1^{\max },$$ (79b)

$$s_2\simeq s_2^{\lambda }[1-\text{exp}(-t∕t_{s_2})],$$ (79c)

$$c_2\simeq 0,$$ (79d)

for t_c1 ≲ ^t ≲ ^t_s2.

The remaining dimensionless timescale necessary for the completion of the scaling analysis is $\stackrel{‒}{\tau }=t∕t_{c_2}$. Rescaling yields

$$\frac{d{\widehat{s}}_1}{d\stackrel{‒}{\tau }}={\mu }_2(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],$$ (80a)

$$\varpi \frac{d{\widehat{c}}_1}{d\stackrel{‒}{\tau }}={\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1,$$ (80b)

$$\nu \frac{d{\widehat{s}}_2}{d\stackrel{‒}{\tau }}=-{\widehat{s}}_2+(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2+{\beta }_2{\alpha }_2{\widehat{c}}_2+r_S{\mu }_1{\widehat{c}}_1,$$ (80c)

$$\frac{d{\widehat{c}}_2}{d\stackrel{‒}{\tau }}=(1+{\kappa }_2)(1+{\sigma }_2)[{\widehat{s}}_2-(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2-{\beta }_2{\widehat{c}}_2],$$ (80d)

where ϖ = t_c1/t_c2. Again, if ϖ ≪ 1, then c₁ is in QSS, in which case

$$\frac{d{\widehat{s}}_1}{d\stackrel{‒}{\tau }}\simeq -{\mu }_2\frac{{\widehat{s}}_1(1+{\sigma }_1)}{1+{\sigma }_1{\widehat{s}}_1}\ge -{\mu }_2,$$ (81)

and s₁ is a slow variable with respect to t_c2.

Next, if ν ≪ 1, then s₂ is in QSS on the t_c2 timescale, which implies

$$s_2\simeq \frac{k_{-3}{c}_2+k_2{c}_1^{\max }}{k_3(e_2^0-c_2)},\therefore s_2^{\lambda }\le s_2\le s_2^{\max }.$$ (82)

Thus, the scaling analysis indicates that

$$s_1\simeq s_1^0,$$ (83a)

$$c_1\simeq c_1^{\max },$$ (83b)

$$s_2\simeq \frac{k_{-3}{c}_2+k_2{c}_1^{\max }}{k_3(e_2^0-c_2)},$$ (83c)

$$c_2\simeq c_2^{\max }[1-\text{exp}(-t∕t_{c_2})],$$ (83d)

for t_s2 ≲ t ≲ t_c2, and the results of the complete scaling analysis allow us to formally construct the composite solutions for s₂ and c₂:

$$s_2^{io}=-s_2^{\lambda }[\text{exp}(-t∕t_{s_2})]+\frac{k_{-3}{c}_2^{io}+k_2{c}_1^{\max }}{k_3(e_2^0-c_2^{io})}-\frac{K_{M_2}}{V_2+{\stackrel{.}{s}}_1^{\epsilon }}{\stackrel{.}{s}}_1^{\epsilon }-s_2^{\max },$$ (84a)

$$c_2^{io}=-c_2^{\max }[\text{exp}(-t∕t_{c_2})]-{\stackrel{.}{s}}_1^{\epsilon }∕k_4.$$ (84b)

Together, (84a) and (84b) provide a uniform asymptotic expansion that is valid for all time (see Figure 8).

Figure 8: A graphical illustration of the accuracy of the composite solutions for the auxiliary reaction mechanism (47)—(48).

The solid black curve is the numerical solution to (49c), and the unfilled circles mark the composite solution (84a). The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1000$, $e_2^0=100$, k₁ = 1, k₂ = 1, k₃ = 1, k₋₃ = 1, k₄ = 2 and k₋₁ = 1. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)]. The substrate concentration has been scaled by its maximum value.

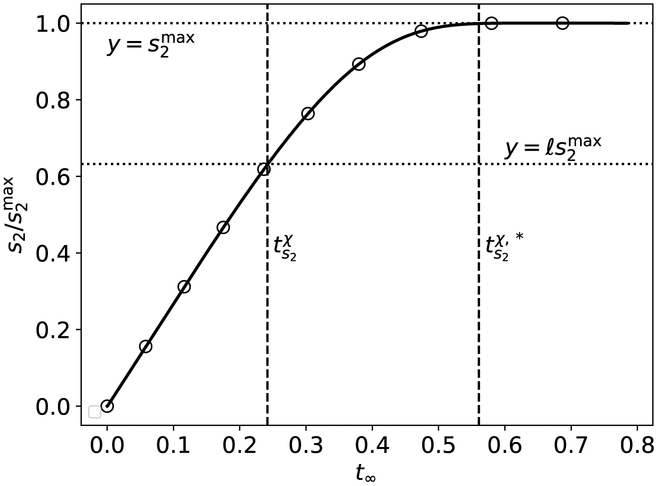
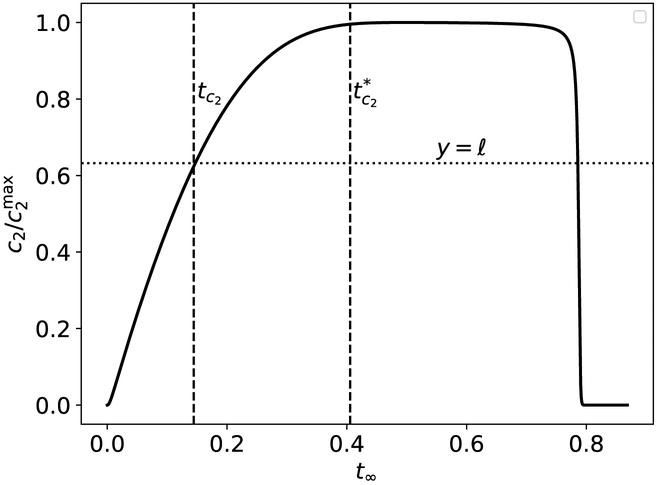
4.3. The lag time appears when there are multiple layers and multiple matching timescales

In the previous subsection, we derived inner (initial fast transient) and outer (quasi-steady-state phase) solutions that are valid when t_c1 ≪ t_s2 ≪ t_c2 ≪ t_s1. Formally, the ordering, t_c1 ≪ t_s2 ≪ t_c2 ≪ t_s1, categorizes t_c1 as a super-fast timescale, t_s2 as a fast timescale, t_c2 as a slow timescale, and t_s1 as a super-slow timescale. From a theoretical perspective, there is utility in estimating the time it takes for s₂ and c₂ to reach x*, at which time the rate of product formation, ṗ, is at its maximum value. Let $t_{s_2}^{\ast }$ denote the actual time it takes s₂ to reach $s_2^{\ast }$, and let $t_{c_2}^{\ast }$ denote the actual time it takes s₂ and c₂ to reach x*. Since t_s2 and t_c2 are characteristic timescales, utilizing them as matching timescales is problematic since the transition regimes, $t_{s_2}\le t\le t_{s_2}^{\ast }$ and $t_{c_2}\le t\le t_{c_2}^{\ast }$, can be quite large. Thus, what we seek are reliable estimates for $t_{s_2}^{\ast }$ and $t_{c_2}^{\ast }$. To construct these estimates, we will utilize the approximation techniques introduced in Section 3. Starting with $t_{c_2}^{\ast }$, the inner solution for the formation of c₂ is

$$c_2\simeq c_2^{\max }[1-\text{exp}(-t∕t_{c_2})].$$ (85)

Although t_c2 is a slow timescale, it is fast with respect to t_s1. Thus, rewriting (85) with respect to T yields

$$c_2\simeq c_2^{\max }[1-\text{exp}(-T∕{\mu }_2)],$$ (86)

and we see that T = μ₂∣ln μ₂∣ provides an estimate for $t_{c_2}^{\ast }$:

$$t_{c_2}^{\ast }\approx -t_{c_2}\text{ln}{\mu }_2.$$ (87)

The estimate given in (87) is the approximate time it takes for ṗ to reach it maximum with respect to the timescale ordering t_c1 ≪ t_s2 ≪ t_c2 ≪ t_s1 (see Figure 9). Formally, the matching timescale $t_{c_2}^{\ast }$ is the lag time, or the time during which the second reaction “lags” behind the first reaction.

Figure 9: The timescale t_c2 is characteristic of the time it takes c₂ to reach $c_2^{\max }$, and the timescale $t_{c_2}^{\ast }$ is the approximate time it takes c₂ to reach $c_2^{\max }$, respectively, in the auxiliary reaction mechanism (47)–(48).

The thick black curve is the numerically-integrated solutions to the mass action equations (49a)–(49d). The leftmost dashed vertical line corresponds to t_c2, and the rightmost dashed vertical line corresponds to $t_{c_2}^{\ast }=-t_{c_2}\text{ln}{t}_{c_2}∕t_{s_1}$. The lower dotted horizontal line corresponds to the scaled characteristic value $\ell c_2^{\max }$, and the upper dotted horizontal line corresponds to $c_2^{\max }$. The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1000$, $e_2^0=100$, k₁ = 1, k₂ = 1, k₃ = 1, k₋₃ = 1, k₄ = 2 and k₋₁ = 1. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)], and c₂ has been numerically scaled by its maximum value. Note that the mass action equations have only been integrated from t = 0 to $t\approx t_{c_2}^{\ast }$ for clarity.

Next we estimate the matching timescale $t_{s_2}^{\ast }$, which is roughly the time it takes for s₂ to reach QSS. The inner solution

$$s_2\simeq s_2^{\lambda }[1-\text{exp}(-t∕t_{s_2})],$$ (88)

can be expressed in terms of its corresponding slow timescale $\stackrel{‒}{\tau }$:

$$s_2\simeq s_2^{\lambda }[1-\text{exp}(-\stackrel{‒}{\tau }∕\nu )].$$ (89)

Employing a direct method yields

$$t_{s_2}^{\ast }\approx -t_{s_2}\text{ln}\nu ,$$ (90)

which we take as our approximation to the matching timescale $t_{s_2}^{\ast }$.

In addition to the estimate (90) obtained by the direct method, we can employ scaling and justify both (90) and (87) by invoking Theorem 1. The scaled mass action equations, (64a)–(64d), can be systematically reduced on the super-slow timescale (i.e., T = t/t_s1). Since ε₂ and μ₁ are, respectively, the smallest parameters with respect to the ordering t_c1 ≪ t_s2 ≪ t_c2 ≪ t_s1, we can write

$$\frac{d{\widehat{s}}_1}{dT}=-\frac{{\widehat{s}}_1({\sigma }_1+1)}{1+{\sigma }_1{\widehat{s}}_1}+\mathcal{O}({\epsilon }_2),$$ (91a)

$${\mu }_2\frac{d{\widehat{c}}_2}{dT}=\frac{{\widehat{s}}_1({\sigma }_1+1)}{1+{\sigma }_1{\widehat{s}}_1}-{\widehat{c}}_2+\mathcal{O}({\epsilon }_2,{\mu }_1),$$ (91b)

which are the scaled, leading-order asymptotic equations on the T-timescale. Applying Theorem 1 to (91a)–(91b) suggests that c₂ should approximately reach QSS when T ≈ μ₂∣ln μ₂∣.

Alternatively, by looking carefully at the scaling obtained with respect to $\stackrel{‒}{\tau }$, the leading order dynamics are given by:

$$\nu \frac{d{\widehat{s}}_2}{d\stackrel{‒}{\tau }}=[-{\widehat{s}}_2+(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2+{\beta }_2{\alpha }_2{\widehat{c}}_2]+r_S{\mu }_1[1+\mathcal{O}({\mu }_2,{\epsilon }_1)],$$ (92a)

$$\frac{d{\widehat{c}}_2}{d\stackrel{‒}{\tau }}=(1+{\kappa }_2)(1+{\sigma }_2)[{\widehat{s}}_2-(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2-{\beta }_2{\widehat{c}}_2].$$ (92b)

Pursuant to Theorem 1, (92a)–(92b) indicate s₂ should reach QSS when $\stackrel{‒}{\tau }\approx \nu \mid \text{ln}\nu \mid$; consequently, we take

$$t_{s_2}^{\ast }\approx -t_{s_2}\text{ln}\nu ,$$ (93)

as the asymptotic estimate (i.e., the matching timescale) of the time it takes for s₂ to reach QSS (see Figure 10).

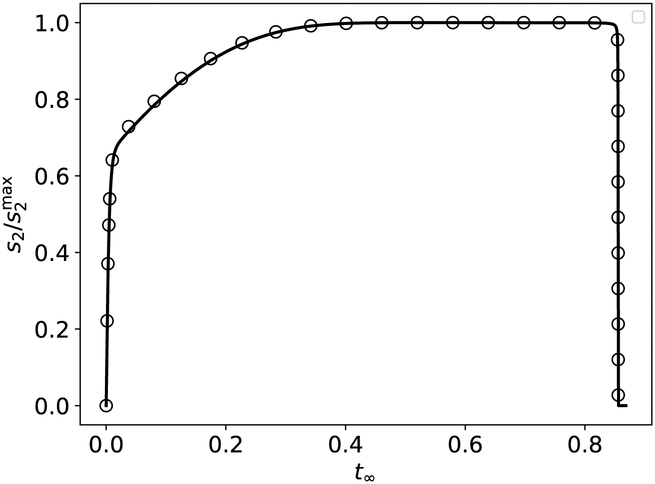
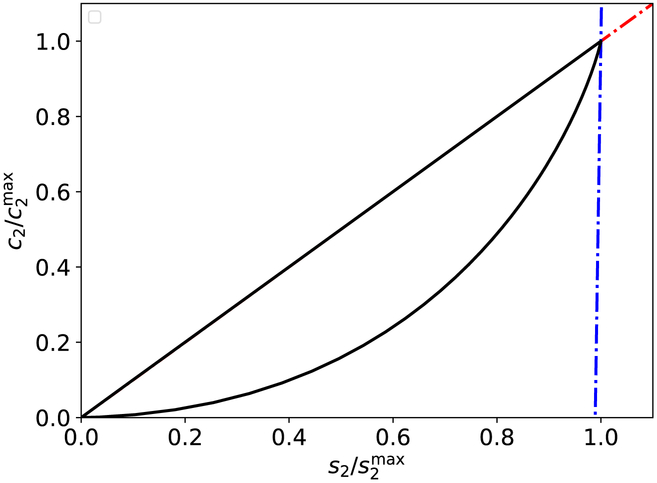
Figure 10: The timescale t_s2 is characteristic of the time it takes s₂ to reach $s_2^{\lambda }$, and the timescale $t_{s_2}^{\ast }$ is the approximate time it takes s₂ to reach $s_2^{\lambda }$, respectively, in the auxiliary reaction mechanism (47)–(48).

The thick black curve is the numerically-integrated solution to the mass action equations (49a)–(49d). The leftmost dashed vertical line corresponds to t_s2, and the rightmost dashed vertical line corresponds to $t_{s_2}^{\ast }=-t_{s_2}\text{ln}{t}_{s_2}∕t_{c_2}$. The lower dotted horizontal line corresponds to the scaled characteristic value $\ell s_2^{\lambda }$, and the upper dashed/dotted vertical line corresponds to $s_2^{\lambda }$. The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1000$, $e_2^0=100$, k₁ = 1, k₂ = 1, k₃ = 1, k₋₃ = 1, k₄ = 2 and k₋₁ = 1. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)], and s₂ has been numerically-scaled by its maximum value. For clarity, the mass action equations have been integrated from t = 0 to $t\approx t_{s_2}^{\ast }$.

4.4. Scaling Analysis: t_s2, t_c2 ≪ t_c1 ≪ t_s1

In the most extreme case, when both t_s2 and t_c2 are much less than t_c1 in magnitude, scaling analysis indicates that both s₂ and c₂ are fast variables over both the τ and T timescales:

$$\frac{d{\widehat{s}}_1}{d\tau }={\epsilon }_1[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],$$ (94a)

$$\frac{d{\widehat{c}}_1}{d\tau }=[{\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1],$$ (94b)

$${\lambda }_1^{-1}\frac{d{\widehat{s}}_2}{d\tau }=[-{\widehat{s}}_2+(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2+{\beta }_2{\alpha }_2{\widehat{c}}_2]+r_S{\mu }_1{\widehat{c}}_1,$$ (94c)

$${\lambda }_2^{-1}\frac{d{\widehat{c}}_2}{d\tau }=(1+{\kappa }_2)(1+{\sigma }_2)[{\widehat{s}}_2-(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2-{\beta }_2{\widehat{c}}_2].$$ (94d)

Recall that λ₁ ≡ t_c1/t_s2 and λ₂ ≡ t_c1/t_c2, and that ${\lambda }_1^{-1}$ and ${\lambda }_2^{-1}$ will be small when t_s2 and t_c2 are super-fast timescales, t_c1 is a fast timescale, and t_s1 is a slow timescale. Consequently, both s₂ and c₂ are given in terms of c₁

$$s_2\simeq \frac{K_{M_2}{k}_2{c}_1}{V_2-k_2{c}_1},$$ (95a)

$$c_2\simeq \frac{k_2{c}_1}{k_4},$$ (95b)

for t ≥ 0. Since the secondary reaction is asymptotically determined by c₁ when t_s2, t_c2 ≪ t_c1 ≪ t_s1, the production rate will reach a maximum when $t\approx t_{c_1}^{\ast }$ (see Figure 11). Thus, the matching timescale $t_{c_1}^{\ast }$ is synonymous with time it takes for ṗ to reach its maximum value.

Figure 11: When t_c2, t_s2 ≪ t_c1, the timescale t_c1 is characteristic of the time it takes ṗ to reach its maximum, and the timescale $t_{c_1}^{\ast }$ is the approximate time it takes c₂ to reach its maximum, respectively, in the auxiliary reaction mechanism (47)–(48).

The thick black curve is the numerically-integrated solution to the mass action equations (49a)–(49d). The leftmost dashed vertical line corresponds to t_c1, and the rightmost dashed vertical line corresponds to $t_{c_1}^{\ast }=-t_{c_1}\text{ln}{t}_{c_1}∕t_{s_1}$. The lower dotted horizontal line corresponds to the scaled characteristic value $\ell s_2^{\lambda }$. The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=100$, $e_2^0=100$, k₁ = 0.01, k₂ = 1, k₃ = 10, k₋₃ = 1, k₄ = 100 and k₋₁ = 1. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)], and c₂ has been numerically scaled by its maximum value.

5. Alternative Orderings of timescale for the auxiliary enzyme reaction

The previous sections and subsections dealt primarily with the ordering t_c1 ≪ t_s2 ≪ t_c2 ≪ t_s1. It is natural to ask what happens when this ordering starts to change, and in this section we will briefly analyze the dynamics of (48) in regimes where the ordering, t_c1 ≪ t_s2 ≪ t_c2 ≪ t_s1, is no longer preserved.

5.1. Scaling Analysis for t_c1 ≪ t_c2 ≪ t_s2 ≪ t_s1: A three versus four timescale perspective

The first ordering we consider is that in which t_c1 is a super-fast timescale, t_c2 is a fast timescale, t_s2 is a slow timescale, and t_s1 is super-slow timescale: t_c1 ≪ t_c2 ≪ t_s2 ≪ t_s1. We will start the analysis by observing the scaling with respect to $\stackrel{‒}{\tau }$:

$$\frac{d{\widehat{s}}_1}{d\stackrel{‒}{\tau }}={\mu }_2(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],$$ (96a)

$$\varpi \frac{d{\widehat{c}}_1}{d\stackrel{‒}{\tau }}=[{\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1],$$ (96b)

$$\frac{d{\widehat{s}}_2}{d\stackrel{‒}{\tau }}={\nu }^{-1}[-{\widehat{s}}_2+(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2+{\beta }_2{\alpha }_2{\widehat{c}}_2]+r_S{\mu }_2{\widehat{c}}_1,$$ (96c)

$$\frac{d{\widehat{c}}_2}{d\stackrel{‒}{\tau }}=(1+{\kappa }_2)(1+{\sigma }_2)[{\widehat{s}}_2-(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2-{\beta }_2{\widehat{c}}_2].$$ (96d)

If ν⁻¹ ≪ 1, then we immediately see that

$$\frac{d{\widehat{s}}_2}{d\stackrel{‒}{\tau }}\simeq r_S{\mu }_2{\widehat{c}}_1+\mathcal{O}({\nu }^{-1}).$$ (97)

Next, because we have assumed in our ordering that t_c1 ≪ t_c2, equation (97) can be reduced further by noting that ${\widehat{c}}_1\simeq 1$:

$$\frac{d{\widehat{s}}_2}{d\stackrel{‒}{\tau }}\simeq r_S{\mu }_2.$$ (98)

If we can then find a bound on r_Sμ₂ by showing that r_Sμ₂ ≤ K and K ~ ν⁻¹, then it follows that s₂ is a slow variable with respect to $\stackrel{‒}{\tau }$. Expanding r_Sλ₂ yields

$$r_S{\mu }_2=\frac{s_1^0}{s_2^{\max }}\frac{t_{c_2}}{t_{s_1}}=\frac{e_2^0}{K_{M_2}}-{\epsilon }_1\frac{k_2{s}_1^0}{K_{M_2}{k}_4}\ge 0,$$ (99)

which implies

$$r_S{\mu }_2\le \frac{e_2^0}{K_{M_2}}\equiv K\le {\nu }^{-1}.$$ (100)

Thus, based on the scaling analysis, we take s₂ ≃ 0 for t ≤ t_c2. The immediate consequence is that c₂ ≃ 0 for t < t_c2, since complex cannot form without the presence of substrate. Thus, no significant change in the concentration of s₂ or c₂ occurs for t < t_c2 when t_c1 ≪ t_c2 ≪ t_s2 ≪ t_s1 (see Figure 12).

Figure 12: No significant change in the concentration of s₂ or c₂ occurs over the timescale t_c2 in the auxiliary reaction mechanism (47)–(48) when t_c1 ≪ t_c2 ≪ t_s2 ≪ t_s1.

The thick black curve is the numerically-integrated solutions to the mass action equations (49a)–(49d). The dashed vertical line corresponds to t_c2 Note that there is no significant increase in the concentration of the intermediate complex over the t_c2 timescale. The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1000$, $e_2^0=1$, k₁ = 1, k₂ = 1, k₃ = 1, k₋₃ = 1, k₄ = 100 and k₋₁ = 1. Time has been mapped to the t_∞ scale: t_∞(t) = 1 — 1/ln[t + exp(1)], and c₂ has been scaled its maximum value.

Next, we scale with respect to the slow timescale, $\stackrel{‒}{T}$:

$$\frac{d{\widehat{s}}_1}{d\stackrel{‒}{T}}={\mu }_1(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],$$ (101a)

$${\epsilon }_1\frac{d{\widehat{c}}_1}{d\stackrel{‒}{T}}={\mu }_1(1+{\kappa }_1)(1+{\sigma }_1)[{\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1]$$ (101b)

$$\frac{d{\widehat{s}}_2}{d\stackrel{‒}{T}}=-{\widehat{s}}_2+(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2+{\beta }_2{\alpha }_2{\widehat{c}}_2+r_S{\mu }_1{\widehat{c}}_1,$$ (101c)

$$ϵ\frac{d{\widehat{c}}_2}{d\stackrel{‒}{T}}={\widehat{s}}_2-(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2-{\beta }_2{\widehat{c}}_2.$$ (101d)

The term r_sμ₁ is $\mathcal{O}(1)$, and ${\widehat{c}}_2$ can be approximated as being in QSS since ϵ ≪ 1 when t_c2 ≪ t_s2. Putting these observations together yields the dimensional equation

$${\stackrel{.}{s}}_2\simeq -\frac{V_2}{K_{M_2}+s_2}{s}_2+k_2{c}_1^{\max },t\lesssim t_{s_2},$$ (102)

which admits an exact solution in the form of a Lambert-W function

$$s_2\simeq s_2^{\max }(1+\psi W\left[-{\psi }^{-1}\text{exp}(-{\psi }^{-1}-\mathrm{\Theta }\cdot t)\right]),t\lesssim t_{s_2},$$ (103)

where $\psi \equiv V_2∕(k_2{c}_1^{\max })$ and $\mathrm{\Theta }\equiv (V_2-k_2{c}_1^{\max }{)}^2∕(V_2{K}_{M_2})$. From (103), we have a new timescale, $t_{s_2}^{\chi }$:

$$t_{s_2}^{\chi }\equiv \frac{K_{M_2}+s_2^{\max }}{V_2}.$$ (104)

Since no significant change in the concentration of any chemical species occurs over t_c2, the kinetic analysis in this regime can be effectively carried out with three timescales: t_c1, $t_{s_2}^{\chi }$, t_s1 (Eilertsen and Schnell, 2018). Additionally, it is also worth noting that rescaling the mass action equations with respect to $T^{\chi }=t∕t_{s_2}^{\chi }$ yields.

$$\frac{d{\widehat{s}}_1}{d{T}^{\chi }}=\frac{t_{s_2}^{\chi }}{t_{s_1}}(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],$$ (105a)

$$\frac{t_{c_1}}{t_{s_2}^{\chi }}\frac{d{\widehat{c}}_1}{d{T}^{\chi }}={\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1,$$ (105b)

$$\frac{d{\widehat{s}}_2}{d{T}^{\chi }}=(1+{\kappa }_2)(1+{\sigma }_2)[-{\widehat{s}}_2+(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2+{\beta }_2{\alpha }_2{\widehat{c}}_2]+{\widehat{c}}_1,$$ (105c)

$$ϵ\frac{d{\widehat{c}}_2}{d{T}^{\chi }}=(1+{\kappa }_2)(1+{\sigma }_2)[{\widehat{s}}_2-(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2-{\beta }_2{\widehat{c}}_2],$$ (105d)

and the term in front of ${\widehat{c}}_1$ in (105c) is euqal to 1. It follows that (105c) is, to leading order, given by

$$\frac{d{\widehat{s}}_2}{d{T}^{\chi }}\simeq -\frac{{\widehat{s}}_2(1+{\sigma }_2)}{1+{\sigma }_2{\widehat{s}}_2}+1.$$ (106)

Furthermore, rescaling the mass action equations with respect to T yields

$$\frac{d{\widehat{s}}_1}{dT}=(1+{\kappa }_1)(1+{\sigma }_1)[-{\widehat{s}}_1+(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1+{\beta }_1{\alpha }_1{\widehat{c}}_1],$$ (107a)

$${\epsilon }_2\frac{d{\widehat{c}}_1}{dT}={\widehat{s}}_1-(1-{\beta }_1){\widehat{c}}_1{\widehat{s}}_1-{\beta }_1{\widehat{c}}_1,$$ (107b)

$$\frac{t_{s_2}^{\chi }}{t_{s_1}}\frac{d{\widehat{s}}_2}{dT}=(1+{\kappa }_2)(1+{\sigma }_2)[-{\widehat{s}}_2+(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2+{\beta }_2{\alpha }_2{\widehat{c}}_2]+{\widehat{c}}_1,$$ (107c)

$${\mu }_2\frac{d{\widehat{c}}_2}{dT}=(1+{\kappa }_2)(1+{\sigma }_2)[{\widehat{s}}_2-(1-{\beta }_2){\widehat{c}}_2{\widehat{s}}_2-{\beta }_2{\widehat{c}}_2],$$ (107d)

from which it directly follows (see Figure 13) that the time it takes for ṗ to reach its maximum is given by

$$t_{s_2}^{\chi ,\ast }\approx -t_{s_2}^{\chi }\text{ln}\frac{t_{s_2}^{\chi }}{t_{s_1}}.$$ (108)

Figure 13: The validity of $t_{s_2}^{\chi }$ and $t_{s_2}^{\chi ,\ast }$ in the auxiliary reaction mechanism (47)–(48) when ϵ ≪ 1.

The thick black curve is the numerically-integrated solution to the mass action equations (49a)–(49d), and the unfilled circles mark the inner solution given by (103). The leftmost dashed vertical line corresponds to $t_{s_2}^{\chi }$, and the rightmost dashed vertical line corresponds to $t_{s_2}^{\chi ,\ast }=-t_{s_2}^{\chi }\text{ln}{t}_{s_2}^{\chi }∕t_{s_1}$. The lower dotted horizontal line corresponds to $y=\ell s_2^{\max }$, and the upper dotted horizontal line corresponds to $y=s_2^{\max }$. The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1000$, $e_2^0=1$, k₁ = 1, k₂ = 1, k₃ = 1, k₋₃ = 1, k₄ = 100 and k₋₁ = 1. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)], and s₂ has been numerically-scaled by its maximum value. Note that the mass action equations have only been integrated from t = 0 to $t\approx t_{s_2}^{\chi ,\ast }$ for clarity.

The timescale (108) is the matching timescale for s₂. It is a very good estimate of the time it takes s₂ to reach QSS, and corresponds to the time it takes the phase-plane trajectory to reach x* when ϵ ≪ 1 (Eilertsen and Schnell, 2018).

5.2. Scaling Analysis: t_c2 ≪ t_c1 ≪ t_s2 ≪ t_s1

In the previous subsection we showed that t_c2 was a “hidden” timescale: no significant accumulation of s₂ and c₂ occurs over t_c2 when t_c1 ≪ t_c2 ≪ t_s2 ≪ t_s1. In this subsection we examine was what happens when t_c2 ≪ t_c1. First, note that

$$\underset{k_4\to \infty }{\text{lim}}{t}_{s_2}^{\chi }=t_{s_2},$$ (109)

and second,

$$\underset{k_4\to \infty }{\text{lim}}{c}_2^{\max }=0,\text{and}\underset{k_4\to \infty }{\text{lim}}{s}_2^{\max }=s_2^{\lambda }.$$ (110)

Finally, since

$$W\left[-{\psi }^{-1}\text{exp}(-{\psi }^{-1}-\mathrm{\Theta }\cdot t)\right]\simeq -{\psi }^{-1}\text{exp}(-{\psi }^{-1}-\mathrm{\Theta }\cdot t),{\psi }^{-1}⪡1,$$ (111)

we can combine (109), (110) and (111) to yield

$$s_2\approx s_2^{\lambda }[1-\text{exp}(-t∕t_{s_2})],\text{for}t\lesssim t_{s_2}.$$ (112)

From a geometrical point of view, the c₂-nullcline gets pressed against the s₂-axis in the phase-plane as k₄ → ∞, and $c_2^{\max }$ is almost negligible in magnitude. Thus, when $k_4\gg k_3{e}_2^0$, the mass action kinetics can essentially be approximated by (112), since $t_{s_2}\approx t_{s_2}^{\chi }$ and $s_2^{\max }\approx s_2^{\lambda }$ as t_c2 → 0. Consequently, t_s2 is approximately characteristic of the time it takes s₂ to reach $s_2^{\max }$ in regimes where t_c2 is a super-fast timescale and $t_{c_2}\ll t_{c_1}\ll t_{s_2}^{\chi }\ll t_{s_1}$.

5.3. Scaling Analysis: t_s2 ≪ t_c1 ≪ t_c2 ≪ t_s1

Another case is when t_s2 is a super-fast timescale. Under this scenerio, the scaled equations indicate that s₂ is in QSS for the duration of the reaction. Geometrically, s₂ will closely follow the s₂-nullcline as it moves in the s₂–c₂ phase–plane. In this case c₂ is asymptotic to

$${\stackrel{.}{c}}_2\simeq -k_4{c}_2+k_2{c}_1,t\ge 0,$$ (113)

and thus t_c2 remains characteristic of the time is takes c₂ to reach its maximum value, and the matching timescale $t_{c_2}^{\ast }$ provides an estimate for the time it takes for ṗ to reach its maximum value (see Figure 14).

Figure 14: The lag time in the auxiliary reaction mechanism (47)–(48) when t_s2 ≪ t_c1 ≪ t_c2 ≪ t_s1.

The thick black curve is the numerically-integrated solution to the mass action equations (49a)–(49d), and the unfilled circles mark the inner solution given by (103). The leftmost dashed vertical line corresponds to t_c2, and the rightmost dashed vertical line corresponds to $t_{c_2}^{\ast }=-t_{c_2}\text{ln}{t}_{c_2}∕t_{s_1}$. The lower dotted horizontal line corresponds to y = ℓ; The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1000$, $e_2^0=1$, k₁ = 1, k₂ = 1, k₃ = 1, k₋₃ = 1, k₄ = 100 and k₋₁ = 1. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ln[t + exp(1)], and c₂ has been numerically-scaled by its maximum value.

5.4. Scaling Analysis: t_c1 ≪ t_c2 ≈ t_s2 ≪ t_s1

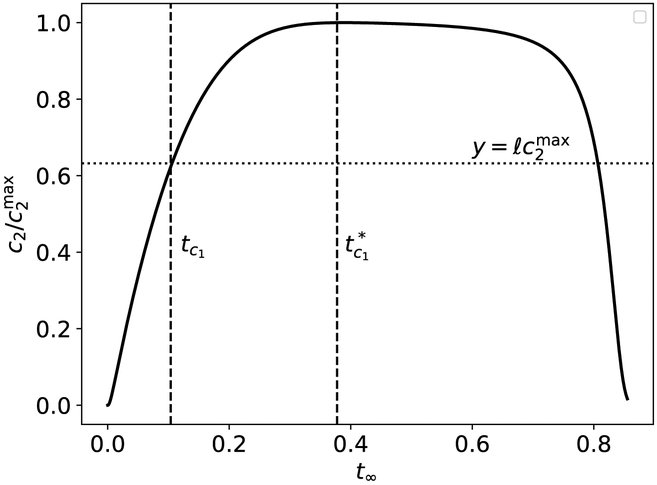
Up until this point, we have been able to derive characteristic timescales that quantify the temporal order of magnitude of a specific trajectory’s rapid approach to QSS. Our success in the derivation of characteristic timescales resides in the fact that, so far, we have only considered regimes in which trajectories are asymptotic to one-dimensional manifolds (i.e., the s₂-nullcline or the c₂-nullcline) in their approach to the zero-dimensional manifold, x*. However, their are many such trajectories that are not asymptotic to a particular manifold in the approach to x*. For example, if t_c1 ≪ t_c2 ≈ t_s2 ≪ t_s1, then it is obvious from both the scaling analysis and the phase-plane dynamics that the trajectory will not follow closely to either nullcline in its approach to x* (see Figure 15). It is not obvious in this case how to go about determining the lag time. However, Theorem 1 suggests that either matching timescale $t_{c_2}^{\ast }$ or $t_{s_2}^{\ast }$ should yield a reasonable approximation to the lag time. Thus, even though the transient solution is unknown, the scaling analysis still provides a good estimate of the time it takes for the secondary reaction to “catch” the primary reaction and for ṗ to reach its maximum value (see Figure 16).

Figure 15: Phase–plane dynamics of the auxiliary reaction mechanism (47)— (48) when t_c1 ≪ t_c2 ≪ t_s2 ≪ t_s1.

The thick black curve is the numerically-integrated solution to the mass action equations (49a)–(49d), the dashed/dotted red curve is the c₂-nullcline and the dashed/dotted blue curve is the stationary s₂-nullcline. Notice that the trajectory does not follow a path that lies close to either nullcline in the approach to x*. The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1000$, $e_2^0=10$, k₁ = 1, k₂ = 1, k₃ = 10, k₋₃ = 1, k₄ = 100 and k₋₁ = 1.

Figure 16: The lag time in the auxiliary reaction mechanism (47)–(48) when t_c1 ≪ t_c2 = t_s2 ≪ t_s1.

This is a close-up of Figure 15 near x*. The thick black curve is the numerically-integrated solution to the mass action equations (49a)–(49d), the dashed/dotted red curve is the c₂-nullcline and the dashed/dotted blue curve is the stationary s₂-nullcline. The solid black circle marks the trajectory when $t=t_{s_2}^{\ast }=-t_{s_2}\text{ln}{t}_{s_2}∕t_{s_1}$. Notice that Tikhonov’s Theorem still provides a reasonable estimate of the lag time, which is synonymous with the matching timescale corresponding to either s₂ or c₂. The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1000$, $e_2^0=10$, k₁ = 1, k₂ = 1, k₃ = 10, k₋₃ = 1, k₄ = 100 and k₋₁ = 1.

6. The region of validity of the timescale estimations

We conclude our analysis by noting that the conditions max{ϵ₂, μ₁, μ₂} ≪ 1 do not provide a universal set of qualifiers to ensure that the phase-plane trajectory approximately adheres to x* after a brief fast transient. To establish criteria that determines a region in parameter space within which our analysis is valid, we first remark that an absolutely necessary condition for the validity of our timescale analysis is $V_2\gg k_2{c}_1^{\max }$. Second, if $V_2\gg k_2{c}_1^{\max }$ holds, then $0<t_{s_2}<t_{s_2}^{\chi }$ since

$$t_{s_2}^{\chi }=t_{s_2}(1+{\kappa }_2)[1+\theta +\mathcal{O}({\theta }^2)],\theta \equiv \frac{k_2{c}_1^{\max }}{V_2}.$$ (114)

Consequently, we take

$$0<\text{min}\{t_{s_2}^{\chi }∕t_{s_1},t_{c_2}∕t_{s_1}\},$$ (115a)

$$\text{max}\{t_{s_2}^{\chi }∕t_{s_1},t_{c_2}∕t_{s_1}\}⪡1,$$ (115b)

as our qualifying set of conditions that must hold in order for the trajectory to closely follow x*. This implies that the natural scaling to employ is given by (107c)–(107d), and gives a universal set of parameters from which to analyze the phase-plane dynamics. For example, if $t_{s_2}^{\chi }\ll t_{s_1}$ but μ₂ ~ 1, then we do not expect the trajectory to closely follow x*. However, we see from the scaled equations that s₂ should deplete in a QSS over the t_s1 timescale as long as $t_{s_2}^{\chi }\ll t_{s_1}$. Thus, the trajectory s₂ “sticks” to the s₂-nullcline, but lags behind x* since μ₂ ~ 1 (see Figure 17). On the other hand, when the phase-plane trajectory does closely follow x*, the scaling given by (107c)–(107d) tells us the component that contributes most to the error in our approximation (see Figure 18).

Figure 17: The trajectory follows the s₂-nullcline in the phase–plane of the auxiliary reaction mechanism (47)-(48) when $t_{s_2}^{\chi }∕t_{s_1}\ll 1$.

The thick black curve is the numerically-integrated solution to the mass action equations (49a)–(49d), the dashed/dotted red curve is the c₂-nullcline and the dashed/dotted blue curve is a snapshot of s₂-nullcline when t ≈ 1.1 · t_s1. The black dot is the corresponding snapshot of the numerical solution to (49a)–(49d). In this simulation, $t_{s_2}^{\chi }∕t_{s_1}\approx 0.001<{\mu }_2\approx 0.1$; consequently, the trajectory follows the s₂-nullcline but fails to closely follow x* (see Movie 1 in Supplementary Materials). The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=100$, $e_2^0=100$, k₁ = 1, k₂ = 1, k₃ = 1, k₋₃ = 1, k₄ = 0.1 and k₋₁ = 1.

Figure 18: The component-wise error when the indicator reaction is fast in the auxiliary reaction mechanism (47)–(48).

The thick black curve is the numerically-integrated solution to the mass action equations (49a)–(49d), the dashed/dotted red curve is the c₂-nullcline and the dashed/dotted blue curve is a snapshot of s₂-nullcline when t ≈ 1.1 · t_s1. The black dot is the corresponding snapshot of the numerical solution to (49a)–(49d). In this simulation, $t_{s_2}^{\chi }∕t_{s_1}\approx 0.0001<{\mu }_2\approx 0.005$; consequently, the trajectory sits “just behind” and slightly above x* (green dot) since the trajectory will be closer to the s₂-nullcline than the c₂-nullcline (see Movie 2 in Supplementary Materials). The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=100$, $e_2^0=100$, k₁ = 1, k₂ = 1, k₃ = 1, k₋₃ = 1, k₄ = 2 and k₋₀ = 1.

7. Discussion

Enzyme catalyzed reactions typically exhibit multiple dynamical regimes; each regime marks a domain over which certain kinetic behavior and approximate rate laws can be assumed to be valid. The approximate rate laws are derived assuming timescale separations. The primary contribution of this paper is to categorize specific types of timescales, particularly with regard to matched asymptotics in enzyme catalyzed reactions. In short, we have shown that in each kinetic regime of a reaction there really exist two distinct timescales that must be considered: characteristic and matching. Characteristic timescales arise naturally when the initial fast transient of a reaction can be approximated with a linear equation. This happens often in enzyme catalyzed models, since the differential equation governing the fast variable becomes linear when the slow variable is held constant. As such, the characteristic timescale should be utilized in scaling analysis, since it determines the relevant length scale of its corresponding regime. However, its limitation resides in the fact that it does not provide a good approximation to the time it takes a reaction to reach QSS. The matching timescale provides a reliable estimate to reach QSS, and determines the temporal boundary of the corresponding regime.

In this work, the fast and slow timescales of the single-enzyme, single-substrate MM reaction mechanism (12) have been revisited. Under the RSA, the established fast timescale, t_c1, of the MM reaction mechanism is a characteristic timescale: it provides the temporal order of magnitude needed for the concentration of complex to accumulate to approximately 63% of its threshold value. This is the appropriate timescale to utilize in the scaling analysis. However, since t_c1 does not provide a good estimate of when the complex concentration reaches its maximum value, it fails to define an appropriate matching timescale. The matching timescale delimits the approximate time point in the course of the reaction when the transition from initial fast transient to steady-state kinetics occurs. By utilizing Tikhonov/Fenichel theory, we have shown that the appropriate matching timescale for the MM reaction mechanism is $t_{c_1}^{\ast }$:

$$t_{c_1}^{\ast }=-t_{c_1}\text{ln}\frac{t_{c_1}}{t_{s_1}}.$$

In this paper, we consider the auxiliary enzyme reaction mechanism (47)–(48) as a multiple timescale case study. This reaction was initially analyzed with the assumption that the auxiliary enzyme concentration is high, and that the primary reaction obeys the RSA. We demonstrated that when the secondary reaction has sufficient speed, the overall kinetics and reaction mechanism is determined by the ratios of four timescales: t_c1, t_s2, t_c2 and t_s1. Six different orderings of these timescales were considered: (i) t_c1 ≪ t_s2 ≪ t_c2 ≪ t_s1, (ii) t_c1 ≪ t_c2 ≪ t_s2 ≪ t_s1, (iii) {t_c2, t_s2} ≪ t_c1 ≪ t_s1, (iv) t_c2 ≪ t_c1 ≪ t_s2 ≪ t_s1, (v) t_s2 ≪ t_c1 ≪ t_c2 ≪ t_s1, and (vi) t_c1 ≪ t_s2 = t_c2 ≪ t_s1. The lag time, which is roughly the time it takes for the rate of product generation to reach its maximum value, was calculated for each specific ordering. As we have shown, the lag time corresponds to a specific matching timescale; specifically, we have demonstrated that the lag time is synonymous with the matching timescale that corresponds to the slow variable when the auxiliary reaction is composed of super-fast, fast, slow and super-slow variables.

The estimation of timescales is perhaps the most challenging component chemical kinetics. The subtle difference between characteristic and matching timescales is often neglected in applications of GSPT. This work provides a useful case study in the interpretation of timescales in enzyme-catalyzed reactions, and the approaches used should be readily applicable to a wide range of singular perturbation problems in mathematical biology.

On a final note, we wish to emphasize that we carried out this analysis by restricting the parameters pertinent to the primary reaction to lie in a regime in which the RSA and QSSA are applicable. This is of course not necessary, and the total quasi-steady-state approximation could have been employed (Borghans et al., 1996; Schnell and Maini, 2002; Tzafriri, 2003; Bersani and Dell’Acqua, 2012; Bersani et al., 2015). The tQSSA is lumping method that it is generally considered to be valid over a much larger parameter range than the QSSA. It has been preivously applied to complex enzyme catalyzed reactions that exhibit both reversibility (Tzafriri and Edelman, 2004) and competition (Pedersen et al., 2006). From a timescale perspective, the tQSSA has an advantage it reduces the total number of timescales in the system by lumping two chemical species into one by defining the total substrate s_T = c₁ + s₁. The disadvantage of this approach is that the lumping of variables inevitably leads to a lower dimensionality system with a potentially different dynamical behavior. So far, the validity and applicability of the tQSSA in the case of both the auxiliary reaction and coupled zymogen activation reactions (Eilertsen et al., 2018) remains open, and we certainly encourage exploration and research in this direction.

Highlights.

• Complex enzyme catalyzed reactions typically consist of multiple regimes with characteristic timescales

• Each regime marks a domain over which certain kinetic behavior and corresponding rate laws can be assumed to be valid

• Characteristic timescales are not ideal for determining when chemical species reach their maximum rates

• Matching timescales precisely determine when the transitions from initial fast transient to steady-state kinetics occurs