Comprehensive evaluation of deep learning architectures for prediction of DNA/RNA sequence binding specificities

Abstract

Motivation

Deep learning architectures have recently demonstrated their power in predicting DNA- and RNA-binding specificity. Existing methods fall into three classes: Some are based on convolutional neural networks (CNNs), others use recurrent neural networks (RNNs) and others rely on hybrid architectures combining CNNs and RNNs. However, based on existing studies the relative merit of the various architectures remains unclear.

Results

In this study we present a systematic exploration of deep learning architectures for predicting DNA- and RNA-binding specificity. For this purpose, we present deepRAM, an end-to-end deep learning tool that provides an implementation of a wide selection of architectures; its fully automatic model selection procedure allows us to perform a fair and unbiased comparison of deep learning architectures. We find that deeper more complex architectures provide a clear advantage with sufficient training data, and that hybrid CNN/RNN architectures outperform other methods in terms of accuracy. Our work provides guidelines that can assist the practitioner in choosing an appropriate network architecture, and provides insight on the difference between the models learned by convolutional and recurrent networks. In particular, we find that although recurrent networks improve model accuracy, this comes at the expense of a loss in the interpretability of the features learned by the model.

Availability and implementation

The source code for deepRAM is available at https://github.com/MedChaabane/deepRAM.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

DNA- and RNA-binding proteins are involved in many biological processes including transcription, translation and alternative splicing (Ferré et al., 2016; Gerstberger et al., 2014). Unfortunately, only some of these binding sites have been identified by biological experiments. Moreover, these experiments are expensive and time-consuming. Position weight matrices (PWMs) are the most common method to characterize the sequence specificity of a protein, thanks to their simplicity and ease of interpretation (Stormo, 2000). However, many studies suggest that sequence specificity can be better captured using more complex models (Kazan et al., 2010; Rohs et al., 2010; Siggers and Gordâ n, 2014).

In recent years, deep neural networks have become the technique of choice for challenging tasks in computer vision (Krizhevsky et al., 2012; LeCun et al., 2015), speech recognition (Hinton et al., 2012), machine translation (Sutskever et al., 2014) and computational biology (Angermueller et al., 2016). Methods based on convolutional neural networks (CNNs) (LeCun et al., 1998) and recurrent neural networks (RNNs) (Hochreiter and Schmidhuber, 1997) have been proposed for the task of identifying protein binding sites in DNA and RNA sequences, and have achieved state-of-the-art performance (Alipanahi et al., 2015; Hassanzadeh and Wang, 2016; Quang and Xie, 2016; Shen et al., 2018).

DeepBind (Alipanahi et al., 2015) was the first deep learning approach for this task. It used a single layer of convolution and demonstrated the accuracy of CNNs as well as their ability to learn signal detectors that recapitulate known motifs. Zeng et al. (2016) explored in more detail the effect of various architecture parameters such as the number of layers and operations such as pooling. Other studies opted for more complex architectures and introduced hybrid models that integrate both CNNs and RNNs. DeeperBind (Hassanzadeh and Wang, 2016) and DanQ (Quang and Xie, 2016) for example, add long short-term memory (LSTM) layer(s) to the DeepBind architecture. The additional RNN layers are designed to improve binding accuracy prediction by learning long-range dependencies between the sequence features learned by the CNN layers. Purely RNN-based methods were also examined: the KEGRU method (Shen et al., 2018) used a layer of bidirectional gated recurrent units (bi-GRUs), combined with a k-mer embedding representation of the input sequence to create an internal state of the network that allows it to capture long-range dependencies and thus obtain good performance. Methods that are specific to modeling RNA-binding proteins (RBPs) were also developed. iDeepS for example, uses both CNN and RNN layers, and identifies sequence and structural motifs simultaneously (Pan et al., 2018).

Despite all these studies, it is still not clear which deep learning architecture performs best for detecting binding in DNA and RNA sequences. A fair and unbiased comparison can be very challenging especially when considering the sensitivity of deep learning methods to the step of model selection: deep neural networks have many hyper-parameters that require careful tuning, and differences in performance can be the result of the use of different model selection strategies (Lipton and Steinhardt, 2018; Melis et al., 2018). Therefore, a meaningful comparison requires the use of a coherent model selection strategy applied uniformly across all architectures. In this study, we conduct a systematic exploration of the performance of different architectures using CNNs and/or RNNs for the study of DNA and RNA sequence binding specificity prediction. For this purpose, we have designed a collection of architecture variants, some of which correspond to published methods by varying the network components, depth and input layer representation. To ensure the objectivity of our evaluation, we used the same model selection strategy and made the pipeline fully automatic to avoid the need for hand-tuning.

Our experiments use datasets collected from the Encyclopedia of DNA Elements (ENCODE) project (ENCODE-Project-Consortium, 2012) and verified binding site of RBPs derived from large-scale CLIP-seq experiments (Stražar et al., 2016). We find that more complex architectures that combine RNNs and CNNs indeed provide improved performance over the vanilla CNN model, and that this advantage increases with increasing number of training examples that are available. However, the improvement in accuracy comes at the expense of the interpretability of the learned models and increased training times. Our results also demonstrate the advantage of using a k-mer embedding to represent the input sequence instead of the standard one-hot encoding, especially for RBP binding site prediction. Finally, we present an end-to-end deep learning toolkit called deepRAM that provides a framework for training and evaluating deep learning architectures for DNA/RNA sequence analysis.

2 Materials and methods

In this study, we present a comprehensive evaluation of different deep learning architectures for the task of predicting DNA- and RNA-protein binding sites. First, we present the benchmark datasets used in our study. Then, we present the architectures used in our experiments. Third, we provide the technical details of the model selection process that we followed to ensure unbiased model comparison. These methods are implemented as an open-source deep learning package called deepRAM that allows users to evaluate different architectures for predicting DNA- and RNA-protein binding sites. Finally, we describe our method for extracting motifs from the learned models.

2.1 Datasets

The deep learning models are evaluated on data from ChIP-seq and CLIP-seq experiments. For ChIP-seq data we used data from 83 ChIP-seq experiments from the ENCODE project that assayed binding of diverse transcription factors. These datasets were used to evaluate deep learning architectures in Alipanahi et al. (2015) and Zhou and Troyanskaya (2015), and we use the same sequences as training/testing examples. The authors of DeepBind split the ChIP peak data into three lists: A, B and C. A is the set of the top 500 even-numbered peaks when considering the ranked list of peaks detected. B is the set of the top 500 odd-numbered peaks and C is the set of remaining peaks. For model training, we use the peaks from A and C, and the peaks from B were used for testing. Positive examples in this binary classification task consist of 101 bp regions centered on each ChIP-seq peak. The negative examples were generated by shuffling the positive sequences while matching dinucleotide composition.

We also evaluate the ability of different architectures to identify RNA-binding sites. We use the same benchmark human dataset used by the developers of iONMF (Stražar et al., 2016) which consists of 31 CLIP-seq experiments over 19 proteins. The data were obtained from (https://github.com/mstrazar/ionmf); original data were retrieved from DoRiNA (Blin et al., 2015) and iCount (http://icount.biolab.si/). Positive sites represented nucleotides that were identified as being within clusters of interaction sites derived from CLIP-seq. Negative sites were extracted from genes not participating in the protein-RNA interaction process in any of the 31 experiments. Each experiment consists of 40 000 examples divided into 30 000 examples for training and 10 000 for testing.

2.2 Model architectures

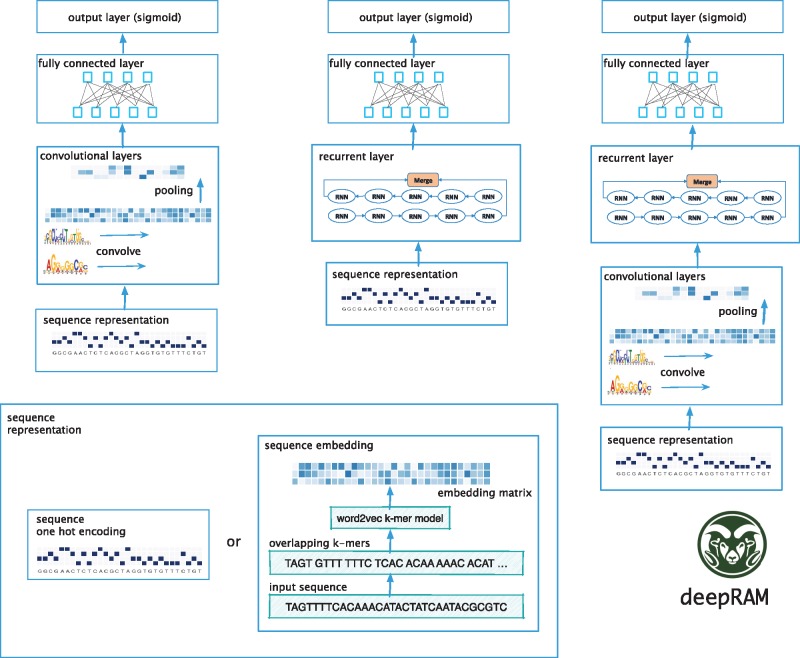
In this section, we describe the deep learning architectures to be evaluated (see Fig. 1). In addition to comparing architectures, we compare two ways of representing the input sequence: either using a one-hot encoding or a k-mer embedding computed using word2vec (Asgari and Mofrad, 2015; Mikolov et al., 2013). When using the one-hot encoding, the input sequence is represented by a 4 × L matrix where L is the length of the sequence and each position in the sequence is associated with a vector of length four with a single non-zero element corresponding to the nucleotide in that position. For the k-mer embedding representation (see Fig. 1), we first split the sequence into overlapping k-mers of length k using a sliding window with stride s and then map each k-mer in the obtained sequence into a d-dimensional vector space using the word2vec algorithm (Mikolov et al., 2013). Word2vec is an unsupervised learning algorithm which maps k-mers from the vocabulary to vectors of real numbers in a low-dimensional space. The embedding representation of k-mers is computed in such a way that their context is preserved, i.e. word2vec produces similar embedding vectors for k-mers that tend to co-occur.

Fig. 1.

Overview of the deep learning architectures evaluated in this work. These include CNN-only models known for their ability to detect motifs (left), RNN-only models (center) which excel at capturing long-term sequence dependencies, and hybrid CNN-RNN models. The input for all variants is either a one-hot encoding or a k-mer embedding of the DNA/RNA sequence obtained using word2vec

Convolutional networks. To apply CNNs to biological sequence data we use 1D convolution. In 1D convolution we slide local signal detectors (filters) along the sequence; subsequent convolutional layers integrate the results of previous layers at increasing spatial scales, generating a representation that is able to abstract away some of the variability observed in binding sites. Each convolutional module is composed of a convolutional layer and a pooling layer (see Fig. 1). A convolutional layer consists of 1D convolution with a specified number of kernels or filters. The results of applying each filter at each position of the sequence is transformed using a non-linear activation function. We use the commonly used rectified linear unit (ReLU), which keeps only positive filter values and sets the remaining to 0, which helps avoid the so-called vanishing gradient problem (Bengio et al., 1994; Maas et al., 2013). More specifically, a convolution layer computes

$$\text{convolution}{\left(X\right)}_{i,k}=\text{ReLU}\left(\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}{W_{\mathit{mn}}}^k{X}_{i+m,n}\right),$$ (1)

where X is the input matrix representing the sequence, i is the index of the output position and k is the index of the filter. Each convolutional filter W^k is an M × N matrix with M being the window size and N being the number of input channels. For the first convolution layer N equals the input representation dimension (four for one-hot encoding or d for the word2vec representation); for higher-level convolutional layers N is the number of filters in the previous convolutional layer. Next, the output of convolution undergoes pooling, which aggregates the outputs from neighboring positions for each filter in order to achieve consistency and invariance to small shifts in the input sequence. In this work, we use max-pooling which computes the maximum value over a fixed number of spatially adjacent overlapping windows over the convolutional layer’s output:

$$\text{pooling}{\left(Y\right)}_{\mathit{ik}}=\max (Y_{\mathit{iP},k},Y_{\mathit{iP}+1,k},\dots ,Y_{\mathit{iP}+P-1,k}),$$ (2)

where Y is the output of the convolutional layer, P is the pooling window size, i is the output position and k is the index of the filter being pooled.

The first convolutional layer can be thought of as a motif detector where each filter is analogous to a PWM and the convolution operation is equivalent to scanning the PWM with a sliding window across the sequence. Additional layers of convolution and pooling enable the network to extract features from larger spatial ranges and potentially capture interactions between motifs, allowing the network to represent more complex patterns than shallower networks. On the flip side, deeper networks have more parameters and require more data for obtaining high levels of performance.

RNN-based models. The second class of architectures we explore are RNN-only models. RNNs have an internal state that is updated as the network reads the input sequence. This internal memory allows RNNs to capture interactions between distant elements along the sequence, and is therefore commonly used in natural language processing (Hirschberg and Manning, 2015). Two types of RNN units were tested using deepRAM: LSTM units (Hochreiter and Schmidhuber, 1997) and GRU units (Cho et al., 2014; Chung et al., 2014). A GRU unit given an input x_t at position t in the sequence performs the following operations:

$$\begin{array}{cc}{z}_t& =\mathrm{\sigma }(W_z\times [h_{t-1},x_t]+b_z),\\ r_t& =\mathrm{\sigma }(W_r\times [h_{t-1},x_t]+b_r),\\ {{\displaystyle \stackrel{\sim }{h}}}_t& =\tanh (W_h\times [r_t\odot h_{t-1},x_t]+b_h),\\ h_t& =(1-z_t)\odot h_{t-1}+z_t\odot {{\displaystyle \stackrel{\sim }{h}}}_t,\end{array}$$ (3)

where $\odot$ is element-wise multiplication, z_t and r_t are the two GRU gates called the update gate and reset gate, respectively; W_z, W_r and W_h are weight matrices, and b_z, b_r and b_h are the biases. h_t is the hidden state that is used as memory to hold information on previous data the network has seen before, and ${{\displaystyle \stackrel{\sim }{h}}}_t$ is the candidate memory state that is considered for potentially replacing h_t. The reset gate controls how much past information to forget and the update gate controls how much information to throw away and what new information to add. The gates and hidden states are vectors of real numbers of the same dimension, which is a tunable hyper-parameter.

LSTM units are more complex than GRU units, and we refer the readers to the original publications for details (Hochreiter and Schmidhuber, 1997). The basic idea of using a gating mechanism in both LSTM and GRU architectures is to capture short- and long-term dependencies in sequences. After the LSTM/GRU has iterated over the sequence, we use its hidden state at the last position, which contains information about the entire sequence, as the output of that layer.

The bi-RNN (bi-GRU/bi-LSTM) is an extension of the regular RNN, which consists of a forward layer and a backward layer, representing traversals of the sequence in both directions. The output of the bi-RNN is then computed by concatenating the output vectors of the two traversals together.

Hybrid models. The third type of architecture we consider is that of hybrid convolutional and recurrent networks (see Fig. 1). The convolution stage that is composed of one or more convolutional modules scans the sequence using a set of 1D convolutional filter in order to capture sequence patterns or motifs. The convolutional stage is followed by an RNN stage which is capable of learning complex high-level grammar-like relationships by considering the orientations and spatial relationships between the motifs.

The final module in all three types of models is composed of one or two fully connected layers to integrate information from the entire sequence followed by a sigmoid layer to compute the probability that the input sequence contains a DNA- or RNA-binding site.

Evaluated architectures. The deepRAM tool provides implementations of several existing architectures: DeepBind (Alipanahi et al., 2015), which uses a single CNN layer; DanQ, which uses a single layer CNN followed by a bidirectional LSTM (Quang and Xie, 2016); KEGRU, which uses k-mer embedding and a layer of GRU units (Shen et al., 2018) and dilated multi-layer CNN (Gupta and Rush, 2017). To fully evaluate the range of deep learning architectures we considered additional variants denoted as DeepBind* (multi-layer CNN), DanQ* (DanQ with multiple layers of convolution), DeepBind-E* (multi-layer CNN with k-mer embedding), ECLSTM (k-mer embedding with single layer CNN and LSTM) and ECBLSTM (k-mer embedding with single layer CNN and bidirectional LSTM). These architectures are summarized in Table 1.

Table 1.

Overview of the models compared in this work

Layers	DeepBind	DeepBinda	Dilated	DanQ	DanQa	DeepBind-Ea	KEGRU	ECLSTM	ECBLSTM
Embedding	−	−	−	−	−	+	+	+	+
Convolution	+	+ (3)	+(3) a	+	+ (3)	+ (3)	−	+	+
Recurrent	−	−	−	bi-LSTM	bi-LSTM	−	bi-GRU	LSTM	bi-LSTM

Note: ‘+’ and ‘−’ denote the presence and absence of the layer type respectively. ‘(.)’ denotes the number of convolution layers if present. In the recurrent layers, if present, the type of RNN is specified.

^aThe dilated architecture consists of three convolution layers, one non-dilated followed by two dilated (dilation = 2) convolution layers.

2.3 Model training, selection and evaluation

Model selection is perhaps the most challenging step in deep learning as the performance of deep learning algorithms is very sensitive to the calibration parameters (Lipton and Steinhardt, 2018). A careful configuration and selection of the hyper-parameters is thus essential. For each dataset, we use automatic calibration that is based on randomly sampling 40 hyper-parameter settings from all possible combinations; each parameter setting is evaluated using its area under the ROC curve (AUC) in 3-fold cross-validation. Next, we use the selected best hyper-parameter setting to train five models using the full training data and choose the model with the best training performance as the final selected model. Multiple models are trained to avoid the effect of random initialization on model performance. This model selection strategy is based on the one used by the authors of DeepBind (Alipanahi et al., 2015).

In the training phase, we consider the number of learning steps as a hyper-parameter. For each of the 40 calibration sets, we train a model for a maximum of 40 000 learning steps and test it on the held out validation set every 5000 learning steps. The iteration with the best validation accuracy is picked as the number learning steps. The number of filters in the first convolutional layer is chosen as part of model selection; the number of filters in each subsequent layer is increased by 50% compared to the layer before it. Some model parameters were chosen on the basis of preliminary experiments that demonstrated consistent behavior across datasets (e.g. embedding k-mer length and embedding stride); complete details of the hyper-parameter space are summarized in Table 2.

Table 2.

deepRAM hyper-parameters, search space and sampling method

Calibration parameters	Search space	Sampling
Embedding dimensionality	50	Fixed
Embedding k-mer length	3	Fixed
Embedding stride	1	Fixed
Motif length	{10, 24}a	Fixed
Number of filters	{16, 32}	Uniform
Pooling window size	3	Fixed
Pooling stride	1	Fixed
RNN hidden size	{20, 50, 80, 100}	Uniform
Dense layer size	{None, 32 units, 64 units}	Uniform
Optimizer	{SGD, Adagrad}	Uniform
Learning rate	[1e-3, 1e-1]	Log uniform
Momentum (SGD)	[0.95, 0.99]	Sqrt uniform
Number of learning steps	[5000:40 000]b	Evaluate all
Weight initialization	{Xavier, normal}	Uniform
CNN initial weight std	[1e-6, 1e-1]	Log uniform
RNN initial weight std	[1e-6, 1e-1]	Log uniform
Fully connected initial weight std	[1e-5, 1e-1]	Log uniform
Weight decay	[1e-10, 1e-1]	Log uniform
Dropout expectation	{0.4, 0.55, 0.7, 0.85, 1}	Uniform

Note: ‘initial weight std’ refers to the SD of the distribution used to choose the weights.

^aTen with k-mer embedding. 24 with one-hot encoding.

^bStep = 5000.

Model training. To train a given model, we minimize the cross-entropy objective function. This is performed by stochastic gradient descent (SGD) or Adagrad, and the choice is made as part of the model selection process. Examples were processed using a batch size of 128 in all experiments. We used multiple regularization schemes including dropout (applied to max-pooling layers/RNN layers/hidden layers), weight decay and early stopping.

We ran our experiments on an Ubuntu server with a TITAN X GPU with 12 GB of memory. Typical running times of each experiment for model selection was between 1 h for a single layer CNN and almost 4 h for a network that includes convolutional and bi-LSTM modules (see details in Supplementary Table S3).

2.4 Motif extraction

In order to make models implemented using deepRAM easily interpretable, we extract motifs from the first convolutional layer following a similar methodology as in DeepBind (Alipanahi et al., 2015). To do so, we feed all test sequences through the convolution stage. For each filter, we extract all sequence fragments that activate the filter and use only activations that are greater than half of the filter’s maximum value. Once all the sequence fragments are extracted, they are stacked and the nucleotide frequencies are counted to form a position frequency matrix (PFM). Sequence logos are then constructed using WebLogo (Crooks et al., 2004). Finally, the discovered motifs are aligned using TOMTOM (Gupta et al., 2007) against known motifs from CISBP-RNA (Ray et al., 2013) for RBPs and JASPAR (Mathelier et al., 2014) for transcription factors.

2.5 deepRAM

deepRAM is an end-to-end deep learning toolkit for predicting protein binding sites and motifs. It is designed to help users run experiments using a variety of architectures and implements the fully automatic model selection strategy described above. This helps avoid the need for hand-tuning and thus removes, making it user friendly without losing its flexibility. While it was designed with ChIP-seq and CLIP-seq data in mind, it can be used for any DNA/RNA sequence binary classification problem.

deepRAM allows users the flexibility to choose a deep learning model by selecting its different components: input sequence representation (one-hot or k-mer embedding), whether to use a CNN and how many layers, and whether to use an RNN, and the number of layers and their type. For CNNs the user can choose to use dilated convolution as well. Once the model is trained, the learned motifs of the first convolutional layer are automatically extracted and visualized using WebLogo, and then matched with known motifs using TOMTOM.

We implemented deepRAM using PyTorch 1.0 (http://pytorch.org/), which supports GPU acceleration. Our implementation has been packaged to make it runnable on any Unix-based system, and is available at: https://github.com/MedChaabane/deepRAM.

3 Results

3.1 Deeper is better

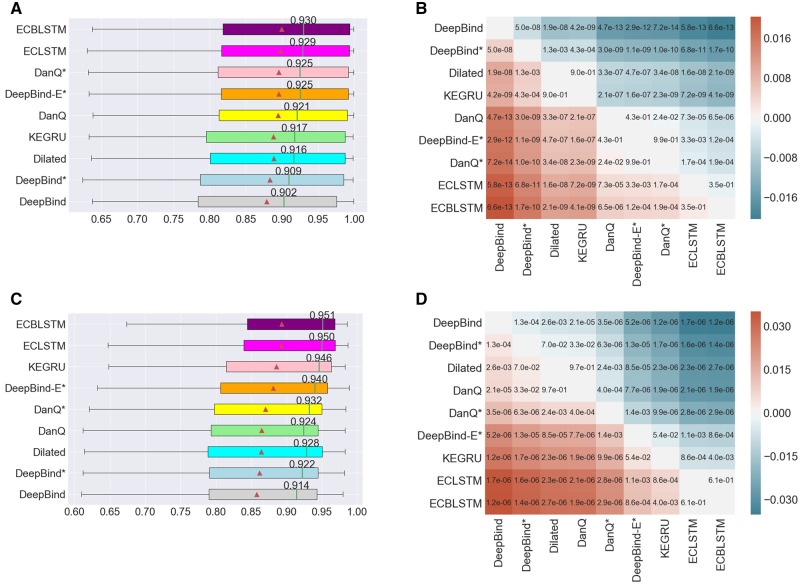
We evaluated and compared the performance of the models introduced in Section 2.2 on the two tasks of predicting DNA- and RNA- protein binding sites (see Fig. 2). Overall, all models performed well with median AUCs >0.90 on ChIP-seq data and >0.91 on CLIP-seq data. The proposed ECBLSTM model (Embedding, Convolution, bi-LSTM) provided the most significant improvement over DeepBind with a median AUC of 0.930 compared with 0.902 for DeepBind on ChIP-seq data, and with a more pronounced gap for CLIP-seq data: 0.951 for ECBLSTM versus 0.914 for DeepBind. All the performance differences described here are statistically significant except when noted explicitly (see Fig. 2). Detailed accuracy values for individual datasets are provided in Supplementary Tables S1 and S2.

Fig. 2.

(A) The distribution of AUCs across 83 ChIP-seq datasets. (B) Heatmap annotated with P-values of pairwise model comparison using the Wilcoxon signed-rank test for ChIP-seq datasets. (C) The distribution of AUCs across 31 datasets for predicting RBP binding sites. (D) Heatmap annotated with P-values of pairwise model comparison using the Wilcoxon signed-rank test for predicting RBP binding sites. In subfigures (A) and (C), the triangle represents the average AUC for the respective model, the annotated vertical line represents the median AUC whose value is indicated. The models are sorted by their average AUC values. In subfigures (B) and (D), the color red or blue at position (i, j) in the heatmap indicates which model has a high average AUC, and its intensity indicates the magnitude of the difference

DeepBind is the simplest model considered here: it uses one-hot sequence encoding, and a single convolutional layer. The results shown in Figure 2 demonstrate that adding multiple convolutional layers, dilated convolution and sequence embedding all provide improved performance over the original DeepBind. The addition of a recurrent module provides further improvement as seen by comparing the performance of ECBLSTM to a model called DeepBind-E* which has multiple convolutional layers and an embedding stage. This shows that adding recurrent connections to capture long-term dependencies between motifs detected by the convolutional layer leads to improved performance. The performance advantage of RNNs is further highlighted by comparing the performance of DanQ where the additional bidirectional LSTM layer has helped improve its performance over DeepBind.

Our results demonstrate the performance advantage of deeper more complex networks. This is in contrast to Zeng et al. (2016) whose findings suggested that simpler models performed best in this task. Furthermore, the finding that more complex networks performed better demonstrates the effectiveness of our model tuning strategy.

We note that iDeepS which is specifically designed for RNA-binding and uses a CNN over sequence and local secondary structure in combination with an LSTM module, achieved a median AUC of 0.917 for the CLIP-seq data, which is less than all the evaluated methods except DeepBind (see Supplementary Figure S7 and Table S4). All the deep learning methods performed better than iONMF which uses multiple sources of data, including k-mer frequency, secondary structure and GO annotations (see Supplementary Table S4). Finally, we also note that in both tasks, our implementation of DeepBind achieved nearly identical performance to the original DeepBind implementation (see Supplementary Figure S3).

3.2 k-mer embedding boosts model performance

We observe that using k-mer embedding to represent input sequences rather than one-hot encoding improves model performance, and more so for the RBP binding datasets. For example, among models with the same architecture, we see that ECBLSTM outperforms DanQ in both tasks (see Fig. 2 and Supplementary Figures S2 and S3). We also observe that in the task of RNA-protein binding site prediction, all models that use embedding representation have median AUC higher than 0.94 while all models that use one-hot encoding have median AUC lower than 0.935 (Fig. 2C). These results suggest that one-hot encoding is not the optimal strategy for representation of DNA and RNA sequences. In contrast, k-mer embedding provides contextual information by learning the statistical information of k-mer co-occurrence relationships in the input sequences.

In this work, we train the k-mer embedding algorithm for each dataset with k = 3 and stride s = 1. Other studies (Min et al., 2017; Shen et al., 2018) have shown that using different values of k-mer length (values in the range of 4–7) does not have considerable effect on model performance. In preliminary experiments, we have evaluated model performance by varying the k-mer length from 3 to 7 and found that k = 3 provided the best performance. In agreement with other studies, we found that model performance increases with decreasing stride values, and found that using stride value equal to 1 led to the best performance.

3.3 Deeper is better with sufficient training data

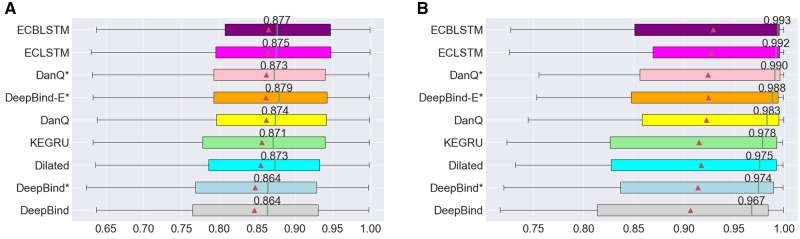
Based on the results shown in Figure 2, one may conclude that relatively complex models tend to perform better than simpler models. However, this statement is based on the evaluation of the overall performance across all experiments and do not take into consideration the effect of the number of training examples. To study this aspect, we divided the ENCODE ChIP-seq datasets into two groups according to the number of training examples. The first group consists of 38 datasets with <10 000 positive training samples, and the second group consists of 45 datasets with more than 10 000 positive training samples. We compare the performance of different models in these two groups and report the results in Figure 3. We observe considerably higher AUCs for the large datasets with median AUCs between 0.967 (DeepBind) and 0.993 (ECBLSTM) compared to median AUCs between 0.864 (DeepBind) and 0.879 (DeepBind-E*) for the small datasets. It is also worth noting that the effect of the number of training examples is more pronounced with hybrid models (see Fig. 3 and Supplementary Figure S4). Indeed, ECBLSTM, ECLSTM and DanQ* tend to perform very strongly for large datasets (median AUCs above 0.983) while interestingly, they fell behind DeepBind-E* when used on smaller datasets. This suggests the need for sufficient training data for hybrid models. Complex models such as ECBLSTM still perform well even for the smaller datasets, demonstrating that our regularization procedure was effective in preventing over-fitting.

Fig. 3.

(A) The distribution of AUCs in predicting DNA-protein binding sites across 38 ChIP-seq experiments with <10 000 peaks. (B) The distribution of AUCs in predicting DNA-protein binding sites across 45 ChIP-seq experiments with more than 10 000 peaks. Figure notation follows the description in Figure 2

3.4 Dilated convolution

Dilated convolution uses filters with gaps to allow each filter to capture information across larger and larger stretches of the input sequence (Yu and Koltun, 2015). Hence, dilated convolution finds usage in applications that benefit from modeling of a wider context without incurring the increased cost of using RNNs (Gupta and Rush, 2017; Kelley et al., 2018; Strubell et al., 2017).

In this work, we evaluate a dilated model which consists of three convolutional modules with dilation parameters equal to 1, 2 and 2 in the first, second and third layers, respectively. We find that the dilated convolutional model outperforms DeepBind* with significant P-values in both tasks (Fig. 2). In addition, the dilated convolutional model had slightly higher median AUC than DanQ in the RBP binding sites datasets, which suggests that dilated convolution can capture long-range relationships similarly to LSTMs. These findings suggest that dilated convolution is a valuable architecture parameter to consider. This is likely to be even more pronounced for longer sequences such as those modeled using the Basenji method for example (Kelley et al., 2018).

3.5 GRU or LSTM?

The results shown so far do not allow a direct comparison of GRU and LSTM units. To make that comparison we performed experiments on two additional architectures: (i) CNN layer followed by bidirectional GRU, using sequence embedding as input and (ii) a single bidirectional LSTM layer using sequence embedding as input. The first architecture is directly comparable to the ECBLSTM architecture, while the second is directly comparable to KEGRU. In both cases we observed negligible difference between the corresponding architectures (see Supplementary Figures S5 and S6).

3.6 Cross-assay performance

Binding assays, and especially in-vivo assays like ChIP-seq, have assay-specific biases (Chen et al., 2012). To test whether complex models are more affected by those biases, we identified three transcription factors in the ChIP-seq collection for which SELEX data are available (MAX, RFX5 and YY1). We then compared the performance of models trained and tested on ChIP-seq data with the performance of models trained on SELEX and tested on ChIP-seq data. In all cases cross-assay performance was lower as expected, and the more complex model (ECBLSTM) performed better than the simplest model (DeepBind), in addition having better same-assay performance (see Supplementary Table S5). This result provides support for the merit of complex deep learning models and demonstrates their ability to learn biologically relevant features.

3.7 Model interpretation and visualization

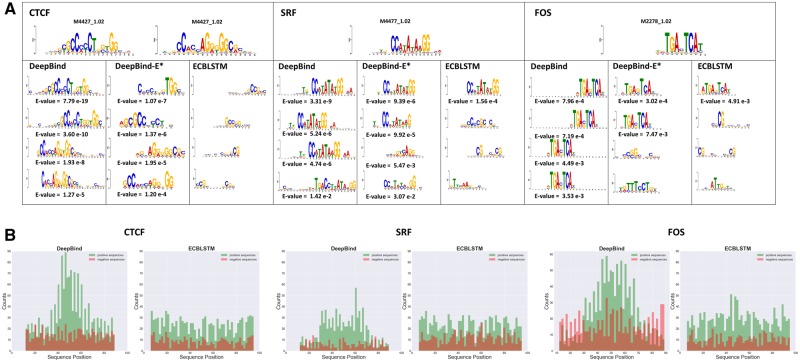
To explore the ability of selected architectures to capture informative motifs, we chose a random sample of ChIP-seq experiments and extracted motifs from the first convolutional layer as described in Section 2.4. As shown in Figure 4A, DeepBind and DeepBind-E* are able to detect informative motifs that match well with known motifs from the JASPAR database. However, ECBLSTM turns out to perform poorly in detecting motifs compared to the two other models and most of its detected motifs are not informative despite the fact that it is the best performing model among all the models we compared. We hypothesize that when combined with RNNs, the CNN filters learn information that is geared toward providing the subsequent recurrent layer with the information it needs, which is of a different nature than the localized information learned by CNN-only models.

Fig. 4.

(A) Examples of motifs detected by first layer convolutional modules learned by DeepBind, DeepBind-E* and ECBLSTM for predicting DNA binding sites of CTCF, SRF and FOS. E-values are displayed below each motif only if it matches with the known motifs for the same Transcription Factor. Known motifs from the JASPAR database are displayed at the top. (B) Histograms of the counts of convolutional filter activations that are considered for extracting motifs along the sequences for models of CTCF, SRF and FOS binding using DeepBind and ECBLSTM

To further investigate the difference between the behavior of hybrid models and CNN-only models, we explored the distribution of sequence fragments with positive activation values for a given filter with DeepBind and ECBLSTM in the positive and negative examples (Fig. 4B). As expected, the number of activated sequence fragments in positive sequences is much higher than in negative sequences in both methods. In addition, we observe that the activated sequence fragments in positive sequences using DeepBind are concentrated in the middle of the sequence, and are uniformly distributed for negative examples. This phenomenon was not observed in the CLIP-seq data, where activated sequence fragments were uniformly distributed for both positive and negative examples. However, using ECBLSTM the activated sequence fragments are distributed uniformly across the sequence for both positive and negative sequences. Noting that the centers of positive sequences correspond to the reported ChIP-seq peaks, we conclude that DeepBind is detecting sequence motifs that represent the binding event while ECBLSTM’s convolution stage is extracting features that span the whole sequence. This is in agreement with our finding that RNNs lead to a representation which has reduced interpretability compared to that of CNNs.

4 Conclusion

In this work, we performed an in-depth analysis and evaluation of the performance of commonly used deep learning architectures for DNA and RNA-binding site prediction. This study was aimed at providing a better understanding of the performance characteristics and advantages of different architectures to help users choose the right architecture for their work. Our experiments demonstrated the accuracy of hybrid CNN/RNN models; however, that requires the availability of sufficient training data, and these networks are harder to interpret and hence their usefulness in motif discovery might be limited. We have made the software used in our experiments available as an easy to use tool to evaluate and analyze various deep learning architectures for DNA/RNA-binding prediction in a user friendly package called deepRAM. We hope this work will stimulate further studies on visualizing and understanding deep models and enhance their usefulness for analyzing biological sequence data.

Conflict of Interest: none declared.