Capsule network for protein post-translational modification site prediction

Abstract

Motivation

Computational methods for protein post-translational modification (PTM) site prediction provide a useful approach for studying protein functions. The prediction accuracy of the existing methods has significant room for improvement. A recent deep-learning architecture, Capsule Network (CapsNet), which can characterize the internal hierarchical representation of input data, presents a great opportunity to solve this problem, especially using small training data.

Results

We proposed a CapsNet for predicting protein PTM sites, including phosphorylation, N-linked glycosylation, N6-acetyllysine, methyl-arginine, S-palmitoyl-cysteine, pyrrolidone-carboxylic-acid and SUMOylation sites. The CapsNet outperformed the baseline convolutional neural network architecture MusiteDeep and other well-known tools in most cases and provided promising results for practical use, especially in learning from small training data. The capsule length also gives an accurate estimate for the confidence of the PTM prediction. We further demonstrated that the internal capsule features could be trained as a motif detector of phosphorylation sites when no kinase-specific phosphorylation labels were provided. In addition, CapsNet generates robust representations that have strong discriminant power in distinguishing kinase substrates from different kinase families. Our study sheds some light on the recognition mechanism of PTMs and applications of CapsNet on other bioinformatic problems.

Availability and implementation

The codes are free to download from https://github.com/duolinwang/CapsNet_PTM.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Protein post-translational modification (PTM) is a key mechanism to regulate protein functions by the covalent addition of chemical groups or proteins. Over 400 types of PTMs have been identified (Khoury et al., 2011), and they influence almost all aspects of cell biology and pathogenesis. Therefore, identifying and understanding PTMs are critical in the studies of biology and diseases. In contrast to experimental methods, computational prediction of PTMs provides a fast and low-cost strategy for proteome annotation and experimental design. The PTM site prediction can be formulated as a classification problem, where machine learning can be applied. Some machine-learning methods have been developed for PTM site prediction. Support vector machine (SVM) was used in Musite (Gao et al., 2010) for general and kinase-specific protein phosphorylation site prediction using the K nearest neighbor score, disorder scores and amino acid frequencies as features. ModPred, a sequence-based PTM site predictor for 23 different modifications, applies logistic regression models using three types of features: sequence-based features, physicochemical properties and evolutionary features (Pejaver et al., 2014). The random forest algorithm was also applied in this area, such as the recently published tool PhosPred-RF for phosphorylation site prediction, which uses the evolutionary information features from position specific soring matrices (Wei et al., 2017). Sulfinator used hidden Markov models to predict sulfotyrosine sites in protein sequences (Monigatti et al., 2002). In our previous work, we presented MusiteDeep (Wang et al., 2017), the first deep-learning framework for predicting general and kinase-specific phosphorylation sites, which took raw protein sequences as input and achieved significant improvement over other well-known tools on the benchmark data. Even though MusiteDeep has demonstrated that deep learning has a prominent advantage in automated complex feature extraction from raw sequences for PTM site prediction, challenges remain, especially in small sample training and model interpretation. Except for a few PTMs, such as phosphorylation, glycosylation and acetylation, known annotations for most other PTMs are limited. The main building block of MusiteDeep is the traditional convolutional neural network (CNN) with scalar neurons, which may not characterize hierarchical relationships between simple and complex features using such small training data.

To address the problems of scalar neurons, a novel deep-learning architecture, known as Capsule Network (CapsNet) was introduced (Sabour et al., 2017). The main building block of CapsNet is the capsule (Hinton et al., 2011), which is a group of neuron vectors, whose activity vector represents the ‘instantiation parameters’ of a specific type of entity. The length of the vector represents the probability of an entity’s existence while the orientation of the vector represents the state of the entity. Taking digit image classification as an example, the length of a digit capsule represents the probability that the digit exists while the orientation can represent various properties, such as the width, scale and thickness of that digit. Capsule provides a unique and powerful deep-learning building block to better model the diverse relationships inside internal representations of a neural network.

CapsNet has not been exploited in many deep-learning applications, especially not at all for protein PTM site prediction. We found that some properties of CapsNet can benefit the PTM site prediction problem although it is highly non-trivial to exploit the application of CapsNet in biological sequence analyses. Three primary benefits set CapsNet apart from previous deep learning methods:

First, capsules are suitable feature representations for PTM substrates. Taking phosphorylation as an example, the sequences surrounding the phosphorylation sites have different patterns corresponding to various catalyzing kinases. As shown in Supplementary Figure S1, amino acids in these flanking sequences have certain patterns for each subgroup, while sequences in the negative groups (without phosphorylation) do not have these patterns. These patterns include one-dimensional sequence profiles and two-dimensional correlated mutations, as well as higher dimensional correlations among amino acids, which are not shown in the figure. The ‘instantiation parameters’ of a capsule enable characterization of all these relationships for distinct kinase families in the feature space (in contrast to 2D image space in the original application of CapsNet). Specifically, the capsule length can represent the probability that the PTM of interest exists, and the capsule orientation can represent the specific sequence properties of substrates as characteristics of PTM subtypes.

Second, CapsNet has outstanding performance for small-sample learning (Sabour et al., 2017). The unique representation capacity of capsule––the change of ‘instantiation parameters’ by a corresponding amount as the viewpoint changes (the ‘equivariant’) while the probability of the sought-after entity being present is invariant (Hinton et al., 2011). This changeability feature makes CapsNet effective in learning from a small fraction of training data since it does not need to see as many samples to generate appropriate representations as other neural networks. For PTM applications, the ‘equivariant’ property will also work. Through the routing-by-agreement learning mechanism (dynamic routing), a prediction capsule for a PTM of interest (positive or negative) becomes activated when its prediction agrees with the specific amino acid relationships, i.e. the specific ‘instantiation parameters’ iteratively defined from the over-represented patterns in the cohort substrates. This property is particularly in demand in PTM site prediction and could be applied to many other biological sequence analysis problems, since known annotations are often limited.

Third, the dynamic routing mechanism can be viewed as a parallel attention mechanism (Bahdanau et al., 2014). In PTM site prediction, this allows the network to attend to some internal capsules related to the prediction. The dynamic routing process is transparent, which helps users identify key features relevant to the PTM recognition mechanism.

Here, we proposed a CapsNet with a multi-layer CNN for protein PTM site prediction, including phosphorylation, N-linked glycosylation, N6-acetyllysine, methyl-arginine, S-palmitoyl-cysteine, pyrrolidone-carboxylic-acid and SUMOylation. Our experiments showed that CapsNet outperformed the baseline CNN architecture MusiteDeep and other well-known tools in most cases, especially in almost all cases involving learning from small training samples. Besides the superior performance in PTM site prediction, CapsNet showed outstanding properties that can explore the internal data distribution related to biological significance. For example, internal capsules could learn features related to kinase families and discover novel kinase-specific motifs when no kinase-specific phosphorylation labels were provided; the robust representations generated by CapsNet have a strong discriminant power in distinguishing kinase substrates from different known or unknown kinase families. We believe that the proposed architecture can also address other modifications with limited annotations better than previous methods. Our study provides an early example use-case of CapsNet in a biological sequence analysis, and may also shed some light on other biological sequence analysis and prediction problems.

2 Materials and methods

The PTM site prediction can be formulated as a binary classification problem, i.e. each potential site can be classified as either the PTM site of interest or not. In particular, a 33-length peptide is extracted from each residue of interest (16 residues at each side). The first step is to convert the input amino acid peptides into real-number vectors by a coding method. Next, a supervised model will be trained on the benchmark training set. Finally, the trained model will be used to predict PTM sites for the benchmark testing set, and its performance will be evaluated by comparing with other methods.

2.1 Benchmark dataset

We built a benchmark dataset by collecting annotations from UniProt/Swiss-Prot (August 2017 release) (Bairoch et al., 2005). In this work, we only trained PTM models for animal species (Metazoa) that were extracted according to the NCBI taxonomy database (Wheeler et al., 2007). For each interested PTM, all the residues annotated by Uniprot/Swiss-Prot with the same type of PTM were used as positive sites, while the residues with the same amino acids excluding the PTM annotations were regarded as the negative sites. The statistics of the data are shown in Table 1.

Table 1.

Benchmark dataset

PTM typesa	# of residuesb	# of non-redundant residuesc
Phosphorylation (S/T)	123 631 (2 468 434)	36 395 (12 177)
Phosphorylation (Y)	8417 (89 316)	2141 (826)
N-linked glycosylation (N)	64 374 (449 108)	10 218 (6564)
N6-acetyllysine (K)	19 884 (265 234)	6376 (1907)
Methyl-arginine (R)	4585 (109 580)	2241 (455)
S-Palmitoylation-cysteine (C)	2589 (16 133)	572 (266)
Pyrrolidone-carboxylic-acid (Q)	1407 (11 070)	623 (154)
SUMOylation (K)	996 (20 910)	334 (108)

^aThe amino acids in parentheses represent the modified residues for each PTM.

^bNumbers outside the parentheses represent the numbers of positive residues; numbers in parentheses represent the numbers of all the candidate residues.

^cTaking the first fold to illustrate the scale of the modified residues in the training sets after removing the redundant sequences (numbers outside the parentheses) and the scale of the modified residues in the testing sets (numbers in the parentheses).

2.2 Input sequence coding

In our previous work, MusiteDeep, a 33-length peptide was coded by the one-of-K coding method, which is a discrete representation with value 1 at the index corresponding to the amino acid in the peptide and 0 at all other positions. In this work, we coded each amino acid by a quantitative representation method proposed by (Venkatarajan and Braun, 2001), which used the multi-dimensional scaling of 237 physical-chemical properties to derive quantitative representations for all 20 naturally occurring amino acids. In their method, five principal components were used to reproduce the main variations of the 237 properties for the 20 amino acids. Here, a 6D vector is used to represent each amino acid, wherein the first 5D represents the five principal components as shown in Table 1 of (Venkatarajan and Braun, 2001). The additional 1D is used to represent a gap in the position, where there is no amino acid at the position within the 33-length fragment. When there was a gap in the position, the first 5D values were all set as 0 and the last 1D was set as 1. On the other hand, the last 1D was set as 0 when there was no gap. The new quantitative representation was constructed by considering the original high-dimensional physical-chemical property space and provided a small dimension of input data, which was thought to be a more efficient representation than the one-of-K coding. The results in Section 3.4 showed that this quantitative representation was slightly better in distinguishing kinase substrates from different families than the one-of-K representation.

2.3 Architecture design

The architecture of the proposed CapsNet, as shown in Figure 1, consists of three 1D convolutional layers (Conv1, Conv2 and PrimaryCaps) and one fully connected layer (PTMCaps). The first two layers are the conventional convolutional layers. They convert the input peptide from its initial representation to the intermediate-level features, which are then fed into the PrimaryCaps and PTMCaps for further feature abstraction. The first two layers were designed to increase the representation power of CapsNet.

Fig. 1.

Architecture of the proposed CapsNet. The input is a 33-length peptide in the 6D quantitative coding. The first two layers are two 1D convolutional layers, each with 200 channels, as well as with size 1 and 9 convolution kernels, respectively. The PrimaryCaps layer is the convolutional capsule layer, which has size 20 convolution kernels and 60 channels of 8D capsules, as described in (Sabour et al., 2017). The PTMCaps layer has two 10D capsules to represent two states of the input peptides—whether the input has the interested PTM site or not. The L2-norm of each capsule vector was calculated indicating the probability of each state

The Conv1 and Conv2 were constructed with similar hyper-parameters like those in MusiteDeep, since they were selected by the Bayesian optimization method (Snoek et al., 2012). Specifically, the first layer (Conv1) has 200 size-1 1D convolution kernels with a stride of 1, and a ReLU activation function (Nair and Hinton, 2010). The first layer also has a dropout technique (Srivastava et al., 2014) with a neuron dropping rate 0.75. The second layer (Conv2) has 200 size-9 1 D convolution kernels with a stride of 1, a ReLU activation function and a dropout technique with a neuron dropping rate 0.75. In other studies, the 1 x 1 convolution kernel provides a more efficient way for dimension reduction and allows for deeper and wider networks (Lin et al., 2013; Szegedy et al., 2015). In our case, the size 1 1D convolution kernels in Conv1 serve as a ‘feature filter’, which sum-pools features across the six physical-chemical channels into single scalar features. The high neuron dropping rate (0.75) applied in the dropout technique was used to prevent the model from over-fitting and to optimize the model generalization capacity.

The PrimaryCaps is the convolutional capsule layer, as described by (Sabour et al., 2017). In our case, one can see the PrimaryCaps as a 1D convolutional layer, which has 60 channels of convolutional capsules. Each capsule in the PrimaryCaps contains eight convolutional units, each of which was the result of a size 20 1D convolution kernel with stride of 1. The first valid dimension of Conv1 was 33, i.e. 33 (fragment length) – 1 (kernel size) + 1; the first valid dimension of Conv2 was 25, i.e. 33 (first dimension of Conv1)—9 (kernel size) + 1 and finally the first valid dimension of PrimaryCaps was 6, i.e. 25 (first dimension of Conv2)—20 (kernel size) + 1; In total, the PrimaryCaps layer has [6, 60] 8D vector capsules and each capsule in the [6, 1] grid shares its weight with others; 8 is the dimension of capsule vectors in the PrimaryCaps used in the original CapsNet (Sabour et al., 2017). Since the length of a capsule represents the probability that the entity presented (Sabour et al., 2017), the convolutional units in the capsule layers need a new activation function, which is called the squashing function, to scale the lengths of capsules to [0, 1] as follows:

$$v_j=\frac{\Vert s_j\Vert }{1+{\Vert s_j\Vert }^2}\frac{s_j}{\Vert s_j\Vert }$$ (1)

where v_j is the vector output of capsule j and s_j is its input. Besides the PrimaryCaps layer, the squashing activation function will be applied to capsules in the following PTMCaps layer.

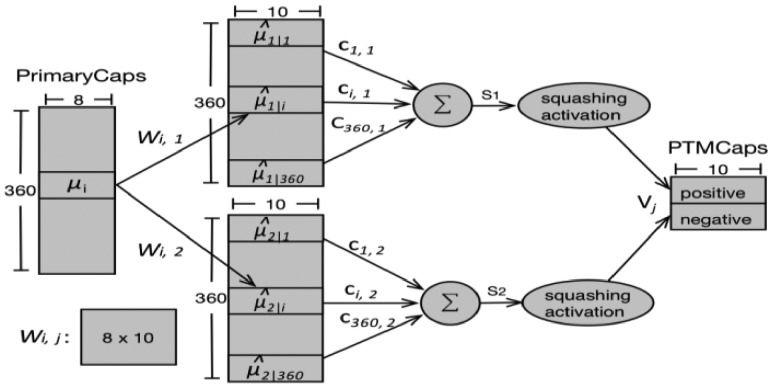
The PTMCaps layer contains two 10D capsules to represent two states of the input peptides: positive and negative (representing whether the input has the interested PTM site or not). This layer accepts inputs from all the capsule outputs in the PrimaryCaps layer. The computation between the PrimaryCaps and PTMCaps was illustrated in Figure 2. We used the same symbols as in the original CapsNet paper (Sabour et al., 2017) wherever possible but displayed the specific parameters used in our experiments. µ_i, i ∈ [1, 360] is an 8D capsule in PrimaryCaps. W_i, j is the weight matrix that conducts the affine transformation. There are two capsules (V_j, _j ∈ [1, 2]) in the PTMCaps, each of which receives inputs from all the capsule outputs in the PrimaryCaps. V_j is a 10D vector which is produced by a weighted sum (s_j) over all outputs (  ${\widehat{\mu }}_{j|i}$) from PrimaryCaps and then through the squashing function [Equation (1)]. Here, the c_i, j are coupling coefficients that are summed to 1 over the two capsules in PTMCaps, i.e. $c_{i,\mathrm{\hspace{0.17em}}1}+c_{i,\mathrm{\hspace{0.17em}}2}=1$ and determined by the iterative dynamic routing process. Please refer to Supplementary Material S1 for the complete dynamic routing algorithm.

Fig. 2.

Computation between the PrimaryCaps and PTMCaps. There are 360 8D capsules (each µ_iis an 8D vector) in PrimaryCaps ${\widehat{u}}_{j|i}$, j ∈ [1, 2]. Each is produced by multiplying µ_iby a weight matrix W_i, j(8 × 10). Capsule V_j (10D vector and j ∈ [1, 2]) in PTMCaps is produced by a weighted sum over all ${\widehat{u}}_{j|i}$ and the squashing non-linear activation function. The parameter c_i, _j was determined by the iterative dynamic routing process

The length of the positive capsule in the PTMCaps layer indicates the probability that the PTM of interest exists, while the length of the negative capsule indicates the probability that the PTM of interest does not exist. Therefore, the L2-norms of the positive and negative capsule vectors were calculated, respectively, and following (Sabour et al., 2017) a separate margin loss function was applied as follows:

$$L_c=Y_c\max {(0,0.9-|\left|v_c\right||)}^2+0.5(1-Y_c)\max {(0,|\left|v_c\right||-0.1)}^2$$ (2)

where, Yc = 1 if the PTM of interest exists. For other hyper-parameters, we used the suggested values 0.9, 0.1 and 0.5 as in (Sabour et al., 2017). The total number of parameters of the whole CapsNet in this work was 3 078 694.

In the prediction process, both positive and negative capsule lengths were calculated, and then the labels were assigned to the query sites according to which one had the larger length.

2.4 Model training

In each experiment, all the deep-learning models were trained using identical training strategies. Training and testing data were generated according to a particular experiment. From one specific training data, 10% of samples were extracted as validation data. To address the unbalanced issues during training, the same bootstrapping method as in Musitedeep (Wang et al., 2017) was applied for CapNet and MusiteDeep. Particularly, given one training data, the models were trained on several balanced training subsets and several independent classifiers were generated. The final results were calculated by averaging the results from all the classifiers. During the training iteration, the early stopping strategy was used; specifically, when the loss of validation did not reduce in some numbers of epochs (one forward and backward pass over the entire training set), the training procedure would be stopped. We used the Adam stochastic optimization method (Kingma and Ba, 2014) with the following parameters: learning rate 0.001, decay rate for the first-moment estimates 0.9 and exponential decay rate for the second-moment estimates 0.999. To train the CapsNet by dynamic routing, we followed the suggestion in (Sabour et al., 2017), i.e. three routing iterations and the same margin loss function with the suggested hyper-parameters. All the deep-learning models were implemented using Keras 2.1.1 and TensorFlow 1.3.0. Model training and testing were performed on a workstation with Ubuntu 16.04.3 LTS system and equipped with GPU Nvidia GTX 1080Ti.

3 Results

3.1 Performance of CapsNet for small training data

To explore the advantage of CapsNet in effective learning from small training data, we compared the performance of CapsNet on different fractions of training samples with MusiteDeep, as well as with a CNN model that has a similar architecture and complexity only excluding the capsule form by converting the PrimaryCaps into a standard CNN and the PTMCaps into a fully connected layer with 10 × 2 neurons. This set of experiments only focuses on phosphorylation of S/T.

To evaluate the performance of these models without the effect of the unbalanced data issue and the issue of similar fragments in the training, validation and testing datasets, we built two balanced, fragment-level non-redundant datasets according to two sequence-similarity conditions. One dataset contained fragments that have no more than 40% sequence similarities. The other dataset contained fragments that have no more than 50% sequence similarities. Each dataset was generated by first randomly selecting an equal size of negative fragments from the raw dataset of phosphorylation (S/T) (Table 1, Column 2) to build the balanced dataset and only one fragment candidate from each homologous sequence cluster of fragments with sequence similarities higher than 40% or 50% remained by CD-HIT (Li et al., 2001). Then, we applied a 10-fold cross-validation method to each dataset. For each fold, we extracted increasing fractions of the training samples according to a series of ratios (0.5%, 1%, 2%, 5%, 10%, 20%, 50%, 90%) and then trained models of CapsNet and other two deep-learning models on the same data fractions and evaluated the performances on the same testing data. Taking the first fold of the dataset with under 40% fragment-level redundancy as an example, the numbers of the experiment series of training samples were 181, 363, 726, 1816, 3632, 7264, 18 160, 32 688 and the number of testing samples was 4036. Other folds contained similar size data. For a fair comparison, to all the compared methods we applied the same quantitative coding method. We noticed that these distinct models have model-specific optimal training processes. It is difficult to train models by their optimal training processes for every experiment; therefore, we applied one consistent and general training strategy for all the models in all these experiments, which is the Adam stochastic optimization method and stopping the training processes after 100 epochs.

We also considered the model variation out of different runs. Therefore, besides the 10-fold cross-validation, each method was trained 10 times using the same fold of training sets but different starting model parameters and it was evaluated by the same fold of testing sets, resulting 100 independent models for each method at each ratio. The distributions of the accuracies of the 100 models at each ratio were displayed by boxplots, as shown in Figure 3. The experimental results show several advantages of CapsNet: (i) Under the small training sample conditions (number of samples below 10 000), CapsNet outperformed other methods significantly (P-value < 0.01 by t-test compared with MusiteDeep), while in large training sample conditions, CapsNet achieved a comparable performance (P-value > 0.01 by t-test compared with MusiteDeep) in all these conditions; (ii) CapsNet had smaller variations and fewer outliers than the other two deep-learning methods, especially in small training sample conditions; (iii) the capsule design in CapsNet improved the performance compared with similar CNN architecture only without the capsule form. All these advantages indicate that CapsNet is more robust in training and more effective in learning from small training data. The comparisons of training and prediction time among different methods are shown in Supplementary Table S1.

Fig. 3.

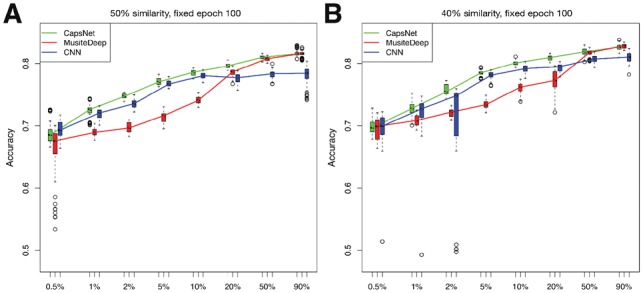
Accuracies of CapsNet, MusiteDeep and CNN for phosphorylation (S/T) trained by different sizes of training samples represented in boxplots. The x-axis represents the sampling ratio of the total training samples. The y-axis represents the accuracies of 10-fold cross-validation with each fold trained 10 times. At each ratio, each method generated 100 independent models. For each sampling ratio, we draw three boxplots beside each other for the three methods in the order of CapsNet, MusiteDeep and CNN. The line in the middle of the box represents the median; the box edges represent the 25th and 75th percentiles; the flattened arrows extending out of the box represent the reasonable extremes of the data (the 1.5 times interquartile ranges from the middle 50% of the data) and the open circles beyond the flattened arrows represent outliers for each experiment. (A) and (B) show results of the datasets with fragment-level sequence similarities less than 50% and 40%, respectively

3.2 Assessment of prediction reliability

According to the design of CapsNet, the capsule length in the output layer can be used to represent the probability that the predicted entity exists. However, the relationship between the capsule length and the prediction confidence was not demonstrated by real data. Here, we tested whether the capsule length in PTMCaps (positive/negative capsule lengths) can reflect the prediction reliability for a specific PTM. The experiments were conducted on the balanced 10-fold cross-validation phosphorylation (S/T) dataset. Specifically, given one fold of the testing data, after the corresponding lengths of the positive/negative capsules in PTMCaps were obtained, we divided these lengths ranging from 0 to 1 into equal-size bins (the size of each bin is 0.05). Next, we used two measures to evaluate the prediction reliability of each bin: (i) the precision (positive predictive value, i.e. the percentage of true PTM sites whose positive capsule lengths were in the interval of the bin) and (ii) the FDR (false discovery rate, i.e. the percentage of false PTM sites whose negative capsule lengths were in the interval of the bin). As shown in Figure 4, the length of the positive capsule and the average precision of 10-fold cross-validation had a very high positive correlation (Pearson correlation 0.97, P-value = 6.4 e–11), while the length of the negative capsule and the average FDR of the 10-fold cross-validation also had a very high positive correlation (Pearson correlation 0.96 P-value = 2.6 e–11), demonstrating that the length of positive/negative capsule alone is a good estimator of the prediction reliability. Then, we used a non-linear least square fitting (function nls in R) to estimate the non-linear regression parameters of each type of capsule, respectively. The estimated analytic mapping from the positive capsule length (x) to the assessed precision (y) is shown in Equation (3).

$$y=1.115x^2$$ (3)

Fig. 4.

Prediction reliability versus capsule length. (A) Precision versus positive capsule length. (B) FDR versus negative capsule length. The x-axis represents the center of each length-bin of the positive/negative capsule in PTMCaps. The y-axis represents the precision/FDR of the corresponding bin. The circles and the bars represent the average precision/FDR and the SD, respectively, for a given capsule length bin from 10-fold cross-validation results. The dashed line represents the non-linear (quadratic) regression of the precision/FDR from a capsule length, which can be used to estimate the prediction reliability for a PTM of interest [Equations (3)–(4)]

The estimated analytic mapping from the negative capsule length (x) to the assessed FDR (y) is shown in Equation (4).

$$y=1.079x^2$$ (4)

Interestingly, these two regressions were very close to y = x². In practical use, for a given protein with a predicted positive/negative capsule length, we can assess its prediction/FDR reliability by substituting it in Equations (3) and (4).

3.3 Comparing the performance of CapsNet in several PTM site predictions with other methods

To demonstrate the performance of CapsNet in practical use, we compared CapsNet with other existing PTM site prediction models. However, these models used different training data and most of them did not provide standalone tools, thereby making it difficult to provide a direct comparison. Also, in this paper, the main objective is to demonstrate the advantages of applying CapsNet in PTM site prediction, rather than developing a comprehensive prediction tool. Therefore, we only chose to compare with several representative machine-learning methods with available tools. The tools we chose to compare were MusiteDeep, Musite and ModPred. Here, MusiteDeep was used as a baseline model of deep learning, Musite was used as a baseline model of the SVM algorithm and ModPred was used as a baseline model of a logistic regression algorithm which provides many types of PTM site predictions in a standalone package. For each PTM, we applied the 10-fold cross-validation on the benchmark dataset described in Table 1 (Column 2) and removed sequences that have more than 30% sequence identity with the testing set from the training set by Blast (Altschul et al., 1990), as shown in Table 1 (Column 3) Since MusiteDeep and Musite provided the customized model training, we used the same training data to train these models. ModPred did not provide the customized model training, and hence we used their pre-trained model as is to predict for all the folds of testing data. We used the areas under ROC curves and the areas under the precision-recall (PR) curves to evaluate the performance. The average areas for each measure and their SD calculated from 10 folds are shown in Table 2. The corresponding ROC and PR curves are shown in Supplementary Figures S2 and S3.

Table 2.

Performances on benchmark datasets

PTM types	Areas under the ROCa				Areas under the PR
	CapsNet	MusiteDeep	Musite	ModPred	CapsNet	MusiteDeep	Musite	ModPred
Phosphorylation (S/T)	0.8470 ± 0.003	0.8629 ± 0.003	0.7983 ± 0.010	0.7973 ± 0.002	0.3437 ± 0.010	0.3422 ± 0.010	0.2155 ± 0.011	0.2018 ± 0.011
Phosphorylation (Y)	0.7171 ± 0.011	0.7224 ± 0.009	0.6942 ± 0.013	0.7331 ± 0.007	0.2620 ± 0.017	0.2595 ± 0.019	0.2195 ± 0.019	0.2425 ± 0.011
N-linked glycosylation (N)	0.9808 ± 8.0e–4	0.9821 ± 0.001	––	0.7916 ± 0.004	0.8382 ± 0.009	0.8416 ± 0.010	––	0.2750 ± 0.006
N6-acetyllysine (K)	0.7280 ± 0.009	0.7266 ± 0.006	––	0.6757 ± 0.008	0.1970 ± 0.013	0.1939 ± 0.009	––	0.1456 ± 0.008
Methyl-arginine (R)	0.9891 ± 0.007	0.9874 ± 0.006	––	0.8004 ± 0.018	0.9352 ± 0.042	0.8564 ± 0.047	––	0.2150 ± 0.055
S-palmitoylation-cysteine (C)	0.7806 ± 0.022	0.7713 ± 0.026	––	0.8553 ± 0.001	0.5003 ± 0.070	0.4873 ± 0.056	––	0.5973 ± 0.043
Pyrrolidone-carboxylic-acid (Q)	0.9256 ± 0.042	0.9229 ± 0.0386	––	0.9113 ± 0.037	0.8333 ± 0.063	0.7772 ± 0.064	––	0.6470 ± 0.076
SUMOylation (K)	0.8680 ± 0.023	0.8675 ± 0.025	––	0.8227 ± 0.015	0.5717 ± 0.062	0.5146 ± 0.058	––	0.3001 ± 0.047

^aThe average and the SD of the areas under the ROC and PR were reported from 10-fold cross-validation. The bold font represents the best performance in the highest value of the PTM type.

It is important to note that we used a very strict non-redundant dataset construction procedure in this experiment, wherein for CapsNet, MusiteDeep and Musite, the training sequences had no more than 30% identity with the testing sequences. However, the testing set could be involved in the training procedure of ModPred, so that the performance could be overestimated. From the comparison results, CapsNet outperformed other methods in most cases. In particular, CapsNet outperformed MusiteDeep for PTMs with small annotation data, such as methyl-arginine with 2241 annotations, S-palmitoyl-cysteine with 572 annotations, pyrrolidone-carboxylic-acid with 623 annotations and SUMOylation with 334 annotations, which were consistent with the results in Section 3.1 that CapsNet learned better than other methods using small training samples. We further investigated the reason why ModPred achieved the significantly outstanding ROC and PR for S-palmitoylation-cysteine and superior ROC for phosphorylation (Y). Because 99% (1509 out of 1524) testing sequences of S-palmitoylation-cysteine, 99% (4555 out of 4596) testing sequences of phosphorylation (Y) were created in UniProt/Swiss-Prot before the year 2012 and ModPred used UniProt/Swiss-Prot 2012 to train their models; hence, these testing data had a significant chance in the training data of ModPred.

3.4 Interpretation of what was learned by capsules

We took the phosphorylation site prediction as an example to present possible biological meanings of the capsules. For this purpose, the annotations of kinase families collected from RegPhos (Lee et al., 2011) were employed to the phosphorylation sites. Eighty-six kinase families contained more than one sample in our dataset, of which 10 kinase families each contained more than 100 samples. Since only the positive capsule in PTMCaps relates to phosphorylation peptides, only the positive capsule in PTMCaps and its coupled primary capsules were considered in the following experiments.

A widely adopted hypothesis for kinase recognition is that the kinases in the same group or family recognize similar sequence patterns of substrates for modification (Brinkworth et al., 2003; Linding et al., 2007; Obenauer et al., 2003). In this phosphorylation example, one intuitive assumption is that substrates catalyzed by the kinases in the same family activate a specific group of capsules. The dynamic routing of CapsNet provides an indication of this assumption. The coupling coefficients c_{i, j} calculated during dynamic routing can be viewed as probabilities of lower-level capsules (in PrimaryCaps) that should be coupled to the higher-level capsules (in PTMCaps) activated by the particular input peptide. By viewing the patterns of the coupling coefficients, we can see the usage of capsules by the inputs. We selected kinase families PKA, CK2, Src and MAPK to represent kinase families from distinct kinase groups. We fed all the peptides that had the annotation in one of these four kinase families to the CapsNet and calculated the coupling coefficients c_i,j (i ∈ [1, 360] and j = 1) between the lower-level capsules in PrimaryCaps and the positive capsule in PTMCaps. In this way, we obtained a 360D vector (the value of each element is from 0 to 1) for a given input peptide. Figure 5 shows a heatmap presented by clustering the coupling coefficients of the four kinase families, indicating that substrates from the same kinase families automatically tend to activate the same group of capsules. A further analysis of some subgroups is shown in Supplementary Figure S4.

Fig. 5.

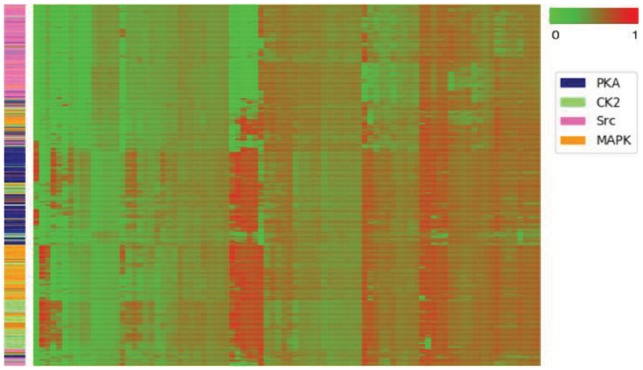
Heatmap of the coupling coefficients for kinase. Rows are samples and columns are the coupling coefficients calculated during dynamic routing. The side colors of rows represent the kinase families. The rows and columns are clustered by a hierarchical clustering method on the coupling coefficients

Next, to investigate the features learned by individual capsules in PrimaryCaps, we generated sequence logos according to the capsules’ responses to the input peptides. Specifically, we fed all the peptides through all the capsules in PrimaryCaps (360 capsules in total), and we aligned the peptides in responses to a particular positive capsule in PTMCaps with a capsule length larger than 0.55 (slightly above the 0.5 threshold that corresponds to the capsule in PrimaryCaps equally coupled to the positive and negative capsules in PTMCaps). Then we generated position frequency matrixes for these aligned peptides and transformed them into sequence logos (motifs) (Ou et al., 2018). Interestingly, some of the motifs converted by the internal capsules are very similar to the ground truth motifs of some kinase families that were constructed by aligning all the peptides from the same kinase families. Three examples of these similar motifs are shown in Figure 6. The P-values of these matches were calculated by aligning the motifs learned by the internal capsules to the constructed ground truth kinase family motifs through the TOMTOM algorithm (Gupta et al., 2007) and are 2.09e–42 for PKA, 0.0 for CK2 and 6.52e–31 for CDK. It is worth mentioning that the internal capsules were trained using the general phosphorylation site data only, without using any labels of kinase families. From this experiment, we see that the internal capsules in the phosphorylation site prediction model may be used as kinase family motif detectors.

Fig. 6.

Examples of motifs converted from capsules compared with the ground truth motifs. The left sequence logos show the ground truth motifs for kinase families PKA CK2 and CDK, which were generated by aligning all the peptides with annotations of these kinase families. The right sequence logos show the corresponding motifs converted from capsules 55, 2 and 83

To show that the PTMCaps capsule learns a more robust representation for phosphorylation, we fed all the peptides that have kinase family annotations to the CapsNet and projected the 10D vector of the positive capsule in PTMCaps to a 2D plot (Fig. 7) by t-SNE (Maaten and Hinton, 2008). As a comparison, the raw quantitative coding representations and the merged representations [H’ in Equation (1) of (Wang et al., 2017)] from MusiteDeep are also shown. Figure 7 shows that representation of kinase substrates from the same kinase family tend to group together for all the methods. To quantitatively evaluate the discriminant power for these representations, we calculated the between/within class scatter ratio (B/W ratio) (Johnson and Wichern, 2002) from the representations in their original dimension of each method and their t-SNE transformed 2D representations. For all the kinase families, the B/W ratio was 0.06 (0.19 for 2D t-SNE) for the raw quantitative coding representations, 0.20 (0.27) for the MusiteDeep representations and 0.54 (0.63) for the capsule representations. To make a clearer display, we also regenerated these t-SNE representations for only four selected kinase families (PKA, CK2, Src and MAPK) and abstained the corresponding B/W ratios: 0.04 (0.21 for 2D t-SNE), 0.19 (0.28) and 0.78 (0.96) for each method, respectively. Strikingly, CapsNet generated much better representations with stronger discriminant power in distinguishing kinase substrates from different kinase families than other representation methods. This is remarkable given that no label of kinase families except for the labels of general phosphorylation was used to guide the training procedure. In addition, we calculated the B/W ratios for the one-of-K coding representation, which is 0.05 (0.16) for all the kinases and 0.03 (0.14) for the selected kinases. Compared with the one-of-K coding, the quantitative coding representations are slightly better in terms of the discriminant power of kinase families. Note that both MusiteDeep and CapsNet use the quantitative coding method for input peptides to generate each high-level representation in Figure 7. In Supplementary Figure S5, the same representations were generated by feeding one-of-K coded peptides to each model. The conclusion did not change, it just obtained lower B/W ratios for both methods compared with coding in the quantitative coding method, indicating that one-of-K coding is less effective than the quantitative coding in this application.

Fig. 7.

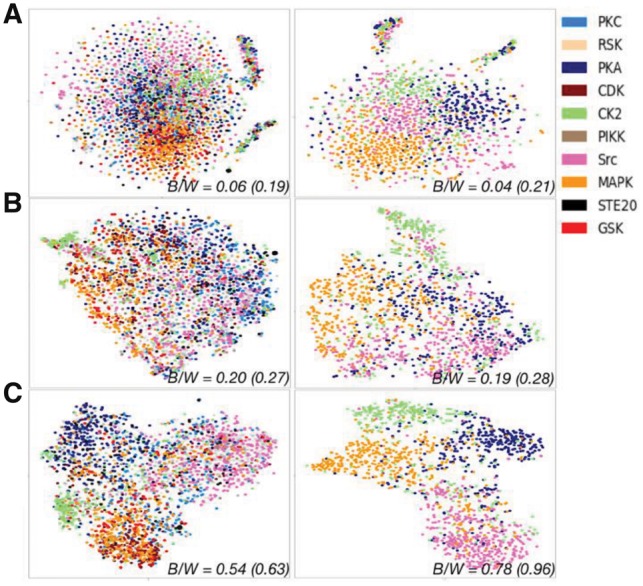
Comparing different representations of peptides after training in quantitative coding by t-SNE. Three types of representations including the raw quantitative coding representations (A), the merged representations of MusiteDeep (B) and the representations from the positive PTMCaps capsule (C) are shown by 2D t-SNE plots. In all the left plots, the colored nodes (non-gray nodes) represent samples from one of the 10 kinase families (listed in the color legend) that have more than 100 samples. The nodes in gray represent samples from other smaller kinase families. All the right plots display regenerated t-SNE representations using only four selected kinase families (PKA, CK2, Src and MAPK). The between/within class scatter ratios (B/W) calculated from the full representations of each method (value outside the parentheses) and their t-SNE transformed 2D representations (value in the parentheses) are labeled. A higher B/W value indicates more separable clusters

4 Conclusions and discussion

CapsNet introduces a new building block to the deep-learning family, which has presented advantages in modeling hierarchical relationships inside of internal representations beyond scalar neural networks in image recognition. In this paper, we proposed a CapsNet for protein PTM site prediction and presented some outstanding properties of capsules in characterizing biologically meaningful features. We used the same network architecture for several PTM types, including phosphorylation, N-linked glycosylation, N6-acetyllysine, methyl-arginine, S-palmitoyl-cysteine, pyrrolidone-carboxylic-acid and SUMOylation. The comparative results show that the proposed CapsNet outperformed the previous deep-learning method MusiteDeep and other well-known tools in most cases, and it provides promising results for practical use, together with the estimated confidence of the predicted label. Although it needs more training time compared with traditional CNN, CapsNet has a similar prediction time, which only takes seconds for thousands of samples.

To test the performance of the proposed CapsNet on small sample data, we compared it with two other deep-learning models constructed using traditional convolutional layers on a series of experiments by gradually increasing protein-sequence training data size. To reduce the over-fitting, all these methods applied very high dropout ratios, e.g. 75%. From the results in 10-fold cross-validation, we found that under such a high dropout ratio, the other two deep-learning models may not converge in some trials; however, this phenomenon rarely occurred in the CapsNet, indicating that CapsNet is a hyper-parameter robust network. In these experiments, CapsNet showed a better performance under the small training sample conditions and a comparable performance under the large training sample conditions against two other deep-learning models.

To explore the biological meanings of the capsules, we conducted three experiments. In the first experiment, by displaying the distribution of coupling coefficients for four selected kinase families from distinct kinase groups, we showed that substrates catalyzed by kinases in the same family would activate a specific combination of internal capsules (Fig. 5). In the second experiment, we showed that the internal capsules could be used as motif detectors (Fig. 6). This procedure is similar to converting convolution kernels into motifs through aligning the sequences that passed the ReLU activation threshold used in DNA function predictions (Alipanahi et al., 2015; Quang and Xie, 2016). The main difference in the method of Alipanahi et al. (2015) or Quang and Xie (2016) is that they either trained a multi-class model or single models with different labels, by which they forced the convolution kernels to learn specific DNA motifs. But in our case, the training procedure of capsules was totally free from kinase labels. Our third experiment showed that the ‘instantiation parameters’ for protein sequences generated from high-level capsules were more robust and had stronger discriminatory power in distinguishing kinase substrates from different kinase families than other representations (Fig. 7). The first and second experiments together showed how internal capsules were activated according to specific types of substrates, i.e. how dynamic routing worked on PTM prediction. The third experiment showed the consequence of the first two experiments demonstrating the effectiveness of the dynamic routing for PTM predication, which indicates the resulting ‘instantiation parameters’ are well suited for protein substrate representations. In contrast to image recognition, capsules learned for protein phosphorylation can be used more than an attention mechanism and likely characterize more complex relationships among amino acids at different sequence positions.

Taken together, CapsNet not only has an outstanding performance in small sample learning but also has a capacity in exploring internal data distribution related to biochemical significance. As a new method in computer vision, CapsNet needs to be further exploited in more deep-learning application domains and much more work should be carried out to understand the characteristics of CapsNet and make it to train more effectively. We believe that CapsNet has a great potential in other biological sequence analysis and prediction problems. With its attention capacity, CapsNet is a valuable tool for biologists to gain a better understanding of underlying biological processes, as shown as the example of the phosphorylation site prediction through the in-depth study of internal capsules.

Funding

This work was supported by the National Institutes of Health award R35-GM126985.

Conflict of Interest: none declared.