Abstract
Motivation
Accurate prediction and interpretation of ligand bioactivities are essential for virtual screening and drug discovery. Unfortunately, many important drug targets lack experimental data about the ligand bioactivities; this is particularly true for G protein-coupled receptors (GPCRs), which account for the targets of about a third of drugs currently on the market. Computational approaches with the potential of precise assessment of ligand bioactivities and determination of key substructural features which determine ligand bioactivities are needed to address this issue.
Results
A new method, SED, was proposed to predict ligand bioactivities and to recognize key substructures associated with GPCRs through the coupling of screening for Lasso of long extended-connectivity fingerprints (ECFPs) with deep neural network training. The SED pipeline contains three successive steps: (i) representation of long ECFPs for ligand molecules, (ii) feature selection by screening for Lasso of ECFPs and (iii) bioactivity prediction through a deep neural network regression model. The method was examined on a set of 16 representative GPCRs that cover most subfamilies of human GPCRs, where each has 300–5000 ligand associations. The results show that SED achieves excellent performance in modelling ligand bioactivities, especially for those in the GPCR datasets without sufficient ligand associations, where SED improved the baseline predictors by 12% in correlation coefficient (r2) and 19% in root mean square error. Detail data analyses suggest that the major advantage of SED lies on its ability to detect substructures from long ECFPs which significantly improves the predictive performance.
Availability and implementation
The source code and datasets of SED are freely available at https://zhanglab.ccmb.med.umich.edu/SED/.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Drug discovery often begins with the screening of a high number of chemical compounds against a therapeutic protein target via biological high-throughput assays in vitro. Subsequently, leading hits are selected based on their bioactivities and optimized to make them stronger binders or more target selective (Unterthiner et al., 2014). However, biological high-throughput assays and bioactivity determinations are usually time and labor intensive. Currently, only a small part of ‘available compounds’ can be synthesizable or available for drug design studies. Thus, it is not possible to employ experimental high-throughput screening assays to determine the bioactivities for all the compounds (Blum and Reymond, 2009), where computer-based virtual screening becomes an important complement to the experimental efforts.
Virtual screening can be classified into receptor-based and ligand-based approaches (Cherkasov et al., 2014). The receptor-based approaches screen compounds via simulating physical interactions between a drug target protein and known compounds, but they are only valid when the 3D structure of the biomolecular target is available (Ceretomassagué et al., 2015). Ligand-based techniques learn the bioactivity of a compound acting with a target protein using known experimental data; of these, machine learning-based methods have been the most popular and widely applied in drug design (Ceretomassagué et al., 2015). A common approach to the machine learning-based virtual screening is to build predictive models through the training on the fixed-length hand-crafted features. Recently, deep learning-based methods have witnessed impressive success in ligand-based virtual screening (Ramsundar et al., 2017; Unterthiner et al., 2014; Wallach et al., 2015; Winkler and Le, 2017; Xu et al., 2017). For instance, in 2012, Merck organized a challenge for the design of machine learning methods to model the bioactivities of ligands acting with target proteins, and methods using deep learning achieved the best performance. Later, Ma et al. (2015) proposed a deep neural net model for determining quantitative structure–activity relationships (QSARs), which demonstrated better performance than random forest models for most of the data they studied (Ma et al., 2015). Most recently, we proposed a weighted deep learning algorithm that takes arbitrarily sized inputs and generates bioactivity predictions which are significantly more accurate than the control predictors with different molecular fingerprints and descriptors (Wu et al., 2018).
In addition to the accurate prediction of ligand bioactivities, comprehensive interpretation of predictors by precise identification of key substructures that control ligand bioactivities is equally important to the virtual screening and drug discovery studies. In this regard, the utilization of the extended-connectivity fingerprints (ECFPs), which are circular fingerprints whose features denote the presence or absence of particular substructures, have been shown beneficial to an accurate interpretation of ligand bioactivities (Rogers and Hahn, 2010). In addition, ECFPs have several useful features: (i) they do not need to be predefined and can code an infinite number of different molecular features, which is critical to the improvement of virtual screening performance; (ii) they can be rapidly calculated; and (iii) the ECFP algorithm can be tailored to produce different kinds of circular fingerprints, optimized for different usages.
In order to precisely predict ligand bioactivities, long ECFPs are required for obtaining optimal performance. For instance, after removing rarely occurring features, Unterthiner et al. created a 43 000-dimensional ECFP vector, where the ECFP12 fingerprints (chemical substructures) with long dimensions were found ideal for representing compound properties in QSARs (Unterthiner et al., 2014). More importantly, the use of long ECFPs can reduce the occurrence of bit collision, which helps determine more accurate substructures of each bit of the input compound molecule in feature retrieval (Rogers and Hahn, 2010). A drawback to the use of long ECFPs is, however, the requirement of greater computational and storage costs. Furthermore, the use of long fingerprints for compounds usually results in extremely sparse data, which may lead to the ‘Curse of Dimensionality’ (i.e. the drastic decrease in prediction performance) in many real-world ligand-based virtual screening campaigns, especially for drug targets without sufficient data. To the best of our knowledge, there have been no previous studies on the efficient utilization of long ECFPs in ligand-based virtual screening with the aim of improving the predictive performance of models and increasing the interpretability of experimental results.
It is generally assumed that ligand bioactivity is determined by some local regions and is usually closely related to a small number of chemical substructures (Crisman et al., 2008). Currently, one of the most popular methods to find the important and explainable substructures is through the least absolute shrinkage and selection operator (Lasso), which is a widely used regression technique for identifying sparse representations (Tibshirani, 1996). However, with high-dimensional ECFPs, the identification of relevant features by solving the Lasso problem remains challenging because it is computationally expensive and may not be possible to load the feature matrix into the main memory (Wang et al., 2013). Fortunately, screening for Lasso helps quickly recognize irrelevant features that have zero components in the solution, and then ignores these in the optimization. Therefore, we can work on a reduced-feature matrix when dealing with the Lasso problem, which would result in substantial savings in computational cost and memory usage, as well as alleviating the ‘Curse of Dimensionality’. Moreover, the irrelevant features removed by screening for Lasso are guaranteed to have zero coefficients in the solution stage, so there is no loss of accuracy or optimality (Wang et al., 2013).
In this work, we describe a novel method that employs screening for Lasso of ECFPs and deep neural nets (SED) for predicting the bioactivities. Our focus will be on the ligands associated with G protein-coupled receptors (GPCRs), mainly because of their significant importance in drug discovery studies, where currently drugs targeting GPCRs account for ∼27% of the global therapeutic drugs market (Hauser et al., 2017). For this purpose, we collect ligands from 16 human GPCR datasets that cover most families of human GPCRs. The testing results show that SED can achieve exceptional performance in terms of predicting ligand bioactivities. In particular, on datasets without sufficient ligand samples, the model performance exhibits a significant improvement just by adopting relevant ECFP features selected by screening for Lasso. If long ECFPs are used, further improvements can be observed. Moreover, in order to precisely interpret bioactivities of ligands interacting with the GPCRs, a case study was performed to examine key substructures which determine ligand bioactivities.
There has been an unfortunate lack of open-source code for virtual screening tools, as most have been designed for commercial usage. In this work, a demonstration program including the source code and data was produced and released on our webserver for the benefit of academic usage. As a general Lasso screening method for long ECFPs and a deep neural network (DNN) model were adopted by our approach for predicting the bioactivities of ligand molecules, it is straightforward for users to design virtual screening models for their targets of interest. All SED code and data are freely available at https://zhanglab.ccmb.med.umich.edu/SED/.
2 Datasets and methods
2.1 Datasets
We first downloaded the ‘all interaction data’ file from GLASS database (http://zhanglab.ccmb.med.umich.edu/GLASS/), which contains 533 470 unique GPCR–ligand interaction entries (Chan et al., 2015). Entries with the match ‘Standard units=nM’ were retained, and GPCR–ligand pairs with multiple bioactivity values were replaced with their median value to reduce the influence of outliers. For each GPCR, an experimental dataset was built with active ligands, which contain the canonical SMILES strings and target-associated bioactivities of these ligands.
For GPCR data, we downloaded the ‘7tmrlist’ file, which includes 3093 GPCRs, from the UniProt database (http://www.uniprot.org/docs/7tmrlist) (The UnitProt Consortium, 2008). After parsing this file, a total of 825 human GPCR proteins were found, of which only 55 had 3D structures available in the PDB (Berman et al., 2000; Zhang et al., 2015) (see also https://zhanglab.ccmb.med.umich.edu/GPCR-EXP/). Sixteen representative GPCRs without a solved structure, having at least 300 ligands, were selected as the experimental targets. These GPCRs are not homologous with each other with the maximum pair-wise sequence identity of 50% (for P0DMS8 and Q99835) and about 80% of pair-wise sequence identity is less than 30%. They cover four GPCR classes (A, B, C and F) and 13 subfamilies (see Supplementary Table S1). Other subfamilies with no or few experimental ligand associations were not considered because the lack of sufficient samples would preclude the construction of reliable models; these include, for instance, the subfamily ‘Sensory receptors’ in Class A, ‘Adhesion receptors’ in Class B, ‘Sensory receptors’ and ‘Orphan receptors’ in Class C, among others (Chan et al., 2015; Isberg et al., 2014). Such diversity of dataset selections is important for examining the generality of the models and to avoid cross-learning from homologous targets during the training process. As the raw bioactivity values of ligands span a large range, we adopted the p-bioactivity metric throughout this work. This is defined as , where is the raw bioactivity that can be evaluated using IC50, EC50, Ki, Kd and so on (Cortes-Ciriano, 2016). In our experimental datasets, the p-bioactivity ranges from −11 to 2.523, where smaller values indicate lower ligand activity.
Some control ligands were added into each GPCR dataset to ensure more robust feature selection and regression models for ligand-based virtual screening. The control ligands, without association with the target GPCR, were randomly selected from the remaining subfamily irrelevant GPCR datasets, representing approximately 20% of the original ligands. As for the control ligands, the p-bioactivity was fixed to −11, which is the upper bound of all GPCR–ligand interaction entries in GLASS database. Supplementary Table S1 presents a detailed description of the 16 GPCR datasets used in this work.
2.2 Methods
We propose a three-stage method to effectively screen key substructures from long ECFPs and then predict the bioactivities of ligands acting with GPCR targets. The proposed SED approach involves three steps: (i) ECFP generation, (ii) key substructure selection and (iii) bioactivity prediction using a DNN regression model (Fig. 1).
Fig. 1.
Schematic of SED. The approach is composed of three stages: long extended-connectivity fingerprint (ECFP) representation for ligand molecules, feature selection by screening for Lasso and construction of deep neural network regression prediction models
2.2.1 Generation of extended-connectivity fingerprints
ECFPs are among the most popular molecular fingerprints. Based on the Morgan algorithm (Morgan, 1965), they are highly suitable for the identification of the presence or absence of particular substructures and are often used for QSAR model building in the lead optimization process (Rogers and Hahn, 2010).
The ECFP generation contains three steps: (i) initial assignment of atom identifiers, (ii) iterative update of identifiers and (iii) duplication removal (Rogers and Hahn, 2010) (also see https://docs.chemaxon.com/). ECFP generation starts with the assignment of an initial integer identifier to every nonhydrogen atom of the input ligand molecule. This integer identifier catches some local information on the corresponding atom such that various properties (e.g. atomic number, connection count) are wrapped into a single identifier by a hash function. Several iterations are then implemented to merge the initial atom identifiers with those of neighbor atoms until a predefined diameter is reached. Each iteration captures a greater circular neighborhood around each atom and packs this into a single integer identifier through the appropriate hashing methods. The final stage of the generation process is to remove multiple identifier representations for identical atom neighborhoods. Here, two neighborhoods are treated as identical if they occupy the same set of chemical bonds or if their hashed integer identifiers are the same.
In this study, ECFPs were generated using three key parameters: diameter, length and count (Rogers and Hahn, 2010) (also see https://docs.chemaxon.com/). The diameter determines the maximum diameter of the circular neighborhoods employed for each atom. This is the main ECFP parameter, regulating the number and maximum size of the atom neighborhoods, and thus determines the length of the identifier list representation and the size of ‘1’ bits in the fixed-length string representation. The parameter ‘length’ defines the length of the bit string representation, whereas the parameter ‘count’ controls whether identical integer identifiers are saved with occurrence counts or kept only once. To decrease the likelihood of bit collision and information loss, the diameter was fixed to 12 in this study; the count was set to the default ‘No’ option, meaning that each identifier was stored only once. The ECFPs were generated by the program GenerateMD, which was authorized by the ChemAxon Ltd. with the free license for academic research.
2.2.2 Feature selection
Consider the ligand sample dataset , where represents the ith ligand molecule that takes the encoding ECFP of each molecule as input and denotes its p-bioactivity value.
Lasso (Tibshirani, 1996) is widely used to obtain sparse data representations or predictive models. Standard Lasso takes the form
| (1) |
where is the ECFP feature matrix, is the p-bioactivity response vector, is the optimal sparse representation and is the regularization parameter.
When the dimension of the ECFP feature space is long, solving the Lasso problem may be challenging because we might not be able to read the data matrix into main memory. To solve large-scale Lasso problems efficiently, the standard Lasso can be written in its dual form (Wang et al., 2013)
| (2) |
where denotes the dual variable and is the jth column of X. Let be the optimal solution of (2) and be the optimal solution of (1). The Karush–Kuhn–Tucker (KKT) conditions are implemented by
| (3) |
| (4) |
where denotes the ith component of . Considering the KKT condition in (4), the following rule holds: denotes an inactive feature.
The inactive features occupy the zero components in the optimal solution, , and can be discarded from the optimization without any sacrifice of the performance of the optimal value in the objective function (1). We refer to this approach as the Safe Screening Rules. SAFE (Ghaoui et al., 2010) is an efficient safe screening method. In SAFE, the ith entry of is removed when
| (5) |
where is the maximal parameter value such that the solution is non-trivial. To fine tune the value of , methods such as cross-validation can be applied to the Lasso problem along with a sequence of parameters . However, this may be very time-consuming. Enhanced Dual Polytope Projection (EDPP) is a much more efficient form of safe screening rules (Wang et al., 2013). An implementation of EDPP is available on GitHub: http://dpc-screening.github.io/lasso.html.
Consequently, the reduced data matrix can be optimized and the original problem (1) can be transformed into
| (6) |
where , is the number of zero components in , , denotes the p-bioactivity responses, is the optimal sparse representation, and is the regularization parameter. Applying the Lasso solver from the SLEP package (Liu et al., 2009) (http://www.yelab.net/software/SLEP/), only a small subset of the original features are selected for use in the final model. This improves the prediction performance and interpretability of regression models.
2.2.3 Deep neural network training
A neural network model is a hierarchical network composed of multiple layers. The lowest layer takes the molecular descriptors as the model input, whereas the uppermost layer outputs the predicted activities. Between the two are one or more hidden layers, which form a very complicated nonlinear transformation from the input descriptors to the output variables. A DNN holds more than one hidden layer and can model complex relationships among the input descriptors.
A standard DNN model is specified by three basic components (Haykin, 1994; Xu et al., 2017). The first is the interconnections between layer nodes. These interconnections are weighted according to the strength of the relationship between nodes, and the input value for a node is a weighted sum of the output values of nodes in the previous layer. The second component is the activation function, which performs the nonlinear transfer of the weighted sum of input values to the output at each node. The final component of a neural network is the optimization scheme, which tunes the weights to best match the activities.
The stage for updating the weight parameters is known as training and proceeds in an iterative fashion. During the optimization process, the weights are tuned to decrease the divergence between the prediction and the real bioactivity. For regression problems, the standard cost function for optimization is the mean square error (MSE). Because of the hierarchical structure of DNNs, the training process for reducing errors is usually called backpropagation. Because DNNs have many hyperparameters, it is time and labor intensive to implement the whole set of grid search. Since most previous studies on applying DNNs for ligand-based virtual screening optimized the adjustable weights in the neural network model, here we adopted the set of hyperparameter values that work well in similar tasks (Ma et al., 2015). The settings are as follows: (i) the DNN has four hidden layers containing 4000, 2000, 1000 and 1000 nodes, respectively; (ii) the dropout rates in the DNN are 0% in the input layer, 25% in the first 3 hidden layers, and 10% in the last hidden layer; (iii) the activation function is the rectified linear unit (ReLU); (iv) no unsupervised pretraining is conducted, and the network weights were initialized as random small values; (v) the size of each mini-batch is 20 and the number of epochs is 200; and (vi) the parameters for the optimization step are fixed to their default values, i.e. the learning rate is 0.05, the momentum strength is 0.9 and the weight cost strength is 0.0001. The DNN model runs in Python, and the code is available at https://github.com/Merck/ DeepNeuralNet-QSAR.
2.3 Evaluation criterion
In the Kaggle challenge organized by Merck in 2012, the correlation coefficient (r2) was used to assess the performance of drug activity predictions. This metric is calculated as
| (7) |
where is the true activity, is the mean of the true activity, is the predicted activity, is the mean of the predicted activity and n is the number of ligand molecules in the dataset. The larger the value of r2, the better the prediction performance.
A common metric for evaluating regression models is the root mean square error (RMSE), given by
| (8) |
where and are the true and predicted activity values, respectively, and n is the number of ligand molecules. The smaller the RMSE value, the better the prediction performance.
To remove the influence of random selection, three sets of control ligands were collected for each GPCR dataset, and the regression model for predicting the ligand bioactivities was trained separately. The mean criterion value of the three models was designated as the final result. Moreover, the Wilcoxon signed-rank test was performed to verify the statistical significance between the performance of the compared methods.
3 Results and discussion
3.1 Performance of top features selected from various ECFPs
We compared the ligand bioactivity prediction performance after feature selection from various sizes of ECFPs. Full-length ECFPs with 1024 bits were used to build the baseline prediction model. All regression models were implemented by DNN. For different sizes of ECFPs, the top 300 dimensions, ranked by the Lasso weight values, were used to construct DNN regression models. The GPCR datasets were divided into two groups according to their number of ligand samples. Datasets with sufficient samples (more than 600) formed Group I, whereas those with insufficient samples (≤600) formed Group II (details are given in the ‘# of ligands’ column in Supplementary Table S1).
The results show that, when the number of ligand samples is sufficient (Group I), baseline methods perform well on all GPCR datasets (r2: 0.9224 ± 0.0181; RMSE: 1.1693 ± 0.1351). Indeed, after feature selection, there is no significant difference between the performance of models based on the top 300 features (r2: 0.9186 ± 0.0189; RMSE: 1.2812 ± 0.2455) and the baseline methods (Wilcoxon signed-rank test, two-tailed P-value = 0.0663) (Table 1). With long ECFPs, the performance of the regression models improved on most GPCR data after feature selection. For example, with 10 240 bits, the Group I GPCR datasets give r2 = 0.9267 ± 0.0273 and RMSE = 1.099 ± 0.1834. When there are insufficient ligand samples in a GPCR dataset (Group II), the performance of the baseline method is often poor (r2: 0.7943 ± 0.1020; RMSE: 1.5655 ± 0.2868). In this case, after feature selection, the performance of models based on the top 300 features exhibits significant improvements (r2: 0.8358 ± 0.0807; RMSE: 1.4110 ± 0.2444). Using long ECFPs, the models achieve further improvements in performance when using the top 300 features, with the average improvement on r2 of 12% and RMSE of 19% against the baseline predictors. In addition, we further consider the effect of the size of ligand samples in the GPCR datasets on model performance. The results show that, after feature selection for the baseline methods, the improvement in r2 on the GPCR datasets of Group II is significantly better than that of Group I (Group I: −0.0026 ± 0.0073; Group II: 0.0572 ± 0.0556) (Supplementary Fig. S1A). Using long ECFPs (based on the best results, highlighted in boldface in Table 1), the improvement in r2 on the GPCR datasets of Group II was again significantly better that of Group I after feature selection (Group I: 0.0093 ± 0.0084; Group II: 0.0554 ± 0.0653) (Supplementary Fig. S1B). These results show that our SED method can improve performance on datasets without sufficient ligand samples.
Table 1.
Performance of deep neural networks with top features selected from various sizes of long ECFPs
| Groupa | GPCRs | ECb | Baselinec |
Top 300 features selected from various sizes |
||||
|---|---|---|---|---|---|---|---|---|
| 1024 | 1024 | 5120 | 10 240 | 51 200 | 102 400 | |||
| I | P08908 | r 2 (↑) | 0.9268 | 0.9249 | 0.9310 | 0.9314 | 0.9227 | 0.9127 |
| RMSE(↓) | 1.0483 | 1.0878 | 0.9968 | 0.9879 | 1.0636 | 1.0982 | ||
| Q9Y5N1 | r 2 (↑) | 0.9513 | 0.9464 | 0.9468 | 0.9598 | 0.9272 | 0.921 | |
| RMSE(↓) | 1.0218 | 0.9627 | 0.9748 | 0.9486 d | 1.0827 | 1.0889 | ||
| P28335 | r 2 (↑) | 0.9096 | 0.9066 | 0.8989 | 0.9095 | 0.8983 | 0.8903 | |
| RMSE(↓) | 1.1475 | 1.1335 | 1.1533 | 1.1184 | 1.1549 | 1.1723 | ||
| P35372 | r 2 (↑) | 0.9034 | 0.8968 | 0.8966 | 0.8954 | 0.8796 | 0.8814 | |
| RMSE(↓) | 1.2931 | 1.3478 | 1.1616 | 1.1547 | 1.2367 | 1.2384 | ||
| Q99705 | r 2 (↑) | 0.9389 | 0.931 | 0.9393 | 0.9436 | 0.9295 | 0.9327 | |
| RMSE(↓) | 1.1132 | 1.2236 | 0.9649 | 0.8928 d | 0.9464d | 0.9351d | ||
| P0DMS8 | r 2 (↑) | 0.8937 | 0.8859 | 0.8864 | 0.8938 | 0.8781 | 0.8555 | |
| RMSE(↓) | 1.1979 | 1.2348 | 1.1987 | 1.1907 | 1.2572 | 1.3375 | ||
| Q16602 | r 2 (↑) | 0.9268 | 0.9326 | 0.9514d | 0.9533 d | 0.9516d | 0.9527d | |
| RMSE(↓) | 1.2783 | 1.8135 | 1.6057 | 1.4746 | 1.4675 | 1.3730 | ||
| P51677 | r 2 (↑) | 0.9329 | 0.9216 | 0.9338 | 0.9405 | 0.9211 | 0.9161 | |
| RMSE(↓) | 1.0194 | 1.2781 | 1.0674 | 1.0280 | 1.0048 | 1.0989 | ||
| P48039 | r 2 (↑) | 0.9180 | 0.9209 | 0.9108 | 0.9147 | 0.9126 | 0.908 | |
| RMSE(↓) | 1.4047 | 1.4495 | 1.4607 | 1.3635 | 1.3699 | 1.3831 | ||
| II | Q9H228 | r 2 (↑) | 0.8152 | 0.8636d | 0.8789d | 0.8870d | 0.9100 d | 0.8942d |
| RMSE(↓) | 1.6521 | 1.3965d | 1.5009 | 1.372d | 1.3231 d | 1.3239d | ||
| Q8TDU6 | r 2 (↑) | 0.8830 | 0.9124 | 0.9329 d | 0.9206d | 0.9165d | 0.9077 | |
| RMSE(↓) | 1.3289 | 1.1804 | 1.0253 d | 1.0906d | 1.1056d | 1.1713 | ||
| Q8TDS4 | r 2 (↑) | 0.9154 | 0.9262 | 0.929 | 0.9222 | 0.9378 d | 0.9348d | |
| RMSE(↓) | 1.0707 | 1.0445 | 1.1328 | 1.1051 | 0.9567 d | 0.9906 | ||
| Q9HC97 | r 2 (↑) | 0.6047 | 0.7097d | 0.7649d | 0.8508 d | 0.8264d | 0.7801d | |
| RMSE(↓) | 1.7889 | 1.5855d | 1.6228d | 1.3631d | 1.3282d | 1.4242d | ||
| P41180 | r 2 (↑) | 0.7784 | 0.7916 | 0.8253d | 0.8435 d | 0.8029 | 0.8217d | |
| RMSE(↓) | 1.9226 | 1.7581 | 1.7082 | 1.5410 d | 1.5869d | 1.5510d | ||
| Q14833 | r 2 (↑) | 0.7429 | 0.7682 | 0.7947 d | 0.7743d | 0.7424 | 0.7302 | |
| RMSE(↓) | 1.6512 | 1.5453 | 1.4635 d | 1.4754d | 1.6216 | 1.6719 | ||
| Q99835 | r 2 (↑) | 0.8203 | 0.8790d | 0.892d | 0.8933d | 0.8999d | 0.9028 d | |
| RMSE(↓) | 1.5439 | 1.3669 | 1.1953d | 1.1924d | 1.155d | 1.1239 d | ||
Group I: original number of ligands >600; II: original number of ligands ≤600.
Evaluation Criterion: ↑ (↓) indicates that larger (smaller) values are better; the best results for each evaluation criterion are highlighted in boldface.
Baseline: full-length ECFPs with 1024 bits.
Indicates that the performance of the method using the top 300 ECFP features selected from various ECFPs is significantly better than that of the baseline methods based on Wilcoxon signed-rank test.
When the number of ligand samples in a GPCR dataset is sufficient, the baseline method usually performs well, and it is difficult to obtain further improvement. This is because the dimension of the ECFPs used in the baseline methods is only 1024, too small for any obvious ‘Curse of Dimensionality’ problems, and therefore the performance will not be significantly improved after feature selection. When long ECFPs are used, the model performance can be improved because more comprehensive information is captured by including more substructures. When the number of ligand samples is insufficient, the baseline methods perform poorly on most GPCR datasets. This is because the ‘Curse of Dimensionality’ probably exists in the baseline methods when 1024-bit ECFPs are used, as this is greater than the number of ligand samples in each dataset. When the most irrelevant features are removed via feature selection, the prediction performance improved significantly, which suggests that the bioactivity of a ligand is related to relatively few substructures. Moreover, when using long ECFPs, the model performance would be further improved by feature selection because more comprehensive information can be captured by the inclusion of larger and more substructures.
3.2 Influence of regression models
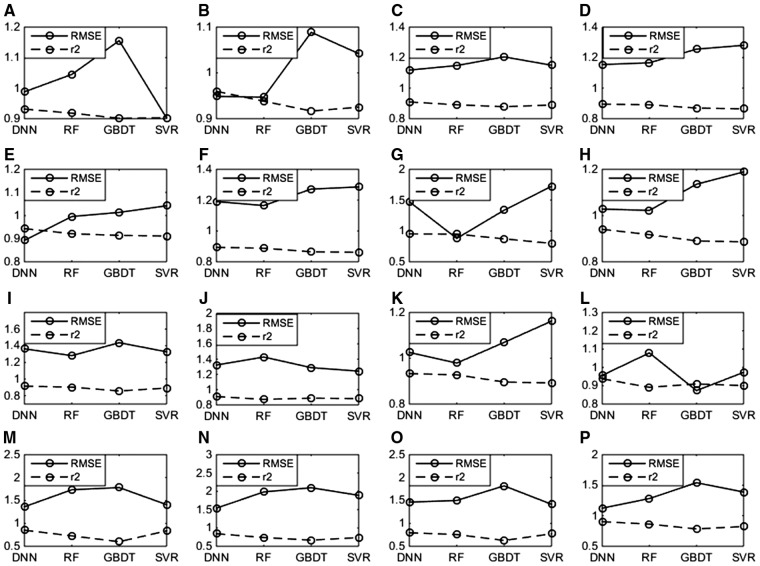
We investigated the dependence of SED on the regression model and applied Gradient Boosting Decision Tree (GBDT), Support Vector Regression (SVR), Random Forest (RF) and DNN to the GPCR datasets. The input of each regression model was the top 300 features selected from the optimal bits of the ECFPs. For each GPCR dataset, the optimal bit is the ECFP length corresponding to the optimal result (highlighted in boldface in Table 1). The optimal parameters of the RF, GBDT and SVR models were obtained through three-fold cross-validation with a standard grid search method, and the optimal model was evaluated by addressing the mean of r2 value of three-fold cross-validation. Specifically, for RF, the number of trees in the forest is set to 1000, and the number of features to consider at each split is set to ‘sqrt’. For GBDT, the learning rate is set to 0.1, and the number of boosting stages to perform is set to 1000. For SVR, the ‘rbf’ kernel type is used, and the gamma is set to 0.2.
Figure 2 shows a head-to-head comparison of SED implementations with different regression models, where the same training and validation datasets in the cross validation have been used. Here, a lower RMSE or higher r2 value indicates better model performance. The results show that the DNN regression models achieve an optimal performance with all GPCR datasets and evaluations, with a mean r2 value of 0.8913 which is 0.047, 0.1147 and 0.0597 higher than that of RF, GBDT and SVR, and a mean RMSE value of 1.1847 which is of 0.0425, 0.1510 and 0.0919 lower than that of RF, GBDT and SVR, respectively (see Fig. 2 and Supplementary Table S2). In addition, the r2 value of DNN statistically significantly better than that of the runner-up method RF (with the two-tailed P-value = 0.0004 in the Wilcoxon signed-rank test). Thus, the DNNregression model was employed in SED because of its robust performance.
Fig. 2.
Effect of regression model on performance. GBDT, Gradient Boosting Decision Tree; SVR, Support Vector Regression; RF, Random Forest; DNN, deep neural network. (A): P08908; (B): Q9Y5N1; (C): P28335; (D): P35372; (E): Q99705; (F): P0DMS8; (G): Q16602; (H): P51677; (I): P48039; (J): Q9H228; (K): Q8TDU6; (L): Q8TDS4; (M): Q9HC97; (N): P41180; (O): Q14833; (P): Q99835
In Supplementary Table S3, we present a comparison of SED with WDL-RF, which was previously developed for modeling ligand bioactivities by combining weighted network learning and random forest regression (Wu et al., 2018). Here, the input to WDL-RF is in the format of canonical SMILES and the bioactivity values of compounds, where the default parameters of the WDL-RF program are adopted, that is the number of module units (L) is set to 4, and 100 and in the random forest regression. The results show that the SED models achieve a better performance with all GPCR datasets and evaluations: the mean r2 value is 0.907 which is 0.243 higher than that by WDL-RF, and the mean RMSE value is 1.185 which is of 0.239 lower than that of WDL-RF (see Supplementary Table S3). The main reason for the better performance of SED over WDL-RF is that SED adopts long molecular fingerprints, with the maximum of 102 400 bits, whereas WDL-RF employs short molecular fingerprints, with only 50 bits.
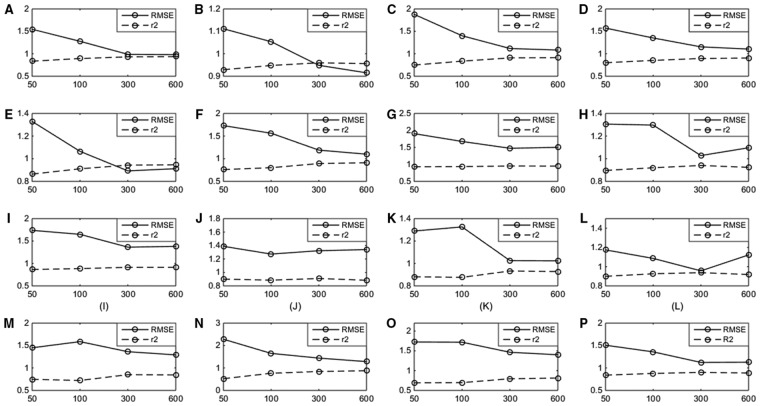
3.3 Effect of number of selected features
We now examine how the prediction of ligand bioactivities is affected by the number of features selected (K), where the features are ranked in order of weight values returned by Lasso. In this paper, we compare the predicted ligand bioactivities given by K = 50, 100, 300, and 600. For each GPCR dataset, the optimal bit is the ECFP length corresponding to the optimal result (highlighted in boldface in Table 1).
The results show that the model performance based on the top 300 features is better than that based on both the top 50 features and top 100 features on all GPCR datasets (Fig. 3). Moreover, the r2 values given by using the top 300 features significantly better than those based on the top 50 features (Wilcoxon signed-rank test, two-tailed P-value < 0.05) on the vast majority of GPCR datasets (14/16), and also obviously superior to those based on the top 100 features (Wilcoxon signed-rank test, two-tailed P-value < 0.05) on most GPCR datasets (9/16) (Fig. 3). Moreover, the r2 values based on the top 300 features are better than those based on the top 600 features on the majority of GPCR datasets (9/16) (Fig. 3). Thus, the default value of K was set to 300 in this study.
Fig. 3.
Dependence of SED performance on the number of selected features. (A): P08908; (B): Q9Y5N1; (C): P28335; (D): P35372; (E): Q99705; (F): P0DMS8; (G): Q16602; (H): P51677; (I): P48039; (J): Q9H228; (K): Q8TDU6; (L): Q8TDS4; (M): Q9HC97; (N): P41180; (O): Q14833; (P): Q99835
3.4 Correlation analysis of selected features
To further verify the effect of feature selection, we performed correlation analysis. For each selected feature, we calculated the Pearson correlation coefficient (PCC) between their values and the ligand bioactivities. A positive value indicates a positive correlation, and vice versa. The greater the absolute value, the stronger the correlation. Here, we focused on the absolute values of the PCCs and considered the top 300 features identified by sparse screening and Lasso (marked as ‘T300’ in Fig. 4). For comparison, another group of 300 features were randomly selected from all dimensions of the ECFPs (marked as ‘R300’ in Fig. 4). The boxes in Figure 4 indicate the distribution of PCCs of the top 300 and random 300 features on each GPCR dataset. The results show that the absolute values of PCCs for the top 300 features are significantly different from those for the random 300 features (Wilcoxon signed-rank test, two-tailed P-value < 0.01). On all GPCR datasets, the mean absolute value of the PCCs for the top 300 features was 0.1537, much higher than that of the random 300 features (0.0333). As a comparison, we also display the data based on the top 100 and 50 features (marked as ‘T100’ and ‘T50’ in Fig. 4). The result shows that the average PCCs for top 100 (0.2074) and top 50 (0.2530) features are slightly higher than that of top 300, but they generally have a larger fluctuation (indicating a lower reliability) than the top 300 ones. Overall, PCCs by all top 300, 100 and 50 features are significantly higher (with P-value < 0.01) than the randomly selected top 300 features, suggesting that our selected features by sparse screening and Lasso are effective and feasible.
Fig. 4.
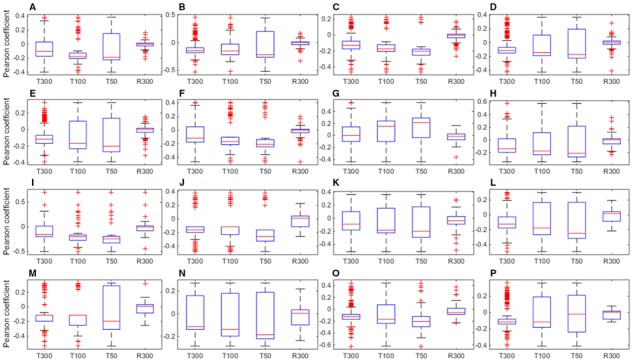
Pearson correlation analysis of selected features. T300, T100 and T50: The top 300, 100 and 50 features identified by screening for Lasso. R300: the 300 features randomly selected from all dimensions of the ECFPs. (A): P08908; (B): Q9Y5N1; (C): P28335; (D): P35372; (E): Q99705; (F): P0DMS8; (G): Q16602; (H): P51677; (I): P48039; (J): Q9H228; (K): Q8TDU6; (L): Q8TDS4; (M): Q9HC97; (N): P41180; (O): Q14833; (P): Q99835
3.5 Case study
Sphingosine 1-phosphate receptor 5 (S1PR5) is a GPCR which binds the lipid-signaling molecule sphingosine 1-phosphate. Its agonists have been proposed as an innovative mechanism for the treatment of neurodegenerative disorders (such as Alzheimer’s disease) and lysosomal storage disorders (such as Niemann–Pick disease) (van der Kam et al., 2014). As shown in Supplementary Table S1, the S1PR5 dataset contains 320 original and 60 control ligand samples. As indicated in Table 2, the regression performance based on the top 300 features is improved significantly when feature selection was applied to the baseline method, which is then improved further when long ECFPs were used. Using 51 200 bits, the model achieved improvements on 12% in r2 and 20% in RMSE compared with the baseline method.
Table 2.
Top 50 substructures identified by SED along with the associated Pearson correlation coefficients
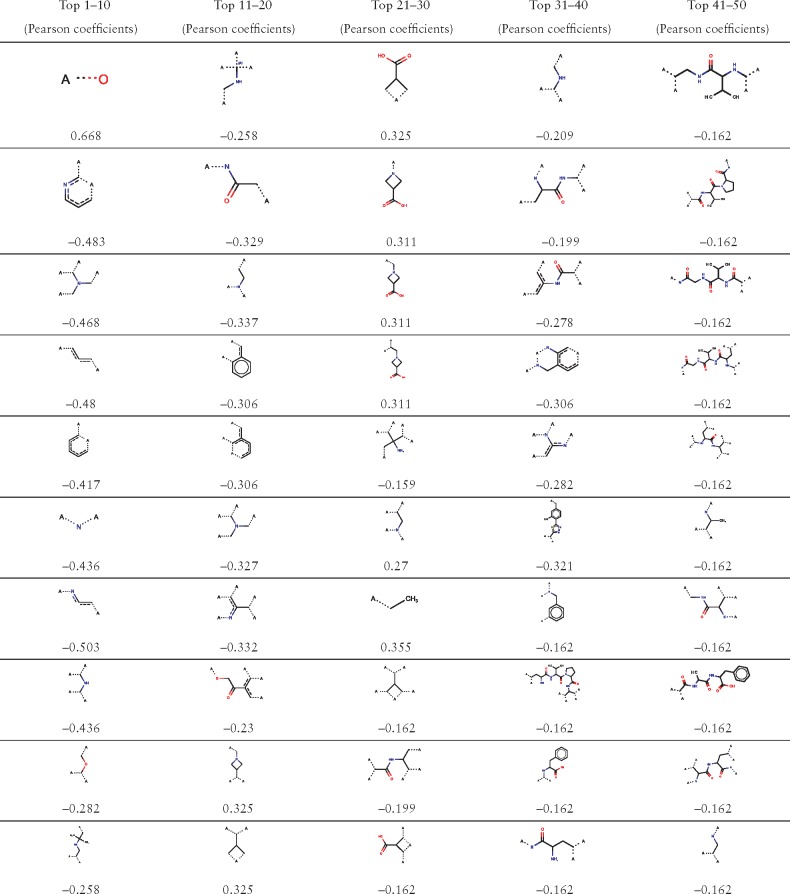
|
Screening for Lasso issued by SED is to identify the key substructures of ECFPs that affect ligand bioactivities. Visualization and correlation analysis of the key substructures which determine ligand bioactivities is important for understanding GPCR–ligand interactions and designing new drugs. The JChem Suite of ChemAxon (Csizmadia, 2000) provides a lookup service for the substructures encoded in ECFP fingerprints. Its ‘ECFPFeatureLookup’ class retrieves substructures corresponding to a given integer identifier or bit position. The program MarvinView was used to visualize substructures. The top 50 substructures identified by SED are presented in Table 2, and the top 51–300 substructures are presented in Supplementary Table S4, along with the associated PCCs between the attribute values of each dimension and ligand bioactivities. The top substructures have the potential of guiding further optimization of lead compounds by constructing new and better ligand molecules.
4 Conclusions
We have developed a novel method, SED, which combines the screening for Lasso of ECFPs with DNNs to predict the bioactivities of GPCR-associated ligand molecules. The method is comprised of three consecutive steps: (i) generation of long ECFPs for ligand samples, (ii) feature selection by screening for Lasso of ECFPs and (iii) bioactivity prediction using a DNN regression model. Large-scale benchmark tests show that SED can generate excellent bioactivity predictions from various datasets. Using GPCR datasets without sufficient ligand samples, the regression model performance exhibits significant improvements by simply adopting the relevant ECFP features selected by screening for Lasso; if long ECFPs are used, the performance can be further improved. The results indicate that the SED method can quickly remove irrelevant features, resulting in a reduced feature matrix for the Lasso problem. This may lead to substantial reductions in computational cost and memory usage, as well as greatly alleviate the potential for the ‘Curse of Dimensionality’. In addition, a visualized study was examined to clearly explore key substructures which determine bioactivities of ligand molecular acting with GPCRs for accurate understanding the experimental results.
At present, the relationship between ligand binding and biology remains unclear. In this regard, the SED method can help to quickly screen key substructures that determine ligand bioactivities. Current results have showed that further improvement can be achieved by models based on the top identified substructures, especially for GPCRs datasets without sufficient ligand samples. Moreover, PCCs between their values and the ligand bioactivities were calculated for each selected feature, where the top substructures tend to have a higher correlation with bioactivity values. These analyses can help provide a better understanding of the success of the SED method, and the top substructures are likely to be new and correct in the context of the machine learning experiment. Ideally, the best and reliable choice for the model controls is to validate the method through biomedical experiments, where the next important work is to apply the SED model to virtual screening for specific drug targets. The work along this line is currently in progress.
The SED source code and datasets are freely available at https://zhanglab.ccmb.med.umich.edu/SED/, with the code usage provided in Supplementary Text S1.
Supplementary Material
Acknowledgement
We thank the ChemAxon Ltd. to provide the free license of the ChemAxon softwares for academic research.
Funding
This work was supported, in part, by the National Science Foundation of China [61872198, 81771478 and 61571233]; the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province [18KJB416005]; the key University Science Research Project of Jiangsu Province [17KJA510003]; the Natural Science Foundation of Nanjing University of Posts and Telecommunications [NY218092]; and the National Science Foundation [DBI1564756].
Conflict of Interest: none declared.
References
- Berman H.M. et al. (2000) The Protein Data Bank. Nucleic Acids Res., 28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blum L.C., Reymond J.L. (2009) 970 million druglike small molecules for virtual screening in the chemical universe database GDB-13. J. Am. Chem. Soc., 131, 8732.. [DOI] [PubMed] [Google Scholar]
- Ceretomassagué A. et al. (2015) Molecular fingerprint similarity search in virtual screening. Methods, 71, 58–63. [DOI] [PubMed] [Google Scholar]
- Chan W.K. et al. (2015) GLASS: a comprehensive database for experimentally validated GPCR–ligand associations. Bioinformatics, 31, 3035–3042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cherkasov A. et al. (2014) QSAR modeling: where have you been? Where are you going to? J. Med. Chem., 57, 4977.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortes-Ciriano I. (2016) Benchmarking the predictive power of ligand efficiency indices in QSAR. J. Chem. Inform. Model., 56, 1576.. [DOI] [PubMed] [Google Scholar]
- Crisman T.J. et al. (2008) Ligand-target interaction-based weighting of substructures for virtual screening. J. Chem. Inform. Model., 48, 1955–1964. [DOI] [PubMed] [Google Scholar]
- Csizmadia F. (2000) JChem: Java applets and modules supporting chemical database handling from web browsers. J. Chem. Inform. Comput. Sci., 40, 323–324. [DOI] [PubMed] [Google Scholar]
- Ghaoui E. et al. (2010) Safe feature elimination in sparse supervised learning. Pacific J. Optim., 8, 667–698. [Google Scholar]
- Hauser A.S. et al. (2017) Trends in GPCR drug discovery: new agents, targets and indications. Nat. Rev. Drug Discov., 16, 829–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haykin S. (1994) Neural Networks: A Comprehensive Foundation. Prentice Hall PTR, Upper Saddle River, New Jersey, pp. 71–80. [Google Scholar]
- Isberg V. et al. (2014) GPCRDB: an information system for G protein-coupled receptors. Nucleic Acids Res., 42, D422.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J. et al. (2009) SLEP: Sparse Learning with Efficient Projections. Arizona State Univ., Tempe, AZ, USA. [Google Scholar]
- Ma J. et al. (2015) Deep neural nets as a method for quantitative structure–activity relationships. J. Chem. Inform. Model., 55, 263–274. [DOI] [PubMed] [Google Scholar]
- Morgan H.L. (1965) The generation of a unique machine description for chemical structures - a technique developed at Chemical Abstracts Service. J. Chem. Document., 5, 107–113. [Google Scholar]
- Ramsundar B. et al. (2017) Is multitask deep learning practical for pharma? J. Chem. Inform. Model., 57, 2068–2076. [DOI] [PubMed] [Google Scholar]
- Rogers D., Hahn M. (2010) Extended-connectivity fingerprints. J. Chem. Inform. Model., 50, 742–754. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. (1996) Regression shrinkage and selection via the lasso. J. R. Statist. Soc. Ser. B Methodol., 58, 267–288. [Google Scholar]
- The UnitProt Consortium (2008) The Universal Protein Resource. Nucleic Acids Res., 35, 193–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unterthiner T. et al. (2014) Deep learning as an opportunity in virtual screening. In: Proceedings of the Deep Learning Workshop at NIPS, Montreal, Canada, pp. 1–9. [Google Scholar]
- Van der Kam E. et al. (2014) The use of selective sphingosine-1-phosphate receptor 5 agonists for the treatment of neurodegenerative disorders such as Alzheimer's disease and lysosomal storage diseases such as Niemann-Pick c disease. Alzheimer’s Dement. J. Alzheimer’s Assoc., 10, P281. [Google Scholar]
- Wallach I. et al. (2015) AtomNet: a deep convolutional neural network for bioactivity prediction in structure-based drug discovery. Mathemat. Z., 47, 34–46. [Google Scholar]
- Wang J. et al. (2013) Lasso screening rules via dual polytope projection. Adv. Neural Inform. Process. Syst., 1070–1078. [Google Scholar]
- Winkler D.A., Le T.C. (2017) Performance of deep and shallow neural networks, the universal approximation theorem, activity cliffs, and QSAR. Mol. Inform., 36, 1–2. [DOI] [PubMed] [Google Scholar]
- Wu J. et al. (2018) WDL-RF: predicting bioactivities of ligand molecules acting with G protein-coupled receptors by combining weighted deep learning and random forest. Bioinformatics, 34, 2271–2282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y. et al. (2017) Demystifying multitask deep neural networks for quantitative structure–activity relationships. J. Chem. Inform. Model., 57, 2490–2504. [DOI] [PubMed] [Google Scholar]
- Zhang J. et al. (2015) GPCR-I-TASSER: a Hybrid approach to G protein-coupled receptor structure modeling and the application to the human genome. Structure, 23, 1538–1549. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.