Abstract
Motivation
MicroRNAs (miRNAs) are important non-coding post-transcriptional regulators that are involved in many biological processes and human diseases. Individual miRNAs may regulate hundreds of genes, giving rise to a complex gene regulatory network in which transcripts carrying miRNA binding sites act as competing endogenous RNAs (ceRNAs). Several methods for the analysis of ceRNA interactions exist, but these do often not adjust for statistical confounders or address the problem that more than one miRNA interacts with a target transcript.
Results
We present SPONGE, a method for the fast construction of ceRNA networks. SPONGE uses ’multiple sensitivity correlation’, a newly defined measure for which we can estimate a distribution under a null hypothesis. SPONGE can accurately quantify the contribution of multiple miRNAs to a ceRNA interaction with a probabilistic model that addresses previously neglected confounding factors and allows fast P-value calculation, thus outperforming existing approaches. We applied SPONGE to paired miRNA and gene expression data from The Cancer Genome Atlas for studying global effects of miRNA-mediated cross-talk. Our results highlight already established and novel protein-coding and non-coding ceRNAs which could serve as biomarkers in cancer.
Availability and implementation
SPONGE is available as an R/Bioconductor package (doi: 10.18129/B9.bioc.SPONGE).
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
MicroRNAs (miRNAs) are ∼23 nt long RNAs that play an important role in the regulation of transcript abundance in mammalian cells. They are estimated to regulate at least half of the genes in the human genome (Friedman et al., 2009) and thus affect important biological processes and show deregulation in many diseases (Jiang et al., 2009). miRNAs regulate their target mRNAs by either degrading them or by preventing their translation (Bartel, 2009). Target recognition is initiated by sequence complementarity of the target transcripts to the seed sequence of the miRNA at position 2–8. To predict miRNA target interactions, a number of sequence-based approaches have been proposed (e.g. Agarwal et al., 2015; John et al., 2004). However, a large fraction of these predictions are false positives, since condition-specific attributes of the cell, such as miRNA abundance, number of miRNA targets and their expression, are not known (Pinzón et al., 2017). Although experimental techniques exist that measure condition-specific miRNA–gene interactions (e.g. Jaskiewicz et al., 2012), these experiments are laborious and costly and often not available for the condition of interest. This motivates the development of computational methods that quantify condition-specific miRNA–gene interaction potential using widely available gene and miRNA expression datasets, reviewed by Muniategui et al. (2013).
Notably, genes sharing binding sites for the same miRNA(s) compete over a limited pool of miRNA molecules, giving rise to a complex gene-regulatory network of competing endogenous RNAs (ceRNAs) (Tsang et al., 2010). A number of cancer-associated genes have been shown to act as ceRNAs (Arvey et al., 2010; Salmena et al., 2011; Tay et al., 2014), including PTEN (Poliseno et al., 2010), CD44 (Jeyapalan et al., 2011), ESR1 (Chiu et al., 2015), BRAF (Karreth et al., 2015), KRAS (Poliseno et al., 2010), MYCN (Powers et al., 2016) and HULC (Wang et al., 2010). These findings motivated the development of computational methods for inferring ceRNA interactions systematically from gene and miRNA expression data, reviewed by Le et al. (2016).
The different methods can be broadly categorized into methods that use (i) only static information, such as the number of miRNA binding sites or binding energy or (ii) methods that use condition-specific information in addition such as expression or Clip-data. One of the most commonly used methods in category (i) is based on the idea to assess the probability that two mRNAs share miRNAs and their binding sites, and to then highlight cases where this probability is much higher than expected by chance, for example by using the hypergeometric test (Li et al., 2014).
With the emergence of large-scale studies providing gene and miRNA expression data for hundreds of samples, a number of methods of category (ii) have been developed (Le et al., 2016). Sumazin et al. (2011) proposed the use of conditional mutual information (CMI) for estimating the effect of a miRNA on a gene–gene interaction in their method HERMES. The advantage of this approach is that it measures non-linear associations, but estimation of significance is done using permutations, later implemented as part of the CUPID software (CUPID step III) (Chiu et al., 2015). Recently the JAMI software has improved the runtime of the extensive CMI computation compared to CUPID (Hornakova et al., 2018), but runtime is still a limiting factor for this approach in applications to very large datasets.
This issue has motivated the use of conceptually simpler and fast linear correlation-based methods, for instance, restricting to only gene–gene correlation values (Du et al., 2016; Xu et al., 2015), gene–miRNA correlation (Zhang et al., 2017) or correlations within triplets of two genes and one miRNA (Liu et al., 2017; Wang et al., 2015). However, in contrast to CUPID, these approaches do not quantify the contribution of the miRNA to the ceRNA interaction in a unified model.
Paci et al. (2014) overcame this issue with the definition of sensitivity correlation (scor), which has similarities to the CMI-based approach. Linear partial correlation can be used to quantify the remaining correlation between two genes after accounting for the effect of one miRNA. scor is then defined as the difference between gene–gene correlation and partial correlation and thus quantifies the contribution of the miRNA in the regulation of two genes. Similar to CMI, scor considers the impact of miRNA regulation on both genes in a single mathematical model and is thus more powerful than the methods proposed in Wang et al. (2015), Zhang et al. (2017), Du et al. (2016), Xu et al. (2015) and Liu et al. (2017). Unlike CMI, however, scor computation is based on efficient estimators of covariance matrices for computing partial correlation and thus allows large-scale ceRNA network inference as demonstrated by Zhang et al. (2016), who inferred lncRNA–mRNA related ceRNA networks for 12 different cancer types.
While the estimation of the scor coefficients is efficient, no theory for the computation of the null distribution of these values exists. Therefore, previous work relied on ad hoc approaches. Paci et al. (2014) selected the top 5% of scor coefficients for downstream analysis, disregarding significance testing. Zhang et al. (2016) addressed this issue by generating a null distribution using permutations based on randomly selected lncRNA–miRNA–mRNA triplets. This null distribution was then used to obtain empirical P-values.
We have identified a number of issues with the current approaches that use scor. First, current correlation-based approaches assume independence between scor values and the gene–gene correlation. However, as we show in this work, the distribution of scor coefficients is strongly affected by gene–gene correlation (Fig. 1A and Supplementary Fig. S1). Thus, previous studies that have used scor values have been biased.
Fig. 1.
Overview of the SPONGE workflow. (A) Predicted and/or experimentally validated gene–miRNA interactions are subjected to regularized regression on gene and miRNA expression data. Interactions with negative coefficients are retained since they indicate miRNA induced inhibition of gene expression. (B) We compute sensitivity correlation coefficients for gene pairs based on shared miRNAs identified in (A). (C) Given the sample number, we compute empirical null models for various gene–gene correlation coefficients (k) and number of miRNAs (m). Sensitivity correlations coefficients are assigned to the best matching null model and a P-value is inferred. (D) After multiple testing correction, significant ceRNA interactions can be used to construct a genome-wide, disease or dataset-specific ceRNA interaction network
Second, we note that many ceRNAs are regulated by several miRNAs. Neglecting joint contributions, many significant ceRNA interactions may be missed. The CUPID approach considers that ceRNA interactions may be mediated by several miRNAs in conjunction. To accommodate this, CUPID pools P-values obtained from individual ceRNA triplets (Chiu et al., 2015). We propose that the contributions of multiple miRNAs should be part of the ceRNA inference model to optimally account for miRNA covariance effects.
Here we present a unified mathematical approach that addresses the above issues. We have developed a Bioconductor/R package called Sparse Partial correlation ON Gene Expression (SPONGE). At the core of SPONGE is a new mathematical framework that is a generalization of scor values for more than one miRNA, which we call multiple miRNA sensitivity correlation (mscor). Assessing the significance of mscor coefficients is difficult due to biases of gene–gene correlation, number of samples and the number of miRNAs. Therefore, we have developed a novel strategy for simulating background distributions that accommodate the aforementioned factors and for inferring P-values for mscor coefficients efficiently. Due to SPONGE’s efficiency, we were able to perform an analysis of the complete human transcriptome across 31 different cancer types combining over 10 000 paired gene and miRNA expression samples using data from The Cancer Genome Atlas (TCGA). Our analysis highlights the potential of ceRNA network inference for hypothesis generation by revealing extensive ceRNA cross-talk. Some of the key regulators have already been reported as ceRNAs while others potentially represent novel biomarkers and drug target candidates.
2 Materials and methods
2.1 SPONGE overview
The objective of SPONGE is to infer a ceRNA interaction network from gene and miRNA expression data of paired samples. In theory, inferring a genome-wide ceRNA network with n genes entails considering interactions for all pairwise combinations. In practice, only gene pairs with shared miRNAs need to be considered. First, SPONGE identifies for each gene those miRNAs that are likely to have a regulatory effect (Fig. 1A). Second, we filter for gene pairs with shared miRNAs and determine their ceRNA interaction scores (Fig. 1B). Third, we assess the significance of each ceRNA interaction using a series of null models (Fig. 1C) adjusting for confounders. Finally, significant interactions are retained for constructing a ceRNA interaction network (Fig. 1D). In the following, we describe each of these steps in detail.
Step 1: Identifying relevant miRNA–gene interactions
SPONGE identifies relevant gene–miRNA interactions in two stages. First, we retain only miRNA–gene pairs for which we have general evidence from external predictive or experimental sources. SPONGE allows for an arbitrary number of data sources to be combined.
Second, we test if the gene and miRNA expression data provides support for these interactions, since we expect many of the putative miRNA–gene interactions in particular to be false positives (Pinzón et al., 2017). Negative correlation of gene and miRNA expression can provide evidence for a miRNA–gene regulation. However, many miRNAs might target a single gene. To take this into account, and to identify the most likely miRNA regulators of each gene, we use regularized regression.
We build an Elastic net regularized linear regression model with the expression of gene g as the dependent variable and the expression of miRNAs as explanatory variables, where are miRNAs predicted or experimentally shown to target g. Elastic net balances lasso (L1) and ridge (L2) penalties using a linear combination of both denoted as a weight factor α. We build a range of Elastic net models to optimize the parameters for α = 0.1, 0.2, …, 1.0 and the optimal shrinkage parameter λ via 10-fold cross validation using the glmnet package (Friedman et al., 2010). We select the best model based on the residual sum of squares. Since miRNAs with positive coefficients are likely caused by effects other than miRNA repression, we retain only miRNAs with negative coefficients, which was previously shown to work well (Muniategui et al., 2012; Schulz et al., 2013). Moreover, SPONGE offers a user-definable coefficient threshold for discarding miRNAs with negligible impact on gene expression (default < −0.05).
In summary, we identify for each gene condition-specific miRNA regulators. This leads to a dramatic reduction of gene pairs that share miRNAs (Fig. 1B) compared to using all predicted miRNA–gene interactions and reduces the runtime of SPONGE. In the next step, we determine the effect strength of ceRNA interactions.
Step 2: Computing sensitivity correlation coefficients
In general, the partial correlation describes to what extent two variables x and y are correlated when controlling for one or up to i additional variables . Paci et al. (2014) proposed to quantify the regulatory contribution of a miRNA in a ceRNA interaction between two genes g1 and g2 by subtracting the partial correlation achieved when controlling for a single miRNA m and refered to this as sensitivity correlation (scor):
| (1) |
Note that this approach does not account for a combinatorial effect of several miRNAs. Consequently, strong ceRNA interactions mediated by several moderate miRNA regulators cannot be detected.
We thus propose to extend the definition of sensitivity correlation considering the effect of multiple miRNAs M for the computation of the partial correlation. In this way, we implicitly incorporate the effect of miRNA-miRNA cross-correlation. We call this multiple miRNAs sensitivity correlation (mscor):
| (2) |
where and i is the number of shared miRNAs between g1 and g2.We compute mscor coefficients efficiently using the R package ppcor (Kim, 2015). In the next step, we establish the significance of each mscor coefficient.
Step 3: Sampling from the mscor null distribution with respect to important parameters
Zhang et al. (2016) proposed to establish the significance of scor coefficients by means of sampling a background distribution from random triplets. This approach, however, disregards that correlation coefficients have smaller variance when the coefficient is high (Fisher, 1915). Moreover, it can be expected that the significance of sensitivity correlation values is linked to the number of samples and the number of miRNAs involved.
To accommodate these biases, we propose a novel algorithm to study the null distribution of mscor coefficients. Our null hypothesis is that the shared miRNAs M do not affect the correlation of two genes g1 and g2. Hence,
| (3) |
| (4) |
To be able to sample random mscor coefficients under this null hypothesis, we first need to construct random covariance matrices that fulfill these conditions. Briefly, we consider a partitioned expression vector with . The correlation matrix of Z can be expressed as:
| (5) |
where
| (6) |
is the correlation matrix between the first two entries of Z. In order to compute the conditional covariance between the first two entries (g1, g2) of Z given , we compute the Schur complement of R/R22 as follows:
| (7) |
where
| (8) |
We can obtain the partial correlation from the conditional covariance as follows:
| (9) |
Our null hypothesis is that . Thus
| (10) |
We have devised sampling strategies that enable us to find values a, b and c such that these conditions are fulfilled, allowing us to construct random covariance matrices under the null.
Most importantly, we can control the gene–gene correlation r12 and the number of miRNAs (via the dimensions of R22) to construct a series of covariance matrices with respect to these important parameters. SPONGE uses these covariance matrices to draw random samples which are subsequently used to estimate empirical P-values for mscor values computed on experimental data. The details of this approach and of our sampling strategy can be found in the Supplementary Material.
The SPONGE R package provides precomputed covariance matrices for a range of gene–gene correlations and number of miRNAs. Given the number of samples in the expression data, SPONGE can efficiently construct a series of null distributions from these covariance matrices. Next, we assign each mscor coefficient to the closest matching null model and infer its P-value via its rank in the random distribution (Fig. 1D). The number of data points sampled for the null distribution determines the maximal precision of this P-value ( by default). Finally, P-values are adjusted for multiple testing within each null model using the method by Benjamini and Hochberg (1995).
Step 4: Constructing a ceRNA network
We filter ceRNA interactions returned by SPONGE by a user-defined significance threshold (FDR < 0.01 by default) and subsequently construct a ceRNA interaction network N = (V, E), where nodes V correspond to genes participating in significant ceRNA interactions and edges correspond to significant ceRNA interactions between two genes.
2.2 Using SPONGE to construct a pan-cancer ceRNA network
We downloaded reprocessed TCGA pan-cancer data from the TOIL project (Vivian et al., 2017) via the UCSC Xena Browser (Goldman et al., 2018). We identified 10 019 samples for which both gene and miRNA expression data were available. Next, we performed log2 transformation and discarded genes and miRNAs not expressed in more than 80% of samples as well as genes and miRNAs with expression variance <0.5.
To consider both coding and non-coding miRNA–gene interactions, we downloaded sequence-based predictions of two methods, namely TargetScan (Agarwal et al., 2015) (v.7.1, downloaded 10/03/2017) and miRcode (Jeggari et al., 2012) (v.11, downloaded 10/03/2017). We included the latter since it also considers non-coding RNAs which have been shown to act as ceRNAs.
TargetScan and miRcode predict target genes for miRNA families. We thus downloaded suitable miRNA family definitions for both datasets (available at the TargetScan website http://www.TargetScan.org/). Note that miRcode uses the miRNA family definitions corresponding to TargetScan v.6. After mapping family ids to miRBase mature miRNA ids (MIMATs) we generated integer matrices in which genes are listed as rows and miRNAs are listed as columns. Each entry of the matrix represents the number of binding sites for the corresponding interaction.
To consider experimental evidence for miRNA–gene interactions, we obtained datasets from miRTarBase (v.6, downloaded 13/03/2017) (Chou et al., 2016) for coding and lncBase (v.2, downloaded 13/03/2017) (Paraskevopoulou et al., 2016) for non-coding genes and generated input matrices as described above.
Matrices, for gene and miRNA expression and miRNA–gene interactions were analyzed with SPONGE. Significant ceRNA interactions were used to construct the pan-cancer ceRNA network.
2.3 Runtime analysis
In order to compare against the runtime of the CMI-based approach of CUPID (Chiu et al., 2015), which similarly uses paired gene and miRNA expression to estimate gene–miRNA–gene triplets, we used the JAMI software (Hornakova et al., 2018). JAMI is a fast reimplementation of CUPID step III that leverages parallelization. We compared the runtime of JAMI to that of SPONGE (without step1: the regression filter) for a fair comparison. We used a subset of the pan-cancer dataset with 200 genes, which form ca. 80 000 gene–miRNA–gene triplets. We ran both tools with default parameters in parallel mode with 16 cores with varying number of samples and genes.
2.4 Survival analysis
For assessing the impact of gene or miRNA expression on the survival probability, we downloaded right-censored TCGA survival data of TCGA patients from the UCSC Xena Browser (Goldman et al., 2018). We divided patients into two groups based on the 50% quantile of the expression vector. Survival probability was computed in R using the survfit function in the R package survival (Therneau and Grambsch, 2000). P-values were computed using the function survdiff in the same package. survdiff tests for significant differences of survival curves using the χ2 statistic. Kaplan Meier plots were generated using the ggsurv function of package survminer.
To test for the enrichment of survival genes in a list of top candidates ranked by degree, we used the following strategy. First, we computed survival P-values based on expression data for all genes as outlined above using the survdiff function. Second, we classified genes into survival-associated and -unassociated (background) genes (FDR < 0.001; Benjamini and Hochberg, 1995) for the purpose of enrichment analysis. Third, we computed enrichment of the candidate gene set in survival-associated compared to background using the hypergeometric test in R.
3 Results
We have devised a method for the statistical evaluation of condition-specific ceRNA interactions from paired miRNA and gene expression data considering contributions for multiple miRNAs: called multiple miRNA sensitivity correlation (mscor). mscor is a generalization of scor previously defined for one miRNA by (Paci et al., 2014) (see Section 2 for details).
3.1 Simulated data reveals dependency of sensitivity correlation on several factors
As mentioned above, no theory existed to describe the distribution of sensitivity correlation values (Paci et al., 2014). However, we wanted to understand how the mscor measure is influenced by confounding factors present in ceRNA relationships: (i) the correlation of two genes, (ii) the number of miRNAs involved in the ceRNA interaction and (iii) the number of samples that are available for estimation. We developed an efficient simulation approach to explore null models in which miRNAs have no effect on the correlation of two genes, hence mscor is zero (see Section 2 and Supplementary Material for details). Our method is able to compute random covariance matrices that fulfill this null hypothesis. This allowed us to simulate datasets for a range of gene–gene correlation coefficients (0.2–0.9 in steps of 0.1), shared miRNAs (1–8) and number of samples (50, 200, 800) and thus to approximate the random distribution of the mscor coefficients under the null hypothesis that mscor is zero.
Figure 1 and Supplementary Figure S1 show our simulation results, which reveal that the null distribution is strongly affected by all three tested parameters. Our findings indicate that large mscor coefficients are more likely to occur by chance when the gene–gene correlation is low and when the number of miRNAs increases. As expected, it is more difficult to obtain significant mscor coefficients with few samples as higher mscor values are obtained with smaller samples sizes by chance. Thus, comparing mscor values without proper adjustment for these parameters would prioritize low gene–gene correlation pairs, interactions with many miRNAs and lead to a bias when tests between studies with different sample numbers are compared.
The above insights led us to develop SPONGE, an R/Bioconductor package to infer ceRNA interactions between pairs of genes. We briefly outline how SPONGE facilitates this in two steps (see Section 2 and Fig. 1). First, we estimate condition-specific miRNA–gene associations from a large set of putative miRNA–gene interactions. This is done using sparse regression of paired gene and miRNA expression data obtained from many samples. Second, ceRNA interactions are predicted using mscor values estimated for all gene–gene pairs that share at least one miRNA from the first step. Statistical significance of mscor values is efficiently computed using the simulation approach described above.
3.2 Considering multiple miRNAs leads to information gain
To demonstrate the advantages of mscor measure over scor, we selected a subset of the TCGA data with 364 liver cancer samples and 1000 randomly selected genes. mscor allows us to incorporate multiple miRNAs in the model and thus to detect ceRNA interactions that only become significant when several miRNAs act in concert. Figure 2A shows that considering all miRNAs lead in most but not all cases to a higher mscor coefficient compared to the individual miRNA with highest scor. However, when also considering significance (FDR < 0.01), the signal to noise ratio increased and led to a clear gain in information, namely consistently higher mscor coefficients for multiple miRNAs. Consequently, SPONGE is able to assess the joint regulatory effect of several miRNAs in a ceRNA relationship in a condition-specific way.
Fig. 2.
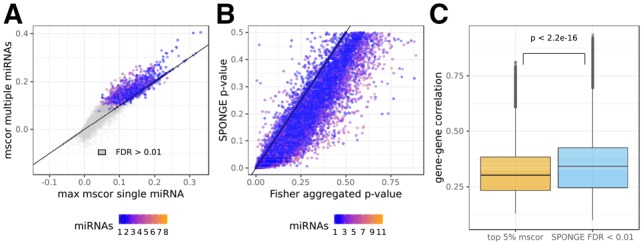
Comparison of sensitivity correlation and SPONGE FDR control on liver cancer data. (A) mscor values (y-axis) compared to maximal scor values (x-axis) for the same gene–gene interaction. (B) mscor P-values obtained from sampling compared to P-value summarization of scor values using Fisher’s method. (C) Boxplot of gene–gene correlations for gene–miRNA–gene triplets obtained after selecting the top 5% ceRNA interactions according to the raw scor values (orange) or based on FDR corrected P-values from SPONGE (blue). t-test P-value between both distributions is shown on top
Our approach correctly adjusts the P-value to the number of miRNAs involved (see Fig. 1C). As CUPID uses a meta-analysis strategy on individual gene–miRNA–gene triplets (Chiu et al., 2015) to obtain one P-value for a set of miRNAs per gene–gene interaction, we sought to compare to such an approach for our measure. We used Fisher’s popular meta-analysis approach to combine P-values (Fischer, 1925) of individual miRNA triplets. Figure 2B shows that aggregated P-values tend to be considerably higher in meta-analysis, illustrating the loss of information and sensitivity compared to assessing significance in a joint model via mscor.
Our simulation suggested that ranking ceRNA interactions by the scor or mscor values would introduce a bias towards interactions with low gene–gene correlation (see Fig. 1C). In Figure 2C, we compared the gene–gene correlation values of the top 5% ceRNA interactions sorted according to mscor with our FDR corrected set of ceRNA interactions. Paci et al. (2014) used 5% as an arbitrary cutoff. We observed that SPONGE selected ceRNA interactions showed significantly higher gene–gene correlation values on average (t-test P-value < 2.2e–16) underlining that sorting without proper correction leads to a bias.
3.3 Runtime comparison with a conditional mutual information-based approach
CMI is an alternative to partial correlation for estimating the effect and significance of a gene–miRNA–gene interaction. We compared the performance of JAMI (Hornakova et al., 2018), a fast implementation of the CMI-based approach of CUPID (Chiu et al., 2015), and SPONGE on a subset of the pan-cancer dataset. Figure 3 illustrates that the SPONGE workflow can be computed fast even for large sample numbers and large number of triplets, while the runtime of JAMI increases dramatically due to the need to rank expression values and due to computationally intensive permutations that are needed for assessing the significance of CMI values. In addition, SPONGE does normally not evaluate each triplet individually, but considers all shared miRNAs in a joint model, giving rise to an additional speedup. SPONGE is thus uniquely suited to infer a genome-wide ceRNA network even on large-scale datasets such as the TCGA pan-cancer data.
Fig. 3.
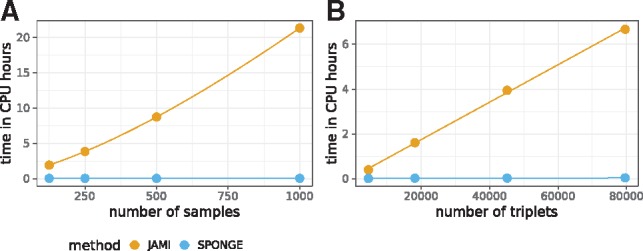
Runtime comparison between SPONGE and JAMI, a fast method for computing ceRNA interactions based on CMI. (A) Runtime for varying number of samples on a fixed set of ca. 80 000 triplets. (B) Runtime for varying number of triplets on a fixed number of samples. Time was measured in CPU hours (y-axis)
3.4 The empirical null model allows strict control over the false positive rate
To study ceRNA interactions in a pan-cancer setting, we applied SPONGE to paired miRNA and gene expression data for 10 019 samples from TCGA (see Section 2) combining data from 31 cancer types. A comprehensive set of putative miRNA–gene interactions was obtained by combining several sources: sequence-based predictions from TargetScan (Agarwal et al., 2015) and miRcode (Jeggari et al., 2012) as well as experimentally validated miRNA–gene interactions from mirTarBase (Chou et al., 2016) and LncBase (Paraskevopoulou et al., 2016).
Considering all possible pairwise combinations of genes, ca. 109 putative ceRNA interactions can be formed. Figure 4 shows how the three-step approach of SPONGE reduces this large set of putative interactions. In the first step, condition-specific gene–miRNA interactions are inferred, which reduces the set of considered ceRNA interactions to 108. However, many of these denote spurious ceRNA interactions that do not pass our selected significance threshold (FDR < 1e–5) in the second filter step. Finally, ca. 106 significant ceRNA interactions are predicted by SPONGE and used to construct a pan-cancer ceRNA interaction network.
Fig. 4.

Analysis of SPONGE ceRNA interactions on the pan-cancer dataset. Barplots show the number of interactions (y-axis) that are initially analyzed (grey), obtained after the regression filter (Step 1) and after computing mscor values and FDR correction of empirical P-values (Step 3). The analysis is shown for miRNA–gene relationships for which miRNA binding sites (seeds) have been predicted (orange bars) and for a large set of true-negative miRNA–gene relationships, investigating miRNAs without seed matches in a given gene (blue bars)
SPONGE estimates ceRNA interaction significance based on simulated null distributions. To determine if this estimation is accurate when applied to real data, we devised a random scenario in which SPONGE should not be able to find significant interactions. We devised a true-negative setting by using only miRNAs as features for a particular gene, which do not have a predicted miRNA binding site in the target gene in any of our considered databases, i.e. miRNAs that have no seed match in the gene (blue bars, Fig. 4). Here only 66 interactions remained significant. Thus, our assumed FDR < 1e–5 appears conservative, which demonstrates the efficacy of SPONGE in filtering for significant miRNA-mediated interactions between genes.
3.5 Pan-cancer ceRNA network analysis
After demonstrating that most of the ceRNA interactions in the pan-cancer network are statistically sound, we proceeded with a more detailed analysis. After processing expression data from 60 498 genes and 2463 mature miRNAs, SPONGE reported 95 541 095 gene–gene interactions after step one from which we retained 914 165 at an FDR threshold of 1e−5 (Fig. 4). 16 935 genes participated in ceRNA cross-talk with a median of 29 interactions per gene and a median of six miRNAs per ceRNA interaction with a maximum of 36 miRNAs per interaction. Table 1 shows the number of genes in different Ensembl gene categories, highlighting that ceRNA interaction is not limited to protein-coding genes with a 3’ UTR. Interestingly, we found a large number of pseudogenes in this pan-cancer analysis, including the two previously reported pseudogenes PTENP1 and BRAFP1 (Sanchez-Mejias and Tay, 2015).
Table 1.
Number of genes participating in significant ceRNA pan-cancer interactions (FDR < 1e−5) divided by Ensembl gene type
| Gene type | Number of genes |
|---|---|
| Protein coding | 12 776 |
| Pseudogenes | 1529 |
| lincRNA | 1086 |
| Antisense | 1025 |
| Processed transcript | 207 |
| Sense intronic | 69 |
| Sense overlapping | 67 |
We further investigated which microRNAs facilitate ceRNA cross-talk by counting how many interactions they participate in. These results are shown in Supplementary Figure S2. Our results highlight that a few miRNAs mediate most of the ceRNA interactions in the network. We observe that these miRNAs have comparably high expression levels, which is in line with what we would expect since ceRNA competition only plays a role if sufficient miRNA copies are present in a cell.
The ceRNA network is based on the pan-cancer TCGA dataset which contains cancer as well as tumor-adjacent samples. To identify which of the key ceRNA regulators are associated with cancer, we filtered for genes which showed high mean expression levels (TPM > 100) and were differentially expressed between cancer and tumor-adjacent samples [t-test, FDR < 0.01 (Benjamini and Hochberg, 1995) and log2 fold change > 1]. Our rationale was to determine genes that are present at sufficient copy numbers to exert cell-relevant ceRNA effects concentrated on genes that are overexpressed in the pan-cancer samples, thus likely mediating oncogenic effects. A total of 141 unique genes were obtained using these criteria (Supplementary Table S1). The 10 genes with the highest number of interactions are shown in Table 2 and in Figure 5.
Table 2.
Top 10 ceRNA regulating genes with highest node degree among genes differentially expressed between cancer and tumor-adjacent samples
| Ensembl gene id | HGNC gene symbol | Degree | |
|---|---|---|---|
| 1 | ENSG00000038427 | VCAN | 1135 |
| 2 | ENSG00000113810 | SMC4 | 923 |
| 3 | ENSG00000166851 | PLK1 | 812 |
| 4 | ENSG00000115414 | FN1 | 698 |
| 5 | ENSG00000142945 | KIF2C | 519 |
| 6 | ENSG00000134013 | LOXL2 | 513 |
| 7 | ENSG00000141756 | FKBP10 | 481 |
| 8 | ENSG00000227036 | LINC00511 | 478 |
| 9 | ENSG00000258947 | TUBB3 | 433 |
| 10 | ENSG00000106089 | STX1A | 391 |
Note: The full table with 141 differentially expressed genes is shown in Supplementary Table S1.
Fig. 5.
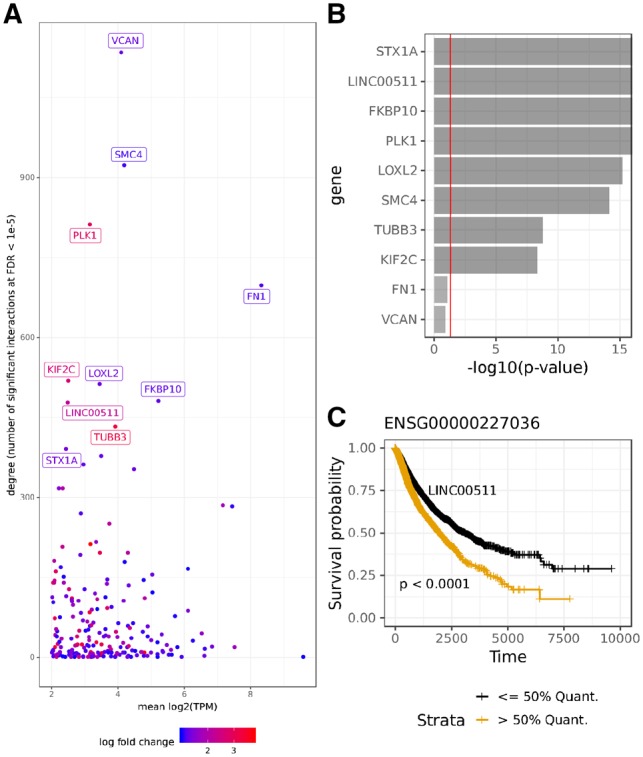
(A) Degree of ceRNA genes with mean expression (TPM > 100) and differential expression between cancer and tumor-adjacent samples (FDR < 0.01 and log fold change > 1). Number of ceRNA interactions (y-axis) is compared to mean expression (x-axis). Differential expression magnitude is shown as color code in the plot. (B) The 10 genes with highest degree ranked by their survival analysis P-value. (C) Kaplan Meier survival plot of the non-coding RNA LINC00511
The gene with the largest number of significant ceRNA interactions is VCAN, which is an established ceRNA (Sanchez-Mejias and Tay, 2015; Tay et al., 2014). In fact, previous work has shown that overexpression of the VCAN 3’UTR sequence alone is able to induce cancer growth in liver cancer cells (Fang et al., 2013). Similarly FN1 is a known ceRNA (Sanchez-Mejias and Tay, 2015).
We used clinical data from TCGA to assess if the expression of the genes identified here is significantly associated with survival probability. Figure 5B shows that among the top 10 genes, 8 are significant (P < 0.05, see Section 2). Among all 141 genes in this analysis (Supplementary Table S1) we find a significant enrichment for survival related genes according to a hypergeometric test (P = 3.75e−10) comparing against the background of other genes.
An intriguing candidate in this list is the linc-RNA LINC00511, which has the highest expression of all non-coding genes in this set and is associated with survival (Fig. 5C). Interestingly, a recent paper has shown that LINC00511 is an oncogenic ceRNA and regulates VEGFA gene expression in pancreatic adenocarcinoma (Zhao et al., 2018). Further, it was found that LINC00511 is a ceRNA for E2F1 and is involved in breast cancer tumourigenesis (Lu et al., 2018). Also, it was found that LINC00511 drives tumourigenesis in non-small-cell lung cancer (Sun et al., 2016). This suggests that LINC00511 is an oncogenic ceRNA that plays an important role in diverse cancer types, as experimental evidence for LINC00511 mediated ceRNA regulation in two cancers already exists. Thus, LINC00511 qualifies as an interesting pan-cancer drug target.
4 Discussion
We identified two major obstacles that prevent the efficient inference of a comprehensive genome-wide ceRNA interaction network. One of the first approaches, CUPID (Chiu et al., 2015; Hornakova et al., 2018; Sumazin et al., 2011), does not scale to the genome-wide level (see Fig.3) due to the use of permutation-based empirical P-value computation for establishing significance and the complexity of estimating CMI. Partial correlation-based approaches employing scor (Paci et al., 2014), on the other hand, are fast but do not accurately determine significance of the estimated effects.
To overcome these two issues, we designed an efficient empirical P-value computation approach by sampling from null models that describe the random distribution of mscor values. Moreover, this approach enabled us to accommodate possible biases introduced by several parameters, namely the number of samples, the gene–gene correlation and the number of shared miRNAs. Our results highlight that the current practice of ranking ceRNA interactions by scor coefficients introduces a bias towards gene pairs with low correlation, which are also more abundant. Furthermore, it became evident that scor cannot be directly compared across datasets with different sample numbers, suggesting that previous studies on unbalanced datasets, where ceRNA network comparisons between cancer and related normal samples were conducted, have likely been biased. We note that null model-based significance analysis is fast, which entails that SPONGE can compute P-values at high numerical precision (P > 1e−6) compared to permutation-based approaches that often limit precision (P > 1e−3) due to excessive runtime.
In this work we have presented a statistical approach to jointly estimate the significance of multiple miRNAs in a ceRNA interaction between two genes. Most genes are regulated by several miRNAs and it can thus be expected that potential ceRNA interaction partners share more than one miRNA between them. This suggests that there is an advantage in considering joint effects of several miRNAs. As far as we are aware only CUPID considers such combinatorial effects when using paired expression data. However, CUPID integrates these effects at the level of triplets, where P-values of triplets involving the same genes are pooled (Chiu et al., 2015), which, as we have shown, results in a loss of sensitivity (Fig. 2B). In contrast, our approach captures the contribution of several miRNAs and their co-expression in a single mathematical model. To this end, we extended the concept of sensitivity correlation to multiple miRNA sensitivity correlation (mscor).
To make this approach broadly available, we developed SPONGE, a R/Bioconductor package which provides a general framework for analyzing sensitivity correlation beyond its current application in ceRNA network inference. SPONGE enabled us to construct the first pan-cancer ceRNA network that systematically infers interactions between all genes within a few days on a typical compute cluster. Notably, close to 16 000 genes are involved in ceRNA regulation. Roughly 12 000 of these are protein-coding genes highlighting that this is a genome-wide phenomenon as proposed by Salmena et al. (2011) and not limited to non-coding RNAs. However, association may not be confused with causation. We cannot rule out that some of the effects we observe are caused by the activity of the proteins encoded by the tested ceRNA genes. For instance, transcription factors or RNA binding proteins may affect the expression of ceRNA interaction partners directly or indirectly.
To further investigate to what extend our results are biased by non-miRNA-mediated regulatory effects, we conducted an in silico control experiment where we observed that almost no significant ceRNA interactions remained when miRNAs were tested for which an actual regulation is unlikely as they have no seed match in either of the genes. This suggests that the majority of SPONGE reported ceRNA interactions can be attributed to miRNA-based association.
Network analysis in which we focused on genes that show moderate to high average expression and that are differentially expressed between cancer and tumor-adjacent samples revealed ceRNA genes with hundreds of interactions, many of which also show a significant association with survival probability. Our findings suggest that many protein-coding genes auch as VCAN and FN1 have an additional regulatory function as a ceRNA. Moreover, SPONGE suggests ceRNA regulation as a potential mechanism to explain why non-coding RNAs such as LINC00511 have a significant impact on survival. This straight-forward analysis thus illustrates the potential of ceRNA networks for hypothesis generation and biomarker discovery.
We note that results might vary depending on the choice and quality of miRNA target interaction databases. To alleviate this issue, we selected datasets based on sequence-based predictions as well as experimentally validated miRNA target interactions. Most of the sequence-based prediction methods focus exclusively on the 3’ UTR of protein-coding genes for detecting miRNA binding sites. Our results indicate that non-coding RNAs make a substantial contribution to miRNA cross-talk such that future miRNA-target annotations should be adapted.
It is important to emphasize that statistical significance does not equal biological relevance. While we have ensured that the pan-cancer ceRNA interactions predicted in this work are likely true associations with respect to our model and its assumptions, understanding which of those individual interactions are of physiological relevance, is another important problem. Large-scale validation of ceRNA interactions is challenging and new methods are needed. One interesting approach is the work by Rzepiela et al., in which miRNA target sensitivity values were estimated using mathematical modelling of miRNA overexpression coupled to single cell expression analyses and may provide a way to prioritize ceRNA targets of functional biological relevance (Rzepiela et al., 2018).
5 Conclusion and outlook
The TCGA pan-cancer analysis performed here provides unique insights into global ceRNA cross-talk in cancer. However, cancer-specific networks will be needed to draw a more comprehensive map of ceRNA regulation where sophisticated network alignment methods are employed to reveal commonalities and differences between cancer types. Generating paired gene and miRNA expression data for healthy tissues in databases like GTEx (Lonsdale et al., 2013) will become crucial for gaining an understanding of tissue-specific ceRNA cross-talk which will in turn present a baseline for detecting cancer-specific aberrations in the network presented here. Recently, single cell protocols that facilitate measurements of multi-omics have become available (Macaulay et al., 2017). We envision that a protocol supporting parallel measurement of microRNA and gene expression will particularly benefit from fast correlation-based approaches like SPONGE for celltype-specific ceRNA network inference.
In many genes, alternative splicing gives rise to a large number of transcripts, many of which differ strongly in their expression. Some of these transcripts are not translated and vary in the miRNA binding sites they carry. Thus, similar to transcripts originating from non-coding genes, they have no apparent biological role but may potentially contribute to ceRNA cross-talk. Considering transcript-level expression data will improve the quality of ceRNA network inference and allow for identifying disease-relevant changes in alternative splicing that act through ceRNA effects.
Note that, to our knowledge, we have devised the first generalized algorithm for sampling covariance matrices in which the partial correlation is equal to the correlation. We envision that this might be relevant beyond the inference of ceRNA interaction networks with possible applications in other scientific disciplines.
Supplementary Material
Acknowledgements
We thank Tariq Khaleeq for sharing his initial work on applications of partial correlation to TCGA data. We thank the contributors of the TCGA consortium. We thank Alexandra K. Kiemer, Stephan Laggai, Sonja M. Kessler and Christina S. Schultheiss for inspriring discussions.
Funding
This work was supported by the DZHK (German Centre for Cardiovascular Research, 81Z0200101). DK was supported by NIH R01GM115836.
Conflict of Interest: none declared.
References
- Agarwal V. et al. (2015) Predicting effective microRNA target sites in mammalian mRNAs. eLife, 4, e05005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arvey A. et al. (2010) Target mRNA abundance dilutes microRNA and siRNA activity. Mol. Syst. Biol., 6, 363.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartel D.P. (2009) MicroRNA target recognition and regulatory functions. Cell, 136, 215–233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y., Hochberg Y. (1995) Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodological), 57, 289–300. [Google Scholar]
- Chiu H.S. et al. (2015) Cupid: simultaneous reconstruction of microRNA-target and ceRNA networks. Genome Res., 25, 257–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou C.-H. et al. (2016) miRTarBase 2016: updates to the experimentally validated miRNA-target interactions database. Nucleic Acids Res., 44, D239–D247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Z. et al. (2016) Integrative analyses reveal a long noncoding RNA-mediated sponge regulatory network in prostate cancer. Nat. Commun., 7, 10982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang L. et al. (2013) Versican 3’-untranslated region (3’-UTR) functions as a ceRNA in inducing the development of hepatocellular carcinoma by regulating miRNA activity. FASEB J., 27, 907–919. PMID: 23180826. [DOI] [PubMed] [Google Scholar]
- Fischer R. (1925) Statistical Methods for Research Workers. Oliver and Boyd, Edinburgh. [Google Scholar]
- Fisher R.A. (1915) Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika, 10, 507. [Google Scholar]
- Friedman J. et al. (2010) Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw., 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
- Friedman R.C. et al. (2009) Most mammalian mRNAs are conserved targets of microRNAs. Genome Res., 19, 92–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman M. et al. (2018) The UCSC Xena Platform for cancer genomics data visualization and interpretation. bioRxiv. doi: 10.1101/326470. https://xena.ucsc.edu/ [Google Scholar]
- Hornakova A. et al. (2018) JAMI-Fast computation of Conditional Mutual Information for ceRNA network analysis. Bioinformatics, 34, 3050–3051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaskiewicz L. et al. (2012) Argonaute CLIP–a method to identify in vivo targets of miRNAs. Methods, 58, 106–112. [DOI] [PubMed] [Google Scholar]
- Jeggari A. et al. (2012) miRcode: a map of putative microRNA target sites in the long non-coding transcriptome. Bioinformatics, 28, 2062–2063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeyapalan Z. et al. (2011) Expression of CD44 3’-untranslated region regulates endogenous microRNA functions in tumorigenesis and angiogenesis. Nucleic Acids Res., 39, 3026–3041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Q. et al. (2009) miR2Disease: a manually curated database for microRNA deregulation in human disease. Nucleic Acids Res., 37, D98–D104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- John B. et al. (2004) Human MicroRNA Targets. PLoS Biology, 2, [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karreth F.A. et al. (2015) The BRAF pseudogene functions as a competitive endogenous RNA and induces lymphoma in vivo. Cell, 161, 319–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S. (2015) ppcor: an R package for a fast calculation to semi-partial correlation coefficients. Commun. Stat. Appl. Methods, 22, 665–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le T.D. et al. (2016) Computational methods for identifying miRNA sponge interactions. Brief. Bioinf., 18, bbw042. [DOI] [PubMed] [Google Scholar]
- Li J.-H. et al. (2014) starBase v2.0: decoding miRNA-ceRNA, miRNA-ncRNA and protein? RNA interaction networks from large-scale CLIP-Seq data. Nucleic Acids Res., 42, D92–D97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C. et al. (2017) Cancer-related triplets of mRNA–lncRNA–miRNA revealed by integrative network in uterine corpus endometrial carcinoma. BioMed Res. Int., 2017, 3859582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lonsdale J. et al. (2013) The Genotype-Tissue Expression (GTEx) project. Nat. Genet., 45, 580.EP –. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu G. et al. (2018) Long noncoding RNA LINC00511 contributes to breast cancer tumourigenesis and stemness by inducing the miR-185-3p/E2F1/Nanog axis. J. Exp. Clin. Cancer Res., 37, 289289–289289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macaulay I.C. et al. (2017) Single-cell multiomics: multiple measurements from single cells. Trends Genet., 33, 155–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muniategui A. et al. (2012) Quantification of miRNA-mRNA Interactions. PLoS One, 7, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muniategui A. et al. (2013) Joint analysis of miRNA and mRNA expression data. Brief. Bioinf., 14, 263.. [DOI] [PubMed] [Google Scholar]
- Paci P. et al. (2014) Computational analysis identifies a sponge interaction network between long non-coding RNAs and messenger RNAs in human breast cancer. BMC Syst. Biol., 8, 83.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paraskevopoulou M.D. et al. (2016) DIANA-LncBase v2: indexing microRNA targets on non-coding transcripts. Nucleic Acids Res., 44, D231–D238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinzón N. et al. (2017) microRNA target prediction programs predict many false positives. Genome Res., 27, 234–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poliseno L. et al. (2010) A coding-independent function of gene and pseudogene mRNAs regulates tumour biology. Nature, 465, 1033–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers J.T. et al. (2016) Multiple mechanisms disrupt the let-7 microRNA family in neuroblastoma. Nature, 535, 246–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rzepiela A.J. et al. (2018) Single-cell mRNA profiling reveals the hierarchical response of miRNA targets to miRNA induction. Mol. Syst. Biol., 14, e8266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salmena L. et al. (2011) A ceRNA hypothesis: the Rosetta Stone of a hidden RNA language? Cell, 146, 353–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Mejias A., Tay Y. (2015) Competing endogenous RNA networks: tying the essential knots for cancer biology and therapeutics. J. Hematol. Oncol., 8, 3030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schulz M.H. et al. (2013) Reconstructing dynamic microRNA-regulated interaction networks. Proc. Natl. Acad. Sci. USA, 110, 15686–15691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumazin P. et al. (2011) An extensive MicroRNA-mediated network of RNA–RNA interactions regulates established oncogenic pathways in glioblastoma. Cell, 147, 370–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun C.-C. et al. (2016) Long intergenic noncoding RNA 00511 acts as an oncogene in non-small-cell lung cancer by binding to EZH2 and suppressing p57. Mol. Ther. Nucleic Acids, 5, e385–e385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tay Y. et al. (2014) The multilayered complexity of ceRNA crosstalk and competition. Nature, 505, 344.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Therneau,T.M. and Grambsch,P.M. (2000) Modeling Survival Data: Extending the Cox Model. Springer, New York.
- Tsang J.S. et al. (2010) Genome-wide dissection of microRNA functions and co-targeting networks using gene-set signatures. Mol. Cell, 38, 140–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vivian J. et al. (2017) Toil enables reproducible, open source, big biomedical data analyses. Nat. Biotechnol., 35, 314–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J. et al. (2010) CREB up-regulates long non-coding RNA, HULC expression through interaction with microRNA-372 in liver cancer. Nucleic Acids Res., 38, 5366–5383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang P. et al. (2015) Identification of lncRNA-associated competing triplets reveals global patterns and prognostic markers for cancer. Nucleic Acids Res., 43, 3478–3489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J. et al. (2015) The mRNA related ceRNA–ceRNA landscape and significance across 20 major cancer types. Nucleic Acids Re., 43, 8169–8182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J. et al. (2017) Inferring miRNA sponge co-regulation of protein-protein interactions in human breast cancer. BMC Bioinformatics, 18, 243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. et al. (2016) Comprehensive characterization of lncRNA–mRNA related ceRNA network across 12 major cancers. Oncotarget, 7, 64148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao X. et al. (2018) Linc00511 acts as a competing endogenous RNA to regulate VEGFA expression through sponging hsa-miR-29b-3p in pancreatic ductal adenocarcinoma. J. Cell. Mol. Med., 22, 655–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



