Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2019 Jul 5;35(14):i354–i359. doi: 10.1093/bioinformatics/btz395

ShaKer: RNA SHAPE prediction using graph kernel

Stefan Mautner 1, Soheila Montaseri 1, Milad Miladi 1, Martin Raden 1, Fabrizio Costa 2, Rolf Backofen 1,3,✉
PMCID: PMC6612843  PMID: 31510707

Abstract

Summary

SHAPE experiments are used to probe the structure of RNA molecules. We present ShaKer to predict SHAPE data for RNA using a graph-kernel-based machine learning approach that is trained on experimental SHAPE information. While other available methods require a manually curated reference structure, ShaKer predicts reactivity data based on sequence input only and by sampling the ensemble of possible structures. Thus, ShaKer is well placed to enable experiment-driven, transcriptome-wide SHAPE data prediction to enable the study of RNA structuredness and to improve RNA structure and RNA–RNA interaction prediction. For performance evaluation, we use accuracy and accessibility comparing to experimental SHAPE data and competing methods. We can show that Shaker outperforms its competitors and is able to predict high quality SHAPE annotations even when no reference structure is provided.

Availability and implementation

ShaKer is freely available at https://github.com/BackofenLab/ShaKer.

1 Introduction

Secondary structure plays an important role for the function of RNA molecules. The conservation of secondary structure is a central feature to determine classes of non-coding RNAs consisting of molecules that have similar structure and function (Bateman et al., 2017; Miladi et al., 2017; Will et al., 2007). In contrast, the importance of structure for mRNA function is less well understood. While there are well-known examples for structured RNA elements in the 5' and 3' untranslated regions with regulatory roles, the situation is more complex for the coding region. Albeit ribosomes show helicase activity, and thus active translation leads to transient unfolding of the mRNA structure, there is evidence for a regulatory role of mRNA structure (Rice et al., 2018).

For that reason, it would be advantageous to know the structure of (m)RNA on a genome-wide level to study such effects. SHAPE-seq (SHAPE=Selective 2′-hydroxyl acylation analyzed by primer extension) experiments offer an approach to investigate mRNA structure on such a large scale (Choudhary et al., 2017; Katrina and Alain, 2017; Rouskin et al., 2014; Zubradt et al., 2017). In such an experiment, free nucleotides of a (folded) RNA are exposed to an acylation process that stops the polymerase in the subsequent sequencing step. Based on that, a reactivity estimation is calculated for each nucleotide. This SHAPE data encode the ‘structuredness’ of the molecule. There are similar experimental methods to SHAPE. One of them is DMS (Russell et al., 2007) which uses dimethyl sulfate to experimentally probe the accessibility of cytosine and adenine only.

While SHAPE experiments showed that mRNA is frequently structured, they often lacked quantitative precision and coverage to determine mRNA structure on an individual gene level. An exception is a recent work by Mustoe and co-workers (Mustoe et al., 2018), who showed translational efficiency is correlated with mRNA structure. Thus so far there is a lack of suitable experimental data, which calls for computational methods to model the missing RNA structure information. Thermodynamic approaches like Mfold (Zuker, 2003) or RNAfold (Lorenz et al., 2011), while successful for short RNAs, have problems in modeling the structure of longer RNAs and especially for mRNAs. Local approaches (Hofacker et al., 2006; Lange et al., 2012) do improve this situation, however, mRNA structure is still very challenging for thermodynamic approaches. In order not to do SHAPE experiment for each RNA, a couple of computational methods were developed to approximate SHAPE information. Sükösd et al. (2013) estimated probability distribution functions for the nucleotides in unpaired, stacked and helix-end regions based on the experimental SHAPE data on two long ribosomal RNAs in the mentioned regions. Another method (Montaseri et al., 2017) is based on k-mers of RNA sequence on helices, loops and the helices that comprise pseudoknot regions as their SHAPE are obtained as the average of available SHAPE data on RNAs in the above regions. In these methods, the real structure of an RNA (or a respective prediction using a thermodynamic model) is required to decompose the given sequence into the mentioned regions and subsequently estimate its SHAPE data.

To the authors’ knowledge, there exists no method to learn and predict SHAPE data on RNA sequences without known structures. For that reason, we set out to predict an RNA’s SHAPE information from its sequence only, using a machine learning approach. We present a new tool called ShaKer, ‘SHAPE prediction using graph Kernel’, which is trained on available experimental SHAPE data to approximate SHAPE experiments in silico. In transcriptome-wide high-throughput studies, for instance, reactivities cannot be obtained if the RNA is not (highly) expressed/transcribed within the cell. For such cases, ShaKer can be trained on other expressed RNAs and used to predict missing data. Furthermore, such in silico SHAPE data might also be useful to improve the prediction of intra-molecular structure (Hajdin et al., 2013; Montaseri et al., 2016) as well as RNA–RNA interaction (Miladi et al., 2019).

To evaluate ShaKer’s performance, we compare its predicted SHAPE information to experimental data and to results from purely thermodynamic modeling when no reference structure is available. ShaKer outperforms the unguided thermodynamic predictions both in terms of accessibility as well as base-pair accuracy. These results suggest that the thermodynamic model may not be sufficient to reflect all the relevant energy terms for the identification of RNA’s functional structure. Furthermore, we compare ShaKer with the approach from Sükösd et al. for given reference structures. Also here, ShaKer shows superior results in both categories. This demonstrates that ShaKer is able to model highly accurate SHAPE information and is well placed to support RNA structure studies with missing information. Since we learn ShaKer’s model from experimental data, the steady growth of available SHAPE experiments will further improve its prediction accuracy.

2 Materials and methods

2.1 Definitions

An RNA sequence is a word over the alphabet of nucleotides {A, C, G, U}. Here, we consider the base pairings AU, CG and GU as complementary. An RNA secondary structure S is a list of pairs of indices that indicate complementary base pairs in the RNA sequence. Each nucleotide can only participate in one base pairing. W.l.o.g., we restrict the base pairs of S to be non-crossing, i.e. there are no two base pairs (i, j), (i′,j′)∈S such that one is not enclosed by the other (i<i′<j<j′). The free energy E(S) of such a secondary structure S can be estimated using the Nearest Neighbor model and experimentally derived parameters (Turner and Mathews, 2010). A reference structure is a structure that was manually curated based on literature. RNA’s SHAPE data are a vector of non-negative real numbers, which assigns to each nucleotide position the respective reactivity estimate.

2.2 Graph processing

In order to encode RNA secondary structure for our machine learning approach, we encode them as labeled graphs. A graph consists of edges (E) and vertices (V) and their labels. The RNA-graph is generated as follows. First, we use the sequence to generate a path graph, where the vertices are labeled according to the nucleotides in the sequence. The edges of the path graph are labeled as ribose-phosphate backbone. Second, we encode the structure by introducing edges between the vertices that correspond to a base pair and label them as hydrogen bond.

Graph kernels, typically used to calculate the distance between graphs, enable graphs to be used with kernelized machine learning methods like support vector machines. The Neighborhood Subgraph Pairwise Distance Kernel (NSPDK) of the ‘EDeN’ package (Costa and Grave, 2010) allows us to extract feature vectors for every node in a graph. NSPDK is a Weisfeiler–Lehman kernel (Leeuwen, 2011), except that it does not only consider the immediate neighborhood of a vertex but considers pairs of neighborhoods of vertices in close proximity. The neighborhood of a vertex is the subgraph that is induced by all vertices that are within a certain number of edges. The NSPDK graph kernel has two main parameters r for the radius of the neighborhood subgraphs and distance d for the maximum distance between neighborhood subgraphs. For a given node v, the following features are extracted

{h(hg(Ns(v)),hg(Ns(w)))|s∈{0..r}∧w∈V ∧ distance(v,w)≤d}.

Where h is a hash function, hg a hash function on graphs and Ns extracts the neighborhood subgraph of a vertex. The size of the resulting vector depends on the bit-length of the hash function h, resulting in a feature vector of size 2bit−length.

2.3 RNA structure and probability estimation

For predicting SHAPE reactivities, we rely both on experimental SHAPE training data as well as secondary structure. In our context it is adequate to work with the structures that are most likely to occur in the thermodynamic model. Conveniently, the ViennaRNA package (Lorenz et al., 2011) provides tools for secondary structure prediction under minimization of the free energy of a given sequence using the nearest neighbor energy models. We use RNAfold to calculate free energy EM of the structure ensemble M and RNAsubopt to sample structures S from M according to their Boltzmann probability. The latter is given by P(S)=exp(−E(S)/RT)/Z, where T denotes the temperature, R the gas constant and Z the ensemble’s partition function computed by −RT log(EM).

2.4 Regression model

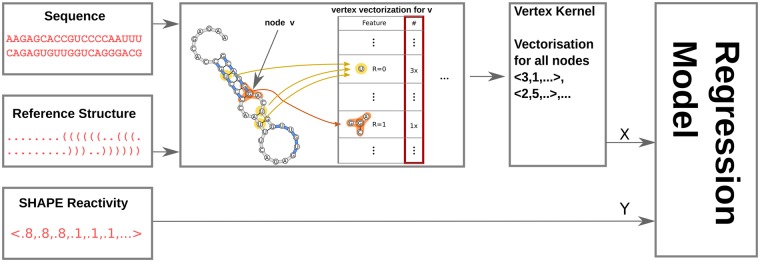
Model training. Gradient tree boosting (Chen and Guestrin, 2016) is an ensemble-based machine learning method that improves on random forest by taking previously trained trees in account. We use a regressor based on this method and train it on experimental SHAPE reactivity values and the feature vectors obtained by vectorizing the vertices of the reference structure induced RNA-graph with the EDeN graph kernel to predict SHAPE values. For each vertex there is exactly one feature vector. See Figure 1 for an overview of this process. In practice, SHAPE annotations can be unavailable for individual positions. Whenever the reactivity annotation for a nucleotide is missing, that vertex is ignored for training.

Fig. 1.

Fig. 1.

Open in a new tab

Schema of the training process. The input data are triplets of sequence, a reference structure and SHAPE reactivity values for the nucleotides in the sequence. We combine the sequence and the structure to form an RNA-graph. Each vertex in the graph is vectorized such that there is one vector per vertex. The vectors are the input and the associated reactivity values the targets for the regressor to train on

Reactivity prediction. Figure 2 shows how we use these tools to estimate SHAPE data for a given sequence of length n. The m structures and the associated probabilities are sampled as described previously. We call the unit norm of the probabilities π. From the sequence and the structures we generate m RNA-graphs whose vertices are vectorized by the graph kernel. Using the trained model, SHAPE reactivities are predicted. Since every nucleotide in the sequence has now m predictions, one corresponding to each RNA structure graph, we compute a weighted average of the reactivities with the probability vector of the sampled structures. This is done by multiplying the n × m matrix of predictions by vector π.

Fig. 2.

Fig. 2.

Open in a new tab

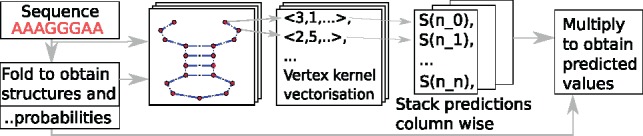
SHAPE reactivity prediction. (left) For a given sequence, possible structures are sampled. Respective Boltzmann probabilities form the unit probability vector π which has as many entries as there were structures sampled. (middle) RNA-graphs of the structures are vectorized and we use the model to predict a SHAPE (S) value for each nucleotide (n_x). We stack the predictions for each graph column wise. (right) We obtain as many predictions for every nucleotide in the sequence as there are sampled structures. We weight these by the probabilities of the structure to obtain the final prediction i.e. we multiply the matrix of predictions with π

Eventually, we are thereby combining the standard thermodynamic model (used for structure sampling and probability computation) with our model trained on experimental SHAPE data. The resulting combined reactivities are thus not biased toward a single (arbitrary) user-provided structure [as done in Sükösd et al. (2013) and Montaseri et al. (2017)] but are guided by the structural ensemble that can be formed by the sequence.

2.5 Hyperparameter optimization

For EDeN we tested parameters r and d in the range of 0.4. We used 16-fold cross-validation on the 16 sequences with a random forest regressor and compared the Spearman’s correlation with the experimental data to determine the best configuration. The default values, 3 and 3, performed best. For the regressor, we generated RNA-graphs from all 16 sequences and vectorized all vertices to obtain a joint dataset. Random search with 3-fold cross-validation was performed to obtain our final parameters. Optimal parameters for RNAsubopt were inspired by Deforges et al. (2017). Namely we sample 60 structures with a maximum base-pair range of 150.

2.6 Software and data

ShaKer is implemented in Python and freely available at github. ShaKer depends on several libraries e.g. NetworkX (Daniel et al., 2008), Matplotlib (Hunter, 2007) and Scikit-learn (Pedregosa et al., 2011).

All data used in this work are made available in an accessible format in our ShaKer github repository. The input is in a single ‘.dbn’ file which is a FASTA file where each sequence is followed by a dot-bracket-string line and a ‘.react’ file that contains a sequence name header followed by pairs of nucleotide position and SHAPE reactivity value.

3 Results

Our ShaKer method predicts SHAPE reactivities for any RNA sequence employing a regression model. The model is based on a graph-kernel encoding secondary structure and is trained on a dataset of RNA sequences with experimentally determined SHAPE reactivities. The main advantage compared to previous approaches is that it does not require a reference structure for the prediction step, which implies that it can be used on RNA with unknown structure.

We tested ShaKer by analyzing the publicly available SHAPE (Deigan et al., 2009; Hajdin et al., 2013; Montaseri et al., 2017) dataset to evaluate the quality of SHAPE reactivity prediction for RNAs with unknown reference structure. Furthermore, we also compared ShaKer to the Sükösd et al. method (Sükösd et al., 2013) and to the thermodynamics-based predictions by RNAfold. The method by Sükösd et al. uses the reference structure and annotates the strength of reactivity using different precalculated probabilistic models for bound and unbound nucleotides. We use the median performance of five runs on the Sükösd et al. method. Our method does not require a reference structure to predict the reactivity profile. However, the prediction quality is necessarily better when using a reference structure as prior information. For that reason, when comparing to Sükösd et al., we provide only the RNA-graph induced by the reference structure to guarantee a fair comparison. The method of Sükösd et al. was derived from SHAPE data of ribosomal RNA; we use the ribosomal RNA in our dataset for training and the rest for testing.

3.1 Accessibility correlation

SHAPE reactivities are a proxy for accessibility of nucleotides. Although it is feasible to directly compare the reactivity vectors of the experimental and predicted SHAPE reactivities, it is more desirable to compare the resulting accessibility profiles as they are directly interpretable. This evaluation is also more reliable than a direct comparison of SHAPE profiles due to the stochastic nature of the structure probing experiments and experiment-specific biases. To make the evaluations comparable between SHAPE values obtained from separate experiments with different conditions, we chose to compare the performances over the SHAPE-assisted accessibility predictions.

Accessibility, also termed unpaired probability, calculates the probability that sequence nucleotides are unpaired across the ensemble of possible structure formations. The accessibility for a given RNA sequence can be predicted using RNAplfold (Lorenz et al., 2016). RNAplfold has two modes for predicting accessibility. The first mode is relying purely on the thermodynamic model for RNA secondary structure. In the second mode, SHAPE data are used as an additional input to assist the prediction of accessibility. Technically, this is solved by transforming SHAPE data into pseudo-energy terms that are used in the evaluation of secondary structures (Deigan et al., 2009; Zarringhalam et al., 2012). The second mode is preferable as accessibility induced by experimental SHAPE data is our best estimation of the true accessibility and thus considered as the ground truth.

We evaluated how simulated SHAPE data improves the prediction of accessibility compared to the pure thermodynamic model. To compare the accessibility of a transcript, we calculate the accessibility profiles using different prediction methods and compare these profiles to the profile generated from SHAPE data using RNAplfold which uses the SHAPE-assisted mode as ground truth. The prediction performance is then assessed using Spearman’s rank correlations against the ground truth. We also report the standard deviation after a ‘±’. The mean can be found before this symbol and marked with a white circle in the figures. As shown in Figure 3, the prediction results by our ShaKer tool induce a better average correlation to the ground truth (0.895 ± 0.18) compared to Sükösd et al. (0.87 ± 0.17) even in the case of a known structure.

Fig. 3.

Fig. 3.

Open in a new tab

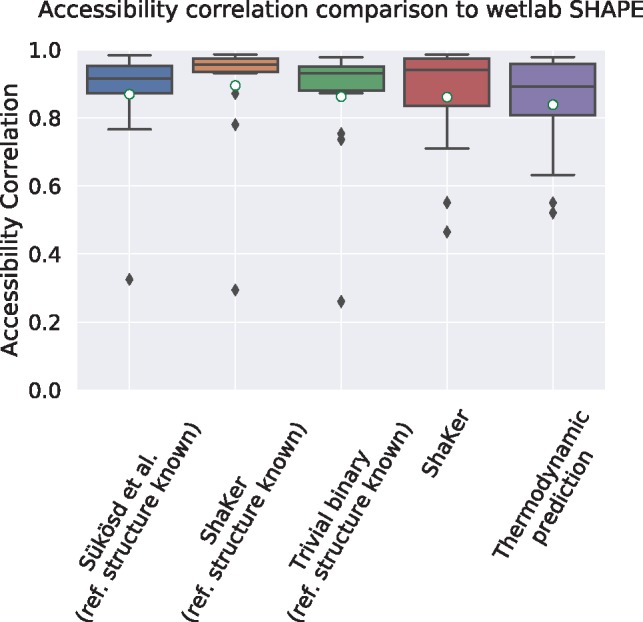
Correlation of accessibility profiles by RNAplfold using predicted SHAPE reactivities compared to the accessibility profile generated from experimental SHAPE data. The first three prediction methods are using a manually curated reference structure. Because of this prior information, all prediction tools result in a high correlation to the profile generated from experimental SHAPE data. The final two plots evaluate the situation for the more realistic application scenario where no reference structure is given. In this case, only ShaKer without structure and RNAplfold without SHAPE data can be compared. The predicted SHAPE data by ShaKer leads to an improved result compared to the pure thermodynamic prediction (mean 0.861±0.17 versus 0.839±0.16)

Since the accessibility is the probability of a position to be unpaired, it is a quantity that is related to the ensemble of all structures. Nevertheless, the reference structure usually has a high weight in the structure ensemble and should dominate accessibility values. To test this role of the reference structure as prior information, one can read off reactivities directly from the reference structure by assigning 1 to an unpaired nucleotide and 0 otherwise. In this case one does not need to consider the scale as RNAplfold will normalize the values. We call this the trivial binary predictor. It scores slightly worse than Sükösd et al. (0.86 ± 0.19), which shows that a given reference structure already provides a strong prior information.

For that reason, we compared the prediction quality for the more realistic case where the reference structure is not given. When the reference structure is not provided to the algorithm, we can only compare to the thermodynamic model since we already used the experimental SHAPE data to compute the reference accessibility and we are not aware of alternative tools. Here, we get an improvement of 2.6% (0.861 ± 0.17 versus 0.839 ± 0.16). This might seem like a small amount, but the folding process also takes into account the sequence, limiting the effect of the SHAPE data on the correlation.

3.2 Base-pair accuracy

One application for SHAPE data is the determination of functionally relevant secondary structure. Providing a folding algorithm with accurate SHAPE data should guide the prediction tool toward the manually curated reference structure. One could use the predicted minimum free energy structure for comparison, however, this would ignore predicted suboptimal structures in the vicinity of the reference structures. Thus, in order to compare a reference structure to a predicted structure ensemble, Lange et al. (Lange et al., 2012) introduced a measure similar to the maximum expected accuracy scoring for structure prediction. Here, the accuracy A of a reference structure in a predicted ensemble of structures is the sum of all probabilities for the base pairs of the reference structure:

A(Sl|R)=∑S|Sl∩S|·P(S|R)=∑(i,j)∈Slp(i,j)

We calculate the probability of a base pair (i, j) under SHAPE input with the Vienna tool set (Lorenz et al., 2011) and report the average to account for varying sequence length.

In Figure 4, we see the evaluations according to the base-pair accuracy metric. When the reference structure is provided to the programs ShaKer (0.892 ± 0.096) performs slightly (1.9%) better than Sükösd et al. (0.875 ± 0.113). Our simulation when the reference structure is not available scores a mean accuracy of 0.679 ± 0.26 while the thermodynamic model alone performs lower with 0.629 ± 0.21. This is significant because it shows that you can use ShaKer to find potentially biologically relevant structures. Since we did not need to resort to using the wet lab data as ground truth, we included it in the evaluation. With 0.73 ± 0.29 it scores better than ShaKer.

Fig. 4.

Fig. 4.

Open in a new tab

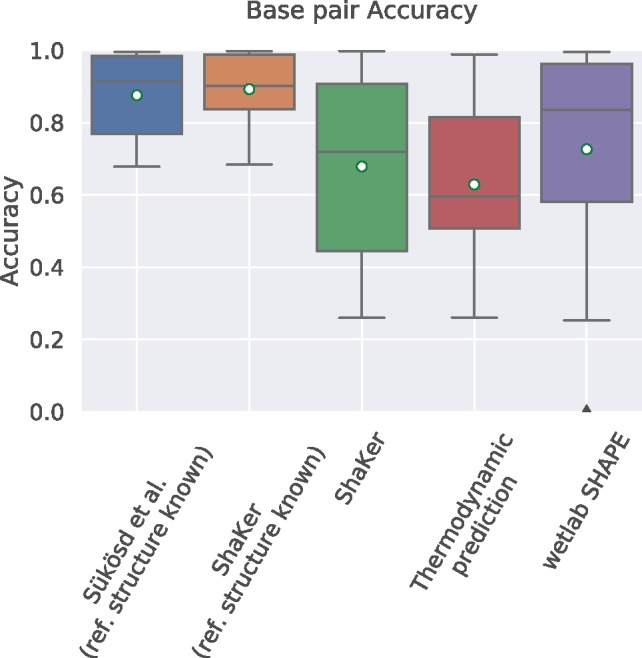
Comparison of base-pair accuracy. Accuracy is the average probability of all base pairs in a single structure over the whole ensemble of possible structures. This structure is the reference structure in this case. We expect good SHAPE data to support the reference structure. In this test ShaKer performs significantly better than the thermodynamic model alone. The experimental data outperform both, which is a testament to its quality. Given the reference structure Sükösd et al. and ShaKer perform even better than SHAPE data which is not surprising since we evaluated for exactly that reference structure. ShaKer performs slightly better than Sükösd et al.

3.3 Structured versus unstructured

The benefits of our method are that we work on structured data and perform structure sampling while Sükösd et al. annotates based on single nucleotides. K-mer approaches are popular in bioinformatics and have a wide array of applications. One could see a k-mer approach as a combination of ShaKer and Sükösd et al. It could learn a sequence bias and quickly annotate sequences without requiring the reference structure.

By supplying ShaKer with path graphs only when training and predicting, we effectively mimic a gapped k-mer algorithm. Intuitively, choosing a vertex in a sequence path graph and its neighbors at distance 1 is effectively the same as selecting a 3-mer from the sequence. Figure 5 shows the performance of ShaKer in this configuration. Structured ShaKer (0.85 ± 0.15) clearly outperforms the unstructured version (0.74 ± 0.24).

Fig. 5.

Fig. 5.

Open in a new tab

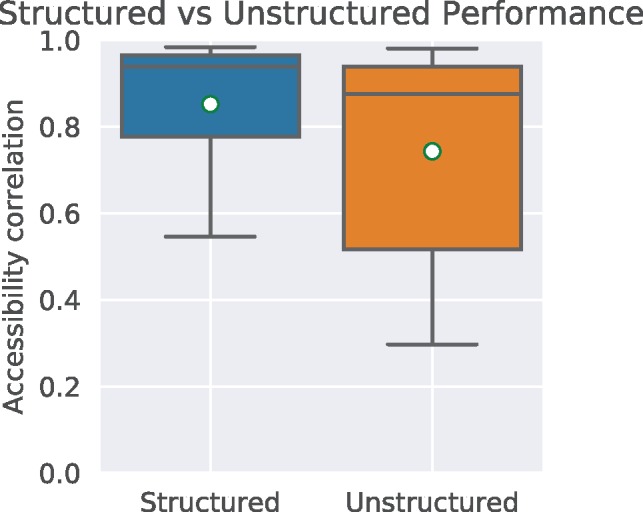
Comparison of ShaKer using structures i.e. RNA-graphs as described earlier and ShaKer using sequence data only. For the unstructured mode, we trained ShaKer on the RNA-graphs but omitted the hydrogen bond edges. Subsequently when predicting, we only predicted on the sequence graph without structure sampling. This effectively mimics gapped k-mers, a popular technique in bioinformatics

4 Discussion

Structure prediction for mRNAs has a limited quality as the transcript is often bound by RNA-binding proteins in vivo. Here, SHAPE-seq experiments offer an approach to investigate mRNA structure on such a large scale. The collected SHAPE reactivities can be used to guide the structure prediction toward the functional structure. However, SHAPE-seq data are limited and will not be available for many organisms or tissues. One way to overcome this problem is to use predicted SHAPE reactivities learned from SHAPE-seq data instead of experimental ones.

We presented ShaKer to predict SHAPE reactivity on arbitrary RNA sequences. In comparison to existing methods as e.g. Sükösd et al. (Sükösd et al., 2013), we do not rely on a manually curated secondary structure for the input RNA. Thus, it can be applied to a large class of RNA sequences with unknown structures. Our ShaKer method learns the association of secondary structure elements and reactivity in a regression approach using a graph kernel to represent secondary structures. To abstract from individual structures, we sample the possible structure space and weight the considered structures with respective Boltzmann probabilities.

For the comparison of the ShaKer method with other tools, we did not compare SHAPE profiles directly but relied on biologically more relevant information for the comparison, namely the accessibility profiles and the base-pair accuracy of the reference structure within the SHAPE-guided predicted structure ensemble. SHAPE reactivities are considered a proxy for the accessibility of positions, which is important information as it provides e.g. hints for binding sites of RNA-binding proteins.

We compared ShaKer with the tool presented by Sükösd et al. (Sükösd et al., 2013) as it established a state-of-the-art SHAPE prediction tool. The latter requires a single input structure. Thus we also only use the reference structure for ShaKer predictions. That way, we compare the predictive power of the learned models. Albeit the secondary structure as prior information already provides a lot of information about accessibility, we were able to improve the already good results by Sükösd et al. by 2.9%.

Our ShaKer approach is, in contrast to Sükösd et al., per se able to predict SHAPE reactivities in the absence of prior information about the structure. This is done by applying our model (trained on experimental SHAPE data) to a sampled set of secondary structures for the given sequence weighted by respective structure probabilities. We show that this approach provides a much better accessibility prediction compared to the pure thermodynamic accessibility profiles as calculated by RNAplfold (+2.6%). The improvement is even more visible when comparing the base-pair accuracy for known reference structures when using RNAplfold with or without ShaKer-predicted SHAPE reactivities (+7.9%). This shows that constraints implied by the ShaKer-predicted reactivities guide structure prediction toward the functional secondary structure. This results from the conversion of the reactivity data into pseudo-energy terms that are extending the thermodynamic model for structure prediction (Lorenz et al., 2016). Thus we conclude that the high-level structure information learned by ShaKer from experimental SHAPE data (in combination with structural ensemble information) implicitly mends the underlying energy model to reflect more complex rules for improved secondary structure prediction.

Next, we will investigate the impact of ShaKer reactivities on sRNA target prediction using IntaRNA (Mann et al., 2017), which is able to incorporate SHAPE structure probing data into RNA–RNA interaction prediction (Miladi et al., 2019).

Finally, ShaKer could be trained on SHAPE experiments under different experimental conditions (such as in vivo or cell-free), and thus can also investigate the effects of these different conditions on other RNAs with unknown SHAPE reactivities.

Funding

This work was supported by the German Research Foundation (DFG) [BA2168/16-1, BA2168/3-3] and Germany’s Excellence Strategy (CIBSS – EXC-2189 – Project ID 390939984).

Conflict of Interest: none declared.

References

  1. Bateman A. et al. (2017) Rfam 13.0: shifting to a genome-centric resource for non-coding RNA families. Nucleic Acids Res., 46, D335–D342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Chen C., Guestrin T. (2016) XGBoost: a scalable tree boosting system. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. pp. 785–794.
  3. Choudhary K. et al. (2017) Comparative and integrative analysis of RNA structural profiling data: current practices and emerging questions. Quant. Biol., 5, 3–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Costa F., Grave K.D. (2010) Fast neighborhood subgraph pairwise distance kernel. In: Proceedings of the 27th International Conference on International Conference on Machine Learning. pp. 255–262. Omnipress.
  5. Daniel A.S. et al. (2008) Exploring network structure, dynamics, and function using NetworkX. In: Proceedings of the 7th Python in Science Conference (SciPy2008). pp. 11–15.
  6. Deforges J. et al. (2017) Two ribosome recruitment sites direct multiple translation events within HIV1 Gag open reading frame. Nucleic Acids Res., 45, 7382–7400. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Deigan K.E. et al. (2009) Accurate SHAPE-directed RNA structure determination. Proc. Natl. Acad. Sci. USA, 106, 97–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hajdin C.E. et al. (2013) Accurate SHAPE-directed RNA secondary structure modeling, including pseudoknots. Proc. Natl. Acad. Sci. USA, 110, 5498–5503. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hofacker I.L. et al. (2006) Local RNA base pairing probabilities in large sequences. Bioinformatics, 22, 614–615. [DOI] [PubMed] [Google Scholar]
  10. Hunter J.D. (2007) Matplotlib: a 2D graphics environment. Comput. Sci. Eng., 9, 90–95. [Google Scholar]
  11. Katrina M.K., Alain L. (2017) Transcending the prediction paradigm: novel applications of SHAPE to RNA function and evolution. Wiley Interdiscip. Rev. RNA, 8, e1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lange S.J. et al. (2012) Global or local? Predicting secondary structure and accessibility in mRNAs. Nucleic Acids Res., 40, 5215–5226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Leeuwen E.J.v. et al. (2011) Weisfeiler-Lehman graph kernels. J. Mach. Learn. Res., 12, 2539–2561. [Google Scholar]
  14. Lorenz R. et al. (2011) ViennaRNA package 2.0. Algorithms Mol. Biol., 6, 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lorenz R. et al. (2016) SHAPE directed RNA folding. Bioinformatics, 32, 145–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Mann M. et al. (2017) IntaRNA 2.0: enhanced and customizable prediction of RNA-RNA interactions. Nucleic Acids Res., 45, W435–W439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Miladi M. et al. (2019) Integration of accessibility data from structure probing into RNA-RNA interaction prediction. Bioinformatics doi:10.1093/bioinformatics/bty1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Miladi M. et al. (2017) RNAscClust: clustering RNA sequences using structure conservation and graph based motifs. Bioinformatics, 33, 2089–2096. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Montaseri S. et al. (2016) Evolutionary algorithm for RNA secondary structure prediction based on simulated SHAPE data. PLoS One, 11, e0166965.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Montaseri S. et al. (2017) Evaluating the quality of SHAPE data simulated by k-mers for RNA structure prediction. J. Bioinform. Comput. Biol., 15, 1750023.. [DOI] [PubMed] [Google Scholar]
  21. Mustoe A.M. et al. (2018) Pervasive regulatory functions of mRNA structure revealed by high-resolution SHAPE probing. Cell, 173, 181–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Pedregosa F. et al. (2011) Scikit-learn: machine learning in Python. J. Mach. Learn. Res., 12, 2825–2830. [Google Scholar]
  23. Rice G.M. et al. (2018) Pervasive regulatory functions of mRNA structure revealed by high-resolution SHAPE probing. Cell, 173, 181–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Rouskin S. et al. (2014) Genome-wide probing of RNA structure reveals active unfolding of mRNA structures in vivo. Nature, 505, 701–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Russell R. et al. (2007) DMS footprinting of structured RNAs and RNA-protein complexes. Nat. Protoc., 2, 2608–2623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Sükösd Z. et al. (2013) Evaluating the accuracy of SHAPE-directed RNA secondary structure predictions. Nucleic Acids Res., 41, 2807–2816. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Turner D.H., Mathews D.H. (2010) NNDB: the nearest neighbor parameter database for predicting stability of nucleic acid secondary structure. Nucleic Acids Res., 38, D280–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Will S. et al. (2007) Inferring non-coding RNA families and classes by means of genome-scale structure-based clustering. PLoS Comput. Biol., 3, e65.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Zarringhalam K. et al. (2012) Integrating chemical footprinting data into RNA secondary structure prediction. PLoS One, 7, e45160.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Zubradt M. et al. (2017) DMS-MaPseq for genome-wide or targeted RNA structure probing in vivo. Nat. Methods, 14, 75–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Zuker M. (2003) Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res., 31, 3406–3415. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES