Integrating read-based and population-based phasing for dense and accurate haplotyping of individual genomes

Abstract

Motivation

Reconstruction of haplotypes for human genomes is an important problem in medical and population genetics. Hi-C sequencing generates read pairs with long-range haplotype information that can be computationally assembled to generate chromosome-spanning haplotypes. However, the haplotypes have limited completeness and low accuracy. Haplotype information from population reference panels can potentially be used to improve the completeness and accuracy of Hi-C haplotyping.

Results

In this paper, we describe a likelihood based method to integrate short-range haplotype information from a population reference panel of haplotypes with the long-range haplotype information present in sequence reads from methods such as Hi-C to assemble dense and highly accurate haplotypes for individual genomes. Our method leverages a statistical phasing method and a maximum spanning tree algorithm to determine the optimal second-order approximation of the population-based haplotype likelihood for an individual genome. The population-based likelihood is encoded using pseudo-reads which are then used as input along with sequence reads for haplotype assembly using an existing tool, HapCUT2. Using whole-genome Hi-C data for two human genomes (NA19240 and NA12878), we demonstrate that this integrated phasing method enables the phasing of 97–98% of variants, reduces the switch error rates by 3–6-fold, and outperforms an existing method for combining phase information from sequence reads with population-based phasing. On Strand-seq data for NA12878, our method improves the haplotype completeness from 71.4 to 94.6% and reduces the switch error rate 2-fold, demonstrating its utility for phasing using multiple sequencing technologies.

Availability and implementation

Code and datasets are available at https://github.com/vibansal/IntegratedPhasing.

1 Introduction

Humans are diploid and haplotype phasing—determination of the sequence of alleles at variant sites on homologous chromosomes—is an important problem in human genomics. Haplotype information is crucial for a number of analyses including identification of genetic variants associated with disease (e.g. compound heterozygotes), detection of IBD (Identity by Descent) segments and genotype imputation (Tewhey et al., 2011). Haplotypes are not directly observed from genotyping or short-read sequencing but can be inferred either directly (using long sequence reads for an individual genome) or indirectly (using a reference panel of haplotypes). A number of algorithms and statistical methods have been developed for haplotype inference from genotype data (Browning and Browning, 2011). Nevertheless, population-based phasing is limited in accuracy for rare variants and in regions with high haplotype diversity in the human genome.

Read-based haplotype phasing is a direct approach for phasing individual genomes and there is increasing interest in haplotype-resolved whole-genome sequencing (Snyder et al., 2015). Read-based phasing is feasible using long reads such as those generated using single molecule sequencing technologies such as Pacific Biosciences (Pendleton et al., 2015). Sequence reads that cover multiple variants provide partial haplotype information and can be assembled into longer haplotypes using computational methods (Levy et al., 2007). To address the computational problem of haplotype assembly, a number of combinatorial and statistical algorithms (Aguiar and Istrail, 2012; Bansal and Bafna, 2008; Duitama et al., 2010; Kuleshov, 2014) have been developed. At the same time, a number of methods that encode long-range haplotype information in short reads and generate virtual long reads have been developed (Duitama et al., 2012; Kitzman et al., 2011; Kuleshov et al., 2014; Peters et al., 2012).

Haplotype assembly is also feasible with paired-end sequencing—pairs of short reads derived from the ends of DNA fragments—but requires long and variable insert lengths to assemble long haplotypes. Hi-C sequencing generates paired-end reads with insert sizes ranging from a few hundred bases to tens of megabases. Selvaraj et al. (2013) exploited this property of Hi-C reads to assemble accurate haplotypes for NA12878 using ∼18 × Illumina whole-genome sequencing. In contrast to haplotyping using long reads which generates 10–100s of disjoint haplotype segments per chromosome, more than 90% of variants phased using Hi-C are connected in a single chromosome-spanning block. Although Hi-C based haplotypes span entire chromosomes, the completeness of the haplotypes is rather low [only 18–22% of the variants per chromosome could be phased using the Hi-C reads (Selvaraj et al., 2013)]. A second limitation is the relatively low accuracy [switch error rate of 1–2% compared to other methods (Edge et al., 2017)]. The low resolution of Hi-C haplotypes is due to non-uniformity in sequence coverage resulting from the use a DNA restriction enzyme in the Hi-C library preparation protocol. Recently, Edge et al. (2017) showed using Hi-C data generated using the MboI restriction enzyme can be used to assemble haplotypes with 65% completeness compared to ∼20% completeness using the HindIII enzyme.

Hi-C sequencing leverages the Illumina technology and does not require specialized equipment unlike other sequencing-based haplotyping methods such as 10X Linked-reads (Zheng et al., 2016). Therefore, improving the completeness and accuracy of Hi-C haplotyping can enhance the use of this approach for phasing human genomes. Similar to Hi-C-based haplotyping, the Strand-seq single-cell sequencing method also generates sparse chromosome-spanning haplotypes (Porubsky et al., 2016). Another singe-cell based haplotyping method, SISSOR, also generates highly accurate haplotypes but with 70% resolution (Chu et al., 2017). One avenue for improving accuracy and completeness is to combine sequence data from multiple technologies. Edge et al. (2017) combined Hi-C data with 10X Linked-read data to assemble haplotypes with very high resolution and low switch error rates. Similarly, Porubsky et al. (2017) showed that combining Strand-seq haplotypes with long-read sequence information enables the reconstruction of dense, chromosome-spanning haplotypes. Ben-Elazar et al. (2016) described a novel algorithmic framework to combine short-range haplotypes with Hi-C reads for phasing. Nevertheless, all of these methods requires sequencing using two or more technologies, and may not be feasible for all genomes.

An alternative approach that does not require additional sequencing is to leverage haplotype information from population reference panels to complement haplotype information of sequence reads. Selvaraj et al. (2013) combined Hi-C haplotypes with statistical phasing to improve the completeness of haplotypes to ∼81%. Kuleshov et al. (2014) developed a statistical method to combine read-based haplotype information with population phase information to improve the contiguity of haplotypes from long reads. Similarly, Delaneau et al. (2013) extended their statistical phasing method (SHAPEIT2) to incorporate haplotype information from sequence reads. They demonstrated that this reduced the switch error rate, particularly for rare variants. However, it is not clear if the Markov model underlying this method can incorporate the long-range haplotype information present in Hi-C reads.

In this paper, we describe a new likelihood based method that integrates long-range haplotype information from sequence reads with short-range haplotype information from population reference panels to dramatically improve the accuracy and completeness of haplotyping human genomes using methods such as Hi-C. Our approach leverages the existing likelihood based method HapCUT2 for read-based haplotype phasing. To incorporate population haplotype information, we use the statistical phasing method SHAPEIT2 to sample haplotypes consistent with the individual’s genotypes and approximate the population haplotype likelihood as a product of second-order distributions. Subsequently, pseudo-reads are used to encode the approximate population likelihood and used as input along with sequence reads for phasing using HapCUT2 (Edge et al., 2017).

We have used this integrative phasing method to investigate the improvement in completeness and accuracy of Hi-C haplotyping using whole-genome sequence data for two different individuals from the 1000 Genomes Project: NA19240 (YRI population) and NA12878 (CEU population). For both these genomes, we demonstrate that our method improves the completeness of haplotypes [>98% single nucleotide variants (SNVs) phased] and reduces the switch error rate by 3–6-fold. We also show that a recent multi-enzyme Hi-C protocol enables the phasing of ∼86.7% of SNVs using Illumina whole-genome sequencing with 36× coverage. In addition, we use whole-genome Strand-seq data to show that our integrated phasing method can improve the completeness and accuracy of haplotyping for any sparse sequencing method.

2 Materials and methods

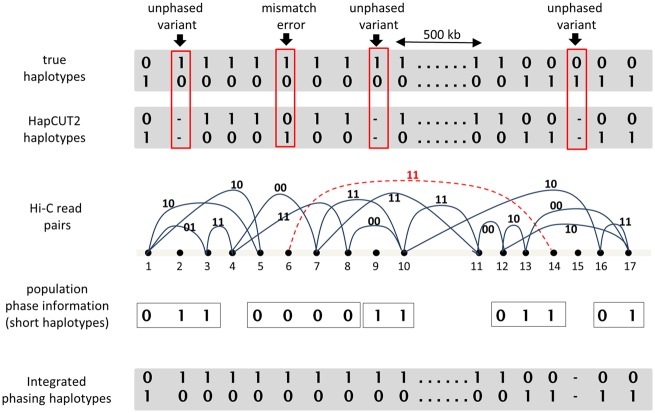
Comparison of Hi-C haplotypes to high-confidence haplotypes (for the NA12878 genome) shows that the vast majority of errors are local errors where a single variant or a small block of variants is incorrectly phased with respect to the chromosome-spanning haplotype block (Edge et al., 2017). Given an individual’s genotypes, one can infer haplotypes using information from a population reference panel (Delaneau et al., 2013). These population-based haplotypes are highly accurate in short blocks (30–100 kb) and provide haplotype information that is complementary to Hi-C sequence reads. Therefore, leveraging haplotype information from population reference panels has great potential to improve the completeness and accuracy of haplotyping using methods such as Hi-C (see Fig. 1 for an illustration). Since sequence reads contain errors (e.g. trans errors in Hi-C) and population-based haplotype information has ambiguity in regions with high population diversity, a probabilistic approach for combining the two sources of haplotype information is needed. Therefore, we consider a joint likelihood model for individual haplotyping that combines the two independent sources of haplotype information.

Fig. 1.

Integrating haplotype information from Hi-C reads and population reference panels to improve accuracy and completeness of haplotyping. Haplotypes assembled using HapCUT2 from Hi-C reads have three unphased variants (2, 9 and 15) and an incorrectly phased variant (#6) with respect to the large haplotype block due to an erroneous Hi-C read (edge connecting variants 6 and 14). Haplotypes estimated using a population reference panel provide accurate short-range phase information. This information can be combined with the Hi-C reads to phase two of the three variants with no sequence information and also correct the phase for variant #6

2.1 Joint likelihood model for haplotyping

We assume that the variants (and genotypes) to be phased are known in advance and only consider heterozygous variants for phasing. For read-based phasing or haplotype assembly, the objective is to find the most likely pair of haplotypes (H = (H¹, H²)) for an individual genome given the genotypes G, aligned sequence reads R and the corresponding set of base error probabilities Q for the reads. In population-based phasing, the goal is to find the most likely pair of haplotypes given the genotypes and a reference panel of population haplotypes (H^p). A joint likelihood based formulation for haplotyping is:

$$\underset{H}{\max }P\left(H||R,Q,H^p\right).$$

We can assume that the reads for the individual are conditionally independent of the haplotypes for other individuals, given H. Under this assumption, it has previously been shown that the joint likelihood can be decomposed as a product of two terms (Delaneau et al., 2013):

$$P\left(H||R,Q,H^p\right)\propto P\left(R||H,Q\right)P\left(H||H^p\right).$$ (1)

The $P\left(R\right|H,Q)$ term corresponds to the read-based likelihood and the $P\left(H\right|H^p)$ is the population-based likelihood of a pair of haplotypes H conditional on the reference panel of haplotypes. The read-based likelihood is simply a product of individual read likelihoods defined as:

$$P\left(R||H,Q\right)=\prod _{r\in R}\frac{P\left(r||H^1,Q\right)+P\left(r||H^2,Q\right)}{2},$$

where $P\left(r\right|H^1,Q)$ and $P\left(r\right|H^2,Q)$ can be calculated using the base error probabilities of the reads as follows:

$$P\left(r||h,Q\right)=\prod _j\left[\mathrm{\delta }\left(r_j,h_j\right)\left(1-{Q_j}^r\right)+\left(1-\mathrm{\delta }\left(r_j,h_j\right)\right){Q_j}^r\right],$$ (2)

where $\mathrm{\delta }(r_j,h_j)=1$ if r_j = h_j and 0 otherwise, and the product is over all variants covered j by the read r (Edge et al., 2017).

Unlike the read-based likelihood, there is no direct expression for the population-based likelihood$P\left(H\right|H^p)$. Different statistical phasing methods use different models for capturing the relationship between an individual’s haplotypes and the haplotypes in a population. SHAPEIT2, a state-of-the-art statistical phasing tool, uses a Markov model for modeling an individual’s haplotypes and utilizes an MCMC algorithm to sample from the posterior distribution of$P\left(H\right|H^p)$. We use the SHAPEIT2 algorithm to obtain haplotype samples from the probability distribution and use these samples to approximate the population haplotype likelihood using lower order distributions.

2.2 Approximating population haplotype likelihood using second-order distributions

We are given a sample of N haplotype pairs for n heterozygous variants for a single individual sampled from the probability distribution$P\left(H\right|H^p)$. Using these samples, it is difficult to estimate the full probability distribution since the number of potential haplotypes for an individual is exponential in n and much larger than N. Therefore, we approximate the probability distribution as a product of lower order distributions using the N samples. This allows us to calculate $P\left(H\right|H^p)$ for any haplotype pair H using a small number of samples. Since we are interested in obtaining short-range haplotype information from the population reference panel, this is a reasonable approximation. For example, given two variant sites x and y, there are only two possible phasings: (00, 11) and (01, 10). Let ${H_x}^1$ be the haplotype allele at variant x in haplotype H¹. We can use the N samples to estimate $P({H_x}^1=0,{H_x}^2=1|{H_y}^1=0,{H_y}^2=1)$ as follows:

$$P({H_x}^1=0,{H_x}^2=1|{H_y}^1=0,{H_y}^2=1)=\frac{c_{\mathit{xy}}\left(00\right)}{c_{\mathit{xy}}\left(00\right)+c_{\mathit{xy}}\left(01\right)},$$

where $c_{\mathit{xy}}\left(00\right)$ is the count of the pair 00 in the N samples at sites x and y. This is also equal to the probability of the phase being (00, 11). Also, $P\left({H_x}^1=1,{H_x}^2=0||{H_y}^1=0,{H_y}^2=1\right)=1-P({H_x}^1=0,{H_x}^2=1|{H_y}^1=0,{H_y}^2=1)$. We can approximate the full distribution as a product of n − 1 second-order distributions:

$$P\left(H||H^p\right)\approx P\left(H_{x_1}\right)\prod _{i=1}^{n-1}P\left(H_{x_{i+1}}||H_{x_i}\right),$$

where $(x_1,x_2,\dots ,x_n)$ is a permutation of the n variants. The number of possible permutations is exponential in n, so how we do choose the permutation for approximating the probability distribution? Chow and Liu (1968) have shown that it is possible to select the second-order approximation that has the minimum Kullback–Leibler distance to the full distribution and hence is the best approximation in the information-theoretic sense. The Chow–Liu algorithm reduces the problem of finding the best permutation or the optimal second-order approximation to finding the maximum spanning tree of a weighted graph where the nodes of the graph correspond to the n variants and the weight of an edge (x, y) is equal to the mutual information between the two variants:

$$I\left(H_x,H_y\right)=\sum _{H_x,H_y}P\left(H_{\mathit{xy}}\right)\hspace{0.17em}\text{log}\hspace{0.17em}\frac{P\left(H_{\mathit{xy}}\right)}{P\left(H_x\right)P\left(H_y\right)}.$$

We can estimate $P\left(H_{\mathit{xy}}\right)$ using the frequency of the pair H_xy in the N haplotype samples. Similarly, we can estimate $P\left(H_x\right)$ and $P\left(H_y\right)$ using the samples.

2.3 Encoding the population haplotype likelihood using pseudo-reads

Our objective is to find a haplotype pair that maximizes the product of the population-based haplotype likelihood $P\left(H\right|H^p)$ and read-based likelihood $P\left(R\right|H,Q)$ [Equation (1)]. HapCUT2 (Edge et al., 2017) uses a graph-cut based iterative method to search for a pair of haplotypes that maximizes$P\left(R\right|H,Q)$. To incorporate the population haplotype likelihood into HapCUT2, we encode each individual term $P\left(H_x\right|H_y)$ in the second-order approximation of $P\left(H\right|H^p)$ as a pseudo-read r with alleles r_x and r_y and base error probabilities q_x and q_y. The allele and error probabilities are chosen such that $P\left(r\right|H_{\mathit{xy}},q_x,q_y)=P(H_x\left|H_y\right)$ for any haplotype pair H. As a result, if we use these pseudo-reads as input to HapCUT2 along with the sequence reads, the likelihood function optimized by HapCUT2 is precisely equal to the product of the read-based likelihood and the second-order approximation of$P\left(H\right|H^p)$.

For this, we define $f_{\mathit{xy}}\left(00\right)=P({H_x}^1=0,{H_x}^2=1|{H_y}^1=0,{H_y}^2=1)$ and$\mathrm{ }{f}_{\mathit{xy}}\left(01\right)=1-f_{\mathit{xy}}\left(00\right)$. We also define $q=0.5-0.5\sqrt{\left|f_{\mathit{xy}}\right(00)-f_{\mathit{xy}}(01\left)\right|}$. Then, the pseudo-read r that covers the two variants x and y is defined as:

• If$\mathrm{ }{f}_{\mathit{xy}}\left(00\right)>f_{\mathit{xy}}\left(01\right)$: r_x = 0, r_y = 0, $q_x=q_y=q$

• else: r_x = 0, r_y = 1, $q_x=q_y=q$.

2.4 Integrated phasing method

Encoding the approximate population haplotype likelihood as pseudo-reads allows us to simply use these pseudo-reads along with the sequence reads as input to HapCUT2 for phasing. We use the Kruskal minimum spanning tree algorithm to find the optimal second-order approximation of the probability distribution. The full algorithm is outlined below:

1. Given individual genotypes G and population reference panel H^p, sample N haplotype pairs using the SHAPEIT2 MCMC method.

2. For each pair of variants (x, y), calculate $I(H_x,H_y)$ using the N samples.

3. Construct a weighted graph G with each variant as a node and the weight of the edge (x, y) = I(H_x, H_y).

4. Compute the maximum spanning tree of G.

5. For each edge in the maximum spanning tree, generate a pseudo-read r.

6. Run HapCUT2 with the sequence reads R and the pseudo-reads as input.

In Step 1, we sample N  = 1000 pairs of haplotypes. In Step 2, for a variant x, if we calculate I(H_x, H_y) for all other variants y, the complexity of the algorithm increases as$O\left(n^2\right)$. To reduce the running time, we compute I(H_x, H_y) only for k variants to the left and right of x where the variants are ordered by their location. We considered different values of k (5–30) and found that using values of k larger than 10 did not change the Minimum Spanning Tree (MST) since for most variants, edges to neighboring variants were selected (data not shown). Therefore, we use k  = 10 for phasing real data. We also remove all edges (x, y) from the graph for which q < 0.8 since these low-confidence edges are not reliable for phasing.

2.5 Measuring haplotyping accuracy

The accuracy of the haplotypes was measured using the switch error rate metric (Duitama et al., 2012; Edge et al., 2017; Kuleshov, 2014). The switch error rate is defined as the fraction of adjacent phased variants for which the phase is incorrect. Two consecutive switch errors correspond to the flipping of the phase of a single variant and are counted separately as a single ‘mismatch’ or short switch error. To calculate the absolute error rate (or the Hamming error rate) of the haplotypes, we compute the hamming distance between the estimated and true haplotypes and divide it by the total number of phased variants.

2.6 Datasets

We evaluated our integrated phasing method using whole-genome Hi-C data for two individuals from the 1000 Genomes Project: NA19240 (YRI population) and NA12878 (CEU population). For NA19240, whole-genome Hi-C data generated by the 1000 Genomes SV project (Clarke et al., 2017) for this individual was downloaded from SRA (project PRJEB11418, accessions ERX1299696-701) and aligned to the hg19 reference human genome sequence using BWA-MEM (option -SP5M). PCR duplicates were marked using the Picard tool (https://broadinstitute.github.io/picard/). The raw data contained 467 million read pairs with reads of length 100 bp. SNV calls from the 1000 Genomes Project were used for phasing and trio-based haplotypes were used for assessing accuracy for these data.

For the NA12878 genome, we utilized Hi-C datasets generated using two different protocols: (i) a multi-enzyme protocol developed by Arima Genomics (Ghurye et al., 2019) and (ii) MboI restriction enzyme based protocol (Rao et al., 2014). The Arima Hi-C dataset for NA12878 was downloaded from SRA (accession SRR6675327) and processed using the same pipeline as used for the NA19240 data. The read length for this dataset was 150 bp and the average depth of coverage was 36×. Similarly, reads for the MboI Hi-C data (Rao et al., 2014) (read length equal to 101 bp) were aligned to the reference genome using BWA-MEM and the aligned reads were down-sampled to match the coverage of the Arima Hi-C dataset. SNV calls generated using an independent Illumina WGS dataset (30× coverage) from the GIAB project (Zook et al., 2016) were used for phasing and high quality phased haplotypes from the Platinum Genomes Project (Eberle et al., 2017) were used for assessing the accuracy of phasing.

In addition, we also leveraged whole-genome Strand-seq data (Porubsky et al., 2016) for NA12878 for analysis. Aligned Strand-seq reads for 133 cells generated by Porubsky et al. (2017) were downloaded from Zenodo (doi: 10.5281/zenodo.830278) and two haplotype fragments were generated for each cell using the list of WC regions identified previously by Porubsky et al. (2016). This was done using the extractHAIRS module of HapCUT2 and a custom script.

The 1000 Genomes reference panel (Auton et al., 2015) (2504 individuals from 25 different populations) was used to estimate haplotypes for each genome using SHAPEIT2 and also to sample haplotype pairs. Since the NA12878 (CEU population) and NA19240 (YRI population) genomes are part of the 1000 Genomes panel, we excluded all individuals from the CEU and YRI populations in the reference panel to avoid any bias. For all datasets, only heterozygous SNVs were considered for phasing. HapCUT2 was run with default parameters. For processing Hi-C datasets, the option ‘−hic 1’ was used.

3 Results

3.1 Accurate haplotyping using Hi-C data for NA19240

First, we applied the integrated phasing method to whole-genome Hi-C data for NA19240. Using the Hi-C reads, 51.3% of the 50 763 SNVs (with heterozygous genotype) on chromosome 20 could be phased and the largest haplotype block contained 19.9% of the SNVs. Using the integrated phasing algorithm, 48 135 pseudo-reads were included for phasing along with the Hi-C reads. The resulting haplotypes covered 97.32% of the SNVs with 96.47% of the SNVs in the largest haplotype block. The haplotypes had very high accuracy with a switch error rate of 0.034% and a mismatch error rate equal to 0.266% (Table 1). Furthermore, the absolute error rate of the Hi-C haplotypes was 0.31% demonstrating that almost all of the errors were local (due to the incorrect phasing of a few variants relative to the chromosome spanning haplotype block).

Table 1.

Comparison of the phasing completeness and accuracy on whole-genome Hi-C data for NA19240

Method	SNVs phased (%)	Absolute error rate (%)	Switch error rate (%)	Mismatch rate (%)	Run time
Reads only	51.30	0.49	0.20	0.365	02:43
Integrated phasing	97.32	0.31	0.034	0.266	08:57
SHAPEIT2	98.67	42.1	0.27	0.76	04:57

Note: Results shown are from the analysis of chromosome 20 only. The run-time is reported as minutes:seconds.

For comparison, we used SHAPEIT2 to phase the SNVs using the 1000 Genomes haplotype reference panel. Phase-informative reads were extracted using the extractPIRs tool and were included for phasing using SHAPEIT2 (Delaneau et al., 2013). 98.67% of the SNVs were phased with a long switch error of 0.27% and a mismatch error rate equal to 0.76%. Although SHAPEIT2 phased more SNVs compared to the integrated phasing method, the switch error rate of the SHAPEIT2 haplotypes was almost 8-fold higher than the haplotypes assembled using the integrated phasing approach (Table 1). In addition, the SHAPEIT2 haplotypes had an absolute error rate of 42.1% due to the presence of long switch errors. As a result, these haplotypes cannot be used to reliably infer the phase between distant pair of variants.

3.2 Comparison of different Hi-C protocols on NA12878 genome

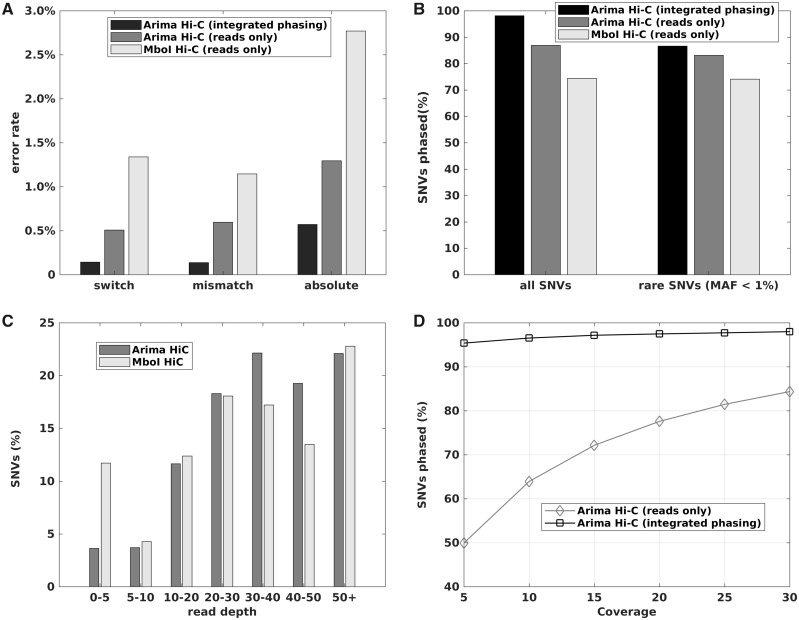
Next, we compared the accuracy and completeness of phasing using whole-genome Hi-C data for NA12878. 72.1% of SNVs (on chromosome 20) could be phased using the MboI Hi-C data with a switch error rate of 1.3% and a mismatch error rate of 1.1%. In comparison, 86.7% of the SNVs were phased by HapCUT2 using the Arima Hi-C reads with 2-fold lower switch and mismatch error rates (Fig. 2A). Furthermore, the largest haplotype block contained 80.92% of the SNVs. The greater completeness and accuracy of the haplotypes assembled using Arima Hi-C data was a result of the improved uniformity in sequence coverage. Analysis of the sequence data showed that 3.63% SNVs had less than 5 × coverage in the Arima Hi-C data. In comparison, the MboI Hi-C data had 11.7% SNVs with such low-coverage (Fig. 2C). Single-enzyme Hi-C using the MboI (or similar) restriction enzyme results in non-uniform sequence coverage due to the preference of the restriction enzyme for specific sequences. The Arima Hi-C protocol utilizes multiple restriction enzymes to digest chromatin which reduces the coverage bias.

Fig. 2.

Completeness and accuracy of haplotyping using Hi-C data for NA12878 (all statistics are for chromosome 20 only). (A) Error rates for haplotypes estimated using HapCUT2 on the MboI and Arima Hi-C datasets, and the integrated phasing algorithm applied to the Arima Hi-C data. (B) Haplotyping completeness (percentage of SNVs phased) across the three different methods. (C) Distribution of read-depth across SNV sites using the Arima and MboI Hi-C datasets (36× coverage). (D) Haplotype completeness for Arima Hi-C data as a function of sequence coverage

Phasing the Arima Hi-C data using the integrated phasing method increased the completeness to 98.14% from 86.7% and improved the accuracy of the haplotypes (Fig. 2). Using sequence reads, the ability to phase a variant does not depend on its population allele frequency but only on the number of links to other variants. Analysis of the phased SNVs showed that the integrated phasing method could phase 86.65% of the rare variants (minor allele frequency <1% in the 1000 Genomes reference panel), 3.5% points more than using Hi-C reads alone (Fig. 2B). This was not surprising, since using a population reference panel, rare variants are less likely to be phased compared to common variants. Analysis of phasing accuracy and completeness for all autosomes (chromosomes 1–22) demonstrated that the integrated phasing algorithm was able to phase 97.65% of SNVs with an average switch (mismatch) error rate equal to 0.038% (0.049%). In comparison, the switch and mismatch error rates using HapCUT2 on the Hi-C reads alone were 0.25 and 0.33% respectively, more than 6-fold higher.

To assess the ability to assemble haplotypes using low-coverage Hi-C data, we down-sampled the Arima dataset to various depths of coverage (5×, 10×, 15×, 20× and 30×) and calculated the completeness and accuracy of the haplotypes using HapCUT2 (reads only) and the integrated phasing method. The results (Fig. 2D) show that using Hi-C reads only, the completeness of the haplotypes increases gradually from 50 to 84.3% as coverage is increased from 5 × to 30 ×. In comparison, using the integrated phasing method, 96.6% of the SNVs can be phased with an absolute error rate of 1.1% at a coverage of 10×. This demonstrated that chromosome-spanning haplotypes with long-range accuracy can be assembled using low-coverage sequencing.

3.3 Analysis of Strand-seq data

Recently, Porubsky et al. (2016) developed a single-cell strand sequencing approach, Strand-seq, and showed that it enables accurate whole-chromosome phasing of diploid genomes. However, only 74.6% of SNVs could be phased for the NA12878 genome using 183 Strand-seq libraries (Porubsky et al., 2016). To assess if our new integrated phasing method could improve the completeness and accuracy of haplotyping using Strand-seq, we applied our method to this dataset.

After processing the raw data (see Section 2.6), 140 fragments were obtained for chromosome 20 and each fragment had allelic information for ∼750 SNVs (1.5% of the total number of heterozygous SNVs) on average. Using these fragments, 71.4% of the SNVs were phased into a single, chromosome-spanning haplotype block using HapCUT2. In comparison, using the integrated phasing method, 94.56% of the SNVs were phased and the chromosome-spanning haplotype block contained 94.1% of the SNVs. In addition, the mismatch error rate was reduced 2-fold, while the long switch error rate was also lower (Table 2). These results demonstrate that the integrated phasing method can significantly improve the completeness and accuracy of haplotyping for multiple sequencing technologies.

Table 2.

Phasing completeness and accuracy on whole-genome Strand-seq data for NA12878

Method	SNVs phased (%)	Switch error rate (%)	Mismatch error rate (%)	Absolute error rate (%)
Reads only	71.38	0.091	0.268	0.905
Integrated phasing	94.56	0.0364	0.134	0.868

Note: Results are shown for data on chromosome 20 only. Switch and mismatch error rates were calculated by comparison to Platinum Genomes haplotypes for NA12878.

4 Discussion

In this paper, we have described a novel likelihood based method that can integrate sparse, long-range haplotype information from sequence reads with haplotype information from population reference panels to enable dense and accurate whole-genome haplotyping of individual genomes. We have demonstrated that this approach significantly improves the completeness and accuracy of haplotype phasing using whole-genome Hi-C data for human genomes. We also find that a new multi-enzyme Hi-C chemistry developed by Arima Genomes significantly improves the completeness of whole-genome haplotyping compared to existing single-enzyme Hi-C data.

Using 30–40× Illumina whole-genome sequencing using the Arima Hi-C protocol, the integrated phasing method can assemble highly accurate and complete haplotypes for human genomes (>98% of variants phased and error rates <0.2%). Recent work (Porubsky et al., 2017) showed that combining data from 10 Strand-seq cells with 10 × Pacific Biosciences long read data was sufficient to phase more than 95% of variants into a single chromosome-spanning block. Here we have shown that it is possible to obtain dense and chromosome-spanning haplotypes with very low error rates using data from a single sequencing technology. Therefore, using low-coverage (∼10×) Hi-C sequencing for genomes in projects such as the Genotype-Tissue Expression (GTEx) project (Lonsdale et al., 2013) would be highly informative since it would provide accurate long-range haplotype information for eQTL mapping as well as information about the 3D structure of the genome.

Our integrated phasing method approximates the haplotype likelihood from a population reference panel using second-order probability distributions that capture the uncertainty in the phase information from population data and can be combined with sequence reads for phasing using HapCUT2. This approach is not limited to Hi-C data and we have shown that it improves the completeness and accuracy of phasing using another sparse haplotyping method, Strand-seq. For Hi-C data, our method significantly outperforms an existing statistical phasing method, SHAPEIT2, in terms of switch error rates. Even though this method can leverage haplotype information from sequence reads (Delaneau et al., 2013), our results indicate that SHAPEIT2 is unable to fully utilize the long-range haplotype information in Hi-C reads.

One limitation of our integrated phasing method is that the ability to phase rare variants that are not linked by sequence reads to other variants is limited by the size of the population reference panel. In this paper, we have used the 1000 Genomes Project reference panel which has haplotypes from 2504 individuals. Use of larger haplotype reference panels such as the recently published HRC panel (McCarthy et al., 2016) with 64 976 haplotypes will likely improve the ability to phase rare variants.