Enhancing the drug discovery process: Bayesian inference for the analysis and comparison of dose–response experiments

Abstract

Motivation

The efficacy of a chemical compound is often tested through dose–response experiments from which efficacy metrics, such as the IC₅₀, can be derived. The Marquardt–Levenberg algorithm (non-linear regression) is commonly used to compute estimations for these metrics. The analysis are however limited and can lead to biased conclusions. The approach does not evaluate the certainty (or uncertainty) of the estimates nor does it allow for the statistical comparison of two datasets. To compensate for these shortcomings, intuition plays an important role in the interpretation of results and the formulations of conclusions. We here propose a Bayesian inference methodology for the analysis and comparison of dose–response experiments.

Results

Our results well demonstrate the informativeness gain of our Bayesian approach in comparison to the commonly used Marquardt–Levenberg algorithm. It is capable to characterize the noise of dataset while inferring probable values distributions for the efficacy metrics. It can also evaluate the difference between the metrics of two datasets and compute the probability that one value is greater than the other. The conclusions that can be drawn from such analyzes are more precise.

Availability and implementation

We implemented a simple web interface that allows the users to analyze a single dose–response dataset, as well as to statistically compare the metrics of two datasets.

1 Introduction

Drug discovery is a highly multidisciplinary process that encompasses the domains of biology, chemistry, computer science and mathematics (Rudin, 2006). A relevant therapeutic target is first identified, then different experiments are set up to analyze its activity under various conditions (Szymański et al., 2011). Such an approach makes it possible to deploy research efforts in a relevant and precise way, as well as in a context where there is a demand and a need for novel therapies.

The drug discovery process generates a very large amount of data, which often makes it difficult to manage and analyze experiment results. Analyses are thus often limited and omit a large amount of information. Intuition hence plays an important role when interpreting the results which can easily lead to biased conclusions. This work aims at developing a methodology that addresses these important issues in the specific context of dose–response experiments.

1.1 Dose–response experiments

The technological and biomedical advancements made in recent years have helped to accelerate the drug discovery process. For a specific assay, various chemical compounds are tested in order to identify those capable of generating a satisfactory response. The studied response is specific to the assay setup and can represent inhibition of cell growth, proliferation of cells etc. High-throughput screening (HTS) allows to quantitatively characterize a very large number of compounds (several thousands per day) in an in vitro or in vivo setting. HTS also allows the rapid elimination of unfit compounds in the context of a specific study (Szymański et al., 2011).

Screen assays are often used to assess the effectiveness of a chemical compound: it evaluates the biological response for a given dose of the compound of interest. It is possible to study single-dose responses as well as a set of responses for a dose gradient (dose–response screen). Assays can also be designed to study the effect of a combination of chemical compounds (synergistic screen). The proposed methodology described in this article is primarily applicable to dose–response screens, but its application could be widen to the other types of assay mentioned.

Dose–response screens are what we could refer to an idealized HTS experiment. It is quite typical that the effectiveness of a set of hits identified through a single-dose assay is validated by a dose–response screen (Editorial, 2007). For a gradient of concentrations, a compound of interest is added to well containing cells (cell lines, patient-derived cells etc.). The set of responses obtained (one for each concentration times the number of replicates) is then used to model a dose–response curve from which efficacy metrics are derived (Pabst et al., 2014) (Fig. 1).

Fig. 1.

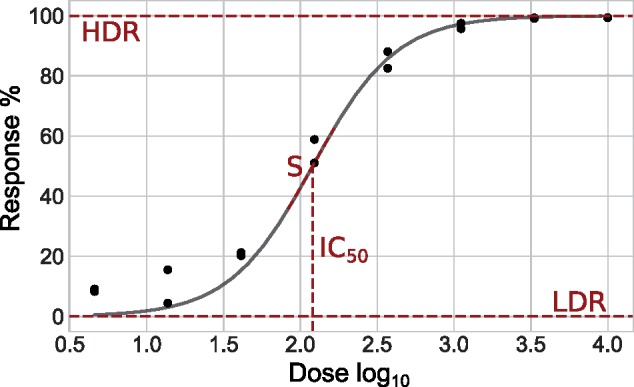
Dose–response curve and efficacy metrics. Example of dose–response curve modeled by non-linear regression. The four commonly reported efficacy metrics are identified in red

From a dose–response curve, four efficacy metrics can be derived:

  IC₅₀: the dose needed to generate a mean response equidistant from minimal and maximal responses (low-dose response (LDR) and high-dose response (HDR)];

HDR–LDR: the asymptotic responses generated for very low and very high doses of the compound, also referred to as the plateaus of the curve; and

    S: the steepness of response transition between the two plateaus.

These metrics can be embedded into a mathematical model, the log-logistic (Equation 1), in which a response f(x) is modeled in terms of a dose x. Although there are different models (Brain and Cousens, 1989; Calabrese, 2002) that can be used for dose–response analysis, the log-logistic is by far the most commonly used (Ritz, 2010).

$$f\left(x\right)=\mathit{LDR}+\frac{\mathit{HDR}-\mathit{LDR}}{1+{10}^{S·({\hspace{0.17em}\text{log}\hspace{0.17em}}_{10}I{C}_{50}-{\hspace{0.17em}\text{log}\hspace{0.17em}}_{10}x)}}$$ (1)

We often seek to identify the compound with the lowest IC₅₀ (Pabst et al., 2014), that is the compound capable of generating a maximal response for the lowest dose.

1.2 Marquardt–Levenberg

The process by which the metrics (or the model’s parameters) are normally estimated is called non-linear regression. The experimental data are used to adjust the parameters of the model such that the difference between the experimental data and the dose–response curve is minimized. The regression can be identified with algorithms such as gradient descent, Gauss-Newton and Marquardt–Levenberg (Levenberg, 1944), the latter being the most widely implemented.

Various software tools are available to estimate a dose–response curve and its associated metrics (Gadagkar and Call, 2015; Naqa et al., 2006; Veroli et al., 2015). Other tools include GraphPad, ActivityBase, the R environment and multiple Python libraries. The vast majority of these tools are not accessible to everyone, either because they are costly or because of they are complex to use. None of them allows for the comparison of two curves which limits the comparative analyzes to a qualitative numerical comparison of parameter estimates.

The non-linear regression approach, as implemented by the Marquardt–Levenberg algorithm, greatly limits the conclusions that can be made: it does not take into account the uncertainty of the estimated efficacy metrics. The certainty of the adjusted parameters and of the dose–response curve in regards to the experimental data is generally evaluated on the basis of intuition, based on visual inspection of the model fit. Complementary methodologies to the non-linear regression are sometimes used to compute confidence intervals. Bootstrap re-sampling (Efron, 1992) and Monte-Carlo simulation are among the most popular.

There is a significant need for a methodology that explicitly quantifies the reliability of the efficacy metrics taking into account the noise over the data, while adjusting the log-logistic model.

1.3 Bayesian inference

Bayesian inference refers to the process of fitting a probabilistic model to a specific dataset and to represent the fitted parameters by probability distributions. The results obtained are both representative of observed and unobserved data Gelman et al., 2014).

Bayesian inference aims to infer the posterior probability of a hypothesis H given a dataset of evidence E and previous knowledge about H. As more elements of E are presented to the model, the posterior of H is updated. The final results are a posterior distribution of the probability of H as described by Bayes Theorem (Equation 2).

$$P(H\hspace{0.17em}|\hspace{0.17em}E)=\frac{P(E\hspace{0.17em}|\hspace{0.17em}H)·P\left(H\right)}{P\left(E\right)}$$ (2)

The probability of H given E is directly proportional to the likelihood $P(E\hspace{0.17em}|\hspace{0.17em}H)$ and to the prior distribution P(E). The latter represents our intuition regarding the value of H. The prior is often defined by anterior evidence and observations, as well as theoretical knowledge. The likelihood evaluates the probability of obtaining E given H (Bernardo and Smith, 2001).

Given a parametric model of data $y\sim f(x\hspace{0.17em}|\hspace{0.17em}\theta )$, it is assumed that θ is a random variable which uncertainty can be described by a distribution, hence the prior. Defining the prior is not a trivial task and using a suboptimal prior can be detrimental to the analysis. In the context of dose–response, y represents an experimental response to dose x, and $\theta$ = {IC₅₀, HDR, S, LDR} defines the log-logistic model.

Various works have already been published on the application of Bayesian inference to the analysis of dose–response experiments (Collis et al., 2017; Cummings et al., 2003; Johnstone et al., 2016; Messner et al., 2001; Smith and Marshall, 2006). Although they span a wide range of experimental contexts and their applications are well demonstrated, most methodology lacks flexibility in the type of data it can analyze. To our knowledge, no work has been done on Bayesian comparative methodology which could be beneficial to dose–response analysis. From a software development perspective, there currently exists various platforms to facilitate the implementation and execution of probabilistic analyses. Among the most frequently cited are Stan (Carpenter et al., 2017) and PyMC3 (Salvatier et al., 2016).

1.4 Objectives

The methodologies currently in place limit the analysis of dose–response screens. To overcome these limitations, a significant weight is given to the intuition of the experimenter which can easily results in incomplete, biased and difficult to reproduce conclusions. These methodologies do not exploit the experimental data to their full informational potential and thereby impede the drug discovery process.

We aim at developing and implementing a Bayesian model for the analysis and comparison of dose–response datasets. The model incorporates the notion of intuition through prior distributions and computes the most probable value distribution for each of the efficacy metrics that define the log-logistic model. The comparison approach computes the most probable value distribution for differences between the metrics of two experiments. Finally, we want to redefine the way experimenters, such as medicinal chemists, analyze and interpret dose–response experiments by including uncertainty in their reasoning and providing them a simple and visual approach to do so.

2 Materials and methods

We separated our work in three main axes: (i) the probabilistic analysis of a single dose–response dataset, (ii) the comparative analysis of two dose–response datasets and (iii) the development of a web interface. The latter encapsulated the methodologies developed in the two first axes.

2.1 Inferring a dose–response curve

We used a hierarchical Bayesian model (Equation 3) to infer the parameters of the log-logistic model (Equation 1) given a dataset y of dose–response data.

$$P(\theta \hspace{0.17em}|\hspace{0.17em}y)=\frac{P(y\hspace{0.17em}|\hspace{0.17em}\theta )·P(\theta )}{P\left(y\right)}$$ (3)

For each component of θ we define a prior distribution $P(\theta )$. We assume that the dose–response data are normally distribution around $f(x;\theta )$ and for some shared value of σ (Equation 4). The value of σ is also inferred but without prior. Its posterior is representative of the noise in the dataset.

$$P(y\hspace{0.17em}|\hspace{0.17em}\theta )\sim \mathcal{N}\left(f\right(x;\theta ),{\sigma }^2)$$ (4)

To obtained the posterior distribution $P(\theta \hspace{0.17em}|\hspace{0.17em}y)$ we use the Markov chain Monte Carlo approach with the No-U-Turn sampler (Carpenter et al., 2017). Summarily, we define a chain as an ensemble of values that approximate $P(\theta \hspace{0.17em}|\hspace{0.17em}y)$. For every i iterations of I, a set of values θ is proposed. It is obtained by sampling a multivariate normal distribution centered at θ_i. The posterior$P(\theta \hspace{0.17em}|\hspace{0.17em}y)$ is calculated and the values of Θ are appended to the chain with a probability given by the ratio of likelihood of θ and θ_i. If Θ is accepted, i becomes i + 1 and ${\theta }_{i+1}=\theta$; if θ is not accepted we say that the iteration as resulted in a divergence and ${\theta }_{i+1}={\theta }_i$. Once i as reach I, a number w of the first iterations is discarded as they are warm-up iterations. Multiple chains C can be run in parallel and their results concatenated to generate the final posterior distribution, which is thus composed of $C\times (I-w)$ values.

Once $P(\theta \hspace{0.17em}|\hspace{0.17em}y)$ is obtained, we compute $\mathcal{N}\left(f\right(x;\theta ),{\sigma }^2)$ for a wide continuous range of hypothetical x. This allow use to derive an inferred dose–response curve, which is really the sequence of median responses for hypothetical and very close to each other doses x. In the same fashion, we are also able to derive a confidence interval around the curve by aligning the $\frac{100-\alpha \text{th}}{2}$ percentiles of every $\mathcal{N}\left(f\right(x;\theta ),{\sigma }^2)$ for the lower bound, and the $100-\frac{100-\alpha \text{th}}{2}$ percentiles for the upper bound. By doing so, we are capable to analyze what the responses might be for untested experimental doses while characterizing their uncertainty. The data can also be analyzed by plotting the histograms of the posterior distributions of θ. Confidence interval and median values can easily be derived from these distributions.

We tested our Bayesian model for various setups and multiple contexts (see Section 3). As demonstrated in the following section, an important aspect of Bayesian inference is the definition of the prior distributions. The current paper only presents analyzes done on inhibition rate (%) responses (see Section 2.4), that is responses that range from more or less 0 to 100, and increase as the doses increase. Our general intuition regarding the values of the efficacy metrics is as follow:

• We would expect the IC₅₀ to be around the median experimental dose (assuming an appropriate range of doses has been tested); We are assuming its value could span a very large range of hypothetical doses while above the absence of compound dose;

• The LDR should have a positive value and should more or less have a maximal value of 100%; We do not assume that its value is caped at nor will reach 100%;

• We would expect the slope (S) to be positive (inhibition rate response); We do not restrict it to have a positive value;

• The LDR should be somewhere around the 0% mark.

Following these elements of intuition, we tested different prior distribution in order to assess their effects on the inferred posterior distributions. Our model could easily be applicable to other type of responses (e.g. survival rate) by adjusting the prior.

2.2 Comparing two dose–response curves

To further our analysis approach and to propose a novel methodology, we adapted our Bayesian model so that we can infer the probability that two curves have significantly different components of θ.

Given two dose–response datasets D₁ and D₂, we are asking What is the probability that θ_k of D₁ will be greater than that of D₂? In order to answer this question, we evaluate the posterior of differences between ${\theta }_{1k}$ and ${\theta }_{2k}$ (Equation 5)

$$P(\Delta \theta \hspace{0.17em}|\hspace{0.17em}{\theta }_1,{\theta }_2)$$ (5)

$\mathit{Posterior}$ distributions are inferred for D₁ and D₂ in parallel. For every accepted Θ appended to the chain, $\Delta \theta ={\theta }_2-{\theta }_1$ is computed and stored. In the end, the w first elements are discarded, just as for the other posterior. We can evaluate the probability that each data has the largest value for θ_k by calculating the ratios of positive (D₁) and negative (D₂) posterior values. To facilitate the interpretation, we plot the histogram of the differences posterior with a contrasted vertical segment marking the median difference. It is also easy to calculate confidence interval and evaluate the reliability of the comparison.

This comparative methodology takes into account the uncertainty of θ which is currently ignored when comparing two dose–response curves. We tested our approach on both synthetic and experimental results, and the results proved to be more informative than the simple qualitative comparison.

2.3 Implementation

Our Bayesian model is implemented in the modeling language Stan (Carpenter et al., 2017). We use 4 chains of 2000 iterations and 1000 warm-ups to compute the posterior. We use the PyStan interface (v2.18.0.0) to work with Stan in the Python (v3.0.0) environment. Our plots are generated with Matplotlib (v3.0.2). When comparing our model to the Marquardt–Levenberg algorithm, we used the optimize package of Scipy (v1.2.0) with default settings to implement the non-linear regression.

For our web interface, we use Flask (v1.0.2) and Python on the server side. On the client side, standard HTML5 and JavaScript is used as well as Jinja and Bootstrap (v3.3.7). Interactivity is mainly provided by the use of jQuery (v2.1.1).

2.4 Dose–response data

We use various datasets to test and demonstrate the efficacy of our proposed approach. We use both synthetic and experimental datasets.

Using synthetic data allow us to evaluate the efficacy of the various approaches tested in a controlled environment. These data are generated from the log-logistic model (Equation 1). For a given set of 10 hypothetical doses x and defined θ = {IC₅₀, HDR, S, LDR}, we compute the associated $f(x;\theta )$ responses. Noise is added to dataset by sampling from $\mathcal{N}(y_j,{\sigma }^2)$ for each response y_j. We used multiple σ to test how well our methodology dealt with noise. The various synthetic datasets used in Section 3 are described in Table 1. When referencing a synthetic dataset, we use the label of Table 1 to which we add the σ value in subscript. For instance, A₀ would describe a dataset with an IC₅₀ of 2.15, a HDR of 60 and a Gaussian noise of $\sigma =0.1$.

Table 1.

Synthetic datasets

Label	HDR	IC 50	σ
A	60	2.15	{0.1, 10 }
B	60	2.0	{0.1, 5, 10 }
C	90	2.15	{0.1, 5, 10 }
S = 0.8 and LDR = 0.0

We also used real experimental data to demonstrate the application of our proposed methodology. The datasets E₁, E₂ and E₃ are from a single assay and represents different compounds. The compounds were tested at eight concentrations against patient-derived leukemic cell. The response measured is representative of cell growth inhibition rate (%). The experimental data were obtained through the Leucegene project.

Our proposed Bayesian model is unaffected by the number of replicates R (number of measured responses for each concentration). R varies from one experimental setting to another: to demonstrate the flexibility of our approach, we generated synthetic datasets with $R=\{1,3\}$ and used experimental datasets with R = 2.

3 Results and discussion

Results presented in this section are obtained by analyzing both synthetic and experimental datasets (Section 2.4). Most of the figures adaptation from our web interface (Section 3.3).

3.1 Bayesian inference on dose–response data

We evaluated the efficacy and limits of our Bayesian model in various experimental contexts. We first compared its results to those obtained by non-linear regression (Marquardt–Levenberg algorithm). We then assessed the effects of various prior in order to define the most appropriate. Last, we discussed the inferred σ posterior distributions for multiple datasets.

3.1.1. Marquardt–Levenberg versus Bayesian inference

We did not optimized the Bayesian prior but they were chosen wisely. As for the Marquardt–Levenberg algorithm, we tested it for both the four-parameters (4P) log-logistic model (Equation 1) and a two-parameters model (2P). In the 2P model, only the IC₅₀ and slope (S) parameters are estimated: the HDR and LDR are fixed to constant values, 100 and 0, respectively. These three approaches are applied to two synthetic datasets with varying noise (A₀ and A₁₀) and on an experimental dataset (E₁). The results are reported in Figure 2.

Fig. 2.

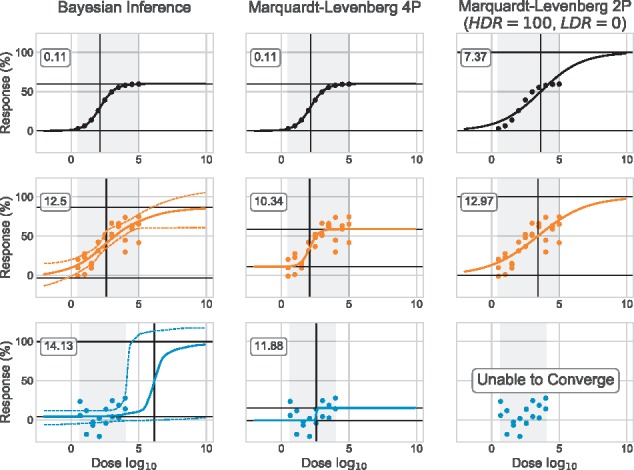
Marquardt–Levenberg versus Bayesian inference. Both synthetic datasets A₀ (black) and A₁₀ (orange) have triplicate (R = 3). The experimental dataset E₁ (blue) displays no response in the range of doses tested. Our Bayesian model is used to estimate dose–response curves with a 95% CI. Marquardt–Levenberg estimates the parameters of the 4P log-logistic model (Equation 1) and of the 2P model (only the IC₅₀ and S parameters are estimated: the HDR and LDR are fixed to constant values, 100 and 0, respectively). HDR and LDR (median values for Bayesian Inference) are represented by horizontal black segments; IC₅₀ (median value for Bayesian Inference). Root mean square error (RMSE) value is identified for each curve. For Bayesian Inference, we used the median curve to compute the residuals

Both Bayesian inference and Marquardt–Levenberg 4P generate the expected values when the data has very little noise (A₀, black dataset). The median HDR and adjusted HDR are the same (60.1) and contrary to the Marquardt–Levenberg 2P, they stay around the 60% mark. As expected, Marquardt–Levenberg 2P generates a dose–response curve that is not representative of the dataset as its HDR is fixed at 100%. This forces the IC₅₀ to shift to the right (3.62) and the slope to flatten (0.286).

When the data are noisier (A₁₀, orange dataset), Marquardt–Levenberg 4P generates curves that resemble the expected model the most. Its curve is steeper (1.36), which can be explained by its high LDR (11.1). The estimated HDR is as expected (58.9) and there is a small shift in the IC₅₀ (2.00). The Marquardt–Levenberg 2P curve is mostly the same as for the A₀ dataset. Interestingly, the Bayesian inference results differ from the previous ones. First, the CI (95%) surrounding the curve is significantly larger. Second, the median HDR now reaches well above 60% (86.5), creating a shift in the IC₅₀ to the right (2.60) and a flatter response (slope of 0.290). Even though the curve seems to represent well the data, the median parameters do not approximate those expected, with the exception of the LDR (−3.17).

When compared with the two datasets presented above, E₁ (blue dataset) completely breaks both Marquardt–Levenberg 4P and 2P. The latter is simply unable to converge (when using Scipy’s implementation, see Section 2.3). As for the former, it returns a very low HDR (15.2) and an unrealistically steep slope (18.9). Confusingly, the IC₅₀ estimated could lead to erroneously conclude that the compound is active (IC₅₀ = 2.58). The Bayesian inference curve better models the absence of response over the range of doses tested. The curve’s inflexion, or IC₅₀, is largely out of the experimental range and reaches a median value of 6.23. The confidence interval surrounding the right side of the curve (outside of the experimental doses range) is extremely wide: its bound span from ∼120 to 0%. The dataset E₁ is not sufficient to infer precisely efficacy metrics, but sufficient to clearly indicate the lack of response for this compound over the range of doses tested. Finally, since the Marquardt–Levenberg 4P directly minimizes the RMSE, it is not surprising that it achieves overall lower values.

It is interesting to interpret the results of Figure 2 by comparing how each methodology handles the concept of intuition. Marquardt–Levenberg 4P has no implemented consideration for it: only the data are considered when computing the estimates for the parameters of the model. This greatly limits the analysis to the range of experimental doses, as the approach assumes that the lower and upper response plateaus have been experimentally observed. This explained the unrealistic dose–response curve obtained for E₁ (absence of the high dose plateau). If we were to analyze this dataset only by looking at its IC₅₀, which is common practice, we would conclude that the tested compound is somewhat active. If we were to further our analysis to the other parameters, we would be puzzled by the very low HDR. The dataset would most likely be discarded because of the small distance between the LDR and HDR estimates and/or because of the unusual shape of the curve. The decision to discard E₁ is entirely based on intuition from the experimenter. The Marquardt–Levenberg 2P does take into account the notion of intuition in its implementation, but in an extreme way. By fixing the HDR and LDR to constant values, we imply that our intuition is rather a certitude. Again, this methodology is highly limiting, since our intuition prevails over the data. This is exactly what happened during the analysis of A₀. In the case where the data do not fit our intuition (E₁), the algorithm simply does not converge and the dataset is discarded. Neither of the Marquardt–Levenberg methodologies are capable of considering both the data and our intuition in a complementary fashion: it is one or the other. As demonstrated in Figure 2 this can highly bias our conclusions.

Our proposed Bayesian inference methodology is a good alternative to the problematic Marquardt–Levenberg. The use of prior allows us to incorporate the notion intuition into the computation in a less drastic way than Marquardt–Levenberg 2P. Thus, the resulting dose–response curve can be expanded to doses that were not tested experimentally. This approach also allows for the quantification of uncertainty, which neither of the Marquardt–Levenberg approaches do. For instance, we can conclude with certainty that E₁ does not support an IC₅₀ within the range of doses tested and the compound can be eliminated from further studies. Even though Bayesian inference is better suited for the analysis of dose–response data than the Marquardt–Levenberg algorithm, it still presents some limitations as demonstrated by the analysis of A₁₀: inappropriate prior combined with high noise can skew the results (Fig. 2). The following section discusses this topic in more details.

3.1.2. Defining prior distributions

We must think of prior as safety nets: when the data are insufficient, the inference gradually falls back on the prior distributions. It is thus important to use appropriate prior that best represent the experimental context. The process of defining the most suitable prior for θ is referenced as prior elicitation. It can either be based on consensus notions regarding θ (Chen et al., 1999), or on beliefs (Albert et al., 2012). The latter corresponds to our aim of mathematically implementing the notion of intuition.

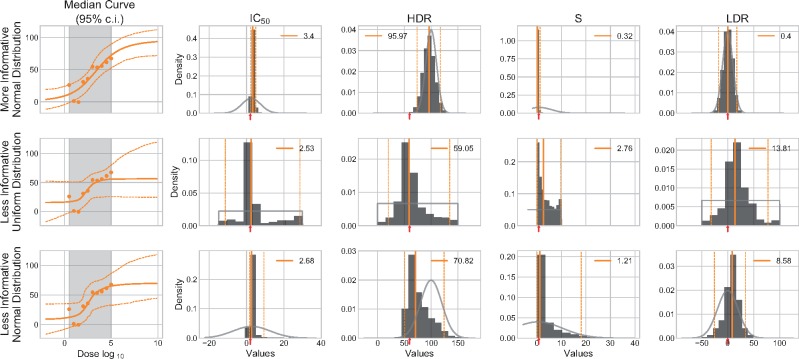
We describe prior in terms of their informativeness which refers to the information that they provide. More informative prior are not necessarily better: they may be too restrictive which can be highly detrimental if they do no complement the data. A prior should be a representation of intuition rather than certitude of what the unobserved data would be. To demonstrate the effects prior informativeness, we tested two sets of prior for the analysis of the synthetic dataset A₀ with R = 1. All prior are normally distributed and for a given parameter, centered around the same value. ‘Informative’ prior have very narrow distributions, while ‘Less Informative’ prior have wider distributions with σ five times bigger than that of the ‘Informative’ (Fig. 3).

Fig. 3.

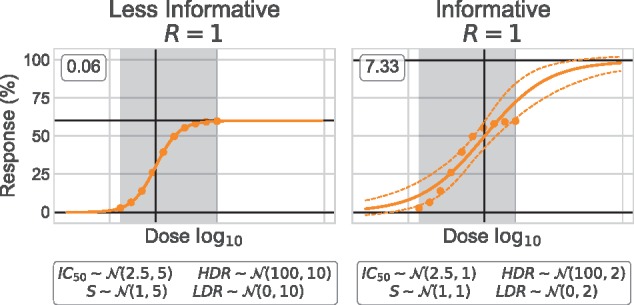
Prior informativeness. Informativeness can be described by the wideness of the distribution. ‘Informative’ (narrow) prior prevail on the data and the inference is biased. ‘Less Informative’ (wide) prior do not overshadow the data and the curve is inferred with high certainty. We used the A₀ dataset with R = 1. The median HDR and LDR are represented by black horizontal segments, and the median IC₅₀ vertical segments. RMSE value is identified for each curve. We used the median curve to compute the residuals

When comparing both Bayesian inferences, it is clear that the ‘Informative’ prior are not suited to the data (Fig. 3). Even though both HDR prior are centered at 100%, the ‘Less Informative’ prior does not prevail over the data and parameters can be inferred as expected (2.14, 60.1, 0.801, 0.032 for the IC₅₀, HDR, S and LDR, respectively). The second curve is reminiscent of the one obtained when using Marquardt–Levenberg 2P (Fig. 2). In such case, the prior are highly restrictive and do not complement the data, causing the inferred curve to mainly be representative of the prior themselves.

Figure 3 illustrates the effect of prior informativeness on 10 data points (R = 1). The undesirable effects of ‘Informative’ prior can be counterbalanced by giving more data points to the Bayesian model. For example, A₀ dataset with R = 5 prevails on the ‘Informative’ setup. In the context of dose–response analysis, it is not always possible to generate large dataset due to cost and material limitations. Prior should thus be defined by less informative distributions.

We tested various setups of prior distributions (Table 2) in order to establish the ones that can generalized to multiple experiments with similar contexts. Again, we used the synthetic dataset A₁₀ with R = 1. The dose–response curves and posterior distributions are presented in Figure 4.

Table 2.

Distributions parameters

Description	IC 50	HDR	S	LDR
More Informative Normal Dist.	$\mathcal{N}(2.5,5)$	$\mathcal{N}(100,10)$	$\mathcal{N}(1,5)$	$\mathcal{N}(0,10)$
Less Informative Uniform Dist.	$\mathcal{U}(-15,45)$	$\mathcal{U}(0,150)$	$\mathcal{U}(-10,10)$	$\mathcal{U}(-50,50)$
Less Informative Normal Dist.	$\mathcal{N}(\widehat{x},10)$	$\mathcal{N}(100,20)$	$\mathcal{N}(0.5,10)$	$\mathcal{N}(0,20)$

Note: $\widehat{x}$, median of experimental doses.

Fig. 4.

Effects of various prior. Three different prior settings (Table 2) are tested on the A₁₀ synthetic dataset with R = 1. Dose–response curves are plotted against the data and with a 95% CI. The posterior of each parameter is represented by an histogram. The colored vertical segments represent the median value (continuous) and its 95% CI (hashed). The numerical median value is indicated in the legend. The expected values (used to generate the synthetic data) are identified by a red arrow on the x-axis. The light gray segment superimposed on the histogram illustrates the contour of the prior distribution

The ‘More Informative Normal Dist.’ prior resulted in a higher than expected HDR (96.0) which generates a shift to the right in the IC₅₀ (3.40). The slope is also flattened by this high HDR and its value diverges greatly from the expected one. Interestingly, the HDR posterior is highly similar to the prior. Similarly, the LDR posterior is also matching its prior. When looking at the data, we notice that there are no clearly define upper and lower plateaus: the inference must thus rely mainly on the prior to define these regions of the dose–response curve. Even though the prior distributions are not highly informative, they are still too informative and force the HDR to reach the theoretical optimal 100.0% even though it is not directly supported by the data.

The ‘Less Informative Uniform Dist.’ prior is the less informative out of the three settings. Only the median HDR is approaching the expected values (59.1) but its CI (95%) is quite large. The other inferred parameters do not resemble those expected, which is not surprising considering the noise present in the data. When comparing the posterior distributions to the prior, we noticed that they were bound by very similar limits with the exception of the slope, which has a lower bound of 0.

The ‘Less Informative Normal Dist.’ prior seems to be a good compromise between the two previously described settings. The median values are not as expected but this can be explained by the noise in the data, mainly in the low dose region. The median HDR is however not too far from the 60% mark. It is interesting to notice the shift between the posterior and the prior of that parameter, which is not observed in the other two settings.

Overall, normally distributed prior ($\mathcal{N}(\mu ,{\sigma }^2)$) appear more appropriate. The uniform distributions prior ($\mathcal{U}(\alpha ,\beta )$) are too uninformative: when data are insufficient, the distribution values suggested by the prior are all equally probable which has the same effect as adding a large amount of new noisy data. This could explain the very large confidence intervals when using uniform prior, with the exceptions of the slope. In addition to the lack of informativeness in regards to the most probable value, uniform distributions are constrained by their α and β parameters. For instance, the slope posterior abruptly stops at 10 which is incidentally the defined β we selected for the slope uniform prior. Comparatively, the normal distribution is not bound and each distribution values as its own probability. We also adjusted our intuition of μ for both the IC₅₀ and slope prior (Table 2). Assuming the experimental doses are sufficient and range on a 2-fold scale, we could expected the IC₅₀ to be near the median experimental dose.

We will be using the ‘Less Informative Normal Dist.’ prior as default settings for now on.

3.1.3. Unresponsive data

So far, we mainly used synthetic datasets to explore the application of our Bayesian model to the analysis of dose–response data. To assess the extend of the applicability of our approach, we applied it to the analysis of a seemingly unresponsive experimental dataset, E₁ (Fig. 5). This type of response is frequent during the drug discovery process and it is of the utmost importance that the analysis approach applied can confidently assess that this compound has an IC₅₀ value above the range of doses tested and must be discarded.

Fig. 5.

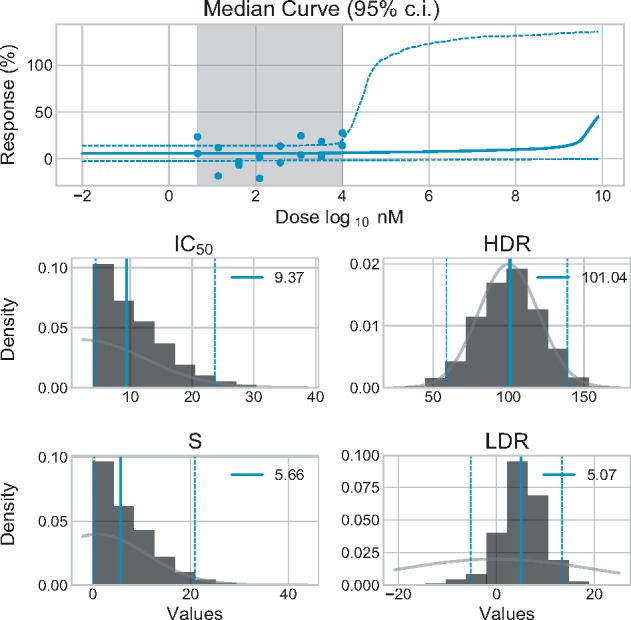
Bayesian inference applied to seemingly unresponsive experimental data. Results obtained for the experimental data E₁ using our default prior settings. Parameters posterior are represented by histograms. Their median values are identified by the colored full vertical segments and the values are reported in the legend. The colored dashed vertical segments mark the 95% CI bounds. The light gray segment superimposed on the histogram illustrates the contour of the prior distributions

On this specific dataset, the responses never reach >30% and there is no clear tendency. The inferred dose–response curve is mainly flat for the entire experimental doses range. The median IC₅₀ is high (9.37). As we expected it, the HDR posterior is highly reminiscent of the prior: the data did not give any indication regarding the response at very high doses. All the parameters’ confidence intervals are quite large. We are not able to determine with certainty the efficacy metrics of the tested compound. We can however conclude with certainty its IC₅₀ is bigger than 5 ${\hspace{0.17em}\text{log}\hspace{0.17em}}_{10}\text{nM}$, which is enough to discard this compound as ineffective. Such a high certainty conclusion cannot be made on seemingly unresponsive dataset with commonly used Marquardt–Levenberg algorithm methodology, without resorting to ad hoc rules.

3.1.4. Inferring noise

Our Bayesian model also infers a posterior distribution for σ (Equation 4), which describe the amount of noise in the dataset. For synthetic datasets (A₀ and A₁₀), the median σ is close to the actual σ used to generate the data (Fig. 6). It is true that we used a Gaussian noise when generating the data, and that our Bayesian model assumes that the responses are from independent identical normal distributions. That being said, the median σ for the experimental dataset E₁ is very close to the standard deviation of responses for this dataset (Fig. 6), which corresponds to interpreting the dose–response as flat and corresponding to the LDR plateau.

Fig. 6.

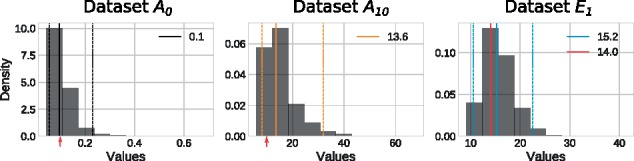
A posterior distribution of σ. posterior distributions obtained by applying our Bayesian model to the synthetic datasets A₀ and A₁₀ (black and orange respectively), and to experimental dataset E₁ (blue). The median σ are represented by the full segments and their values are reported in the legend. The dashed segments mark the bounds of a 95% CI. For the two synthetic datasets, the real value of σ is identified by a red arrow on the x-axis. For the experimental dataset, the standard deviation of the responses is represented by the red full segment and its value is reported in the legend

3.2 Comparison of two dose–response datasets

To further the analysis of dose–response data, we proposed a novel comparison methodology.

As mentioned in Section 2.2, the comparison is done by inferring the posterior of the difference between two values of an efficiency metric. From these posterior, we can derive the probability that a dataset has the largest value for a given efficiency metric. The uncertainty identified through the individual dose–response inference is carried to our comparison analysis, which allows to characterize the uncertainty of the difference.

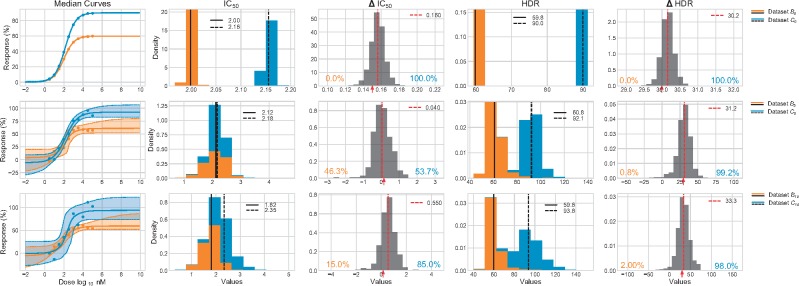
When comparing the synthetic datasets B₀ and C₀ (Fig. 7), we can conclude with great certainty that the C₀IC₅₀ is larger than that of B₀, even though the difference between the value is quite small (∼0.15). We can also conclude with great certainty that C₀ has a higher HDR than B₀. The precision of both datasets ($\sigma =0.1$) allows us to draw these conclusions without doubt.

Fig. 7.

Comparison of synthetic datasets. Three pairs of synthetic datasets with R = 1 are compared: B₀ to C₀, B₅ to C₅ and B₁₀ to C₁₀. Each pair of datasets differs in their IC₅₀ and HDR values. The 95% CI of each median curve is represented by the colored shaded regions. For both IC₅₀ and HDR, the stacked individual posterior are represented by the colored histograms. Their median are marked by black segments. The numerical values are reported in the legend. The Δ IC₅₀ and Δ HDR posterior are represented by gray histograms. The true difference is identified by a red arrow on the x-axis (0.15 for the IC₅₀ and 30 for the HDR). The median values of the differences posterior are identified by the red hashed segments, and the numerical values are reported in the legend. The probability (in %) that a dataset has the largest value for a given parameter is identified on the graph in the color corresponding to the dataset

In contrast, when comparing B₅ to C₅ (Fig. 7) we cannot make such conclusion. These two datasets share the same parameter values as B₀ and C₀, respectively, but they were generated with increased noise (σ = 5). The inferred IC₅₀ are more uncertain and their posterior distributions overlap. When comparing their respective median IC₅₀, one could easily concludes that the B₅ dataset has a larger IC₅₀ than the C₅ dataset (2.29 > 2.15) and that the B₅ compound is thus less effective than that of C₅. This conclusion is highly biased: the uncertainty of the inferred IC₅₀ does not allow for the identification of significantly greater value as demonstrated by the ΔIC₅₀posterior. If we take a look at the comparison of HDR values, we notice that the uncertainty does not affect the comparison: the values are different enough that the two posterior do not overlaps. We thus can conclude with certainty the C₅HDR is greater than the B₅HDR even when considering their respective uncertainty.

Similar results have been observed when comparing the two highly noisy (σ = 10) that are B₁₀ and C₁₀ (Fig. 7). The difference in median IC₅₀ is even greater but the Δ IC₅₀posterior tends more toward the expected conclusion. The HDR comparison is still highly convincing despite an higher level of uncertainty in the individual HDR posterior.

To highlight the informative gain of our comparative approach, we compared and analyzed two experimental datasets (E₂ and E₃) using two methodologies: (i) the commonly used numerical comparison of IC₅₀ and (ii) our differences posterior approach.

3.2.1 Numerical comparison

When comparing the IC₅₀ median values, we notice they differ by 0.11 log₁₀ nM (Fig. 8A) which is equivalent to ∼32 nM. We would conclude that the E₃ dataset has a larger IC₅₀ than that of the E₂ dataset. The E₂ compound is thus seemingly more effective than the E₃ compound.

Fig. 8.

Comparison of experimental datasets. Datasets E₂ and E₃ are compared. (A) The 95% CI of each median curve is represented by the colored shaded regions. The individual posterior are represented by the stacked colored histograms. The median values are indicated by black segments and the numerical values are reported in the legend. The Δ posterior are shown as gray histograms with their median values represented by red hashed segments. The probability (in %) that a dataset has the largest value for a given efficiency metric is identified on the graph in the color corresponding to the dataset. (B) Pairwise comparison of the individual posterior. Each dot a single value of the posterior for a given efficiency metric. Datasets are identified by their colors

3.2.2 Differences posterior

When we first look at the Δ IC₅₀posterior we cannot conclude that one of the IC₅₀ is greater than the other. The IC₅₀ were not inferred with enough certainty, because of the noise present in the data, for us to conclude that their values are significantly different. The HDR are however significantly different, despite the great uncertainty of E₂HDR(Fig. 8A). The Δ HDR posterior identify the E₃ dataset as the one with the overall largest HDR. It is also interesting to note that the difference between the two HDR is quite large, with median difference of almost 23% (Fig. 8A). The E₃ also have the overall largest S(Fig. 8A). When combining all of these information, we can conclude that the E₃ compound is more effective at generating a maximal response than the compound of E₂.

The two conclusions greatly differ and the one drawn from the numerical comparison is biased. The numerical comparison methodology is highly limited as it only considers one efficacy metric and does not consider the uncertainty associated to its values. It is preferable to consider all four metrics to get a more complete characterization of the efficacy of a compound. We must also evaluate the probabilities of certainty on the metrics as well as on the comparison itself to ensure our conclusions are as precise as is appropriate.

Last, interpreting pairwise plots of the posterior distributions can also help to draw informed conclusions. This sort of representation can identify inter-parameter dependencies which should be considered when analyzing posterior distributions. We can observe in Figure 8B that both datasets are distinguishable by pairing their HDR and S, which was not observable from the analysis of the histograms of Figure 8A.

3.3 BiDRA: an online tool

The two previous sections demonstrated how well and how much more information can be gathered when using our proposed Bayesian methodology for the analysis and comparison of dose–response data. The conclusions drawn from such analyses are less prone to bias compared with other commonly used methodologies. We are aware that the implementation and subsequent application of our Bayesian approach is not within everyone’s reach. We thus decided to develop an easy-to-use web interface, BiDRA (Bayesian inference for dose–response analysis).

The interface proposes both the analysis of a single dataset (Sections 2.1 and 3.1) and the comparison of two datasets (Sections 2.2 and 3.2). For both analyses, the user simply uploads the dataset(s) in a comma-separated values (CSV) format with the first column corresponding to the doses and the second representing the associated responses. It is important that the doses be log-transformed since we are using the log-logistical model (Equation 1). The data type must then be specified: Inhibition if the response increases with the dosage; Activity is the response decreases as the dosage increases. The HDR and LDR prior are adjusted according to the response type. We suggest default prior distributions (Section 3.1.2), assuming the data represent some sort of rate (%). The user can however easily specify his own μ and σ for each parameter.

The results are returned in both a figure and in a table. For the single dataset inference, the median dose–response curve as well as the posterior of all efficacy metrics and the σ are plotted. The returned results are similar to Figure 5. For the two datasets analysis, the individual inference plots are returned as well a figure describing the comparison. The latter includes the stacked individual posterior as well as the differences posterior. As an example, Figure 8A was obtained from BiDRA. For every computed posterior, we return its median and the bounds for 10, 5 and 1% CIs in a table.

The interface is accessible (https://bidra.bioinfo.iric.ca/) and does not require any authentication. The interface is not connected to any database and the analysis is not saved. We plan on adjusting the interface as our work progresses (see Section 4).

4 Implications

We propose in this article a Bayesian inference methodology for the analysis of dose–response data. This approach is then extended to directly infer differences in efficacy metrics between two dose–response experiments.

Our approach addresses two limitations of the commonly used Marquardt–Levenberg algorithm: first, it yields a single point estimate for each efficacy metrics, with no assessment of the uncertainty for these values. The experimenter is then left to decide on whether to accept or reject a given fit based on its intuition. This process is typically manual leading to possible biases and difficulty to reproduce analysis results. The second limitation is that the Marquardt–Levenberg algorithm relies entirely on the experimental data to estimate the efficacy metrics. In cases where the data are insufficient to determine one of the efficacy metrics, this algorithm will settle for the mostly likely value without consideration for experimentally sound boundaries. These limitations are compounded by the fact that there exists no methodology to support direct comparison of dose–response curves besides numerically comparing the efficacy metrics. The Bayesian inference approach we describe here allows us to incorporate in the analysis of dose–response the notion of experimental intuition to guide the identification of plausible ranges for each of the efficacy metrics. This reduces the necessity for careful inspection of curve fitting and provides a sound statistical framework to communicate the reliability of estimates to the experimenter. Our approach shares similarities to the ones presented in Collis et al. (2017), Cummings et al. (2003), Johnstone et al. (2016), Messner et al. (2001) and Smith and Marshall (2006); as it implements a simple hierarchical Bayesian model. We consider as part of our analysis all efficacy metrics of the log-logistic model (Equation 1). We also propose a novel and informative approach to compare two dose–response curves, again unambiguously conveying estimates uncertainty as posterior distributions of the differences for efficacy metrics of interest. In practice, these distributions are either communicated as a probability that one value is larger for one experiment than in the other, or as a confidence interval on the difference.

As mentioned by Johnstone et al. (2016), the Bayesian inference still have some limitations even though it provides numerous advantages when compared with the usual non-linear regression approach. As for Marquardt–Levenberg, computation time increases with the number of data points under consideration: the analysis of A₁₀ (R = 3) (Fig. 2) took ∼0.8 s, while the analysis of A₁₀ (R = 1) (Fig. 4) took ∼0.5 s (Intel, i9-7920X). Comparatively, the comparison of B₁₀ and C₁₀ (both R = 1) (Fig. 7) took ∼3 s. In most practical settings, the computational time necessary for these analyses is insignificant to the time required for actually performing the experiments being analyzed. A more important limitation to consider is the difficulty to clearly express the relative weight of the prior in the analysis. As shown in Section 3.1.2, an inappropriate prior can greatly alter the posterior distributions. This effect is mostly seen for the HDR and LDR as they often depend on extrapolation of the experimental data. As a general rule of thumb, the prior informativeness should not outweigh the data information and least informative prior should be favored in most situations.

That being said, we do think our approach to directly compare two dose–response will provide a useful tool to support the drug discovery process, either at the stage of secondary validation following a primary screen or during compound optimization. Considering distributions of probable values instead of single point estimates brings more depth to interpretation efficacy metrics and supports better informed decision from the experimenters. These benefits are also attained through a method that better support automated analysis as we greatly reduced the necessity for manual inspection of each fit.

Finally, we would also like to emphasis the flexibility of the proposed framework. We are currently exploring the use of this approach in the context of primary screens based on high-throughput, single-dose assays or to the more complex context of two-compounds synergistic dose–response assays. There are currently no established methodologies for the analysis of these types of assay. We think that Bayesian inference would be highly beneficial and could help to more reliably identify compound hits as well as better quantification of compounds interactions.