Drug repositioning based on bounded nuclear norm regularization

Abstract

Motivation

Computational drug repositioning is a cost-effective strategy to identify novel indications for existing drugs. Drug repositioning is often modeled as a recommendation system problem. Taking advantage of the known drug–disease associations, the objective of the recommendation system is to identify new treatments by filling out the unknown entries in the drug–disease association matrix, which is known as matrix completion. Underpinned by the fact that common molecular pathways contribute to many different diseases, the recommendation system assumes that the underlying latent factors determining drug–disease associations are highly correlated. In other words, the drug–disease matrix to be completed is low-rank. Accordingly, matrix completion algorithms efficiently constructing low-rank drug–disease matrix approximations consistent with known associations can be of immense help in discovering the novel drug–disease associations.

Results

In this article, we propose to use a bounded nuclear norm regularization (BNNR) method to complete the drug–disease matrix under the low-rank assumption. Instead of strictly fitting the known elements, BNNR is designed to tolerate the noisy drug–drug and disease–disease similarities by incorporating a regularization term to balance the approximation error and the rank properties. Moreover, additional constraints are incorporated into BNNR to ensure that all predicted matrix entry values are within the specific interval. BNNR is carried out on an adjacency matrix of a heterogeneous drug–disease network, which integrates the drug–drug, drug–disease and disease–disease networks. It not only makes full use of available drugs, diseases and their association information, but also is capable of dealing with cold start naturally. Our computational results show that BNNR yields higher drug–disease association prediction accuracy than the current state-of-the-art methods. The most significant gain is in prediction precision measured as the fraction of the positive predictions that are truly positive, which is particularly useful in drug design practice. Cases studies also confirm the accuracy and reliability of BNNR.

Availability and implementation

The code of BNNR is freely available at https://github.com/BioinformaticsCSU/BNNR.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The process of new drug discovery is time-consuming and tremendously expensive (Chong et al., 2007). It has been showed that the average time of developing a new drug is more than 13.5 years and the cost exceeds $1.8 billion dollars (Paul et al., 2010). Discovering new and reliable indications for commercialized drugs allows the pharmaceutical industry and the research community to reduce time and costs, because the existing commercialized drugs have already owned safety, efficacy and toleration data after various tests and clinical trials. The process of identifying new applications for existing drugs is known as drug repositioning. In fact, some successfully repositioned drugs, such as sildenafil, raloxifene and thalidomide, have generated generous revenues for their patent holders or companies. Therefore, drug repositioning is an effective strategy for developing new drugs.

Computational drug repositioning has attracted increasing attention, since manual investigation is time-consuming. With the development of high throughput technology and continuously updating databases, quite a few computational approaches have been proposed, including network-based analysis, machine learning, text mining and semantic inference approaches. The network-based methods are popular and fundamental for drug repositioning. Based on a network of drugs, diseases and targets (proteins), Martinez et al. (2015) proposed an approach named DrugNet to predict new use for existing drugs. DrugNet can perform both drug–disease and disease–drug prioritization by propagating information in the heterogeneous network. Gottlieb et al. (2011) integrated drug similarities and disease similarities to obtain primary features to support a computational approach called PREDICT to identify unknown drug–disease associations. Wang et al. (2013) constructed a heterogeneous drug–target graph, which contains intra-similarity information and drug–target association information. Based on the guilt-by-association principle, heterogeneous graph based inference (HGBI) algorithm (Wang et al., 2013) was proposed to predict new drug–target associations. HGBI is also used for predicting drug–disease associations (Wang et al., 2014). Luo et al. (2016) exploited the available information of drug–disease associations to enhance drug similarity and disease similarity. The MBiRW algorithm, which used some comprehensive similarity measures and Bi-Random Walk (BiRW) algorithm, is implemented on the drug–disease heterogeneous network to predict potential drug–disease associations.

Matrix factorization and matrix completion techniques have been applied to drug repositioning in recent years. Dai et al. (2015) incorporated the interaction network of genes and developed a matrix factorization model. Taking advantage of the information in genes network, the association between drug and disease can be predicted and new indications for known drugs can be obtained. Luo et al. (2018) constructed a heterogeneous network by integrating drug–drug network, disease–disease network and drug–disease association network, and then R⁴SVD (Li and Yu, 2017) was employed to efficiently compute the dominant singular values and the corresponding singular vectors of the association matrix. Based on the Singular Value Thresholding (SVT) algorithm (Cai et al., 2010), a Drug Repositioning Recommendation System (DRRS) has been proposed to rank the potential associations between drugs and diseases by completing the drug–disease association matrix. In fact, the methods based on random walks are equivalent to certain special cases of those using matrix completions. For example, MBiRW is equivalent to finding the eigenvector with respect to the largest eigenvalue of the association matrix. However, the above matrix completion algorithms are operated in a noiseless setting, assuming that the drug–disease associations are correctly derived and the disease–disease as well as drug–drug similarities are accurately measured. But in reality, drugs and diseases vary in many aspects and it is difficult to construct a single measure to precisely describe the similarity relationship among drugs or diseases. Occasionally, such similarity is misleading. For example, a disease caused by bacteria may have highly similar symptoms as one caused by virus, which should be treated by completely different drugs. Moreover, in the matrix completions algorithms, typically, 1’s in the drug–disease association matrix denote known drug–disease associations while 0’s represent the unknowns. The predicted values are expected to be within the range of [0, 1], indicating the likeliness of the predicted associations. However, the above matrix factorization and completion approaches are unable to avoid the situations that the predicted values fall out of the [0, 1] range, which brings difficulty in biological interpretation.

In this study, assuming that similar drugs share the similar molecular pathway to treat similar diseases, we consider the prediction of drug–disease association as a noisy matrix completion problem and develop a bounded nuclear norm regularization (BNNR) method to address this problem. First of all, we construct a heterogeneous drug–disease network, which is composed of drug–drug, drug–disease and disease–disease sub-networks. Then, BNNR is implemented to recover the missing entries in the adjacency matrix of this heterogeneous network while tolerating the potential noise in drug–drug and disease–disease similarities calculations. Finally, we evaluate the performance of BNNR on various datasets and compare it with several state-of-the-art methods. Our results show that our approach has superior capability of predicting hidden drug–disease associations. The main contributions of our BNNR model include:

• BNNR performs noisy matrix completion by incorporating nuclear norm regularization, which effectively addresses overfitting and leads to better improved accuracy as shown in our results;

• Our BNNR model incorporates a range constraint, which enforces all predicted matrix entry values within the specific interval;

• Our BNNR model is able to deal with noisy data efficiently; and

• An efficient iterative scheme is designed to numerically solve the BNNR model.

2 Materials and methods

In this section, we describe the BNNR model to predict the potential indications for existing drugs, which is organized as follows. First, we describe the datasets used in this study. Then, we depict the construction of the drug–disease heterogeneous network and its adjacency matrix to be completed. Finally, we present the BNNR model, solved by alternating direction method of multipliers (ADMM), to fill out the unknown associations between drugs and diseases. The overall workflow of BNNR is illustrated in Figure 1.

Fig. 1.

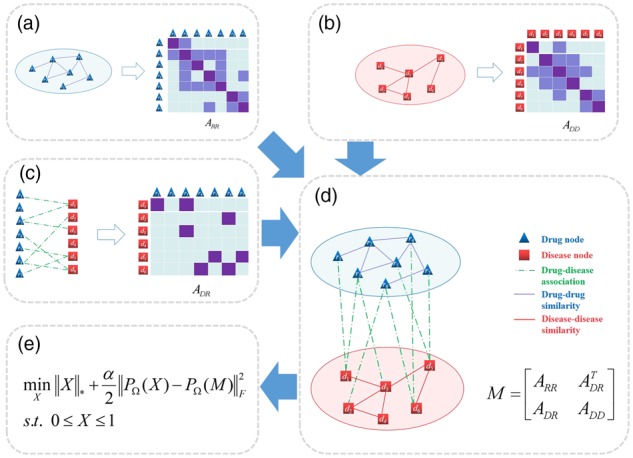
The overall workflow of BNNR. (a) Drug–drug network and its similarity matrix. (b) Disease–disease network and its similarity matrix. (c) Drug–disease association network and its association matrix. (d) The heterogeneous drug–disease network and its adjacency matrix. (e) The model of BNNR

2.1 Datasets

We use the gold standard dataset to predict new drug indications, which is obtained from (Gottlieb et al., 2011) collecting comprehensive associations from multiple data sources. There are 593 drugs, 313 diseases and 1933 validated drug–disease associations. Drugs are collected from the DrugBank database (Wishart et al., 2006) and diseases are extracted from the Online Mendelian Inheritance in Man (OMIM) dataset (Ada et al., 2002).

The similarities between drugs are calculated by the Chemical Development Kit (CDK) (Steinbeck et al., 2003) according to the chemical structures of all drug compounds in the Canonical Simplified Molecular Input Line-Entry System (SMILES) (Weininger, 1988). We firstly download the Canonical SMILES format of all drugs from DrugBank. Then, we utilize CDK to calculate a binary fingerprint for each drug. Finally, the Tanimoto score (Tanimoto, 1958) measuring the similarity of pairwise drugs is calculated with respect to their chemical fingerprints, which is in the range of [0, 1].

Disease–disease similarities are obtained from MimMiner (Van Driel et al., 2006), which measure the number of appearance of MeSH (medical subject headings vocabulary) terms of two diseases in the medical descriptions obtained from the OMIM database.

2.2 Construction of the heterogeneous network

We construct a heterogeneous drug–disease network, which integrates the drug–drug, disease–disease and drug–disease association networks. Let $R=\{r_1,r_2,...,r_m\}$ and $D=\{d_1,d_2,...,d_n\}$ denote a set of m drugs and n diseases, respectively. For the drug–drug network, the edge between two drugs is weighted by the pairwise drug similarity value. Similarly, the edge between two diseases is weighted by the pairwise disease similarity value. Then, the drug–disease association network is treated as a bipartite graph G(R, D, E), where $E\left(G\right)=\left\{e_{\mathit{ij}}\right\}\subseteq R\times D$ contains edges representing known associations between drug r_i and disease d_j. In this heterogeneous drug–disease network, drug–drug network and disease–disease network are connected by drug–disease associations. Figure 1a–d illustrates the construction of the heterogeneous network.

The adjacency matrix of the drug–disease heterogeneous network is then defined as:

$$M=\left[\begin{array}{cc}{A}_{\mathit{RR}}& A_{\mathit{DR}}^{\mathit{T}}\\ A_{\mathit{DR}}& A_{\mathit{DD}}\end{array}\right],$$

where the sub-matrices A_RR and A_DD denote the adjacency matrices of drug network and disease network and their weights are set as the pairwise drug and disease similarities, respectively, in range [0, 1]. A_RR and A_DD are dense which include rich correlation information among drugs and diseases. In contrast, due to the fact that drug–disease associations are rare, A_DR is usually extremely sparse, where 1’s denote known drug–disease associations and 0’s correspond to the unknowns. After all, our goal is to fill out the unknown elements in A_DR as the predicted scores of potential associations between drugs and diseases.

2.3 BNNR for predicting drug–disease associations

Assuming a low-rank structure, the general matrix completion problem (Ramlatchan et al., 2018) to fill out the missing entries is formulated as:

$$\begin{array}{c}{\displaystyle \underset{X}{\min }}\hspace{0.17em}\mathit{rank}\left(X\right)\\ s.t.{\mathcal{P}}_{\mathrm{\Omega }}\left(X\right)={\mathcal{P}}_{\mathrm{\Omega }}\left(M\right),\end{array}$$

where $M\in {\mathbb{R}}^{(m+n)\times (m+n)}$ is the given incomplete matrix, rank(.) denotes the rank function, Ω is a set containing index pairs (i, j) of all known entries in M and ${\mathcal{P}}_{\mathrm{\Omega }}$ is the projection operator onto Ω.

$${\left({\mathcal{P}}_{\mathrm{\Omega }}\right(X\left)\right)}_{\mathit{ij}}=\left\{\begin{array}{c}{X}_{\mathit{ij}},\hspace{1em}(i,j)\in \Omega \\ \hspace{1em}0,\hspace{1em}\hspace{1em}(i,j)\notin \Omega \end{array}.\right.$$

Unfortunately, the rank minimization problem is known to be NP-hard. The rank minimization in the above matrix completion model is often relaxed to a nuclear norm minimization problem such that:

$$\begin{array}{c}{\displaystyle \underset{X}{\min }}{\Vert X\Vert }_{*}\\ s.t.{\mathcal{P}}_{\mathrm{\Omega }}\left(X\right)={\mathcal{P}}_{\mathrm{\Omega }}\left(M\right),\end{array}$$ (1)

where ${\Vert X\Vert }_{*}$ denotes the nuclear norm of X, which is defined as the sum of all singular values of X. The nuclear norm minimization model is a convex optimization problem. Many algorithms have been designed to provide numerical solutions for the above model or alternative forms, including the fixed point continuation with approximate SVD (FPCA) (Ma et al., 2011), the accelerated proximal gradient algorithm (APG) (Toh et al., 2010), the SVT algorithm (Cai et al., 2010) and the ADMM (Boyd et al., 2011; Chen et al., 2012; Wen et al., 2010). Candes et al. (2013) showed that the solution obtained by optimizing the nuclear norm is equivalent to the one by rank minimization under certain conditions, minimizing the nuclear norm.

For predicting drug–disease associations, the elements in the drug similarity matrix A_RR and disease similarity matrix A_DD are within the interval of [0, 1]. The elements in the association matrix A_RD are either 0 or 1. As a result, the predicted values in the unknown entries are expected to be in the interval of [0, 1], where a predicted value closer to 1 indicates that this is likely to be an indication and vice versa. Nevertheless, in the above matrix completion models (1), the entries in the completed matrix can be any real value in (−∞, +∞). A predicted value out of the interval [0, 1] is meaningless in the application context. Hence, it is important to add a bound constraint to the matrix completion model to ensure that the uncovered missing elements are within the interval of [0, 1].

Moreover, since there may be a lot ‘noise’ in the drug and disease data, particularly when measuring the drug–drug and disease–disease similarities, the drug repositioning model should effective tolerate the potential noise. A matrix completion model to tolerate noise is:

$$\begin{array}{c}{\displaystyle \underset{X}{\min }}{\Vert X\Vert }_{*}\\ s.t.\left|\right|{\mathcal{P}}_{\mathrm{\Omega }}\left(X\right)-{\mathcal{P}}_{\mathrm{\Omega }}\left(M\right)|{|}_F\le ϵ,\end{array}$$

where ϵ measures the noise level. However, for this model with the inequality constraint, choosing the appropriate parameter is challenging, because the noise level is not explicitly known. Moreover, it is not straightforward to come up with an efficient solver for this model. Therefore, we relax the constraint satisfaction model into a regularization model. Introducing the soft regularization term not only enables tolerance to the unknown noise (Chen et al., 2012; Hu et al., 2013; Ma et al., 2011; Toh et al., 2010), but also provides computational convenience.

Putting all pieces together, we propose a BNNR method, which minimizes the nuclear norm as the regularization term and ensures the recovered matrix elements within a specific interval. The BNNR model is described as follows:

$$\begin{array}{c}{\displaystyle \underset{X}{\min }}{\Vert X\Vert }_{*}+\frac{\mathrm{\alpha }}{2}{\Vert {\mathcal{P}}_{\mathrm{\Omega }}\left(X\right)-{\mathcal{P}}_{\mathrm{\Omega }}\left(M\right)\Vert }_F^2\\ s.t.\hspace{0.33em}0\le X\le 1,\end{array}$$ (2)

where α is parameter balancing the nuclear norm and the error term. Note that we use $0\le X\le 1$ to denote $0\le X_{\mathit{ij}}\le 1$ for all elements in X throughout this paper. We derive a simple but effective numerical scheme using ADMM to solve (2).

Model (2) is solved by an iterative method. Starting from the initial solution$\mathrm{ }{X}_1={\mathcal{P}}_{\mathrm{\Omega }}\left(M\right)$. It is important to notice that the objective function in (2) is convex. By introducing an auxiliary matrix W, (2) can be optimized using the ADMM framework in the following equivalent form.

$$\begin{array}{cc}{\displaystyle \underset{X}{\min }}{‖X‖}_{*}+\frac{\mathrm{\alpha }}{2}{‖{\mathcal{P}}_{\mathrm{\Omega }}\left(W\right)-{\mathcal{P}}_{\mathrm{\Omega }}\left(M\right)‖}_F^2& \\ \mathrm{s}.\mathrm{t}.\mathrm{ } X=W, & \hspace{0.33em}\\ 0\le W\le 1.& \hspace{0.33em}\end{array}$$ (3)

Accordingly, the augmented Lagrangian function becomes

$$\begin{array}{c}\mathcal{L}(W,X,Y,\mathrm{\alpha },\mathrm{\beta })={\Vert X\Vert }_{*}+\frac{\mathrm{\alpha }}{2}{\Vert {\mathcal{P}}_{\mathrm{\Omega }}\left(W\right)-{\mathcal{P}}_{\mathrm{\Omega }}\left(M\right)\Vert }_F^2\\ +\mathit{Tr}\left(Y^T\right(X-W\left)\right)+\frac{\mathrm{\beta }}{2}{\Vert X-W\Vert }_F^2,\end{array}$$ (4)

where Y is the Lagrange multiplier and β > 0 is the penalty parameter. At the k-th iteration, BNNR requires alternatively computing$\mathrm{ }{W}_{k+1},\hspace{0.33em}{X}_{k+1}$ and$\mathrm{ }{Y}_{k+1}$.

Compute $\mathrm{ }{W}_{k+1}$: We fix X_k and Y_k to minimize $\mathcal{L}(W,X_k,Y_k,\mathrm{\alpha },\mathrm{\beta })$ for$\mathrm{ }{W}_{k+1}$. We hereby take full advantage of the inverse operator to obtain an exact and closed-form solution.

$$\begin{array}{c}{W}_{k+1}=\underset{0\le W\le 1}{\arg \mathrm{ }\min }\mathcal{ }\mathcal{L}(W,X_k,Y_k,\mathrm{\alpha },\mathrm{\beta })\\ =\underset{0\le W\le 1}{\arg \mathrm{ }\min \mathrm{ }}\frac{\mathrm{\alpha }}{2}{\Vert {\mathcal{P}}_{\mathrm{\Omega }}\left(W\right)-{\mathcal{P}}_{\mathrm{\Omega }}\left(M\right)\Vert }_F^2\\ \hspace{1em}+\mathit{Tr}\left({Y_k}^T\right(X_k-W\left)\right)+\frac{\mathrm{\beta }}{2}{\Vert X_k-W\Vert }_F^2.\end{array}$$ (5)

Here, W* is the optimal solution of ${\displaystyle \underset{W}{\arg \mathrm{ }\min }} \mathcal{L}(W,X_k,Y_k,\mathrm{\alpha },\mathrm{\beta })$, if and only if

$$\mathrm{\alpha }{\mathcal{P}}_{\mathrm{\Omega }}^{*}\left({\mathcal{P}}_{\mathrm{\Omega }}\right(W^{*})-{\mathcal{P}}_{\mathrm{\Omega }}(M\left)\right)-Y_k-\mathrm{\beta }(X_k-W^{*})=0$$ (6)

holds, where ${\mathcal{P}}_{\mathrm{\Omega }}^{*}$ denotes the adjoint operator of$\mathrm{ }{\mathcal{P}}_{\mathrm{\Omega }}$. Then, a closed-form solution becomes

$$\begin{array}{c}{W}^{*}={(\mathcal{I}+\frac{\mathrm{\alpha }}{\mathrm{\beta }}{\mathcal{P}}_{\mathrm{\Omega }}^{*}{\mathcal{P}}_{\mathrm{\Omega }})}^{-1}(\frac{1}{\mathrm{\beta }}{Y}_k+\frac{\mathrm{\alpha }}{\mathrm{\beta }}{\mathcal{P}}_{\mathrm{\Omega }}^{*}{\mathcal{P}}_{\mathrm{\Omega }}(M)+X_k)\\ =(\mathcal{I}-\frac{\mathrm{\alpha }}{\mathrm{\alpha }+\mathrm{\beta }}{\mathcal{P}}_{\mathrm{\Omega }}^{*}{\mathcal{P}}_{\mathrm{\Omega }})(\frac{1}{\mathrm{\beta }}{Y}_k+\frac{\mathrm{\alpha }}{\mathrm{\beta }}{\mathcal{P}}_{\mathrm{\Omega }}^{*}{\mathcal{P}}_{\mathrm{\Omega }}(M)+X_k)\\ =(\frac{1}{\mathrm{\beta }}{Y}_k+\frac{\mathrm{\alpha }}{\mathrm{\beta }}{\mathcal{P}}_{\mathrm{\Omega }}(M)+X_k)\\ -\frac{\alpha }{\alpha +\beta }{\mathcal{P}}_{\Omega }(\frac{1}{\beta }{Y}_k+\frac{\alpha }{\beta }{\mathcal{P}}_{\Omega }(M)+X_k),\end{array}$$ (7)

where $\mathcal{I}$ is the identity operator. ${(\mathcal{I}+\frac{\mathrm{\alpha }}{\mathrm{\beta }}{\mathcal{P}}_{\mathrm{\Omega }}^{*}{\mathcal{P}}_{\mathrm{\Omega }})}^{-1}$ denotes the inverse operator of $(\mathcal{I}+\frac{\mathrm{\alpha }}{\mathrm{\beta }}{\mathcal{P}}_{\mathrm{\Omega }}^{*}{\mathcal{P}}_{\mathrm{\Omega }})$ and is equal to $\mathcal{I}-\frac{\mathrm{\alpha }}{\mathrm{\alpha }+\mathrm{\beta }}{\mathcal{P}}_{\mathrm{\Omega }}^{*}{\mathcal{P}}_{\mathrm{\Omega }}$ (Yang and Yuan, 2012). It’s worth noting that$\mathrm{ }{\mathcal{P}}_{\mathrm{\Omega }}^{*}{\mathcal{P}}_{\mathrm{\Omega }}={\mathcal{P}}_{\mathrm{\Omega }}$. Considering the interval $\left[\mathrm{0,1}\right]$ constraint, we limit the range of the elements of $W_{k+1}$ to [0, 1] such that

$$\begin{array}{c}{W}_{k+1}={\mathcal{Q}}_{\left[\mathrm{0,1}\right]}\left(W^{*}\right),\end{array}$$ (8)

where ${\mathcal{Q}}_{\left[\mathrm{0,1}\right]}$ is the projection operator defined as

$${\left({\mathcal{Q}}_{\left[\mathrm{0,1}\right]}\right(W^{*}\left)\right)}_{\mathit{ij}}=\left\{\begin{array}{c}1,\hspace{1em}\hspace{1em}{W}_{\mathit{ij}}^{*}>1\\ W_{\mathit{ij}}^{*},\hspace{1em}0\le W_{\mathit{ij}}^{*}\le 1\\ 0,\hspace{1em}\hspace{1em}{W}_{\mathit{ij}}^{*}<0\end{array}\right..$$

Compute$\mathrm{ }{X}_{k+1}$: Alternatively, we fix $W_{k+1}$ and Y_k to compute$\mathrm{ }{X}_{k+1}$.

$$\begin{array}{c}{X}_{k+1}=\underset{X}{\mathrm{argmin}} \mathcal{L}(W_{k+1},X,Y_k,\mathrm{\alpha },\mathrm{\beta })\\ =\underset{X}{\mathrm{argmin}}{\Vert X\Vert }_{*}+\mathit{Tr}\left({Y_k}^T{Y}_k^T\right(X-W_{k+1}\left)\right)+\frac{\mathrm{\beta }}{2}{\Vert X-W_{k+1}\Vert }_F^2\\ =\underset{X}{\mathrm{argmin}}{\Vert X\Vert }_{*}+\frac{\mathrm{\beta }}{2}{\Vert X-(W_{k+1}-\frac{1}{\mathrm{\beta }}{Y}_k)\Vert }_F^2\\ ={\mathcal{D}}_{\frac{1}{\mathrm{\beta }}}(W_{k+1}-\frac{1}{\mathrm{\beta }}{Y}_k),\end{array}$$ (9)

where ${\mathcal{D}}_{\mathrm{\tau }}\left(X\right)$ is the singular value shrinkage operator (Cai et al., 2010; Ma et al., 2011) defined as

$${\mathcal{D}}_{\mathrm{\tau }}(X)=\sum _{i=1}^{{\mathrm{\sigma }}_i\ge \mathrm{\tau }}({\mathrm{\sigma }}_i-\mathrm{\tau })u_i{v_i}^T,$$

where σ_i is the singular values of X which is larger than τ, while u_i and v_i are the left and right singular vectors corresponding to σ_i, respectively.

Compute $\mathrm{ }{Y}_{k+1}$: Finally, $Y_{k+1}$ is calculated as

$$Y_{k+1}=Y_k+\mathrm{\gamma }\mathrm{\beta }(X_{k+1}-W_{k+1}),\hspace{1em}\mathrm{\gamma }\in (0,\frac{\sqrt{5}+1}{2}),$$ (10)

where γ is the learning rate, which is set to 1 in this study for simplicity (Hu et al., 2013). Putting all pieces together, Algorithm 1 presents an iterative BNNR scheme for solving (2). Based on the assumption that similar diseases tend to be treated by similar drugs, because of the common molecular pathways, there exist certain low-rank structures governing drug–disease associations. Minimizing the nuclear norm of the target matrix, BNNR reveals the low-rank structures and provides a way to recover the missing entries. After supplying the adjacency matrix of the drug–disease heterogeneous network to BNNR, we can obtain an updated drug–disease association matrix$\mathrm{ }{A}_{\mathit{DR}}^{*}$, where the unknown entries in A_DR are filled up. The entries in $A_{\mathit{DR}}^{*}$ with predicted values (scores) close to 1 indicate the potential drug–disease associations.

Algorithm 1.

BNNR Algorithm

Input: The drug similarity matrix $A_{\mathit{RR}}\in {\mathbb{R}}^{m\times m}$, the disease similarity matrix$\mathrm{ }{A}_{\mathit{DD}}\in {\mathbb{R}}^{n\times n}$, the drug–disease association matrix$\mathrm{ }{A}_{\mathit{DR}}\in {\mathbb{R}}^{n\times m}$, parameters α and β.

Output: Predicted association matrix$\mathrm{ }{A}_{\mathit{DR}}^{*}$.

$M\leftarrow \left[\begin{array}{cc}{A}_{\mathit{RR}}& {A_{\mathit{DR}}}^T\\ A_{\mathit{DR}}& A_{\mathit{DD}}\end{array}\right];$

initialize $X_1=P_{\mathrm{\Omega }}\left(M\right),W_1=X_1,Y_1=X_1,\mathrm{\gamma }=1;$ //Ω is a set of indices of all known entries in M.

$k\leftarrow 1$;

repeat

$W_{k+1}\leftarrow {\mathcal{Q}}_{\left[\mathrm{0,1}\right]}\left(W^{*}\right);$

$X_{k+1}\leftarrow {\mathcal{D}}_{\frac{1}{\mathrm{\beta }}}(W_{k+1}-\frac{1}{\mathrm{\beta }}{Y}_k);$

$Y_{k+1}\leftarrow Y_k+\gamma \beta (X_{k+1}-W_{k+1});$

$k\leftarrow k+1$;

until convergence

$\left[\begin{array}{cc}{A}_{RR}^{*}& A_{DR}^{*}{}^T\\ A_{DR}^{*}& A_{DD}^{*}\end{array}\right]\leftarrow W_k;$

return $A_{\mathit{DR}}^{*}.$

3 Results and discussion

3.1 Evaluation metrics

To evaluate the performance of BNNR, a 10-fold cross-validation is conducted to verify the candidate diseases for given drugs. All known drug–disease associations are randomly divided into 10 exclusive subsets of approximately equal size. Each subset is treated as the testing set in turn, while the remaining nine subsets are used as the training set. The 10-fold cross-validation is repeated 10 times with random subset division and the average accuracy values are showed as the final results.

After the association matrix of the drug–disease heterogeneous network is completed, the predicted scores of all drug–disease associations are obtained. For each drug, the predicted scores of its associations with the diseases are ranked in descending order. The score of the candidate association exceeding a given threshold is considered as a positive prediction; otherwise, negative. For increasing threshold values, true positive rate (TPR) and false positive rate (FPR) will be calculated to generate the receiver-operating characteristic (ROC) curve. Precision and recall (equivalent to TPR) are obtained to plot the precision–recall (PR) curve (Davis et al., 2006). Meanwhile, due to the fact that the top-ranked results are of most interest, the number of correctly identified drug–disease associations using different thresholds will be illustrated. The area under the ROC curve (AUC) and top-ranked results are presented to compare the overall performance of BNNR with a variety of existing methods in this study.

3.2 Parameter setting

In BNNR algorithm, there are two parameters needed to be determined, including α and β. For the parameters α and β, we perform cross-validation on the training dataset to determine, which are determined from {0.1, 1, 10, 100}. Table 1 reports AUC values calculated by BNNR when α and β are ranging from {0.1, 1, 10, 100} in 10-fold cross-validation, where the best AUC values are displayed in bold. One can find that BNNR achieves the best performance when α = 1 and β = 10.

Table 1.

The AUC values using different α and β values in 10-fold cross-validation on the gold standard dataset

α\β	0.1	1	10	100
0.1	0.757	0.785	0.879	0.888
1	0.863	0.921	0.933	0.899
10	0.854	0.921	0.926	0.890
100	0.862	0.919	0.925	0.889

Meanwhile, we terminate the BNNR algorithm when the following stopping criterions are satisfied:

$$f_k\le \mathit{tol}1,\frac{|f_{k+1}-f_k|}{\mathit{max}\{1,|f_k\left|\right\}}\le \mathit{tol}2,$$ (11)

where$\mathrm{ }{f}_k=\frac{{\Vert X_{k+1}-X_k\Vert }_F}{{\Vert X_k\Vert }_F}$, tol1 and tol2 are the given tolerances, which are set as 2 × 10⁻³ and 10⁻⁵ in BNNR algorithm, respectively.

3.3 Compare with other methods

BNNR is compared with four latest methods for drug repositioning: HGBI (Wang et al., 2013), DrugNet (Martinez et al., 2015), MBiRW (Luo et al., 2016) and DRRS (Luo et al., 2018). Based on the guilt-by-association principle and the interpretation of information flow, HGBI is designed for predicting disease-associated drugs. DrugNet is based on propagation flow algorithm, which can perform both drug–disease and disease–drug prioritization. MBiRW and DRRS are our previous works, MBiRW uses comprehensive similarity measures and BiRW algorithm to infer drug–disease association. DRRS constructs a heterogeneous drug–disease network and conducts prediction based on the matrix completion of SVT algorithm to predict potential indications for drugs.

Although DRRS and BNNR are based on the same heterogeneous drug–disease network, BNNR can exploit more accuracy association information due to better robustness. BNNR has several distinct advantages compared with DRRS: First, BNNR could fit the whole network better. Since the values of similarity matrices computed in silico may include noisy information, BNNR has a relaxed penalty function to cope with noisy entries, while DRRS attempts to fit all entries. Second, BNNR has more interpretable predicted values. The bounded constraint ensures that all predicted associations are within [0, 1]. In contrast, the predicted association scores may be negative or >1 in DRRS. Third, the regularization term based on nuclear norm is able to address overfitting effectively. This enables us to design an appropriate stop criterion for BNNR to directly obtain the optimal solution without the need of designating a part of known drug–disease associations as the validation set to identify the optimal rank.

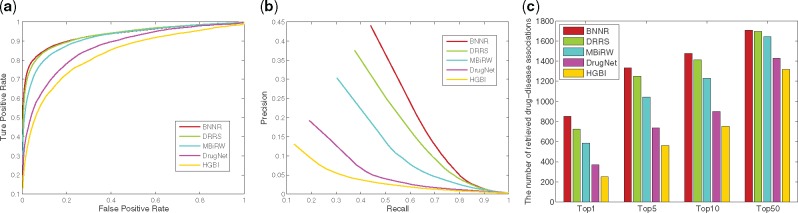
To ensure a fair comparison, the parameters in the compared approaches are set to the default values according to the authors’ recommendation (HGBI: α = 0.4; MBiRW: α = 0.3, l  =  2, r  =  2; DRRS: τ and δ are two adaptive parameters) and cross-validation (DrugNet: α is chosen from {0.1, 0.2, …, 0.9}). The overall results of 10-fold cross-validation for all methods are depicted by ROC curve, PR curve and top-ranked results in Figure 2. As shown in Figure 2, the BNNR method outperforms the other methods in terms of AUC values of the ROC curves, precisions and top-ranked indications. Specifically, BNNR reports AUC value of 0.932, while HGBI, DrugNet, MBiRW and DRRS have 0.829, 0.868, 0.917 and 0.930, respectively. The more significant gains are in precision. BNNR obtains prediction precision of 0.440, which is significantly higher than HGBI (0.130), DrugNet (0.192), MBiRW (0.304) and DRRS (0.375). It is important to note that BNNR can successfully rank 44.0% true drug–disease associations at top 1, which is 13.6 and 6.5% higher than MBiRW and DRRS, respectively. One true drug–disease association is treated as a retrieved association when its predicted rank is higher than the specified top rank threshold. These approaches identify different numbers of true drug–disease associations with respect to different rank cutoffs, which are presented in Figure 2c. For instance, among the 1933 true drug–disease associations, 1333 associations are identified at top 5 by BNNR, while in comparison, only 561, 738, 1044 and 1251 associations are predicted by HGBI, DrugNet, MBiRW and DRRS, respectively. In practice, precision is a more important measure of the drug–disease association prediction performance, because a more precise prediction provides correct indication for existing drugs with higher probability, which can lead to budget and time reduction.

Fig. 2.

The performance of all methods in predicting drug–disease association for 10-fold cross-validation. (a) ROC curve of prediction results. (b) PR curve of predicting candidate diseases for drugs. (c) The number of correctly retrieved drug–disease associations for various rank thresholds

3.4 Predicting indications for new drugs

To assess the capability of BNNR in predicting potential indications for new drugs, we choose these drugs which have only one known drug–disease association to conduct a de novo test. For each of these drugs, the known disease association is removed in turn as the test sample and other existing associations are used as training sample.

For a new drug without any known drug–disease association, BNNR is able to predict its drug–disease associations by taking advantage of the similarity information of the novel drug in adjacency matrix. Also, due to the fact that there is no drug–disease association information for the novel drug, the similarity information is more important than the existing drug–disease association information for the other drugs, which should be given heavier weights. Equivalently, association matrix is multiplied by a weight coefficient 0.7 in this study.

As shown in Figure 3 for the de novo test, BNNR achieves AUC value of 0.830, while HGBI, DrugNet, MBiRW and DRRS have inferior results with 0.746, 0.782, 0.818 and 0.824, respectively. For top-ranked results, BNNR outperforms all methods at top 5, 10 and 50, except for being inferior to DRRS at top 1.

Fig. 3.

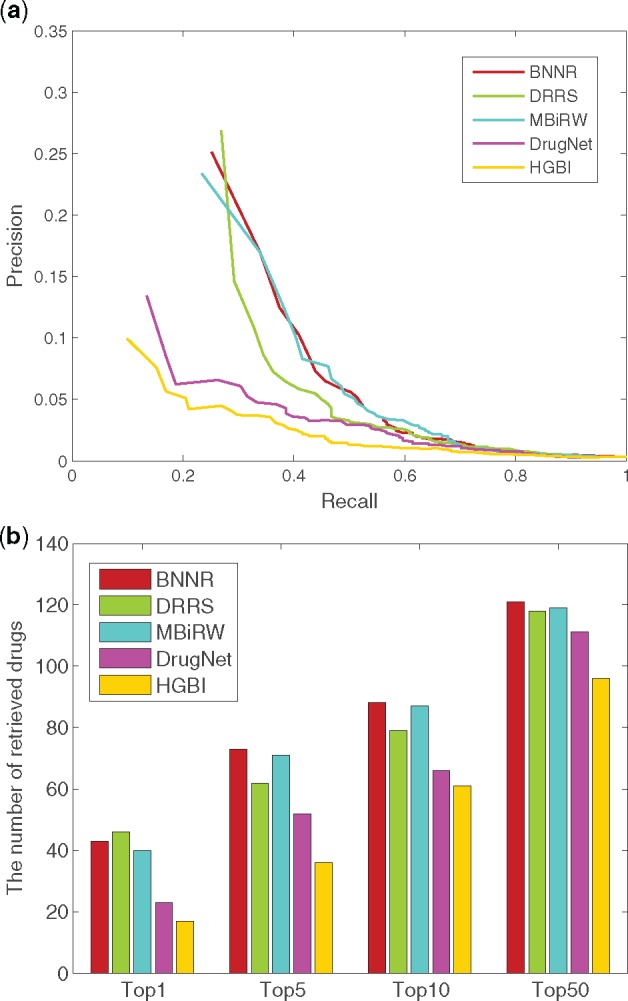
The performance of all methods in predicting potential diseases for new drugs. (a) PR curve of prediction results. (b) The number of retrieved drugs for various rank thresholds

3.5 Case studies

In these case studies, we apply BNNR to predict new uses for already approved drugs in practical applications. In the process of identifying novel drug–disease associations, we treat all known drug–disease associations in the gold standard dataset as the training set and regard the missing drug–disease pairs as the candidate set. After the prediction scores of all candidate pairs are computed by BNNR, we rank the candidate diseases by the predicted scores for each drug.

In order to confirm whether the predicted diseases are true or not, we choose Levodopa, Doxorubicin, Amantadine and Flecainide as the representative drugs to validate their potential diseases predicted by BNNR and then list the confirmed information of top-5 candidate diseases for them. We confirm the potential diseases associated with the given drug by authoritative public databases, such as DrugBank, CTD (Davis et al., 2013) and KEGG (Kanehisa et al., 2014). The predicted results and the supporting evidences are summarized in Table 2. For each representative drug, more than three new drug–disease associations on top-5 have been reported in the public databases. It demonstrates the effectiveness of BNNR in predicting novel indications for drugs in practical use.

Table 2.

The top five candidate diseases for Levodopa, Doxorubicin, Amantadine and Flecainide

Drugs (DrugBank IDs)	Top five candidate diseases (OMIM IDs)	Evidences
Levodopa (DB01235)	Parkinson disease (168600)	KEGG/DB/CTD
	Dementia (125320)	DB/CTD
	Multiple sclerosis (126200)	CTD
	Pheochromocytoma (171300)	CTD
	Hyperplastic myelinopathy (147530)
Doxorubicin (DB00997)	Small cell cancer of the lung (182280)	CTD
	Dohle bodies (223350)
	Testicular germ cell tumor (273300)	CTD
	Reticulum cell sarcoma (267730)	CTD
	Leukemia (109543)	KEGG/DB/CTD
Amantadine (DB00915)	Parkinson disease (168600)	KEGG/DB/CTD
	Dementia (125320)	DB/CTD
	Restless legs syndrome (102300)
	Alzheimer disease (104300)	CTD
	Malignant hyperthermia (217150)
Flecainide (DB01195)	Atrial fibrillation (608583)	CTD
	Cardiac arrhythmia (115000)	DB/CTD
	Diastolic hypertension (608622)	CTD
	Nephropathy-hypertension (161900)
	Hyperplastic myelinopathy (147530)

Furthermore, BNNR identifies other new indications including: Levodopa for hyperplastic myelinopathy; Doxorubicin for dohle bodies; Amantadine for restless legs syndrome and malignant hyperthermia; Flecainide for nephropathy-hypertension and hyperplastic myelinopathy. These predicted associations are not yet reported in current literature, but may have a greater likelihood of existing. There are great opportunities to research and validate these associations for medical researchers and pharmaceutical companies.

3.6 The effects of bounded constrain and regularization model of BNNR on performance

In order to evaluate the effectiveness of bounded constraint [0, 1] and regularization model, we compare BNNR with two models in 10-fold cross-validation. The first model is BNNR without bounded constraint [0, 1] (referred to as NNR), while the other one is BNNR without regularization term (referred to as BNN). Specifically, NNR is defined as:

$${\displaystyle \underset{X}{\min }}{\Vert X\Vert }_{*}+\frac{\alpha }{2}\Vert {{\mathcal{P}}_{\Omega }(X)-{\mathcal{P}}_{\Omega }(M)\Vert }_F^2,$$ (12)

and BNN is defined as:

$$\begin{array}{c}{\displaystyle \underset{X}{\min }}{\Vert X\Vert }_{*}\hfill \\ \mathit{s}.\mathit{t}.{\mathcal{P}}_{\Omega }(X)={\mathcal{P}}_{\Omega }(M)\hfill \\ 0\le X\le 1.\hfill \end{array}$$ (13)

One can find that incorporating the regularization term leads to more robust prediction results compared to simply minimizing the nuclear norm, where the noise in similarity measures is tolerated. Moreover, constraining the predicted association values within [0, 1] further improves the prediction accuracy. This is shown in the 10-fold cross-validation results illustrated in Figure 4.

Fig. 4.

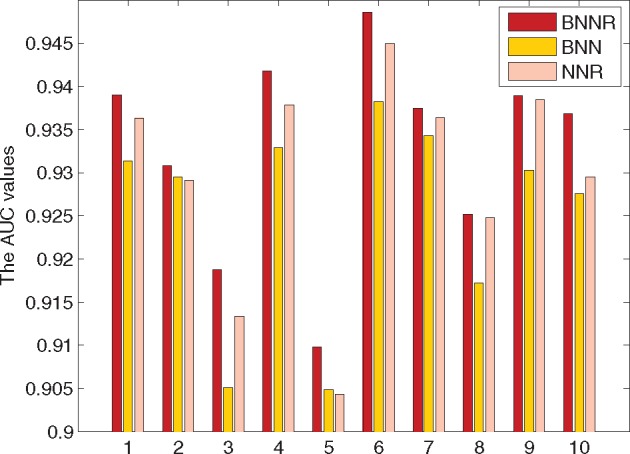
Performance comparison of BNNR, NNR and BNN in 10-fold cross-validation in terms of AUC values

To further verify the robustness of BNNR, we increasingly add random noises to the drug–drug and disease–disease similarity matrices. The noise entries are drawn independently from $\mathcal{N}(\mathrm{0,1}/20)$ and noise rate is the proportion of the contaminated entries with respect to all components of similarity matrix. We set the noise rate in [0, 0.3] with an increase step size of 0.06. BNNR and BNN are compared in 10-fold cross-validation in terms of AUC values. Without a surprise, as shown in Figure 5, the AUC values decrease gradually as the noise rate increases in both BNNR and BNN. However, the decrease of BNNR is much slower compared to BNN, indicating that BNNR is able to better tolerate noisy similarity computations. This also explains why BNNR leads to better prediction accuracy when the nuclear norm regularization term is incorporated.

Fig. 5.

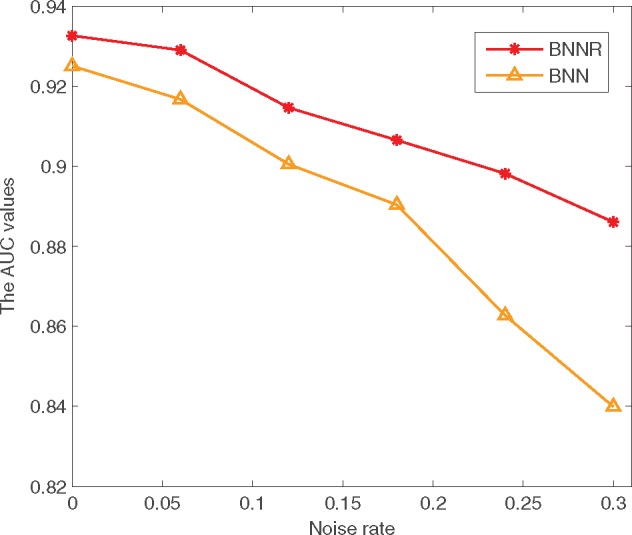
Performance comparison of BNNR and BNN under different noise rates in terms of AUC values

3.7 Experiments on the other datasets

In order to illustrate the adaptability of BNNR in different datasets, we perform BNNR on the two other datasets including Cdataset and DNdataset, which are used in our previous work (Luo et al., 2016, 2018). Cdataset (Luo et al., 2016) contains 663 drugs collected in DrugBank, 409 diseases obtained in OMIM database and 2352 known drug–disease associations. DNdataset (Martinez et al., 2015) includes 1490 drugs registered in DrugBank, 4516 diseases annotated by Disease Ontology (DO) terms and 1008 known drug–disease associations. We evaluate the robustness of our method on these two datasets by performing 10-fold cross-validation and the de novo test. The parameters of BNNR for Cdataset and DNdataset are set as Section 3.2. (For Cdataset, α = 1 and β = 10. For DNdataset, α = 1 and β = 1.)

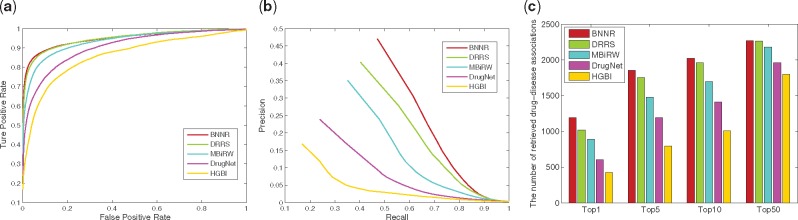
For Cdataset, as shown in Figure 6, BNNR obtains AUC value of 0.948 in 10-fold cross-validation, while HGBI, DrugNet, MBiRW and DRRS have 0.858, 0.903, 0.933 and 0.947, respectively. The PR curves illustrate that BNNR obtains the best precision with 0.471, while HGBI, DrugNet, MBiRW and DRRS have 0.168, 0.239, 0.351 and 0.403, respectively. Meanwhile, BNNR outperforms the other methods on top rank results. More specifically, at top-5 rank, 1855 associations out of 2532 are identified by BNNR, while only 796, 1193, 1481 and 1753 associations are predicted by HGBI, DrugNet, MBiRW and DRRS, respectively. In the de novo test, PR curve and top rank results are illustrated in Figure 7. BNNR obtains AUC value of 0.812, while HGBI, DrugNet, MBiRW and DRRS have 0.732, 0.785, 0.804 and 0.819, respectively. DRRS achieves slightly better performance than BNNR. In addition, BNNR outperforms the other methods with respect to different top-ranked thresholds. Specifically, for 177 drug associations, BNNR retrieves 87(49.2%) drugs at top 10 rank, while HGBI, DrugNet, MBiRW and DRRS have 48(27.1%), 61(34.5%), 80(45.2%) and 78(44.0%), respectively.

Fig. 6.

The performance of all methods in predicting drug–disease associations for 10-fold cross-validation on Cdataset. (a) ROC curve of prediction results. (b) PR curve of predicting candidate diseases for drugs. (c) The number of correctly retrieved drug–disease associations for various rank threshold

Fig. 7.

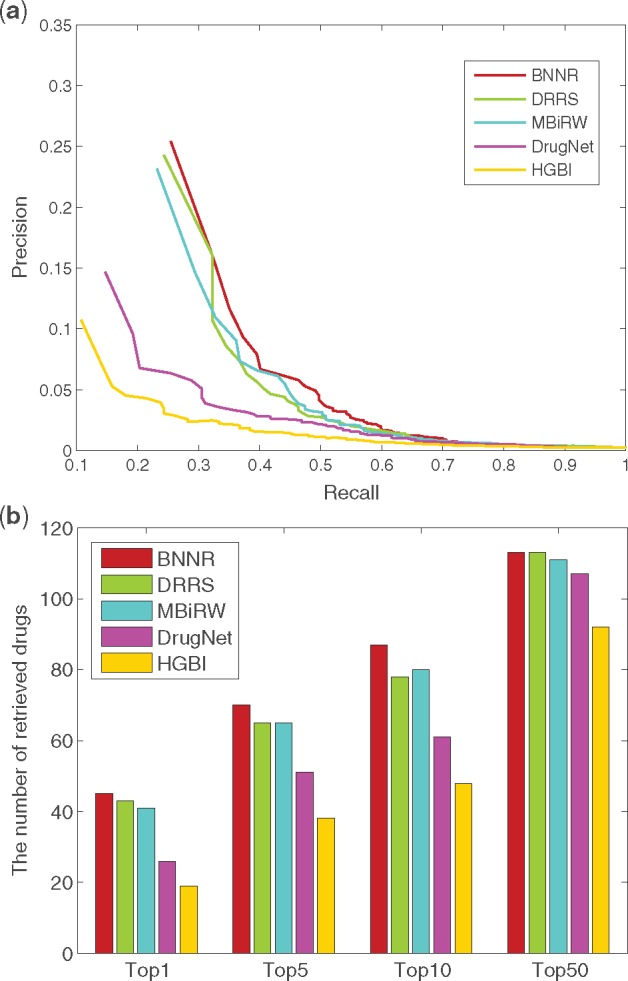
The performance of all methods in predicting potential diseases for new drugs on Cdataset. (a) PR curve of prediction results. (b) The number of retrieved drugs for various rank thresholds

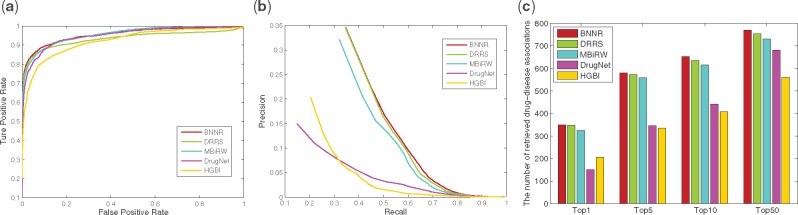
For DNdataset, as shown in Figure 8, BNNR obtains AUC value of 0.955 in 10-fold cross-validation, while HGBI, DrugNet, MBiRW and DRRS have 0.921, 0.950, 0.956 and 0.934, respectively. The PR curves show that BNNR obtains the best precision with 0.347, while HGBI, DrugNet, MBiRW and DRRS have 0.204, 0.150, 0.321 and 0.346, respectively. It is a noteworthy fact that BNNR has better AUC value and precision compared to other methods. Meanwhile, BNNR outperforms the other methods on top rank results from four different thresholds. In de novo test, PR curve and top rank results of de novo test are illustrated in Figure 9. BNNR obtains AUC value of 0.956, which is slightly worse than DrugNet and MBiRW, while HGBI and DRRS have 0.928 and 0.946, respectively. BNNR surpasses the other methods on top rank results: for 347 test drug associations, BNNR retrieves 145 drugs at top 1 rank, while HGBI, DrugNet, MBiRW and DRRS have 111, 84, 136 and 134, respectively.

Fig. 8.

The performance of all methods in predicting drug–disease association for 10-fold cross-validation on DNdataset. (a) ROC curve of prediction results. (b) PR curve of predicting candidate diseases for drugs. (c) The number of correctly retrieved drug–disease associations for various rank threshold

Fig. 9.

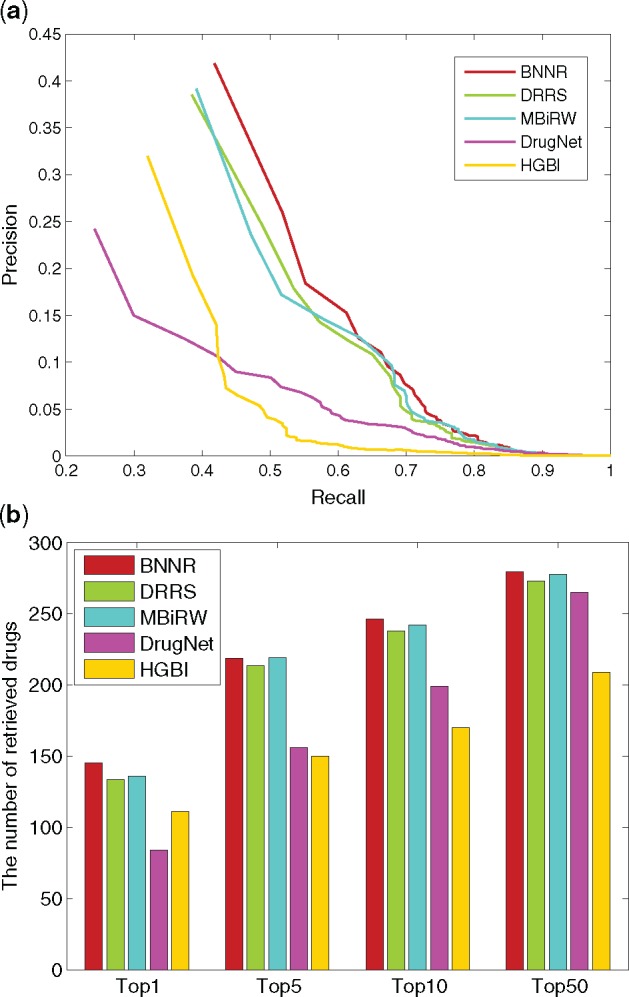
The performance of all methods in predicting potential diseases for new drugs on DNdataset. (a) PR curve of prediction results. (b) The number of retrieved drugs for various rank thresholds

3.8 Computation time comparisons

In order to compare the computational efficiency of different methods, we have conducted a 10-fold cross-validation on the gold standard dataset, Cdataset and DNdataset. The running times of these methods were obtained on a Linux server with CPU 2.30 GHz and 128 GB memory, which are shown in Supplementary Table S1. The average running time of BNNR is more than HGBI and DrugNet but less than MBiRW and DRRS on the gold standard dataset. Although HGBI is much faster than the others, it yields the lowest precision and AUC values. Moreover, compared to DrugNet on a bigger dataset such as DNdataset, BNNR is more computationally efficient.

4 Conclusions

This study has developed a novel method named BNNR for drug repositioning. BNNR not only can restrict all predicted matrix entry values within a specific interval, but also exhibit robustness to tolerate potentially noisy similarity calculations. The results of cross-validation and de novo experiments have demonstrated that BNNR is an effective prediction approach. Especially, comparing with the existing drug repositioning methods, BNNR yields both the best AUC value and the best precision in most measures. Our case studies have confirmed the reliability of the identified new drug–disease associations. In the future, we plan to integrate drug–target information into the existing heterogeneous networks to further improve the prediction ability of BNNR.

Funding

This work was supported by the National Natural Science Foundation of China under Grant number (61732009, 61622213, 61772552 and 61420106009).

Conflict of Interest: none declared.