Locality-sensitive hashing for the edit distance

Abstract

Motivation

Sequence alignment is a central operation in bioinformatics pipeline and, despite many improvements, remains a computationally challenging problem. Locality-sensitive hashing (LSH) is one method used to estimate the likelihood of two sequences to have a proper alignment. Using an LSH, it is possible to separate, with high probability and relatively low computation, the pairs of sequences that do not have high-quality alignment from those that may. Therefore, an LSH reduces the overall computational requirement while not introducing many false negatives (i.e. omitting to report a valid alignment). However, current LSH methods treat sequences as a bag of k-mers and do not take into account the relative ordering of k-mers in sequences. In addition, due to the lack of a practical LSH method for edit distance, in practice, LSH methods for Jaccard similarity or Hamming similarity are used as a proxy.

Results

We present an LSH method, called Order Min Hash (OMH), for the edit distance. This method is a refinement of the minHash LSH used to approximate the Jaccard similarity, in that OMH is sensitive not only to the k-mer contents of the sequences but also to the relative order of the k-mers in the sequences. We present theoretical guarantees of the OMH as a gapped LSH.

Availability and implementation

The code to generate the results is available at http://github.com/Kingsford-Group/omhismb2019.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Measuring sequence similarity is the core of many algorithms in computational biology. For example, in the overlap–layout–consensus paradigm to assemble genomes (e.g. Jaffe et al., 2003; Myers et al., 2000), the first overlap step consists of aligning the reads against one another to determine which pairs have a significant alignment (an overlap). In meta-genomics, sequencing reads, or longer sequences created from these reads, are aligned against known genomes, or against one another to cluster the sequences, to determine the constituent species of the sample. Sequence similarity is also at the heart of the many general sequence aligners, either genome to genome [e.g. MUMmer4 (Marçais et al., 2018), LASTZ (Harris, 2007)] or reads to genome [e.g. Bowtie2 (Langmead and Salzberg, 2012), BWA (Li and Durbin, 2010)], that are used in countless pipelines in bioinformatics.

Despite many algorithmic and engineering improvements [e.g. implementation on SIMD (Zhao et al., 2013) and GPU (Liu et al., 2012)], computing the sequence alignment or edit distance between two sequences takes approximately quadratic time in the length of the input sequences, which remains computationally expensive in practice. Given that the edit distance is likely not computable in strong subquadratic time (Backurs and Indyk, 2015), most aligners rely on heuristics to more quickly detect sequences with a high probability of having an alignment.

Recent aligners, such as Mash (Ondov et al., 2016), Mashmap (Jain et al., 2017), or overlappers such as MHap (Berlin et al., 2015), use a method called ‘locality-sensitive hashing’ (LSH) to reduce the amount of work necessary (Indyk and Motwani, 1998). The procedure is a dimensionality reduction method and works in two steps. First, the sequences (or part of the sequences) are summarized into sketches that are much smaller than the original sequences while preserving important information to estimate how similar two sequences are. Second, by directly comparing those sketches (with no need to refer to the original sequences) or by using these sketches as keys into hash tables, the software finds pairs of sequences that are likely to be similar. A more thorough, and computationally expensive, alignment procedure may then be used on the candidate pairs to refine the actual alignments.

In an LSH method, the distance between sketches is used as a first approximation for the distance between the sequences. That is, with high probability, two sequences which are very similar must have sketches which are similar, and conversely dissimilar sequences have dissimilar sketches. More precise definition of these concepts is given in Section 2.

Instead of using an LSH for the edit distance or an alignment score, in practice sequence alignment programs use the minHash LSH (Broder, 1997) for the Jaccard similarity or an LSH for the Hamming distance as a proxy for the edit distance. Although these two techniques have proven themselves useful in practice, they suffer from one major flaw: neither the Jaccard similarity nor the Hamming similarity directly corresponds to the edit distance (see Section 2.2 for examples). In fact, it is possible to find sequences that are indistinguishable according to the Jaccard similarity, but have large edit distance. Similarly, with the Hamming distance, there exist sequences with very low edit distance that are completely dissimilar according to the Hamming similarity.

Depending on the problem and the software implementation, the cases above can lead to false negatives (an alignment is missed) and a decrease in precision, or false positives (a nonexistent potential alignment reported) and extra computational work. An LSH method for edit distance instead of the proxy Jaccard or Hamming similarities would reduce both of these issues.

Although multiple definitions are possible for sequence similarity (or distance), in this study, we focus on the edit distance (a.k.a. Levenshtein distance, Levenshtein, 1966), which is the number of operations (mismatch, insertion, deletion) needed to transform a string into another one.

Two methods that are LSH for the edit distance have been described previously. Bar-Yossef et al. (2004) propose a sketch that can distinguish, with some probability, between sequences with edit distance $\le t$ from sequences with edit distance $\ge {\left(\mathit{tn}\right)}^{2/3}$, where n is the length of the sequences, for any $t\le \sqrt{n}$. They use an indirect method to obtain an LSH for the edit distance: first they embed the edit distance space into a Hamming space with low distortion, and second, apply an LSH on the Hamming space. That is, the input sequence is first transformed into a bit vector of high dimension, then sketching for the Hamming distance is applied to obtain an LSH for the edit distance.

Similarly, Ostrovsky and Rabani (2007) propose a two-step method, where the edit distance space is first embedded into an ${\ell }_1$ space with low distortion, then a sketching algorithm for the ${\ell }_1$ (Kushilevitz et al., 2000) is used to obtain an LSH for the edit distance. This method can distinguish between sequences with edit distance $\le t$ and edit distance $\ge t·2^{c\sqrt{\hspace{0.17em}\text{log}\hspace{0.17em}n\hspace{0.17em}\text{log}\hspace{0.17em}\hspace{0.17em}\text{log}\hspace{0.17em}n}}$, for some constant c.

We propose a simpler and direct method that is an LSH for the edit distance. Our method is an extension to the minHash method. We call our method OMH for Order Min Hash, and it can be seen as a correction of the minHash method. The probability of hash collision in the OMH method is the product of two probabilities. The first is the probability to select a k-mer from the set of common k-mers between the two sequences. This probability is similar to minHash that estimates the Jaccard similarity between the k-mer contents of two sequences. However, there is one key difference: the minHash method estimates the Jaccard similarity which treats sequences as sets of k-mers, and the number of occurrences of each k-mer in the sequences is ignored, whereas OMH estimates the weighted Jaccard, where the number of occurrences of a k-mer in a sequence is significant, i.e. the weighted Jaccard works with multi-sets. The second probability is the likelihood that the common k-mers appear in the same relative order in the two sequences. Therefore, OMH is sensitive not only to the k-mer content of the sequences but also to the order of the k-mers in the sequences.

The sketch proposed for OMH is only slightly bigger than the sketch for minHash while maintaining significantly more information about the similarity of two sequences. In addition to providing an estimate for the edit distance between two sequences, it also provides an estimate of the k-mer content similarity (the weighted Jaccard) and how similar the relative order is between the common k-mers of the two sequences.

Section 2 summarizes the notation used though out and main results. Detailed proofs of the results are given in Section 3. Section 4 discusses some practical consideration on the implementation of the sketches.

2 Main results

2.1 Concepts and definitions

Similarity and dissimilarity. A dissimilarity is a function $d:\mathcal{U}\times \mathcal{U}\to [0,1]$ that indicates the distance between two elements in the universe $\mathcal{U}$. d satisfies the triangle inequality and $d(x,y)=0$ means that x  =  y. In other words, a dissimilarity is a normalized distance. A similarity is a function $s(·,·)$ such that $1-s$ is a dissimilarity. Hence, a dissimilarity defines a similarity and vice versa. We will therefore use either of the terms ‘edit dissimilarity’ or ‘edit similarity’.

Given two strings $S_1,S_2\in {\Sigma }^n$ of length n (where Σ is the alphabet of size $\sigma =\hspace{0.17em}|\hspace{0.17em}\Sigma \hspace{0.17em}|\hspace{0.17em}$), the Hamming dissimilarity ${\mathrm{H}}_{\mathrm{d}}(S_1,S_2)$ is the number of indices at which S₁ and S₂ differ divided by n: ${\mathrm{H}}_{\mathrm{d}}(S_1,S_2)=\hspace{0.17em}|\hspace{0.17em}\{i\in [n]\hspace{0.17em}|\hspace{0.17em}{S}_1[i]\ne S_2[i\left]\right\}\hspace{0.17em}|\hspace{0.17em}/n$ ($\left[n\right]$ denotes the set $\{0,\dots ,n-1\}$). The edit dissimilarity ${\mathrm{E}}_{\mathrm{d}}(S_1,S_2)$ (a.k.a. normalized edit distance) is the minimum number of indels (short for insertion or deletion) and mismatches necessary to transform S₁ into S₂, divided by n. Given two sets A and B, the Jaccard similarity is $\mathrm{J}(A,B)=\hspace{0.17em}|\hspace{0.17em}A\cap B\hspace{0.17em}|\hspace{0.17em}/\hspace{0.17em}|\hspace{0.17em}A\cup B\hspace{0.17em}|\hspace{0.17em}$.

Gapped LSH. Let $\mathcal{H}$ be a set of hash functions defined on a set $\mathcal{U}$ (the universe). A probability distribution on the set $\mathcal{H}$ is called $(s_1,s_2,p_1,p_2)$-sensitive for the similarity s when

$$s(x,y)\ge s_1\Rightarrow \underset{h\in \mathcal{H}}{\mathrm{Pr}}\left[h\right(x)=h(y\left)\right]\ge p_1,$$ (1)

$$s(x,y)\le s_2\Rightarrow \underset{h\in \mathcal{H}}{\mathrm{Pr}}\left[h\right(x)=h(y\left)\right]\le p_2,$$ (2)

where $s_1\ge s_2$ and $p_1\ge p_2$. A similarity admits a gapped LSH scheme if there exists a distribution on a set of hash functions that is $(s_1,s_2,p_1,p_2)$-sensitive. In the definition above, the probability is taken over the choice of the hash function in $\mathcal{H}$ and the implications hold for any choice of x and $y\in \mathcal{U}$. In a gapped LSH, the probability of a hash collision is increased ($\ge p_1$) between similar elements, and less likely ($\le p_2$) for dissimilar elements.

In the following, the probabilities are always taken over the choice of the hashing function, even though we may omit the ‘$h\in \mathcal{H}$’ subscript.

LSH. An LSH for a similarity is a family of hash functions that is $(r,r,r,r)$-sensitive for any $r\in (0,1)$. Equivalently, the family of hash functions satisfies $\mathrm{Pr}\left[h\right(x)=h(y\left)\right]=s(x,y)$. In practice a gapped LSH is typically used to put elements into a hash table where there is high likelihood of a collision, whereas a full LSH can be used as a direct estimator of the underlying measurement.

minHash sketch. Let the universe $\mathcal{U}$ be a family of sets on the ground set X (i.e. $\mathcal{U}\subset \mathcal{P}\left(X\right)$). The minHash LSH for the Jaccard similarity is defined as the uniform distribution on the set ${\mathcal{H}}_{\min }=\left\{h_{\pi }\right(A)={\min }_{x\in A}\pi (x)\hspace{0.17em}|\hspace{0.17em}\pi \hspace{0.17em}\text{is}\hspace{0.17em}\mathrm{a}\hspace{0.17em}\text{permutation}\hspace{0.17em}\text{of}\hspace{0.17em}\mathrm{X}\}$. That is, the hash function selects the smallest element of the set A according to some ordering π of the elements of the ground set X. This family of hash functions is $(s,s,s,s)$-sensitive for any value of $s\in [0,1]$, or equivalently $\mathrm{Pr}\left[h\right(A)=h(B\left)\right]=\mathrm{J}(A,B)$.

LSH for Hamming similarity. The Hamming similarity between two sequences with same length n is the proportion of positions which are equal: ${\mathrm{H}}_{\mathrm{s}}(S_1,S_2)=\hspace{0.17em}|\hspace{0.17em}\{i\in [n]\hspace{0.17em}|\hspace{0.17em}{S}_1[i]=S_2[i\left]\right\}\hspace{0.17em}|\hspace{0.17em}/n$. For the Hamming similarity, the uniform distribution on $\mathcal{H}=\left\{h_i\right(S)=S[i]\hspace{0.17em}|\hspace{0.17em}i\in [n\left]\right\}$ satisfies $\mathrm{Pr}\left[h\right(S_1)=h(S_2\left)\right]={\mathrm{H}}_{\mathrm{s}}(S_1,S_2)$.

String k-mer set. For a sequence S, the set of its constituent k-mers is ${\mathcal{M}}_k\left(S\right)=\left\{S\right[i:k]\hspace{0.17em}|\hspace{0.17em}i\in [\hspace{0.17em}|\hspace{0.17em}S\hspace{0.17em}|\hspace{0.17em}-k+1\left]\right\}$, where $S[i:k]$ is the substring of length k starting at index i. By extension, the Jaccard similarity between two sequences is the Jaccard similarity between their k-mer sets: $\mathrm{J}(S_1,S_2)=\mathrm{J}\left({\mathcal{M}}_k\right(S_1),{\mathcal{M}}_k(S_2\left)\right)$.

Weighted Jaccard. The weighted Jaccard similarity on multi-sets (or weighted sets) is defined similarly to the Jaccard similarity on sets, where the intersection and union take the multiplicity of the elements into account. More precisely, a multi-set A is defined by an index function ${\chi }_A:\mathcal{U}\to \mathbb{N}$, where ${\chi }_A\left(x\right)$ gives the multiplicity of x in A (zero if not present in A). The index function of the intersection of two multi-sets is the minimum of the index functions, and for the union it is the maximum. Then, the weighted Jaccard is defined by

$${\mathrm{J}}^{\mathrm{w}}(A,B)=\frac{\sum _{x\in \mathcal{U}}\min \left({\chi }_A\right(x),{\chi }_B(x\left)\right)}{\sum _{x\in \mathcal{U}}\max \left({\chi }_A\right(x),{\chi }_B(x\left)\right)}.$$

This is a direct extension to the set definitions, where the index function takes values in {0, 1}.

2.2 Jaccard and Hamming similarities differ from edit similarity

Similarly to the definition of the LSH, we say that a similarity f₁ is a $(s_1,s_2,t_1,t_2)$-proxy for the similarity f₂ if

$$f_1(x,y)\ge s_1\Rightarrow f_2(x,y)\ge t_1$$ (3)

$$f_1(x,y)\le s_2\Rightarrow f_2(x,y)\le t_2$$ (4)

That is high similarity for f₁ implies high similarity for f₂, and the converse. Because of the similar structure between the definitions of sensitivity and proxy, if f₁ is not a proxy for f₂ (for any non-trivial choice of parameters $s_1,s_2,t_1,t_2$), then an LSH for f₁ is not an LSH for f₂.

We show here that neither the Hamming similarity nor the Jaccard similarity is a good proxy for the edit dissimilarity. More precisely, only one of the implications above is satisfied.

Jaccard similarity differs from edit similarity. A low Jaccard similarity does imply a low edit similarity (Equation 4). On the other hand, consider the sequence $S_1=0\dots 01\dots 1$ that has n − k 0s followed by k 1s, and S₂ with k 0s followed by n − k 1s (k fixed, n arbitrarily large). The k-mer sets of S₁ and S₂ are identical, hence $\mathrm{J}(S_1,S_2)=1$, while the edit similarity is $\le 2k/n$. These sequences are indistinguishable according to the Jaccard similarity while having arbitrarily small edit similarity (Equation 3 not satisfied).

Weighted Jaccard similarity differs from edit similarity. Consider two de Bruijn sequences: sequences of length σ^k containing every k-mer exactly once (van Aardenne-Ehrenfest and de Bruijn, 1951). There is a very, very large number of such sequences [${(\sigma !)}^{{\sigma }^{k-1}}/{\sigma }^n$], and although any two such sequences have exactly the same k-mer content, they might otherwise have a very low edit similarity. Both the Jaccard and weighted Jaccard similarities fail to distinguish between de Bruijn sequences, regardless of their mutual edit dissimilarity.

For example, the two sequences 1111011001010000111 and 0000101001111011000 of length 19 each contain exactly the 16 possible 4-mers; hence, their Jaccard and weighted Jaccard similarities are 1. Their edit similarity is only $\approx 0.37$. By comparison, two random binary sequences of length 19 have an average edit similarity of $\approx 0.62$ and an average Jaccard similarity of $\approx 0.36$. In other words, these two de Bruijn sequences are much more dissimilar than two random sequences despite having a perfect Jaccard similarity.

More generally, both Jaccard and weighted Jaccard similarities treat sequences as bags of k-mers. The information on relative order of these k-mers within the sequence is ignored, although it is of great importance for the edit similarity. In contrast, an OMH sketch does retain some information on the order of the k-mers in the original sequence. In the case of the two de Bruijn sequences above, the proportion of pairs of k-mers that are in the same relative order in the two sequences is 0.4. The expected similarity between the OMH sketches of these sequences is also equal to 0.4.

Hamming similarity differs from edit similarity. A high Hamming similarity does imply a high edit similarity (Equation 3). The opposite is not true however. Consider the sequences of length n, $S_1=0101\dots 01$ and $S_2=1010\dots 10$. These sequences have a Hamming similarity of 0 and an edit similarity of $\ge 1-2/n$ (two indels). That is, these sequences are as dissimilar as possible according to the Hamming dissimilarity, but an arbitrarily high edit similarity (Equation 4 not satisfied).

The Hamming similarity is very sensitive to the absolute position in the string. A single shift between two sequences has a large impact on the Hamming similarity but only a unit cost for the edit similarity. An OMH sketch on the other hand only contains relative order between k-mers and is indifferent to changes in absolute position.

2.3 LSH for the edit similarity

An LSH for the edit similarity must be sensitive to the k-mer content of the strings and the relative order of these k-mers, but relatively insensitive to the absolute position of the k-mers in the string. This motivates the definition below. Similarly to the minHash, k-mers are selected at random by using a permutation on the k-mers. Additionally, to preserve information about relative order, $\ell$k-mers are selected at once and recorded in the order they appear in the sequence (rather than the order defined by the permutation).

Additionally, the method must handle repeated k-mers. Two copies of the same k-mer occur at different positions in the sequence, and it is important for the relative ordering between k-mers to distinguish between these two copies. We make k-mers unique by appending to them their ‘occurrence number’.

More precisely, for a string S of length $\hspace{0.17em}|\hspace{0.17em}S\hspace{0.17em}|\hspace{0.17em}=n$, consider the set ${\mathcal{M}}_k^w\left(S\right)$ of the pairs of the k-mers and their occurrence number. If there are x copies of m in sequence S, then the x pairs $(m,0),\dots ,(m,x-1)$ are in the set ${\mathcal{M}}_k^w\left(S\right)$, and the occurrence number denotes the number of other copies of m that are in the sequence S to the left of this particular copy. That is, if m is the k-mer at position i in S (i.e. $m=S[i:k]$), then its occurrence number is $\hspace{0.17em}|\hspace{0.17em}\{j\in [i]\hspace{0.17em}|\hspace{0.17em}S[j:k]=m\}\hspace{0.17em}|\hspace{0.17em}$. This set is the ‘multi-set’ of the k-mer content of string S, or the ‘weighted set’ of k-mers where the number of occurrences is the weight of the k-mer (hence the w superscript). We call a pair (m, i) of a k-mer and an occurrence number a ‘uniquified’ k-mer.

A permutation π of ${\Sigma }^k\times \left[n\right]$ defines two functions $h_{\ell ,\pi }^w$ and $h_{\ell ,\pi }$. $h_{\ell ,\pi }^w\left(S\right)=\left(\right(m_1,o_1),\dots ,(m_{\ell },o_{\ell }\left)\right)$ is a vector of length $\ell$ of elements of ${\mathcal{M}}_k^w\left(S\right)$ such that:

• the pairs (m_i, o_i) are the $\ell$ smallest elements of ${\mathcal{M}}_k^w\left(S\right)$ according to π,

• the pairs are listed in the vector in the order in which the k-mer appears in the sequence S. That is, if i < j, $m_i=S[x:k]$ and $m_j=S[y:k]$, then x < y.

The vector $h_{\ell ,\pi }\left(S\right)=(m_1,\dots ,m_{\ell })$ contains only the k-mers from $h_{\ell ,\pi }^w\left(S\right)$, in the same order. The OMH method is defined as the uniform distribution on the set of hash functions ${\mathcal{H}}_{k,\ell }=\{h_{\ell ,\pi }\hspace{0.17em}|\hspace{0.17em}\pi \hspace{0.17em}\mathrm{a}\hspace{0.17em}\text{permutation}\hspace{0.17em}\text{of}\hspace{0.17em}{\Sigma }^k\times [n\left]\right\}$.

For extreme cases, where $\ell =n-k+1$, the vector contains overlapping k-mers that cover the entire sequence S. In that case, equality of the hash values implies strict equality of the sequences.

At the other extreme, where $\ell =1$, the vectors contain only one k-mer and no relative order information is preserved. In that case, only the k-mer content similarity between S₁ and S₂ matters.

The weighted Jaccard similarity ${\mathrm{J}}^{\mathrm{w}}(S_1,S_2)$ of two sequences is the weighted Jaccard of their k-mer content (seen as multi-set). Because k-mers were made unique by their occurrence number in ${\mathcal{M}}_k^w\left(S\right)$, the weighted Jaccard similarity is equivalently defined as ${\mathrm{J}}^{\mathrm{w}}(S_1,S_2)=\mathrm{J}\left({\mathcal{M}}_k^w\right(S_1),{\mathcal{M}}_k^w(S_2\left)\right)$.

Theorem 1. When$\ell =1$, OMH is an LSH for the weighted Jaccard similarity:

$$\mathrm{Pr}\left[h_{1,\pi }\right(S_1)=h_{1,\pi }(S_2\left)\right]={\mathrm{J}}^{\mathrm{w}}(S_1,S_2).$$ (5)

Proof. This proof is similar to that of minHash and the Jaccard similarity (Broder, 1997). Because every uniquified k-mer in ${\mathcal{M}}_k^w\left(S_1\right)\cup {\mathcal{M}}_k^w\left(S_2\right)$ has the same probability of being selected, the probability of having a hash collision is the same as selected a k-mer from the intersection where the probability of picking a k-mer is weighted by its maximum occurrence number. □

As we shall see in Section 4.4, the weighted Jaccard similarity contains approximately the same information as the Jaccard similarity with respect to the edit similarity.

For the general case $1<\ell <n-k+1$, we shall prove the following theorem in Section 3 that OMH is a gapped LSH for the edit dissimilarity.

Theorem 2. For any$\ell \in [2,n-k]$and any$1>s_1\ge s_2>0$, there exist functions$p_{n,k,\ell }^1(·)$and$p_{n,k,\ell }^2(·)$such that OMH is$\left(s_1,s_2,p_{n,k,\ell }^1\left(s_1\right),p_{n,k,\ell }^2\left(s_2\right)\right)$-sensitive for the edit distance.

The actual functions p¹ and p² are explicitly defined in Section 3, but they may not be easily expressed with elementary functions in general.

3 Proofs of main results

We shall now prove Theorem 2 that OMH is sensitive for the edit similarity by exhibiting the relations between parameters $(s_1,s_2,p_1,p_2)$ that satisfy Equations (1) and (2). We will break the proof in two lemmas that provide the relations between s₁, p₁ and between s₂, p₂. In the following, S₁ and S₂ are two sequences of length n. The number of k-mers in each of these sequences is $n_k=n-k+1$.

In the following, we assume that a binomial coefficient $(\begin{array}{c}n\\ k\end{array})$ where n is negative or null is equal to 0. In these proofs, it means that the probability of choosing elements from the empty set is zero.

Lemma 1. ${\mathrm{E}}_{\mathrm{s}}(S_1,S_2)\ge s_1\Rightarrow \mathrm{Pr}\left[h_{\ell ,\pi }\right(S_1)=h_{\ell ,\pi }(S_2\left)\right]\ge p_1$ when

$$p_1=\frac{\left(\begin{array}{c}n-n(k+2)(1-s_1)\\ \ell \end{array}\right)}{\left(\begin{array}{c}{n}_k+\mathit{kn}(1-s_1)\\ \ell \end{array}\right)}.$$ (6)

Proof. The situation is similar to the minHash method. Suppose that ${\mathrm{E}}_{\mathrm{s}}(S_1,S_2)\ge s_1$, then the edit dissimilarity ${\mathrm{E}}_{\mathrm{d}}(S_1,S_2)=1-{\mathrm{E}}_{\mathrm{s}}(S_1,S_2)\le 1-s_1$ and the number of mismatches and indels is $\le n(1-s_1)$. Any alignment between s₁ and s₂ has at most $n(1-s_1)$ mismatches and indels, because ${\mathrm{E}}_{\mathrm{d}}(S_1,S_2)\le 1-s_1$. Therefore, there are at least $n_k-\mathit{kn}(1-s_1)$k-mers in the aligned bases, as an error (mismatch or indel) affects at most k consecutive k-mers.

Similarly, the size of the set ${\mathcal{M}}_k^w\left(S_1\right)\cup {\mathcal{M}}_k^w\left(S_2\right)$ is maximized when all the k-mers that are not part of the alignment are different. Then, $\hspace{0.17em}|\hspace{0.17em}{\mathcal{M}}_k^w\left(S_1\right)\cup {\mathcal{M}}_k^w\left(S_2\right)\hspace{0.17em}|\hspace{0.17em}$ is at most $n_k+\mathit{kn}(1-s_1)$.

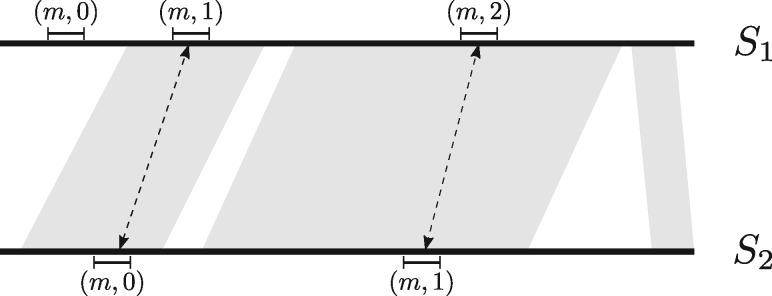
We estimate the probability to have a hash collision from the number of uniquified k-mers in the aligned bases. As seen in Figure 1, it is possible for a k-mer m with different occurrence numbers to be part of the aligned bases. Any permutation that has $(m,0)$ in the lowest $\ell$ uniquified k-mers does not lead to a hash collision. Let x be the number of k-mers in the aligned bases with occurrence number that disagree between S₁ and S₂. Therefore, there are at least x k-mers outside of the aligned bases representing at least $x+k-1$ unaligned bases. Given that the edit similarity is $\ge s_1$, the number of unaligned bases is at most $2n(1-s_1)$ and $x+k-1\le 2n(1-s_1)$. Consequently, the number of k-mers in the aligned bases to choose from is at least the number of k-mers in the aligned bases ($n_k-\mathit{kn}(1-s_1)$) minus the number of k-mers with disagreeing occurrence number (x) $n-n(k+2)(1-s_1)$.

Fig. 1.

For an alignment between S₁ and S₂, the gray area represents the aligned bases. A particular k-mer m is shown with its occurrence numbers. The occurrence number of the matched k-mer pairs in the aligned bases may not agree (as in this example). For every such m with a mismatch occurrence number in the aligned bases, there must exist an instance of m outside the aligned bases [$(m,0)$ in S₁ here]

Every element of ${\mathcal{M}}_k^w\left(S_1\right)\cup {\mathcal{M}}_k^w\left(S_2\right)$ has an equal probability to be in the lowest $\ell$ elements according to a permutation π; therefore, the probability of having a hash collision is:

$$\begin{array}{c}\mathrm{Pr}\left[h_{\ell ,\pi }\right(S_1)=h_{\ell ,\pi }(S_2\left)\right]\ge \mathrm{Pr}\left[h_{\ell ,\pi }^w\right(S_1)=h_{\ell ,\pi }^w(S_2\left)\right]\hfill \\ \ge \frac{\left(\begin{array}{c}n-n(k+2)(1-s_1)\\ \ell \end{array}\right)}{\left(\begin{array}{c}{n}_k+\mathit{kn}(1-s_1)\\ \ell \end{array}\right)}.\hfill \end{array}$$ (7)

This defines the relationship between p₁ and s₁ as in Equation (6).

□

For the proof of Equation (2), we will consider its contrapositive

$$\mathrm{Pr}\left[h_{\ell ,\pi }\right(S_1)=h_{\ell ,\pi }(S_2\left)\right]\ge p_2\Rightarrow {\mathrm{E}}_{\mathrm{s}}(S_1,S_2)>s_2.$$ (8)

That is for any two sequences with high probability of having a hash collision, the edit similarity of the sequences must be high.

To have a high probability of collision between two sketches, the sequences must (i) have a large number of common k-mers and (ii) these common k-mers should be mostly in the same relative order. The first condition corresponds to the sequences having a large weighted Jaccard similarity.

The second condition is related to common subsequences (CSs) between sequences of k-mers. A ‘common subsequence’ between $\left(a_i\right)$ and $\left(b_i\right)$ is a sequence of elements that are in both $\left(a_i\right)$ and $\left(b_i\right)$ and appear in the same order (formally an increasing function $\phi$ such that $a_{\phi \left(i\right)}=b_{\phi \left(i\right)}$). We emphasize here that the ‘sequences’ considered here are not DNA sequences, but ordered lists of k-mers ${\left(a_i\right)}_{i\in \mathbb{N}}$.

If the sequences S₁ and S₂ have a long CS of k-mers, then the probability to pick $\ell$k-mers in the same order between the common k-mers of S₁ and S₂ will be high. In turn, the presence of a long CS of k-mers implies a high similarity.

Considering Equation (8), we are looking for the lowest similarity (s₂) that is achievable given a high probability (p₂) of hash collision. This is done in two parts: (i) finding the lowest weighted Jaccard between S₁ and S₂ given the high hash collision rate and (ii) constructing a worse case example of having many CSs of k-mers while not having any long CS. This second problem is equivalent to finding, for a given L, a single sequence with as many as possible increasing subsequences of length L (see Lemma 3).

Lemma 2. ${\mathrm{E}}_{\mathrm{s}}(S_1,S_2)\le s_2\Rightarrow \mathrm{Pr}\left[h_{\ell ,\pi }\right(S_1)=h_{\ell ,\pi }(S_2\left)\right]\le p_2$ when

$$p_2=\frac{{\left(\frac{n_k}{n{s}_2-k+1}\right)}^{\ell }\left(\begin{array}{c}n{s}_2-k+1\\ \ell \end{array}\right)}{\left(\begin{array}{c}{n}_k\\ \ell \end{array}\right)}.$$ (9)

Proof. We use the notation $\left\{h_{\ell ,\pi }^w\right(S\left)\right\}$ for the set of elements in the vector $h_{\ell ,\pi }^w\left(S\right)$ (in other words, because all the elements are unique by construction, the elements without order).

As mentioned above, we consider the contrapositive state in Equation (8). We have that

$$\begin{array}{c}{p}_2<\mathrm{Pr}\left[h_{\ell ,\pi }\right(S_1)=h_{\ell ,\pi }(S_2\left)\right]=\hfill \\ \mathrm{Pr}\left[h_{\ell ,\pi }\right(S_1)=h_{\ell ,\pi }(S_2)\hspace{0.17em}|\hspace{0.17em}\{h_{\ell ,\pi }^w\left(S_1\right)\}=\{h_{\ell ,\pi }^w\left(S_2\right)\left\}\right]\hfill \\ ·\mathrm{Pr}\left[\right\{h_{\ell ,\pi }^w\left(S_1\right)\}=\{h_{\ell ,\pi }^w\left(S_2\right)\left\}\right].\hfill \end{array}$$ (10)

Under the conditional event (C) that $\{h_{\ell ,\pi }^w(S_1)\}=\{h_{\ell ,\pi }^w(S_2)\}$, we have $h_{\ell ,\pi }(S_1)=h_{\ell ,\pi }(S_2)\iff h_{\ell ,\pi }^w(S_1)=h_{\ell ,\pi }^w(S_2)$. The reverse implication ($\Leftarrow$) is always true as h is obtained from h^w by using only the k-mer in each element. The forward implication ($\Rightarrow$) holds thanks to (C). Given that the k-mers are listed in order in which they appear in the respective sequences, they are also listed in order of their occurrence number, and because the content in the weighted vectors h^w is the same, the equality of the unweighted vectors h implies equality of the weighted vectors.

Let $m=\hspace{0.17em}|\hspace{0.17em}{\mathcal{M}}_k^w\left(S_1\right)\cap {\mathcal{M}}_k^w\left(S_2\right)\hspace{0.17em}|\hspace{0.17em}$ be the size of the intersection of the weighted k-mer sets. The event (C) occurs when the $\ell$ smallest k-mers/occurrence number pairs according to the permutation π belong to the intersection ${\mathcal{M}}_k^w\left(S_1\right)\cap {\mathcal{M}}_k^w\left(S_2\right)$. Therefore,

$$\begin{array}{c}\mathrm{Pr}\left[\right\{h_{\ell ,\pi }^w\left(S_1\right)\}=\{h_{\ell ,\pi }^w\left(S_2\right)\left\}\right]=\frac{\left(\begin{array}{c}\hspace{0.17em}|\hspace{0.17em}{\mathcal{M}}_k^w\left(S_1\right)\cap {\mathcal{M}}_k^w\left(S_2\right)\hspace{0.17em}|\hspace{0.17em}\\ \ell \end{array}\right)}{\left(\begin{array}{c}\hspace{0.17em}|\hspace{0.17em}{\mathcal{M}}_k^w\left(S_1\right)\cup {\mathcal{M}}_k^w\left(S_1\right)\hspace{0.17em}|\hspace{0.17em}\\ \ell \end{array}\right)}\hfill \\ \le \frac{\left(\begin{array}{c}m\\ \ell \end{array}\right)}{\left(\begin{array}{c}{n}_k\\ \ell \end{array}\right)}.\hfill \end{array}$$ (11)

Consider now the sequences $M_k^w\left(S_1\right)$ and $M_k^w\left(S_2\right)$ of the elements of ${\mathcal{M}}_k^w\left(S_1\right)\cap {\mathcal{M}}_k^w\left(S_2\right)$ listed in the order in which they occur in S₁ and S₂, respectively. Both of these sequences have length m. Then, the event that $h_{\ell ,\pi }\left(S_1\right)=h_{\ell ,\pi }\left(S_2\right)$ under the condition (C) is equivalent to having the hash function $h_{\ell ,\pi }^w$ picking a CS of length $\ell$ between $M_k^w\left(S_1\right)$ and $M_k^w\left(S_2\right)$. Because the elements of these sequences are never repeated (it is a list of uniquified k-mers), the problem of finding CSs between $M_k^w\left(S_1\right)$ and $M_k^w\left(S_2\right)$ is identical to finding increasing subsequences (IS) in a sequence of integers of length m (Fredman, 1975; Hunt and Szymanski, 1977).

$$\mathrm{Pr}\left[h_{\ell ,\pi }\right(S_1)=h_{\ell ,\pi }(S_2)\hspace{0.17em}|\hspace{0.17em}(C\left)\right]\le \underset{\pi \in \left[m\right]!}{\max }\mathrm{Pr}[\text{pick}\hspace{0.17em}\text{IS}\hspace{0.17em}\text{of}\hspace{0.17em}\text{length}\hspace{0.17em}\ell \hspace{0.17em}\text{in}\hspace{0.17em}\pi (\left[m\right]\left)\right],$$ (12)

where $\left[m\right]!$ is the set of all permutations of $\left[m\right]$. Together, Equations (10–12), and Lemma 3 imply that the following holds for any choice of sequences S₁, S₂:

$$\begin{array}{c}{p}_2<\underset{\begin{array}{c}\ell \le m,\\ m\le n_k\end{array}}{\max }\frac{{\left(\frac{m}{L}\right)}^{\ell }\left(\begin{array}{c}L\\ \ell \end{array}\right)}{\left(\begin{array}{c}m\\ \ell \end{array}\right)}\frac{\left(\begin{array}{c}m\\ \ell \end{array}\right)}{\left(\begin{array}{c}{n}_k\\ \ell \end{array}\right)}\hfill \\ <\frac{{\left(\frac{n_k}{L}\right)}^{\ell }\left(\begin{array}{c}L\\ \ell \end{array}\right)}{\left(\begin{array}{c}{n}_k\\ \ell \end{array}\right)},\hfill \end{array}$$ (13)

where L is the length of the longest CS between $M_k^w\left(S_1\right)$ and $M_k^w\left(S_2\right)$. The function on the right-hand side of Equation (13) is an increasing function of L, equal to 0 when $L<\ell$, and equal to 1 when $L=n-k+1$. Given that $s_2\ge E_s(S_1,S_2)\ge (L+k-1)/n$, replacing L by $n{s}_2-k+1$ in Equation (13) gives the desired relation between s₂ and p₂ of Equation (9).□

Finally, we prove the relationship between the length of the longest increasing subsequence (LIS) and the largest number of sequences of maximal length.

Lemma 3. For $i,n,\ell \in \mathbb{N},\hspace{0.17em}n\ge i\ge \ell$, for any sequence of length n with an LIS of at most i, the largest number of increasing subsequences of length $\ell$ is

$${\left(\frac{n}{i}\right)}^{\ell }\left(\begin{array}{c}i\\ \ell \end{array}\right),$$

and this bound is tight.

Proof. The proof relies on the properties of patience sorting (Aldous and Diaconis, 1999). Patience sorting for a shuffled deck of cards works as follows:

• The algorithm creates stacks of cards where in each stack the cards are in decreasing order from the bottom to the top of the stack. The stacks are organized in a line, left to right.

• At each round, the next card of the deck is examined and added to the top of the left most stack it can go on, i.e. the left most stack with a top card whose value is higher than the new card.

• If no existing stack is suitable, a new stack is created to the right with the new card.

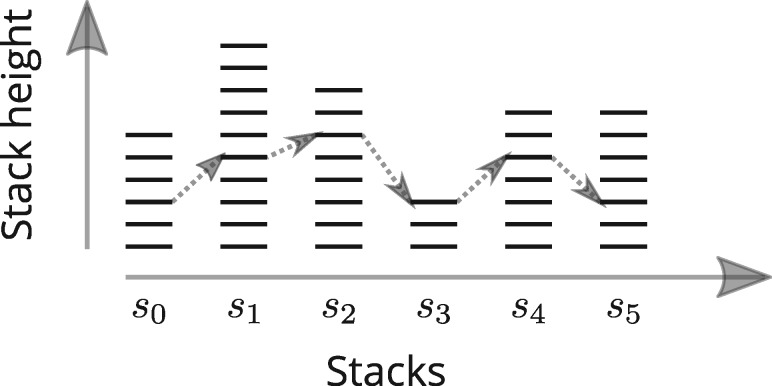
After all the cards are drawn and organized in stacks (see Fig. 2), the following properties hold: (i) no two cards from an increasing subsequence in the original deck are in the same stack, and (ii) the number of stacks is equal to the LIS (see Aldous and Diaconis, 1999, Lemma 1).

Fig. 2.

An example of stacks created when sorting a deck of cards. The LIS is 6, with the arrows showing a possible increasing subsequence of maximal length. To maximize the number of possible subsequences of maximum length, the height of the stacks have to be equal

Fix $i\prime \in [\ell ,i]$ and a sequence S of length n with LIS of $i\prime$. At the end of patience sorting of S, let $\mathbf{s}=(s_0,\dots ,s_{i\prime -1})$ be the vector of the height of each of the stacks. Then, an upper bound on the number of increasing subsequence of length $\ell$ in S is

$$g\left(\mathbf{s}\right)=\sum _{\begin{array}{c}A\subset [i\prime ]\\ \hspace{0.17em}|\hspace{0.17em}A\hspace{0.17em}|\hspace{0.17em}=\ell \end{array}}\prod _{j\in A}{s}_j.$$ (14)

This is an upper bound as every choice of $\ell$ elements from different stacks does not necessarily define a valid increasing subsequence of S. We show that g reaches its maximum when $s_0=\cdots =s_{i\prime -1}=n/i\prime$.

Because the set $C=\{\mathbf{s}=(s_0,\dots ,s_{i\prime })\hspace{0.17em}|\hspace{0.17em}\sum _j{s}_j=n\}$ is compact, g reaches a maximum on C. Suppose that in s, not all the s_j are equal; without loss of generality, assume that $s_{i\prime -2}$ and $s_{i\prime -1}$ are distinct. Set $\alpha =(s_{i\prime -2}+s_{i\prime -1})/2$ and consider the point $\mathbf{s}\prime =(s_0,\dots ,s_{i\prime -3},\alpha ,\alpha )$. Let us also use the notation

$$\rho \left(x\right)=\sum _{\begin{array}{c}A\subset [i\prime -2]\\ \hspace{0.17em}|\hspace{0.17em}A\hspace{0.17em}|\hspace{0.17em}=x\end{array}}\prod _{j\in A}{s}_j.$$

Then, we split the sum in $g(\mathbf{s}\prime )$ into the terms containing neither $s_{i\prime -2}$ nor $s_{i\prime -1}$ ($=\rho \left(\ell \right)$), the terms that contain one of $s_{i\prime -2}$ or $s_{i\prime -1}$ ($=2\alpha \rho (\ell -1)$) and the terms that contain both ($={\alpha }^2\rho (\ell -1)$), and we use the inequality ${\alpha }^2>s_{i\prime -2}{s}_{i\prime -1}$ (arithmetic mean is larger than geometric mean):

$$\begin{array}{c}g(\mathbf{s}\prime )=\rho \left(\ell \right)+2\alpha \rho (\ell -1)+{\alpha }^2\rho (\ell -2)\hfill \\ >\rho \left(\ell \right)+(s_{i\prime -2}+s_{i\prime -1})\rho (\ell -1)+s_{i\prime -2}{s}_{i\prime -1}\rho (\ell -2)\hfill \\ =g\left(\mathbf{s}\right).\hfill \end{array}$$

Hence, $g\left(\mathbf{s}\right)$, where s contains two distinct values, is not maximum, and g must reach its maximum when all the s_j are equal. Furthermore, in that case $s_j=n/i\prime$.

Therefore,

$$\underset{\mathbf{s}\in C}{\max }g\left(\mathbf{s}\right)=\sum _{\begin{array}{c}A\subset \left[i\right]\\ \hspace{0.17em}|\hspace{0.17em}A\hspace{0.17em}|\hspace{0.17em}=\ell \end{array}}{\left(\frac{n}{i\prime }\right)}^{\ell }={\left(\frac{n}{i\prime }\right)}^{\ell }\left(\begin{array}{c}i\prime \\ \ell \end{array}\right)\triangleq m_{n,\ell }(i\prime ).$$ (15)

The function $m_{n,\ell }(·)$ defined above is increasing and the maximum is reached for $i\prime =i$.

Finally, consider the sequence S(i, n), i divides n, defined by blocks:

$$\underset{\text{block} 1}{\underbrace{(n/i-1)\cdots 0}}\underset{\text{block} 2}{\underbrace{(2n/i-1)\cdots (n/i)}}\cdots \underset{\text{block}i}{\underbrace{(n-1)\cdots (n-n/i)}}.$$

Each block is of length n/i, the numbers in each blocks are in decreasing order, and the start of the blocks are in increasing order: block j is the decreasing sequence $(\mathit{jn}/i-1)\cdots \left(\right(j-1)n/i)$.

When the patience sorting algorithm is applied to the list S(i, n), the stacks are filled up one by one, from bottom to top and from left to right, and have the same height of n/i. Therefore, any choice of one element in each stack is a valid increasing subsequence of S(i, n) and the bound of Equation (15) is attained. □

Finally, we can restate and prove the main theorem.

Theorem 2. For any$\ell \in [2,n-k]$and any$1>s_1\ge s_2>0$, there exist functions$p_{n,k,\ell }^1(·)$and$p_{n,k,\ell }^2(·)$such that OMH is$\left(s_1,s_2,p_{n,k,\ell }^1\left(s_1\right),p_{n,k,\ell }^2\left(s_2\right)\right)$-sensitive for the edit distance.

Proof. It is a direct consequence of Lemma 1 and Lemma 2. □

4 Discussion

4.1 Parameters ${\mathrm{s}}_1,{\mathrm{p}}_1,{\mathrm{s}}_2,{\mathrm{p}}_2$

To have a proper LSH method, the conditions $p_1\ge p_2$ must hold. This condition means that the method is able to distinguish with some probability between dissimilar ($\le s_2$) and similar ($\ge s_1$) sequences. Figure 3 shows the functions p¹ (blue lines) and p² (red lines) from Theorem 2 for varying values of $\ell$.

Fig. 3.

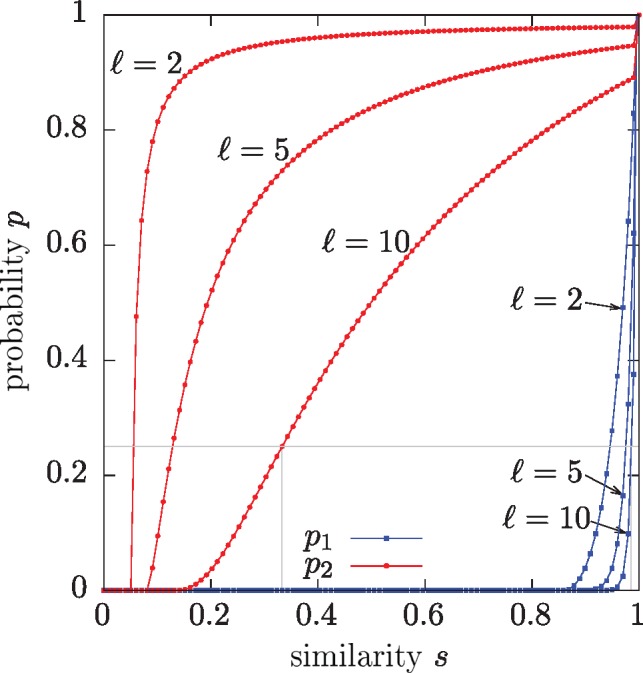
The relationships between the similarity thresholds s₁ and s₂, and the probabilities p₁ and p₂, for n = 100, k = 5. Given a probability, e.g. $p_1=p_2=0.25$ shown by the horizontal gray line, the OMH method can distinguish between similarities below s₂ (below left vertical gray line) and from similarities above s₁ (above the right vertical gray line). The functions are defined at discrete points, when ns is integral, represented by the circles and squares

At the limit, taking $p_1=p_2=p$, the method can distinguish between any s₁ and s₂ such that $p^1\left(s_1\right)\ge p$ and $p^2\left(s_2\right)\le p$ (gray lines on Fig. 3). For larger values of $\ell$, the gap between distinguishable values is reduced, although at the cost of having high values for s₁.

4.2 Choice of parameter $\ell$

The main difference between OMH and the minHash methods is the choice of $\ell$k-mers, where minHash corresponds to the case of $\ell =1$ (ignoring the slight difference between Jaccard and weighted Jaccard). It might seem surprising at first that OMH is an LSH for edit dissimilarity for any values of $\ell$, except for the extremes of $\ell =1$ and $\ell =n-k+1$.

The proof of Theorem 2 is consistent with this analysis. For both these extreme values of $\ell$, Equation (13), which relates the probability p₂ to the similarity s₂, becomes trivially true ($p_2<1$). This means that even a certain hash collision (probability of 1) provides no guarantee on the relative order of common k-mers between the two sequences (i.e. the length of the longest subsequence L = 1: only one k-mer is guaranteed to align). On the other hand, any other value of $\ell$ leads to an actual bound in Equation (13).

For example, when $\ell =2$, the minimum number of k-mers that must align in proper order as a function of the collision probability p₂ is

$$L=\frac{n-k+1}{(n-k)(1-p_2)+1}.$$ (16)

Even in the case where n is very large, then $L\approx 1/(1-p_2)$, the number of properly aligning k-mers becomes large when the probability of collision p₂ is close to 1. This is in contrast to the minHash, where a probability of collision of 1 (i.e. a Jaccard similarity of 1) does not guarantee that more than two k-mers properly align (see example in Section 2.2).

In practice, the parameter $\ell$ should be relatively small, say $2\le \ell \le 5$. Increasing the value of $\ell$ has two effects on the OMH method. First, it increases the minimum edit similarity that is detectable by the method, as there must be at least $\ell +k-1$ bases in the alignment of the two sequences for OMH to have a non-zero probability of hash collision. Second, a larger value of $\ell$ implies that the probability of hash collision is small, which requires storing a higher number of vectors in a sketch to obtain a low variance. There is a trade-off between how sensitive the scheme is to relative order (high value of $\ell$) and the smaller size for the sketch (low value of $\ell$).

4.3 Practical sketches for OMH

In our implementation, the OMH sketch for a sequence S contains more than just the list of vectors $h_{\ell ,\pi }\left(S\right)$. In practice, we store

• the length of the sequence $\hspace{0.17em}|\hspace{0.17em}S\hspace{0.17em}|\hspace{0.17em}$,

• a list of m vectors $h_{\ell ,\pi }\left(S\right)$ and associated order vector $r_{\ell ,\pi }\left(S\right)=(r_0,\dots ,r_{\ell -1})$.

Recall that the k-mers in the vector $h_{\ell ,\pi }\left(S\right)$ are listed in the order in which they appear in S. The order vector $r_{\ell ,\pi }$ is a permutation of the indices $\left[\ell \right]$ that can reorder the k-mers according to π. That is, $h_{\ell ,\pi }\left(S\right)=(m_0,\dots ,m_{\ell -1})$ and i < j imply that $\pi (m_{r_i},o_{r_i})<\pi (m_{r_j},o_{r_j})$ (where, as in the definition, o_i is the occurrence number of the k-mer m_i). The total space usage of a sketch is $O(\text{log}\hspace{0.17em}\hspace{0.17em}|\hspace{0.17em}S\hspace{0.17em}|\hspace{0.17em}+m\ell (k\hspace{0.17em}\text{log}\hspace{0.17em}\sigma +\text{log}\hspace{0.17em}\ell \left)\right)$.

The reason for the order vector in the sketch is to recover both an estimate of the weighted Jaccard between the two sequences and how well these common k-mers properly align. More precisely, given two sketches for S₁ and S₂, the number of collisions $h_{\ell ,\pi }\left(S_1\right)=h_{\ell ,\pi }\left(S_2\right)$ and the number of collisions in the reordered k-mers according to the order vector $o_{\ell ,\pi }$ give an estimate of the weighted Jaccard ${\mathrm{J}}^{\mathrm{w}}(S_1,S_2)$. Using this estimate, the sizes of S₁ and S₂ from the sketches, and the formula $\hspace{0.17em}|\hspace{0.17em}{\mathcal{M}}_k^w\left(S_1\right)\hspace{0.17em}|\hspace{0.17em}+\hspace{0.17em}|\hspace{0.17em}{\mathcal{M}}_k^w\left(S_2\right)\hspace{0.17em}|\hspace{0.17em}=\hspace{0.17em}|\hspace{0.17em}{\mathcal{M}}_k^w\left(S_1\right)\cup {\mathcal{M}}_k^w\left(S_2\right)\hspace{0.17em}|\hspace{0.17em}+\hspace{0.17em}|\hspace{0.17em}{\mathcal{M}}_k^w\left(S_1\right)\cap {\mathcal{M}}_k^w\left(S_2\right)\hspace{0.17em}|\hspace{0.17em}$, we can recover estimates for the size of the intersection and union of the weighted k-mer sets. Finally, formulas (10) and (11) give the probability for $\ell$k-mers from the intersection to be in the same alignment order between the two sequences. The case where the Jaccard similarity is not sufficient to assess that the sequences have a high edit similarity is precisely the case when this last probability is low.

In other words, the extra $O(\text{log}\hspace{0.17em}\ell )$ bits of information per k-mer in the OMH sketch compared with a weighted minHash sketch corresponds to the supplemental information given by OMH compared with minHash. Given that $\ell$ is small in practice, the cost for this extra information is also very small.

For genomics sequences, it is traditional to compute the minHash using ‘canonical’ k-mers (defined as a k-mer or its reverse complement, whichever comes first lexicographically). In the OMH sketches, it is not possible to use canonical k-mers as this in incompatible with the order information encoded in the vector $h_{\ell ,\pi }\left(S\right)$. Rather, two sketches, one for the forward strand and one for the reverse are stored. Comparing two sequences requires doing two sketches comparisons.

The size of an OMH sketch is $O\left(\mathit{km}\ell \right)$.

4.4 Weighted Jaccard and OMH

Even though the Jaccard and minHash sketches are regularly used as a measure of the k-mer content similarity in computational biology software, the weighted Jaccard similarity has been heavily studied and used in other contexts, such as large database document classification and retrieval (e.g. Shrivastava, 2016; Wu et al., 2017), near duplicate image detection (Chum et al., 2008), duplicate news story detection (Alonso et al., 2013), source code deduplication, time series indexing (Luo and Shrivastava, 2017), hierarchical topic extraction (Gollapudi and Panigrahy, 2006), or malware classification (Drew et al., 2017) and detection (Raff and Nicholas, 2017).

The weighted Jaccard, compared with the unweighted Jaccard, gives a more complete measure of the similarity between two sets or sequences. Obviously, when no elements are repeated, the two similarities are equal. On the other hand, in the case of many repeated elements, the difference can be significant.

For example, returning to the example from Section 2.2 where $S_1=0\dots 01\dots 1$ with n – k 0s followed by k 1s and S₂ with k 0s followed by n – k 1s, the edit similarity is very low: ${\mathrm{E}}_{\mathrm{s}}(S_1,S_2)\le 2k/n$. The Jaccard similarity is $\mathrm{J}(S_1,S_2)=1$, in other words, these two sequences are indistinguishable according to the Jaccard similarity. On the other hand, the weighted Jaccard is also very low: ${\mathrm{J}}^{\mathrm{w}}(S_1,S_2)=1/(n-k)$, much more similar to the edit similarity.

In the case of two de Bruijn sequences that might have very low edit similarity, the Jaccard and weighted Jaccard are both equal to 1, as every k-mer occurs exactly once. Therefore, in this case the weighted Jaccard provides no extra information. The OMH sketching method, being also sensitive to the relative orders of the k-mers (see Equation 10), would have a probability of hash collision much lower than 1.

In Figure 4, we generated 1 million random binary sequences (σ = 2) of length n = 100. Each string is then randomly mutated a random number of times (up to 100 times) to obtain a pair of sequences with a random edit dissimilarity. Then, for each pair, we compute the actual edit dissimilarity, Hamming dissimilarity, the exact—i.e. not estimated by minHash—Jaccard and weighted Jaccard similarities. Additionally, the OMH sketch (with $\ell =2$ and m = 500) is also computed for each pair. The graph shows the median and first quartiles computed over the million pairs of sequences. Even for sequences with high edit dissimilarity (>0.4), the Jaccard similarity remains very high. However, the weighted Jaccard and OMH are more sensitive to the edit dissimilarity.

Fig. 4.

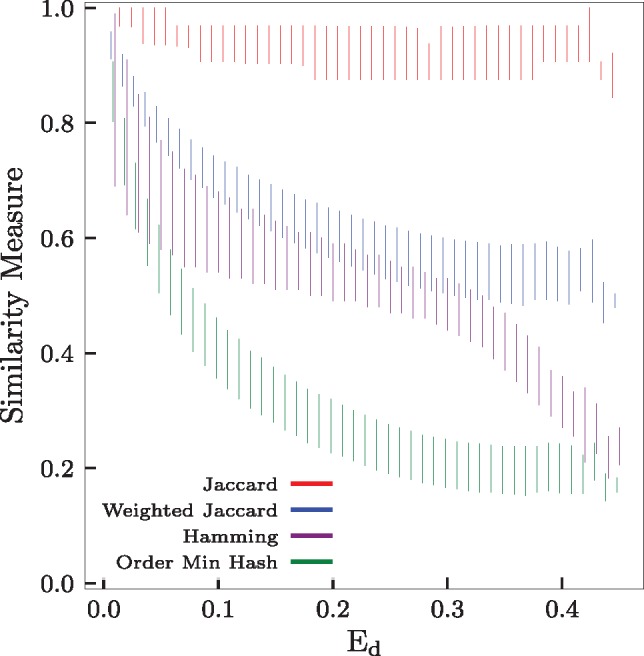
Evolution of the Jaccard, weighted Jaccard, Hamming and OMH against the edit dissimilarity on randomly generated binary sequences. In average, the Jaccard similarity stays high, even for sequences with high edit dissimilarity, unlike the weighted Jaccard, Hamming or OMH which are much more sensitive to the edit dissimilarity

4.5 Using sketches for phylogeny reconstruction

Genomic rearrangement in bacteria often involves mobile genomic elements known as ‘insertion sequences’ (IS). Lee et al. (2016) studied the frequencies and locations of these insertions and found that the positions are largely driven by the locations of existing copies. Although the locations of these inserts may vary across the genome, there are only a small number of inserted sequences that occur regularly. Consequently, the k-mer content of the genomes remains almost unchanged through these insertion events.

To test the effectiveness of OMH to recover the history of these insertion events, we simulated a family of Escherichia coli genomes by inserting these IS elements. We randomized the order of the four most common sequences (IS1, IS5, IS2, and IS186) and insert one into the genome at each of four generations of produced genomes. The location of the insertion was randomly chosen from the list of locations where the same sequence had been previously identified. Starting with E.coli K-12 MG1655 (NC_000913.2) we created two children by inserting the first element in the randomized order at two separate locations. For the next generation, we created two children for each of the individuals by choosing two random locations at which to insert the next sequence. For all the children in a generation, the same IS is inserted. We then measured all pairwise dissimilarities and created a phylogeny using the distances computed by OMH and weighted Jaccard.

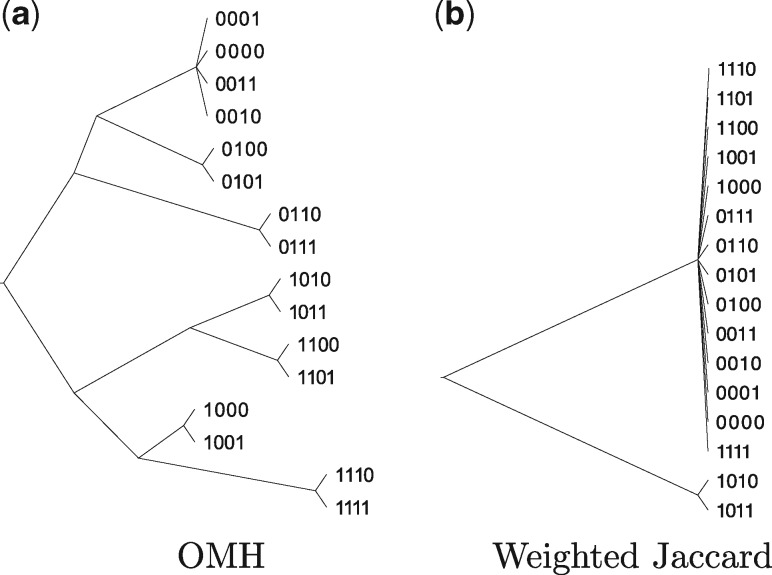
Figure 5 shows two phylogenies of the 16 final sequences with $m=10\hspace{0.17em}000$, k = 22, $\ell =3$. We chose $\ell$ to provide high differentiation between OMH and Jaccard, and m to provide high sensitivity to sequence perturbation. The binary sequences are the path used to create the child, i.e. siblings in the last generation would have the same three-digit prefix. OMH recovered the structure of the tree except for the four nodes at the top of the tree. Weighted Jaccard on the other hand cannot resolve most of the lineages as the sequences are very similar at the level of k-mer content. The experiment was repeated 10 times, and in each a similar tree was recovered (see Supplementary Fig. S1).

Fig. 5.

Phylogenies of the 16 child sequences produced by inserting IS elements into the Escherichia coli genome when distance is measured by both (a) OMH and (b) weighted Jaccard with $m=10\hspace{0.17em}\hspace{0.17em}000$, k = 22, $\ell =3$. In general, OMH is able to recover more of the lineage structure than Jaccard because the k-mer content is very similar even though the sequences are inserted at different locations

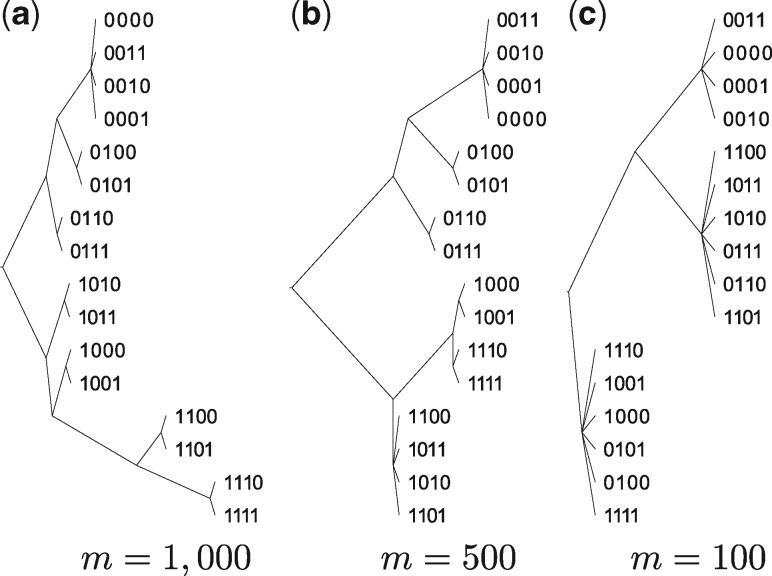
To test the robustness of OMH to lower values of m, and in turn the necessary computational resources, we reconstructed the tree above with $m=1000,500,$ and 100 (see Fig. 6). Even for low values of m, OMH is able to recover most of the tree structure, which is not recovered by weighted Jaccard even with a much larger m.

Fig. 6.

Phylogenies of the 16 child sequences produced by inserting IS elements into the Escherichia coli genome when distance is measured by OMH k = 22, $\ell =3$ and m equals to (a) 1000, (b) 500 and (c) 100. As m increases, OMH recovers more accurately the general structure of the tree

5 Conclusion

We presented the OMH method that is an LSH for the edit dissimilarity. Unlike the Jaccard similarity, which is only sensitive to the k-mer content of a sequence, OMH additionally takes into account the relative order of the k-mers in a sequence.

The OMH method is a refinement of the weighted Jaccard similarity that is used extensively in many related fields, such as document classification and duplicate detection. However, despite the advantages of the weighted Jaccard similarity, it has not yet been widely adopted by the bioinformatics community. Using weighted Jaccard and OMH for estimating edit similarity in bioinformatics applications can help reduce the number of false-positive matches which can in turn avoid unnecessary computations.