Abstract
Motivation
Mass spectrometry imaging (MSI) characterizes the spatial distribution of ions in complex biological samples such as tissues. Since many tissues have complex morphology, treatments and conditions often affect the spatial distribution of the ions in morphology-specific ways. Evaluating the selectivity and the specificity of ion localization and regulation across morphology types is biologically important. However, MSI lacks algorithms for segmenting images at both single-ion and spatial resolution.
Results
This article contributes spatial-Dirichlet Gaussian mixture model (DGMM), an algorithm and a workflow for the analyses of MSI experiments, that detects components of single-ion images with homogeneous spatial composition. The approach extends DGMMs to account for the spatial structure of MSI. Evaluations on simulated and experimental datasets with diverse MSI workflows demonstrated that spatial-DGMM accurately segments ion images, and can distinguish ions with homogeneous and heterogeneous spatial distribution. We also demonstrated that the extracted spatial information is useful for downstream analyses, such as detecting morphology-specific ions, finding groups of ions with similar spatial patterns, and detecting changes in chemical composition of tissues between conditions.
Availability and implementation
The data and code are available at https://github.com/Vitek-Lab/IonSpattern.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Mass spectrometry imaging (MSI) characterizes the spatial distribution of chemical composition of complex biological samples such as tissues. It is broadly applied in biological and clinical research, including diagnosis and prognosis of disease and the study of drug delivery (Jones et al., 2012; Spengler, 2015). MSI experiments rely on ionization techniques, among which matrix-assisted laser desorption ionization (MALDI), desorption electrospray ionization (DESI) and nano-DESI are the most widely used. In a MALDI-MSI experiment, a tissue section is coated with a matrix, which absorbs the energy of laser and aids extraction and ionization of molecules from tissue section (Aichler and Walch, 2015). For DESI-MSI, primary charged droplets generated by electrospray ionization are sprayed upon the tissue section and molecules are ionized and desorbed in secondary droplet (Wu et al., 2013).
The ions of proteins or peptides (for MALDI), or of lipids or metabolites (for DESI and MALDI) are separated according to their ratios of mass over charge (m/z). This produces a mass spectrum, i.e. a graph where the x axis represents the m/z of the ions, and the y axis is the intensity (related to the abundance of the ions). MSI experiments collect mass spectra in a raster pattern throughout a tissue. A color representation of the intensities of one m/z across the locations is referred to as an ion image. Mass spectrometric workflows differ in their spatial resolution, mass resolution and the dynamic range of the intensity signals (Watrous et al., 2011). A typical experiment contains spectra with tens of thousands of m/z, collected across hundreds to tens of thousands of locations, across multiple tissues sections of a biological replicate, and across multiple biological replicates from multiple conditions, thus producing high-dimensional datasets with complex structures of variation.
Many tissues have distinct morphological structures. For example, the cerebral cortex, corpus callosum and caudate putamen are a few of the hundreds within a mouse brain. Treatments and conditions affect the ion distributions in the tissue, often in ways that are morphology-specific (Delcourt et al., 2018; Norris and Caprioli, 2013). For example, most neurodegenerative diseases have regionally confined subsets of neurons that are selectively vulnerable to disease (Cleveland and Rothstein, 2001). Examination of the regional selectivity of a drug delivered to a targeted area in the tissue helps understand the effectiveness of the treatment (Prasad et al., 2018). Evaluating the selectivity and the specificity of ion localization and regulation is therefore biologically and clinically important.
Despite the name ‘imaging’, MSI differs from other imaging techniques in its highly quantitative and multivariate nature of the measurements, large between-experiment differences, and a small sample size. Therefore, most common methods for image analysis are inappropriate. Currently the exploration of ion-selective and morphology-selective patterns is mostly done by hand. As the spatial resolution, the mass resolution, and the number of biological replicates increase, MSI routinely generates thousands of ion images in a single experiment (Watrous et al., 2011). A manual exploration of the images becomes impossible in practice.
Statistical methods complementing manual exploration perform image segmentation and differential analysis (Jones et al., 2012; Watrous et al., 2011). Multivariate methods for image segmentation, e.g. principle component analysis (PCA), hierarchical clustering and K-means, detect regions (or, components) of the tissues with homogeneous chemical composition. Their output is a single set of components for all the ions. For differential analysis, t-test and analysis of variance (ANOVA) average the abundances of an ion across all the locations in each tissue. Their output is the change in ion abundance between tissue replicates from different conditions. Overall, these methods lose the information on either the heterogeneity of the spatial distribution across the ions, or the specificity or selectivity of ion localization within the tissues (de Muller et al., 2017).
This article contributes an algorithm, and a workflow for the analyses of individual ion images, that overcomes the limitations above. The approach, based on Dirichlet Gaussian Mixture Model (DGMM) that we call spatial-DGMM, detects ion-specific tissue components with homogeneous spatial composition. This is the first application of Gaussian mixture models (GMM) in MSI. We show that spatial-DGMM accurately segments ion images, and can distinguish ions with homogeneous or heterogeneous spatial distribution in experiments in diverse MALDI- and DESI-based MSI workflows. We also demonstrate that the extracted spatial information is useful for downstream analyses, such as detecting morphology-specific ions, finding groups of ions with similar spatial patterns, and detecting changes in chemical composition.
2 Background
2.1 Multivariate analyses of MSI
2.1.1 Classical multivariate analyses
Unsupervised multivariate analyses are commonly used for MSI visualization and segmentation. High-dimensional spectra are visualized in lower dimensions, e.g. by PCA (Bonnel et al., 2011; Jones et al., 2011) and non-negative matrix factorization (Jones et al., 2011). For image segmentation, K-means and hierarchical clustering are most commonly used (Bonnel et al., 2011; Jones et al., 2011). However, the classical multivariate analyses do not account for the spatial dependence of the locations, or for the fact that ions may have subtle but important differences in the spatial distribution in the tissue. As a motivating example, Figure 1a presents a sample of known composition, an oil painting (described in greater details in Section 4). Figure 1b illustrates that a PCA analysis of the MSI experiment of the painting, although useful, failed to effectively distinguish subregions of homogeneous color.
Fig. 1.
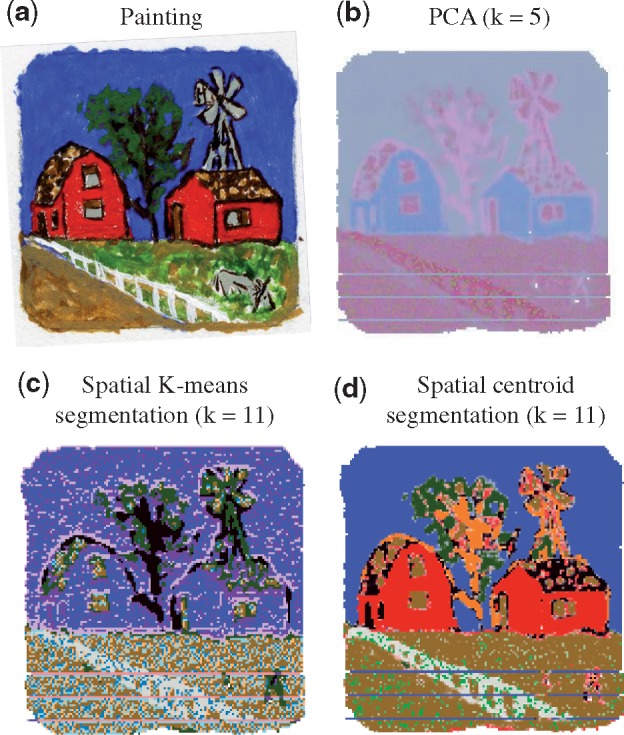
Multivariate analysis of the MSI experiment with an oil painting. (a) The painting representing the ground truth. Each color has a unique chemical composition, and is a homogeneous component of the image. (b) PCA analysis of all the ions. k represents the number of principle components. Colors are principle components, and intensity of each color is the score of the location in that principle components. (c) Spatial K-means segmentation of all the ions. k represents the number of segments. Colors are segments. (d) Spatial shrunken centroid segmentation of all the ions. k represents the number of segments. Colors are segments. k in (b–d) was chosen to best visualize the structure of the painting
2.1.2 Spatial multivariate analyses
Spatial K-means (Alexandrov and Kobarg, 2011) and spatial centroid segmentation (Bemis et al., 2016), designed specifically for MSI, account for the spatial dependency between locations and for the similarity of mass spectra at each location. As shown in Figure 1c and d, these methods provide less noisy image segmentation, and preserve sharp edges. However, the segmentation does not uncover the differences of spatial distribution between the ions. For example, the ion images in Figure 2a and c show that m/z 650.17 and m/z 321.25 are color-specific. Such specificity of ion localization cannot be deduced from Figure 1c and d.
Fig. 2.
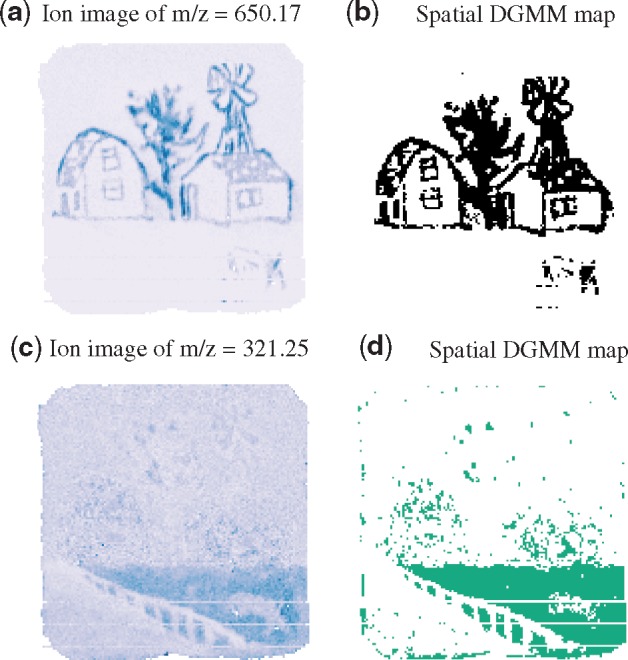
Univariate analysis of the MSI experiment of an oil painting. (a) Ion image of m/z 650.17 specific to the color black. (b) Spatial-DGMM segmentation of the ion selects the color-specific locations, K = 2 and . (c) Ion image of m/z 321.25 specific to the grass area in the painting. (d) Spatial-DGMM segmentation of the ion selects the grass-specific locations, K = 2 and . K is the number of components estimated by GMM and is the number of components estimated by spatial-DGMM
2.2 Univariate analyses of MSI
2.2.1 Capturing morphological patterns of individual ions
Univariate methods analyze ion images as in Figure 2a and c, one image at a time. Many analyses first specify a region of interest (ROI) selected by an optical image of the tissue, or determined by the location of a pre-defined marker ion. Then, the colocalization of the ion image and of the ROI is manually examined. Alternatively, computational methods define ROI as a binary vector containing the values of 1 for tissue locations inside the ROI, and 0 outside. A correlation coefficient between the binary matrix and the ion intensity quantifies the extent of colocalization (Alexandrov et al., 2010; Trede et al., 2012). The method is simple and fast, but fails when an ion is localized in multiple regions of the tissue, when the ROI is relatively small, or when the ion contains outlying intensity values (Bemis et al., 2016).
Another group of methods quantitatively capture the spatial distribution of individual ions. One example is a homogeneity index based on a texture analysis technique (Prasad et al., 2018). It provides automated measure of homogeneity, but cannot comprehensively capture ions selective to multiple areas of the tissue. Another example is morphometric analysis (de Muller et al., 2017). It characterizes the number of objects in the total surface of an ion image; however, the biological interpretation of the ‘number of objects’ and of the ‘total surface’ may be a challenge.
2.2.2 Differential analysis
To examine changes in ion abundance between conditions, it is common to average the intensity of a m/z in each replicate tissue, and use the averages as input to t-test or ANOVA. Alternative tissue summaries, more complex than the averaging, have also been proposed (Bemis et al., 2019; Cassese et al., 2016). However, these summaries are not designed to distinguish patterns of ion distribution within a tissue.
2.3 Mixture models
Mixture modeling has long been a popular approach for finding patterns in data; however, it has not yet been adopted for MSI. A popular class is GMM (Zivkovic, 2004). GMM assume that the data contain sub-structures, each following a Gaussian distribution. GMM have a small number of parameters, estimated by the expectation maximization (EM). However, GMM assume that the individual data points (such as locations of the tissue) are independent, and do not make use of the spatial information.
A common way to relax the assumption of independence, and to incorporate the spatial information is to use a Markov random field (MRF; Blekas et al., 2005). GMM can also be extended with Dirichlet priors to form DGMMs (Nikou et al., 2010). This simplifies parameter estimation as compared to GMM when incorporating spatial dependence using an MRF. Instead of using MRF, spatial dependence can also be incorporated to the Dirichlet priors (Nguyen and Wu, 2011). However, these methods assume that neighboring locations contribute to spatial smoothness equally, which is not true in MSI data.
This article adapts DGMM to MSI experiments, by incorporating spatial dependence in a way that is specifically designed for MSI. The proposed method, spatial-DGMM, assigns spatial weights to neighboring locations based on both spatial proximity and spectral similarity. Since MSI experiments have many m/z features, and since different m/z have different spatial distributions, spatial-DGMM estimates the number of Gaussian components separately for each m/z. The output of spatial-DGMM, which we call spatial-DGMM map, is illustrated in Figure 2b and d. Spatial-DGMM uncovers ions m/z 650.17 and m/z 321.25 of spatial distributions specific to colors, which is hidden in the results of multivariate segmentation (Fig. 1c and d). Below, we show that it delimits ion images in ways that are specific to the underlying structures, and provides meaningful information for downstream statistical analyses.
3 Materials and methods
In this section, we first introduce the notation and the existing DGMM. Then, we introduce the proposed extension, and the iterative Expectation-Maximization algorithm for spatial-DGMM parameter estimation. Finally, we review the overall proposed data analysis workflow.
3.1 Notation
Let denote the ion intensity at location i at one of the N locations. Let and denote the vector of prior and posterior probabilities of ith location to belong to each of the K Gaussian components. Let denote the discrete label of the ith location, where if location i belongs to component j, and 0 otherwise; and and denote the mean intensity and the standard deviation of each Gaussian component.
3.2 Dirichlet gaussian mixture model
Ion images (such as in Fig. 2a and c) have regions of distinct average intensity. Within each region, the ion intensity is relatively homogeneous, and the variation is random. Gaussian mixture models represent such regions as components, and assume that the ion intensity within each component approximately follows a Gaussian distribution. In a Gaussian mixture model, the probability density at xi is
| (1) |
where is defined as
| (2) |
The parameters of interest are , and the log-likelihood is
| (3) |
Dirichlet Gaussian mixture models extend the basic GMM by assuming that the indicators of component membership are random variables (Nikou et al., 2010). Each is one realization from a multinomial distribution with parameters . Therefore, the probability distribution of the vector zi is
| (4) |
The hyperprior distribution of ξi is defined as a Dirichlet process
| (5) |
where , is the vector of Dirichlet parameters. Integrating Equations 4 and 5, the probability distribution of component membership zi simplifies to
| (6) |
In particular, the probability of the event where the ith location on the tissue belongs to component j is
| (7) |
It is the prior probability before knowing xi, thus .
In DGMM the parameters of interest are . An iterative optimization such as the expectation maximization (EM) algorithm is typically used for parameter estimation. At the iteration t of the algorithm, the parameters of are updated, and the posterior probability of the event where location i belongs to component j is derived
| (8) |
3.3 Spatial-DGMM
Since biological tissues have spatial substructures, the ion intensities in neighboring locations are correlated. Therefore, the probabilities of locations belonging to each Gaussian component should also be spatially dependent. To incorporate spatial dependence, we were inspired by the work in Nguyen and Wu (2011), which incorporated a linear filter to the posterior probabilities of DGMM. At each iteration t of the EM algorithm, the linear filter linearly combines the posterior probabilities of the neighboring locations to achieve spatial smoothing. Unlike Nguyen and Wu (2011), we define weighted linear combinations
| (9) |
where is the vector of indexes of neighboring locations of location i. The weights express the proximity of location m to location i.
The weights are designed specifically for MSI. Similarly to Alexandrov and Kobarg (2011), we consider the fact that neighboring locations may be similar in chemical composition, but they may also be different, e.g. if they fall on opposite sides of edges separating distinct morphological structures. The similarity of chemical composition of the two locations can be quantified by the similarity of their mass spectra. Specifically, denote the spatial coordinate of the location i, and Si= the spectrum of intensities of all the m/z values at that location. The weights combine the spatial distance and the spectrum similarity as:
| (10) |
The tuning parameters λ1 and λ2 reflect the scale and the relative importance of spatial and spectrum similarities.
Following Nguyen and Wu (2011), we incorporate to the Dirichlet parametrization, such that the prior probability of the location i to belong to component j can depend on the posterior probabilities of the neighboring locations. The revised Dirichlet distribution is
| (11) |
The parameter β represents the extent of spatial dependence, and is estimated from the data. Similar to Equations 4–7, the prior is:
| (12) |
3.4 Parameter estimation
Algorithm 1.
Expectation maximization algorithm
1. procedure DGMM()
2. Initialization:
3. if Initialization=“km” then
4. μj kmeans(xi)
5.
6. end if
7. if Initialization=“gmm” then
8. gmm()
9. end if
10.
11. (Equations 12 and 8)
12. parameter estimation:
13. fort = 1 to tmaxdo
14. compute (Equation 9)
15. compute (Equation 12)
16. compute (Equation 8)
17.
18. if Simulated Annealing then
19. pick kc from
20. and
21. ifthen
22.
23. end if
24.
25. end if
26. Stop when
27. end for
28. return
29. end procedure
The process of parameter estimation is summarized in Algorithm 1. The inputs are a vector of ion intensities , a N × N matrix W of weights of location i relative to location j, Kmax is the maximum number of Gaussian components, tmax is the maximum number iterations, and ε is the stopping tolerance. The parameters of interest are . Although spatial-DGMM has more parameters than DGMM, the complexity of the parameter space is reduced by the spatial smoothing. We initialize the parameters with either GMM or K-means and initialize and β = 1. The negative log-likelihood is
| (13) |
The estimation relies on EM algorithm, an iterative method for minimizing the negative log likelihood with respect to all the parameters in presence of latent variables. At the iteration t in the E step, we calculate as in Equation 8 and write the expectation of negative log-likelihood as
| (14) |
The M step of the algorithm minimizes the function above with respect to parameters Θ by gradient descent. Each parameter is updated with respect to its partial gradient
| (15) |
where η is the learning step. All have closed form and are subject to the constrains. The partial gradients of each parameter are
| (16) |
The algorithm alternates between the E step and the M step, until it reaches either the stopping criterion or tmax.
To avoid local optima, we enhanced the M step with simulated annealing. At each iteration the step randomly picks a Gaussian component kc, and randomly assign another value to its mean. The proposal for the random assignment is a Gaussian distribution centered at the current mean, with variance proportional to a temperature parameter T. The current mean is replaced by the new mean if its log-likelihood increased. The parameter T decreases after each iteration, making it less likely to sample a new mean far away from the current mean after each iteration. Our evaluations indicate that the simulated annealing prevents the EM algorithm from being trapped in local optima when the initialization is poor.
The approach is implemented in R and is available open-source. Analysis of the datasets in this article on a laptop with 2.7GHz CPU and 12G RAM took between 2 and 5 s per ion image.
3.5 Proposed data analysis workflow
The overall proposed spatial-DGMM workflow is overviewed in Figure 3. It consists of data pre-processing (black boxes), fitting the spatial-DGMM model to the observed intensities of an ion in a tissue (red boxes) and model-based inference from the output of spatial-DGMM (blue boxes).
Fig. 3.
The proposed workflow of data analysis with spatial-DGMM. Black: data processing; red: model fitting; and blue: model-based inference
3.5.1 Data pre-processing
Typical MSI pre-processing steps include baseline correction, normalization, peak picking, peak alignment and peak binning (Ràfols et al., 2018). Since the technical variance between different MS analyses can be quite large, normalization of spectra across locations and tissues reduces this variation. Different normalization methods can be used, such as total ion current (TIC) normalization, median normalization and normalization based on an internal standard. Smoothing eliminates non-systematic noise in the mass spectra. Peak picking summarizes the mass spectra, and reduces the m/z features to a subset of meaningful analytes. In the following, we assume that the input to spatial-DGMM are pre-processed m/z features across locations on one or multiple tissues, from one or several conditions.
3.5.2 Model fitting
The number of Gaussian components in an ion image corresponds to the number of morphological sub-structures in the spatial distribution of the ion. A single Gaussian component implies a homogeneous spatial distribution, and multiple Gaussian components imply a heterogeneous spatial distribution of that ion. Since different ions have different spatial distributions, we estimate the ion-specific number of Gaussian components from the data, as follows.
The Bayesian information criterion (BIC) is a common approach to estimating the number of components K in GMM. Therefore, we use it to initialize K in spatial-DGMM. However, BIC tends to overestimate the model complexity and K. Our simulations demonstrated that when K is too large, spatial-DGMM tends to return empty components, i.e. components with no mapped locations. Based on these observations, the proposed workflow estimates K using GMM and BIC, fits spatial-DGMM with multiple initializations and multiple neighborhood radii given K, and selects the mode of the numbers of non-empty Gaussian components in these initializations. Finally, spatial-DGMM is re-fit using the number of components .
3.5.3 Model-based inference
Model-based inference summarizes the fit of spatial-DGMM in ways that are useful for downstream statistical analyses. It consists of predicting component labels for each location i, estimating an overlap between a component with a pre-defined ROI, estimating distances between the spatial-DGMM maps of two ions, and estimating the mean ion intensities of each component.
The component labels for each location i are predicted as the label of component with highest posterior probability:
| (17) |
The overlap between the components detected by spatial-DGMM map and a pre-determined ROI is quantified by a match score
| (18) |
Ions with a Gaussian component of high matching score are viewed as morphology-specific.
Distances between the spatial-DGMM maps of two ions are estimated as the proportion of locations belonging to component j with identical component labels between two spatial-DGMM maps. Mathematically, we define the distance between two spatial-DGMM maps M1 and M2 as:
| (19) |
where if and 1 otherwise. This is used as input to clustering ions with similar spatial patterns.
The mean intensities of each component estimated from the model are used as input for differential analysis with t-test or ANOVA. In an unsupervised manner, as the components are ranked by their mean intensities in each condition, the compared components are mapped between conditions by their relative order. In a supervised manner, the compared components can be mapped manually between conditions or guided by other source of images.
4 Data
4.1 Simulated Data 1
To evaluate the accuracy of ion spatial-DGMM in presence of noise, we simulated 10 ion images with complex morphology. The images had three morphological components: 1 = circle, 2 = background and 3 = triangle, with mean intensities of and . The spatial variation in each ion was simulated according to the intrinsic conditional auto-regression (ICAR) model (Bemis et al., 2019), namely , where xi is the intensity of location i, and the mean intensity of morphological component k of location i. The term expressed the spatial auto-correlation , with standard deviation τ = 5. W is the N × N matrix that takes values of 1 for pairs of locations that are direct neighbors, and 0 otherwise. ϵi is the random noise of location i, varied from to .
4.2 Simulated Data 2
To evaluate the utility of spatial-DGMM for finding ions with similar patterns, we simulated four groups of ions with different morphologies, 10 ions per group. m/z 1–10 had three morphological components: 1 = circle, 2 = background and 3 = triangle, with μ1 varying from 65 to 116, and μ3 varying from 200 to 512. m/z 11–20 had two morphological components: 1 = background and 2 = triangle, with and μ2 varying from 265 to 571. m/z 21–30 had two morphological components: 1 = circle and 2 = background, with μ1 varying from 72 to 124 and . m/z 31–40 had homogeneous spatial distribution with μ varying from 134 to 193. The spatial variation was simulated with the ICAR model as above, and for all m/z.
4.3 Farmhouse painting
The experiment was used to evaluate spatial-DGMM in a real-life situation with known truth. In the oil painting on paper each color has a unique chemical composition, representing a component of the image. The painting was affixed to a glass slide. A DESI-MSI experiment with an LTQ linear ion trap mass spectrometer (Thermo Finnigan) acquired mass spectra from 12 600 locations, with m/z range 100–1000, and produced 10 800 m/z features. The data were analyzed with Cardinal (Bemis et al., 2015). At each location, the intensities were normalized with TIC and smoothed using Gaussian kernel. About 187 m/z features with signal to noise ratio >6 and occurring in >1% of the locations were retained for the analyses. The m/z in the original spectra were binned to the selected 187 m/z features.
4.4 Amyotrophic lateral sclerosis mouse brain
Amyotrophic lateral sclerosis (ALS) is a neurodegenerative disease of the brain and spinal cord (Cleveland and Rothstein, 2001). The brain of one mouse expressing a human ALS mutation (G93A) was collected at Day 45 after birth, sectioned, mounted, coated with 2,5-Dihydroxybenzoic acid (DHB) matrix using the TM Sprayer (HTX Technologies) and analyzed by MALDI-MSI using solariX 9.4 T FTICR MS (Bruker Daltonics) in positive mode. The spatial resolution was 100 μm with a mass range of m/z 609.44–1400. The data were converted from flexImaging (Bruker Daltonics) to imzML format and processed with Cardinal (Bemis et al., 2015). There were ∼1800 locations on the tissue and ∼1733 m/z features per location. For each location, the m/z were binned to a mass resolution of 2500. After the same pre-processing procedure as for the Farmhouse painting, 60 m/z features were retained for the analyses.
4.5 CpG and saline pre-conditioned mouse brain
CpG is an unmethylated oligodeoxynucleotide that stimulates the toll-like receptor 9 and induces neuroprotection against ischemic damage. Brain tissue sections of three saline (control) and four CpG pre-conditioned mice were collected and analyzed by nano-DESI MSI using an LTQ-orbitrap (Thermo Fisher Scientific) in positive mode (Bemis et al., 2019). The spatial resolution was approximately 40 × 200 μm with the mass range of 100–1500. The data in RAW format were converted to NetCDF format using Xcalibur (Thermo Fisher Scientific) and processed with Cardinal (Bemis et al., 2015). There were ∼2000 locations on the tissue and ∼7475 m/z features per location. For each location, m/z were binned to a mass resolution of 5800, and processed as above. About 433 m/z features were retained.
5 Results
5.1 Spatial-DGMM accurately segments ion images
We evaluated the accuracy of spatial-DGMM at varying levels of noise, in terms of estimates of the mean intensity of each component, and in terms of classifying tissue locations to their components (Section 3.5). Figure 4 compares the performance of spatial-DGMM to that of GMM on Simulated Data 1 (For comparison of spatial-DGMM and GMM on experimental data in section 4.4 and 4.5, Supplementary Figs. S1 and S2). With low noise, both GMM and spatial-DGMM suggest the correct number of morphological components (), have low estimation errors, and low misclassification rates.
Fig. 4.
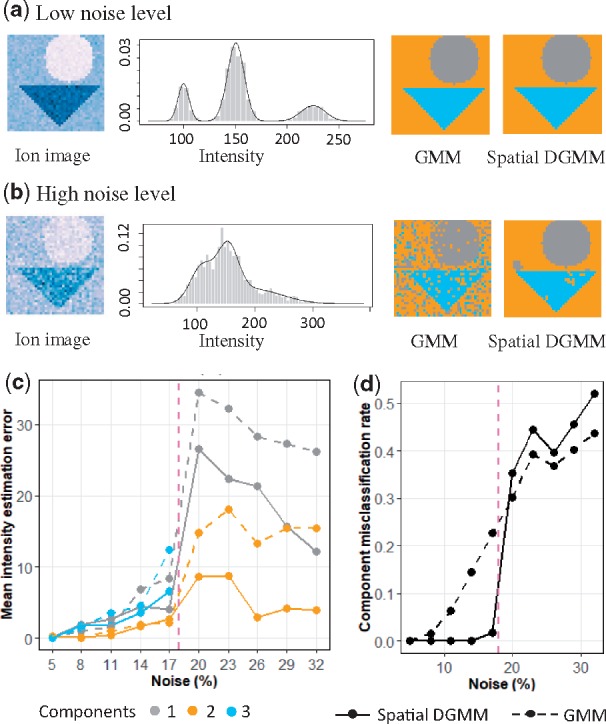
Accuracy of spatial-DGMM on the Simulated Dataset 1. (a) Ion image, histogram of ion intensities, GMM segmentation and spatial-DGMM segmentation for the simulated dataset with a low noise (). (b) As in (a), for the simulated dataset with a high noise (). (c) Estimation error of mean intensity of each morphological component versus noise (in % of intensity). (d) Misclassification rate versus noise level (in % of intensity). Only two Gaussian components were inferred with noise above 20%. K = 3 for noise level smaller than 20% of mean intensity and K = 2 for noise level equal or greater than 20% of mean intensity. In all the cases Kmax = 4 and . Kmax is the initialized maximum number of components, K is the number of components estimated by GMM and is the number of components estimated by spatial-DGMM
As the noise increases, the component map derived by GMM becomes uncertain, and the estimation error and the misclassification rate rapidly increase. Spatial-DGMM, on the other hand, leverages the information from the neighboring locations, has a lower estimation and misclassification error. In this particular simulation the 1.5-fold change between the mean intensities of the components is obscured when the noise exceeds 20%. GMM and spacial GMM only detect two morphological components, thus inflating the estimation and the misclassification errors.
5.2 Spatial-DGMM uncovers ion distributions hidden by multivariate segmentation
The experimental datasets allow us to evaluate the ability of spatial-DGMM to uncover ion-specific and morphology-specific information, in experiments with DESI (farmhouse painting), MALDI (ALS mouse brain) and nano-DESI (saline and CpG mouse brain) acquisitions.
5.2.1 Farmhouse painting
Although the multivariate analyses in Figure 1 uncovered the general outlines of the painting, the results lacked color specificity. For example, the spatial shrunken centroids in Figure 1d highlighted color red (walls), color blue (sky) and color dark green (leaves), but failed to distinguish colors light green (grass), color brown (earth) and color gray (windows). In contrast, images of individual ions in Figure 2 reflect color localization: m/z 650.17 (Fig. 2a) was specific to color black, and m/z 321.25 was selective (i.e. had a higher intensity) for color light green (Fig. 2c). Spatial-DGMM (Fig. 2b and d) automatically detected these ion-specific patterns.
5.2.2 ALS mouse brain
Figure 5 leads to the same conclusion. Spatial shrunken centroids and spatial K-means were strongly affected by the noisy ions, and missed the anatomic sub-structures of the mouse brain tissue. Spatial-DGMM successfully distinguished ions with informative (i.e. heterogeneous) spatial distribution from those with uninformative (i.e. homogeneous) spatial distribution. For example, DGMM finds characteristic patterns in m/z 868.33 and 838.63, which can be lipids (phosphatidylcholines) known to be present in both gray and white matter. DGMM detects relatively homogeneous distributions of m/z 896.57 and 681.14 across the tissue. We can interpret m/z 896.57 as driven not by the anatomic structure but by the cellular organization. m/z 681.14 is not known to be associated with the brain, and may arise from the matrix.
Fig. 5.
Segmentation of an ALS mouse brain. (a) Multivariate segmentation with spatial shrunken centroids, neighborhood radius = 1 and shrinkage parameter = 3. (b) Multivariate segmentation with spatial K-means. (c) Ion image of m/z 868.33. (d) Univariate spatial-DGMM of m/z 868.33, Kmax = 5, K = 4 and . (e) Ion image of m/z 838.33. (f) Univariate spatial-DGMM of m/z 838.33, Kmax = 5, K = 4 and . (g) Ion image of m/z 681.14. (h) Univariate spatial-DGMM of m/z 681.14, Kmax = 5, K = 4 and . (i) Ion image of m/z 896.57. (j) Univariate spatial-DGMM of m/z 896.57, Kmax = 5, K = 5 and . In d, f, h and j, Kmax is the initialized maximum number of components, K is the number of components estimated by GMM and is the number of components estimated by spatial-DGMM
5.2.3 Saline and CpG mouse brain
Figure 6 makes a similar point for a Sal pre-conditioned mouse brain tissue. Spatial shrunken centroids and spatial K-means produced three structured segments (and an additional segment stochastically distributed across the tissue). However, the multivariate segments could not fully represent the ion-specific spatial distributions. m/z 756.51 had a higher intensity in the upper and the central parts of the tissue, and spatial-DGMM highlighted that. For m/z 798.50, spatial-DGMM only detected two morphological components, and was consistent with the ion image.
Fig. 6.
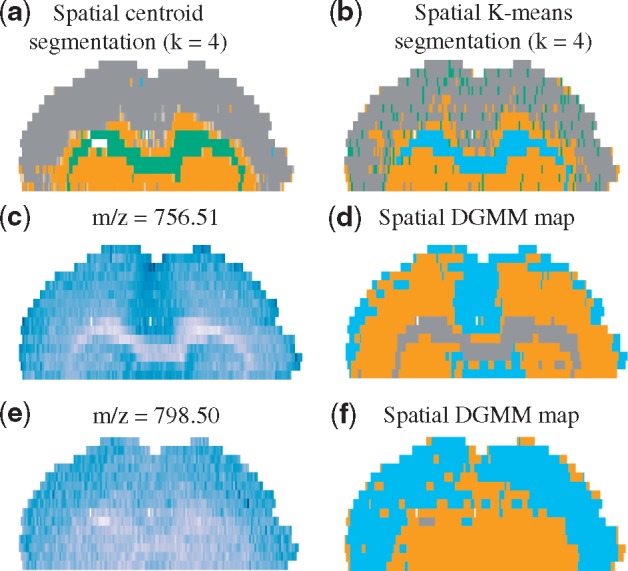
Segmentation of a Sal pre-conditioned mouse brain. (a) Multivariate segmentation with spatial shrunken centroids, neighborhood radius = 1, shrinkage parameter = 3. (b) Multivariate segmentation with spatial K-means. (c) Ion image of m/z 756.51. (d) The spatial-DGMM map of m/z 756.51 . (e) Ion image of m/z 798.50. (f) The spatial-DGMM map of m/z 798.50 . In d and f, Kmax is the initialized maximum number of components, K is the number of components estimated by GMM and is the number of components estimated by spatial-DGMM
5.3 Spatial-DGMM maps the distribution of ions to morphologically relevant regions
In many applications it is important to map the spatial distributions of an ions as present in (or absent from) a ROI (such as a known morphological region) of the tissue. Therefore, we evaluated the overlap between the components of ion distributions selected by spatial-DGMM and the regions of interest (Equation 18). We compared the results to those of Pearson correlation between the ion intensities and the binary vector indicating the region.
Figure 7 illustrates the results in the case of a Sal mouse brain tissue. The ROI in Figure 7a, obtained by spatial shrunken centroid segmentation, approximated corpus callosum. The image of m/z 844.67 shows a clear selectivity for this segment; however, it is also systematically over-represented in other regions of the brain (Fig. 7b). As the result, the Pearson correlation is relatively low (−0.51). Spatial-DGMM, on the other hand, had the matching score of 0.78, indicating a high ion selectivity for this region (Fig. 7c).
Fig. 7.
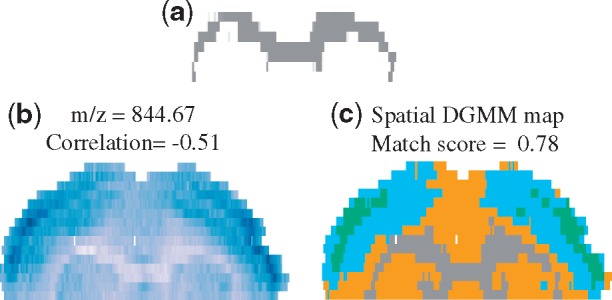
Selectivity of ion localization to a morphological structure in a Sal mouse brain tissue. (a) A region of interest, obtained by spatial shrunken centroid segmentation and approximating corpus callosum. (b) Ion image of m/z 844.67, the correlation is calculated between ion image and binary matrix indicating the area of interest. (c) Morphological component map of (b) modeled by spatial-DGMM
5.4 Spatial-DGMM helps cluster ions with similar spatial distributions
Grouping ions with similar spatial distributions helps understand the biological processes in the tissue. We evaluated the ability of hierarchical clustering to group such ions in Simulated Data 2, using two types of inputs. The first input was the intensities of the individual locations in the image. In this simulation, this input for each ion was a 1600-dimensional vector of noisy measurements lacking spatial information, and the ions were compared using Euclidean distance. The second input was the spatial-DGMM map generated by the proposed model. In this simulation, the input for each ion was a categorical 1600-dimensional vector, where the entries were the component labels of each location. The ions were compared as defined in Equation 19.
Figure 8a shows the simulated ion images of the four ion groups, where 10 replicate ions per group have a same spatial distribution. Figure 8b illustrates that, due to the noise and to the high dimensionality of the input data, the hierarchical clustering failed to consistently group some of the ions with the same spatial distribution. Clustering the ions in the space of the spatial-DGMM components, on the other hand, could more fully characterize the similarity between the spatial distributions.
Fig. 8.
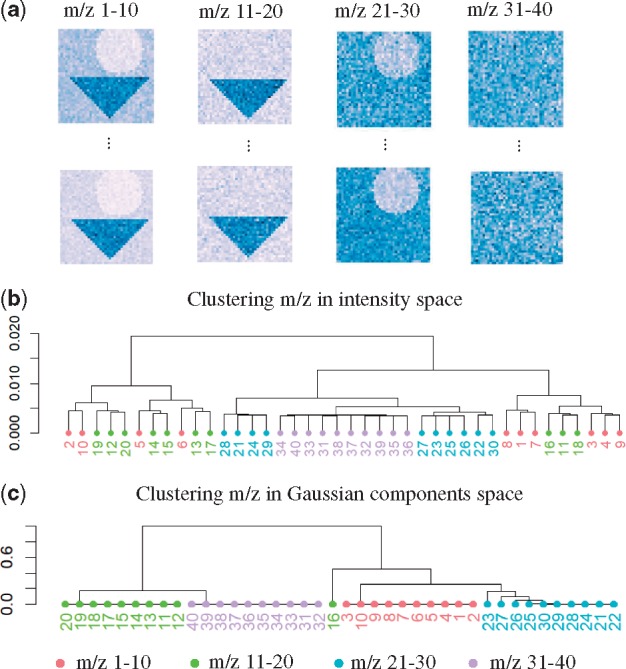
Hierarchical clustering of ions with similar spatial distributions in Simulated Dataset 2. (a) Simulated morphological components for ions 1–10, 11–20, 21–30 and 31–40. (b) Hierarchical clustering of ions in the location space. (c) Hierarchical clustering of ions in the Gaussian components space generated by spatial-DGMM. for m/z 1–10, 16; for m/z 11–15, 17–30; for m/z 31–40. K is the number of components estimated by GMM and is the number of components estimated by spatial-DGMM
5.5 Spatial-DGMM uncovers differences in ion abundance between conditions
Many MSI experiments characterize changes in chemical compositions of tissues between conditions. We evaluated the utility of spatial-DGMM for this purpose in the CpG and saline pre-conditioned mouse brains experiment. Figure 9 illustrates the comparison for m/z 826.76. Figure 9a and b highlights the heterogeneity of the distribution of this ion in a CpG and a saline tissues. Spatial-DGMM detected three morphological components with distinct mean values in the tissues (Fig. 9c and d).
Fig. 9.
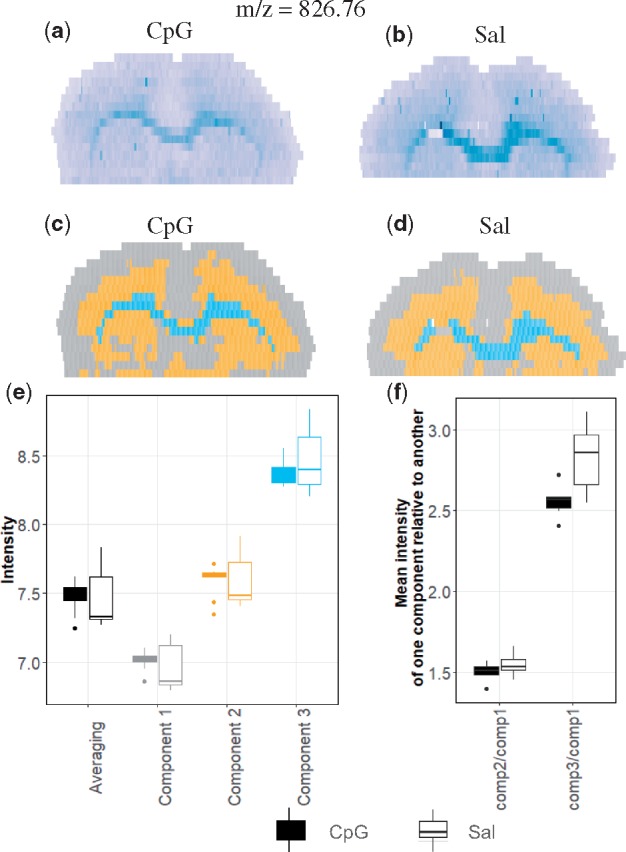
Changes in chemical composition in mouse brains between CpG and Sal conditions. (a) Ion image (m/z 826.76) of one of the four biological replicates of CpG pre-conditioned mouse brain. (b) Image of the same ion of one of the three biological replicates of saline pre-condition. (c) Spatial-DGMM component map of (a). (d) Spatial-DGMM component map of (b). (e) Comparison between the CpG and the Saline pre-conditioned mice. Black boxplots summarize the average intensities of m/z 826.76 in each tissue. Color boxplots summarize the average intensities of m/z 826.76 in each component detected by spatial-DGMM. (f) Paired comparison between the CpG and the Saline pre-conditioned mice. The boxplots summarize relative mean intensities of the components in a same tissue. The CpG pre-conditioned group had a smaller intensity of Component 3 relative to Component 1
When the analysis averaged the intensities of this ion separately in each tissue and over all the replicate tissues, we found no apparent difference in abundance between the two conditions (black boxes in Fig. 9e). However, when comparing the mean intensities of the components detected by spatial-DGMM the differences were more pronounced, and revealed that in Components 1 and 2 the ion was regulated in the direction opposite to that in Component 3 (colored boxes in Fig. 9e).
Finally, as an alternative way to gain insight into the regulation, we compared the relative mean intensities of the ion between pairs of components in each group (Fig. 9f). The ratio is an indicator of the difference between the two morphological components within each tissue. As we can see from Figure 9d, the mean intensity of Component 3 relative to Component 1 was visibly regulated between two conditions. This information is overlooked when not taking the tissue morphology into account.
6 Discussion
We proposed a novel workflow spatial-DGMM for MSI experiments. Spatial-DGMM segments an ion image of a tissue into a data-driven number of Gaussian components, that reflect morphological sub-structures in the analyzed tissue. We showed the application of GMM in MSI for the first time. The number of Gaussian components can be used to distinguish ions with homogeneous or heterogeneous spatial distributions. In addition, spatial-DGMM quantitatively extracts statistical summaries of the Gaussian components, such as their mean intensities and variances, spatial location and overlap with a pre-defined ROI.
We demonstrated using simulated data that spatial-DGMM accurately estimates the correct number of Gaussian components, and their properties. Applied to experimental data from different experimental workflows, specifically DESI-MSI, MALDI-MSI and nano-DESI MSI with diverse characteristics, spatial-DGMM uncovered ion-specific patterns that could not be found via multivariate analysis. We also explored downstream applications of spatial-DGMM, and demonstrated its utility for selecting ions colocalizing with a region-of-interest, clustering ions with similar spatial patterns and detecting morphology-specific changes in ion abundance between conditions.
The limitations of spatial-DGMM are related to its assumptions. Spatial-DGMM assumes that ion intensities within a unique morphological sub-structure approximately follow a Gaussian distribution. In reality, the data may have more complex distributions. The accuracy of estimating the number of morphological components and their properties depends on the extent of differences of the intensities in these components, and on the associated noise. Despite the limitations, we believe that spatial-DGMM will help gain useful information from ion images, and will become an important tool for practical applications of MSI.
Supplementary Material
Acknowledgements
The authors are grateful to Dr Christina Ferreira and Prof. Graham R. Cooks (Purdue University) for providing access to the farmhouse painting experiment, and to Prof. Ingela Lanekoff (Uppsala University) and Prof. Julia Laskin (Purdue University) for providing access to the CpG and Saline pre-conditioned mouse brain experiment.
Conflict of Interest: none declared.
Funding
This work was supported in part by the award NSF-BIO/DBI 1759736 to O.V.
References
- Aichler M., Walch A. (2015) MALDI imaging mass spectrometry: current frontiers and perspectives in pathology research and practice. Lab. Invest., 95, 422.. [DOI] [PubMed] [Google Scholar]
- Alexandrov T. et al. (2010) Spatial segmentation of imaging mass spectrometry data with edge-preserving image denoising and clustering. J. Proteome Res., 9, 6535.. [DOI] [PubMed] [Google Scholar]
- Alexandrov T., Kobarg J.H. (2011) Efficient spatial segmentation of large imaging mass spectrometry datasets with spatially aware clustering. Bioinformatics, 27, i230.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bemis K. et al. (2015) Cardinal: an R package for statistical analysis of mass spectrometry-based imaging experiments. Bioinformatics, 31, 2418.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bemis K. et al. (2016) Probabilistic segmentation of mass spectrometry images helps select important ions and characterize confidence in the resulting segments. Mol. Cell. Proteomics, 15, 1761–1772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bemis K.A. et al. (2019) Statistical detection of differentially abundant ions in mass spectrometry-based imaging experiments with complex designs. Int. J. Mass Spectrom., 437, 49. [Google Scholar]
- Blekas K. et al. (2005) A spatially constrained mixture model for image segmentation. IEEE Trans. Neural Netw., 16, 494.. [DOI] [PubMed] [Google Scholar]
- Bonnel D. et al. (2011) Multivariate analyses for biomarkers hunting and validation through on-tissue bottom-up or in-source decay in MALDI-MSI: application to prostate cancer. Anal. Bioanal. Chem., 401, 149.. [DOI] [PubMed] [Google Scholar]
- Cassese A. et al. (2016) Spatial autocorrelation in mass spectrometry imaging. Anal. Chem., 88, 5871–5877. [DOI] [PubMed] [Google Scholar]
- Cleveland D.W., Rothstein J.D. (2001) From Charcot to Lou Gehrig: deciphering selective motor neuron death in ALS. Nat. Rev. Neurosci., 2, 806. [DOI] [PubMed] [Google Scholar]
- de Muller G.P. et al. (2017) Automated morphological and morphometric analysis of mass spectrometry imaging data: application to biomarker discovery. J. Am. Soc. Mass Spectrom., 28, 2635.. [DOI] [PubMed] [Google Scholar]
- Delcourt V. et al. (2018) Spatially-resolved top-down proteomics bridged to MALDI MS imaging reveals the molecular physiome of brain regions. Mol. Cell. Proteomics, 17, 357.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones E.A. et al. (2011) Multiple statistical analysis techniques corroborate intratumor heterogeneity in imaging mass spectrometry datasets of myxofibrosarcoma. PLoS One, 6, e24913.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones E.A. et al. (2012) Imaging mass spectrometry statistical analysis. J. Proteomics, 75, 4962.. [DOI] [PubMed] [Google Scholar]
- Nguyen T.M., Wu Q.M.J. (2011) Dirichlet Gaussian mixture model: application to image segmentation. Image Vis. Comput., 29, 818. [Google Scholar]
- Nikou C. et al. (2010) A Bayesian framework for image segmentation with spatially varying mixtures. IEEE Trans. Image Process., 19, 2278.. [DOI] [PubMed] [Google Scholar]
- Norris J.L., Caprioli R.M. (2013) Analysis of tissue specimens by matrix-assisted laser desorption/ionization imaging mass spectrometry in biological and clinical research. Chem. Rev., 113, 2309.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prasad M. et al. (2018) Drug-homogeneity index in mass spectrometry imaging. Anal. Chem., 90, 13257.. [DOI] [PubMed] [Google Scholar]
- Ràfols P. et al. (2018) Signal preprocessing, multivariate analysis and software tools for MALDI-TOF mass spectrometry imaging for biological applications. Mass Spectrom. Rev., 37, 281.. [DOI] [PubMed] [Google Scholar]
- Spengler B. (2015) Mass spectrometry imaging of biomolecular information. Anal. Chem., 87, 64.. [DOI] [PubMed] [Google Scholar]
- Trede D. et al. (2012) SCiLS Lab: software for analysis and interpretation of large MALDI-IMS datasets. In: Proceedings of OurCon, p.50, September 3-5, 2012, Ourense, Spain.
- Watrous J.D. et al. (2011) The evolving field of imaging mass spectrometry and its impact on future biological research. J. Mass Spectrom., 46, 209.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu C. et al. (2013) Mass spectrometry imaging under ambient conditions. Mass Spectrom. Rev., 32, 218.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zivkovic Z. (2004) Improved adaptive gaussian mixture model for background subtraction. Pattern Recognit., 2, 28. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




