Abstract
Motivation
Alternative splicing generates multiple isoforms from a single gene, greatly increasing the functional diversity of a genome. Although gene functions have been well studied, little is known about the specific functions of isoforms, making accurate prediction of isoform functions highly desirable. However, the existing approaches to predicting isoform functions are far from satisfactory due to at least two reasons: (i) unlike genes, isoform-level functional annotations are scarce. (ii) The information of isoform functions is concealed in various types of data including isoform sequences, co-expression relationship among isoforms, etc.
Results
In this study, we present a novel approach, DIFFUSE (Deep learning-based prediction of IsoForm FUnctions from Sequences and Expression), to predict isoform functions. To integrate various types of data, our approach adopts a hybrid framework by first using a deep neural network (DNN) to predict the functions of isoforms from their genomic sequences and then refining the prediction using a conditional random field (CRF) based on co-expression relationship. To overcome the lack of isoform-level ground truth labels, we further propose an iterative semi-supervised learning algorithm to train both the DNN and CRF together. Our extensive computational experiments demonstrate that DIFFUSE could effectively predict the functions of isoforms and genes. It achieves an average area under the receiver operating characteristics curve of 0.840 and area under the precision–recall curve of 0.581 over 4184 GO functional categories, which are significantly higher than the state-of-the-art methods. We further validate the prediction results by analyzing the correlation between functional similarity, sequence similarity, expression similarity and structural similarity, as well as the consistency between the predicted functions and some well-studied functional features of isoform sequences.
Availability and implementation
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
In recent years, the study of functional genomics has expanded from the gene level to the transcript level. Due to alternative splicing, exons of multi-exon genes are selectively included in the transcription process, thus generating multiple isoforms from a single gene. Isoforms carry specific, sometimes distinct or even opposing, biological functions. Moreover, the expression of an isoform is often specific to tissue, developmental stage or environmental conditions, which is responsible for the diversity and adaptability of cellular activities (Sulakhe et al., 2018; Wang et al., 2008). Therefore, delineating the functions of isoforms is crucial to the study of functional complexity and diversity of genomes.
Despite their importance, the specific functions of the vast majority of isoforms are still poorly understood to date. Although many well-established databases exist (Bairoch et al., 2004; Kanehisa et al., 2000) for gene functional annotation, very few functions have been annotated at the isoform level. Owing to the large number of isoforms, systematic and global analysis of isoform functions experimentally is impractical in a short period. Therefore, efficient computational methods that can provide high-throughput and accurate predictions of isoform functions are in great demand. Given the availability of annotated gene functions, supervised learning has been successfully applied for gene function prediction (Kulmanov et al., 2017; Mostafavi et al., 2008). In contrast, the lack of isoform-level functional ground truth annotation makes isoform function prediction much more challenging.
Several methods have been proposed for isoform function prediction recently, including iMILP (Li et al., 2014b), mi-SVM (Eksi et al., 2013), WLRM (Luo et al., 2017) and DeepIsoFun (Shaw et al., 2018). The basic idea of these methods is to distribute the functional annotation of a gene to all of its isoforms using techniques such as multiple instance learning (MIL) and domain adaptation. However, these methods suffer from the limitation that they infer isoform functions from the information contained in expression profiles alone. The experimental results suggest that the prediction accuracy of these methods is less than desirable: the best area under the receiver operating characteristics curve (AUC) achieved by these methods is around 0.7 and the best area under the precision–recall curve (AUPRC) is around 0.3 (Shaw et al., 2018).
Different types of biological data may carry complementary information of isoform functions, and hence a systematic integration of such information might lead to a substantial improvement in prediction accuracy (Li et al., 2016; Sulakhe et al., 2018). In particular, we may divide informative biological data into the following two types. (i) Data of individual isoforms: An isoform sequence may contain some functional sites, say active or binding sites, signal peptides and motifs. These sites, although very short, could provide strong signals about the functions of an isoform. Another source of information is (evolutionarily) conserved domains. Compared with functional sites, conserved domains are much longer, and their conservation during the evolutionary process may imply their important biological functions. Both functional sites and conserved domains could be identified from an isoform sequence, and it is well-known that the presence or absence of such sequence features can significantly influence its functions. For example, Taneri et al. (2004) studied the impact of alternative splicing on transcription factors in mouse and reported that alternative splicing can delete DNA binding domains, generating tissue-specific protein isoforms with distinct functions. (ii) Data between isoforms: From the expression profiles of isoforms, we could easily identify the co-expression relationship between isoforms (Ellis et al., 2012). This co-expression relationship has been used to predict isoform functions in the aforementioned methods as co-expressed isoforms tend to share similar biological functions. These two types of biological data come in different forms: the functional sites and conserved domains can be represented as strings while the co-expression relationship is usually represented as a network. How to integrate such different forms of data in isoform function prediction remains as a challenge.
In this paper, we present a novel approach, named DIFFUSE (Deep learning-based prediction of IsoForm FUnctions from Sequences and Expression), that integrates both isoform sequences and expression profiles to predict isoform functions. Our approach goes through two stages to integrate various information into a unified predictive model. In the first stage, a deep neural network (DNN) is designed to capture features from isoform sequences and conserved domains. Taking the sequence and conserved domains of an isoform as the input, the DNN computes an initial score that measures how likely the isoform has the function under consideration. In the second stage, a conditional random field (CRF) is designed to exploit the co-expression relationship between isoforms. By combining the initial scores computed by the DNN with the co-expression relationship, the CRF assigns isoforms functional labels based on the initial scores while trying to keep highly co-expressed isoforms attaining the same labels. To overcome the lack of isoform-level training labels, we propose an iterative semi-supervised training algorithm based on the MIL framework similar to the one in (Andrews et al., 2002). Specifically, our approach first initializes all isoforms of genes that have the function under consideration with positive labels and the other isoforms with negative labels. The initial functional labels are then used to train the model parameters. The new parameters of the model are next used to update the label of each isoform from positive genes. In each iteration, these two steps are performed alternately. Note that the isoforms of the same gene may be assigned different labels an update, which would encourage the model to capture features that can differentiate the functions of different isoforms.
To evaluate the performance of DIFFUSE, we first measure its prediction accuracy using the gene-level functional annotation in Gene Ontology (GO) as done in Li et al. (2014b), Eksi et al. (2013), Luo et al. (2017) and Shaw et al. (2018). DIFFUSE achieves an average AUC of 0.840 and AUPRC of 0.581 over 4184 functional categories. We also compare DIFFUSE with the existing methods on several datasets. Four state-of-the-art isoform function prediction methods proposed in Li et al. (2014b), Eksi et al. (2013), Luo et al. (2017) and Shaw et al. (2018) are included in the comparison. The results demonstrate that our method significantly outperforms the others. We further analyze the divergence of the predicted functions of isoforms from the same gene. The scarcity of experimentally verified isoform functions makes the validation of predicted functions difficult. We thus conduct a series of computational experiments to indirectly validate our predictions. More specifically, we first analyze how functional similarity is correlated with isoform sequence, expression and structural similarities. Our analysis shows that the similarity of predicted functions has higher correlation with isoform structural similarity than with sequence similarity or expression similarity, which accords previous studies (Illergård et al., 2009). The predictions are then further validated by assessing their consistency with the presence or absence of some well-studied functional sequence features followed by a targeted literature search.
2 Materials and methods
2.1 Datasets
Isoform sequences of the human genome are downloaded from the NCBI Reference Sequences database (RefSeq GRCh38.p12; Pruitt et al., 2012). To ensure sequence quality, only manually curated RefSeq records are recruited in our computational experiments. The ‘Coding DNA Sequence’ (CDS) is extracted for each isoform using the RefSeq CDS annotation file. Two or more isoforms corresponding to the same CDS are treated as a single isoform. For each isoform, we search it against the NCBI Conserved Domain Database (Marchler-Bauer et al., 2015) to acquire its conserved domains.
Isoform expression profile data are obtained from the literature (Shaw et al., 2018). It consists of human isoform RNA-seq data from the NCBI Reference Sequence Archive (SRA) (Leinonen et al., 2011) consisting of 334 studies and 1735 experiments. Only isoforms that appear in both the sequence data and the expression data are kept. This results in a total of 39 375 isoforms from 19 303 genes consisting of 9032 multiple isoform genes (MIGs) and 10 271 single isoform genes (SIGs).
We adopt the functional categories defined by GO, and download gene functional annotation from the UniProt Gene Ontology Annotation database (Huntley et al., 2015). To ensure the annotation quality, we only keep manually curated GO terms and skip terms with the ‘IEA’ evidence code. Similar to (Li et al., 2014b;Shaw et al., 2018), we also ignore GO terms that are too specific or general. Finally, 4184 GO terms associated with the numbers of genes in the range of 10–1000 are considered in this study.
2.2 Methods
2.2.1. Overview
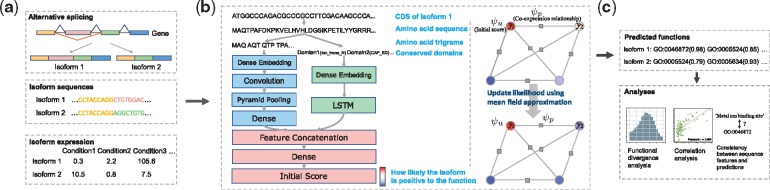
As mentioned before, DIFFUSE predicts isoform functions by integrating the information of isoform sequences, conserved domains and expression profiles into a unified predictive model. More specifically, we train a model for each GO term. The inference procedure of the model consists of two stages. In the first stage, taking the sequence and conserved domains of an isoform as the input, the DNN computes an initial score in the range of [0, 1] measuring how likely the isoform has the GO term. In the second stage, the CRF makes a final prediction by considering both the initial scores and the co-expression relationship among isoforms. To overcome the lack of annotated isoform functions, we develop a semi-supervised algorithm following (Andrews et al., 2002) to train both the DNN and CRF together iteratively. To help training the DNN, protein sequences from the SwissProt (Boutet et al., 2016) database are also used as training data. To avoid potential information leak between the training and test data, we consider clusters of orthologous groups (COGs) and make sure that each COG is never split between the training and test data. A schematic illustration of DIFFUSE as well as the analyses to be performed in our study is given in Figure 1, and more details of the method are discussed below.
Fig. 1.
Overview of our computational pipeline. (a) Alternative splicing generates multiple isoforms from a gene with different sequences and expression profiles. (b) The DIFFUSE model contains two key components, a DNN and a CRF. The DNN consists of several layers and components including a CNN and an LSTM. Its input consists of trigrams generated from a CDS or protein sequence and conserved domains. It computes an initial score indicating how likely the output label is positive. The CRF can be represented as a complete graph G over variables y, which denote the labels of isoforms. Each unary clique or pairwise clique in G induces a unary potential or a pairwise potential denoted as ψu or ψp. The CRF makes predictions by minimizing a Gibbs energy composed of ψu’s and ψp’s. The initial scores are factored into ψu’s while the co-expression relationship is factored into ψp’s. The DNN and CRF are trained together using an iterative semi-supervised learning algorithm based on MIL, where the positive likelihood of each isoform is initialized with its initial score and then updated iteratively through the mean field approximation. (c) Several analyses are conducted in our study to support or validate our predicted isoform functions
2.2.2. Exploring sequence features using a DNN
DNNs are known to be effective in capturing biological sequence features (Kulmanov et al., 2017; Zhang et al., 2017). Here, we design a DNN consisting of two components (Fig. 1b) to capture informative features from isoform sequences and conserved domains, respectively. We use a convolutional neural network (CNN) to extract sequence features. Specifically, we first translate each isoform CDS to an amino acid sequence. Then, each sequence is represented as a series of overlapping trigrams, denoted as s = (). Each trigram is embedded as a continuous vector by the dense embedding layer [denoted as embed()] (Bengio et al., 2003). Note that the vector representations are optimized during the training process and thus are able to capture similarities between the trigrams. We then employ a 1D convolutional layer with multiple convolution filters [denoted as conv()] to scan the encoded sequence and detect the functional sites. After that, pooling [denoted as pool()] and dense [denoted as dense()] layers are used to reduce the dimensionality of the hidden features.
A big challenge here is that the lengths of isoform sequences vary a lot. Due to the fixed size of pooling window and stride, the output size of a normal pooling layer depends on the length of the input sequence, which makes connecting the pooling layer to the following dense layer impossible. To address this problem, we adopt a ‘pyramid pooling’ layer in our model, which is widely used in computer vision (He et al., 2014). We modify it, however, as a 1D pooling layer. The pyramid pooling layer can generate a fixed-length output regardless of the input sequence length. Specifically, it uses multi-level pooling bins. Pooling bins at different levels have sizes proportional to the sequence length with different ratios. The number of bins at each level is fixed. High level pooling bins capture global features while low level bins capture local features.
Conserved domains are the building blocks of proteins. Their duplication, fusion and recombination during evolution produce proteins with novel structures and functions. In addition, the order of domains is also conserved during evolution (Kummerfeld et al., 2009). Rearrangement of domains can influence functions of a protein. We use a recurrent neural network to capture domain features. Domain order information is considered in the network structure design. Specifically, we order the conserved domains of an isoform as a sequence, denoted as d = (), where each domain is represented by a unique ID. Then, we use the same dense embedding technique to embed each ID into a vector representation. To capture the order information of domains, we apply the recurrent layer with long short-term memory (LSTM) units [denoted as LSTM()] to process the encoded domain sequence. The output of the last LSTM unit is used as the feature vector from the domain component.
Feature vectors from both the sequence and domain components are then concatenated to form a unified feature representation. Finally, the unified representation is fed into a logistic regression layer [denoted as logit()] to compute the initial score as follows. Formally, given isoform sequence s and sequence of domains d, the initial score computed as follows:
| (1) |
2.2.3. Exploring co-expression relationship using a CRF
The function of an isoform is sometimes determined by its interacting partners that are often co-expressed. To capture the co-expression relationship among isoforms, we design a CRF in the second stage (Fig. 1b). Co-expression networks are first derived from the RNA-seq data. Specifically, we construct a co-expression network for each SRA study using the WGCNA algorithm (Langfelder et al., 2008), which has been widely used in the studies of weighted correlation network analysis. To ensure the network quality, we only consider SRA studies with at least 10 experiments. This results in a total of 42 networks. For each pair of isoforms, the absolute value of the Pearson correlation coefficient (PCC) between their expression profiles is assigned as the corresponding edge weight using the soft threshold method of WGCNA.
We denote the sequence, domains and expression profile of an isoform i as , and , and use a binary scalar to denote its label, indicating whether the isoform has the function under consideration or not. The CRF model aims to assign each isoform a label by minimizing a Gibbs energy function, which is defined as:
| (2) |
The Gibbs energy is characterized by both the initial scores from the DNN and the co-expression relationship between isoforms. The unary potential comes from the initial scores, which is defined as and . The co-expression relationship is considered in the pairwise potential, which is defined as:
| (3) |
where is the edge weight between isoform i and isoform j in the lth co-expression network and is a label compatibility function defined as that is used to penalize highly co-expressed isoforms with differently assigned labels. The weights θ1 and θ2 control the relative importance of the unary potential ψu and pairwise potential ψp in the Gibbs energy, and discussed in the following section.
By finding a label assignment that minimizes the Gibbs energy , we aim to assign each isoform an label with low unary energy and, at the same time, ensure that highly co-expressed isoforms get the same label. Because of the computational complexity of exact inference, we apply an efficient approximation algorithm named the mean field approximation similar to (Krähenbühl et al., 2011). Here, minimizing the Gibbs energy is formulated as maximizing the following probability:
| (4) |
where is a normalization constant. Instead of computing the exact distribution , the approximation algorithm computes a distribution that minimizes the KL-divergence , where the distribution Q is defined as a product of independent marginals:
| (5) |
Minimizing the KL-divergence yields the following iterative update equation:
| (6) |
Qi is initialized with the unary potential and updated iteratively according to Equation (6) until convergence, which gives the final output of our model.
2.2.4. Training the model with the MIL framework
Algorithm 1:
Model training
Initialization: Initialize the label of each instance in a positive or negative bag as or 0, respectively. Initialize DNN parameters w and CRF parameters θ.
Parameter update: Fix instance labels and update model parameters.
1: Compute and use SGD to update w.
2: Compute and use L-BFGS-B to update θ.
Label update: Fix model parameters and update instance labels.
3: for each instance i in positive bags do
4:
5: end for
6: for each positive bag bdo
7: if, for all instances i belonging to bag b then
8: , for all instances i belonging to bag b
9:
10: end if
11: end for
Due to the lack of ground truth isoform labels, the conventional supervised training algorithm cannot be directly applied to our model. Hence, we adopt a semi-supervisd model training algorithm under the MIL framework similar to the one in (Andrews et al., 2002), which is outlined in Algorithm 1. In the MIL framework, each gene is treated as a bag, the isoforms of a gene are treated as the instances in the bag, and only the ground truth labels of the bags (i.e. genes) are required. A positive bag refers to a gene that has the function under consideration. Clearly, a positive bag should contain at least one positive instance, while a negative bag should contain no positive instances. We first initialize the instances of positive bags with positive labels, and the others with negative labels. Then, the model parameters can be optimized with the initial labels in the normal supervised learning manner. In particular, given the training instances , the loss function in terms of the DNN parameters w is defined as the sum of the negative log likelihoods:
| (7) |
Gradients in terms of w can be computed and the stochastic gradient descent (SGD) algorithm is used to optimize w. Similarly, the CRF parameters θ are optimized by minimizing the negative log-likelihood using the L-BFGS-B algorithm (Zhu et al., 1997), which is defined as:
| (8) |
Here, the second term is a regularization term to reduce over-fitting, where is a free parameter that determines how much to penalize large weights. L-BFGS-B requires to compute the gradient of in terms of θ. However, the number of terms in Z of is exponential in the number of instances, making the gradient computation intractable. We therefore use an approximate gradient algorithm given in Sutton et al. (2012), which approximates the true gradient by replacing P with the marginals Q:
| (9) |
| (10) |
After updating the parameters of the model, we perform inference for each instance in positive bags using the new model. Instance labels are then updated according to the inference: . For each positive bag, if all its instances are assigned with negative labels, we select the instance with the largest positive prediction score in the bag as positive. The parameter update step and the label update step are repeated alternately until convergence.
2.2.5. Implementation details
A large number of manually reviewed protein sequences with annotated GO terms are available on the SwissProt (Boutet et al., 2016) database. Most proteins in the database represent the canonical isoforms of genes and therefore will not help improve the model’s ability to differentiate the isoform functions of the same gene. However, they are still precious resources that can help our DNN learn important functional features from sequences and domains. We download 89 459 eukaryotic (other than human) protein sequences with GO annotation from the SwissProt database. Conserved domain data are downloaded accordingly using the same method described before. The data are used to train the DNN. Specifically, given the sequence, domains and ground truth label of each protein instance, the initial score and loss of DNN are computed for the instance and then the loss is used to update the DNN parameters.
We partition our data into the training, validation and test sets with the proportions of 70%, 10% and 20%, respectively. To avoid potential information leak (i.e. isoforms with very similar sequences and similar functions appear in different components of the partition), we split the data according to two criteria. First, we require that isoforms of the same gene are partitioned into the same set. Second, since our data contains proteins from different eukaryotes, we forbid orthologous genes to be split. In other words, we consider COGs (Tatusov et al., 2000) and require that all genes of the same COG are partitioned together. COGs (10 308) are downloaded from the EggNOG database (Huerta-Cepas et al., 2016). Note that the SwissProt proteins are only used for training our model and are not involved in testing. Hyperparameters of the model are manually tuned based on the model performance on the validation data. The validation data are then merged with the training data to train a final model for each GO term before we assess its performance in terms of AUC and AUPRC.
In our computational experiments, the Adam optimizer (Kingma et al., 2014) is used to optimize the DNN. The sizes of the embedding vectors for both amino acid trigrams and domain unique IDs are 32. We use 64 convolution filters with length 32 and stride 1. The pyramid pooling layer consists of pooling bins from four levels, with 1, 2, 4 and 8 bins at each level, respectively. To prevent over-fitting the model, the dropout (Srivastava et al., 2014) technique is adopted. The DNN model is implemented using the Keras library with TensorFlow (Abadi et al., 2016) as the backend. The SciPy package is used for implementing the L-BFGS-B algorithm. To accelerate the training process, NVIDIA K80 GPUs are used.
3 Results and validation
In this section, we first evaluate the performance of DIFFUSE and the effectiveness of each component of the model. We then study the divergence of isoform functions predicted by our method from the same gene. To validate our predictions, we analyze the correlation between functional similarity, sequence similarity, expression similarity as well as structural similarity. The predicted functions are further validated by assessing their consistency with some well-studied functional sequence features. Finally, a targeted literature search is performed to directly confirm some of the isoform functions considered above.
3.1 Prediction of isoform functions
3.1.1. Prediction performance of DIFFUSE
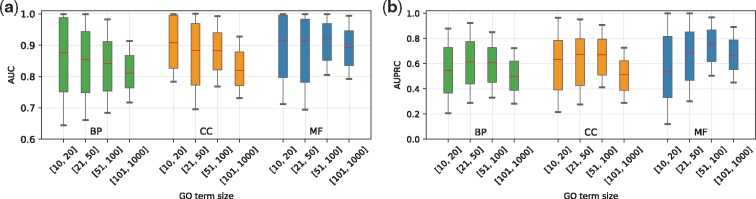
Since annotated isoform functions are generally unavailable, following the evaluation procedure used in previous isoform function prediction studies (Eksi et al., 2013; Li et al., 2014b;Luo et al., 2017; Shaw et al., 2018), we first evaluate the performance of our method using gene-level functional annotation. For each GO term, the maximum prediction score among the isoforms of a gene is taken to check its consistency with the gene annotation. To investigate how the prediction performance may be influenced by GO branches and the number of positive genes, we divide all the GO terms into 12 groups based on GO branch and term size, which is defined as the number of genes associated with a GO term. Specifically, we first divide GO terms into three groups based on the three main GO branches [i.e. Biological Process (BP), Molecular Function (MF) and Cellular Component (CC)]. Then, the terms of each group are divided into four subgroups with term sizes in the ranges of [10, 20], [21, 50], [51, 100] and [101, 1000], respectively. Both AUC and AUPRC are used to evaluate the performance for each GO term. Since the baseline for AUPRC (ratio of positive genes in the test set) is different for different GO terms, to make comparison across different groups more fair, we unify the AUPRC baseline as 0.1 for all terms by duplicating positive genes in the test set. Out of the 4184 GO terms, 3037 are in the BP group, 432 in CC and 715 in MF.
The (numerical, also called macro) average AUC value for BP, CC and MF is 0.829, 0.850 and 0.881, and the average AUPRC values are 0.563, 0.586 and 0.656, respectively. The distributions of AUC and AUPRC values in different groups are shown in Figure 2. Interestingly, we observe that more positive genes do not yield higher performance. The groups with the largest term sizes (i.e. range [101, 1000]) in fact have relatively low AUC and AUPRC values compared with the other groups. This phenomenon has been observed in several previous studies as well (Li et al., 2014b; Shaw et al., 2018). A possible explanation is that as the term size increases, the biological features (i.e. sequences and expression) of isoforms associated with a GO term become more heterogeneous and the correlation between the functional similarity and the similarities of the biological features decreases, as discussed in Shaw et al. (2018).
Fig. 2.
Performance evaluation in terms of AUC and AUPRC. GO terms are divided into groups based on the three main GO branches and term sizes. (a) Distributions of AUC scores over GO terms in different groups. (b) Distributions of AUPRC scores
3.1.2. Performance comparison with the existing methods
We compare DIFFUSE with four state-of-the-art isoform function prediction methods including mi-SVM (Eksi et al., 2013), iMILP (Li et al., 2014b), WLRM (Luo et al., 2017), and DeepIsoFun (Shaw et al., 2018). The comparison focuses on a small set of GO terms, GO Slim (Consortium, 2004), which provides a broad overview of the ontology content. 96 GO terms are kept after the term size filtration aforementioned. To make a comprehensive comparison, besides the dataset analyzed above (called Dataset#1), we include two other datasets from the literature (Eksi et al., 2013; Li et al., 2014b). In particular, Dataset#2 contains RNA-seq data for 29 806 human isoforms of 18 923 genes, which were generated from 29 SRA human studies consisting of 455 experiments. Dataset#3 contains RNA-seq data for 16 191 mouse isoforms of 13 692 genes, which were generated from 116 SRA studies consisting of 365 experiments. The corresponding sequence, domain and annotation data are collected by following the same procedure described in Section 2. The average AUC and AUPRC values are reported in Table 1. Note that iMILP performs a three-class classification rather than two-class. While all other methods treat genes without a GO annotation as negatives of this GO term, iMILP selects negative genes according a more stringent criterion and treats the others as unknowns. Here, we assess the AUC and AUPRC of iMILP based only on the positive genes and selected negative genes, which might incur some favorable bias for the method. Nonetheless, significant improvements by our method have been observed. DIFFUSE achieves improvements of 14.5%, 14.7% and 14.7% in terms of AUC and 84.5%, 83.9% and 81.9% in terms of AUPRC over the best performance of the other methods on the three datasets, respectively. Some example receiver operating characteristic curves and precision–recall curves on two GO terms achieved by the methods are illustrated in Supplementary Figure S3a–d. The performance of DIFFUSE on the training data is given in Supplementary Table S1 to show that the model is not grossly overtrained.
Table 1.
Comparison between DIFFUSE and other isoform function prediction methods
| Method | Dataset#1 |
Dataset#2 |
Dataset#3 |
|||
|---|---|---|---|---|---|---|
| AUC | AUPRC | AUC | AUPRC | AUC | AUPRC | |
| DIFFUSE | 0.835 | 0.585 | 0.828 | 0.537 | 0.817 | 0.524 |
| DeepIsoFun | 0.729 | 0.280 | 0.722 | 0.257 | 0.712 | 0.231 |
| WLRM | 0.685 | 0.265 | 0.667 | 0.237 | 0.672 | 0.201 |
| mi-SVM | 0.668 | 0.248 | 0.671 | 0.221 | 0.706 | 0.235 |
| iMILPa | 0.678 | 0.317 | 0.662 | 0.292 | 0.639 | 0.288 |
Since iMILP classifies an isoform into three classes rather than two classes for a given GO term (i.e. positive, negative or unknown), we measure its AUC and AUPRC values using only the positive and negative classes. The best performance values are highlighted in bold.
3.1.3. Analyzing the effects of model components
To evaluate the contribution of some key components and biological features used in our model, we perform an ablation study by removing these components/features from model and measuring how the performance of the model is affected. Specifically, we remove the CRF component, conserved domain features and sequence features from DIFFUSE, respectively, and test its performance on GO Slim. We observe that the average AUC drops 1.7% (from 0.835 to 0.821) and the average AUPRC drops 7.5% (from 0.585 to 0.541) without the CRF. The average AUC drops 3.7% (from 0.835 to 0.804) and the average AUPRC drops 21.2% (from 0.585 to 0.461) without using conserved domains. The average AUC drops 4.6% (from 0.835 to 0.797) and the average AUPRC drops 27.9% (from 0.585 to 0.422) without using sequences (Fig. 3a). The results suggest that the CRF component is very effective in capturing the co-expression relationship and conserved domains contain important functional information (as known before), and both contribute significantly to the performance of DIFFUSE. Moreover, although conserved domains are extracted from sequences, they cannot completely replace sequences. Some example receiver operating characteristic curves and precision–recall curves on two GO terms achieved by the above four variants of DIFFUSE are illustrated in Supplementary Figure S3e–h.
Fig. 3.
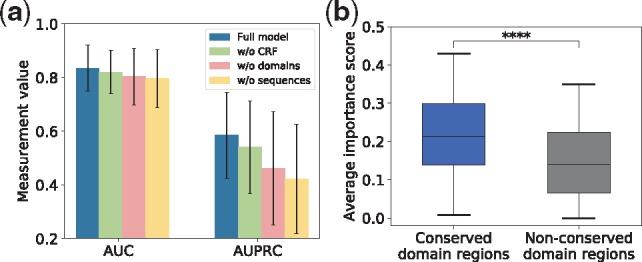
(a) The average AUC and AUPRC values over the terms in GO Slim for DIFFUSE (blue), DIFFUSE without CRF (green), DIFFUSE without using conserved domains (pink) and DIFFUSE without using sequences (yellow). (b) Average importance scores for conserved domain regions and non-conserved domain regions are calculated for each isoform-GO term pair. There is a clearly a significant difference between these two regions as supported by the one-sided Wilcoxon test (****P < 0.0001)
3.1.4. Importance of local sequence features in function prediction
Deep learning models are usually considered as ‘black boxes’. In the bioinformatics domain, however, understanding the rationales behind decisions made by a model is very important to the potential users of the model. Here, we use the saliency map (Simonyan et al., 2013), a deep learning visualization technique, to help us understand what parts of an isoform sequence are most influential in the classification decision. Briefly, a saliency map calculates the derivative of the output of the DNN with respect to the variable at each input position, so we can see the influence of each position of the input sequence on the output score. We denote the value of derivative at each position as its ‘importance score’. The Keras-vis tool (Kotikalapudi et al., 2017) is used to calculate the saliency map and the method in Lanchantin et al. (2017) is used to obtain the importance score of each amino acid residue of the input sequence. Since conserved domains are known to be rich in functional sites, residues inside conserved domains are expected to have higher importance scores on average.
To test this hypothesis, for each isoform-GO pair, we compute a saliency map and calculate the importance score for each amino acid residue of the isoform. For each saliency map, we calculate the average importance score of all amino acid residues inside conserved domains and that of all amino acid residues outside conserved domains, respectively. As expected, we observe significantly higher average importance scores in conserved domains (Fig. 3b).
3.1.5. Analyzing the divergence of isoform functions
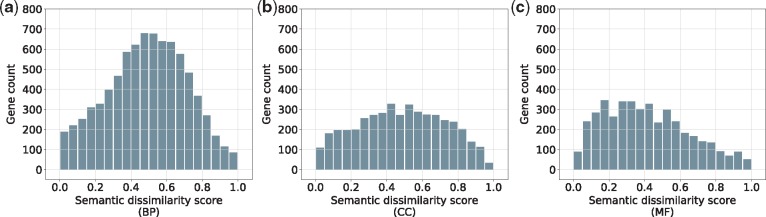
Delineating the specific functions of the isoforms is the ultimate goal of isoform function prediction. Hence, it would be useful to analyze the divergence of the predicted functions of the isoforms from each gene, as done in Li et al. (2014b) and Shaw et al. (2018). We estimate the similarity of predicted functions for each pair of isoforms in terms of the semantic similarity score using GOssTo (Caniza et al., 2014), again considering the three GO branches separately. The semantic dissimilarity score of two isoforms is then defined as one minus their similarity score. For each MIG, the functional divergence of its isoforms is calculated by averaging the semantic dissimilarity scores of all pairs of its isoforms sharing predicted functions in the same GO branch. Out of the 9032 MIGs, 8924 (5444 or 5521) MIGs have at least two isoforms assigned GO terms in the BP (CC or MF, respectively) branch by DIFFUSE. Among these MIGs, 90.3% (8060 out of 8924), 81.1% (4415 out of 5444) and 76.5% (4222 out of 5521) are estimated to have functional divergent isoforms (i.e. semantic dissimilarity scores greater than 0) with respect to BP, CC and MF, respectively. The dissimilarity score distributions for MIGs that have functional divergent isoforms are shown in Figure 4, where the mean score values are 0.490, 0.482 and 0.411 for BP, CC and MF, respectively. A similar pattern of distributions was observed in a previous study (Li et al., 2014b).
Fig. 4.
Distributions of semantic dissimilarity scores of MIGs that have functionally divergent isoforms. The range of semantic dissimilarity score [0, 1] is equally divided into 20 bins. For each bin, we count how many MIGs have semantic dissimilarity scores in this range. The three GO branches are considered separately
As discussed above, functional divergence among isoforms of the same gene is expected. It remains unclear, however, to what extent isoforms have divergent functions. Therefore, we further investigate the functional divergence of isoforms by testing its consistency with the (protein) structural divergence of isoforms. In other words, for a gene with isoforms that share similar functions (i.e. low semantic dissimilarity score), the protein structures of these isoforms are expected to be similar, and vice versa. The protein structure of an isoform can be represented as a contact map, which is a 2D matrix of distance between all possible amino acid residue pairs and can be used to estimate protein structural similarities. Contact maps are predicted using the RaptorX (Peng et al., 2011) server. Due to the computational intensity of contact map prediction, we predict contact maps for isoforms of 300 randomly selected MIGs with at most 500 amino acids. For each GO branch separately, we divide the genes into two groups by the median semantic dissimilarity score, resulting in a high functional similarity group and a low functional similarity group. For each gene, we calculate the average structural similarity score over all its isoform pairs, measured by the Contact Map Overlap using the software AI-Eigen (Di Lena et al., 2010). As anticipated, we observe significantly higher structural similarities between isoforms of MIGs in the high functional similarity groups for all three GO branches (Fig. 5).
Fig. 5.
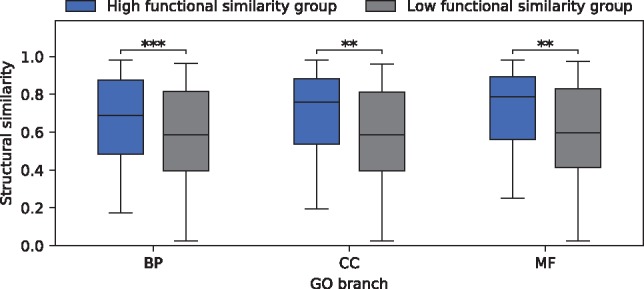
Average structural similarity between isoforms of MIGs with low or high functional similarities. Significant differences are observed in all the GO branches according to the Kruskal–Wallis tests (with P-values ***P = 5.77e-04, **P = 2.50e-03 and **P = 3.30e-03 for BP, CC and MF, respectively). Note that the semantic dissimilarity score can only be calculated for MIGs containing two or more isoforms with GO terms in the same branch. This results in 296 (167 or 155) out of the 300 MIGs considered for the BP (CC or MF) branch
3.2 Validation of predicted isoform functions
The scarcity of experimentally verified functions of isoforms raises a great a challenge to the validation of our predicted isoform functions. To address this challenge, we first indirectly validate the predicted functions by analyzing how they are correlated with isoform sequences, expression as well as protein structures. The predictions are further validated by evaluating their consistency with some well-studied UniProt sequence features related to functions. Finally, we directly validate a small set of predicted isoform functions analyzed above by a targeted literature search.
3.2.1. Correlations between functional, sequence and expression similarities
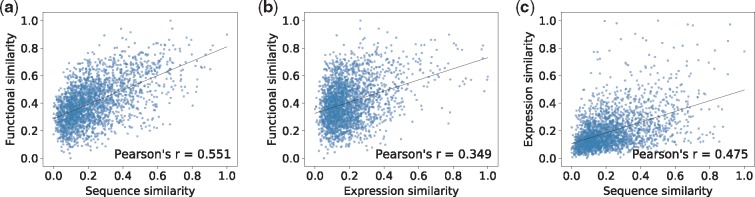
Our method is based on the assumption that isoforms with similar sequences and/or expression profiles should have similar functions. To check that our predicted functions indeed have this property, we test whether similar biological features indeed lead to similar predictions and vice versa, as done in Shaw et al. (2018). (Hence, this is more of a sanity check on our computational model than a proper validation of our predicted isoform functions.) We group the 39 375 isoforms into 2492 clusters with sizes in the range of [10, 20] based on hierarchical clustering, where the bit score of BLAST (Altschul et al., 1997) is used to measure the pairwise distance of isoforms. Then the average functional similarity, sequence similarity and expression similarity are estimated over all isoform pairs within each cluster. Different from the last subsection, here the functional similarity between isoforms is measured by the negative value of the Euclidean distance between their predicted functions (as two vectors). The expression similarity is measured by the PCC of two expression profiles and the sequence similarity is measured by the pairwise global alignment score of two isoform protein sequences normalized by the alignment length. Each similarity is normalized to the range of [0, 1]. Then, the PCC is used to measure the pairwise correlations between functional similarity, sequence similarity and expression similarity, as shown in Figure 6. Clearly, isoforms with similar sequences or expression profiles tend to have similar predicted functions. Interestingly, functional similarity seems to be more correlated with sequence similarity than with expression similarity and only a moderate correlation is found between sequence similarity and expression similarity, which explains why these two biological features can be combined to improve function prediction. To further verify these isoform-level correlations, we perform the same computational experiment at the gene level where the gene functional annotation, the longest isoform sequence of each gene and gene expression profiles are used to estimate the above three similarities. Very similar PCC values are obtained as shown in Supplementary Figure S1.
Fig. 6.
Correlations between functional similarity, sequence similarity and expression similarity. The isoforms are grouped into 2492 clusters by hierarchical clustering. The average pairwise functional similarity, sequence similarity and expression similarity are estimated for the isoforms in each cluster. The PCC is used to measure the strength of correlation
3.2.2. Correlation between functional and structural similarities
Previous studies (Illergård et al., 2009) have shown that protein structures are more conserved than sequences. Hence, isoforms with similar functions are expected to have more similar structures than sequences. We further test how the predicted functions are correlated with protein structures represented as contact maps. Again, we download contact maps from the RaptorX server for 1500 isoforms of MIGs. We focus on MIGs rather than SIGs in this test since the functions of their isoforms are currently unknown. The isoforms are grouped into 99 clusters with sizes in the range of [10, 20] and the average functional similarity, sequence similarity and structural similarity are measured for each cluster using the same methods described above. As expected, a higher PCC is found between functional similarity and structural similarity (Fig. 7). Furthermore, we perform the same computational experiment on 600 random SIGs using their annotated functions and obtain a consistent PCC between functional similarity and structural similarity (see Supplementary Fig. S2). These analyzes indirectly support our prediction results.
Fig. 7.
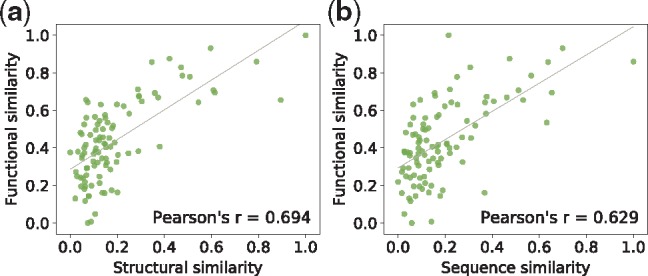
1500 isoforms of MIGs are grouped into 99 clusters. The average pairwise functional similarity, sequence similarity and structural similarity are estimated for each cluster. (a) The correlation between functional similarity and structural similarity. (b) The correlation between functional similarity and sequence similarity
3.2.3. Consistency with well-studied UniProt sequence features
A recent review (Sulakhe et al., 2018) reported a set of function-related sequence features (as defined by UniProt; Breuza et al., 2016) associated with a list of isoforms. The presence or absence of these functional sequence features can be used to infer potential isoform functions. Three of the functional sequence features can be mapped to GO terms, which are ‘Metal ion binding site’ (to GO: 0046872), ‘ATP binding site’ (to GO: 0005524) and ‘Nuclear localization signal’ (to GO: 0005634). We then map the list of isoforms reported in this review to our isoform dataset. For each GO term, we check the consistency between the presence or absence of the corresponding sequence feature in associated isoforms and the functional predictions concerning this GO term. To quantify the consistency for the three GO terms separately, the Jaccard indices are calculated as in the literature (Yang et al., 2016). The same computational experiment is repeated for the three other methods as well to compare. The Jaccard indices of DIFFUSE are 0.674, 0.700 and 0.700 for GO: 0046872, GO: 0005524 and GO: 0005634, respectively, which are significantly higher than those of DeepIsofun (0.548, 0.595 and 0.579), WLRM (0.514, 0.578 and 0.580), mi-SVM (0.534, 0.517 and 0.569) and iMILP (0.560, 0.581 and 0.521). The detailed results concerning the three GO terms are shown in Supplementary Tables S2–S4.
3.2.4. Validation via the literature
We further perform an exhaustive literature search for experimentally verified functions of the isoforms analyzed above (i.e. appearing in Supplementary Tables S2–S4). Functions or strong functional evidence for 14 isoforms of 6 genes have been found. Out of the 14 isoforms, our method predicted correct functions for 11 of them (Table 2), which is significantly more accurate than the other methods. It is worth mentioning that 13 of the 14 functions reported in the literature are consistent with the presence or absence of their corresponding UniProt sequence features. This suggests that the UniProt sequence features may serve as a good benchmark to validate predicted isoform functions.
Table 2.
Literature support for 14 isoforms of 6 genes on two GO terms
| GO term | Gene | Isoform | Literature evidence | Prediction method |
||||
|---|---|---|---|---|---|---|---|---|
| DIFFUSE | DeepIsoFun | WLRM | mi-SVM | iMILP | ||||
| GO: 0046872 | ACE | P12821-1 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ |
| P12821-3 | ∘ | ∘ | ∘ | × | ∘ | ∘ | ||
| ACMSD | Q8TDX5-1 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |
| Q8TDX5-2 | × | ∘ | ∘ | ∘ | ∘ | ∘ | ||
| GCH1 | P30793-1 | ∘ | ∘ | ∘ | × | × | ∘ | |
| P30793-2 | × | × | × | × | ∘ | × | ||
| P30793-4 | × | × | ∘ | ∘ | ∘ | ∘ | ||
| GO: 0005634 | ADK | P55263-1 | ∘ | ∘ | ∘ | ∘ | ∘ | × |
| P55263-2 | × | ∘ | × | ∘ | ∘ | ∘ | ||
| AIFM1 | O95831-1 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |
| O95831-3 | × | ∘ | ∘ | ∘ | × | × | ||
| O95831-4 | × | × | × | ∘ | × | × | ||
| PPP1R8 | Q12972-1 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |
| Q12972-3 | × | × | ∘ | × | × | ∘ | ||
| Accuracy | 78.6% | 71.4% | 50.0% | 64.3% | 64.3% | |||
Note: Positive and negative results are represented as circles and crosses in the table. Experimental evidence concerning relevant functions have been found for six genes in the literature: ACE (Corradi et al., 2006), ACMSD (Pucci et al., 2007), GCH1 (Auerbach et al., 2000), ADK (Cui et al., 2009), AIFM1 (Delettre et al., 2006) and PPP1R8 (Chang et al., 1999). The best performance value is highlighted in bold.
4 Discussion
As discussed in recent reviews (Li et al., 2016; Sulakhe et al., 2018), the integration of various types of biological information is needed to improve isoform function prediction. In this paper, we proposed a deep learning-based method, called DIFFUSE, that integrates sequence, conserved domain and expression information into a unified predictive model. DIFFUSE greatly outperformed the existing methods in our comprehensive computational experiments. However, the performance of DIFFUSE could be further improved in several aspects. First, the co-expression networks derived from RNA-seq data are specific to different tissues and conditions, which may be correlated with specific GO terms. Li et al. (2014b) used a search algorithm to identify the best performing subset of co-expression networks for each GO term. However, the algorithm is time-consuming. We believe that an efficient algorithm that can search for a good combination of co-expression networks specific to each GO terms could be designed and integrated into our method. Moreover, in the model training procedure, we decoupled the DNN and CRF training stages, assuming that the DNN parameters were fixed when optimizing the CRF parameters. A recent work (Zheng et al., 2015) demonstrated the advantage of formulating the CRF as a layer in the DNN to enable end-to-end training with the usual back-propagation algorithm. This could further improve the performance of our model.
As demonstrated in our paper (also a well-known fact), isoform functions are more correlated with protein structures than anything else. Hence, it is natural to consider incorporating protein structures in isoform function prediction (Li et al., 2014a). However, large-scale determination of 3D protein structures for isoforms accurately is computationally prohibitive. Nonetheless, contact maps have been used to represent protein structures approximately and they are easier to compute (Wang et al., 2017). We have used them in the validation of our predictions in this work and plan to explore how to incorporate them into our model in the future.
Funding
This work was supported in part by the National Science Foundation [IIS-1646333], the National Natural Science Foundation of China [61772197, 31671369, 31770775, 61872216, 61472205 and 81630103] and the National Key Research and Development Program of China [2018YFC0910404 and 2018YFC0910405].
Conflict of Interest: none declared.
Supplementary Material
References
- Abadi M. et al. (2016) TensorFlow: a system for large-scale machine learning. In OSDI, Vol. 16, pp. 265–283. [Google Scholar]
- Altschul S.F. et al. (1997) Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res., 25, 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews S. et al. (2002) Multiple instance learning with generalized support vector machines. In AAAI/IAAI, pp. 943–944.
- Auerbach G. et al. (2000) Zinc plays a key role in human and bacterial GTP cyclohydrolase I. Proc. Natl. Acad. Sci., 97, 13567–13572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bairoch A. et al. (2004) The universal protein resource (UniProt). Nucleic Acids Res., 33, D154–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengio Y. et al. (2003) A neural probabilistic language model. J. Mach. Learn. Res., 3, 1137–1155. [Google Scholar]
- Boutet E. et al. (2016) UniProtKB/Swiss-Prot, the manually annotated section of the UniProt KnowledgeBase: how to use the entry view In Plant Bioinformatics, Springer, pp. 23–54. [DOI] [PubMed] [Google Scholar]
- Breuza L. et al. (2016) The UniProtKB guide to the human proteome. Database, 2016, bav120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caniza H. et al. (2014) GOssTo: a stand-alone application and a web tool for calculating semantic similarities on the Gene Ontology. Bioinformatics, 30, 2235–2236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang A.C. et al. (1999) Alternative splicing regulates the production of ARD-1 endoribonuclease and NIPP-1, an inhibitor of protein phosphatase-1, as isoforms encoded by the same gene. Gene, 240, 45–55. [DOI] [PubMed] [Google Scholar]
- Consortium G.O. (2004) The Gene Ontology (GO) database and informatics resource. Nucleic Acids Res., 32, D258–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corradi H.R. et al. (2006) Crystal structure of the N domain of human somatic angiotensin I-converting enzyme provides a structural basis for domain-specific inhibitor design. J. Mol. Biol., 357, 964–974. [DOI] [PubMed] [Google Scholar]
- Cui X.A. et al. (2009) Subcellular localization of adenosine kinase in mammalian cells: the long isoform of AdK is localized in the nucleus. Biochem. Biophys. Res. Commun., 388, 46–50. [DOI] [PubMed] [Google Scholar]
- Delettre C. et al. (2006) Identification and characterization of AIFsh2, a mitochondrial apoptosis-inducing factor (AIF) isoform with NADH oxidase activity. J. Biol. Chem., 281, 18507–18518. [DOI] [PubMed] [Google Scholar]
- Di Lena P. et al. (2010) Fast overlapping of protein contact maps by alignment of eigenvectors. Bioinformatics, 26, 2250–2258. [DOI] [PubMed] [Google Scholar]
- Eksi R. et al. (2013) Systematically differentiating functions for alternatively spliced isoforms through integrating RNA-seq data. PLoS Comput. Biol., 9, e1003314.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis J.D. et al. (2012) Tissue-specific alternative splicing remodels protein–protein interaction networks. Mol. Cell, 46, 884–892. [DOI] [PubMed] [Google Scholar]
- He K. et al. (2014) Spatial pyramid pooling in deep convolutional networks for visual recognition In: European Conference on Computer Vision, Springer, pp. 346–361. [DOI] [PubMed] [Google Scholar]
- Huerta-Cepas J. et al. (2016) eggNOG 4.5: a hierarchical orthology framework with improved functional annotations for eukaryotic, prokaryotic and viral sequences. Nucleic Acids Res., 44, D286–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huntley R.P. et al. (2015) The GOA database: Gene Ontology annotation updates for 2015. Nucleic Acids Res., 43, D1057–1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Illergård K. et al. (2009) Structure is three to ten times more conserved than sequence—a study of structural response in protein cores. Proteins, 77, 499–508. [DOI] [PubMed] [Google Scholar]
- Kanehisa M. et al. (2000) KEGG: kyoto encyclopedia of genes and genomes. Nucleic Acids Res., 28, 27–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma D.P. et al. (2014) Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
- Kotikalapudi,et al. (2017) Keras-vis. https://github.com/raghakot/keras-vis. GitHub.
- Krähenbühl P. et al. (2011) Efficient inference in fully connected crfs with gaussian edge potentials. In Advances in Neural Information Processing Systems, pp. 109–117.
- Kulmanov M. et al. (2017) DeepGO: predicting protein functions from sequence and interactions using a deep ontology-aware classifier. Bioinformatics, 34, 660–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kummerfeld S.K. et al. (2009) Protein domain organisation: adding order. BMC Bioinform., 10, 39.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanchantin J. et al. (2017) Deep motif dashboard: visualizing and understanding genomic sequences using deep neural networks In Pacific Symposium on Biocomputing 2017, World Scientific, pp. 254–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langfelder P. et al. (2008) WGCNA: an R package for weighted correlation network analysis. BMC Bioinform., 9, 559.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leinonen R. et al. (2011) The sequence read archive. Nucleic Acids Res., 39, D19–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H.D. et al. (2014a) The emerging era of genomic data integration for analyzing splice isoform function. Trends Genet., 30, 340–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W. et al. (2014b) High-resolution functional annotation of human transcriptome: predicting isoform functions by a novel multiple instance-based label propagation method. Nucleic Acids Res., 42, e39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H.D. et al. (2016) A proteogenomic approach to understand splice isoform functions through sequence and expression-based computational modeling. Briefings Bioinform., 17, 1024–1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo T. et al. (2017) Functional annotation of human protein coding isoforms via non-convex multi-instance learning In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, pp. 345–354. [Google Scholar]
- Marchler-Bauer A. et al. (2015) CDD: NCBI’s conserved domain database. Nucleic Acids Res., 43, D222–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostafavi S. et al. (2008) GeneMANIA: a real-time multiple association network integration algorithm for predicting gene function. Genome Biol., 9, S4.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng J. et al. (2011) RaptorX: exploiting structure information for protein alignment by statistical inference. Proteins, 79, 161–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruitt K.D. et al. (2012) NCBI Reference Sequences (RefSeq): current status, new features and genome annotation policy. Nucleic Acids Res., 40, D130–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pucci L. et al. (2007) Tissue expression and biochemical characterization of human 2-amino 3-carboxymuconate 6-semialdehyde decarboxylase, a key enzyme in tryptophan catabolism. FEBS J., 274, 827–840. [DOI] [PubMed] [Google Scholar]
- Shaw D. et al. (2018) DeepIsoFun: a deep domain adaptation approach to predict isoform functions. Bioinformatics, bty1017. [DOI] [PMC free article] [PubMed]
- Simonyan K. et al. (2013) Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv preprint arXiv:1312.6034.
- Srivastava N. et al. (2014) Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res., 15, 1929–1958. [Google Scholar]
- Sulakhe D. et al. (2018) Exploring the functional impact of alternative splicing on human protein isoforms using available annotation sources. Brief. Bioinform., bby047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton C. et al. (2012) An introduction to conditional random fields. Found. Trends Mach. Learn., 4, 267–373. [Google Scholar]
- Taneri B. et al. (2004) Alternative splicing of mouse transcription factors affects their DNA-binding domain architecture and is tissue specific. Genome Biol., 5, R75.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatusov R.L. et al. (2000) The COG database: a tool for genome-scale analysis of protein functions and evolution. Nucleic Acids Res., 28, 33–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang E.T. et al. (2008) Alternative isoform regulation in human tissue transcriptomes. Nature, 456, 470.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S. et al. (2017) Accurate de novo prediction of protein contact map by ultra-deep learning model. PLoS Comput. Biol., 13, e1005324.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang E.W. et al. (2016) SDEAP: a splice graph based differential transcript expression analysis tool for population data. Bioinformatics, 32, 3593–3602. [DOI] [PubMed] [Google Scholar]
- Zhang S. et al. (2017) TITER: predicting translation initiation sites by deep learning. Bioinformatics, 33, i234–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng S. et al. (2015) Conditional random fields as recurrent neural networks. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 1529–1537.
- Zhu C. et al. (1997) Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw., 23, 550–560. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.