Abstract
A critical question in life-course research is whether the relationship between a risk factor and mortality strengthens, weakens, or remains constant with age. The objective of this paper is to shed light on the importance of measurement scale in examining this question. Many studies address this question solely on the multiplicative (relative) scale and report that the hazard ratio of dying associated with a risk factor declines with age. A wide set of risk factors have been shown to conform to this pattern including those that are socioeconomic, behavioral, and physiological in nature. Drawing from well-known principles on interpreting statistical interactions, we show that evaluations on the additive (absolute) scale often lead to a different set of conclusions about how the association between a risk factor and mortality changes with age than interpretations on the multiplicative scale. We show that on the additive scale the excess death risks posed by key socio-demographic and behavioral risk factors increase with age. Studies have not generally recognized the additive interpretation, but it has relevancy for testing life-course theories and informing public health interventions. We discuss these implications and provide general guidance on choosing a scale. Data from the U.S. National Health Interview Survey are used to provide empirical support.
Keywords: Socioeconomic status, Obesity, Smoking, Life-course, Health inequalities, Mortality, Statistical interaction
Highlights
-
•
Studies often conclude that the effect of demographic and behavioral risk factors on mortality weakens with age.
-
•
We show that this conclusion is premature as studies often fail to interpret their findings on the additive scale.
-
•
We show empirically that on the additive scale the excess death risks posed by key risk factors strengthens with age.
-
•
The general pattern of increasing susceptibility by age on the additive scale has not been previously recognized.
-
•
We argue that the pattern has critical implications for sociological theory and public health policy.
Introduction
A critical question in life-course research is whether the relationship between a risk factor and mortality strengthens, weakens, or remains constant with age. Life-course concepts such as cumulative disadvantage, for example, predict that the association between social factors (e.g., educational attainment) and mortality strengthens with age (Ross & Wu, 1996). Other hypotheses, such as the “age-as-leveler,” predict a weakening of these relationships with age (House et al., 1994, 1990). From a public health perspective, beliefs that the dangers of a behavioral factor (e.g., smoking, obesity) are small at older ages can lead to complacency in targeting these risks among older adults. Measures of demographic interest such as a risk factor's population attributable risk fraction and its influence on life expectancy are dependent on how the magnitude of the association between a risk factor and mortality changes with age.
We shed light on the importance of measurement scale in evaluating whether a risk factor's association with mortality strengthens, weakens, or remains constant with age, which is essentially a statistical interaction between a risk factor and age. It is well-known that statistical interactions can be interpreted on an additive (absolute) or multiplicative (relative) scale and that this choice is often consequential to the conclusion one reaches. To claim that the effect of a risk factor “strengthens” or “weakens” with age requires an underlying measurement scale as a basis to make the judgement. In many instances, however, researchers do not acknowledge the scale dependency of their findings. We show that failure to do so often results in premature conclusions about how the effect of a risk factor on mortality changes over the life-course.
The choice of which measurement scale—additive or multiplicative—should be used to interpret an interaction among risk factors in a given research context has been debated and discussed in the epidemiological literature since at least the 1970s (Brown, 1986; Rothman, Greenland, & Walker, 1980; Walter, 2000; Walter & Holford, 1978). The issue remains of central importance. For example, the choice of measurement scale is receiving considerable attention in the epidemiological literature on evaluating whether health disparities are improving or deteriorating (Harper et al., 2008; Harper & Lynch, 2007; King, Harper, & Young, 2012; Moonesinghe & Beckles, 2015). We believe that the issue has not received adequate attention in the specific context of evaluating how the effects of a risk factor change over the life-course. Moreover, there has been little recognition of the importance of measurement scale in testing life-course theories such as cumulative disadvantage. Our main objective is to apply the logic of measurement scale to the evaluation of risk factor by age interactions and consider its importance to testing sociological theories.
Our paper is structured as follows. First, we highlight the importance of scale by providing a brief review of prior literature on this topic. Second, we present the intuitions behind additivity and multiplicativity in the context of risk factor by age interactions. Third, we discuss the importance of these intuitions to testing life-course theories and concepts. Fourth, we present results from an exploratory analysis of major risk factors for mortality using the U.S. National Health Interview Surveys. In this exploratory analysis, we consider three factors that are socio-demographic in nature (sex, race, educational attainment) and two that are behavioral in nature (cigarette smoking, obesity). Obesity is not a behavior per se, but closely tied to diet and physical activity. In the Discussion, we raise issues that researchers may want to consider in choosing a measurement scale.
We use the term “risk factor” to encompass socio-demographic and behavioral factors. Socio-demographic factors including one's sex, educational attainment, or race are structural in nature, shaping an individual's access to resources and affecting health through myriad inter-related pathways. Behavioral factors are also influenced by structural forces, but can also be considered proximal risk factors in that they directly affect physiological functioning. We consider these important distinctions in the Discussion.
Relevancy of scale to the interpretation of statistical interactions
The relevancy of measurement scale to the interpretation of statistical interactions has received considerable attention in epidemiology. Perhaps the earliest consideration in modern epidemiology dates to debates between Brown and Harris (1978) and Tennant and Bebbington (1978) on the social causes of depression. Brown and Harris (1978) concluded that “stressful life events” and “intimacy problems” exhibited a positive statistical interaction in their effects on depression. They reported that the effect of social isolation on depression was stronger when intimacy problems were present and the effect of intimacy problems on depression was stronger when social isolation was present. Brown and Harris (1978) based their conclusion using an absolute measure of difference, the risk difference. Re-analyzing Brown and Harris’ (1978) data, Tennant and Bebbington (1978) refuted their conclusion. Tennant and Bebbington (1978) used log-linear models, basing their evaluation on relative risks. Using relative risks, a conclusion of no statistical interaction was reached—the relative risks of depression associated with each risk factor was similar across levels of the other variable.
Both sets of authors correctly interpreted their findings, but they used different reference scales to test for the presence of dependency. Brown and Harris' (1978) interpretation was based on the additive scale and Tennant and Bebbington's (1978) was based on the multiplicative scale. Subsequent work formalized the basic mathematics behind statistical interactions raising general awareness of the importance of scale to the interpretation of statistical interactions (Brown, 1986; Rothman et al., 1980; Walter & Holford, 1978). Recently, this issue has been central to debates on how to interpret gene by environment interactions (Gauderman et al., 2017; Ritz et al., 2017; Schwartz, 2006; van der Mei, Otahal, Taylor, & Winzenberg, 2014) and how to interpret whether the magnitude of health disparities are increasing or decreasing over time (Harper et al., 2008; Harper & Lynch, 2005, 2007; Moonesinghe & Beckles, 2015). A main lesson from these debates is that choice of scale is often consequential to conclusions.
The interpretation of age x risk factor interactions
We motivate our discussion using the example of smoking, age, and mortality. Table 1 shows a cross-classification of age and smoking. For simplicity, smoking and age are treated as dichotomous (smoker/nonsmoker, young/old). Let be the mortality rate among young non-smokers (i.e., baseline hazard), the mortality rate among old smokers, the mortality rate among old non-smokers, and the mortality rate among young smokers.
Table 1.
Additive and multiplicative interactions in a hypothetical case of smoking, age, and mortality.
| (a) Additive Interaction | ||
|---|---|---|
| Old Age | Young Age | |
| Smoker | ||
| Non-Smoker |
|
|
| (b) Multiplicative Interaction | ||
| Old Age |
Young Age |
|
| Smoker | ||
| Non-Smoker | ||
Note: is the rate of death and HR is the hazard ratio. The superscripts A and M denote the additive and multiplicative predictions, respectively.
If smoking and age are interacting in an additive way the mortality of the highest risk group (old smokers) would be a sum:
| (1) |
The term is just the rate difference associated with getting older among non-smokers and is the rate difference associated with smoking among the young. The super-script A denotes the additive prediction for . A strictly additive relationship necessarily implies that the rate difference associated with smoking is the same for the young and old and the rate difference associated with getting older is the same for smokers and non-smokers. This constancy is why the rate difference is naturally suited to test for an additive interaction—if the rate difference of a risk factor depends on the presence of another risk factor, the risk factors are not interacting in a strictly additive manner.
Multiplicativity, on the other hand, is best tested with ratio measures. Table 1b provides the relationship. If the two risk factors are operating in a strictly multiplicative way, would be:
| (2) |
where = is the hazard ratio for smoking among the young and = is the hazard ratio for getting older among non-smokers. The super-script M denotes the multiplicative prediction for . Strict multiplicativity implies constancy of the hazard ratios for each risk factor across levels of the other risk factor (e.g., and ). A departure from multiplicativity would occur if the hazard ratio for a risk factor differed across levels of the other risk factor. Thus, ratio measures including the hazard ratio, relative risk, or odds ratio are naturally suited to assess departures from a multiplicative interaction.
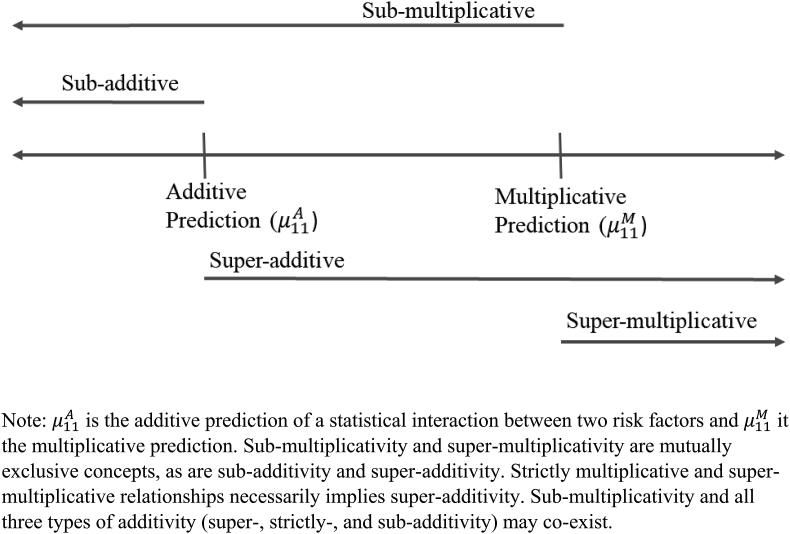
It is important to note that additivity and multiplicativity fall along a single continuum (Fig. 1). Risk factors need not interact in a strictly additive or multiplicative way. The multiplicative prediction, however, will always result in a higher value than the additive prediction (i.e., as long as each risk factor increases the risk of the outcome. If we find that the hazard ratio for a risk factor is smaller at old compared to young ages, for example, we would state that the risk factor and age are interacting sub-multiplicatively (because the observed is less than ). In this case, the relationship on an additive scale is ambiguous. The relationship could be super-additive (), additive (), or sub-additive (). Each of these descriptors is consistent with sub-multiplicativity.
Fig. 1.
Additivitiy and multiplicativity along a continuum.
Note: is the additive prediction of a statistical interaction between two risk factors and it the multiplicative prediction. Sub-multiplicativity and super-multiplicativity are mutually exclusive concepts, as are sub-additivity and super-additivity. Strictly multiplicative and super-multiplicative relationships necessarily implies super-additivity. Sub-multiplicativity and all three types of additivity (super-, strictly-, and sub-additivity) may co-exist.
Table 2 presents a concrete example. It shows death rates by smoking status for those ages 65 and 75. On the multiplicative scale, the association of cigarette smoking with mortality declines over age as evidenced by the declining hazard ratio (from 2.88 to 2.45, sub-multiplicativity). The rate difference, however, increases from 15.92 to 35.83 deaths per 1000 person-years. Therefore, the hazard of smoking would be stated to increase over age on an additive scale. Older smokers suffer an incrementally higher death risk associated with their smoking compared to younger smokers in an additive sense. Such an interpretation is missed if one solely focuses on the relative measure.
Table 2.
Additive (absolute) and multiplicative (relative) relationships using the case of smoking, age, and death.
| Age 65 | Age 75 | |
|---|---|---|
| Never Smoker | 8.48 | 24.72 |
| Current Smoker | 24.39 | 60.56 |
| Hazard Ratio = 2.88 Rate Difference = 15.92 |
Hazard Ratio = 2.45 Rate Difference = 35.83 |
Note: Estimates obtained from Model 1 of Table 2 in Mehta and Preston (2012). Data were from the 1987-2003 U.S. National Health Interview Surveys (excluding 1989 and 1996) with death linkage through December 31, 2006. Rates and rate differences are in units of deaths per 1000 person-years. Men and women combined.
By design, log-linear regression models (e.g., logistic, proportional hazards) force risk factors to operate multiplicatively because additivity on a logarithmic scale implies multiplicativity on the untransformed scale. Researchers often use a product term between a risk factor and age to relax the multiplicative relation. A hazard ratio that deviates from 1.00 on this product term is interpreted as a signal that there is a statistical interaction between the risk factor and age. HRs<1.00 on the product term, for example, are interpreted as a signal that the risk factor's association with mortality declines over age (often stated as “weakening”). This finding, however, only implies that the hazard ratio declines over age. Without further investigation, it is not immediately apparent if older, compared to younger, individuals suffer less, equally, or more from the dangers of the risk factor in an additive sense.
Life-course concepts and public health practice
A prominent concept in sociology labeled cumulative disadvantage posits that the association of education with health or mortality will increase with age because health-promoting “[r]esources associated with education cumulate through life.” (Ross & Wu, 1996, p. 106). A key prediction is that educational disparities in health or death risks will grow stronger with age. An alternative viewpoint is the age-as-leveler. The age-as-leveler posits that socioeconomic status’ association with age tends to be strongest at middle age and then weakens in old age (House et al., 1994, 1990). Explanations for leveling include mortality selection, the convergence in behavioral differences, and the redistributive nature of old-aged entitlements (Benzeval, Green, & Leyland, 2011; House, Kessler, & Herzog, 1990; Marang-van de Mheen, Shipley, Witteman, Marmot, & Gunning-Schepers, 2001).
Despite the interest in testing these concepts, there has been no guidance given as to which measurement scale one should use to interpret age-related changes. Studies have largely interpreted findings from log-linear models and as such implicitly on the multiplicative scale (Beckett, 2000; de Mheen et al., 2001; Dupre, 2007; Hoffmann, 2011; Knesebeck, Lüschen, Cockerham, & Siegrist, 2003; Lauderdale, 2001; Lynch, 2003). The “age-as-lever” has been given empirical support in mortality studies of various populations based on evidence that the hazard ratio associated with low SES or being a race/ethnic minority decline by age (de Mheen et al., 2001; Elo & Preston, 1996; Hoffmann, 2011; Lauderdale, 2001), but this finding is not universal (Dupre, 2007; Lynch, 2003). Studies of other health outcomes have also reached varying conclusions with some supporting cumulative disadvantage (Shuey & Willson, 2008; Willson, Shuey, & Elder, 2007), age-as-leveler (Boen, 2016; Brown, Richardson, Hargrove, & Thomas, 2016), or persistent inequality (Ferraro & Farmer, 1996), the latter of which reflects a constancy in the magnitude of the association across age.
Choice of scale is also relevant to the age dependency in the effect of behavioral risk factors such as obesity and cigarette smoking. Whether the mortality risks associated with obesity rise or fall with age, for example, has elicited much attention (Hanley, 2017; Masters, Powers, & Link, 2013; Zheng & Dirlam, 2016). Studies of large epidemiological cohorts have reported that the hazard ratios of death associated with obesity decline with age (Prospective Studies Collaboration, 2009; Flegal, Graubard, Williamson, & Gail, 2005; Prospective Studies; Stevens et al., 1998). The smaller hazard ratios in old age has been attributed to the competing risks in old age, the biasing effects of disease-induced weight loss, and the protective aspects of excess caloric reserves (Mehta, 2015; Zheng & Dirlam, 2016). Such an interpretation suggests that obesity should not be targeted as aggressively among older individuals compared to younger individuals. An interpretation of the interaction on the additive scale has not been critically evaluated and may result in a different conclusion.
Methods
Data
Data are from the IPUMS National Health Interview Survey (NHIS) database (https://ihis.ipums.org/ihis/) (Lynn, Rivera Dreq, Griffin, King, & Williams, 2016). NHIS is an annual cross-sectional study of non-institutionalized U.S. residents. IPUMS NHIS contain harmonized NHIS variables and death linkages. Since 1997, the NHIS selected one member of a household to receive a comprehensive set of questions on health and behaviors. Our analysis is based on individuals in these sample adult files in the 1997-2009 surveys. At time of our study, mortality information at quarter-year intervals is available through December 31, 2011. We focus on individuals who were aged 40-84 years at the time of survey (n = 224,914). We eliminate observations that had missing information on any of the risk factors (n = 13,027, 5.8% of eligible observations) or had incomplete information that precluded death linkage (an additional 9320 respondents). Our main analytic sample consists of 202,567 unique individuals who contributed 1,646,097 person-years of follow-up and 28,388 deaths.
Risk factors
Binary variables for the presence of each risk factor are constructed based on respondent reports. The higher risk category is assigned a value of one. Male (vs. female) is used as the high-risk category for sex. We use a racial identification of being black as the marker of racial disadvantage because of the persistently higher mortality of blacks relative to other U.S. racial groups. Those who identified as being black/African American on a question asking about racial background are categorized as black and included Hispanic and non-Hispanic blacks. Among Hispanics, a relatively low mortality population, being Black has been shown to be associated with worse health (Chinn & Hummer, 2016; Elo, Mehta, & Huang, 2011). Low education is defined as having a high school degree (HS) or GED as the highest level of attained schooling. The reference group are those with education beyond high school including those with some college or post-secondary degrees. Cigarette smokers are those who reported currently smoking cigarettes. Former and never smokers are the reference category. Obesity is defined a body mass index (BMI) of 30 kg/m2 or higher calculated from self-reports of height and weight. Those with a BMI of <30 kg/m2 serve as the reference.
Analysis
We perform two sets of analyses—a descriptive bivariate analysis and a multivariate analysis. The multivariate analysis is based on Poisson regression models. Both sets of analyses are conducted on a person-year file constructed from information on survey year, year of death, and censoring year.
For the bivariate analysis, we compute unadjusted death rates for those with and without the risk factor by 10-year age category between ages 40 and 89 years. The large sample size of the NHIS facilitates stable estimates within 10-year age categories. Age is treated as time-varying over follow-up. From these death rates, we compute the age-specific hazard ratios and rate differences.
The bivariate approach does not impose any parametric form on changes in the hazard ratios and rate differences over age, which is advantageous. We analyze the age pattern of the hazard ratios and rate differences first visually and then with the aid of a linear regression model. The mid-point of each 10-year age category is used in the linear regression. A coefficient of zero on the age variable in the linear regression models predicting the hazard ratio indicates a strictly multiplicative relationship. Similarly, a coefficient of zero in models predicting the rate difference indicates a strictly additive relationship. Departures from multiplicativity and additivity are then assessed.
The usual approach to investigating risk factor by age interactions is to produce hazard ratios from a log-linear regression model controlling for other confounders. We perform such an approach. We model death rates using discrete-time models with a log-link and Poisson distribution. A first model includes age measured in single years, the dummy variable for the risk factor under consideration, and an interaction between the risk factor and age. A second model includes adjustments for all socio-demographic characteristics (male, black, low education), time in study, and calendar year of exposure. As log-linear models naturally produce hazard ratios, we are able to assess the age by risk factor interaction on the multiplicative scale directly. To assess the interaction on the additive scale, we further estimate the relative excess risk due to interaction (RERI) (Rothman, 1986; VanderWeele & Knol, 2014). The RERI is often used to assess the direction of a statistical interaction on the additive scale from from log-linear models. A RERI of zero indicates no interaction on the additive scale, a RERI<0 indicates sub-additivity, and a RERI>0 indicates super-additivity.
Analyses by birth cohorts are also performed using the NHIS 1986-2009 to increase the observation window. We focus on the three risk factors (male, black, education) that were collected on all persons during 1986–2009. Three birth cohorts are followed (1920-9, 1930-9, and 1940-9). Each cohort is observed over three 10-year age spans beginning at ages 40-9 (1940-9 cohort), 50-9 (1930-9 cohort), and 60-9 (1920-9 cohort). The birth cohort analysis includes 539,372 individuals contributing 7,646,136 person-years and 145,980 deaths.
Results
Male (44%) and low education (51%) are the most prevalent risk factors (Table 3). Twenty-seven percent of the sample is obese and 21% are current smokers. Fourteen percent are black. The mean attained age is 56.2 years.
Table 3.
Descriptive characteristics of sample, 1997-2009 National Health Interview Survey.
| Characteristic | Percentage (unless noted otherwise) |
|---|---|
| Age (mean, years) | 56.2 |
| Male | 44.4 |
| Black | 14.0 |
| Low education | 50.7 |
| Obese (body mass index≥30 kg/m2) | 26.7 |
| Current smoker | 21.1 |
| Number | |
| Sample size | 202,567 |
| Person-years | 1,646,097 |
| Deaths | 28,388 |
Note: Ages 40-84 at time of survey. Death linkages are through December 31, 2011. Age is age over follow-up. Other characteristics pertain to time at survey. Low education defined as having a HS degree or GED.
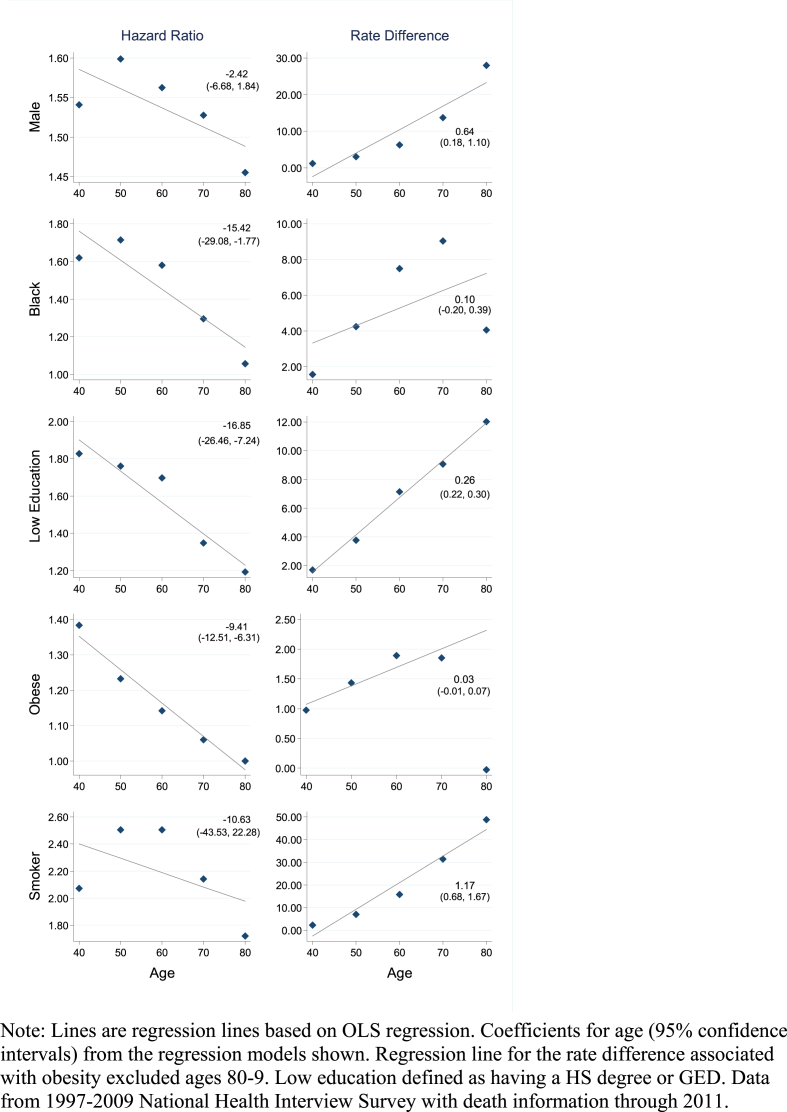
Fig. 2 shows age-specific hazard ratios and rate differences (per 1000 person-years) computed from the tabulated death rates. A clear regularity is evident from Fig. 2. Hazard ratios tend to decline and rate differences tend to rise over age. This pattern is confirmed by the coefficients on the age variable from the linear regressions through the points. The coefficients for the hazard ratios are all negative and the coefficients for the rate differences are all positive. The pattern implies that while the hazard ratio declines over age, the absolute association tends to grow stronger with age. There are, however, a few deviations. For male, black, and smoking the hazard ratio increases between ages 40-9 and 50-9. For obesity, the rate difference sharply drops after ages 70-9.
Fig. 2.
Hazard ratios and rate differences (per 1000 person-years) by 10-year age group for each risk factor.
Note: Lines are regression lines based on OLS regression. Coefficients for age (95% confidence intervals) from the regression models shown. Regression line for the rate difference associated with obesity excluded ages 80-9. Low education defined as having a HS degree or GED. Data from 1997-2009 National Health Interview Survey with death information through 2011.
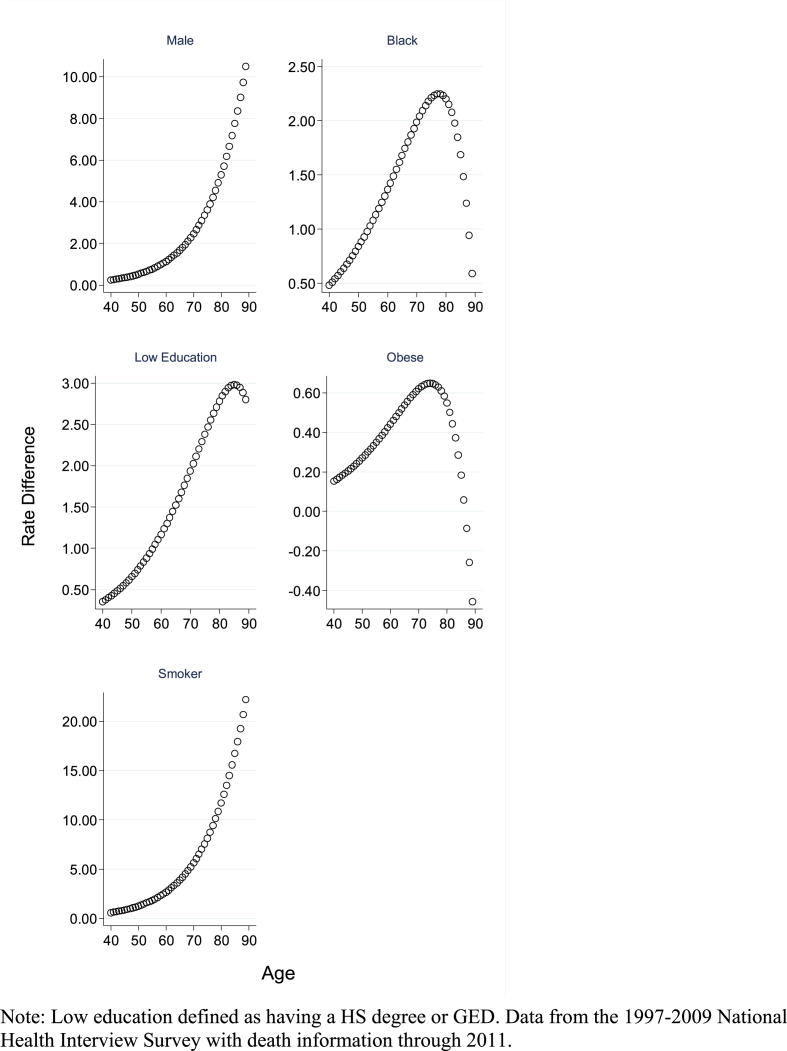
Table 4 shows hazard ratios and RERIs from the multi-variate regression models predicting death rates as a function of age measured in single years. Panel A shows the unadjusted model and Panel B shows the adjusted model. The main effect shown is pertinent to the hazard ratio at age 65 associated with each risk factor. The interaction effects are the proportionate change in the hazard ratio for each single year of age. As indicated in Panels A and B, the interaction effects are all less than 1.00 indicating a declining hazard ratio over age. In contrast, the RERIs, which evaluate the interaction on the additive scale, are all positive indicating a super-additive relationship. This finding is reinforced in Fig. 3, which plots the predicted rate difference by single year of age. As we find in the main analysis, the rate difference for black and obese declines at the oldest ages.
Table 4.
Coefficients from Poisson regression models and the relative excess risk due to interaction (RERI).
| Characteristic | Panel A: Unadjusted |
Panel B: Adjusted |
||||
|---|---|---|---|---|---|---|
| Main Effect | Interaction on Multiplicative Scale | Interaction on Additive Scale (RERI) | Main Effect | Interaction on Multiplicative Scale | Interaction on Additive Scale (RERI) | |
| Male | 0.459*** | −0.003** | 0.047*** | 0.492*** | −0.004*** | 0.056*** |
| Black | 0.406*** | −0.016*** | 0.019*** | 0.390*** | −0.016*** | 0.022*** |
| Low Education | 0.431*** | −0.013*** | 0.028*** | 0.424*** | −0.011*** | 0.034*** |
| Obese | 0.145*** | −0.007*** | 0.005*** | 0.119*** | −0.005*** | 0.007*** |
| Current Smoker | 0.867*** | −0.011*** | 0.107*** | 0.788*** | −0.008*** | 0.109*** |
Note: Age measured in single years and centered at age 65 years. Main effects pertain to the coefficient at age 65. All models include main effect for age (not shown). The interaction on the relative scale is the coefficient for the product term of the risk factor with age. A negative value indicates a negative (i.e., sub-multiplicative) relationship. RERI tests for the presence and direction of interaction on the additive scale. A positive value indicates a super-additive interaction on the additive scale. Panel A are from models that only include the respective risk factor, age, and their interaction. Panel B includes adjustments for all socio-demographic characteristics (male, black, low education), time in study, and calendar year of exposure. Low education defined as having a HS degree or GED. Data from 1997-2009 National Health Interview Survey with deaths through 2011. ***p < .001; **p < .01.
Fig. 3.
Rate difference (per 1000 person-years) for each risk factor estimated from the Poisson regression models shown in Panel B in Table 4.
Note: Low education defined as having a HS degree or GED. Data from the 1997-2009 National Health Interview Survey with death information through 2011.
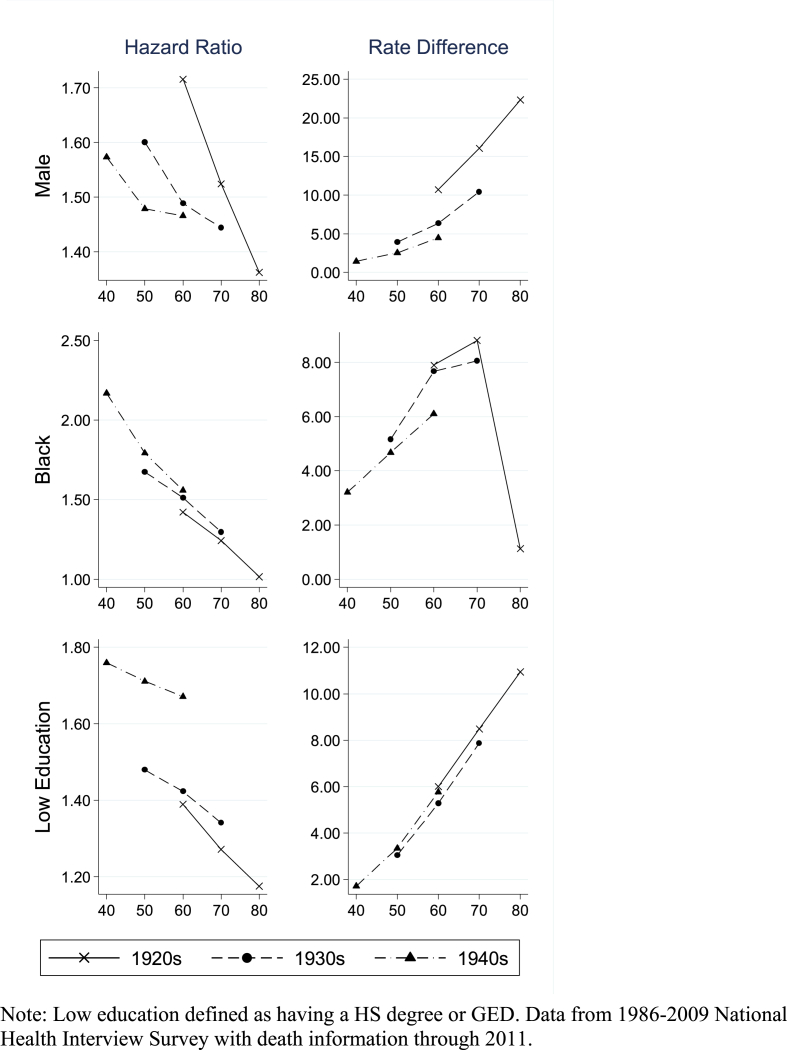
We next turn to the birth cohort analyses of the three socio-demographic risk factors. (Fig. 4). The pattern of declining hazard ratios and increasing rate differences across all of the risk factors is evident for the three birth cohorts (1920-9, 1930-9, 1940-9). One exception is a sharp decline in the rate difference for obesity between ages 70-9 and 80-9 in the 1920s birth cohort.
Fig. 4.
Hazard ratios and rate differences (per 1000 person-years) by 10-year age group for cohorts born during 1920-9, 193-9, and 1940-9.
Note: Low education defined as having a HS degree or GED. Data from 1986-2009 National Health Interview Survey with death information through 2011.
Discussion
Studies often conclude that the magnitude of a risk factor's association with mortality declines with age, but this claim is often made by only considering the change on the multiplicative (relative) scale using the relative risk or hazard ratio. We show that when one uses the rate difference, an additive (absolute) measure, the prevailing pattern is in the opposite direction: the rate difference associated with many major risk factors rise with age. The generalizability of this pattern across major risk factors, to our knowledge, has not been recognized previously. By arraying risk factors from different domains in one setting, we are positioned to observe whether general patterns. The fact that a consistent pattern is observed from tracking birth cohorts increases our confidence in our main conclusions.
We did not develop causal models for each of the risk factors. We aimed, rather, to identify whether there are basic empirical regularities in risk factor by age interactions across many major risk factors for mortality. Our findings were robust to a basic set of controls. We use binary exposures to aid our exposition of the relevant interpretive issues, but the concepts are pertinent to multi-category or continuous exposures.
Our results underscore that choice of scale is not trivial. It is important to emphasize that choosing an interpretative scale should be a separate decision than choosing a statistical model. The latter choice should be dictated by concerns about statistical fit (Spiegelman, Khudyakov, Wang, & Vanderweele, 2017). Log-linear models are often preferable. Methods are readily available to test for the presence and direction of an interaction on the additive scale in these models using measures such as the RERI.
We do not endeavor to argue for the adoption of one scale over the other here, rather we would like to raise some issues that may be helpful to researchers. At minimum, we believe that researchers should explicitly consider the issue of interpretative scale in theory or hypothesis testing. Ideally, theories or hypotheses should be developed from a rich understanding of underlying mechanisms that would naturally point to the most appropriate test. Of course, this is not always feasible.
Tests of departures from additivity have long been recognized to be relevant in public health policy contexts (Blot & Day, 1979; Harper & Lynch, 2005; Mehta & Preston, 2016; Rothman et al., 1980; VanderWeele & Knol, 2014). One reason is that a test of departure from additivity provides unambiguous information as to which subgroup of a population would reap maximum benefits from an intervention. Take, for example, the interaction between obesity and smoking in their effects on mortality. If the two risk factors positively interact on the additive scale (i.e., super-additivity), an obese smoker would reap the largest reduction in mortality from effective interventions of either one of the risk factors. There is no such test on the multiplicative scale. Also pertinent to policy, of course, is the joint distribution of the risk factors in a population, but this distribution does not by itself inform which individuals suffer the most from a particular set of risk factors.
Another useful property of testing departures from additivity is in the context of the population attributable risk fraction, which is often useful for public health priority setting. If an interaction of two risk factors departs from additivity then identifying the number of deaths (or disease cases) in a population that is attributable to each risk factor will depend on the correlation of the risk factors. If there is no interaction on the additive scale, the correlation among the risk factors has no bearing on the number of attributable deaths for each factor. If obesity and smoking are strictly additive in their effects, for example, we do not need to know the number of obese smokers to properly identify the number of deaths attributable to obesity or smoking in the population (Mehta & Preston, 2016).
A more complicated set of issues arise in testing life-course theories and hypotheses such as cumulative disadvantage and age-as-leveler. To test whether educational attainment differences in mortality widen with age, for example, should we test for departures from additivity or multiplicativity? We believe that some insight is gained from considering the mechanisms through which these disparities arise and propagate over the life course. Prior work has hypothesized that risk factors will be additive in their effects if they target unrelated diseases or bodily systems (Mehta & Preston, 2016; Weinberg, 2012). Strict multiplicativity could be expected in more limited circumstances as when risk factors contribute to a multistep disease process including in certain carcinogenic models (Siemiatycki & Thomas, 1981).
The postulated mechanisms through which social disadvantage is related to health are many encompassing psychosocial processes, environmental exposures, access to resources and information, and behavioral factors. Together, these mechanism impact multiple bodily systems and oftentimes target overlapping physiological processes, e.g., stress pathways and obesity both operating through inflammatory and cardiovascular pathways (Geronimus, Hicken, Keene, & Bound, 2006; McEwen & Seeman, 1999). Furthermore, physiological damage done in the past or that are a result of normal aging processes may make the body increasingly vulnerable to further insults as it ages. It seems reasonable, then, to hypothesize that interactions between age and markers of social disadvantage (low education, being black) or even behavioral factors (obesity, smoking) would grow on an additive scale, and part of this association may be related to the overall increase in risk of death with age. Testing against the additive prediction may, therefore, prove insightful. However, given that the appropriate scale to test a theory is not always clear-cut, we agree with prior calls that it is often beneficial to present findings on both scales (Harper & Lynch, 2005; Vandenbroucke et al., 2007; VanderWeele & Knol, 2014).
Our results indicate that being black or having low education, two markers of social disadvantage, do in fact deviate from the additive prediction. They operate in a super-additive way. Being disadvantaged at older age may have a larger negative health effect than at younger ages because the experience of social disadvantage at old age is operating on physiological systems already damaged from being a member of a socially disadvantaged group throughout life. Such an explanation is consistent with cumulative disadvantage processes, although it does not require “[r]esources associated with education [to] cumulate through life.” (Ross & Wu, 1996, p. 106) All it requires is that some damage done in the past makes the body more susceptible to being socially disadvantaged in the present. Such a process would favor policies improving the circumstances of younger individuals with the goal of preventing physiological damage that can make the body more susceptible to insults later in life.
Noteworthy is that the hazard associated with being black declined after ages 70-79. This finding appears in line with the documented racial crossover of black-white mortality differences (Fenelon, 2013), although we did not observe an actual cross-over. High levels of age misreporting among older blacks in cohorts born during the beginning of the 20th century and earlier have been postulated to result in an underestimation of black mortality and contribute to the crossover (Elo & Preston, 1994; Hussey & Elo, 1997). The 80-9 age group in our sample covered cohorts born during 1902–1931 and we found a small excess risk associated with being black in this group. Differential selective mortality by race at younger ages has also been hypothesized to explain the crossover (Fenelon, 2013).
The excess death risks associated with being male relative to being female also were super-additive. This pattern is consistent with findings reported in Wisser and Vaupel (2014), which studied absolute male-female mortality differences for 10-year birth cohorts in European countries since 1860. Wisser and Vaupel (2014) found that excess male mortality (on the additive scale) rose quickly over age from age 40 for cohorts born since 1900. They postulated that the pattern represented a synergistic interaction between age and risky behaviors: the effect of risky behaviors, which males are more likely to engage in, rises with age in an additive sense.
Interpreting the pattern for behavioral factors, which are not fixed over life, requires additional considerations. What explains the growth in the excess risk of smoking on the additive scale? In the United States, age and smoking duration positively correlate because few U.S. smokers pick up the habit after age 30 (Holford et al., 2014). It has been difficult, therefore, in U.S. samples to separate the age pattern of the effects of current smoking from the effects of smoking duration (Flanders, Lally, Zhu, Henley, & Thun, 2003). The pattern we observe is broadly consistent with work indicating that the effect of an additional year of smoking on lung cancer mortality increases the longer one smokes (Doll & Peto, 1978; Flanders et al., 2003), what we have termed super-additive.
The excess risks of obesity under additivity increased until about age 60 years after which it plateaus and then after ages 70-9 years declines. Reverse causal processes associated with disease-induced weight loss may become increasingly important with age producing an artefactual decline in the mortality risks associated with obesity (Mehta, 2015; Stokes & Preston, 2016). It is plausible, however, that the smaller association at the oldest age (80-9 years) is real and reflective of the protective properties of nutritional or caloric reserves in frailer populations. Nonetheless, our findings suggest that the mortality risks of obesity increase by age on an additive scale up until the oldest ages. The clear implication for public health and clinical practice is that obesity should be aggressively treated in the older population. Conclusions based only on the relative scale may result in an under-valuing of the damaging health effects of obesity at older ages (Flegal, Kit, Orpana, & Graubard, 2013; Hughes, 2013; Sairenchi et al., 2005; Wang, 2015, 2015; Willett, Hu, & Thun, 2013).
The nature of risk factor by age interactions will be a net result of many processes, some of them offsetting the impact of others. Mortality selection is a prominent explanation for observed declines in the effect of a risk factor over age (Beckett, 2000; Fenelon, 2013; Lynch, 2003; Sautter, Thomas, Dupre, & George, 2012; Vaupel, Manton, & Stallard, 1979; Zajacova, Goldman, & Rodríguez, 2009). Our results do not necessarily indicate that selection is inoperable, but rather one force out of many in shaping how the effect of a risk factor changes with age. Moreover, if the mortality associated with risk factors do in fact rise with age in an additive sense this should not imply that risk factors should not be treated aggressively in the young as eliminating a risk factor earlier in life will reap benefits throughout the life-course. Thus, evaluations on which age groups to target require considerations beyond that of the age-dependency of the effects of risk factors.
Many life-course studies evaluating how the effect of a risk factor on mortality changes with age draw conclusions from the multiplicative scale using measures such as the relative risk or hazard ratio. We believe that this choice is often made implicitly without recognition of the scale dependency of the claim. We show that a contradictory pattern emerges when interpretations are made on the additive scale. This contradictory pattern, namely that of increasing susceptibilities with age in an additive sense, appears to be a prevailing pattern across major socio-demographic and behavioral risk factors for mortality. We believe that researchers should appreciate and engage with the complexities that arise from the differing patterns in drawing conclusions.
Ethics approval
This research consisted entirely of a secondary analysis of de-identified data that is publicly available and therefore does not constitute human subjects research.
Acknowledgments
This research was supported by the National Institute on Aging (R03AG060404 and R03AG053463). The authors are also grateful for support from the Michigan Center on the Demography of Aging (MiCDA, NIA: P30 AG012846). The authors would also like to thank Samuel Preston, Nikkil Sudharsanan, and Jeffrey McCullough for helpful comments.
References
- Beckett M. Converging health inequalities in later life-an artifact of mortality selection? Journal of Health and Social Behavior. 2000;41:106–119. doi: 10.2307/2676363. [DOI] [PubMed] [Google Scholar]
- Benzeval M., Green M.J., Leyland A.H. Do social inequalities in health widen or converge with age? Longitudinal evidence from three cohorts in the west of Scotland. BMC Public Health. 2011;11:947. doi: 10.1186/1471-2458-11-947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blot W.J., Day N.E. Synergism and interaction: Are the equivalent? American Journal of Epidemiology. 1979;110:99–100. doi: 10.1093/oxfordjournals.aje.a112793. [DOI] [PubMed] [Google Scholar]
- Boen C. The role of socioeconomic factors in Black-White health inequities across the life course: Point-in-time measures, long-term exposures, and differential health returns. Social Science & Medicine. 2016;170:63–76. doi: 10.1016/j.socscimed.2016.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown G.W. Statistical interaction and the role of social factors in the aetiology of clinical depression. Sociology. 1986;20:601–606. doi: 10.1177/0038038586020004009. [DOI] [Google Scholar]
- Brown G.W., Harris T. Tavistock; 1978. Social origins of depression: A study of psychiatric disorder in women. [Google Scholar]
- Brown T.H., Richardson L.J., Hargrove T.W., Thomas C.S. Using multiple-hierarchy stratification and life course approaches to understand health inequalities: The intersecting consequences of race, gender, SES, and age. Journal of Health and Social Behavior. 2016;57:200–222. doi: 10.1177/0022146516645165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chinn J.J., Hummer R.A. Racial disparities in functional limitations among hispanic women in the United States. Research on Aging. 2016;38:399–423. doi: 10.1177/0164027515620244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doll R., Peto R. Cigarette smoking and bronchial carcinoma: Dose and time relationships among regular smokers and lifelong non-smokers. Journal of Epidemiology & Community Health. 1978;32:303–313. doi: 10.1136/jech.32.4.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupre M.E. Educational differences in age-related patterns of disease: Reconsidering the cumulative disadvantage and age-as-leveler hypotheses. Journal of Health and Social Behavior. 2007;48:1–15. doi: 10.1177/002214650704800101. [DOI] [PubMed] [Google Scholar]
- Elo I.T., Mehta N.K., Huang C. Disability among native-born and foreign-born blacks in the United States. Demography. 2011;48:241–265. doi: 10.1007/s13524-010-0008-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elo I.T., Preston S.H. Estimating African-American mortality from inaccurate data. Demography. 1994;31:427–458. [PubMed] [Google Scholar]
- Elo I.T., Preston S.H. Educational differentials in mortality: United States, 1979-85. Social Science & Medicine. 1996;42:47–57. doi: 10.1016/0277-9536(95)00062-3. [DOI] [PubMed] [Google Scholar]
- Fenelon A. An examination of black/white differences in the rate of age-related mortality increase. Demographic Research. 2013;29:441–472. doi: 10.4054/DemRes.2013.29.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferraro K.F., Farmer M.M. Double jeopardy, aging as leveler, or persistent health inequality? A longitudinal analysis of white and black Americans. J. Gerontol. B. Psychol. Sci. Soc. Sci. 1996;51:S319–S328. doi: 10.1093/geronb/51b.6.s319. [DOI] [PubMed] [Google Scholar]
- Flanders W.D., Lally C.A., Zhu B.-P., Henley S.J., Thun M.J. Lung cancer mortality in relation to age, duration of smoking, and daily cigarette consumption results from cancer prevention study II. Cancer Research. 2003;63:6556–6562. [PubMed] [Google Scholar]
- Flegal K.M., Graubard B.I., Williamson D.F., Gail M.H. Excess deaths associated with underweight, overweight, and obesity. Journal of the American Medical Association. 2005;293:1861–1867. doi: 10.1001/jama.293.15.1861. [DOI] [PubMed] [Google Scholar]
- Flegal K.M., Kit B.K., Orpana H., Graubard B.I. Association of all-cause mortality with overweight and obesity using standard body mass index categories: A systematic review and meta-analysis. Journal of the American Medical Association. 2013;309:71–82. doi: 10.1001/jama.2012.113905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauderman W.J., Mukherjee B., Aschard H., Hsu L., Lewinger J.P., Patel C.J. Update on the state of the science for analytical methods for gene-environment interactions. American Journal of Epidemiology. 2017;186:762–770. doi: 10.1093/aje/kwx228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geronimus A.T., Hicken M., Keene D., Bound J. “Weathering” and age patterns of allostatic load scores among blacks and whites in the United States. American Journal of Public Health. 2006;96:826–833. doi: 10.2105/AJPH.2004.060749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanley J.A. Correction of selection bias in survey data: Is the statistical cure worse than the bias? American Journal of Epidemiology. 2017;185:409–411. doi: 10.1093/aje/kww175. [DOI] [PubMed] [Google Scholar]
- Harper S., Lynch J. 2005. Methods for measuring cancer disparities: Using data relevant to healthy people 2010 cancer-related objectives (No. 05–5777), NCI cancer surveillance monograph series, Number 6. Bethesda, MD. [Google Scholar]
- Harper S., Lynch J. National Cancer Institute; Bethesda, MD: 2007. Selected comparisons of measures of health disparities: A review using databases relevant to healthy people 2010 cancer-related objectives (No. Number 7), NCI cancer surveillance monograph series. [Google Scholar]
- Harper S., Lynch J., Meersman S.C., Breen N., Davis W.W., Reichman M.E. An overview of methods for monitoring social disparities in cancer with an example using trends in lung cancer incidence by area-socioeconomic position and race-ethnicity, 1992-2004. American Journal of Epidemiology. 2008;167:889–899. doi: 10.1093/aje/kwn016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann R. Illness, not age, is the leveler of social mortality differences in old age. J. Gerontol. Ser. B. 2011;66B:374–379. doi: 10.1093/geronb/gbr014. [DOI] [PubMed] [Google Scholar]
- Holford T.R., Levy D.T., McKay L.A., Clarke L., Racine B., Meza R. Patterns of birth cohort–specific smoking histories, 1965–2009. American Journal of Preventive Medicine. 2014;46:e31–e37. doi: 10.1016/j.amepre.2013.10.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- House J.S., Kessler R.C., Herzog A.R. Age, socioeconomic status, and health. The Milbank Quarterly. 1990;68:383–411. doi: 10.2307/3350111. [DOI] [PubMed] [Google Scholar]
- House J.S., Lepkowski J.M., Kinney A.M., Mero R.P., Kessler R.C., Herzog A.R. The social Stratification of aging and health. Journal of Health and Social Behavior. 1994;35:213–234. [PubMed] [Google Scholar]
- Hughes V. The big fat truth. Nat. News. 2013;497:428. doi: 10.1038/497428a. [DOI] [PubMed] [Google Scholar]
- Hussey J.M., Elo I.T. Cause-specific mortality among older african-Americans: Correlates and consequences of age misreporting. Social Biology. 1997;44:227–246. [PubMed] [Google Scholar]
- King N.B., Harper S., Young M.E. Use of relative and absolute effect measures in reporting health inequalities: Structured review. BMJ. 2012;345 doi: 10.1136/bmj.e5774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von dem Knesebeck O., Lüschen G., Cockerham W.C., Siegrist J. Socioeconomic status and health among the aged in the United States and Germany: A comparative cross-sectional study. Social Science & Medicine. 2003;57:1643–1652. doi: 10.1016/S0277-9536(03)00020-0. [DOI] [PubMed] [Google Scholar]
- Lauderdale D.S. Education and survival: birth cohort, period, and age effects. Demography. 2001;38:551–561. doi: 10.1353/dem.2001.0035. [DOI] [PubMed] [Google Scholar]
- Lynch S.M. Cohort and life-course patterns in the relationship between education and health: A hierarchical approach. Demography. 2003;40:309–331. doi: 10.2307/3180803. [DOI] [PubMed] [Google Scholar]
- Lynn B., Rivera Dreq J., Griffin R., King M.L., Williams K. University of Minnesota; Minneapolis: 2016. IPUMS health surveys: National health Interview survey, Version 6.2. [Google Scholar]
- Marang-van de Mheen P.J., Shipley M.J., Witteman J.C., Marmot M.G., Gunning-Schepers L.J. Decline of the relative risk of death associated with low employment grade at older age: The impact of age related differences in smoking, blood pressure and plasma cholesterol. Journal of Epidemiology & Community Health. 2001;55:24–28. doi: 10.1136/jech.55.1.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masters R.K., Powers D.A., Link B.G. Obesity and US mortality risk over the adult life course. American Journal of Epidemiology. 2013;177:431–442. doi: 10.1093/aje/kws325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McEwen B.S., Seeman T. Protective and damaging effects of mediators of stress. Elaborating and testing the concepts of allostasis and allostatic load. Annals of the New York Academy of Sciences. 1999;896:30–47. doi: 10.1111/j.1749-6632.1999.tb08103.x. [DOI] [PubMed] [Google Scholar]
- Mehta N., Preston S. Continued increases in the relative risk of death from smoking. American Journal of Public Health. 2012;102:2181–2186. doi: 10.2105/AJPH.2011.300489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta N., Preston S. Are major behavioral and sociodemographic risk factors for mortality additive or multiplicative in their effects? Social Science & Medicine. 2016;154:93–99. doi: 10.1016/j.socscimed.2016.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta N. International encyclopedia of the social & behavioral sciences, J.D. Wright (Editor-in-chief) Elsevier; Oxford: 2015. Obesity and mortality; pp. 75–81. [Google Scholar]
- van der Mei I.A.F., Otahal P., Jr., Simpson S., Taylor B., Winzenberg T. Meta-analyses to investigate gene-environment interactions in neuroepidemiology. Neuroepidemiology. 2014;42:39–49. doi: 10.1159/000355439. [DOI] [PubMed] [Google Scholar]
- de Mheen P.J.M. -v., Shipley M., Witteman J., Marmot M., Gunning-Schepers L. Decline of the relative risk of death associated with low employment grade at older age: The impact of age related differences in smoking, blood pressure and plasma cholesterol. Journal of Epidemiology & Community Health. 2001;55:24–28. doi: 10.1136/jech.55.1.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moonesinghe R., Beckles G.L.A. Measuring health disparities: A comparison of absolute and relative disparities. PeerJ. 2015;3 doi: 10.7717/peerj.1438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prospective Studies Collaboration Body-mass index and cause-specific mortality in 900 000 adults: Collaborative analyses of 57 prospective studies. The Lancet. 2009;373:1083–1096. doi: 10.1016/S0140-6736(09)60318-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritz B.R., Chatterjee N., Garcia-Closas M., Gauderman W.J., Pierce B.L., Kraft P. Lessons learned from past gene-environment interaction successes. American Journal of Epidemiology. 2017;186:778–786. doi: 10.1093/aje/kwx230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross C.E., Wu C.L. Education, age, and the cumulative advantage in health. Journal of Health and Social Behavior. 1996;37:104–120. [PubMed] [Google Scholar]
- Rothman K.J. Little, Brown and Company; Boston, MA: 1986. Modern epidemiology. [Google Scholar]
- Rothman K.J., Greenland S., Walker A.M. Concepts of interaction. American Journal of Epidemiology. 1980;112:467–470. doi: 10.1093/oxfordjournals.aje.a113015. [DOI] [PubMed] [Google Scholar]
- Sairenchi T., Iso H., Irie F., Fukasawa N., Yamagishi K., Kanashiki M. Age-specific relationship between blood pressure and the risk of total and cardiovascular mortality in Japanese men and women. Hypertens. Res. Off. J. Jpn. Soc. Hypertens. 2005;28:901–909. doi: 10.1291/hypres.28.901. [DOI] [PubMed] [Google Scholar]
- Sautter J.M., Thomas P.A., Dupre M.E., George L.K. Socioeconomic status and the black–white mortality crossover. American Journal of Public Health. 2012;102:1566–1571. doi: 10.2105/AJPH.2011.300518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz S. National Academies Press (US; 2006. Modern epidemiologic approaches to interaction: Applications to the study of genetic interactions. [Google Scholar]
- Shuey K.M., Willson A.E. Cumulative disadvantage and black-white disparities in life-course health trajectories. Research on Aging. 2008;30:200–225. doi: 10.1177/0164027507311151. [DOI] [Google Scholar]
- Siemiatycki J., Thomas D.C. Biological models and statistical interactions: An example from multistage carcinogenesis. International Journal of Epidemiology. 1981;10:383–387. doi: 10.1093/ije/10.4.383. [DOI] [PubMed] [Google Scholar]
- Spiegelman D., Khudyakov P., Wang M., Vanderweele T.J. Evaluating public health interventions: 7. Let the subject matter choose the effect measure: Ratio, difference, or something else entirely. American Journal of Public Health. 2017;108:73–76. doi: 10.2105/AJPH.2017.304105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens J., Cai J., Pamuk E., Williamson D., Thun M.J., Wood J. The effect of age on the association between body-mass index and mortality. New England Journal of Medicine. 1998;338:1–7. doi: 10.1056/NEJM199801013380101. [DOI] [PubMed] [Google Scholar]
- Stokes A., Preston S.H. How dangerous is obesity? Issues in measurement and interpretation. Population and Development Review. 2016;42:595–614. doi: 10.1111/padr.12015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tennant C., Bebbington P. The social causation of depression: A critique of the work of Brown and his colleagues. Psychological Medicine. 1978;8:565–575. doi: 10.1017/S003329170001878X. [DOI] [PubMed] [Google Scholar]
- Vandenbroucke J.P., Elm E. von, Altman D.G., Gøtzsche P.C., Mulrow C.D., Pocock S.J. Strengthening the reporting of observational studies in epidemiology (STROBE): Explanation and elaboration. PLoS Medicine. 2007;4:e297. doi: 10.1371/journal.pmed.0040297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T.J., Knol M.J. A tutorial on interaction. Epidemiologic Methods. 2014;3:33–72. [Google Scholar]
- Vaupel J.W., Manton K.G., Stallard E. The impact of heterogeneity in individual frailty on the dynamics of mortality. Demography. 1979;16:439–454. doi: 10.2307/2061224. [DOI] [PubMed] [Google Scholar]
- Walter S.D. Choice of effect measure for epidemiological data. Journal of Clinical Epidemiology. 2000;53:931–939. doi: 10.1016/s0895-4356(00)00210-9. [DOI] [PubMed] [Google Scholar]
- Walter S.D., Holford T.R. Additive, multiplicative, and other models for disease risks. American Journal of Epidemiology. 1978;108:341–346. doi: 10.1093/oxfordjournals.aje.a112629. [DOI] [PubMed] [Google Scholar]
- Wang Z. Age-dependent decline of association between obesity and mortality: A systematic review and meta-analysis. Obesity Research & Clinical Practice. 2015;9:1–11. doi: 10.1016/j.orcp.2014.01.006. [DOI] [PubMed] [Google Scholar]
- Weinberg C.R. Interaction and exposure modification: Are we asking the right questions? American Journal of Epidemiology. 2012;175:602–605. doi: 10.1093/aje/kwr495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willett W.C., Hu F.B., Thun M. Overweight, obesity, and all-cause mortality. Journal of the American Medical Association. 2013;309:1681–1682. doi: 10.1001/jama.2013.3075. [DOI] [PubMed] [Google Scholar]
- Willson A.E., Shuey K.M., Elder, G.H Cumulative advantage processes as mechanisms of inequality in life course health. American Journal of Sociology. 2007;112:1886–1924. doi: 10.1086/512712. [DOI] [Google Scholar]
- Wisser O., Vaupel J.W. MPIDR working paper WP 2014-2015. 2014. The sex differential in mortality: A historical comparison of the adult-age pattern of the ratio and the difference. [Google Scholar]
- Zajacova A., Goldman N., Rodríguez G. Unobserved heterogeneity can confound the effect of education on mortality. Mathematical Population Studies. 2009;16:153–173. doi: 10.1080/08898480902790528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng H., Dirlam J. The body mass index-mortality link across the life course: Two selection biases and their effects. PLoS One. 2016;11 doi: 10.1371/journal.pone.0148178. [DOI] [PMC free article] [PubMed] [Google Scholar]