Identifying progressive imaging genetic patterns via multi-task sparse canonical correlation analysis: a longitudinal study of the ADNI cohort

Abstract

Motivation

Identifying the genetic basis of the brain structure, function and disorder by using the imaging quantitative traits (QTs) as endophenotypes is an important task in brain science. Brain QTs often change over time while the disorder progresses and thus understanding how the genetic factors play roles on the progressive brain QT changes is of great importance and meaning. Most existing imaging genetics methods only analyze the baseline neuroimaging data, and thus those longitudinal imaging data across multiple time points containing important disease progression information are omitted.

Results

We propose a novel temporal imaging genetic model which performs the multi-task sparse canonical correlation analysis (T-MTSCCA). Our model uses longitudinal neuroimaging data to uncover that how single nucleotide polymorphisms (SNPs) play roles on affecting brain QTs over the time. Incorporating the relationship of the longitudinal imaging data and that within SNPs, T-MTSCCA could identify a trajectory of progressive imaging genetic patterns over the time. We propose an efficient algorithm to solve the problem and show its convergence. We evaluate T-MTSCCA on 408 subjects from the Alzheimer’s Disease Neuroimaging Initiative database with longitudinal magnetic resonance imaging data and genetic data available. The experimental results show that T-MTSCCA performs either better than or equally to the state-of-the-art methods. In particular, T-MTSCCA could identify higher canonical correlation coefficients and capture clearer canonical weight patterns. This suggests that T-MTSCCA identifies time-consistent and time-dependent SNPs and imaging QTs, which further help understand the genetic basis of the brain QT changes over the time during the disease progression.

Availability and implementation

The software and simulation data are publicly available at https://github.com/dulei323/TMTSCCA.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Brain imaging genetics studies the relationship between the quantitative traits (QTs) extracted from neuroimaging data and genotypic data such as single nucleotide polymorphisms (SNPs). This research methodology is expected to uncover the genetic basis of brain structure and function, thereby further offers new opportunities to interpret the relationships between genetic variations and brain disorders (Potkin et al., 2009; Saykin et al., 2015; Shen et al., 2010).

During the last decade, many efforts have been made to explore computational methods to identify the correlation between QTs and genetic factors (Du et al., 2016, 2018; Hao et al., 2017; Shen et al., 2010; Vounou et al., 2010, 2012; Wang et al., 2012b; Witten and Tibshirani, 2009; Yan et al., 2014). The early imaging genetic studies (Shen et al., 2010; Vounou et al., 2010) used pairwise univariate analysis to identify single-SNP-single-QT associations. To improve the identification power, the multivariate sparse regression methods were introduced later (Vounou et al., 2012; Wan et al., 2011; Wang et al., 2012b). They either regressed a set of SNPs for a few candidate QTs, or regressed a set of QTs for a few candidate SNPs, and the relationship among predictors is usually taken into consideration via the regularization.

Recently, sparse canonical correlation analysis (SCCA) becomes popular in imaging genetics since it can identify bi-multivariate associations between multiple SNPs and multiple imaging QTs without pre-selecting candidate biomarkers (Du et al., 2016; Witten and Tibshirani, 2009; Yan et al., 2014). Most existing SCCA methods only employ neuroimaging data of one time point, e.g. the baseline, to study their correlation with SNPs. Neuroimaging techniques show improved power in investigating the characteristics of neurodegenerative progression in the spectrum from healthy controls (HCs) to patients with Alzheimer’s disease (AD) (Cheng et al., 2019). Thus, the brain structure and function along with the disease diagnosis change over time other than remain stationary. For example, a HC subject might progress to mild cognitive impairment (MCI) patient, and further to AD several years later; while another HC subject could remain healthy during these years. Therefore, understanding how the genetic factors modulate the trajectory of disease progression is particularly important and interesting.

The aforementioned methods might be insufficient to discover deep-seated imaging genetic relationship due to the ignorance of rich temporal information carried by the imaging data across multiple time points. To date, there are a few methods studying imaging genetics using the longitudinal phenotypic data. A common issue is that a pre-selection of candidate risk biomarkers is required before conducting the actual imaging genetic analysis. For example, Vounou et al. (2010) proposed a two-step method which first selected a small set of disease-related imaging voxels which can distinguish AD subjects from HC ones. Then a sparse reduced-rank regression was applied to identify those disease relevant SNPs by using the pre-selected voxels as responses and SNP as predictors (Vounou et al., 2012). Given the complexity of the human brain (Mai et al., 1997), only including a small proportion might be insufficient since this may lose important information carried by cerebral components which are not included (Shen et al., 2010). Wang et al. (2012a) proposed a sparse regression model which uses a small set of pre-selected SNPs as responses and the brain-wide imaging phenotypes as predictors. Instead of identifying disease relevant SNPs (Vounou et al., 2010), it identifies disease relevant brain imaging phenotypes with common influence on all candidate SNPs (Wang et al., 2012a). Recently, Hao et al. (2017) proposed a temporally constrained group SCCA (TGSCCA) which simplified the multi-set/multi-view SCCA (mSCCA) model (Witten and Tibshirani, 2009) by dropping the pairwise association between longitudinal imaging phenotypes. Both TGSCCA and mSCCA require that one set of variables (SNPs) being associated with several sets of variables (longitudinal imaging QTs across multiple time points) simultaneously, which might be too strict to make full use of the complementary information embedded in different period of imaging data. Moreover, TGSCCA identified time-consistent markers for imaging QTs, which only revealed those relevant markers being shared by all time points. As a result, it could not uncover the heterogeneous progressive patterns of human brain. Neuroimaging studies have shown that the human brain cerebral decline, e.g. the atrophy in AD, presents regional differences in the atrophy rates (Fox and Schott, 2004; Harper et al., 2017). This implies that, in many cases, the common progressive pattern is shared by multiple time points, but not all (Lee et al., 2010; Wang et al., 2011). This regional variations may trace back to the involvement of different SNPs at different time points. Therefore, developing longitudinal imaging genetics methods, with the ability of identifying a trajectory of progressive and time-dependent imaging genetic patterns, is of great importance and meaning. This could further help uncover the diverse genetic factors’ roles in affecting brain changes over the disease progression.

In this article, using the longitudinal brain imaging QTs across multiple time points, we propose a novel Temporal Multi-Task SCCA (T-MTSCCA) framework which learns bi-multivariate associations between intermediate phenotypes and genotypes simultaneously. In this new model, each SNP or QT is denoted as a feature, and an SCCA task is conducted between each longitudinal imaging modality and SNPs. Distinct from mSCCA and TGSCCA who learn only one canonical weight vector for SNPs, our T-MTSCCA learns a canonical weight matrix for SNPs, where each column corresponds to one canonical weight of one SCCA task. This means that our method can make full use of the complementary information carried by imaging QTs at different time points. The inherent linkage disequilibrium (LD) (Pritchard and Przeworski, 2001) structure is taken into consideration by the group ${\ell }_{2,1}$-norm (${\mathrm{G}}_{2,1}$-norm) (Wang et al., 2012b) to make the model practical. The ${\ell }_{2,1}$-norm is used to jointly select an individual feature for SNPs and phenotypic QTs. The longitudinal imaging QTs naturally present a temporal pattern across multiple time points, we use a fuse pairwise group lasso to accommodate this temporal relationship. In addition, the ${\ell }_1$-norm for both SNPs and imaging QTs assures a time-dependent feature selection, indicating its capability in finding markers which are only effective at a specific time point. We derive an efficient algorithm and show its convergence to a local optimum.

In the experiments, to evaluate the performance of T-MTSCCA, we used synthetic datasets with different characters and a real neuroimaging genetic dataset from the Alzheimer’s disease neuroimaging initiative (ADNI) (Mueller et al., 2005) cohort. The real data included longitudinal structural magnetic resonance imaging (MRI) measurements over a two year period and 1085 SNPs near the APOE gene. Compared with two state-of-the-art methods, on both synthetic and real datasets, our method yielded improved canonical correlation coefficients, and clear canonical weight profiles showing its capability in identifying relevant biomarkers. Moreover, T-MTSCCA also identified time-dependent and progressive imaging and genetic markers, demonstrating it is a potential alternative method in longitudinal brain imaging genetics.

2 Materials and methods

Throughout this article, we denote scalars as italic letters, vectors as boldface lowercase letters and matrices as boldface uppercase letters. The i-th row and j-th column of matrix $\mathbf{X}=(x_{i,j})$ are denoted as ${\mathbf{x}}^i$ and ${\mathbf{x}}_j$, respectively. The i-th matrix of a set of matrices is denotes as ${\mathbf{X}}_i$. The Euclidean norm of x is denoted as ${\Vert \mathbf{x}\Vert }_2$ and the Frobenius norm of X is defined as ${\Vert \mathbf{X}\Vert }_{\mathrm{F}}=\sqrt{\sum _i\sum _j{x}_{i,j}^2}$.

2.1 The sparse canonical correlation analysis

Canonical correlation analysis (CCA) combined with sparse learning techniques is widely used in imaging genetics. Suppose we have T matrices, i.e. ${\mathbf{X}}_i(i\in [1,\dots ,T])$ and T canonical weights ${\mathbf{w}}_i$, the SCCA can be formally defined as:

$$\underset{{\mathbf{w}}_1,\dots ,{\mathbf{w}}_T}{\min }\sum _{t<k}-{\mathbf{w}}_t^{\top }{\mathbf{X}}_t^{\top }{\mathbf{X}}_k{\mathbf{w}}_k+{\lambda }_t\Omega \left({\mathbf{w}}_t\right)$$ (1)

$$s.t. {\Vert {\mathbf{X}}_t{\mathbf{w}}_t\Vert }_2^2=1, \forall t.$$

$\Omega \left({\mathbf{w}}_t\right)$ is the sparsity-inducing term to select those features of interest and λ_t is the parameter to control the strength of sparsity. So far, SCCA studies have involved the Lasso (${\ell }_1$-norm) (Parkhomenko et al., 2009; Witten and Tibshirani, 2009), group Lasso (Chen and Liu, 2012; Du et al., 2017) and graph Laplacian regularization (Chen and Bushman, 2013; Du et al., 2016; Yan et al., 2014), to name a few. For the sake of description, we name an SCCA method based on the number of matrices involved. For example, we call it two-view or two-set SCCA (SCCA for short) when t = 2, and most existing studies are in this category. The multi-view or multi-set SCCA (mSCCA) studies the associations among three or more matrices ($t\ge 3$).

The temporally constrained group SCCA (TGSCCA) (Hao et al., 2017) is introduced by relating the SNP data to the imaging data at each time point separately while enforcing a shared canonical loading on the genetic side, i.e.

$$\underset{\mathbf{u},{\mathbf{v}}_1,\dots ,{\mathbf{v}}_T}{\min }\sum _{t=1}^T-{\mathbf{u}}^{\top }{\mathbf{X}}^{\top }{\mathbf{Y}}_t{\mathbf{v}}_t+{\lambda }_u\Omega \left(\mathbf{u}\right)+{\lambda }_v\Omega \left(\mathbf{V}\right)$$ (2)

$$s.t. {\Vert \mathbf{X}\mathbf{u}\Vert }_2^2=1, {\Vert {\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2=1, \forall t.$$

$\mathbf{X}\in {\mathbb{R}}^{n\times p}$ here represents the genotype SNPs data with n subjects and p SNPs, ${\mathbf{Y}}_t\in {\mathbb{R}}^{n\times q}(t=1,\dots ,T)$ represents the longitudinal phenotype data with q imaging QTs, where T is the number of time points and $\mathbf{V}=[{\mathbf{v}}_1 {\mathbf{v}}_2 \cdots {\mathbf{v}}_T]$.

2.2 The T-MTSCCA

In this subsection, we aim to investigate the association between genotypes and longitudinal imaging phenotypes. In view that imaging phenotypes show regional variations over time owing to the impact of genotypes, the computational model should account for the regional variations. Inspired by the success of multi-task regression in imaging genetics studies (Wang et al., 2012a, b), we propose a novel temporal multi-task SCCA (T-MTSCCA) method for longitudinal imaging genetics as follows:

$$\underset{{\mathbf{u}}_t,{\mathbf{v}}_t}{\min }\sum _{t=1}^T-{\mathbf{u}}_t^{\top }{\mathbf{X}}^{\top }{\mathbf{Y}}_t{\mathbf{v}}_t+\Omega \left(\mathbf{U}\right)+\Omega \left(\mathbf{V}\right)$$ (3)

$$s.t. {\Vert \mathbf{X}{\mathbf{u}}_t\Vert }_2^2=1,{\Vert {\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2=1, \forall t,$$

where $\mathbf{U}=[{\mathbf{u}}_1 {\mathbf{u}}_2 \cdots {\mathbf{u}}_T],\hspace{0.17em}\mathbf{V}=[{\mathbf{v}}_1 {\mathbf{v}}_2 \cdots {\mathbf{v}}_T]$ and T is the number of time points (SCCA tasks). $\Omega \left(\mathbf{U}\right)$ and $\Omega \left(\mathbf{V}\right)$ are the regularization terms for selection of time-dependent and time-consistent genotypic and imaging phenotypic markers.

T-MTSCCA has three advantages over previous models mSCCA and TGSCCA. First, T-MTSCCA is a multi-task bi-multivariate method which jointly learns related SCCA tasks. The neurodegenerative disorders, e.g. AD, usually deteriorate gradually, implying the brain structure and function, might show little difference between two consecutive visits. This indicates that the longitudinal imaging QTs remain stable during this period, which further reveals that these SCCA tasks regarding associations between genotypes and longitudinal imaging phenotypes are correlated longitudinally. According to the multi-task learning theory (Argyriou et al., 2006), T-MTSCCA is expected to yield enhanced performance owing to these longitudinally correlated SCCA tasks. Second, T-MTSCCA learns a weight matrix U with T vectors corresponding to T SCCA tasks. That is, an SCCA task will promote correlated tasks instead of enforcing them to be the same, which is meaningful when these tasks (associations between SNPs and longitudinal imaging phenotypes at different time points) are not perfectly related (Lee et al., 2010). This strategy seeks common ground while reserving differences and offers a unique opportunity to identify both time-consistent and time-dependent markers simultaneously. Third, the blended regularization $\Omega \left(\mathbf{U}\right)$ subsumes ${\mathrm{G}}_{2,1}$-norm, ${\ell }_{2,1}$-norm and ${\ell }_1$-norm, and thus assures diverse sparsity including time-dependent, time-consistent and smoothness crossing multiple time points but not all. $\Omega \left(\mathbf{V}\right)$ is also a blended regularization performing diverse feature selection for heterogeneous progressive patterns of imaging QTs. Therefore, T-MTSCCA is promising in discovering complex regional variations existing in the progression of neurodegenerative disorders (Fox and Schott, 2004), and further identifying the deep-seated QT loci being responsible for the disorders.

2.2.1. Regularization for genotypes via group-sparsity and individual-sparsity

It is well known that the genetic markers, i.e. SNPs, affect the brain structure and function both conjointly at group level and individually. SNPs could exhibit different temporal patterns longitudinally, being supported by the truth that the human brain cerebral decline exhibits regional variations longitudinally (Fox and Schott, 2004). Therefore, in order to take into consideration these complex temporal patterns, $\Omega \left(\mathbf{U}\right)$ is defined as:

$$\Omega \left(\mathbf{U}\right)={\lambda }_{u1}{\Vert \mathbf{U}\Vert }_{{\mathrm{G}}_{2,1}}+{\lambda }_{u2}{\Vert \mathbf{U}\Vert }_{2,1}+{\lambda }_{u3}\sum _{i=1}^p{\Vert {\mathbf{u}}^i\Vert }_1,$$ (4)

where ${\lambda }_{u1},\hspace{0.17em}{\lambda }_{u2}$ and ${\lambda }_{u3}$ are non-negative tuning parameters.

Specifically, the ${\mathrm{G}}_{2,1}$-norm is formulated as follows:

$${\Vert \mathbf{U}\Vert }_{{\mathrm{G}}_{2,1}}=\sum _{k=1}^K{\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}=\sum _{k=1}^K\sqrt{\sum _{i\in g_k}\sum _{t=1}^T{(u_t^i)}^2}.$$ (5)

${\mathbf{U}}^k$ is the k-th submatrix of U whose rows is indexed by g_k. $\mathcal{G}={\left\{g_k\right\}}_{k=1}^K$ denotes K groups in accordance with the LD structure. This norm assures group sparsity since it penalizes SNPs in the same group (e.g. LD) jointly, meaning they will be selected or unselected simultaneously (Wang et al., 2012b). The penalization is practical owing to packaging SNPs in the same LD block together, which makes the model consistent with the genotype mechanism.

The ${\ell }_{2,1}$-norm is defined as:

$${\Vert \mathbf{U}\Vert }_{2,1}=\sum _{i=1}^p{\Vert {\mathbf{u}}^i\Vert }_2=\sum _{i=1}^p\sqrt{\sum _{t=1}^T{(u_t^i)}^2}.$$ (6)

This regularization emphasizes on a single variable across multiple tasks, and could help identify a single SNP that plays a role in the brain development or disease progression via affecting the longitudinal imaging phenotypes. Finally, the temporal pattern implies that a SNP could not always play a role during the disease progression. Therefore, we use the ${\ell }_1$-norm for each ${\mathbf{u}}^i$ to induce sparsity across all time points for each individual SNP, i.e.

$${\Vert {\mathbf{u}}^i\Vert }_1=\sum _{t=1}^T\left|u_t^i\right|.$$ (7)

This penalty is focused on selecting the relevant features at a specific time point. It is worth noting that, combining the three terms together, they can not only identify active SNPs shared by all time points, but also identify SNPs being only relevant at a specific time point.

2.2.2. Regularization for longitudinal imaging phenotypes via time-consistent and time-dependent sparsity

The regularization aiming for sparsity with respect to imaging QTs is also desirable, being motivated by the fact that different imaging QTs play different roles during the disease progression. According to Equation (3), there is one canonical weight vector for imaging QTs at a specific time point. Then across multiple times points, an imaging QT describes the trajectory of the disease progression at this specific brain area. Based on the analysis earlier, regional variations, i.e. one brain region may remain stable while another may change significantly, should be taken into consideration.

On this account, we introduce a novel time-consistent and time-dependent constraint which is defined as follows:

$$\Omega \left(\mathbf{V}\right)={\lambda }_{v1}{\Vert \mathbf{V}\Vert }_{{\text{FP}}_{2,1}}+{\lambda }_{v2}{\Vert \mathbf{V}\Vert }_{2,1}+{\lambda }_{v3}\sum _{j=1}^q{\Vert {\mathbf{v}}^j\Vert }_1,$$ (8)

where ${\lambda }_{v1},\hspace{0.17em}{\lambda }_{v2}$ and ${\lambda }_{v3}$ are non-negative tuning parameters.

The fused pairwise ${\ell }_{2,1}$-norm (${\text{FP}}_{2,1}$-norm) (Du et al., 2017) is defined as:

$${\Vert \mathbf{V}\Vert }_{{\text{FP}}_{2,1}}=\sum _{j=1}^q\sum _{t=1}^{T-1}\sqrt{{(v_t^j)}^2+{(v_{t+1}^j)}^2}.$$ (9)

This norm first imposes the ${\ell }_2$-norm for two adjacent time points of one QT, then uses the ${\ell }_1$-norm for all QTs spanning the whole brain. As a result, the intermediate temporally stable pattern of one QT is considered as well as the sparsity among all QTs. Moreover, ${\text{FP}}_{2,1}$-norm is convex and thus could be easily optimized compared to the non-convex fused Lasso of TGSCCA (Hao et al., 2017). The ${\ell }_{2,1}$-norm:

$${\Vert \mathbf{V}\Vert }_{2,1}=\sum _{j=1}^q{\Vert {\mathbf{v}}^j\Vert }_2=\sum _{j=1}^q\sqrt{\sum _{t=1}^T{(v_t^j)}^2},$$ (10)

is used to assure the cross-task relationship for each imaging QT. Thus it could select or discard those imaging QTs remaining stable across all time points. Finally, as stated, the brain areas exhibit distinct atrophy patterns (Fox and Schott, 2004). Therefore, identifying time-dependent imaging QTs is also very important to understand the disease pathology. We use the ${\ell }_1$-norm penalty, i.e.

$${\Vert {\mathbf{v}}^j\Vert }_1=\sum _{t=1}^T\left|v_t^j\right|,$$ (11)

for each ${\mathbf{v}}_t$ to assure the individual-sparsity at a specific time point.

Obviously, either the ${\text{FP}}_{2,1}$-norm, ${\ell }_{2,1}$-norm or ${\ell }_1$-norm alone is insufficient due to the regional variations of both healthy and pathological brains. Therefore, we use all of them to regularize the longitudinal imaging QTs to account for both time-consistent and time-dependent feature selection. This make T-MTSCCA a very practical model, and thus suitable for longitudinal brain imaging genetics.

2.3 The optimization algorithm and its convergence

Writing the regularizers for genotypes and imaging phenotypes explicitly, the T-MTSCCA becomes:

$$\begin{array}{cc}\hfill & {\displaystyle \underset{{\mathbf{u}}_t,{\mathbf{v}}_t}{\min }}\sum _{t=1}^T-{\mathbf{u}}_t^{\top }{\mathbf{X}}^{\top }{\mathbf{Y}}_t{\mathbf{v}}_t+{\lambda }_{u1}{\Vert \mathbf{U}\Vert }_{{\mathrm{G}}_{2,1}}+{\lambda }_{u2}{\Vert \mathbf{U}\Vert }_{2,1}\hfill \\ \hfill & +{\lambda }_{u3}\sum _{i=1}^p{\Vert {\mathbf{u}}^i\Vert }_1+{\lambda }_{v1}{\Vert \mathbf{V}\Vert }_{{\text{FP}}_{2,1}}+{\lambda }_{v2}{\Vert \mathbf{V}\Vert }_{2,1}+{\lambda }_{v3}\sum _{j=1}^q{\Vert {\mathbf{v}}^j\Vert }_1\hfill \\ \hfill & s.t. {\Vert \mathbf{X}{\mathbf{u}}_t\Vert }_2^2=1,{\Vert {\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2=1,\forall t.\hfill \end{array}$$ (12)

Since $\forall t,\hspace{0.17em}{\Vert \mathbf{X}{\mathbf{u}}_t\Vert }_2^2=1$ and ${\Vert {\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2=1$, Equation (12) is equivalent to:

$$\begin{array}{cc}\hfill & {\displaystyle \underset{{\mathbf{u}}_t,{\mathbf{v}}_t}{\min }}\sum _{t=1}^T{\Vert \mathbf{X}{\mathbf{u}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+{\lambda }_{u1}{\Vert \mathbf{U}\Vert }_{{\mathrm{G}}_{2,1}}+{\lambda }_{u2}{\Vert \mathbf{U}\Vert }_{2,1}\hfill \\ \hfill & +{\lambda }_{u3}\sum _{i=1}^p{\Vert {\mathbf{u}}^i\Vert }_1+{\lambda }_{v1}{\Vert \mathbf{V}\Vert }_{{\text{FP}}_{2,1}}+{\lambda }_{v2}{\Vert \mathbf{V}\Vert }_{2,1}+{\lambda }_{v3}\sum _{j=1}^q{\Vert {\mathbf{v}}^j\Vert }_1\hfill \\ \hfill & s.t. {\Vert \mathbf{X}{\mathbf{u}}_t\Vert }_2^2=1,{\Vert {\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2=1,\forall t.\hfill \end{array}$$ (13)

It is hard to solve Equation (13) above due to its non-convexity in the quadratic term and non-smooth in regularization terms. But the objective is biconvex in U and V even if it is still non-smooth. In particular, this objective is convex in U with all ${\mathbf{v}}_t$’s fixed; and it is convex in ${\mathbf{v}}_t$ with U and the rest of ${\mathbf{v}}_{t\prime }(t\prime \ne t)$ fixed. Therefore, the solution can be easily attained via first using smoothing approximations of non-smooth terms, and then applying the efficient smooth optimization such as the alternative search method (Gorski et al., 2007).

2.3.1. Updating U

When V is fixed, the Lagrangian of Equation (13) regarding U writes:

$$\begin{array}{cc}\hfill & {\displaystyle \underset{\mathbf{U}}{\min }}\sum _{t=1}^T{\Vert \mathbf{X}{\mathbf{u}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+{\lambda }_{u1}{\Vert \mathbf{U}\Vert }_{{\mathrm{G}}_{2,1}}+{\lambda }_{u2}{\Vert \mathbf{U}\Vert }_{2,1}+{\lambda }_{u3}\sum _{i=1}^p{\Vert {\mathbf{u}}^i\Vert }_1\hfill \\ \hfill & +{\gamma }_u\sum _{t=1}^T{\Vert \mathbf{X}{\mathbf{u}}_t\Vert }_2^2,\hfill \end{array}$$ (14)

with those constants vanish. Now this equation transforms to a multi-task regression problem.

We take its derivative with respect to each ${\mathbf{u}}_t$ and set it to zero, i.e.

$$-{\mathbf{X}}^{\top }{\mathbf{Y}}_t{\mathbf{v}}_t+{\lambda }_{u1}{\tilde{\mathbf{D}}}_1{\mathbf{u}}_t+{\lambda }_{u2}{\overline{\mathbf{D}}}_1{\mathbf{u}}_t+{\lambda }_{u3}{\mathbf{D}}_{1t}{\mathbf{u}}_t+(1+{\gamma }_u){\mathbf{X}}^{\top }\mathbf{X}{\mathbf{u}}_t=0.$$ (15)

${\tilde{\mathbf{D}}}_1$ is a block diagonal matrix with the k-th diagonal block as $\frac{1}{2{\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}}{\mathbf{I}}_k$ (${\mathbf{I}}_k$ is an identity matrix with size being equal to the k-th submatrix ${\mathbf{U}}^k$, and $1\le k\le K$), ${\overline{\mathbf{D}}}_1$ is also a diagonal matrix whose i-th diagonal element is $\frac{1}{2{\Vert {\mathbf{u}}^i\Vert }_2}(1\le i\le p)$ and ${\mathbf{D}}_{1t}$ is a diagonal matrix with the i-th diagonal element being $\frac{1}{2\left|u_t^i\right|}$.

This equation indicates that every ${\mathbf{u}}_t$ can be solved in closed form. Simple mathematical derivation yields the updating rule for each ${\mathbf{u}}_t$, i.e.

$${\mathbf{u}}_t={({\lambda }_{u1}{\tilde{\mathbf{D}}}_1+{\lambda }_{u2}{\overline{\mathbf{D}}}_1+{\lambda }_{u3}{\mathbf{D}}_{1t}+(1+{\gamma }_u){\mathbf{X}}^{\top }\mathbf{X})}^{-1}{\mathbf{X}}^{\top }{\mathbf{Y}}_t{\mathbf{v}}_t.$$ (16)

Since ${\tilde{\mathbf{D}}}_1,\hspace{0.17em}{\overline{\mathbf{D}}}_1$ and ${\mathbf{D}}_{1t}$ ($t=1,2,\dots ,T$) are latent variables which depend on U, we can solve Equation (16) using the efficient iterative algorithm (Wang et al., 2011, 2012b).

2.3.2. Updating V

Now with U being fixed, the objective with respect to ${\mathbf{v}}_t$ writes:

$$\begin{array}{c}{\displaystyle \underset{{\mathbf{v}}_t}{\min }}{\Vert \mathbf{X}{\mathbf{u}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+{\lambda }_{v1}{\Vert \mathbf{V}\Vert }_{{\text{FP}}_{2,1}}+{\lambda }_{v2}{\Vert \mathbf{V}\Vert }_{2,1}+{\lambda }_{v3}{\Vert {\mathbf{v}}_t\Vert }_1+{\gamma }_v{\Vert {\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2.\hfill \end{array}$$ (17)

Taking the derivative with respect to ${\mathbf{v}}_t$ and setting it to zero, we have,

$$-{\mathbf{Y}}_t^{\top }\mathbf{X}{\mathbf{u}}_t+{\lambda }_{v1}{\tilde{\mathbf{D}}}_{2t}{\mathbf{v}}_t+{\lambda }_{v2}{\overline{\mathbf{D}}}_2{\mathbf{v}}_t+{\lambda }_{v3}{\mathbf{D}}_{2t}{\mathbf{v}}_t+(1+{\gamma }_v){\mathbf{Y}}_t^{\top }{\mathbf{Y}}_t{\mathbf{v}}_t=0.$$ (18)

Then, we arrive at:

$${\mathbf{v}}_t={({\lambda }_{v1}{\tilde{\mathbf{D}}}_{2t}+{\lambda }_{v2}{\overline{\mathbf{D}}}_2+{\lambda }_{v3}{\mathbf{D}}_{2t}+(1+{\gamma }_v){\mathbf{Y}}_t^{\top }{\mathbf{Y}}_t)}^{-1}{\mathbf{Y}}_t^{\top }\mathbf{X}{\mathbf{u}}_t,$$ (19)

where ${\overline{\mathbf{D}}}_2,\hspace{0.17em}{\tilde{\mathbf{D}}}_{2t}$ and ${\mathbf{D}}_{2t}$ ($t=1,2,\dots ,T$) are all diagonal matrices. In particular, the j-th diagonal element of ${\tilde{\mathbf{D}}}_{2t}$ is $\frac{1}{2\sqrt{{(v_{t-1}^j)}^2+{(v_t^j)}^2}}+\frac{1}{2\sqrt{{(v_t^j)}^2+{(v_{t+1}^j)}^2}}$ ($1\le j\le q,\hspace{0.17em}1\le t\le T$) (The j-th diagonal elements of ${\tilde{\mathbf{D}}}_{2t}$ is $\frac{1}{2\sqrt{{(v_t^j)}^2+{(v_{t+1}^j)}^2}}$ when t = 1, and $\frac{1}{2\sqrt{{(v_{t-1}^j)}^2+{(v_t^j)}^2}}$ when t = T.). The j-th diagonal element of ${\overline{\mathbf{D}}}_2$ is $\frac{1}{2{\Vert {\mathbf{v}}^j\Vert }_2}$, and that of ${\mathbf{D}}_{2t}$ is $\frac{1}{2\left|v_t^j\right|}$. This closed form shows that each ${\mathbf{v}}_t$ can be obtained via the alternative iteration algorithm too.

Now that U and V are solved, respectively, we summarize the optimization procedure in Algorithm 1, which guarantees to converge to a local optimum. In the iteration, Steps 1, 3 and 5 are computationally trivial. Steps 4 and 6 solve a system of linear equations, both of which are well studied in literature and can be solved efficiently.

Algorithm 1.

The T-MTSCCA algorithm

Require:

 The genotype data matrix $\mathbf{X}\in {\mathbb{R}}^{n\times p}$, longitudinal imaging phenotype data matrices of T time points ${\mathbf{Y}}_t\in {\mathbb{R}}^{n\times q},\hspace{0.17em}t\in [1,T]$, the pre-tuned ${\lambda }_{u1},\hspace{0.17em}{\lambda }_{u2},\hspace{0.17em}{\lambda }_{u3}$, γ_u, ${\lambda }_{v1},\hspace{0.17em}{\lambda }_{v2},\hspace{0.17em}{\lambda }_{v3}$ and γ_v.

Ensure:

 Canonical weights U and V.

1: Initialize $\mathbf{U}\in {\mathbb{R}}^{p\times T},\hspace{0.17em}\mathbf{V}\in {\mathbb{R}}^{q\times T}$;

2: while not convergence do

3:  Update ${\tilde{\mathbf{D}}}_1,\hspace{0.17em}{\overline{\mathbf{D}}}_1$ and ${\mathbf{D}}_{1t}$ ($t=1,2,\dots ,T$);

4:  Solve U according to Equation (16), and scale ${\mathbf{u}}_t$ as that ${\Vert \mathbf{X}{\mathbf{u}}_t\Vert }_2^2=1$;

5:  Update ${\overline{\mathbf{D}}}_2,\hspace{0.17em}{\tilde{\mathbf{D}}}_{2t}$ and ${\mathbf{D}}_{2t}$ ($t=1,2,\dots ,T$);

6:  Solve ${\mathbf{v}}_t$ alternatively according to Equation (19), and scale ${\mathbf{v}}_t$ so that ${\Vert {\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2=1$;

7: end while

2.3.3. Convergence analysis

The following theorem holds for Algorithm 1.

Theorem 1.

The objective decreases in each iteration of Algorithm 1. Proof. Denote the current estimate of U and V, respectively, as U and V (with a slight abuse of notation, for notational convenience), and their refined estimates using the updating rules in Equations (16) and (19) as $\widehat{\mathbf{U}}$ and $\widehat{\mathbf{V}}$. Denote the objective function value of problem (13) as $f(\mathbf{U},\mathbf{V})$.

According to the update rule in Equation (16), we have,

$$\begin{array}{cc}\hfill & \sum _{t=1}^T{\Vert \mathbf{X}{\widehat{\mathbf{u}}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+{\lambda }_{u1}\text{Tr}\left({\widehat{\mathbf{U}}}^{\top }{\tilde{\mathbf{D}}}_1\widehat{\mathbf{U}}\right)+{\lambda }_{u2}\text{Tr}\left({\widehat{\mathbf{U}}}^{\top }{\overline{\mathbf{D}}}_1\widehat{\mathbf{U}}\right)+{\lambda }_{u3}\sum _{t=1}^T{\widehat{\mathbf{u}}}_t^{\top }{\mathbf{D}}_{1t}{\widehat{\mathbf{u}}}_t\hfill \\ \hfill & +{\gamma }_u\text{Tr}\left({\widehat{\mathbf{U}}}^{\top }{\mathbf{X}}^{\top }\mathbf{X}\widehat{\mathbf{U}}\right)\le \sum _{t=1}^T{\Vert \mathbf{X}{\mathbf{u}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+{\lambda }_{u1}\text{Tr}\left({\mathbf{U}}^{\top }{\tilde{\mathbf{D}}}_1\mathbf{U}\right)\hfill \\ \hfill & +{\lambda }_{u2}\text{Tr}\left({\mathbf{U}}^{\top }{\overline{\mathbf{D}}}_1\mathbf{U}\right)+{\lambda }_{u3}\sum _{t=1}^T{\mathbf{u}}_t^{\top }{\mathbf{D}}_{1t}{\mathbf{u}}_t+{\gamma }_u\text{Tr}\left({\mathbf{U}}^{\top }{\mathbf{X}}^{\top }\mathbf{X}\mathbf{U}\right)\hfill \\ \hfill & \Rightarrow \sum _{t=1}^T{\Vert \mathbf{X}{\widehat{\mathbf{u}}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+{\lambda }_{u1}\sum _{k=1}^K\frac{{\Vert {\widehat{\mathbf{U}}}^k\Vert }_{\mathrm{F}}^2}{2{\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}}+{\lambda }_{u2}\sum _{i=1}^p\frac{{\Vert {\widehat{\mathbf{u}}}^i\Vert }_2^2}{2{\Vert {\mathbf{u}}^i\Vert }_2}\hfill \\ \hfill & +{\lambda }_{u3}\sum _{i=1}^p\sum _{t=1}^T\frac{|{{{\displaystyle \hat{u}}}_t^{\mathit{i}}|}^2}{2\left|u_t^i\right|}+{\gamma }_u{\Vert \mathbf{X}\widehat{\mathbf{U}}\Vert }_{\mathrm{F}}^2\le \sum _{t=1}^T{\Vert \mathbf{X}{\mathbf{u}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+{\lambda }_{u1}\sum _{k=1}^K\frac{{\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}^2}{2{\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}}\hfill \\ \hfill & +{\lambda }_{u2}\sum _{i=1}^p\frac{{\Vert {\mathbf{u}}^i\Vert }_2^2}{2{\Vert {\mathbf{u}}^i\Vert }_2}+{\lambda }_{u3}\sum _{i=1}^p\sum _{t=1}^T\frac{|u_t^i{|}^2}{2\left|u_t^i\right|}+{\gamma }_u{\Vert \mathbf{X}\mathbf{U}\Vert }_{\mathrm{F}}^2.\hfill \end{array}$$

Applying ${\Vert {\widehat{\mathbf{U}}}^k\Vert }_{\mathrm{F}}-\frac{{\Vert {\widehat{\mathbf{U}}}^k\Vert }_{\mathrm{F}}^2}{2{\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}}\le {\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}-\frac{{\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}^2}{2{\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}}$, ${\Vert {\widehat{\mathbf{u}}}^i\Vert }_2-\frac{{\Vert {\widehat{\mathbf{u}}}^i\Vert }_2^2}{2{\Vert {\mathbf{u}}^i\Vert }_2}\le {\Vert {\mathbf{u}}^i\Vert }_2-\frac{{\Vert {\mathbf{u}}^i\Vert }_2^2}{2{\Vert {\mathbf{u}}^i\Vert }_2}$ and $|{{\displaystyle \hat{u}}}_t^{\mathit{i}}|-\frac{|{{{\displaystyle \hat{u}}}_t^{\mathit{i}}|}^2}{2\left|u_t^i\right|}\le \left|u_t^i\right|-\frac{|u_t^i{|}^2}{2\left|u_t^i\right|}$ [Lemma 1 in (Wang et al., 2012b)] to Equation (2.3.3) with respect to each group and individual features, respectively, we arrive at:

$$\begin{array}{cc}\hfill & \sum _{t=1}^T{\Vert \mathbf{X}{\widehat{\mathbf{u}}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+{\lambda }_{u1}\sum _{k=1}^K{\Vert {\widehat{\mathbf{U}}}^k\Vert }_{\mathrm{F}}+{\lambda }_{u2}\sum _{i=1}^p{\Vert {\widehat{\mathbf{u}}}^i\Vert }_2+{\lambda }_{u3}\sum _{i=1}^p\sum _{t=1}^T|{{\displaystyle \hat{u}}}_t^{\mathit{i}}|\hfill \\ \hfill & +{\gamma }_u{\Vert \mathbf{X}\widehat{\mathbf{U}}\Vert }_{\mathrm{F}}^2\le \sum _{t=1}^T{\Vert \mathbf{X}{\mathbf{u}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+{\lambda }_{u1}\sum _{k=1}^K{\Vert {\mathbf{U}}^k\Vert }_{\mathrm{F}}\hfill \\ \hfill & +{\lambda }_{u2}\sum _{i=1}^p{\Vert {\mathbf{u}}^i\Vert }_2+{\lambda }_{u3}\sum _{i=1}^p\sum _{t=1}^T\left|u_t^i\right|+{\gamma }_u{\Vert \mathbf{X}\mathbf{U}\Vert }_{\mathrm{F}}^2.\hfill \end{array}$$

Writing in matrix form, we obtain:

$$\begin{array}{cc}\hfill & \sum _{t=1}^T{\Vert \mathbf{X}{\widehat{\mathbf{u}}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+\lambda u1{\Vert \widehat{\mathbf{U}}\Vert }_{{\mathrm{G}}_{2,1}}+{\lambda }_{u2}{\Vert \widehat{\mathbf{U}}\Vert }_{2,1}+{\lambda }_{u3}\sum _{i=1}^p{\Vert {\widehat{\mathbf{u}}}^i\Vert }_1\hfill \\ \hfill & +{\gamma }_u\sum _{t=1}^T{\Vert \mathbf{X}{\widehat{\mathbf{u}}}_t\Vert }_2^2\le \sum _{t=1}^T{\Vert \mathbf{X}{\mathbf{u}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+\lambda u1{\Vert \mathbf{U}\Vert }_{{\mathrm{G}}_{2,1}}+{\lambda }_{u2}{\Vert \mathbf{U}\Vert }_{2,1}\hfill \\ \hfill & +{\lambda }_{u3}\sum _{i=1}^p{\Vert {\mathbf{u}}^i\Vert }_1+{\gamma }_u\sum _{t=1}^T{\Vert \mathbf{X}{\mathbf{u}}_t\Vert }_2^2.\hfill \end{array}$$

This reveals that, in each iteration of Equation (16), the objective decreases, namely, $f(\widehat{\mathbf{U}},\mathbf{V})\le f(\mathbf{U},\mathbf{V})$.

Similarly, we can prove the convergence of updating ${\mathbf{v}}_t$’s one by one. Combined, in equations with respect to each ${\mathbf{v}}_t$ yields:

$$\begin{array}{cc}\hfill & \sum _{t=1}^T{\Vert \mathbf{X}{\widehat{\mathbf{u}}}_t-{\mathbf{Y}}_t{\widehat{\mathbf{v}}}_t\Vert }_2^2+\lambda v1{\Vert \widehat{\mathbf{V}}\Vert }_{{\text{FP}}_{2,1}}+{\lambda }_{v2}{\Vert \widehat{\mathbf{V}}\Vert }_{2,1}+{\lambda }_{v3}\sum _{j=1}^q{\Vert {\widehat{\mathbf{v}}}^j\Vert }_1\hfill \\ \hfill & +{\gamma }_v\sum _{t=1}^T{\Vert {\mathbf{Y}}_t{\widehat{\mathbf{v}}}_t\Vert }_2^2\le \sum _{t=1}^T{\Vert \mathbf{X}{\widehat{\mathbf{u}}}_t-{\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2+\lambda v1{\Vert \mathbf{V}\Vert }_{{\text{FP}}_{2,1}}+{\lambda }_{v2}{\Vert \mathbf{V}\Vert }_{2,1}\hfill \\ \hfill & +{\lambda }_{v3}\sum _{j=1}^q{\Vert {\mathbf{v}}^j\Vert }_1+{\gamma }_v\sum _{t=1}^T{\Vert {\mathbf{Y}}_t{\mathbf{v}}_t\Vert }_2^2,\hfill \end{array}$$

from which it follows that $f(\widehat{\mathbf{U}},\widehat{\mathbf{V}})\le f(\widehat{\mathbf{U}},\mathbf{V})$.

Combining two conclusions above yields $f(\widehat{\mathbf{U}},\widehat{\mathbf{V}})\le f(\widehat{\mathbf{U}},\mathbf{V})\le f(\mathbf{U},\mathbf{V})$, which completes the proof. □

Since both objectives of problems Equations (14) and (17) are lower bounded by zero and the T-MTSCCA problem is biconvex, the overall iteration algorithm will converge to a local optimum. In our experiments, we terminate Algorithm 1 when ${\max }_{i,t}|{{\displaystyle \hat{u}}}_t^{\mathit{i}}-u_t^j|\le ϵ$ and ${\max }_{j,t}|{{\displaystyle \hat{v}}}_t^{\mathit{i}}-v_t^j|\le ϵ$ satisfy, where ϵ is the pre-set error bound. We use $ϵ={10}^{-5}$ in this article empirically based on experiments.

3 Experimental results and discussions

3.1 Experimental setup

In the experiments, we compare T-MTSCCA with two close counterparts including the mSCCA (multi-view SCCA) and TGSCCA (temporally constrained group SCCA) using both synthetic data and real neuroimaging genetic data. The mSCCA computes pairwise correlation coefficients between the SNPs data and the imaging QTs data including that between every two modalities of imaging QTs at different time points (Witten and Tibshirani, 2009). TGSCCA is similar to mSCCA by dropping the pairwise correlation terms between those imaging QTs data at different time points (Hao et al., 2017).

We use the nested 10-fold cross-validation method to find the optimal parameters. These parameters generating the highest cross-task mean testing correlation coefficient will be chosen as the optimal parameters, i.e. $\mathrm{CV}(\lambda ,\beta ,\gamma )=\frac{1}{10}{\sum }_{j=1}^{10}{\sum }_{t=1}^{T}Co\mathit{rr}({\overline{\mathbf{X}}}_j{\mathbf{u}}_{j,t},{\overline{\mathbf{Y}}}_{j,t}{\mathbf{v}}_{j,t})$, where ${\overline{\mathbf{X}}}_j$ and ${\overline{\mathbf{Y}}}_{j,t}$ are the j-th fold which are the complementary sets used for testing, and ${\mathbf{u}}_{j,t}$ and ${\mathbf{v}}_{j,t}$ are the canonical weights estimated from the training set. To further reduce the time effort, we fix ${\gamma }_u=1$ and ${\gamma }_v=1$ since they result in two scaling steps in Algorithm 1, and thus only affect the magnitude of U and V (Chen and Liu, 2012). This indicates that the relative relationship among each variables remain the same. Finally, we tune these parameters from candidate range ${10}^i$ ($i=-5,-4,\dots ,0,\dots ,4,5$), within which the results are from less-sparsity to over-sparsity. Once determined, we use the tuned parameters to obtain the final training and testing results. In each experiment, all methods are stopped if ${\max }_i\left|u_i^{(t+1)-u_i^{(t)}}\right|\le ϵ$ and ${\max }_j\left|v_j^{(t+1)-v_j^{(t)}}\right|\le ϵ$, with ϵ being the tolerable error. ϵ is set to ${10}^{-5}$ empirically in this article.

3.2 Results on simulation data

In this simulation study, to evaluate the T-MTSCCA method, we used four synthetic datasets with distinct properties which could thoroughly access the performance. First, we generated one sparse vector $\mathbf{u}\in {\mathcal{R}}^{p\times 1}$ and four successive sparse vectors ${\mathbf{v}}_t\in {\mathcal{R}}^{q\times 1}$. In particular, several non-zero variables are shared by all ${\mathbf{v}}_t$’s while some ones are time-dependent. Then, using a latent vector $\mathbf{z}\in {\mathcal{R}}^{n\times 1}$, we create X by ${\mathbf{x}}_i\sim N(z_i\mathbf{u},e·{\mathbf{I}}_{p\times p})$, and each ${\mathbf{Y}}_t$ by ${\mathbf{y}}_{t,i}\sim N(z_i{\mathbf{v}}_t,e·{\mathbf{I}}_{q\times q})$. Being embedded with different strengths of noise, the first three datasets share the same ground truth, i.e. n = 80, p = 100 and q = 120, on which could show one method’s performance under different noises. The fourth dataset simulated a large and complex imaging genetic problem (n = 500, p = 2000 and q = 600). The details of the ground truths are presented in Figure 2 (top row).

Fig. 2.

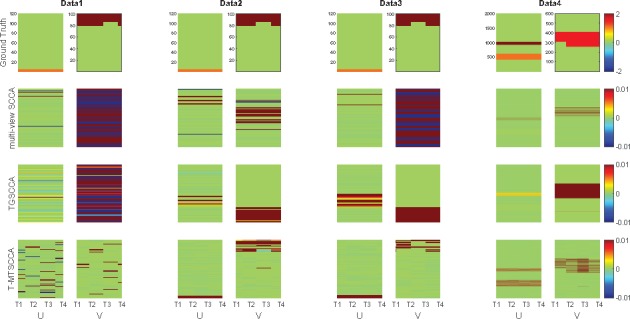
Heat maps of canonical weights on synthetic data. Rows 1–4: Ground truth, mSCCA, TGSCCA and T-MTSCCA, respectively. In each row, U is on the left panel and V is on the right. Within each panel, there are four canonical weights associating with four time points. For our method, there are four canonical weights corresponding to four time points, i.e. T1, T2, T3, T4, for both U and V. For mSCCA and TGSCCA, the weight matrix U is stacked by the same canonical weight vector u.

We presented the testing canonical correlation coefficients (CCCs) in Figure 1 (training CCCs are omitted due to the space limitation). The CCCs, i.e. CCC_T1, CCC_T2, CCC_T3, CCC_T4, of each method were calculated between X and ${\mathbf{Y}}_t$ at every time point. In this figure, all methods obtained low testing CCCs, indicating they were over-fitted when the true CCC was quite low. As expected, their performances improve as the CCC increased. T-MTSCCA and TGSCCA obtained better CCCs than mSCCA on data 2 and data 3 attributing to the temporal constraints. On data 4 with thousands of variables, T-MTSCCA and TGSCCA also hold better CCCs than mSCCA, which demonstrates they were suitable for longitudinal imaging genetics.

Fig. 1.

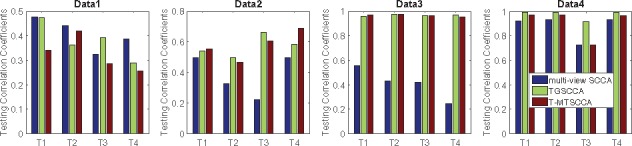
Comparison of the mean canonical correlation coefficients (CCCs) obtained from 10-fold cross-validation trials. The CCCs at all time points are illustrated, where CCC_T1 is calculated between the SNP data and the imaging data at T1, and so forth.

In addition, the ability of feature selection, i.e. the selected SNPs and imaging QTs at intermediate time points, is also important. To make the results stable, we averaged the canonical weights across 10-folds and shown them in Figure 2. The actual U and V were shown on the top row followed by those estimated by mSCCA, TGSCCA and T-MTSCCA. Within each method’s panel, the canonical weights associated with all time points were stacked vertically. It is clear that T-MTSCCA identified a clear and clean pattern in terms of both U and V, whose non-zero variables were consistent to the ground truth. TGSCCA also obtained acceptable results due to its temporal constraint for the intermediate imaging QTs. It is worth mentioning that T-MTSCCA also identified time-dependent non-zero variables for U and V thanks to its novel time-dependent penalties. This is very interesting since, combined with the time-consistent penalty, our T-MTSCCA can not only identify those active variables at a specific time point, but also identify those active variables shared by all time points. To summarize, the results on this four distinct synthetic datasets demonstrate that T-MTSCCA could be a competitive alternative method for longitudinal bi-multivariate association’s identification.

3.3 Results on real neuroimaging genetic data

The real genotyping and brain imaging data used in this article were obtained from the ADNI database (adni.loni.usc.edu). The primary goal of ADNI has been to test whether serial MRI, positron emission tomography (PET), other biological markers and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. For up-to-date information, see www.adni-info.org.

The longitudinal neuroimaging data were from 408 non-Hispanic Caucasian participants, including 125 healthy controls (HC), 192 MCI and 91 AD subjects at the baseline screening. Table 1 shown the demographic information. We used MRI T1-weighted imaging including baseline (BL), Month 06 (M6), Month 12 (M12) and Month 24 (M24) in this work. These preprocessed imaging data, i.e. the voxel-based morphometry (VBM), were aligned to each participant’s same visit scan. Then the normalized gray matter density maps were created from MRI data in the standard Montreal Neurological Institute (MNI) space as $2\times 2\times 2$ mm³ voxels via the SPM software (Ashburner and Friston, 2000). Based on the MarsBaR AAL atlas (Tzourio-Mazoyer et al., 2002), we further extracted 116 ROI level measurements of mean gray matter densities. Finally, we removed the cerebellum area and obtained 90 imaging measures, and finally used them as phenotypes of four time points in the experiments. Before the experiment, the imaging measures were adjusted by removing the effects of the baseline age, gender, education and handedness.

Table 1.

Participant characteristics

	HC	MCI	AD
Num (n)	125	192	91
Gender (M/F)	73/52	122/70	65/26
Handedness (R/L)	112/13	178/14	86/5
Age (mean ± SD)	74.44 ± 6.58	75.26 ± 6.85	74.12 ± 7.07
Education (mean ± SD)	15.62 ± 2.96	16.27 ± 2.83	16.14 ± 2.64

The genotyping data of the same 408 subjects were downloaded from the ADNI website too. The SNPs were generated by the Human 610-Quad or OmniExpress Array (Illumina, Inc., San Diego, CA, USA), and preprocessed according to the standard quality control (QC) and imputation steps. We included 1085 SNPs from the neighbor of the APOE gene based on the ANNOVAR annotation (see the Supplementary file). We aim to study associations between SNPs and longitudinal brain imaging measures, and identify those time-consistent and time-dependent markers in this ADNI dataset.

3.3.1. Improved bi-multivariate association

We applied three methods to this real neuroimaging genetic data. mSCCA and TGSCCA yielded one canonical weight u and four canonical weights ${\mathbf{v}}_t$ associating with four longitudinal time points. By calculating association between SNPs and each imaging QTs of different time points, we obtained four CCCs for them. Our method naturally generated four pairs of canonical weights, and thus there were four CCCs with respect to four time points. We denoted these four CCCs as CCC_BL, CCC_M6, CCC_M12 and CCC_M24 for the sake of description, and presented them in Figure 3 separately. In this figure, the testing CCCs was shown with those training ones omitted due to the space limitation. As expected, owing to the utilization of temporal regularization, both TGSCCA and T-MTSCCA obtained better CCCs than mSCCA. This shows their effectiveness in longitudinal bi-multivariate association studies.

Fig. 3.

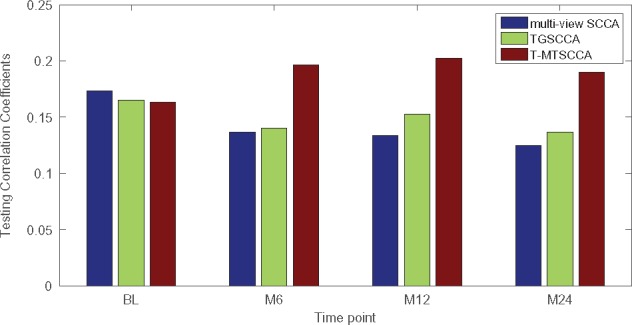
Comparison of the mean canonical correlation coefficients (CCCs) obtained from 10-fold testing trials on ADNI.

3.3.2. Identification of time-consistent and time-dependent SNPs

Besides the CCC which showing the strength of the association, the identification of longitudinally active SNPs and imaging QTs is of great importance. These time-dependent patterns help uncover the basis of the diverse progression stages of diseases. We illustrated the weight matrix U, whose absolute values show the importance of SNPs, of each method in Figure 4. In this figure, each subfigure denotes a method, within which each row corresponds to one canonical weight at one time point. mSCCA and TGSCCA only reported one canonical weight vector with respect to SNPs, and thus, we stacked u for four times. T-MTSCCA yielded four ${\mathbf{u}}_t$’s, with each being associated to one time point. Finally, the canonical weights across 10-folds were averaged to make a stable selection.

Fig. 4.

Comparison of canonical weights in terms of SNPs averaged from 10-fold cross-validation trials. Each row corresponds to a SCCA method: (1) mSCCA; (2) TGSCCA and (3) T-MTSCCA. For our method, there are four rows corresponding to four time points, i.e. BL, M6, M12 and M24. For mSCCA and TGSCCA, the four rows are stacked by the same u.

T-MTSCCA yielded a clear time-consistent and time-dependent pattern with respect to selected features (SNPs) across multiple time points owing to the jointly learning and the novel constraint. TGSCCA and mSCCA could only identify time-consistent imaging QTs. The reason is that both methods output only one canonical weight vector based on their modeling strategy, and thus cannot identify those ones being involved at a specific time point. This reveals that our method performs cleverly and suitably in longitudinal feature selection studies. For the selected features, we observed that the SNPs identified by T-MTSCCA have been reported to show increasing risk for AD or MCI progression in previous studies. Specifically, there are evidences showing that rs76692773 (TOMM40) and rs112262807 (PVRL2) were AD-risk loci. rs141622900 (APOC1) is a determinant of the cholesterol efflux Capacity (CEC) (Low-Kam et al., 2018), whose reduction is a sign of MCI or AD (Yassine et al., 2016). rs76075198 (CEACAM19) is a loci associated to Dyslipidemia which shares some pathology with AD (Carlsson, 2010). It warrants further investigation to confirm the effects of the remaining loci since they were within in AD-associated genes such as PVRL2 (rs7343130), and RELB (rs141652051) (Nho et al., 2017), BCL3 (rs7249244 and rs2927462) (Xiao et al., 2017), CEACAM19 (rs141846480) (Jansen et al., 2019), CLPTM1 (rs12983572) (Hao et al., 2018). TGSCCA and mSCCA also identified AD-associated loci such as rs57537848 (Nazarian et al., 2019) and rs76692773, as well as loci falling within AD-risk genes such as rs1166329 (PVRL2) and rs7249244 (BCL3) which have not been reported to be associated with AD or MCI. Given these meaningful results, further investigation, such as a post-refined analysis, is warranted to confirm the role of these SNPs during the AD progression. It is interesting that all three method did not identify rs429358 which is a well-known AD risk locus. This might stem from the reduced effect of rs429358 in the AD progression, and, of course, it warrants further investigation to conform this. In summary, the results regarding SNPs selection show that the proposed method can not only identify SNPs being effective across multiple time points, but also identify those being only effective at a specific time point. This reveals that T-MTSCCA could be suitable to identify meaningful genetic markers in a longitudinal scenario.

3.3.3. Identification of time-consistent and time-dependent QTs

We want to know the dynamic patterns of imaging QTs longitudinally as well, which shows the interior behavior of diseases progression. We averaged each ${\mathbf{v}}_t$ across 10-folds to assure a stable selection. These averaged results of every method on each imaging modality (BL, M6, M12 and M24) were shown in Figure 5. Since TGSCCA could not yield sparse results due to the lack of individual sparse-inducing term, we show the top 10 imaging QTs with the highest absolute weight values. As expected, mSCCA identified irregular non-zero imaging QTs which is time-dependent for each individual time point due to the lack of temporal constraint. TGSCCA and T-MTSCCA yielded consistent imaging markers across all time points, indicating their ability in finding time-consistent markers. T-MTSCCA also identified imaging QTs being only effective at one time point, e.g. baseline screening in this study. We then investigated this by conducting a two-view SCCA between SNP data and imaging data at each time point separately (results were not shown due to the space limitation). These four independent tasks showed that the association pattern at BL is not closely correlated to those of the three successive time points, i.e. M6, M12 and M24. Therefore, there is a significant difference with respect to the non-zero imaging QTs between BL and M6, M12 and M24. This, on the contrary, demonstrates the value of T-MTSCCA for its time-dependent feature selection.

Fig. 5.

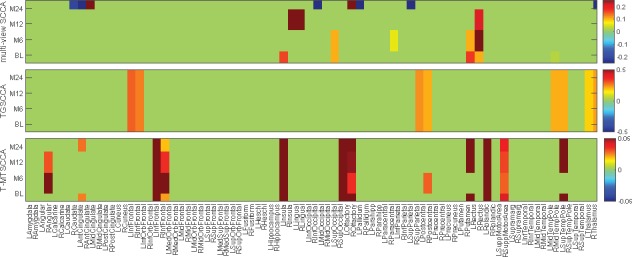
Comparison of canonical weights in terms of each imaging QTs averaged from 10-fold cross-validation trials. Each row corresponds to a SCCA method: (1) mSCCA; (2) TGSCCA and (3) T-MTSCCA. Within each panel, there are four rows corresponding to four time points of imaging QTs, i.e. BL, M6, M12 and M24.

T-MTSCCA identified seven imaging markers across all time points, indicating its ability in discovering time-consistent features. A literature search shows that all these brain areas are relevant to MCI or AD. For examples, the right angular gyrus, in which the glucose metabolism shows significant reduction, is associated to aging-associated cognitive decline (AACD) (Hunt et al., 2007). The right middle frontal gyrus, the orbitofrontal cortex, the left insula, the left lingual gyru, and the left occipital were reported as AD-relevant brain regions in previous studies (Holroyd et al., 2000; Van Hoesen et al., 2000; Yao et al., 2010). T-MTSCCA also reported several AD-associated imaging QTs, such as the right fusiform gyrus (Wang et al., 2015) and the left precuneus, at baseline. It is worth mentioning that the left precuneus has been demonstrated to be associated with early onset AD (Karas et al., 2007). This is promising since T-MTSCCA could successfully identify the neurodegenerative biomarker at its early stage. In addition, T-MTSCCA also captured the aging-associated areas, such as the left calcarine cortex which shows predominantly atrophy with age (Bakkour et al., 2013). This is interesting that, due to the unsupervised modeling strategy, our method could capture the temporal characters of the brain change happening to both HCs and ADs, thereby it can also be applied to brain aging studies. TGSCCA and mSCCA also identified imaging markers that were associated with MCI or AD, e.g. the left and right olfactory and the left and right parahippocampal gyri. To summarize, T-MTSCCA identified both time-consistent and time-dependent imaging QTs, which could help uncover the different changing patterns during different periods in MCI and AD progression, as well as the change caused by aging. This finally reveals that, using time-consistent and time-dependent constraints simultaneously, T-MTSCCA could be very promising in longitudinal brain imaging genetics.

4 Conclusion

Studying the associations between multiple genetic markers and brain imaging measurements is an important task in brain science, with the aim to uncover the genetic basis of the brain structure, function and disorder. Longitudinal study is widely used in biomedical studies where the brain imaging measures are collected repeatedly over long periods of time. These longitudinal data carry rich information with respect to the disorder progression and brain aging. Most existing imaging genetics methods only use the baseline neuroimaging data, and thus ignore useful information embedded in the longitudinal imaging data across multiple time points. In this article, we present a novel temporal multi-task SCCA (T-MTSCCA) method which can identify time-consistent and time-dependent phenotypic and genotypic markers simultaneously. Being distinct from existing temporal SCCA, T-MTSCCA treats those temporally correlated SCCA jointly other than enforcing them to be the same. This strategy seeks common ground while reserving differences and can identify both time-consistent and time-dependent markers, and thus has better modeling ability. An efficient algorithm is proposed to optimize the problem, which is guaranteed to converge to a local optimum.

We compared T-MTSCCA with two state-of-the-art counterparts, i.e. the mSCCA (multi-view SCCA) (Witten and Tibshirani, 2009) and TGSCCA (temporally constrained group SCCA) (Hao et al., 2017) using both synthetic data and neuroimaging genetic data from the ADNI database. On the synthetic data, T-MTSCCA obtained better CCCs than the benchmarks and identified clearer canonical weight patterns which were consistent to the ground truths. On the real neuroimaging genetic data, our method obtained better or equal CCCs to mSCCA and TGSCCA at multiple time points. It succeeds in identifying a small set of SNPs and brain imaging QTs from all markers involved. It is worth noting that our method can not only find out time-consist features for SNPs and imaging QTs across multiple time points, but also identified time-dependent markers at baseline. These identified imaging QTs and SNPs were highly correlated to AD or MCI, and thus demonstrated that the proposed temporal multi-task SCCA could be a powerful alternative method in longitudinal brain imaging genetics. T-MTSCCA also identified aging-associated areas in elderly subjects. In the future, we aim to extend T-MTSCCA to the genome-wide brain-wide study, since the GWAS-oriented longitudinal brain imaging genetics is a major challenge.