Reactive school closure weakens the network of social interactions and reduces the spread of influenza

Significance

The effectiveness of school-closure policies to mitigate seasonal and pandemic influenza is controversial, mostly because of the lack of empirical evidence about the behavior of the population during the implementation of these policies. In this study, we measure the behavior of the population during regular school/work days and when schools/classes are closed as a consequence of a school-closure policy. We leverage the obtained data to develop an innovative data-driven predictive-modeling framework to reduce the uncertainty surrounding school-closure policies.

Abstract

School-closure policies are considered one of the most promising nonpharmaceutical interventions for mitigating seasonal and pandemic influenza. However, their effectiveness is still debated, primarily due to the lack of empirical evidence about the behavior of the population during the implementation of the policy. Over the course of the 2015 to 2016 influenza season in Russia, we performed a diary-based contact survey to estimate the patterns of social interactions before and during the implementation of reactive school-closure strategies. We develop an innovative hybrid survey-modeling framework to estimate the time-varying network of human social interactions. By integrating this network with an infection transmission model, we reduce the uncertainty surrounding the impact of school-closure policies in mitigating the spread of influenza. When the school-closure policy is in place, we measure a significant reduction in the number of contacts made by students (14.2 vs. 6.5 contacts per day) and workers (11.2 vs. 8.7 contacts per day). This reduction is not offset by the measured increase in the number of contacts between students and nonhousehold relatives. Model simulations suggest that gradual reactive school-closure policies based on monitoring student absenteeism rates are capable of mitigating influenza spread. We estimate that without the implemented reactive strategies the attack rate of the 2015 to 2016 influenza season would have been 33% larger. Our study sheds light on the social mixing patterns of the population during the implementation of reactive school closures and provides key instruments for future cost-effectiveness analyses of school-closure policies.

One of the key lessons learned from the 2009 H1N1 influenza pandemic was the pivotal role of young individuals in spreading the infection. School-age children were the most affected age group (1–4) and the most susceptible to infection (5–7). Moreover, influenza transmission at the population level was substantially lower when schools were closed (e.g., due to regular holidays) (8–13). For this reason, as well as due to the time consuming process of vaccine development and large-scale distribution, school-closure policies are considered by health officials around the world as a viable strategy to mitigate the spread of a new influenza pandemic (14).

Countries like Japan, Bulgaria, and Russia have already used school-closure policies to mitigate influenza spread (15), demonstrating that logistic and social challenges of school-closure strategies can be overcome. Nonetheless, the effectiveness of school-closure policies as nonpharmaceutical interventions for mitigating influenza epidemics and pandemics is still disputed (14, 15). Indeed, mathematical modeling studies are struggling to provide public health officials with a definitive indication in favor of school-closure policies, despite leveraging high resolution data on social interactions (16), analyzing detailed influenza transmission datasets (17), and using state-of-the-art modeling approaches (18–24). The lack of a clear indication is mostly due to a shortage of data about the behavior and mixing patterns of the population as a whole while such strategies are in place.

Previous studies have focused on the analysis of the contact patterns of the population during weekends and holidays. In particular, the analysis of data from a large-scale survey on human-mixing patterns relevant for the transmission of infectious diseases conducted in eight European countries (25) shows that the reproduction number of airborne infectious diseases may decrease up to 20% from workdays to weekends and from regular to holiday periods (26). A modeling study based on the same data found a mitigation effect of the Christmas holidays on influenza spread (27). Similarly, the analysis of influenza sentinel data revealed a 24% reduction in child-to-child transmission during school holidays compared with in-school days (17). Other studies have focused on the student population only. They have highlighted a reduction of up to 65% in face-to-face conversational contacts recollected by secondary school students during periods when schools are closed (28), provided an accurate description of the social interactions of students at school (16), and clarified the patterns of influenza transmission between students (29). However, to estimate the effect of reactive school-closure strategies, specific data on population-level human-mixing patterns collected precisely during the implementation of such policies are needed. In fact, it is far from guaranteed that during the application of a policy entailing short-lasting unscheduled school closures, the (student and nonstudent) population will behave in the same way as during weekends or vacation periods.

In Russia, gradual school-closure policies are performed every year to mitigate the spread of seasonal influenza (a description of the policy can be found in the next section). This offers us the invaluable chance to directly measure the variation in human contact patterns caused by the policy. To do so, we performed a diary-based contact survey (25, 30) in the city of Tomsk, Russia during the 2015 to 2016 influenza season by recruiting students of two schools and their household members. Data were collected when the schools were regularly open and when students could not attend school because their classes were closed as a consequence of the school-closure policy.

By integrating the collected contact survey data with publicly available micro and macro sociodemographic data, we develop a highly detailed time-varying contact network based on an innovative hybrid survey-modeling framework. This approach enables us to perform computer simulations of the social interactions between individuals to estimate human-mixing patterns at the population level and simulate influenza spread. Indeed, this goes beyond the state-of-the-art data-driven, network, and multiplex network models of infectious diseases transmission, which are based either on an homogenous mixing assumption within entire populations or within the particular settings where transmission can occur (e.g., households, schools) (18, 19, 23, 31, 32). Our results provide evidence of the influenza mitigation impact of school-closure policies.

Results

Contact Pattern.

We perform a diary-based contact survey, to quantify human-mixing patterns during regular school/work days and when the school-closure strategy is implemented. The school-closure strategy implemented in Russia works as follows. Once the influenza epidemic has been declared, students showing acute respiratory infection (ARI) symptoms are not allowed to enter the school and the number of absent students is monitored daily. If the fraction of absent students of a class exceeds a certain threshold, then the class is closed for 1 wk; if the fraction of absent students of the entire school exceeds a certain threshold, then the entire school is closed for 1 wk. A description of the policy is reported in Box 1. An overview of the survey methodology is reported in Materials and Methods, and details are reported in SI Appendix, section 1. We analyzed a total of 7,009 contacts, reported by the 450 study participants (see Table 1). A contact is defined as a two-way conversation of at least five words in the physical presence of another person (25, 30).

Table 1.

Number of contacts and sample size by characteristics of study participant

Category	School/Class Open		School/Class Closed
	N	Mean	N	Mean	Difference
	(%)	(95% CI)	(%)	(95% CI)	(P*)
Student	259	14.2	100	6.7	7.5
	(57.6)	(13.0 to 15.3)	(55.2)	(5.9 to 7.5)	(<0.0001)
Adult (worker or not employed)	191	10.4	81	8.4	2.0
	(42.4)	(9.3 to 11.6)	(44.8)	(7.2 to 9.6)	(0.018)
Worker	158	11.2	70	8.7	2.5
	(35.1)	(9.8 to 12.6)	(38.7)	(7.3 to 10.1)	(0.012)
Not employed	33	6.9	11	6.4	0.5
	(7.3)	(5.2 to 8.5)	(6.1)	(4.5 to 8.2)	(0.678)
Total	450	12.6	181	7.4	5.2
	(100.0)	(11.7 to 13.4)	(100.0)	(6.7 to 8.1)	(<0.0001)

^*Two-sided t test.

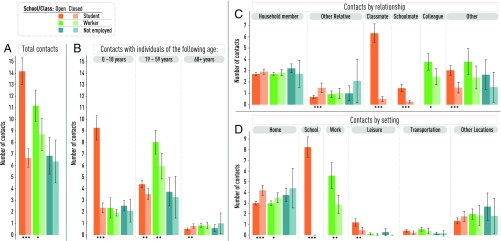
We find that the number of contacts is highly dependent on the activity status of the participant, which is categorized as student, worker, or not employed nonstudent (for simplicity also referred as not employed—e.g., stay-at-home parents and retired individuals). The number of contacts also heavily depends on the school/class status (i.e., either regularly open or closed as a result of the school-closure policy). Results are summarized in Table 1 and Fig. 1A. When the school-closure strategy is not in place, students are the category showing the highest number of contacts per day with 14.2 contacts (95% CI: 13.0 to 15.3), followed by workers with 11.2 contacts (95% CI: 9.8 to 12.6), and not employed nonstudents with 6.9 contacts (95% CI: 5.2 to 8.5). When the school-closure strategy is in place, the estimated number of contacts highly differs for students not attending school as a consequence of the strategy and for their household members. In particular, students and workers show a statistically significant decline in their number of contacts. For students, the average daily number of contacts drops to 6.7 (95% CI: 5.9 to 7.5; 53% reduction), becoming similar to the value observed for not employed nonstudents. For workers, it drops to 8.7 contacts per day (95% CI: 7.3 to 10.1; 19% reduction). This reduction is caused by two factors: first, the number of workers reporting zero contacts at work increased by 23.2%; second, for the workers who reported at least one contact in the workplace, the number of contacts decreased by 1.5 contacts per day. Not employed individuals show a slight (not statistically significant) reduction in their number of contacts as well.

Fig. 1.

Number of contacts. (A) Mean daily number of contacts by activity status of the participant (i.e., student, worker, or not employed) and school/class status (i.e., either open or closed as a result of the school-closure policy) based on the contact survey data. The asterisks below the bars denote the level of significance of the reduction (two-sided t test): ^* P <0.05, ^** P <0.01, ^*** P <0.001. (B) As in A, but split by age group of the contacted individual. (C) As in A, but split by relation between the participant and the contact. (D) As in A, but split by location where the reported contact took place.

By breaking down contacts by the age of the contacted individuals (Fig. 1B), we find that the school-closure policies induced students to significantly reduce their number of contacts with individuals aged 0 to 18 y (75% reduction) and 19 to 59 y (20% reduction), while simultaneously increasing contacts with individuals aged 60 y or more (52% increase), although their absolute value remains low (i.e., less than one contact per day). In parallel, workers show a 26% reduction of contacts with individuals aged 19 to 59 y.

The analysis of the locations where contacts took place and the relationships among the contacted individuals help to explain the aforementioned patterns (Fig. 1 C and D). In particular, the drop in the number of contacts between students and individuals aged 0 to 18 y is mostly ascribable to the dramatic decrease in the number of contacts with classmates (decreasing from 6.3 contacts per day to 0.5) and schoolmates (decreasing from 1.5 contacts per day to 0.3). Students also show a significant decrease in the number of contacts during leisure activities (61% decrease) and in the number of contacts with unrelated individuals (50% decrease). On the other hand, they show a statistically significant increase in the number of contacts at home (40% increase) and in the number of contacts with other (nonhousehold member) relatives (119% increase). The school-closure strategy also alters the behavior of the adult working population. Workers who are members of households directly affected by the school-closure strategy show a significant decrease in the number of contacts with work colleagues (regardless of the social setting where the contact occurs; 35% reduction) and, in particular, contacts taking place at the workplace (i.e., including both work colleagues and other individuals they can contact in the workplace such as customers; 48% reduction). The strategy appears not to significantly affect the contact patterns of the not employed population.

Contact Network at the Population Level.

The closure of a specific school or class affects mixing patterns not only of the students of that school and of the members of the households where these students live. In fact, the strategy leads to a cascade of indirect effects that should be taken into account to generalize contact survey results at the population level. For instance, we expect to observe a change in the contact pattern within a workplace if one or more employees are members of households having students directly affected by the school-closure strategy. Therefore, we develop a time-varying contact network based on a hybrid survey-modeling framework to estimate to what extent the school-closure policy shapes the mixing patterns of the population. First, we develop a highly detailed synthetic population of 515,202 agents—the number of inhabitants of Tomsk—based on macro- and microlevel sociodemographic data on the Tomsk Oblast population. Second, contacts between individuals (i.e., edges between nodes of the generated network) are simulated as a Markov process based on the distributions of the number of contacts by setting and relationship conditional on the activity status of the respondent, as estimated from the contact survey. An overview of the adopted methodology is reported in Materials and Methods (see SI Appendix, section 2 for details and for a validation of the time-varying contact network).

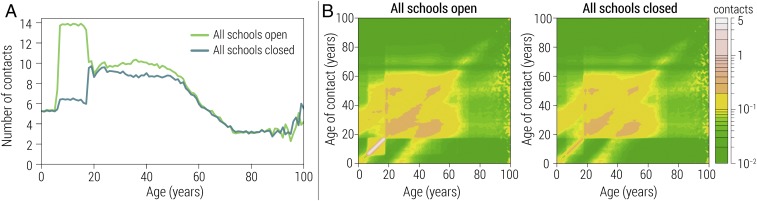
We consider the extreme scenario where all schools are closed at the same time to illustrate to the maximum effect of the school-closure policy in shaping mixing patterns of the population. Our modeling analysis shows a reduction of about eight contacts per day for school-age individuals and about one contact per day for adults (individuals aged 25 to 54 y), while we find no substantial variation for other age groups (Fig. 2A).

Fig. 2.

Estimated number of contacts at the population level. (A) Estimated mean daily number of contacts by age by assuming that all schools are either regularly open or closed at the same time as a consequence of the school-closure policy. (B) Estimated mean daily number of contacts by age of contact and contacted individuals, by assuming that all schools are regularly open (Left) and that all schools are closed at the same time as a consequence of the school-closure policy (Right).

By breaking down contacts by the age of contacting and contacted individuals, we can visualize the mixing patterns in the form of contact matrices by age (Fig. 2B). We find that the contact matrix shows three main diagonals representing contacts between household members. These diagonals are not affected by the school-closure policy. The central part of the matrix (i.e., contacts between individuals aged 19 to 60 y) shows a slight reduction when schools are closed due to the decrease in the number of contacts in the workplace. The most evident change occurs for school-age individuals—in Russia students generally attend the same school building from the age of 6 to 17 y. The bottom left part of the matrix, which includes contacts between schoolmates, drops from more than one contact per day to about zero when all schools are closed at the same time. Even more evident is the effect on contacts between classmates, which dominates the contact matrix when schools are open and decreases from about six to less than one contact per day when schools are closed. A reduction in contact between school-age individuals and adults is rather evident as well, implying that the increase of contacts with other relatives taking care of children during the school closure is not enough to offset the decrease of contacts with adults in the school setting (e.g., teachers and other school employees), during leisure time, and on means of transportation.

The 2015 to 2016 Influenza Season.

We develop a dynamical model of influenza transmission over our time-varying contact network. The model is at the individual-level and explicitly considers all households, students, schools, and so on, thus allowing the mechanistic simulation of school-closure policies. See Materials and Methods and SI Appendix, sections 3 and 4 for details. We validate the model against empirical epidemiological and social data collected during the 2015 to 2016 influenza season (i.e., the season when the contact survey has been conducted). A vaccination campaign covering about 30% of the population had been carried out in September to November 2015. Thereafter, influenza started to spread in the region in early December, before the winter vacations, and ended after the spring vacations. Moreover, in the week of February 8 to February 16, 2016, extraordinary measures were implemented, including, among others, the dismissal of children in educational institutions of the region, as well as the prohibition of mass cultural, sport, and other events. Details are reported in SI Appendix, section 4.4.

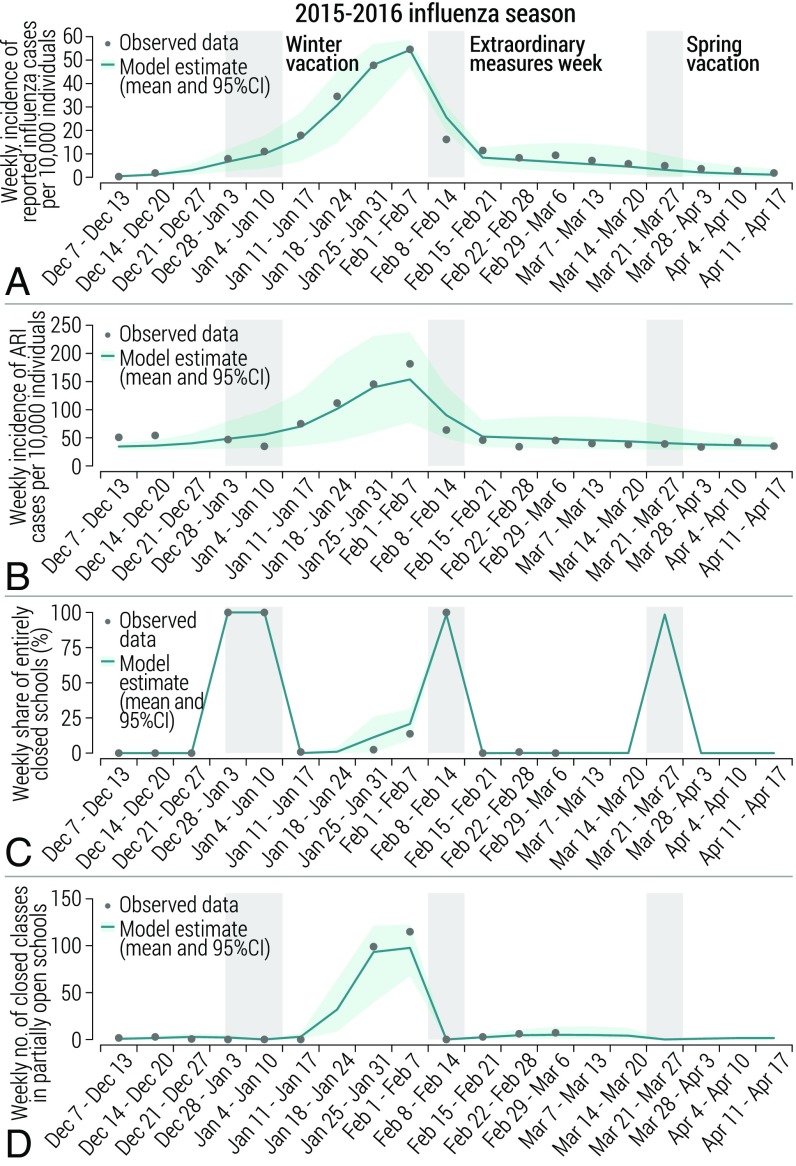
We use the 2015 to 2016 influenza season as a benchmark to assess the reliability of our model. In particular, we validate the output of the model against four temporal indicators of special interest for this study: (i) the reported weekly incidence of influenza cases (calculated as the weekly incidence of ARI cases multiplied by the share of samples testing positive for influenza in that week), (ii) the weekly incidence of ARI cases, (iii) the weekly number of schools that are entirely closed, and (iv) the weekly number of classes that are closed in partially open schools. The model is able to capture the observed dynamics for all of the considered indicators (Fig. 3). In particular, the mean absolute error for the weekly incidence of influenza cases per 10,000 individuals is 1.8 and all data-points fall well inside the 95% CI, except for the week when extraordinary measures were in place (Fig. 3A). However, a lower reporting rate was likely observed during the week when extraordinary measures were in place. The model is also able to capture the temporal trend of the ARI incidence, including the initial and final phase of the influenza season, characterized by a negligible number of influenza cases and nearly constant ARI incidence (of about 50 cases per 10,000 individuals) (Fig. 3B). We find a good agreement in the weekly number of schools that are entirely closed (Fig. 3C) and of the weekly number of classes that are closed in partially open schools as an effect of the reactive school-closure strategy (Fig. 3D). Moreover, we estimate the effective reproduction number of influenza (i.e., the average number of secondary infections generated by a typical case) to be 1.24 (95% CI: 1.20 to 1.27), in agreement with the literature for seasonal influenza (33). We estimate that on average one out of 3.5 influenza symptomatic cases are reported to the surveillance system, in agreement with the values (one out of 3.1 to 3.7) found in the literature (34).

Fig. 3.

The 2015 to 2016 influenza season. (A) Weekly incidence of reported influenza cases as observed in the data (calculated as the weekly ARI incidence multiplied by the share of collected samples testing positive for influenza in that week) and as estimated by the model (calculated as the incidence of symptomatic cases multiplied by the reporting rate). (B) Weekly incidence of ARI cases as observed in the data and as estimated by the model. (C) Weekly share of schools that are entirely closed as observed in the data and as estimated by the model. (D) Weekly number of closed classes in partially open schools as observed in the data and as estimated by the model.

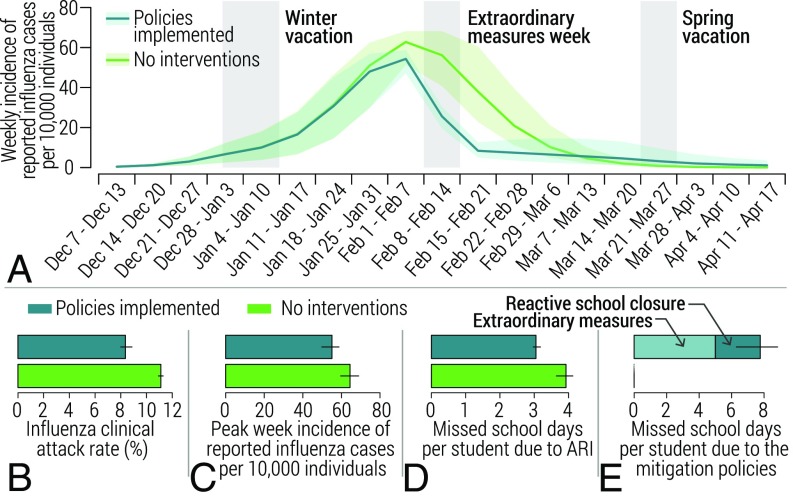
We use the calibrated model to provide a counterfactual scenario where we assume that no mitigation measures were in place during the 2015 to 2016 influenza season. Our results show that the implemented measures had a remarkable effect in altering the temporal dynamics of the epidemic and in mitigating influenza spread (Fig. 4A). In particular, we estimate that, on average, in the absence of any reactive mitigation strategies, the influenza attack rate would have been 33.0% larger (Fig. 4B), the peak week incidence of symptomatic cases would have been 17.1% larger (Fig. 4C), and the number of school days missed per student due to ARI would have been 28.7% larger (Fig. 4D). On the other hand, the implemented measures led students to miss on average 7.8 school days: 5 linked to the extraordinary measures that were in place for 1 wk and 2.8 d linked to the reactive school-closure strategy (Fig. 4E). Additional counterfactual scenarios are discussed in SI Appendix, section 5.7.

Fig. 4.

Effect of the mitigation policies implemented during the 2015 to 2016 influenza season. (A) Weekly incidence of reported influenza cases as estimated by the calibrated model accounting for the performed mitigation policies and as resulting from the simulation of a counterfactual scenario not accounting for the interventions. Note that both scenarios account for winter and spring school vacations. (B) Estimated influenza clinical attack rate (which accounts for all symptomatic cases of influenza) in the two aforementioned scenarios. (C) As in B, but for the peak week incidence of reported influenza cases. (D) As in B, but for the number of school days missed per student due to ARI. (E) As in B, but for the number of school days missed per student due to the implementation of the mitigation policies.

Impact of School-Closure Policies.

The fundamental epidemiological parameter controlling the dynamics of the system is the effective reproduction number $R_e$ or, if the population is fully susceptible (as is generally the case for pandemics), the basic reproduction number $R_0$. We explore a wide spectrum of values of $R_0$ (namely, 1.2 to 2.0), which extends beyond the maximum value for seasonal influenza ($R_e$ usually $\le 1.4$) (33).

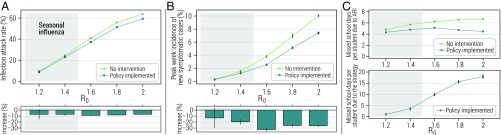
In the absence of any intervention, we estimate the infection attack rate (which includes all influenza infections, independently whether an individual developed symptoms or not) and the peak week incidences of symptomatic cases (an important indicator of the maximum stress that the health system and the work force endures as a consequence of an epidemic) to highly depend on $R_0$ (Fig. 5 A and B). Similarly, the estimated number of school days missed because of either influenza symptomatic infection or other ARI increases with $R_0$, although the pattern is less marked (Fig. 5C). For all analyzed values of $R_0$, a reactive school-closure strategy mimicking policy currently implemented in Russia leads to a reduction of the infection attack rate of about 8 to 10% (Fig. 5A). The strategy has a much larger effect (up to more than 30%) in reducing the peak week incidence (Fig. 5B). We also observe a slight decrease in the number of school days missed due to ARI (Fig. 5C, Top). The number of missed school days per student due to the strategy is moderate for low values of $R_0$ (e.g., less than 4 d for $R_0\le 1.4$), while it exceeds 2 wk for $R_0\ge 1.8$ (Fig. 5C, Bottom).

Fig. 5.

Impact of school-closure policies. (A) Estimated mean infection attack rate of an influenza epidemic for different values of $R_0$ when the epidemic is left untreated and when the Russian school-closure policy is implemented. The small vertical lines represent 95% CI. Bottom shows the estimated mean percentage increase when the policy is implemented. Vertical lines represent standard errors. (B) As in A, but for the peak week incidence of symptomatic cases. (C) As in A, Top, but for the number of school days missed per student due to influenza infection or other ARI over the entire course of the influenza season. Bottom shows the estimated number of school days missed per student due to the school-closure policy.

Our estimates of the impact of the school-closure policies are quite stable with respect to variations on protocol used to declare the start of the influenza epidemic and to variations of the infectiousness of symptomatic infectious individuals relative to asymptomatic ones. On the other hand, the larger the student absenteeism rate induced by noninfluenza ARI or the fraction of influenza infections leading to symptoms (such as fever), the larger the effect of the policy. Results of these sensitivity analyses are reported in SI Appendix, section 5. In addition, we performed a sensitivity analysis on the effect of preschools/kindergartens. This analysis shows that the estimated effect of reactive school-closure strategies remains stable under different hypotheses on the mixing pattern of children attending preschools/kindergartens (SI Appendix, section 6).

Discussion

Previous studies investigated the changes in human-mixing patterns during vacations (26, 27), analyzed in detail student contact patterns at school (16, 28, 29), and showed the effect of school vacations in shaping the spread of influenza (8–13). However, our results provide a quantitative assessment of human-mixing patterns during reactive school-closure strategies and highlight their effect in shaping the network of social interactions of the (student and nonstudent) population. We find that the policy induces a marked drop in the overall number of daily interactions. Indeed, this is induced by the dramatic reduction of the number of contacts of students with their classmates, other schoolmates, and other unspecified individuals, along with the moderate decrease in the number of contacts between workers and their colleagues. This combined decrease is not offset by the mild increase in the number of contacts between students and nonhousehold relatives, suggesting that school-closure policies may contribute to limiting influenza spread.

We perform a modeling study entailing the measured behavior of students and other members of their families in the days when a reactive school-closure strategy is implemented. Our results quantify the effect of the reactive school-closure policy implemented during the 2015 to 2016 influenza season in Tomsk. We find that the implemented measures greatly reduced the impact of the epidemic (one out of three cases is estimated to be averted). More generally, we find that for values of the reproduction number typical of seasonal influenza (i.e., up to 1.4), the reactive school-closure policy has a positive mitigation effect at a relatively moderate number of additional missed school days per students (generally lower than 4 d). Additional work is needed to identify the optimal school-closure policies (e.g., for how long classes/schools have to close, which student absenteeism thresholds triggering the closures to use) and under which circumstances reactive school closures are cost-effective. In particular, such a modeling exercise should take into account all direct and indirect costs associated with the illness such as the cost of the treatment (including rare but expensive complications), the risk of death, and the loss of human capital (e.g., measured as school days missed for student and loss of productivity for workers) (35).

The growing number of contact surveys performed across the globe (25, 30, 36–44) and the availability of detailed micro- and/or macro-level socio-demographic data for nearly every country of the world allow the extension of the introduced modeling framework to several other countries. Moreover, the definition of contact that we adopted (i.e., holding a conversation in the physical presence of another) is the general standard for the analysis of airborne infectious diseases. As such, our framework has a much wider scope than the study of influenza in one specific region.

Finally, as there are no available data to compare our results with, we must remark that it is impossible to know to what extent our findings on mixing patterns during the implementation of the school-closure policy applies to other locations and countries. For instance, the way workers may be taking time off from work is culturally specific and the population sampled to perform the contact survey may not be representative for other locations. As a consequence, it is also unclear to what extent the effect of the reactive school-closure policy implemented in Russia would translate to another country.

Conclusion

To provide health decision makers with evidence in favor of or against school-closure policies for the mitigation of influenza pandemics and epidemics, comprehensive modeling analyses of alternative types of school-closure strategies (e.g., reactive school closure at the city neighborhood level, strategies solely based on monitoring ARI incidence rates) should be conducted along with an economic analysis of the direct and indirect costs of the policies. Our work, nonetheless, provides (i) empirical evidence about the behavior of the (student and nonstudent) population during the implementation of the school-closure strategies and (ii) a hybrid survey-modeling approach to estimate human-mixing patterns and simulate the spread of infectious diseases with an unprecedented level of detail and whose potential in terms of supporting the health decision-making process goes well beyond the assessment of school-closure strategies.

Materials and Methods

Summary of Survey Methodology.

Two schools in Tomsk, Russia were willing to participate in this study and participants were recruited among the students of these two schools and the adult members of their households. One of the schools follows the typical organization of the Russian school system: an entire 11-y cycle with students essentially aged 6 to 17 y. The second school covers a 9-y cycle with students essentially aged 6 to 15 y. Out of the 259 participating students, 234 were recruited from the 11-y cycle school (90.3%) and 25 from the 9-y cycle school (9.7%). The difference in the number of contacts of students between the two schools is not statistically significant (two-side t test, P = 0.61): on average students of the 11-y cycle school have 14.1 (95% CI: 12.9 to 15.3) contacts per day and students of the 9-y cycle school have 15.0 (95% CI: 11.7 to 18.3) contacts. According to Tomsk official administrative records, 80% of the schools of the city follow the 11-y cycle and cover 93% of city school students, while 10% follow the 9-y cycle (4% of city students). Special higher education preparation schools comprise the remaining 10% (3% of city students). The two schools participating in the study are representative for their type of educational cycle in terms of total number of students, average class size, and student-to-teacher ratio (SI Appendix, section 1.2). Moreover, the territories assigned to the two schools have typical characteristics (e.g., household size and national identity) of the city population (SI Appendix, section 1.2).

All participants were asked to fill in a contact diary. The contact diary was divided into the following three sections.

• i)Basic information. We collected information on the activity status (student, worker, or not employed) and age of the study participant, and number and age of all household members. Note that no other information (e.g., sex, education level) of the participants were collected due to concerns about individual identifiability brought up at an introductory meeting with the schools’ principals held during the study design phase.
• ii)Contact pattern for a regular school/work day. Student participants were instructed to fill in this section on a day (from Monday to Friday) when they regularly attended school. Worker participants were similarly instructed to fill in this section on a day when they did not miss work. We collected information about the number and characteristics of each contact made during that day. In particular, for each contacted individual, participants reported the age (or the age bracket, if the exact age of the contacted person was unknown), setting where the contact took place (home, school, workplace, leisure, means of transportation, other), and relationship with the contacted individual (household member, other relative, classmate, other schoolmate, work colleague, other).
• iii)Contact pattern when the strategy is in place. Student participants were instructed to fill in this section on a day (from Monday to Friday) when they do not attend school because their classes or the entire school are closed as a consequence of the school-closure policy. Nonstudent participants filled in this section of the diary on a day when the student member of their households could not attend school as a consequence of the school-closure strategy.

Before the start of the data-collection phase, study participants were orally trained on how to fill in the diary. Detailed information on the contact diaries can be found in SI Appendix, section 1, along with the original template of the diary (SI Appendix, section 7). Data were collected within the research initiative ContactPatterns (www.contact-patterns.org) and individual contact diaries are openly available from ref. 45.

Ethics Statement.

In accordance with Russian regulations, all participants (or parents/legal guardians for underage individuals) signed an informed consent agreement. The study was approved by the Ethical Committee of the Siberian State Medical University (Protocol 5168/I).

Synthetic Population.

We leverage public sources of macrolevel (e.g., census) and microlevel (e.g., household surveys) data to construct a synthetic population of the city of Tomsk. Each agent of the synthetic population corresponds to an individual in the real population. Each agent has an associated age, belongs to a certain household (whose size and composition is based on actual data), and attends a certain school if she/he is a student or a workplace if she/he is a worker. School and workplace sizes are derived from actual data. Students of each school are further stratified in grades and classes depending on their age, and the proper number of teachers is assigned to each school to comply with teacher-to-student ratio data. The synthetic population enables us to characterize four different social settings where contacts can occur (i.e., home, school, workplace, general community/other setting) and six relations (i.e., household member, schoolmate, classmate, teacher, work colleague, other). The resulting synthetic population has been validated against independent data. Details in SI Appendix, section 2).

Time-Varying Contact Network.

We use the developed synthetic population to perform stochastic simulations on the daily contacts between individuals. This allows us to generalize the results of the survey, which, by design, includes only households having students.

In particular, we leverage the contact survey data to estimate distributions of the daily number of contacts between individuals conditional on the activity status of the individual, the setting where the interaction occurs (we consider the four settings available in the synthetic population), and the relationship with the contacted individual (we consider the five relations available in the synthetic population, where “other individuals” are further divided into individuals aged 0 to 17 and 18+ y). The resulting conditional distributions can be denoted as $B\left(e;l,r\right)$, where $e=\left\{\text{student},\text{worker},\text{not employed}\right\}$ represents the activity status of the individual responsible for the contact, $l=\left\{\text{home},\text{school},\text{workplace},\text{general community}\right\}$ represents the setting where the contact occurs, and $r=\left\{\text{household member},\text{schoolmate},\text{classmate},\text{teacher},\text{work}\hspace{0.17em}\text{colleague},\text{other0}-17,\text{other}18+\right\}$ represents the relationship to the contacted individual. Note that the class worker includes the special case of teachers, for which different distributions are used.

At each time step of the simulation (corresponding to 1 d) and for each individual, we stochastically determine the contacts (i.e., the edges of the network) with individuals in each setting and for each relation by performing a random sampling from the proper conditional distributions. For instance, if agent $i$ is a worker, then we sample the number of contacts that $i$ has with his work colleagues in the general community from $B\left(\text{worker};\text{general community},\text{work colleague}\right)$. Basically, this Markov process defines a time-varying network of contacts. Details are reported in SI Appendix, section 2.

Influenza Transmission Model.

On top of the time-varying contact network, we develop a mechanistic model of influenza transmission at the individual level. The model enables us to simulate the diffusion of influenza in the population and estimate the impact of school-closure policies in mitigating influenza spread. Briefly, influenza transmission is simulated as a stochastic SLIAR (susceptible, latent, infectious symptomatic, infectious asymptomatic, removed) model. Essentially, given an edge between a susceptible node $i$ and an infectious (either symptomatic or asymptomatic) node $j$, the susceptible individual can acquire the infection with probability $p_i=\beta \sigma \left(a_i\right)$, where $\beta$ is the influenza transmission rate per contact, and $\sigma \left(a_i\right)$ is the susceptibility to infection that depends on the age of the individual, $a_i$. By sampling from a Bernoulli distribution of probability $p_i$ we stochastically determine whether individual $i$ has been infected and thus she/he proceeds to the latent compartment, or if she/he remains in the susceptible status. Latent individuals are not able to transmit the infection and after an average time of 1.5 d (46) (the latent period) move either to the symptomatic infectious stage with probability $\rho =0.37$ (47) or to the asymptomatic infectious stage with probability $1-\rho$. Infectious individuals, either symptomatic or asymptomatic, move to the removed stage after an average of 1.3 d, in such a way that the generation time (i.e., the interval of time between two generations of cases) is on average 2.8 d (48). See SI Appendix, section 3 for details.

By analyzing seroprevalence data collected before and right after the 2009 H1N1 influenza pandemic, we estimated age-specific susceptibility to infection rates specific for the Russian population (SI Appendix, section 4.3). Values of the transmission rate were determined in such a way that $R_0$ is in the range of 1.2 to 2 (33). Symptomatic and asymptomatic individuals are assumed to have the same level of infectiousness. We performed a sensitivity analysis on this parameter (SI Appendix, section 5).

The explicit representation of each individual, class, and school allows for the simulation of school-closure policies, including the one currently in use in Russia (Box 1), in a mechanistic way (SI Appendix, section 3). The simulation of the school-closure policy requires a model of student absenteeism rates induced by noninfluenza ARI over time and the identification of a threshold for the declaration of the start of the influenza season. Such information were derived from the analysis of the ARI and influenza data for Russia in six seasons (SI Appendix, section 4).