Significance
Growing evidence suggests that cytoskeleton-mediated transmission of mechanical forces from the extracellular matrix (ECM) to the nucleus alters nuclear mechanics and architecture and these alterations can, in turn, impact the ability of the cell to respond to its mechanical microenvironment by regulating important nuclear functions including gene expression in both normal and diseased cells. Using a chemomechanical model together with micropatterning experiments, we elucidate how the physical properties of the microenvironment impact the properties of the nucleus by regulating the mechanisms through which mechanical forces are directly and indirectly transmitted from the ECM to the nucleus. This information can be used to understand how chromosome configurations are altered in response to changes in nuclear mechanical properties following cues from the microenvironment.
Keywords: nuclear mechanics, mechanotransduction, cell geometry, cytoskeletal mechanics
Abstract
Cells sense mechanical signals from their microenvironment and transduce them to the nucleus to regulate gene expression programs. To elucidate the physical mechanisms involved in this regulation, we developed an active 3D chemomechanical model to describe the three-way feedback between the adhesions, the cytoskeleton, and the nucleus. The model shows local tensile stresses generated at the interface of the cell and the extracellular matrix regulate the properties of the nucleus, including nuclear morphology, levels of lamin A,C, and histone deacetylation, as these tensile stresses 1) are transmitted to the nucleus through cytoskeletal physical links and 2) trigger an actomyosin-dependent shuttling of epigenetic factors. We then show how cell geometric constraints affect the local tensile stresses and subsequently the three-way feedback and induce cytoskeleton-mediated alterations in the properties of the nucleus such as nuclear lamina softening, chromatin stiffening, nuclear lamina invaginations, increase in nuclear height, and shrinkage of nuclear volume. We predict a phase diagram that describes how the disruption of cytoskeletal components impacts the feedback and subsequently induce contractility-dependent alterations in the properties of the nucleus. Our simulations show that these changes in contractility levels can be also used as predictors of nucleocytoplasmic shuttling of transcription factors and the level of chromatin condensation. The predictions are experimentally validated by studying the properties of nuclei of fibroblasts on micropatterned substrates with different shapes and areas.
Cells are known to respond to external physical signals by regulating the physical properties of their cytoskeletal structures (1). In addition to the cytoskeleton, recent studies show that external physical signals can also alter the physical properties of the nucleus through (i) cytoskeletal physical links (e.g., perinuclear stress fibers) that transmit mechanical stresses from cell anchorages to the nucleus (2) and (ii) a contractility-dependent cascade of biochemical pathways that changes the chromatin structure by nucleocytoplasmic translocation of epigenetic factors (3). Cytoskeleton-mediated changes in the physical properties of the nucleus have been observed to be correlated with alterations in nuclear architecture and gene expression (4). For example, it has been observed that compressive forces on fibroblast cells reduce actomyosin contractility, depolymerize apical actin filaments, and cause histone deacetylation, which has been observed to be correlated with chromatin condensation, reduction of transcriptional activity, and inducing quiescence in fibroblasts (5). In addition to chromatin, cytoskeleton-mediated changes in the physical properties of the nucleus can be induced by alterations in the mechanical properties of the nuclear envelope. For example, lamin A,C levels in mesenchymal stem cells have been observed to increase with increasing myosin II contractility resulting from increases in substrate stiffness (6).
Recent experimental studies show that alterations in the physical properties of the nucleus can, in turn, induce changes in the cytoskeletal organization. For example, it was observed that lamin A,C-deficient mouse embryonic fibroblast cells lack apical stress fibers (7) and show lower contractility (8). Furthermore, partial knockdown of lamin A,C in mesenchymal stem cells was observed to be correlated with a reduction in myosin II contractility (9). Much of what we know about these reciprocal relationships are derived from qualitative observations; mathematical models that describe the three-way coupling between the focal adhesions, the cytoskeleton, and the nucleus can provide a predictive framework for elucidating how forces generated at the cell–extracellular matrix (ECM) interface activate nuclear signal transduction pathways. At present, it remains largely unknown how the physical properties of the ECM impact the three-way coupling and subsequently alter the generation, transition, and distribution of mechanical stresses that induce the changes in the physical properties of the nucleus.
To study how the physical properties of the microenvironment including cell substrate shape, area, and stiffness impact the properties of the nucleus, we developed a 3D chemomechanical model that accounts for the dynamic reciprocities between the adhesions, the cytoskeleton, and the nucleus. We show that cell geometry controls this feedback loop by regulating the local tensile stresses that are generated at the mature focal adhesions. We then elucidate how these stresses regulate nuclear morphology, levels of lamin A,C, and histone deacetylation by altering actomyosin contractility level and reorganizing the cytoskeleton. Finally, we study how disruption of cytoskeletal components can affect the components of the feedback loop and subsequently alter nuclear morphology and mechanics.
Results
Cell Geometric Constraints Regulate Cell Contractility, Actin Organization, and Formation of Focal Adhesions.
To study the effect of cell geometric constraints on contractility, actin organization, and focal adhesions, we first study NIH 3T3 mouse fibroblast cells cultured on two extreme geometries of fibronectin-coated micropatterns: 1) a rectangle with an aspect ratio of 1:5 and a substrate surface area of 1,600 µm2 (large and elongated geometry) and 2) a circle with a substrate surface area of 500 µm2 (small and symmetric geometry). As shown in SI Appendix, Fig. S1, both cells are subject to the same initial conditions: 1) The cell contractility and the cytoskeletal stiffness in both cells are initially uniform (independent of spatial location) and isotropic (independent of direction) and the cell contractility and stiffness are initially the same everywhere in the cytoplasm with no preferential alignment of phosphorylated myosin motor dipoles and actin filaments; 2) both cells have the same initial density of phosphorylated myosin motors and thus the same magnitude of initial (isotropic) contractility; 3) the nucleus is initially assumed to be a sphere; and 4) the stiffness of the adhesion layer is initially low (immature focal adhesions and weak connections between the cell and its substrate) and uniform.
We show that for an elongated substrate geometry (Fig. 1A), the initial isotropic contractility of the cell generates an anisotropic stress field, particularly at the cell boundaries (SI Appendix, Figs. S2 and S3) where the adhesion layer experiences higher tensile stresses at the two ends along the long axis of the cell (SI Appendix, Fig. S4). In response to these tensile stresses, the stiffness of the connections to the substrate (adhesion layer) increases at the two ends, representing the stress-dependent formation of mature focal adhesions observed in our experiments (Fig. 2B). The local tensile stresses that arise at the mature focal adhesions activate mechanotransductive feedback mechanisms that are controlled by stress-activated signaling pathways such as the Ca2+ and the Rho–Rock pathways (10, 11) (Fig. 1B). As a result, the cell contractility will be no longer isotropic (SI Appendix, Fig. S5) since these stress-activated signaling pathways promote phosphorylation of myosin motors (SI Appendix, Fig. S6) which leads to an increase in the density of force dipoles and subsequently the cell contractility along the direction of the tensile stresses. In addition to , the stress in the actin filament network and the cytoskeletal stiffness also change in an orientation-dependent manner in the presence of the anisotropic tensile stress field (Fig. 1 C and D and SI Appendix, Fig. S7). SI Appendix, Figs. S2 and S3 show the polarization of the stress in the actin filament network as both cell contractility and substrate resistance increase along the long axis of the cell. This polarization of is accompanied by cytoskeletal stiffening in the direction of the maximum tensile principal stress representing the formation of stress fibers in this direction (Fig. 2A and Movie S1). The prediction for the orientation of stress fibers in the direction of the maximum principal stress is found to be consistent with our experimental observations. For example, the model predicts the formation of stress fibers along the long axis of the cell in the apical plane while stress fibers are interestingly formed at 45° at the corners of the basal plane (Fig. 2F), which supports our assumption that stress fibers are formed in the direction of the maximum principal stress.
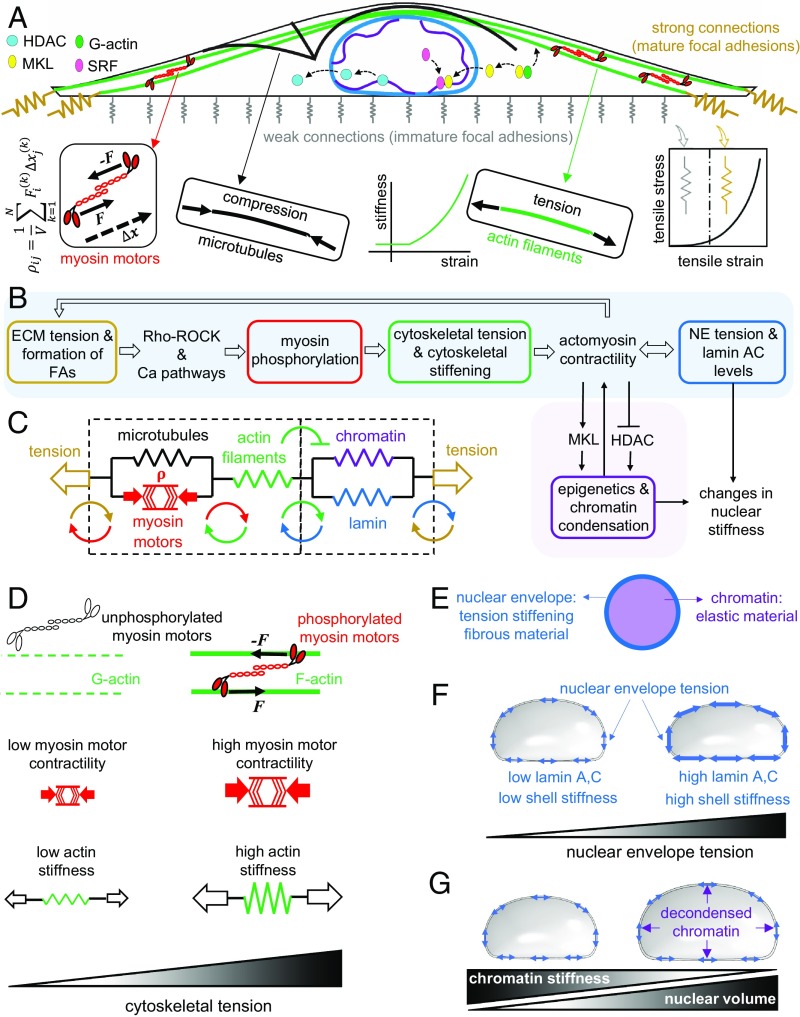
Fig. 1.
A mechanochemical feedback model for cytoskeletal and nuclear mechanics. A contractile cell on a large and elongated adhesive substrate (A). The model is composed of 1) the focal adhesions, 2) the cytoskeleton, and 3) the nucleus. When the tensile stress exerted by the contractile cell to the adhesion layer exceeds a certain threshold, the stiffness of the connections to the substrate increases and mature focal adhesions are formed. The formation of mature focal adhesions (at the two ends for elongated substrate geometries) generates higher resistance against cell contraction and subsequently higher cytoskeletal tension. The tensile stresses arise at the mature focal adhesions activate the Ca2+ and the Rho–Rock signaling pathways which promote cell contractility through phosphorylation of myosin molecular motors (B). The increase in cell contractility leads to higher compression in microtubules and higher tension in actin filaments (C). In addition to the cell contractility , the stiffness of actin filaments in our model increases with tension in an orientation-dependent manner to capture the fact that cells respond to tension by increasing their own stiffness through recruitment and alignment of actin filaments along the direction of the tensile stress (D). The increase in actomyosin contractility alters nuclear morphology and nuclear stiffness through 1) cytoskeletal physical links that transmit the stresses generated at the mature focal adhesions to the nucleus (sky blue path in B) and 2) a cascade of biochemical pathways that changes chromatin stiffness by nucleocytoplasmic shuttling of epigenetic factors (pink path in B). The nuclear envelope (E) is modeled as a filamentous network material (lamin network) which stiffens with tension to capture the fact that lamin A,C level and strain stiffening of the nuclear envelope increase with actomyosin contractility (F), while chromatin is treated as an elastic material (E) whose stiffness increases (decreases) with chromatin condensation (decondensation) in proportion to nuclear level of HDAC predicted by our model (G).
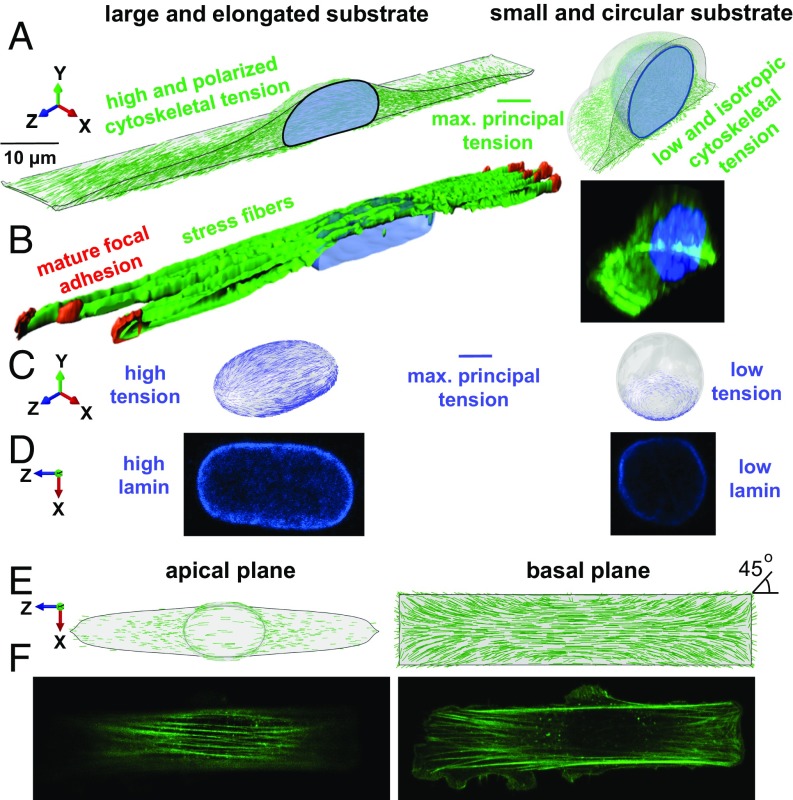
Fig. 2.
Cell geometric constraints regulate cell contractility, actin organization, and nuclear envelope lamina stiffness. (A and B) NIH 3T3 mouse fibroblast cells are cultured on fibronectin-coated micropatterned substrates with two extreme geometries: a rectangle with an aspect ratio of 1:5 and a substrate surface area of 1,600 µm2 (large and elongated substrate geometry), and a circle with a substrate surface area of 500 µm2 (small and circular substrate geometry). Cells on the rectangular substrate have higher and polarized 1) contractility, 2) cytoskeletal tension, and 3) cytoskeletal stiffness leading to a flattened and elongated nuclear morphology (C). As a result, tension is generated in the nuclear envelope lamina of rectangular cells correlated with their higher levels of lamin A,C and nuclear envelope stiffness (D). Stress fibers are formed along the long axis of the cell in the apical plane (E) and at 45° at the corners of the basal plane (F).
On the other hand, our simulations show that when cells are constrained on circular substrates, myosin II-driven tensile stresses are distributed uniformly at the cell periphery leading to the formation of uniform focal adhesions at the cell boundary (12). Compared with the rectangular cell, our model predicts lower and isotropic 1) contractility, 2) cytoskeletal tension, and 3) cytoskeletal stiffness for the circular cell (Fig. 2A, SI Appendix, Fig. S8, and Movie S2); while these predictions are consistent with our experimental observations, actin filaments in the circular substrate geometry are organized in Fig. 2B as short filament networks and mesh-like structures (lower cytoskeletal stiffness). Furthermore, compared with the cells on the rectangular substrate, cells on the circular substrate have lower levels of phosphorylated myosin light chain (p-MLC), which is a well-established marker for cytoskeletal myosin II contractility (SI Appendix, Fig. S9).
As shown by our simulations (Fig. 2A) and experiments (Fig. 2B), cells on the rectangular substrate have a significantly different nuclear morphology compared with the cells on the circular pattern. While it remains almost rounded (aspect ratio ≈ 1) in the circular geometry, the nucleus becomes flattened (lower height) and elongated (higher aspect ratio) in the rectangular geometry. Next, we assess whether this actomyosin-dependent alteration in nuclear morphology (from a round in the circular substrate geometry to an elongated and flattened morphology in the rectangular substrate geometry) induces changes in the stiffness of the nuclear envelope.
Tension at the Lateral Side and Curvature at the Poles of the Nucleus Increase with Actomyosin Contractility.
Lamin A,C is an important contributor to the mechanical stiffness of the nuclear envelope. It has been shown that lamin A,C-deficient mouse embryonic fibroblasts (7) and lamin A,C knockout mouse embryonic fibroblasts (2) have increased nuclear deformability and subsequently decreased nuclear stiffness. To investigate how the actomyosin-dependent alteration in nuclear morphology may change the level of lamin A,C, we measure the stiffness of the nuclear envelope in our computational model for both substrate geometries (Fig. 2C).
First, our model shows how the tensile stresses that arise at the mature focal adhesions of the rectangular cell are transmitted to the nucleus (Fig. 1 B and C); the reciprocal relationships between tension-dependent formation of focal adhesions, actomyosin contractility, and cytoskeletal stiffening in our model provide a link between the focal adhesions and the nucleus (formation of stress fibers) through which the myosin II-driven tensile stresses generated at the focal adhesions are transmitted to the nucleus.
Second, our model shows how these tensile stresses regulate nuclear deformation and subsequently nuclear morphology; as previously described, cells on the elongated substrate experience higher cytoskeletal tension along the long axis which stiffens the cytoskeleton in this direction (formation of stress fibers) and imposes significant vertical (SI Appendix, Fig. S10A) and lateral (SI Appendix, Fig. S10B) compressive forces on the nucleus, leading to a flattened and elongated nuclear morphology. The complex traction force field (exerted by the stress fibers on the nuclear envelope) which induces this alteration in nuclear morphology is shown in SI Appendix, Fig. S10 (black arrows). In addition to this inward traction force field, the nuclear envelope also experiences outward mechanical forces from the nuclear interior including 1) the resistance forces due to chromatin deformations regulated by the chromatin elastic modulus and 2) the internal pressure due to fluid content and chromatin decondensation regulated by the Poisson’ ratio and the prestress , respectively, as described in SI Appendix, section 3.2 (Fig. 1 E and G). As the inward forces reduce nuclear height (SI Appendix, Fig. S10A) and width (SI Appendix, Fig. S10B), the nucleus elongates in the direction of the long axis of the cell. The inward and outward forces are balanced by the mechanical resistance of the nuclear envelope (SI Appendix, Fig. S11). The model shows how the nuclear envelope in the rectangular cell is stretched (red arrows in SI Appendix, Fig. S10) as the nucleus deforms from a round to a flattened and elongated geometry. Our simulations show that far from the cap of the nucleus the nuclear envelope is stretched along the long axis of the cell (the z-direction in Fig. 2), while at the cap the nuclear envelope is mainly stretched in the circumferential direction of the X–Z plane. The nuclear envelope, treated as a fibrous material (Fig. 1E), then stiffens as it is stretched, thus capturing the experimentally observed increase of lamin A,C level with actomyosin contractility (13) (Fig. 1F). In contrast, our simulations show that the nucleus on the circular substrate experiences lower and isotropic tension (Fig. 2C) leading to an almost round morphology and lower nuclear envelope lamina stiffness.
To investigate how fibroblasts respond to these mechanical forces generated in the nuclear envelope, we measure lamin A,C levels in both substrate geometries based on immunofluorescence staining. Our experiments show that cells on the rectangular substrate have significantly higher levels of lamin A,C (Fig. 2D). This indicates that the nucleoskeletal protein lamin A,C increases in proportion to tension to stiffen the nuclear envelope lamina network perhaps to protect the nuclear membrane from rupture (6). Interestingly, our simulations show that the maximum tensile strain in the nuclear envelope occurs at the lateral side (SI Appendix, Fig. S12), while nuclear rupture is often observed at the poles (and not at the side) where the curvature is high (14, 15) (SI Appendix, Fig. S13). In the next section, we show that the round nuclear morphology and the observed softening of the nuclear envelope lamina of circular cells can cause invagination of the nucleus by microtubules.
Cell Geometric Constraints Induce Microtubule Associated Nuclear Invaginations.
Cytoskeletal microtubules have been observed to buckle due to the internally generated actomyosin contractile stresses (16), indicating that microtubules are compressively loaded in physiological conditions. This observation has been further supported by the finding that microtubules buckling decreases (increases) when actomyosin contractility decreases (increases) upon treatment with cytochalasin D (thrombin) (17). To study how buckling of microtubules changes with actomyosin contractility, we model microtubules as discrete elastic filaments, emanating from the microtubule organizing center (MTOC), in both circular and rectangular substrates (Fig. 3 A and B). All microtubules are tied together at one end to have the same displacement at that end (MTOC displacement), while the other end extends to the cell membrane (also see SI Appendix, section 8 for more details). Our simulations show that microtubules are compressively loaded by the cell contraction and buckle between the nucleus and the cell membrane in both rectangular and circular substrate geometries. Note that microtubules in living cells may buckle with shorter wavelengths since they are laterally reinforced by their surrounding network of cytoskeletal intermediate filaments and actin microfilaments (16). Interestingly, in the circular cell, we observe that the MTOC indents the nucleus, leading to a nuclear invagination as shown in Fig. 3B. Our simulations show that the MTOC in the rectangular cell is pushed toward the cell boundary by the nucleus (Movie S3), while in the circular cell the MTOC pushes against the nucleus and forms a local indentation in the nucleus (Movie S4). Consistent with these simulations, our experiments show that microtubules can only indent the nuclei of circular cells (Fig. 3D), while they buckle without being able to indent the nuclei of rectangular cells (Fig. 3C). To test whether microtubules are involved in the observed nuclear abnormality (crescent-shaped nuclear morphology), circular cells were treated with nocodazole (an inhibitor of microtubule polymerization). Fig. 3G shows that the disruption of microtubules reduces nuclear invaginations in circular cells supporting our observation that the MTOC pushes against the nucleus and forms a local indentation in the nucleus of circular cells.
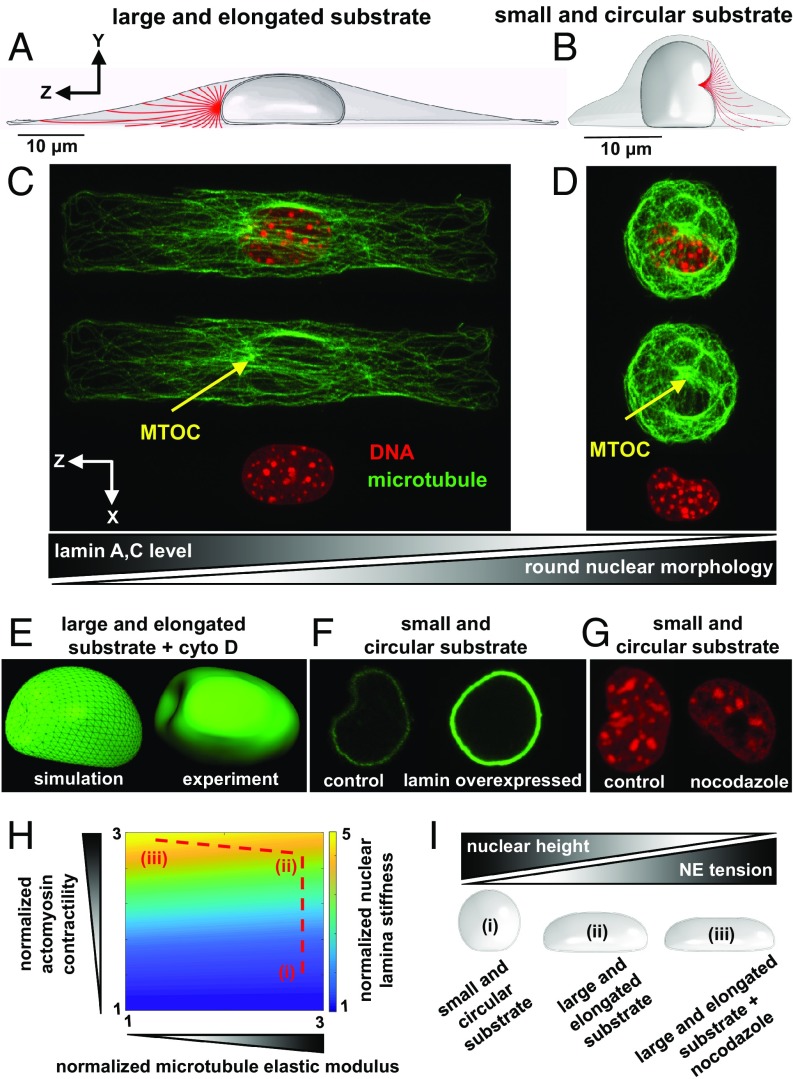
Fig. 3.
Nuclei with low levels of lamin A,C and round morphologies are indented by the MTOC. Microtubules in large and elongated cells buckle without being able to significantly indent the nucleus as the MTOC is pushed toward the cell boundary by the nucleus (A and C). In contrast, cells on small and circular substrates exhibit crescent-shaped nuclear morphologies as the MTOC pushes against the nucleus and forms a local indentation in the nucleus (B and D). Similar to the circular cell, the nucleus is indented by the MTOC when actin filaments are depolymerized in the rectangular cell (E). Overexpression of lamin A,C (F) and nocodazole treatment (G) rescue nuclear invagination in circular cells. Cell geometric constraints and polymerization of microtubules reduce nuclear lamina stiffness by decreasing actomyosin contractility (H); compared with small and circular cells (i), cells on large and elongated substrates (ii) show increased contractility which in turn leads to stiffening of the nuclear envelope lamina network in proportion to actomyosin-driven tension in the nuclear envelope. Depolymerization of microtubules in large and elongated cells (iii) further increases actomyosin contractility and subsequently nuclear lamina stiffness. The actomyosin-driven reduction in nuclear height tenses and stiffens the nuclear envelope lamina network (I).
We also find that the MTOC indentation of the nucleus in the circular cell decreases when we increase nuclear lamina stiffness in our model (SI Appendix, Fig. S14). These simulations suggest that loss of lamin A,C (nuclear lamina stiffness) may play an important role in the experimentally observed nuclear invagination of circular cells. To test this possibility, we overexpress lamin A,C in circular cells using transient transfection before culturing them. Fig. 3F shows that overexpression of lamin A,C partially rescues abnormal nuclear morphology in circular cells.
Our simulations in Fig. 3B show that constraining cells on small and circular substrates leads to rounding and softening of the nucleus, which in turn can cause nuclear invagination by the MTOC. To further test the model prediction, we simulate depolymerization of actin filaments in the rectangular cell in the presence of microtubules. To this end, we set the stiffness of the actin filament network in our simulations, which subsequently leads to a significant reduction in contractility and softening of the cytoskeleton as experimentally reported in refs. 18 and 19. As a result, the compressive forces on the nucleus are removed and the nucleus becomes round. Also, the nuclear lamina tension is released and the nuclear envelope becomes softer (lower level of lamin A,C). Finally, our simulations in Fig. 3E show that, similar to the circular cell, the MTOC forms a local indentation in the nucleus when actin filaments are disrupted in the rectangular cell. To validate the model predictions, fibroblasts on the rectangular substrate were treated with inhibitors of actomyosin contractility. Upon disruption of actin filaments, both p-MLC (SI Appendix, Fig. S15) and lamin A,C (9) levels decrease, nuclear height increases (SI Appendix, Fig. S16), and the MTOC indents the nucleus (Fig. 3E). These experiments support the prediction of the model that loss of nuclear lamina stiffness together with nuclear rounding can cause indentation of the nucleus by the MTOC. Since both nuclear envelope and microtubules are found in our studies to be involved in the determination of nuclear morphology, we next study how nuclear envelope stiffness changes with depolymerization of microtubules.
Microtubule Depolymerization Increases Nuclear Envelope Lamina Stiffness by Promoting Actomyosin Contractility.
Microtubule depolymerization is known to increase cell contractility by promoting phosphorylation of myosin light chain (20). The increase in cell contractility upon depolymerization of microtubules has been shown to require GEF-H1, which is a RhoA-specific guanine nucleotide exchange factor whose activity increases by depolymerization of microtubules (21). The activated GEF-H1, in turn, activates the Rho–Rock signaling pathway which promotes phosphorylation of myosin light chain and subsequently cell contractility.
Microtubules in our active model bear compressive stresses due to the cell contractility . Consistent with experimental studies, depolymerization (polymerization) of microtubules in our model leads to higher (lower) phosphorylation of myosin motors, which in turn increases (decreases) the cell contractility . This is shown in Fig. 3H and SI Appendix, Fig. S17, where a reduction in the bulk modulus of the microtubule network increases the contractility in our model, in agreement with the experimentally observed activation of the Rho–Rock pathway. This increase in (upon depolymerization of microtubules) generates higher tension in the actin filament network, , and subsequently stiffens the actomyosin network (formation of stress fibers), in agreement with ref. 22. Our simulations predict that this increase in actomyosin contractility due to microtubule depolymerization, in turn, decreases nuclear height [in agreement with our experiments (23)] and subsequently stretches and stiffens the nuclear lamina network as shown in Fig. 3H.
Since lamin A,C and chromatin are both important contributors to the mechanical stiffness of the nucleus (2, 24–26), in addition to the nuclear lamina network stiffness, we also measure changes in chromatin structure to investigate whether depolymerization of microtubules causes condensation/decondensation of chromatin in these cells. We find that depolymerization of microtubules upon nocodazole treatment does not cause significant changes in chromatin condensation level (SI Appendix, Fig. S18). Since microtubule depolymerization does not significantly change chromatin stiffness, the predicted nuclear envelope stiffening upon nocodazole treatment is expected to increase the total stiffness of the nucleus. Our finding is consistent with atomic force microscopy experiments on cardiac myocytes where the total stiffness of the nucleus increases with depolymerization of microtubules (27).
To summarize our results on the mechanical interaction between the cytoskeleton and the nucleus, we provide a phase diagram in Fig. 3H to illustrate how both cell geometric constraints (e.g., cells on small and circular geometries) and microtubule polymerization cause nuclear envelope softening by decreasing actomyosin contractility. Note that alterations in the physical properties of the nucleus can, in turn, induce changes in the cytoskeletal organization. In general, cytoskeletal tension and subsequently actomyosin contractility in the model decrease with increasing nuclear deformability (SI Appendix, Fig. S17), which is consistent with experimental observations where lamin A,C-deficient mouse embryonic fibroblast cells lack apical stress fibers (7) and show lower actomyosin contractility (8). Also, note that nuclear tension and lamin A,C have been reported to increase with increasing myosin II contractility resulting from increases in matrix stiffness (9, 13). To test our model, we measured nuclear envelope tension and stiffness in the rectangular cell simulated on deformable substrates with different stiffness. As substrate stiffness increases, our simulations in SI Appendix, Fig. S19 show 1) formation of mature focal adhesions at the two ends (consistent with experimental results in refs. 1 and 28), 2) higher contractility (9), 3) higher cytoskeletal tension and subsequently higher traction forces on the substrate [in agreement with traction force microscopy experiments (29)], 4) formation of stress fibers (30), and 5) stiffening of the cytoskeleton [consistent with atomic force microscopy experiments (30, 31)]. These cytoskeletal changes lead to higher actomyosin-dependent compressive forces on the nucleus and subsequently decreasing nuclear height with increasing substrate stiffness (consistent with experimental observations in ref. 9). Finally, both tension and stiffness in the nuclear envelope increase with matrix stiffness showing the ability of the model to capture the scaling of nuclear envelope tension and matrix stiffness (6).
Substrate Aspect Ratio Induces Cytoskeleton-Mediated Alterations in Nuclear Morphology.
As the circular and rectangular cells have different substrate surface areas and shapes, we test whether shape alone can regulate actin organization and nuclear morphology. To this end, we study fibroblasts cultured on fibronectin-coated micropatterned substrates with the same substrate surface area (1,600 µm2) but various aspect ratios (1:1, 1:3, and 1:5). First, we investigate the orientation of stress fibers and we show that stress fibers are formed in the direction of the maximum principal stress as previously described in Fig. 2 E and F. This can be better observed in the square geometry by comparing our experiments in Fig. 4D with our simulations in Fig. 4E.
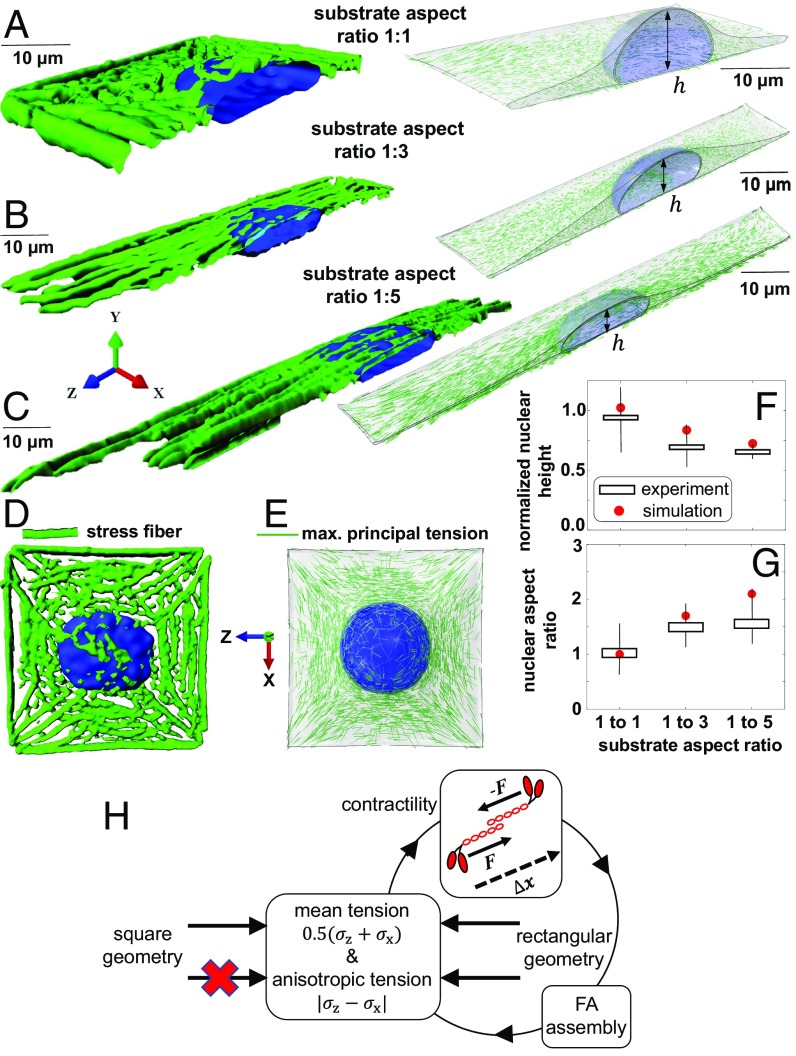
Fig. 4.
Substrate aspect ratio induces alterations in prenuclear actin organizations and nuclear morphology. Fibroblasts on fibronectin-coated micropatterned substrates with the same substrate surface area of 1,600 µm2 but various aspect ratios (A–C). Stress fibers (D) are formed in the direction of the maximum principal stress (E). Formations of apical stress fibers lead to flattening (F) and elongation (G) of the nucleus in the rectangular substrate geometries as actomyosin contractility increases with anisotropy in tensile stresses (H).
Then, we study whether substrate aspect ratio can change the level of actomyosin contractility and induce alterations in nuclear morphology. As shown in Eq. 1 and described in SI Appendix, section 2.6, our model accounts for a positive feedback loop between the average of contractility and the average of cytoskeletal tension . We will show in the next section that as a result of this feedback actomyosin contractility increases with substrate surface area as cells on larger areas sense higher resistance from their substrates, form stronger connections to the substrates, and subsequently experience higher cytoskeletal tension. These predictions agree with experimental results in ref. 12, where both total focal adhesion area and traction force increase with micropattern surface area. The feedback between the averages of contractility and stress also enables us to capture the fact that actomyosin contractility increases with the stiffness of the microenvironment (32) (SI Appendix, Figs. S19 and S20). In addition to the feedback between and , the model also accounts for a positive feedback between the average of contractility and the anisotropy in tension, (which represents the difference between the stress components in different directions). As a result, the mean contractility not only increases with substrate area (SI Appendix, Fig. S21), but it also increases with anisotropy in the components of the stress tensor (Fig. 4H). This is shown in Figs. 4 A–C and 5B where, for the same substrate area, the model predicts that actomyosin contractility increases with cell elongation. This is in excellent agreement with our experiments which show that cells on the square geometry have lower levels of p-MLC (SI Appendix, Fig. S22) and F-actin (Fig. 5B) compared with the cells on the rectangular geometries. Similar to the actin organization in the circular geometry (Fig. 2B), our experiments show that cells on the square geometry lack apical stress fibers (Fig. 4 A and D), while actin filaments in the elongated substrate geometries are organized as stress fibers along the long axis of the cell (Fig. 4 B and C), indicating that cell aspect ratio can alone regulate prenuclear actin organization by controlling the magnitude and the direction of tension in the cytoskeleton. Note that as our simulations show in SI Appendix, Fig. S23 the feedback between and is not enough to capture the experimentally observed increases in actomyosin contractility with increasing substrate aspect ratio. This indicates that cell elongation not only induces polarized contractility along the long axis of the cell but it also induces an increase in the volume averaged of tension in the cytoskeleton as myosin phosphorylation increases with cell elongation (Fig. 4H).
Fig. 5.
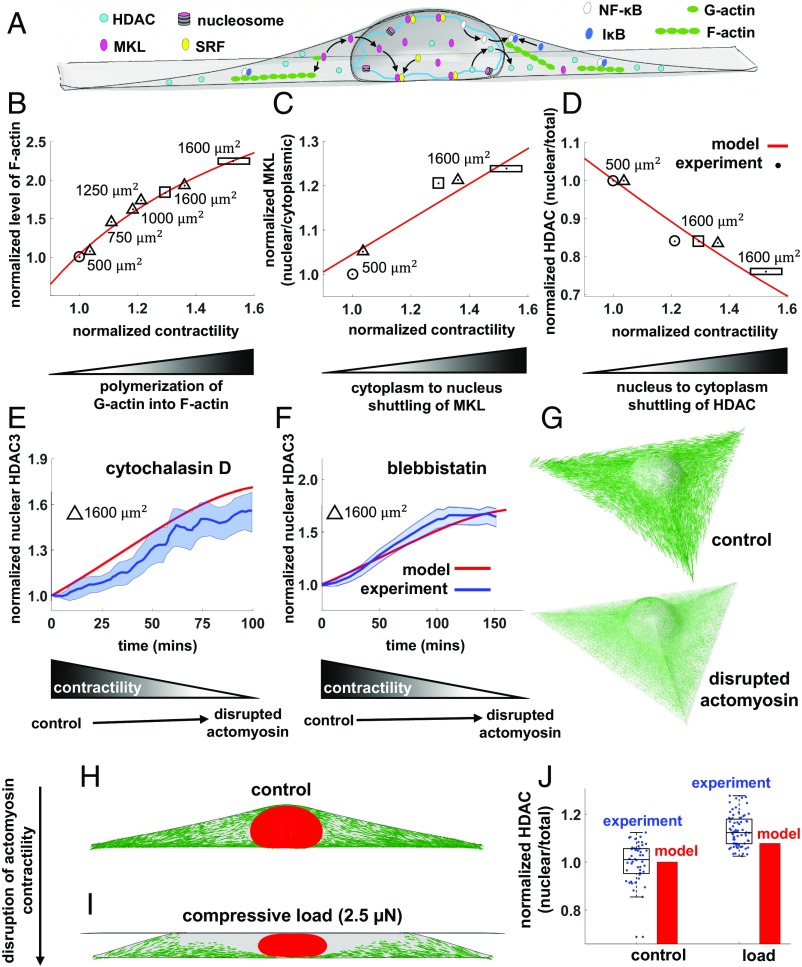
Cell geometric constraints induce chromatin condensation through nuclear translocation of HDAC driven by decreases in actomyosin contractility. The level of contractility, represented by in our model, regulates nucleocytoplasmic translocations of epigenetic and transcription factors (A). Cells on large and elongated substrates have higher contractility (compared with small and circular cells) and higher levels of polymerized F-actin (B). As G-actin is polymerized into F-actin, MKL unbinds from G-actin and shuttles to the nucleus, leading to higher nuclear accumulations of MKL in large and elongated cells (C). On the other hand, decreasing by constraining cells on smaller and unpolarized substrates (D) or by using actomyosin inhibitors (E–G) leads to translocation of HDAC to the nucleus. Similar to geometric constraints and actomyosin inhibitors, compressive forces on fibroblasts cause disruption of actomyosin contractility (H and I) and translocation of HDAC to the nucleus (J).
To further test the effect of tension anisotropy on the level of actomyosin contractility, we simulate actomyosin contractility of cells encapsulated within 3D microniches with two different geometries: 1) a cylinder and 2) a triangular prism. As illustrated in SI Appendix, Fig. S24, cells in both microniches are constrained in all three directions and have the same base area, height, and volume. Our simulations show that tension anisotropy in the triangular prism is higher than the cylinder and subsequently cells have significantly higher actomyosin contractility in the triangular prism than in the cylinder. This is in agreement with experimental results for human mesenchymal stem cells in ref. 33, where the level of myosin II in triangular prism cells is significantly higher than cylindrical cells. Our simulations in SI Appendix, Fig. S24 again show that the higher contractility of triangular prism cells cannot be captured if we do not account for the effect of tension anisotropy on actomyosin contractility.
We finally show that these changes in actin organizations with cell aspect ratio are correlated with alterations in nuclear morphologies as depicted in Fig. 4 E and F. For the rectangular substrate geometries (1:3 and 1:5 aspect ratios), the positive feedback between the cell-generated tensile stress and the tension-dependent formation of mature focal adhesions (Figs. 1 B and C and 4H) leads to the formation of stress fibers along the long axis of the cell (Fig. 4 B and C). The model predicts that these stress fibers form an arch bridge above the nucleus, exert an active compressive load on the nucleus, and provide physical links between the nucleus and mature focal adhesions. As a result, the nuclear height decreases, and the nucleus elongates in the direction of the long axis of the cell. This prediction agrees with our experiments that show the nuclei on the rectangular substrate geometries are more flattened (lower height) and elongated (higher nuclear aspect ratio) compared with the square substrate geometry (Fig. 4 F and G).
Cell Geometric Constraints Regulate Actomyosin-Mediated Spatial Redistribution of Transcriptional and Epigenetic Regulators and Cause Chromatin Condensation.
We next study the effect of substrate area on contractility, focal adhesions, and nuclear shape. We model fibroblasts (of the same initial volume) on circular micropatterned substrates with surface areas of 500 and 1,600 µm2. Starting with the same density of phosphorylated myosin motors for both cases (SI Appendix, Fig. S1), our simulations show that cells on the larger substrate area form stronger connections to the substrate at the cell periphery and subsequently have higher cytoskeletal tension and actomyosin contractility. These predictions are experimentally confirmed as cells on larger substrates exhibit higher levels of p-MLC (SI Appendix, Fig. S25) and F-actin (Fig. 5B) and increased assembly of focal adhesion (34).
Our experiments show that cells constrained on smaller substrate areas have decreased nuclear volume and increased histone acetylation levels (SI Appendix, Fig. S25). We thus hypothesize that the reduction of actomyosin contractility in constrained cells causes cytoplasmic-to-nuclear translocation of histone deacetylase 3 (HDAC3), which in turn can lead to lower histone acetylation level and subsequently chromatin compaction. To test that disruption of actomyosin contractility leads to 1) nuclear translocation of HDAC, 2) chromatin condensation, and 3) reduction of nuclear volume, we treat rectangular micropatterned fibroblasts with actomyosin contractility inhibitors (SI Appendix, Fig. S15). We find that drug-induced disruption of actomyosin contractility also causes nuclear accumulation of HDAC3 (SI Appendix, Fig. S26), chromatin compaction (SI Appendix, Fig. S27), and reduction of nuclear volume and area (SI Appendix, Fig. S16). These results are also confirmed for fibroblasts cultured on unpatterned substrates (SI Appendix, Figs. S28 and S29). Note that the substrate surface area of our rectangular micropattern approximately represents the spreading area of fibroblasts on rigid unpatterned substrates (35).
To quantitatively describe the actomyosin contractility-dependent translocation of transcription and epigenetic factors, we include the reaction–diffusion equations for the transport of these proteins (SI Appendix, section 4) in our model. To this end, we use the mean contractility to couple our mechanical simulations with the model for nucleocytoplasmic shuttling of epigenetic and transcription factors. The overall average of contractility in the cytoskeleton is determined from our simulations for substrates with different shapes and areas and then is introduced as an input to our signaling model to predict the steady-state 1) cytoplasmic levels of G-actin and F-actin, 2) cytoplasmic and nuclear levels of megakaryoblastic acute leukemia factor-1 (MKL), and 3) cytoplasmic and nuclear levels of HDAC. To assess whether the level of actomyosin contractility can be used to predict the relative nucleocytoplasmic levels of these proteins, we first train the signaling model on different substrate geometries using our experimental data (SI Appendix, section 4) and we then test the model predictions for new geometries. We also test the trained model for fibroblasts treated with actomyosin inhibitors and cells under vertical compression.
Our simulations show more than twofold increase in the level of F-actin in the large and elongated cell compared with the cell on the small and circular substrate geometry (Fig. 5B), in excellent agreement with our experiments. The higher polymerization of G-actin into F-actin in the rectangular cell is not surprising as the mean contractility in the rectangular cell is significantly higher than the circular cell. Since actin polymerization is known to regulate cytoplasmic to nuclear shuttling of MKL, a cofactor of SRF, we monitor cytoplasmic and nuclear levels of MKL for both rectangular and circular substrate geometries. Our simulations show a higher nuclear level of MKL in the rectangular cell, which is consistent with our experimental observation. Since MKL binds to G-actin in the cytoplasm (36), MKL is expected to be concentrated in the cytoplasm in the circular cell where there is less polymerized F-actin (Fig. 5C). As more G-actin is polymerized into F-actin in the rectangular cell, MKL unbinds from G-actin and shuttles to the nucleus, leading to an increase in the nuclear level of MKL as predicted by our simulations in Fig. 5C. Next, we study nucleocytoplasmic shuttling of HDAC3, which can impact the physical properties of chromatin as previously observed. Concomitant with the lower level of contractility, the model predicts higher nuclear accumulation of HDAC3 in the circular cell (Fig. 5D), which leads to chromatin condensation and reduction of nuclear volume. The increased nuclear level of HDAC3 in the circular substrate and the subsequent chromatin condensation are also shown by our experiments in Fig. 5D and SI Appendix, Fig. S30, respectively. To ensure that the observed chromatin condensation in circular cells is associated with the increased nuclear level of HDAC, we inhibit HDACs by treating rectangular cells with trichostatin A (TSA). As shown in SI Appendix, Fig. S31, fibroblasts exhibit chromatin decondensation upon TSA treatment. Also, we have previously shown that TSA-treated fibroblasts have higher levels of histone H3 acetylated at lysine 9 and significantly higher nuclear volume (3).
We next test whether the trained model can predict the translocation of HDAC upon treating fibroblasts with actomyosin inhibitors. To this end, we first experimentally measure changes in the nuclear level of HDAC as actomyosin contractility decreases upon treatment of fibroblasts with cytochalasin D (Fig. 5E) and blebbistatin (Fig. 5F). We then simulate the disruption of the actomyosin network (SI Appendix, section 4.4) and we measure the subsequent changes in the mean contractility which is used as an only input to the previously trained signaling model. The model predictions are shown in Fig. 5 E–G and are in excellent agreement with our experiments.
Finally, we use the trained model to predict the translocation of HDAC upon compression of fibroblasts (5). To this end, we simulate the compression of the rectangular cell using a rigid flat plate. Our simulations show that applying a vertical compressive force of 2.5 µN causes a dramatic drop in the maximum tensile principal stress in the apical regions which leads to depolymerization of apical stress fibers (Fig. 5 H and I). The model prediction is in agreement with our experimental results in SI Appendix, Fig. S32, where we apply the same compressive force on rectangular fibroblast. We also find that similar to the effect of geometric constraints and actomyosin inhibitors, the disruption of actomyosin contractility upon applying the compressive force leads to higher nuclear accumulation of HDAC and subsequently chromatin condensation (SI Appendix, Fig. S33 and section 9). As depicted in Fig. 5J, the trained model shows relatively good agreement with our experimental results.
Taken together, the comparison of the theoretical results with our experiments shows that the level of actomyosin contractility is an indicator of the relative nucleocytoplasmic levels of MKL, HDAC3, and other related molecules and it can be therefore used to predict the nucleocytoplasmic translocations of the epigenetic factors for substrates with different shapes and areas. The feedback between compartmentalization of epigenetic factors, nuclear stiffness, and the level of cytoskeletal contractility is depicted in Fig. 6; for small and circular substrate geometries, our simulations from the mechanical model predict low levels of contractility. As contractility decreases, the signaling model predicts nuclear shuttling of HDAC3 and cytoplasmic shuttling of MKL (Fig. 5 C and D). The nuclear accumulation of HDAC3, in turn, causes chromatin stiffening in our model, while the cytoplasmic shuttling of MKL leads to a further decrease in contractility as shown in Fig. 6B.
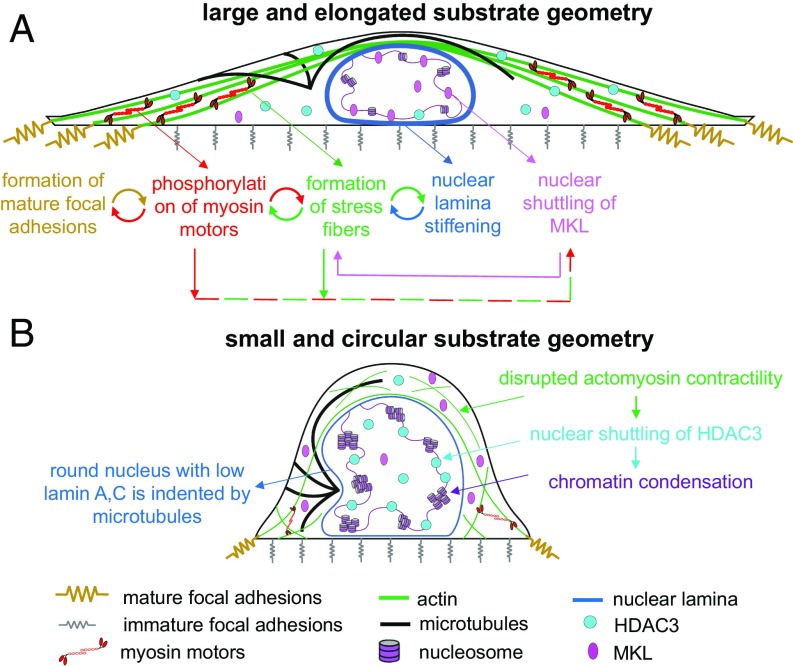
Fig. 6.
A model summarizing how cell geometry regulates focal adhesion formation, cell contractility, actin organization, nuclear morphology, and nuclear stiffness. Cell geometry controls the dynamic reciprocities between the focal adhesions, the cytoskeleton, and the nucleus by regulating the local tensile stresses that are generated on the cell substrate. For example, cells on large and rectangular substrates (A) generate high, polarized (along the long axis of the cell), and localized tensile stresses (at the two ends), while cells on small and circular geometries (B) generate low, isotropic (independent of direction), and uniform tension on the cell periphery. These mechanical stresses 1) are transmitted to the nucleus through cytoskeletal physical links and 2) trigger an actomyosin-dependent shuttling of epigenetic factors, causing alterations in nuclear morphology, nuclear stiffness (both nuclear envelope and nuclear interior), and gene expression.
Discussion
Using a chemomechanical model, we showed how the physical properties of the microenvironment, including cell substrate area, shape, and stiffness, impact the properties of both cytoskeleton and nucleus by regulating the dynamic reciprocities between tension-dependent formation of focal adhesions, phosphorylation of myosin motors, polymerization of actin filaments, stiffening of the nuclear envelope lamina network, and nucleocytoplasmic shuttling of epigenetic factors. The parameters in our model were obtained by using data on different micropatterned substrate geometries (see SI Appendix, Fig. S34 for more details). The model was then tested by comparing its following predictions with micropatterning experiments for new substrate geometries and by using pharmacological treatments to up- or down-regulate different components of the model.
We first showed how the formation of focal adhesions connects the cell to the substrate and generates tension in the cytoskeleton through the maturation of the focal adhesions, which in turn is governed by the magnitude and anisotropy of stresses in different substrate geometries. In response (and proportional) to the strengthening of the adhesions, our feedback model predicts how the nonuniform increase of cell contractility leads to the formation of stress fibers and stiffening of the cytoskeleton in the direction of the maximum principal tension, while these cytoskeletal changes induce alterations in the physical properties of the nucleus. We determined the orientations of stress fibers and we showed how they remodel the nucleus by applying inward compressive forces. As these forces reduce the nuclear height and width, the nucleus elongates along the long axis of the cell and tension is generated in the nuclear envelope. The magnitude of tension in the nuclear envelope predicted by our simulations was found to be correlated with the experimentally observed level of lamin A,C. We also showed that the phosphorylation of myosin motors and polymerization of actin filaments not only increase with the average of tension in the cytoskeleton (dominated by the substrate surface area) but they also increase with anisotropy of tension in the cytoskeleton (dominated by the substrate aspect ratio).
Combining our mechanical model with a model for nucleocytoplasmic shuttling of transcription and epigenetic factors enabled us to describe the actomyosin-dependent translocation of these proteins. The model shows that nuclear accumulation of HDAC3 and condensation of chromatin coincide with fluid exiting the nucleus and the shrinkage of the nuclear volume. The model also predicts the role of microtubules and actin filaments on the physical properties of the nucleus. We found that depolymerization of microtubules leads to stiffening of the nuclear envelope lamina network. Also, we showed how depolymerization of actin filaments in highly contractile cells can cause nuclear invaginations. In summary, our model predicts how the physical properties of the extracellular microenvironment induce alterations in the organization and mechanics of both cytoskeleton and nucleus. Given the predictive power of the model as illustrated by extensive experimental tests, it can potentially be used to describe abnormal nuclear morphology in diseases like progeria, cancer, fibrosis, and dilated cardiomyopathy.
Materials and Methods
A 3D Chemomechanical Feedback Model for Cytoskeletal and Nuclear Mechanics.
To understand the role of substrate geometry on nuclear mechanics, we develop a chemomechanical model that accounts for all of the key cellular components involved in the transmission of mechanical stimuli from the cell–matrix interface to the nucleus. These components are shown in Fig. 1, which include 1) the cytoskeleton, 2) the nucleus, and 3) the focal adhesions. We use the model to study fibroblasts cultured on fibronectin-coated micropatterned substrates. In our study, we focus on the stationary behavior of cells where cells have adopted the shape of the substrate while the model can be readily extended to study time-dependent behavior of cells as shown in our recent publications (37). All our experiments are also carried out in the stationary configuration where fibroblasts are fully constrained to the micropatterned substrate before and after drug treatment.
A 3D active model for the actomyosin system.
As shown in Fig. 1 A and C, the cytoskeletal model is composed of three elements: 1) the myosin molecular motors; 2) the cytoskeletal components that are in compression (e.g., microtubules); and 3) the cytoskeletal components that are in tension (e.g., actin filaments).
Myosin molecular motors.
In our coarse-grained finite element model, we treat the average density of the phosphorylated myosin motors per unit volume as a symmetric tensor, , whose components represent cell contractility in different directions (SI Appendix, section 2.1). To capture the fact that cell contractility increases with tension (tensile stresses activate the Ca2+ and the Rho–Rock signaling pathways which promote phosphorylation of myosin motors), the average of the cell contractility in all three directions, , is related to the average of stress, , as follows:
| [1] |
where is the bulk modulus of the cytoskeletal components that are in compression (e.g., microtubules) and is the cell contractility in the quiescent state (SI Appendix, section 2.1). Eq. 1 shows that in the presence of tension , the cell contractility increases with the tensile stress where this stress-dependent feedback mechanism is regulated by the volumetric chemomechanical feedback parameter ; a large value of leads to a greater overall density of phosphorylated myosin motors and subsequently higher contractility. We will show that the average of contractility not only increases with the average of stress but it also increases with anisotropy in the components of the stress tensor. This is captured in our model by assuming that the cell contractility increases with the anisotropic tension , where are the eigenvalues of the stress tensor (SI Appendix, section 2.6). As we show below, this term which has not been considered in prior models for the actomyosin system accounts for the fact that myosin phosphorylation increases in response to anisotropy in tension while this increase in regulated by the anisotropic chemomechanical feedback parameter . Eq. 1 also shows that the volumetric chemical stiffness parameter regulates the cell contractility in the absence of tension by maintaining the contractility at a quiescent level,. Similarly, the deviatoric contractility tensor , which measures the degree of contractility polarization, is related to the deviatoric stress tensor as follows:
| [2] |
where is the shear modulus of the cytoskeletal components that are in compression, is the deviatoric chemomechanical feedback parameter which represents the tendency of the feedback mechanism to induce polarization in contractility (along the orientations where the stresses are tensile), and is the deviatoric chemical stiffness parameter which ensures that the cells are not polarized when the stresses are isotropic. Note that the feedback parameters should be chosen according to the stability criterion described in SI Appendix, section 6 to ensure that the feedback gain does not lead to instabilities.
Cytoskeletal components in compression (e.g., microtubules).
Experimental studies show that the internally generated cell contractile forces can compressively load microtubules (16). While microtubules are compressively loaded by contractile forces represented by the tensor , part of this internally generated stress is transmitted to the ECM and the nucleus through the tensile stress in the actin filament network, . The balance of forces requires that the sum of the stresses in the actin and microtubule networks equal the cell generated contractile stress:
| [3] |
where is the compressive stress that resists the active forces (generated by the cell contractility ), while and are the stiffness and strain tensors of the cytoskeletal components that are in compression (see also SI Appendix, section 2.2 and Fig. S7A). Note that the microtubule network that bears most of the compressive stresses is treated in a coarse-grained continuum sense unless stated otherwise.
Cytoskeletal components in tension (e.g., actin filaments).
As described in detail in SI Appendix, section 2, in addition to the cell contractility the stiffness of the actin filament network and the stress it carries, , also change in an orientation-dependent manner as a function of the stiffness of the extracellular environment. It has been reported (32, 38) that cells actively respond to external stiffness by increasing their own stiffness, which is correlated with the recruitment and alignment of actin filaments whose orientations coincide with the directions of the principal tensile stresses. Therefore, we assume that the stiffness of the actin filament network increases with tension (but not in compression) in an orientation-dependent manner (along the tensile principal directions of the stress tensor, ) to capture the tension-induced cell stiffening observed in refs. 38 and 39 (see SI Appendix, section 2.3 for more details).
Note that in animal cells these three cytoskeletal components are also accompanied by intermediate filaments which have been shown to play an important mechanical role in cell integrity particularly at large deformations (40, 41). The characteristic properties of intermediate filaments that enable them to undergo large deformations have been elucidated by multiscale modeling of these filaments (42). In addition to their ability to withstand large mechanical deformations, intermediate filaments may also laterally reinforce microtubules under physiological compressive forces which in turn can significantly increase the compressive forces that microtubules can withstand (16). Furthermore, intermediate filaments have been shown to have a considerable contribution to cytoplasmic stiffness (43–46) and protect the nucleus from excessive deformations (SI Appendix, section 7).
Model for the nucleus.
The lamina network in the nuclear envelope and chromatin are the key components that determine the mechanical properties of the nucleus (2, 24–26). Therefore, the nucleus is modeled as an elastic thin layer (representing the nuclear envelope) filled with an elastic material which represents chromatin and other subnuclear components (SI Appendix, Fig. S35A).
Experimental studies show that the nucleus also displays viscous properties (24); however, the timescale for its viscous relaxation has been measured to be around 80 s (47), which is significantly smaller than the time it takes the nucleus to fully spread on micropatterned substrates (48). Thus, the elastic properties used in our model are the mechanical properties of the nucleus after the viscous effects have relaxed.
Nuclear envelope.
The nuclear envelope is one of the major components of the nucleus which provides the nucleus with structural integrity. The nuclear envelope is made up of 1) the inner and outer membranes and 2) the nuclear lamina, which is a complex peripheral mesh-like network underneath the inner nuclear membrane and is composed of lamins (including lamins A,C and B1,B2) and nuclear membrane-associated proteins (SI Appendix, section 3.1).
We model the nuclear envelope as a filamentous network material which stiffens along the tensile principal axes of the stress tensor. This is consistent with the fibrous nature of the lamin network as observed in the lamina of the mammalian cell nuclei (49). Furthermore, both lamin A,C (50) and lamin B1 (51) networks were experimentally observed to stiffen in tension.
Chromatin.
Uniaxial stretch tests of single isolated nuclei (SI Appendix, Fig. S35) show that chromatin, unlike the nuclear envelope lamina network, does not exhibit strain stiffening even at large extensions (50). Therefore, chromatin is modeled as a linear elastic material (SI Appendix, section 3.2), where the Poisson’s ratio determines the amount of fluid that can be expelled. Our experimental results show that alterations in the level of actomyosin contractility trigger a cascade of biochemical pathways leading to nucleocytoplasmic shuttling of epigenetic factors (i.e., HDAC3) and subsequently changes in chromatin structures and nuclear stiffness. These changes in chromatin stiffness are included in our model by increasing (decreasing) the elastic modulus of chromatin with condensation (decondensation) in proportion to HDAC3 nuclear levels as discussed in the section on chemomechanical signaling.
Stress-dependent formation of focal adhesions.
Three-dimensional reconstruction of confocal images of fibroblasts on large rectangular micropatterned substrates shows that stress fibers are connected to the mature focal adhesion sites at the two ends along the long axis of the cell (Fig. 2B). Through these focal adhesions, mechanical forces can be transmitted from the cytoskeleton to the substrate, and vice versa. The formation and maturation of these focal adhesion complexes in cells are known to be tension-dependent (52). To capture the tension-dependent formation of the focal adhesions, we use a continuum model that treats the adhesion layer shown in SI Appendix, Fig. S4C as a set of initially soft nonlinear mechanical elements (SI Appendix, Fig. S4A) that stiffen with tension (SI Appendix, Fig. S4B). As shown in SI Appendix, Fig. S4D, when the tensile stress exerted by the cell to the adhesion layer exceeds a certain threshold, mature focal adhesions are formed, and the cell is connected to the substrate. Below this threshold, the stiffness of the adhesion layer remains low and the substrate experiences negligible forces.
Model for nucleocytoplasmic shuttling of transcription and epigenetic factors.
Our experimental results show that alterations in the level of actomyosin contractility and subsequently the density of F-actin can induce nucleocytoplasmic translocation of transcription and epigenetic factors. For example, we have shown that while the total level of myocardin-related transcription factor (MRTF-A, also known as MKL) remains constant, nuclear accumulation of MKL increases linearly with the total density of actin (3). As another example, while the total level of p65, an NF-κB transcription factor subunit, remains constant, the nuclear-to-cytoplasmic ratio of p65 decreases remarkedly with actin density (3). These examples show that the actomyosin system can possibly serve as a potential substrate for MRTF-A, p65, MKL, HDAC3 and other related molecules (Fig. 5A) (3, 5, 35). Thus, the level of actomyosin contractility can be used as an indicator to predict the relative levels of these proteins in the nucleus and the cytosol. To this end, we combine our mechanical model with steady-state reaction–diffusion equations for the transport of these proteins (signaling model described in SI Appendix, section 4). With the average contractility at hand (known from our mechanical model simulations), the signaling model enables us to quantitatively predict the contractility-dependent translocation of the epigenetic factors such as HDAC3 and MKL.
Supplementary Material
Acknowledgments
This work is supported by National Cancer Institute Awards U01CA202177 and U54CA193417 (to V.B.S.), National Institute of Biomedical Imaging and Bioengineering Award R01EB017753 (to V.B.S.), the NSF Center for Engineering Mechanobiology (CMMI-154857), and Ministry of Education (MOE)-Tier3 grant Singapore (to G.V.S.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1902035116/-/DCSupplemental.
References
- 1.Discher D. E., Janmey P., Wang Y. L., Tissue cells feel and respond to the stiffness of their substrate. Science 310, 1139–1143 (2005). [DOI] [PubMed] [Google Scholar]
- 2.Makhija E., Jokhun D. S., Shivashankar G. V., Nuclear deformability and telomere dynamics are regulated by cell geometric constraints. Proc. Natl. Acad. Sci. U.S.A. 113, E32–E40 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jain N., Iyer K. V., Kumar A., Shivashankar G. V., Cell geometric constraints induce modular gene-expression patterns via redistribution of HDAC3 regulated by actomyosin contractility. Proc. Natl. Acad. Sci. U.S.A. 110, 11349–11354 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Le Beyec J., et al. , Cell shape regulates global histone acetylation in human mammary epithelial cells. Exp. Cell Res. 313, 3066–3075 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Damodaran K., et al. , Compressive force induces reversible chromatin condensation and cell geometry dependent transcriptional response. Mol. Biol. Cell 10.1091/mbc.E18-04-0256 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Swift J., et al. , Nuclear lamin-A scales with tissue stiffness and enhances matrix-directed differentiation. Science 341, 1240104 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kim J.-K., et al. , Nuclear lamin A/C harnesses the perinuclear apical actin cables to protect nuclear morphology. Nat. Commun. 8, 2123 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.van Loosdregt I. A. E. W., et al. , Lmna knockout mouse embryonic fibroblasts are less contractile than their wild-type counterparts. Integr. Biol. 9, 709–721 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Buxboim A., et al. , Coordinated increase of nuclear tension and lamin-A with matrix stiffness outcompetes lamin-B receptor that favors soft tissue phenotypes. Mol. Biol. Cell 28, 3333–3348 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Katoh K., et al. , Rho-kinase–mediated contraction of isolated stress fibers. J. Cell Biol. 153, 569–584 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Matthews B. D., et al. , Ultra-rapid activation of TRPV4 ion channels by mechanical forces applied to cell surface beta1 integrins. Integr. Biol. 2, 435–442 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Versaevel M., Grevesse T., Gabriele S., Spatial coordination between cell and nuclear shape within micropatterned endothelial cells. Nat. Commun. 3, 671 (2012). [DOI] [PubMed] [Google Scholar]
- 13.Buxboim A., et al. , Matrix elasticity regulates lamin-A,C phosphorylation and turnover with feedback to actomyosin. Curr. Biol. 24, 1909–1917 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Xia Y., et al. , Nuclear rupture at sites of high curvature compromises retention of DNA repair factors. J. Cell Biol. 217, 3796–3808 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stephens A. D., et al. , Chromatin histone modifications and rigidity affect nuclear morphology independent of lamins. Mol. Biol. Cell 29, 220–233 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brangwynne C. P., et al. , Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J. Cell Biol. 173, 733–741 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang N., et al. , Mechanical behavior in living cells consistent with the tensegrity model. Proc. Natl. Acad. Sci. U.S.A. 98, 7765–7770 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Haase K., Pelling A. E., Investigating cell mechanics with atomic force microscopy. J. R. Soc. Interface 12, 20140970 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rotsch C., Radmacher M., Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: An atomic force microscopy study. Biophys. J. 78, 520–535 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kolodney M. S., Elson E. L., Contraction due to microtubule disruption is associated with increased phosphorylation of myosin regulatory light chain. Proc. Natl. Acad. Sci. U.S.A. 92, 10252–10256 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chang Y.-C., Nalbant P., Birkenfeld J., Chang Z.-F., Bokoch G. M., GEF-H1 couples nocodazole-induced microtubule disassembly to cell contractility via RhoA. Mol. Biol. Cell 19, 2147–2153 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu B. P., Chrzanowska-Wodnicka M., Burridge K., Microtubule depolymerization induces stress fibers, focal adhesions, and DNA synthesis via the GTP-binding protein Rho. Cell Adhes. Commun. 5, 249–255 (1998). [DOI] [PubMed] [Google Scholar]
- 23.Ramdas N. M., Shivashankar G. V., Cytoskeletal control of nuclear morphology and chromatin organization. J. Mol. Biol. 427, 695–706 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Pajerowski J. D., Dahl K. N., Zhong F. L., Sammak P. J., Discher D. E., Physical plasticity of the nucleus in stem cell differentiation. Proc. Natl. Acad. Sci. U.S.A. 104, 15619–15624 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mazumder A., Roopa T., Basu A., Mahadevan L., Shivashankar G. V., Dynamics of chromatin decondensation reveals the structural integrity of a mechanically prestressed nucleus. Biophys. J. 95, 3028–3035 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lammerding J., et al. , Lamin A/C deficiency causes defective nuclear mechanics and mechanotransduction. J. Clin. Invest. 113, 370–378 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lee H., et al. , Cytoskeletal prestress regulates nuclear shape and stiffness in cardiac myocytes. Exp. Biol. Med. (Maywood) 240, 1543–1554 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Goffin J. M., et al. , Focal adhesion size controls tension-dependent recruitment of α-smooth muscle actin to stress fibers. J. Cell Biol. 172, 259–268 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Oakes P. W., Banerjee S., Marchetti M. C., Gardel M. L., Geometry regulates traction stresses in adherent cells. Biophys. J. 107, 825–833 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Solon J., Levental I., Sengupta K., Georges P. C., Janmey P. A., Fibroblast adaptation and stiffness matching to soft elastic substrates. Biophys. J. 93, 4453–4461 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tee S.-Y., Fu J., Chen C. S., Janmey P. A., Cell shape and substrate rigidity both regulate cell stiffness. Biophys. J. 100, L25–L27 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hall M. S., et al. , Fibrous nonlinear elasticity enables positive mechanical feedback between cells and ECMs. Proc. Natl. Acad. Sci. U.S.A. 113, 14043–14048 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bao M., Xie J., Piruska A., Huck W. T. S., 3D microniches reveal the importance of cell size and shape. Nat. Commun. 8, 1962 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gallant N. D., Michael K. E., García A. J., Cell adhesion strengthening: Contributions of adhesive area, integrin binding, and focal adhesion assembly. Mol. Biol. Cell 16, 4329–4340 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mitra A., et al. , Cell geometry dictates TNFα-induced genome response. Proc. Natl. Acad. Sci. U.S.A. 114, E3882–E3891 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Miralles F., Posern G., Zaromytidou A.-I., Treisman R., Actin dynamics control SRF activity by regulation of its coactivator MAL. Cell 113, 329–342 (2003). [DOI] [PubMed] [Google Scholar]
- 37.Pakshir P., et al. , Dynamic fibroblast contractions attract remote macrophages in fibrillar collagen matrix. Nat. Commun. 10, 1850 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Icard-Arcizet D., Cardoso O., Richert A., Hénon S., Cell stiffening in response to external stress is correlated to actin recruitment. Biophys. J. 94, 2906–2913 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pourati J., et al. , Is cytoskeletal tension a major determinant of cell deformability in adherent endothelial cells? Am. J. Physiol. 274, C1283–C1289 (1998). [DOI] [PubMed] [Google Scholar]
- 40.Bertaud J., Qin Z., Buehler M. J., Intermediate filament-deficient cells are mechanically softer at large deformation: A multi-scale simulation study. Acta Biomater. 6, 2457–2466 (2010). [DOI] [PubMed] [Google Scholar]
- 41.Ackbarow T., Buehler M. J., Superelasticity, energy dissipation and strain hardening of vimentin coiled-coil intermediate filaments: Atomistic and continuum studies. J. Mater. Sci. 42, 8771–8787 (2007). [Google Scholar]
- 42.Qin Z., Buehler M. J., Kreplak L., A multi-scale approach to understand the mechanobiology of intermediate filaments. J. Biomech. 43, 15–22 (2010). [DOI] [PubMed] [Google Scholar]
- 43.Wang N., Stamenović D., Contribution of intermediate filaments to cell stiffness, stiffening, and growth. Am. J. Physiol. Cell Physiol. 279, C188–C194 (2000). [DOI] [PubMed] [Google Scholar]
- 44.Mendez M. G., Restle D., Janmey P. A., Vimentin enhances cell elastic behavior and protects against compressive stress. Biophys. J. 107, 314–323 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lowery J., Kuczmarski E. R., Herrmann H., Goldman R. D., Intermediate filaments play a pivotal role in regulating cell architecture and function. J. Biol. Chem. 290, 17145–17153 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Eckes B., et al. , Impaired mechanical stability, migration and contractile capacity in vimentin-deficient fibroblasts. J. Cell Sci. 111, 1897–1907 (1998). [DOI] [PubMed] [Google Scholar]
- 47.Guilak F., Tedrow J. R., Burgkart R., Viscoelastic properties of the cell nucleus. Biochem. Biophys. Res. Commun. 269, 781–786 (2000). [DOI] [PubMed] [Google Scholar]
- 48.Vishavkarma R., et al. , Role of actin filaments in correlating nuclear shape and cell spreading. PLoS One 9, e107895 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Turgay Y., et al. , The molecular architecture of lamins in somatic cells. Nature 543, 261–264 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Stephens A. D., Banigan E. J., Adam S. A., Goldman R. D., Marko J. F., Chromatin and lamin A determine two different mechanical response regimes of the cell nucleus. Mol. Biol. Cell 28, 1984–1996 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Panorchan P., Schafer B. W., Wirtz D., Tseng Y., Nuclear envelope breakdown requires overcoming the mechanical integrity of the nuclear lamina. J. Biol. Chem. 279, 43462–43467 (2004). [DOI] [PubMed] [Google Scholar]
- 52.Chen C. S., Alonso J. L., Ostuni E., Whitesides G. M., Ingber D. E., Cell shape provides global control of focal adhesion assembly. Biochem. Biophys. Res. Commun. 307, 355–361 (2003). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.