Buckling and twisting of advanced materials into morphable 3D mesostructures

Significance

The growing availability of 3D manufacturing methods has implications across diverse applications, from ship building to microelectronics processing. Systems with sizes in the micrometer and millimeter regime are of particular interest, where few techniques offer the necessary range of capabilities in throughput, materials compatibility, and design versatility. Recently reported techniques for mechanically guided 3D assembly offer many appealing features, but limitations remain, such as those in formation of structures with chiral features and morphable shapes. Here we present concepts that allow controlled introduction of twisting into 3D mesostructures. The results provide access to many classes of previously unachievable 3D architectures, as illustrated through nearly 2 dozen examples in diverse materials and across a wide span of length scales.

Abstract

Recently developed methods in mechanically guided assembly provide deterministic access to wide-ranging classes of complex, 3D structures in high-performance functional materials, with characteristic length scales that can range from nanometers to centimeters. These processes exploit stress relaxation in prestretched elastomeric platforms to affect transformation of 2D precursors into 3D shapes by in- and out-of-plane translational displacements. This paper introduces a scheme for introducing local twisting deformations into this process, thereby providing access to 3D mesostructures that have strong, local levels of chirality and other previously inaccessible geometrical features. Here, elastomeric assembly platforms segmented into interconnected, rotatable units generate in-plane torques imposed through bonding sites at engineered locations across the 2D precursors during the process of stress relaxation. Nearly 2 dozen examples illustrate the ideas through a diverse variety of 3D structures, including those with designs inspired by the ancient arts of origami/kirigami and with layouts that can morph into different shapes. A mechanically tunable, multilayered chiral 3D metamaterial configured for operation in the terahertz regime serves as an application example guided by finite-element analysis and electromagnetic modeling.

Three-dimensional structures of functional materials are of growing interest due to their utility in areas ranging from energy storage and generation devices (1–4), to plasmonic and photonic nanosystems (5, 6), mechanical and optical metamaterials (7–9), and biomedical devices (10–13). A collection of recently reported methods for forming 3D mesoscale systems of relevance for these applications exploits compressive buckling of 2D precursors selectively bonded to prestretched elastomer substrates (14–20). These assembly techniques are intrinsically compatible with the most sophisticated planar technologies and with broad classes of functional thin-film materials, including device-grade semiconductors. Additional attractive features include high speed, parallel operation, and access to a wide breadth of feature sizes, from nanometers to centimeters. These capabilities lead to design opportunities that lie outside of those supported by existing 3D fabrication methods based on 3D printing (21–23), thin-film folding and wrinkling (24–27), and actuation of active materials (28–32). A key limitation is that the existing version of the process involves only in- and out-of-plane translational displacements in the transformation of 2D precursors into 3D architectures, thereby constraining the classes of 3D geometries that can be achieved. In particular, systems that involve strong degrees of out-of-plane chirality or folding, controlled locally across a structure, are not possible.

Chiral structures are ubiquitous in nature, from biomolecules such as essential amino acids and certain proteins, to climbing plant tendrils, twisted leaves, and seashells. Chiral features are also commonly present in architecture and art such as spiral elements in towers and staircases. Chirality not only provides geometric handedness and efficient use of space, but also leads to unique chemical, electronic, and optical properties across a range of length scales in naturally occurring and manmade systems. As specific examples, structural chirality serves as the basis for spectroscopic instruments (33), optical systems (34), and plasmonic sensors (35). Scalable fabrication of 3D chiral structures with general architectures and in high-performance materials remains challenging in the micrometer and millimeter range due to the limitations of conventional top-down and bottom-up fabrication methods.

Here, we introduce a strategy that overcomes this restriction where controlled rotations, in addition to translational displacements, occur as a result of a complex combination of forces imparted through the bonding sites of the precursor. The method relies on elastomeric assembly substrates formed into interconnected segments that rotate relative to one another during uniaxial or biaxial stretching. Release involves a 2-stage process that first directs transformation of a 2D precursor into an initial 3D structure by conventional buckling and then introduces strong and well-defined levels of rotational twist (up to 45°) to yield the final shape. Examples of more than 20 different structures, each with finite-element analysis (FEA) of their assembly as a guide, highlight capabilities in forming such chiral architectures and in reversibly morphing their geometries via elastic deformations of the substrate. In addition to the creation of chiral structures, controlled twisting also enables local, large degrees of folding of structures, yielding unique 3D shape transformations that are not achievable using other techniques. Examples include opening and closing of box structures, creased structures, and complex spatially varying foldable cage structures. Mechanically tunable chiral metamaterials that operate in the terahertz regime illustrate some unique shapes and morphing/tuning options with relevance in photonics.

Results and Discussion

Buckling and Twisting Concepts and Design Principles.

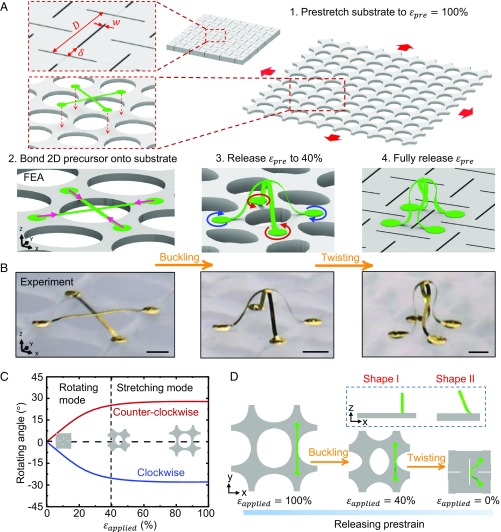
Fig. 1A presents a schematic illustration of the steps for forming 3D mesostructures on segmented assembly substrates, which we refer to here as kirigami substrates, via FEA. The scheme begins with the creation of a collection of cuts through the thickness of a sheet of a silicone elastomer (Dragon Skin, Smooth-On) by laser ablation. The pattern illustrated here divides the elastomer into connected square units with sizes $D$, with gaps of width $w$, and with spacings $\delta$, between orthogonal cuts (Fig. 1A and SI Appendix, Fig. S1A). Biaxially stretching the elastomer to a strain of 100% deforms the elastomer in a manner that causes adjacent units to rotate in opposite directions. When the strain exceeds ∼40%, the rotation angle at the center of a unit (where the rotation is the largest) plateaus to a fixed value (∼30° for the kirigami pattern shown in SI Appendix, Fig. S1), such that further stretching only induces additional overall deformations of the substrate, without further rotations (Fig. 1C and SI Appendix, Fig. S1 B and C). Through this sequence, the cuts transform from rectangular to ellipsoidal to approximately circular shapes.

Fig. 1.

Three-dimensional morphable mesostructures formed by mechanically guided buckling and twisting on elastomeric kirigami substrates. (A) Conceptual illustration of the fabrication process, through a sequence of FEA results: (i) prestretching a substrate with engineered kirigami cuts (key geometric parameters labeled in the magnified image) to 100% biaxial strain; (ii) bonding of a 2D precursor onto the prestretched kirigami substrate at selected regions (circular pads); (iii) releasing of the substrate prestrain to 40%, thereby causing the structure to buckle; (iv) further releasing of the substrate prestrain to 0%, thereby causing the structure to twist. (B) Experimental images (optical) of 3D structures that correspond to those predicted by FEA in A. (C) Plot of the rotation angles at the centers of an individual square unit in a typical kirigami elastomer substrate as a function of the applied biaxial strain. (D) Schematic illustration [top view and side view (dashed Inset)] of 2 different 3D ribbon shapes on a kirigami substrate at different stages of released prestrain. Shape I results from the release of stretching of the square units in the substrate (ε_prestrain = 40%), thereby causing a buckling deformation of the ribbon. Shape II results from the release of both stretching and rotating of these units (ε_prestrain = 0%), thereby causing twisting of the ribbon. (Scale bars, 500 µm.)

The next step involves laminating a 2D precursor onto this prestretched elastomer with bonding sites aligned to designated locations on selected units. Initial relaxation of the prestrain (from 100 to 40% strain) releases the overall stretching of the units, thereby transforming the 2D precursor into a 3D shape through buckling induced by compressive stresses. Further relaxation (from 40 to 0% strain) releases the shear stresses associated with the individual units, thereby causing rotations through associated forces at the bonding sites. These rotations transform the initial 3D structure into a distinct geometry with chiral character, as schematically illustrated by the twisting of a ribbon bonded to 2 adjacent rotating units (Fig. 1D). Fig. 1B shows optical images of a 3D ribbon structure (ribbon width: 130 µm, ribbon length: 320 µm, diameter of circular bonding pads: 520 µm) made of polyimide (PI; 9 µm in thickness) coated with layers of metal (Cr/Au, 10 nm/100 nm in thickness) at various stages of the assembly process, as illustrated by the FEA results in Fig. 1A. In addition to the overall similarity of experimental and computational shapes, the measured height (1.27 mm) of the structure after full release also agrees well with the FEA results (1.17 mm). This good correspondence between FEA predictions and experimental observations indicates the high level of control associated with the assembly process, and validates the use of computational techniques to guide design choices, as described in examples introduced subsequently. The detailed procedures for fabrication, transfer, and bonding are in Methods and SI Appendix, Fig. S2.

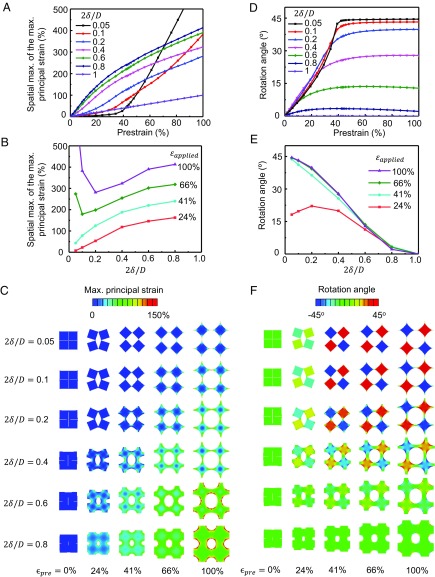
FEA serves not only as a means for predicting shape transformations, but also for revealing the nature of deformations in the substrates, including the dependence of the maximum principal strains and the unit rotation angles as functions of geometric parameters of the cuts. In the case of small spacings between orthogonal cuts $\left(2\delta /D=0.05\right)$, a clear transition from the rotating mode to the stretching mode appears when the biaxial prestrain increases beyond 40% (Fig. 2A). This transition becomes less sharp with further increase of the $2\delta /D$ ratio. Fig. 2B illustrates the spatial maximum of the maximum principal strain as a function of $2\delta /D$ at different prestrain levels. With large (>66%) prestrain, an optimal $2\delta /D$ ratio minimizes this strain, located at the narrow connections between units (for small $2\delta /D$) or along the cuts (for large $2\delta /D$), as visualized in Fig. 2C. The $2\delta /D$ ratio is also a key parameter in determining the achievable rotation angle in the assembly process. The maximum rotation angle at prestrain >40% increases with decreasing $2\delta /D$, with a maximum rotation angle close to 45° (Fig. 2 D and E). Fig. 2F presents the distribution of rotation angles as functions of $2\delta /D$ and the applied prestrain. The measured rotation angles at the centers of the unit cells from experiments match with values predicated by FEA with high accuracy (SI Appendix, Fig. S1B). Optical images of the unit-cell deformation with different $2\delta /D$ ratios and biaxial prestrain appear in SI Appendix, Fig. S1C. While a small $2\delta /D$ (<0.4) provides a large rotation angle, the associated principal strains can reach levels that could lead to fracture of the substrate. Another geometric parameter, the cut width (characterized by $w/D$), has a much smaller influence on the spatial maximum of the maximum principal strain and the rotation angle (SI Appendix, Fig. S3). Given the above design considerations, typical parameters chosen in the experiments reported here ($D$ = 2 mm, $w$ = 100 µm, $\delta$ = 400 µm) enable maximum rotation angles of ∼30°, restricted only by the fracture limits of the elastomer and the resolution of the laser ablation process to form the cuts.

Fig. 2.

Dependence of the spatial maximum of the maximum principal strain and the unit rotation angles on the stretched kirigami substrate, as a function of geometric parameters of the cuts and applied biaxial prestrain from FEA. (A) Plots of the spatial maximum of the maximum principal strain as a function of the biaxial prestrain with different values of $2\delta /D$ (from 0.05 to 1). (B) Plots of the spatial maximum of the maximum principal strain as a function of $2\delta /D$ with different biaxial prestrain (24, 41, 66, and 100%). (C) Color representations of the distributions of the maximum principal strain in kirigami substrates with different $2\delta /D$ values and biaxial prestrain. (D) Plots of the rotation angle at the centers of the unit cells as a function of the biaxial prestrain with different $2\delta /D$ values (from 0.05 to 1). (E) Plots of the rotation angle at the centers of unit cells as a function of the $2\delta /D$ values with different biaxial prestrain (24, 41, 66, and 100%). (F) Color representations of the distributions of rotation angle in kirigami substrates with different $2\delta /D$ values and biaxial prestrain. The cutting width $w/D$ is 0.02 in these plots.

Three-Dimensional Morphable Architectures with Diverse Geometries and Materials.

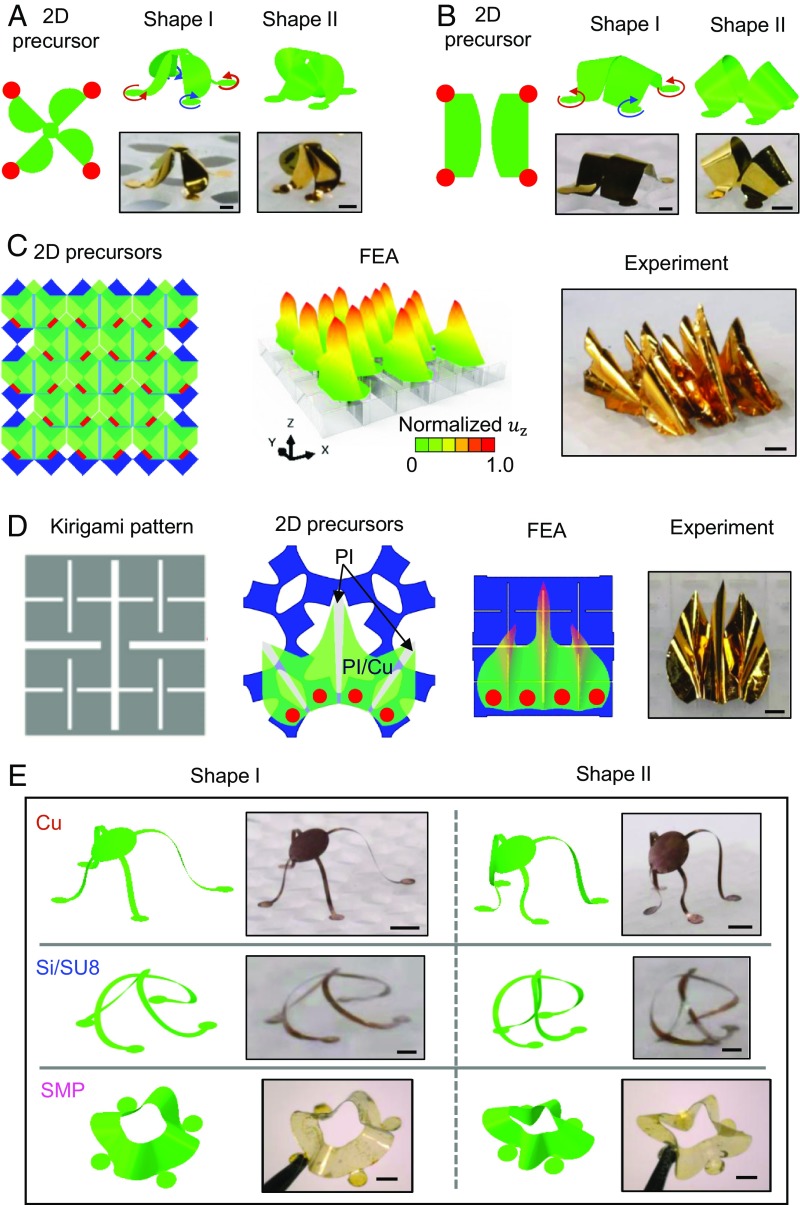
Fig. 3 presents a collection of additional 3D structures in diverse geometries and materials, including those composed of ribbons, membranes, and ribbons/membranes, each with FEA results and corresponding optical images of experimental results. The transformations between the 3D shape I and shape II allow for controlled, strong degrees of twisting of structures to generate structural chirality in a propeller shape (Fig. 3A). Additionally, local twisting of ribbons or membranes in opposite directions creates folding deformations, as shown in the opening and closing of a box structure (Fig. 3B), and origami-inspired structures. The origami designs rely on patterns in PI/copper (3 µm/1 µm in thickness) bilayers that create locations of folding deformations, specifically where the copper is selectively removed (fabrication procedures shown in SI Appendix, Fig. S4). The absence of copper decreases the bending stiffness by a factor of ∼7.8, thereby inducing folding deformations in the regions composed only of PI (referred to as creases). Various other examples of 3D morphable mesostructures created uniquely by buckling and twisting appear in SI Appendix, Fig. S5. SI Appendix, Fig. S6 shows 3 precursor designs that incorporate creases and/or cuts to create morphable structures, including a standing mesh (width: 98 µm) supported by frames, connected stages, and walls (3 structures in the right column in SI Appendix, Fig. S5). The quantitative agreement of the heights of these 3D structures in shape II between FEA and experiments (SI Appendix, Table S1) further validates the predictive feature of the assembly process.

Fig. 3.

Three-dimensional morphable mesostructures based on buckling and twisting with diverse geometries and materials. (A) Two-dimensional geometries, FEA predictions, and experimental images (optical) of a morphable 3D chiral, propeller structure. (B) Two-dimensional geometries, FEA predictions, and experimental images (optical) of a morphable 3D box structure. Shape I and shape II correspond to the 3D shapes after releasing of the stretching mode (prestrain from 100 to 40%) and releasing of the rotating mode (prestrain from 40 to 0%). (C) Two-dimensional geometries, FEA predictions (showing normalized displacements in z direction), and experimental images (optical) of an array of creased structures based on twisting-induced folding. (D) Two-level square substrate cut pattern, 2D geometries, FEA predictions, and experimental images (optical) of a structure with multiple creases. (E) FEA predictions and experimental images (optical) of 3 mesostructures constructed with diverse materials. Scale bars, 1 mm for structures in A–D; 2 mm for Cu structures (E, Top); and 500 μm for Si/SU8 and SMP structures (E, Middle and Bottom).

The twisting-incorporated assembly process provides access to a wide range of sophisticated 3D architectures, including those in which the shapes change significantly at different stages of release of the substrate. SI Appendix, Fig. S7 presents flower-like structures that consist of 2 levels of connected, arrow-like features (overall lateral dimension: 12.9 mm, smallest width: 90 µm, thickness: 9 µm) where the associated “legs” bond to targeted units of the substrate. Buckling (release of the prestrain from 100 to 40%) raises the arrow tips off of the substrate. Local twisting (prestrain 40–0%) of the 2 legs in opposite directions “closes” the arrows to a unified, upward arrangement. The transformations from 2D to various 3D shapes occur continuously and reversibly, controlled by mechanically stretching and releasing the elastomeric kirigami substrate.

Structures with lateral dimensions, characteristic feature sizes, and thicknesses as small as ∼250, 30, and 2 µm, respectively, can be achieved simultaneously (SI Appendix, Fig. S8A), with the potential to scale to much larger or smaller dimensions. The assembly process occurs in a single-step manner, applicable to arrays of isolated or connected structures, over large areas. SI Appendix, Fig. S8B presents an example of a collection of 3D architectures (precursors shown in SI Appendix, Fig. S8C) formed simultaneously, together with FEA simulations. Fig. 3C shows another design that incorporates sharp creases (length: 2.3 mm, width: 160 µm) along the central axis of each unit of the structure in an array that forms in a dense collection (13 structures in a 6 × 6 mm² area) of thin (thickness: 4 µm) wedge-type features (individual precursor shown in SI Appendix, Fig. S9). A similar array appears in SI Appendix, Fig. S10. Kirigami substrates with hierarchical patterns of cuts allow for enhanced sophistication in the rotations of selected bonding sites (36, 37), thereby creating various types of previously unobtainable architectures. Fig. 3D presents a corrugated structure (lateral dimension: 4 mm, thickness: 4 µm) that results from assembly on a substrate (60% prestrain) that has 2-level square cuts (substrate deformation shown in SI Appendix, Fig. S11). These 3D structures are potentially useful for a broad range of applications including novel manipulators, actuators, and textured surfaces for controlled wetting and adhesion.

In addition to PI, the same process applies equally well to many other types of thin-film materials, including copper (thickness: 3 µm), silicon (thickness: 1.5 µm)-epoxy (SU8, Microchem; thickness: 7 µm) bilayers (ribbon width: 130 µm; fabrication process illustrated in SI Appendix, Fig. S12), and shape memory polymer (SMP; thickness: 10 µm) (Fig. 3E). The use of SMP allows for the creation of freestanding 3D structures by leveraging its shape fixation property (38).

Incorporation of Twisting into Loading-Path Controlled Mechanical Assembly.

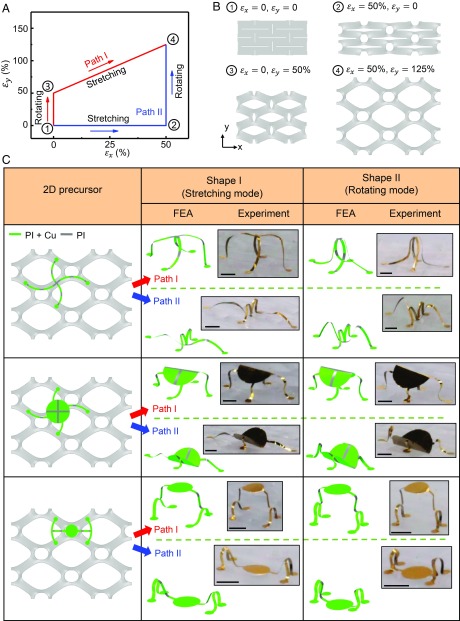
Controlled, temporal sequences in the release of prestrain along different directions, together with specialized precursor designs, can yield multiple, distinct modes of 3D buckling on biaxially prestrained elastomer platforms (39). This route to morphable structures is compatible with the types of kirigami platforms and rotational deformations introduced here. An example of stretching a kirigami substrate with a rectangular pattern of cuts (aspect ratio = 2.5; SI Appendix, Fig. S13) along 2 different loading paths appears in Fig. 4 A and B (this design avoids wrinkling that can occur in thin substrates (1 mm in thickness) with square patterns (aspect ratio = 1.0) under uniaxial stretching (SI Appendix, Fig. S14)). Loading path I corresponds to stretching from the fully released state (state 1) along the y axis to an intermediate state (state 3) in a rotating mode, then fully stretching to the final state (state 4) in a stretching mode. Along loading path II, the substrate passes through a stretching mode first (state 1–2), followed by a rotating mode (state 2–4). Through careful design of 2D precursors, release from state 4 to state 1 via these 2 different loading paths can create 4 distinct, morphable 3D shapes, driven by multistable buckling mechanics. Fig. 4C highlights 3 exemplary, origami-inspired precursor designs (PI/copper, 3 µm/1 µm in thickness), along with the FEA predictions and corresponding experimental (optical) images of such shape transformations (ribbon width: 150 µm; experimental images of precursors shown in SI Appendix, Fig. S15). The combination of loading-path controlled buckling mechanics and twisting enabled by kirigami substrates enables these and other unique and diverse shape morphing capabilities, as validated by computational modeling.

Fig. 4.

Morphable 3D mesostructures constructed by incorporating twisting into a loading-path controlled scheme for mechanical assembly on kirigami substrates. (A) Temporal sequence of changes in applied strains for 2 different loading paths. (B) Undeformed and deformed configurations of an elastomeric substrate with rectangular units (aspect ratio = 2.5) at different positions (corresponding to the positions in A) along the loading paths. (C) Two-dimensional geometries, FEA predictions, and experimental images (optical) of 3 morphable 3D mesostructures that result from different loading paths on kirigami substrates. (Scale bars, 1 mm.)

Mechanically Tunable Optical Chiral Metamaterials.

As mentioned previously, the 3D twisting deformations supported by the use of kirigami substrates provide access to strongly chiral structures, of potential utility in optics (9, 40, 41). Examples of chiral optical metamaterials include stacked-planar structures with mutually twisted patterns (42–44), 3D helices fabricated by direct laser writing and metal deposition (40), and 3D kirigami nanostructures fabricated by focused ion-beam milling and irradiation (9). The approaches introduced here allow access to these and other related geometries, with additional capabilities in the integration of semiconductors and other advanced materials in single or multilayered patterned layouts and in the reversible tuning of the geometries by elastic deformations of the assembly substrate. The latter creates opportunities in reconfigurable or switchable optical and optoelectronics components (45, 46).

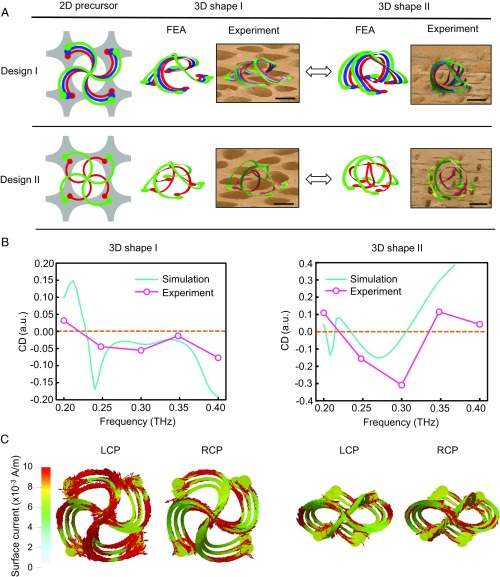
Fig. 5A presents 2 examples of microstructures [PI (2.2 µm in thickness) coated with Cr/Au (10 nm/100 nm in thickness)] assembled on kirigami substrates via transfer printing, consisting of a trilayer or bilayer of mutually twisted or conjugated rosettes. For each design, controlled release of the substrate provides access to 2 morphable 3D shapes. The distinct microscale (lateral dimension: 200–300 µm, ribbon width: 40 µm, diameter of contact pads: 70 µm) geometries of these 2 shapes give rise to mutually detuned resonant responses in the terahertz (THz) range. Experimental measurements of a helical microstructure (design I structure shown in Fig. 5A) under left-handed and right-handed circularly polarized light (LCP and RCP) exhibit wavelength-dependent chirality, or asymmetric absorption, in the 0.2–0.4 THz range (Fig. 5B, measured time-domain data shown in SI Appendix, Fig. S16). The circular dichroism (CD) characterizes the chirality, defined as CD = A(λ)_LCP − A(λ)_RCP, where A is the absorption and λ is the wavelength. The simulated CD spectral response (Fig. 5B) from finite-element method-based electromagnetic simulation (Methods) correlates with the experimental trends. The observed discrepancies may originate from structural imperfections and/or slight misalignments among the 3 layers during the transfer printing part of the fabrication process.

Fig. 5.

Applications of 3D morphable multilayered microstructures as mechanically tunable optical chiral metamaterials. (A) Two-dimensional geometries, FEA predictions, and scanning electron microscope images of 2 exemplary 3D morphable multilayered microstructures on kirigami substrates with 2 different 3D shapes. (B) Measured and simulated optical CD of a morphable 3D trilayer microstructure with two 3D shapes (design I in A) in the 0.2–0.4-THz frequency range. (C) Simulated time-averaged surface current distributions in the 3D morphable microstructure with two 3D shapes (design I in A) under LCP and RCP. (Scale bars, 200 µm.)

In addition, mechanically stretching and releasing the substrate allows for smooth modulation of the optical chirality among these 2 and intermediate states, via twisting/untwisting the trilayer helical structures. Notably, this type of mechanical tuning can flip the sign of the optical chirality in certain ranges of frequencies. For instance, LCP light absorbs more strongly than RCP light at 0.36 THz in shape I; the opposite is true for shape II, as indicated in the numerically simulated induced surface currents (Fig. 5C). Electromagnetic simulations also suggest that increased levels of tunable optical chirality can be achieved in arrays of such microstructures (SI Appendix, Fig. S17).

Conclusions

In summary, the concepts described here provide means for introducing well-controlled twisting deformations into processes for mechanically driven geometrical transformation of planar, 2D structures into 3D architectures. The results enable key features, such as out-of-plane helical layouts, that were previously impossible to achieve. The approach utilizes elastomeric substrates with patterns of cuts that lead to deformations including both local rotation and elongation under applied strain, in distributions that can be designed precisely by use of computational approaches. Upon release of applied strain, these platforms impart forces and torques to lithographically defined positions across 2D precursors bonded to their surfaces, to affect 2D to 3D transformation. Over a dozen 3D morphable mesostructures with length scales ranging from micrometers to centimeters, across material classes from polymers and metals, to inorganic semiconductors assembled on kirigami substrates, illustrate the key ideas and validate the utility of computational modeling as a design tool. A mechanically tunable optical chiral metamaterial structure serves as an application example, where a 3D multilayer geometry with local twisting shape transformations gives rise to broadband modulation of resonant dichroic responses in the THz frequency range. The compatibility of these ideas and schemes with advanced thin-film materials and planar microsystems technologies suggest a significant breadth of opportunities in 3D reconfigurable electronic/optoelectronic metamaterials, biomedical devices, and many others.

Methods

Fabrication of 3D Morphable Mesostructures on Kirigami Substrates.

Preparation of 2D precursors began with spin coating (3,000 rpm for 30 s) and curing (180 °C for 2 min) a thin layer of poly(methyl methacrylate) (PMMA) onto a clean glass slide, followed by spin coating and curing (260 °C for 1 h) a layer of polyimide (2–9 µm depending on pattern size; PI-2545, HD MicroSytems). A bilayer of chromium (Cr, 10 nm) and gold (Au, 100 nm) deposited on the PI layer by electron beam evaporation and patterned by photolithography and wet etching served as a hard mask for oxygen plasma etching of the PI. Immersion in acetone overnight dissolved the underlying PMMA layer, thereby allowing the structures to be retrieved from the glass slide and transferred to a water-soluble tape (polyvinyl alcohol, PVA). Deposition of Ti/SiO₂ (10 nm/50 nm in thickness) via electron beam evaporation through a shadow mask onto the back sides of the structures defined the bonding sites. A thin (∼0.7 mm) sheet of silicone elastomer (Dragon Skin, Smooth-On) with cuts created by laser ablation (VLS3.50, Universal Laser Systems; 40% power, 30% speed, and 1,000 pulses per inch) served as the kirigami assembly platform. Exposing the 2D precursors and the elastomer surface to surface hydroxyl groups created by exposure to UV-ozone facilitated bonding. Prestretching the elastomer to an equal biaxial strain of 100%, laminating the 2D precursors/PVA tape onto the stretched elastomer and heating (70 °C for 10 min) led to strong adhesion at sites registered to the rotating units in the kirigami elastomer. Dissolving the PVA tape with water and releasing the prestrain transformed the 2D precursors into 3D mesostructures.

Fabrication of 3D Origami-Inspired Mesostructures.

The process began by spin coating and curing PMMA (same procedure as described above) and PI (1,500 rpm for 60 s, 3 µm in thickness) on a glass slide, followed by the deposition of titanium (Ti, 10 nm) and copper (Cu, 1 µm) by electron beam evaporation. Photolithography and wetting etching defined the Cu pattern. Deposition of a layer of Cr/Au (10 nm/100 nm in thickness) followed by photolithography and wet etching yielded a hard mask for oxygen plasma etching of the PI. The remaining steps followed the procedures described above.

Fabrication of 3D Silicon/SU8 Mesostructures.

Preparation of the 2D precursors began with patterning the top silicon layer (1.5 µm in thickness) on a silicon-on-insulator wafer using photolithography and dry etching of silicon, followed by spin coating (3,000 rpm for 30 s) and baking of an adhesive layer (Omni-coat). Spin coating (3,000 rpm for 40 s; 7 µm in thickness) and lithographically patterning a photodefinable epoxy (SU8, Microchem) created a supporting layer for the silicon. Oxygen plasma etching (190 mT, 100 W, 1 min) removed the exposed adhesive layer. A brief (90-s) immersion of the sample in hydrofluoric acid (HF, 49%) partially undercut the SiO₂ layer. Another photolithography step using AZ 5214 on top of the SU8 layer defined the bonding sites. Immersion in HF (49%) for 4 h fully undercut the SiO₂. Electron beam evaporation then formed a bilayer of Ti/SiO₂ (10 nm/50 nm in thickness). The remaining steps (transfer printing, buckling) are similar to the procedures described above. Cleaning the 2D precursor by immersion in acetone removed the AZ 5214 before buckling.

Fabrication of 3D Freestanding Mesostructures Using SMP.

Preparation of the 2D precursors began with spin coating a thin layer of water-soluble polymer [poly(4-styrenesulfonic acid), Sigma-Aldrich] onto a glass slide, followed by spin coating (3,000 rpm for 60 s; 10 µm in thickness) a mixture of epoxy monomer E44 (molecular weight ∼450 g/mol, China Petrochemical Corporation) and curing agent poly (propylene glycol) bis (2-aminopropyl) ether (Jeffamin D230, Sigma-Aldrich) with a weight ratio of 44:23. After baking the mixture (110 °C for 1 h) in an oven, a thin layer of Cr/Au (10 nm/50 nm) deposited on the SMP by electron beam evaporation and patterned by photolithography and wet etching formed a hard mask for oxygen plasma etching of the SMP. Immersion in water for 48 h dissolved the underlying water-soluble polymer and enabled transfer of the 2D precursors to a PVA tape. Deposition of Ti/Au/Ti/SiO₂ (5 nm/100 nm/5 nm/50 nm in thickness) via electron beam evaporation through a shadow mask defined the bonding sites. The buckling steps followed the procedures described above. Thermal treatment (70 °C for 5 min) in an oven fixed the shapes of the buckled 3D SMP structures, and immersion of the 3D structures on the stretched elastomer in Au etchant for ∼5 h released the structures from the elastomer substrate and removed the Au layer.

Modeling of Mechanically Guided Buckling and Twisting.

Computational models of postbuckling analyses used FEA software (ABAQUS) to predict the final 3D configurations. We used 8-node solid elements (C3D8R) and 4-node shell elements (S4R) for the silicone substrate and 2D precursors, respectively. Convergence of mesh sizes was tested to ensure computational accuracy. Frictionless contact was implemented to model the interface between 2D precursors and substrate. The hyperelastic model following the Mooney–Rivlin law described below,

$$U=C_{10}\left({\overline{I}}_1-3\right)+C_{01}\left({\overline{I}}_2-3\right)+\frac{1}{D_1}{\left(J^{el}-1\right)}^2,$$

was employed for the simulation of silicone substrate deformation, where $C_{10}$ = 0.02228 MPa, $C_{01}$ = 0.7228 MPa, and $D_1$ = 0.72289 MPa⁻¹, given by the initial elastic modulus $E_{substrate}$ = 0.166 MPa and the Poisson ratio ${\nu }_{substrate}$ = 0.49 for isotropic elastic material at small strain. Linear elastic material models were used for PI, copper, silicon, and SU8 given the small strain. The elastic modulus (E) and Poisson’s ratio $\left(\upsilon \right)$ are E_PI = 2.5 GPa and $\upsilon$_PI = 0.34 for PI; E_Cu = 119 GPa and $\upsilon$_Cu = 0.34 for copper (Cu); E_Si = 130 GPa and $\upsilon$_Si = 0.27 for silicon; E_SU8 = 4.02 GPa and $\upsilon$_SU8 = 0.22 for SU8. For the SMP used in this work, a multibranch viscoelastic model is described with parameters listed in previous work (38).

Modeling of Optical Chirality of 3D Microstructures.

The numerical simulation of 3D chiral microstructures used the commercial finite-element method package CST (Computer Simulation Technology GmbH). The geometrical configuration meshes exported from the mechanical model, including the substrate and the microstructure at both stages, defined the material boundaries. The simulation used plane-wave excitation, with LCP and RCP. The calculation of the dissymmetry factor g, i.e., the normalized CD determining the chiral interaction observed at the far field, used the calculated scattering cross-sections σ: g = 2(σ^RCP − σ^LCP)/(σ^RCP + σ^LCP). At representative frequencies the surface current supported by the microstructure was extracted, for both polarizations, and numerically rendered using ParaView vector field visualization.

Terahertz Electromagnetic Measurements.

A 1-mm-thick <110> ZnTe crystal excited by 35-fs, 800-nm pulses produced by a Ti:sapphire amplifier at a 1-kHz repetition rate generated the terahertz beam. Another identical ZnTe crystal detected the transmitted THz beam via the standard electrooptic sampling technique with a weak 800-nm probe pulse, matched photodiodes, and lock-in detection. The use of 2 identical quarter-waveplates (optimal at 0.3 THz) converted the polarization of the terahertz beam between linear polarization and circular polarization. A Fourier transform converted the measured time-domain electric field strength data (20-ps duration with 0.05-ps time step) to frequency spectra.