Solar thermal desalination as a nonlinear optical process

Significance

One critical challenge of solar thermal distillation is the need to collect and focus sunlight, since purified water output increases with increasing solar intensity. Here we show substantial increases in the efficiency of solar thermal distillation by redistributing direct sunlight intensity with small focusing elements rather than by increasing overall intensity with large solar concentrators. This is because solar thermal distillation depends upon the saturation vapor pressure of water, which has an exponential temperature dependence, making purified water output exponentially dependent upon light intensity. This observation should redirect design efforts to focus on exploiting this nonlinearity, rather than increasing solar collector size, for higher-performance solar water purification systems within a small footprint, suitable for portability and use in remote locations.

Abstract

The ever-increasing global need for potable water requires practical, sustainable approaches for purifying abundant alternative sources such as seawater, high-salinity processed water, or underground reservoirs. Evaporation-based solutions are of particular interest for treating high salinity water, since conventional methods such as reverse osmosis have increasing energy requirements for higher concentrations of dissolved minerals. Demonstration of efficient water evaporation with heat localization in nanoparticle solutions under solar illumination has led to the recent rapid development of sustainable, solar-driven distillation methods. Given the amount of solar energy available per square meter at the Earth’s surface, however, it is important to utilize these incident photons as efficiently as possible to maximize clean water output. Here we show that merely focusing incident sunlight into small “hot spots” on a photothermally active desalination membrane dramatically increases––by more than 50%––the flux of distilled water. This large boost in efficiency results from the nearly exponential dependence of water vapor saturation pressure on temperature, and therefore on incident light intensity. Exploiting this inherent but previously unrecognized optical nonlinearity should enable the design of substantially higher-throughput solar thermal desalination methods. This property provides a mechanism capable of enhancing a far wider range of photothermally driven processes with supralinear intensity dependence, such as light-driven chemical reactions and separation methods.

Currently, half of the population of the world faces water scarcity (1, 2). One possible solution to meet this increasing water demand is to efficiently convert abundant alternative water sources, such as seawater, brackish water, processed water, or underground reservoirs to potable water (1–4). Because of the increasing energy consumption and cost of conventional water purification technologies like reverse osmosis (5) with increasing water salinity, there has been a rapidly increasing demand for the development of sustainable distillation methods. As a result, a general approach of using localized photothermal heating to drive solar water purification processes has been a topic of intense recent research interest worldwide, and many variations of this process have recently been demonstrated (6–24). One approach for water purification, powered by sunlight and appropriate for portability to remote locations, is nanophotonics-enabled solar membrane distillation (NESMD) (25). This process relies on a membrane coated with broadband light-absorbing nanoparticles that, when illuminated by sunlight, provides localized heating (11, 21) of the input saline water flowing along the illuminated side of the membrane. This induces evaporation through the membrane, and distilled water is condensed on the membrane’s opposite side. By locally focusing incident sunlight onto the light-absorbing face of the membrane, we observe dramatic increases in the distillate flux. The multilens array, directly arranged on the device surface, generates heterogeneous intensity patterns while keeping the total input power constant. The large flux increases are conceptually distinct from what could be achieved by increasing the total intensity and power, for example, by using solar concentrators. In fact, the presence of lenses at the input face is likely responsible for a small decrease in total absorbed sunlight due to back-reflection.

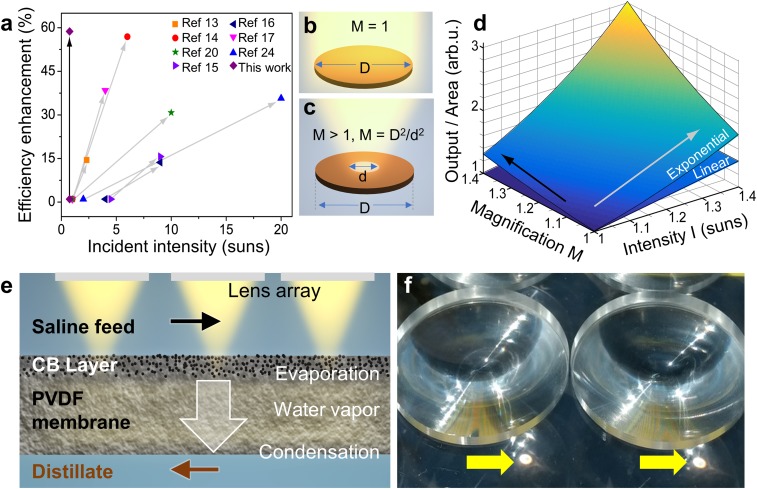
Many groups (13–17, 20, 24) have also observed sizable increases in distilled water flux by increasing solar intensity in localized heating-based systems (Fig. 1A), but thus far this effect has remained unexplained. The observed increases in distillate flux have been shown to result in an increase in efficiency, which has been attributed to the increased steam temperature (13, 14, 17, 20). Here we show that the origin of this distillate flux enhancement arises from the exponential dependence of the saturation vapor pressure of water on temperature [p_sat(T)] (26). Since the temperature increase in these systems is in a range that scales approximately linearly with optical intensity, the solar distillation process is exponentially dependent on optical intensity. Based on this realization, we show that focusing elements, like an array of lenses directly on the input surface of a photothermal membrane distillation system, can substantially increase the distillate flux without increasing device footprint.

Fig. 1.

Signal/output per unit area of linear and nonlinear processes at different intensities and magnifications: NESMD with lens array. (A) Efficiency enhancement under one sun illumination––this work––compared with several solar thermal devices described in the literature that showed efficiency enhancements with increasing solar intensity on the active device surface. (A and B) Schematic of uniform illumination of a circular area of diameter D. (C) Schematic of focused illumination at a spot diameter d by light focusing, defining magnification M. (D) Output per unit area for linear and exponential processes for different illumination intensities and different values of magnification. (E) Schematic of the cross-section of a solar thermal membrane distillation device under focused illumination. Saline feed and purified distillate flow are on the top and bottom, respectively, of a CB-coated PVDF membrane in a countercurrent configuration. The illuminated area is covered with a lens array to concentrate the incident light on the coated membrane surface. (F) Close-up photograph of part of the input face of the 4 in. × 8 in. NESMD device with a 2-in.-diameter Fresnel lens array showing ∼5-mm localized spots of focused sunlight (yellow arrows).

Processes that scale linearly with light intensity, such as photocurrent generation, are limited by the active area of a device, but processes that scale supralinearly with incident light are instead constrained by light intensity. For example, light-driven chemical reactions (27–31) are nonlinear functions of input light intensity because of their Arrhenius temperature dependence. A rigorous expression for the temperature dependence of the saturation vapor pressure of water can be obtained from the second law of thermodynamics, by integrating the Clausius–Clapeyron equation (26). In practice, semiempirical correlations for ${\text{p}}_{\text{sat}}\left(\text{T}\right)$ can be used to fit tabulated data. In the range between 20 and 90 °C, the regime of most solar thermal desalination demonstrations, the saturated vapor pressure of water can be well-approximated by an analytical exponential relation, ${\text{p}}_{\text{sat}}\left(\text{T}\right)={\text{p}}_0{\text{e}}^{\text{γT}}$, with ${\text{p}}_0$ as the base pressure at 0 °C and $\text{γ}$ as the fitting parameter (SI Appendix, Fig. S1). All calculations in the work reported here employed more accurate fittings (i.e., Antoine equation) for ${\text{p}}_{\text{sat}}\left(\text{T}\right)$ (Methods and SI Appendix, sections 1, 2).

The effect of light focusing on processes that vary linearly and exponentially with incident light intensity, as parametrized by lens magnification, is shown in Fig. 1 B–D. We examine the simple case of uniform light illumination of a circular surface with diameter $\text{D}$ (Fig. 1B) with light focusing to a smaller area with diameter $\text{d}$ (Fig. 1C) scaled by the magnification factor $\text{M}={\text{D}}^2/{\text{d}}^2$. With light focusing, an $\text{M}\times$ smaller active area gets illuminated with $\text{M}\times$ larger intensity at the same incident power. This illustrates how an exponentially nonlinear optical process improves substantially with increased magnification for a given light intensity, easily overcoming the reduction in illumination area. Fig. 1D shows the influence of light magnification (black arrow) and light intensity (gray arrow) on an exponentially nonlinear optical process compared with a linear process, where an array of lenses covers the surface area of a light-driven system under natural incident intensity (sunlight). A magnification of M = 1 describes a lensless system where, with increasing intensity, the output is enhanced for both a linear and an exponential light-dependent process. The output per area due to the exponentially nonlinear process of solar thermal distillation is enhanced by increasing both intensity and light focusing. The apparent gain for the linear case would be lost upon normalization to the total light-collecting area if the larger values of light intensities originate from a larger area, such as with a solar concentrator. A schematic of the NESMD (25) system under an array of focusing elements is shown in Fig. 1E, and a photograph of the input face of the device, where the focusing spots are clearly observable, are shown in Fig. 1F.

Two solar thermal membrane distillation devices with dimensions 4 in. × 8 in. and 4 in. × 16 in. were fabricated (SI Appendix, Fig. S2). The polyvinylidene difluoride (PVDF) membranes were coated with a carbon black (CB) nanoparticle-laden surface layer using a scalable, spray-based coating method (Methods and SI Appendix, section 3). CB nanoparticles were embedded up to ∼5 μm below the surface of the hydrophobic PVDF membranes facilitating the concentration of light energy within this thin top layer (21) (SI Appendix, Figs. S3 and S4). Square arrays of 1-in.- (focal length f = 25 mm) and 2-in.-diameter (f = 32 mm) Fresnel lenses were positioned above the input face of the membrane by means of a custom-made, grooved acrylic sheet so that the focal spot diameter was ∼5 mm for both lens arrays (Fig. 1 E and F).

The solar experiments were conducted at Alamogordo, New Mexico, USA (32.8995° N, 105.9603° W) under an average solar intensity of ∼700 W/m² (see Methods for details). The purified water fluxes for both devices with and without the lens arrays are shown in Fig. 2A. For unfocused solar illumination, both systems (gray bars) produce a distillate flux that almost doubles with the twofold increase in active device area demonstrating the scalability of this approach (25). For the 4 in. × 8 in. system, increases of ∼38% and ∼58% were observed in the distillate flux with 1- and 2-in.-lens arrays, respectively, relative to the lensless case. The flux increases observed for the 4 in. ×16 in. system were ∼22% and ∼30%, respectively. The larger flux increases for the shorter length device can be explained by the lower intrinsic efficiency of the 8-in. lensless device relative to the 16-in. one (gray bars in both cases, see SI Appendix, section 4). In all experiments, a faster distillate speed, 50 mL/min (still within the laminar flow regime, see SI Appendix, section 8), was maintained compared with the feed speed of 5 mL/min to more efficiently remove heat from the membrane–distillate interface, sustaining vapor diffusion across the membrane. This is easily achievable with two independent pump systems and separate reservoirs for the fluids.

Fig. 2.

Effect of light focusing on temperature and distillate flux in NESMD systems. (A, Left) Comparison of distillate flux rates of the 4 in. × 8 in. and 4 in. × 16 in. NESMD systems without lens array (gray), with 1-in.-diameter lens array (blue), and with 2-in.-diameter lens array (red). These values correspond to the purified water flux contribution obtained by solar illumination by subtracting the distillate flux values obtained for the same NESMD system in the dark. Experimental flux rates (solid bars); theoretical flux rates (cross-hatched columns). (Right) photographic images of 4 in. × 8 in. NESMD device input face without lens array (gray border), with 1-in.-lens array (blue border), and with 2-in.-lens array (red border). (B) Simulated temperature maps for 4 in. × 8 in. NESMD systems (i) without lens array, (ii) with 1-in.-lens array, and (iii) with 2-in.-lens array. (C) Simulated distillate flux maps for 4 in. × 8 in. NESMD systems (i) without lens array, (ii) with 1-in.-lens array and (iii) with 2-in.-lens array. Solar intensity is 0.7 kW/m²; feed and distillate input temperatures are 20 °C. Feed and distillate speeds are 5 mL/min and 50 mL/min, respectively. Thickness of both feed and distillate channels is 2 mm.

A finite element method-based model incorporating photothermal heating, Navier–Stokes equations for fluid dynamics, Fourier equations for thermal transport, and diffusion equations for mass transfer was used to analyze the effect of light focusing on distillate flux (see Methods for details). The theoretical flux values shown in Fig. 2A (cross-hatched columns) were calculated by averaging the flux for CB layer thicknesses in the range of 2–5 μm (SI Appendix, Fig. S5) and agree well with the experimental values.

The substantial increases in distillate flux due to focusing can be explained in terms of the nonlinear temperature dependence of ${\text{p}}_{\text{sat}}$. The lens array redistributes the incident light, creating quasi-2D “hot spots” in the light-absorbing region of the membrane, where rapid evaporation occurs. The enhanced flux in the hot spots more than counterbalances the reduction in flux in the rest of the device, resulting in an overall higher flux rate. Simulated temperature maps for the 4 × 8 in. device without lenses and with 1- and 2-in.-lens arrays are shown in Fig. 2B with corresponding distillate flux rates shown in Fig. 2C. The temperature distribution for the lensless cases is homogeneous, with a 3–4 °C temperature increase (SI Appendix, section 5 and Fig. S6). However, with focusing, the focal spot regions reach substantially higher temperatures, inducing confined regions of high water vapor concentration with dramatically increased diffusion through the membrane (Fig. 2C and SI Appendix, Fig. S7). Localized distillate flux rates up to ∼30 kg/m²⋅h appear to be achieved in the d = 5 mm hot spots of the 4 in. × 8 in. device created by the 2-in.-lens array (Fig. 2 C, iii). The corresponding localized flux rates for a 4 in. × 16 in. device appear to be as high as ∼50 kg/m²⋅h (SI Appendix, Figs. S9 and S10).

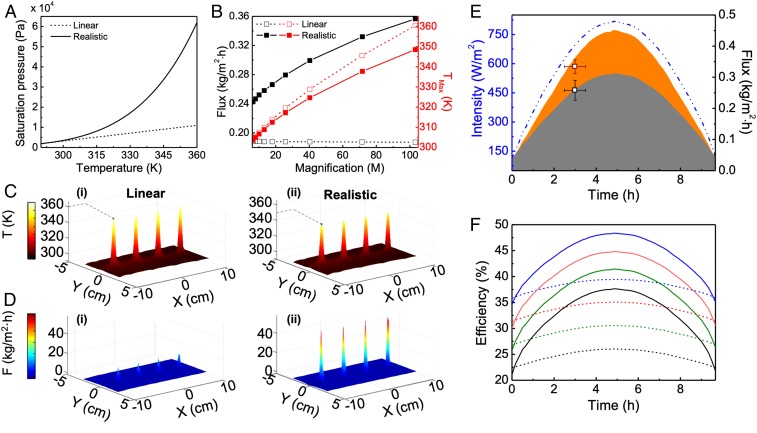
To better understand how the nonlinearity in the system increases the flux rates, we compare the distillate flux yields calculated using the realistic (exponential) (32) versus linearized ${\text{p}}_{\text{sat}}\left(\text{T}\right)$ (Fig. 3A) near room temperature. The average flux rates (black lines) and highest temperatures $\left({\text{T}}_{\text{Max}}\right)$ reached (red lines) for a 4 in. × 8 in. membrane with a 2-in-lens array for different magnification factors are shown in Fig. 3B. The linear slope changes the base flux value but does not affect the trend of flux rates with increased focusing (SI Appendix, section 6 and Fig. S10). The exponential and linear models exhibit similar ${\text{T}}_{\text{Max}}$ trends (red curves in Fig. 3B) with the sublinear ${\text{T}}_{\text{Max}}$ increase in the exponential case resulting from heat transfer between the thin hot spots and the feed channel (SI Appendix, section 7). However, only the realistic model yields a significant increase of the flux rate with focusing, highlighting the role played by ${\text{p}}_{\text{sat}}$ in the distillation process. Even if many parameters of the distillation process depend on temperature, ${\text{p}}_{\text{sat}}\left(\text{T}\right)$ can be identified as the leading cause of the nonlinear trend observed (SI Appendix, section 9).

Fig. 3.

Comparison of results for realistic and linearized models of ${\text{p}}_{\text{sat}}$. (A) Saturation pressure variation with temperature for the realistic (solid) and linear (dashed) models of ${\text{p}}_{\text{sat}}$. (B) Simulated flux (black) for linear (dashed) and realistic (solid) models with magnification for a 4 in. × 8 in. system with 2-in.-diameter lens array. Simulated ${\text{T}}_{\text{Max}}$ (red, right axis) for linear (dashed) and realistic (solid) models for increasing magnification $\text{M}$. (C) Simulated (i) temperature maps for (i) linear and (ii) realistic models; (D) Simulated flux maps for (i) linear and (ii) realistic models. (E) Calculated flux production from 4 in. × 16 in. NESMD with 2-in.-diameter lens array with 5-mm focal spots (orange area) and bare NESMD (dark-gray area) under varying solar intensity (dashed blue line) for more than 9 h. (F) Comparison of efficiencies of a lensless 4 in. × 16 in. NESMD (dashed lines) and 4 in. × 16 in. NESMD with 2-in.-diameter lens array with 5-mm focal spots (solid lines) for different ambient temperatures [20 °C (black), 25 °C (green), 30 °C (red), 35 °C (blue)] for solar intensity variations shown with dashed blue line in E. Feed and distillate speeds are 5 mL/min and 50 mL/min respectively.

While the temperature maps for the linear (Fig. 3 C, i) and realistic models (Fig. 3 C, ii) are comparable, the flux maps (Fig. 3 D, i and ii) show remarkable differences, with the flux in the realistic model being ∼5× larger than in the linear case. This observation explains the flux increases with intensity observed in other solar distillation systems (13–17, 20, 24) as being fundamentally due to the exponential nature of ${\text{p}}_{\text{sat}}\left(\text{T}\right)$.

A simple explanation for why the lensed system is more efficient can be obtained from energy considerations. Solar thermal membrane distillation can be viewed as an ensemble of thermal processes where, in steady state, the heat generated through light-to-heat conversion eventually has to dissipate. The relevant thermal processes are heat used to evaporate water, heat lost to the feed and distillate leaving the device, and the latent heat of condensation, as vapor is transported through the membrane. Since heating of the distillate is primarily due to the condensation of fresh water, the only process associated with loss is heat transported out by the feed. By increasing the local temperature, due to the nonlinear dependence of ${\text{p}}_{\text{sat}}\left(\text{T}\right)$, the energy transfer pathways are altered to promote the efficient evaporation of water, while minimizing the loss of heat via the exiting feed flux. This is illustrated in SI Appendix, Fig. S10, which shows that feed output temperature decreases with magnification for the realistic ${\text{p}}_{\text{sat}}\left(\text{T}\right)$ model. Moreover, as reported in Fig. 3B, the ${\text{T}}_{\text{Max}}$ trend shows larger values for the linear case which is consistent with evaporation being a cooling mechanism for the feed: Larger distillation rates reached for the realistic model imply lower temperature hot spots. While the overall energy balance is not affected by the lenses, light concentration allows heat to be redistributed among the different thermal transport phenomena to promote water evaporation.

To observe the effect of light focusing on solar thermal membrane distillation under realistic operating conditions, we monitored purified water production under naturally varying sun intensities with and without a 2-in.-lens array over a 9-h period (Fig. 3E and SI Appendix, Fig. S20). The experimental flux rates under these same conditions were obtained at hour 3 only, to avoid reorientation of the unit to follow the motion of the sun. At an ambient temperature of 20 °C, the 4 in. × 16 in. system with the 2-in.-lens array yields a water production rate of 2.79 L/m²⋅per day, a 27% increase over the 2.04-L/m²⋅per day for the lensless case. Additional increase in flux rates can be obtained at higher ambient temperatures due to an increased water vapor concentration across the membrane (25) (SI Appendix, sections 10–12 and Figs. S18–S20). Larger flux rates directly translate to higher efficiencies, as shown in Fig. 3F for varying ambient temperatures. Solar thermal membrane distillation with lenses always exhibits higher efficiencies, especially at peak sunlight, for all ambient temperatures considered.

While similar efficiency increases could be achieved using conventional solar concentrators, multilens arrays have practical advantages like direct application to device surface without requiring any additional infrastructure. They also allow partial focusing even without sun-tracking mechanisms since the majority of lens foci should fall on the active device area for a wider range of incident angles. Furthermore, they can be combined even with nonflat surfaces for additional design flexibility. They also achieve equal flux to the case without multilens focusing at lower incident solar intensities (SI Appendix, Fig. S18). For solar photothermal desalination, increased flux rates have a direct impact on the minimum area necessary to achieve a desired water production rate, diminishing its footprint and reducing its cost. Taking advantage of this nonlinear behavior will also open the door to substantially higher throughput solar desalination designs. Similar enhancements should be achievable in any photothermally driven system where the underlying process scales supralinearly with temperature and concomitantly, light intensity, such as solar-driven chemical reactors (27–29) and separation processes (33). The incorporation of more advanced focusing systems such as metasurfaces (34, 35) and plasmonic nanoantennas (36) capable of subwavelength light focusing are likely to further boost the efficiencies and performance of photothermal distillation systems.

Materials and Methods

Membrane Fabrication with Spray Coating.

Scalability is one of the many advantages that a solar thermal membrane distillation system has over conventional membrane distillation (MD). To be able to practically scale up this approach, the method to coat evaporating membrane has to be scalable as well. PVDF membranes were chosen as the diffusion media due to their high hydrophobicity, good mechanical strength, chemical and thermal stability, and high oxidation resistance (37). A previously demonstrated electrospinning method (25) to coat the PVDF membrane becomes expensive and time-consuming when attempting to coat large membrane surfaces. Here, we have developed a low-cost time effective method to coat the PVDF membrane (Pall Corp.) with CB nanoparticles. The costing solution is prepared by dissolving 150 mg CB (Cabot Corp.) and 50 mg poly(vinyl alcohol) (PVA) (Sigma Aldrich, 87–90% hydrolyzed, average molecular weight 30,000–70,000) in 50 mL ethanol. The solution is then sonicated for 1 h. The same PVA (100 mg) is dissolved in 50 mL deionized (Millipore) water. CB solution is spray coated with an airbrush (Master Airbrush) and air compressor (Airbrush-Depot model TC-20) onto the PVDF membrane followed by drying in ambient conditions. It is important to not wet the membrane while spraying the CB solution as this may lead to the CB nanoparticles getting adsorbed deep into the PVDF membrane, reaching the bottom side of the membrane. Spray coating a thin layer of the ethanol solution allows quick evaporation and leads to the CB nanoparticles (NPs) getting adsorbed into a few-micrometers-thick layer at the top of the PVDF. The PVDF membrane is hydrophobic whereas the CB nanoparticles are hydrophilic; therefore, adding PVA to the CB solution helps in adhering CB nanoparticles to the PVDF surface. After spray coating each layer uniformly, it is blown dry with nitrogen. Following five layers of CB, two layers of the PVA in deionized water solution are spray coated to make sure that the nanoparticles adhere well to the substrate. The process is repeated five times (for a total of 35 layers) until a uniform black coat of CB is formed on the substrate. This process can further be used to coat any length of the PVDF membrane. To allow the PVA to cross-link and better stick to the surface, the spray-coated membrane is placed under direct sunlight for 1 h. SI Appendix, Fig. S3A shows a photograph of an ∼80-cm-long PVDF membrane uniformly spray coated with CB nanoparticles. We have successfully been able to coat >2-m-long PVDF membranes manually. Scanning electron microscopy images of the spray-coated PVDF membranes confirm that the carbon nanoparticles do not block the membrane pores and create uniform coverage on the membrane surface as shown in SI Appendix, Fig. S3 B and C. The ability to coat any size of the PVDF membrane can allow one to build an NESMD device with a desired purified water capacity for any given application. Comparison of Monte Carlo simulations and the diffuse reflectance of the spray-coated CB coatings shows that the spray-coating method can result in more absorptive CB coatings compared with those produced by electrospinning (25) (SI Appendix, Fig. S4). There is a balancing act to producing optimal CB absorbing layers. Increasing the concentration of CB increases the absorption of sunlight, but also blocks more membrane pores. The concentration of CB nanoparticles providing high absorption coefficient with minimally loading the membrane is obtained by comparing the experimental and Monte Carlo simulated diffuse reflectance for PVDF membranes with increasing CB nanoparticle concentrations (SI Appendix, Fig. S4). The experimental diffuse reflectance spectra are obtained for the CB coating with increasing numbers of spray-coated layers using UV-vis–near-infrared spectrophotometer (Agilent Cary 5000). The cross-sectional image of the CB-coated PVDF membrane shows that the CB nanoparticles penetrate a depth of 3–5 μm on top of the membrane surface. Considering an average CB nanoparticle layer thickness of 3 μm and the scattering coefficients for the PVDF and PVA layers (25) we chose the coating layers corresponding to absorption coefficient of around 3,200 cm⁻¹ for this study to get maximum solar absorption with minimal CB particle loading of 0.1 mg/cm² (SI Appendix, Fig. S4). The salt rejection for the spray-coated membrane is >99%. It is calculated using the percentage reduction in salinity from feed to distillate (25).

Experimental Conditions.

The device framework was constructed out of polycarbonate (38). The experimental module components are shown in SI Appendix, Fig. S2. The saline feed is flowed on top of the CB spray-coated PVDF membrane. The distillate is maintained in a closed loop on the bottom of the membrane and any addition to the distillate from the evaporation through the membrane is recorded from the mass gain in the loop with a weighing scale (Torbal AD500) in real time. Both the 1-in. (Thorlabs FRP125 - Ø1-in. Fresnel lens, f = 25 mm) and 2 in.-(Thorlabs FRP232 - Ø2-in. Fresnel lens, f = 32 mm) diameter Fresnel lens array is incorporated on grooved and machined 5-mm-thick acrylic sheets on top of the device. The saline feed glass container is placed inside the water bath (SoCal Biomed) whereas the closed loop on the distillate side has a 1-m-long copper tube inserted in the water bath to maintain equal input temperatures for feed and distillate. Peristaltic pumps (Cole Parmer, UX-73160-32) are used to maintain the feed speed of 5 mL/min and distillate speed of 50 mL/min.

Finite Element Method Modeling.

Modeling has been performed using COMSOL Multiphysics 5.3a. The details of the model for solar thermal membrane distillation systems can be found elsewhere (25). Here we summarize the adopted method and we expand over the features introduced in this work (SI Appendix, Figs. S11–S16). The model features two countercurrent flows for feed and distillate, which are described by laminar flows with low Reynolds number (SI Appendix, section 8). The speeds at which feed and distillate enter the device at ambient temperature are given by ${\text{Q}}_{\text{feed}}=5/\text{min}$ and ${\text{Q}}_{\text{dist}}=50\hspace{0.17em}\text{mL}/\text{min}$, respectively. The effect of lens array addition is modeled as a heterogeneous heat source distribution. Heat sources are modeled by thin cylinders with diameters equal to the lens focal spot diameter and with a height equal to the penetration depth of CB NPs in the PVDF membrane,${\text{t}}_{\text{abs}}$, estimated to be between 2 and 5 µm; see SI Appendix, Fig. S12. In these regions, the heat source distribution is homogeneous on the XY plane and exponentially decreases in the Z direction as ${\text{Q}}_{\text{focus}}\left(\text{z}\right)={\text{αMI}}_1{\text{e}}^{-\text{αz}}$, where $\text{α}=3.2\times {10}^5{\text{m}}^{-1}$ is the estimated CB NPs absorption coefficient and $\text{M}={{\text{d}}_{\text{focus}}}^2/{{\text{d}}_{\text{lens}}}^2$ is the lens magnification ratio with ${\text{d}}_{\text{lens}}=2{\text{r}}_{\text{lens}}$. Additional heat sources are placed in the region not covered by the lenses which collect unfocused sunlight:${\text{Q}}_{\text{sun}}\left(\text{z}\right)={\text{αI}}_2{\text{e}}^{-\text{αz}}$. Given the presence of polycarbonate (refractive index ${\text{n}}_{\text{poly}}=1.58$) and the lenses (refractive index ${\text{n}}_{\text{lens}}=1.52$), the input intensities are ${\text{I}}_1={\text{I}}_0{\text{T}}_{\text{lens}}{\text{T}}_{\text{poly}}$ and ${\text{I}}_2={\text{I}}_0{\text{T}}_{\text{poly}}$, with ${\text{I}}_0$ being the natural sunlight intensity, ${\text{T}}_{\text{lens}}=1-{\left({\text{n}}_{\text{lens}}-1\right)}^2/{\left({\text{n}}_{\text{lens}}+1\right)}^2\cong 96\text{\%}$, and ${\text{T}}_{\text{poly}}=1-{\left({\text{n}}_{\text{poly}}-1\right)}^2/{\left({\text{n}}_{\text{poly}}+1\right)}^2\cong 95\text{\%}$. Water evaporation and condensation are modeled through molecular diffusion,$\nabla \cdot \left[\text{D}\nabla \text{c}\right]=0$, within the membrane where the temperature-dependent concentrations of water molecules at the feed/membrane and membrane/distillate interfaces represent the boundary conditions. $\text{D}$ is the diffusion coefficient of water molecules in air and it is estimated using Bruggemann’s correlation and depends here on the membrane porosity and temperature (25). Latent heat of evaporation/condensation is accounted for as a vapor-concentration-dependent heat flux which leaves the feed/membrane and enters the membrane/distillate interface:${\text{Q}}_{\text{evap}/\text{cond}}=\pm {\text{H}}_{\text{vap}}\left(\text{T}\right)\text{c}$. Additional exchanged heat fluxes include: emitted black-body radiation, ${\text{Q}}_{\text{rad}}=-\text{εσ}\left({\text{T}}^4-{\text{T}}_{\text{amb}}^4\right)$, which is here applied to the membrane surface where CB NPs are placed and considered as perfect emitters $\left(\text{ε}\approx 1\right)$ and natural convective losses, ${\text{Q}}_{\text{conv}}=-\text{h}\left(\text{T}-{\text{T}}_{\text{amb}}\right)$, applied to the polycarbonate surfaces with $\text{h}\approx 5\hspace{0.17em}\text{W}/\left({\text{m}}^2\text{K}\right)$. Heat transfer equations are solved in all of the domains and are coupled to Navier–Stokes equations which are solved in the feed and distillate channels and feature no-slip boundary conditions. The diffusion equation is solved in the membrane domain only. All of the utilized temperature-dependent parameters utilized in the model are reported in SI Appendix, section 9 and Figs. S15–S17) with grid size convergence (SI Appendix, Fig. S14) and Reynolds number under operational conditions (SI Appendix, Fig. S13).