Plastic responses to novel environments are biased towards phenotype dimensions with high additive genetic variation

Significance

Theory suggests that populations can evolve by genetic modification of environmentally induced responses. We demonstrate that such plastic responses to novel environments tend to occur along trait dimensions that have high genetic variation. This suggests that selection for or against environmentally induced phenotypes typically will be effective. That organisms respond to environmental novelty and genetic variation in similar ways can be explained by how development is wired. This makes it challenging to distinguish if plasticity or genetic constraints shape evolutionary responses following environmental change.

Abstract

Environmentally induced phenotypes have been proposed to initiate and bias adaptive evolutionary change toward particular directions. The potential for this to happen depends in part on how well plastic responses are aligned with the additive genetic variance and covariance in traits. Using meta-analysis, we demonstrate that plastic responses to novel environments tend to occur along phenotype dimensions that harbor substantial amounts of additive genetic variation. This suggests that selection for or against environmentally induced phenotypes typically will be effective. One interpretation of the alignment between the direction of plasticity and the main axis of additive genetic variation is that developmental systems tend to respond to environmental novelty as they do to genetic mutation. This makes it challenging to distinguish if the direction of evolution is biased by plasticity or genetic “constraint.” Our results therefore highlight a need for new theoretical and empirical approaches to address the role of plasticity in evolution.

Populations that encounter novel environments must often adapt to persist. The rate and direction of adaptive change depends on the phenotypic and genetic variation that is exposed to natural selection. The “plasticity-first” hypothesis proposes that environmentally induced phenotypic variation initiates and directs adaptive genetic divergence along particular trajectories (1, 2). This has been demonstrated experimentally (3, 4), and the observation that plastic responses sometimes are aligned with population divergence in morphology, physiology, and behavior makes it a plausible explanation for adaptive divergence in the wild (5–10). However, whether or not evolutionary divergence generally is disposed to follow the direction of environmentally induced phenotypes is contested and poorly understood (reviewed in refs. 2 and 11–14).

Adaptation following exposure to novel or stressful environments is hypothesized to involve the refinement, exaggeration, or elimination of ancestrally plastic responses through quantitative genetic change. This is possible only when there is heritable variation along the dimensions of the phenotype that are plastic. In quantitative genetics, this variation is described in terms of additive genetic variance and covariance between traits, commonly referred to as the G matrix. The predicted change in phenotype under directional selection on standing genetic variation has been considered a quantitative genetic estimate of evolvability (15). Quantitative genetic evolvability is highest in the direction of phenotypic space with the most additive genetic variance. All else being equal, quantitative genetic evolvability of environmentally induced phenotypes will therefore be high when the direction of phenotypic plasticity is well aligned with the axis of maximum additive genetic variation in novel environments. We refer to this alignment as the short-term evolutionary potential (ref. 1, p. 142) of environmentally induced phenotypes or plastic responses.

There are reasons to believe that the direction of plasticity and the main axis of genetic variation can be aligned. Both genetic and environmental perturbation produce their phenotypic effects through development, and phenotypes that are induced by mutation can often also be induced by environmental factors, and vice versa (1). The G matrix is partly a result of the distribution of mutational effects (in addition to, e.g., selective loss of variation) and will therefore tend to reflect how traits are coregulated in development (16). Indeed, models demonstrate that correlational selection can produce developmental interactions that channel the phenotypic effects of mutation along dimensions of trait combinations that were favored in the past (17–21). Since phenotypic accommodation involves the coordinated adjustment of traits that need to function together (1), it too relies on developmental interactions that likely are products of correlational selection. Selecting for environmentally induced phenotypes may therefore change developmental regulation of phenotypes such that it increases the additive genetic variation along the dimensions of the phenotype that are plastic (22). If so, it implies that selection in the direction or opposition of plastic responses to novel environments will typically be effective, which may predispose the population to evolve in the short term along the phenotype dimensions that are plastic.

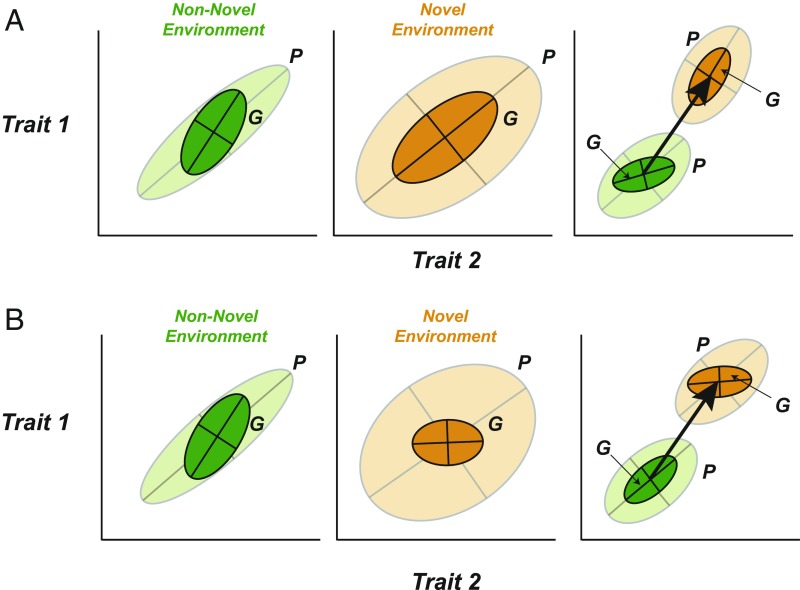
Here we use a meta-analysis to test if plastic responses are biased toward trait dimensions that harbor high levels of additive genetic variation. Plastic responses can be described by a “plasticity vector” that quantifies the change in mean phenotypic trait values between two environments, expressed as the distance between the multivariate phenotype means. We chose to focus on environmental conditions to which the population is not (yet) adapted, since this is the most contentious scenario for plasticity-driven evolution. The potential for adaptive divergence along the trait dimensions that are environmentally responsive will be high when (i) genetic variation underlying phenotypic variance and covariance (the P matrix) increases in the novel environment and (ii) the plastic response (“plasticity vector”) falls along the main axis of G, while the orientation of G stays the same in the novel environment, or (iii) the plastic response does not fall along the main axis of G, but the orientation of G rotates in the novel environment such that it aligns with the direction of plasticity (Fig. 1). Our meta-analysis tests how common these scenarios are.

Fig. 1.

Alternative scenarios describing differences in the short-term evolutionary potential of environmentally induced phenotypes. Ellipses depict multivariate phenotypic (P, light color) and genotypic (G, dark color) variation for two traits (Trait 1 and Trait 2). Arrows connecting the centroids of nonnovel (green) and novel (orange) environments are the plasticity vectors that describe the change in multivariate mean phenotype (P) between two environments. (A) Plastic responses to novel environments can be said to have high evolutionary potential if there is ample genetic variation underlying P and the vector of plastic response is well-aligned with the major axis of genetic variation in the novel environment (i.e., dark orange ellipse). (B) Plastic phenotypic responses can be said to have low evolutionary potential if there is limited genetic variation underlying P and the vector of plastic response does not align with the major axis of genetic variation in the novel environment.

Results

We conducted a systematic search of the literature (see Materials and Methods for more detail) and identified 21 studies across 19 species where G and P matrices could be compared (i.e., 32 environmental comparisons of G and P with n = 64 effects total). We also identified 32 studies (n = 98 effects) across 30 species that could be used to derive estimates of the quantitative genetic evolvability in the direction of plasticity. This larger number of studies could be included because we only needed a vector of trait means and G matrices to generate effect sizes (see Materials and Methods for more detail). Data were taxonomically biased toward insects with a total of 56 effect sizes, whereas fish and plants had 18 and 16 effect sizes, respectively. There were also G matrices estimated for one snail and one frog species (having six and two effects, respectively). Matrix size varied from 2 to 11 traits (mean = 4.16, n = 98), and the novel environments were imposed under conditions that were either “stressful” (resulting in decreased survival) or “nonstressful,” and using different breeding designs. Given these factors can affect G (23–25) we controlled for them in our analysis (see below and Materials and Methods for more details).

Changes in Additive Genetic Variance in Response to Novel Environments.

We first explored if novel environmental conditions result in an increase in additive genetic variation (i.e., “cryptic genetic variation”; refs. 23 and 24) by generating effect sizes that contrasted the structure of G between nonnovel and novel environments. Nonnovel environments were those that the populations were considered to be well adapted to, or in which populations had been reared for at least five generations or more, whereas novel environments were those that were manipulated outside normal rearing conditions. We quantified changes in additive genetic variation by calculating a number of effect sizes describing changes in G across environments (see Materials and Methods for more detail). Here we focus on those describing the change in total standardized genetic variation (SDV) and the change in the proportion of additive genetic variation along the major axis of G (i.e., ${\mathit{g}}_{max}$) $\left(P{V}_{max}\right)$ as these capture how heritable variation may be released in response to novel conditions. For some studies, novel environments were considered stressful and/or led to a decrease in survival (see Materials and Methods). Using a metaregression model we therefore tested whether the observed changes in G depended on whether the novel environment was “stressful” or “nonstressful.” We also tested whether the type of breeding design (“full-sib” vs. “half-sib”) and the number of traits impacted the magnitude of change.

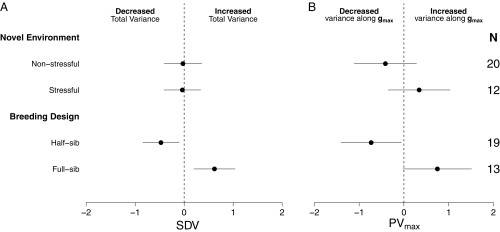
Across studies, there was little evidence for a release of cryptic genetic variation (overall meta-analytic mean from intercept-only models: SDV: = −0.12, 95% CI = −0.47 to 0.23; $P{V}_{max}=$ −0.06, 95% CI = −0.68 to 0.55). However, there was a high amount of between-study variance in effect sizes (proportion of between-study variance $\left[I_{st}^2\right]$: SDV: = 0.84; $P{V}_{max}=$ 0.73). When controlling for the number of traits, breeding design, and whether or not the environmental manipulation was stressful there was evidence that variance can increase in novel environments. Specifically, trait variance significantly increased in novel environments for studies using full-sib breeding designs [SDV: overall mean estimate (logit scale) = 0.62, 95% CI = 0.086 to 1.159; Fig. 2A and see SI Appendix, Table S2], with ∼61% of the total additive genetic variation falling along ${\mathit{g}}_{max}$ [$P{V}_{max}$: overall mean estimate (logit scale) = 0.465, 95% CI = −0.5 to 1.43; Fig. 2B and see SI Appendix, Table S2]. However, G matrices estimated using half-sib breeding designs actually exhibited a lower total additive genetic variance in novel environments and a lower proportion of additive genetic variance along ${\mathit{g}}_{max}$ compared with studies using full-sib breeding designs (by ∼35%; Fig. 2 A and B). Whether the novel environment was stressful or not did not impact the change in additive genetic variance (Fig. 2 A and B).

Fig. 2.

Mean effect sizes comparing the change in genetic variation across environments for studies where novel environmental manipulations were stressful (Stressful/Nonstressful) and with different breeding designs (Half-sib vs. Full-sib). (A) Total SDV between G matrices across environments. (B) Change in the proportion of variation along ${\mathit{g}}_{max}$ (PV_max) between G matrices across environments. Note that in all cases effect sizes are means for a study for an average number of traits and are independent of other factors (i.e., marginalized means) in the model (see Materials and Methods).

Evaluating the Short-Term Evolutionary Potential of Environmentally Induced Phenotypes.

The potential for environmentally induced phenotypes to bias evolutionary divergence depends on the degree to which plastic responses fall along dimensions of the phenotype that harbor heritable variation (Fig. 1A). We derived new effect size measures inspired by Hansen and Houle (15) to test this prediction. We first quantified how much additive genetic variation fell in the direction of the plastic response (defined as ${\pi }_e$) and then derived a measure of quantitative genetic evolvability (sensu ref. 15), defined as the alignment between the plastic response vector and main axes of additive genetic variation $\left({\mathit{g}}_{max}\right)$, in both the nonnovel and novel environment (denoted as ${\theta }_e$; see Material and Methods for details). We also explored the relationship between G and P within and across environments and present these results in SI Appendix, Tables S2 and S3. We explicitly tested whether there were significant changes in how the plastic response vector aligned with additive genetic variation when a population moves from a nonnovel to novel environment using a metaregression model contrasting environment type (nonnovel vs. novel), after controlling for trait number and breeding design.

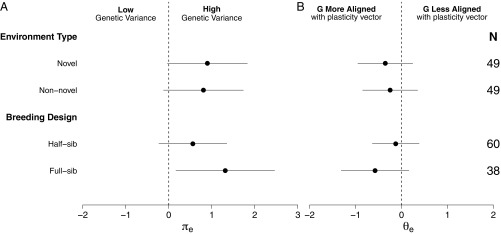
On average, there was substantial additive genetic variance in traits along the plasticity vector in both the nonnovel and novel environments (average variance of 69.14% in the nonnovel and 71.06% in the novel; Fig. 3A and SI Appendix, Table S3). Plastic responses fell between 32 and 42° from the major axis of additive genetic variation (i.e., ${\mathit{g}}_{max}$_x; Fig. 3B and see SI Appendix, Table S3). This alignment between the plasticity vector and ${\mathit{g}}_{max}$ was significantly greater than expected under random alignment (SI Appendix, Table S1).

Fig. 3.

Mean effect sizes comparing plastic responses to G in nonnovel and novel environments (Nonnovel vs. Novel) and using different breeding designs (Half-sib vs. Full-sib). (A) Proportion of genetic variation along the plastic response vector $\left({\pi }_e\right)$. (B) The alignment between the plastic response vector and main axes of genetic variation ${\mathit{g}}_{max}$ $\left({\theta }_e\right)$. Negative values indicate that the plastic response vector and ${\mathit{g}}_{max}$ is fully aligned (i.e., ∼0°), whereas positive values indicate that the plastic response vector and ${\mathit{g}}_{max}$ is not aligned (i.e., ∼90°). Values of 0 indicate that the plastic response vector and ${\mathit{g}}_{max}$ are 45° to one another. Note that in all cases effect sizes are means for a study for an average number of traits and are independent of other factors (i.e., marginalized means) in the model (Materials and Methods).

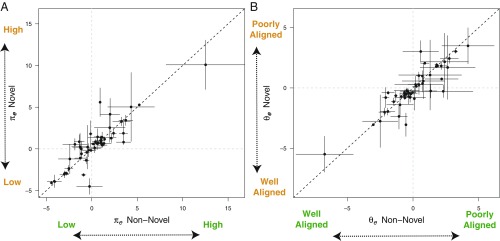
However, the angle between the plastic response vector and ${\mathit{g}}_{max}$ (i.e., ${\theta }_e$) for the nonnovel and novel environments varied substantially across studies (between-study heterogeneity; $I_{st}^2$ = 0.80; Fig. 4). These findings suggest that results depend on the types of traits measured, the type of environmental exposure, and/or past selective history; disentangling these sources of variation, however, is not possible with the existing data. In some studies, the rotation of the G matrix made the plasticity vector align better in the novel environment than in the nonnovel environment, whereas the opposite occurred in other studies (Fig. 5).

Fig. 4.

(A) The total amount of genetic variation along the plastic response vector as a proportion of the maximum amount of variation in any direction, ${\pi }_e$. Smaller values on the axes (i.e., negative numbers) correspond to situations where genetic variation along the plasticity vector is low (“Low” label) whereas larger positive values correspond to situations where genetic variation along the plasticity vector is high (“High” label) for the nonnovel (green text) and novel (orange text) environments. (B) The angle between the plastic response vector and ${\mathit{g}}_{max}$ $\left({\theta }_e\right)$ in novel and nonnovel environments across all studies. Labels correspond to values on the axes where the plasticity vector does not align with the major axis of genetic variation, ${\mathit{g}}_{max}$, (Poorly Aligned) or where ${\mathit{g}}_{max}$ aligns with the plasticity vector (Well Aligned) in both the nonnovel (green text) and novel (orange text) environments. Axes are on the transformed scale to facilitate comparisons with analyses. Large negative values (e.g., −8) indicate that the plastic response vector and ${\mathit{g}}_{max}$ is fully aligned (i.e., ∼0°), whereas large positive values (e.g., 8) indicate that the plastic response vector and ${\mathit{g}}_{max}$is not aligned (i.e., ∼90°). Values of 0 indicate that the plastic response vector and ${\mathit{g}}_{max}$ are 45° to one another. Mean effect sizes and 95% sampling intervals are depicted.

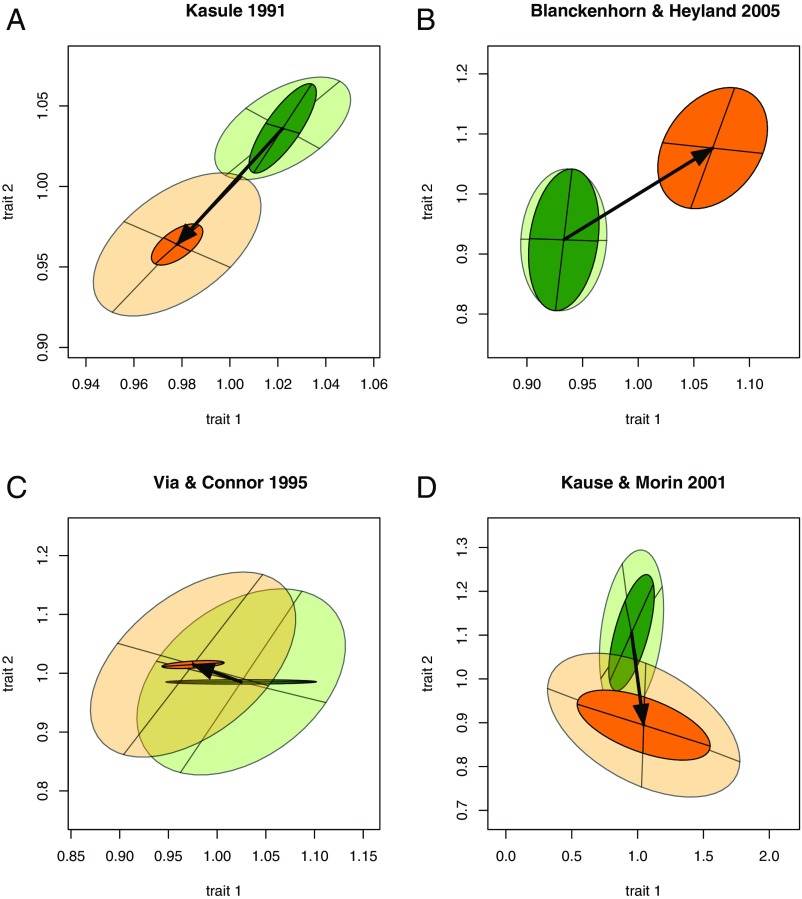
Fig. 5.

Examples of studies (with two trait matrices) with high (A and B) or low (C and D) alignment between the direction of plastic responses and standing genetic variation. Arrows are plastic response vectors; large light ellipses are P matrices and smaller dark ellipses are G matrices. Colors correspond to the nonnovel (green) and novel (orange) environments. (A) Kasule (44) used the cotton stainer bug (Dysdercus fasciatus) to estimate quantitative genetic variation in fecundity and adult size under stressful conditions using a half-sib breeding design. (B) Blanckenhorn and Heyland (45) used a full-sib breeding design to estimate quantitative genetic variation for hind limb size and development time in the yellow dung fly (Scathophaga stercoraria) under stressful conditions. (C) Via and Conner (46) studied the flour beetle (Tribolium castaneum) using a half-sib breeding design to estimate quantitative genetic variation for pupal weight and development time under nonstressful conditions. (D) Kause and Morin (47) studied the sawfly (Priophorus pallipes) and estimated quantitative genetic parameters for development time and body size using a full-sib breeding design under stressful environmental conditions.

Discussion

West-Eberhard suggested that “genes are followers, not leaders, in adaptive evolution” (1). Evolutionary exaggeration or reduction of environmentally induced phenotypes requires heritable variation along the dimensions of the phenotype that are plastic. Our results demonstrate that the alignment between plastic responses to a novel environment and the main axis of genetic variation is greater than expected by chance (Fig. 4 and SI Appendix, Table S1). This may reflect developmental systems responding similarly to environmental and genetic inputs. Such developmental biases should facilitate adaptive divergence in response to selection on environmentally induced phenotypes, making plasticity appear to take the lead in adaptive evolution (1).

It is not fully understood why genetic and environmental perturbations should have similar phenotypic effects. However, theoretical models have demonstrated that evolved regulatory systems tend to produce developmental biases that reflect correlational selection in the past (reviewed in refs. 20 and 26). For example, multivariate selection can predispose developmental systems to respond plastically in the direction of trait covariance (22). Similar biases in phenotypes can occur in response to mutation (e.g., ref. 21). The matrix of mutational variance and covariance (the M matrix; refs. 27 and 28) is a more appropriate estimate of developmental bias than G since the latter also reflects the effects of selection and drift. Nevertheless, G is often assumed to represent how phenotypes vary in response to genetic variation (e.g., refs. 29 and 30). In other words, since both the direction of plasticity and the G matrix capture how trait development is regulated, plastic responses and the major axis of additive genetic variation may commonly be aligned. Our results suggest that this may indeed be the case for many traits, even for plastic responses to environments to which organisms are not adapted.

Exposure to a novel or stressful environment may also be associated with a general increase in additive genetic variation (23). The release of “cryptic genetic variation” is sometimes considered central to plasticity-first models of evolution (2, 31). While additive genetic variation generally increased in novel environments, studies using half-sib breeding designs actually supported a decrease in additive genetic variance. This difference between breeding designs suggests that maternal or paternal effects contribute significantly to the phenotypic variation that is expressed in novel environments, and that the variance contributed by parental effects may result in better alignment with the plastic response. This result provides a more nuanced understanding of previous work; without effectively disentangling environmental and genetic effects studies may overestimate how much genetic variation is “cryptic” (32, 33).

While these results suggest substantial scope for population divergence in the direction of plasticity, the impact of plasticity on evolutionary trajectories depends on the strength and form of selection operating on the phenotype distribution in novel environments—information that is often missing. For example, the studies in our meta-analysis rarely estimated selection on phenotypes in the novel environment (this also means we were unable to account for any selection that may have occurred due to mortality). This is not surprising given that estimating selection demands additional or more complex experiments. To date, only one study appears to have explicitly addressed the alignment between ${\mathit{g}}_{max}$, plasticity, and selection (34). Lind et al. (34) showed that, in water fleas, adaptive plasticity in response to fish predator cues was well-aligned with ${\mathit{g}}_{max}$ and the response to survival selection; however, the same was not true in response to midge predatory cues. It is unclear if this difference is related to the strength of past selection, but the water flea clones were considered to be well-adapted to both predator regimes (which is why the study was not included in our meta-analysis).

That evolutionary responses are not easily predicted on the basis of either selection or variability is also evident by a compilation of 16 long-term study populations, which showed that, as environments change, the relationship between heritable variation in single traits (i.e., h²) and selection is weak (35). Indeed, some of the studies in the present analysis found that the direction of plasticity and standing genetic variation were poorly aligned. On the basis of the theoretical models described above, it may appear reasonable to conclude that such instances of poor alignment simply reflect that individuals fail to successfully accommodate to novel conditions. However, this interpretation is complicated not the least by the fact that G also reflects selective removal of genetic variation (36). This means that most additive genetic variance detected by the studies in this meta-analysis could be selectively neutral in the ancestral environment. If so, the alignment between additive genetic variance and the direction of plasticity can be interpreted as if plasticity is biased toward dimensions of the phenotype that have been weakly, rather than strongly, selected in the past. This ambiguity in the interpretation of an alignment between plastic responses and G calls for theoretical and empirical studies that can demonstrate how developmental evolution shapes plasticity and standing genetic variation, the latter through phenotypic effects of mutation and selective removal of phenotypes.

Our findings have important implications for testing the plasticity-first hypothesis. Such tests are often done by comparing ancestral-descendent populations (2, 5, 6, 19, 37–39). Typically, studies identify a set of traits that have diverged between the populations and establish whether ancestral populations show plasticity in the direction of descendent populations for those traits. However, while the alignment between plastic responses and the major axis of genetic variation make plasticity-led divergence more likely, it also makes it challenging to distinguish signatures of plasticity-led evolution from evolutionary divergence biased by the phenotypic effects of genetic mutation (i.e., “genetic constraints”; refs. 29 and 30). More generally, quantitative genetic estimates are likely to provide limited insights into more long-term evolution (40, 41). Distinguishing the distinct empirical traces of environmentally and genetically induced developmental biases in evolution will thus require identification of appropriate “null” models (38). Ancestral-descendant comparisons in natural populations combined with theoretical modeling and experimental evolution studies will likely be necessary to assess the role of plasticity in adaptive diversification.

Materials and Methods

Literature Searches and Data Collection.

We did two literature searches for studies containing either (i) ‘G matri*’ AND ‘P matri*’ AND ‘environ*’ or (ii) ‘genetic covariance’ AND ‘phenotyp* covariance’ AND ‘environ*’ in the title, abstract or keywords to find studies that estimated G and P matrices in multiple environments. In both searches we used Web of Science and Scopus (search date October 9, 2017), given that different search engines can yield different results (42). We restricted our subject areas to biology, plant sciences, evolutionary biology, ecology, developmental biology, and agriculture. In addition, we extracted P and G correlation/covariance matrices from primary studies collated by previous meta-analyses exploring the environmental sensitivity of G (33, 43) and a meta-analysis compiling environmental effects on additive genetic variance (32).

To be included in our meta-analysis, the primary study had to (i) conduct a quantitative genetic breeding design in two or more environments, where one environment was considered representative for the population or species (i.e., nonnovel), and one or more environments were novel, (ii) measure two or more phenotypic traits, and (iii) present G and P correlation/covariance matrices for these traits or G along with trait means in both environments. We defined a novel environment as one where the source population had not been experienced in the recent past (more than five generations) or where the authors had clearly stated the novelty of the environment within the paper. We further classified novel environments as stressful if (i) authors clearly stated that the environment was stressful and/or (ii) a decreased survival in the novel environment was evident. We acknowledge that novel environments not deemed stressful by authors or where mortality data were not provided may also be considered stressful in many cases, but the distinction is nevertheless potentially important since selective mortality can influence estimates of genetic and phenotypic variation. Relevant studies deemed to meet the above criteria based on title and abstracts were screened by two of the authors (D.W.A.N. and R.R.). In some studies, only correlation matrices were provided. These studies were included if we could obtain additive genetic variance estimates for the set of traits so that correlation matrices could be converted to covariance matrices (necessary for generating effect sizes, see below). In instances where only part of the necessary data were available (e.g., only G and not P, missing sample sizes, no variance estimates, etc.) we estimated G and P from raw data if they were deposited from the authors in repositories or contacted authors directly for the relevant information. If this information could not be obtained we excluded the study, or in some cases the trait, from our analysis. See SI Appendix, Fig. S1 for a full PRISMA diagram. All raw matrix data extracted from studies (44–75), code, and analyses can be found at https://osf.io/fz7sr/.

Moderator (Predictor) Variables.

We collected a number of moderator variables which we a priori expected to explain variation in effect sizes. These included the number of traits quantified (i.e., total size of the G matrix), stressfulness of environment, and the study design used to estimate G matrices (i.e., half-sib or full-sib) which distinguished narrow-sense and broad-sense estimates of additive genetic variation, respectively. For meta-analyses involving comparison of G across environments, we also categorized effect sizes as having come from studies where the novel environment was considered stressful (i.e., stressful vs. nonstressful) and included this in the relevant analyses. However, it is important to note that our main aim is not to isolate specific environmental predictors of variation in effect size but to assess the extent to which the direction of plasticity and the main axis of additive genetic variance is aligned for populations exposed to a novel environment.

Matrix-Based Effect Sizes and Sampling Variance.

We were specifically interested in comparing G and P matrices within and across nonnovel and novel environments and determining how stressfulness of the novel environment, trait number, and study design impacted the magnitude of changes in matrices. In addition, we were also interested in the degree to which plastic responses (i.e., the plasticity vectors) align with genetic variation (G) in nonnovel and novel environments. These questions require effect size estimates that can be used to compare various aspects of matrices and their alignments (details on effect size measures used are discussed below). Estimation of G and P occurs with varying levels of precision (76), and any comparisons both within and between environments should attempt to account for the effects of sampling variance to avoid potentially erroneous conclusions.

We took a flexible meta-analytic approach to effect size and sampling variance estimation with matrices that allowed us to make use of traditional multilevel meta-analytic models, which more effectively weight studies based on their precision. Given that no single matrix effect size captures all aspects of how matrices can change, we used a series of alternative effect size measures (Fig. 6 A–D and described in detail below) and generated their corresponding sampling variances for comparing G and P matrices within and across environments (Fig. 6E). While we compared both G and P to themselves across environments, we focus on comparisons of G only. This is appropriate since G and P typically were very similar (see analysis code and results at https://osf.io/fz7sr/). Before simulations, any nonpositive-definite matrices (i.e., nonpositive eigen values) were “bent” to make them positive-definite, and we excluded any matrix row and column entry where trait genetic or phenotypic variances were zero or negative (33). This ensured that all matrices used for simulations were positive definite.

Fig. 6.

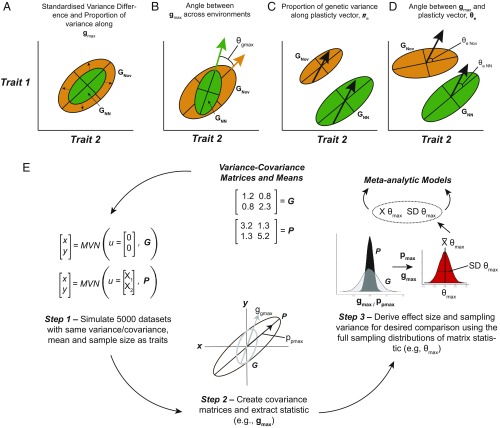
(A–D) Examples of the different effect size measures describing changes in G and P within and across nonnovel (green-“NN”) and novel (orange-“Nov”) environments. While both G and P were compared to each other, and themselves, within and across environments, we present effect sizes comparing G matrices only for simplicity. See text for more details. (E) Schematic example of the Monte Carlo simulations used to generate effect sizes and corresponding sampling variance described in A–D.

To estimate sampling variability for matrix-based effect sizes, we used Monte Carlo simulations where each positive definite covariance matrix $\left(\mathbf{\Sigma }\right)$, along with its respective sample size (number of families or sires for G and number of individuals for P), was used to generate 5,000 simulated datasets of each trait matrix from a paper. Sets of traits had the same covariance structure as the covariance matrix taken from each paper, but with random variation (simulated) added. Traits were assumed to follow a multivariate normal distribution [$MVN\sim \left(\overline{x},\mathbf{\Sigma }\right)$, where $\overline{x}$ is a vector of means (zeros for G and the mean of each trait for P), with a length the size of the number of traits] (Fig. 6E). Matrix effect sizes generated in this way have the benefit of propagating sampling variance from different study designs across different environments and from different matrices (i.e., G and P). Covariance matrices generated from the 5,000 simulated datasets were then used to calculate various matrix-based statistics (described below). From these distributions, we took the average of the distribution as the average effect for the study and the variance of the distribution as the studies corresponding sampling variance.

To ensure that a few traits were not disproportionately impacting effect sizes, we standardized the trait means along with P and G matrices. For comparing quantitative genetic evolvabilities, as quantified by the additive genetic variances within and between populations, these data should be standardized by the mean (15, 77). Since we were also interested in the plastic response, which is measured as the change in trait means, we cannot simply divide by the trait means for each study within each environment. We therefore first calculated the average of the trait means within each study (μ) as

$$\mathit{\mu }=\frac{{\overline{\mathit{x}}}_{\mathit{NN}}+{\overline{\mathit{x}}}_{\mathit{Nov}}}{2},$$

where ${\overline{\mathit{x}}}_{\mathit{NN}}$ is the vector containing the mean phenotypic trait values in the nonnovel environment (i.e., NN) and ${\overline{\mathit{x}}}_{\mathit{Nov}}$ is the vector of mean phenotypic trait values in the novel environment (i.e., Nov). Next, we standardized means $\left({\overline{\mathit{x}}}_{\mathit{\mu }}\right)$ and covariance matrices $\left({\mathbf{\Sigma }}_{\mathit{\mu }}\right)$ as

$${\overline{\mathit{x}}}_{\mathit{\mu }}\equiv \frac{\overline{\mathit{x}}}{\mathit{\mu }}$$

$${\mathbf{\Sigma }}_{\mathit{\mu }}\equiv \mathbf{\Sigma }\mathrm{\oslash }\left(\mathit{\mu }{\mathit{\mu }}^{\mathit{\text{'}}}\right),$$

where $\overline{\mathit{x}}$ is the vector with means for a given study and environment, and $\mathbf{\Sigma }$ is a covariance matrix (either the G or the P matrix). $\mathrm{\oslash }$ denotes an elementwise division. Below we describe in detail how we calculated different matrix-based effect sizes using the standardized means and covariance matrices, but to simplify notation we drop the subscript $\mathit{\mu }$ in the remainder of the text.

Comparing changes in standardized variance.

We calculated the change in the total additive genetic variation of the multivariate phenotype (Fig. 6A). The total amount of variation was first calculated for each matrix as the sum of all diagonal elements of $\mathbf{\Sigma }$ (i.e., the trace of the covariance matrix). We then calculated the standardized difference in total variance between the nonnovel and novel G matrices $\left(SD{V}_G\right)$ as

$$SDV=2\frac{tr\left({\mathbf{\Sigma }}_{Nov}\right)–tr\left({\mathbf{\Sigma }}_{NN}\right)}{tr\left({\mathbf{\Sigma }}_{Nov}\right)+tr\left({\mathbf{\Sigma }}_{NN}\right)},$$

where the $tr\left({\mathbf{\Sigma }}_{NN}\right)$ and $tr\left({\mathbf{\Sigma }}_{Nov}\right)$ are the traces of the covariance matrices in the nonnovel environment and novel environment, respectively. We did not take the absolute difference in variance because we were interested in, and also had specific predictions for, how variance should change in response to novel environmental conditions. Positive standardized effect sizes indicate that total variance in multivariate phenotypes from novel environments were larger than total variance in nonnovel environments.

Comparing proportion of variation along major axes of G.

We also estimated the proportion of variation in G $\left(P{V}_{\mathbf{G}\_\text{max}}\right)$ that was along the major axis of additive genetic variation (i.e., along ${\mathit{g}}_{max}$) for each environment (Fig. 6A). We quantified the proportion of total variance along ${\mathit{g}}_{max}$ as

$$P{V}_{max}=\frac{{\lambda }_{max}}{tr\left(\text{Σ}\right)},$$

where ${\lambda }_{max}$ is the first eigenvalue (i.e., the amount of variation along the first eigenvector) and the $tr\left(\text{Σ}\right)$ is the trace of the covariance matrix. Given that $P{V}_{max}$ is a proportion, we logit-transformed it to normalize its distribution and sampling error.

Comparing major axes of genetic and phenotypic variation.

Second, we explored how the orientations of G and P change within and across environments by calculating the angle between the major axes of variation (Fig. 6B). The major axis of variation for a covariance matrix is described by its first eigenvector. To compare within environments, we calculated the angle between ${\mathit{g}}_{max}$ and ${\mathit{p}}_{max}$ (${\theta }_{NN}$ or ${\theta }_{Nov}$ depending on the environment), which are the first eigenvectors of G and P, respectively. To compare across the environments, we calculated the angle between the nonnovel ${\mathit{g}}_{max}$ and novel ${\mathit{g}}_{max}$ $\left({\theta }_G\right)$, or the angle between the nonnovel ${\mathit{p}}_{max}$ and novel ${\mathit{p}}_{max}$ $\left({\theta }_P\right)$, depending on whether the angle was calculated for the genetic or phenotypic variation. The angle between the two first eigenvectors was calculated as

$$\theta =\frac{180}{\pi }{\text{cos}}^{-1}\left(\frac{v_{1\_max}\cdot v_{2\_max}}{\sqrt{v_{1\_max}\cdot v_{1\_max}}\cdot \sqrt{v_{2\_max}\cdot v_{2\_max}}}\right),$$

where $v_{1\_max}$ is the first eigenvector of one of the covariance matrices and $v_{2\_max}$ is the first eigenvector of the other covariance matrix. This calculation results in angles varying between 0° and 180° and so we subtracted from 180° any angle between 180° and 90° to yield angles between 0° and 90° (33). To normalize the distribution of angles we divided them by 90 and performed a logit transformation.

Assessing short-term evolutionary potential of plastic responses.

Finally, to investigate the short-term evolutionary potential along the dimensions of plastic responses we tested whether or not the plastic response vector—the change in mean trait values between the nonnovel to novel environment—was aligned with the G matrices of the nonnovel and the novel environment. First, we calculated the vector $\mathrm{\Delta }\overline{\mathit{x}}$ describing the change in mean trait values:

$$\mathrm{\Delta }\overline{\mathit{x}}={\overline{\mathit{x}}}_{\mathit{NN}}-{\overline{\mathit{x}}}_{\mathit{Nov}}.$$

Next, we projected the G matrices for both the nonnovel and novel environments on the vector $\mathrm{\Delta }\overline{\mathit{x}}$ to calculate the amount of variance in G in the direction of vector $\mathrm{\Delta }\overline{\mathit{x}}$ (i.e., $e_{\mathrm{\Delta }\overline{x}}$) using equation 1 in ref. 15:

$$e_{\mathrm{\Delta }\overline{x}}=\frac{\left(\mathrm{\Delta }\overline{\mathit{x}}\right)\text{'}\mathit{G}\mathrm{\Delta }\overline{\mathit{x}}}{{\left|\mathrm{\Delta }\overline{\mathit{x}}\right|}^2}.$$

To estimate how much variation was present in the direction of the plastic response compared with the maximum amount of variation in any direction, we divided $e_{\mathrm{\Delta }\overline{x}}$ by the first eigenvalue of G $\left({\lambda }_{\mathit{G}\_max}\right)$, to calculate the evolutionary potential of plasticity (Fig. 6C):

$${\pi }_e=\frac{e_{\mathrm{\Delta }\overline{x}}}{{\lambda }_{G\_max}}.$$

Given that ${\pi }_e$ is a proportion, we logit-transformed it to normalize its distribution and sampling error. To test whether ${\pi }_e$ was significantly larger than expected for any random alignment between the plastic response and G, we also calculated a null expectation for the evolutionary potential of plasticity $\left({\pi }_0\right)$:

$${\pi }_0=\frac{{\overline{\lambda }}_G}{{\lambda }_{G\_max}},$$

in which ${\overline{\lambda }}_G$ is the average of all eigenvalues for G. Next, we subtracted the logit of ${\pi }_0$ from the logit of ${\pi }_e$ to estimate the difference between the observed and expected evolutionary potential in the direction of plasticity $\left({\pi }_{e-0}\right)$:

$${\pi }_{e-0}=\text{logit}\left({\pi }_e\right)-\text{logit}\left({\pi }_0\right).$$

When the lower boundary of the credible interval for the intercept of the meta-analytic model (as described below) for ${\pi }_{e-0}$ is larger than zero, the evolutionary potential in the direction of plasticity is higher than what we would expect for a random alignment between $\mathrm{\Delta }\overline{\mathit{x}}$ and ${\mathit{g}}_{max}$. We also calculated the angle between $\mathrm{\Delta }\overline{\mathit{x}}$ and the first eigenvector of G $\left(v_{\mathit{G}\_max}\right)$ (Fig. 6D):

$${\theta }_e=\frac{180}{\pi }{\text{cos}}^{-1}\left(\frac{\mathrm{\Delta }\overline{\mathit{x}}\cdot v_{\mathit{G}\_max}}{\sqrt{\mathrm{\Delta }\overline{\mathit{x}}\cdot \mathrm{\Delta }\overline{\mathit{x}}}\cdot \sqrt{v_{\mathit{G}\_max}\cdot v_{\mathit{G}\_max}}}\right).$$

This calculation results in angles varying between 0° and 180° and so we subtracted from 180° any angle between 180° and 90° to yield angles between 0° and 90°. To normalize the distribution of angles we divided them by 90 and then performed a logit transformation.

Meta-Analysis.

We meta-analyzed effect sizes using multilevel meta-analytic and metaregression models (78) with the R package metafor (79). In all models, effects were weighted by their sampling variance from the simulations and we included “study” as a random effect. For analyses comparing environments, each study contributed multiple estimates and so we included a random slope of environment type in the study-level random effect to account for this nonindependence. However, only a random intercept was included if variance in the slope failed to converge in the model. Given that there was strong overlap between study and species we did not include a species-level random effect or phylogeny in our models to avoid confounding estimates (80). The package metafor does not estimate a residual variance by default so we included an observation-level random effect in all our models. Multiple environments were manipulated in some studies, and given quantitative genetic designs often separated families across these environments, this introduces a level of nonindependence between effect sizes (80). Given the limited sample sizes, we did not account for this level of dependence; however, we acknowledge this may lead to inflated type I error rates.

We used intercept only meta-analytic models to quantify total $\left(I_t^2\right)$ and between study $\left(I_{st}^2\right)$ heterogeneity in effects (81, 82) as

$$I_{st}^2=\frac{{\sigma }_{st}^2}{{\sigma }_{st}^2+{\sigma }_e^2+{\sigma }_m^2}$$

$$I_t^2=\frac{{\sigma }_{st}^2+{\sigma }_e^2}{{\sigma }_{st}^2+{\sigma }_e^2+{\sigma }_m^2}$$

$${\sigma }_m^2=\frac{{\displaystyle \sum w_i\left(k-1\right)}}{\left[{\left({\displaystyle \sum w_i}\right)}^2-{\displaystyle \sum w_i^2}\right]},$$

where ${\sigma }_m^2$ is an estimate of the total sampling variability derived from $w_i$, the weight or inverse of the sampling variance, and k the total number of effects. ${\sigma }_{st}^2$ and ${\sigma }_e^2$ are the between- and within-study variance estimates. $I_{st}^2$ can be interpreted as the proportion of variation in effects resulting from differences between studies, which includes differences such as species, trait types, and methodological approaches that vary across studies. In contrast, $I_t^2$ is the total proportion of variation in effects beyond sampling variance. If $I_t^2$ is high, then this suggests that the effects observed are not simply the result of sampling variability.

We ran metaregression models to explore how our predicted moderator variables explained variation in effects. For each effect size, we included main effects for moderators we hypothesized would explain variation in effects when sample sizes allowed. These included (i) the number of traits, (ii) environment type (nonnovel and novel—only for analyses comparing the alignment between the plasticity vector and G), (iii) the type of novel environment (i.e., stressful or nonstressful—only for analyses comparing G across environments), and (iv) the breeding design (i.e., half-sib or full sib). Given the limited sample sizes and uneven taxonomic sampling we restricted models to estimating main effects of the above moderators only. Models comparing G and P across environments were run separately. We calculated the marginalized mean effect size (and confidence intervals) for different subgroups of categorical predictors by taking the weighted average of the mean (and sampling variance) of one level in factor 1 (e.g., half-sib for the breeding design factor) across both levels of factor 2 (i.e., stressed and nonstress for the novel environment factor). We did this for all combinations to produce mean estimates unconditional on other categorical factors in the model. We checked funnel plot (i.e., effect size as a function of sampling error) asymmetry to look for evidence of publication bias. However, we found no clear evidence for publication bias in any of the effect sizes (SI Appendix, Fig. S2).