Abstract
Based on a Bayesian decision theoretic approach, we optimize frequentist single- and adaptive two-stage trial designs for the development of targeted therapies, where in addition to an overall population, a pre-defined subgroup is investigated. In such settings, the losses and gains of decisions can be quantified by utility functions that account for the preferences of different stakeholders. In particular, we optimize expected utilities from the perspectives both of a commercial sponsor, maximizing the net present value, and also of the society, maximizing cost-adjusted expected health benefits of a new treatment for a specific population. We consider single-stage and adaptive two-stage designs with partial enrichment, where the proportion of patients recruited from the subgroup is a design parameter. For the adaptive designs, we use a dynamic programming approach to derive optimal adaptation rules. The proposed designs are compared to trials which are non-enriched (i.e. the proportion of patients in the subgroup corresponds to the prevalence in the underlying population). We show that partial enrichment designs can substantially improve the expected utilities. Furthermore, adaptive partial enrichment designs are more robust than single-stage designs and retain high expected utilities even if the expected utilities are evaluated under a different prior than the one used in the optimization. In addition, we find that trials optimized for the sponsor utility function have smaller sample sizes compared to trials optimized under the societal view and may include the overall population (with patients from the complement of the subgroup) even if there is substantial evidence that the therapy is only effective in the subgroup.
Keywords: Adaptive design, optimal design, enrichment design, precision medicine, subgroup analysis
1 Introduction
A major challenge in the development of targeted therapies is the identification and confirmation of subgroups of patients where a treatment is effective. To address this issue, a range of clinical trial designs and statistical methodology have been proposed.1–4 An important field of application is oncology, where the better understanding of the molecular basis of the disease leads the development of therapies that directly act on specific molecular mechanisms and therefore may be effective in special subgroups of patients only. In this work, we consider a setting, where there is a priori biological plausibility that the treatment effect is larger or only present in a subgroup defined by a binary biomarker. However, there is still uncertainty if the treatment is effective at all and if so, if the treatment effect is larger or only present in a subpopulation of biomarker positive patients. To address this uncertainty, clinical trials testing for a treatment effect in the full population and a subgroup can be performed.
While in standard parallel group clinical trials the statistical power to demonstrate a treatment effect in a dedicated primary endpoint is typically the basis for the planning of clinical trials, the consideration of power alone does not sufficiently represent the losses and gains of correct and incorrect test decisions when several subgroups are tested. Subgroup analyses are challenging because several types of risks are associated with inference on subgroups. On the one hand, by disregarding a relevant subpopulation a treatment option may be missed due to a dilution of the treatment effect in the full population. In addition, even if the diluted treatment effect can be demonstrated in an overall population, it is not ethical to treat patients that do not benefit from the treatment when they can be identified in advance.5,6 On the other hand, selecting a spurious subpopulation increases the risk to restrict an efficacious treatment to too narrow a fraction of a potential benefiting population. In order to account for these risks, we apply a decision theoretic framework and define utility functions that quantify the expected benefits as well as the costs of a particular clinical trial.
Decision theoretic approaches are based on utility functions that map actions to a numeric scale representing the values of these actions. Optimal actions are then defined as the actions that maximize these utility functions. In the application to clinical trials the set of actions are families of trial designs, specified by sample sizes, allocation ratios, stopping and adaptation rules (for adaptive designs), as well as inference procedures. The utilities represent the value of trial outcomes (as e.g. the rejection of a null hypothesis or the size of observed treatment effects), adjusted for the cost of the trial and may also depend on the true treatment effects (see Hee et al.7 for a recent review on the application of decision theoretic approaches to guide clinical trial design). When applying the approach to optimize enrichment designs, the utilities also account for the size of the population for which an efficacy claim is made.8–12 Because the outcome of the trial as well as the true treatment effects are unknown at the time of planning, the optimization relies on expected utilities. Here, the expectation is taken over a prior distribution on the effect sizes as well as the distribution of trial outcomes given the effect sizes. The optimal design based on the decision theoretic approach is then defined as the design with the largest expected utility.
We derive optimized clinical trial designs in the setting of a parallel group trial comparing the means of a normally distributed outcome and consider utility functions from the perspective of different stakeholders: a sponsor's as well as a societal view. We assume that the utility of the sponsor is the net present value (NPV), while for the societal perspective it is the expected health benefit (adjusted for the cost of the trial).
We especially focus on single-stage and adaptive partial enrichment designs. Partial enrichment designs are designs, where the prevalence of the subgroup in the trial is a design parameter and may differ from the prevalence in the underlying population.8,13 Therefore, we can choose to make the subpopulation over- or underrepresented. Adaptive designs,14–17 on the other hand, are two-stage designs, where in a first stage patients are recruited from the full population. Then, in an interim analysis, based on interim data, the trial design of the second stage may be modified. For example recruitment may be limited to patients in a subgroup of biomarker positive patients and/or the sample size may be adapted. In the proposed adaptive partial enrichment designs, in addition the prevalence of the subgroup in the second stage sample can be chosen adaptively, based on the first stage data. The adaptations may be based on all information observed at the interim analysis, including information on secondary and surrogate endpoints and safety information.
Using numerical optimization and a dynamic programming approach, we determine optimal single and two-stage designs optimizing the total sample size of the trial, the prevalence of the subgroup in the trial, and, for the adaptive designs, the optimal adaptation rule. The adaptation rule is a function of the first stage data that determines the population selected for the second stage as well as the second stage sample size in the overall population and the sample size in the subgroup, which may imply different subgroup prevalences in the first and second stage. An adaptation option is also stopping for futility, which corresponds to a second stage sample size of zero.
In this manuscript, we extend earlier work on decision theoretic approaches to optimize single-stage designs12 and optimal adaptive enrichment designs.11 We derive optimal single- and adaptive two-stage partial enrichment designs with optimal adaptation rules that go beyond subgroup selection and allow one to choose optimal second stage sample sizes in the full population and the subgroup conditional on the first stage data using a backwards induction algorithm. The use of Bayesian decision theoretic methods has also been proposed to optimize clinical development programs and in models that account for errors in the determination of the patient's biomarker status.8,18,19 An alternative line of research optimizes multiple testing procedures in one and two-stage designs based on a decision theoretic approach.9,10,12,20
The remainder of the paper is structured as follows: In Section 2, the considered single-stage and adaptive enrichment designs are introduced. In Section 3, the utility functions are discussed and in Section 4, we derive the optimized trial designs. We present the results of a case study in Section 5 and conclude with a discussion in Section 6.
2 Testing scenario and trial designs
Consider a parallel group trial comparing the means of a normally distributed endpoint in a population F that is divided into a subgroup S of biomarker positive patients and its complement , the biomarker negative patients. Let denote the treatment effects in the subgroups and the overall treatment effect, where λ denotes the prevalence of the subgroup in the considered patient population, which is assumed to be known. We consider a setting, where there is a biological rationale that the treatment effect might be higher (or only present) in S compared to and consider one-sided tests of the null hypotheses and .
Next, we define single-stage and adaptive two-stage designs to test HF and HS controlling the family-wise error rate (FWER) at a pre-specified one-sided level α. In Sections 2.1 and 2.2, these tests are defined for given sample sizes in the subgroups (for single stage designs) or given first stage sample sizes and second stage sample sizes functions (for adaptive designs). In Section 4, we optimize these sample sizes and sample size functions.
2.1 Single-stage designs
We consider single-stage designs with partial and with full enrichment. Partial enrichment designs include biomarker positive and biomarker negative patients, while full enrichment designs include biomarker positive patients only.
2.1.1 Single-stage designs with partial enrichment
A single-stage partial enrichment design is a clinical trial with biomarker positive and biomarker negative patients per treatment arm. Thus, the trial prevalence of the biomarker positive subgroup is given by , where denotes the overall sample size per treatment arm. We define Z-test statistics to compare the outcomes in subgroup S, its complement and the full population F
| (1) |
where denotes the estimated mean treatment effects and their standard error which is assumed to be known. The treatment effect estimates in the subgroups are the mean differences of the outcomes in S and . In the full population, the treatment effect estimate is given by . Note that is a weighted average of the treatment effect estimates in S and , where the weights are given by the population prevalence λ and not the trial prevalence γ.13 Therefore, it gives an unbiased estimate of the overall treatment effect in the underlying population. Note that ZF can be rewritten as a weighted sum of the test statistics in S and
| (2) |
with (see online supplementary material, Section S1). The standard errors are given by and , where denotes the variance of the observations in the treatment and control group. For simplicity, this variance is assumed to be homogeneous across the subpopulations and treatment groups. For the generalization to unequal variances, the definitions of and the weights in equation (2) have to be adjusted accordingly.
Note that we use the re-weighted test statistics ZF because the standard Z-statistics computed from the pooled sample in the full population may have an expectation different from zero even if . This occurs if the means in the two subpopulations have different signs and the effects cancel out in the underlying patient population but not in the trial population. Furthermore, by the definition of ZF, the vector of test statistics (ZS, ZF) follows a multivariate normal distribution with means , variances 1 and covariance .
To adjust for multiplicity for the test of the two hypotheses HF and HS, we apply a Bonferroni correction. While more powerful testing procedures could be used, we chose the conservative Bonferroni test to limit the computational complexity (especially in the adaptive setting below this allows us to utilize numerical integration rather than to have to rely on simulations). In addition, to avoid test decisions where HF is rejected but the rejection is driven by a strong effect in a single subpopulation only, we additionally require that a sufficient positive Z-test statistic is observed in each subpopulation to reject HF (called consistency criterion6,12,21). The decision function of the resulting multiple test for HF and HS, whose components take the value 1 if the corresponding hypotheses are rejected and zero otherwise, is then given by
| (3) |
where is a pre-chosen consistency threshold, bq denote the quantiles of the standard normal distribution, and the indicator function. Thus, HF is only rejected if there is a significant treatment effect in F at the Bonferroni adjusted level and, in addition, in both subgroups a significant treatment effect at level η is observed. Given this decision function, a partially enriched single-stage design is fully specified by the sample sizes in the subgroup and its complement. We denote the family of single-stage enrichment designs by .
2.1.2 Fully enriched single-stage designs
In the single-stage full enrichment design, patients from the full population are screened but only biomarker positive patients are included in the trial (i.e. n = nS). Only hypothesis HS is tested and the decision function of the respective test is given by
| (4) |
where ZS is defined as in equation (1). Note that HS can be tested at full level α since only one hypothesis is under investigation (because is set to zero). A single-stage fully enriched design d is specified by the sample size nS and we define d = nS and denote the family of single-stage full enrichment designs by .
2.2 Adaptive two-stage designs
For an adaptive two-stage design, let denote the number of patients per treatment arm recruited in the subgroup and its complement in stage k = 1, 2. The corresponding total per treatment arm sample size in stage k is denoted by . The trial prevalence of the biomarker positive subgroup in stage k is given by . We assume that in the first stage patients from S and are recruited (i.e. ). In the interim analysis, the trial may be either stopped for futility, continued only in S or continued in the full population. The second stage sample sizes can be chosen based on the interim data. In accordance with equations (1) and (2), we define the stage k test statistics and , where all variables in equations (1) and (2) are replaced by the corresponding stage k quantities denoted by the superscript . Note that the second stage statistics are not cumulative test statistics but computed from the second stage data only. We define an adaptive two-stage test that combines the test statistics of the first and second stage with the inverse normal combination function, with equal weights for the two-stages. The combined test statistics are then given by , where are pre-defined, non-negative weights such that . Note that follows a standard normal distribution under the respective null hypothesis, even if the second stage sample size is chosen in a data dependent way, see literature.22–24 This comes at the cost, that the stage-wise test statistics are combined with weights that need to be pre-defined and are not adjusted to the actual stage-wise sample sizes. To adjust for multiple testing, we apply the Bonferroni correction and define the adaptive multiple test for HF and HS setting its decision function, denoted by , equal to equation (3) replacing the single-stage test statistics Zi by the combination test statistics . If no patients in are recruited in the second stage such that , we set and . If the trial is stopped for futility and the second stage sample sizes are zero, we set .
We assume that the second stage sample sizes are adaptively chosen and can be written as function of the vector of first stage test statistics (for notational convenience we drop the argument of the functions ). Given the decision function , an adaptive two-stage enrichment design d is fully specified by the first stage sample sizes and the second stage sample size functions and we define , where the first two elements are numbers and the second two components functions from . Let denote the family of adaptive two-stage enrichment designs.
3 Utility functions
Let denote the family of considered one- and two-stage trial designs. As in Ondra et al.,12 we define two types of utility functions for the trial designs representing either a societal perspective or a commercial sponsor perspective. The societal utility function models the total public health benefit, whereas the sponsors utility function models the total revenue of the sponsor. Let denote the true treatment effects in the subgroup and the full population. Then the utility from a societal perspective is modelled as
| (5) |
where N denotes the expected number of future patients, r is a reward parameter, are lower thresholds for the effect size that represent, for example the minimal clinically relevant effect size that outweighs the treatment cost and/or known side effects, C(d) denotes the costs of the trial with design d defined in equation (7), and denote the test procedure of design d. Note that the utility function also depends on the trial data through the test decisions ψS and ψF that are functions of the respective Z-statistics. Given that the hypothesis test rejects the null hypothesis of no treatment effect in a certain population, the utility increases linearly with the true treatment effect and the population size. If the true treatment effect is smaller than the respective threshold, but the hypothesis test rejects, the utility takes negative values.
From a sponsor perspective, we define a utility that models a setting where the price of the drug depends on the effect size estimate from the pivotal trial as well as the size of the market and set
| (6) |
where denotes the positive part and, compared to the utility from a societal perspective, the effect sizes δF as well as δS have been replaced by their respective point estimates as defined in Section 2.1 for single-stage designs. For adaptive designs, the point estimates of the treatment effect in S and F are computed based on the subgroup estimates of the pooled data from the two stages. Note that the sponsor utility does not depend on the true treatment effects. However, it depends on the trial data through the treatment effect estimates and, as above, through the test decisions. Note that, in contrast to the societal utility function, the sponsor's utility depends on the positive part of rather than the difference . If the sponsor observes a treatment effect lower than the clinically relevant threshold, we assume that payors and/or patients will not be willing to pay for the treatment and that it will not be marketed, leading to zero gain. In this case the sponsor's utility equals . For the societal utility function in contrast, false decisions (where a treatment is licensed in a population where the true treatment effect is smaller than the threshold) give a negative contribution to the utility, in addition to the trial costs.
For both utility functions, the trial costs C(d) are modelled as
| (7) |
where for single-stage designs we set and . The costs are composed of trial setup costs , the biomarker development costs , screening costs to identify biomarker positive patients and costs per patient in the trial. The screening costs are proportional to the number of patients that have to be screened to recruit biomarker positive patients in stage k = 1, 2 and depend on the population prevalence (the lower the prevalence the larger the number of patients that need to be screened) and the sample sizes in the trial and are given by (see online supplementary material, Section S2).
| (8) |
4 Optimizing trial designs
The utilities defined in equations (5) and (6) depend on the trial outcomes and are therefore unknown at the planning stage of the trial. The societal utility is even unknown after the trial is performed because it depends on the unknown true treatment effects. However, given a prior distribution on the effect sizes in the two subgroups, we can compute expected utilities and determine optimal trial designs that maximize these expected utilities.
4.1 Expected utilities
The expected utility for a trial design is given by
| (9) |
where for the societal and for the sponsor utility function, and the expectation is taken both over a prior distribution on the effect sizes and the sampling distribution of the data given the effect sizes δ.
The expected utility for partially enriched single-stage designs is given by
| (10) |
where denotes the joint density of the Z-statistics given the effect sizes and design . Since are independent, is the product of two univariate normal densities with means , and variance 1. For the full enrichment design, the computation of the expected utility reduces to an integral over the marginal prior on δS and the marginal sampling distribution of ZS given δS (see online supplementary material, Section S5).
The expected utility of an adaptive enrichment design is given by an integral over the joint sampling distribution of the stage-wise test statistics of the two-stages k = 1, 2 as well as the prior distribution on δ. Let denote the joint density of the first stage test statistics and the conditional joint density of the second stage test statistics conditional on , where denotes the sample sizes in the first stage and the sample sizes in the second stage. Note that are functions of the vector of first stage test statistics . The joint sampling distribution of the stage-wise test statistics of the two stages is then given by the product , where each factor is the product of two univariate normal densities with means and variance 1, where and k = 1, 2 denote the standard errors of the stage-wise treatment effect estimates. Note that depend on the second stage sample sizes and therefore are functions of the interim test statistics . Then, the expected utility for an adaptive enrichment design is given by
| (11) |
where the inner two integrals integrate over the sampling distribution of the stages and the outer integral over the prior. For first stage outcomes where the adapted second stage sample size in both subgroups is zero (stopping for futility) and are not defined. However, for these outcomes and the utility no longer depends on the second stage test statistics such that we can arbitrarily set in the integral above. Similarly, if only the second stage sample size in is zero then and we can set .
4.2 Determining the optimal design
We consider the optimization problem for single-stage designs () and for adaptive designs (). For single-stage partial enrichment designs, the design d is fully specified by the sample sizes nS and . Thus, to find the optimal design we numerically maximize equation (10) in the sample sizes . Similarly, for the full enrichment designs we optimize the corresponding expected utility function in nS. The optimal single-stage design is then given by the optimal partial enrichment or the optimal full enrichment design, whichever gives the higher expected utility.
To determine optimal adaptive enrichment designs d as defined in Section 2.2, we use a dynamic programming approach. We first rewrite the objective function (10) to (see online supplementary material, Section S3)
| (12) |
where
and denotes the posterior distribution of the effect sizes given the first stage data. is the conditional expected utility, given the first stage test statistics if design d is used. For a specific it depends only on the value of evaluated at but not the entire function .
Given first stage sample sizes and first stage test statistics the optimal second stage sample sizes , which maximize the conditional expected utility, are given by
| (13) |
The optimal first stage sample sizes are then given by
| (14) |
where the functions are defined in equation (13). The optimal adaptive enrichment design is then given by , where the second component is a function of the first stage test statistics. By the dynamic programming principle, the solutions (13) and (14) maximize equation (12) and thus also equation (11). Note that optimization can be performed under constraints on minimal and maximal sample sizes, by maximizing the utilities over respective restricted sets of sample sizes.
If the optimal single-stage or adaptive trial leads to a non-positive utility, the optimal option is to perform no trial and to retain both null hypotheses. This leads to an expected utility of zero.
5 Examples
We derive optimized trial designs for a range of scenarios to investigate the dependence of the optimum designs on the prior, the type of utility function (societal or sponsor) and the cost of the biomarker development and determination. We compare optimized adaptive enrichment designs with single-stage designs for both the weak and the strong biomarker prior for a grid of population subgroup prevalences from 10% to 90% in steps of 10%.
To explore the gain in expected utility by allowing the subgroup prevalence in the trial to differ from the population subgroup prevalence λ, we in addition consider optimized single-stage designs, where the prevalence of the subgroup in the trial is equal to the population prevalence such that . For the latter, we optimize the expected utilities in the overall per arm sample size n. We refer to these designs as fixed trial prevalence designs.
As priors π0 on the effect size δ we considered two scenarios, a weak and a strong biomarker prior (see Table 1). Both, the weak and the strong biomarker prior are discrete joint prior distributions on the effect sizes , with weights on the points . The weak biomarker prior reflects a situation where the predictive property of the biomarker is questionable, whereas the strong biomarker prior reflects a situation where there is a strong belief that the treatment is only effective in the subgroup S. Note that the prior distributions of the effect sizes in the subgroups are not independent. The Pearson correlation between the effect sizes is 0.54 for the weak biomarker prior and 0.23 for the strong biomarker prior. The variance of the outcomes was set to in both groups.
Table 1.
Weak and strong biomarker prior. Each column specifies an effect size vector and its prior probabilities under the weak and the strong biomarker prior.
| δS | 0 | 0.3 | 0.3 | 0.3 |
| 0 | 0 | 0.15 | 0.3 | |
| Weak biomarker prior | 0.2 | 0.2 | 0.3 | 0.3 |
| Strong biomarker prior | 0.2 | 0.6 | 0.1 | 0.1 |
In the examples below, the clinically relevant thresholds were set to , assuming that the minimal clinical relevant effect is a third of the maximal effect sizes considered in the prior and the consistency parameter is such that a weak positive trend needs to be observed in both subgroups to reject HF without substantially compromising the power for the test of HF (see Section S6 in the online supplementary material for results for other parameter values). The weights in the combination test were set to and the significance level to . The adaptive enrichment designs were optimized over stage-wise sample sizes with a minimum of 25 subjects per arm, stage and subgroup. Specifically, the first stage sample sizes were chosen from a grid, starting at 25 and increasing in steps of 30% up to 265 (note that, however, the maximum sample size 265 was never identified as optimal in the investigated scenarios). The second stage sample sizes for each interim outcome were optimized with the L-BFGS-B algorithm of the optim function of R,25 setting the second stage maximum sample size to 500 (for simplicity we treated the optimization problem as continuous in the sample sizes). The minimal and maximal sample sizes for single-stage designs were set to the sum of the stage-wise minimal and maximal sample sizes of the adaptive enrichment designs. We considered two scenarios for the cost and reward parameters that differ in the biomarker development costs and the biomarker determination costs (i.e. the screening costs). For both cases the reward parameter is set to €, the per patient cost to € and the fixed costs of the trial to €.
Case 1. Biomarker with costs.
The costs for biomarker determination are € and for the biomarker development €.
Case 2. Biomarker with negligible costs.
The biomarker costs and are set to zero.
5.1 Optimized utilities
For Case 1, optimized utilities of adaptive enrichment designs, single-stage enrichment designs and single-stage fixed trial prevalence designs are shown in Figure 1 (Case 2 is shown in the online supplementary material, Section S4). Since the single-stage designs with fixed prevalence (dotted lines) are a subclass of the single-stage designs the utility of optimized single-stage designs with a fixed prevalence is always lower or equal than the optimized utility for single-stage designs. The difference is largest when the prevalence is either very low or very large: then optimized single-stage trials with need to recruit a large number of patients to reach the required minimal sample size in S and .
Figure 1.
Case 1. Optimized utilities as function of the population prevalence for adaptive enrichment trials (solid lines), single-stage designs (dashed lines) and single-stage designs restricted to a fixed prevalence (FP) (dotted lines). Red lines show the sponsor utility and blue lines the societal utility.
5.1.1 Weak biomarker prior
For the sponsor view, the expected utilities of the optimized single-stage partial enrichment designs are at least 10% larger compared to the fixed trial prevalence designs if the population prevalence λ is in the range of 0.1–0.5 and for . For the societal view, such an increase is observed for prevalences of 0.1,0.2, and 0.9. Note that for the societal view and a prevalence of 0.1 among the fixed trial prevalence designs ‘no trial’ is the optimal design (leading to a utility of 0) while the optimal partial enrichment design has a positive expected utility. The optimized adaptive enrichment designs lead to a further improvement in expected utility compared to single-stage partial enrichment designs for both the sponsor and the societal utility functions. The improvement exceeds 10% for all considered prevalences under the sponsor view and for prevalences up to 0.5 for the societal view.
5.1.2 Strong biomarker prior
For the sponsor view, increases of more than 10% in the expected utility are observed for prevalences from 0.2 to 0.6 and a prevalence of 0.9 (with increases from 14% to 651% in expected utility) if an optimized single-stage partial enrichment design is used instead of a fixed trial prevalence design. For the societal view, such improvements occur for prevalences of 0.3 and above. For the latter the optimal design is the full enrichment design in these setting and the expected utilities increase by 13% to 572% and, for a prevalence of 30%, where the optimal fixed prevalence trial is to perform no trial, the relative increase becomes infinite.
The benefit of optimized adaptive enrichment designs compared to single-stage partial enrichment designs is substantial for the sponsor view, with improvements above 10% for all considered prevalences. For a prevalence of 0.1, only the adaptive enrichment designs lead to a positive expected utility. For the societal view, an improvement in expected utility of more than 10% is observed for a prevalence of 0.3 only, where it reaches 37%.
5.2 Optimized designs
Figures 2 and 3 (see online supplementary material, Section S4 for Case 2) show the (expected) sample sizes of the optimized designs.
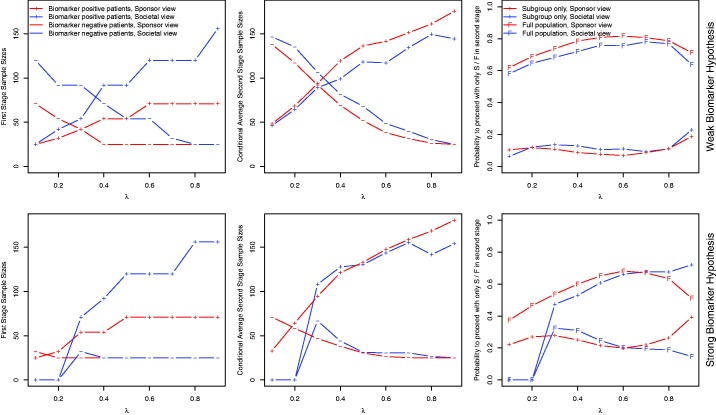
Figure 2.
Case 1. Optimized trial designs for the single-stage designs. For single-stage designs the sample sizes stratified by subgroup S and are shown. For the single-stage designs with restricted trial prevalence (, dotted lines) the total sample size is shown. Red lines correspond to the sponsor view, blue lines to the societal view.
Figure 3.
Case 1. Optimized trial designs for adaptive enrichment designs. The first column show the optimal first stage sample sizes, the second column the average second stage sample sizes conditional on the event that they are larger than zero. The third column shows the probability that the second stage is conducted in S only/in F.
5.2.1 Weak biomarker prior
For very small and very large prevalences, the total sample sizes of fixed trial prevalence designs are very large because of the lower bound on the sample size in each subgroup. An exception is the optimal design for the societal utility function and very low prevalence, where all such trials have negative expected utility (and are outperformed by the option to perform no trial which leads to an expected utility of zero). For the single-stage partial enrichment designs, the optimal number of patients recruited from S () is monotonically increasing (decreasing) in λ for both the societal and the sponsor view, however, for the latter with the exception of the case where . These monotone relationships are due to the increased reward that can be gained by rejecting HS (and the decreased additional gain by rejecting HF) as the prevalence increases. Furthermore, the optimal samples sizes under the sponsor view are lower than under the societal view. For the weak biomarker prior and intermediate or large prevalences, the sponsor optimal sample size for is given by the lower sample size bound of 50. For very large prevalences, a fully enriched trial is optimal for both the societal and the sponsor perspective.
For the adaptive enrichment designs, Figure 3 shows the optimized first stage sample sizes and the conditional expected second stage sample sizes, conditional on the event that the respective population is continued to the second stage. The last column of Figure 3 shows the probability to recruit in the second stage only biomarker positive patients and the probability to continue in the full population. The first stage and conditional expected second stage sample sizes in S are essentially monotonically increasing in the prevalence (the minor deviation from monotonicity observed might be due to the discrete grid used in the optimization of the first stage sample sizes) for both the sponsor and the societal view. However, for the sponsor view lower first stage sample sizes are used.
5.2.2 Strong biomarker prior
If the prevalence is very small, all considered single-stage trial designs lead to negative expected utilities, for both the sponsor and the societal utility function, and the expected utilities are maximized if no trial is performed. For the societal utility function, the fixed trial prevalence designs lead to negative utilities also for somewhat larger prevalences. When the societal utility function is optimized, then, with the exception of very low prevalences, among the general enrichment designs the fully enriched design is optimal. In contrast, for the sponsor a more aggressive strategy is optimal also under the strong biomarker prior, and the optimal sample size in is given by the lower bound 50. Only for very large prevalences, the fully enriched design is also optimal for the sponsor. This is due to the fact that a positive trend needs to be observed in S and to reject HF (due to the consistency threshold η), which becomes more challenging as increases. But for large λ rejecting HF brings little benefit compared to rejecting HS only.
For the adaptive enrichment designs, first stage sample sizes in S are similar to those for the weak biomarker prior, however, the sample size in is lower or equal. Again we observe that optimizing the sponsor expected utility leads to lower first stage sample size than optimizing the societal utility. For very low prevalences, the optimal strategy for the societal perspective remains to conduct no trial, even if optimized adaptive enrichment designs are used. However, for the sponsor view, the range of prevalences, for which performing a trial is the optimal solution is larger. A striking difference between the sponsor and the societal perspective is observed in the probabilities to continue to the second stage in the full population. Optimizing the societal utility function leads to a strategy that continues more likely in the subpopulation only, while the sponsor tends to continue in the full population. This is due to the fact that the sponsor can profit from a positive result in the full population, even if the treatment is only effective in the subpopulation.
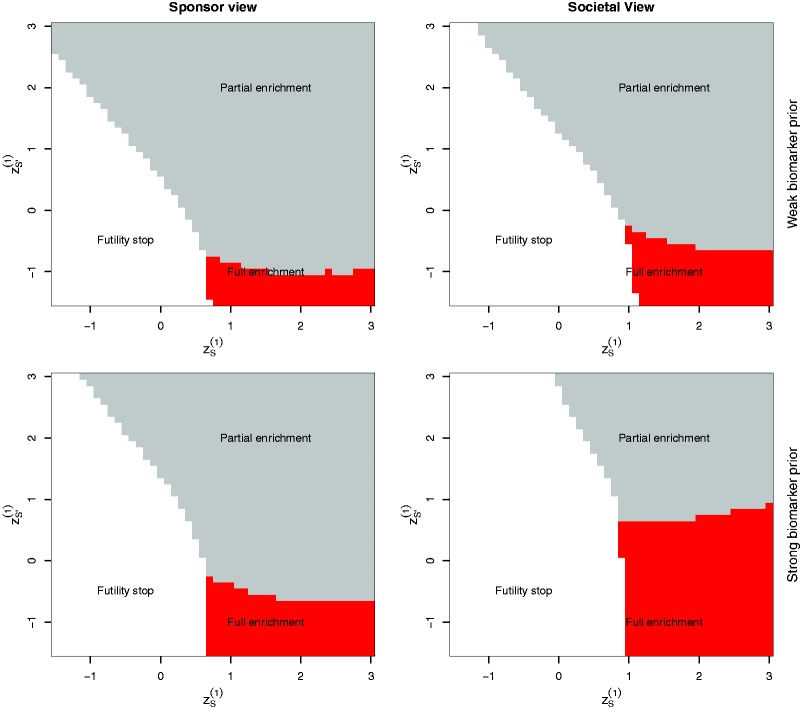
Figure 4 illustrates the optimal adaptation rules for Case 1 and a population subgroup prevalence (see online supplementary material, Section S4 for Case 2). The optimal second stage design is full enrichment (i.e. ) if, in the interim analysis, a large treatment effect in S but a low effect in is observed and it is unlikely that the trial will be successful to reject HF. Note that for the societal perspective, the region where a full enrichment trial is optimal is much larger under the strong biomarker prior than under the weak biomarker prior. For the sponsor view, this difference is much less pronounced and the region where the sponsor continues with the full population is large also under the strong biomarker prior.
Figure 4.
Optimized interim decisions under the weak and the strong biomarker prior for Case 1 and as function of the first stage test statistics . Grey (red) areas correspond to regions where patients from S and (only S) are recruited in the second stage of the trial, respectively. White areas correspond to regions where a futility stop is optimal. Note that the first stage sample sizes have been optimized as well and therefore differ between the considered scenarios.
5.2.3 Operating characteristics of optimized designs under specific alternatives
To illustrate the properties of the optimized procedures under specific treatment effect constellations (rather than averaged over a prior), we computed the operating characteristics of single-stage and adaptive designs optimized under the sponsor and societal perspective under the null hypothesis and specific alternatives, see Table 2. Here, we considered the parameters of Case 1 and a population prevalence of . In all considered scenarios, the average sample numbers in the subgroup are larger under the societal than the sponsor view. Under the weak biomarker prior also the probability for a correct decision (i.e. to show efficacy in S only if there is no effect in the complement and to show an effect in the full population if the trial is effective overall) is larger for the optimal designs under the societal view compared to designs optimized under the sponsor view. In contrast, under the strong biomarker prior, the optimal design from the societal perspective outperforms the optimal sponsor design (with respect to the probability of a correct decision) only in cases where the treatment effect is confined to the subgroup. Under the strong biomarker prior, the design optimized under the sponsor perspective has better performance if there is in fact some treatment effect in the complement. We also find that the optimized adaptive designs have a larger probability for a correct decision compared to single-stage designs, with one notable exception: under the strong biomarker prior and the societal utility function, the optimal single-stage design is a fully enriched design which has probability 0 to reject HF. Therefore, it outperforms the adaptive designs in the case where there is only a treatment effect in S.
Table 2.
Operating characteristics of optimized single- and adaptive two-stage designs optimized under the weak and strong biomarker prior for the parameters of Case 1 and a population prevalence of .
| Societal view |
Sponsor view |
|||||||
|---|---|---|---|---|---|---|---|---|
| Treatment effect δ | (0, 0) | (0.3, 0) | (0.3, 0.15) | (0.3, 0.3) | (0, 0) | (0.3, 0) | (0.3, 0.15) | (0.3, 0.3) |
| Weak biomarker prior | ||||||||
| Adaptive designs | ||||||||
| P(futility stop) | 0.58 | 0.04 | 0.02 | 0.01 | 0.43 | 0.05 | 0.03 | 0.02 |
| P(full enrichment) | 0.12 | 0.28 | 0.08 | 0.01 | 0.1 | 0.16 | 0.06 | 0.02 |
| P(partial enrichment) | 0.3 | 0.68 | 0.9 | 0.97 | 0.47 | 0.79 | 0.9 | 0.96 |
| Average sample number in S | 164 | 212 | 199 | 179 | 162 | 174 | 174 | 172 |
| Average sample number in | 82 | 98 | 112 | 113 | 57 | 69 | 70 | 66 |
| Power to reject HF | 0.011 | 0.226 | 0.627 | 0.907 | 0.010 | 0.173 | 0.453 | 0.744 |
| Power to reject only HS | 0.010 | 0.626 | 0.268 | 0.051 | 0.010 | 0.574 | 0.342 | 0.129 |
| Single stage designs | ||||||||
| Power to reject HF | 0.011 | 0.225 | 0.614 | 0.901 | 0.010 | 0.160 | 0.378 | 0.641 |
| Power to reject only HS | 0.010 | 0.575 | 0.245 | 0.043 | 0.011 | 0.552 | 0.374 | 0.184 |
| Strong biomarker prior | ||||||||
| Adaptive designs | ||||||||
| P(futility stop) | 0.64 | 0.03 | 0.02 | 0.02 | 0.5 | 0.04 | 0.03 | 0.02 |
| P(full enrichment) | 0.25 | 0.76 | 0.59 | 0.39 | 0.16 | 0.28 | 0.14 | 0.04 |
| P(partial enrichment) | 0.11 | 0.21 | 0.38 | 0.59 | 0.34 | 0.68 | 0.83 | 0.93 |
| Average sample number in S | 188 | 237 | 231 | 221 | 164 | 187 | 187 | 184 |
| Average sample number in | 30 | 32 | 37 | 43 | 37 | 46 | 49 | 52 |
| Power to reject HF | 0.008 | 0.098 | 0.265 | 0.507 | 0.009 | 0.155 | 0.384 | 0.661 |
| Power to reject only HS | 0.011 | 0.797 | 0.639 | 0.422 | 0.011 | 0.637 | 0.440 | 0.216 |
| Single stage designs | ||||||||
| Power to reject HF | 0 | 0 | 0 | 0 | 0.010 | 0.160 | 0.379 | 0.643 |
| Power to reject only HS | 0.025 | 0.874 | 0.874 | 0.874 | 0.011 | 0.558 | 0.378 | 0.186 |
Note: The operating characteristics are given under the global null (where the Power corresponds to the type I error rate) and several alternative hypotheses. For the adaptive designs the probabilities of the interim decisions futility stop, full enrichment, partial enrichment and the average sample numbers (across both stages) are given. For all designs the power to reject F and the power to reject S only are reported. Note that the power to reject any null hypothesis is given by the sum of the two.
5.3 Sensitivity analyses if several prior distributions are under consideration
To investigate the robustness of optimized single-stage and adaptive enrichment designs with respect to the choice of the prior distribution, we consider designs optimized for a prior and evaluate its expected utilities under a different prior π0.
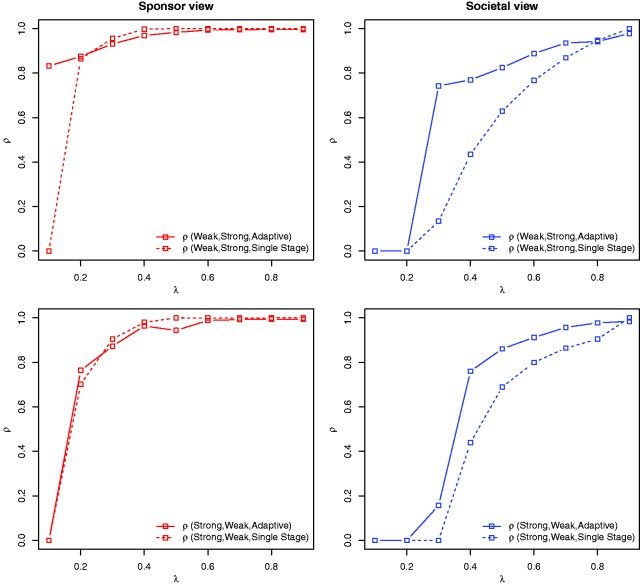
For a prior distribution p and for let denote the design maximizing for all designs d in a family of designs . Later, we consider the families of single-stage and the family of adaptive designs. For convenience we drop the index x below. Consider two different prior distributions π0 and , possibly arising due to two different expert opinions. We are interested in a measure quantifying to which extent the expected utility drops if trial designs are optimized under a prior that differs from the prior used to calculate the expected utility. To this end, we define for a given family of designs the proportion
Thus, ρ is the ratio of the expected utilities under the prior π0 if designs and are applied. By definition of it follows that and hence . Large values of ρ indicate that designs and perform almost equally well under prior π0. Hence, if ρ is close to one, the trial design is robust with respect to the prior specification, since the utilities obtained by using the designs and do not differ by much.
Figure 5 shows the proportions as function of the population prevalence, where π0 is the weak, and the strong biomarker prior and vice versa. We consider Single-Stage, Adaptive} and investigate the sponsor and the societal utility functions. For the societal view, adaptive enrichment designs are for many scenarios substantially more robust with respect to the prior specification than single-stage trial designs and they retain a larger proportion of the expected utility than single-stage designs. This holds for both scenarios, designs optimized for the weak and evaluated under the strong biomarker prior and the other way round. For the sponsor view, the robustness of single-stage and adaptive enrichment designs is very similar, with the exception of under the weak biomarker prior and if the design is optimized under the strong biomarker. The optimal single-stage design under the strong biomarker prior is to perform no trial while the adaptive designs include patients from S and in the first stage which is favourable under the weak biomarker prior.
Figure 5.
Case 1. is the ratio of the expected utilities under the prior π0 if designs (the optimal design from family under prior ) and (the optimal design from family under π0) are applied. The proportion ρ is shown for several prior distributions and families of designs , for both the sponsor and the societal view.
6 Discussion
In this work, we apply a decision theoretic approach to optimize single-stage and adaptive partial enrichment designs with general adaptation rules. To make the dynamic programming approach for adaptive enrichment designs feasible, we considered simple adaptive Bonferroni tests for which the expected utilities could be computed by numeric integration rather than having to rely on Monte Carlo simulation. We showed that single-stage partial enrichment designs can substantially improve the expected utility compared to designs where the prevalence in the subgroup coincides with the population prevalence. In many settings, a further increase in expected utility can be achieved by adaptive enrichment designs. Especially, if there is substantial uncertainty about the population that benefits from the drug (modelled by the weak biomarker prior), the stepwise approach of the adaptive design achieves a higher expected utility. Importantly, we also investigated the sensitivity of the optimized designs with respect to the prior distribution and showed that optimal adaptive enrichment designs are not as dependent on expert information as single-stage trial designs, because they can ‘learn’ from the observed interim data and allow for interim design adaptations. Stabilization of performance due to mis-specified biomarker priors can also be achieved by adaptive alpha allocation in a full population study, assuming biomarker positive and negative populations are both present in adequate proportions.20
Adaptive designs are more complex to analyse and execute26 which may result in higher setup costs. While in the numerical example the same cost parameters as for single-stage designs were used, the utility-based approach allows one to easily account for different costs in the planning of the trial. A further limitation of our approach is the assumption that the endpoints can be immediately observed. If the endpoint is delayed, the efficiency of adaptive designs is reduced, because the primary outcome is available only for a part of the recruited patients at the time of the interim analysis. This, however, can be ameliorated if information on short-term surrogate endpoints is available. In that case, the effectiveness of adaptive trials will depend on the ability of short-term endpoints to predict treatment effects on long-term endpoints.
The proposed decision theoretic framework was derived for multivariate normally distributed test statistics, resulting from the comparison of means of a normally distributed outcome. However, multivariate normal test statistics arise, at least asymptotically, also for other endpoints such as, for example, binary, or time to event outcomes and the results can be generalized to these settings. For time to event endpoints, however, special care has to be taken in the implementation of adaptive designs to control the FWER.27–30
The considered utility functions are linear in the size of the subgroup and the observed or actual effect sizes. This assumption can be relaxed to account for settings where a sponsor's drug development program is optimized across a number of competing candidate compounds. Then, the utility can be modelled as the marginal expected gain per invested capital which can be approximated by the ratio of the expected gain and trial costs. Furthermore, to account for regulatory incentives for the development of medicines in orphan indications, the drug's net present value in small groups may be modelled to be larger than predicted by the model considered here. Similarly, in the societal view a larger weight may be put on smaller populations as a step to address the ethical issue of drug development in small populations.
A further extension of the considered model is the choice of optimized weights in the combination function. Also the multiple testing procedure can be improved by replacing the Bonferroni adjustment by a weighted Bonferroni test with optimized weights or by applying (adaptive) closed tests that also take the correlation of the test statistics into account. In addition, one can drop the assumption that the population prevalence of the subgroup is known in advance by introducing a prior for λ. Then the expected utility is computed over a prior on the effect sizes and the population prevalence. Finally, the utility function can be extended to include also secondary outcomes and safety endpoints to better model the overall effect of a drug. However, with increasing complexity of the underlying model, the computational burden increases and can become a constraint in the implementation of the optimization approach.
We investigated two utility functions, representing a sponsor and a societal view and found several discrepancies in the resulting optimized designs. Especially, we saw that with the prospect of a large market, a commercial sponsor may be incentivized to develop a treatment in too large a population. Note, however, that the incentive to search for positives in the full population may be exaggerated in our approach which considers absolute net benefit. That is, pursuing opportunities with low probability of success may at times increase the net benefit, but the same investment in a different opportunity might have a more attractive marginal benefit/cost ratio.8 Thus, it is unclear to which degree sponsors would choose to develop drugs in over-broad populations. In addition, to avoid approval of a drug in too large a market, we assumed that besides the hypothesis test a consistency condition is applied and at least a positive trend in both subpopulations must be observed to demonstrate a positive treatment effect in the full population. The results in Ondra et al.12 show, however, that if licensing the treatment in F in a stratified framework (allowing for testing HF and HS simultaneously) becomes too difficult, it maybe optimal for a sponsor to conduct a clinical trial without subgroup tests, where the biomarker information is ignored.
Overall, the results suggest that single-stage and adaptive two-stage partial enrichment designs can lead to substantial improvements of expected utilities. The actual benefit, however, depends on the cost structure, the prevalence of the subgroup, the expected effect sizes and the type of utility function and must be assessed separately for each individual setting. This can be challenging if little data for the elicitation of priors and other parameters is available. In addition, for the utility functions representing the societal view, the necessity to project health benefits and monetary costs to the same scale can be difficult.
Supplementary Material
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This project has received funding from the European Union's 7th Framework Programme for research, technological development and demonstration under the IDEAL Grant Agreement no. 602552 (to SJ, CFB, FK) and the InSPiRe Grant Agreement no. 602144 (to TO, NS, MP).
Supplemental material
Supplemental material for this article is available online.
References
- 1.Lipkovich I, Dmitrienko A, D'Agostino RB. Tutorial in biostatistics: exploratory subgroup analysis in clinical trials. Stat Med 2017; 36: 136–196. [DOI] [PubMed] [Google Scholar]
- 2.Ondra T, Dmitrienko A, Friede T, et al. Methods for identification and confirmation of targeted subgroups in clinical trials: a systematic review. J Biopharm Stat 2016; 26: 99–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Antoniou M, Jorgensen AL, Kolamunnage-Dona R. Biomarker-guided adaptive trial designs in phase II and phase III: a methodological review. PLoS One 2016; 11: e0149803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Alosh M, Huque MF, Bretz F, et al. Tutorial on statistical considerations on subgroup analysis in confirmatory clinical trials. Stat Med 2016; 36: 1334–1360. [DOI] [PubMed] [Google Scholar]
- 5.Millen BA, Dmitrienko A, Ruberg S, et al. A statistical framework for decision making in confirmatory multipopulation tailoring clinical trials. Ther Innov Regul Sci 2012; 46: 647–656. [Google Scholar]
- 6.Millen BA, Dmitrienko A, Song G. Bayesian assessment of the influence and interaction conditions in multipopulation tailoring clinical trials. J Biopharm Stat 2014; 24: 94–109. [DOI] [PubMed] [Google Scholar]
- 7.Hee SW, Hamborg T, Day S, et al. Decision-theoretic designs for small trials and pilot studies: a review. Stat Methods Med Res 2016; 25: 1022–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Beckman RA, Clark J, Chen C. Integrating predictive biomarkers and classifiers into oncology clinical development programmes. Nat Rev Drug Discov 2011; 10: 735–748. [DOI] [PubMed] [Google Scholar]
- 9.Rosenblum M, Liu H, Yen EH. Optimal tests of treatment effects for the overall population and two subpopulations in randomized trials, using sparse linear programming. J Am Stat Assoc 2014; 109: 1216–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rosenblum M, Fang X and Liu H. Optimal, two stage, adaptive enrichment designs for randomized trials using sparse linear programming. Johns Hopkins University, Department of Biostatistics Working Paper, 2014.
- 11.Graf AC, Posch M, Koenig F. Adaptive designs for subpopulation analysis optimizing utility functions. Biom J 2015; 57: 76–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ondra T, Jobjörnsson S, Beckman RA, et al. Optimizing trial designs for targeted therapies. PLoS One 2016; 11: e0163726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhao YD, Dmitrienko A, Tamura R. Design and analysis considerations in clinical trials with a sensitive subpopulation. Stat Biopharm Res 2010; 2: 72–83. [Google Scholar]
- 14.Wang SJ, O'Neill RT, Hung HMJ. Approaches to evaluation of treatment effect in randomized clinical trials with genomic subset. Pharm Stat 2007; 6: 227–244. [DOI] [PubMed] [Google Scholar]
- 15.Brannath W, Zuber E, Branson M, et al. Confirmatory adaptive designs with Bayesian decision tools for a targeted therapy in oncology. Stat Med 2009; 28: 1445–1463. [DOI] [PubMed] [Google Scholar]
- 16.Wang SJ, James Hung HM, O'Neill RT. Adaptive patient enrichment designs in therapeutic trials. Biom J 2009; 51: 358–374. [DOI] [PubMed] [Google Scholar]
- 17.Jenkins M, Stone A, Jennison C. An adaptive seamless phase II/III design for oncology trials with subpopulation selection using correlated survival endpoints. Pharm Stat 2011; 10: 347–356. [DOI] [PubMed] [Google Scholar]
- 18.Krisam J, Kieser M. Decision rules for subgroup selection based on a predictive biomarker. J Biopharm Stat 2014; 24: 188–202. [DOI] [PubMed] [Google Scholar]
- 19.Krisam J, Kieser M. Performance of biomarker-based subgroup selection rules in adaptive enrichment designs. Stat Biosci 2015; 8: 8–27. [Google Scholar]
- 20.Chen C, Beckman RA. Hypothesis testing in a confirmatory phase III trial with a possible subset effect. Stat Biopharm Res 2009; 1: 431–440. [Google Scholar]
- 21.Millen BA, Dmitrienko A. Chain procedures: a class of flexible closed testing procedures with clinical trial applications. Stat Biopharm Res 2011; 3: 14–30. [Google Scholar]
- 22.Bretz F, Koenig F, Brannath W, et al. Adaptive designs for confirmatory clinical trials. Stat Med 2009; 28: 1181–1217. [DOI] [PubMed] [Google Scholar]
- 23.Wassmer G, Brannath W. Group sequential and confirmatory adaptive designs in clinical trials, Heidelberg: Springer, 2016. [Google Scholar]
- 24.Bauer P, Bretz F, Dragalin V, et al. Twenty-five years of confirmatory adaptive designs: opportunities and pitfalls. Stat Med 2016; 35: 325–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.R Core Team. R: a language and environment for statistical computing, Vienna, Austria: R Foundation for Statistical Computing, 2016. www.R-project.org/. [Google Scholar]
- 26.Stallard N, Hamborg T, Parsons N, et al. Adaptive designs for confirmatory clinical trials with subgroup selection. J Biopharm Stat 2014; 24: 168–187. [DOI] [PubMed] [Google Scholar]
- 27.Bauer P, Posch M. Modification of the sample size and the schedule of interim analyses in survival trials based on data inspections by H. Schäfer and H.-H. Müller, Statistics in Medicine 2001; 20: 3741–3751. Stat Med 2004; 23: 1333–1334. [DOI] [PubMed] [Google Scholar]
- 28.Jenkins M, Stone A, Jennison C. An adaptive seamless phase II/III design for oncology trials with subpopulation selection using correlated survival endpoints. Pharm Stat 2011; 10: 347–356. [DOI] [PubMed] [Google Scholar]
- 29.Mehta C, Schäfer H, Daniel H, et al. Biomarker driven population enrichment for adaptive oncology trials with time to event endpoints. Stat Med 2014; 33: 4515–4531. [DOI] [PubMed] [Google Scholar]
- 30.Magirr D, Jaki T, Koenig F, et al. Sample size reassessment and hypothesis testing in adaptive survival trials. PLoS One 2016; 11: e0146465. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.