Abstract
Advanced brain imaging techniques make it possible to measure individuals’ structural connectomes in large cohort studies non-invasively. Given the availability of large scale data sets, it is extremely interesting and important to build a set of advanced tools for structural connectome extraction and statistical analysis that emphasize both interpretability and predictive power. In this paper, we developed and integrated a set of toolboxes, including an advanced structural connectome extraction pipeline and a novel tensor network principal components analysis (TN-PCA) method, to study relationships between structural connectomes and various human traits such as alcohol and drug use, cognition and motion abilities. The structural connectome extraction pipeline produces a set of connectome features for each subject that can be organized as a tensor network, and TN-PCA maps the high-dimensional tensor network data to a lower-dimensional Euclidean space. Combined with classical hypothesis testing, canonical correlation analysis and linear discriminant analysis techniques, we analyzed over 1100 scans of 1076 subjects from the Human Connectome Project (HCP) and the Sherbrooke test-retest data set, as well as 175 human traits measuring different domains including cognition, substance use, motor, sensory and emotion. The test-retest data validated the developed algorithms. With the HCP data, we found that structural connectomes are associated with a wide range of traits, e.g., fluid intelligence, language comprehension, and motor skills are associated with increased cortical-cortical brain structural connectivity, while the use of alcohol, tobacco, and marijuana are associated with decreased cortical-cortical connectivity. We also demonstrated that our extracted structural connectomes and analysis method can give superior prediction accuracies compared with alternative connectome constructions and other tensor and network regression methods.
Keywords: Brain networks, Connectome, Diffusion MRI, Principal brain networks, Tensor PCA, Tractography, Traits, White matter
1. Introduction
The human brain structural connectome, defined here as the collection of white matter fiber tracts connecting different regions of the brain [Parkand Friston, 2013; Fornito et al., 2013; Craddock etal., 2013; Jones et al., 2013], plays a crucial role in how the brain responds to everyday tasks and life’s challenges. There has been a huge interest in studying connectomes and understanding how they vary for individuals in different groups according to traits and substance exposures. The majority of such studies have focused on functional connectomes [Park and Friston, 2013; Finn et al., 2015; Bjork and Gilman, 2014; Smith et al., 2015; Price, 2012; Toschi et al., 2018] due to the difficulties of recovering reliable structural connectomes [Maier-Hein et al., 2017; Reveley et al., 2015]. Recent advances in noninvasive brain imaging and preprocessing have produced huge brain imaging datasets (e.g., the Human Connectome Project [Van Essen et al., 2013] and the UK Biobank [Miller et al., 2016]) along with sophisticated tools to routinely extract brain structural connectomes for different individuals. Relying on high quality imaging data and many different traits for a large number of study participants obtained in the Human Connectome Project (HCP) [Glasser et al., 2013; 2016b], this article focuses on analyzing relationships between brain structural connectomes and different traits using novel data science tools applied to the HCP data.
Estimation of the structural connectome often relies on a combination of diffusion magnetic resonance imaging (dMRI) and structural MRI (sMRI). dMRI collects information on the diffusion of water molecules in the brain [Behrens et al., 2003; Parker et al., 2003; Jbabdi et al., 2015]. As water diffusion tends to occur along fiber tracts in white matter, dMRI provides information on the locations and directions of the tracts. Tractography [Basser et al., 2000; Descoteaux et al., 2009; Girard et al., 2014] constructs tracts from dMRI data, yielding a very large number of 3D curves connecting different brain regions. These data are enormous and complex, and statistical analysis of them is not straight forward. Challenges comes from several aspects. First, the dimensionality of each subject’s data (p) is extremely large (each subject usually contains >1 million 3D curves), but the sample size (n) is relatively small. This problem is referred to the large p small n problem in statistics [Dunson, 2018]. Second, the data are geometrically structured and it is unclear how to efficiently summarize the geometric information and link this information to traits and phenotypes. Last but not least, alignment and building correspondence between tracts across subjects are very hard. For these reasons, it is typical to parcellate the brain into anatomical regions of interest (ROIs) using sMRI [Desikan et al., 2006; Destrieux et al., 2010] according to pre-defined templates [Desikan et al., 2006; Destrieux et al., 2010; Glasser et al., 2016a]. This allows coarse alignment of different individuals (by mapping the template to individual space), and connectome data reduction into a connectivity matrix.
Although reconstruction errors inevitably occur [Maier-Hein et al., 2017; Reveley et al., 2015; Thomas et al., 2014], advances in imaging techniques [Setsompop et al., 2012] and preprocessing pipelines [Girard et al., 2014; Smith et al., 2012; Zhang et al., 2018; Donahue et al., 2016] have improved the reconstruction of structural connectomes [Donahue et al., 2016]. In this paper, we will explore whether existing structural connectome reconstruction together with proposed novel analysis methods are sufficient to detect (potentially subtle) associations between connectomes and various human traits [Ingalhalikar et al., 2014; Shah et al., 2017; Lim and Kang, 2015]. We will also compare the structural connectomes with other type of connectomes, eg., local structural connectomes [Powell et al., 2018; Yeh et al., 2016], in predicting traits. This comprehensive connectome-trait analysis will give us a systematic understanding of which and how human traits are related to the structural connectome.
In our analysis framework, we rely on a new structural connectome processing pipeline, and improved methods for representing brain connectomes [Zhang et al., 2018]. Previous statistical approaches focus primarily on reducing the connectome to a binary adjacency matrix containing 0–1 indicators of any fiber connections between ROIs. The adjacency matrix is then further reduced to topological summary statistics of the brain graph, providing low-dimensional numerical summaries to be used in statistical analyses [Watts and Strogatz, 1998; Durante et al., 2017; Sporns and Zwi, 2004]. Such connectome simplification is appealing due to its interpretability, but leads to an enormous loss of information. Instead, we use a tensor network representation that incorporates multiple features measuring the strength and nature of white matter tracts between each pair of brain ROIs. This representation better preserves information in the tractography data, and allows flexibility in examining associations with traits. We extend principal components analysis (PCA) to tensor network data via a semi-symmetric tensor decomposition method, which produces brain connectome PC scores for each subject. These scores can be used for visualization and efficient inference on relationships between connectomes and human traits. The main contributions of this paper can be summarized as follows:
In conjunction with a recent dMRI preprocessing pipeline PSC (Population-based Structural Connectome [Zhang et al., 2018] analysis pipeline, available at https://github.com/zhengwu/PSC_Pipeline), this paper provides additional flexible statistical toolboxes to the neuroscience community for statistically analyzing structural connectomes in large cohort studies. The toolboxes are publicly available along with the PSC GitHub repository, providing functions of 1) mapping high-dimensional connectomes to low-dimensional space for visualization; 2) hypothesis testing of connectome distribution difference; and 3) relating brain connectomes with human traits. The code and test data can be downloaded from https://github.com/zhengwu/Tensor.
We develop a novel tensor network PCA (TN-PCA) method to map high-dimensional tensor network data to low-dimensional vectors for network-trait visualization and subsequent statistical analyses. Different from previous multiplex network analysis methods which extract topological features such as motifs and community structures [Bentley et al., 2016; Bassett et al., 2011; Battiston et al., 2017; De Domenico et al., 2016], TN-PCA deals with the “raw” network data - symmetric matrices - and represents them with basis networks and coefficients. The objective function in our method is to minimize some discrepancy between recovered networks and original networks. Topological features can simplify statistical analyses and reduce dimensionalities of the data, while maintaining interpretability. However, our methods are more data adaptive and do not restrict consideration to a pre-defined set of features, which may lead to a loss of information about aspects of brain structure that relate to traits. By comparing with state of the art tensor and network regression methods, we demonstrate good predictive power of TN-PCA and its ability in explaining more detailed relationship between connectomes and traits.
Based on our analysis of data from 1076 individuals and 175 traits, we find strong relationships between structural cortical-cortical connectomes and multiple traits, particularly those related to cognition and substance use. Our systematical analyses show that traits related to positive lifestyles, such as good reading ability, high fluid intelligence, and good motor skills, tend to have positive correlations on cortical-cortical brain connections. On the other hand, substance use, including binge drinking, tobacco, and marijuana use, can reduce cortical-cortical connections. Among all traits, the substance use, especially high alcohol use, degenerates structural connectomes. The proposed method achieves about 81% classification accuracy when classifying binge drinkers from the ones with no or little alcohol.
2. Methods
2.1. Data sets
We focus on three data sets in this paper, which contain about 1221 dMRI scans form 1067 subjects.
Human Connectome Project (HCP) data set: The HCP aims to characterize human brain connectivity in about 1200 healthy adults and to enable detailed comparisons between brain circuits, behavior and genetics at the level of individual subjects [Van Essen et al., 2012]. Customized scanners were used to produce high-quality and consistent data to measure brain connectivity. The release in 2017, containing various traits, structural MRI (sMRI) and diffusion MRI (dMRI) data for 1065 healthy adults, can be easily accessed through ConnectomeDB. The rich trait data, high-resolution dMRI and sMRI make it an ideal data set for studying relationships between connectomes and human traits.
A full dMRI session in HCP includes 6 runs (each approximately 10min), representing 3 different gradient tables, with each table acquired once with right-to-left and left-to-right phase encoding polarities, respectively. Each gradient table includes approximately 90 diffusion weighting directions plus 6 b0 acquisitions interspersed throughout each run. Within each run, there are three shells of b = 1000, 2000, and 3000 s/mm2 interspersed with an approximately equal number of acquisitions on each shell. The directions were optimized so that every subset of the first N directions is also isotropic. The scans were done by using the Spin-echo EPI sequence on a 3 T customized Connectome Scanner. See Van Essen et al., [2012] and Glasser et al., [2013] for more details about the data acquisition and preprocessing of the HCP. Such settings give the final acquired image with isotropic voxel size of 1.25 mm, and 270 diffusion weighted scans distributed equally over 3 shells.
HCP test-retest data set: A subset of HCP participants were recruited to undergo the full 3T HCP imaging and behavioral protocol for a second time. We identified and successfully processed structural connectome data from 44 subjects (88 scans).
Sherbrooke test-retest data set: Different from the high-resolution HCP data set, this data set [Cousineau et al., 2016; Zhang et al., 2016; Chamberland et al., 2017] represents a clinical-like acquisition using a 1.5 T SIEMENS Magnetom. There are 11 subjects with 3 acquisitions for each subject. A total of 33 acquisitions, from 11 healthy participants, were included. The diffusion space (q-space) was acquired along 64 uniformly distributed directions, using a b-value of b = 1000 s/mm2 and a single b0 (=0 s/mm2) image. The dMRI has a 2 mm isotropic resolution. An anatomical T1-weighted 1 × 1 × 1 mm3 MPRAGE (TR/TE 6.57/2.52 ms) image was also acquired.
2.2. Brain connectome extraction
From the raw diffusion MRI (dMRI) and structural MRI (sMRI) data, we want to reliably extract the brain structural connectome data. Fig. 1 illustrates our data processing pipeline.
Fig. 1.
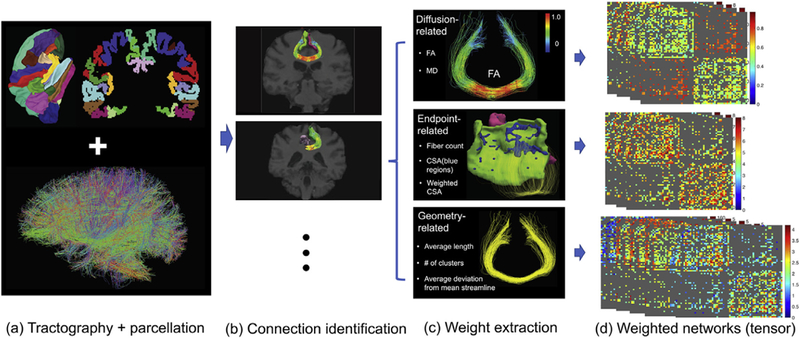
Pipeline of the preprocessing steps to extract weighted networks from the dMRI and sMRI image data. (a) Desikan-Killiany parcellation and the tractography data for an individual’s brain; (b) extraction of streamlines between two ROIs; (c) feature extraction from each connection and (d) extracted weighted networks.
HARDI tractography construction: A reproducible probabilistic tractography algorithm [Girard et al., 2014; Maier-Hein et al., 2017] is used to generate the whole-brain tractography data set of each subject for all data sets. The method borrows anatomical information from high-resolution T1-weighted imaging to reduce bias in reconstruction of tractography. Also the parameters were selected based on evaluation of various global connectivity metrics (e.g., valid connections, invalid connections, and average bundle coverage) in [Girard et al., 2014]. In the generated tractography data, each streamline has a step size of 0.2 mm. On average, 105 voxels were identified as the seeding region (white matter and gray matter interface region) for each individual in the HCP data set (with isotropic voxel size of 1.25 mm). For each seeding voxel, we initialized 16 streamlines to generate about 106 streamlines for each subject. For the Sherbrooke test-retest data set, we also generated about 106 streamlines for each subject. Diffusion MRI data in the Sherbrooke test-retest were resampled to have isotropic voxel size of 1.0 mm and we initialized 10 streamlines in each seeding voxel.
Network node definition: We use the popular Desikan-Killiany atlas [Desikan et al., 2006] to define brain regions of interest (ROIs) corresponding to the nodes in the structural connectivity network. The Desikan-Killiany parcellation has 68 cortical surface regions with 34 nodes in each hemisphere. Freesurfer software [Dale et al., 1999; Fischl et al., 2004] is used to perform brain registration and parcellation. Fig. 1 column (a) illustrates the Desikan-Killiany parcellation and reconstructed tractography data after subsampling.
Connectome tensor extraction: With the parcellation of an individual brain, we extract a set of weighted matrices to represent the brain’s structural connectome. To achieve this goal, for any two ROIs, one needs to first extract the streamlines connecting them. Alignment of the parcellation (on T1 image) and tractography data (dMRI image) is done using Advanced Normalization Tools (ANTs) [Avants et al., 2011]. To extract streamlines connecting ROI pairs, several procedures are used to increase the reproducibility: (1) each gray matter ROI is dilated to include a small portion of white matter region, (2) streamlines connecting multiple ROIs are cut into pieces so that we can extract the correct and complete pathway and (3) apparent outlier streamlines are removed. Extensive experiments have illustrated that these procedures can significantly improve the reproducibility of the extracted weighted networks, and readers can refer to Zhang et al., [2018] for more details.
To analyze the brain as a network, a scalar number is usually extracted to summarize each connection. For example, in the current literature [Fornito et al., 2013; Smith et al., 2013; Jones et al., 2013], fiber count is considered as a measure of the coupling strength between ROI pairs. However, fiber count can be unreliable due to tractrography algorithms and noise in the dMRI data [Maier-Hein et al., 2017; Fornito et al., 2013]. Instead of only using the count as the “connection strength”, we include multiple features of a connection to generate a tensor network for each brain. The tensor network has a dimension of P × P × M, where M represents the number of features and P represents the number of ROIs. Each of the M matrices is a weighted network and describes one aspect of the connection. As illustrated in the third column of Fig. 1, the following features are extracted.
Endpoint-related features: We consider the features generated from the end points of streamlines for each ROI pair. The first feature we extract is the number of endpoints, which is the same as the count of streamlines. Another feature we extracted is connected surface area (CSA), which is proposed in Zhang et al., [2018]. To extract CSA, at each intersection between an ROI and a streamline, a small circle is drawn, and the total area covered by these circles is the CSA. A weighted version of CSA is calculated by dividing the total surface area of the two ROIs.
Diffusion-related features: Diffusion metrics, such as FA, characterize the water diffusivity at a particular location or voxel. We extract these diffusion metrics along white matter streamlines for each ROI pair.
Geometry-related features: Geometric features such as the average length and cluster configuration [Zhang et al., 2018] that can characterize the geometry of extracted streamlines are extracted. The average fiber length is easy to get. To get the cluster number in each connection, we use the Quickbundle method [Garyfallidis et al., 2012] with a fixed threshold. The cluster number reflects the geometry of the bundle and is robust to some confounding effects in the tractography reconstruction, such as the seeding strategy.
Applying the pipeline in Fig. 1, we processed the Sherbrooke test-retest data set with 11 subjects and 3 repeated scans per subject (for our reproducibility study), and the HCP data set with 1065 subjects (from the release of HCP data set in 2017) [Van Essen et al., 2013]. For each subject, 12 weighted networks were extracted: three endpoint-related features (count of streamlines, connected surface area (CSA) and weighted CSA), four diffusion-related features (mean and max values of fractional anisotropy (FA) and mean diffusivity (MD)), and five geometry-related features (cluster number, average length and mean deviations from a template streamline).
2.3. Traits identification
HCP uses a reliable and well-validated battery of measures that assess a wide range of human functions, which are called traits in this paper. The core of this battery is comprised of the tools and methods developed by the NIH Toolbox for Assessment of Neurological and Behavioral function [Gershon et al., 2013]. The Toolbox includes measures of cognitive, emotional, motor and sensory processes in healthy individuals. These measures were selected using a consensus building process, and were developed and validated using state-of-the-art assessment methodologies, including item response theory and computer adaptive testing. Moreover, five important areas not fully covered by the Toolbox were also included by the HCP - additional measures of visual processing; personality and adaptive function; delay discounting (as a measure of self-regulation and neuroeconomic decision making); fluid intelligence (as a measure of higher order relational reasoning); and behavioral measures of emotion processing. Specific trait scores for each subject can be easily accessed from the HCP data sharing website (ConnectomeDB: http://www.humanconnectome.org/).
In our analysis, we identified 175 trait measures for each subject in the HCP data set. The 175 trait measures are from eight categories describing a human’s status and behavior: cognition, motor, substance use, psychiatric and life function, sense, emotion, personality, and health. Each of these trait measures is classified as a binary, an ordinal or a continuous variable (by manual inspection of the trait definition). Fig. 2 shows a plot of the proportion of non-NAs for each trait and the trait type. A detailed description of these traits is included in the Excel spreadsheet of Supplementary Material II. In total, we will analyze relationships between 13,176 (1098 scans and 12 weighted networks per scan) weighted networks and 186,375 (1065 subjects in the HCP and 175 traits per subject) trait measures.
Fig. 2.
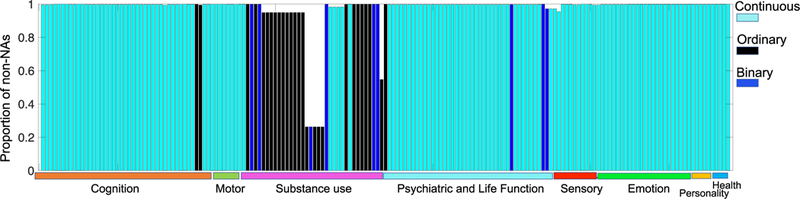
Plot of 175 selected trait measures. The y-axis indicates the proportion of non-NA values for each trait and the y-axis shows the types of traits.
2.4. Tensor-network principal components analysis
Our focus is on inferring relationships between brain structural connectomes and human traits. To address this goal using the extracted connectome representation, it is necessary to develop a statistical approach to assess associations between tensor network representations of the brain connectome and traits. A key problem in this respect is how to estimate low-dimensional features summarizing the brain tensor network without losing valuable information. If the connectome data for each individual could be reorganized into a vector, Principal Components Analysis (PCA) could be used to extract brain connectome PC scores for each individual. However, vectorizing the network would discard valuable information about the network structure. Instead, we propose to use a semi-symmetric tensor generalization of PCA, named tensor-network PCA (TN-PCA), to perform the dimensionality reduction.
To begin, we need some notation which is largely adapted from Kolda and Bader [2009b]. Let be an N-mode tensor, and we denote matrices as X, vectors as x and scalars as x. The outer product is denoted by The scalar product of two tensors is defined as The Frobenius norm of a tensor The n-mode multiplication of tensor with a matrix denoted by gives a tensor in where each element is the product of mode-n fiber of multiplied by A. When A degenerates to a vector a, i.e. we have which is an N − 1-mode tensor.
For simplicity, we will only consider three-mode tensors here, but all of the methods can be easily extended to higher-order tensors. We will work with a tensor network, which is a concatenation of network adjacency matrices where P represents the number of nodes and N represents the number of subjects. For example, if we only use the count feature, by concatenating all subjects’ count adjacency matrices in the HCP data, we get a tensor of 68 × 68 × 1065 (if all features are included, we will have a tensor of 68 × 68 × 12 × 1065). We say that our tensor network is semi-symmetric as every frontal slice, :,:,n, is a symmetric matrix:
Given the special structure of our semi-symmetric tensor network, existing tensor decompositions are not ideal for conducting TN-PCA. Consider an extension of the popular Tucker model [Tucker, 1966] which forces the first two Tucker factors to be equal to account for the semi-symmetric structure:
| (1) |
where are orthogonal matrices that form the Tucker factors and is the Tucker core; under certain restrictions on the Tucker core, this model will result in a semi-symmetric tensor. Interestingly, when standard algorithms for estimating Tucker models (e.g. Higher-Order SVD and Higher-Order Orthogonal Iteration, HOSVD and HOOI, respectively [Tucker, 1966; De Lathauwer et al., 2000a; Kolda and Bader, 2009a]) are applied to semi-symmetric tensors, they result in tensor factorizations that follow model (1); this fact can be easily verified and is also discussed in De Lathauwer et al., [2000a]. Despite the ease of implementation of Tucker models for semi-symmetric tensors, these approaches are not ideal for studying and embedding brain networks. The semi-symmetric Tucker core makes it difficult to directly interpret the effects and prevalence of tensor network components (eigenvectors associated with V) across the population. Further, the assumption that the population factors, U, are orthogonal is likely overly restrictive and limits the Tucker model’s ability to fit brain connectome data well.
Because of this, we consider another popular tensor decomposition model: the CP decomposition, which models a tensor as a sum of rank one tensors: [Carroll and Chang, 1970; Harshman, 1970]. As with the Tucker model, it is clear that the first two factors must be equivalent to yield a CP model appropriate for semi-symmetric tensors:
| (2) |
Here, vk and uk are P and N vectors, respectively, that form the kth CP factor and dk is the kth positive CP scaling parameter. It is clear that (2) needs no further restrictions to yield a semi-symmetric tensor. Yet, this model may not be ideally suited to modeling our population of brain connectomes. If there are no restrictions on the CP factors V as is typical in CP models, then the columns of V could be highly correlated and fail to span the eigen-space of the series of brain networks. Hence, we propose to add an additional orthogonality constraint on the CP factors V, but leave U unconstrained. Note that this form of orthogonality in one factor but not the other is distinct from the various forms of orthogonal tensor decompositions proposed in the literature [Kolda, 2001].
We estimate our CP model for semi-symmetric tensors by solving the following least squares problem:
| (3) |
As with the typical CP problem, this is non-convex but is instead biconvex in v and u. The most common optimization strategy employed is block coordinate descent which alternates solving a least squares problem for all the K factors, for V with U fixed and for U with V fixed [Kolda and Bader, 2009a]. For our problem with the additional orthogonality constraints, this approach is computationally prohibitive. Instead, we propose to use a greedy one-at-a-time strategy that sequentially solves a rank-one problem, a strategy sometimes called the tensor power method [De Lathauwer et al., 2000b; Allen, 2012]. The single-factor CP method can be formulated as
| (4) |
where is the projection matrix with denoting the previously estimated factors. (4) Uses a Gram-Schmidt scheme to impose orthogonality on vk via the projection matrix Pk−1; it is easy to verify that (4) is equivalent to (3) [Allen, 2012].
To solve (4), we employ a block coordinate descent scheme by iteratively optimizing with respect to u and then v; each coordinate-wise update has an analytical solution:
| (5) |
| (6) |
Here, Emax(A) refers to the eigenvector corresponding to the maximum eigenvalue of matrix A. We can show that this scheme converges to a local optimum of (4). More properties about this greedy decomposition method, such as uniqueness, convergence and some statistical characteristics can be found in recent papers [Li and Huang, 2018; Sun et al., 2017] in more general scenarios.
Putting together these pieces, we present our tensor power algorithm for solving (3) in Algorithm 1. After we greedily estimate a rank-one factor, we use subtraction deflation. Overall, this algorithm scales well computationally compared to the Tucker model which requires computing multiple SVDs of potentially large matricized tensors.
Algorithm 1 Tensor power method for semi-symmetric CP decomposition (TN-PCA Algorithm) Let χ be a three-way tensor concatenating M brain networks. The tensor power method for semi-symmetric CP decomposition of χ is given as:
-
(a)Find the semi-symmetric single-factor CP decomposition for and iteratively update until convergence:
-
(b)
CP Scaling:
-
(c)
Projection:
-
(d)
Deflation:
When applied to tensor brain networks, our new semi-symmetric tensor decomposition results in a method for TN-PCA. Specifically, each uk denotes the subject mode and each denotes the rank-one network mode. The subject-modes give the low-dimensional vector embeddings of the brain network for each subject; we use these to associate structural connectomes with traits. Each of these brain components acts similarly to the principal components in the regular PCA analysis. From k = 1 to K, the brain components explain more and more variation of the data across subjects. The subject mode score uk(i) indicates the expression weight of in the subject i. We call the weighted sum of network modes, the principal brain network, which gives a one network summary that captures the most variation in the structural connectomes across all subjects. We do not enforce vk to be sparse, and therefore each network mode and the principal brain network are densely connected. To obtain more meaningful sparse connectivity, we employ a threshold-based method in our experiments.
Note that K here refers to the number of components for estimating the original tensor . There are a few possible ways of selecting K for different purposes. If we want to better represent the original data using low-dimensional vectors, we can select K based on the cumulative proportion of variation explained (CPVE) by the K components. We define the CPVE as follows: Let define analogously. The cumulative proportion of variation explained by the first k high-order components is [Allen, 2012]. In another scenario, if our goal is to use (the low-dimensional representation of weighted networks) for predicting traits, K here can be a tuning parameter of the predictive model, and we select K based on the prediction accuracy.
2.5. Relating connectomes to traits
To relate the networks to various traits, we rely on the low-dimensional representations UK. There are many advantages of using the vector UK(i) to represent the ith subject’s brain connectivity, e.g., (i) we recover the network from Uk(i) through (ii) the low-dimensional vector representations bring us flexibility to utilize various existing statistical tools to study the relationship between the brain networks and human traits; and (iii) TN-PCA is flexible and easily deal with high-order tensors, e.g. a four-mode tensor, by simply include another vector in the outer product.
Hypothesis testing of distribution difference: For each trait, we sort the 1065 HCP subjects according to their scores, and extract two groups of subjects: 100 subjects with the highest trait scores and 100 subjects with the lowest scores. For discrete traits, it is sometimes not possible to identify exactly 100 subjects; in such cases, we randomly select subjects on the boundary as needed. We compare the embedded vectors of networks (rows of UK) from the two groups and test the null hypothesis that the two samples are from the same distribution against the alternative that they are from different distributions. We use the Maximum Mean Discrepancy (MMD) [Gretton et al., 2012] to perform hypothesis tests. False discovery rate (FDR) is controlled using Benjamini and Hochberg [1995].
Relating brain connectomes with traits: We are interested in studying relationships between traits and brain connectomes for all HCP subjects. In particular, we are interested in two types of results. First, we want to see if brain structural connectomes can be used to predict various traits. Second, for those traits that can be predicted by brain connectomes, we would like to identify how the connectome changes with trait values by flagging the subset of connections with the largest differences.
Let vector, which contains one type of trait score for each of the N subjects, and let Uk be an N × K matrix containing the embedded networks in for N subjects. Our first analysis focuses on predicting yi using brain PC scores and demographic covariates such as age and gender. Subjects in the HCP are randomly allocated into a training data set (66% of the subjects), a validation data set (17% of the subjects) and a test data set (17% of the subjects). We then train various machine learning methods (e.g., simple linear/logistic regression, random forests, support vector machines and XGboost) to predict the trait scores. The prediction accuracy is evaluated using the root- mean-square error (RMSE) for both continuous and ordinal traits and the classification accuracy for binary traits. To evaluate whether brain connectomes are important in predicting traits, we compare with a reduced model, where only demographic covariates are used as predictors. The model containing brain connectomes is referred to as the full model, and the model without brain connectomes is referred to as the baseline model.
For each trait, we define a measure ρ to evaluate the importance of brain connectomes. For trait p, let denote the RMSE or (1-classification accuracy) of the full model, and for the baseline model. The measure ρ for trait p is calculated as The best model (including the tuning parameters in each machine learning method) is selected based on the validation data set, and then is applied to the test data set for performance evaluation. We then evaluate ρ for different combinations of networks and traits.
The next question that we are interested in is, for each trait, how the connectome varies across levels of the trait? Depending on a trait’s type, we apply different methods to identify the subset of networks or edges. For continuous traits we use canonical correlation analysis (CCA) [Hotelling, 1936] and for categorical traits we use linear discriminant analysis (LDA) [Fisher, 1936]. For a continuous trait, the problem of finding a subset of edges that are highly correlated with the trait using CCA is equivalent to finding a direction (in the network embedding space) such that the correlation between the trait scores and the projection scores are maximized, i.e.,
| (7) |
If we assume that both are centered, the unit vector w obtained in (7) describes changes of networks in the embedding space with increases of the trait score. To map this direction w back on to the brain network for interpretability, we let come from the TN-PCA analysis, and s is a scaling parameter (which will be explained in the next paragraph). Confounding influence of age and gender can be regressed out from y before fitting the model in (7). For a categorical trait, e.g., we use LDA to identify edge changes from low to high scores. The idea is to find a w in that best separates the two classes of networks. Let be the means, and be the covariances of the embedded networks. The separation of the two groups is defined in the embedding space in the following way:
| (8) |
It is clear that S achieves the maximum when
In both CCA and LDA methods, we only identify a unit vector w, reflecting the global trend in network changes with increasing traits, and there is no scale information included in w. This makes the comparison of network changes across different traits challenging. Hence, we want to define a proper scale s for each trait such that Δnet reflects the magnitude of network changes with increases in that particular trait. Since in this paper the w’s are always inferred from two groups of subjects (with high and low trait scores even for continuous traits), we dichotomize the subjects and use their mean differences in the network embedding space to define s. To be more specific, for a selected trait, letting be the mean embedding vectors for subjects with low and high trait scores respectively, we define
3. Results
3.1. Comparative studies of TN-PCA model
In this section, we compare the proposed TN-PCA via CP decomposition with other tensor decompositions, namely the Higher-Order SVD (HOSVD) and Higher-Order Orthogonal Iteration (HOOI) [Tucker, 1966; De Lathauwer et al., 2000a; Kolda and Bader, 2009a].
First, we study how well the HOOI, HOSVD and our new CP algorithm for semi-symmetric tensor decompositions perform in simulations. We simulate data from the following semi-symmetric tensor model: where is a P × P × N semi-symmetric tensor and Wishart(I, P) to ensure the noise follows a semi-symmetric structure. Also, we take D to be a diagonal tensor to most fairly compare the CP and Tucker models, letting For the tensor factors, V is randomly sampled from the Stiefel manifold; U is either generated from the Stiefel manifold or generated as non-orthogonal iid norm-one Gaussian vectors to evaluate both the orthogonal and non-orthogonal U cases. Each of our scenarios is studied for a set of tensors with size P = 100, M = 500 for various ranks K, and under various signal-to-noise (SNR) levels, where the SNR is defined as We evaluate each tensor decomposition algorithm according to two metrics: the relative difference between the true and estimated and the cumulative proportion of variation explained by the first K components. All simulations were repeated ten times with the average results reported (see Fig. 3).
Fig. 3.
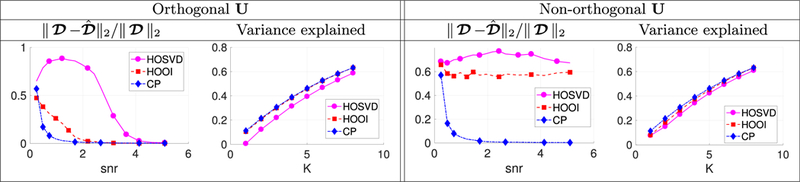
Simulation results in terms of structural recovery (left columns) and variance explained (right columns) for the proposed TN-PCA via a new semi-symmetric CP model compared to the existing HOSVD and HOOI methods.
The results presented in Fig. 1 show that our new CP model for semi- symmetric tensors compares favorably to the algorithms based on the Tucker model, the HOSVD and HOOI. This is especially true in terms of structural recovery (left columns), where our model is able to recover the structure at lower SNRs and when the U factors are not orthogonal. In terms of variance explained (right columns), our CP model shows marginal improvements over the Tucker model; the added flexibility of the non-diagonal Tucker core may help explain more variance in the data even if the lower-dimensional structural recovery is poor. In a real data analysis presented in Supplement I, we also demonstrate the flexibility of the proposed TN-PCA. HOOI requires carefully tuning of K to avoid lack-of-model fit issues, but our new semi-symmetric CP model does not suffer from this problem (we can simply choose K that explains most of the variance in the data without worrying about model mis-specification).
3.2. Exploratory analysis: connectome visualization and classification
The TN-PCA approach approximates the brain tensor network using K components, with the components ordered to have decreasing impact. Individuals are assigned a brain connectome PC score for each of the K components, measuring the extent to which their brain tensor network expresses that particular tensor network component. In this section, we demonstrate how to use these PC scores for visualization of brain connectomes in large cohort studies and statistical analysis of connectomes, such as classification.
In the following study, we use the CSA network as an example. Fig. 4 (a) and (b) show brain PC scores for each of CSA networks in the Sherbrooke and HCP test-retest data sets using K = 3. Each marker represents multiple scans from the same subject (3 scans per subject in Sherbrooke and 2 scans per subject in HCP). Even using only K = 3 components (for data visualization), the CSA brain networks display a clear clustering pattern, suggesting that not only are the extracted connectomes from the repeated scans reproducible but also that we can distinguish between different subjects based on only three components. To formally assess this, we applied nearest neighbor clustering to the PC scores for different types of weighted networks separately (3-way tensor decomposition) and jointly (4-way tensor decomposition) under different K. Fig. 5 shows the results (some non-discriminative features are excluded based on the results in Supplementary Fig. 1).
Fig. 4.
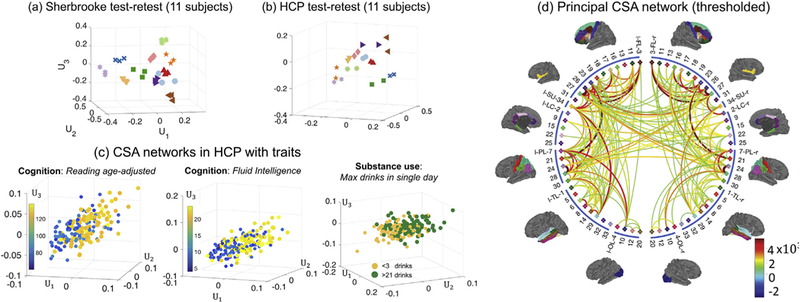
Illustration of connectome visualization using TN-PCA. In (a) and (b), we display brain PC scores for CSA networks from the HCP and Sherbrooke test-retest data sets. Each unique marker represents multiple scans from the same subject (3 scans per subject in Sherbrooke and 2 scans per subject in HCP). In (c), we show PC scores with traits. For each cognition trait, we selected 100 subjects with low trait scores and 100 subjects with high scores. For the substance use trait (alcohol use), we selected subjects with <3 drinks and subjects with > 21 drinks. In (d), we display the principal CSA brain network calculated using all 1065 subjects from the HCP data set. For display purposes, we thresholded the dense principal brain network to keep only the 200 most connected edges.
Fig. 5.
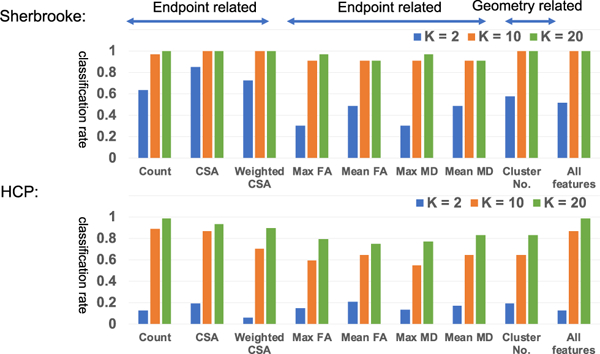
Classification results on the Sherbrooke and HCP test-retest data sets. The results are based on nearest neighbor classification. “K” here indicates the number of component in TN-PCA.
We have the following interesting observations. First, with a moderate K, e.g, K = 10, we can almost perfectly cluster the repeated scans of all subjects based on endpoint features such as the count, CSA, and cluster number. Zhang et al., [2018] also showed that some of the endpoint features have better reproducibilities. One possible explanation is that the pattern of fiber curves connecting gray matter (GM) carries more discriminative information. WM fiber tracts usually group tightly in deep WM regions and start fanning when reaching the interface of WM and GM regions. Studies have shown that these fanning regions will be affected in earlier stage of brain diseases [Granberg et al., 2017], indicating the importance of the ending-point connection patterns. The fanning pattern can be partially captured by the endpoint features. Second, we can obtain very good classification rates by jointly using all features. Third, although the HCP data have better resolution, it seems that the classification results of HCP are not better than for Sherbrooke. There are several reasons. There are more subjects (44 vs. 11) and fewer scans (2 vs. 3) per subject in the HCP than Sherbrooke. More subjects with fewer scans per subject increase the variation in the data, and thus require more PC coefficients to represent each network and it also makes the classification difficult. Also, scan intervals in the HCP (about 60% of them are > 5 months) are much larger than Sherbrooke (1–2 weeks). Differences between scans of a subject in the HCP test-retest is naturally larger than Sherbrooke.
TN-PCA allows one to visualize relationships between structural connectomes and various traits in the HCP data. Based on CSA networks, Fig. 4 (c) displays the first three brain PC scores along with three selected traits (two cognition, one substance use). For the two cognition traits (oral reading test score and fluid intelligence), we selected 100 subjects with low trait scores and 100 subjects with high scores and plotted their brain PC scores. For the substance use trait (max drinks in a single day), we plot subjects with low (<3 alcohol drinks) and high values (>21 alcohol drinks). We can clearly observe a separation between different groups of subjects in these plots, indicating that brain connection patterns are different for these two groups (measured by the CSA feature; we have similar findings on some other features, e.g. the fiber count).
Principal brain networks can also be obtained as a byproduct of TN-PCA. We define the rank K principal brain network to be the network given by the sum of the first K rank-one tensor network components from TN-PCA. Similar to examining patterns amongst features by exploring the PC loadings, the principal brain network exhibits major patterns of structural connectivity that explain most of the variation across the population. Fig. 4 (d) displays the thresholded principal brain network derived from the CSA networks of 1065 subjects from the HCP data set; here, we take K = 30 and threshold the edges so that the 200 most connected pairs of brain regions are displayed. The principal brain network gives a visual summary of all the structural connectomes in the HCP population. Compared to the mean network for the HCP population (shown in Supplementary Fig. 2), our principal brain network yields additional insights into which structural connections tend to have major differences across subjects. Specifically, we see that there is large variation in the strength of connections within hemispheres as well as a few strong inter-hemispheric connections that vary across subjects. As we will investigate in the next sections, these variations in brain connections across subjects may be related to differences in traits.
3.3. Statistical inference: relating connectome to traits
In this section, we study distribution differences of brain connectomes across different groups, evaluate the prediction power of brain connectomes and infer how the connectome varies across levels of traits.
Hypothesis testing of connectome distribution difference:
We first assess whether there are significant differences in distribution of brain PC scores among subjects having low versus high values for each trait. Out of the 1065 HCP subjects, we identified groups of 100 subjects having the highest and lowest traits. We used the Maximum Mean Discrepancy (MMD) test [Gretton et al., 2012] to obtain p values for differences in the brain connectomes across the two groups for each trait. Results are shown in Fig. 6. Fig. 6 (a) shows p values for the CSA weighted networks. Different thresholds for significance based on false discovery rate (FDR) control using Benjamini and Hochberg [1995] are marked with different colored lines. Corresponding results for 7 types of weighted networks are shown in Fig. 6 (b).
Fig. 6.
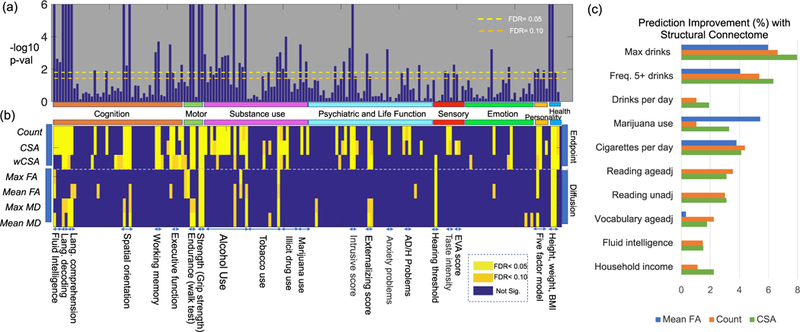
Relation between structural brain connectomes and various traits. Panels (a) and (b) show hypothesis testing results for 175 traits and 7 different weighted networks. In (a), we show p-values (−log10 scale) of the CSA weighted networks with different traits. Two different FDR thresholds are used (different colored dash lines). In (b), we present hypothesis testing results for different combinations of traits and networks. Each row shows a type of weighted network and each column shows a particular trait. The significance is displayed based on different FDR values. Panel (c) shows the top 10 traits in terms of their predictability based on brain connectomes adjusting for age and gender as covariates. The prediction improvement ratio ρp for the pth trait is shown.
Based on these results, many traits are significantly related to brain structural connectomes. Traits in the same domain are placed next to each other in Fig. 6 (b). The block patterns of significance add evidence that brain structural connectomes relate more broadly to these trait domains. In the cognitive domain, structural connectomes are related to fluid intelligence, language decoding and comprehension, working memory, and some executive functions. In the motor domain, connectomes are related to endurance and strength. In the substance use domain, connectomes are related to alcohol consumption, tobacco, illicit drug and marijuana use. In the sensory domain, connectomes are related to hearing and taste. In the emotion domain, connectomes are related to negative emotions, such as anger and anxiety. In the health domain, connectomes are related to height, weight and BMI. Again, we see that endpoint-related features are more discriminative according to the hypothesis testing results; more traits are significant adjusting for false discoveries using features such as count, CSA and weighted CSA than when using diffusion-related features.
Prediction of traits using connectomes:
We are interested in comparing our global structural connectome with other types of connectomes, such as local structural connectomes [Powell et al., 2018; Yeh et al., 2016] and functional connectomes, in teams of predicting human traits. To directly compare with the local structural connectome, we utilize a subset of traits that have been used in Powell et al., [2018] in a similar setting: a linear regression model is applied within a cross-validation paradigm (5-fold cross-validation) with K = 60. For functional connectomes, we utilize the Desikan-Killiany atlas and the resting state fMRI data to calculate a 68 × 68 correlation matrix for each subject and then the same procedures (TN-PCA and linear regression) are applied to evaluate the prediction power. The results are shown in Table 1, where column 4 shows the correlation between the predicted and the observed traits and column 5 shows the p-value of the correlation being zero for the count structural connectome. We can see that our structural connectome has better prediction ability than the local structural connectome. When compared with the functional connectome, structural connectomes are better for most traits, but a few traits can be predicted better with functional connectomes.
Table 1.
Comparison of trait prediction results based on different brain connectomes.
| Model Response | Index | Local structural connectome (correlation) | Functional connectome (correlation) | Global structural connectome (correlation) | P-value |
|---|---|---|---|---|---|
| Total household income | 1 | −0.0029 | 0.1279 | 0.1342 | 0.0510 |
| Years of education completed | 2 | 0.0729 | 0.0619 | 0.1536 | 0.0257* |
| Picture Sequence Memory Test | 3 | 0.0977 | 0.1066 | 0.0671 | 0.3306 |
| Card Sort Test | 4 | −0.0299 | 0.0591 | 0.0522 | 0.4493 |
| Inhibitory Control and Attention Test | 5 | −0.0001 | 0.1120 | 0.0931 | 0.1760 |
| Penn Progressive Matrices: Number of correct responses | 6 | 0.0849 | 0.2400 | 0.2411 | 0.0004** |
| Penn Progressive Matrices: Total skipped items | 7 | 0.0733 | 0.1976 | 0.2106 | 0.0021** |
| Penn Progressive Matrices: Median reaction time for correct responses | 8 | 0.0086 | 0.1125 | 0.1218 | 0.0769 |
| Oral Reading Recognition Test | 9 | 0.0008 | 0.2393 | 0.3020 | <0.0001** |
| Picture Vocabulary Test | 10 | 0.0481 | 0.2091 | 0.2622 | <0.0001** |
| Processing Speed Test | 11 | −0.0569 | 0.0891 | 0.0552 | 0.423 |
| Delay Discounting: Area under the curve for discounting of 200 | 12 | 0.0275 | 0.0808 | 0.1483 | 0.0309* |
| Delay Discounting: Area under the curve for discounting of 4000 | 13 | 0.0802 | 0.2268 | 0.0911 | 0.1864 |
| Line Orientation: Total number correct | 14 | 0.0951 | 0.1254 | 0.2536 | 0.0002** |
| Line Orientation: Median reaction time divided by expected number of clicks for correct | 15 | −0.0572 | 0.0243 | 0.0974 | 0.1578 |
| Line Orientation: Total positions off for all trials | 16 | 0.0014 | 0.2191 | 0.2248 | 0.0010** |
| Memory Test: Total number of correct responses | 17 | 0.0474 | 0.0273 | 0.1034 | 0.1335 |
| Memory Test: Median reaction time for correct responses | 18 | −0.0391 | 0.0473 | 0.0404 | 0.5589 |
| List Sorting Working Memory Test | 19 | 0.0793 | 0.1121 | 0.0939 | 0.1723 |
| Body mass index | 20 | 0.2736 | 0.2770 | 0.1933 | 0.0047** |
| Sleep Quality Index | 21 | −0.0314 | 0.0747 | 0.0455 | 0.5092 |
Correlations in the first column are copied from Powell et al., [2018], whose experiment setting is similar to us but with fewer subjects. In the last column, * indicates significance based on α = 0.05 and ** indicates significance after FDR based on α = 0.05.
To better study the relationship between connectomes and traits and to account for some potential confounding effects, we consider a more comprehensive strategy: a baseline model that only uses demographic variables of age and gender as predictors is compared with a full model that also includes brain connectome PC scores. In this scenario, the 1065 subjects in the HCP data set are randomly divided into three groups: a training group containing 66% of the subjects, a validation group containing 17%, and a test group containing 17%. We trained various machine learning algorithms for prediction using the training data set, with the number of components K treated as a tuning parameter. The prediction improvement of the full model over the baseline model is measured using the relative ratio ρ. For each trait, the best model (with the highest ρ) is selected based on the validation data set. Panel (a) of Supplementary Fig. 3 presents the results for the validation and test data sets based on an average of 50 runs. According to the values of ρ with the test data set, we selected the 10 traits yielding the largest predictive improvements based on connectomes. The ρ’s for these 10 traits are displayed in Fig. 6 panel (c). The 10 traits come from two domains: substance use (5 traits) and cognition (5 traits).
Among the five traits of substance use, three of them are related to alcohol use, one to cigarette use and the last one to marijuana use. A close inspection of the two alcohol use traits was performed and the results are presented in the Supplementary Fig. 3 panels (c) and (d). Consider the trait that measures lifetime max drinks in a single day as one example; it is an ordinal variable ranging from 1 to 7, with 1 corresponding to less than 3 drinks and 7 to more than 21 drinks. For subjects with reported values from 1 to 7, our model with the brain connectome PC scores predicted mean values for each group as 1.97,1.83,2.67,2.91,3.13,4.04, respectively, showing a clear increasing pattern. In another example presented in Fig. 4, we extracted subjects with value 1 (light drinkers, totaling 191) and 7 (binge drinkers, totalling 93) and used LDA to perform binary classification. Based on the brain connectome PC scores alone, we obtain a classification accuracy of 80.99%. These results suggest that using only the brain connectomes, we can distinguish with surprising accuracy between individuals with low and binge alcohol consumption.
Of the five leading cognitive traits, three are related to language and vocabulary decoding ability, one to fluid intelligence, and the other to household income (we loosely classify the household income into the cognition category). A close inspection of the language decoding trait is presented in the Supplementary Fig. 3 panel (b). The language decoding trait score (after age adjustment) can be predicted ~4% better (p < 0.0002) under a random forest model with the additional CSA PC scores (the model is selected based on validation data). On the test data set, the correlation between the predicted trait and the subject self-reported trait is r = 0.27 (based on an average of ten runs). If we restrict the analysis to the 200 subjects with the highest and lowest traits (plotted in the first column of panel (c) in Fig. 4), the correlation increases to r = 0.45. Similar results are observed for the traits of fluid intelligence and vocabulary decoding. Given that these trait scores are only a rough measure of a person’s cognitive function, the results are very promising, indicating that brain structural connectomes can partially account differences in cognitive abilities.
Effects of parcellation and inclusion of subcortical brain regions: Parcellation is very important for connectome analysis [Glasser et al., 2016a, a; Desikan et al., 2006; Destrieux et al., 2010]. Different parcel-lation schemes will affect the representation of the brain connectome and its power in predicting traits [Zalesky et al., 2010]. Here we evaluated how a different parcellation will affect our analysis and whether inclusion of subcortical brain regions can be helpful. The result is presented in the Supplementary Fig. 6. We found that including subcortical regions is helpful in predicting most of the traits, but simply increasing the par- cellation resolution does not always help. This finding is consistent with the result in Zhang et al., [2018] - the reproducibility of networks obtained by the Destrieux parcellation is lower than that by the Desikan parcellation. One possible reason is the misalignment between subjects. A coarse parcellation is often more robust to misalignment. Another reason is statistical due to the increasing dimension of the data.
Effects of motion: A recent study has shown that motion can systematically affect the structural connectivity derived from dMRI data [Baum et al., 2018] even after complicated preprocessing steps, e.g., motion and eddy correction. Although HCP has spent a lot of effort in minimizing head motion during MR scans [Marcus et al., 2013], we still want to investigate whether motion affects our analysis. To analyze motion in dMRI, we extracted all b0 images (they are sampled evenly across the whole dMRI scan in HCP) for each subject, and aligned the first b0 image to subsequent b0 images using FSL FLIRT [Jenkinson and Smith, 2001], restricting to only six degrees of freedom. We quantified motion through analyzing head translation and rotation, separately. The translation displacement was measured using the L2 norm. Fig. 7 (a) (with a unit of mm) shows the histogram of translation displacements. To measure rotation size, we mapped each rotation matrix to the tangent space at identity using the log map defined in Zhang et al., [2019], and measured the length of the tangent vector using Frobenius norm. Fig. 7 (b) shows the histogram of rotation displacements. We can observe that both displacements follow approximately a normal distribution but with a heavy tail, indicating that there are some subjects having big motions. Using the two quantities, we defined a subject as big movement outlier if he/she has either a translation or a rotation greater than the 99 percentile. In total, 95 subjects were identified to have big movements. We selected four traits from Table 1 and conducted the same analysis as the one producing Table 1 but excluded the 95 subjects. Fig. 7 (c) shows the percentage of mean squared error (MSE) decrease after removing the subjects with big motions. We see that these outlying individuals with large head motion are negatively impacting performance, suggesting that we can future improve our results by properly correcting motion or removing subjects with big motion.
Fig. 7.
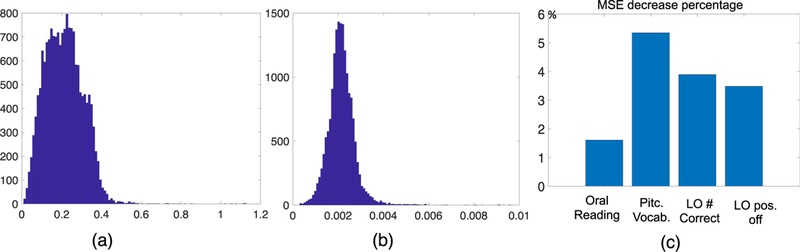
Motion analysis of HCP dataset. (a) histogram of head translation displacements; (b) the histogram of rotation displacements; and (c) percentage of MSE decrease after removing subjects with big translations and rotations.
Empirical comparison of prediction models: TN-PCA reduces dimensionalities of tensor network data, providing a convenient way of linking structural connectomes with traits. Here, we are interested in comparing trait prediction accuracies of different methods. There are a few new methods available for predicting traits using network data. For simplification, we used the count matrix as the predictor and chose four traits that can be accurately predicted from Table 1 as the responses. For TN-PCA, a regular linear regression model was used to predict traits from coefficients (this model is denoted as LR-TNPCA). We compared it with a few other models. The first one is the CP tensor regression model (CPR) proposed in Zhou et al., [2013], where we let the coefficient matrix be rank one (higher ranks gave worse results in this application). This tensor regression model is a popular way of predicting scalars from tensor data. A few recent variants using Bayesian principles can be found in Guha-niyogi et al., [2017] and Guha and Rodriguez [2018]. Another method to compare is the supervised bi-linear regression (BLR) [Wang et al., 2019] model, which emphasizes signal sub-network selection. In our implementation of BLR, we set the number of components as 10 and selected the L1 penalty parameter based on cross-validation. In addition, we compared with simple PCA with linear regression (LR-PCA), where the simple PCA is done by vectorizing the network and performing regular PCA. The mean square error (MSE) from five-fold cross-validation was used to measure the goodness of fit. Table 2 shows the result.
Table 2.
Comparison of trait prediction using different models.
| Model Response | LR-TNPCA (K = 6) | LR-TNPCA (K = 27) | LR-PCA (K = 6) | LR-PCA (K = 27) | CPR (K = 1) | BLR (K = 10) |
|---|---|---|---|---|---|---|
| Oral Reading Recognition Test | 202.05 | 204.52 | 204.18 | 209.89 | 252.10 | 200.40 |
| Picture Vocabulary Test | 214.51 | 218.98 | 219.95 | 221.76 | 257.22 | 216.07 |
| Line Orientation: Total number correct | 18.54 | 19.01 | 18.18 | 18.62 | 21.88 | 18.76 |
| Line Orientation: Total positions off for all trials | 201.79 | 203.32 | 202.55 | 211.51 | 259.02 | 200.74 |
In each cell, we show the mean squared error between predicted value and real value.
From the result, we can see that a simpler model in general favors predictive accuracy. This discovery is also confirmed by Wang et al. (2019), where only a few brain connections are selected to predict traits. In terms of the prediction power, TN-PCA is better than the simple PCA and much better than the CP tensor regression. BLR has better results in some cases, since it is a supervised method, trying to identify sparse connections that can best predict traits. However, BLR needs a careful parameter tuning to select model parameters. The simplicity of TN-PCA, its predictive power and its interpretability make it a good choice for analyzing the structural tensor networks.
Interpreting relationships between traits and connectomes: Having established that a particular trait is significantly associated and can be predicted with the brain connectome, it is important to infer how the connectome varies across levels of the trait. For example, is the association specific to certain sub-networks and in what direction is the association? We start by studying how brain connectome PC scores vary with the trait, and then map these changes back to network using the method presented in the Methods section. The following analyses are based on K = 30 (results are robust for K~20–60). We selected three representative traits: language reading age-adjusted score, lifetime max drinks consumed in a single day and the use of marijuana. The language reading score is a continuous variable, and the other two are categorical. We study how the CSA network changes with increases in these traits.
For the language reading trait, the plot of the top 3 PC scores for the 100 subjects with the highest scores and 100 with the lowest scores is shown in panel (c) of Fig. 4. Panel (a) in Fig. 8 shows the network change (Δnet) with the trait; we show only the 50 edges that change most. There are four major white matter connections that increase significantly with reading ability. They connect the left and right frontal lobes (FL) and parietal lobes (PL): (rFL, lFL), (rFL, rPL), (lFL, lPL), (rPL, lPL). On closer inspection, the strongest connections are among left and right brain nodes of 27-superior frontal, 26-middle frontal (BA 46), 28-superior parietal and 24-precuneus (Supplement III has detailed information on each ROI). These regions have shown strong associations with language ability in previous studies of Positron Emission Tomography (PET), functional MRI [Edwards et al., 2010; Price, 2012] and cortical thickness [Porter et al., 2011]. There were no edges that decreased significantly with increasing reading ability. This result is robust to adjustment for age and gender.
Fig. 8.

Top 50 pairs of brain regions in terms of their changes in CSA connectivity with increasing traits. (a) Results for increasing language reading score; (b) Results for max drinks; (c) Results for marijuana use. We also display the correlation and binary classification rates obtained from CCA and LDA, providing measures of differences in brain connectivity networks between subjects with different trait scores.
Lifetime max drinks is an ordinal variable ranging from 1 to 7, with 1 corresponding to less than 3 drinks and 7 more than 21 drinks. The third column in Fig. 4 (c) shows the top 3 brain PC scores for individuals with a max drink score of 1 (191 light drinkers) and 7 (93 binge drinkers). The separation between light and binge drinkers suggests structural con- nectome differences between the two groups. Panel (b) in Fig. 8 shows the result of using LDA to identify brain network changes between light and binge drinkers (Δnet). As max drinks increases, inter-hemisphere connections (especially the connections between rFL, lFL, rPL, and lPL) decrease. Different from the language reading trait, we observe that Δnet for alcohol drinking are mostly associated with the frontal lobes. Previous studies (e.g., [Moselhy et al., 2001]) have provided evidence of relationships between alcoholism and dysfunction and deficits in the frontal lobe. This analysis shows evidence that binge drinking might cause severe damage to structural connectivity. We repeated this analysis for marijuana use (583 used and 481 did not), and show the result in panel (c) of Fig. 8. Similarly to alcohol, marijuana use is also associated with decreases in inter-hemisphere connections.
To assess how well subjects with different trait scores can be distinguished based on their brain connectomes, we calculated the correlation between traits and their predictive values for continuous traits and the classification rate for categorical traits, based on The results are presented in Fig. 8. The correlation between the projected UK(i,:) and the language reading score is 0.45 for the 200 subjects, indicating a strong relationship between reading abilities and the subjects’ brain networks. The classification rate is 80.99% for binge versus light drinking. More specifically, the sensitivity (a binge drinker is identified as a binge drinker) is 59.1% and the specificity (a light drinker is identified as a light drinker) is 91.6%. The classification rate for marijuana use or not is 59.68% (sensitivity: 26.8%, specificity: 86.8%). This rate is surprisingly high for alcohol, indicating sizable differences in these subjects’ brain structural connectomes, while the rate for marijuana is only slightly better than chance.
From the networks presented in Fig. 8, we extract their corresponding white matter tracts and display them in Fig. 9. These white matter tracts are from two selected subjects with high and low trait scores. Among the connections shown in Fig. 8, cross-hemisphere connections are particularly interesting. These connections are roughly classified into two types: (lFL, rFL) and (lPL, rPL). The first row of panel (a) in Fig. 9 plots differences in these two types of connections between subjects with high (125.2) and low (67.27) reading scores. The streamlines corresponding to these connections are shown in the second row. The subject with a high reading score has richer and thicker structural connections in both (lFL, rFL) and (lPL, rPL); this pattern is common for subjects with similarly high reading scores. Fig. 9 panel (b) shows similar results for selected light and binge drinkers; in this case differences between the subjects are detectable but subtle. More detailed results for the two pairs of subjects are displayed in the Supplementary Figs. 4 and 5.
Fig. 9.
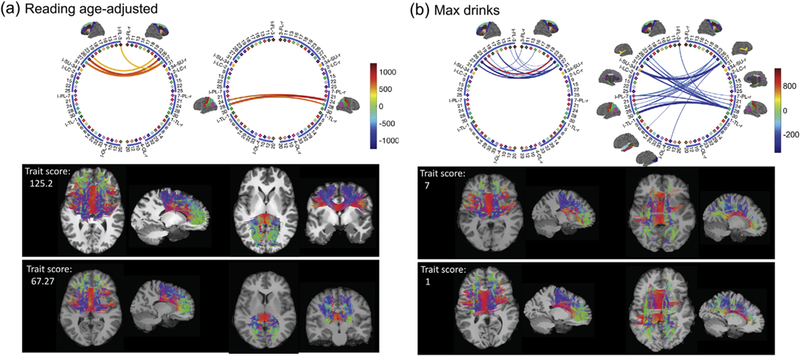
Network difference (based on CSA network) and the corresponding streamlines for selected subjects in the HCP data set. Among the 50 pairs of brain regions identified in Fig. 8, we focus on cross-hemisphere connections. Such connections are either between (lFL, rFL) or (lPL, rPL). In (a) we show the differences between subjects with high (125.2) and low (67.27) reading scores. The streamlines corresponding to these connections are shown in the second row. Similar results are plotted in (b) for two selected subjects with light and binge drinking.
4. Discussion
Using state-of-the-art data science tools applied to data from the Human Connectome Project, we find that many different human traits are significantly associated with the brain structural connectome. Over-all, and consistent with results in previous studies of functional connectomes [Smith et al., 2015; Finn et al., 2015], positive attributes tend to have positive association with structural connectomes, while negative attributes have a negative relationship. Examples of positive traits include high language learning ability, fluid intelligence and motion ability; high levels of such variables tend to be indicative of stronger interconnections in the brain. Examples of negative traits include a high level of alcohol intake and the use of marijuana; such variables tend to be indicative of weaker interconnections.
Given inevitable errors in connectome reconstruction and in measuring human traits, such as alcohol intake, it is surprising how strong the statistical relationships are. For example, we chose to highlight results for reading scores and alcohol intake as being particularly interesting. Using our data science methods, the correlation between the measured reading score and our predicted value based on an individual’s brain connectome was 0.45 (focusing on subjects with particularly low or high scores). In addition, and even more remarkably, the classification accuracy in attempting to distinguish between a light drinker and an individual with a history of binge drinking based only on their brain connectome was surprisingly high. (See Supplementary Fig. 5 for more results on alcohol).
Implementations of the data processing pipeline, TN-PCA method, and the corresponding statistical methods for prediction and interpretation are all freely available in GitHub. They provide an end-to-end solution: from the “raw” imaging data to the analyses of relationships between brain connectomes and individual traits. These methods should be highly useful in the neuroscience community. We note that our results show interesting associations, and it is important to design follow up studies to establish causality. For example, do individuals with less connected brains have more of a tendency for substance abuse or does substance abuse cause a decrease in connectivity? The direction of this relationship has a fundamental impact on the clinical and public health implications of our results. Also of critical importance is the plasticity of the connectome; for example, if a binge drinker modifies their drinking behavior does the brain gradually return to a normal connectivity pattern over time? If an individual having a low reading score works hard to improve their score through coursework, tutoring and exercises, then does the brain connectivity also improve? Does this intervention have a direct causal effect on the connectome?
Given the increasing quality of data on structural connectomes, and in particular the sizable improvements in robustness and reproducibility, we are now at the point in which large, prospective studies can be conducted to answer some of the above important questions. The tools developed and used in this article should be helpful in analyzing data from such studies. On the method side, it is important moving forward to continue to develop more informative and reproducible measures of connectivity between pairs of brain regions, and also to reduce sensitivity to the somewhat arbitrary number and choice of regions of interest. An additional important direction is linking structural and functional connectivity together in one analysis, which can potentially be accomplished via a minor modification of the proposed TN-PCA approach. In addition, a more interpretable TN-PCA that allows sparsity is an appealing future direction.
In a recent paper, Baum et al., [2018] discussed the effect of head motion on the structural connectivity derived from dMRI data. They show that even after complicated preprocessing steps, e.g., motion and eddy correction, head motion can still impact the reconstructed structural connectivity in a consistent and length-dependent manner. HCP spent a lot of effort in minimizing head motion during MR scans [Marcus et al., 2013]. Subjects are trained to keep their heads still in a mock scanner prior to the initial acquisition. During the actual scan, the head is stabilized using cushions on the sides and top of the head. During structural and diffusion sessions, participants watch a movie. The movie pauses for 5s when head motion exceeds a specified threshold, providing immediate feedback to participants that they have moved too much. Images will be reacquired after visual inspection by a trained technologist. But we know that head motion is a concern for MRI and universally exists [Power et al., 2012; Satterthwaite et al., 2013]. Following the suggestion from an anonymous reviewer, we conducted a smaller scale analysis by removing subjects with big motions. The finding suggests that we can improve our analysis by correcting head motion or simply removing subjects with a big motion from the data.
Supplementary Material
Acknowledgment
This research is partially supported by grant MH118927 of the United States National Institute of Health (NIH). Allen acknowledges support from NSF DMS-1554821 and NeuroNex-1707400 and Zhu acknowledges support from NIH MH086633 and MH116527. Data were provided in part by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657). We thank Maxime Descoteaux, Kevin Whittingstall and the Sherbrooke Molecular Imaging Center for the acquisition and sharing of the test-retest data. We also thank the three anonymous reviewers for their insightful comments, which have helped improve the paper significantly.
Footnotes
Supplement
Supplementary materials to this article can be found online at https://doi.org/10.10167j.neuroimage.2019.04.027.
References
- Allen G, 2012. Sparse higher-order principal components analysis. In: International Conference on Artificial Intelligence and Statistics, pp. 27–36. [Google Scholar]
- Avants BB, Tustison NJ, Song G, Cook PA, Klein A, Gee JC, 2011. A reproducible evaluation of ANTs similarity metric performance in brain image registration. Neuroimage 54, 2033–2044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A, 2000. In vivo fiber tractography using DT-MRI data. Magn. Reson. Med. 44, 625–632. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Wymbs NF, Porter MA, Mucha PJ, Carlson JM, Grafton ST, 2011. Dynamic reconfiguration of human brain networks during learning. Proc. Natl. Acad. Sci. Unit. States Am. 108, 7641–7646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battiston F, Nicosia V, Chavez M, Latora V, 2017. Multilayer motif analysis of brain networks. Chaos: An Interdisciplinary Journal of Nonlinear Science 27, 047404. [DOI] [PubMed] [Google Scholar]
- Baum GL, Roalf DR, Cook PA, Ciric R, Rosen AF, Xia C, Elliott MA, Ruparel K, Verma R, Tunç B, et al. , 2018. The impact of in-scanner head motion on structural connectivity derived from diffusion MRI. Neuroimage 173, 275–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens T, Johansen-Berg H, Woolrich M, Smith S, Wheeler-Kingshott C, Boulby P, Barker G, Sillery E, Sheehan K, Ciccarelli O, et al. , 2003. Noninvasive mapping of connections between human thalamus and cortex using diffusion imaging. Nat. Neurosci. 6, 750–757. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y, 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B 289–300. [Google Scholar]
- Bentley B, Branicky R, Barnes CL, Chew YL, Yemini E, Bullmore ET, Vértes PE, Schafer WR, 2016. The multilayer connectome of Caenorhabditis elegans. PLoS Comput. Biol. 12, 1–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjork JM, Gilman JM, 2014. The effects of acute alcohol administration on the human brain: insights from neuroimaging. Neuropharmacology 84, 101–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll J, Chang J, 1970. Analysis of individual differences in multidimensional scaling via an N-way generalization of Eckart-Young decomposition. Psychometrika 35, 283–319. [Google Scholar]
- Chamberland M, Girard G, Bernier M, Fortin D, Descoteaux M, Whittingstall K, 2017. On the origin of individual functional connectivity variability: the role of white matter architecture. Brain Connect. 7, 491–503. [DOI] [PubMed] [Google Scholar]
- Cousineau M, Garyfallidis E, Côté MA, Jodoin PM, Descoteaux M, 2016. Tract- profiling and bundle statistics: a test-retest validation study. In: Proceedings of: International Society of Magnetic Resonance in Medicine (ISMRM) Singapore. [Google Scholar]
- Craddock RC, Jbabdi S, Yan CG, Vogelstein JT, Castellanos FX, Di Martino A, Kelly C, Heberlein K, Colcombe S, Milham MP, 2013. Imaging human connectomes at the macroscale. Nat. Methods 10, 524–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI, 1999. Cortical surface-based analysis: I. segmentation and surface reconstruction. Neuroimage 9, 179–194. [DOI] [PubMed] [Google Scholar]
- De Domenico M, Sasai S, Arenas A, 2016. Mapping multiplex hubs in human functional brain networks. Front. Neurosci. 10, 326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Lathauwer L, De Moor B, Vandewalle J, 2000a. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 21, 1253–1278. [Google Scholar]
- De Lathauwer L, De Moor B, Vandewalle J, 2000b. On the best rank-1 and rank-(r 1, r 2,..., rn) approximation of higher-order tensors. SIAM J. Matrix Anal. Appl. 21 1324–1342. [Google Scholar]
- Descoteaux M, Deriche R, Knosche TR, Anwander A, 2009. Deterministic and probabilistic tractography based on complex fibre orientation distributions. IEEE Trans. Med. Imaging 28, 269–286. [DOI] [PubMed] [Google Scholar]
- Desikan RS, Segonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ, 2006. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 31, 968–980. [DOI] [PubMed] [Google Scholar]
- Destrieux C, Fischl B, Dale A, Halgren E, 2010. Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. Neuroimage 53, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donahue CJ, Sotiropoulos SN, Jbabdi S, Hernandez-Fernandez M, Behrens TE, Dyrby TB, Coalson T, Kennedy H, Knoblauch K, Van Essen DC, et al. , 2016. Using diffusion tractography to predict cortical connection strength and distance: a quantitative comparison with tracers in the monkey. J. Neurosci. 36, 6758–6770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunson DB, 2018. Statistics in the big data era: Failures of the machine. Stat. Probab. Lett. 136, 4–9. [Google Scholar]
- Durante D, Dunson DB, Vogelstein JT, 2017. Nonparametric Bayes modeling of populations of networks. J. Am. Stat. Assoc. 112, 1516–1530. [Google Scholar]
- Edwards E, Nagarajan SS, Dalal SS, Canolty RT, Kirsch HE, Barbaro NM, Knight RT, 2010. Spatiotemporal imaging of cortical activation during verb generation and picture naming. Neuroimage 50, 291–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn ES, Shen X, Scheinost D, Rosenberg MD, Huang J, Chun MM, Papademetris X, Constable RT, 2015. Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nat. Neurosci. 18, 1664–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Salat DH, van der Kouwe AJ, Makris N, Seégonne F, Quinn BT, Dale AM, 2004. Sequence-independent segmentation of magnetic resonance images. Neuroimage 23, S69–S84. [DOI] [PubMed] [Google Scholar]
- Fisher RA, 1936. The use of multiple measurements in taxonomic problems. Ann. Hum. Genet. 7, 179–188. [Google Scholar]
- Fornito A, Zalesky A, Breakspear M, 2013. Graph analysis of the human connectome: promise, progress, and pitfalls. Neuroimage 80, 426–444. [DOI] [PubMed] [Google Scholar]
- Garyfallidis E, Brett M, Correia MM, Williams GB, Nimmo-Smith I, 2012. Quickbundles, a method for tractography simplification. Front. Neurosci. 6, 175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gershon RC, Wagster MV, Hendrie HC, Fox NA, Cook KF, Nowinski CJ, 2013. NIH toolbox for assessment of neurological and behavioral function. Neurology 80, S2–S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard G, Whittingstall K, Deriche R, Descoteaux M, 2014. Towards quantitative connectivity analysis: reducing tractography biases. Neuroimage 98, 266–278. [DOI] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M, et al. , 2016a. A multimodal parcellation of human cerebral cortex. Nature 536, 171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Smith SM, Marcus DS, Andersson JL, Auerbach EJ, Behrens TE, Coalson TS, Harms MP, Jenkinson M, Moeller S, et al. , 2016b. The human connectome project’s neuroimaging approach. Nat. Neurosci. 19, 1175–1187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, et al. , 2013. The minimal preprocessing pipelines for the human connectome project. Neuroimage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granberg T, Fan Q, Treaba CA, Ouellette R, Herranz E, Mangeat G, Louapre C, Cohen-Adad J, Klawiter EC, Sloane JA, Mainero C, 2017. In vivo characterization of cortical and white matter neuroaxonal pathology in early multiple sclerosis. Brain 140, 2912–2926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gretton A, Borgwardt KM, Rasch MJ, Scholkopf B, Smola A, 2012. A kernel two- sample test. J. Mach. Learn. Res. 13, 723–773. [Google Scholar]
- Guha S, Rodriguez A, 2018. Bayesian regression with undirected network predictors with an application to brain connectome data arXiv:1803.10655. [Google Scholar]
- Guhaniyogi R, Qamar S, Dunson DB, 2017. Bayesian tensor regression. J. Mach. Learn. Res. 18, 1–31. [Google Scholar]
- Harshman R, 1970. Foundations of the Parafac Procedure: Models and Conditions for an “Explanatory” Multimodal Factor Analysis. UCLA Working Papers in Phonetics. [Google Scholar]
- Hotelling H, 1936. Relations between two sets of variates. Biometrika 28, 321–377. [Google Scholar]
- Ingalhalikar M, Smith A, Parker D, Satterthwaite TD, Elliott MA, Ruparel K, Hakonarson H, Gur RE, Gur RC, Verma R, 2014. Sex differences in the structural connectome of the human brain. Proc. Natl. Acad. Sci. Unit. States Am. 111, 823–828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jbabdi S, Sotiropoulos SN, Haber SN, Van Essen DC, Behrens TE, 2015. Measuring macroscopic brain connections in vivo. Nat. Neurosci. 18, 1546. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Smith S, 2001. A global optimisation method for robust affine registration of brain images. Med. Image Anal. 5, 143–156. [DOI] [PubMed] [Google Scholar]
- Jones DK, Knosche TR, Turner R, 2013. White matter integrity, fiber count, and other fallacies: the do’s and don’ts of diffusion MRI. Neuroimage 73, 239–254. [DOI] [PubMed] [Google Scholar]
- Kolda T, Bader B, 2009a. Tensor decompositions and applications. SIAM Rev. 51, 455–500. [Google Scholar]
- Kolda TG, 2001. Orthogonal tensor decompositions. SIAM J. Matrix Anal. Appl. 23, 243–255. [Google Scholar]
- Kolda TG, Bader BW, 2009b. Tensor decompositions and applications. SIAM Rev. 51, 455–500. [Google Scholar]
- Li J, Huang F, 2018. Guaranteed Simultaneous Asymmetric Tensor Decomposition via Orthogonalized Alternating Least Squares arXiv:1805.10348. [Google Scholar]
- Lim JS, Kang DW, 2015. Stroke connectome and its implications for cognitive and behavioral sequela of stroke. Journal of Stroke 17, 256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier-Hein KH, Neher PF, Houde JC, Coôtée MA, Garyfallidis E, Zhong J, Chamberland M, Yeh FC, Lin YC, Ji Q, et al. , 2017. The challenge of mapping the human connectome based on diffusion tractography. Nat. Commun. 8, 1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcus DS, Harms MP, Snyder AZ, Jenkinson M, Wilson JA, Glasser MF, Barch DM, Archie KA, Burgess GC, Ramaratnam M, et al. , 2013. Human connectome project informatics: quality control, database services, and data visualization. Neuroimage 80, 202–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KL, Alfaro-Almagro F, Bangerter NK, Thomas DL, Yacoub E, Xu J, Bartsch AJ, Jbabdi S, Sotiropoulos SN, Andersson JL, et al. , 2016. Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nat. Neurosci. 19, 1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moselhy HF, Georgiou G, Kahn A, 2001. Frontal lobe changes in alcoholism: a review of the literature. Alcohol Alcohol 36, 357–368. [DOI] [PubMed] [Google Scholar]
- Park HJ, Friston K, 2013. Structural and functional brain networks: from connections to cognition. Science 342, 1238411. [DOI] [PubMed] [Google Scholar]
- Parker GJ, Haroon HA, Wheeler-Kingshott CA, 2003. A framework for a streamline- based probabilistic index of connectivity (PICo) using a structural interpretation of MRI diffusion measurements. J. Magn. Reson. Imaging 18, 242–254. [DOI] [PubMed] [Google Scholar]
- Porter JN, Collins PF, Muetzel RL, Lim KO, Luciana M, 2011. Associations between cortical thickness and verbal fluency in childhood, adolescence, and young adulthood. Neuroimage 55, 1865–1877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powell MA, Garcia JO, Yeh FC, Vettel JM, Verstynen T, 2018. Local connectome phenotypes predict social, health, and cognitive factors. Network Neuroscience 2, 86–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE, 2012. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage 59, 2142–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price CJ, 2012. A review and synthesis of the first 20 years of PET and fMRI studies of heard speech, spoken language and reading. Neuroimage 62, 816–847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reveley C, Seth AK, Pierpaoli C, Silva AC, Yu D, Saunders RC, Leopold DA, Frank QY, 2015. Superficial white matter fiber systems impede detection of long- range cortical connections in diffusion MR tractography. Proc. Natl. Acad. Sci. Unit. States Am. 112, E2820–E2828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Gerraty RT, Ruparel K, Loughead J, Calkins ME, Eickhoff SB, Hakonarson H, Gur RC, Gur RE, et al. , 2013. An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data. Neuroimage 64, 240–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Cohen-Adad J, Gagoski B, Raij T, Yendiki A, Keil B, Wedeen VJ, Wald LL, 2012. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage 63, 569–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah A, Lenka A, Saini J, Wagle S, Naduthota RM, Yadav R, Pal PK, Ingalhalikar M, 2017. Altered brain wiring in Parkinson’s disease: a structural connectome-based analysis. Brain Connect. 7, 347–356. [DOI] [PubMed] [Google Scholar]
- Smith RE, Tournier JD, Calamante F, Connelly A, 2012. Anatomically-constrained tractography: improved diffusion MRI streamlines tractography through effective use of anatomical information. Neuroimage 62, 1924–1938. [DOI] [PubMed] [Google Scholar]
- Smith RE, Tournier JD, Calamante F, Connelly A, 2013. SIFT: Spherical- deconvolution informed filtering of tractograms. Neuroimage 67, 298–312. [DOI] [PubMed] [Google Scholar]
- Smith SM, Nichols TE, Vidaurre D, Winkler AM, Behrens TE, Glasser MF, Ugurbil K, Barch DM, Van Essen DC, Miller KL, 2015. A positive-negative mode of population covariation links brain connectivity, demographics and behavior. Nat. Neurosci. 18, 1565–1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Zwi JD, 2004. The small world of the cerebral cortex. Neuroinformatics 2, 145–162. [DOI] [PubMed] [Google Scholar]
- Sun WW, Lu J, Liu H, Cheng G, 2017. Provable sparse tensor decomposition. J. R. Stat. Soc. Ser. B 79, 899–916. [Google Scholar]
- Thomas C, Frank QY, Irfanoglu MO, Modi P, Saleem KS, Leopold DA, Pierpaoli C, 2014. Anatomical accuracy of brain connections derived from diffusion MRI tractography is inherently limited. Proc. Natl. Acad. Sci. Unit. States Am. 111, 16574–16579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toschi N, Riccelli R, Indovina I, Terracciano A, Passamonti L, 2018. Functional connectome of the five-factor model of personality. Personality Neuroscience 1, e2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker L, 1966. Some mathematical notes on three-mode factor analysis. Psychometrika 31, 279–311. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium WMH, et al. , 2013. The Wu-Minn human connectome project: an overview. Neuroimage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens T, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW, et al. , 2012. The human connectome project: a data acquisition perspective. Neuroimage 62, 2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Zhang Z, Dunson DB, 2019. Symmetric bilinear regression for signal subgraph estimation. IEEE Trans. Signal Process. 67, 1929–1940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH, 1998. Collective dynamics of ‘small-world’ networks. Nature 393, 409–410. [DOI] [PubMed] [Google Scholar]
- Yeh FC, Badre D, Verstynen T, 2016. Connectometry: a statistical approach harnessing the analytical potential of the local connectome. Neuroimage 125, 162–171. [DOI] [PubMed] [Google Scholar]
- Zalesky A, Fornito A, Harding IH, Cocchi L, Yucel M, Pantelis C, Bullmore ET, 2010. Whole-brain anatomical networks: does the choice of nodes matter? Neuroimage 50, 970–983. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Descoteaux M, Dunson DB, 2016. Nonparametric bayes models of fiber curves connecting brain regions. J. Am. Stat. Assoc. arXiv 1612.01014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, Descoteaux M, Dunson DB, 2019. Nonparametric bayes models of fiber curves connecting brain regions. J. Am. Stat. Assoc. Online. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, Descoteaux M, Zhang J, Girard G, Chamberland M, Dunson D, Srivastava A, Zhu H, 2018. Mapping population-based structural connectomes. Neuroimage 172, 130–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H, Li L, Zhu H, 2013. Tensor regression with applications in neuroimaging data analysis. J. Am. Stat. Assoc. 108, 540–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


