Approaches to treatment effect heterogeneity in the presence of confounding

Summary

The literature on causal effect estimation tends to focus on the population mean estimand, which is less informative as medical treatments are becoming more personalized and there is increasing awareness that subpopulations of individuals may experience a group-specific effect that differs from the population average. In fact, it is possible that there is underlying systematic effect heterogeneity that is obscured by focus on the population mean estimand. In this context, understanding which covariates contribute to this treatment effect heterogeneity (TEH) and how these covariates determine the differential treatment effect is an important consideration. Towards such an understanding, this paper briefly reviews three approaches used in making causal inferences and conducts a simulation study to compare these approaches according to their performance in an exploratory evaluation of TEH when the heterogeneous subgroups are not known a priori. Performance metrics include the detection of any heterogeneity, the identification and characterization of heterogenerous sub-groups, and unconfounded estimation of the treatment effect within subgroups. The methods are then deployed in a comparative effectiveness evaluation of drug-eluting versus bare-metal stents among 54 099 Medicare beneficiaries in the continental United States admitted to a hospital with acute myocardial infarction in 2008.

1 |. INTRODUCTION

Literature on estimation of the causal effect of a treatment on an outcome tends to focus on the population mean estimand, which is appropriate for many research questions. However, technological advances and subsequent increases in the quantity and quality of biomedical data has led to an interest in personalized medicine, the mining of large observational data sources to construct treatments tailored to the covariate distribution of a population.¹ The resulting research question then involves determination of treatment effect heterogeneity (TEH), the existence of an underlying partition of the population into subgroups across which the treatment effect varies systematically. Although the causal effect research question has evolved from one of a population-level average effect to one of subgroup-specific effects, methods for population-level average effect estimates still dominate the literature on causal effect estimation. The goal of this discussion is to evaluate the extent to which several common methods for causal effect estimation simultaneously adjust for confounding and allow for an exploratory investigation of subgroup-specific treatment effects, in potentially high-dimensional settings without any prior knowledge of the number or specific characteristics of these subgroups.

Subgroup analysis methods originated in the clinical trial setting,^2,3 and have been generalized for use in observational studies⁴ with limitations.^2,3,5,6,7 Many methods for subgroup detection in observational studies have grown out of the genetics and bioinformatics literature, but are not designed for comparative evaluation or causal inference.^{8,9,10,11,12,13,14,15} In light of these issues there have been a number of proposed applications of modern machine-learning methods such as regression trees^16,17 to TEH, including the development of non-parametric causal forests comprised of “honest” trees,^18,19,20 the use of trees to identify members of a subgroup with an “enhanced” treatment effect,²¹ and a weighted ensemble of estimators.²²

This paper contributes the ongoing discussion by considering exploratory subgroup detection and TEH estimation in high-dimensional settings when manual evaluation of effect modifiers is not feasible, accomplished in conjunction with confounding adjustment. Achievement of these goals is defined as correct estimation of the number of underlying subgroups, interpretable characterization of the subgroups by observed covariates, and unconfounded estimation of the treatment effect within each subgroup. The discussion continues in §1.1 with a brief overview of causal inference and treatment effect estimation. In §1.2 we more formally define TEH and distinguish it from other but related causal concepts, and in §2 we introduce regression trees as a modeling procedure well-suited for our treatment of TEH identification as a classification problem.

We then discuss three general classes of modeling approach that have been used for causal effect estimation: 1) modeling the outcome conditional on covariates and treatment (e.g., linear regression), 2) modeling the treatment conditional on covariates (e.g., propensity score estimation), and 3) modeling the outcome and treatment jointly conditional on covariates. Evaluation of the ability of each approach to identify TEH is done by describing, implementing, and comparing representative modern methods from each model class: Bayesian Additive Regression Trees (BART)²³, propensity scores estimated with Generalized Boosted Models (GBM)²⁴, and the Facilitating Score (FS)²⁵, respectively. Note that these specific methods are not investigated based on any judgment of optimality or superiority over other methods, and such judgment is not the focus of this paper. Rather, evaluation of each of these representative methods is meant to assess the relative strengths and weaknesses of its respective class of modeling approach for the purposes of identifying and estimating TEH. BART and propensity scores with GBM were chosen as modern methods that have recently emerged as popular approaches to overall causal effect estimation. FS is a recently-proposed approach from the machine learning literature that is similarly rooted in tree-based approaches, designed specifically for the purposes of estimating TEH. In §3 each method is compared qualitatively, in §4 via simulation study, and in §5 in the context of an actual CER investigation. The discussion is concluded in §6.

1.1 |. Notation and Estimation of the Overall Average Treatment Effect

Let i index individuals within a sample of size n, randomly sampled from a much larger population of interest. T_i is a binary indicator of an individual’s point exposure status and X_i a p-dimensional vector of measured pre-treatment covariates. Lowercase t_i, x_i are realizations of their uppercase counterparts. Y_1i and Y_0i represent the potential outcomes that would have been observed had individual i been assigned to treatment or control, respectively. On the difference scale, the causal effect of treatment on individual i is Y_1i − Y_0i. The Fundamental Problem²⁷ precludes observation of this individual treatment effect (ITE), so we instead consider the average treatment effect (ATE) as our estimand, defined in (1).

$$\text{E}\left[Y_1-Y_0\right]=\text{E}\left[Y_1\right]-\text{E}\left[Y_0\right]$$ (1)

$$={\text{E}}_{F_X}\{\text{E}[Y|T=1,\mathit{X}=\mathit{x}]-\text{E}[Y|T=0,\mathit{X}=\mathit{x}]\}.$$ (2)

There are variables associated with both T and Y such that the quantity measured in (2) is not a treatment effect (TE), but a spurious measure of association that is in part due to dissimilarities in their distribution across treatment arms. These problematic covariates are referred to as confounders, defined here as the subset of X required for strong ignorability²⁹ to hold. For the purposes of this discussion, we assume that the available covariates measured in X contain (at least) all confounders required to satisfy the assumption of strong ignorability and estimate causal treatment effects. The notation above also implies the Stable Unit Treatment Value Assumption (SUTVA).²⁸

1.2 |. Treatment Effect Heterogeneity

Variables $\mathit{E}=\left\{E_1,E_2,\dots \right\}\subseteq \mathit{X}$ that define subpopulations across which the treatment effect differs are called effect modifiers,³⁰ with effect modification being synonymous with TEH. As noted by Hernán & Robins³⁰ and Rothman³¹, whether a variable is an effect modifier depends on the scale on which the effect is being measured, be it additive as used here, multiplicative, or the odds ratio. To reflect this dependence, some authors use the terminology effect-measure modification. It is possible for a variable to be both an effect modifier and a confounder, which further emphasizes the importance of simultaneous confounder adjustment and TEH identification.

Mapping these statements back to our notation, effect modifiers E comprise a subset of X, a collection of variables which deserve some clarification. First note that identifying TEH requires that causal effect identifiability assumptions (e.g., strong ignorability in §1.1) defined at the population level must hold within each subgroup. An implication is that achievement of ignorability is particular to a subpopulation, meaning that each subpopulation has its own set of confounders, and its own set of relationships among the confounders, treatment, and outcome. For example, a particular variable can be a confounder in more than one subpopulation but have different relationships with the outcome in each. Thus let variables X be the union of effect modifiers E and confounder sets from each subpopulation.

Our conceptualization of effect modification is different from that of causal^{32, p. 268} or biologic^{31, p. 202} interaction, the combined effect of treatment T and a second exposure on the outcome Y. In this context, it is of interest whether the effect of T depends on the value of this second treatment (or vice versa in the symmetric argument)^{33,Definition 2}. Contrastingly, effect modifiers are characteristics of observational units used to define subpopulations^{33,Definition 1}. Our conceptualization of effect modification is also different from that of mediation, a causal concept that aims to understand “how an effect occurs”³² by considering the pathways between T and Y and variables on those pathways, termed mediators. Effect modification is a causal concept that aims to understand “for whom an effect occurs”.³²

2 |. REGRESSION TREES FOR CHARACTERIZING TEH

Assuming that strong ignorability is satisfied by measured covariates X and a modeling approach has been selected (as will be discussed in §3), there are different estimation procedures that an analyst could consider in fitting a model to data. One such procedure is the fitting of a step function with a classification or regression tree (CART).

A classifier or classification rule is “a systematic way of predicting what class a case is in”.¹⁶ In the most general sense, identifying TEH amounts to classifying observations according to how the treatment affects their outcome. A tree is one type of classifier, a sequence of binary covariate-based decision rules with its depth equal to the maximum number of decisions that have to be made to classify an observation. The tree represents a partitioning of the covariate space into terminal nodes or “leaves”, where within each leaf, observations are of the same class (i.e., a classification tree) or the predicted outcome is constant (i.e., a regression tree). To prevent overfitting (i.e., an overly-fine partitioning of the covariate space that is particular to the sample used to build the tree), an oversized tree is “grown” (constructed) then “pruned” (modified by removing “branches”, subtrees that do not contain the root node). Trees are summed into a new larger tree by adding each observation’s predictions from the summand trees. Boosting is the summing of many low-depth trees (i.e., “weak learners”) into a larger tree, a method known to improve predictive performance.¹⁷ Bootstrap aggregation (bagging) is the averaging of many full-sized trees, as grown from bootstrap samples.^{17, Chapter 8.7}

In our causal context, similar to that of Hill²³, component trees are not intended to address confounding; the virtue of BART and other tree-based ensemble methods is the complexity (e.g., high order interaction terms) of the model built from the the summing of the simple component trees, a flexibility that is very difficult to achieve with traditional regression. In exchange for this flexibility, however, we lose the ability to characterize the partition created by terminal node membership. Terminal node membership is not used to make final subgroup determinations; in practice an ensemble method yields a set of n predictions, and it is this set that is partitioned.

CART does not require the prespecification of any relationships between Y, T, and/or X, and the relationships that it does estimate are quite flexible. Further, CART is potentially nonparametric and is able to yield valid estimates when data are missing at random. CART has relevance to the goal of identifying TEH because the classifications can be thought of as the detection and characterization of subgroups by effect modifiers. As discussed in the previous section, each subgroup has its own set of confounders, and its own set of relationships among Y, T, and X. These subgroup-specific relationships can be thought of as (statistical) interactions between treatment, confounders, and effect modifiers. Achievement of subgroup-specific ignorability can be thought of as the detection of many (potentially) high-order interactions, making CART a natural choice for TEH estimation.

3. |. TREATMENT EFFECT MODELING APPROACHES

There are several approaches an analyst could pursue in modeling the treatment effect, and within each approach, several methods to choose from. In this section we describe three classes of approach and from each, a representative method that has been previously used for the explicit purpose of causal effect estimation. For each representative method, we outline its statistical framework and discuss how it may be used to identify subgroups.

The tree-based methods highlighted here average across many simple or unstable models, improving variance but losing direct interpretability of the estimated subgroups. Further, the analyst must a priori specify a maximum number of possible subgroups to investigate, relying on the ability to collapse across subgroups if the data indicate fewer. After deciding on a method and how to use that method to assign group membership, interpretation of which characteristics define each subgroup relies on the analyst’s ability to inspect covariates distributions within each group to infer what characterizes them. Assuming ignorability is satisfied by some subgroup-specific confounder covariate set X_subgroup, unconfounded subgroup-specific treatment effect estimation is possible. TEH is present if the estimated treatment effects vary across the subgroups.

A necessary condition for such estimation is that the analyst can extrapolate the relationships estimated from the treatment arm to the control arm, and vice versa. This extrapolation relies on positivity, the assumption that within every level of X_subgroup, the probability of treatment is bounded away from 0 and 1. This is an assumption that our causal interpretations rely on, and should be empirically justified. Our ability to provide such justification depends on the estimation method, so the discussion of each estimation method includes an examination of positivity.

3.1 |. Modeling Class 1: Outcome conditional on covariates and treatment

By far the most common modeling approach is to model the conditional mean of Y | X, T. The overwhelmingly most popular class of models within this approach is parametric linear regression, which models the conditional mean as a linear combination of covariates. To see how this modeling approach allows for causal inference, consider the linear regression model

$$\text{E}[Y|\mathit{X},T]={\beta }_0+{\beta }_1{X}_1+\dots +{\beta }_p{X}_p+{\gamma }_{0}T+{\gamma }_{1}T{X}_1.$$ (3)

SUTVA and ignorability allow the difference in conditional means to represent the conditional average treatment effect (ATE):

$${\gamma }_0+{\gamma }_1{X}_1=\underset{\text{difference in conditional means}}{\underbrace{\text{E}[Y|\mathit{X},T=1]-\text{E}[Y|\mathit{X},T=0]}}=\text{E}\left[Y_1|\mathit{X}\right]-\text{E}\left[Y_0|\mathit{X}\right]=\underset{\text{conditional ATE}}{\underbrace{\text{E}\left[Y_1-Y_0|\mathit{X}\right]}}.$$ (4)

First considering the case where γ₁ ≡ 0, we see that the conditional ATE is γ₀, constant for all values of X. Because of the collapsibility of the mean, γ₀ is also the marginal average treatment effect. If ${\gamma }_1\ne 0,$ then the linear predictor contains a (statistical) interaction term, which embeds the a priori belief that the average treatment effect is not additive and its magnitude depends on the value of X₁. Use of (statistical) interaction terms is one way of specifying possible TEH, but requires knowledge of the covariates that define the underlying subgroups, infeasible when considering a large number of covariates.

Another set of methodologies within this modeling class estimate the disease risk score,^34,35 a special case of Mietennen’s confounder score³⁶ and used when the outcome is binary. A disease risk score is the conditional probability of experiencing the outcome while unexposed to treatment $\text{Pr}(Y=1|\mathit{X},T=0)$ and is a tool for ranking subjects on how “case-like” they are.^{36, p.611} Related to the disease risk score is the prognostic score, a recasting of the disease risk score in the language of potential outcomes.³⁷ In both cases, observations are stratified by score and the treatment effect estimated within each stratum.

Representative Method: Bayesian Additive Regression Trees (BART)

A popular alternative to parametric regression for estimating (3) is Bayesian Additive Regression Trees (BART)^38,39 which we will explore in some detail for its potential to provide exploratory analysis of TEH. Following the notation of Chipman, George, & McCulloch³⁸ let ${\mathcal{T}}_j,j=1,\dots ,m$ represent a tree with B_j terminal nodes; that is, a partition of the population into B_j subgroups. Let $M_j=\left\{{\mu }_{b_j}|b_j=1,\dots ,B_j\right\}$ be the set of mean outcomes across the subpopulations defined the terminal nodes of tree ${\mathcal{T}}_j$. Also let $g\left({\mathit{x}}_i,t_i|{\mathcal{T}}_j,M_j\right)$ represent the mapping of observed covariate and treatment pair (x_i, t_i) to a terminal node within tree ${\mathcal{T}}_j$ with mean ${\mu }_{b_j}\in M_j.$ An individual’s outcome is then modeled as the sum of m trees

$$Y_i={\epsilon }_i+\sum _{j=1}^{m}g\left({\mathit{x}}_i,t_i|{\mathcal{T}}_j,M_j\right),{\epsilon }_i~N\left(0,{\sigma }^2\right)$$ (5)

where m is fixed. This is an example of boosting, the construction of a large tree by summing together simple trees. In the Bayesian model, the m simple trees and outcome variance σ² are the unknown parameters; the data are y the vector of observed outcomes, and X the matrix of observed covariate data. A Gibbs sampler is used to sample from the posterior distribution of the boosted tree. Each posterior draw is used to generate a predicted outcome ${\widehat{Y}}_i$ for all observations i. Notationally, let the kth posterior draw be denoted as ${\widehat{\mathcal{T}}}^{(k)}=\left(\left({\widehat{\mathcal{T}}}_1^{(k)},{\widehat{M}}_1^{(k)}\right),\dots ,\left({\widehat{\mathcal{T}}}_m^{(k)},{\widehat{M}}_m^{(k)}\right),{\widehat{\sigma }}^{(k)}\right),$ and the vector of n predicted outcomes generated from this tree denoted as ${\widehat{\mathit{Y}}}^{(k)}.$ The set $\widehat{\mathcal{T}}=\left\{{\widehat{\mathcal{T}}}^{(1)},{\widehat{\mathcal{T}}}^{(2)},\dots ,{\widehat{\mathcal{T}}}^{(K)}\right\}$ denotes the K posterior draws.

As Hill²³ contributes in her reframing of BART from a predictive methodology into a methodology for causal effect estimation, ${\widehat{\mathit{Y}}}^{(k)}$ is the vector of predicted potential outcomes, corresponding to the treatment actually received. ${\widehat{\mathit{Y}}}_{\text{counterfactual}}^{(k)}$ is another vector of predicted potential outcomes, but corresponding to the treatment not received. The ITE predicted from $\widehat{\mathcal{T}}$^(k) is then the appropriate difference in the predicted potential outcomes. This prediction of ITEs is repeated $\forall {\widehat{\mathcal{T}}}^{(k)}\in \widehat{\mathcal{T}}$ (envision a K × n matrix, with the i^th column representing K samples from the posterior distribution of the ITE for the i^th observation). Estimates of the ITE for each individual (as well as σ²) are then obtained by summarizing across the K posterior draws, for example, by averaging to take the posterior mean estimate. It is this averaging across K boosted trees (rather than inference based on one boosted tree) that differentiates BART from traditional boosted methods.

Although subgroup estimation is not explicitly part of the model specification or estimation output, the analyst is still able to investigate the empirical distribution of ITEs for clues. For example Foster et al.²¹ refer to ${\widehat{\mathit{Y}}}_{\text{counterfactual}}^{(k)}$ as the “virtual twin” of ${\widehat{\mathit{Y}}}^{(k)}$, and suggest regressing the predicted ITEs on X, towards finding a single subgroup with a treatment effect that is “enhanced“ relative to the ATE. Hill²³ proffers visualization of the modes of the predicted ITEs (by histogram for example) for hints about the underlying number of subgroups. Alternatively, the analyst can a priori set the number of subgroups to ten (say), and group observations based on deciles of the empirical distribution and estimate a TE within each subgroup.

When using BART or other outcome regression models, valid causal inference relies on positivity, but empirical positivity violations (e.g., a level of X_subgroup with only treated observations) will not be automatically evident. In fact, outcome regression will yield causal effect estimates whether or not positivity is violated. This issue can be partially overcome by assuming any empirical violations are random rather than deterministic⁴⁰, and checking that the unconditional probability of treatment within the finite subgroup sample is bounded away from 0 and 1.

3.2 |. Modeling Class 2: Treatment conditional on covariates

Modeling T | X is referred to as propensity score estimation, where the propensity score e(X) = Pr(T = 1 | X) is the conditional probability of treatment⁴¹. This modeling approach is typically employed as part of a covariate dimension reduction strategy, where the analyst attempts to satisfy ignorability by conditioning on e(X) rather than the covariates individually^{41, Theorem 3}. The use of e(X) allows us to adjust for confounding while averting the need to model how each covariate relates to the outcome of interest or at least alleviating the consequences of misspecifying such a model⁴².

Propensity score methods are used in designing observational comparative studies, that is, the structuring “to obtain, as closely as possible, the same answer that would have been obtained in a randomized experiment comparing the same analogous treatment and control conditions in the same population”⁴³. This can be accomplished, for example, by matching or subclassifying treated and untreated observations with similar values of the propensity score. A key benefit of this approach is that it permits the analyst to empirically judge the plausibility of the hypothetical study design before analysis of any outcome. After grouping observations on the propensity score, the analyst can empirically assess covariate balance, the similarity of covariate distributions among treated and control units with similar values of the propensity score.

In addition to empirical verification of the hypothetical study design and covariate balance, use of propensity scores to adjust for confounding empirically alerts the analyst to violations of the positivity assumption: when the propensity score model discriminates treatment groups too well, it yields subgroups that are homogeneous with respect to treatment, thus empirical justification of causal interpretation is absent, the treatment effect is undefined, and overall inference must be restricted to observations with defined treatment effect estimates.

Estimation of the propensity score itself has traditionally been done via logistic regression, but the literature shows movement towards more flexible alternatives. For example, Woo et al. ⁴⁴ evaluate the use of generalized additive models in propensity score estimation, where the linear predictor is replaced with a flexible additive function. Ghosh⁴⁵ generalizes propensity score estimation as an example of confounder dimension reduction and discuss the theoretical validity of “covariate sufficiency” in causal inference.

Representative Method: Generalized Boosted Models (GBM)

One of the most popular flexible alternatives to traditional logistic regression is the use of generalized boosted models (GBM)²⁴. We use this method to estimate the conditional log odds of treatment logit $\left[\text{Pr}\left(T_i=1|{\mathit{X}}_i\right)\right],$ by summing together many low-depth regression trees. Again following the notation of Chipman, George, & McCulloch,³⁸ let $g\left({\mathit{x}}_i|{\mathcal{T}}_j,M_j\right)$ represent a mapping of an observed covariate value to a terminal node within tree ${\mathcal{T}}_j$ with mean ${\mu }_{b_j}\in M_j=\left\{{\mu }_{b_j}|b_j=1,\dots ,B_j\right\}$. In this model, ${\mu }_{b_j}$ is the mean log odds of treatment for observations in terminal node b_j.

The estimation algorithm is initialized at tree ${\mathcal{T}}_0$ with B₀ = 1 node and $M_0=\{\text{logit}(\overline{t})\}\text{where}\overline{t}$ is the unconditional proportion of treated individuals in the sample. During the jth of m iterations, a low-depth tree fit to residuals $\left[r_i=t_i-\text{expit}\left[g\left({\mathit{x}}_i|{\mathcal{T}}_{j-1},M_{j-1}\right)\right]\right],$ where expit $\left[g\left({\mathit{x}}_i|{\mathcal{T}}_{j-1},M_{j-1}\right)\right],$ is the predicted probability of treatment based on the tree from the previous iteration. Let the number of nodes on this residual tree be denoted by ${\mathit{B}}_j^{*}\text{and}{b}_{j\mathcal{l}}^{*}$ represent the set of observations in terminal node $\mathcal{l}\in \left\{1,\dots ,B_j^{*}\right\}$ For each terminal node $b_{j\mathcal{l}}^{*}$ an update is calculated and added to ${\mathcal{T}}_{j-1}$ to generate ${\mathcal{T}}_j.$ The end result of this algorithm is a sequence of trees with increasingly better fit to the data. To prevent overfitting, the algorithm is stopped at the iteration that minimizes some average measure of covariate imbalance across the two treatment arms (e.g., the average standardized absolute mean difference, or the Kolmogorov-Smirnov statistic).

The resulting estimated propensity score can be used to group individuals, but such grouping requires an a priori specification of the number of subgroups. The analyst could set the number of subgroups to ten (say) and group observations based on deciles of the empirical propensity score distribution, then estimate a TE within each subgroup.

Recall, however, that our goal is to group observations that are similar, where the desired similarity is in the ITE. While estimating differential effects across groups defined by the estimated propensity score is commonplace, note that these groups are not defined based on observations’ ITE. Rather, observations are grouped based on the likelihood of receiving treatment, so assessment of TEH is typically restricted to whether the treatment effect varies with values of the estimated propensity score. This can provide an overall assessment of the presence of TEH, but as the propensity score is a scalar summary of a multivariate covariate vector, deriving clinical or scientific interpretability from knowing that the treatment effect varies with the propensity score is challenging. Thus TEH across values of the propensity score does not provide the specificity of heterogeneity we are interested in. If an effect modifier is associated with Y and not T – in other words, if an effect modifier is not also a confounder –then propensity score methods will not be able to detect it. By ignoring outcome data and focusing solely on the relationship between T and X, the propensity score model has difficulty learning about who experiences the treatment effect differently.

3.3 |. Modeling Class 3: Outcome and treatment jointly, conditional on covariates

A relatively recent approach is considering the conditional joint distribution of the outcome and treatment by modeling (Y, T) | X. Nelson & Noorbaloochi⁴⁶ define a multidimensional sufficient summary S(X), a balancing score such that $(Y,T)\perp \perp \mathit{X}|\mathit{S}(\mathit{X}).$ Wang, Parmigiani, & Dominici⁴⁷ take a Bayesian variable selection perspective, defining a Bayesian adjustment for confounding (BAC) methodology for estimating average treatment effects with linear regression models by averaging over the posterior probability of covariate inclusion in a joint model for (Y, T).

Representative Method: Facilitating Score (FS)

The representative approach from this model class that we investigate in detail is that of Su et al.,²⁵ who define the multidimensional facilitating score ${\mathit{a}}_0(\mathit{X})$ as a statistic that satisfies the following conditional independence:

$$\mathit{X}⫫\left(Y_0,Y_1,T\right)|{\mathit{a}}_0(\mathit{X})\stackrel{\text{relaxation}}{\Rightarrow }\underset{\text{addresses confounding}}{\underbrace{\mathit{X}⫫T|{\mathit{a}}_0(\mathit{X})}}\text{and}\underset{\text{addresses effect modification}}{\underbrace{\mathit{X}⫫\left(Y_0,Y_1\right)|{\mathit{a}}_0(\mathit{X})}}.$$ (6)

Estimation of ${\mathit{a}}_{\text{0}}\text{(}\mathit{X}\text{)}$ involves joint modeling of (Y₀, Y₁, T), precluded by the Fundamental Problem.²⁷ Thus Su et al.²⁵ instead propose a multidimensional weak facilitating score a(X), that satisfies the following as derived from the above relaxation:

$$\underset{\text{addresses confounding}}{\underbrace{\mathit{X}⫫T|\mathit{a}(\mathit{X})}}\text{and}\underset{\text{addresses effect modification}}{\underbrace{\text{E}\left[Y_1-Y_0|\mathit{X}\right]=\text{E}\left[Y_1-Y_0|\mathit{a}(\mathit{X})\right]}}.$$ (7)

The weak FS a(X) is therefore a balancing score, and conditioning on a(X) defines a subpopulation within which the average treatment effect is constant. This is the first method discussed thus far that has explicitly addressed the issue of TEH.

To estimate the weak FS, Su et al.²⁵ use the conditional independence

$$\text{(}Y,T)⫫\mathit{X}|\mathit{h}\left(\mathit{X}\right)$$ (8)

for a statistic h(X). The validity of this independence is a consequence of a factorization theorem applied to the joint distribution of observed data $f_{Y,T|\mathit{X}}(y,t|\mathit{x}\text{)}.$^{25, Theorem 7} By this theorem, the statistic h(X) that fulfills the preceding conditional independence also fulfills definition (7) of a weak facilitating score.^{25, Theorem 3} This then allows for indirect estimation of the weakFS by jointly modeling (Y, T). Regression trees¹⁶ are used for this modeling, where the fact that the joint conditional density $f_{Y\text{,}T|\mathit{X}}(y,t|\mathit{x})$ is constant within a terminal node implies $(Y,T)⫫\mathit{X}$ within that node. This within-node independence implies (8); that is, that the facilitating score is constant within a given node. Because a single tree model is known to be unstable (i.e., a small change in the data can result in a large change in the final tree structure),^{17, p.312} Su et al.²⁵ propose an aggregated grouping strategy (similar to bagging) to average across K possible tree structures. Again adopting the notation of Chipman, George, & McCulloch,³⁸ to generate one possible tree structure, a bootstrap sample is generated to grow and prune tree ${\mathcal{T}}_k$ to B_k terminal nodes. This tree is then applied to the original data. An n × n pairwise distance matrix D_k is generated from the resulting tree classifications, where matrix element

$$d_{i{i}^{\prime }}^{(k)}=\{\begin{array}{ll}1\hfill & \text{if observations}\left\{i,i^{\prime }\right\}\text{fall into the same terminal node of}{\mathcal{T}}_k\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (9)

The distance matrices are then averaged to obtain $\mathit{D}=\frac{1}{K}{{\mathbf{\sum }}_{k=1}^K\mathit{D}}_k,$ and a clustering algorithm (e.g., multidimensional scaling, partitioning around mediods) applied to D to obtain the final data stratification. The end product is the assignment of each observation to a subgroup, and a TE can be estimated within each.

Similar to BART, issues of sparsity may preclude empirical justification of positivity, but this can be partially overcome through assumptions made of the larger subpopulation that the sample represents and checking that the unconditional probability of treatment within each subgroup is bounded away from 0 and 1. We note that although the estimation algorithm of Su et al.²⁵ ensures empirical subgroup positivity through particular stopping rules within the node-splitting procedure, these rules also increase the potential to conceal true subgroups. For example, if there is a tree node that contains observations from two subgroups but there are too few treatment observations, the procedure will not split that node and inference will be made on the whole node.

4 |. COMPARISON OF METHODOLOGIES: SIMULATION STUDY

We evaluate the ability of the three approaches discussed in §3 to identify TEH by considering the representative method from each approach; these methods are summarized in Table 1.

TABLE 1.

Summary of statistical methods being compared.

Approach	Representative Method	Summary + Assumption	Simulation Notes
Y | X, T	Bayesian Additive Regression Trees (BART)38,39 & application to causal effect estimation23	Tree-based modeling of potential outcomes.	Used recommended prior and hyperparameter values.39
T | X	Propensity score estimation with Generalized Boosted Regression (GBM)24	Tree-based modeling of logit[e(x)].  $T⫫\mathit{X}\left|e\right(\mathit{X}).$	Used recommended parameter values.24, pp.409–10
Y,T | X	Tree-based Facilitating Score (FS) estimation25	Tree-based modeling of $\begin{array}{l}{f}_{Y,T|\mathit{X}}(Y,T|\mathit{X})\\ \mathit{X}⫫T|\mathit{h}(\mathit{X})\text{and}\\ \text{E}\left[Y_1-Y_0|\mathit{X}\right]=\\ \text{E}\left[Y_1-Y_0|\mathit{h}(\mathit{X})\right].\end{array}$	Used aggregated grouping to generate K = 100 trees of maximum depth 8, from a bootstrap sample of ⅔ of the total dataset. Each node has ≥ 20 observations, with ≥ 5 observations from each treatment group.25

4.1 |. Data Structure and Analysis

Letting ${\mathcal{l}}_1\in \left\{A,B,C,D,D^{*}\right\}$ denote a particular simulation scenario, Table 2 defines possible underlying correlation structures for $\left\{Y,T,X_1,\dots ,X_6,E_1,E_2,E_3\right\}.$ Let $Y~N({\mu }_{{\mathcal{l}}_1},1)$ denote the continuous outcome, and $T~\text{Bern}(p_{{\mathcal{l}}_1})$ the binary treatment. There is one covariate associated with the treatment only, X₅ ~ Bern(0.5). There is one covariate associated with the outcome only, X₆ ~ N(0,1). There are four confounders of the effect of treatment on outcome, $\left(X_1,X_2,X_3,X_4\right)\stackrel{\text{i.i.d.}}{~}N(0,1).$ In addition, there are three binary effect modifiers, $\left(E_1,E_2,E_3\right)\stackrel{\text{i}.\text{i}.\text{d}.}{~}\text{Bern}(0.5).$ These three variables define eight subgroups (Group 1, …, Group 8), with six unique treatment effects among them. As determined by ${\mu }_{{\mathcal{l}}_1}$ and the eight unique values of (E₁, E₂, E₃), the subgroup-specific ATEs are 1, 2, 5, 5, 6, 6, 9, and 10. Regardless of the underlying data generation mechanism, models are fit using all available covariates (similar to what might be done in practice).

TABLE 2.

Summary of data generation scenarios for Simulation Study 4.

${\mathcal{l}}_1$	Data Generation Scenario	Definition
A	confounding and no effect modification	$\begin{array}{l}{p}_{{\mathcal{l}}_1}=\text{expit}\left(0.1X_1-0.1X_2+1.1X_3-1.1X_4+0.4X_5\right)\\ {\mu }_{{\mathcal{l}}_1}=-3.85+0.5X_1-2X_2-0.5X_3+2X_4+X_6+5T\end{array}$
B	effect modification and no confounding	$\begin{array}{l}{p}_{{\mathcal{l}}_1}=\text{expit}\left(0.4X_5\right)\\ {\mu }_{{\mathcal{l}}_1}=-3.85+X_6-E_1-2E_3+5T+T{E}_1+4T{E}_2-4T{E}_3\end{array}$
C	effect modification and confounding effect modifiers	$\begin{array}{l}{p}_{{\mathcal{l}}_1}=\text{expit}\left(0.1X_1-0.1X_2+1.1X_3-1.1X_4+0.4X_5\right)\\ {\mu }_{{\mathcal{l}}_1}=-3.85+0.5X_1-2X_2-0.5X_3+2X_4+X_6-E_1-2E_3\\ +5T+T{E}_1+4T{E}_2-4T{E}_3\end{array}$
D	effect modification and confounding by	$\begin{array}{l}{p}_{{\mathcal{l}}_1}=\text{expit}(0.1X_1-0.1X_2+1.1X_3-1.1X_4+0.4X_5\\ -0.1E_1+1.1E_2-4E_3)\\ {\mu }_{{\mathcal{l}}_1}=-3.85+0.5X_1-2X_2-0.5X_3+2X_4+X_6-E_1-2E_3\\ +5T+T{E}_1+4T{E}_2-4T{E}_3\hfill \end{array}$
D*	effect modification and nonlinear confounding by effect modifiers	$\begin{array}{l}{p}_{{\mathcal{l}}_1}=\text{expit}(0.1X_1-0.1X_2+1.1X_3-1.1X_4+0.4X_5\hfill \\ \begin{array}{l}-0.1E_1+1.1E_2-4E_3)\\ {\mu }_{{\mathcal{l}}_1}={\left(-3.85+0.5X_1-2X_2-0.5X_3+2X_4+X_6-E_1-2E_3\right)}^2\end{array}\hfill \\ +5T+T{E}_1+4T{E}_2-4T{E}_3\hfill \end{array}$

Within one of the 1000 simulation iterations, a dataset of size n = 1500 is generated according to §4.1 and TEH evaluated using each of the methods described in §3. In the case of BART and GBM, such evaluation is done by partitioning the estimated probability distribution (be it of the outcome or treatment) into deciles, then estimating a TE within each subgroup defined by the deciles. In the case of the facilitating score (FS), the dissimilarity matrix D is partitioned into 10 subgroups using the partitioning around mediods method and a TE estimated within each. In practice the analyst will know neither the number nor relative sizes of the true underlying subgroups; thus success of a method is judged in part by its ability to group similar observations together. Typical measures of concordance are complicated by our estimation of more subgroups (ten) than truly exist in the population (eight), as well as the unequal sizes of the true subgroups, leading to members of true subgroups necessarily split across estimated subgroups. This process is explained in detail below, as is our proposed measure of concordance. Example code used to simulate these data and estimate partitions is available online.²⁶

4.2 |. Results

To summarize the results of a single simulation iteration, subgroups are numbered in ascending order by the estimated treatment effect. If an individual is in a subgroup for which there is an undefined treatment effect (e.g., its subgroup is entirely comprised of individuals on treatment), it is assigned to an “undefined” subgroup. For example, if only seven of ten subgroups have a defined treatment effect, then the 8th, 9th, and 10th subgroups are empty and the individuals in the three subgroups are all reassigned to the same “undefined” subgroup. In the ordering of subgroups, the “undefined” group is placed last.

The estimated partition is cross-tabulated with the eight true groupings, which are also ordered by the magnitude of their average treatment effect (envision a 8×11 table where each row corresponds to true subgroup membership and each column corresponds to estimated subgroup membership). Within this cross-tabulation table, row percentages for each of the q = 1,2,…, 8 rows are calculated representing the proportion of units in true treatment group q that are assigned each of the estimated sub-groups (columns). This table of row percentages is constructed for each simulation iteration. The resulting collection of tables is averaged over the 1000 simulation iterations to yield a single table of cell-specific averages. A single average indicates how often a method places an individual from true subgroup q in to each of the 11 estimated subgroups. Averages for the different data generation scenarios and the different estimation methodologies are visualized in Figure 1.

FIGURE 1.

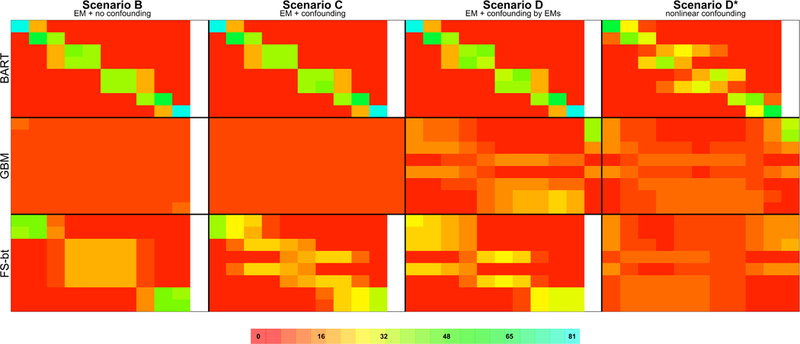
Visualization of results from Simulation Study 4. Details regarding how the figure was constructed, and how to interpret the figure, are given in §4.2. A full, annotated version of this image, including the quantities visualized by the colors as well as a summary of Simulation Scenario A, can be found in Appendix 2 of the Supplementary Materials

To ease explanation, consider the fourth block in the second row of Figure 1 –the table summarizing data generated under Scenario D* and using GBM to address TEH. The last row of this table summarizes results for observations in Group 8, the true subgroup with the largest ATE. While not displayed here (but displayed in the full, annotated version of this image in Appendix 2 of the Supplementary Materials), the number visualized by the red cell color is “4”, the average percentage of units in Group 8 that were assigned to the estimated subgroup with the smallest treatment effect. This average is taken across the simulations for which this estimated subgroup had membership. For this first cell, the average is taken across all 1000 simulation iterations, because by design, there is always membership in the smallest group. Consider, however, the 10th cell in this row visualizing the value “20”. On average across the 8 simulations for which there was membership in the 10th subgroup, 20% of units in Group 8 were assigned to the subgroup with the tenth (i.e., largest) treatment effect. Of special note is the “37” visualized in the 11th column of the first row; on average across the 92 simulation iterations for which there was at least one estimated subgroup with an undefined treatment effect, 37% of observations in Group 1 were placed in an estimated subgroup having an undefined treatment effect. Said simply, using GBM to estimate TEH, over one-third of observations in true Group 1 can be expected to have an undefined treatment effect. We note that GBM was the only estimation procedure that yielded subgroups with an undefined treatment effect; the cell-specific averages presented for BART and FS were across all 1000 simulation iterations. The denominators for the cell-specific averages presented for GBM are not explicitly provided within the figure, but are contained in Appendix 1 of the Supplementary Materials.

Measures of concordance between Figure 1 and what we expect to see are given in Table 3. Defining “truth” as the color arrangement we expect to see for a particular estimation method and simulation scenario, we calculate the Euclidean distance of each observed cell color (i.e., a block in Figure 1 ) from its expected cell color, in red-green-blue (RGB) color space. We then average these cell-specific distances over the 80 cells to get a summary measure of how far our observed data are from what we expect. (Note that the 11th undefined column was omitted from these calculations, under the assumption that membership in this column is reflected by absence in the remaining 10 columns included in the calculation.) Scaling these distances by the maximum distance (the distance between random assignment of and perfect assignment), we get a measure of distance from what we expect to see on the [0,1] scale. Letting (R_c, G_c, B_c) represent the expected color of cell c and (r_c, g_c, b_c) the observed color, we define this distance in Equation (10) below.

TABLE 3.

Summary of “specificity” (column 1) and “sensitivity” (columns 2–5) calculations for Simulation Study 4, with quantities calculated according to Equation (10) and given as percentages.

	Scenario A confounding and no effect modification	Scenario B effect modification and no confounding	Scenario C effect modification and confounding	Scenario D effect modification and confounding by EMs	Scenario D* effect modification & nonlinear confounding by EMs
Bayesian Additive Regression Trees (BART) $\begin{array}{l}+\text{partitioning}\widehat{ITE}\\ \text{distribution into deciles}\end{array}$	95.1	98.0	97.9	96.3	61.8
Generalized Boosted Models (GBM) $\begin{array}{l}+\text{partitioning}\widehat{e(\mathit{X})}\\ \text{distribution into deciles}\end{array}$	98.5	1.0	0.6	11.0	1.3
Facilitating Score (FS) + partitioning D into 10 subgroups using PAM	95.6	42.6	30.5	23.3	−2.9

$$\frac{1}{80\text{cells}}\sum _{c\in \left\{80\text{cells}\right\}}\sqrt{{\left(R_c-r_c\right)}^2+{\left(G_c-g_c\right)}^2+{\left(B_c-b_c\right)}^2}$$ (10)

Scaling this quantity by the distance between detecting no heterogeneity and detecting the exact partition of the data, then subtracting from 1, we get a measure of concordance that is similar to the traditional definition of sensitivity, in that we are conditioning on the truth and measuring agreement with this truth. Note that when the truth is ‘no heterogeneity’ as in simulation scenario A, we are calculating a measure of specificity. Sensitivity and specificity for each estimation procedure is presented in Table 3.

Figure 2 presents a second summary of the simulation results. The structure of this grid is pattered after Figure 1, where each row is an estimation method, and each column is a data generation scenario. Letting j = 1,…, 1000 denote the simulation iteration, the ten treatment effect estimates generated during the jth iteration are plotted, with the x-axis corresponding to magnitude; this is repeated for all 1000 simulation iterations. For each estimated treatment group (e.g., TE(1)), a boxplot is used to help visualize the distribution of estimates in that group. Recall from §4.2, the estimated treatment groups are always sorted from smallest TE to largest; so TE(1) will always be the estimated subgroup with the smallest treatment effect. For clarity, the x-axes of the forest plots have been omitted, but there are vertical dashed lines denoting the true average treatment effects (1,2,5,6,9,10)

FIGURE 2.

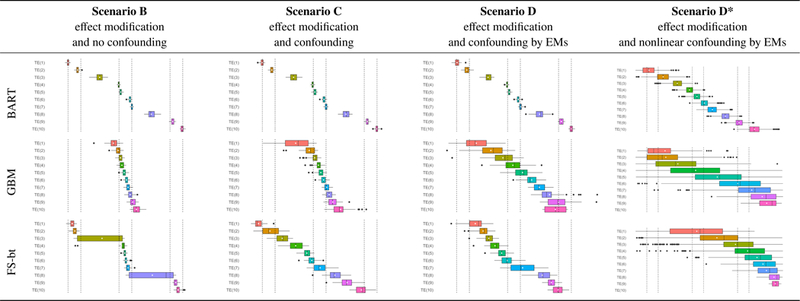
Box plots of point estimates of the ATE across 1000 replicates of each simulation scenario, with layout analogous to that of Figure 1 in the main text. For clarity, the x-axes of the plots have been omitted, but there are vertical dashed lines denoting the true average treatment effects (1,2,5,6,9,10). Summary results for Simulation Scenario A can be found in Appendix 3.1 of the Supplementary Materials.

4.3 |. Discussion

Figure 1 is a qualitative metric that allows for broad comparisons of the “performance” of each TEH identification strategy under several different data generation scenarios, where “performance” refers to the ability of the method to group truly similar observations together. For BART and GBM, deciles are used to define the estimated subgroups; for our sample size of 1500, each of the 10 estimated subgroups is expected to contain 150 individuals. While there is no analogous sample size imposed on the subgroups estimated by FS, the groups tend to contain between 110 and 180 individuals. If we consider that individuals in true Group 1 have value (E₁, E₂, E₃) = (0,0,1) and $\text{Pr}\left\{\left(E_1,E_2,E_3\right)=(0,0,1)\right\}=1/2^3=0.125,$ then we expect 0.125×1500 ≈ 188 individuals to be in Group 1. In a procedure that does a good job of grouping truly similar observations together, we’d expect to see Group 1 concentrated within the first estimated decile and the remaining 188 – 150 = 38 observations in the contiguous decile.

Looking at the results from BART we see exactly what we expect given the particular data generation scenario. Under Scenario A there is no effect modification, and observations from each of the true Groups are evenly distributed across the estimated subgroups (as seen in Appendix 2 of the Supplementary Materials). Under Scenarios B, C, and D, where effect modification is present, 150/188 = 80% of observations in true Group 1 are in the first estimated decile, and 38/188 = 20% are in the contiguous decile. These percentages are reflected in the underlying cell color; the full range of colors is given by the scale at the bottom of the figure. In true Group 2 there are 188 individuals, with 150 – 38 = 112 in the second decile and 188 – 112 = 76 in the third. Again, we see exactly what we expect, with 112/188 = 60% of true Group 2 in the second decile and 76/188 = 40% in the third, and these percentages reflected in the underlying cell color. As demonstrated by these percentages, because the true subgroup sizes are not multiples of the estimated subgroup sizes, the estimated subgroups are heterogenous with respect to the true subgroups.

This heterogeneity is also made obvious in Figure 2. We expect the first estimated subgroup to be completely comprised of individuals from true Group 1 and the second estimated subgroup to have 38/150 = 25% from true Group 1 and 112/150 = 75% from true Group 2. Thus we would expect the treatment effect of the first estimated subgroup (i.e., TE(1)) to be 1, and the estimated treatment effect of the second estimated subgroup to be 25% × 1 + 75% × 2 = 1.75, and this is exactly what we see under Scenarios B, C, and D for BART. Of note is the boxplot associated with the third estimated subgroup, which we expect to be comprised of 76/150 = 51% from true Group 2 and 74/150 = 49% from true Group 3, with an expected treatment effect of 51%×2+49%×5 = 3.5. This particular boxplot echoes the feature of Figure 1 where the estimated subgroups are heterogenous with respect to the true subgroups. This also emphasizes the importance of estimating a large number of subgroups relative to the true number, because the analyst will want the estimated subgroups to be homogeneous.

Returning to the BART results under Scenarios A (in Appendix 2 of the Supplementary Materials), B, C, and D (in Figure 1), not only is the distribution of true Groups 1 and 2 as expected, the distribution of all eight true Groups is as we would expect. Within these scenarios BART does an excellent job of grouping truly similar observations. This is demonstrated by the clustering of large percentages in a given row, and the diagonal pattern of cell coloring. As explained in detail above, the spread over three versus two columns is purely a function of the true group size; larger groups will spread over more columns. Table 3 quantifies this concordance, reporting high “sensitivities” across all simulation scenarios. We do see, however, that when there’s high nonlinearity in the outcome model as in Scenario D* there is some degradation in performance.

Next considering the GBM analysis, the results confirm our earlier hypothesis, that an effect modifier must be associated with treatment for the propensity score to have any chance of detecting the resulting TEH. Under Scenario B where there is effect modification but the EMs are not associated with treatment (i.e., the EMs are not confounders), GBM does no better than random assignment of observations. This is demonstrated by the equal (≈ 10%) allocation of each true subgroup (rows) across the ten estimated subgroups (columns), by the relatively uniform red coloring across the summary table, and by the relatively small “sensitivity” reported in Table 3. However in Scenario D where all three EMs are associated with treatment, GBM is able to detect some of the underlying data structure. Looking generally at the distribution of cell percentages/coloring in this table, we see two blocks of orange & yellow coloring, in the upper left and the lower right. What is being manifested in this separation is GBM’s detection of the one EM (E₃) that has a strong association with treatment relative to the other two EMs (logistic regression coefficients of (E₁, E₂, E₃) = (−0.1,1.1, −4)) and the other covariates in the dataset (see Table 2 ). The four rows (the first, second, third, and fifth) with more orange coloring on the left represent the four true subgroups with E₃ = 1 and the remaining four rows represent the subgroups with E₃ = 0.

Perhaps the most interesting aspect of the results from GBM is the 11th “undefined” column, where the method is alerting us to positivity violations. There are certain combinations of EMs that lead to extreme average propensity score values within that subgroup. For example, observations with (E₁, E₂, E₃) = (0,0,1) and (E₁, E₂, E₃) = (1,0,1) have average propensity scores of 0.06 and 0.04, respectively. Such a low average propensity score means that in finite settings like this one, where GBM is able to (somewhat) correctly group these observations together, often the estimated subgroups will not have any treated observations and the TE will be undefined. Figure 1 quantifies this, with brighter colors in the 11th column indicating more extreme positivity issues.

Now looking towards the results generated by FS, under Scenario B where there is effect modification and no confounding, the blocks of color suggest that the method is able to group observations by the magnitude of their treatment effect, rather than their covariate values: true subgroups with ATEs of 1 and 2 are grouped together (rows 1 and 2), as are true subgroups with ATEs of 5 and 6 (rows 3 through 6), and true subgroups with ATEs 9 and 10 (rows 7 and 8). A preliminary investigation of PAM partitioning the data into 20 subsamples revealed four large groups, implying that specifying more subgroups would have detected more structure, but that not all structure would have been detected due to the relatively weak association between E₁ and Y.

Comparing the FS results of Scenario C to Scenario B, we see the beginnings of a bifurcation of the middle block of observations. Because we have now introduced covariates that have treatment and outcome associations of similar strength to E₂, the decision trees constructed by FS choose E₂ less often as a variable that defines a decision rule, instead choosing the other covariates. Because E₂ has become relatively less important in defining subgroups, the movement of observations is towards the groups defined by strong EM E₃. Thus, the third and fifth rows, which have value E₃ = 1, are moving towards the grouping of the first and second rows which also have value E₃ = 1; similarly for the fourth and sixth rows with value E₃ = 0.

Our final comments on FS are about Scenario D, which demonstrates a potential pitfall of empirical positivity enforcement through algorithmic stopping rules. As expected, FS is able to group observations by strong EM E₃. Different from Scenario C where E₃ is not associated with treatment, here E₃ has a strong negative association with treatment. Thus observations with E₃ = 1, those in rows 1, 2, 3, and 5, have very low values of the propensity score. Decision tree nodes with these observations cannot be split any further because the stopping rule requiring a minimum number of treated observations will have been triggered. Comparatively, observations with E₃ = 0 have moderate propensity score values, so are able to be further divided by E₂.

While the above simulation study was intentionally simplistic in its data generation, Appendix 5 in the Supplementary Materials present an analogous simulation where data are generated to more directly mimic the covariate distribution observed in the CER investigation of §5. The general conclusions of this supplementary simulation study are the same as those presented here.

5 |. COMPARISON OF METHODOLOGIES: CER FOR CARDIOVASCULAR STENTS IN MEDICARE BENEFICIARIES

Drug-eluting stents (DES) have been widely adopted as a non-inferior alternative to bare-metal stents (BMS) for treatment following myocardial infarction (MI),⁴⁸ with clinical-trials evidence indicating important effect modification by diabetes⁴⁹ and age.^50,51,52 In this data analysis, we consider the comparison of drug-eluting stents (DES) to bare-metal stents (BMS) as treatment of myocardial infarction (MI), by looking at the association of each with the two-year revascularization rate. Our goal in this exploratory analysis is to evaluate whether TEH is present, as determined by the three estimation methods under consideration and using our knowledge of their operating characteristics.

5.1 |. Data Structure

De-identified inpatient data on 38 covariates were generated by 54 099 Medicare beneficiaries hospitalized in the continental United States in 2008 with their first MI. An unadjusted comparison of the two-year revascularization rate in DES and BMS patients yields a risk difference of −0.055, indicative of a worse outcome with BMS and thus consistent with the literature, but thought to be confounded by patient characteristics that help determine treatment choice. As summarized in Table 4, patients receiving BMS generally have a higher baseline risk profile.

TABLE 4.

Baseline characteristics (% experiencing unless otherwise indicated) and one-year hospital readmission rate for DES (“treated”) and BMS (“untreated”) patients (columns 1 and 2). See §5.1 for details on the population that generated these data.

	DES (30562)	BMS (23537)
Race: white	90.2	90.1
Male	57.2	57.8
Age (years)	74.9	76.2
Region
west	16.0	13.7
midwest	27.7	30.0
south	40.6	38.8
northeast	15.7	17.5
COPD	15.7	16.9
Asthma	2.6	2.5
Prior Coronary artery bypass graft (CABG) performed	0.4	1.1
Prior congestive heart failure	6.8	7.1
Prior myocardial infarction	3.0	2.8
Unstable angina	3.2	2.3
Chronic atherosclerosis	90.6	88.4
Respiratory failure	2.3	2.6
Hypertension	69.2	65.8
Prior stroke	1.0	1.3
Cerebrovascular disease (non stroke)	2.7	3.1
Renal failure	5.4	6.2
Pneumonia	6.7	8.5
Malnutrition	1.2	2.2
Dementia	3.3	5.3
Functional disability	1.3	1.7
Peripheral vascular disease	4.4	4.7
Trauma in the past year	3.5	4.3
Major psychiatric disorder	1.2	1.6
Liver disease	0.2	0.5
Severe hematological disorder	0.4	0.7
Anemia	14.6	18.2
Depression	4.8	4.9
Parkinsons/Huntington	0.9	1.0
Seizure disorder	1.1	1.4
Chronic fibrosis	1.4	1.6
Vertebral fractures	0.6	0.7
Cancer	3.6	6.3
Eligible for Medicaid	12.0	13.2
Diabetes	29.9	26.3
Revascularization within two years	22.0	27.5

To evaluate TEH, each of the three estimation methods were applied to the data. In the case of BART and GBM, such evaluation was done by partitioning the estimated probability distribution (be it of the outcome or treatment) into 500 quantiles, then estimating a TE within each subgroup defined by these quantiles. In the case of FS, the dissimilarity matrix D is partitioned into 500 subgroups using PAM and a TE estimated within each.

5.2 |. Results

The results of this data analysis are summarized in Figure 3. For each estimation method, the subgroup-specific treatment effects (the risk difference) and associated uncertainty intervals are plotted in ascending order. The red vertical line denotes the marginal estimated risk difference. None of the estimation methods were able to estimate 500 subgroups, for differing reasons. In the case of BART, there were several hundreds of patients with the same estimated ITE, and those subgroups could not be disaggregated. Furthermore, the relatively small within-group and between-group variation is a manifestation of an important distinction in the BART estimation procedure: what is being calculated within each subgroup is an average of estimates (ITEs), rather than a function of observed outcomes. For GBM, 24 of the 500 subgroups had an undefined treatment effect (i.e., at least one treatment arm with less than 2 observations), 3 for FS.

FIGURE 3.

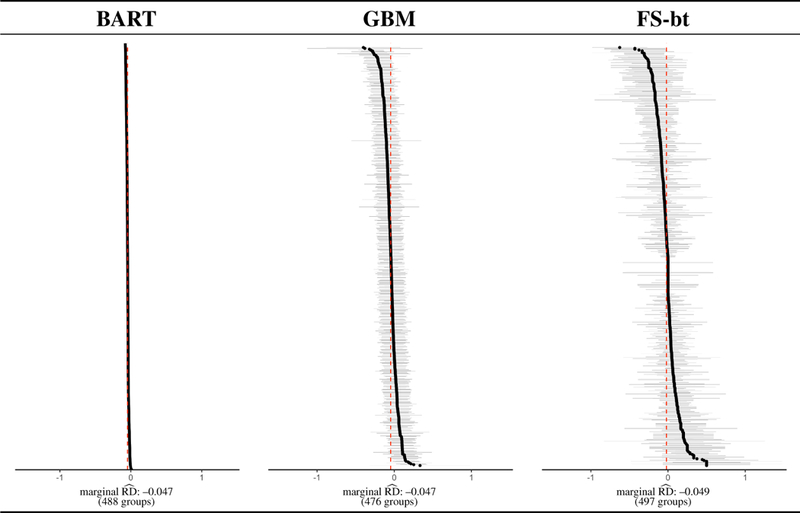
Visualization of results from the data analysis of §5. Details regarding how the figure was constructed, and how to interpret the figure, are given in §5.2.

Focusing on the results from BART (which proved most promising in the simulation studies), we investigate whether any individual covariates exhibit a clear association with subgroup membership. Towards this goal, we plot ITEs and subgroup average ITEs across the distribution of each covariates, as illustrated for four covariates in Figure 4. To ease explanation, consider the top-most plot marked age. The y-axis represents the subgroup-specific average age in years, and the x-axis represents the subgroup-specific ATE (again measured on the risk-difference scale). A red dot represents a subgroup, generated as described earlier: the 54 099 posterior means are partitioned into 500 subgroups, and the average age and average TE (taken as the average of the posterior mean ITEs within that subgroup) are plotted. Thus, we expect 500 red dots in this single plot. To generate the values that the gray dots represent, we applied the subgrouping process used on the posterior means (i.e., partitioned into 500 subgroups and calculated subgroup-specific averages) to each of the 1000 posterior draws of 54 099 ITEs, and plotted a random subset of 100.

FIGURE 4.

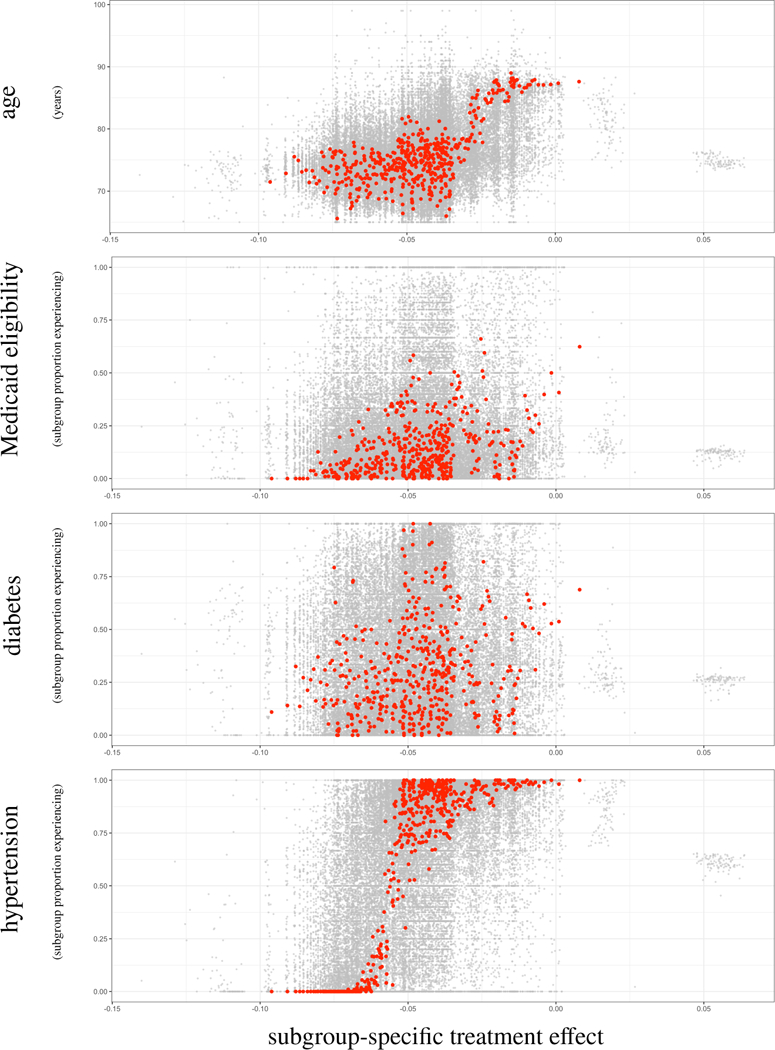
Visualization of results from the data analysis of §5. Covariates displayed are age, Medicaid eligibility, prior diabetes diagnosis, and prior hypertension diagnosis. The y-axis represents the subgroup-specific average, and the x-axis represents the subgroup-specific ATE (on the risk-difference scale). A red dot represents a subgroup, generated as described in §5.2: the 54099 posterior means are partitioned into 500 subgroups, and the average covariate measure (e.g., average age) and average TE (taken as the average of the posterior mean ITEs within that subgroup) are plotted. Thus, we expect 500 red dots in a single plot. To generate the values that the gray dots represent, we applied the subgrouping process used on the posterior means (i.e., partitioned into 500 subgroups and calculated subgroup-specific averages) to each of the 1000 posterior draws of 54099 ITEs, and plotted a random subset of 100.

5.3 |. Discussion

A qualitative analysis of the forest plots in in Figure 3 suggests that none of the three estimation procedures detect any treatment effect heterogeneity; the variability in subgroup-specific estimates is as one might expect from sampling variability. However the successful performance of BART in the simulation studies leads us to further investigation, as displayed in Figure 4.

Considering Figure 4, there is evidence of quantitative effect modification by age; it appears that DES lead to better outcomes in younger patients, a benefit that decreases to nearly zero in older patients. These conclusions are supported by the literature, where it is known that DES generally leads to better outcomes than BMS but the increased comordibities, bleeding risk, and frailty of elderly patients may negate the beneficial effects.^50,51,52 There is also compelling evidence of quantitative effect modification by hypertension, where absence of hypertension is associated with better outcomes within DES patients, as compared to BMS patients. The figure does not imply effect modification by Medicaid eligibility or diabetes.

The lack of evidence of effect modification by diabetes may come as a surprise because of the physiological^53,54 and randomized clinical trial⁴⁹ evidence that supports the general understanding among clinicians that the effect of stent type on adverse cardiovascular outcomes is different within diabetic patients. However what we are seeing is a well-known issue with measurement of diabetes prevalence: it is subject to high rates of misclassification.⁵⁵ High blood pressure, on the other hand, is positively associated with diabetes⁵⁶ and is much easier to determine. So in fact, it is possible that we are seeing the effect modification of diabetes through a proxy.

6 |. CONCLUSIONS

The goal of a TEH estimation method is to provide a partitioning of the covariate space into interpretable subgroups, identifiable by covariate values. Such a partition would be extracted from the data, rather than specified a priori by the researcher. Historically, detection of TEH has involved identification of effect modifiers by subject matter experts, then an evaluation of the estimated treatment effect within each subgroup. This sort of a priori specification precluded exploratory analyses of TEH (for good reason, out of a desire to constrain the type I and II error rates), treated confounding and TEH as separate issues, and was not scalable to high-dimensional data. Uncertainty in confounder and/or effect modifier selection was not addressed by these methods. Thus out of necessity, we have seen an evolution of estimation procedures to match the increased complexity of our research questions and our data.

We contribute to the ongoing discussion by briefly reviewing and evaluating three general classes of modeling approach, through a performance comparison of representative modern methods from each class. We considered the ability of each method to detect subgroups in an exploratory, hypothesis-generating manner. Our simulation studies revealed that GBM, as a representation of using propensity scores to estimate causal effects, is not able to detect effect modifiers that are not associated with treatment; that is, effect modifiers that are not also confounders. However, GBM is able to alert the analyst to positivity violations whereas the representative methods from the other modeling classes extrapolate, possibly inappropriately. For example, FS, as a representation of the joint modeling of outcome and treatment conditional on covariates, potentially fails to disaggregate when the treatment prevalence is extreme, leading the analyst to draw conclusions on the aggregate. BART, as a representation of modeling the outcome conditional on covariates, does not require observations in both treatment arms to calculate the subgroup ATE so positivity violations may go unnoticed. The ability of each method to estimate an unbiased subgroup-specific treatment effect is related to its ability to group similar observations together, and to the number of subgroups that the sample is initially partitioned into by the analyst. When the initial partition is too coarse, the resulting subgroups are still heterogeneous with respect to the true subgroups, leading to biased treatment effect estimates. The conclusions drawn from our simulation studies were used to evaluate the results of a comparative effectiveness analysis, looking at the effect of stent type on an adverse cardiovascular outcome. Diabetes status and age are known in the cardiovascular literature as an effect modifier, and presented itself as such in our analysis, although through the correlated hypertension covariate.

Our analyses do have some limitations, that present opportunities for future work. Our heuristic study was designed to gain some intuition about the more mathematically-rigorous evaluative measures, so we do not address measurement of uncertainty in the subgroup-specific treatment effect estimates, nor any of the classical statistical performance metrics (e.g., consistency). There are also potential problems with using the same data to estimate subgroups and treatment effects, and future work would explore ways to avoid this. Future work would also explore ways to estimate the number of underlying subgroups from the data, rather than a priori specification by the analyst. Lastly, we explicitly explored methods designed to “automatically” detect which of the measured variables are confounders and/or effect modifiers. This was motivated by the desire to address settings where the sheer number of measured covariates or limited contextual knowledge precluded prior specification of such variables. However, such analyses entail important limitations. All methods we consider rely on the assumption that the entirety of X is measured pretreatment and thus unaffected by T. If this assumption was violated, such automated procedures could be susceptible to forms of bias such as posttreatment selection bias or M-bias. Furthermore more, if the available variables in X do not contain important confounders or proxies, then the methods explored here would still suffer from unobserved confounding bias.