Abstract
Prediction of disease progress is of great importance to Alzheimer disease (AD) researchers and clinicians. Previous attempts at constructing predictive models have been hindered by undersampling, and restriction to linear associations among variables, among other problems. To address these problems, we propose a novel Bayesian data-mining method called Bayesian Outcome Prediction with Ensemble Learning (BOPEL). BOPEL uses a Bayesian-network representation with boosting to allow the detection of nonlinear multivariate associations, and incorporates resampling-based feature selection to prevent over-fitting caused by undersampling. We demonstrate the use of this approach in predicting conversion to AD in individuals with mild cognitive impairment (MCI), based on structural magnetic-resonance and magnetic-resonance–spectroscopy data. This study included 26 subjects with amnestic MCI. The converter group (n = 8) included subjects who met MCI criteria at baseline, but who converted to AD within 5 years. The non-converter group (n = 18) consisted of subjects who met MCI criteria at baseline and at 5-year follow-up. We found that BOPEL accurately differentiated MCI converters from non-converters, based on baseline volumes of the left hippocampus, the banks of the right superior temporal sulcus, the right entorhinal cortex, the left lingual gyrus, and the rostral aspect of the left middle frontal gyrus. Prediction accuracy was 0.81, sensitivity was 0.63 and specificity was 0.89. We validated BOPEL’s predictive model with an independent data set constructed from the Alzheimer Disease Neuroimaging Initiative database, and again found high predictive accuracy (0.75).
1. Introduction
Prediction of disease progress is of great importance to researchers studying Alzheimer disease (AD) [Chao et al. 2010; Chetelat et al. 2005a; Petersen et al. 2008], and to clinicians taking care of these patients. Mild cognitive impairment (MCI) is defined as a transitional state between normal aging and early dementia. Amnestic MCI patients progress to AD at an annual rate of 10–15% [Petersen & Negash 2008]; this progression rate is much higher than the population AD incidence rate of 1–2% per year.
Magnetic-resonance (MR) examination provides a noninvasive and reliable means for examining brain structure and function. Due to the rapid evolution of this technology, researchers now have the potential to improve prognostic accuracy by combining information from several modalities.
Consequently, many researchers have attempted to use MR-derived features to identify the subset of MCI patients that will develop AD [Davatzikos et al. 2010; Devanand et al. 2007; Dickerson et al. 2001; Jack et al. 1999; Killiany et al. 2000; Korf et al. 2004; Modrego 2006]. For example, Killiany et al. [Killiany et al. 2000] constructed a discriminant model to differentiate patients with MCI who ultimately developed AD within 3 years, from those who did not. Using volumes of the banks of the superior temporal sulcus and anterior cingulated as regions of interest, the model based on a discriminant function achieved sensitivity = 0.68 and specificity = 0.48. Most investigations of prediction of AD conversion have generated predictive models based on conventional statistical analysis or machine-learning approaches, including discriminant function analysis [Killiany et al. 2000], logistic regression [Devanand et al. 2007; Dickerson et al. 2001; Korf et al. 2004], and support vector machines [Cuingnet et al. 2010; Davatzikos et al. 2010]. Many of these analyses have been hindered by undersampling, that is, a small number of subjects relative to a large number of observed variables. Undersampling often leads to over-fitting, a situation in which the predictive model describes noise, rather than true associations among the variables being observed.
To address these problems, we propose a novel outcome-prediction approach that we call Bayesian Outcome Prediction with Ensemble Learning (BOPEL). Constructing outcome-prediction models based on image data is a challenging problem. Generalizability, a model’s ability to correctly classify a future case sampled from the same population used to generate the predictive model, is a crucial characteristic of a predictive model, in that it directly bears on the utility of applying that predictive model in the clinic. However, in many studies, the number of variables observed greatly exceeds the number of subjects. If the outcome-prediction method does not incorporate feature selection or regularization, the resulting predictive model is prone to overfitting. In overfitting, a model is not only modeling the variation observed in the population, but also the variation due to noise. An overfitted model usually has poor generalizability. BOPEL uses regularization [Koller et al. 2009], feature selection [Duda et al. 2001], and ensemble learning [Duda et al. 2001] to address the overfitting problem. BOPEL is based on a Bayesian-network (BN) representation, which has an embedded Bayesian regularization procedure; this approach has achieved high prediction accuracy in a variety of applications [Friedman et al. 1997]. BOPEL also incorporates resampling methods [Duda et al. 2001] to stabilize the feature-selection process, and it utilizes boosting [Freund et al. 1996] to improve prediction performance.
In this paper, we applied BOPEL to an ongoing study of neuroanatomic and neurochemical features that may predict conversion from MCI to AD; we refer to this study as PCD (prediction of cognitive decline). To validate the generated model, we applied it to an independent test sample acquired from the same population used to generate the predictive model. This independent test data set was constructed based on the Alzheimer Disease Neuroimaging Initiative (ADNI) database.
2. Materials
Subjects in the PCD study included 26 subjects with amnestic MCI. These individuals were recruited by the State-funded Alzheimer disease Research Center of California, University of California San Francisco, and Memory Disorders Clinic at the San Francisco Veterans Affairs Medical Center.
All participants had MCI at baseline, based on Petersen’s criteria [Petersen 2003]. All subjects were diagnosed after an extensive clinical evaluation, including a detailed history, physical, and neurological examination, neuropsychological screening, and study partner interview. Study partners had regular contact with, and knew the subject for, at least 10 years. As part of the neurological examination, all subjects and study partners were queried about initial and current symptoms, under the following categories: (1) memory, (2) executive, (3) behavioral, (4) language, (5) visuospatial, (6) motor, and (7) other. The neuropsychological screening battery included the Mini Mental Status Examination (MMSE) [Folstein et al. 1975], the Weschsler Adult Intelligence Scale [Wechsler 1997], the Delis-Kaplan Executive Function System (DKEFS- Trail-making test; Color Word Interference test, FAS & category fluency tests) [Delis et al. 2001], the California Verbal Learning Test [Delis et al. 2000], and the Weschsler Memory Scale Visual Reproduction Test [Wechsler 1987]. The interview with the study partner was based on the Clinical Dementia Rating (CDR) to assess functional abilities, and on the Neuropsychiatric Inventory to evaluate behavior. Screening for depression was based on the 30-item Geriatric Depression Scale (self-report) and an interview with the study partner. Diagnosis was determined by consensus involving the neurologist, neuropsychologist, and nurse using only the diagnostic information described above.
Subjects were excluded if they met criteria for dementia (Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition (DSM-IV)), a history of a neurological disorder, current psychiatric illness, head trauma with loss of consciousness greater than 10 minutes, severe sensory deficits, substance abuse.
Each participant underwent clinical and neuropsychological assessments annually. The diagnosis of AD was based on the National Institute of Neurologic and Communicative Disorders and Stroke and Alzheimer Disease and Related Disorders Association (NINCDS-ADRDA) criteria [Tierney et al. 1988].
We divided these 26 participants into two groups. The converter group (n = 8) included subjects who met MCI criteria at baseline, but within up to 5 years of follow-up met the NINCDS- ADRDA criteria for AD. The non-converter group (n = 18) contained subjects who met MCI criteria at baseline and at follow-up.
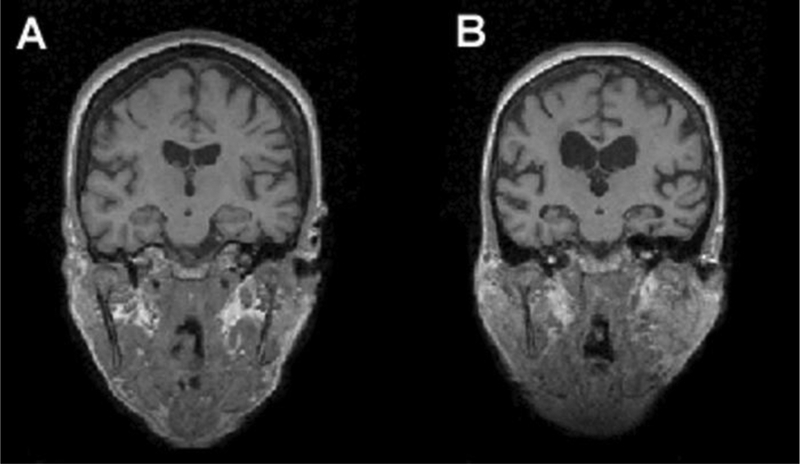
Each individual underwent structural MR examination and MR spectroscopy (MRS) at baseline. For each subject, high resolution T1-weighted MR images were acquired, with parameters: magnetization prepared rapid gradient echo imaging with TR/TE/TI = 300/9.7/4 ms, 15° flip angle, 256 × 256 field of view. The T1-weighted volumes consisted of 154 1.5-mm thick coronal images with 1 mm × 1 mm in-plane resolution. The reconstructed image voxel size was 1 mm × 1 mm × 1.5 mm. Figure 1 depicts the baseline T1-weighted images for two subjects in the PCD study. In light of results in the literature indicating that structural MR-based models can identify the subset of MCI patients that will develop AD [Dickerson et al. 2001; Killiany et al. 2000], we too used features derived from these structural-MR examinations to build a predictive model for AD conversion.
Figure 1.
Baseline T1-weighted MR images. A) is a 77.4 year old female MCI subject who remained stable within 5 years; B) is a 76.5 year old female MCI subject who converted to AD after 2.4 years.
For single-voxel proton spectroscopy, the voxel was placed in the lowest portion of the posterior aspect of the parietal lobe, such that it did not overlap with the occipital lobe. Acquisition parameters were TR/TE/TM = 11800/20/10 ms, voxel volume was 8.1 mL, with dimensions of approximately 22.5 mm left-right, 24 mm anterior-posterior, and 15 mm superior-inferior, to cover most of the posterior cingulate gray matter. We selected the posterior cingulate region because several studies have reported metabolic changes in this region in MCI and AD patients [Chantal et al. 2004; Kantarci et al. 2000].
3. Methods
From a machine-learning perspective, outcome prediction is a supervised-learning problem with two time points: baseline and outcome, respectively. We can formulate this outcome-prediction problem as one of generating a model from data and/or expert knowledge:
| (1) |
where C is the outcome variable, and Xi is feature i measured at baseline, and p is the number of features. We denote the set of features {Xi} by X. In this paper, we assume that C is binary. The feature vector X can include imaging-derived features—such as regional gray-matter volume—feature vector X can include imaging-derived features—such as regional gray-matter volume—and/or demographic variables, such as age.
3.1. Background
A Bayesian network B is a probabilistic graphical model that represents a joint probability distribution over a set of variables X = {Xi}. B is defined formally as a pair B = {G, Θ}, where G is the graphical structure of the Bayesian network, and Θ represents the parameters that quantify the distribution over X. G is a directed acyclic graph (DAG), in which the edge Xi → Xj represents a probabilistic association between Xi and Xj. The parent set and child set of Xi are denoted by pa(Xi) and child(Xi), respectively. A BN represents a factorization of Pr(X1, …, Xp). That is,
| (2) |
In a BN, each node Xi is associated with a conditional probability distribution Pr(Xi | pa(Xi)) (if Xi has no parents, it is associated with a marginal distribution). When variables in the Bayesian network are continuous, it is often assumed that Pr(Xi | pa(Xi)) is Gaussian. In this case, Pr(X1, …, Xp) will be Gaussian as well. However, assuming that Pr(X1, …, Xp) follows a multivariate Gaussian distribution could be too restrictive for many applications. Therefore, we herein adopt the discrete BN representation. When {Xi} are discrete, Pr(Xi | pa(Xi)) are represented as tables. Discrete BNs can model any distribution among {Xi}; therefore, we adopt the discrete BN representation in this paper. In a discrete BN, θijk = Pr(Xi = k | pa(Xi) = j) represents the conditional probability that node Xi assumes state k given that its parent set assumes joint state j. Θ = { θijk }.
A BN can be used as a predictive model [Friedman et al. 1997], in which prediction is performed by using Bayes’ rule. In particular, we can apply BN inference algorithms [Cowell 1998] to a BN model B to predict the value of C given evidence X, by computing Pr(C | X).
There are different classes of BN models, based on constraints on allowed model structures [Friedman et al. 1997]. One such BN-model class is called naïve Bayes, in which C is a root node, and the baseline tests X are represented as children of C. Naïve Bayes require fewer computational resources than unrestricted BN models, yet the former have been shown to demonstrate excellent classification performance in empirical studies [Rash 2001].
BN-generation algorithms can suffer from over-fitting. To prevent over-fitting, BOPEL incorporates ensemble-learning methods, which reduce model variability via averaging [Fred et al. 2005]. Ensemble learning can stabilize the model-generation process, even when data are undersampled [Fred & Jain 2005], and can improve classification performance [Breiman 1996; Breiman 2001; Freund & Schapire 1996].
3.2. Data preprocessing and feature extraction
Most structural MR studies of AD conversion have been based on regional volumes. We used Freesurfer (an MRI brain image processing software package) [Fischl et al. 2004] to process T1-weighted brain MR images and to compute regional volumes (for each of 70 structures) and intracranial volumes. A brief description of this data-processing pipeline is as follows (see [Dale et al. 1999; Fischl et al. 1999; Fischl et al. 2004] for details): First, each scan was corrected for motion, normalized for intensity, and resampled to 1 × 1 × 1 mm. Then, extracerebral tissue was removed using a watershed skull-stripping algorithm, and images were segmented to identify dorsal, ventral, and lateral extent of the gray-white matter boundary, to provide a surface representation of cortical white matter. Then we generated a surface tessellation for each white-matter volume, by fitting a deformable template. We generated the gray matter-cerebrospinal fluid surface using a similar process. These surfaces were used to guide registration. After registering each scan to a probabilistic atlas [Fischl et al. 2004], we obtained automated parcellation of each hemisphere into 35 regions. After parcellation, we computed the volume of each region. This automated procedure for volume calculation has been validated by several different research groups [Desikan et al. 2006; Fischl et al. 2004; Tae et al. 2008]. Finally, we normalized these regional volumes to total intracranial volume, and then normalized each feature to zero mean and unit variance.
To process the MRS image data, we first used the GAVA software application [Soher et al. 2007] to perform baseline correction of the MRS data; GAVA uses a parametric model of known spectral components (metabolites) to fit metabolite resonances. GAVA generated 7 neurochemical baseline features, which are metabolite levels in the posterior cingulate as determined from MRS: Myo-inositol (mI), NAA, Creatine (Cr), Choline (Cho), NAA/Cho, NAA/Cr, and Cho/Cr. We normalized these features to zero mean and unit variance.
3.3. Bayesian outcome prediction with ensemble learning (BOPEL)
BOPEL includes two components: predictive-model generation, and application of this model for prediction. The predictive-model–generation component takes the outcome, MR and MRS variables as input, and constructs a predictive model Bpred. BOPEL’s prediction component uses Bpred to infer the state of the outcome variable for a new patient, based on the states of the variables corresponding to the available baseline tests X.
The input to BOPEL’s model-generation process consists of a training data set, D = {X1, …, Xp, C}, where C is a binary outcome variable that assumes a value in {0, 1}, and Xi is a baseline feature (continuous or discrete). The output of BOPEL’s model-generation process is a predictive model Bpred.
Given a training set D, our goal is to automatically construct a predictive BN model Bpred; this process is referred to as BN generation. The most widely used approach to solving this problem is search-and-score based; that is, it defines a fitness metric, or score, which measures the goodness-of-fit of the candidate BN structure to the observed data, and uses a search method to find the BN structure that optimizes this metric. For this purpose, we need a metric to evaluate how well a Bayesian-network structure G models data D, while penalizing increasing model complexity to avoid over-fitting. The K2 score, as the marginal likelihood Pr(D|G), is among the most widely used BN-scoring functions [Cooper et al. 1992; Herskovits 1991]. It is defined as
| (3) |
where G is the graphical structure of predictive model Bpred, ri is the number of states of the ith variable, qi is the number of joint states of the parents of the ith variable, Nijk is the number of samples in D for which the ith variable assumes its kth state and its parents assume their jth joint state, and .
In addition to a scoring metric, BN generation requires a search procedure to generate candidate BN structures. The search for an optimal BN model is NP-hard [Chickering 1996], so we must employ heuristic-search methods to find a solution. Another way to reduce the search space is to restrict the class of BN models under consideration; in BOPEL, we restrict search to naïve Bayes predictive models, because these models retain excellent prediction performance in empirical studies [Rash 2001].
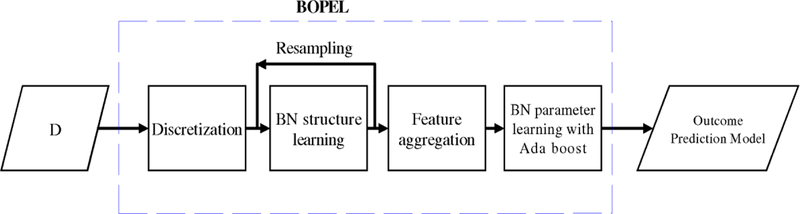
Figure 2 illustrates BOPEL’s predictive-model–generation process. First, BOPEL converts any continuous baseline variables into corresponding discrete variables: for each continuous feature fi, we apply a binary threshold thi. We find the optimal threshold based on the resulting binary variable’s K2 score. That is,
| (4) |
where fi(thi) is the thresholding operator, and C → fi (i.e., C is a parent of fi) in G. We use the global line search method (http://solon.cma.univie.ac.at/software/ls/) to search for th*.
Figure 2.
An overview of the BOPEL algorithm.
After discretization, BOPEL performs feature selection; that is, BOPEL identifies a highly predictive subset of variables in X. Feature selection often ameliorates the curse of dimensionality, avoids over-fitting, increases classification accuracy, and reduces computation time. BOPEL uses BN-structure generation for feature selection, which has been widely employed for generating BN predictive models [Friedman et al. 1997]. In BOPEL, the feature-selection process finds a subset of features X* such that
| (5) |
where B is a Bayesian network in which C is a root node; BOPEL employs greedy search to find X*. After BOPEL generates the BN structure G, the child set of C constitutes the selected features. For example, if, after structure generation, we found that G contained the edges C → X1, and C → X3, then the selected feature set would be {X1, X3}.
One problem with this approach is that the feature-selection process may not be stable; that is, it may not return similar results given small perturbations of the input D. This instability may be due to the use of heuristic search, or due to small sample size, among other causes. To solve this problem, we employ ensemble learning to stabilize the feature-selection process. In particular, we apply bootstrap resampling to D, resulting in a re-sampled data set Di. Then, for each Di, we generate a BN model Bi, from which we obtain the feature set, Xi(C), from the children of C in Bi. If we resample the training data n times, we obtain a feature ensemble {X1(C), …, Xn(C)}. In the feature-aggregation step, we calculate the frequency of each feature in this ensemble, andthereby associate each feature in the ensemble with a frequency. We rank {Xi} based on these frequencies, and choose the top-ranked features as the aggregated feature set. The number of highly ranked features to be included in the model is determined based on internal cross-validation. We denote this ensemble-derived aggregated feature set by Xe.
Given Xe, we can construct a BN Be with Xe as the children of C. We then use maximum-likelihood methods [Thiesson 1995] to estimate the parameters for this model. We can then use Be to predict outcomes for new cases. However, there is not an exact correspondence between data likelihood and label-prediction accuracy [Friedman et al. 1997]; that is, Be may not achieve high prediction accuracy, even though it consists of the most frequently identified predictive features. To solve this problem, we use boosting, one form of ensemble learning, to generate an ensemble of predictive models. BOPEL employs boosting for BN-parameter estimation as follows. We start with a BN model with fixed structure (child(C) = Xe), and training data D; our goal is to generate a model ensemble Ξ. First, we initialize the weight of each instance di in D as wi = 1/|D|, and we initialize Ξ to the empty set. In iteration k, we use the weighted instances to estimate the parameters of the BN, which yields a BN model Bk; we then calculate the error, errk, of Bk as the total sum weight of the instances that Bk classifies incorrectly. If errk > 0.5, we end the algorithm. Otherwise, let βk = errk / (1 – errk); we multiply the weights of the correctly classified instances by βk, rescale {wi} by , and add Bk to Ξ.
For a new case, BOPEL first preprocesses the data and extracts features, then computes the state of C that has the highest weighted vote based on Ξ, and returns that state of C as the predicted outcome.
4. Results
During the 5-year follow-up period, 8 of the 26 subjects had progressed to probable AD. Table 1 lists these subjects’ baseline demographic characteristics and a subset of the memory scores and measures of functional activities. The mini–mental state examination (MMSE) is a questionnaire test to screen for cognitive impairment; a higher score is better (total possible was 30). The CVTR score (from the California Verbal Learning Test II) measures total recall from 5 learning trials; a higher score is better. The functional activities questionnaire (FAQ) [Pfeffer et al. 1982] measures functional abilities; a lower score is better.
Table 1.
Baseline demographic variables.
| Non-converters (n = 18) | Converters (n = 8) | p-value | |
|---|---|---|---|
| Age, years (mean, SD) |
75.1 (SD 7.9) | 76.3 (SD 7.7) | 0.57 |
| Sex (female:male) |
4:14 | 2:6 | 1.0 |
| Handedness (right:left) |
16:2 | 8:0 | 1.0 |
| Education, years (mean, SD) | 16.2 (SD 2.9) | 17.3 (SD 3.0) | 0.59 |
| MMSE (mean, SD) |
27.7 (SD 1.4) | 26.8 (SD 2.7) | 0.11 |
| CVTR | 37.7 (SD 16.6) | 30 (SD 8.7) | 0.13 |
| FAQ | 4.9 (SD 6.6) | 5.4 (SD 7.4) | 0.89 |
We used the Wilcoxon rank-sum test to detect group differences for continuous variables (age, education, MMSE, CVTR, and FAQ), and the Fisher exact statistic to detect group differences for categorical variables (sex and handedness). We found no significant difference in age, sex, handedness, education, MMSE, CVTR, or FAQ. We included age, sex, handedness, education, and MMSE as potential predictive variables for BOPEL.
We used BOPEL to construct a model for predicting whether or not a subject with MCI would convert to AD within 5-year period, based on structural MR and MRS features at baseline, and the demographical variables age, sex, handedness, education, and MMSE.
We used leave-one-out cross validation (LOOCV) to evaluate BOPEL’s prediction accuracy. In LOOCV, we partition the data set D into Ntotal data sets (Ntotal is the total number of subjects in the study); in each iteration, one subject is left out to test the predictive model, and a model is generated based on the remaining subjects.
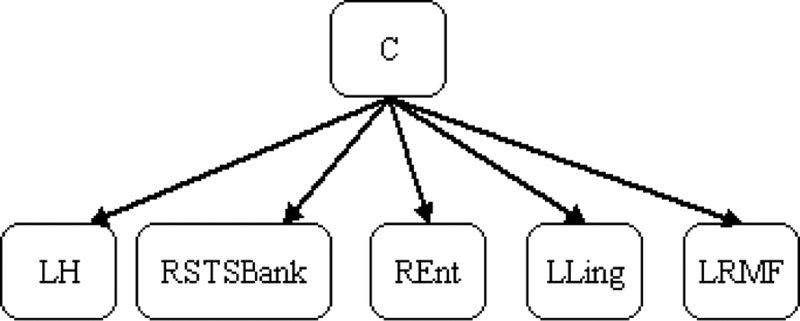
In this manner, we generated 26 training data sets, and 26 predictive models. We found that the selected features Xe were stable across different predictive models. In particular, of the 26 predictive models that BOPEL generated during cross validation, 9 (35%) contained the same feature set, consisting of volumes of the left hippocampus (LH), the banks (i.e., adjacent cortical areas) of the right superior temporal sulcus (RSTSBank), the right entorhinal (REnt) cortex, the left lingual gyrus (LLing), and of the left rostral middle frontal gyrus (LRMF). Figure 3 shows the structure of the corresponding BN. Let M* denote this five-variable set. Other models differed only slightly from M* (i.e., by the inclusion or exclusion of no more than 2 variables). This high concordance was probably due to our use of ensemble learning to stabilize the model-generation process.
Figure 3.
The structure of the Bayesian network M* generated by BOPEL. In this Bayesian network, C represents whether or not a subject with MCI will progress to AD. LH = left hippocampus, RSTSBank = the banks (i.e., adjacent cortical areas) of the right superior temporal sulcus, REnt = right entorhinal cortex, LLing = left lingual gyrus, LRMF= left rostral middle frontal gyrus.
To estimate the consistency of feature selection, we defined edge frequency as
where I[condition] is a function that returns the value 1 if a condition is true, otherwise, it returns the value 0, and childi(C) is the child set of C in the ith model. The 26 models that BOPEL generated in the course of LOOCV contained a total of 13 different features. Of these features, 5 had frequency greater than 0.5 (that is, they were included in the majority of models): LH (frequency = 1.0), RSTSBank (frequency = 0.65), REnt (frequency = 0.80), LLing (frequency = 0.88), and LRMF (frequency = 0.58). We consider these features to be stable; that is, they were frequently detected across a series of perturbations of the data. These features exactly correspond to the features of M*. Table 2 lists baseline volumes for these five structures, for the converter and non-converter groups.
Table 2.
Mean regional volumes that were predictive of AD conversion; standard deviations are in parentheses. We first adjusted these regional volumes to total intracranial volume, and then normalized them to zero mean and unit variance.
| Non-converters (n = 18) | Converters (n = 8) | Discretization cutoff | P-value | |
|---|---|---|---|---|
| The left hippocampus | 0.29 (0.99) | −0.65 (0.69) | 0.178 | 0.012 |
| The right superior temporal sulcus bank | 0.34 (0.96) | −0.77 (0.61) | −0.771 | 0.002 |
| The right entorhinal cortex | 0.42 (0.86) | −0.95 (0.55) | 0.605 | < 0.001 |
| The left lingual gyrus | 0.41 (0.83) | −0.93 (0.69) | −0.104 | 0.001 |
| The left rostral middle frontal gyrus | 0.38 (0.88) | −0.85 (0.71) | −0.660 | 0.002 |
We defined predictive accuracy (acc) as
where Ncorr is the number of correctly labeled subjects, and we defined the error rate (err) as 1 – acc. Sensitivity is the proportion of subjects who progress to AD and are labeled as converters by BOPEL. Specificity is the proportion of subjects who do not progress to AD and are labeled as non-converters by BOPEL. Positive predictive value (PPV) is the proportion of subjects with positive test results (labeled as converters) who are correctly labeled. Negative predictive value (NPV) is the proportion of subjects with negative test results (labeled as non-converters) who are correctly labeled. As estimated by LOOCV, BOPEL’s accuracy was 0.81, sensitivity was 0.63, and specificity was 0.89, positive predictive value was 0.71, and negative predictive value was 0.84.
To validate the model generated by BOPEL, we used an independent data set constructed from the Alzheimer Disease Neuroimaging Initiative (ADNI) database [Jack et al. 2008a] (http://www.loni.ucla.edu/ADNI). In the ADNI database (version 2010-11-20), there were 397 subjects with MCI at baseline. We found that the age distribution of the ADNI database was quite different from that of the PCD data set. Since age is an important factor in AD pathology, we selected subjects in the ADNI database that were age-matched to subjects in the PCD study. The gender distributions of the ADNI database and the PCD study were also different. To correct for bias introduced by gender-distribution differences, we selected subjects in the ADNI database that were sex-matched to subjects in the PCD study. That is, the PCD data set and the ADNI validation data set were age-, and sex-matched. A general practice in the machine-learning community is to ensure that the class distributions of the training data set and the validation data set are comparable. For our purposes, the proportions of converters in the PCD data set and the ADNI validation data set should be comparable. We thus selected 48 of these subjects to build a validation data set; Table 3 lists demographic information for these subjects.
Table 3.
Mean demographic variables for ADNI validation data set; standard deviations are in parentheses.
| Non-converters (n = 30) | Converters (n = 18) | p-value | |
|---|---|---|---|
| Age (mean, SD) |
75.1 (6.0) | 74.2 (3.5) | 0.53 |
| Sex (female:male) |
6:24 | 4:14 | 1.0 |
| Education (mean, SD) |
15.6 (2.6) | 15.3 (2.9) | 0.73 |
| MMSE (mean, SD) |
28.0 (1.3) | 26.1 (2.5) | 0.009 |
Baseline T1-weighted MR examinations for these subjects were acquired according to the ADNI acquisition protocol [Jack et al. 2008a], and regional brain volumes were calculated by the ADNI investigators using FreeSurfer. We normalized these regional volumes to total intracranial volume, and then normalized each feature to zero mean and unit variance. The ADNI MR-acquisition protocol does not include MRS data. However, since the final diagnostic model based on the PCD data set only used features from structural MRI; the lack of MRS data in the ADNI validation data set had no effect on our validation.
Applying the predictive model built based on the PCD data set (which did not incorporate any information from the ADNI validation data set), and classifying subjects in the ADNI validation data set (converter or non-converter), we found that BOPEL’s prediction accuracy was 0.75, sensitivity was 0.56, specificity was 0.87, positive predictive value was 0.71 and negative predictive value was 0.76. Given complete independence of the data we used to build our predictive model and the test (ADNI) data, this experiment indicates that BOPEL’s model accurately predicts MCI-AD conversion.
5. Conclusion and Discussion
We found that BOPEL uses baseline structural-MR data to predict MCI to AD conversion with high accuracy. Of note, prediction accuracy was almost as high for independently acquired ADNI subjects.
BOPEL, a Bayesian approach to outcome prediction, has the following advantages over other approaches. First, it is accurate: BOPEL uses a BN representation with boosting to increase model-representation capacity, and incorporates resampling-based feature selection to prevent over-fitting. Second, the generated predictive model is stable even when data are undersampled, which is commonly the case in outcome-prediction studies: as demonstrated by the high concordance rate for Xe, ensemble learning increases the likelihood that the generated predictive model will be stable. Third, the models generated by BOPEL are declarative in nature, and can be easily understood. Other approaches, such as logistic regression, also have this advantage, however support vector machines and RBF networks do not.
In our analysis of data from the PCD study to predict AD conversion, we found that five features were predictive of AD conversion. These features were volumes of the left hippocampus (frequency = 1.0), the banks of the right superior temporal sulcus (frequency = 0.65), the right entorhinal cortex (frequency = 0.80), the left lingual gyrus (frequency = 0.88), and the left rostral middle frontal gyrus (frequency = 0.58).
We found that volumes of the left hippocampus and of right entorhinal cortex are predictive of conversion from MCI to AD. Hippocampus and entorhinal cortex are among the biomarkers most consistently found to predict AD conversion [Devanand et al. 2007; Jack et al. 1999]. Devanand et al. [Devanand et al. 2007] evaluated the utility of MR hippocampal and entorhinal cortex atrophy in predicting AD conversion. They used logistic regression to build the predictive model, and found that hippocampal and entorhinal cortical atrophy contributes to the prediction of conversion to AD.
We also found that the volume of the banks of the right superior temporal sulcus was a predictor of AD conversion. Killiany et al. conducted discriminant function analysis, including a total of 14 variables: each of the 11 regions-of-interest, and age, sex, and intracranial volume for each subject. They reported that the volume of the banks of the right superior temporal sulcus contributed significantly to the discrimination of patients with MCI who ultimately developed AD within 3 years, from those who did not [Killiany et al. 2000]. The superior temporal sulcus region has been thought to play a role in memory, or in controlling or regulating attention necessary for memory [Salzmann 1995].
In this study, we identified the lower baseline volumes of the left lingual gyrus was predictive of AD conversion. Chetelat et al. analyzed MR images of 18 amnestic MCI individuals (7 converters) using voxel-based morphometry, and reported that the lingual gyri had lower baseline gray matter value in converters [Chetelat et al. 2005b]. Their finding is consistent with our finding. We found that lower baseline volume of the left rostral middle frontal gyrus was predictive of AD conversion. This biomarker for AD conversion is also reported in [Whitwell et al. 2008]. Whitewell et al. used voxel-based morphometry to assess patterns of gray matter atrophy in the MCI converter and MCI non-converter groups. They found that MCI converters show greater loss in the left rostral middle frontal gyrus.
We found hemispheric (left-right) differences in the five brain regions that are predictive of AD conversion: three of these regions are in the left cerebral hemisphere, and two are in the right hemisphere. Of existing studies that use regional volumes to predict AD conversion, some [Devanand et al. 2007; Dickerson et al. 2001; Killiany et al. 2000] have combined the volumes of left- and right-sided structures. However, Chételat et al. [Chetelat et al. 2005b] used voxel-based morphometry to map structural changes associated with conversion from MCI to AD and reported “essentially symmetrically distributed” GM loss in converters (Figure 5 in [Chetelat et al. 2005b]). Their findings suggest that there are no left-right differences in regions characterizing AD conversion. The discrepancy between Chetelat’s and our results can be explained as follows. First, our study was atlas-based, whereas Chételat’s study was voxel-based; therefore, the feature types in our and Chételat’s studies are not directly comparable. Second, Chételat et al. did not build a predictive model; their goal was to find regions demonstrating significantly greater GM loss in converters relative to non-converters. It is possible that features manifesting group differences were not included in our predictive model. For example, in our study, baseline MMSE demonstrates some degree of group difference (p-value=0.11). However, baseline MMSE was not included in the predictive model because this feature provided no additional predictive power given the five features included in the model. Third, there are some differences between the study population in Chételat’s study and that of the PCD study. One significant difference is education. Subjects in the PCD study were more educated (mean education is more than 16 years), relative to subjects in Chételat’s study (mean education is 10 years).
We included MRS features into the PCD study because several studies had demonstrated that MRS features differentiate normal elderly subjects, patients with AD, and patients with MCI [Chantal et al. 2004; Kantarci et al. 2000; Schuff et al. 2002]. We found that the final predictive model generated by BOPEL did not include MRS features. This result suggests that, given structural MR features, the additional predictive value of MRS features to predict AD conversion is not significant. However, we should be cautious accepting this finding because of small sample size.
In this study, we used the ADNI validation data set (a subset of the ADNI database) to validate the generated predictive model. Predicting AD conversion based on the ADNI study is a very challenging problem. In a recent study of predicting AD conversion based on ADNI, Cuingnet et al. [Cuingnet et al. 2010] used a SVM-based predictive model which used regional cortical-thickness as predictor variables. For evaluation, they randomly split the set of participants into two groups of the same size: a training set and a testing set. They reported sensitivity = 0.27 and specificity = 0.85. We obtained sensitivity = 0.56, and specificity = 0.87 for a subset of ADNI subjects. Relative to Cuingnet’s model, our model had much better sensitivity with similar specificity. However, we should be cautious regarding this finding since we only used a subset of ADNI subjects.
In this study, we used cross-validation and an independent validation data set to estimate model accuracy. However, most of the studies in [Devanand et al. 2007; Dickerson et al. 2001; Killiany et al. 2000; Korf et al. 2004; Modrego 2006] reported discrimination accuracy only. That is, most researchers computed prediction accuracy by applying the predictive model to the training data that generated the model. For instance, Dickerson et al. [Dickerson et al. 2001] built a predictive model with sensitivity = 0.83 and specificity = 0.72, based on entorhinal cortex as the neuroanatomic marker, and logistic regression as the classification approach. However, these sensitivity and specificity measures were obtained by applying the logistic regression to the same training data set. Relative to the accuracy estimated by cross-validation or an independent validation data set, discrimination accuracy yields an optimistic estimate of model generalizability and performance [Chen et al. 2010]. This is well recognized in the machine learning community [Duda et al. 2001].
This study focuses on predicting conversion from MCI to AD based on neuroanatomic and neurochemical features. This predictive model can provide valuable information regarding the mechanisms of AD physiopathology. However, our results do not imply that only neuroanatomic and/or neurochemical features can predict AD conversion. Other imaging-derived or non-imaging features may also be predictive of AD conversion. Predictors of conversion from MCI to AD include neuropsychological predictors, neuroradiological markers, AOPE genotype, depression, and blood and CSF biomarkers. For neuroradiological markers, Small et al. reported features derived from Positron Emission Tomography (PET) images obtained with 2-deoxy-2-[F-18]fluoro-D-glucose (after injection of FDDNP) can differentiate subjects with MCI from these with AD and normal controls [Small et al. 2006]. Jack et al. [Jack et al. 2008b] found that Pittsburgh Compound B (PiB) and MRI provided complementary information to discriminate between cognitively normal, amnestic MCI, and AD subjects; furthermore, diagnostic classification using both PiB and MR was superior to using either modality in isolation. With respect to neuropsychological predictors, Dierckx et al. [Dierckx et al. 2009] reported a score of 0 or 1 out of 6 on the Memory Impairment Screen plus as a good indicator of progression to AD among MCI patients. For blood and CSF biomarkers, many studies have focused on the discriminative power of β-amyloid and tau proteins to predict AD conversion. For example, Mitchell [Mitchell 2009] performed a meta-analysis including six studies with MCI subjects, and found that P-tau was modestly successful in predicting progression to dementia in MCI.
Overall, different predictors provide complementary information, and combining them can improve sensitivity and specificity. We plan to include these features in a BOPEL analysis and build more accurate model of AD conversion.
BOPEL is based on the discrete, rather than continuous, Bayesian-network representation. We adopted a Bayesian network classifier based on discrete variables, because it has been found to achieve high classification accuracy, it can represent nonlinear multivariate associations among variables, and it readily supports embedded feature selection. However, using discrete Bayesian networks in BOPEL required that we threshold all continuous variables, possibly leading to loss of information. Given that BOPEL accurately predicted AD conversion in individuals with MCI for the PCD data set, and for an independent data set constructed from the ADNI database, it is likely that thresholding did not cause severe loss of information in this study. In future work, we plan to implement methods for analyzing these data that do not involve discretization, to determine the effects of discretization on our results.
The automated procedure for volume calculation provided by FreeSurfer has been validated by several groups of investigators. Desikan et al. [Desikan et al. 2006] assessed the validity of this automated volume calculation system by comparing the regions-of-interest (ROIs) generated by FreeSurfer to those generated by manual tracing. They used intraclass correlation coefficients to measure the degree of mismatch between FreeSurfer and manual tracing. They found that the automated ROIs were very similar to the manually generated ROIs, with an average intraclass correlation coefficient of 0.835. Similarly, Tae et al. [Tae et al. 2008] reported that FreeSurfer’s automated hippocampal volumetric methods showed good agreement with manual hippocampal volumetry, with intraclass correlation coefficients of 0.846 (right) and 0.848 (left). This automated procedure for volume calculation was also used in the ADNI study.
In this paper, we restricted the Bayesian-network classifier architecture to the naïve Bayes class. There exist other types of Bayesian-network classifiers, such as unrestricted Bayesian-network classifiers [Friedman et al. 1997] and Bayesian-network classifier with inverse-tree structure [Chen et al. 2005]. In the future, we will examine whether the performance of BOPEL can be improved by using other types of Bayesian-network classifiers.
We also plan to extend our current work to evaluate BOPEL on data sets with large sample sizes, and on other biomedical data sets. There are a few relatively large-scale studies, such as the ADNI study [Jack et al. 2008a], in which 400 subjects who have MCI were recruited. Analyzing these data will allow us to quantify the effects of sample size on BOPEL’s prediction accuracy.
In these experiments we focused on outcome prediction for a single categorical outcome variable. Many other studies to predict who will develop AD in patients with MCI [Davatzikos et al. 2010; Devanand et al. 2007; Jack et al. 1999; Killiany et al. 2000; Korf et al. 2004; Modrego 2006] followed a similar overall approach. Other researchers have focused on a continuous outcome variable, such as predicting the time taken for MCI conversion to AD; this problem is usually modeled using regression. An interesting direction for our future work is to combine the ensemble learning used in BOPEL with regression analysis, which could provide an estimate of number of years till conversion.
Acknowledgement
Drs. Chen and Herskovits are supported by National Institutes of Health grant R01 AG13743, which is funded by the National Institute of Aging, and the National Institute of Mental Health; this work was also supported by the American Recovery and Reinvestment Act. This work is supported by National Institutes of Health grant R03 EB-009310. Dr. Chen is supported by ITMAT Fellowship from University of Pennsylvania.
Data collection and sharing for this project was funded by the Alzheimer Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: Abbott, AstraZeneca AB, Bayer Schering Pharma AG, Bristol-Myers Squibb, Eisai Global Clinical Development, Elan Corporation, Genentech, GE Healthcare, GlaxoSmithKline, Innogenetics, Johnson and Johnson, Eli Lilly and Co., Medpace, Inc., Merck and Co., Inc., Novartis AG, Pfizer Inc, F. Hoffman-La Roche, Schering Plough, Synarc, Inc., as well as non-profit partners the Alzheimer Association and Alzheimer Drug Discovery Foundation, with participation from the U.S. Food and Drug Administration. Private sector contributions to ADNI are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of California, Los Angeles. This research was also supported by NIH grants P30 AG010129, K01 AG030514, and the Dana Foundation.
Appendix
Brain structures included in the analysis:
For the PCD dataset, the summary statistics and discretization threshold of 70 brain structures are listed in Table 4. For each structure, we calculate the mean and standard deviation of structure volume (adjusted by intracranial volumes). Then we normalize it to zero-mean and unit variance. After that, we discretize the normalized variable using the discretization threshold.
Table 4.
Neuroanatomic features used in the PCD study.
| Name | Mean volume (SD) | threshold | Name | Mean volume (SD) | threshold | |
|---|---|---|---|---|---|---|
| Left hippocampus | 219(36) | 0.18 | Right parsOpercularis | 212(36) | 0.13 | |
| Right Hippocampus | 221(37) | −0.73 | Left parsOrbitalis | 109(14) | 0.08 | |
| Left Bankssts | 153(28) | −0.36 | Right parsOrbitalis | 153(26) | 0.17 | |
| Right Bankssts | 144(25) | −0.77 | Left parsTriangularis | 175(29) | −0.36 | |
| Left CaudalAnteriorCingulate | 115(26) | −0.18 | Right parsTriangularis | 214(28) | −0.38 | |
| Right CaudalAnteriorCingulate | 126(22) | −0.20 | Left pericalcarine | 103(15) | 0.19 | |
| Left CaudalMiddleFrontal | 361(69) | 0.00 | Right pericalcarine | 120(21) | −0.03 | |
| Right CaudalMiddleFrontal | 335(51) | −0.13 | Left postcentral | 560(74) | −0.16 | |
| Left Cuneus | 158(26) | −0.06 | Right postcentral | 517(78) | −0.52 | |
| Right Cuneus | 169(34) | −0.19 | Left posteriorCingulate | 199(37) | 0.00 | |
| Left Entorhinal | 105(37) | −0.79 | Right posteriorCingulate | 192(25) | −0.87 | |
| Right Entorhinal | 98(30) | −0.60 | Left precentral | 703(100) | 0.13 | |
| Left Fusiform | 516(82) | −0.53 | Right precentral | 728(111) | −0.44 | |
| Right Fusiform | 522(69) | 0.09 | Left precuneus | 516(72) | −0.57 | |
| Left inferiorParietal | 675(121) | −0.58 | Right precuneus | 535(98) | −0.77 | |
| Right inferiorParietal | 837(142) | −0.87 | Left rostral AnteriorCingulate | 140(36) | −0.61 | |
| Left inferiorTemporal | 612(75) | −0.7022 | Right rostralAnteriorCingulate | 107(19) | −0.50 | |
| Right inferiorTemporal | 592(87) | 0 | Left rostralMiddleFrontal | 858(121) | −0.66 | |
| Left isthmusCingulate | 143(28) | 0.078 | Right rostralMiddleFrontal | 883(115) | −0.57 | |
| Right isthmusCingulate | 124(26) | −0.80 | Left superiorFrontal | 1294(179) | −0.33 | |
| Left lateralOccipital | 758(111) | −0.02 | Right superiorFrontal | 1260(172) | 0.00 | |
| Right lateralOccipital | 719(104) | −0.09 | Left superiorParietal | 752(109) | −0.03 | |
| Left lateralOrbitofrontal | 424(49) | −0.63 | Right superiorParietal | 747(99) | 0.06 | |
| Right lateralOrbitofrontal | 425(53) | −0.68 | Left superiorTemporal | 646(102) | −0.42 | |
| Left lingual | 359(64) | −0.10 | Right superiorTemporal | 612(75) | 0.21 | |
| Right lingual | 358(57) | 0.24 | Left supramarginal | 614(92) | −0.69 | |
| Left medialOrbitofrontal | 250(46) | 0.14 | Right supramarginal | 584(90) | −0.24 | |
| Right medial Orbitofrontal | 273(33) | −0.46 | Left frontalPole | 37(9) | 0.05 | |
| Left middleTemporal | 594(105) | 0.25 | Right frontalPole | 50(12) | −0.25 | |
| Right middleTemporal | 663(101) | −0.88 | Left temporalPole | 107(26) | 0.079 | |
| Left parahippocampal | 128(27) | −0.72 | Right temporalPole | 115(23) | −0.38 | |
| Right parahippocampal | 115(21) | −0.50 | Left transverseTemporal | 65(11) | −0.26 | |
| Left paracentral | 200(37) | −0.29 | Right transverseTemporal | 49(8) | −0.17 | |
| Right paracentral | 217(36) | −0.15 | Left insula | 371(43) | −0.75 | |
| Left parsOpercularis | 276(64) | 0.11 | Right Insula | 376(38) | −0.95 |
References
- Breiman L Bagging predictors. Machine Learning 1996; 26 (2):123–40. [Google Scholar]
- Breiman L Random Forests. Machine Learning 2001; 45 (1):5–32. [Google Scholar]
- Chantal S, Braun CM, Bouchard RW et al. Similar 1H magnetic resonance spectroscopic metabolic pattern in the medial temporal lobes of patients with mild cognitive impairment and Alzheimer disease. Brain Res 2004; 1003 (1–2):26–35. [DOI] [PubMed] [Google Scholar]
- Chao LL, Buckley ST, Kornak J et al. ASL perfusion MRI predicts cognitive decline and conversion from MCI to dementia. Alzheimer Dis Assoc Disord 2010; 24 (1):19–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen R, Herskovits EH. A Bayesian Network Classifier with Inverse Tree Structure for Voxel-wise MR Image Analysis. Proceedings of the eleventh conference of SIGKDD 2005:4–12. [Google Scholar]
- Chen R, Herskovits EH. Machine-learning techniques for building a diagnostic model for very mild dementia. Neuroimage 2010; 52 (1):234–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chetelat G, Eustache F, Viader F et al. FDG-PET measurement is more accurate than neuropsychological assessments to predict global cognitive deterioration in patients with mild cognitive impairment. Neurocase 2005a; 11 (1):14–25. [DOI] [PubMed] [Google Scholar]
- Chetelat G, Landeau B, Eustache F et al. Using voxel-based morphometry to map the structural changes associated with rapid conversion in MCI: a longitudinal MRI study. Neuroimage 2005b; 27 (4):934–46. [DOI] [PubMed] [Google Scholar]
- Chickering DM. Learning Bayesian networks is NP-complete. AI&STAT. V 1996. [Google Scholar]
- Cooper GF, Herskovits EH. A Bayesian method for the induction of probabilistic networks from data. Machine Learning 1992; 9:309–47. [Google Scholar]
- Cowell R Introduction to Inference for Bayesian Networks In: Proceedings of the NATO Advanced Study Institute on Learning in Graphical Models. Series Introduction to Inference for Bayesian Networks. Kluwer Academic Publishers; 1998; p. 9––26. [Google Scholar]
- Cuingnet R, Gerardin E, Tessieras J et al. Automatic classification of patients with Alzheimer’s disease from structural MRI: A comparison of ten methods using the ADNI database. Neuroimage 2010. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage 1999; 9 (2):179–94. [DOI] [PubMed] [Google Scholar]
- Davatzikos C, Bhatt P, Shaw LM et al. Prediction of MCI to AD conversion, via MRI, CSF biomarkers, and pattern classification. Neurobiol Aging 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delis DC, Kaplan E, Kramer JH. Delis-Kaplan Executive Function System. San Antonio, TX.: Psychological Corporation; 2001. [Google Scholar]
- Delis DC, Kramer JH, Kaplan E et al. California Verbal Learning Test® – Second Edition (CVLT® –II). San Antonio: The Psychological Corporation; 2000. [Google Scholar]
- Desikan RS, Segonne F, Fischl B et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 2006; 31 (3):968–80. [DOI] [PubMed] [Google Scholar]
- Devanand DP, Pradhaban G, Liu X et al. Hippocampal and entorhinal atrophy in mild cognitive impairment: prediction of Alzheimer disease. Neurology 2007; 68 (11):828–36. [DOI] [PubMed] [Google Scholar]
- Dickerson BC, Goncharova I, Sullivan MP et al. MRI-derived entorhinal and hippocampal atrophy in incipient and very mild Alzheimer’s disease. Neurobiol Aging 2001; 22 (5):747–54. [DOI] [PubMed] [Google Scholar]
- Dierckx E, Engelborghs S, De Raedt R et al. Verbal cued recall as a predictor of conversion to Alzheimer’s disease in Mild Cognitive Impairment. Int J Geriatr Psychiatry 2009; 24 (10):1094–100. [DOI] [PubMed] [Google Scholar]
- Duda R, Hart R, Stork DG. Pattern Classification (second edition). New York: Wiley; 2001. [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage 1999; 9 (2):195–207. [DOI] [PubMed] [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C et al. Automatically Parcellating the Human Cerebral Cortex. Cerebral Cortex 2004; 14:11–22. [DOI] [PubMed] [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. “Mini-mental state”. A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res 1975; 12 (3):189–98. [DOI] [PubMed] [Google Scholar]
- Fred A, Jain AK. Combining Multiple Clusterings Using Evidence Accumulation. IEEE Transactions on pattern analysis and machine intelligence 2005; 27 (6):835–50. [DOI] [PubMed] [Google Scholar]
- Freund Y, Schapire R. Experiments with a new boosting algorithm. Machine Learning: Proceedings of the Thirteenth International Conference, 1996:148–56. [Google Scholar]
- Friedman N, Geiger D, Goldszmidt M. Bayesian network classifiers. Machine Learning 1997; 29:131–63. [Google Scholar]
- Herskovits EH. Computer-based probabilistic-network construction: Stanford University; 1991. [Google Scholar]
- Jack CR Jr., Bernstein MA, Fox NC et al. The Alzheimer’s Disease Neuroimaging Initiative (ADNI): MRI methods. J Magn Reson Imaging 2008a; 27 (4):685–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR Jr., Lowe VJ, Senjem ML et al. 11C PiB and structural MRI provide complementary information in imaging of Alzheimer’s disease and amnestic mild cognitive impairment. Brain 2008b; 131 (Pt 3):665–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR Jr., Petersen RC, Xu YC et al. Prediction of AD with MRI-based hippocampal volume in mild cognitive impairment. Neurology 1999; 52 (7):1397–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kantarci K, Jack CR Jr., Xu YC et al. Regional metabolic patterns in mild cognitive impairment and Alzheimer’s disease: A 1H MRS study. Neurology 2000; 55 (2):210–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killiany RJ, Gomez-Isla T, Moss M et al. Use of structural magnetic resonance imaging to predict who will get Alzheimer’s disease. Ann Neurol 2000; 47 (4):430–9. [PubMed] [Google Scholar]
- Koller D, Friedman N. Probabilistic Graphical Models: Principles and Techniques: The MIT Press; 2009. [Google Scholar]
- Korf ES, Wahlund LO, Visser PJ et al. Medial temporal lobe atrophy on MRI predicts dementia in patients with mild cognitive impairment. Neurology 2004; 63 (1):94–100. [DOI] [PubMed] [Google Scholar]
- Mitchell AJ. CSF phosphorylated tau in the diagnosis and prognosis of mild cognitive impairment and Alzheimer’s disease: a meta-analysis of 51 studies. J Neurol Neurosurg Psychiatry 2009; 80 (9):966–75. [DOI] [PubMed] [Google Scholar]
- Modrego PJ. Predictors of conversion to dementia of probable Alzheimer type in patients with mild cognitive impairment. Curr Alzheimer Res 2006; 3 (2):161–70. [DOI] [PubMed] [Google Scholar]
- Petersen RC. Mild cognitive impairment clinical trials. Nat Rev Drug Discov 2003; 2 (8):646–53. [DOI] [PubMed] [Google Scholar]
- Petersen RC, Negash S. Mild cognitive impairment: an overview. CNS Spectr 2008; 13 (1):45–53. [DOI] [PubMed] [Google Scholar]
- Pfeffer RI, Kurosaki TT, Harrah CH Jr., et al. Measurement of functional activities in older adults in the community. J Gerontol 1982; 37 (3):323–9. [DOI] [PubMed] [Google Scholar]
- Rash I An empirical study of the naive Bayes classifier. IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence 2001. [Google Scholar]
- Salzmann E Attention and memory trials during neuronal recording from the primate pulvinar and posterior parietal cortex (area PG). Behav Brain Res 1995; 67 (2):241–53. [DOI] [PubMed] [Google Scholar]
- Schuff N, Capizzano AA, Du AT et al. Selective reduction of N-acetylaspartate in medial temporal and parietal lobes in AD. Neurology 2002; 58 (6):928–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Small GW, Kepe V, Ercoli LM et al. PET of brain amyloid and tau in mild cognitive impairment. N Engl J Med 2006; 355 (25):2652–63. [DOI] [PubMed] [Google Scholar]
- Soher BJ, Young K, Bernstein A et al. GAVA: spectral simulation for in vivo MRS applications. J Magn Reson 2007; 185 (2):291–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tae WS, Kim SS, Lee KU et al. Validation of hippocampal volumes measured using a manual method and two automated methods (FreeSurfer and IBASPM) in chronic major depressive disorder. Neuroradiology 2008; 50 (7):569–81. [DOI] [PubMed] [Google Scholar]
- Thiesson. Accelerated quantification of Bayesian networks with incomplete data In Proceedings of the First International Conference on Knowledge Discovery and Data Mining; 1995. 306–11 p. [Google Scholar]
- Tierney MC, Fisher RH, Lewis AJ et al. The NINCDS-ADRDA Work Group criteria for the clinical diagnosis of probable Alzheimer’s disease: a clinicopathologic study of 57 cases. Neurology 1988; 38 (3):359–64. [DOI] [PubMed] [Google Scholar]
- Wechsler D Wechsler Adult Intelligence Scale®—Third Edition (WAIS®–III); 1997.
- Wechsler D Wechsler Memory Scale-Revised. New York: The Psychological Corporation; 1987. [Google Scholar]
- Whitwell JL, Shiung MM, Przybelski SA et al. MRI patterns of atrophy associated with progression to AD in amnestic mild cognitive impairment. Neurology 2008; 70 (7):512–20. [DOI] [PMC free article] [PubMed] [Google Scholar]