NONPARAMETRIC INFERENCE FOR IMMUNE RESPONSE THRESHOLDS OF RISK IN VACCINE STUDIES

Abstract

An important objective in vaccine studies entails identifying an immune response which is predictive of disease risk. Nonparametric methods are developed for inference on immune response thresholds that are associated with specified levels of disease risk, including where the risk level is zero. This threshold is defined as the minimum immune response value above which disease risk is less than or equal to the desired level. The proposed nonparametric methods are compared to previously developed parametric methods in simulation studies. The methods are extended for use in studies that only measure the immune response in a subset of participants, such as case-cohort or case-control studies, and with right censored time to disease outcomes. Finally, these methods are used to estimate neutralizing antibody thresholds for virologically confirmed dengue risk using data from two recent dengue vaccine trials.

1. Introduction.

Infectious disease is one of the most prevalent causes of death globally. In 2010 approximately 15 million deaths worldwide were caused directly by infectious disease [12]. Historically, the use of vaccines to reduce the burden of infectious diseases has been extremely effective. Previously devastating illnesses such as smallpox and measles have been dramatically reduced, and sometimes eradicated completely, due to vaccination [14]. However, infectious diseases such as HIV/AIDS, malaria, and tuberculosis continue to cause millions of deaths worldwide as their treatment and prevention have proved difficult [14]. As a result, it is imperative that the effectiveness of vaccines continues to be studied.

One goal of vaccine research entails finding an immune response which is predictive of the clinical outcome of interest. Here we consider a binary outcome which is generically referred to as disease. The inferential goal is to estimate the minimum immune response value above which the risk of disease is less than or equal to some specified value (e.g., 0.01%). This value of immune response is referred to as a risk threshold and the specified risk upper bound is referred to as a risk level. Inference about these thresholds can be useful to regulatory agencies, policymakers, and public health officials in assessing disease risk in a vaccinated population. In particular, for the sake of cost and efficiency, studies of new formulations of existing vaccines and studies of existing vaccines in new populations often collect data only on immune responses and do not also assess disease outcomes. In these studies, estimated risk thresholds can be used to predict disease risk for the new vaccine formulation or in the new population.

There are two common approaches employed in vaccine efficacy trials to identify immune response thresholds of risk. The first approach entails fitting parametric or semiparametric models to quantify an immune response’s association with disease risk (e.g., White et al. [31], Storsaeter et al. [28], Chan et al. [6], Jokinen and Åhman [19], Dunning [11], Haynes et al. [16]) and these methods can be adapted for inference on risk thresholds. However, such models are subject to mis-specification, especially when drawing inference about immune response thresholds associated with zero disease risk. The second approach considers specifically the zero risk threshold. This approach (e.g., Andrews, Borrow and Miller [1], Jódar et al. [18], Borrow, Balmer and Miller [3], Black et al. [2]) assumes the existence of an immune response threshold which perfectly discriminates whether an individual is protected from disease. In addition, disease risk is assumed to be independent of vaccination status given the immune response, i.e., Prentice’s [25] full mediation condition for a valid surrogate endpoint is assumed. In contrast, this paper introduces methods for inference about risk thresholds corresponding to specified disease risk levels which are non-parametric and do not require Prentice’s full mediation condition to hold.

The remainder of this paper’s structure is as follows. Section 2 details inference about a risk threshold in a standard vaccine study design. Section 3 describes simulation studies evaluating the inferential methods described in Section 2. Section 4 extends the methods to studies where the immune response is only measured in a subset of participants, such as case-cohort or case-control studies, and where some individuals’ disease outcomes are censored. Section 5 presents an application of these methods to two recent dengue vaccine trials. Section 6 concludes the paper and offers further discussion.

2. Methods.

2.1. Risk Threshold.

Suppose a vaccine is evaluated in a randomized trial, possibly placebo-controlled, in which all participants are initially disease-free and n individuals receive vaccine. (Unless indicated otherwise, the methods described below only utilize data observed from the n vaccinated individuals. Thus the methods can also be applied in observational cohort studies where a random sample of n vaccinated individuals is followed prospectively.) Let Z denote treatment assignment with Z = 1 denoting vaccine and Z = 0 denoting control, where control refers to a placebo or absence of treatment. Suppose there is an immune response associated with the likelihood of developing disease. Let S denote an individual’s immune response, with S measured after the individual receives their assigned treatment (vaccine or control). Let Y denote an individual’s outcome, with Y = 1 denoting disease and Y = 0 otherwise; assume Y is measured some time after S. While for simplicity we assume that all n participants have S measured before Y occurs, under a random censoring assumption the methods also apply for inference on participants at-risk for Y when S is measured.

For risk level c ∈ [0, 1], define the risk threshold when vaccinated to be

$$v_c=\inf \{v:\text{Pr}(Y=1|Z=1,S\ge v)\le c\}.$$

In other words, the risk of disease is no greater than c in the stratum of individuals with immune response at least v_c. Such thresholds are useful for understanding the risk of disease in a vaccinated population. For example, suppose c = 0.01 and Pr(S ≥ v_c|Z = 1) = 1; then the risk of disease in the vaccinated population is at most 1%. As described in the Introduction, these thresholds have utility in assessing disease risk at the population level in settings where only immune response data are available.

An alternative target parameter might be v_alt = inf{v : Pr(Y = 1|Z =1, S = v) ≤ c}. This alternative parameter has a straightforward interpretation at the individual level, providing an upper bound on disease risk for an individual with immune response v_alt. However, this parameter does not have a straightforward population level interpretation, and thus is of less utility to regulatory agencies or policymakers regarding the population level disease risk when vaccinated. An exception is in settings where it is plausible to assume there is a monotonic relationship between the immune response and disease risk, i.e., Pr[Y = 1|S = v, Z = 1] is a non-increasing function of v. If monotonicity is assumed, then disease risk would be at most c in the stratum of individuals with immune response at least v_alt. Below non-parametric methods are proposed which do not require such a monotonicity assumption, and thus v_c is the target parameter of interest.

Below, methods are considered for estimation and confidence intervals (CIs) of v_c. Assume n independent copies of (S, Y) are observed in the vaccinated individuals. The estimators of v_c considered below are motivated by the equalities

$$\text{Pr}(Y=1|S\ge v)=\frac{\text{Pr}(Y=1,S\ge v)}{\text{Pr}(S\ge v)}=\frac{{\int }_v^{\infty }\text{Pr}(Y=1|S=s)d{F}_S(s)}{{\int }_v^{\infty }d{F}_S(s)}$$ (1)

where F_S(s) is the cumulative distribution function (CDF) of S. Here and elsewhere distributions are conditional on Z = 1 unless stated otherwise. The denominator of (1) can be estimated consistently by ${\sum }_{i=1}^{n}I\left(S_i\ge v\right)/n$. Nonparametric and parametric estimators for the numerator of (1) are considered below, which in turn lead to estimators of v_c. For now assume c > 0; the special case where c = 0 is considered in Section 2.2.

Note Pr(Y = 1, S ≥ v) can be estimated consistently by ${\sum }_{i=1}^{n}I(Y_i=1,S_i\ge v)/n$, which motivates the following proposed nonparametric estimator of v_c

$${\widehat{v}}_c=\min \left\{S_j:\frac{{\sum }_{i=1}^{n}I\left(Y_i=1,S_i\ge S_j\right)}{{\sum }_{i=1}^{n}I\left(S_i\ge S_j\right)}\le c,j\in \{1,\dots ,n\}\right\}.$$ (2)

In words, ${\widehat{v}}_c$ is the minimum v of the set of observed immune responses such that in the stratum of individuals with immune response at least v, the proportion developing disease is no greater then c. Note that ${\widehat{v}}_c$ is not well-defined for c such that the estimated disease risk conditional on S ≥ S_j exceeds c for all j = 1, …, n. In particular, let $\widehat{\text{P}}\text{r}(Y=1|S\ge S_j)={\sum }_{i=1}^{n}I(Y_i=1,S_i\ge S_j)/{\sum }_{i=1}^{n}I\left(S_i\ge S_j\right)$ and ${\widehat{p}}_{\min }=\min \{\widehat{\text{P}}\text{r}(Y=1|S\ge S_j):j=1,\dots ,n\}$. For $c<{\widehat{p}}_{\text{min}}$, ${\widehat{v}}_c$ is not well-defined because the right side of (2) equals the minimum of the empty set. Examples from two simulated data sets are shown in Figure 1. These data were generated from logistic regression models of the form Pr[Y = 1|S ≥ v] = expit(β₀ + β₁v) for different values of β₀ and β₁, where expit denotes the inverse of the logit function. In the left panel of Figure 1, ${\widehat{p}}_{\min }=0$ such that ${\widehat{v}}_c$ is well-defined for all c ∈ [0, 1]. On the other hand, in the right panel of Figure 1, ${\widehat{p}}_{\min }>0$ so ${\widehat{v}}_c$ is only well-defined for $c\in \left[{\widehat{p}}_{\min },1\right]$. Note that ${\widehat{v}}_c$ being well-defined is separate from existence of v_c, as ${\widehat{v}}_c$ not being well-defined may be a result of sampling variation or insufficient sample size.

Fig 1:

Panels a) and b) display nonparametric estimates of disease risk conditional on S ≥ v for each observed v from two simulated data sets. These estimates are denoted $\widehat{\text{P}}\text{r}(Y=1|S\ge v)$. For each data set, the minimum of these estimates is denoted by ${\widehat{\text{P}}}_{\text{min}}$.

The estimator ${\widehat{v}}_c$ is compared with parametric methods that estimate p(v) = Pr(Y = 1|S = v) using a regression model, denoted $\widehat{p}(v)$. These parametric estimators of v_c are of the form

$$\min \left\{S_j:\frac{{\sum }_{i=1}^{n}I\left(S_i\ge S_j\right)\widehat{p}\left(S_i\right)}{{\sum }_{i=1}^{n}I\left(S_i\ge S_j\right)}\le c,j\in \{1,\dots ,n\}\right\}.$$ (3)

Following Storsaeter [28], p(v) may be modeled by p(v) = expit(β₀ + β₁v). Define the parametric estimator ${\widehat{v}}_c^l$ by (3) with $\widehat{p}(v)=\text{expit}\left({\widehat{\beta }}_0+{\widehat{\beta }}_{1}v\right)$, where ${\widehat{\beta }}_0$ and ${\widehat{\beta }}_1$ are maximum likelihood estimators of β₀ and β₁.

Dunning’s scaled logit model [11] suggests another parametric estimator. Suppose individuals are either immune or susceptible to disease. Let λ denote the risk of disease given an individual is susceptible. Let π(v) denote the probability an individual is susceptible given an immune response v and suppose p(v) = λπ(v), where π(v) = expit(β_0d + β_1dv). Denote the parametric estimator corresponding to Dunning’s scaled logit model by ${\widehat{v}}_c^d$, defined as (3) with $\widehat{p}(v)=\widehat{\mathrm{\lambda }}\text{expit}\left({\widehat{\beta }}_{0d}+{\widehat{\beta }}_{1d}v\right)$, where $\widehat{\mathrm{\lambda }}$, ${\widehat{\beta }}_{0d}$ and ${\widehat{\beta }}_{1d}$ are maximum likelihood estimators of λ, β_0d and β_1d.

For each of the three estimators described above, a corresponding (1 ‒ α) CI for v_c can be computed using the bootstrap percentile method [13] as follows. First, B independent bootstrap samples, each consisting of n copies of (S, Y), are drawn with replacement from {(S₁, Y₁), …, (S_n, Y_n)}. Then for each of the B samples, the estimator for v_c is calculated. A (1 − α) CI for v_c is given by the α/2 and (1 − α/2) percentiles of the B estimates of v_c.

2.2. Threshold for Zero Risk.

Recall v₀ is the lowest immune response threshold above which an individual has no risk of disease when vaccinated. When v₀ exists, the distribution of S given Y = 1 is truncated with an upper truncation point at v₀ such that f_S(v|Y = 1) = 0 for v ≥ v₀, where f_S(v|Y = 1) is the conditional density of S given Y = 1. The parametric models discussed in Section 2.1 imply non-zero values for Pr(Y = 1|S = v) for all v. As a result, these models are guaranteed to be mis-specified when finite v₀ exists. While these parametric models could be extended to allow for zero-risk above some truncation point, the corresponding threshold estimators would not in general be expected to perform well when the parametric component of the model is mis-specified. Below, three nonparametric estimators of v₀ are considered instead.

The first nonparametric estimator is ${\widehat{v}}_0$, the estimator ${\widehat{v}}_c$ from Section 2.1 when c = 0. Suppose there are m vaccinated individuals who develop disease (i.e., Y = 1) and let S_v(1) < S_v(2) < … < S_v(m) denote their ordered immune response values. Then ${\widehat{v}}_0=\min \left\{S_j:S_j>S_{v(m)},j=1,\cdots ,n\right\}$.

The second nonparametric estimator considered uses Cooke’s [9] method for estimating an upper truncation point, defined as

$${\tilde{v}}_0=S_{v(m)}+\sum _{i=1}^{m-1}{(i/m)}^m\left(S_{v(i+1)}-S_{v(i)}\right).$$

This estimator is motivated by the general result that

$$v_0=E\left(S_{v(m)}\right)+{\int }_0^{v_0}{F}^m(s)ds$$ (4)

where F ^m(s) is the CDF of S_v(m). Due to independence, F ^m(s) = F (s) where F_(s) is the CDF of S given Y = 1. Plugging in the sample maximum and empirical CDF $\widehat{F}(s)$ into the right side of (4) yields ${\tilde{v}}_0$. Cooke [9] also derived an asymptotic (1 – α) CI for an upper truncation point, adopted here for v₀. This interval is denoted $\left(L_0^c,U_0^c\right)$, where $L_0^c=S_{v(m)}+\{{(\alpha /2)}^{-1}-1{\}}^{-1}\left(S_{v(m)}-S_{v(m-1)}\right)$ and $U_0^c=S_{v(m)}+{\left\{{(1-\alpha /2)}^{-1}-1\right\}}^{-1}\left(S_{v(m)}-S_{v(m-1)}\right)$.

Another approach to drawing inference about v₀ was proposed by Siber et al. [27]. Unlike the methods described above, this approach requires data from both vaccinated and control individuals. A key assumption of Siber et al.’s method is that Pr(Y = 1|Z = z, S ≤ v₀) = Pr(Y = 1|S ≤ v₀) and Pr(Y = 1|Z = z, S > v₀) = Pr(Y = 1|S > v₀) for z = 0, 1 (i.e., disease status is independent of treatment conditional on the immune response). In other words, Prentice’s [25] full mediation condition for a valid surrogate endpoint is assumed. Define vaccine efficacy (VE) as VE = 1 − p_v/p_c, where p_v = Pr(Y = 1|Z = 1) and p_c = Pr(Y = 1|Z = 0). Let ${\widehat{v}}_0^S$ denote the estimator of v₀ proposed by Siber et al. To calculate ${\widehat{v}}_0^S$, VE is first estimated using the sample proportions of disease for vaccine and control, denoted ${\widehat{p}}_v$ and ${\widehat{p}}_c$ respectively. Under the Prentice mediation assumption above, VE = 1 − Pr(S ≤ v₀|Z = 1)/ Pr(S ≤ v₀|Z = 0). Thus, if v₀ were known, VE could be estimated by $1-\widehat{\text{P}}\text{r}\left(S\le v_0|Z=1\right)/\widehat{\text{P}}\text{r}\left(S\le v_0|Z=0\right)$, where $\widehat{\text{P}}\text{r}\left(S\le v_0|Z=z\right)$ denotes the proportion of individuals in treatment arm z with immune response less then or equal to v₀. Therefore, ${\widehat{v}}_0^S$ is calculated by determining the immune response v such that ${\widehat{p}}_v/{\widehat{p}}_c=\widehat{\text{P}}\text{r}(S\le v|Z=1)/\widehat{\text{P}}\text{r}(S\le v|Z=0)$. Siber et al. also proposed a (1 – α) CI for v₀, denoted $\left(L_0^s,U_0^s\right)$. Let (L_VE, U_VE) be a (1 – α) CI for VE. Then $L_0^s$ is calculated by determining the immune response v such that $L_{\text{VE}}=1-\widehat{\text{P}}\text{r}(S\le v|Z=1)/\widehat{\text{P}}\text{r}(S\le v|Z=0)$ The upper limit $U_0^s$ is calculated analogously U_VE. This method has some disadvantages. It requires data on both vaccine and control and the assumption of Prentice’s full mediation condition may not hold in practice. Furthermore, ${\widehat{v}}_0^s$ may not exist or be unique.

3. Simulation Studies.

3.1. Inference on v_c for c > 0.

This section reports the results of simulation studies evaluating the methods described in Section 2 for constructing point estimates and 95% CIs for specified risk thresholds. For inference on v_c for c > 0, data were simulated for n independent vaccinated individuals. Immune response S was generated from a gamma distribution with mean and variance 4. Disease outcome Y given S was generated from a Bernoulli distribution with Pr(Y = 1|S = v) according to one of the four following models. The logit model was defined by Pr(Y = 1|S = v) = expit(β₀ + β₁v) for 0 ≤ v < ∞. The probit model was defined by Pr(Y = 1|S = v) = Φ(β_0p + β_1pv) for 0 ≤ v < ∞ where Φ(·) is the CDF of the standard Normal distribution. The step model was defined by Pr(Y = 1|S = v) = γ for 0 ≤ v ≤ v₀, 0 < γ < 1 and Pr(Y = 1|S = v) = 0 otherwise. Finally, the scaled logit model was defined by Pr(Y = 1|S = v) = λ expit(β_0d + β_1dv) for 0 ≤ v < ∞ with λ = 0.5. Each model’s parameters were determined by fixing the marginal disease risk when vaccinated, i.e., p_v. For the logit, probit, and scaled logit models, the slope parameter was set to −5 to reflect a higher immune response being associated with lower risk of disease. For each model, 1000 datasets were generated each with sample size n = 12, 500. For each dataset, ${\widehat{v}}_c$, ${\widehat{v}}_c^l$, and ${\widehat{v}}_c^d$ from Section 2 were calculated and corresponding 95% CIs for v_c were computed using the bootstrap percentile methods with B = 2000.

Table 1 presents the simulation results for each of the four models of Pr(Y = 1|S = v). The reported results include the empirical bias of each estimator, the average CI widths and the empirical CI coverage rates for each model.

Table 1.

Results of simulation study described in Section 2.1 based on 1000 simulated datasets each with sample size 12,500 where Bias denotes empirical bias, Width denotes average CI width and Cov denotes empirical CI coverage rate. The proposed nonparametric estimator is denoted by ${\widehat{v}}_c$, the parametric estimator based on a logistic regression model by ${\widehat{v}}_c^l$, and the parametric estimator based on Dunning’s scaled logit model by ${\widehat{v}}_c^d$.

Model	pv	c	vc	${\widehat{v}}_c$			${\widehat{v}}_c^l$			${\widehat{v}}_c^d$
				Bias	Width	Cov	Bias	Width	Cov	Bias	Width	Cov
Logit	0.01	0.001	1.31	0.00	0.29	0.93	0.00	0.23	0.93	0.00	0.24	0.93
		0.005	0.82	0.00	0.20	0.95	0.00	0.19	0.94	0.00	0.19	0.95
		0.009	0.47	−0.02	0.38	0.95	−0.02	0.37	0.95	−0.02	0.38	0.95
	0.10	0.009	2.01	0.00	0.10	0.94	0.00	0.08	0.94	0.00	0.08	0.94
		0.01	1.98	0.00	0.10	0.95	0.00	0.08	0.94	0.00	0.08	0.94
		0.05	1.43	0.00	0.09	0.95	0.00	0.08	0.96	0.00	0.08	0.96
Probit	0.01	0.001	1.00	0.00	0.13	0.93	0.00	0.12	0.94	0.00	0.12	0.94
		0.005	0.73	0.00	0.14	0.95	0.00	0.13	0.95	0.00	0.13	0.96
		0.009	0.47	−0.02	0.33	0.94	−0.02	0.33	0.94	−0.01	0.33	0.94
	0.10	0.009	1.82	0.00	0.06	0.94	0.00	0.05	0.92	0.01	0.05	0.92
		0.01	1.80	0.00	0.06	0.95	0.00	0.06	0.92	0.00	0.05	0.92
		0.05	1.41	0.00	0.07	0.95	0.00	0.07	0.95	0.00	0.07	0.95
Step	0.01	0.001	1.16	0.00	0.05	0.94	0.28	0.25	0.00	0.00	0.05	0.91
		0.005	0.97	0.00	0.15	0.96	−0.01	0.20	0.40	0.00	0.13	0.95
		0.009	0.61	−0.04	0.53	0.95	−0.20	0.41	0.73	−0.05	0.51	0.95
	0.10	0.009	2.39	0.00	0.03	0.95	0.70	0.14	0.00	0.00	0.03	0.76
		0.01	2.38	0.00	0.04	0.96	0.63	0.14	0.00	0.00	0.03	0.77
		0.05	1.95	0.00	0.11	0.95	−0.16	0.14	0.00	−0.01	0.09	0.94
Scaled	0.01	0.001	1.43	0.00	0.29	0.95	0.10	0.25	0.69	−0.01	0.25	0.95
		0.005	0.94	0.00	0.21	0.94	−0.03	0.22	0.91	0.00	0.20	0.94
		0.009	0.57	−0.04	0.47	0.94	−0.08	0.42	0.91	−0.04	0.47	0.94
	0.10	0.009	2.48	0.00	0.11	0.95	0.48	0.15	0.00	0.00	0.09	0.95
		0.01	2.45	0.00	0.10	0.96	0.44	0.14	0.00	0.00	0.09	0.96
		0.05	1.84	0.00	0.11	0.96	−0.10	0.13	0.13	0.00	0.10	0.96

In general, the empirical bias of ${\widehat{v}}_c$ was negligible and the corresponding CIs had coverage rates approximately equal to the nominal level 0.95. In contrast, the parametric estimator ${\widehat{v}}_c^l$ performed poorly when the assumed model was mis-specified, with ${\widehat{v}}_c^l$ having substantial bias and the associated CIs failing to achieve the nominal coverage level. While the parametric estimator ${\widehat{v}}_c^d$ had low bias for all models, the associated CIs had coverage rates well below 0.95 in some scenarios when the assumed model was mis-specified. In scenarios where the parametric models were correctly specified, CIs based on the nonparametric estimator tended to have similar width to CIs computed using the parametric estimator, indicating minimal loss of efficiency associated with using the non-parametric estimator.

3.2. Inference on v₀.

For inference on v₀, data were simulated for n independent individuals, assigned to vaccine or control in a 1:1 allocation. Immune response S was generated from a gamma distribution with mean and variance 4 when vaccinated and with mean and variance 2 when assigned control. Disease outcome Y given S and Z was generated from a Bernoulli distribution using the logit, probit, and step models. The logit model was defined by Pr(Y = 1|Z = 0, S = v) = expit(γ₀ + γ₁v) for 0 ≤ v <∞ and Pr(Y = 1|Z = 1, S = v) = expit(β₀ + β₁v) for 0 ≤ v ≤ v₀ with γ₀ = β₀ and β₁ = −5. The probit model was defined by Pr(Y = 1|Z = 0, S = v) = Φ(γ_0p + γ_1pv) for 0 ≤ v |< ∞ and Pr(Y = 1|Z = 1, S =v) = Φ(β_0p + β_1pv) for 0 ≤ v ≤ v₀ with γ_0p = β_0p and β_1p = −5. Finally, the step model was defined by Pr(Y = 1|Z = z, S = v) = ω for 0 ≤ v ≤ v₀, 0 < ω < 1 and Pr(Y = 1|Z = z, S = v) = 0 otherwise for z = 0, 1. Each model’s parameters were determined by fixing the marginal disease risks when assigned control and when vaccinated, i.e., p_c and p_v. For each model, 1000 datasets were generated each with sample size n = 25, 000. For each dataset, ${\widehat{v}}_0$, ${\tilde{v}}_0$, and ${\widehat{v}}_0^s$ were calculated and 95% CIs for v₀ were computed using the bootstrap percentile method with ${\widehat{v}}_0$ and B = 2000, and the methods from Cooke and Siber et al. Table 2 presents the simulation results.

Table 2.

Results of simulation study described in Section 2.2 based on 1000 simulated datasets each with sample size 25,000 and a 1:1 vaccine:control allocation where Bias denotes empirical bias, Width denotes average CI width and Cov denotes empirical CI coverage rate. The proposed nonparametric estimator is denoted by ${\tilde{v}}_0$, Siber’s estimator by ${\widehat{v}}_0^s$, and the maximum immune response value for the vaccinated and diseased sample by ${\widehat{v}}_0$.

Model	(pc, pv)	v0	${\widehat{v}}_0$			${\tilde{v}}_0$	$\left(L_0^c,U_0^c\right)$		${\widehat{v}}_0^s$	$\left(L_0^s,U_0^s\right)$
			Bias	Width	Cov	Bias	Width	Cov	Bias	Width	Cov
Logit	(0.10, 0.01)	2.00	−0.19	0.25	0.01	−0.13	4.31	0.94	−0.80	0.13	0.00
	(0.30, 0.10)	2.00	0.00	0.01	0.65	0.00	0.08	0.95	0.45	0.19	0.00
Probit	(0.10, 0.01)	2.00	−0.73	0.14	0.00	−0.69	2.84	0.77	−0.77	0.25	0.00
	(0.30, 0.10)	2.00	0.00	0.01	0.00	0.00	0.17	0.96	0.45	0.19	0.00
Step	(0.10, 0.01)	1.20	0.00	0.01	0.74	0.00	0.13	0.95	0.00	0.24	0.99
	(0.30, 0.10)	2.47	0.00	0.00	0.85	0.00	0.03	0.95	0.00	0.20	0.96

In general, the difference in bias between ${\tilde{v}}_0$ and ${\widehat{v}}_0$ was negligible. The boostrap CIs corresponding to ${\widehat{v}}_0$ never reached the nominal coverage level 0.95. Cooke’s [9] method generally performed well in terms of bias and CI coverage, except for the probit model simulations when p_v = 0.01, in which case the estimator was biased and the CI coverage was lower then 0.95. In general, the estimator ${\widehat{v}}_0^s$ performed poorly when the assumed models were mis-specified (logit and probit models), with ${\widehat{v}}_0^s$ having substantial bias and the associated CIs failing to achieve the nominal coverage level.

4. Extensions.

4.1. Background.

The methods in Section 2 assume each individual’s immune response and disease status are observed. However, in some studies this assumption may not hold. Two examples are studies with nested sub-sampling of S by design and with right censoring of Y. Common sub-sampling designs are case-control and case-cohort designs. Here case refers to individuals who develop disease during the study, and control refers to individuals who are disease-free at the end of study follow-up. There are multiple types of case-control studies [29], and and in this section we consider extensions of the methods above for the “cumulative case-control study” type, for which S is measured for all cases and for a random sample of controls [10, 29].

The extended methods also apply for a case-cohort sampling design, for which S is measured for all individuals randomly sampled into a subcohort at enrollment and also for all cases not sampled into the subcohort [24]. Our methods do not apply for case-control studies with risk-set sampling of S, which sample one or more control participants at each point in time when an event Y = 1 occurs [29]. In rare event studies such as our motivating application of preventive vaccine efficacy trials, risk-set sampling provides negligible benefits compared to cumulative case-control sampling, and cumulative case-control or case-cohort studies are the norm for vaccine efficacy trials.

In addition, in some studies the time to disease is right censored for some individuals, e.g., due to loss to follow-up. Methods for this scenario need to account for missing data from right censoring as well as to the sub-sampling design.

4.2. Methods.

Consider the vaccinated sample from the trial detailed in Section 2.1. We describe the methods for cumulative case-control sampling. Among individuals with Y = 0, proportion p₀ are randomly selected, by Bernoulli or without replacement sampling, to form the control group, denoted G₀. Similarly, a proportion p₁ of individuals with Y = 1 are randomly selected to form the case group, denoted G₁. Denote the union G₀ ⋃ G₁ by G. For individual i, let M_i = 1 if i ∈ G and M_i = 0 otherwise for i =1, …, n. For now, suppose Y is observed for all n individuals but S is observed only for individuals in G.

As in Section 2, point estimation and a corresponding (1 – α) CI for v_c are desired. The scenario where c = 0 is not considered in this section. To adjust for the missing immune response data, individuals are weighted by their probability of being selected into G conditional on Y using inverse probability weighting [17]. For individual i, let p₀ = Pr(i ∈ G|Y_i = 0) and let p₁ = Pr(i ∈ G|Y_i = 1). Denote the corresponding empirical proportions by ${\widehat{p}}_0$ and ${\widehat{p}}_1$ respectively. Then following Robins et al. [26], the weight for individual i, denoted W_i, is defined as $W_i=1/{\widehat{p}}_0$ if Y_i = 0 and $W_i=1/{\widehat{p}}_1$ if Y_i = 1. The weighted nonparametric estimator ${\widehat{v}}_c^w$ is defined as

$${\widehat{v}}_c^w=\min \left\{S_j:\frac{{\sum }_{i=1}^n{W}_{i}I\left(M_i=1\right)I\left(Y_i=1,S_i\ge S_j\right)}{{\sum }_{i=1}^n{W}_{i}I\left(M_i=1\right)I\left(S_i\ge S_j\right)}\le c,j\in \{1,\dots ,n\}\right\}.$$

This nonparametric estimator is compared to parametric estimators of the form

$$\min \left\{S_j:\frac{{\sum }_{i=1}^n{W}_{i}I\left(M_i=1\right)I\left(S_i\ge S_j\right)\widehat{p}\left(S_i\right)}{{\sum }_{i=1}^n{W}_{i}I\left(M_i=1\right)I\left(S_i\ge S_j\right)}\le c,j\in \{1,\dots ,n\}\right\}$$ (5)

where p(v) = Pr(Y = 1|S = v) is estimated by a parametric regression model, denoted $\widehat{p}(v)$. Estimators ${\widehat{v}}_c^{wl}$ and ${\widehat{v}}_c^{wd}$ are defined by (5) using the logit and scaled logit models respectively from Section 2.1 for p(v). The regression parameters for p(v) are estimated using weighted maximum likelihood with weight W_iI(M_i = 1) for individual i. Except in the special case where the sampling probabilities are the same for the disease and non-diseased group, not weighting will in general lead to biased estimates of p(v). The bootstrap percentile method is used to construct a (1 – α) CI for v_c.

The estimator ${\widehat{v}}_c^w$ and corresponding bootstrap CI can also be used for a cumulative case-cohort design or for a two-phase sampling design, which is defined as an extension of the cumulative case-control design that uses stratified random sampling of cases and controls within strata of a discrete covariate V with K levels that is measured in all n participants [4]. For the latter extension, the estimated inverse probability weights W_i are now defined using ${\widehat{p}}_{yk}$ that are estimates of Pr(i ∈ G|Y_i = y, V_i = k), which again may be obtained as empirical fractions.

For the methods to provide valid point and confidence interval estimation of the full population-level parameters p(v) and v_c (i.e., as if S had been measured in all n participants), the bootstrap is used with sampling type (Bernoulli or without-replacement) the same as that used for the observed data set. Validity of the methods relies on consistent estimation of (p₀, p₁) or the p_yk, which is readily achieved in studies where the investigator designs which individuals to sample from (barring a substantial amount of happen-stance missing data).

Now suppose that the n individuals are monitored starting at time 0 for incident disease. Let T_i denote the time until disease or survival time. Suppose survival times are subject to right censoring and let C_i denote the censoring time for individual i. Assume T_i is independent of C_i, and that we observe min{T_i, C_i} and δ_i = I(T_i ≤ C_i), where δ_i = 0 indicates censoring. Consider some time t₀ > 0 and suppose the outcome of interest is Y_i = I(T_i ≤ t₀), i.e., disease by t₀. Let V (t₀| S ≥ v) = 1 − Pr(Y = 1|S ≥ v) denote the survival function at time t₀, conditional on S ≥ v In this scenario, ${\widehat{v}}_c^w$ needs to be adjusted since it ignores the right censoring. The proposed nonparametric estimator ${\widehat{v}}_c^{wk}$ is defined as

$${\widehat{v}}_c^{wk}=\min \left\{S_j:1-{\widehat{V}}_w\left(t_0|S\ge S_j\right)\le c,j\in \{1,\dots ,n\}\right\}$$

where ${\widehat{V}}_w(t|S\ge v)$ is the weighted Kaplan-Meier estimator [23] of V (t|S ≥ v) with weight W_iI(M_i = 1, S_i ≥ v) for individual i. The bootstrap percentile method is used to construct a (1 – α) CI for v_c.

Note in the preceding paragraph that Y_i is defined for a particular time point t₀. Thus the corresponding immune response threshold v_c, i.e., the target parameter of inference, is also (implicitly) defined in terms of t₀. More generally, we can consider the target parameter of interest to be a function of time, say v_c(t), and the approach described above can be used to draw inference about v_c(t) by evaluating ${\widehat{v}}_{ck}$ over a grid of values of t.

4.3. Simulation Studies.

The methods in Section 4.2 were examined in simulation studies with and without right censoring. Data were simulated for n independent vaccinated individuals. Immune response S was generated as in Section 3.1 and 1000 datasets were generated each with sample size n = 12, 500.

First, the simulations without right censoring are discussed. For these simulations, Y was generated as in Section 3.1. Define $n_0={\sum }_{i=1}^{n}I\left(Y_i=0\right)$. For each dataset, cumulative case-control sampling was done, where subsets G₀ and G₁ were selected without replacement of size ⌊p₀n₀⌋from those with Y = 0 and ⌊p₁(n − n₀) ⌋ from those with Y = 1 respectively, where p₀ =0.2 and p₁ = 1 and ⌊·⌋denotes the floor function. Then, ${\widehat{v}}_c^w$, ${\widehat{v}}_c^{wl}$, and ${\widehat{v}}_c^{wd}$ were calculated as well as 95% bootstrap CIs with B = 2000. Simulation results are presented in Table 3.

Table 3.

Results of first simulation study described in Section 4.3 based on 1000 simulated datasets each with sample size 12,500 where Bias denotes empirical bias, Width denotes average CI width and Cov denotes empirical CI coverage rate. The proposed weighted nonparametric estimator is denoted by ${\widehat{v}}_c^w$, the weighted parametric estimator using logistic regression by ${\widehat{v}}_c^{wl}$ and the weighted parametric estimator using Dunning’s scaled logit model by ${\widehat{v}}_c^{wd}$.

Model	pv	c	vc	${\widehat{v}}_c^w$			${\widehat{v}}_c^{wl}$			${\widehat{v}}_c^{wd}$
				Bias	Width	Cov	Bias	Width	Cov	Bias	Width	Cov
Logit	0.01	0.001	1.31	0.00	0.29	0.94	0.00	0.26	0.94	−0.02	0.25	0.93
		0.005	0.82	0.00	0.20	0.95	0.00	0.20	0.96	0.00	0.20	0.97
		0.009	0.47	−0.02	0.39	0.97	−0.02	0.39	0.97	−0.01	0.40	0.96
	0.10	0.009	2.01	0.00	0.10	0.95	0.00	0.10	0.95	0.00	0.10	0.95
		0.01	1.98	0.00	0.10	0.95	0.00	0.10	0.96	0.00	0.10	0.96
		0.05	1.43	0.00	0.09	0.96	0.00	0.10	0.97	0.00	0.10	0.96
Probit	0.01	0.001	1.00	0.00	0.13	0.94	0.00	0.15	0.95	−0.01	0.13	0.94
		0.005	0.73	0.00	0.14	0.96	0.00	0.13	0.96	0.00	0.13	0.97
		0.009	0.47	−0.02	0.33	0.94	−0.02	0.34	0.95	−0.01	0.34	0.95
	0.10	0.009	1.82	0.00	0.06	0.95	0.00	0.06	0.94	0.00	0.06	0.93
		0.01	1.80	0.00	0.06	0.95	0.00	0.06	0.93	0.00	0.06	0.93
		0.05	1.41	0.00	0.08	0.97	0.00	0.08	0.97	0.00	0.08	0.97
Step	0.01	0.001	1.16	0.00	0.05	0.94	0.28	0.25	0.00	0.00	0.05	0.91
		0.005	0.97	0.00	0.15	0.95	−0.10	0.21	0.51	−0.01	0.16	0.95
		0.009	0.61	−0.04	0.50	0.96	−0.15	0.39	0.83	−0.05	0.49	0.96
	0.10	0.009	2.39	0.00	0.03	0.94	0.69	0.24	0.00	0.00	0.04	0.86
		0.01	2.38	0.00	0.04	0.97	0.64	0.23	0.00	0.00	0.04	0.88
		0.05	1.95	0.00	0.12	0.97	−0.16	0.16	0.01	0.00	0.12	0.96
Scaled	0.01	0.001	1.43	0.00	0.29	0.94	0.10	0.30	0.77	0.00	0.26	0.95
		0.005	0.94	0.00	0.21	0.97	−0.02	0.23	0.95	0.00	0.22	0.98
		0.009	0.57	−0.03	0.45	0.97	−0.07	0.42	0.95	−0.03	0.45	0.96
	0.10	0.009	2.48	0.00	0.11	0.95	0.48	0.24	0.00	0.00	0.10	0.95
		0.01	2.45	0.00	0.11	0.95	0.44	0.22	0.00	0.00	0.10	0.96
		0.05	1.84	0.00	0.12	0.97	−0.10	0.16	0.24	0.00	0.12	0.97

The results were similar to those in Table 1. In general, the empirical bias of ${\widehat{v}}_c^w$ was negligible and the corresponding CIs had coverage rates approximately equal to the nominal level 0.95. In contrast, the parametric estimator ${\widehat{v}}_c^{wl}$ performed poorly when the assumed model was mis-specified, with ${\widehat{v}}_c^{wl}$ having substantial bias and the associated CIs failing to achieve the nominal coverage level. The parametric estimator ${\widehat{v}}_c^{wd}$ had low bias for all models, however the associated CIs had coverage rates below 0.95 in some scenarios when the assumed model was mis-specified. The widths of CIs corresponding to ${\widehat{v}}_c^w$ were nearly identical to the widths of CIs corresponding to ${\widehat{v}}_c$ in Table 1, indicating a minimal loss in efficiency due to case-control sampling.

Next, results from simulations with right censoring are presented. Survival times were generated using accelerated failure time (AFT) models, adapted from Chan et al. [6]. In particular, T was generated by log(T) = β₀ + β₁S + ∊ where S was generated from a gamma distribution with mean and variance 4 and ∊ was generated from either a standard Normal distribution or logistic distribution (location parameter 0 and scale parameter 1). To reflect an increasing survival time for higher immune response values, β₁ was set to 2 and β₀ was determined after fixing p_v. Disease outcome Y was defined by Y = I(T ≤ t₀) with t₀ = 40. Censoring time C was generated as min {E, t₀} where E followed an exponential distribution with mean t₀. Sets G₀ and G₁ were generated using p₀ = 0.2 and p₁ = 1 respectively. Given c, for each dataset, ${\widehat{v}}_c^{wk}$ and ${\widehat{v}}_c^w$ were computed along with 95% bootstrap CIs with B = 2000.

Table 4 presents the simulation results for each AFT model. In general, the empirical bias of ${\widehat{v}}_c^{wk}$ was negligible and the corresponding CIs had coverage rates approximately equal to the nominal level 0.95. In contrast, ${\widehat{v}}_c^w$ generally had high bias and the corresponding CIs failed to achieve the nominal coverage level, which is expected since ${\widehat{v}}_c^w$ does not account for the right censoring.

Table 4.

Results of second simulation study described in Section 4.3 based on 1000 simulated datasets each with sample size 12,500 where Bias denotes empirical bias, Width denotes average CI width and Cov denotes empirical CI coverage rate. The proposed weighted nonparametric estimator is denoted by ${\widehat{v}}_c^{wk}$ and the weighted nonparametric estimator which ignores censoring by ${\widehat{v}}_c^w$.

Model	pv	c	vc	${\widehat{v}}_c^{wk}$			${\widehat{v}}_c^w$
				Bias	Width	Cov	Bias	Width	Cov
Log−Normal	0.01	0.001	1.43	−0.01	0.40	0.93	−0.19	0.32	0.39
		0.005	0.92	−0.01	0.34	0.95	−0.47	0.45	0.01
		0.009	0.50	−0.04	0.49	0.95	−0.30	0.14	0.01
	0.10	0.009	2.19	0.00	0.17	0.95	−0.20	0.13	0.00
		0.01	2.16	0.00	0.16	0.95	−0.20	0.13	0.00
		0.05	1.49	0.00	0.15	0.95	−0.43	0.20	0.00
Logistic	0.01	0.001	2.41	0.02	1.11	0.93	−0.30	0.78	0.66
		0.005	1.32	0.00	0.34	0.95	−0.47	0.70	0.11
		0.009	0.64	−0.04	0.71	0.95	−0.44	0.16	0.01
	0.10	0.009	2.88	0.00	0.35	0.95	−0.27	0.27	0.04
		0.01	2.82	0.00	0.31	0.94	−0.27	0.26	0.03
		0.05	1.706	0.00	0.20	0.96	−0.44	0.23	0.00

The simulations study above was repeated with sample size 6500. Results (not shown) were similar to those in Table 4, except the CIs had larger average widths.

5. Application.

5.1. Data.

In this section, the methods described above are used to estimate neutralizing antibody thresholds for virologically confirmed dengue risk levels using data from two recent dengue vaccine trials. With an estimated 390 million dengue infections per year and anti-viral treatment for dengue unavailable, continued research on dengue vaccination is important [21]. CYD14 and CYD15 were Phase 3 placebo-controlled studies aimed at evaluating the efficacy and safety of the dengue vaccine CYD-TDV in children. Following these two studies, CYD-TDV became the first dengue vaccine to be licensed, beginning with Mexico in 2015 [22].

CYD14 was conducted in five Asian-Pacific countries (Indonesia, Malaysia, Philippines, Thailand, and Vietnam), with participants 2–14 years old [5]. CYD15 was conducted in five Latin American countries (Columbia, Brazil, Mexico, Puerto Rico, and Honduras), with participants 9–16 years old [30]. The protocols for these two studies were harmonized. For both studies, participants were randomized in a 2:1 ratio to CYD-TDV vaccine or placebo. Participants received doses at the start of the study (month 0), at month 6, and at month 12 with follow-up visits at months 13 and 25. The primary endpoint was time until virologically confirmed dengue disease from any of four serotypes between months 13 and 25 (referred to simply as “dengue” below). The primary objective was to estimate vaccine efficacy against dengue occurring between months 13 and 25 in the per-protocol population (those with dengue occurring between months 0 and 13 were excluded). Both studies used a case-cohort sampling design where a subset of participants was randomly selected for neutralizing antibody titers measurement before the first dose and at months 7, 13, and 25. All cases (dengue) also had antibody titers measured. The magnitude of neutralizing antibodies to each of the four serotypes represented in the CYD-TDV vaccine were measured as 50% neutralization titer at the log₁₀ scale; thus participants in the case-cohort subset had four PRNT₅₀ values.

Pooled analysis of participants 9–16 years old from both trials indicated that antibody response was positively associated with VE and that vacci-nation was associated with decreased dengue risk [20] (here and in Section 5.2, antibody response refers to the average of the four serotype-specific antibody titers from the month 13 measurements in the case-cohort subset). In a pooled analysis of participants 9–16 years old from both trials, the estimated VE was 65.6% (95% CI of 60.7%, 69.9%) using a Cox regression model with vaccine status and study participation as covariates [15].

5.2. Results.

Motivated by these results, risk thresholds when vaccinated were estimated using the CYD14, CYD15 and pooled CYD14 and CYD15 (CYD14/15) data. The participants included in the statistical analysis were those who did not develop dengue and were not right censored prior to month 13 and had titers measured, i.e., the case-cohort subset. These participants were analyzed according to the treatment group to which they were randomized, irrespective of per-protocol criteria. For the pooled analysis, only participants between 9 and 16 years old were included because 9 and older is the indication for the licensed vaccine. When analyzing the CYD14 and CYD15 data individually, there were no age restrictions. The analysis included 6454 participants in CYD14 with 104 cases, 13,376 participants in CYD15 with 183 cases, and 16,623 participants in CYD14/CYD15 with 216 cases. For CYD14, CYD15, and CYD14/CYD15, 1145, 1458, and 2088 participants respectively had measured antibody data.

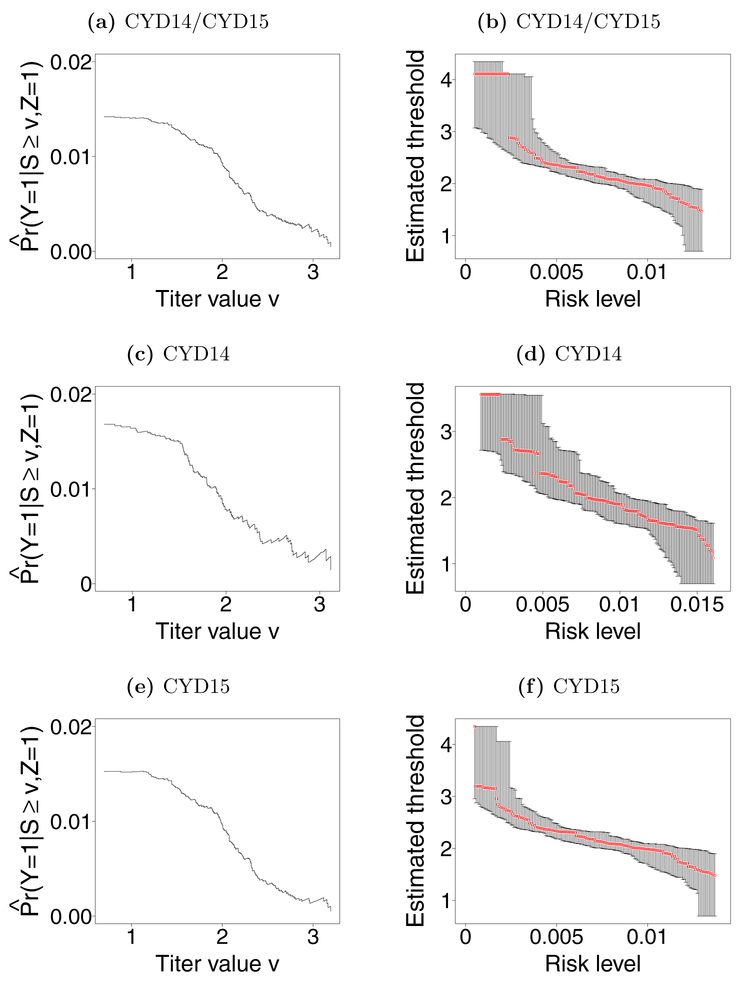
Let Y denote dengue status, with Y = 1 denoting presence of dengue between months 13 and 25. Figures 2a – 2c display estimates of Pr(Y = 1|Z = 1, S ≥ v) for each observed antibody response v in the vaccine arm for CYD14, CYD15 and CYD14/CYD15 respectively. Estimates were computed using the weighted Kaplan-Meier estimator in Section 4.2 to account for case-cohort sampling and right censored outcomes, with weights equal to the inverse of the sample proportions having an observed antibody response in the strata of individuals with and without dengue. These proportions were 1 among individuals with dengue for each dataset and were 0.164, 0.100, 0.114 for CYD14, CYD15, and CYD14/15 respectively among individuals without dengue. All three figures indicate decreasing dengue risk as antibody response increases. Figures 2d – 2f show estimates and 95% CI for risk thresholds over a range of risk levels for CYD14, CYD15, and CY14/15. Due to the case-cohort sampling and right censoring, point estimates and CIs were constructed using ${\widehat{v}}_c^{wk}$ as described in Section 4.2 with B = 5000.

Fig 2:

Panels a), c), and e) show estimated disease risk conditional on S ≥ v by log₁₀ titer at month 13 when vaccinated for 9–16 years olds in CYD14 and CYD15 pooled (CYD14/15), CYD14 all ages, and CYD15 all ages, respectively. These estimates were calculated for each observed antibody response v in the data and are denoted by $\widehat{\text{P}}\text{r}(Y=1|Z=1,S\ge v)$. Panels b), d), and f) show estimates (red points) and 95% CIs for risk thresholds over a range of risk levels for CYD14/15, CYD14, and CYD15 respectively.

6. Discussion.

In this paper, nonparametric methods for inference on risk thresholds were presented and examined through simulation studies. Extensions of these methods for studies with sub-sampling of the immune response, such as case-cohort and cumulative case-control and two-phase studies, and with right censoring of the outcome, were also considered. Simulation studies were presented demonstrating that the proposed nonparametric estimators tended to have minimal bias and the corresponding bootstrap CIs typically cover at approximately the nominal level. In contrast, estimators and CIs based on parametric models or Siber et al. [27] tended to not perform well empirically when the additional underlying assumptions did not hold.

The nonparametric methods were used for inference on neutralizing antibody risk thresholds for specified risk levels of virologically confirmed dengue for the CYD-TDV vaccine. In new populations adopting the CYD-TDV vaccine, these risk thresholds may helpful for policymakers and public health officials in estimating the risk of dengue based solely on the distribution of antibody concentrations. Similarly, these risk thresholds may be helpful in indirect evaluation of new candidate dengue vaccines on the basis of antibody titer data alone by providing initial estimates of disease risk by titer thresholds; one application is informing Go/No-Go decisions for down-selecting vaccines for advancement to efficacy trials.

In some settings it may be of interest to draw inference about immune response risk thresholds within certain subgroups. In this case the proposed method can be used by restricting the analysis to participants with particular (baseline) covariate values, resulting in estimates of covariate-specific risk thresholds. This would allow indirect evaluation of vaccine efficacy for sub-populations of interest or for new populations whose covariate distributions differ from those studied in the original efficacy trial(s). In particular, if a covariate that is correlated with both the immune response and disease has a different distribution in the two settings (e.g., if the new population is older), then the covariate-conditional thresholds would be needed for predicting vaccine efficacy in immune response threshold subgroups in the new population.

There are several possible avenues of future research related to the methods considered here. For example, unlike the frequentist approach used in this paper, Bayesian methods could be developed for inference about thresholds of risk. Advantages of a Bayesian approach would include not relying on asymptotic approximations and allowing prior information on thresholds to be incorporated into the inference. On the other hand, a disadvantage of the Bayesian approach is that the results will depend on the (subjective) choice of the prior.

Another possible area of further research would be to extend the methods developed here to allow for diagnostic uncertainty. Throughout this paper it was assumed that the true disease status is observed for each individual. However, in some settings the presence of disease may be measured with error. Extensions of the proposed methods to allow for diagnostic uncertainty will naturally depend on the particular setting under consideration, e.g., whether the sensitivity and specificity of the diagnostic instrument are known, whether a validation subsample is available where the true disease status is known, and so forth. Existing measurement error methods, such as multiple imputation [8], could potentially be combined with the non-parametric approach developed here.

Future research could entail extending the nonparametric method presented here to the setting where it is assumed the risk threshold is a monotonic function of immune response. If this monotonicity assumption is correct, nonparametric methods that leverage this assumption would be expected to outperform the approach in this paper. That said, the non-parametric methods considered here have the appealing property of not relying on such a monotonicity assumption, and thus should provide valid inference regardless of whether such an assumption holds.

Future research could also examine developing confidence bands for a set of risk levels. The CIs presented here provide only point-wise coverage. Lastly, methods for testing for the existence of risk thresholds is a possible area of future research. There has been some development on methods for this type of inference for a risk level of zero [7], however for general risk thresholds no such methods exist.