The influence of sample selection on the structure of psychopathology symptom networks: an example with alcohol use disorder

Abstract

Increasingly, the structure of mental disorders has been studied in the form of a network, characterizing how symptoms or criteria interact with and influence each other. Many studies of psychiatric symptoms and diagnostic criteria employ community or population-based surveys using co-occurrence of the symptoms/criteria to form the networks. However, given the overall low prevalence rates of mental disorders and their symptoms in the general population, the vast majority of those surveyed may not exhibit or endorse any symptoms and yet are often included in network analyses. Consequently, because network models are built on associations between symptoms/criteria, much of the observed variability is driven by individuals who are asymptomatic. Using data from the National Epidemiological Survey of Alcohol and Related Conditions (NESARC) Wave 2 and NESARC-III, we explore the effect of these “asymptomatic” observations on the estimated relations among diagnostic criteria of alcohol use disorder to determine the effects of such observations on estimated networks. We do so using the eLasso tool, as well as with traditional measures of correlation between binary variables (the Φ coefficient and odds ratio). We find that when the proportion of asymptomatic individuals are systematically culled from the sample, the estimated pairwise relations are often significantly affected, even changing signs in some cases. Our findings indicate that researchers should carefully consider the population(s) included in their sample and the implications it has on their interpretations of pairwise similarity estimates and resulting generalizability and reproducibility of estimates of network structures.

General Scientific Summary:

Network representations of psychopathological symptoms are becoming increasingly popular in clinical research, modeling how diagnostic symptoms interact with each other, often in terms of co-occurrence. This study examines the influence of restrictions on the observations included in a sample used to estimate the network relations, demonstrating how a clinical and national sample can identify very different network structures.

Introduction

In network form, a system is modeled as a set of nodes representing the objects or variables being studied, and edges, modeling connections or relationships among the nodes. For example, a researcher may have a social network from a school of students (the nodes) and the observed friendships connecting pairs of students (the edges). Network analyses are not limited to social relations among individuals, but can also be used to model a wide variety of systems in many different fields. One of these new fields is symptom or criteria networks. In these models, the symptoms or criteria of a disorder are represented by the nodes, and the edges indicate the relationships between each pair. This allows the researcher to utilize the statistics unique to the field of network analysis, such as centrality measures, to answer different types of questions. Studies have already examined the relations among symptoms of specific disorders such as substance use disorders (SUD; Rhemtulla et al., 2016), post-traumatic stress disorder (McNally et al., 2015), or depression (Kendler et al., 2018; Fried et al., 2016a), and comorbidity of different disorders (Borsboom et al., 2011; Boschloo et al., 2015; Afzali et al., 2017).

Estimating Criteria Networks

Different from traditional networks, the associations among symptoms (the desired edges) are not observed. Instead, they must be inferred from non-network data such as diagnostic surveys where the presence/absence of symptoms is recorded for each individual as binary variables¹. The recent surge in network analysis has largely been driven by the development of methods to build these networks from non-network sources. The eLasso method was developed to create networks from binary data specifically for psychological applications and is implemented using the R package IsingFit (van Borkulo et al., 2014). This method allows researchers to easily estimate symptom networks from binary variables.

The algorithm attempts to infer the edges of the undirected graph underlying the P variables (symptoms) of interest (j=1,…,P). The estimation proceeds by selecting one variable at a time ( X _j ) as the dependent variable, then using the remaining P-1 variables (denoted as X_\j) as the predictors, an ℓ1-regularized logistic regression model is fit. This process is repeated P times with each variable taking a turn as the dependent variable. Estimated regression coefficients are retained at each step. For each pair of variables there will be two values, one where the first is the dependent variable, and the other where the second is the dependent variable. The regularization method is utilized to eliminate spurious edges, producing a more sparse network. For the network model to consider the two variables “connected”, neither of the parameters can be zero, following the “and” rule (as opposed to the “or” rule where only one of the parameters must be nonzero to be included). If both of the parameters are non-zero, then the weight (i.e., strength) of the connection is the average of the parameter values. The network weights are collected in the adjacency matrix A = a_jk, where the weight between criterion j and k is given by a_jk.

Sample Selection

The aim of estimating these symptom networks is to reveal true underlying and potentially causal relations among the symptoms. The usefulness of these estimated relations, however, is heavily dependent on the sample included in the study. The assumption of these studies is that all individuals included in the network analyses are at risk for the diagnoses or syndromes under study, but this might not always be the case. For example, if an individual has not used a substance for the last year (or for his or her lifetime), there is arguably zero risk of developing or manifesting a symptom of SUD. This individual will by definition not meet criteria for any feature of an SUD. Similarly, because a diagnosis of posttraumatic stress disorder (PTSD) requires that one have a history of trauma, PTSD symptoms are not assessed or possible if there is no trauma exposure.

When including broad populations, such as from national surveys, the issue to consider is that of population heterogeneity, where data are analyzed as though they are sampled from a single homogenous population, though the true parameter values differ within the sample (Muthén, 1989b). In network analysis, this would be the case where in one subsample the criteria being studied relate to each other differently than in another subsample. In the case of SUD, we are unaware of any empirical demonstration that network analyses on individuals who are at high risk for disorder (by virtue of meeting at least one criterion) reveal the same network structure as those network analyses that include both at-risk and not at risk individuals. This concern has been demonstrated in factor analysis. In considering the structure of depression criteria, Fried et. al. (2016b) demonstrated that those individuals whose depression improves over time have a different dimensionality in their data than those whose depression continues. These findings from factor analytical research shed light on the potential problem of estimating these networks over the entire population in the presence of unmodeled mixtures of subpopulations.

On the other hand, systematically removing individuals might impose artificial constraints on the estimated network. Restricting the population to a clinical sample to study the relations between symptoms is similar to the classic problem of selection bias in the psychometric literature (Meredith, 1964). For example, Muthén (1989a) discussed the implications of applying a factor analysis directly to a subpopulation that was selected based on a function of the observed scores, such as examining the factor structure of test items for a university admissions test, where the subpopulation being studied (admitted students) are selected as a function of their scores on the test. In psychopathology, this could be seen as similar to studying the structure of psychological symptoms when the admittance into treatment could be seen as de facto evidence of endorsement of some number of criterial symptoms. Muthén demonstrated how differences in sign of factor loadings and estimated covariances between factors can result on the basis of selection effects on a subpopulation of individuals based on a composite of the indicators associated with a factor.

As this literature alludes to the sensitivity of association measures to sample composition, it is clear that the estimated network of relations among symptoms is almost certainly subject to the same potential pitfalls as latent variable models. These concerns seem especially relevant to network analyses of binary data (i.e., present versus absent) because, as we discuss below, including individuals who do not meet any criteria for a diagnosis in network analyses may dramatically inflate estimates of the degree of relation among criteria. It is well known that the marginal distributions of the variable measures (i.e., their prevalence rates) often influence pairwise similarity measures (Warrens, 2008). Similarly, in behavioral genetics research the effects of ascertainment bias are often discussed, reflecting the situation where the methods used to obtain the sample included in the study differentially select people from the population. For example, McGue (1992) demonstrated how the improper choice of pairwise versus probandwise concordance measures can lead to incorrect conclusions in a study.

Ultimately, researchers must find a balance between analyzing, 1) a potentially heterogeneous population including large numbers of people who are irrelevant to the question at hand and could overestimate associations, or 2) a subset of data selected on the basis of either observed variables (e.g., risk status or positive symptom report) or ascertainment from a population that can be assumed to implicitly impose a similar type of selection (e.g., sampling from a clinical setting). In producing a symptom network, the researcher is making a statement about the true underlying structure of linkages and inferring causal relationships between them. Including individuals that have little or no risk for the disorder or its symptoms may drastically affect network structure. However, choosing to remove asymptomatic individuals from the sample induces the known problems associated with selection. Determining whether to include or exclude asymptomatic individuals is a difficult decision; nonetheless, we show that, due to their inability to add meaningful information to the relationship between pairs of symptoms, their inclusion is questionable.

Working with clinical samples, most observations should exhibit at least a few criteria, as these define the disorders. However, some network research is conducted using the data from large epidemiological surveys of the general population, where we do not expect to see particularly high rates of any given mental disorder. For example, one widely cited estimate of past-year prevalence of having any mental disorder is 26.2%, suggesting that roughly 73.8% of the population does not have any disorder over the previous year (Kessler et al., 2005). Even if this is an underestimate, owing to incomplete surveying of all possible mental disorders, the proportion with no diagnosis is high and likely to be much higher when considering single disorders. Consequently, within nationally representative surveys the majority of the data may be “asymptomatic,” where x⁽ⁱ⁾ is a vector of zeros. For example, Lane and Sher (2015) demonstrated in their analysis of criteria in the National Epidemiological Survey of Alcohol and Related Conditions (NESARC) Wave 2, that 15,789 of the 22,177 past year drinkers endorsed zero criteria. The crucial question, then, is whether this is adding useful information to the model, or inflating relationships among variables.

The Present Study

The focus of the current study is to determine how robust estimates of network edges are, depending on the way the sample was conditioned, with particular consideration of the proportion of asymptomatic individuals. For comparison, we also consider the impact on factor models of the same data. These models provide a benchmark, as factor models are typically used to study disorders based on their symptoms.

We elected to investigate alcohol use disorder (AUD) as it has the highest prevalence of any disorder in the general population (Goldstein et al., 2015), and therefore should contain the fewest number of asymptomatic individuals that could potentially obscure the pattern of network edges. Thus, our findings should be a conservative estimate of the impact of asymptomatic individuals in network analyses that is likely applicable to all disorders. Specifically, we examine the effect of systematically including varying numbers of asymptomatic observations on the estimated relationship among pairs of variables using the eLasso method to estimate networks from two large population surveys on alcohol use using the P = 11 criteria defined in the DSM-5 to diagnose AUD. For each of the surveys, networks are estimated from four different “filters” on the sample: (1) the full data, (2) only past-year drinkers, (3) past year binge drinkers, and finally (4) past year symptomatic - observations that have at least one observed criterion (i.e. removing all the asymptomatic observations). The second through fourth subsets provide examples of analyses on increasingly higher risk subpopulations, though not necessarily clinical samples. The effects of including the large number of individuals who report no criteria are assessed by examining the estimated edges and centrality measures across the different subsets. Following this, we examine the effects of increasing numbers of asymptomatic observations on pairwise correlations and odds ratios to gauge the magnitude of this critical methodological issue. Binary symptom data, though not the sole source of diagnostic outcome determinations, are still a primary source for making diagnostic decisions across the entire spectrum of disorders, and the conditional data subsets in the current analyses cover a broad range of sample compositions observed in literatures examining the structure of different clinical diagnoses (e.g., population, clinical, subclinical, comorbid). As a result, we would expect the set of analyses that we present to be broadly representative of various data sources that might be considered for analysis.

Method

Samples

Conducted by the National Institute on Alcohol Abuse and Alcoholism (NIAAA), these are large nationally representative samples of civilian, non-institutionalized adults in the U.S. population. For this study the data from NESARC Wave 2 and NESARC-III surveys were used. NESARC Wave 2 is a follow up survey, conducted in 2004–2005, to the first wave. There was an 87% retention rate from the first to the second wave giving a sample of n=34,653 (Grant et al., 2007). NESARC-III was conducted in 2012–2013 with a new sample of n=36,309 (Grant et al., 2015). Only those aged 21 and older were included in the final data in order to keep the ages similar. This left n=34,629 for NESARC Wave 2, and n=34,712 for NESARC-III. The average age of respondents in NESARC Wave 2 [and III] was 49.08 (SD=17.29) [and 46.85 (SD=16.95)]. The samples were 43.56% and 42.02% male, respectively. NESARC Wave 2 was 58.20% White, 19.00% Black and 18.34% Hispanic. NESARC-III was 53.59% White, 21.17% Black and 18.89% Hispanic.

Measures

For NESARC Wave 2, DSM-5 AUD criteria were scored using the Alcohol Use Disorder and Associated Disabilities Interview Schedule—DSM-IV Version 4 (AUDADIS-IV; Grant, Dawson, & Hasin, 2001). The AUDADIS-IV is a fully structured diagnostic interview designed to assess alcohol, drug, and other mental disorders in both general and clinical populations according to DSM-IV criteria. In addition to the DSM-IV AUD criteria, the AUDADIS at this wave also included items related to craving, allowing scoring for all DSM-5 AUD criteria. Using a subsample of 1,899 respondents, fair to good test-retest and inter-rater reliability have been demonstrated for Wave 2 Axis I and II AUDADIS-IV diagnoses (Grant et.al, 2003; Ruan et al, 2008). Kappas indicated good agreement for AUD past-year and lifetime diagnoses, κ=0.74 and κ=0.70, respectively. In NESARC-3, the Alcohol Use Disorder and Associated Disabilities Interview Schedule 5 (AUDADIS-5) was used to measure DSM-5 criteria for AUDs. Test-retest reliability of AUDADIS-5 and DSM-5 AUD categorical diagnoses (κ = 0.60 and κ = 0.62, respectively) and dimensional criteria scales (intraclass correlation coefficient [ICC], 0.83 and 0.85, respectively) was substantial in a large general population sample.

AUD Criteria

The DSM-5 defines 11 criteria for the diagnosis of AUD (APA, 2013). Briefly, they are: larger amounts/longer use (LL), inability to cut down (CD), spend a lot of time obtaining/drinking/recovering from its effects (TS), craving (CR), failure to fulfill major roles and obligations (FF), social/interpersonal problems (SI), give up activities (GU), hazardous use (HZ), use despite physical/psychological problems (PP), tolerance (TL), and withdrawal (WD)². For this study, only the data for the past-year occurrences of the criteria were included due to concerns with unreliability of reports of lifetime symptoms (e.g., Haeny, Littlefield, & Sher, 2014a, 2014b; Moffitt et al., 2010; Vandiver & Sher, 1991). A diagnosis of AUD is given to an individual who exhibits two or more of these symptoms.

Centrality

Node centrality measures assess a node’s role within a given network. Three are included here that are commonly used as descriptive statistics in psychopathology applications of network analysis: betweenness and closeness, both based on shortest paths, and strength, based on a node’s immediate neighbors (Opsahl, Agneessens, & Skvoretz, 2010). It should be noted that in the case of negative edges, the absolute values are used in the calculation of these measures. All were calculated within the R package qgraph (Epskamp et al., 2012).

AUD Networks

First, two networks were constructed using all of the observations in NESARC Wave 2 and NESARC-III, giving the estimated “full” networks. The “past year drinker” networks include only those reporting that they consumed at least one drink of alcohol in the past 12 months. Both the full and past year drinker networks contain large numbers of asymptomatic observations: for NESARC Wave 2 81.45% and for NESARC III 77.50% of individuals in the full data set are asymptomatic. Participants in the “full” data who have not had any alcohol in the past year are asymptomatic individuals both naturally, as most of the criteria³ require consumption of alcohol, and systematically, as the structure of the interview was such that they were not assessed in non-drinkers. Removing non-drinkers reduces the percentage of asymptomatic individuals to 71.06% for Wave 2 and 68.47% for III. The “past year symptomatic” networks were calculated using only individuals who exhibit at least one criterion, reducing the counts of asymptomatic individuals to zero. The “binge” networks include only observations who report having a binge episode in the past year, defined as having five or more drinks for males or four or more drinks for females within two hours. The “binge” samples include some asymptomatic individuals, but they make up a smaller percentage of the data as would be expected: 31.52% of NESARC Wave 2 and 31.24% of NESARC III. These samples do filter out some individuals who exhibit one or more symptoms (4,044 from Wave 2 and 4,400 from III). This overlap is depicted in supplementary Figure 1. The prevalence rates of the criteria and sample sizes for each of these datasets are presented in Table 1. Table 2 contains the prevalence rates for criterion counts (each potential count of total criteria from 0 to 11).

Table 1.

Unweighted prevalence rates (%) of the criteria for each dataset and subsample. Only the unweighted prevalence rates are included here because the unweighted data are used in the network estimation method.

Sample	LL	CD	TS	CR	FF	SI	GU	HZ	PP	TL	WD	N
NESARC Wave 2
Full Data	8.8	8.1	1.8	2.7	0.7	1.5	0.6	6.8	3.3	4.4	5.0	34,629
PY Drink	13.8	12.7	2.8	4.2	1.1	2.4	1.0	10.6	5.1	6.8	7.8	22,160
PY Binge	41.5	30.8	11.5	14.2	4.5	9.7	4.3	32.9	17.7	16.5	23.3	3,458
PY Symptomatic	47.7	43.8	9.8	14.4	3.7	8.3	3.4	36.7	17.6	23.6	26.8	6,412
NESARC III
Full Data	10.6	9.9	3.8	7.8	1.5	4.5	1.4	8.0	5.2	5.7	7.7	34,712
PY Drink	14.8	13.8	5.3	10.9	2.1	6.4	2.0	11.2	7.3	8.0	10.9	24,773
PY Binge	40.8	32.5	18.4	29.8	7.4	20.1	7.1	29.4	23.3	21.6	30.7	4,959
PY Symptomatic	47.0	43.9	16.9	34.6	6.6	20.2	6.3	35.5	23.2	25.4	34.4	7,810

Note: The 11 criteria are larger amounts/longer use (LL), inability to cut down (CD), spend a lot of time obtaining/drinking/recovering from its effects (TS), craving (CR), failure to fulfill major roles and obligations (FF), social/interpersonal problems (SI), give up activities (GU), hazardous use (HZ), use despite physical/psychological problems (PP), tolerance (TL), and withdrawal (WD).

Table 2.

Unweighted prevalence rates (%) of the criterion counts for each dataset and subsample.

Sample	0	1	2	3	4	5	6	7	8	9	10	11
NESARC Wave 2
Full Data	81.5	8.6	4.2	2.2	1.3	0.9	0.5	0.3	0.2	0.2	0.1	0.1
PY Drink	71.1	13.4	6.6	3.4	2.0	1.3	0.8	0.4	0.4	0.3	0.2	0.1
PY Binge	31.5	22.1	16.1	9.6	6.1	4.9	3.2	2.0	1.4	1.4	1.0	0.7
PY Symptomatic	0.0	46.3	22.9	11.6	6.9	4.6	2.7	1.5	1.3	1.0	0.7	0.5
NESARC III
Full Data	77.5	8.8	4.3	2.8	1.9	1.2	1.0	0.7	0.6	0.4	0.4	0.2
PY Drink	68.5	12.4	6.1	3.9	2.7	1.7	1.4	1.0	0.9	0.6	0.5	0.3
PY Binge	31.2	17.0	12.3	9.6	7.6	5.3	4.6	3.4	3.3	2.1	2.0	1.6
PY Symptomatic	0.0	39.2	19.3	12.3	8.6	5.4	4.5	3.1	2.8	1.9	1.7	1.1

Results

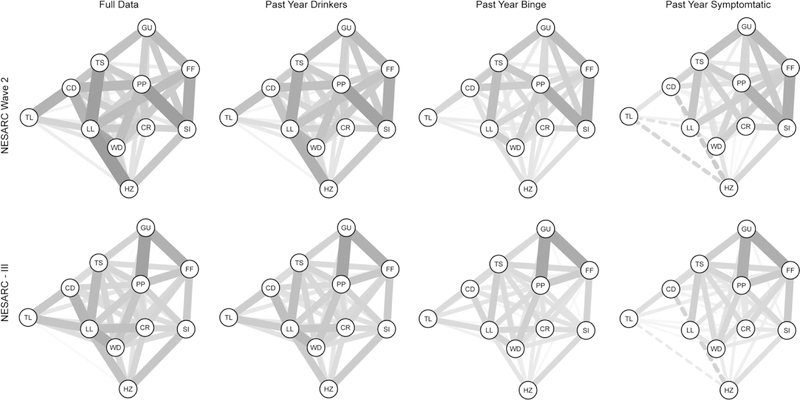
The plots of each estimated network can be found in Figure 1, and the estimated edge weights for the NESARC Wave 2 data are in Table 3a, and NESARC-III in Table 3b. As can be seen in Figure 1, each dataset produces four visually different networks from the different restrictions on the data samples. To summarize the differences between the networks, Spearman correlations between the edge weights were calculated, and can be found in the upper triangle of Table 5; bold values indicate the correlation between different versions of the same dataset (e.g., different filterings) within wave, and the entries with asterisks denote the consistency/replicability of the same filtered network across wave. In NESARC Wave 2, the correlation of .99 between the edge weights of the full data and the past year drinkers indicates that very little changes when applying the “drank in the past year” filter. The general trend in differences between edges in these two networks is a decrease in magnitude, with the removal of non-drinkers (who, again, are asymptomatic).

Figure 1.

Graphs of the estimated networks. The continuous lines represent positive relationships and dashed are negative. Thicker/darker edges indicate stronger relationships. Plots were created using the “averageLayout” function in the R package qgraph to obtain the layouts averaging over the two full network layouts (Epskamp et al., 2012). This was used to maintain node placement across graphs. The 11 criteria are: larger amounts/longer use (LL), inability to cut down (CD), spend a lot of time obtaining/drinking/recovering from its effects (TS), craving (CR), failure to fulfill major roles and obligations (FF), social/interpersonal problems (SI), give up activities (GU), hazardous use (HZ), use despite physical/psychological problems (PP), tolerance (TL), and withdrawal (WD).

Table 3a.

Edge weights for the NESARC Wave 2 networks estimated using the eLasso method. Each entry in the table corresponds to the edge between the row criterion and column criterion.

		CD	TS	CR	FF	SP	GU	HZ	PP	TL	WD
Full Data	LL	1.52	1.86	1.08	1.34	0.55		1.90	0.96	0.89	1.74
	CD		0.29	0.98		0.53	1.15	0.64	1.41	1.55	0.83
	TS			0.93	0.44	0.35	1.27	0.59	1.03	0.62	0.64
	CR					0.93	0.76	0.62	1.04	0.36	0.73
	FF					1.65	1.38		0.92		1.06
	SI						1.07	1.15	1.88	0.31
	GU								0.99	0.39
	HZ								0.60	0.38	0.89
	PP									0.28	1.30
	TL										0.55
1+ Drink in Past Year	LL	1.21	1.67	0.92	1.21	0.49		1.56	0.85	0.68	1.49
	CD		0.27	0.84		0.48	1.01	0.44	1.26	1.25	0.68
	TS			0.92	0.46	0.37	1.26	0.58	1.01	0.61	0.64
	CR					0.91	0.78	0.56	1.00	0.33	0.68
	FF					1.64	1.38		0.91		1.06
	SI						1.07	1.08	1.81	0.31
	GU								0.96	0.42
	HZ								0.54	0.26	0.77
	PP									0.26	1.22
	TL										0.47
1+ Binge in Past Year	LL	0.67	1.32	0.46	0.88	0.19	0.47	0.67	0.40	0.29	1.02
	CD		0.15	0.54	0.43	0.09	1.00	0.09	1.04	0.84	0.44
	TS			0.79	0.40	0.31	1.16	0.50	1.10	0.73	0.42
	CR					0.81	0.77	0.50	0.82		0.62
	FF					1.62	1.36	0.32	0.72		0.73
	SI						0.95	0.69	1.64	0.41	0.11
	GU								0.76	0.45
	HZ								0.56		0.34
	PP									0.08	0.95
	TL										0.40
1+ Criteria in Past Year	LL	−0.24	1.17	0.27	0.97	0.32	0.38		0.39	−0.35	0.36
	CD		0.28	0.23	0.35	0.33	0.90	−0.59	0.65
	TS			0.93	0.53	0.45	1.25	0.57	0.98	0.60	0.63
	CR				0.09	0.87	0.84	0.13	0.84		0.40
	FF					1.62	1.41	0.34	0.89		0.98
	SI						1.08	0.82	1.59	0.30	0.10
	GU								0.87	0.60
	HZ								0.24	−0.48
	PP										0.88
	TL

Table 3b.

Edge weights for the NESARC-III networks estimated using the eLasso method. Each entry in the table corresponds to the edge between the row criterion and column criterion.

		CD	TS	CR	FF	SI	GU	HZ	PP	TL	WD
Full Data	LL	1.49	1.39	1.28	−0.02	0.65	−0.08	1.23	1.01	1.18	1.60
	CD			0.69		0.73	0.69	0.42	0.84	1.14	0.53
	TS			0.85	0.76	0.53	0.92	0.45	0.88	0.74	0.88
	CR				0.87	0.84	0.47	0.88	0.77	0.55	0.96
	FF					1.07	1.57		1.13		0.81
	SI							1.18	0.92	0.30	0.76
	GU							-0.08	1.82	0.26	0.63
	HZ								0.61	0.16	0.80
	PP									0.55	1.17
	TL										0.71
1+ Drink in Past Year	LL	1.29	1.29	1.12		0.58	−0.05	1.04	0.92	1.03	1.43
	CD			0.58	0.30	0.67	0.73	0.29	0.78	1.02	0.44
	TS			0.82	0.77	0.53	0.92	0.41	0.87	0.73	0.85
	CR				0.84	0.79	0.48	0.73	0.73	0.48	0.86
	FF					1.06	1.58		1.11		0.79
	SI							1.06	0.89	0.29	0.71
	GU								1.77	0.29	0.63
	HZ								0.55		0.67
	PP									0.53	1.11
	TL										0.63
1+ Binge in Past Year	LL	0.85	0.98	0.84		0.23		0.58	0.76	0.77	0.89
	CD		0.14	0.22	0.34	0.61	0.73		0.43	0.60	0.23
	TS			0.72	0.82	0.62	0.79	0.34	0.75	0.77	0.76
	CR				0.65	0.71	0.31	0.42	0.62	0.19	0.47
	FF					0.91	1.67	0.19	1.03	0.10	0.68
	SI						0.19	0.77	0.63	0.18	0.57
	GU								1.74	0.34	0.49
	HZ								0.45		0.40
	PP									0.56	0.96
	TL										0.32
1+ Criteria in Past Year	LL	0.08	0.97	0.28		0.28			0.57	0.26	0.56
	CD		0.21	−0.16	0.41	0.32	0.75	−0.52	0.46	0.20	−0.13
	TS			0.74	0.81	0.56	0.97	0.42	0.86	0.70	0.75
	CR				0.79	0.53	0.54		0.54	0.06	0.31
	FF					1.07	1.61	0.36	1.06		0.70
	SI						0.26	0.67	0.80	0.21	0.48
	GU								1.62	0.44	0.61
	HZ								0.34	−0.27
	PP									0.42	0.83
	TL										0.19

Table 5.

Correlations between the networks (upper triangle) and EFA models (lower triangle) for the NESARC Wave 2 data and NESARC III data.

	Full-2	PYD-2	PYB-2	PYS-2	FD-III	PYD-III	PYB-III	PYS-III
NESARC Wave 2
Full Data		.99	.83	.49	.69*	.69	.55	.30
PY Drink	.97		.87	.58	.69	.69*	.58	.38
PY Binge	.99	.95		.78	.49	.52	.50*	.50
PY Symptomatic	.73	.84	.66		.24	.33	.46	.74*
NESARC III
Full Data	.87*	.93	.83	.88		.99	.87	.51
PY Drink	.81	.90*	.76	.95	.97		.92	.61
PY Binge	.89	.94	.87*	.85	.99	.95		.79
PY Symptomatic	.57	.73	.51	.94*	.86	.93	.51

The values of the edges of the past year binge networks fall between the full data/past year drinker and past year symptomatic networks. The binge drinking networks correlate most strongly to that of the past year drinkers. Being the most restricted, the past year symptomatic network demonstrates the least similarity to the full data. Removing the asymptomatic individuals from the full data results in some of the edges being reduced or removed, such as the relatively thick edge, indicating a strong relationship, between LL (larger/longer) and HZ (hazardous use), which is removed in both Wave 2 and III symptomatic networks. The pattern of removed edges is quite different between the networks. Considering the edges in a strictly binary sense, for NESARC Wave 2 74.5% of the edges are consistently present/not present across the four networks, and 76.3% for III. No edge in NESARC III is removed in all four networks. Three are consistently removed in NESARC Wave 2 (a_FF,TL, a_GU,WD, and a_GU,HZ), but the remainder that are missing in one of the networks are present in another. Some edges become negative (indicated by the dashed lines). In the full data network, all of the existing edges are positively valued in NESARC Wave 2, and NESARC-III has three very small negative edges⁴. Four of the estimated edges in Wave 2 become negative in the symptomatic data: a_CD,LL, a_LL,TL, a_CD,HZ and a_HZ,TL. In NESARC-III, four edges become negative: a_CD,CR a_CD,WD, a_CD,HZ, and a_HZ,TL.

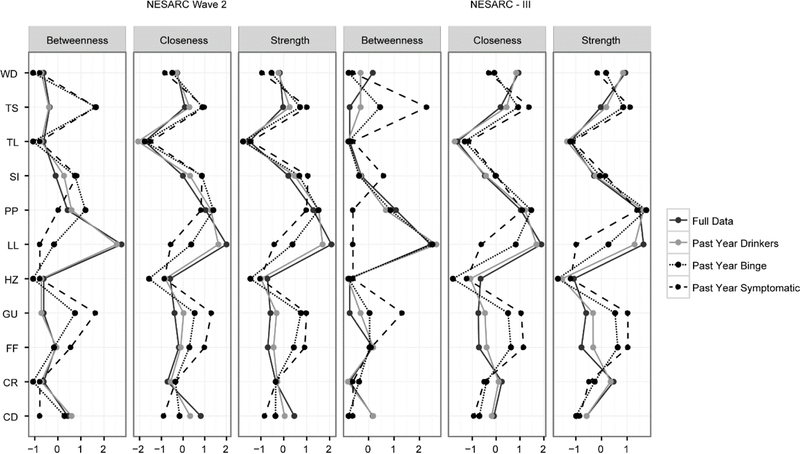
The changes in the network structure between the full and reduced graphs is reflected in the differences for the node centrality statistics. Figure 2 contains the standardized node centralities. These are very different between the full and reduced networks. One of the most notable changes here is the LL (larger/longer) criterion. In both NESARC Wave 2 and NESARC-III the LL criterion is the most central across the various centrality statistics when the network is estimated from the full data or past year drinkers, and falls to being one of the least central in the past year symptomatic networks. The GU (give up pleasurable activities) criterion displays the opposite pattern, with higher centrality measures in the symptomatic networks than in the full. This is quite notable given that LL and GU are the most and least prevalent criteria, respectively. The relative centrality statistics are typically emphasized in papers employing these types of network analyses, where finding the most central criteria or symptom is often the goal of the study. Centrality changes between networks sampled from the same data demonstrates the vastly different interpretations researchers are likely to find. Analogous to these measures in the factor analysis results one might look at the changes in factor scores (Table 4) between the different samples. The loadings for LL, like the centrality statistics, decrease with the increasingly restricted sample. GU also shows a pattern that matches centrality statistics as its loadings increase. The notable difference here is the change in magnitude, the factor loadings appear more stable across sample conditions.

Figure 2.

Standardized network statistics produced using the “centralityPlot” function in qgraph. These reflect the relative importance of each symptom (node) compared to the rest of its network. The 11 criteria are: larger amounts/longer use (LL), inability to cut down (CD), spend a lot of time obtaining/drinking/recovering from its effects (TS), craving (CR), failure to fulfill major roles and obligations (FF), social/interpersonal problems (SI), give up activities (GU), hazardous use (HZ), use despite physical/psychological problems (PP), tolerance (TL), and withdrawal (WD).

Table 4.

Factor loadings for unidimensional factor models for NESARC Wave 2 and NESARC-III

	TL	CD	LL	TS	GU	PP	WD	FF	HZ	SI	CR
NESARC Wave 2
Full Data	0.491	0.550	0.578	0.677	0.551	0.703	0.577	0.575	0.509	0.666	0.634
PY Drink	0.482	0.548	0.577	0.663	0.522	0.695	0.573	0.549	0.506	0.648	0.621
PY Binge	0.477	0.518	0.486	0.680	0.561	0.700	0.548	0.583	0.425	0.662	0.643
PY Symptomatic	0.261	0.305	0.321	0.640	0.601	0.631	0.423	0.623	0.276	0.675	0.579
NESARC III
Full Data	0.693	0.640	0.684	0.754	0.571	0.753	0.668	0.590	0.607	0.684	0.699
PY Drink	0.678	0.630	0.673	0.736	0.526	0.730	0.651	0.548	0.589	0.654	0.668
PY Binge	0.609	0.559	0.600	0.709	0.547	0.699	0.603	0.557	0.525	0.616	0.640
PY Symptomatic	0.498	0.424	0.444	0.690	0.611	0.699	0.515	0.622	0.317	0.619	0.639

Note: The 11 criteria are larger amounts/longer use (LL), inability to cut down (CD), spend a lot of time obtaining/drinking/recovering from its effects (TS), craving (CR), failure to fulfill major roles and obligations (FF), social/interpersonal problems (SI), give up activities (GU), hazardous use (HZ), use despite physical/psychological problems (PP), tolerance (TL), and withdrawal (WD).

Finally, the replicability across data can be assessed by examining the correlation between the edge weights of the same filtering at NESARC Wave 2 and NESARC-III. For instance, the correlation between the network derived from the full data at both waves is .69; with the highest correlation (.74) between the two waves being for the networks that reflect the structure among symptomatic individuals only. At first, this may seem surprising; however, Steinley et al. (2017) noted that a large number of rows with all zeros can place strong constraints on the possible network structures and edge weights. As such, potential variability in the observed edge weights is shrunk, resulting in lower correlations between the ordering of the magnitude of the edge weights.

Comparisons to Factor Models

Given the natural correspondence between latent variable models and network models (see Marsman et al., 2018), one might expect the same issues that affect network models to affect latent variable models. While it is true that for every network model, there is a corresponding latent variable model, it does not follow that the best fitting network model corresponds to the best fitting latent variable model. Given the strong support for single-factor models for AUD (see Hasin et al., 2013), we fit unidimensional factor models to each of the filtered datasets at both waves.

Table 4 contains the factor loadings for the unidimensional factor models when fit to each of the filtered datasets. The correlations between the factor scores are found in the lower triangle of Table 5. As with the correlations between the edge weights, bold values indicate the consistency within Waves and the values with asterisks indicate the replicability across waves. The average correlation between the full data and the most restricted data within wave based on symptomatic individuals only is (.73 + .86)/2 = .795 for the factor model; whereas, it is appreciably lower, (.51 + .49)/2 = .50, for the network model. Likewise, the replicability for the symptomatic data across waves is .94 for the factor model and .74 for the network model.

Contingency Tables and the Influence of Asymptomatic Individuals

Untangling the problem from the complexity of the eLasso algorithm, the effect of having many asymptomatic cases in binary data can be demonstrated with pairwise measures such as correlations or odds ratios. For binary variables, a contingency table can easily be calculated, as presented in Table 6. Consider two binary variables $x_j^{\left(i\right)}$ and $x_k^{\left(i\right)}$ measured over $i=1,\dots ,n$ observations. Each observation can be in one of four states; two that represent agreement, $x_j^{\left(i\right)}=x_k^{\left(i\right)}=1$ and $x_j^{\left(i\right)}=x_k^{\left(i\right)}=0$, and two disagreement, $x_j^{\left(i\right)}=1$ and $x_k^{\left(i\right)}=0$ or $x_j^{\left(i\right)}=0$ and $x_k^{\left(i\right)}=1$. Counting occurrences of each of these states over all n observations gives us the 2×2 contingency table, and the basis for a number of similarity measures, including the correlation coefficient (phi coefficient, $\varphi$, in the binary case) and odds ratio (OR). These measures compare the number of agreements to disagreements, but neither discriminate between the states where both are present or both are absent. In applications to low prevalence rate data, raw agreement is inflated by the many observations where both are absent. We can see this occur in NESARC Wave 2 for the relationship between HZ and CD; recall that their edge changed signs between networks. In the full sample, 879 individuals have both, 1,928 have only HZ, 1,473 have only CD, and 30,349 have neither. These values give $\varphi =.29$ and OR=9.39, a positive association. When the individuals with no AUD symptoms are removed, the 30,349 is reduced to 2,132 (while the other three counts remain the same). This changes the estimated similarity measures to $\varphi =-.10$ and OR=.66, indicating the variables are negatively associated. This issue is elaborated on in the Supplementary Materials.

Table 6.

Contingency table to measure the agreement between two variables. Each of the n observations will fall into one of the four categories, as a person either qualifies for both criteria (a), only criteria j (b), only criteria k (c) or neither criteria (d).

	xk = 1	xk = 0
xj = 1	a	b
xj = 0	c	d

It is well known that the marginal distributions of the variable measures (prevalence rates) influence pairwise similarity measures (Warrens, 2008). In ecological studies, different types of association measures are often used that exclude the mutual absences of locations and organisms for rare species, as traditional measures would indicate that they are highly associated even if they do not occur together often (Janson & Vegelius, 1981). Traditional methods to estimate networks, however, are typically based on correlations or odds ratios (including the IsingFit models, based on logistic regression output) that disregard the common occurrence of extremely large counts of mutual absences.

Discussion

Concurrent with increasing numbers of studies employing network analyses of psychiatric symptomatology, there has been increasing attention to factors that could systematically affect reproducibility. The degree of asymptomatic individuals is one such factor that has obvious a priori importance since some studies are based on epidemiological surveys where many individuals are likely to be asymptomatic and others are based on clinical samples where, by definition, most if not all individuals will be symptomatic. Our analyses demonstrate that choices as to how to define the sample of interest change rates of observations that exhibit zero criteria present, which in basic correlations or the more sophisticated network estimation algorithm can produce (sometimes dramatically) different results. In this study, the variables considered are symptoms of AUD, whose prevalence rate is estimated to be only 13.9% of the population (Grant et al., 2015), and the individual criteria have sample prevalence rates of 1% to 15%. With these rates, the majority of the observations for any pair of variables are $x_j^{\left(i\right)}=x_k^{\left(i\right)}=0$ cases. The $\varphi$ coefficient (Pearson correlation) and the odds ratio analyses demonstrate in a basic pairwise example, how the addition of many $x_j^{\left(i\right)}=x_k^{\left(i\right)}=0$ observations can change the sign of a relationship from negative to positive. While pairwise partial correlations, as the Ising models approximate, might buffer some of this effect, we demonstrated here that conditioning the samples in different ways changes these estimated networks.

The changes in the interpretation of these estimated network edges go beyond the pairwise differences, however, as the node centrality statistics show very different patterns for the full and reduced networks. Centrality measures are commonly utilized in network research for the information they convey. In many network studies of symptom variables, the question of interest is which ones are more central to the disorder. The changes in centrality results and conclusions when the asymptomatic observations are removed from the data reinforce the importance of considering this issue in network analyses⁵.

In comparing centrality statistics across progressively more alcohol-involved subsamples we observed several striking findings. Specifically, the LL criterion is the most central across the various centrality statistics when the network is estimated from the full data or past year drinkers, and falls to being one of the least central in the past-year symptomatic networks. In contrast, the GU (give up pleasurable activities) criterion displays the opposite pattern, with higher centrality measures in the symptomatic networks than in the full data. It is worth noting that the assessment of LL in general population surveys has been found to be problematic in that it is typically reported at low levels of use, is more associated with social motives for drinking than with compulsive drinking (Karriker-Jaffe, Widbrodt, & Greenfield, 2015), and is often found to be one of the most prevalent AUD symptoms as was true in the NESARC samples. Additionally, it is one of the least severe criteria when judged from the perspective of its relatively low correlations with various external criteria including consumption, health problems, and psychiatric comorbidity (Lane & Sher, 2015). In contrast, GU is the most severe criterion with respect to the same external criteria (Lane & Sher, 2015). Moreover, GU is conceptually associated with the notion of “salience” of drinking behavior introduced by Edwards and Gross (1976) in their seminal description of the alcohol dependence syndrome and subsequently incorporated into the International Classification of Diseases- 10 (World Health Organization, 1992) dependence criteria set (“the progressive neglect of alternative pleasures or interest”) as well as the DSM-III-R (American Psychiatric Association, 1987) substance dependence criteria set. Conceptually, it can be viewed as an operationalization of the notion of addictive drugs (and behaviors) “hijacking reward systems,” a commonly accepted notion in neurobiological models of addiction (Gardner, 2015). From this perspective, the centrality statistics from the more restricted models are more consistent with what we know about addiction and are, in a sense, seemingly more “valid.” Therefore, the change in centrality associated with increasingly affected samples might prove to be a useful tool in identifying criteria that warrant further scrutiny.

While we find the systematic changes in centrality associated with progressively higher risk subsamples to be of interest, the identification of symptoms with low centrality across samples (and subsamples) are of interest in their own right. In the current analysis, hazardous use (HZ) and tolerance (TL) showed consistently low centrality. Based on other considerations beyond centrality, both empirical (e.g., psychometric) and conceptual (e.g., failure to distinguish substance-related pathology from simple heedlessness, context dependence), we have argued that HZ is a problematic criterion and should not be included in substance use disorder criteria sets (Martin, Sher, & Chung, 2011). The issue surrounding the diagnostic importance of tolerance is more complex. We recently reported (Verges et al., 2018) that there was virtually no association between self-reported alcohol sensitivity and other symptoms of alcohol dependence after controlling for the heaviness of consumption patterns among daily drinkers. We speculate that tolerance is an intermediate phenotype that puts one at risk for addiction by virtue of the fact that it facilitates high-level exposures but is not part of addiction itself. However, even if one were to assume that TL is a key symptom of addiction on conceptual grounds, the assessment of tolerance is extremely difficult and self-reported tolerance does not show expected relations with drinking history in longitudinal studies (O’Neill & Sher, 2000), possibly because of vagaries of when presumed changes in drug sensitivity occurred over the course of one’s drinking career. The foregoing discussion highlights the potential utility of looking at stability and change in centrality measures across varying levels of affectedness of samples as a type of “diagnostic” that can point to problematic candidate symptoms of disorder.

Thus, the proportion of unaffected individuals comprising the sample and used to estimate the network influences the values of the network’s edges, potentially changing the sign of some of the relationships. Here, the case was considered where many asymptomatic observations/individuals were included, inflating the relationships. On the other hand, the same would be true if the quantity d = 0, where all the observations with neither criterion are cut. In this case, regardless of how many $x_i^{\left(j\right)}=x_i^{\left(k\right)}=1$ observations there are, the correlation or odds ratio can never be positive. In the present study, this extreme case never occurs as in the symptomatic data because only those with a sum score of zero are removed. This suggests that the absence of both criteria in an observation is not meaningless, but it must be interpreted relative to the sample.

With regards to interpretation, using a sample that is representative of the entire population is likely to produce a graph with more edges indicating pairs of symptoms are positively related. When all of the asymptomatic individuals are included there is a certain truth to the high correlations: that among all people the behaviors associated with AUD are associated with each other because they co-occur in people with AUD, and do not co-occur in those without any symptoms of AUD (the majority). Therefore, when the question of interest is how the symptoms functionally relate to each other relative to the other symptoms, the full sample may not be the best choice for this estimation. This points to the problem of generalizing from population samples to clinical samples (e.g., Lane, Steinley, & Sher, 2016). Thus, it is recommended that the researcher estimating these relationships should pay special attention to the base rates of modeled symptoms in their sample before interpreting the measures of relationships between binary variables. Regardless of interpretation, generalization across population-based and clinic-based samples is likely to be low for the reasons described above.

So far, we have been agnostic on the question of whether or not asymptomatic individuals should or should not be included in a given analysis. In practice, researchers frequently condition their data in ways that affect the proportion of unaffected individuals. For example, in many areas of alcoholism research, individuals who are lifetime abstainers or past year abstainers are excluded in etiological and nosological research since, by definition, they are not at risk for most “past year” AUD symptoms. That is, the issue is not just one of clinical versus nonclinical samples but whether one is at risk for disorder (e.g., past-year drinker) and is likely graded as a function of degree-of-risk for a, say, past year diagnosis (e.g., past year drinker vs. past-year heavy drinker). The symptomatic networks were created from a sample conditioned on the variables being modeled (by requiring at least one criterion to be present) which is not recommended practice. While a true clinical sample does not overtly condition on these criteria it may exhibit a sort of “stealth” conditioning as it is unlikely that a person in treatment would have no symptoms. Other types of stealth conditioning could occur when the ascertainment strategy is confounded with a specific symptom/criterion (e.g., the prevalence of hazardous use in a clinical sample of DUI offenders, withdrawal in a clinical sample drawn from detoxification centers).

In representative samples, we might expect the asymptomatic individuals to represent the “healthy” population. While we have demonstrated mathematically the influence of their inclusion in inter-criterion relationships, there are other potential confounding issues. For example, as noted above, in considering the structure of depression criteria, Fried et. al. (2016) demonstrated that those individuals whose depression improves over time have a different dimensionality in their data than those whose depression continues. These findings from factor analytical research shed light on the potential problem of estimating these networks over the entire population.

We do, however, want to highlight several issues that are likely to emerge as more researchers apply network analyses to large data. First, often structured or semi-structured interviews use skip-outs in order to increase the efficiency of the interview and save time. For example, because either (a) depressed mood or (b) loss of interest or pleasure in activities over a period of two weeks is required for current major depressive disorder, some interviews will instruct the interviewer to skip to the next section (and not ask about the remaining seven criteria) if neither (a) nor (b) are present. The remaining seven criteria are then considered absent, and zeros populate the scores for these. In addition to other problems associated with skip outs and network data (Hoffman et al., 2018b), this practice is likely to increase the number of cases with zero criteria, and, thus, make the data more vulnerable to the issues we describe here (i.e., inflate edges in networks). Second, most network analyses of psychopathology symptoms, by using all available cases, seem to assume that network structure is consistent across subgroups (e.g., gender, age, comorbid conditions). However, our analyses suggest that this is not likely to be the case, especially when certain subgroups are more likely to have asymptomatic cases. For example, because antisocial personality disorder is more prevalent among men, there will be more asymptomatic cases among women (affecting network structure if all cases are included), and the antisocial symptom network for men compared to women could be different, perhaps dramatically so, simply because of base rate differences in symptoms/criteria. This same issue applies when examining network structure of different age groups (young adults compared to older adults) or of different comorbidity subgroups (e.g., major depressive disorder-generalized anxiety disorder compared to major depressive disorder-alcohol use disorder comorbidity groups).

Recommendations & Future Directions

What is “best practice” for network analysis of psychiatric symptoms is unclear at this time. We do, however, offer the following recommendations to those who plan to apply these network analyses to psychiatric symptom data. It is very important for the researcher to define and refine the over-arching research question. Is a general population sample, likely replete with asymptomatic cases, appropriate for the question at hand? Is it of theoretical interest to assess symptom network structure in those individuals who are at no- or at low-risk of developing or having the disorder? Using all the observations in large epidemiological data sets limits the generalization of results; one cannot generalize from population samples to clinical samples. Similarly, results from network analyses conducted on clinical samples cannot be readily generalized to population samples. Additionally, subgroups of individuals at varying levels of risk for disorder may have significantly different prevalence rates for individual symptoms which will in turn influence the estimates of associations among symptoms. The analysis might be improved by conducting separate network estimations for the different groups. Finally, we urge caution against an uncritical adoption of a dimensional perspective on psychopathology that may lead the researcher to include all observations, even those who do not manifest any of the symptoms of interest.

Regardless of what is considered best practices for revealing the most valid network structures, our findings suggest there is little reason to expect generalization or replicability across general population, high-risk, and clinical samples using techniques commonly employed. Consequently, these network structures need to be viewed as highly sample-dependent⁶. Indeed, variability in the relative prevalence of diagnostic criteria across diagnostic instruments, as well as demographic strata (Lane, Steinley, & Sher, 2016), suggest that even if two similarly ascertained samples are drawn, differing relative thresholds of different criteria across different diagnostic instruments can also materially affect findings. This has been demonstrated specifically for network models, showing marked differences in networks built from the same sample but using different thresholds to dichotomize the criteria (Hoffman et al., 2018a).

With increasing focus on the problem of reproducibility in the biomedical and behavioral sciences, researchers are looking at different approaches to addressing this problem to improve the speed of scientific progress. The NIH, for example, is considering more options for data transparency, such as providing the data online (Collins & Tabak, 2014). A similar concept is that of comprehensive reporting, where studies release more detail about the particular methodology used, to reduce the rate of false positives due to cherry picking methodology (Carp, 2012). The general idea is that the more that is known about the entire scientific process behind a specific study, the better its true conclusions can be understood and replicated. We recommend that transparent reporting of data include the base rates of individual symptoms/criteria as well as the overall distribution of positive criteria/symptom endorsements, which is easily reported as demonstrated in Table 2.

The types of findings reported here should goad the development of refined methodology for producing robust estimates of symptom networks and clearer discussion of what various findings indicate. This study suggests a further path for methodological developments in directions of similarity measures that are less vulnerable to the influence of the selected sample, such as the ecological association between measures. As noted, in the ecological literature, looking at the associations between species, researchers specifically select association measures that do not include the mutual absences. While still based on the values of a contingency table like that of Table 6, they do not include the quantity d in their calculation. In this study, if the network edges were formed using one of these measures, the resulting networks from the full sample, past year drinkers, and symptomatic sample would be equal. This is because the method of reducing the sample only removes asymptomatic individuals, who only contribute to the count of mutual absences that is ignored by these statistics. Substantively, this reflects the idea that individuals who have no psychopathological symptoms do not provide useful information about the relationships between the symptoms.

Conclusion

Network analysis methods have the potential to be useful tools for examining the relationships among symptoms of psychopathology, opening up a variety of new measures to consider the interactions between and importance of individual symptoms. However, the methods used to estimate the network structure from binary data are underdeveloped with many complications that must be addressed. As demonstrated here, the results of the IsingFit model must be viewed as highly sample dependent and great caution should be exercised in generalizing between population-based and clinical samples.

We note that the analysis herein has compared network models to factor models has focused on binary indicators. It is very well possible that if continuous indicators were used, there would the robustness of factor model would be further increased; however, it is possible that the robustness of the network models would be increased as well given that they would be estimated via Gaussian Graphical Models instead of Ising Models. Furthermore, with continuous indicators, it is possible that the differences between general populations and clinical samples will be mitigated due to the natural decrease in individuals with “all zeros” as a byproduct of an increased number of response options.

The common factor model seems to be more resilient to filtering data based on inclusion criteria when compared to the network model. This is true if we think about the robustness of the structure within a dataset or the consistency/replicability of structures across datasets. An avenue for future research is exploring the degree to which this holds across more complex network structures and various factor models, as well as exploring the mechanism guiding the improved performance of the factor model. Likely, this is in part due to the fact that the factor model is estimating many fewer parameters (for instance, the common factor model for 11 variables, is only estimating 22 parameters [e.g., 11 factor loadings and 11 uniquenesses]) than the IsingFit model (estimating 55 edge weights⁷; P(P-1)/2 = 11(10)/2 = 55). Additionally, the goal of the factor model is much less ambitious. The factor model is aggregating information across several variables to maximize reliability; on the other hand, the IsingFit model is focusing on estimating each of the pairwise relationships between variables. In an exploratory data analysis context (albeit focused on mixture modeling, but the same general guidelines apply), Steinley and Brusco (2011) argued that it is easy to overfit the data, providing the illusion of good model fit while being unable to replicate the precise findings.