Towards high resolution monitoring of water flow velocity using flat flexible thin mm-sized resistance-typed sensor film (MRSF)

Abstract

Novel flexible thin mm-sized resistance-typed sensor film (MRSF) fabricated using ink-jet printing technology (IPT) was developed in this study to monitor water flow rate in pipelines in real time in situ mode. The mechanism of MRSF is that the mm-sized interdigitated electrodes made by printing silver nanoparticles on an elastic polyimide film bend under different flow rates, leading to variation of the resistance of the sensor at different degrees of curvature. Continuous flow tests showed that MRSF possessed a high accuracy (0.2 m/s) and excellent sensitivity (0.1447/ms⁻¹). A model of sensor resistance and flow velocity was established to unfold the correlation between the fundamentals of fluid mechanics and the mechanic flexibility of sensor materials. An analytical model yielded a high coefficient of determination (R² > 0.93) for the relationship between the resistance increment of the MRSF and the square of the flow velocity at the velocity range of 0.25–2 m/s. Furthermore, a temperature-correction model was developed to quantify the effect of water temperature on the sensor resistance readings. MRSF exhibited a low temperature coefficient of resistance (TCR, 0.001) at the water temperature range of 20–60 °C. Computational fluid dynamics (CFD) simulations using the finite element method were conducted and confirmed both the underlying load assumptions and the deformation characteristics of the sensor film under various flow and material conditions. High-resolution monitoring of water flow rate using MRSF technology was expected to save at least 50% energy consumption for a given unit, especially under flow fluctuation. MRSF possesses a great potential to perform real-time in situ monitoring at high accuracy with ultralow cost, thus enabling the feedback control at high spatiotemporal resolution to reduce the overall energy consumption in water and wastewater systems.

Graphical abstract

Highlights

• •Resistance-type flexible MRSF sensors were developed to monitor water flow velocity.
• •Higher accuracy and excellent sensitivity comparable to commercial flow sensors.
• •Analytical and computational models were developed to establish the correlation.
• •The impact of temperature change on the MRSF resistance variation was determined.
• •High resolution monitoring of water flow using MRSF is expected to save at least 50% energy consumption.

1. Introduction

Water flow velocity measurement is critical for system monitoring, feedback control, process analysis, and energy consumption, since it directly affects the operation and loading capacity of each treatment unit in water and wastewater treatment plants. Real-time in situ accurate measurement can provide first-hand information for the quantity of the inlet and outlet throughout each unit and the treatment plant as a whole (Evans et al., 2004). For instance, wastewater flow in a combined sewer system under shocks (e.g. heavy rainfall or snowmelt) can be 1.2–1.4 times or even twice as that in normal days (Müller and Krauth, 1998), leading to substantial fluctuation to wastewater treatment plant (WWTPs). Almost all the water-quality parameters, such as chemical oxygen demand (COD), biological oxygen demand (BOD), ammonium (NH₄—N) and phosphorous could be diluted to 33%–45% of those in the normal condition (Müller and Krauth, 1998; Mines et al., 2007; Kim et al., 2017), leading to the lack of nutrient and organic matters to microorganisms in activated sludge or biofilms (Schalk-Otte et al., 2000; Mohan et al., 2007), unnecessary high aeration intensity and ultimately deteriorating the treatment efficiency. Thus, it is critical to monitor the transient variations of water flow of diverse treatment units at a high spectral-temporal resolution and enhance the resilience and robustness of WWTPs at an energy-saving mode.

Traditional water flow sensors widely used include orifices flowmeters and turbine flowmeters (Morrison et al., 2001; Baker, 2004; Singh et al., 2004; Manshoor et al., 2011). Specifically, orifice flowmeter measures the flow velocity by the liquid differential pressure through the flowmeter, and normally has low accuracy (error: 2–4% of real flow rate) due to the low contraction in the downstream (McCabe et al., 1985; Flow, 1995; Seader et al., 1997; Baker, 2005; DiGiacomo, 2011), and imposes high installation requirements (e.g. needs the straight pipeline length to be at least 6–20 times the pipeline diameter at both upstream and downstream) (McCabe et al., 1985; Flow, 1995; Seader et al., 1997; Baker, 2005; DiGiacomo, 2011). Similarly, the turbine flowmeter has high installation requirements to remain accurate (approximately 10 upstream pipe diameters) (Yeh et al., 1987; Svedin et al., 2003). The moving parts of turbine flowmeter tend to get sticky overtime, making it unsuitable for measuring wastewater flow.

Last decade has seen the development of novel electromagnetic and ultrasonic flow sensors (e.g. Dynasonics TFX Ultra Ultrasonic Flow and Meter GF Signet 2551 Magmeter) (Wang et al., 2007a) capable of measuring the flow in a wide range of pipelines (diameter: 6.25 mm—3m) for different types of fluids (e.g. wastewater, activated sludge, slurry, crude oil) with almost zero pressure drop (Paulsen et al., 2001; Wang et al., 2007a; Meter, 2018). However, these new types of sensors are costly (>$2000 each piece) (Monitors, 2018), leading to prohibitively high costs for mass deployment across treatment plants and long-distance pipelines. In addition, the accuracy and sensitivity of electromagnetic and ultrasound flowmeters are directly impacted by liquid viscosity (e.g. concentrated contaminant solution, particles) and temperature, leading to measurement errors and frequent re-calibration (Meter, 2018). Furthermore, these types of flowmeters can only be used in weak magnetic field, and have high requirement of maintenance and repair (Meter, 2018). Thereby, there is an urgent need to develop low-cost, easy-fabrication, easy-installation, and low-maintenance flowrate sensors.

Flat sensors printed on flexible thin polyimide Kapton film using inkjet printing technology (IPT) could be a solution for accurate flow velocity monitoring in pipelines. IPT has been used to fabricate diverse types of water quality electrochemical sensors (e.g. pH, temperature, conductivity, dissolved oxygen and chloride) with the distinct advantages of easy fabrication, high sensitivity and selectivity, excellent durability, high tolerance to wastewater impurities and low fabrication cost (<$0.2 per sensor) over other fabrication methods (e.g. photolithography) (Yan et al., 2011, 2013; Xu et al., 2016, 2017). For the flow sensor, mm-sized interdigitated silver nanoparticle ink lines can be printed onto an elastic polyimide film, and then sliced into a pipeline vertically and perpendicularly facing to water flow. The elastic film is expected to bend under different flow velocities, and the resistance of the silver nanoparticles ink lines will consequently change with the bending deflection (and associated curvature) of the film, through which the flow velocity can be monitored in a real time in situ mode.

The breakthrough of this study lies in the development of flat thin mm-sized resistance-type sensor film (MRSF) capable of monitoring flow velocities in situ at low fabrication cost and with minimal installation and maintenance needs, and the development of a series of analytical and Computational Fluid Dynamics (CFD) models using the finite element method to elucidate the impacts of flow velocity and temperature on the MRSF accuracy. There were five tasks in this study. First, an analytical mathematical model was established to determine the correlation of MRSF material mechanic flexibility, bending curvature and flow velocity. Second, MRSFs with two film thicknesses were examined at different flow velocities in a lab-scale continuous flow system, and site-by-side compared with a commercial paddlewheel flow sensor. Using the Arbitrary Lagrangian Eulerian (ALE) technique (Hughes et al., 1981; Duarte et al., 2004) the flow in the vicinity of the thin-film sensor was simulated using CFD in the COMSOL modeling framework and the effected deformation of the sensor was analyzed. Third, the impact of temperature on the resistance readings of MRSFs was examined in water solution at various temperatures. A model considering the absolute error of sensor, the actual flow velocity, the temperature change, temperature coefficient of resistance (TCR), and flexural rigidity was established. Fourth, the long-term stability of MRSFs was examined by submerging in wastewater for over 4 weeks, with the resistance of MRSFs being measured and the surface property being observed before and after the immersion. Finally, the energy saving in terms of aeration and chemical dosage through high resolution monitoring of water velocity using MRSFs was simulated in an anoxic/aerobic WWTP under flow fluctuation.

2. Materials and methods

2.1. Mechanisms of mm-sized resistance-type sensor film (MRSF)

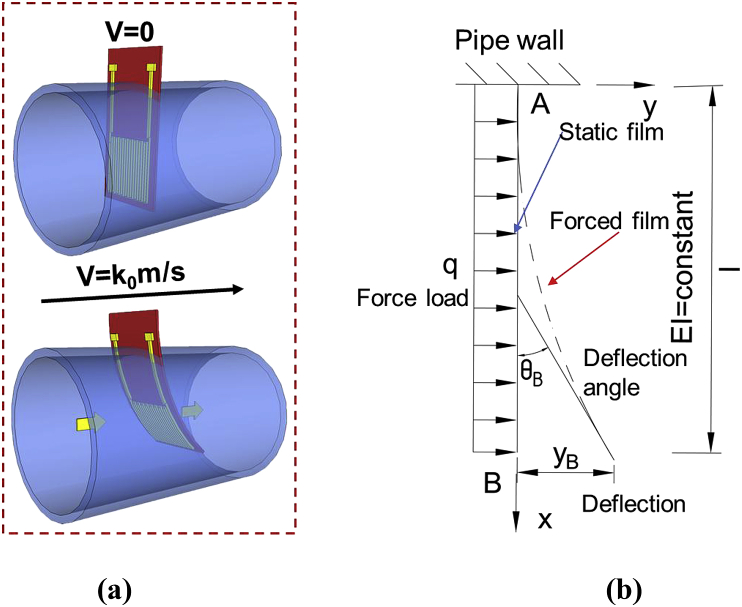
The fundamental mechanism of mm-sized resistance-type sensor film (MRSF) is the variation of the sensor resistance with the curvature degree of the interdigitated silver nanoparticle ink printed on the flexible thin polyimide Kapton film at different water flow velocities. Specifically, the Kapton film is held fixed on one end and is free to bend on the free end in analogous fashion to a cantilever beam. The Kapton film remains completely vertical when the liquid in the pipeline is static, and the resistance of MRSF at this position is recorded as the baseline. Then the Kapton film is bent when the liquid flows through the pipeline and the curvature increases with the flow velocity (Fig. 1a). There are two main assumptions to simplify the force analysis and calculation. First, the flow near the pipe wall moves very slowly due to the no-slip boundary condition while the flow near the center of the pipe is the fastest (Munson et al., 2014). However, due to the small diameter of the pipe (plastic pipe, internal diameter (ID) < 10 cm), the flow velocity of the liquid is assumed to be almost uniform across the pipeline section in this study to simplify the calculations (Munson et al., 2014). This is a reasonable assumption, particularly for turbulent flows and the associated flow velocity profile. It was verified that this is indeed the case with high resolution CFD simulations, which will be discussed in the Results Section. Second, due to the slim thickness (<150  μm) of the sensor Kapton film, the whole film would be simplified as a one-unit area (e.g. from Point A to Point B) in the force analysis (Fig. 1b), where Point A is fixed on the pipeline wall and Point B is free and deformed under the influence of the flow. The deflection and the deflection angle of Point B are y_B and ${\mathbf{\theta }}_{\mathbf{B}}$, respectively. Q is the load caused by the liquid flow, and the quantity EI (Boresi et al., 1993) is referred to as the flexural rigidity (Fig. 1b).

Fig. 1.

Schematic diagram of the MRFS bending from the static status to water flow velocity (${\mathit{k}}_0$) in a pipeline (a) and free-body diagram of the MRSF cross section (b).

2.2. Analytical model for the dependence of MRSF resistance on curvature at different flow velocities

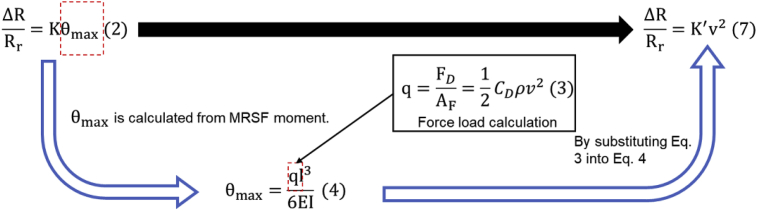
A series of models were integrated to establish the correlation between the mechanical flexibility of MRSF film, bending curvature and water flow velocity (Fig. 2). To start with, the MRSF was essentially a resistance temperature detector (RTD) (Rosal et al., 2010; Blasdel et al., 2015), with the resistance being linearly related to the length of the sensor (Eq. (1)) (Xu et al., 2016, 2017)

$$\text{R}=\frac{{\text{ρ}}_{\text{s}}\text{L}}{{\text{A}}_{\text{R}}}$$ (1)

Where ρ_s is resistivity, L is the length, and $A_R$is the cross-sectional area. The unique configuration of the flat flexible thin MRSF (Fig. 1a) made the resistance increase with the length of the resistor. Therefore, the relative resistance increment of MRSF was proportionally related to the maximum deflection angle (or curvature) of the MRSF caused by the liquid flow (Pang et al., 2012) as described in Eq. (2).

$$\frac{\Delta \text{R}}{{\text{R}}_{\text{r}}}={\text{Kθ}}_{\text{max}}$$ (2)

Where K is the deflection coefficient, R_r is the static MRSF reference resistance at 20 $°C$, $\Delta \text{R}$ is the difference between the resistance of the bending MRSF and the baseline resistance of the static MRSF at 20 $°C$, $\frac{\Delta \text{R}}{{\text{R}}_{\text{r}}}$ is the relative resistance increment of the MRSF, ${\text{θ}}_{\text{max}}$ is the maximum deflection angle of all the points on the MRSF, which typically occurs at the free end for a cantilever beam.

Fig. 2.

The derivation process of the models considering the mechanic flexibility, sensor resistance and the water flow velocity.

The drag force experienced by an object immersed in a moving fluid is described in Eq. (3) (Munson et al., 2014).

$${\mathbf{F}}_{\mathbf{D}}=\frac{1}{2}{\mathit{A}}_{\mathit{F}}{\mathit{C}}_{\mathit{D}}\mathit{\rho }{\mathit{v}}^2$$ (3)

Where ${\mathbf{F}}_{\mathbf{D}}$ is the drag force, which is by definition the force component in the direction of the flow velocity, $\mathbf{\rho }$ is the mass density of the fluid, v is the flow velocity, ${\mathbf{A}}_{\mathbf{F}}$ is the film area perpendicular to the flow, and ${\mathbf{C}}_{\mathbf{D}}$ is the drag coefficient, which, in general, depends on the Reynolds number.

The maximum deflection angle $\text{θ}$_max occurred on the far end of the MRSF (Point B in Fig. 1b) (Boresi et al., 1993; Ugural and Fenster, 2011).

$${\text{θ}}_{\text{max}}=\frac{{\text{qL}}^3}{6\text{EI}}$$ (4)

Where q is the continuous load applied on the MRSF, equals to the force on the unit area ($F_D/A_F$). By substituting Eq. (3) into Eq. (4), the maximum deflection angle $\text{θ}$_max is shown in Eq. (5).

$${\text{θ}}_{\text{max}}=\frac{{\text{C}}_{\text{D}}{\text{ρL}}^3}{12\text{EI}}{\text{v}}^2$$ (5)

Substituting Eq. (5) into Eq. (2), the relationship between the relative change of the sensor resistance and the flow velocity could be described in Eq. (6).

$$\frac{\Delta \text{R}}{{\text{R}}_{\text{r}}}=\text{K}\frac{{\text{C}}_{\text{D}}{\text{ρL}}^3}{12\text{EI}}{\text{v}}^2$$ (6)

The liquid used for flow velocity tests in this study was tap water at 20 $°C$, and its density was stable around 1000 kg/m³ (Tanaka et al., 2001). The flexural rigidity (EI) and the film length (L) were kept the same after fabrication. Therefore, the relationship between the MRSF resistance and the flow velocity is simplified in Eq. (7).

$$\frac{\Delta \text{R}}{{\text{R}}_{\text{r}}}={\text{K}}^{\text{'}}{\text{v}}^2$$ (7)

Where K’ is the adjusted deflection coefficient. Therefore, a linear model between the relative resistance increment and the square of the flow velocity was established in this study. The whole calculation process was simplified by substituting the force load into the MRSF moment equation (Fig. 2).

2.3. Fabrication of MRSF

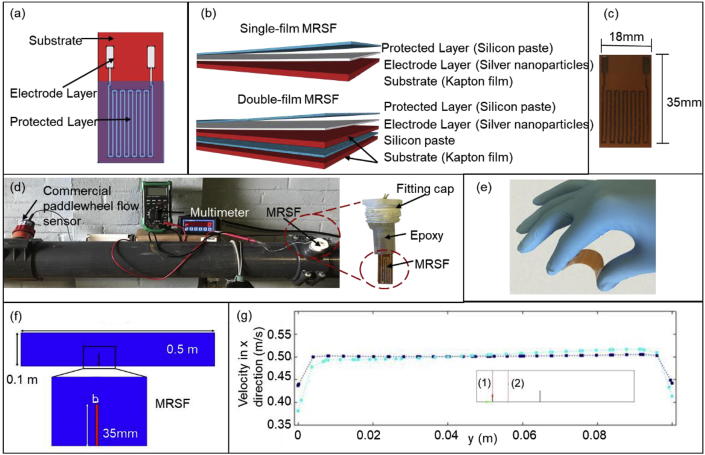
A clean polyimide Kapton film (thickness: 127 μm, American Durafilm) was washed with deionized water (DI water) and ethanol (Sigma-Aldrich Co.) to remove any residual organic/inorganic trace on the film surface. The silver ink was prepared by mixing silver (Ag) nanoparticles (SunTronic^® Silver, Sigma-Aldrich Co.) and ethylene glycol (Fisher Scientific Co.) at the ratio of 3:1. The silver ink on the Kapton film was printed using a Dimatix materials printer (ModelDMP-2800, FUJIFILM Dimatix, Inc.), in which liquid crystal polymer printer cartridges (Model DMCLCP-11610, FUJIFILM Dimatix, Inc.) were used to house the silver ink. The printing pattern was designed using the AutoCAD program and transferred by the LinkCAD program. The sensor was printed as the resistance temperature detector (RTD) (Fig. 3a), which was designed as a 15 μm space between the ink drops by using a customized printing waveform, with each pattern being printed using two jets for facile detection of any potential clog. The printing process was performed as described in previous studies (Xu et al., 2016, 2017). After the printing, the whole sensor on the film was coated with the silicon paste (DOW corning 732 multipurpose sealant) using a small brush to protect the electrodes directly contacting the liquid solution, and then air-dried for 20 min.

Fig. 3.

Diagram of the MRSF configuration (a), sectional view of single-film and double-film MRSFs (b), the image of an MRSF (c), and the lab-scale continuous flow setup (d), the demonstration of a flat flexible thin MRSF (e), schematic of flow domain and film sensor (f), and flow velocity across the pipe upstream and near the film sensor (g).

For the single-film MRSF, there were three layers including the substrate layer, electrode layer, and protective layer (Fig. 3b). The size of the single-film MRSF was 35 mm × 18 mm × 0.2 mm (length by width by thickness, E = 2.5 Gpa) (Fig. 3c). The connect pad was printed on the top of the MRSF to connect with a multimeter (Mastech MS828 Digital AC/DC Auto Range Digital Multimeter) through copper wires. In addition, two-film MRSF (size:35 mm × 18 mm × 0.3 mm (length by width by thickness), E = 8.5 GPa) was fabricated by sticking two Kapton FPC ((Flexible printed circuits) films together using silicon glue (Clear window and door sealant, GE) (Fig. 3b). The single-film MRSF and two-film MRSF were compared to determine the impact of the bending stiffness on the correlation between the sensor resistance and the flow velocity, since the increase in the MRSF resistance was expected to be correlated with the flexural rigidity of the film material. The resistance of MRSFs was measured as around 535 Ω after fabrication.

2.4. Tests in a lab-scale continuous flow pipeline system and comparison with a commercial flow sensor

The water flow velocity in sewage piping and pumping systems should exceed 0.6 m/s (EPA (Office of Water), 2002; Nayyar, 1992; Board, 2004; Jones et al., 2006) to avoid the settling and deposition of solids on pipelines, while the flow velocity should be lower than 2.0 m/s (EPA (Office of Water), 2002; Nayyar, 1992; Board, 2004; Jones et al., 2006) to avoid potential wear and tear to pipelines. In this study, the flow rate range was applied from 0.25 m/s to 2 m/s, which covered the normal range (0.6 m/s- 2 m/s) in wastewater treatment plants (WWTPs) and the low range (0.25 m/s-0.6 m/s) at slow flow scenario. The whole experiment setup consisted of a pump (Unimount 125, U.S. Electronical Motors) with an adjustable Butterfly valve (Spears Co., USA) to control the flow rate of tap water (conductivity: 4.42 μS/cm, temperature: 20 °C) from the university water supply system, a commercial paddlewheel sensor (FP-5300 flow sensor, OMEGA Engineering, Inc) for comparison, a test pipeline (I.D.: 9.86 cm, Schedule 80 PVC Pipe, McMaster-Carr Company), and two 4″ PVC saddle fittings (OMEGA Engineering, Inc) for installing the commercial sensor and MRSF onto the pipeline. Before the tests, the MRSF (length: 3.5 cm; width: 1.8 cm) was inserted into the fitting screw cap (I.D: 2.6 cm, Model: 450–010, Spears Co.) and then glued onto the cap using an Epoxy (5 m quick-cure epoxy, JSP) (Fig. 3d). Afterwards, the fitting cap with the glued MRSF was vertically installed into the pipeline. The two types MRSFs (single-film and double-film) were examined in the pipeline individually.

During the tests, the valve for controlling the flow rate was gradually opened to increase the flow rate steadily from 0.25 m/s (the minimal value) to 2 m/s (the maximum value). The tests were replicated for three times at each velocity. The MRSF would bend under different flow rates (Fig. 3e), leading to variation of the resistance of the sensor at different degrees of curvature. The resistance of the MRSF was recorded using a digital multimeter (Mastech MS828 Digital AC/DC Auto Range Digital Multimeter) and the value of the commercial flow sensor was recorded 1 min after adjusting the valve in order to obtain the readings at the stable flow status.

2.5. Model simulation of MRSF curvature at different flow rates using the COMSOL Multiphysics

Using the arbitrary Lagrangian Eulerian (ALE) technique (Hughes et al., 1981; Duarte et al., 2004), the flow in the vicinity of the thin MRSF sensor was simulated and the effected deformation of the sensor was analyzed. The flow simulation in the pipe mirrored the experimental conditions and was conducted in the COMSOL Multiphysics (COMSOL, Inc, Burlington, MA, USA) modeling framework. Water flows from left to right and in the middle of the channel it imposes drag force on the deformable sensor, which is fixed at the bottom of the pipe. The computational method handles the deformation (bend) of the sensor by the moving mesh technique. Navier-Stokes equations are solved for moving coordinates in order to calculate the velocity field and the strain, stress, and deformation experienced by the sensor as computed by the model. The channel is assumed to be 0.5 m × 0.1 m and the sensor has a height of 35 mm (Fig. 3f). The Young's modulus of the sensor is set at 2.5 GPa and the film thickness was varied between 0.2 and 0.3 mm in order to account for possible imperfections. Using the equivalence of flexural rigidity, the thickness and Young's modulus of the sensor were modified to simulate a less-computationally demanding model considering the size of the domain as well as the moving mesh technique. A triangular mesh consisting of 19,014 domain elements and 398 boundary elements was used in all the simulations (Fig. S1).

2.6. Temperature correction of MRSF

Because the MRSF is based on the variation of the resistance of the interdigitated electrodes under different flow velocities, the influence of the variation of liquid temperature on the silver ink should be minimized to avoid the measurement error. In this study, MRSF was put into water with varied temperatures to examine the stability of the resistance readings. Briefly, the working electrode and counter/reference electrodes of the MRSF were individually connected to a potentiostat (Gamry Reference 600). Then the MRSF was immersed into the DI water in a beaker on the heater (Thermolyne 1000 hotplate). A commercial temperature sensor (Thermo Scientific Orion 3-star conductivity meter) was put into the beaker near the MRSF. The water solution was heated from 20 °C to 60 °C that simulated adversely low and high wastewater temperature (LaPara et al., 2001), during which the MRSF was applied with the current-time program at a setting potential 0.2 V, and the resistance (ohm) of the MRSF was recorded every 100 s for the duration of 2300 s.

2.7. Long-term stability of MRSF for 4-week operational period

Long term stability of the MRSF is important for flow velocity monitoring, especially in wastewater pipelines. Electrode fouling caused by the attachment of inorganic and organic constituents is an inevitable phenomenon that would affect the monitoring accuracy and signal sensitivity in long run (Zhu et al., 2009; Pikaar et al., 2011). The electrode fouling would increase the electrode resistance by destroying the electrode surface structure. To minimize biofouling, the whole electrode part (silver particles) of MRSFs was protected by a silicon glue layer, which covered the whole electrode part. The MRSF stability in wastewater was examined within 4-week operational period. Multiple pieces of MRSFs were immersed into static wastewater (chemical oxygen demand (COD): 250–350 mg L⁻¹ and biological oxygen demand (BOD): 100–300 mg L⁻¹) collected from the influent section of the University of Connecticut Wastewater Treatment Plant (UConn WWTP). A MRSF sample was taken from the wastewater every week, and gently rinsed by DI water for 5 s before the surface observation using a digital microscope (Nikon Labophot). The MRSF resistances were measured at the room temperature (20 °C) using a digital multimeter (Mastech MS828 Digital AC/DC Auto Range Digital Multimeter) weekly throughout the 4-week period to determine the electrode fouling extent. In addition, bacterial attachment on a solid surface had been found to correlate with the surface hydrophilicity (Li and Logan, 2004; Fraiwan et al., 2013). Thereby, the static contact angles of the MRSF were examined in duplicate tests using a CAM 101 optical surface tension meter before and after the immersion to elucidate the sensor surface hydrophilicity (KSV Instrument Inc.) (Hua et al., 2003).

3. Results and discussion

3.1. Calibration of MRSF at different flow velocities and validated by the commercial flow sensor

Considering the flow velocity was 0.25–2 m/s in this study, the diameter of the pipe was 0.0986 m, $\text{ρ}$ was 1000 $\text{kg}/{\text{m}}^3$, and $\text{μ}$ was 0.001 Pa s at the 20 $°C$, the Reynolds number (R_e) ranged from 2.4 × 10⁴ to 1.97 × 10⁵, indicating that the flow in this study is indeed turbulent (Ergas and Rheinheimer, 2004). The flow results are reasonable and clearly indicate the existence of a turbulent flow velocity profile with almost constant flow velocity over most of the pipe cross-section (Fig. 3g). For the film dimensions and the flow conditions, ${\text{C}}_{\text{D}}$varies modestly between 1.1 and 1.9. Because the flow in this study was turbulent, and ${\text{C}}_{\text{D}}$ was approximately constant, the model between the MRSF's resistance and the flow velocity as shown in Fig. 2 and Eq. (7) was considered acceptable.

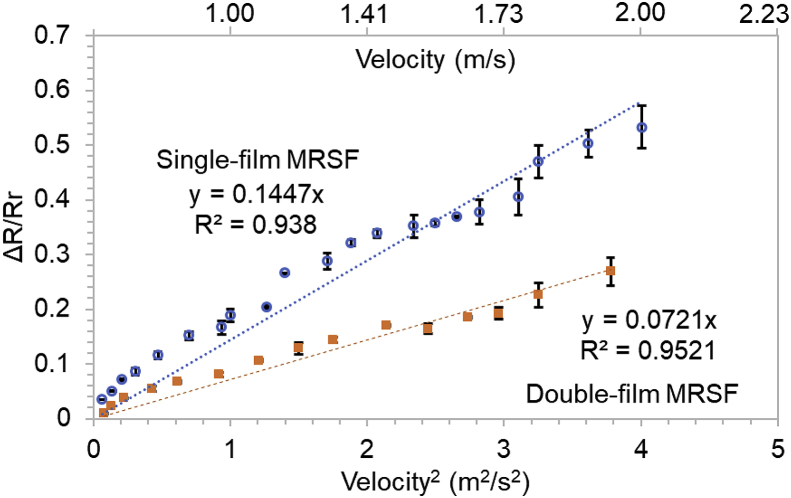
The sensitivity (K′) of the single-film MRSF was 0.1447/ms⁻¹, and the K’ of the double-film MRSF is 0.0721/ms⁻¹ (Fig. 4), implying that the single-film MRSF was more sensitive than double-film MRSF. The model previously reported (Wang et al., 2007b; Zhang et al., 2010) was built upon the absolute resistance change with the flow velocity, which had a problem of the different original resistances caused by the fabrication process, such as inkjet printing or the photolithography (Xu et al., 2016, 2017). In contrast, the relative resistance change $\left(\frac{\Delta \text{R}}{{\text{R}}_{\text{r}}}\right)$ deployed in this study minimized the influence caused by the different sensor fabrication processes. Previous studies had found that resistance change was 125 Ω/ms⁻¹ at the original resistance of 17,000 Ω, meaning the sensitivity was 0.007/ms⁻¹ based on the relative resistance change (Zhang et al., 2010). The maximum sensitivity was 0.0284 Ω/ms⁻¹ at the original resistance of 5 Ω (Wang et al., 2007b), meaning that the sensitivity was 0.00568/ms⁻¹ based on the relative resistance change. Sensor sensitivity ranging from 0.652 × 10⁻⁵ to 4.489 × 10⁻⁵/ms⁻¹ had been reported (Su et al., 2002). MRSF exhibited a much better sensitivity (Single-film MRSF: 0.1447/ms⁻¹; Double-film MRSF: 0.0721/ms⁻¹) than these studies (Su et al., 2002; Kao et al., 2007; Wang et al., 2007b, 2009; Zhang et al., 2010), which was attributed to the flexible thin Kapton film (Fig. 3e) and the excellent adhesion of silver nanoparticle ink onto the film, while the sensors in previous studies were fabricated from piezo-shaped silicon material (SiO_x or SiN_x) using photolithography and resulted in a rigid structure that was less flexible under water flow (Su et al., 2002; Kao et al., 2007; Wang et al., 2007b, 2009; Zhang et al., 2010). Such a high sensitivity offers MRSFs a distinct advantage to real-time detect the transient variation of wastewater flow of each treatment unit across WWTPs, leading to a swift and proactive control strategy to save energy consumption and sustain good treatment efficiency.

Fig. 4.

The responses of the resistance readings (ΔR/R_r) of the single-film and double-film MRSFs to the square of the flow velocity (V²) in the range from 0.2 to 2 m/s.

In addition, due to the same density and dimension of two types of sensors tested (single-film and double-film) (Eq. (6)), the sensitivity of sensors was only related to the flexural rigidity (EI) of the sensor material, which was only affected by the film thickness (Boresi et al., 1993; Kao et al., 2007; Wang et al., 2009; Ugural and Fenster, 2011). Based on E = 2.5 GPa and I = 1.2 × 10⁻¹⁴ m⁴, an estimation of flexural rigidity for the Kapton film with a thickness of 0.2 mm resulted in 3 × 10⁻⁵ N m², which was consistent with the experimental values reported for PET (polyethylene terephthalate) (Price, 1966). The sensitivity of the single-film MRSF was slightly higher than twice that of the double-film MRSF (Fig. 4). It should be noted that the double-film MRSF was fabricated by gluing two pieces of single layer Kapton film using silicon paste, which increased the flexural rigidity and slightly reduced the sensitivity of the double-film MRSF. The ${\text{R}}^2$ values for the relative resistance increment of the MRSF as a function of the square of the flow velocity were 0.94 and 0.95 for single-film and double-film, respectively (Fig. 4), indicating a high sensor resolution (precision), similar to previous studies (Su et al., 2002; Kao et al., 2007; Wang et al., 2007b, 2009; Zhang et al., 2010).

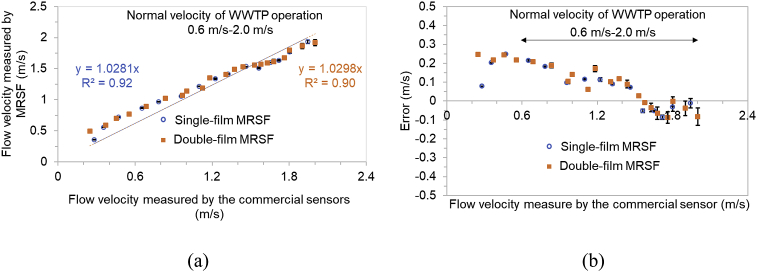
Single-film MRSF and double-film MRSF exhibited an excellent correlation with the commercial paddlewheel flow sensor, with a slope of 1.0298 and 1.0281, respectively (Fig. 5a). Both slopes were tested against the ideal slope of one according to the following hypotheses

$${\text{H}}_0:{\beta }_1=1$$

$${\text{H}}_1:{\beta }_1\ne 1$$

Fig. 5.

The side-side comparison of the single-film and double-film MRSFs with the commercial paddlewheel flow sensor in the range from 0.2 m/s to 2 m/s (a) and the flow velocity disparity (error: m/s) between the MRSFs and the commercial flow sensor (b).

In both cases we cannot reject the hypothesis that the slope is equal to one with p = 0.2079 and 0.3016 for single-film and double-film MRSF, respectively. The R² values were above 0.90, indicating the good linearity between the flow velocity measured by the MRSF and the commercial sensor. The flow velocity disparity between the MRSF and the commercial sensor would be recognized as the error (accuracy: ±1%) in this study. The error of MRSFs was between −0.1–0.25 m/s throughout all the tests and decreased with the flow velocity (Fig. 5b). In the flow velocity range (0.6 m/s- 2 m/s) that usually occurs in the WWTP operation, the error of MRSFs was between −0.1–0.2 m/s (Fig. 5), which met the EPA standard (less than 10% of the flow rate) (Baker, 2005). At the low flow velocity (0.25 m/s- 0.6 m/s), the error of MRSFs was 0.1–0.25 m/s, which was beyond the permissible error by EPA standards (Baker, 2005), meaning that MRSF could not accurately measure the low flow velocity, but could still be used as the warning indicator for the occurrence of low flow velocity specially to prevent the particle deposition in pipeline (EPA (Office of Water), 2002; Nayyar, 1992; Board, 2004; Jones et al., 2006). A small error (2% of the flow rate) had been found in previous studies (Wang et al., 2007b), which was caused by the relative stable mechanical structure of the sensor (cantilever-beam structure). In contrast, a study using the similar structure as MRSF had found a high error (16.7%) at the low flow velocity (<0.2 m/s) (Zhang et al., 2010). Single-film and double-film MRSF exhibited the similar accuracy in this study, implying that there was no significant relationship between the sensitivity and the accuracy (Fig. 5).

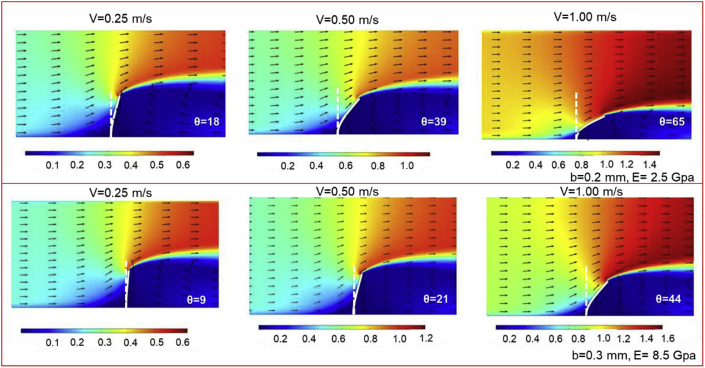
3.2. Calibration result of MRSF validated by the CFD simulations

In the CFD model, the deflection angle and the flow velocity around the film of the sensor were investigated under three different inlet velocities (0.25, 0.5, and 1 m/s), which were imposed on the left boundary of the channel and for two different film thicknesses (0.2 and 0.3 mm) (Fig. 6). In order to observe the deformation of the sensor in time, a transient study was conducted until the CFD model reached a steady-state condition typically in less than 10 s. However, all results were compared at 10 s for consistency (Fig. 6). Comparing the deflection angle at varied velocities for the MRSF with 0.2 mm thickness, the deflection angle at the 0.5 m/s velocity was almost twice that of 0.25 m/s, which was consistent with the linear relation implied by the experiment (Fig. 4). When the velocity increased to 1  m/s, the deflection angle was a little bit less than two times that of 0.5 m/s, which was again considered consistent with what is shown in Fig. 4. This pattern held true at MRSF of 0.3 mm (Fig. 6), which confirmed both the underlying load assumptions and the deformation characteristics of the sensor film under various flow and material conditions. Comparing the deflection angle at different MRSF at the velocity of 0.25 m/s, the deflection angle at the 0.2 mm MRSF was twice of that at 0.3 mm which was consistent with the linear relation implied by the experiment shown in Fig. 4. When the velocity increased, this ratio decreased (Fig. 6) and reached a plateau at 1.3 for flow velocity of 1.475 m/s (data not shown here). Overall, the CFD simulations showed a clear dependence of deflection angle on the square of flow velocity with ${\text{R}}^2$ 0.93 and 0.98 for single-film and double-film MRSFs, respectively. The fact that CFD simulation results showed similar deformation behavior and flow dependence lends credence to the experimental protocols.

Fig. 6.

Flow patterns in the proximity of the film sensor for different flow velocities and material properties and deformation angles of the film sensor for different flow velocities and material properties.

3.3. Temperature influence on MRSFs real-time flow monitoring

Water flowmeters based on the electronic mechanism (e.g. electromagnetic) are normally affected by the temperature and require re-calibration (Paulsen et al., 2001; Wang et al., 2007a; Meter, 2018). As the RTDs (resistance temperature detector), the resistance of MRSFs was expected to decrease with temperature. Therefore, temperature correction should be applied for MRSF calibration. The relationship between MRSF resistance and temperature is described as below (Eq. (8)) (Xu et al., 2016, 2017).

$$\frac{{\text{R}}_{\text{r}}-{\text{R}}_{\text{r}}^{\text{'}}}{{\text{R}}_{\text{r}}^{\text{'}}}=\text{α}\Delta \text{T}$$ (8)

Where ${\mathbf{R}}_{\mathbf{r}}$ is the static MRSF resistance at the actual temperature (Ω), ${\mathbf{R}}_{\mathbf{r}}^{\text{'}}$ is the static MRSF resistance at 20 °C (Ω). α Is the temperature coefficient of resistance (TCR) ((Ω/Ω)/°C), which is regarded as the sensitivity of a temperature sensor (Lee and Lee, 2003; Lee et al., 2008, 2011). ΔT is the difference between the actual temperature and the reference temperature (20 °C) (°C).

The test results of MRSF in different water temperatures (20–60 °C) showed that at the fixed potential set by the potentiostat program, the resistance of MRSF (R = V/I) dropped with the temperature (Fig. S2), since silver nanoparticles coated as the resistor on the sensor film had a positive temperature coefficient (0.001) (Xu et al., 2016, 2017). The temperature coefficient of resistance (α, 0.001) of MRSF (Fig. S2) was half of that in the previous study (0.002) (Xu et al., 2016, 2017), indicating that the resistance hardly changed with temperature variation. The sensitivity of the RTDs was only affected by the MRSF material. Normally, the temperature coefficient of pure metal material (e.g. gold, zinc, and cooper) was higher than 0.0035, while the temperature coefficient of the mixed metal material (e.g. manganin) was close to zero (Kasap, 2006). Some semiconductor materials (e.g. carbon, silicon and germanium) typically have negative temperature coefficient of resistance (Kasap, 2006). The temperature coefficient of pure metal would decrease when mixed with the material having the negative temperature coefficient. The silver ink used for MRSF was the mixture of silver nanoparticles and ethylene glycol (an organic carbon to dissolve silver nanoparticles), and thus having a low temperature coefficient of resistance (α in this model, 0.001) than pure silver (0.0038 at 20 °C) (Kasap, 2006).

The flow velocity without the temperature correction, termed as the apparent flow velocity was calculated from Eq. (9).

$$\text{v'}=\sqrt[2]{\frac{\text{R}-{\text{R}}_{\text{r}}}{{\text{K}}^{\text{'}}{\text{R}}_{\text{r}}}}$$ (9)

Where R is the resistance measured by the multimeter at the actual temperature. When the temperature correction was executed, the standard reference resistance (${\mathbf{R}}_{\mathbf{r}}$) at 20 °C in Eq. (9) should be replaced by the reference resistance at actual temperature (${\mathbf{R}}_{\mathbf{r}}^{\text{'}}$). The absolute error was the difference between the apparent flow velocity (v’) and the actual flow velocity (v) as shown in Eq. (10).

$$\text{Absolute}\text{Error}={\text{v}}^{\text{'}}-\text{v}=\sqrt[2]{\frac{\text{R}-{\text{R}}_{\text{r}}^{\text{'}}}{{\text{R}}_{\text{r}}^{\text{'}}}}-\sqrt[2]{\frac{\text{R}-{\text{R}}_{\text{r}}}{{\text{K}}^{\text{'}}{\text{R}}_{\text{r}}}}$$ (10)

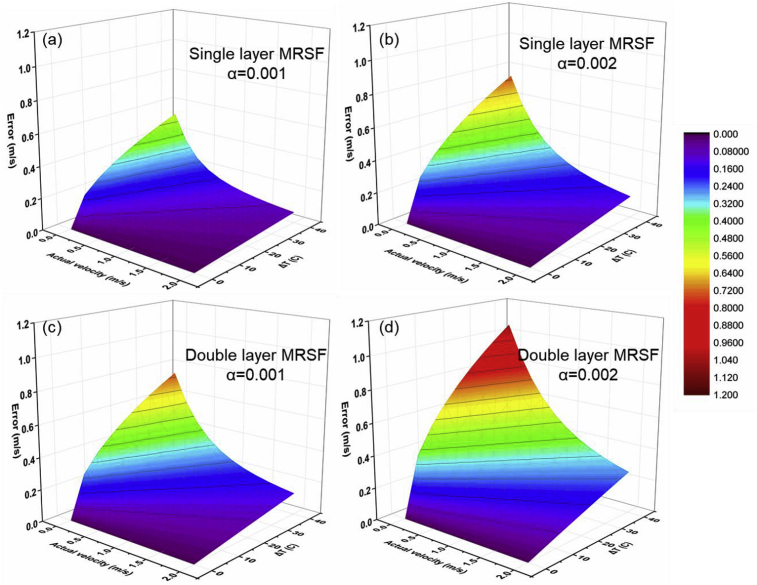
The error increased with the temperature at the same actual flow velocity (Fig. 7), demonstrating that the temperature change ($\Delta \mathit{T}$) would cause the error only if the TCR (temperature coefficient of resistance) is not zero. At the same $\Delta \mathit{T}$, the error decreased with the actual flow velocity (Fig. 7). The increase in the flow velocity and the temperature would increase the MRSF resistance, so that when the flow velocity increases, the temperature change ($\Delta \mathit{T}$) would generate less error and the effect of flow velocity on the increase of resistance would become dominant. For MRSFs with the same EI (flexural rigidity) and different TCRs (Fig. 7a/7c and Fig. 7 b/7 d), the MRSF with lower TCR exhibited less error than the one with higher TCR at the same flow velocity and temperature change. The MRSF with small TCR (0.001) caused less error than the milli-electrode array (MEA) printed on a single film in the previous study (0.002) (Xu et al., 2016, 2017). The comparison of the MRSFs with different EIs (Fig. 7a/7 b and Fig. 7c/7 d) showed that the MRSF with higher EI (double-film MRSF) had bigger error than that with lower EI (single-film MRSF) at the same flow velocity and temperature change, since the MRSF with lower EI (single-film MRSF) was more sensitive than double-film MRSF (K’ = 0.0721). The low flow velocity would cause more deflection of double-film MRSF, resulting in high resistance. Therefore, to reduce the absolute error incurred by temperature change, the TCR should be reduced by integrating the electrode material with lower EI materials (e.g. thinner Kapton films or more elastic films).

Fig. 7.

The variation of the error (the disparity between MRSFs and commercial flow sensor, z-axis) with the flow velocity (0.2 m/s −2 m/s, x-axis) and temperature change (ΔT, ºC, y-axis). (a) Single-film MRSF with low TCR (α = 0.001), (b) single-film MRSF with high TCR (α = 0.002), (c) double-film MRSF with low TCR (α = 0.001), and (d) double-film MRSF with high TCR (α = 0.002).

The temperature coefficient of resistance (TCR, 0.001) in this study was much smaller than that (0.0019–0.0039) in previous studies (Glatzl et al., 2016; Xu et al., 2016, 2017; Shikida et al., 2017), and the temperature had lower impact on the MRSF than other flat flow sensors. The TCR of capacitance-typed flow sensors (Nguyen et al., 2014, 2015) varied from 0.2% to 2% when the temperature changed. However, the error caused by the temperature has no a fixed pattern. Due to the relationship among the error and the actual flow velocity, temperature change, TCR and EI (flexural rigidity) in this study, the temperature impact on the MRSF could be neglected by integrating the temperature MEA (Xu et al., 2016, 2017) on the MRSF. In addition, the relationship among the absolute error and the actual flow velocity, temperature change, TCR and EI of the material was established in models (Eq. (10), Fig. 7) that could be used to minimize the error of the flow monitoring in real time mode.

3.4. Long-term stability test of MRSF in wastewater

Long-term stability is of primary concern for monitoring wastewater flow velocity. Electrode surface fouling caused by the attachment of inorganic/organic particles has been well known to cause the deterioration of the accuracy and stability of electronic sensors (Geise et al., 1991; Manica et al., 2003). The 4-week immersion in wastewater showed that the MRSF surface did not have obvious change based on macroscopic observation (Fig. S3). There was no significant change (less than 0.04%) of the MRSF resistance during 4 weeks of immersion in wastewater (Fig. S3). There were two main reasons for the good long-term stability of MRSF. First, the MRSF consisted of three layers from top to bottom: the silicon glue layer, the electrode layer (silver ink) and the substrate (Kapton film) (Fig. 3b). The silicon layer and the Kapton film isolate the electrode layer from the wastewater and thus preventing the direct attachment of inorganic/organic particles on the electrode layer (Xu et al., 2016, 2017). Second, the silicon glue layer coated on the MRSF surface (shown in Fig. 3b) enhances the hydrophobic property of the Kapton film and thus alleviating bacterial adhesion (Urbain et al., 1993; Stevik et al., 2004). The contact angle increased after the Kapton film was coated with silicon glue (Fig. 8), indicating that the surface of the MRSF (Kapton film/silicon layer) became more hydrophobic and prevented the attachment of inorganic/organic particles.

Fig. 8.

Contact angle of single-film and double-film MRSFs before and after the silicon glue coated on the sensor surface. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

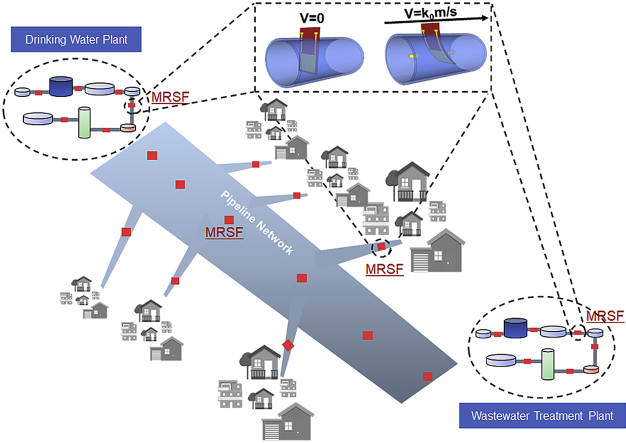
3.5. Towards energy-saving WWTPs through high-resolution monitoring of flow rate using MRSFs

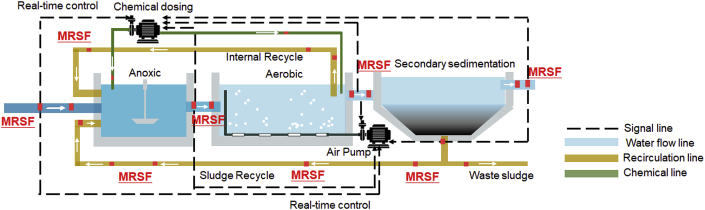
Flexible MRSFs (Fig. 3e) installed across a given WWTP consisting of anoxic/aerobic units (e.g. influent, anoxic tank, aeration tank, effluent), sludge pipeline and chemical dosage pipeline would detect the fluctuation of flow rate throughout each unit and facilitate precise and proactive control, and thus sustaining the stable operational status under transient shock and saving energy and chemical consumption (Fig. 9). For example, under flow fluctuation (e.g. heavy rainfall or snowmelt or overflow in combined flow systems), organic carbon sources could be diluted to 33%–45% compared with normal flow condition (Müller and Krauth, 1998; Mines et al., 2007; Kim et al., 2017). Accurate real-time monitoring this sharp jump of the incoming flow and the drop of carbon source in a WWTP is expected to save 42%–51% electric power for aeration and 53–64% chemical dosage (mainly carbon source (methanol) cost) for denitrification (Table S1) (Gernaey et al., 2004; Pai, 2007; Zeng et al., 2010). Therefore, the MRSF developed exhibited high accuracy, excellent signal stability over a broad range of water flow velocity, good temperature-resistance and long-term robustness, which poses a great potential to be mass deployed in water/wastewater treatment plants for high precision monitoring and energy-saving operation.

Fig. 9.

Diagram of high resolution MRSF monitoring and swift control of each treatment unit in an anoxic/aerobic WWTP.

4. Conclusions

Novel mm-sized resistance-typed sensor film (MRSF) was developed in this study as a flow velocity sensing technology and examined in a lab-scale continuous flow system under different flow velocities. MRSF exhibited high accuracy (−0.1  m/s – 0.2  m/s) and excellent sensitivity (Single-film MRSF: 0.1447/ms⁻¹; Double-film MRSF: 0.0721/ms⁻¹), which exceeded the commercial flow sensor and similar types sensors reported. Single-film MRSF possessed twice the sensitivity of double-film MRSF based on the EI (the flexural rigidity) of the sensor film material. The sensor models were developed to establish the correlation between flow velocity, temperature change, TCR, and EI. The results showed that the MRSF with higher EI (double-film) had bigger error than that with lower EI (single-film) at the same flow velocity and temperature change. Four-week tests in wastewater showed the surface of MRSF was still intact and exhibited a high stability for long-term applications. Computational fluid dynamics simulations were conducted and confirmed both the underlying load assumptions and the deformation characteristics of the sensor film under various flow and material conditions. The novel monitoring system would consume at least 50% less energy compared to the existing monitoring system and it would be much cheaper.

Appendix A. Supplementary data

The following is the supplementary data to this article: