Abstract
Both the total amount and the distribution of heterozygous sites within individual genomes are informative about the genetic diversity of the population they belong to. Detecting true heterozygous sites in ancient genomes is complicated by the generally limited coverage achieved and the presence of post-mortem damage inflating sequencing errors. Additionally, large runs of homozygosity found in the genomes of particularly inbred individuals and of domestic animals can skew estimates of genome-wide heterozygosity rates. Current computational tools aimed at estimating runs of homozygosity and genome-wide heterozygosity levels are generally sensitive to such limitations. Here, we introduce ROHan, a probabilistic method which substantially improves the estimate of heterozygosity rates both genome-wide and for genomic local windows. It combines a local Bayesian model and a Hidden Markov Model at the genome-wide level and can work both on modern and ancient samples. We show that our algorithm outperforms currently available methods for predicting heterozygosity rates for ancient samples. Specifically, ROHan can delineate large runs of homozygosity (at megabase scales) and produce a reliable confidence interval for the genome-wide rate of heterozygosity outside of such regions from modern genomes with a depth of coverage as low as 5–6× and down to 7–8× for ancient samples showing moderate DNA damage. We apply ROHan to a series of modern and ancient genomes previously published and revise available estimates of heterozygosity for humans, chimpanzees and horses.
Keywords: inbreeding, heterozygosity, effective population size, Ancient DNA, Runs of homozygosity
In diploid organisms, single nucleotide differences observed between paternal and maternal chromosomes are called heterozygous sites. As the history underlying both chromosomes can be viewed under a coalescence process, heterozygous sites result from mutations which occurred in the genealogy, backward in time. The number of neutral polymorphic sites segregating in a given population both depends on the average coalescence, which itself depends on the effective population size , and the mutation rate (μ) (Kimura 1969). Consequently, parameters such as the Watterson’s θ, where for diploid organisms (Watterson 1975), are essential in population genetics and have been widely used to infer past population demographies.
If both parents are unrelated, the number of heterozygous sites at equilibrium is expected to be , which is for small values of θ (Watterson 1975). Several tools have been released to infer the number of heterozygous sites at equilibrium, also referred to as the heterozygosity, from either raw sequence alignment files (Haubold et al. 2010; Korneliussen et al. 2014), multiple sequence alignments (Gronau et al. 2011; Adams et al. 2018) and SNP arrays (Purcell et al. 2007; Yang et al. 2011; Browning and Browning 2015; Szpiech et al. 2017). The underlying methodology has been recently reviewed by Yengo et al. (2017).
However, if both parents are related, large stretches of the offspring genome will be identical by descent (IBD). At such loci, no or very few heterozygous sites will be found, resulting in the presence of runs of homozygosity (ROH). Such ROHs can be informative about an individual’s demographic history (Ceballos et al. 2018). The total length of such genomic loci depends on the type of inbreeding (Wright 1922) and the length of such regions depends on how far back in the genealogy the inbreeding event took place (Fisher 1954; Keller et al. 2011), considering that recombinations reduce the length of ROHs with time. A number of statistical packages have been released to investigate the impact of inbreeding on individual fitness (Stoffel et al. 2016).
Inbreeding can be due to small group size, cultural practice (Alvarez et al. 2009) as well as reproductive management procedures such as those underpinning domestic livestock (Wiener and Wilkinson 2011). ROHs have therefore been detected in a number of domestic animals, including sheep (Purfield et al. 2017), cattle (Purfield et al. 2012), pigs (Bosse et al. 2012) and donkeys (Renaud et al. 2018). A first class of methods aimed at the detection of ROH in modern samples have relied on pre-called genotypes (McQuillan et al. 2008; Pemberton et al. 2012) and allele frequencies for the population of interest (Narasimhan et al. 2016). Even without the additional layer of complexity represented by the uncertainty in calling genotypes, available methods show limitations and generally require ad-hoc tuning of their parameters to fit the properties of the data at hand (Howrigan et al. 2011). A second limitation is the use of allele frequencies. Such information is not always available especially for rare breeds or remote populations. Elevated drift or distant split times between the population providing the allele frequencies and the sample often make such information inapplicable. Another class of methods has relied on weighted-likelihood methods using genotype data for several individuals (Blant et al. 2017).
In recent years, methodological advances in ancient DNA (aDNA) research have opened access to the complete genome sequence of ancient human individuals (Llamas et al. 2017b), domesticates (Frantz et al. 2016; Gaunitz et al. 2018), pathogens (Rasmussen et al. 2015), and extinct species (Miller et al. 2008; Green et al. 2010; Reich et al. 2010). Ancient genomes provide time-stamped genetic snapshots which are instrumental for understanding how the genetic makeup of modern species came to be. However, aDNA molecules are generally poorly preserved and co-extracted together with a large fraction of genetic material from environmental microbes (Der Sarkissian et al. 2014). This results in a relatively low amount of endogenous molecules, which makes the recovery of high coverage genomes for ancient individuals often prohibitively expensive (Orlando et al. 2015). As a consequence, the vast majority of the ancient genomes currently available have only been sequenced to low coverage (Marciniak and Perry 2017).
Inferring heterozygosity on the basis of low sequence coverage data are difficult but several methods have been proposed to do so (Bryc et al. 2013; Korneliussen et al. 2014; Kousathanas et al. 2017). In addition to coverage limitation, the presence of post-mortem damage, which introduces nucleotide misincorporations, and potential contamination either stemming from microbial sources or present-day humans (Llamas et al. 2017a), make heterozygosity estimates in ancient samples particularly difficult. Despite these limitations, a method has been developed to address the problem of inferring heterozygosity for ancient samples (Kousathanas et al. 2017). Additionally, other methods have leveraged the power of allele frequencies or recombination maps to predict IBD tracks and infer runs of homozygosity in ancient samples (Narasimhan et al. 2016; Vieira et al. 2016). However, the necessary allele frequencies are not always available for past populations or populations poorly represented by public datasets. Furthermore, drift in the lineage of the reference panel or in the sample might skew allele frequencies. Finally, the presence of long and prevalent ROHs can drive down the genome-wide estimate of heterozygosity (Prüfer et al. 2014).
Here, we introduce ROHan, a method to jointly estimate the local and global heterozygosity rates as well as long ROHs. This method is suitable for both modern and ancient DNA samples given that data are provided at sufficient depth-of-coverage. Our method relies on a maximum weighted likelihood method to first estimate the rate of heterozygosity locally. It then applies an HMM to simultaneously identify regions in ROHs and compute Watterson’s θ for regions that were identified as non-ROH. Our method operates on aligned DNA fragments in BAM format on an individual basis. It does not require allele frequencies or any information provided by the reference genome, and only makes use of the sequence data underlying a given sample. The source code is available at http://grenaud.github.io/ROHan/.
Using genomic simulations incorporating aDNA damage, and investigating the effect of coverage, population size and inbreeding, we show that ROHan is more accurate and robust than previous methods aimed at inferring rates of heterozygosity. We demonstrate that ROHan can infer global and local rates of heterozygosity for modern samples with coverage as low as 5–6× and in ancient samples as low as 7–8× even in the presence of substantial damage. For inbred samples, our method can correctly identify large ROHs at the megabase scale. Masking such regions provides more accurate estimates of global rates of heterozygosity genome-wide than current methods not aided by external allele frequencies.
We also tested ROHan on modern and ancient empirical samples for both human and non-human species. Specifically, we used our methodology on a dozen low-coverage samples from the 1000 Genomes project Phase III (1000 Genomes Project Consortium et al. 2015) and show that our estimates are consistent with the ones presented by the Simons Genome Diversity Project (Mallick et al. 2016) for similar populations sequenced to higher coverage. We also provide heterozygosity estimates for a range of ancient humans spanning a whole range of post-mortem damage and coverage. Additionally, applying our methodology to individual chimpanzee genomes, we obtain more consistent estimates than those reported in the original publication (de Manuel et al. 2016). Finally, we ran ROHan on several horse samples, both modern and ancient, and confirm that the genome of the endangered Przewalski’s horses shows a large fraction of ROHs and low heterozygosity. This is in contrast to their Eneolithic direct ancestors, which showed larger genetic diversity and were not found to be inbred.
Materials and Methods
Our method proceeds in three steps. It first estimates genome-wide coverage (step 1), then estimates local rates of heterozygosity using a user-specified genomic window size (step 2) and finally runs an HMM over the local rate of heterozygosity to simultaneously identify regions in ROH and genome-wide θ (step 3). This section presents the underlying probabilistic model as well as our simulation framework.
Computational model
The first step is to get an estimate of the genome-wide coverage from the average per base coverage at a few genomic loci. As the genomic windows are relatively large (100 kbp–1 Mbp), using 10 randomly selected genomic windows provides a sufficiently accurate estimate of the genome-wide coverage. The actual coverage achieved at each individual site is further used in step 2 in order to weight its contribution to the likelihood function by comparing with the genome-wide coverage. Further details about the coverage correction are found in the text below, where we also use the word fragment to describe individual sequences aligned against a reference genome. This is so to help distinguish the actual physical molecules sequenced from reads, which represent the raw data as obtained from the sequencing instrument. For ultra-fragmented aDNA fragments, reads are often longer than the size of the molecules present in DNA libraries. It is thus crucial to reconstruct the original DNA fragment given the raw reads by removing sequencing adapters at the ends and potentially merging overlapping mates (Kircher 2012).
We first detail how we obtain the local rates of heterozygosity and follow by presenting the HMM model.
Let us define the following variables:
Data:
b: any DNA base such .
: a DNA base post-deamination.
: the ancestral base.
ϵ: the probability of a sequencing error for a given base.
m: the probability of a mismapping event occurring as given by the mapping quality.
: either a derived base if a mutation occurred or equal to the ancestral base otherwise.
h: heterozygosity rate.
θ: Watterson’s theta.
: all possible 16 genotypes .
G: a given genotype such that .
: the observed base at genomic position i and depth j.
: the entire data over a genomic window such that .
: Set of all bases at genomic position i such that .
: the ratio of transitions over transversions.
: coverage at site i.
Probabilistic events:
M: a mismapping event on a specific fragment.
E: a sequencing error for a specific base on a specific fragment.
: denotes the complementary event of any event A.
We consider 16 distinct genotypes instead of 10. For instance, we consider to be a distinct genotype from . The use of 16 genotypes has previously been suggested in the literature to account for indels (Luo et al. 2017).
Local estimates of heterozygosity:
For a given genomic window, we seek to find that satisfies the following:
| (1) |
As does not depend on the heterozygosity rate h, it is not included in downstream calculations to calculate . By applying a uniform prior on h, we have:
| (2) |
By assuming that site i represents an independent observation, we use a weighted log-likelihood approach (Hadi and Luceño 1997) to estimate the total log-likelihood:
| (3) |
where is the weight depending on coverage at site i. This weight is aimed at modeling the certainty in having all the reads correctly mapped at the current site given the genome-wide coverage. To do this, the probability of observing the given coverage at site i given the genome-wide coverage is computed under three potential scenarios: (i) all reads originally came from the locus where they are mapped (ii) a single original locus mapped to two regions in the reference genome (iii) two original loci mapped to a single region in the reference genome. For instance, if the genome-wide coverage is 20×, under scenario (i), the coverage should follow a Poisson distribution with whereas under scenario (ii) the rate will be half the genome-wide coverage and the coverage at that site will follow a Poisson distribution with . Likewise, under scenario (iii), the coverage should follow a Poisson distribution with . Therefore, the weight at a given site represents the probability of an absence of duplication over the remaining possibilities given the coverage at that site and the genome-wide coverage. The exact derivation of such weights are detailed in Appendix A. It is worth noting that, as the derivation of the calculation assumes a Poisson distribution for the coverage at a given site, ancient samples might have a greater variance in their coverage due to nucleosome positioning (see Hanghøj et al. (2016)). This effect could cause sites to be incorrectly weighted and data to be unnecessarily thrown away. Finally, the likelihood of observing the data at site i is given by marginalizing over each 16 genotypes:
| (4) |
is the prior on the genotype given the heterozygosity rate. The term is the genotype likelihood. Both are defined in the following sections.
Genotype prior:
To compute , the prior probability on the genotype given heterozygosity rate h, we consider two possibilities:
- G is homozygous with probability such that . The probability that the G is homozygous is given by:
(5)
where is simply representing the genomic frequency of occurrence the base b in the genome. For humans, this is and .
- 2. G is heterozygous with probability h such that and . The prior on the genotype is therefore the probability that was the ancestral base multiplied by the probability that a specific mutation happened:
(6)
The term depends on the type of mutation:
- For transitions, we compute the probability of a transition occurring given the transition/transversion ratio:
(7) - For transversions, as there are two transversions from a given ancestral base, we consider each to be equally likely:
(8)
Genotype likelihood:
For a given genotype G and heterozygosity rate h, the genotype likelihood is computed by assuming that each base at site i represents independent observations. Since coverage at site i is :
| (9) |
as depends the genotype we rewrite . Since we could have sampled from either chromosome with equal probability, this expression is calculated as follows:
| (10) |
For a given base b (either or ), the probability of observing depends on whether the fragment to which , pertains to is mismapped:
| (11) |
where M is the event that a mismapping event occurred on the DNA fragment where is located. is defined in Equation 17. To quantify M, we simply use the mapping quality of the read as our simulations confirm this as a reasonable approximation (see Appendix B). However, due to problems in assembly and the presence of repetitive regions, ROHan can also use a mappability track if the mapping quality does not fully encompass the probability of a mismapping. This is recommended for very short aDNA fragments with some post-mortem damage as computing the mapping quality for such data are not straightforward (Günther and Nettelblad 2018).
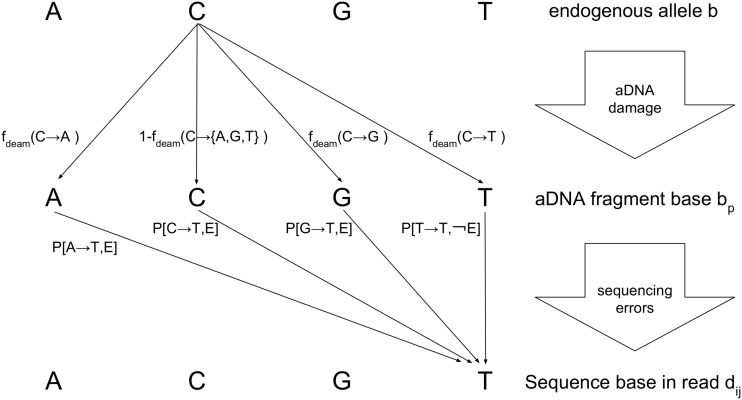
If the aDNA fragment is correctly mapped, two potential events can create a mismatch between the sampled base b and the observed - a deamination event or a sequencing error. We consider both events to be successive as both could have occurred (see Figure 1).
Figure 1.
A schematic representation of two events that can cause a mismatch given a fragment correctly mapped: aDNA damage such as deamination potentially and/or a sequencing error.
We consider the base to be the base after a potential post-mortem deamination reaction. For the Illumina sequencing technology, this base can be construed as the base on the flowcell prior to cluster amplification. As this base is a nuisance parameter, we marginalize over it:
| (12) |
the latter term is given by the rate of misincorporation due to deamination:
| (13) |
where is rate of substitution from original base b to . These substitutions should generally be 0 if unless there is a type of chemical damage which cannot be due to sequencing errors. These rates are given as input by the user and must be as accurate as possible. Scripts, test data and recommendations to estimate these damage rates accurately are found in the README provided with the software. Given the base , the probability of observing depends on whether a sequencing error happened or not:
| (14) |
where is simply defined by the frequency of base can pick a simple frequency of for all pairs of bases but due to the idiosyncrasies of Illumina sequencers (Nakamura et al. 2011), empirical Illumina base substitution frequencies are supplied with the software. In such cases, this expression simply becomes:
| (15) |
where is the frequency of substitution from base to base given that a sequencing error has occurred. These frequencies can be obtained using a sequencing run where DNA libraries have been pooled together with a DNA library constructed on a known genome. In the case of the frequencies supplied with the software, such frequencies were computed using Illumina control reads aligned to the PhiX174 genome.
Finally, in the absence of a sequencing error, the first term in Equation 14 becomes:
| (16) |
Thus far, we have assumed that the DNA fragment for base is correctly mapped. In Equation 11, the second term accounts for when this fragment is mismapped. In this case, the probability of observing this base is completely independent of b:
| (17) |
where is the expected frequency of occurred of . This is usually straightforward but aDNA damage can skew these frequencies by decreasing the probability of finding cytosines at the 5′ end due to deamination. For aDNA, these frequencies depend on the position of the fragment considered and the length of the fragment. Further detailed can be found in Appendix C.
To decrease runtime at the cost of increased memory usage, rates of base substitution for a given mapping quality and base quality can be precomputed as the probability space is already discretized due to the use of integers to represent quality scores and mapping quality.
As the goal is to find from Equation 1, we use a gradient descent with momentum (Rumelhart et al. 1986) to find the heterozygosity rate with the highest likelihood. ROHan precomputes the genotype likelihoods and computes prior probabilities for all 16 genotypes at each iteration of the gradient descent. For a given genomic window, the error bounds for is obtained using the following:
| (18) |
The quantity is an approximate SE for and 1.96 is an approximation of the 97.5 percentile point of a normal distribution.
We noticed that low-coverage samples consistently yielded underestimates due to heterozygous sites appearing as homozygous resulting from the limited chance of sampling the other allele. While for sites with high depth of coverage this is unlikely, for a coverage of 2× for instance, this will happen with a probability of . A correction factor was applied to the heterozygosity estimates to overcome this limitation. After the optimization has converged for a local estimate of heterozygosity, this estimate is multiplied by this corrective factor to retrieve reliable estimates (see details in Appendix D).
Hidden Markov Model:
We use a modified 2-state HMM where the first state corresponds to being in an ROH whereas the second corresponds to being in a non-ROH region. We can transition to the other state with probability p or stay in the same state with probability . We use a single transition parameter p for both states.
We have implemented a customized forward and backward algorithm where features were added to account for chromosomal start/end and undefined genomic windows. This was implemented by modifying the HMM to ignore the probability of transition from a state at the end of a chromosome to the beginning as those are independent. This applies as well for undefined regions. Finally, to account for genomic windows having more defined sites than others, the log-likelihood in the forward algorithm is weighted by the fraction of sites that are defined in the particular window.
Given the local heterozygosity estimate, we compute the expected value of segregating sites S in that genomic window by multiplying the estimated heterozygosity rate by the size of the window. This number of segregating sites in a genomic window constitute our emitted variables.
We are left with computing the emission probabilities which are the probability of a specific state generating a given observation (e.g., ). To compute this, each state has an internal parameter θ corresponding to Watterson’s theta estimate which is used to compute the probability of emitting a given number of segregating sites in a genomic window. This parameter θ for the state outside of an ROH corresponds to the genome-wide θ excluding runs of homozygosity. The same parameter for the state representing being inside an ROH stands for the low number of segregating sites found in ROH due to either germline or somatic mutations or potential miscalls due to other sources of minor error (e.g., exogenous fragments). The next paragraphs detail how we compute the probability of emitting a certain number of segregating sites S given the internal parameter θ.
For a given small non-recombining locus (NRL), it has been reported that S should follow a geometric distribution with parameter (Watterson 1975). However, a sufficiently large genomic window will be composed of multiple NRLs.
As the sum of geometric distributions is a negative binomial distribution, it has also been suggested in the literature that, for a sufficiently large genomic window, the number of segregating sites follows a negative binomial distribution (Pitters 2017). Using coalescence simulations, we confirmed that a negative binomial distribution was indeed a better fit than a standard binomial distribution (see Appendix E).
We construe S along a genomic window of length L to be the sum of the segregating sites of exactly s NRLs. For a given genome-wide θ, the geometric rate for any single NRL is given by . We obtain the following:
| (19) |
To infer the parameters given the local estimates of heterozygosity, we use a Markov Chain Monte Carlo (MCMC) approach to obtain point estimates as well as error bounds. Please refer to Rydén (2008) for a discussion about the use of expectation-maximization vs. MCMC for HMMs.
As local estimates of heterozygosity can differ greatly especially at low coverage, we run the MCMC three times, once using the lower bound estimates for h, a second time using the point estimates and finally, using the upper bound estimates. Once the three MCMC chains have converged, the minimum and maximum values are used as the lower and upper bound of the confidence interval. The average of the MCMC running on the mid values is used as the point estimate.
Simulations
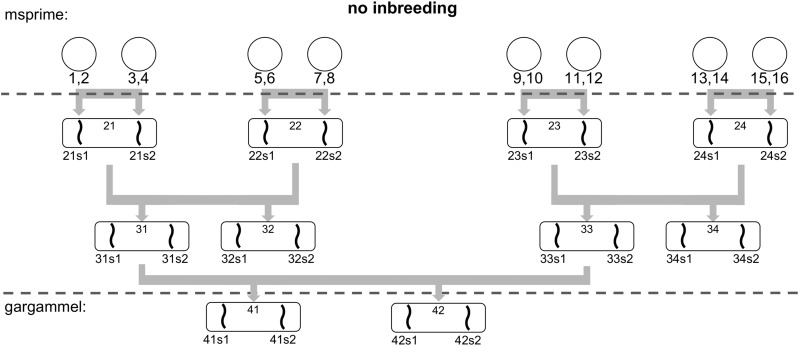
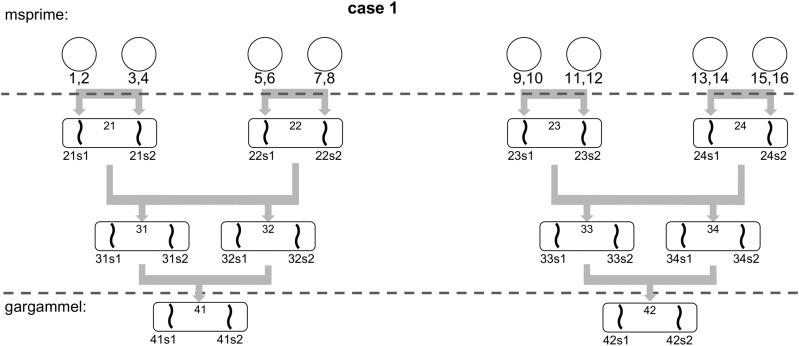
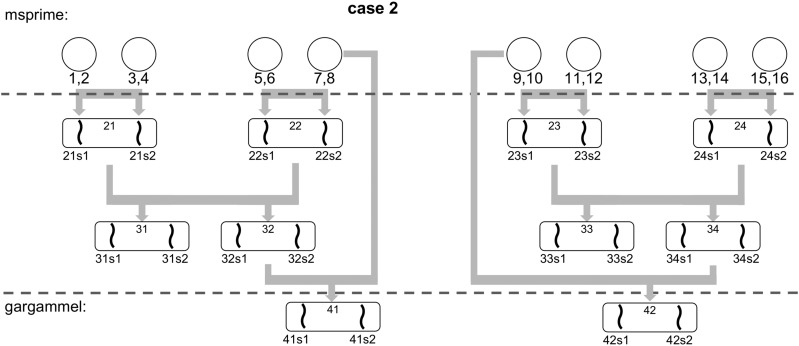
To test our methodology, we simulated a set of non-inbred and inbred datasets, using the full human chromosome 1 from hg19 as the genomic reference. To avoid gaps, unresolved bases were filled using a second-order Markov chain trained on the human genome. A total of 16 unrelated haploid chromosomes were generated using msprime (Kelleher et al. 2016) to form eight diploid individuals. We used the recombination map from HapMap phase II (International HapMap Consortium et al. 2007) in msprime to generate a complete human chromosome 1. As msprime does not currently assign actual bases to the segregating sites, we used the base in the human reference as ancestral allele and added mutations with a of 2.1.
A total of five different effective population sizes were used (see Table 1). The individual haploid chromosomes were recombined to produce a sexual gamete using the recombination map from HapMap phase II (International HapMap Consortium et al. 2007). The number of recombinations was on par with rates previously reported in the literature (Li 2011). These gametes were combined in a pairwise fashion to create a diploid individual (see Figure 2 for a schematic overview of the non-inbred pedigree). The 16 haploid chromosomes were combined to form four grandparents, four parents (two siblings per couple) and finally two diploid individuals corresponding to the great-grandchildren of the original 16 haploid chromosomes. These two diploid individuals are used as input to gargammel (Renaud et al. 2016) to simulate DNA sequencing reads with errors. We simulated a coverage of 30×. These initial 30× genomes were then downsampled to evaluate the program performance at low-coverage data.
Table 1. Simulated values of effective population size and expected θ.
| μa | ||
|---|---|---|
| 3,000 | 2 10−8 | 0.00024 |
| 5,000 | 2 10−8 | 0.00040 |
| 7,000 | 2 10−8 | 0.00056 |
| 9,000 | 2 10−8 | 0.00072 |
| 12,000 | 2 10−8 | 0.00096 |
per site per generation.
Figure 2.
The pedigree of two simulated individuals in absence of inbreeding. The generation of the full chromosomes is achieved using the 16 initial haploid chromosomes and recombination maps to simulate recombinations.
To simulate post-mortem damage, we used three types of aDNA damage profiles: (1) a high rate of post-mortem deamination consistent with the use of a double-stranded DNA protocol for library preparation (Meyer and Kircher 2010) using the ATP2 sample from Gamba et al. (2014); (2) a medium rate of post-mortem deamination from a double-stranded DNA library building protocol from the LaBraña sample described in Sánchez-Quinto et al. (2012) and (3) a low rate of post-mortem deamination corresponding to the damage found in a single-strand aDNA library (Gansauge and Meyer 2013) using the Ust’-Ishim sample from Fu et al. (2014). Please see Appendix F.1 for further details about the substitution rates and patterns considered.
Sequencing reads were simulated using a read length of 125 bp in the single-end mode with the sequencing error profile of an Illumina HiSeq2500. To further test the robustness of our model, we also drastically increased the simulated error rates (see Appendix F.2 for details).
The in silico sequencing adapters were trimmed using leeHom (Renaud et al. 2014) and mapping was conducted using a customized version of BWA version 0.5.9.
To test ROHan’s ability to infer ROHs, we tested three scenarios of inbreeding: 1) between siblings (F = ) 2) between a grandparent and grandchild (F = ), and; 3) between first cousins (F = ). Please refer to Appendix F.3 for the simulated pedigrees for details).
To evaluate the estimate of heterozygosity on a small but substantial chromosomal region due to the demanding computational resources, we subsampled the first 15 Mbp of chromosome 1 and ran ROHan, ATLASv1.0 and ANGSD v0.919-14 (refer to Appendix G for the precise commands). For ANGSD, we used the recommended genotype likelihood model (“-GL 1”) for estimating θ (see Appendix G for a brief discussion regarding this parameter). We evaluated the robustness of such software to low coverage, aDNA damage, and various effective population sizes. As the original sequence of the chromosomes used for simulation was available, we could evaluate the number of segregating sites at both the local and global levels.
We also evaluated BCFtools/RoH (Narasimhan et al. 2016) using version 1.4.1 of BCFtools and PLINK (Purcell et al. 2007) v1.90 to assess their accuracy to predict large and medium size ROH compared to ROHan. We simulated an extra 1000 chromosomes in msprime and used the allele frequencies from those. The population providing these 1000 chromosomes was the same as the one from which the 16 haploid chromosomes were taken from as to provide an ideal test set. However, to test the robustness of BCFtools/RoH to allele frequencies from more distant populations, we repeated the simulations by joining the population from which the BAM files are generated and the population providing the allele frequency farther back in time, arbitrarily at 150 and 500 KYA. The former case would correspond to trying to infer ROHs in an ancient Khoe-Sān individual and the latter in a Neanderthal individual while using allele frequencies from a Eurasian population.
Data availability
The authors state that all data necessary for confirming the conclusions presented in the manuscript are represented fully within the manuscript. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.8251400.
Results
Simulated data
Local heterozygosity estimates:
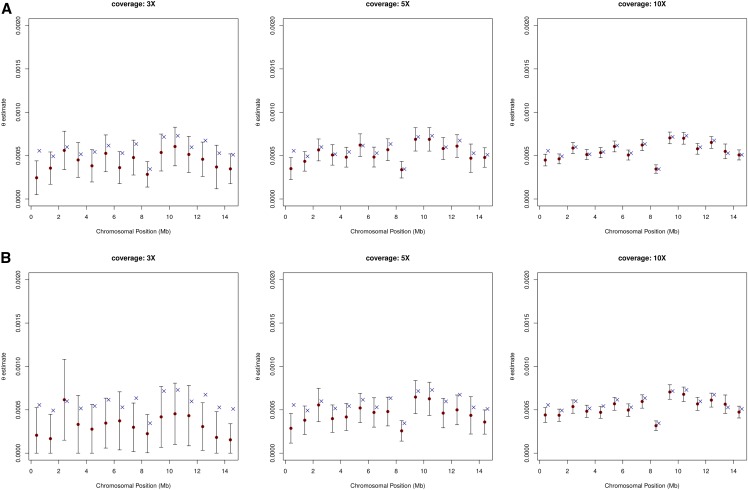
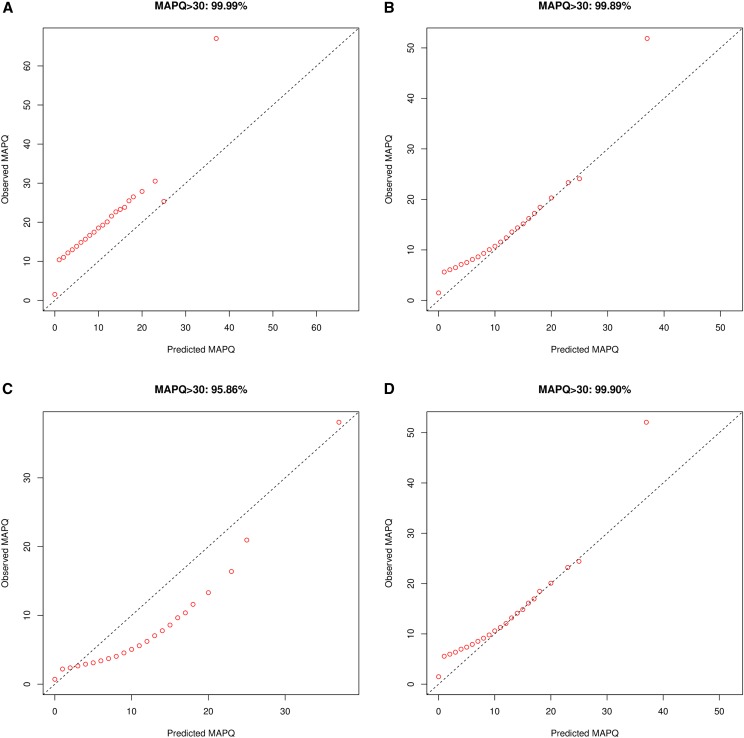
We start by evaluating ROHan’s ability to estimate local heterozygosity rates using genomic windows of 1 Mb and simulated data. As mentioned above, ROHan computes local estimates of heterozygosity rates which are then used to infer the genome-wide estimate of θ. As we have the sequence of the chromosomes used in the simulations, we could compare the estimated rate of heterozygosity to the simulated one. The results in absence of post-mortem DNA damage and for various depth of coverage are found in Figure 3. For coverage equal to 3×, we find that the point estimate is generally inferior to the expected value and that confidence intervals are large. At 5× coverage, we find narrower confidence intervals and point estimates closer to the expected value. This trend toward higher precision and accuracy is confirmed when increasing coverage to 10×. It is noteworthy that the first genomic window seems to be consistently underestimated in our experimental framework, probably due to a poor correlation between the reported and true mapping qualities or due to the lower mappability of the region (16% of the first window of 1 Mbp consisted of unresolved bases (“N”) whereas 3.7% of the first 15 Mbp were unresolved).
Figure 3.
Comparison between the simulated local rates of heterozygosity vs. the predicted ones using windows of 1 Mbp for simulated data without any aDNA damage patterns at various rates of coverage. The original 30× simulated data were downsampled at 3× (left), 5× (middle) and 10× (right) and the effect on the predicted rate of heterozygosity at a local level was compared to the simulated one using an effective population of 7000. (A) Simulations without aDNA damage. (B) Simulations using the high damage patterns of the ATP2 sample. The red dot represents the maximum-likelihood point estimate, the black whiskers represent the 95% confidence interval and the dark blue cross represent the simulated value.
The Supplemental Material (see Supplemental Material, Figures S1–S6) provides the results of more extensive simulations, including effective population sizes of 3000 and 9000, coverage variation between 3, 5 and 10×, and for various types of nucleotide misincorporation patterns due to the ancient DNA damage. At , we notice large confidence intervals at a coverage of 3× regardless of the damage patterns considered. For samples greatly affected by post-mortem damage (e.g., the ATP2 sample), ROHan even fails to produce confidence intervals overlapping with the expected value, and often provides underestimates. For this type of damage patterns, the results improve in accuracy with a coverage of 5×. However one can still see the impact of having a high rate of aDNA damage on both precision and accuracy. At 10× coverage, there is little difference in terms of accuracy between the sample with heavy damage compared to the ones with either very little or no damage at all. Although the confidence interval obtained generally comprises the expected value, the point estimate recovered is generally slightly underestimated.
Global heterozygosity estimates:
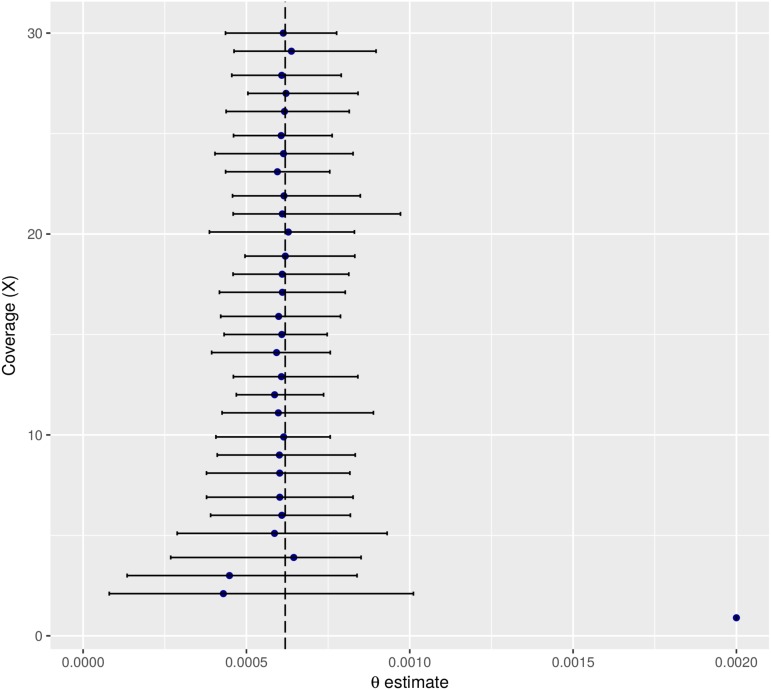
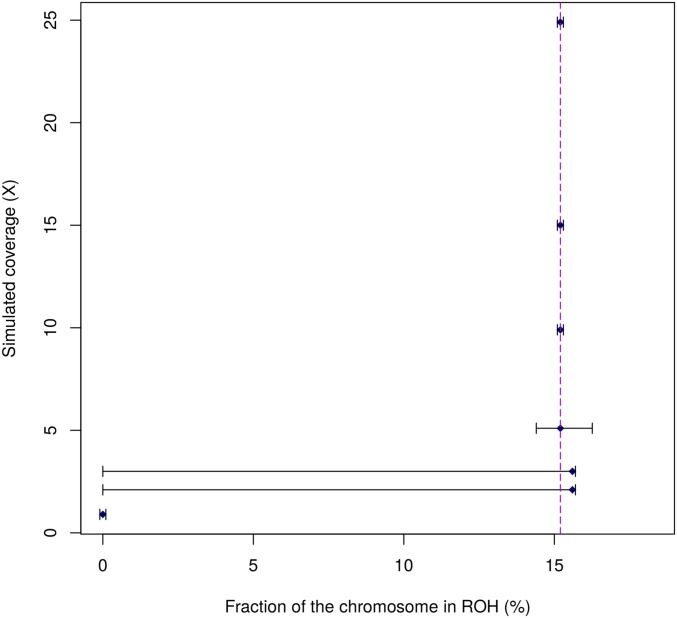
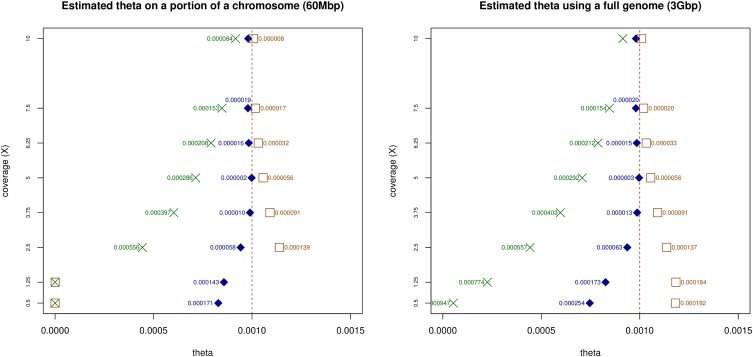
In ROHan, the local estimates of heterozygosity are used together with an HMM to compute the genome-wide estimate of Watterson’s θ. We compared the simulated value for the entire 15 Mbp of simulated data to the global estimates of θ for the same data. This was done for various levels of heterozygosity, aDNA damage and coverage. The results obtained when considering a sample with medium rates of damage associated with a double-stranded DNA library building protocol can be found in Figure 4. The remaining results obtained can be found in the Supplemental Material (see Figures S7–S11).
Figure 4.
Global estimate of θ using 15 Mbp of simulated data at various coverage with an of 9000 and simulated damage rates from the La Braña sample, showing medium rate of post-mortem damage. The dotted line represents the target rate of heterozygosity.
In general, the only time where the confidence interval did not include the simulated values was at 0.9× for the cases with medium and high rates of aDNA damage associated with a double-stranded DNA library building protocol. However, analyses carried out on the basis of 1×–3× coverage data were imprecise. From coverage of 8× and above, the point estimate recovered was stable and close to the simulated value (although slightly underestimated), regardless of the amount of aDNA damage considered. Decreasing coverage generally resulted in underestimated values.
We compared our results to those obtained with ATLAS and ANGSD, using the same 15 Mbp simulations (see Figures S12–S24). In general, we found that ATLAS undercompensated for either sequencing errors or aDNA damage, which leads to overestimates in the value of θ. This issue is consistent at a coverage of 10× or higher, but can be introduced at lower coverage depending on the aDNA damage level considered. Furthermore, the confidence interval for the point estimate rarely includes the expected value. While ANGSD does not provide confidence intervals, it consistently returns underestimated values in absence of aDNA when coverage is inferior to 10×. In the presence of little to moderate aDNA damage, largely overestimated values are returned, however, the recovered estimates converge to the expected value given sufficient coverage (20×–30×). In the presence of high levels of aDNA damage, ANGSD consistently returns largely overestimated values, regardless of the coverage considered. We found that this effect could be mitigated by disregarding transitions (C,G T,A transitions are the most prevalent nucleotide misincorporation resulting from post-mortem damage (Briggs et al. 2007)) and restricting the analyses to transversions only. For instance, using an effective population size of 9000, using only transversions can help the point estimate converge to the expected value as long as high-coverage data (15×–20×) are provided (see Figure S21).
As some sequencing runs can have very high error rates, we sought to test whether ROHan’s model for sequencing errors was robust to elevated sequencing error rates. We repeated the simulation while increasing the rate of sequencing errors to 1.6% which represents a 10 fold increase compared to previous simulations, first in the absence of aDNA damage (see Figure S31). The results indicate that generally, ROHan is sufficiently robust as long as coverage equal to 4× and above are considered. When high sequencing error rates are combined the highest levels of simulated aDNA damage, the point values recovered appears consistently underestimated until high-coverage data are available (20×–25×) but the confidence intervals include the expected value from coverage values above 10×.
To further assess how effective ROHan was in handling post-mortem cytosine deamination (which introduces an excess of nucleotide misincorporations in the sequencing data), we re-ran ROHan but forcing the model’ probabilities of aDNA damage to zero. Results show that while the estimates retrieved on simulations carried out in the absence of aDNA damage were accurate, those carried out in the presence of increasing levels of aDNA damage consistently returned overestimates, regardless of the coverage considered (see Figure S26). This is expected as an underestimate of the error mechanically leads to an overestimate of θ. We also sought to evaluate how errors in evaluating damage rates would impact the final θ estimates. Our results show that errors in estimating damage rates of 15–20% do not seem to have a significant impact on the genome-wide estimate (see Figure S27). As previously mentioned, scripts to evaluate rates of damage are provided with the software. To test the accuracy of such scripts, the rate of evaluated damage was compared to the simulated one and their impact on θ was evaluated (see Supplemental Section S.1.1.5). Rates of aDNA damage while accounting for potentially polymorphic positions seem to be correctly evaluated on samples with a coverage of 4× and above and point estimates for θ seem accurate for coverage of 7× and above using the highest rates of simulated aDNA damage.
Finally, we sought to test whether blending two different libraries with drastic different rates of aDNA damage has a significant impact on the predicted rates of heterozygosity. Such situations can happen when different molecular tools are used during library preparation (Rohland et al. 2015), and when different extracts from the same individual are used during library preparation (Seguin-Orlando et al. 2014) (see Figure S28). As expected, the measured rates of damage on the new dataset was intermediate between the ones of the original sets (i.e., aDNA data showing the highest damage levels and no damage, respectively). Although the point estimates were consistently underestimated for all coverage considered (2× – 28×), all confidence intervals retrieved intercepted the expected values. Relatively accurate point estimates were obtained from 10× to 12× coverage and above.
In terms of runtime, running ROHan on a 10× dataset consisting of the human chromosome 1 (250 Mbp), and using eight Intel Xeon cores at 2.20 GHz took 55 m and ∼3.3 G of RAM for the estimate of the local heterozygosity for a modern sample (i.e., no damage). For a sample with deamination (damage from the La Braña sample), the runtime was ∼53 m and the memory usage reached 7.7 G. Running the HMM to map ROHs took 8m54s on a single core.
Infer ROHs in inbreed samples:
We tested ROHan, PLINK and BCFtools/RoH on a simulated chromosome corresponding to human chromosome 1 for various inbreeding scenarios as well as different levels of coverage. For inbreeding scenario 1 (mating between full siblings) and in the absence of aDNA damage, we find that ROHan can accurately estimate the total proportion of the genome in an ROH using windows of 1 Mbp for the estimate of the local heterozygosity as long as at least 5× coverage data are provided (see Figure 5). The results for the remaining inbreeding scenarios indicate similar performance and are presented in the Supplemental Results (see Figure S34).
Figure 5.
Estimates of the proportion of the genome in an ROH as predicted by ROHan on a simulated full chromosome of 250 Mbp at various depths of coverage compared to the simulated rate using the original simulated chromosomes from the diploid organism. The proportion of ROH reflects inbreeding between siblings. The dotted line represents the target fraction of the genome in a ROH obtained from the simulated chromosome. Whiskers represent the 95% confidence interval. Both the detection of segregating sites for the computation of the theoretical value as well as ROHan used a window size of 1 Mbp.
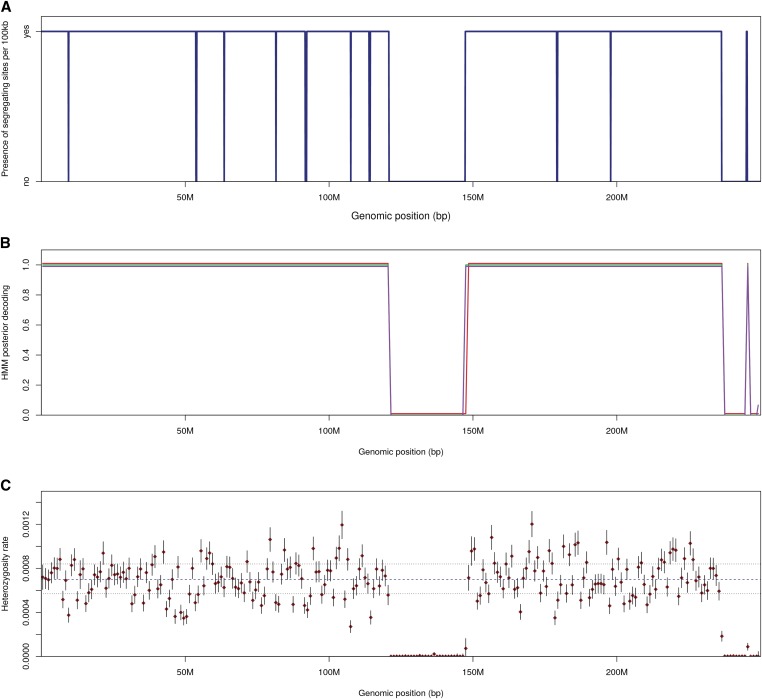
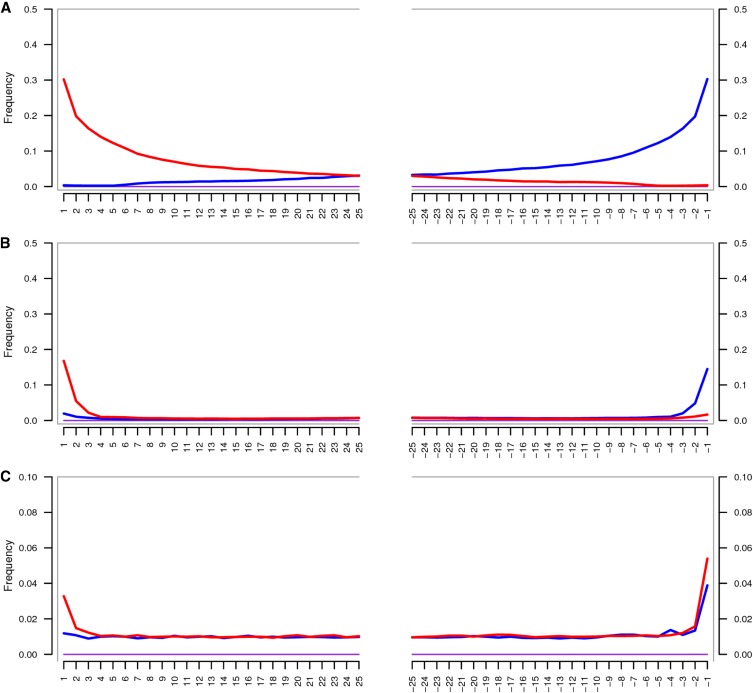
A visualization of the output for a single chromosome can be found in Figure 6. Expectedly, the ROHs delineated by ROHan were found to be of uneven sizes due to uneven recombination rate across the chromosome (see Figure S33 for the distribution of segregating sites). Both the centromere region and the last portion of the chromosome were associated with a local depression of the heterozygosity rate and were correctly decoded by ROHan. The accuracy achieved for different coverage and window sizes for the local estimate of heterozygosity can be found in the Supplemental Results (see Figures S35–S41). In short, when using large windows for the local estimates of heterozygosity (500 kb–1 Mb), large ROH can be confidently identified at 1× coverage and above. However, full accuracy starts at a coverage of 5× for large ROHs of at least 1 Mb. Using smaller windows for estimating local h values (100–250 kb) generally leads in the correct identification of ROHs if data at 5×–10× coverage are provided.
Figure 6.
Visualizing ROHan’s output on a simulated inbred chromosome at a coverage of 6.9× where both parents are siblings. (A) The distribution of segregating sites on the chromosome using windows of 100 kbp to show smaller ROHs. The absence of segragating sites indicates over a large region indicates an ROH. (B) The HMM posterior probability decoding of not being in an ROH. The red line corresponds to the estimate obtained using the lower bound for the local estimates of heterozygosity, the green line to the point estimate (mid-points) and the magenta line using the upper bound. (C) The local heterozygosity estimate with a window size of 1 Mbp where the dotted lines represent the global θ estimate using the lower, mid and upper bounds. The red dots represent the point estimate of the local heterozygosity rate. The vertical lines correspond to the 95% confidence intervals for that given locus.
Comparison to existing tools reveals that PLINK seems to reliably predict large ROHs at a coverage of 10× and above but also seems to overpredict some small ROHs, an effect which tends to disappear as coverage increases (see Figure S42). In comparison, the results for BCFtools/RoH for both long and short ROHs seem stable at 10× and above but seems to predict fewer small ROHs compared to PLINK (see Figure S43). However, the allele frequencies used for computation were selected to be perfectly known. Therefore, this simulation framework does not assess the method’s performance in the case where allelic frequencies are obtained from a distant population. To test the robustness of BCFtools/RoH to this, we repeated the test using join times between the lineage providing the allele frequency and the simulated chromosomes at 150 and 500 KYA (see Figures S44 and S46, respectively). At a split time of 150 KYA, large ROHs could be detected at ∼5–10× but the signal was too unstable to resolve short ROHs. Using a split time of 500k years, even large ROHs were difficult to delineate, regardless of the coverage considered.
As ROHan requires the user to specify the size of the genomic window used for the estimate of local rates of heterozygosity, we finally sought to evaluate the accuracy of our methodology if different sizes of genomic windows were specified. To achieve this, we ran ROHan on two simulated sets, with a simulated of 3000 and 9000 respectively and with window sizes of 100, 250, 500 and 1000 kbp. The results for such tests are found in the Supplemental Results section (see Figures S29 and S30). We found that when using smaller windows of 100 kbp, confidence intervals tend to be stable ∼8–10×. For windows of 250 kbp, a coverage of 7–8× and above is recommended whereas for windows of 500 kbp, we obtain reliable estimates at a coverage of 6–7× and above. Finally, for windows of 1 Mbp, confidence intervals seem stable ∼5× and above. Due to limited computational resources, it should be noted that these tests were run without added simulated aDNA damage.
Empirical samples
In the following section, we applied our methodology to empirical data, where in contrast to simulations, the correct value of the heterozygosity rate or the location of ROHs are not known in advance. As our methodology is both applicable to ancient and modern samples and human as well as non-human animals, we investigated all four possibilities. Overall, we found that our results mostly agreed with previously reported estimates, excepting a few cases where the new estimates recovered appear to be more consistent with the literature.
Modern samples
Humans:
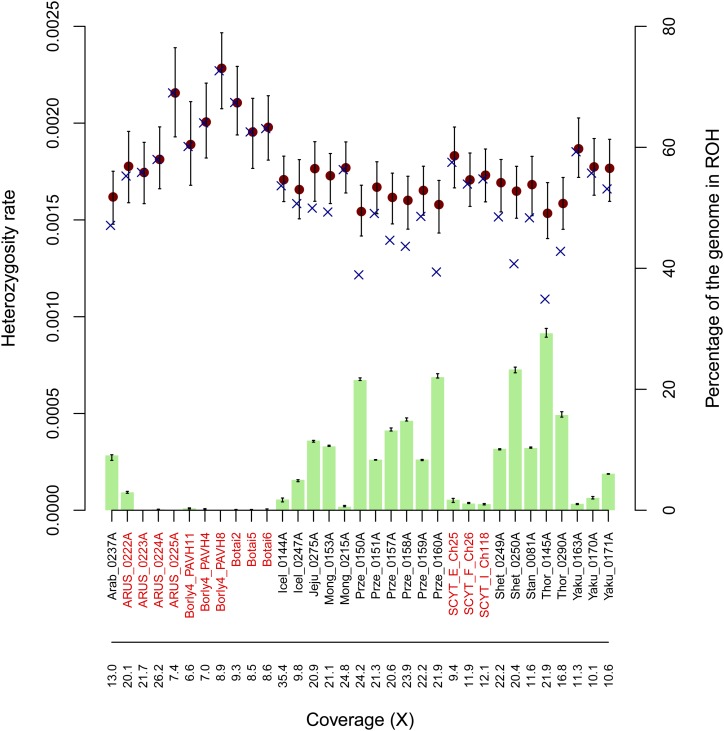
We first downloaded 26 present-day human genomes in BAM format from 1000 Genomes Project Phase 3 (1000 Genomes Project Consortium et al. 2015), all of which had relatively limited coverage (7.8× on average). We sought to evaluate (1) whether the genome data are indicative of inbreeding in these individuals and (2) whether the genome-wide θ estimates recovered from ROHan are compatible with the ones obtained by the Simons Genome Diversity Project (Mallick et al. 2016) which had access to data at a much higher depth of coverage for the same populations (43× on average). We considered various individuals with ancestry from Africa, Eurasia and Indigenous People of the Americas. It is expected that heterozygosity will vary according to drift and that individuals of African ancestry will have the highest heterozygosity rate (Ramachandran et al. 2005).
We found that only four the 26 individuals considered showed signs of minor inbreeding (i.e., ∼0.03–0.17% of their genome consisted of ROHs; see Table 2). The results for the remaining individuals are found in the Supplemental Results (see Table S4). We also found that our estimates of θ for these low-coverage individuals were consistent with the ones obtained by Mallick et al. (2016) while using higher coverage genomes. This shows the robustness of our method to samples with lower coverage.
Table 2. Estimated values of θ for human samples with medium coverage.
| sample IDa | pop. code | coverage (×) | ROHan | from | in ROH (%) | ||
|---|---|---|---|---|---|---|---|
| θ | SGDPb | ||||||
| HG02367 | CDX | 7.2 | 8.059 | 6.873 | 9.301 | 7.937–8.218 | 0.138 |
| NA21141 | GIH | 7.8 | 9.099 | 7.998 | 10.209 | 8.636c | 0.069 |
| HG04222 | ITU | 8.2 | 9.248 | 8.186 | 10.323 | 8.266–8.875 | 0.173 |
| HG03139 | ESN | 7.3 | 11.498 | 10.166 | 12.866 | 10.923–11.441 | 0.035 |
Four different individuals from the 1000 Genomes Project Phase III (1000 Genomes Project Consortium et al. 2015) for which minor amounts of long ROHs were detected. The population codes are as follows: CDX, Chinese Dai in Xishuangbanna; China GIH, Gujarati Indian from Houston; Texas ITU, Indian Telugu from the UK; ESN, Esan in Nigeria. ROHs inferred on chromosome 11 are plotted in Figure S48.
reported θ from the same population.
closest from Kashmiri Pandits.
To further test the robustness of our method to lower depths of coverage, we downloaded five individuals from the Simons Genome Diversity Project (Mallick et al. 2016) from five distinct populations: Bergamo, Czech, Karitiana, Japanese and Yoruba. Duplicates were removed using samtools’ rmdup and the bam files were subsampled using samtools view to coverages between 1 and 30 (Li et al. 2009). Our results show that at high coverage, our estimates of heterozygosity are on par with the ones reported in the original publication (see Figure S50). ROHan’s estimates seem to be robust down to coverages of 3–4×.
non-Humans:
We next considered the high-coverage chimpanzee data from (de Manuel et al. 2016), including three animals from three different geographical locations in Africa (Western, Central and Eastern) and sequenced at an average coverage of 24.6× (Table 3). In the original publication, heterozygosity rates were reported on an individual basis and Watterson’s θ were computed for each of the three populations using G-PhoCS (Gronau et al. 2011). Using ROHan, we found little evidence of large ROHs in those samples. Consistently with the original publication, we find Central chimpanzees to have a greater effective population size than the Eastern ones which in turn, have a greater effective population size than the Western chimpanzees. The genome-wide θs reported for each individual by ROHan are consistent with the ones reported by G-PhoCS for their population of origin and significantly larger than those originally reported by de Manuel et al. (2016). These per-individual heterozygosity rates reported in the original publication were computed by filtering the genotype calls using genotype quality. ROHan estimates also appear on par with the estimates produced by another method (ANGSD), which we demonstrated on the basis of simulations to converge to the correct value at equivalent coverage. As all three programs reported higher levels of heterozygosity than the original ones computed on genotype calls, it is therefore more likely that these heterozygosity rates were slightly underestimated, possibly due to the filtering by genotype quality.
Table 3. Estimated values of θ for chimpanzee samples with high coverage.
| sample IDa | population | coverage (×) | ROHan | ANGSD | reported heterozygosityb | |||
|---|---|---|---|---|---|---|---|---|
| θ | in ROH (%) | θ | ||||||
| Bwambale | Eastern | 20.9 | 18.373 | 16.930 | 19.841 | 0–0.0358 | 15.050 | 12.9 (15.6 *) |
| Lara | Central | 25.2 | 19.968 | 18.685 | 21.463 | 0–0.504 | 18.042 | 14.7 (22.7 *) |
| Linda | Western | 27.6 | 8.6686 | 7.8807 | 9.520 | 0–0.649 | 8.042 | 6.2 (8.3 *) |
Estimates of genome-wide θ by ROHan, ANGSD and from the original publication for three chimpanzees from Western, Central and Eastern Africa. * The first number was the heterozygosity estimate on the individual itself whereas the second number was the estimate for Watterson’s θ for the population.
from de Manuel et al. (2016).
Ancient samples
Humans:
We next used publicly available ancient hominin genomes sequenced in various aDNA research centers and encompassing a full range of post-mortem DNA damage to estimate genome-wide θ and detect ROHs using ROHan. For comparison purposes, we ran ANGSD with and without including transitions in the calculation. We also report the heterozygosity rate previously measured, if available (see Table 4).
Table 4. Estimated values of θ for ancient hominin samples.
| sample | ANGSD | ROHan | coverage | damagea | reported | source | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| name | θ | b | θ | (X) | 5 | 3 | or | |||
| Vindija 33.19 | 3.477 | 1.836 | 1.973 | 1.531 | 2.402 | 26.49 | 36.11 | 38.16 | 1.6 | c |
| Barçın 31 | 13.330 | 0.346 | 3.695 | 1.723 | 5.805 | 3.14 | 35.49 | 33.19 | N/A | d |
| Andronovo 505 | 7.526 | 2.823 | 5.761 | 4.829 | 6.745 | 9.47 | 13.96 | 13.94 | N/A | e |
| Loschbour | 5.441 | 5.403 | 7.514 | 6.430 | 8.271 | 17.67 | 4.04 | 1.79 | 4.75–6.62 | f |
| Wezmeh Cave 1 | 6.803 | 4.056 | 8.079 | 6.988 | 9.218 | 12.74 | 22.04 | 23.13 | 11.0 | g |
| Stora Karlsö 12 | 7.501 | 7.835 | 8.593 | 7.964 | 9.233 | 86.62 | 3.52 | 21.77 | N/A | h |
| Stuttgart | 7.137 | 6.727 | 8.761 | 7.758 | 9.650 | 19.59 | 4.14 | 4.42 | 7.42–10.59 | i |
| Ust’-Ishim | 7.662 | 7.732 | 9.859 | 8.741 | 10.641 | 36.00 | 2.56 | 4.95 | 7.7 | j |
Rate of C to T substitutions at the 5′ end and G to A at the 3′ end. For samples that used the single-stranded DNA protocol for library preparation, the rate of C to T is reported at the 3′ instead of the G to A.
ANGSD’ is the θ estimate using only transversions and multiplying the estimate by +1 (3.1).
We found a very low rate of heterozygosity for the Vindija Neanderthal 33.19 sample, despite the presence of extensive aDNA damage signatures. Likewise, for the Stuttgart early Neolithic farmer, both ANGSD’s and ROHan’s θ estimates are similar to the one obtained in the original publication by Lazaridis et al. (2014). However, for both the Loschbour and Ust’-Ishim hunter-gatherers, ROHan estimates seem slightly higher than the ones originally reported. In general, ROHan estimates are consistent with those obtained by ANGSD using transversions only, except when low-to-moderate coverage data are available (e.g., Barcin 31, Andronovo505 and Wezmeh Cave 1, sequenced at 3.14, 9.47 and 12.74× coverage, respectively). For the Wezmeh Cave 1 early Neolithic farmer sample from Broushaki et al. (2016), the obtained heterozygosity rate using both ANGSD and ROHan are not consistent with the estimates reported by the original publication which were computed using ATLAS. Following the results from our simulations, we can assume that, at an equivalent coverage (13×), ANGSD provides underestimates of θ while ATLAS provides overestimates. ROHan is expected to return accurate estimates, albeit at the cost of large confidence intervals. This is consistent with our observations.
Subsampling the Neanderthal Vindija 33.19 sample down to 1× provided an ideal empirical test case of the robustness of our method, in case it is applied to a difficult sample combining both high levels of aDNA damage and very low rates of heterozygosity. We obtained confidence intervals encompassing the global heterozygosity estimates retrieved from the full data at a coverage of 9× and above (see Figure S49). However, the point values retrieved for coverage inferior to 12× were consistently underestimated. Furthermore, the estimates of rates of aDNA damage at the highest coverage (30×) seemed robust (down to 4×) to subsampling the data to a lower coverage (See Table S5).
non-Humans:
We next sought to evaluate the heterozygosity of one ancient dog from Ireland, which dates back to 4.8 KYA and whose genome was sequenced in Frantz et al. (2016). Raw reads were downloaded from the European Nucleotide Archive (ENA), trimmed using leeHom v.1.1.5 (Renaud et al. 2014) and aligned using BWA (Li and Durbin 2009) 0.5.10. Using ROHan, we obtained an estimate of genome-wide θ of 1.29 10−3 (95% confidence interval: 1.18 10−3–1.42 10−3). The estimate retrieved in ANGSD when considering all substitution types was more than doubled (θ = 2.97 10−3). However, restricting the analysis to transversions only lowered the θ estimate to 0.99 10−3 as the original sample had extensive damage. In this case, the estimate was obtained by multiplying by +1 (3.1) to obtain a comparable value (including both transitions and transversions). Both the original and ROHan estimates are in agreement with previously reported values of θ for modern wolf and dog breeds (Wang et al. 2013).
Finally, we ran ROHan on 13 ancient and 20 modern horse genomes as an example of domestic animals were ROHs could potentially be identified.
Specifically, the 20 modern domestic horses represented a wide range of breeds, including Arabian (Arab_0237A), Mongolian (Mong_0153A, Mong_0215A), Thoroughbred (Thor_0145A, Thor_0290A), Yakutian (Yaku_0163A, Yaku_0170A, Yaku_0171A), Icelandic (Icel_0144A, Icel_0247A), Jeju (Jeju_0275A), Standardbred (Stan_0081A) and Shetland horses (Shet_0249A, Shet_0250A) (Wade et al. 2009; Kim et al. 2013; Do et al. 2014; Jäderkvist et al. 2014; Metzger et al. 2014; Der Sarkissian et al. 2015; Frischknecht et al. 2015; Librado et al. 2015; Leegwater et al. 2016), as well as six endangered Przewalski’s horses (Prze_0150A, Prze_0151A, Prze_0157A, Prze_0158A, Prze_0159A, Prze_0160A) (Der Sarkissian et al. 2015). The 13 ancient horses considered spanned a large temporal range, from the 19th century to 43 KYA, and represented both wild horses that lived prior to domestication, Eneolithic early domesticates and Iron Age domesticates (Schubert et al. 2014; Librado et al. 2015, 2017; Gaunitz et al. 2018). More specifically we have Yakutian (ARUS_0222A), ancient Russian horses (ARUS_0223A, ARUS_0224A, ARUS_0225A), from the Borly4 site in Kazakhstan (Borly4_PAVH11, Borly4_PAVH4, Borly4_PAVH8), the Botai culture (Botai2,Botai5, Botai6) and Scythian kurgan (SCYT_E_Ch25, SCYT_F_Ch26, SCYT_I_Ch118). Corresponding results are presented in Figure 7.
Figure 7.
The predicted genome-wide θ for several ancient and modern horse samples. ROHan’s θ point estimates outside ROHs are shown as brown dots, together with their confidence intervals. Genome-wide estimates including inferred ROHs are indicated with a blue cross, while the green bars indicate the total fraction of the genome consisting of ROHs. The population of origin and the original names of the different horse samples are found in Table S6.
We found that the individual used while sequencing the horse reference genome (Twilight (Wade et al. 2009)) showed the largest fraction of the genome within ROHs. This is not surprising as this individual was selected to facilitate the genome assembly due to its extreme inbreeding levels. Likewise, we found that the six endangered Przewalski’s horses have a substantial fraction of their genome in ROHs, in line with previous estimates (Der Sarkissian et al. 2015). Even when masking ROHs, the estimates of θ are in the lower range of those estimated in all other samples, be it modern or ancient. This is expected for a population founded in the early 20th century from a limited number of only 12–15 founders (Der Sarkissian et al. 2015). Interestingly, Eneolithic early domesticates from the Botai culture (Botai2, Botai6, Botai5) and the Borly4 archaeological site (Borly4_PAVH4,Borly4_PAVH8,Borly4_PAVH11) have recently been shown to represent the direct ancestors of modern Przewalski’s horses (Gaunitz et al. 2018). Their genome was characterized by no detectable inbreeding and was associated with higher θ estimates, in line with the demographic collapse that followed the discovery of Przewalski’s horses in the late 19th century (Der Sarkissian et al. 2015).
We found that three wild horses that lived 5–43 KYA, and that belonged to a now-extinct archaic lineage (Schubert et al. 2014; Librado et al. 2015), also carried genomes showing no inbreeding. However, the θ estimates returned for the 16k years-old animal (ARUS_0225A) were higher than those returned for the other two individuals (ARUS_0223A and ARUS_0224A), despite these being sequenced to an average coverage of 7.4×, 21.7× ad 26.2×, respectively. No such genomes were sequenced using molecular tools limiting the impact of post-mortem DNA damage. Recalling our simulation results showing that ROHan θ point estimates were generally underestimated when limited coverage was available, and that precise estimates are difficult to obtain in the presence of extensive DNA damage, we consider that additional data are necessary before the true heterozygosity of individuals belonging to this lineage is determined. Similarly, we anticipate that the θ point estimates recovered for the three Scythian domesticates (SCYT_E_Ch25, SCYT_F_Ch26, SCYT_I_Ch118) considered here are likely to be in fact underestimated, given that these were only sequenced to an average coverage between 9.4 and 12.1×. To further assess the impact of post-mortem DNA damage on θ estimates, we reran ROHan on seven modern horse samples, including four Przewalski’s horses, forcing the model to account for aDNA damage. We obtained lower θ estimates by an average of 1.3 segregating sites per 10 kbp which represents an average of 9% of the original θ value returned (see Table S7). This demonstrates that our damage model can over-penalize the substitutions present in the sequencing data as long as they show similar signatures of post-mortem damage, skewing the θ point estimates downward on ancient individuals. Analyses comparing ancient and modern genome data should correct such bias if they are aimed at quantifying genetic diversity loss through time.
Discussion
We have explained our methodology for jointly inferring ROHs and the genome-wide θ for regions flagged outside ROHs. Using simulations, we found that both our model and state-of-the-art methods cannot provide reliable estimates in the presence of limited coverage data and/or post-mortem DNA damage, unless significant amounts of data are available. For modern samples, the point estimate for θ seems to be underestimated for samples with coverage inferior to 5×–6×. For ancient samples showing substantial levels of post-mortem DNA damage, a minimal coverage of 8×–10× is required to retrieve meaningful point estimates. In all simulations, ROHan returned more accurate genome-wide θ estimates than existing tools, especially with limited coverage data. We mentioned that users must supply the desired window size for the local heterozygosity estimates and the sensitivity to short ROHs depends on this window size. The choice of the window size depends on available coverage where higher coverage allows for smaller window sizes for the local estimate of heterozygosity. This also entails that our method is not suited for measuring distant and continuous inbreeding. Another limitation is that we do not account for present-day (human) contamination or exogenous DNA such as microbial contamination in aDNA samples, which can disrupt sequence diversity patterns underlying otherwise long blocks of low heterozygosity. Such situations are expected to reduce the length of inferred ROHs.
Our tests with BCFtools/RoH show that having accurate allele frequencies can improve the inference accuracy while delineating ROHs. However, using allele frequencies can also add biases, as the analyzed samples do not necessarily belong to the panel population used for estimating the genome-wide distribution of allele frequencies. The impact of such an ascertainment bias can be especially acute in non-model organisms and non-human animals such as domesticates, where breeds of economical relevance generally retain most of the research focus.
A drawback of our approach entails to the use of quality scores as being representative of the true probability of a sequencing error. This would be especially problematic in the presence of batch effects, i.e., when comparing two samples not sequenced with the same technology and/or instrument, or if different basecallers were used. Any underestimate of the real probability of error will lead to an overestimate of heterozygosity and vice-versa. This is shown in the analyses that considered that aDNA damage could be present in modern samples, which resulted in a significant drop in the θ point estimate recovered. This suggests that the presence of even limited amounts of sequencing errors showing signatures similar to those observed in ancient samples can significantly impact estimates. Reciprocally, it follows that overestimating rates of aDNA damage in ancient samples will lead to underestimates of the rate of heterozygosity. Since our methodology expects users to provide rates of damage that exclude potential polymorphic positions and sequencing errors, we recommend caution when comparing ancient samples to modern samples, or to other ancient samples that either have been analyzed using different molecular tools or show drastically different rates of aDNA damage.
Another problematic aspect is flagging regions with a low number of segregating sites as either ROHs or non-ROHs regions. A low mutation rate in a specific region of the genome or recent positive selection can results in regions with a low number of segregating sites. Furthermore, individuals with a small effective population size will have genomic windows with a low number of segregating sites by chance. On the other hand, genuine regions with ROHs can have some levels of segregating due to de novo mutations, be it germline or somatic. As both scenarios are difficult to tease apart, our algorithm will hesitate to identify these regions as ROHs or non-ROHs and the probability of assignment to either class will be low. We recommend care when identifying ROHs using ROHan on samples with a very low value of θ in non-ROHs regions and caution that the probability of being in an ROH which is produced by our method should also be considered.
Throughout the manuscript, we have assumed that for an aDNA sample, an individual is composed of a single library. This can potentially affect our computations as the rates of aDNA damage are provided by the user and can sometimes represent the average across the genome for all libraries. Ideally, we should allow users to provide read group specific aDNA damage rates. This approach however is likely to require additional RAM as the computation for the nucleotide substitutions are pre-computed and stored for speed as the cost of memory. Other avenues for further improvements of our model include accounting for base compositional bias, such as %GC bias, which can introduce uneven coverage along the genome and potentially skew the weights considered for the likelihoods function. This effect might be magnified in those ancient genomes showing patterns of depth-of-coverage variation on par with nucleosomal protection (Pedersen et al. 2014; Hanghøj et al. 2016).
Acknowledgments
We would like to thank Anders Albrechtsen, Martin Sikora, Fernando Racimo, Pablo Librado and Filipe Vieira for help running software, helpful discussions and feedback. We are indebted to Laurent Frantz for questions relating to ancient dog data as well as Martin Kuhlwilm and Marc de Manuel Montero for providing us access to the chimpanzee data. We also would like to acknowledge Ziheng Yang, Jerome Kelleher and Vagheesh Narasimhan for their help running software. G.R. was supported by a Marie-Curie Individual Fellowship (MSCA-EF-752657). This work was supported by the Danish National Research Foundation (DNRF94); Initiative d’Excellence Chaires d’attractivité, Université de Toulouse (OURASI), and; the Villum Fonden miGENEPI research project. We also thank The Lundbeck Foundation, the Carlsberg Foundation, the Novo Nordisk Foundation and KU 2016. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 681605).
Appendix A: Weighted Likelihood
Maximum-likelihood methods tend to be very sensitive to the assumptions made about the data and outliers (Astrom 1979). If the data deviate from the assumptions made, a potential problem is that the algorithm might yield an incorrect estimate.
Filtering by mapping quality is not immune to copy number variation (CNVs), and mapping qualities are in this case often miscalculated (Ruffalo et al. 2012; Langmead 2017). The depth of coverage can be indicative of a CNV at a specific site (Fromer et al. 2012). To mitigate the impact of potential CNV, previous studies have often filtered sites by applying a minimum (Meynert et al. 2014) or maximum (Li 2014) depth filter. Furthermore, it is also possible that two reads sampled from two different genomic locations find themselves mapped to the same location, and that the mapping quality does not fully reflect this as the original location of one read is not detected by the mapper. Similarly, it is possible that two reads sampled from a single location get mapped to two different locations.
Initial attempts have shown that the unweighted likelihood function was not sufficiently robust to very low coverage samples, whereby the confidence intervals were not sufficiently large. At very low genome-wide coverage (i.e., 3×) it is difficult to ascertain whether all of the DNA fragments mapped at a specific site are genuinely stemming from this particular location.
For instance, if a site has coverage 2× for a sample with a genome-wide coverage of 3×, it could be that (i) all of the fragments were correctly matched at the correct location; (ii) we sampled from two original genomic loci with a coverage of 1× each, and they got mapped to the same location in the reference genome used; (iii) we sampled three reads from a single original genomic location, which got separated into two genomic loci in the reference genome, one having a coverage of 2× and the other having coverage of 1×. At a genome-wide coverage of 3×, it is difficult to tease these three scenarios apart.
However, at higher genome-wide coverage (20×), it is easier to state that the majority of fragments mapped to the specific site are unlikely to have been generated by a CNV. The aforementioned three mismapping scenarios at a genome-wide coverage of 20× are much more unlikely, as we can compute the probability of sampling 10 or 40 reads using a Poisson distribution with a lambda of 20. Furthermore, we sought to downweight sites with coverage outside the expected value (e.g., a site with coverage of 50× where the genome-wide average coverage is 10×).
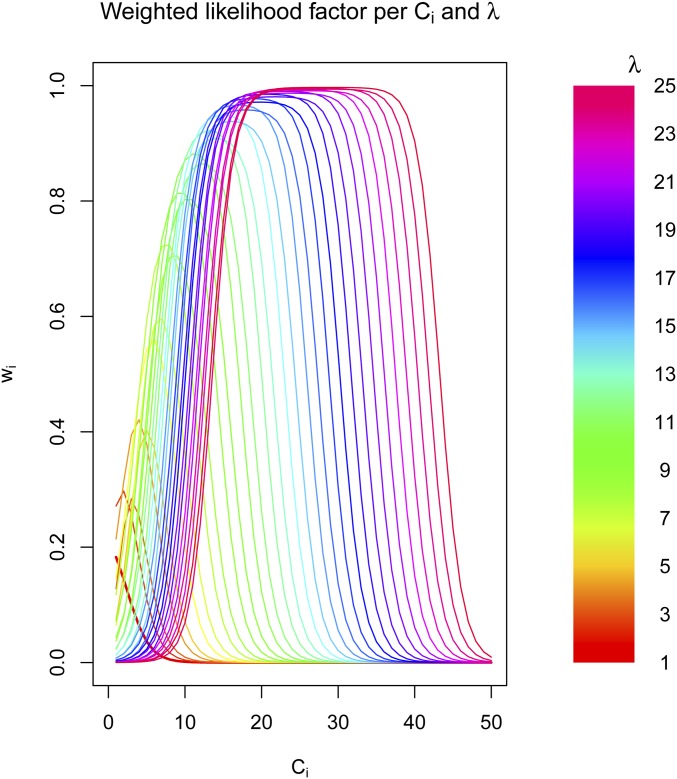
To add robustness to our maximum-likelihood algorithm, we used the genome-wide average coverage as well as the coverage of the specific site in a weighted maximum-likelihood approach (Hadi and Luceño 1997).
In the main text, we defined the weight at site i as a function of the coverage at site i () and the genome-wide coverage (λ). We define the following events:
S = no duplicated alignments or collapses mapping have occurred; the sampled region is the one contained in the reference. The coverage observed in the mapped region should be the genomic average (λ).
T = there was a single region of origin for the reads, but the reference contains two distinct regions where the fragments can map to; the coverage observed in the mapped region is half the genomic average ().
C = there were two different regions of origin for the reads, but they now map to a single location; the coverage observed in the mapped region should twice the genomic average ().
Let denote the complement or negation of an event. We defined weight as:
| (1) |
The probability of not having a duplication or collapsed region depends on the genome-wide average coverage and the local one. We compute this quantity using Bayes’ rule:
| (2) |
| (3) |
for a case T:
| (4) |
for case C:
| (5) |
Finally, the prior probability on λ given not having a duplication is given by the ratio
| (6) |
where is simply the Poisson of λ at genomic rate λ:
| (7) |
and where is the sum of the Poisson of λ at genomic rate λ:
| (8) |
All of those functions are used to define the weight given the coverage at site i () and the genome wide coverage (λ). To visualize the weights for different values of () and the genome-wide coverage (λ), please refer to Figure A1.
Appendix B: Accuracy of the Mapping Quality
Our model uses the mapping quality as a proxy to quantify the probability that a fragment is mismapped. We sought to evaluate the accuracy of this proxy by measuring the observed mapping quality, defined as the fragment of mismapped fragments on a PHRED scale, against the predicted mapping quality. The correlation between the predicted and observed mapping quality was plotted (see Figure B1). Generally, although this correlation is not perfect, predicted mapping quality is a reasonably good proxy for the probability that a fragment is mismapped.
Appendix C: Frequency of Nucleotides for Mismapped Fragments
We describe in this section how the probabilities of finding a specific base given that the fragment is mismapped is obtained. In the main manuscript, we mention that the probability of finding a specific base is given by the natural frequencies of these nucleotides:
| (9) |
where is the observed base at genomic position i and depth j, b is the endogenous base samples from the chromosome and M denotes a mismapping event having occurred. In the human genome we generally find that and . However aDNA damage can shift these probabilities. For instance, if there is a high rate of observed substitution from cytosine to thymine due to deamination, the frequency of cytosines will be decreased but the probability of finding a thymine will be increased. Let be the frequency of base in the presence of deamination. This is obtained by marginalizing over each possible original base b:
| (10) |
where represents the frequency of observed substitution from b to due to deamination. This frequency is supplied by the user and is position dependent.
Appendix D: Low-Coverage Correction
Let be the coverage at site i. At heterozygous sites, the distribution of the two alleles and will follow a binomial distribution. This entails that, given that site i is heterozygous, we will only observe base with probability . Similarly, we will only observe with probability . We will therefore only observe a single base at heterozygous sites with probability . Although this is not significant at high-coverage, at coverage 3×, we will only observe a single base at heterozygous sites with probability . This consistently caused our model to underestimate the heterozygosity rate. To correct this, we multiply the upper, lower, and mid estimate of θ estimates by the following factor:
| (11) |
Empirical evidence shows that this corrected for the underestimate at low coverage, while not affecting estimates at higher coverage, as term 11 is roughly 1 for higher values of . To illustrate this, we ran ROHan with and without low-coverage correction the Yoruba sample presented later in Figure S50, which was subsampled at various depths of coverage. At high coverage (30×), our estimate of θ for this sample is 11.9 10 (95% CI:11.1–12.9 10). The original publication reported estimates of between 11.1 and 11.810 depending on the method used (Mallick et al. 2016). When subsampling down to 2× coverage, our θ estimates become: 12.3 10 (95% CI: 8.3–16.4 10), and, at 3×, 12.410 (95% CI: 9.4–15.4 10). Although the point values are slightly overestimated, the confidence range obtained overlaps the value recovered with high-coverage data. This demonstrates the validity of our correction scheme. However, if no correction factor is applied, our θ estimates become, at 2×, 8.910 (95% CI:5.9–11.8), and, at 3×, 9.310 (95% CI:7.0–11.6). Although the truth for this sample is not known, our point estimates at 30× seem consistent with those reported by completely different algorithms in the original publication. If this estimate is considered reliable, using the correction factor seems to overestimate θ by roughly 0.510 (4.2%), whereas, without this correction factor, an underestimate of about 2.6–310 (23.5%) segregating sites was observed.
Appendix E: The Number of Segregating Sites in a Genomic Locus
As described in the main manuscript, ROHan first computes local estimates of heterozygosity then proceeds by running an HMM to infer the genome-wide θ as well as to mark ROH vs. non-ROH regions. We defined the HMM as a two states model where one corresponds to the ROH state and the other corresponds to the non-ROH state. For a local estimate of heterozygosity, we can infer the expected number of segregating sites by multiplying the estimate of heterozygosity times the size of the genomic window.
For a given genome-wide estimate of θ used by the non-ROH HMM state, we must now define the probability of observing a certain number k of segregating sites (denoted ) given θ.
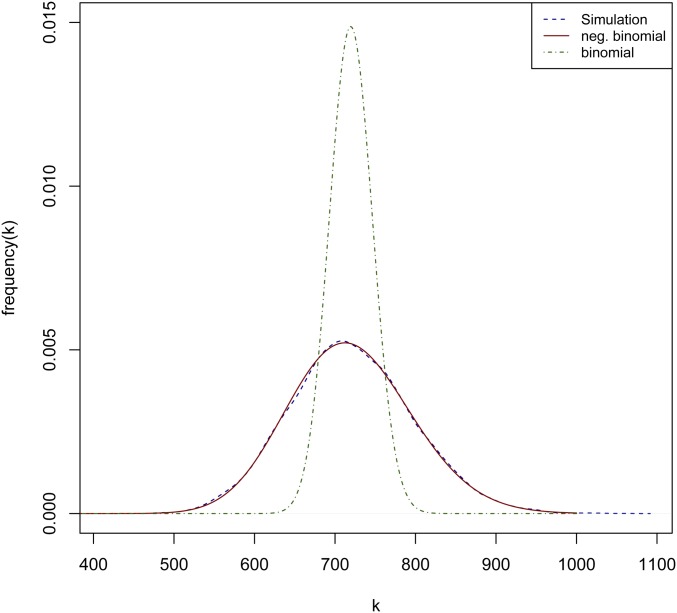
In our simulations, was one possible value of effective population size and the mutation rate per nucleotide per generation was also used. As , this is approximately our heterozygosity rate since . We used Hudson’s ms (Hudson 2002) to visualize the distribution of 10,000 genomic loci with size of 1 Mbp:
The results are plotted in Figure E1, and show a distribution with a wide variance centered at ∼720.
Some previous work by Yang (1996) computed the probability of having a certain number of segregating sites in very small but highly divergent loci using a Jukes-Cantor model to compute the probability of being in a stationary Markov state for a single base combined with a binomial distribution for an entire locus:
| (12) |
however, for a large locus, the variance is not sufficiently large (see Figure E1).
As the number of segregating sites in a small nonrecombining locus (NRL) is geometrically distributed with parameter (Watterson 1975), one can construe the number of segregating sites for a large recombining locus as the sum of segregating sites for multiple NRLs. The sum of multiple geometric distributions is a negative binomial distribution (DeGroot 1986). It has also been previously suggested that the number of segregating sites along a large genomic window follows a negative binomial distribution (Pitters 2017). We therefore modeled our large genomic window of N sites as the sum of s NRLs, each generating segregating sites with rate . The equation for the number of segregating sites becomes:
| (13) |
We found the negative binomial distribution to be more consistent with the distribution obtained using coalescence simulations (see Figure E1).
Appendix F: Genomic Simulations
F.1 Simulating aDNA damage
The final diploid organism was used as input for gargammel (Renaud et al. 2016). The simulated adapters used were AGATCGGAAGAGCACACGTCTGAACTCCAGTCACCGATTCGATCTCGTATGCCGTCTTCTGCTTG and AGATCGGAAGAGCGTCGTGTAGGGAAAGAGTGTAGATCTCGGTGGTCGCCGTATCATTT. The distribution of the simulated fragment sizes was taken from the empirical fragment sizes from the Ust’-Ishim individual (Fu et al. 2014). High rates of damage stemming from deamination were taken from the ATP2 sample (Gamba et al. 2014), intermediate rates of damage from a double-stranded library were taken from the LaBraña sample (Sánchez-Quinto et al. 2012), and low rates of damage from a single-stranded library were taken from the Ust’-Ishim sample (Fu et al. 2014). The rates of damage were plotted (see Figure F1).
F.2 Adding simulated sequencing errors
gargammel by default uses the ART package to add sequencing errors in addition to aDNA damage. We used two values of the per-base quality score shift ( option) to obtain different rates of sequencing error (see Table F1). The default value of 0 is on par with the rate of sequencing errors previously reported in the literature for Illumina sequencers (see Schirmer et al. 2016). To test the robustness of our software to additional errors, we multiplied by 10 the number of sequencing errors ().
F.3 Simulated inbreeding cases
As mentioned in the main text, full simulations of chromosomes were performed for 16 haploid genomes using msprime (Kelleher et al. 2016). These genomes were then recombined using custom programs and a recombination map from HapMap phase II (International HapMap Consortium et al. 2007). In addition to a noninbred pedigree, three other cases of inbred pedigrees were simulated. The first was incest between siblings (see Figure F2). The second involved incest between a grandparent and a grandchild (see Figure F3). For the first case, the predicted rate of identity by descent is and for the second (see Wright 1922). The third case simulated incest between first cousins (see Figure F4) and the predicted rate of identity by descent is
Appendix G: Comparison with other Software
Although there are, as of writing, no published methods to infer genome-wide rates of θ for potentially inbred samples, we compared ROHan’s ability to infer genome-wide rates of θ for non-inbreed samples using only 15 M. We evaluated two software aimed at performing such task namely ATLAS (Kousathanas et al. 2017) and ANGSD (Korneliussen et al. 2014). ATLAS version 1.0 was used with the following command:
atlas task=splitRGbyLength bam=[IN].bam readGroups=singleEndReadgroups.txt
$ atlas task=estimatePMD bam=[IN]_splitRG.bam fasta=ref.fa chr=1 length=25
$ atlas task=recal bam=[IN]_splitRG.bam pmdFile=[IN]_splitRG_PMD_input_Empiric.txt chr=1
limitWindows=20 verbose
$ atlas window=15000126 task=estimateTheta bam=[IN]_splitRG.bam
$ pmdFile[IN]_splitRG_PMD_input_Empiric.txt recal=][IN]_splitRG_recalibrationEM.txt
We also tried adding “equalBaseFreq” to the recalibration, but the effect on the predicted θ was not significant (5.58006e-06). Also, ANGSD version 0.915 built with htslib v1.3.2-132-g609120d was used using the following commands:
$ angsd – P 1 –i [IN].bam –gl 1 –C 50 –ref ref.fa –anc ref.fa –fold 1 –minQ 20 –minmapq 30 –dosaf 1 –out [IN].angsd
$ realSFS [IN].angsd.saf.idx > [IN].angsd.sfs
$ angsd –P 1 –i [IN].bam –gl 1 –C 50 –ref ref.fa –anc ref.fa –fold 1 –minQ 20 –minmapq 30 –dosaf 1 –out [IN].angsdl –pest [IN].angsd.sfs
$ realSFS [IN].angsdl.saf.idx > [IN].angsdl.ml
Finally, we used the number found in the second column divided by the sum of the first and second column to obtain our estimate of θ.
The unit of information in ANGSD is the (diploid) genotype likelihood, which is specified via the “-gl” parameter. The error model specified by “-gl 1” corresponds to the SAMtools error model, whereas “-gl 2” assumes that the qscores are correct and does no error modeling or correction. We tested both parameters on a full simulated genome where a base every 1000 was made to be polymorphic and sequencing errors were added (see Figure G1). We also tested ROHan on the same dataset. The dataset was downsampled to various depths of coverage.
As expected in the presence of no damage signal and quality scores with no error “-gl 2” outperforms “-gl 1”. ROHan is more accurate than both in all cases, with the exception of a full genome at 0.5×. We emphasize that the results for these scenarios are global estimates in the context of no damage signals. In all analyses presented in the main manuscript, we used the error correcting “-gl 1” model even though using “-gl 2” could have improved the performance of the ANGSD based results. The performance of the genotype likelihood-based approaches in ANGSD is dependent on the choice of genotype likelihood model and there is currently no unified “best” genotype likelihood model that encapsulates all idiosyncrasies of sequencing data. However, the documentation for ANGSD for estimating heterozygosity currently lists “-gl 1” as ANGSD is most often used with empirical (and not synthetic data) where the assumption of perfect correlation between quality scores and error rates is not guaranteed.
For BCFtools/RoH, we used the following command to genotype:
$ bcftools mpileup –Ou –f [REF] [IN].bam — bcftools call –m -Oz –o [OUT].vcf.gz
using version 1.4.1 of BCFtools. The genotypes were then used as input into the following command:
$ mergeVCF_AF [PREFIX].af.gz [OUT].vcf.gz | bcftools roh –AF-tag AF1KG –m [genetic\_map]
where mergeVCF_AF is a script that merges the allele frequencies as a field in the VCF file. The [genetic_map] corresponds to the exact recombinations map used for simulations.
For PLINK, we used the vcf files produced above using bcftools and ran the following:
$ plink ––homozyg ––vcf [OUT].vcf.gz ––out [OUT]
where PLINK version v1.90 was used.
Figure A1.
The value of the weights for different values of local coverage () and genome-wide coverage (λ).
Figure B1.
Predicted vs. observed mapping quality. Fragments either carried (A) no damage, (B) Ust’-Ishim level damage, (C) ATP2 level damage, or (D) LaBraña level damage. An effective population size of =9000 was used.
Figure E1.
Comparison of the distribution of the number of segregating sites for 10,000 simulated loci of 1 Mb and different distributions. First, a negative binomial distribution for 100 NRLs on 1 Mb with probability . Second, a binomial distribution for 1 Mb with probability 0.00072.
Figure F1.
mapDamage2 nucleotide misincorporation profiles for ATP2 (A), LaBraña (B), and Ust’-Ishim (C). First cousins (see Figure F4) and the predicted rate of identity by descent (IDB) is .
Figure F2.
First case of simulated inbreeding where parents are siblings, the probability of IBD is .
Figure F3.
Second case of inbreeding where one of the parents in a grandparent of the other parent. The probability of IBD is .
Figure F4.
Third case of inbreeding where parents are first cousins. The probability of IBD is .
Figure G1.
Use of the “-gl 1” (samtools) vs. “-gl 2” (GATK) in ANGSD to specify the model of error compared to ROHan on a simulated set with a heterozygosity of 0.001. The green crosses are the point estimates for θ ANGSD using “-gl 1” whereas the orange squares are using “-gl 2”, the blue diamonds are ROHan’s point estimate of θ. The numbers next to the dots represent the absolute value of the error of the point estimate.
Table F1. Parameters used during simulations of sequencing errors using the ART software.
| Profile of the Illumina sequencing system | Observed error rate (per base) | |
|---|---|---|
| 0 | HiSeq 2500 (HS25) | 0.0016 |
| −10 | HiSeq 2500 (HS25) | 0.0160 |
Rates of sequencing errors with the default value (i.e., -qs 0) were consistent with empirical rates found by Schirmer et al. (2016). The second rate (i.e., -qs −10) represents an sequencing run with an extreme error rate.
Footnotes
Supplemental material available at Figshare: https://doi.org/10.25386/genetics.8251400.
Communicating editor: N. Risch
Literature Cited
- Adams R. H., Schield D. R., Card D. C., Corbin A., Castoe T. A., 2018. ThetaMater: Bayesian estimation of population size parameter θ from genomic data. Bioinformatics 34: 1072–1073. 10.1093/bioinformatics/btx733 [DOI] [PubMed] [Google Scholar]
- Allentoft M. E., Sikora M., Sjögren K.-G., Rasmussen S., Rasmussen M., et al. , 2015. Population genomics of bronze age Eurasia. Nature 522: 167–172. 10.1038/nature14507 [DOI] [PubMed] [Google Scholar]
- Alvarez G., Ceballos F. C., Quinteiro C., 2009. The role of inbreeding in the extinction of a European royal dynasty. PLoS One 4: e5174 10.1371/journal.pone.0005174 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Astrom K., 1979. Maximum likelihood and prediction error methods. IFAC Proceedings Volumes 12: 551–574. 10.1016/S1474-6670(17)53976-2 [DOI] [Google Scholar]
- Blant A., Kwong M., Szpiech Z. A., Pemberton T. J., 2017. Weighted likelihood inference of genomic autozygosity patterns in dense genotype data. BMC Genomics 18: 928 10.1186/s12864-017-4312-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosse M., Megens H.-J., Madsen O., Paudel Y., Frantz L. A., et al. , 2012. Regions of homozygosity in the porcine genome: consequence of demography and the recombination landscape. PLoS Genet. 8: e1003100 10.1371/journal.pgen.1003100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs A. W., Stenzel U., Johnson P. L., Green R. E., Kelso J., et al. , 2007. Patterns of damage in genomic DNA sequences from a Neandertal. Proc. Natl. Acad. Sci. USA 104: 14616–14621. 10.1073/pnas.0704665104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broushaki F., Thomas M. G., Link V., López S., van Dorp L., et al. , 2016. Early neolithic genomes from the eastern fertile crescent. Science 353: 499–503. 10.1126/science.aaf7943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning S. R., Browning B. L., 2015. Accurate non-parametric estimation of recent effective population size from segments of identity by descent. Am. J. Hum. Genet. 97: 404–418. 10.1016/j.ajhg.2015.07.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryc K., Patterson N., Reich D., 2013. A novel approach to estimating heterozygosity from low-coverage genome sequence. Genetics 195: 553–561. 10.1534/genetics.113.154500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceballos F. C., Joshi P. K., Clark D. W., Ramsay M., Wilson J. F., 2018. Runs of homozygosity: windows into population history and trait architecture. Nat. Rev. Genet. 19: 220–234. 10.1038/nrg.2017.109 [DOI] [PubMed] [Google Scholar]
- DeGroot M. H., 1986. Probability and Statistics, Ed. 2 Addison-Wesley, Reading, MA. [Google Scholar]
- de Manuel M., Kuhlwilm M., Frandsen P., Sousa V. C., Desai T., et al. , 2016. Chimpanzee genomic diversity reveals ancient admixture with bonobos. Science 354: 477–481. 10.1126/science.aag2602 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Der Sarkissian C., Ermini L., Jónsson H., Alekseev A., Crubezy E., et al. , 2014. Shotgun microbial profiling of fossil remains. Mol. Ecol. 23: 1780–1798. 10.1111/mec.12690 [DOI] [PubMed] [Google Scholar]
- Der Sarkissian C., Ermini L., Schubert M., Yang M. A., Librado P., et al. , 2015. Evolutionary genomics and conservation of the endangered Przewalski’s horse. Curr. Biol. 25: 2577–2583. 10.1016/j.cub.2015.08.032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do K.-T., Kong H.-S., Lee J.-H., Lee H.-K., Cho B.-W., et al. , 2014. Genomic characterization of the przewalski’s horse inhabiting Mongolian steppe by whole genome re-sequencing. Livest. Sci. 167: 86–91. 10.1016/j.livsci.2014.06.020 [DOI] [Google Scholar]
- Fisher R. A., 1954. A fuller theory of “junctions” in inbreeding. Heredity 8: 187–197. 10.1038/hdy.1954.17 [DOI] [Google Scholar]
- Frantz L. A., Mullin V. E., Pionnier-Capitan M., Lebrasseur O., Ollivier M., et al. , 2016. Genomic and archaeological evidence suggest a dual origin of domestic dogs. Science 352: 1228–1231. 10.1126/science.aaf3161 [DOI] [PubMed] [Google Scholar]
- Frischknecht M., Jagannathan V., Plattet P., Neuditschko M., Signer-Hasler H., et al. , 2015. A non-synonymous HMGA2 variant decreases height in Shetland ponies and other small horses. PLoS One 10: e0140749 10.1371/journal.pone.0140749 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fromer M., Moran J. L., Chambert K., Banks E., Bergen S. E., et al. , 2012. Discovery and statistical genotyping of copy-number variation from whole-exome sequencing depth. Am. J. Hum. Genet. 91: 597–607. 10.1016/j.ajhg.2012.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Q., Li H., Moorjani P., Jay F., Slepchenko S. M., et al. , 2014. Genome sequence of a 45,000-year-old modern human from western Siberia. Nature 514: 445–449. 10.1038/nature13810 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gamba C., Jones E. R., Teasdale M. D., McLaughlin R. L., Gonzalez-Fortes G., et al. , 2014. Genome flux and stasis in a five millennium transect of European prehistory. Nat. Commun. 5: 5257 10.1038/ncomms6257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gansauge M.-T., Meyer M., 2013. Single-stranded DNA library preparation for the sequencing of ancient or damaged DNA. Nat. Protoc. 8: 737–748. 10.1038/nprot.2013.038 [DOI] [PubMed] [Google Scholar]
- Gaunitz C., Fages A., Hanghøj K., Albrechtsen A., Khan N., et al. , 2018. Ancient genomes revisit the ancestry of domestic and Przewalski’s horses. Science 360: 111–114. 10.1126/science.aao3297 [DOI] [PubMed] [Google Scholar]
- 1000 Genomes Project Consortium, . A. Auton, Brooks L. D., Durbin R. M., Garrison E. P., et al. , 2015. A global reference for human genetic variation. Nature 526: 68–74. 10.1038/nature15393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green R. E., Krause J., Briggs A. W., Maricic T., Stenzel U., et al. , 2010. A draft sequence of the Neandertal genome. Science 328: 710–722. 10.1126/science.1188021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gronau I., Hubisz M. J., Gulko B., Danko C. G., Siepel A., 2011. Bayesian inference of ancient human demography from individual genome sequences. Nat. Genet. 43: 1031–1034. 10.1038/ng.937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Günther T., Nettelblad C., 2018. The presence and impact of reference bias on population genomic studies of prehistoric human populations. bioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Günther T., Malmström H., Svensson E. M., Omrak A., Sánchez-Quinto F., et al. , 2018. Population genomics of Mesolithic Scandinavia: investigating early postglacial migration routes and high-latitude adaptation. PLoS Biol. 16: e2003703 10.1371/journal.pbio.2003703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hadi A. S., Luceño A., 1997. Maximum trimmed likelihood estimators: a unified approach, examples, and algorithms. Comput. Stat. Data Anal. 25: 251–272. 10.1016/S0167-9473(97)00011-X [DOI] [Google Scholar]
- Hanghøj K., Seguin-Orlando A., Schubert M., Madsen T., Pedersen J. S., et al. , 2016. Fast, accurate and automatic ancient nucleosome and methylation maps with epiPALEOMIX. Mol. Biol. Evol. 33: 3284–3298. 10.1093/molbev/msw184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haubold B., Pfaffelhuber P., Lynch M., 2010. mlRho–a program for estimating the population mutation and recombination rates from shotgun-sequenced diploid genomes. Mol. Ecol. 19: 277–284. 10.1111/j.1365-294X.2009.04482.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofmanová Z., Kreutzer S., Hellenthal G., Sell C., Diekmann Y., et al. , 2016. Early farmers from across europe directly descended from Neolithic Aegeans. Proc. Natl. Acad. Sci. USA 113: 6886–6891. 10.1073/pnas.1523951113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howrigan D. P., Simonson M. A., Keller M. C., 2011. Detecting autozygosity through runs of homozygosity: a comparison of three autozygosity detection algorithms. BMC Genomics 12: 460 10.1186/1471-2164-12-460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson R. R., 2002. Generating samples under a Wright–Fisher neutral model of genetic variation. Bioinformatics 18: 337–338. 10.1093/bioinformatics/18.2.337 [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium, . K. A. Frazer, Ballinger D. G., Cox D. R., Hinds D. A., et al. , 2007. A second generation human haplotype map of over 3.1 million SNPs. Nature 449: 851–861. 10.1038/nature06258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jäderkvist K., Andersson L., Johansson A., Árnason T., Mikko S., et al. , 2014. The DMRT3 ‘Gait keeper’ mutation affects performance of Nordic and Standardbred trotters. J. Anim. Sci. 92: 4279–4286. 10.2527/jas.2014-7803 [DOI] [PubMed] [Google Scholar]
- Kelleher J., Etheridge A. M., McVean G., 2016. Efficient coalescent simulation and genealogical analysis for large sample sizes. PLOS Comput. Biol. 12: e1004842 10.1371/journal.pcbi.1004842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller M. C., Visscher P. M., Goddard M. E., 2011Quantification of inbreeding due to distant ancestors and its detection using dense single nucleotide polymorphism data. Genetics 189: 237–249. 10.1534/genetics.111.130922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H., Lee T., Park W., Lee J. W., Kim J., et al. , 2013. Peeling back the evolutionary layers of molecular mechanisms responsive to exercise-stress in the skeletal muscle of the racing horse. DNA Res. 20: 287–298. 10.1093/dnares/dst010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M., 1969. The number of heterozygous nucleotide sites maintained in a finite population due to steady flux of mutations. Genetics 61: 893–903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kircher M., 2012. Analysis of high-throughput ancient DNA sequencing data, pp. 197–228 in Ancient DNA. Springer, New York: 10.1007/978-1-61779-516-9_23 [DOI] [PubMed] [Google Scholar]
- Korneliussen T. S., Albrechtsen A., Nielsen R., 2014. ANGSD: analysis of next generation sequencing data. BMC Bioinformatics 15: 356 10.1186/s12859-014-0356-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kousathanas A., Leuenberger C., Link V., Sell C., Burger J., et al. , 2017. Inferring heterozygosity from ancient and low coverage genomes. Genetics 205: 317–332. 10.1534/genetics.116.189985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B., 2017. A tandem simulation framework for predicting mapping quality. Genome Biol. 18: 152 10.1186/s13059-017-1290-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazaridis I., Patterson N., Mittnik A., Renaud G., Mallick S., et al. , 2014. Ancient human genomes suggest three ancestral populations for present-day Europeans. Nature 513: 409–413. 10.1038/nature13673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leegwater P. A., Vos-Loohuis M., Ducro B. J., Boegheim I. J., Steenbeek F. G., et al. , 2016. Dwarfism with joint laxity in Friesian horses is associated with a splice site mutation in B4GALT7. BMC Genomics 17: 839 10.1186/s12864-016-3186-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., 2014. Toward better understanding of artifacts in variant calling from high-coverage samples. Bioinformatics 30: 2843–2851. 10.1093/bioinformatics/btu356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R., 2009. Fast and accurate short read alignment with Burrows–Wheeler transform. Bioinformatics 25: 1754–1760. 10.1093/bioinformatics/btp324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Handsaker B., Wysoker A., Fennell T., Ruan J., et al. , 2009. The sequence alignment/map format and SAMtools. Bioinformatics 25: 2078–2079. 10.1093/bioinformatics/btp352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W., 2011. On parameters of the human genome. J. Theor. Biol. 288: 92–104. 10.1016/j.jtbi.2011.07.021 [DOI] [PubMed] [Google Scholar]
- Librado P., Der Sarkissian C., Ermini L., Schubert M., Jónsson H., et al. , 2015. Tracking the origins of Yakutian horses and the genetic basis for their fast adaptation to subarctic environments. Proc. Natl. Acad. Sci. USA 112: E6889–E6897. 10.1073/pnas.1513696112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Librado P., Gamba C., Gaunitz C., Der Sarkissian C., Pruvost M., et al. , 2017. Ancient genomic changes associated with domestication of the horse. Science 356: 442–445. 10.1126/science.aam5298 [DOI] [PubMed] [Google Scholar]
- Llamas B., Valverde G., Fehren-Schmitz L., Weyrich L. S., Cooper A., et al. , 2017a From the field to the laboratory: controlling DNA contamination in human ancient DNA research in the high-throughput sequencing era. Sci. Technol. Archaeol. Res. 3: 1–14. [Google Scholar]
- Llamas B., Willerslev E., Orlando L., 2017b Human evolution: a tale from ancient genomes. Philos. Trans. R. Soc. Lond. B Biol. Sci. 372: 20150484 10.1098/rstb.2015.0484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo R., Schatz M. C., Salzberg S. L., 2017. 16GT: a fast and sensitive variant caller using a 16-genotype probabilistic model. Gigascience 6: 1–4. 10.1093/gigascience/gix045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallick S., Li H., Lipson M., Mathieson I., Gymrek M., et al. , 2016. The Simons genome diversity project: 300 genomes from 142 diverse populations. Nature 538: 201–206. 10.1038/nature18964 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marciniak S., Perry G. H., 2017. Harnessing ancient genomes to study the history of human adaptation. Nat. Rev. Genet. 18: 659–674. 10.1038/nrg.2017.65 [DOI] [PubMed] [Google Scholar]
- McQuillan R., Leutenegger A.-L., Abdel-Rahman R., Franklin C. S., Pericic M., et al. , 2008. Runs of homozygosity in European populations. Am. J. Hum. Genet. 83: 359–372. 10.1016/j.ajhg.2008.08.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzger J., Tonda R., Beltran S., Águeda L., Gut M., et al. , 2014. Next generation sequencing gives an insight into the characteristics of highly selected breeds vs. non-breed horses in the course of domestication. BMC Genomics 15: 562 10.1186/1471-2164-15-562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer M., Kircher M., 2010. Illumina sequencing library preparation for highly multiplexed target capture and sequencing. Cold Spring Harb. Protoc. 2010: pdb.prot5448 10.1101/pdb.prot5448 [DOI] [PubMed] [Google Scholar]
- Meynert A. M., Ansari M., FitzPatrick D. R., Taylor M. S., 2014. Variant detection sensitivity and biases in whole genome and exome sequencing. BMC Bioinformatics 15: 247 10.1186/1471-2105-15-247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller W., Drautz D. I., Ratan A., Pusey B., Qi J., et al. , 2008. Sequencing the nuclear genome of the extinct woolly mammoth. Nature 456: 387–390. 10.1038/nature07446 [DOI] [PubMed] [Google Scholar]
- Nakamura K., Oshima T., Morimoto T., Ikeda S., Yoshikawa H., et al. , 2011. Sequence-specific error profile of Illumina sequencers. Nucleic Acids Res. 39: e90 10.1093/nar/gkr344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narasimhan V., Danecek P., Scally A., Xue Y., Tyler-Smith C., et al. , 2016. BCFtools/RoH: a hidden markov model approach for detecting autozygosity from next-generation sequencing data. Bioinformatics 32: 1749–1751. 10.1093/bioinformatics/btw044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orlando L., Gilbert M. T. P., Willerslev E., 2015. Reconstructing ancient genomes and epigenomes. Nat. Rev. Genet. 16: 395–408. 10.1038/nrg3935 [DOI] [PubMed] [Google Scholar]
- Pedersen J. S., Valen E., Velazquez A. M. V., Parker B. J., Rasmussen M., et al. , 2014. Genome-wide nucleosome map and cytosine methylation levels of an ancient human genome. Genome Res. 24: 454–466. 10.1101/gr.163592.113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pemberton T. J., Absher D., Feldman M. W., Myers R. M., Rosenberg N. A., et al. , 2012. Genomic patterns of homozygosity in worldwide human populations. Am. J. Hum. Genet. 91: 275–292. 10.1016/j.ajhg.2012.06.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitters, H. H., 2017 On the number of segregating sites. arXiv preprint arXiv:1708.05634.
- Prüfer K., Racimo F., Patterson N., Jay F., Sankararaman S., et al. , 2014. The complete genome sequence of a neanderthal from the altai mountains. Nature 505: 43–49. 10.1038/nature12886 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prüfer K., de Filippo C., Grote S., Mafessoni F., Korlević P., et al. , 2017. A high-coverage neandertal genome from Vindija Cave in Croatia. Science 358: 655–658. 10.1126/science.aao1887 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S., Neale B., Todd-Brown K., Thomas L., Ferreira M. A., et al. , 2007. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81: 559–575. 10.1086/519795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purfield D. C., Berry D. P., McParland S., Bradley D. G., 2012. Runs of homozygosity and population history in cattle. BMC Genet. 13: 70 10.1186/1471-2156-13-70 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purfield D. C., McParland S., Wall E., Berry D. P., 2017. The distribution of runs of homozygosity and selection signatures in six commercial meat sheep breeds. PLoS One 12: e0176780 10.1371/journal.pone.0176780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran S., Deshpande O., Roseman C. C., Rosenberg N. A., Feldman M. W., et al. , 2005. Support from the relationship of genetic and geographic distance in human populations for a serial founder effect originating in Africa. Proc. Natl. Acad. Sci. USA 102: 15942–15947. 10.1073/pnas.0507611102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen S., Allentoft M., Nielsen K., Orlando L., Sikora M., et al. , 2015. Early divergent strains of Yersinia pestis in Eurasia 5,000 years ago. Cell 163: 571–582. 10.1016/j.cell.2015.10.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich D., Green R. E., Kircher M., Krause J., Patterson N., et al. , 2010. Genetic history of an archaic hominin group from Denisova Cave in Siberia. Nature 468: 1053–1060. 10.1038/nature09710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renaud G., Stenzel U., Kelso J., 2014. leeHom: adaptor trimming and merging for Illumina sequencing reads. Nucleic Acids Res. 42: e141 10.1093/nar/gku699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renaud G., Hanghøj K., Willerslev E., Orlando L., 2016. gargammel: a sequence simulator for ancient DNA. Bioinformatics 33: 577–579. 10.1093/bioinformatics/btw670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renaud G., Petersen B., Seguin-Orlando A., Bertelsen M. F., Waller A., et al. , 2018. Improved de novo genomic assembly for the domestic donkey. Science Advances 4: eaaq0392 10.1126/sciadv.aaq0392 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohland N., Harney E., Mallick S., Nordenfelt S., Reich D., 2015. Partial uracil–DNA–glycosylase treatment for screening of ancient DNA. Philos. Trans. R. Soc. Lond. B Biol. Sci. 370: 20130624 10.1098/rstb.2013.0624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruffalo M., Koyutürk M., Ray S., LaFramboise T., 2012. Accurate estimation of short read mapping quality for next-generation genome sequencing. Bioinformatics 28: i349–i355. 10.1093/bioinformatics/bts408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rumelhart D. E., Hinton G. E., Williams R. J., 1986. Learning representations by back-propagating errors. Nature 323: 533–536. 10.1038/323533a0 [DOI] [Google Scholar]
- Rydén T., 2008. Em vs. Markov chain Monte Carlo for estimation of hidden markov models: a computational perspective. Bayesian Anal. 3: 659–688. 10.1214/08-BA326 [DOI] [Google Scholar]
- Sánchez-Quinto F., Schroeder H., Ramirez O., Ávila-Arcos M. C., Pybus M., et al. , 2012. Genomic affinities of two 7,000-year-old Iberian hunter-gatherers. Curr. Biol. 22: 1494–1499. 10.1016/j.cub.2012.06.005 [DOI] [PubMed] [Google Scholar]
- Schirmer M., D’Amore R., Ijaz U. Z., Hall N., Quince C., 2016. Illumina error profiles: resolving fine-scale variation in metagenomic sequencing data. BMC Bioinformatics 17: 125 10.1186/s12859-016-0976-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schubert M., Jónsson H., Chang D., Der Sarkissian C., Ermini L., et al. , 2014. Prehistoric genomes reveal the genetic foundation and cost of horse domestication. Proc. Natl. Acad. Sci. USA 111: E5661–E5669. 10.1073/pnas.1416991111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seguin-Orlando A., Korneliussen T. S., Sikora M., Malaspinas A.-S., Manica A., et al. , 2014. Genomic structure in Europeans dating back at least 36,200 years. Science 346: 1113–1118. 10.1126/science.aaa0114 [DOI] [PubMed] [Google Scholar]
- Stoffel M. A., Esser M., Kardos M., Humble E., Nichols H., et al. , 2016. inbreedR: an R package for the analysis of inbreeding based on genetic markers. Methods Ecol. Evol. 7: 1331–1339. 10.1111/2041-210X.12588 [DOI] [Google Scholar]
- Szpiech Z. A., Blant A., Pemberton T. J., 2017. GARLIC: genomic autozygosity regions likelihood-based inference and classification. Bioinformatics 33: 2059–2062. 10.1093/bioinformatics/btx102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vieira F. G., Albrechtsen A., Nielsen R., 2016. Estimating IBD tracts from low coverage NGS data. Bioinformatics 32: 2096–2102. 10.1093/bioinformatics/btw212 [DOI] [PubMed] [Google Scholar]
- Wade C., Giulotto E., Sigurdsson S., Zoli M., Gnerre S., et al. , 2009. Genome sequence, comparative analysis, and population genetics of the domestic horse. Science 326: 865–867. 10.1126/science.1178158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G., Zhai W., Yang H., Fan R., Cao X., et al. , 2013. The genomics of selection in dogs and the parallel evolution between dogs and humans. Nat. Commun. 4: 1860 10.1038/ncomms2814 [DOI] [PubMed] [Google Scholar]
- Watterson G., 1975. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 7: 256–276. 10.1016/0040-5809(75)90020-9 [DOI] [PubMed] [Google Scholar]
- Wiener P., Wilkinson S., 2011. Deciphering the genetic basis of animal domestication. Proc. R. Soc. Lond. B Biol. Sci. 278: 3161–3170. 10.1098/rspb.2011.1376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S., 1922. Coefficients of inbreeding and relationship. Am. Nat. 56: 330–338. 10.1086/279872 [DOI] [Google Scholar]
- Yang J., Lee S. H., Goddard M. E., Visscher P. M., 2011. Gcta: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 88: 76–82. 10.1016/j.ajhg.2010.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z., 1996. Statistical properties of a DNA sample under the finite-sites model. Genetics 144: 1941–1950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yengo L., Zhu Z., Wray N. R., Weir B. S., Yang J., et al. , 2017. Detection and quantification of inbreeding depression for complex traits from SNP data. Proc. Natl. Acad. Sci. USA 114: 8602–8607. 10.1073/pnas.1621096114 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors state that all data necessary for confirming the conclusions presented in the manuscript are represented fully within the manuscript. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.8251400.