Multi-View Maximum Entropy Clustering by Jointly Leveraging Inter-View Collaborations and Intra-View-Weighted Attributes

Abstract

As a dedicated countermeasure for heterogeneous multi-view data, multi-view clustering is currently a hot topic in machine learning. However, many existing methods either neglect the effective collaborations among views during clustering or do not distinguish the respective importance of attributes in views, instead treating them equivalently. Motivated by such challenges, based on maximum entropy clustering (MEC), two specialized criteria—inter-view collaborative learning (IEVCL) and intra-view-weighted attributes (IAVWA)—are first devised as the bases. Then, by organically incorporating IEVCL and IAVWA into the formulation of classic MEC, a novel, collaborative multi-view clustering model and the matching algorithm referred to as the view-collaborative, attribute-weighted MEC (VC-AW-MEC) are proposed. The significance of our efforts is three-fold: 1) both IEVCL and IAVWA are dedicatedly devised based on MEC so that the proposed VC-AW-MEC is qualified to effectively handle as many multi-view data scenes as possible; 2) IEVCL is competent in seeking the consensus across all involved views throughout clustering, whereas IAVWA is capable of adaptively discriminating the individual impact regarding the attributes within each view; and 3) benefiting from jointly leveraging IEVCL and IAVWA, compared with some existing state-of-the-art approaches, the proposed VC-AW-MEC algorithm generally exhibits preferable clustering effectiveness and stability on heterogeneous multi-view data. Our efforts have been verified in many synthetic or real-world multi-view data scenes.

I. INTRODUCTION

Multi-view data originating from the same objects but acquired from inconsistent observing views are nearly omnipresent in reality [1]–[5]. The attributes as well as dimensionalities to describe the same objects usually vary in different views, which is referred to as the heterogeneity across views. For example, patient’s health status is commonly measured in terms of multiple physiological metrics, such as hemogram characters, urine tests, and medical images (e.g., X-ray or magnetic resonance images) [6]. Despite the diversity of specific items in these metrics, by combining them, doctors are able to more completely, objectively understand a patient’s health condition due to the fact that these physiological metrics are the manifestations of the same patient’s health condition but from inconsistent perspectives.

Clustering on heterogeneous multi-view data is a common challenge for conventional clustering models, such as k-means [7]–[9], fuzzy c-means (FCM) [10]–[14], and maximum entropy clustering (MEC) [13]–[19], as it still belongs to ongoing problems in the effective use of data affiliated to each view. There are two natural solutions to cope with such type of data scene with multiple views. One is the feature fusion strategy. As the features existing in every view are from multiply possible viewpoints, for completely delineating objects, it certainly makes sense to combine all of these features together and then perform clustering on such regenerated data. The other is the result fusion strategy. That is, data affiliated to each view are first independently clustered. Then, to seek the consensus among views, a certain method capable of combining the results of all views, such as clustering ensemble [12], [28]–[30] or kernel combination [12], [27], is used to obtain the eventual, overall clustering decision. These two strategies, however, are sometimes inefficient and even unfeasible, despite the acceptable outcomes in quite a few cases in practice. For instance, feature fusion is prone to feature presentations with very high data dimensionalities and to making any clustering technique intractable, whereas result fusion could suffer from unstable performance due to the separate clustering in individual view, particularly in the situation where either failed partitions occur in some views or distinct outcome diversities exist among views.

In contrast, as one of the most promising clustering techniques for heterogeneous multi-view data, collaborative multi-view clustering [7], [12], [31]–[33] has aroused a large quantity of research interest in recent years. Such a technique features three points: (1) Clustering is concurrently conducted from multiple views on the same target objects; (2) the attributes and data dimensionalities used to depict the same target objects are usually inconsistent in different view spaces; and (3) last and most importantly, the collaborations (namely, interactions) among views are pursued throughout the entire clustering procedure to mine the underlying, consentaneous clustering knowledge across these views, which facilitates the overall preferable decision. Because collaborative multi-view clustering not only more completely considers the characteristics of target objects from multiple views but also takes advantage of the agreement among all involved views during clustering, its final decision, obtained under the principle of seeking common ground while reserving difference, commonly appears to be more reliable than those of the other two strategies. To facilitate explanation, the three mentioned clustering strategies for heterogeneous multi-view data, i.e., feature fusion, result fusion, and inter-view collaboration, are generally designated as multi-view clustering in our manuscript. So far, quite a bit of work regarding multi-view clustering has been conducted [7], [12], [20]–[22], [24]–[33], but most of the existing approaches focus on the strategies of feature or result fusion, and the literature associating multi-view learning with MEC is seldom met. As another type of regularization method for crisp k-means [13], [14], MEC is characterized by a more delicate mathematic formulation and a more interpretable connotation than FCM that has been commonly regarded as the most classic representative of soft partition clustering [13], [14], [34]–[36]. Specifically, by incorporating the Shannon-entropy-based diversity measure, MEC aims at the unbiased probability assignment throughout clustering [14], [15], in addition to pursuing the best intra-cluster homogeneity as well as inter-cluster separation. In addition, most existing methods do not differentiate the individual impact of attributes in each view, but regard them equally. This often weakens the realistic performance of algorithms. It is reasonable to increase the impact of attributes in one view that show high distinguishability, and vice versa. These challenges mentioned above motivate our research.

Our work in this paper proceeds in two steps. First, two specialized criteria, i.e., the criterion of inter-view collaborative learning (IEVCL) and the criterion of intra-view-weighted attributes (IAVWA), are presented. As indicated by their names, these two criteria take the responsibility for the inter-view interaction and the intra-view attribute-differentiation, respectively. Second, by delicately incorporating IEVCL and IAVWA into the framework of the classic MEC, we put forward the collaborative MEC-based multi-view clustering method named view-collaborative, attribute-weighted maximum entropy clustering (VC-AW-MEC). The core contributions of our efforts lie in the following three aspects:

1. Based on the working mechanism of MEC, we dedicatedly design both IEVCL and IAVWA. As such, we figure successfully out the effective strategies for the MEC model for coping with as many multi-view data scenes as possible.

2. IEVCL aims to find the agreement across all views during clustering, whereas IAVWA takes the responsibility for adaptively discriminating the individual impact of the attributes within one view.

3. By organically incorporating IEVCL and IAVWA, VC-AW-MEC features preferable clustering effectiveness and stability on heterogeneous multi-view data, compared with some existing state-of-the-art approaches.

The remainder of this paper is organized as follows. Some related work is reviewed in Section II. The criteria of IEVCL and IAVWA, and the whole framework and algorithm procedure with respect to VC-AW-MEC are introduced in Section III step by step. The experimental studies as well as significant analyses are conducted in Section IV. Also, some conclusions are given in the last section.

II. RELATED WORK

A. MULTI-VIEW CLUSTERING

As revealed in Introduction, there have been three strategies of multi-view clustering so far. That is,

1. The feature-fusion strategy [20]–[24]. This is actually a mechanism of a priori fusion. Namely, by juxtaposing the features in all views, the original multiple views are concatenated into a single one before clustering. This could be the least sophisticated form of multi-view learning;

2. The result-fusion strategy [12], [25]–[30]. Such strategy belongs to the mechanism of a posterior fusion. That is, the data in all views are first processed separately, and then the tricks of result combination, e.g., clustering ensemble [28]–[30] or kernel combination [27], are enlisted to seek the clustering consensus among all views;

3. The collaborative multi-view clustering strategy [5], [7], [12], [31]–[33], [47]–[49]. This strategy strives for interview collaboration during clustering by means of mining as well as exploiting the agreement across all views. For example, two efficient iterative algorithms designated as multi-view kernel k-means (MVKKM) and multi-view spectral clustering (MVSpec) [7], respectively, were proposed by optimizing the intra-cluster variance from different perspectives as well as minimizing inter-view disagreement. As an extension of fuzzy k-means (equivalently, fuzzy c-means [13], [14]), Co-FKM [12] was proposed by constituting a specific organization for each view in addition to introducing a penalty term to measure the disagreement of organizations in different views. A novel non-negative matrix factorization (NMF) based multi-view clustering method (MultiNMF) [49] was presented by searching for a factorization that gives compatible clustering solutions across multiple views.

Moreover, multi-view clustering is actually not isolated from other state-of-the-art clustering methodologies in machine learning, such as multi-task clustering [39], [40] and co-clustering [38], [41]. Multi-task clustering is devoted to completing multiple, relevant clustering tasks concurrently via certain synergistic learning criteria. For instance, the learning shared subspace for multitask clustering (LSSMTC) [39] algorithm learns a subspace shared by all the tasks, through which the knowledge in one task can be transferred to each other. In the sense of concurrent clustering, multi-view clustering is similar to multi-task clustering to a certain extent. However, all of the views in the former are regarded as coming from the same objects but from different perspectives, whereas different tasks in the latter are usually associated with different targets. As for co-clustering, it performs clustering on the target data set from the perspectives of row (i.e., example) and column (i.e., attribute) simultaneously [38], [41]. Differing from multi-view clustering, co-clustering strives for good results based on the duality between data examples and attributes/features in the only view space. For example, the dual regularized co-clustering (DRCC) algorithm [41] was developed in terms of both the data manifold and feature manifold, and the co-clustering was eventually formulated as the problem of semi-nonnegative matrix tri-factorization.

B. MAXIMUM ENTROPY CLUSTERING (MEC)

In a broad sense, MEC implies a series of clustering methods of which the objective functions are composed of certain forms of maximizing entropy [15]–[19], [42], although the specific frameworks may vary in different algorithms. As one of the well-known representatives of this category of approaches, the work proposed in [15] is employed as the foundation of our study. It can be briefly reviewed as follows.

Let X = {x_j | x_j ∈ R^d, j = 1, 2, …, N} denote a given data set, where d and N denote the data dimension and data capacity, respectively. Suppose that this data set contains C (2 ≤ C < N) potential clusters. Then, the objective function of classic MEC can be represented as

$$\begin{gathered} \underset{U,V}{\text{min}}\left(\sum _{i=1}^C\sum _{j=1}^N{\mu }_{ij}{\Vert x_j-v_i\Vert }^2+\gamma \sum _{i=1}^C\sum _{j=1}^N{\mu }_{ij}\text{ln}{\mu }_{ij}\right) \\ \text{s.t. }0\le {\mu }_{ij}\le 1\text{\hspace{0.17em}\hspace{0.17em}and }\sum _{i=1}^C{\mu }_{ij}=1 \\ 1\le i\le C,1\le j\le N \end{gathered}$$ (1)

where, ∥x_j − v_i∥² is the distance measure between pattern x_j and cluster centroid v_i; U ∈ R^C×N is the membership matrix consisting of μ_ij (i = 1, …, C; j = 1, … N), and μ_ij denotes the membership degree of object x_j to cluster centroid v_i; V ∈ R^d×C is the cluster centroid matrix composed of all cluster centroids v₁, …, v_C; and γ > 0 is the regularization parameter.

There are two terms in (1). The first measures the total deviation regarding all data instances to every estimated cluster centroid with membership values μ_ij (i = 1, …, C; j = 1, N) being weight factors. The second term is exactly the Shannon entropy term derived from the Shannon diversity measurement in information theory [14], [15], [18], [37], [38], [53]–[57], i.e., $D{I}_S=-\sum _{i=1}^n{p}_i\text{\hspace{0.17em}ln\hspace{0.17em}}{p}_i$. This term aims at unbiased probability assignments (i.e., the membership degrees in (1)) while agreeing with whatever information is given, according to the principle of maximum entropy inference (MEI) [14], [15].

Using the Lagrange optimization, the update equations of cluster prototype v_i and membership μ_ij in (1) can be derived as

$$v_i=\frac{\sum _{j=1}^N{\mu }_{ij}{x}_j}{\sum _{j=1}^N{\mu }_{ij}},i=1,2,\dots ,C;$$ (2)

$${\mu }_{ij}=\frac{\text{exp}\left(-\frac{\Vert x_j-v_i{\Vert }^2}{\gamma }\right)}{\sum _{k=1}^C\text{exp}\left(-\frac{\Vert x_j-v_k{\Vert }^2}{\gamma }\right)},i=1,2,\dots ,C;j=1,2,\dots ,N.$$ (3)

As revealed in [13], like FCM, MEC is devised as another methodology to fuzzify crisp k-means. Apparently, benefiting from MEI, compared with FCM, MEC has a nicer formulation and a more meaningful connotation [14].

C. MEC VERSUS HETEROGENEOUS MULTI-VIEW DATE

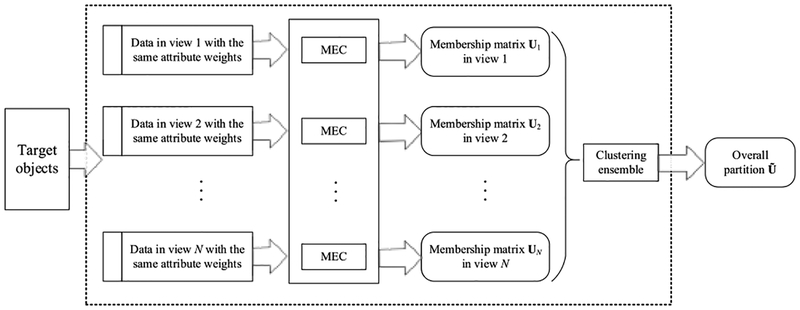
Feature fusion and result fusion are two available countermeasures for conventional MEC for handling heterogeneous multi-view data. For feature fusion, it is needed to concatenate different attributes in all views. Here some preprocessing with respect to some attributes could be necessary, e.g., normalizing each dimension [27], so that all involved attributes can be comparable to each other. As for result fusion, Fig. 1 illustrates one usual workflow, in which the clustering ensemble, as the last but the most important step of the entire procedure, is recruited. Specifically, MEC is first used to separately handle the data affiliated to each view and to attain the individual partition matrices (namely, membership matrices) — U₁, U₂, …, U_N. Then, via a certain clustering ensemble strategy imposing upon these partition matrices, the overall decision $\tilde{U}$ is eventually achieved.

FIGURE 1.

The workflow of conventional MEC versus heterogeneous multi-view data with result fusion.

Remarks: As is evident, traditional MEC fails to take into account two aspects of challenge in the scene of heterogeneous multi-view data. On the one hand, the lack of interactive learning among views, i.e., inter-view collaborations, during the entire clustering procedure is the most serious drawback. It only processes each view separately regardless of their potential correlations. Although the final clustering result is able to be comprehensively obtained in terms of the strategy of result fusion, the reliability of the overall decision is vulnerable to the underlying data distortion existing in certain views. On the other hand, all attributes are currently treated equally in any view, which brings probably about two issues. First, the attributes owning larger orders of magnitude could dominate the similarity measurement between two data instances. Second, the consistent weight assigned to every attribute could restrict the distinguishability of similarity measure, even if the orders of magnitude of all of the attributes are almost close. Motivated by these problems, we attempt to propose our own schema for handling heterogeneous multi-view data in the following section.

III. VIEW-COLLABORATIVE, ATTRIBUTE-WEIGHTED MAXIMUM ENTROPY CLUSTERING

Before introducing our novel framework regarding collaborative multi-view MEC, two dedicated criteria need to be first presented as the bases of our work.

A. TWO SPECIALIZED CRITERIA FOR COLLABORATIVE MULTI-VIEW MEC

1). THE CRITERION OF INTER-VIEW COLLABORATIVE LEARNING (IEVCL)

For the purpose of collaborative learning among views, the clustering knowledge in one view is designed to learn from that in other views in our scheme. Specifically, let k (k ∈ [1, K]) denote the view index and K be the total view number, μ_ij,k denote the membership degree of object j (j ∈ [1, N]) to cluster i (i ∈ [1, C]) in the kth view, and Σ_{k′ ≠k} μ_ij,k′ signify the sum of the membership degrees with respect to object j (j ∈ [1, N]) to cluster i (i ∈ [1, C]) in all of the other views excluding view k; then, the formula of our IEVCL criterion is devised as

$${\tilde{\mu }}_{ij,k\eta }=\eta {\mu }_{ij,k}+\frac{1-\eta }{K-1}\sum _{\begin{array}{c}{k}^{\prime }\ne k\\ k^{\prime }=1\end{array}}^K{\mu }_{ij,k^{\prime }}$$ (4)

where ${\tilde{\mu }}_{ij,k\eta }$ is the synthetic membership degree regarding object j (j ∈ [1, N]) to cluster i (i ∈ [1, C]) in view k, and η ∈ (0, 1] is a trade-off factor.

As is evident, in any view k, membership degree ${\tilde{\mu }}_{ij,k\eta }$ is synthetically generated by incorporating the clustering knowledge in all of the other views into the current one, with parameter η balancing their individual impact. In order to fuse the knowledge outside the current view well, the average of {μ_ij,k′ | k′ ≠ k}, i.e., Σ_{k′ ≠k} μ_ij,k′ / (K − 1), is adopted in our study. In this way, the clustering knowledge obtained in every view is capable of being shared with each other, which is undoubtedly conducive to generating a desirable, insightful decision over all views.

2). THE CRITERION OF INTRA-VIEW-WEIGHTED ATTRIBUTES (IAVWA)

The IAVWA criterion aims to discriminate individual importance with respect to each attribute in any view. For this purpose, based on the original formulation of MEC in the form of (1), we derive IAVWA as

$$\begin{gathered} \text{min}\left(\begin{array}{c}{\delta }_{ij,k}=\sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2\\ +{\lambda }_2\sum _{l=1}^{d_k}{w}_{l,k}\text{ln}{w}_{l,k}\end{array}\right) \\ \text{s.t. }\sum _{l=1}^{d_k}{w}_{l,k}=1 \end{gathered}$$ (5)

in which d_k represents the data dimensionality in view k; w_l,k is the weight of the lth attribute in the kth view; $x_{jl,k}\in x_{j,k}={\left[x_{j1,k},x_{j2,k},\dots ,x_{j{d}_k,k}\right]}^{\text{T}}$ signifies the lth attribute value of the jth object in the kth view; likewise, $v_{il,k}\in v_{i,k}={\left[v_{i1},k,v_{i2},k,\dots ,v_{i{d}_k,k}\right]}^{\text{T}}$ denotes the lth dimensional value of the ith cluster centroid in the kth view; and λ₂ > 0 is a regularization coefficient.

There are two terms in the formula of IAVWA. The first term, ${\sum }_{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2$, calculates the weighted distance sum regarding object j to cluster centroid i in view k with w_l,k, l = 1, …, d_k, acting as the weight factors. The second one, ${\sum }_{l=1}^{d_k}{w}_{l,k}\text{ln}{w}_{l,k}$, similar to Σ_i Σ_jμ_ij ln μ_ij in the formulation of MEC (see (1)), is the Shannon entropy term to achieve unbiased probability assignments during clustering according to the MEI principle.

B. THE NOVEL FRAMEWORK OF VC-AW-MEC

Now, by means of both IEVCL and IAVWA, we can present our VC-AW-MEC model for multi-view collaborative clustering. With the same notations as those in (1), (4), and (5), we formulate the framework of VC-AW-MEC as

$$\begin{array}{l}\text{min}\left(\begin{array}{l}{J}_{\text{VC}-\text{AW}-\text{MEC}}\left(U_1,V_1,w_1,\dots ,U_K,V_K,w_K\right)\\ =\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N\left({\tilde{\mu }}_{ij,k\eta }\sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2\right)\\ +{\lambda }_1\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N{\mu }_{ij,k}\text{ ln }{\mu }_{ij,k}\\ +{\lambda }_2\sum _{k=1}^K\sum _{l=1}^{d_k}{w}_{l,k}\text{ ln }{w}_{l,k},\\ {\tilde{\mu }}_{ij,k\eta }=\eta {\mu }_{ij,k}+\frac{1-\eta }{K-1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K{\mu }_{ij,k^{\prime }}\end{array}\right)\\ \text{s.t. }{\mu }_{ij,k}\in [0,1],w_{l,k}\in [0,1],\sum _{i=1}^C{\mu }_{ij,k}=1,\sum _{l=1}^{d_k}{w}_{l,k}=1,\\ 1\le i\le C,1\le j\le N,1\le k\le K\end{array}$$ (6)

where, x_jl,k ∈ x_j,k, v_il,k ∈ v_i,k, U_k = [μ_ij,k]_C×N, V_k = [v_{1, k}, …, v_C,k]^T, $w_k={\left[w_{1,k},\dots ,w_{d_k,k}\right]}^{\text{T}}$, and λ₁ > 0, λ₂ > 0 are two regularization parameters.

In (6), ${\sum }_{k=1}^K{\sum }_{i=1}^C{\sum }_{j=1}^N\left({\tilde{\mu }}_{ij,k\eta }{\sum }_{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2\right)$ measures the total deviation regarding all objects to all cluster centroids in all views, and the remainder, i.e., ${\lambda }_1{\sum }_{k=1}^K{\sum }_{i=1}^C{\sum }_{j=1}^N{\mu }_{ij,k}\text{ln}{\mu }_{ij,k}+{\lambda }_2{\sum }_{k=1}^K{\sum }_{l=1}^{d_k}{w}_{l,k}\text{ln}{w}_{l,k}$, is composed of two maximum entropy terms used to pursue unbiased probability assignments throughout clustering. Here, both membership degree μ_ij,k and weight factor w_l,k are regarded as two types of probability. More exactly, in view k, the former indicates the probability that object j belongs to cluster i, whereas the latter designates the probability that attribute l dominates the similarity measurement between object j and cluster centroid i.

Theorem 1: The necessary conditions to minimize the objective function J_VC-AW-MEC in (6) yield the following updating equations regarding the cluster centroids, membership degrees, and weight factors:

$$v_{il,k}=\frac{\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }{w}_{l,k}{x}_{jl,k}}{\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }{w}_{l,k}}$$ (7)

$$w_{l,k}=\frac{\text{exp}\left(-\frac{\sum _{i=1}^C\sum _{j=1}^N\left({\tilde{\mu }}_{ij,k\eta }{\left(x_{jl,k}-v_{il,k}\right)}^2\right)}{{\lambda }_2}\right)}{\sum _{q=1}^{d_k}\text{exp}\left(-\frac{\sum _{i=1}^C\sum _{j=1}^N\left({\tilde{\mu }}_{ij,k\eta }{\left(x_{jq,k}-v_{iq,k}\right)}^2\right)}{{\lambda }_2}\right)}$$ (8)

$${\mu }_{ij,k}=\frac{\text{exp}\left(-\frac{\eta \sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2+\frac{1-\eta }{K1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}{\left(x_{jl,k^{\prime }}-v_{il,k^{\prime }}\right)}^2}{{\lambda }_1}\right)}{\sum _{r=1}^C\text{exp}(\frac{n\sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{rl,k}\right)}^2+\frac{1-\eta }{K1}\sum _{k^{\prime }=1,k^{\prime }\ne k}\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}{\left(x_{jl,k^{\prime }}-v_{rl,k^{\prime }}\right)}^2}{{\lambda }_1})}$$ (9)

where ${\tilde{\mu }}_{ij,k\eta }=\eta {\mu }_{ij,k}+\frac{1-\eta }{K-1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K{\mu }_{ij,k^{\prime }}$.

The proof of Theorem 1 is given in Appendix A.

To generate the overall clustering decision $\tilde{U}$ over all views, the geometric mean [12], [30], [43] of all membership degrees in all views, i.e., the Kth root of the product of U₁, …, U_K, is enlisted in our VC-AW-MEC model:

$$\tilde{U}=\sqrt[K]{\prod _{k=1}^K{U}_k}$$ (10)

As such, the overall tendencies/probabilities of all object to all cluster centroids are capable of being measured comprehensively [43].

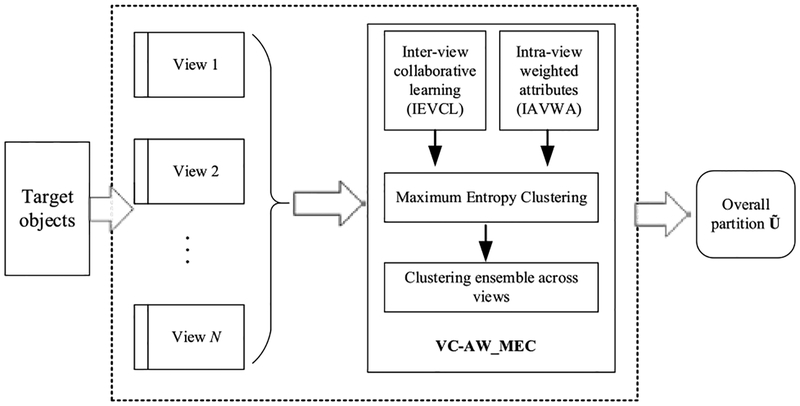
The workflow of our proposed VC-AW-MEC model versus heterogeneous multi-view data is illustrated in Fig. 2.

FIGURE 2.

The workflow of VC-AW-MEC versus heterogeneous multi-view data.

C. THE VC-AW-MEC ALGORITHM

Echoing Fig. 2, the algorithm procedure of VC-AW-MEC is detailed Algorithm 1.

The computational complexity of the proposed VC-AW-MEC algorithm is analyzed as follows. In each iteration, for calculating U_k, V_k, and w_k, k = 1, …, K, the computing cost is $O\left(KNC+KC+{\sum }_{k=1}^K{d}_k\right)$. Thus, the total computational complexity of VC-AW-MEC is $O\left(max\_iter\times \left(KNC+KC+{\sum }_{k=1}^K{d}_k\right)\right)$.

Based on the Zangwill’s convergence theorem [14], [50], the convergence of our proposed VC-AW-MEC algorithm can be proved. Please refer to Section Appendix B for the details.

IV. EXPERIMENTAL RESULTS

A. SETUP

We attempt to demonstrate the effectiveness of our proposed VC-AW-MEC algorithm on heterogeneous multi-view data in this section. For this purpose, five related, well-established competitors, i.e., LSSMTC [39], DRCC [41], MVKKM [7], Co-FKM [12], and MultiNMF [49] were used to compare with each other. Among them, LSSMTC belongs to multi-task clustering, DRCC features co-clustering, and MVKKM, Co-FKM, and MultiNMF are the representatives of collaborative multi-view clustering. In addition, to validate the realistic performance of VC-AW-MEC with distinctive interview collaborations as well as intra-view-weighted attributes in multi-view data scenes, the strategies of “MEC + feature fusion” (denoted as MEC-FF) and “MEC + result fusion” (denoted as MEC-RF, in which (10) was also recruited for generating the eventual decision matrix $\tilde{U}$) were employed in our experiments. As such, we got three MEC-based multi-view clustering approaches — MEC-FF, VC-AW-MEC, and MEC-RF, and they belong to the modalities of priori fusion, inter-view collaboration, and posterior fusion, respectively. Both the synthetic and real-world multi-view data scenes were used, which will be introduced in detail below.

For the purpose of fair comparison, three well-established validity metrics, Normalized Mutual Information (NMI) [14], [17], Rand Index (RI) [14], [44], and Davies-Bouldin Index(DBI) [14], [44], were used throughout our experiments. Both NMI and RI belong to external criteria dependent on given labels, whereas DBI is one internal criterion that appraises clustering effectiveness based purely on the inherent quantities or features in the data set, such as intra-cluster homogeneity as well as inter-cluster separation. Their definitions are briefly reviewed as follows.

1). NMI

$$NMI=\frac{\sum _{i=1}^C\sum _{j=1}^C{N}_{i,j}\text{log}N\cdot N_{i,j}/N_i\cdot N_j}{\sqrt{\sum _{i=1}^C{N}_i\text{log}{N}_i/N\cdot \sum _{j=1}^C{N}_j\text{log}{N}_j/N}}$$ (11)

where N_i,j denotes the number of agreements between cluster i and class j, N_i is the number of data points in cluster i, N_j is the number of data points in class j, and N signifies the data size of the whole dataset.

2). RI

$$RI=\frac{f_{00}+f_{11}}{N(N-1)/2}$$ (12)

where f₀₀ denotes the number of any two data points belonging to two different clusters, f₁₁ denotes the number of any two data points belonging to the same cluster, and N is the total number of data points.

3). DBI

$$DBI=\frac{1}{C}\sum _{k=1}^C\underset{k^{\prime }\ne k}{\text{max}}\frac{{\delta }_k+{\delta }_{k^{\prime }}}{{\Delta }_{k{k}^{\prime }}},$$ (13-1)

where

$${\delta }_k=\frac{1}{n_k}\sum _{x_j^k\in C_k}\Vert x_j^k-v_k\Vert ,{\Delta }_{k{k}^{\prime }}=\Vert v_k-v_{k^{\prime }}\Vert ,$$ (13-2)

C denotes the cluster number in the dataset, $x_j^k$ denotes the data instance belonging to cluster C_k, and n_k and v_k separately signify the data size and the centroid of cluster C_k.

Both NMI and RI take values within the interval [0,1]. The higher the value of NMI or RI, the better clustering performance is indicated. Conversely, smaller values of DBI are preferred, which convey that both the inter-cluster separation and intra-cluster homogeneity are concurrently acceptable.

For parameter settings, the grid search strategy [14] was used to seek the optima of core parameters in all involved approaches. These parameters as well as their trial ranges are listed in Tables 1 and 2. Referring to the recommendations in [7], [12], [39], and [41], we determined the trial ranges of core parameters in the competitive approaches. Taking VC-AW-MEC as an example, we explain how to determine the best parameter settings: The given range of each parameter was first evenly divided into several subintervals; after that, in the form of repeated implementations of the VC-AW-MEC algorithm, the multiply nested loops were executed with one parameter locating at one loop and the subintervals of this parameter being the steps of the matching loop. Meanwhile, the clustering effectiveness was recorded in terms of the recruited validity indices, i.e., NMI, RI, and DBI. After the eventual termination of these nested loops, the optimal parameter settings were achieved, i.e., the ones corresponding to the best clustering effectiveness within the given trial ranges.

TABLE 1.

Parameter settings in multi-task clustering and co-clustering algorithms.

Algorithms	Core parameters and settings
Multi-task clustering: LSSMTC	Task number T= 2 Parameter l ∈ {2,22,23,24} Parameter λ ∈ {0.15, 0.25, 0.5, 0.75}
Co-clustering: DRCC	Parameter λ ∈ {0.1, 1, 10, 100, 500, 1000} Parameter μ ∈ {0.1, 1, 10, 100, 500, 1000}

TABLE 2.

Parameter settings in multi-view clustering algorithms.

Algorithms	Core parameters and settings
VC-AW-MEC	Trade-off factor η ∈ [0.01,0.05: 0.05: 1] Regularization coefficient λ1λ2 ∈ {1e−4,1e−3,1e−2,1e−1,1,1e1,1e2,1e3,1e4}
MEC-FF	Regularization coefficient γ ∈ {1e−4,1e−3,1e−2,1e−1,1,1e1,1e2,1e3,1e4}
MEC-RF	Regularization coefficient γ ∈ {1e−4,1e−3,1e−2,1e−1,1,1e1,1e2,1e3,1e4}
MVKKM	Exponent p ∈ {1, 1.3, 1.5, 2, 4, 6} Gaussian kernel width σ ∈ {τ / 64, τ / 32, τ / 16, τ / 8, τ / 4, τ / 2, τ, 2τ, 4τ, 8τ, 16τ, 32τ, 64τ} where τ is the mean pairwise norm of data set
MultiNMF	λv, ∈ {0, 0.001, 0.01, 0.02}, v=1, …, K
Co-FKM	Fuzzifier m ∈ [1.05: 0.05: 2.5] Parameter $\eta \in \left[0:0.01:\frac{K-1}{K}\right]$ where K is the total view number

All experiments were carried out on a PC with Intel i5–4590 3.3 GHz CPU and 4 GB RAM, Microsoft Windows 7 64 bit, and MATLAB 2011b. The best clustering performance of each approach is reported in terms of the means and standard deviations of NMI, RI, and DBI after 20 runs on each data set. It should be mentioned that, unlike NMI and RI, the calculation of DBI depends on the data itself. Therefore, due to the data inconsistency in different views, the geometric means [12], [30], [43] of DBI scores over all views, similar to (10), were adopted as the final DBI value for one method in one multi-view data scene.

B. IN SYNTHETIC MULTI-VIEW DATA SCENE

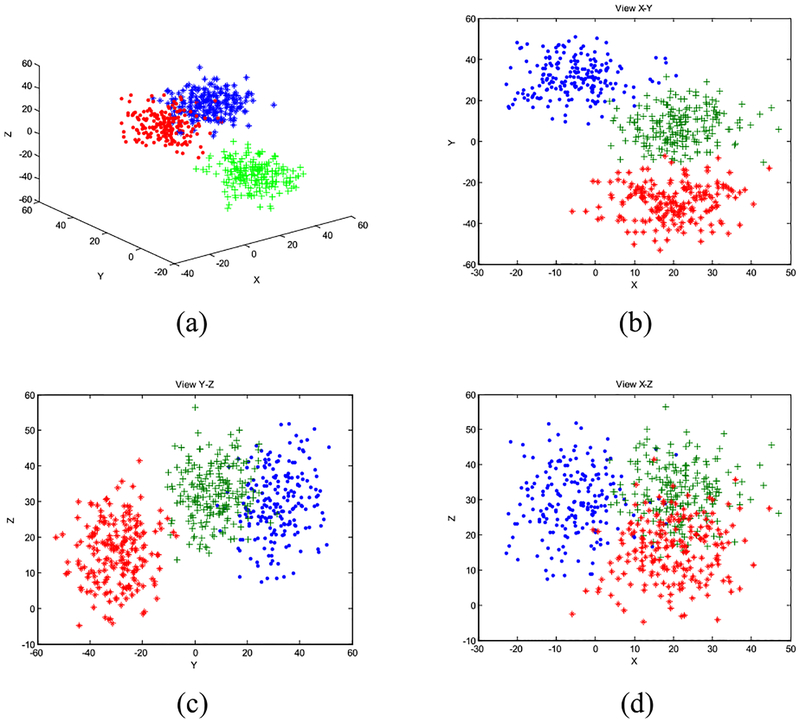
Here, we artificially generated a 3-D data scene, as shown in Fig. 3(a), in which 600 data points, owning the X, Y, and Z coordinate values simultaneously, are potentially affiliated with 3 clusters. This scene contains three views: X–Y (Fig. 3(b)), Y–Z (Fig. 3(c)), and X–Z (Fig. 3(d)). As indicated in Fig. 3, if observed from view X–Y, the 600 examples can be easily, exactly divided into three clusters, whereas from the other views, both Y–Z and X–Z, due to the overlap among clusters, the three clusters are difficult to correctly separate.

FIGURE 3.

Artificial 3-view data scene. (a) 3-D illustration of all data points. (b) View X–Y. (c) View Y–Z. (d) View X–Z.

We implemented LSSMTC, DRCC, MVKKM, Co-FKM, MultiNMF, MEC_FF, MEC_RF, and VC-AW-MEC in such an artificial multi-view data scene, respectively. Their individual clustering performance, measured in terms of the employed validity indices, is listed in Table 3 in which the top 3 scores of each index are marked with “①,” “②,” and “③,” respectively.

TABLE 3.

Performance comparisons of involved approaches in synthetic 3-view data scene.

Data scene	Algorithm	NMI-mean	NMI-std	RI-mean	RI-std	DBI-mean	DBI-std
Artificial 3-view data scene	LSSMTC	0.6305	0.0134	0.8339	0.0073	1.6996	0.0415
	DRCC	0.8988	0	0.9674	1.17E-16	1.2135	2.34E-16
	MVKKM	0.9249	0	0.9762③	2.34E-16	0.9869	0
	Co-FKM	0.9314②	1.17E-16	0.9804②	1.17E-16	0.9895	1.17E-16
	MultiNMF	0.9266③	0.0106	0.9704	0.0055	0.9203②	0.0532
	MEC-FF	0.9173	2.16E-16	0.9761	1.17E-16	0.9855③	5.23E-17
	MEC-RF	0.7610	0.1873	0.8865	0.1076	1.1787	0.3082
	VC-AW-MEC	0.9547①	0	0.9984①	1.17E-16	0.9057①	2.34E-16

Based on Table 3, our analyses are as follows.

1. In such a synthetic multi-view scene, aside from MEC-RF, all of the other multi-view clustering approaches, i.e., MVKKM, Co-FKM, MultiNMF, MEC-FF, and VC-AW-MEC, achieved satisfactory clustering performance. In addition, owing to the desirable inter-view collaboration, MVKKM, Co-FKM, MultiNMF, and VC-AW-MEC outperform the others.

2. Despite the overlap of clusters in some views (see Figs. 3(c) and (d)), by putting the features in all views together, MEC-FF, the feature fusion-based MEC method, also got comparatively high NMI and RI scores. Nonetheless, it should be clarified that the clustering performance of MEC-FF depends largely on the inherent quality itself of the combined features. If and only if the combination of features from all views is profitable, MEC-FF can exhibit superiority against the others.

3. MEC-RF belongs to the strategy of result-fusion. It is difficult for conventional MEC to handle the data distributions in views Y–Z and X–Z (i.e., Figs. 3(c) & 3(d)), as some clusters are heavily mixed. Consequently, unsatisfactory clustering results of MEC in these two views weakened the entire performance of MEC-RF even if the trick of clustering ensemble was utilized.

4. As one representative of multi-task clustering, LSSMTC did not attain desirable results with each view acting as one task on such artificial, heterogeneous multi-view data. In contrast, DRCC, one co-clustering approach, due to the duality utilization from the perspectives of record and attribute synchronously, obtained better NMI and RI scores.

5. Benefiting from jointly leveraging the interview collaborations and intra-view-weighted attributes, VC-AW-MEC achieved the best NMI, RI, and DBI scores, even compared with some state-of-the-art approaches with the collaborations among views, such as MVKKM, MultiNMF, and Co-FKM.

C. IN REAL-WORLD MULTI-VIEW DATA SCENES

1). THE CONSTRUCTION OF MULTI-VIEW SCENES

To further validate the realistic effectiveness of our proposed VC-AW-MEC algorithm, several real-world multi-view data scenes were also used for our experimental studies:

(1). Multi-view data scenes from the UCI machine learning repository¹

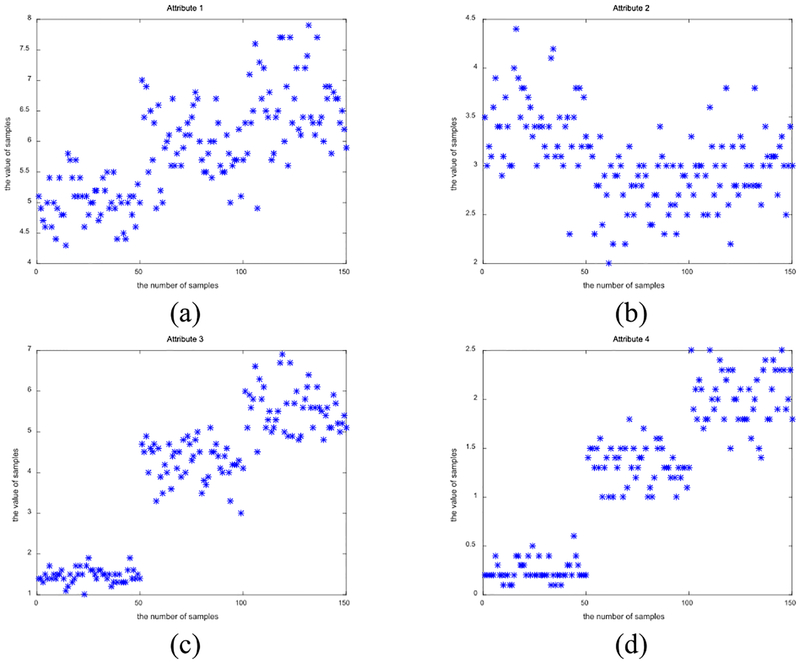
Four data sets from the UCI repository—Iris, Multiple Features (MF), Image Segmentation (IS), and Water Treatment Plant (WTP), were recruited to constitute the real-world multi-view data scenes for our experiments. As shown in Fig. 4, the data distributions of the four original attributes in Iris are inconsistent; the last two dimensions appear to be easily separated but not the others. Thus, via the pairwise combinations of attributes in Iris: 1&3 and 2&4, we generated the 2-view Iris data scene. MF contains 2,000 patterns of handwritten digits affiliated with 10 categories (‘0’–’9’). Each pattern is characterized by 649 features that have been explicitly divided into 6 views. IS is an outdoor image data set composed of 2,310 instances. Each image is depicted by 19 features from the viewpoints of shape and color separately. WTP comes from the daily measures of sensors in an urban waste water treatment plant. It contains 527 instances depicted by 38 attributes from 4 different views.

FIGURE 4.

Data distributions of different attributes in Iris. (a) Distribution in attribute 1. (b) Distribution in attribute 2. (c) Distribution in attribute 3. (d) Distribution in attribute 4.

The details regarding the four real-world multi-view scenes from the UCI repository are listed in Tables 4 and 5.

TABLE 4.

UCI data sets to construct real-world multi-view data scenes.

Data set	Description	Data size	Dimension	Cluster number	View number
Iris	Classes of iris plants	150	4	3	2
Multiple Features (MF)	Handwritten digits represented by multiple features	2,000	649	10	6
Image Segmentation (IS)	Outdoor images	2,310	19	7	2
Water Treatment	The dataset coming from	527	38	13	4
Plant (WTP)	the daily measures of sensors in an urban waste water treatment plant

TABLE 5.

Depictions of Iris, MF, IS, and WTP multi-view data scenes.

Data scene	View	Composition of Each View	Dimension	Size
Iris	View 1	Attributes 1&3	2	150
	View 2	Attributes 2&4	2
MF	Mfeat-fou view	76 Fourier coefficients of the character shapes	76	2,000
	Mfeat-fac view	216 profile correlations	216
	Mfeat-kar view	64 Karhunen-Love coefficients	64
	Mfeat-pix view	240 pixel averages in 2 × 3 windows	240
	Mfeat-zer view	47 Zemike moments	47
	Mfeat-mor view	6 morphological variables	6
IS	Shape view	9 features about the shape information of 7 images	9	2,310
	RGB view	10 features about the RGB values of 7 images	10
WTP	Input view	The first 22 features describing different input conditions.	22	527
	Output view	The 23th-29th features describing the output demands.	7
	Performance input view	The 30th-34th features describing the performance input demands.	5
	Global performance input view	The 35th-38th features describing the global performance input demands.	4

(2). Multi-view data scenes in image segmentation

Two multi-view scenes regarding image segmentation were also enlisted to validate the practicability of the proposed VC-AW-MEC method. Specifically, seven types of textures from the Brodatz texture database² and one animal, hand-labelled image from the Berkeley segmentation database³ were used. The 7 categories of Brodatz textures are shown in Fig. 5 (a). Using these textures, we first constructed a texture image with 100 × 100 = 10, 000 resolution, and then the Gabor filter [45], [46] was adopted to extract the texture features from this image. With three different sets of parameter value for the Gabor filter, as shown in Table 6, we finally generated the 3-view Brodatz texture-segmentation data scene. The test image (No. 296059) in the Berkeley repository (Berke-296059 for short) was used in our work. We resized it to the 100 × 66 resolution and relabeled it by hand, as shown in Fig. 5(b). Extracting the color features of pixels in this image from the channels of R, G, and B, respectively, we achieved another 3-view image-segmentation data scene. We detail these two multi-view real-image segmentation scenes in Table 6.

FIGURE 5.

Involved real-world images for multi-view clustering. (a) Texture image composed of 7 Brodatz textures. (b) Berke-296059 from Berkeley segmentation repository.

TABLE 6.

Depictions of two multi-view real-image-segmentation scenes.

Data scene	View	View depiction	Dimension	Data size
Brodatz texture-image segmentation	View 1	A filter bank with 5 orientations and 2 frequencies starting from 0.2 was created. Then, 10 dimensional features were extracted from each pixel in this image by applying the filter bank.	10	10,000
	View 2	A filter bank with 5 orientations and 3 frequencies starting from 0.3 was created. Then, 15 dimensional features were extracted from each pixel of the image by applying the filter bank.	15
	View 3	A filter bank with 6 orientations and 5 frequencies starting from 0.4 was created. Then, 30 dimensional features were extracted from each pixel of the image by applying the filter bank.	30
Berke-296059 image segmentation	View R	The features of R channel of all pixels in Berke-296059.	1	6,600
	View G	The features of G channel of all pixels in Berke-296059.
	View B	The features of B channel of all pixels in Berke-296059.

2). CLUSTERING RESULT ANALYSES

We ran the eight employed approaches in these six real-world multi-view data scenes, respectively, and their individual clustering scores measured in terms of NMI, RI, and DBI are listed in Table 7. In light of the prerequisite of LSSMTC that the data dimensions of all tasks must be consistent, LSSMTC cannot work in some of these multi-view scenes, such as MF, IS, WTP, and Brodatz texture segmentation, and its score in such case is marked with “−” in Table 7. In addition, one of the realistic segmentation outcomes of each adopted approach in each of the two image-segmentation multi-view scenes is illustrated in Figs. 6 and 7.

TABLE 7.

Performance comparisons of involved approaches on real-world multi-view data sets.

Data sets	Algorithm	NMI-mean	NMI-std	Rl-mean	Rl-std	DBI-mean	DBI-std
Iris with 2 views	LSSMTC	0.5300	0.0272	0.7664	0.0071	7.0324	3.2386
	DRCC	0.7419	1.17E-16	0.8737	1.17E-16	0.8260①	1.17E-16
	MVKKM	0.8552②	1.17E-16	0.9402②	1.17E-16	0.8907	2.34E-16
	Co-FKM	0.8308	1.17E-16	0.9341③	0	0.8903	1.17E-16
	MultiNMF	0.8520③	0.0187	0.9095	0.0149	0.8847	0.0101
	MEC-FF	0.7419	1.17E-16	0.8737	1.17E-16	0.8260①	1.17E-16
	MEC-RF	0.6727	0.0762	0.8013	0.0558	1.1125	0.7402
	VC-AW-MEC	0.8642①	1.17E-16	0.9495①	1.17E-16	0.8307③	2.34E-16
MF with 6 views	LSSMTC	—	—	—	—	—	—
	DRCC	0.7179	1.17E-16	0.9252	0	3.2781②	0
	MVKKM	0.6766	0	0.9180	1.17E-16	3.7234	9.36E-16
	Co-FKM	0.8521②	0.0433	0.9666②	0.0131	4.1374	0.6814
	MultiNMF	0.7644	0.0478	0.7139	0.0918	4.1492	0.0402
	MEC-FF	0.7856③	0.0000	0.9555③	1.17E-16	4.3052	4.19E-16
	MEC-RF	0.6999	0.0393	0.9263	0.0121	3.2976③	0.1569
	VC-AW-MEC	0.8840①	0.0404	0.9717①	0.0175	3.1964①	0.3109
IS with 2 views	LSSMTC	—	—	—	—	—	—
	DRCC	0.5320	0	0.8169	0	2.3537	0
	MVKKM	0.5859	0	0.7942	0	3.6544	0
	Co-FKM	0.5772	0.0007	0.8434	0.0055	2.1294	0.0610
	MultiNMF	0.6142③	0.0173	0.8669	0.0241	2.1144③	0.0690
	MEC-FF	0.6139	0.0060	0.8765②	0.0049	1.8354①	0.0655
	MEC-RF	0.6143②	0.0125	0.8674③	0.0068	2.1898	0.5000
	VC-AW-MEC	0.6547①	0.0006	0.8793①	0.0008	1.9475②	0.1846
WTP with 4 views	LSSMTC			—		—
	DRCC	0.2029	0.0103	0.7051	0.0061	4.1516	0.2427
	MVKKM	0.2106	2.93E-17	0.4082	5.85E-17	0.7662①	1.17E-16
	Co-FKM	0.2003	0.0070	0.7019	0.0048	3.2781②	0.0104
	MultiNMF	0.2072	0.0060	0.7059	0.00777	4.2160	0.0642
	MEC-FF	0.2304②	0.0081	0.6278②	0.0020	5.2373	0.1947
	MEC-RF	0.2204③	0.0141	0.6212③	0.0040	6.8078	0.4719
	VC-AW-MEC	0.2391①	0.0072	0.6281①	0.0020	4.1130③	0.2593
Brodatz texture segmenta tion with 3 views	LSSMTC	—	—	—	—		—
	DRCC	0.6468	1.17E-16	0.8994	0	2.2064	0
	MVKKM	0.4926	0.0575	0.8222	0.0371	2.8394	0.4484
	Co-FKM	0.6740③	0.0251	0.9132③	0.0158	2.0681③	0.0802
	MultiNMF	0.6433	0.0501	0.8685	0.0650	2.1140	0.0960
	MEC-FF	0.6897①	0.0188	0.9169②	0.0104	2.0350②	0.1500
	MEC-RF	0.5345	0.0358	0.8437	0.0190	2.5442	0.2064
	VC-AW-MEC	0.6826②	0.0002	0.9188①	3.01E-05	1.9678①	5.37E-05
Berke-29 6059 segmenta tion with 3 views	LSSMTC	0.4098	0.0015	0.7109	3.44E-04	0.8049③	0.0033
	DRCC	0.4561	5.85E-17	0.7067	0	0.7819②	1.17E-16
	MVKKM	0.4721	0.0097	0.7417	0.0291	0.8431	0.0338
	Co-FKM	0.5176③	0	0.7541	1.17E-16	1.1414	2.34E-16
	MultiNMF	0.4793	0.0182	0.7565	0.0117	0.8956	0.0189
	MEC-FF	0.4819	4.90E-05	0.7664③	5.62E-05	0.7231①	0.0578
	MEC-RF	0.5559②	0.0711	0.7747②	0.0624	1.3270	0.5245
	VC-AW-MEC	0.6061①	1.17E-16	0.8426①	0	0.8242	4.68E-16

FIGURE 6.

Segmentation results of involved approaches on Brodatz texture image. (a) VC-AW-MEC. (b) MEC-FF. (c) MEC-RF. (d) DRCC. (e) Co-FKM. (f) MVKKM. (g) MultiNMF.

FIGURE 7.

Segmentation results of involved approaches on Berke-29605. (a) LSSMTC. (b) MEC-FF. (c) MEC-RF. (d) MVKKM. (e) Co-FKM. (f) DRCC. (g) MultiNMF. (h) VC-AW-MEC.

Observing these experimental results, we can also draw some conclusions below.

1. In general, the conclusions we achieve in the synthetic multi-view data scene still hold here.

2. As was already revealed, MEC-FF no longer exhibited stable effectiveness in some of these real-world multi-view scenes. For example, in Iris, MF, and Berke-296059, the NMI scores of MEC-FF are obviously worse than those of our proposed VC-AW-MEC.

3. In both IS and WTP, the three MEC-based multi-view approaches—VC-AW-MEC, MEC-RF, and MEC-FF, ranked top 3 in terms of the well-accepted NMI and RI indices. This reflects, to a certain extent, the superiority of MEC against other clustering techniques, e.g., the k-means-based MVKKM and the FCM-based Co-FKM, due to the optimization of maximum entropy.

4. The NMI and RI scores of the proposed VC-AW-MEC always ranked top 2 in all of these involved multi-view data scenes. This confirms our efforts in this paper, i.e., IEVCL aims at finding the consensus among all views. Meanwhile, IAVWA strives for adaptively determining the appropriate weights of attributes in each view. By organically incorporating these two mechanisms, it does make sense that VC-AW-MEC achieves preferable clustering outcomes.

5. As is revealed, as an internal criterion, DBI has the underlying drawback that the smallest value does not necessarily indicate the best information retrieval [14]. For example, MEC-FF gets the smallest DBI score in Iris and Berke-29605, while its NMI scores are rather common.

D. PARAMETER ROBUSTNESS ANALYSES

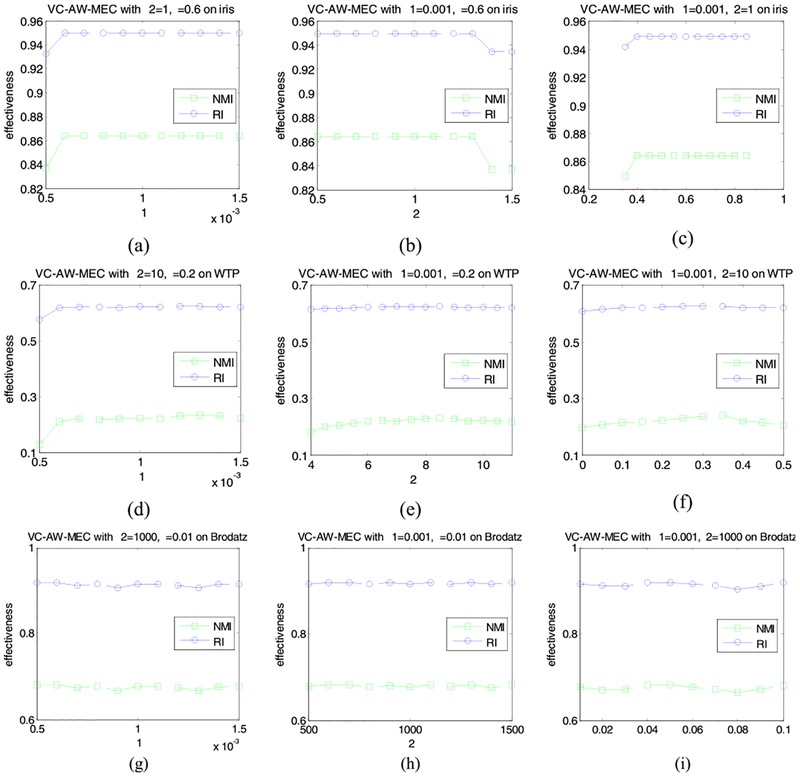
Lastly, we evaluated the robustness of our VC-AW-MEC algorithm with respect to its three core parameters, i.e. the trade-off factors η and the two regularization parameter λ₁, λ₂, in all of the involved multi-view data scenes. In each data scene, we took turns fixing two of the three parameters and gradually varied the third one until VC-AW-MEC achieved the optima by grid search. Here we only recorded the values of the two external metrics, i.e., NMI and RI. Due to the limit of paper length, we only report our experimental results in three real-world multi-view data scenes: Iris with 2 views, WTP with 4 views, and Brodatz texture segmentation with 3 views.

In Iris with 2 views, VC-AW-MEC roughly reached the optima with λ₁ = 1e⁻³, λ₂ = 1 and η = 0.6; in WTP with 4 views, with λ₁ = 1e⁻³, λ₂ = 1e¹ and η = 0.2; and in Brodatz texture segmentation with 3 views, with λ₁ = 1e⁻³, λ₂ = 1e³ and η = 0.01. The effectiveness curves of VC-AW-MEC in these three data scenes are illustrated in Fig. 8, where Fig. 8(a)–(c) show the cases in Iris, Fig. 8(d)–(f) are in WTP, and Fig. 8(g)–(i) are in Brodatz texture segmentation.

FIGURE 8.

Effectiveness curves of VC-AW-MEC with respect to three core parameters λ₁, λ₂, and η in the multi-view data scenes of Iris, WTP, and Brodatz texture segmentation. (a) Iris – λ₁. (b) Iris – λ₂. (c) Iris – η. (d) WTP – λ₁. (e) WTP – λ₂. (f) WTP – η. (g) Brodatz texture segmentation-λ₁. (h) Brodatz texture segmentation -λ₂. (i) Brodatz texture segmentation -η.

As revealed in Fig. 8, the clustering effectiveness of VC-AW-MEC is relatively stable when the three core parameters are within proper ranges, which demonstrates that VC-AW-MEC features the good robustness against parameter settings.

V. CONCLUSIONS

To propose a MEC-based approach competent in coping with heterogeneous multi-view data, two dedicated criteria—IEVCL and IAVWA are first put forward. IEVCL focuses on mining the consensus among multiple views during clustering, while IAVWA strives for properly differentiating the due weights of all attributes within one view. Then, by delicately fusing conventional MEC, IEVCL, and IAVWA, the core VC-AW-MEC model is achieved. VC-AW-MEC proves its superiority against many existing, state-of-the-art approaches in both the artificial and real-world multi-view data scenes.

As for the follow-up work, the strategy of weighted view fusion is afoot. That is, the due weights of all views during collaborative learning are worthy of further investigation, which is one of the available pathways to further promote the performance of our MEC-based multi-view learning schema.

Biographies

PENGJIANG QIAN received the Ph.D. degree from Jiangnan University, Wuxi, Jiangsu, China, in 2011. He is currently an Associate Professor with the School of Digital Media, Jiangnan University. He has been a Research Scholar with Case Western Reserve University, Cleveland, OH, USA, where he is involved in medical image processing. He has authored or co-authored over 40 papers published in international/national journals and conferences, such as IEEE TNNLS, IEEE TSMC-B, IEEE TFS, IEEE Transactions on Cybernetics, and Pattern Recognition. His research interests include data mining, pattern recognition, bioinformatics and their applications, such as analysis and processing for medical imaging, intelligent traffic dispatching, and advanced business intelligence in logistics.

JIAXU ZHOU is currently pursuing the M.S. degree with the School of Digital Media, Jiangnan University, Wuxi, Jiangsu, China. His research interests include pattern recognition and bioinformatics.

YIZHANG JIANG received the Ph.D. degree from Jiangnan University, Wuxi, Jiangsu, China, in 2016. He has been a Research Assistant with the Computing Department, Hong Kong Polytechnic University, for more than one year. He is currently an Instructor with the School of Digital Media, Jiangnan University. He has published over 20 papers in international journals, including IEEE TFS, IEEE TNNLS, IEEE Transactions on Cybernetics, Information Sciences, and so on. His research interests include pattern recognition, intelligent computation, and their applications.

FAN LIANG received the Ph.D. degree from Beihang University in 2013. He is currently a Visiting Scholar with Case Western Reserve University, Cleveland, OH, USA, where he is involved in research on medical imaging. He has authored or co-authored over 30 papers published in international/national journals and conferences. His research interests include robot control, motion compensation method, reinforcement learning, simulation and modeling, Internet of Things, and their applications.

KAIFA ZHAO is currently pursuing the M.S. degree with the School of Digital Media, Jiangnan University, Wuxi, Jiangsu, China. His research interests include pattern recognition and data mining.

SHITONG WANG received the M.S. degree in computer science from Nanjing University of Aeronautics and Astronautics, China, in 1987. He visited London University and Bristol University, U.K., Hiroshima International University, and Osaka Prefecture University, Japan, the Hong Kong University of Science and Technology, and Hong Kong Polytechnic University, as a Research Scientist for over six years. He is currently a Full Professor with the School of Digital Media, Jiangnan University, China. He has published about 100 papers in international/national journals. He has authored seven books. His research interests include artificial intelligence, neuro-fuzzy systems, pattern recognition, and image processing.

KUAN-HAO SU received the Ph.D. degree from National Yang-Ming University, Taiwan, in 2009. He is currently a Research Associate with the Department of radiology, Case Western Reserve University, Cleveland, OH, USA. His research interests include molecular imaging, tracer kinetic modeling, pattern recognition, and machine learning.

RAYMOND F. MUZIC, JR., received the Ph.D. degree from Case Western Reserve University, Cleveland, Ohio, USA, in 1991. He has lead or been a team member on numerous funded research projects. He has also had the pleasure to serve as an advisor for doctoral students. He is currently an Associate Professor of radiology, biomedical engineering, and general medical sciences—oncology—with Case Western Reserve University. He has authored or co-authored approximately 50 peer-reviewed articles. His research interests include the development and application of quantitative methods for medical imaging.

APPENDIX

A. PROOF OF THEOREM 1

Proof: It is clear that (6) can be rewritten as

$$\begin{array}{l}\text{min}\left(\begin{array}{l}{J}_{\text{VC}-\text{AW}-\text{MEC}}\left(U_1,V_1,w_1,\dots ,U_K,V_K,w_K\right)=\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N\left({\tilde{\mu }}_{ij,k\eta }\sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2\right)+{\lambda }_1\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N{\mu }_{ij,k}\text{ln}{\mu }_{ij,k}+{\lambda }_2\sum _{k=1}^K\sum _{l=1}^{d_k}{w}_{l,k}\text{ln}{w}_{l,k},\hfill \\ \iff \hfill \\ J_{\text{VC}-\text{AW}-\text{MEC}}\left(U_1,V_1,w_1,\dots ,U_K,V_K,w_K\right)=\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N\left({\mu }_{ij,k}\left(\eta \sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2+\frac{1-\eta }{K-1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}\times {\left(x_{jl,k^{\prime }}-v_{il,k^{\prime }}\right)}^2\right)\right)+{\lambda }_1\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N{\mu }_{ij,k}\text{ln}{\mu }_{ij,k}+{\lambda }_2\sum _{k=1}^K\sum _{l=1}^{d_k}{w}_{l,k}\text{ln}{w}_{l,k},\hfill \end{array}\right)\\ \text{s.t. }{\mu }_{ij,k}\in [0,1],w_{l,k}\in [0,1],\sum _{i=1}^C{\mu }_{ij,k}=v1,\sum _{l=1}^{d_k}{w}_{l,k}=1,\\ 1\le i\le C,1\le j\le N,1\le k\le K\end{array}$$ (A.1)

Using the Lagrange optimization, the minimization of J_VC-AW-MEC can be transformed into the following unconstrained minimization problem:

$$\begin{gathered} L=\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N\left({\tilde{\mu }}_{ij,k\eta }\sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2\right)+{\lambda }_1\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N{\mu }_{ij,k}\text{ln}{\mu }_{ij,k}+{\lambda }_2\sum _{k=1}^K\sum _{l=1}^{d_k}{w}_{l,k}\text{ln}{w}_{l,k}+\sum _{j=1}^N{\alpha }_j\left(1-\sum _{i=1}^C{\mu }_{ij,k}\right)+\sum _{k=1}^K{\beta }_k\left(1-\sum _{l=1}^{d_k}{w}_{l,k}\right) \\ \iff L=\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N\times \left({\mu }_{ij,k}\left(\eta \sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2+\frac{1-\eta }{K-1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}{\left(x_{jl,k^{\prime }}-v_{il,k^{\prime }}\right)}^2\right)\right)+{\lambda }_1\sum _{k=1}^K\sum _{i=1}^C\sum _{j=1}^N{\mu }_{ij,k}\text{ln}{\mu }_{ij,k}+{\lambda }_2\sum _{k=1}^K\sum _{l=1}^{d_k}{w}_{l,k}\text{ln}{w}_{l,k}+\sum _{j=1}^N{\alpha }_j\left(1-\sum _{i=1}^C{\mu }_{ij,k}\right)+\sum _{k=1}^K{\beta }_k\left(1-\sum _{l=1}^{d_k}{w}_{l,k}\right) \end{gathered}$$ (A.2)

where α_j (j ∈ [1, N]) and β_k (k ∈ [1, K]) are the Lagrange multipliers.

Next, let us set the derivatives to zero with respect to v_il,k, μ_ij,k, and w_l,k:

$$\frac{\partial L}{\partial v_{il.k}}=-2\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }{w}_{l,k}\left(x_{jl,k}-v_{il,k}\right)=0$$ (A.3)

We subsequently obtain (7) by rearranging (A.3).

$$\begin{gathered} \frac{\partial L}{\partial {\mu }_{ij,k}}=\eta \sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2+\frac{1-\eta }{K1}\times \sum _{k^{\prime }=1,k^{\prime }\ne k}^K\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}{\left(x_{jl,k^{\prime }}-v_{il,k^{\prime }}\right)}^2+{\lambda }_1\left(1+\text{ln}{\mu }_{ij,k}\right)-{\alpha }_j=0 \\ \iff \text{ln}{\mu }_{ij,k}=\frac{\left({\alpha }_j-{\lambda }_1-\eta \sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2-\frac{1-\eta }{K1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}{\left(x_{jl,k^{\prime }}-v_{il,k^{\prime }}\right)}^2\right)}{{\lambda }_1} \\ {\mu }_{ij,k}=\text{exp}\left(\frac{{\alpha }_j-{\lambda }_1}{{\lambda }_1}\right)\times \text{exp}\left(\frac{\left(-\eta \sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2-\frac{1-\eta }{K1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}{\left(x_{jl,k^{\prime }}-v_{il,k^{\prime }}\right)}^2\right)}{{\lambda }_1}\right) \end{gathered}$$ (A.4)

$\sum _{r=1}^C{\mu }_{rj,k}=1$, based on (A.4), we get

$$\begin{gathered} \text{exp}\left(\frac{{\alpha }_j-{\lambda }_1}{{\lambda }_1}\right)\sum _{r=1}^C\times \text{exp}\left(-\frac{\left(\eta \sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2+\frac{1-\eta }{K1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}{\left(x_{jl,k^{\prime }}-v_{rl,k^{\prime }}\right)}^2\right)}{{\lambda }_1}\right)=1 \\ \iff \text{exp}\left(\frac{{\alpha }_j-{\lambda }_1}{{\lambda }_1}\right) \\ =1/\sum _{r=1}^C\text{exp}\left(-\frac{\eta \sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{rl,k}\right)}^2+\frac{1-\eta }{K1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}\times {\left(x_{jl,k^{\prime }}-v_{rl,k^{\prime }}\right)}^2}{{\lambda }_1}\right) \end{gathered}$$ (A.5)

By substituting (A.5) into (A.4), we can immediately attain (9).

Likewise,

$$\begin{gathered} \frac{\partial L}{\partial w_{l,k}}=\sum _{i=1}^C\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }{\left(x_{jl,k}-v_{il,k}\right)}^2+{\lambda }_2\left(1+\text{ln}{w}_{l,k}\right)-{\beta }_k=0 \\ \iff \text{ln}{w}_{l,k}=\frac{{\beta }_k-{\lambda }_2-\sum _{i=1}^C\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }{\left(x_{jl,k}-v_{il,k}\right)}^2}{{\lambda }_2} \\ \iff w_{l,k}=\text{exp}\left(\frac{{\beta }_k-{\lambda }_2}{{\lambda }_2}\right)\times \text{exp}\left(-\frac{\sum _{i=1}^C\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }{\left(x_{jl,k}-v_{il,k}\right)}^2}{{\lambda }_2}\right) \end{gathered}$$ (A.6)

Due to $\sum _{q=1}^{d_k}{w}_{q,k}=1$ and via (A.6), we get

$$\begin{gathered} \text{exp}\left(\frac{{\beta }_k-{\lambda }_2}{{\lambda }_2}\right)\sum _{q=1}^{d_k}\text{exp}\left(-\frac{\sum _{i=1}^C\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }{\left(x_{iq,k}-v_{iq,k}\right)}^2}{{\lambda }_2}\right)=1 \\ \iff \text{exp}\left(\frac{{\beta }_k-{\lambda }_2}{{\lambda }_2}\right)=1/\sum _{q=1}^{d_k}\times \text{exp}\left(-\frac{\sum _{i=1}^C\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }{\left(x_{jq,k}-v_{iq,k}\right)}^2}{{\lambda }_2}\right) \end{gathered}$$ (A.7)

Substituting (A.7) into (A.6), (8) can be achieved. □

B. PROOF OF CONVERGENCE OF VC-AW-MEC

For the convergence of iterative optimization issues, the well-known Zangwill’s convergence theorem [50], [14] is extensively adopted as a standard pathway. Let us first review this theorem blow.

Lemma 1 (Zangwill’s Convergence Theorem): Let D denote the domain of a continuous function J, and S ⊂ D be its solution set. Let Ω signify a map over D that generates an iterative sequence {z_(t+1) = Ω_(t+1)(z_(t)), t = 0, 1, …} with z₍₀₎ ∈ D. Suppose that

1. {z_(t), t = 1, 2 …} is a compact subset of D.

2. The continuous function, J: D → R, satisfies that

   1. if z ∉ S, then for any y ∈ Ω(z), J(y) < J(z);
   2. if z ∈ S, then either the algorithm terminates or for any y ∈ Ω(z), J(y) ≤ J(z).

3. Ω is continuous on D - S.

Then either the algorithm stops at a solution or the limit of any convergent subsequence is a solution.

Likewise, we use this theorem to demonstrate the convergence of VC-AW-MEC as follows.

Definition 1: For the kth view, let $M_{U_k}$ denote the set that

$$M_{U_k}=\left\{U_k\in R^{CN}|\begin{array}{l}{\mu }_{ij,k}\in [0,1],1\le i\le C,1\le j\le N\hfill \\ {\sum }_{i=1}^C{\mu }_{ij,k}=1,1\le j\le N.\hfill \end{array}\right\}$$ (A.8)

Definition 2: For the kth view, let $M_{w_k}$ denote the set that

$$M_{w_k}=\left\{w_k={\left[w_{1,k},\dots ,w_{d_k,k}\right]}^{\text{T}}|\begin{array}{l}{w}_{l,k}\in [0,1],1\le l\le d_k\hfill \\ {\sum }_{l=1}^{d_k}{w}_{l,k}=1.\hfill \end{array}\right\}$$ (A.9)

Definition 3: For the kth view, the function $G_{1,k}:M_{U_k}\times M_{w_k}\to R^{C{d}_k}$ is defined as G_1,k(U_k, w_k) = V_k, in which $v_{i,k}={\left(v_{i1,k},\cdots ,v_{i{d}_k,k}\right)}^{\text{T}}\in V_k$, 1 ≤ i ≤ C is calculated by (7).

Definition 4: For the kth view, the function $G_{2,k}:R^{C{d}_k}\times M_{w_k}\to M_{U_k}$ is defined G_2,k(V_k, w_k) = U_k, in which $U_k\in M_{U_k}$ consisting of μ_ij,k, 1 ≤ i ≤ C, 1 ≤ j ≤ N, is calculated by (9).

Definition 5: For the kth view, the function $G_{3,k}:M_{U_k}\times R^{C{d}_k}\to M_{w_k}$ is defined as G_3,k(U_k, V_k) = w_k, in which $w_k={\left[w_{1,k},\dots ,w_{d_k,k}\right]}^{\text{T}}$ is calculated by (8).

Definition 6: For the kth view, the objective function J_VC-AW-MEC, _k(U_k, V_k, w_k) is defined as

$$J_{\text{VC-AW-MEC}}{{}_{,}}_k(U_k,V_k,w_k)=\sum _{i=1}^C\sum _N^{j=1}\left({\mu }_{ij,k}\left(\eta \sum _{l=1}^{d_k}{w}_{l,k}{\left(x_{jl,k}-v_{il,k}\right)}^2+\frac{1-\eta }{K-1}\sum _{k^{\prime }=1,k^{\prime }\ne k}^K\sum _{l=1}^{d_k}{w}_{l,k^{\prime }}\times {\left(x_{jl,k^{\prime }}-v_{il,k^{\prime }}\right)}^2\right)\right)++{\lambda }_1\sum _{i=1}^C\sum _{j=1}^N{\mu }_{ij,k}\text{ln}{\mu }_{ij,k}+{\lambda }_2\sum _{l=1}^{d_k}{w}_{l,k}\text{ln}{w}_{l,k},$$ (A.10)

in which v_il,k ∈ v_i,k, V_k = [v_1,k, …, v_C,k]^T, $U_k={\left[{\mu }_{ij,k}\right]}_{C\times N},w_k={\left[w_{1,k},\dots ,w_{d_k,k}\right]}^{\text{T}}$ and λ₁ > 0, λ₂ > 0 are the two regularization parameters.

Please refer to (A.1) for the derivation of (A.10) from (6).

Definition 7: For the kth view, the map $T_k:M_{U_k}\times R^{C{d}_k}\times M_{w_k}\to M_{U_k}\times R^{C{d}_k}\times M_{w_k}$ is defined as T_k = A_3,k∘A_2,k∘A_1,k for the iteration in VC-AW-MEC, where A_1,k, A_2,k, and A_3,k are further defined as

$$\begin{gathered} A_{1,k}:M_{U_k}\times M_{w_k}\to R^{C{d}_k},A_{1,k}\left(U_k^{(t)},w_k^{(t)}\right)=G_{1,k}\left(U_k^{(t)},w_k^{(t)}\right) \\ =V_k^{(t+1)}, \\ {A}_{2,k}:R^{C{d}_k}\times M_{w_k}\to M_{U_k}\times R^{C{d}_k},A_{2,k}\left(V_k^{(t+1)},w_k^{(t)}\right) \\ =\left(G_{2,k}\left(V_k^{(t+1)},w_k^{(t)}\right),V_k^{(t+1)}\right) \\ =\left(U_k^{(t+1)},V_k^{(t+1)}\right), \end{gathered}$$

and

$$A_{3,k}:M_{U_k}\times R^{C{d}_k}\to M_{U_k}\times R^{C{d}_k}\times M_{w_k},A_{3,k}(U_k^{(t+1)},V_k^{(t+1)})=\left(U_k^{(t+1)},V_k^{(t+1)},G_{3,k}\left(U_k^{(t+1)},V_k^{(t+1)}\right)\right)==\left(U_k^{(t+1)},V_k^{(t+1)},w_k^{(t+1)}\right),\text{ i.e., }{T}_k$$

is a composition of three embedded maps: A_1,k, A_2,k, and A_3,k, and

$$\begin{gathered} T_k\left(U_k^{(t)},V_k^{(t)},w_k^{(t)}\right)=A_{3,k}\circ A_{2,k}\circ A_{1,k}\left(U_k^{(t)},V_k^{(t)},w_k^{(t)}\right) \\ =A_{3,k}\circ A_{2,k}\left(A_1\left(U_k^{(t)},w_k^{(t)}\right),w_k^{(t)}\right) \\ =A_{3,k}\circ A_{2,k}\left(V_k^{(t+1)},w_k^{(t)}\right) \\ =A_{3,k}\left(U_k^{(t+1)},V_k^{(t+1)}\right) \\ =\left(U_k^{(t+1)},V_k^{(t+1)},w_k^{(t+1)}\right). \end{gathered}$$

Theorem 2: In the kth view, suppose that the data X_k {x_1,k, …, x_N,k} contain at least C (C < N) distinct points and that $\left(U_k^{(0)},V_k^{(0)},w_k^{(0)}\right)$ is the start of the iteration of T_k with $U_k^{(0)}\in M_{U_k},w_k^{(0)}\in M_{w_k}$, and $G_{1,k}\left(U_k^{(0)},w_k^{(0)}\right)=V_k^{(0)}$; then the iteration sequence $\left\{\left(U_k^{(t)},V_k^{(t)},w_k^{(t)}\right),t=1,2,\cdots \right\}$ is contained in a compact subset of $M_{U_k}\times R^{C{d}_k}\times M_{w_k}$.

Proof: Suppose that $U_k^{(0)}\in M_{U_k}$ and $w_k^{(0)}\in M_{w_k}$ are randomly initialized, and that λ₁ > 0, λ₂ > 0 are fixed; then, $v_k^{(0)}=G_{1,k}\left(U_k^{(0)},w_k^{(0)}\right)$ can be calculated via (7) as

$$v_{il,k}^{(0)}=\frac{\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }^{(0)}{w}_{l,k}^{(0)}{x}_{jl,k}}{\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }^{(0)}{w}_{l,k}^{(0)}}$$ (A.11)

Let ${\rho }_{j,k}^{(0)}=\frac{{\tilde{\mu }}_{ij,k\eta }^{(0)}{w}_{l,k}^{(0)}}{\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }^{(0)}{w}_{l,k}^{(0)}}$; then, (A.11) is equivalent to

$$v_{il,k}^{(0)}=\sum _{j=1}^N{\rho }_{j,k}^{(0)}{x}_{jl,k}$$ (A.12-1)

with

$$\sum _{j=1}^N{\rho }_{j,k}^{(0)}=\frac{\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }^{(0)}{w}_{l,k}^{(0)}}{\sum _{j=1}^N{\tilde{\mu }}_{ij,k\eta }^{(0)}{w}_{l,k}^{(0)}}=1$$ (A.12-2)

Thus, $v_{il,k}^{(0)}\in conv\left(X_{l,k}=\left\{x_{1l,k},\dots ,x_{Nl,k}\right\}\right)$ and $v_k^{(0)}\in {\left[{\left[conv\left(X_{l,k}\right)\right]}^{d_k}\right]}^C={\left[conv\left(X_{l,k}\right)\right]}^{C{d}_k}$, where conv(X_l,k) and ${\left[conv\left(X_{l,k}\right)\right]}^{C{d}_k}$ denote the convex hull of X_l,k and the (C × d_k)-fold Cartesian product of the convex hull of X_l,k, respectively.

Iteratively, $U_k^{(1)}=G_{2,k}\left(V_k^{(0)},w_k^{(0)}\right)$ is computed via (9) and $U_k^{(1)}\in M_{U_k}$, and $w_k^{(1)}=G_{3,k}\left(U_k^{(1)},V_k^{(0)}\right)$ is computed via (8) and $w_k^{(1)}\in M_{w_k}$. Also, similar to the analyses in (A.11) and (A.12), we know that $V_k^{(1)}=G_{1,k}\left(U_k^{(1)},w_k^{(1)}\right)$ also belongs to ${\left[conv\left(X_{l,k}\right)\right]}^{C{d}_k}$. Therefore, as such, all iterations of T_k must belong to $M_{U_k}\times {\left[conv\left(X_{l,k}\right)\right]}^{C{d}_k}\times M_{w_k}$.

Because both $M_{U_k}$ and $M_{w_k}$ in the forms of (A.8) and (A.9) are closed and bounded [50], [51], they are therefore compact. ${\left[conv\left(X_{l,k}\right)\right]}^{C{d}_k}$ is also compact [50]. Thus, $M_{U_k}\times {\left[conv\left(X_{l,k}\right)\right]}^{C{d}_k}\times M_{w_k}$ is consequently a compact subset of $M_{U_k}\times R^{C{d}_k}\times M_{w_k}$. □

Proposition 1: In the kth view, if $w_k^{*}\in M_{w_k}$, $U_k^{*}\in M_{U_k}$, λ₁ > 0, and λ₂ > 0 are fixed, and the function ${\Theta }_k:R^{C{d}_k}\to R$ is defined as Θ_k(V_k) = J_VC-AW-MEC, $k\left(U_k^{*},V_k,w_k^{*}\right)$, then $V_k^{*}$ is a global minimizer of Θ_k over $R^{C{d}_k}$ if and only if $V_k^{*}=G_{1,k}\left(U_k^{*},w_k^{*}\right)$.

Proof: It is easy to prove that Θ_k(V_k) is a strictly convex function when $w_k^{*}\in M_{w_k}$, $U_k^{*}\in M_{U_k}$, λ₁ > 0, and λ₂ > 0 are fixed. This means Θ_k(V_k) at most has one minimizer over $R^{C{d}_k}$, and it is also a global minimizer. Furthermore, based on the Lagrange optimization, we know that $V_k^{*}=G_{1,k}\left(U_k^{*},w_k^{*}\right)$ is a global minimizer of Θ_k(V_k) over $R^{C{d}_k}$. □

Proposition 2: In the kth view, if $w_k^{*}\in M_{w_k}$, $V_k^{*}\in R^{C{d}_k}$, λ₁ > 0, and λ₂ > 0 are fixed, and the function ${\Upsilon }_k:M_{U_k}\to R$ is defined as ϒ_k(U_k) = J_VC-AW-MEC, $k\left(U_k,V_k^{*},w_k^{*}\right)$, then $U_k^{*}$ is a global minimizer of ϒ_k over $R^{C{d}_k}$ if and only if $U_k^{*}=G_{2,k}\left(V_k^{*},w_k^{*}\right)$.

Proof: It is easy to prove that ϒ_k(U_k) is a strictly convex function when $w_k^{*}\in M_{w_k}$, $V_k^{*}\in R^{C{d}_k}$, λ₁ > 0, and λ₂ > 0 are fixed. This means ϒ_k(U_k) at most has one minimizer over $M_{U_k}$, and it is also a global minimizer. Furthermore, based on the Lagrange optimization, we know that $U_k^{*}=G_{2,k}\left(V_k^{*},w_k^{*}\right)$ is a global minimizer of ϒ_k(U_k) over $M_{U_k}$. □

Proposition 3: In the kth view, if $V_k^{*}\in R^{C{d}_k}$, $U_k^{*}\in M_{U_k}$, λ₁ > 0, and λ₂ > 0 are fixed and the function ${\Gamma }_k:M_{w_k}\to R$ is defined as Γ_k(w_k) = J_VC-AW-MEC, $k\left(U_k^{*},V_k^{*},w_k\right)$, then $w_k^{*}$ is a global minimizer of Γ_k over $M_{w_k}$ if and only if $w_k^{*}=G_{3,k}\left(U_k^{*},V_k^{*}\right)$.

Proof: It is easy to prove that Γ_k(w_k) is a strictly convex function when $V_k^{*}\in R^{C{d}_k}$, $U_k^{*}\in M_{U_k}$,λ₁ > 0, and λ₂ > 0 are fixed. This means Γ_k(w_k) at most has one minimizer over $M_{w_k}$, and it is also a global minimizer. Furthermore, based on the Lagrange optimization, we know that $w_k^{*}=G_{3,k}\left(U_k^{*},V_k^{*}\right)$ is a global minimizer of $M_{w_k}$. □

Theorem 3: Let

$$S_k=\left\{\begin{array}{c}\left(U_k^{*},V_k^{*},w_k^{*}\right)\\ \in M_{U_k}\times R^{C{d}_k}\times M_{w_k}\end{array}|\begin{array}{l}{J}_{\text{VC}-\text{AW}-\text{MEC},k}\left(U_k^{*},V_k^{*},w_k^{*}\right)\\ <J_{\text{VC}-\text{AW}-\text{MEC},k}\left(U_k,V_k^{*},w_k^{*}\right),\\ \forall U_k\in M_{U_k}\text{ and }{U}_k\ne U_k^{*}\\ \text{and}\\ J_{\text{VC}-\text{AW}-\text{MEC},k}\left(U_k^{*},V_k^{*},w_k^{*}\right)\\ <J_{\text{VC}-\text{AW}-\text{MEC},k}\left(U_k^{*},V_k^{*},w_k\right),\\ \forall w_k\in M_{w_k}\text{ and }{w}_k\ne w_k^{*}\\ \text{and}\\ J_{\text{VC}-\text{AW}-\text{MEC},k}\left(U_k^{*},V_k^{*},w_k^{*}\right)\\ <J_{\text{VC}-\text{AW}-\text{MEC},k}\left(U_k^{*},V_k,w_k^{*}\right),\\ \forall V_k\in R^{C{d}_k}\text{ and }{V}_k\ne V_k^{*}\end{array}\right\}$$ (A.13)

denote the solution set of the optimization problem min J_VC-AW-MEC, _k (U_k, V_k, w_k). Let λ₁ > 0 and λ₂ > 0 take the specific values, suppose that X_k = {x_1,k, …, x_N,k} contains at least C (C < N) distinct points. For $\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)\in M_{U_k}\times R^{C{d}_k}\times M_{w_k}$, if $\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)=T_k\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)$, then $J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)\le J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)$ and the inequality is strict if $\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)\notin S_k$.

Proof: As $\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)=T_k\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)$, we arrive immediately at ${\stackrel{⌢}{V}}_k=G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right)$, ${\stackrel{⌢}{U}}_k=G_{2,k}\left({\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)$, and ${\stackrel{⌢}{w}}_k=G_{3,k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k\right)$, according to Definition 7, and we have $J_{\text{VC}-\text{AW}-\text{MEC},k}\left(T_k\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left(G_{2,k}\left(G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right),{\overline{w}}_k\right),G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right),G_{3,k}\left(G_{2,k}\left(G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right),{\overline{w}}_k\right),G_{1,k}\left(U_k,{\overline{w}}_k\right)\right)\right)$. It is obvious that, if $\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)\in S_k$, the conditions ${\overline{V}}_k=G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right)$, ${\overline{U}}_k=G_{2,k}\left({\overline{V}}_k,{\overline{w}}_k\right)$, and ${\overline{w}}_k=G_{3,k}\left({\overline{U}}_k,{\overline{V}}_k\right)$ must simultaneously hold; otherwise, at least one of them does not hold. Specifically,

1. For $\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)\in S_k$, i.e., ${\overline{V}}_k=G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right)$, ${\overline{U}}_k=G_{2,k}\left({\overline{V}}_k,{\overline{w}}_k\right)$, and ${\overline{w}}_k=G_{3,k}\left({\overline{U}}_k,{\overline{V}}_k\right)$ we have $J_{\text{VC}-\text{AW}-\text{MEC}}{}_{,k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC}}{}_{,k}\left(G_{2,k}\left(G_{1,k}\left(U_k,{\overline{w}}_k\right),{\overline{w}}_k\right),G_{1,k}\left(U_k,{\overline{w}}_k\right),G_{3,k}\left(G_{2,k}\left(G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right),{\overline{w}}_k\right),G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right)\right)\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left(G_{2,k}\left({\overline{V}}_k,{\overline{w}}_k\right),{\overline{V}}_k,G_{3,k}\left(G_{2,k}\left({\overline{V}}_k,{\overline{w}}_k\right),{\overline{V}}_k\right)\right)=J_{\text{VC}-\text{AW}-\text{MEC}}{}_{,k}\left({\overline{U}}_k,{\overline{V}}_k,G_{3,k}\left({\overline{U}}_k,{\overline{V}}_k\right)\right)=J_{\text{VC}-\text{AM}-\text{MEC},k}\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)$;

2. For ${\overline{V}}_k\ne G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right)$, according to Proposition 1, we attain $J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)>J_{\text{VC}-\text{AW}-\text{MEC}}{}_{,k}\left({\overline{U}}_k,G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right),{\overline{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)$. Further, based on Propositions 2 and 3, we have $J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)\ge J_{\text{VC}-\text{AW}-\text{MEC},k}\left(G_{2,k}\left({\stackrel{⌢}{V}}_k,{\overline{w}}_k\right),{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)\ge J_{\text{VC}-\text{AW}-\text{MEC}}{}_{,k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,G_{3,k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k\right)\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)$. Thus, we arrive at $J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)<J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)$;

3. For ${\stackrel{⌢}{V}}_k={\overline{v}}_k=G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right)$ but ${\overline{U}}_k\ne G_{2,k}\left({\overline{V}}_k,{\overline{w}}_k\right)=G_{2,k}\left({\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)={\stackrel{⌢}{U}}_k{}_k$, according to Proposition 1, we attain $J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right),{\overline{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)$. Further, based on Propositions 2 and 3, we know that $J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)>J_{\text{VC}-\text{AW}-\text{MEC},k}\left(G_{2,k}\left({\stackrel{⌢}{V}}_k,{\overline{w}}_k\right),{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)\ge J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,G_{3,k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k\right)\right)=J_{\text{VC}-\text{AW}-\text{MEC}}{}_{,k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)$ Thus, we arrive at $J_{\text{VC}-\text{AW}-\text{MEC}}{}_{,k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)<J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)$;

4. For ${\stackrel{⌢}{V}}_k={\overline{V}}_k=G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right)$, ${\overline{U}}_k={\widehat{U}}_k=G_{2,k}\left({\overline{V}}_k,{\overline{w}}_k\right)=G_{2,k}\left({\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)$, but ${\stackrel{⌢}{w}}_k=G_{3,k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k\right)=G_{3,k}\left({\overline{U}}_k,{\overline{V}}_k\right)\ne {\overline{w}}_k$ we arrive at $J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,G_{1,k}\left({\overline{U}}_k,{\overline{w}}_k\right),{\overline{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left(G_{2,k}\left({\stackrel{⌢}{V}}_k,{\overline{w}}_k\right),{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)=J_{\text{VC}-\text{AM}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)$. Further, according to Proposition 3, we know that $J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\overline{w}}_k\right)>J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,G_{3,k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k\right)\right)=J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\widehat{w}}_k\right)$. Thus, we arrive at $J_{\text{VC}-\text{AM}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)<J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)$;

Combining the cases (1)–(4), we know $J_{\text{VC}-\text{AM}-\text{MEC},k}\left({\stackrel{⌢}{U}}_k,{\stackrel{⌢}{V}}_k,{\stackrel{⌢}{w}}_k\right)\le J_{\text{VC}-\text{AW}-\text{MEC},k}\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)$ and the inequality is strict if $\left({\overline{U}}_k,{\overline{V}}_k,{\overline{w}}_k\right)\notin S_k$. □

Theorem 4: Let λ₁ > 0 and λ₂ > 0 take the specific values; suppose that X_k = x_1,k, …, x_N,k} contains at least C (C < N) distinct points; then, the map $T_k:M_{U_k}\times R^{C{d}_k}\times M_{w_k}\to M_{U_k}\times R^{C{d}_k}\times M_{w_k}$ is continuous on $M_{U_k}\times R^{C{d}_k}\times M_{w_k}$.

Proof: As defined in Definition 7, the map T_k = A_3,k ○ A_2,k ○ A_1,k is a composition of three embedded maps, i.e., A_1,k, A_2,k, and A_3,k. Thus, if all of A_1,k, A_2,k, and A_3,k are continuous, T_k = A_3,k ○ A_2,k ○ A_1,k is consequently continuous. To prove A_1,k(U_k, w_k) = G_1,k(U_k, w_k) is continuous, it equals to showing that G_1,k(U_k, w_k) is continuous. As G_1,k(U_k, w_k) is computed by (7) and it is continuous, A_1,k is reasonably continuous. To prove A_2,k(V_k, w_k) = (G_2,k(V_k, w_k), V_k) is continuous, it equals to demonstrating that G_2,k(V_k, w_k) is continuous. As G_2,k(V_k, w_k) is calculated via (9), and (9) is definitely continuous when λ₁ and η are fixed, G_2,k(V_k, w_k) is continuous. Thus, A_2,k is continuous. Likewise, to prove A_3,k(U_k, V_k) = (U_k, V_k, G_3,k(U_k, V_k)) is continuous, it equals to showing that G_3,k(U_k, V_k) is continuous. As G_3,k(U_k, V_k) is computed by (8) and it is continuous, A_3,k is consequently continuous.

Combining them, this theorem can be proven. □

Theorem 5: In any view k (k = 1, …, K), let X_k = {x_1,k, …, x_N,k}contain at least C (C < N) distinct points and J_VC-AW-MEC, _k(U_k, V_k, w_k) be in the form of (A.10); suppose that $\left(U_k^{(0)},V_k^{(0)},w_k^{(0)}\right)$ is the start of the iterations of T_k with $U_k^{(0)}\in M_{U_k}$, $w_k^{(0)}\in M_{w_k}$, and $V_k^{(0)}=G_{1,k}\left(U_k^{(0)},w_k^{(0)}\right)$; then, the iteration sequence, $\left\{\left(U_k^{(t+1)},V_k^{(t+1)},w_k^{(t+1)}\right)=T_k\left(U_k^{(t)},V_k^{(t)},w_k^{(t)}\right),t=0,1,\dots \right\}$, either terminates at a point $\left(U_k^{*},V_k^{*},w_k^{*}\right)$ in the solution set S_k of J_{VC-AW-MEC, k}, or there is a subsequent converging to a point in S_k.

Based on the Zangwill’s convergence theorem, Theorem 5 immediately holds under the premises of Theorems 3, 4, and 5.

Theorem 6 (Convergence of VC-AW-MEC): According to Theorem 5, the entire iteration procedure of VC-AW-MEC is convergent.

Proof: Based on Theorem 5, we know that for any view k (k = 1, …, K), the optimization of min J_VC-AW-MEC, k (U_k, V_k, w_k) is resoluble and its iteration procedure is convergent. Furthermore, because min $J_{\text{VC}-\text{AW}-\text{MEC}}(U,V,w)=\text{min}\left(\sum _{k=1}^K{J}_{\text{VC}-\text{AM}-\text{MEC},k}\left(U_k,V_k,w_k\right)\right)$, the convergence of VC-AW-MEC certainly holds. □