Predicting Molecular Energy using Force-Field Optimized Geometries and Atomic Vector Representations Learned from Improved Deep Tensor Neural Network

Abstract

The use of neural networks to predict molecular properties calculated from high level quantum mechanical calculations has made significant advances in recent years, but most models need input geometries from DFT optimizations which limit their applicability in practice. In this work, we explored how machine learning can be used to predict molecular atomization energies and conformation stability using optimized geometries from Merck Molecular Force Field (MMFF). Based on the recently introduced deep tensor neural network (DTNN) approach, we first improved its training efficiency and performed an extensive search of its hyperparameters, and developed a DTNN_7ib model which has a test accuracy of 0.34 kcal/mol mean absolute error (MAE) on QM9 dataset. Then using atomic vector representations in the DTNN_7ib model, we employed transfer learning (TL) strategy to train readout layers on the QM9_M dataset, in which QM properties are the same as in QM9 [calculated at the B3LYP/6–31G(2df,p) level] while molecular geometries are corresponding local minima optimized with MMFF94 force field. The developed TL_QM9_M model can achieve an MAE of 0.79 kcal/mol using MMFF optimized geometries. Furthermore, we demonstrated that the same transfer learning strategy with the same atomic vector representation can be used to develop a machine learning model that can achieve an MAE of 0.51 kcal/mol in molecular energy prediction using MMFF geometries for an eMol9_C_M conformation dataset, which consists of 9959 molecules and 88,234 conformations with energies calculated at the B3LYP/6–31G* level. Our results indicate that DFT-level accuracy of molecular energy prediction can be achieved using force-field optimized geometries and atomic vector representations learned from deep tensor neural network, and integrated molecular modeling and machine learning would be a promising approach to develop more powerful computational tools for molecular conformation analysis.

Graphical Abstract

I. INTRODUCTION

Molecular conformation analysis is essential in elucidating molecular structure-property relationship and is often a prerequisite for structure based molecular design^1–3. Reliable identification of low-energy conformers for simple small molecules can be achieved with high-level quantum mechanical calculations⁴, but would be computationally demanding for more complicated drug-like molecules³. Currently in structure based rational drug design, computational estimation of ligand conformation stability is mostly dependent on molecular mechanical force fields^{3, 5–7}, which is computationally efficient but is limited by the accuracy of force fields.

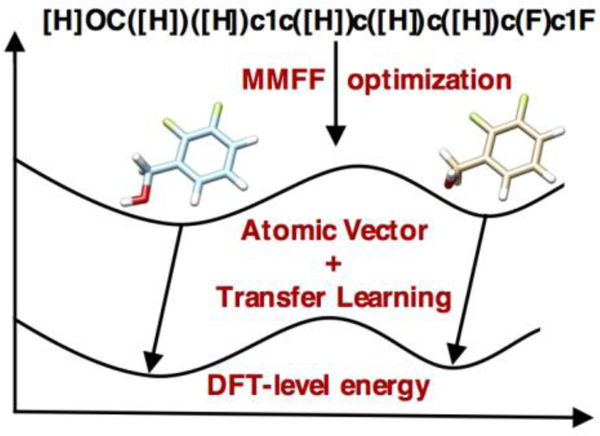
In recent years, machine-learning based methods have made remarkable progresses in molecular energy predictions^8–52. One significant advance is deep tensor neural network (DTNN)¹⁰, which employs atomic number and interatomic distance matrix as the input and utilizes a flexible graph neural network to predict molecular properties based on atomic vector representations. In DTNN, initial atomic vector $c_i^{\left(0\right)}$ for an atom i is initialized based on its atomic number and then iteratively updated to final atomic vector $c_i^{\left(T\right)}$ by using T interaction blocks (ib). Each ib is a tensor layer to model intermolecular interactions with other atoms in the molecule, and T = 2 or 3 has been utilized in DTNN. $c_i^{\left(T\right)}$ is then fed into two fully connected readout layers to predict an atomic energy contribution $E_i$, and the sum of all atom-wise energies in a molecule is the total molecular energy E. With this relatively simple and flexible neural network, DTNN achieved a test accuracy of 0.84 kcal/mol MAE for the QM9 dataset^53–55. Subsequently, several deeper neural network models with more sophisticated network architectures have been developed and the state of the art performance in predicting molecular energies is progressing rapidly. For example, SchNet^56–57, which utilizes continuous-filter convolutions with filter-generating subnetworks to model the interaction terms and more atom-wise layers in interaction block, has achieved a much smaller MAE on QM9 dataset. However, such impressive test accuracy has so far only achieved with DFT optimized geometries, which limits the efficiency of these neural network based models in practical applications, such as for identifying low-energy conformers in high-throughput screening. Thus, we are motivated to investigate whether and how machine learning can be used to accurately predict DFT calculated molecular atomization energies and conformation stability using optimized geometries with Merck Molecular Force Field (MMFF)⁵. In 2017, Raghunathan et al¹⁶. introduced Δ-machine learning method which linearly combines low-level quantum chemical properties and machine learning corrections to get highly accurate predictions. Different from their work, no baseline atomization energy of MMFF is needed in our current work, and transfer learning (TL) strategy^58–59 together with atom representation learned from deep-learning model are utilized to directly evaluate DFT-level atomization energies based on MMFF optimized geometries.

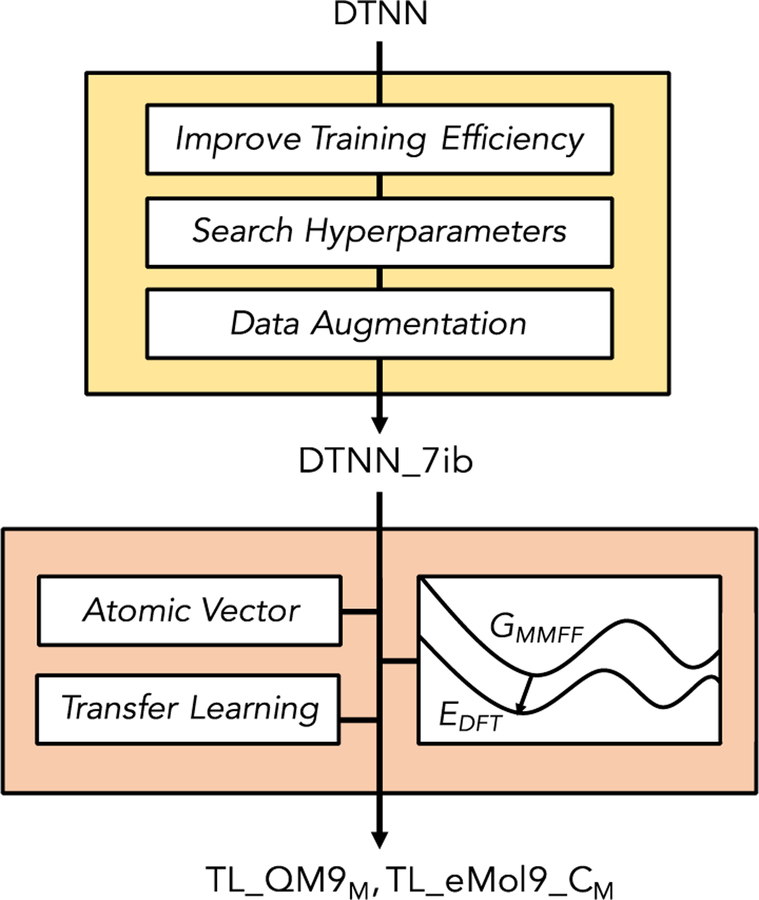
Our overall workflow is illustrated in Figure 1. First, we demonstrated importance of training efficiency improvement, hyperparameter search and data augmentation in the optimization of machine learning models. Based on the same DTNN architecture, we developed a DTNN_7ib model which is a DTNN model with 7 interaction blocks and has a much-improved test accuracy of 0.34 kcal/mol MAE on the QM9 dataset. Then, we built two new data sets QM9_M and eMol9_C_M, in which geometries are optimized with the MMFF94 force field and molecular energies are calculated with a DFT method at the corresponding DFT-minimized geometry in same local minima, and explored transfer learning strategy using atomic vector representations from the DTNN_7ib model. The results from TL_QM9_M and TL_eMol9_C_M, which are two models developed with QM9_M and eMol9_C_M dataset respectively, indicate that our presented machine learning strategy can achieve DFT-level accuracy of molecular energy prediction using force-field optimized geometries. Finally, we generated another new data set Plati_C_M beyond nine heavy atoms to test the generality and applicability of the developed TL_eMol9_C_M model in molecular conformation analysis. All of our presented machine learning models, corresponding source codes as well as data sets are freely available on the web at: https://www.nyu.edu/projects/yzhang/IMA.

Figure 1.

Overall workflow of exploring how machine learning can be used to predict molecular atomization energies and conformation stability using force-field optimized geometries.

II. DATASET

A critical component in developing machine learning models is dataset. In this work, besides employing the QM9 dataset, we have generated three new data sets: QM9_M, eMol9_C_M, and Plati_C_M, as listed in Table 1 and described in detail below.

Table 1.

Datasets^a used for machine learning model development and evaluation.

Dataset	Geometry	Energy	#Moleculeb	#Conformationsb	#Heavy Atoms
QM9	B3LYP/6–31G(2df,p)	B3LYP/6–31G(2df,p)	99,000/1,000/33,885	99,000/1,000/33,885	[1, 9]
QM9M	MMFF94	B3LYP/6–31G(2df,p)	99,000/1,000/33885	99,000/1,000/33,885	[1, 9]
eMol9_CM	MMFF94	B3LYP/6–31G*	8111/500/1,348	~66,000/~6,000/~16,000c	[1, 9]
Plati_CM	MMFF94	B3LYP/6–31G*	0/0/74	0/0/4,076	[10, 12]

^aQM9 dataset is generated by Ramakrishnan et al⁵³. Other three datasets are prepared by ourselves.

^bNumber of molecules and conformations in the training/validation/test sets are shown respectively.

^ceMol9_C_M has been random split into train/validation/test sets using five different random seeds based on molecule types. Thus, the numbers of conformations for train/validation/test sets in different splits are different.

QM9, which includes ~134k structures with 9 or less heavy atoms (C, O, N, F) from GDB-9 dataset, has become the most widely-used dataset for developing machine-learning models to predict quantum-chemical molecular energies. In the QM9 dataset, all molecular geometries are optimized at B3LYP/6–31G(2df,p) level and corresponding molecular properties are calculated at the same level⁵³. We use this dataset for developing and benchmarking the DTNN_7ib model from DTNN model.

QM9_M dataset is built based on QM9 dataset, and the sole difference is in the molecular geometries. The molecular geometries in QM9_M dataset were obtained from the optimization of the molecular geometries in QM9 dataset with MMFF94 force field using RDKit⁶⁰. Molecular properties in QM9_M dataset are kept the same as in QM9 dataset. The QM9_M dataset is developed to explore whether DTNN_7ib model can be directly applied for energy prediction with force-field optimized geometries.

eMol9_C_M dataset is a newly generated conformation dataset, and it is designed to develop models for energy prediction of low-energy conformers with force-field optimized geometries. This dataset is built based on eMolecules⁶¹ dataset, which contains SMILES (Simplified Molecular-Input Line-Entry System) of purchasable compounds, and QM9 dataset. Firstly, the molecules are selected from the overlap set of the eMolecules and QM9. For each selected compound, we employed RDKit to generate up to 300 conformations from SMILES using ETKDG⁶² method. Similar conformations have been removed after Butina⁶³ clustering with 0.2 Å RMSD cutoff, and redundant mirror-image conformations have been cleaned after the RMSD calculation between each pair of conformations by ArbAlign⁶⁴ with consideration of symmetry. Secondly, each conformation was minimized with MMFF94, and B3LYP/6–31G* minimization⁶⁵ was conducted on MMFF optimized geometry to get corresponding DFT-level energy. Here, 6–31G* basis set has been applied since it speeds up the computation in comparison with the 6–31G(2df, p) basis set which was used for developing QM9 dataset. Since DFT energies in the eMol9_C_M dataset are calculated by different basis set as in QM9 dataset, it would be a more stringent applicability test for transfer learning with atomic embedding obtained in the DTNN_7ib model. The eMol9_C_M dataset includes 88,234 conformations from 9,959 molecules, and its distribution of RMSD between each pair of MMFF optimized geometry and DFT optimized geometry is shown in Figure S1.

Plati_C_M dataset is created to evaluate the extrapolation performance of TL_eMol9_C_M model and it includes 4076 conformations for 74 molecules with 10 to 12 number of heavy atoms from Platinum dataset⁶⁶, which is a dataset of protein-bound ligand conformations whose high-quality X-ray structures have been determined and are available from the PDB database⁶⁷. Conformation generation procedure for Plati_C_M dataset is the same as the procedure used for eMol9_C_M.

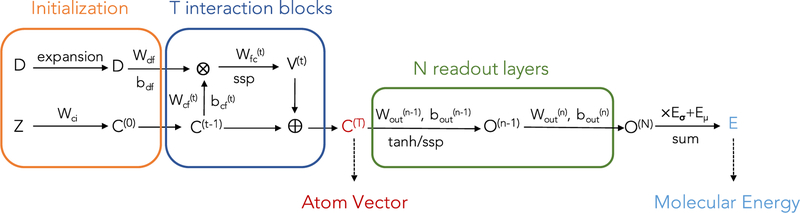
A. Neural Network Model Architecture

As illustrated in Figure 2, DTNN_7ib has the same network architecture as DTNN. The difference between two models is hyperparameter setting, which has been shown in Table 2. Inputs of DTNN_7ib for a molecule with n atoms include an atomic number vector $Z= \left[ Z_1\dots Z_n\right]$ and an interatomic distance matrix Dcomputed from their 3D coordinates. Each interatomic distance is described by a vector from the following Gaussian function:

$${\widehat{d}}_{ij}={[\exp (-\frac{{(D_{ij}-k\text{Δ}\mu )}^2}{2{\sigma }^2})]}_{0\le k\le {\mu }_{max}/\text{Δ}\mu }$$

where ${\mu }_{max}$, $\text{Δ}\mu$ and $\sigma$ are the hyperparameters of a DTNN model. Here, we set $\sigma$ has same value as $\text{Δ}\mu$, which can also be different.

Figure 2.

Illustration of the model architecture.

Table 2.

Hyperparameters searched for interaction blocks during the model optimization.

Hyperparameters	Test Valuesa
${\mu }_{max}$	3, 4, 5, 6, 8, 10, 20
$\text{Δ}\mu$	0.1, 0.2
number of interaction blocks	2, 3, 4, 5, 6, 7, 8
share/distinct weights	shared, distinct
activation function	tanh, shifted softplus

^aHyperparameters used in DTNN_7ib are in bold, and hyperparameters used in the original DTNN model are underlined.

For initial atomic vector $c_i^{\left(0\right)}$ of atom i, it is initialized randomly based on its atomic number, and optimized during training. At t (1 ≤ t ≤ T) interaction block, an updated atomic vector $c_i^{\left(t\right)}$ is obtained by aggregating its atomic environment term $V_i^{\left(t\right)}= {\sum }_{j\ne i}{v}_{ij}^{\left(t\right)}$ with $c_i^{\left(t-1\right)}$:

$$c_i^{\left(t\right)}=c_i^{\left(t-1\right)}+ \sum _{j\ne i}{v}_{ij}^{\left(t\right)}$$

The interaction vector $v_{ij}^{\left(t\right)}$ between atom i and atom j is computed as flowing:

$$v_{ij}^{\left(t\right)}=f_{act}\left[W_{fc}^{\left(t\right)}\left(\left(W_{cf}^{\left(t\right)}{c}_j^{\left(t-1\right)}+b_{cf}^{\left(t\right)}\right)\circ \left(W_{df}{\widehat{d}}_{ij}+b_{df}\right)\right)\right]$$

where $c_j^{\left(t-1\right)}$ is the current atom vector for neighboring atom $j \left(j\ne i\right)$,${\widehat{d}}_{ij}$ is the expanded distance vector between atom i and atom j, ∘ is the element-wise multiplication of two matrices, and $f_{act}$ is the activation function. After generating the final atomic vector $c_i^{\left(T\right)}$, 2 fully connected layers are added as readout layers to predict the atomic energy for atom i, and the sum of atomic energies of all atoms in the molecule is the molecular energy.

Using atomic vector representations in the DTNN_7ib model, we employed transfer learning strategy and retrained readout layers for QM9_M and eMol9_C_M datasets to develop two new machine learning models: TL_QM9_M and TL_eMol9_C_M, respectively, which use MMFF optimized geometries as inputs. For both TL models, the number of readout layers has been increased to 4 and activation function in readout layers has been changed into shifted softplus (ssp).

B. Neural Network Model Implementation, Training and Evaluation

All neural network models in this work were implemented with TensorFlow (version 1.4.1)⁶⁸. To improve data-input efficiency, all input data were saved in the tfrecord format and data import pipelines were built using tf.data API. Meanwhile, cyclic cosine annealing training schedule⁶⁹ together with Adam optimizer was utilized to improve training efficiency, in which the learning rate at i iteration is as following:

$$\text{α}\left(i\right)=\frac{{\text{α}}_0}{2}\left(\cos \left(\frac{\text{πmod}(i-1,\lceil \frac{I}{M}\rceil }{\lceil \frac{I}{M}\rceil }\right)+1\right)$$

where ${\text{α}}_0$ is the initial learning rate, I is the number of total iterations, M is the number of total cycles. Here, ${\text{α}}_0$= 0.001 and M = 8.

To train the DTNN_7ib model, QM9 dataset have been split randomly into training (99k), validation(1k) and test set (33,885), and 400k iterations with batch size equals to 100 have been employed. In order to improve atomic vector representations, we have augmented the training data set with 1.5 k distant diatomic systems, in which two atoms have distance between 20 Å and 30 Å and their molecular energy is assumed to be the sum of their atomic reference energies. Thus, the total training set includes 100.5k molecules. MAE of validation set has been checked every 1k iterations and the model with the lowest MAE has been picked as our final model. The average performance of five models trained upon data split by different random seed have also been computed.

The training/validation/test split for developing transfer learning models are also shown in Table 1. To avoid any training-testing overlap bias, the split for developing TL_QM9_M is the same as in optimizing DTNN_7ib, and eMol9_C_M dataset has been divided by molecule types. Both models were trained using the same training schedule as DTNN_7ib. To evaluate model performance, besides normal absolute error (Error_A), which is the error between predicted energy and target energy for each conformation, we also computed relative error (Error_R) to consider model’s ability on conformation stability calculation. The relative error can be computes as

$${\text{Error}}_{\text{R}}=\frac{{\sum }_i^n\text{error}\_\text{metric}\left(E_i^{\left(c\right)}-E_i^{\text{min}}\right)}{n}$$

where error_metric can be MAE or RMSE, $E_i^{\left(c\right)}$ is the energy of conformation c for molecule i and $E_i^{\text{min}}$ is the lowest energy of the molecule i, and n is the number of total molecules. This relative error also enables us to compare different methods without the limitation of different reference energy. Success rate for finding the right lowest conformation for all molecules in the test set has also been calculated.

IV. RESULT and DISCUSSION

A. DTNN_7ib

One significant advance in developing neural network models to predict DFT molecular energies is DTNN, which achieved a test accuracy of 0.84 kcal/mol MAE for the QM9 dataset. Subsequently, several more recent works, including SchNet, have achieved much-improved test accuracy with more sophisticated network architectures. Thus, one interesting question is whether DTNN itself can be significantly improved by hyperparameter searching, which is an important element of machine learning model development. However, one key challenge is its training efficiency since it took about a week to optimize the published DTNN model (162h for ib = 3 on an NVIDIA Tesla K40 GPU), while hyperparameter searching needs to train many models. Here we accelerated training data input efficiency by using tfrecord and tf.data API, and our reimplemented DTNN code can achieve a speed-up of more than ten times in comparison with using the original code downloaded from https://github.com/atomistic-machine-learning/dtnn. Meanwhile, we employed a cyclic cosine annealing training schedule (cyclic training schedule) instead of commonly-used learning rate exponential decay training schedule. As shown in Figure S2, the model training efficiency and performance can be significantly improved by using cyclic training schedule.

With more efficient model training, we first examined the atomic vector size (number of basis functions) on model performance. As shown in Figure S3, in comparison with an atomic vector size of 30 used in the DTNN model, a better performance can be achieved by increasing the size to 256, which has more flexibility to encode atomic environment. With the atomic vector size of 256, we then explored hyperparameter space of interaction block by grid search, as shown in Table 2 and Figure S4. Hyperparameters we searched include: shared/distinct weights for different interaction blocks (ibs), ${\mu }_{max}$, $\text{Δ}\mu$, number of interaction blocks and activation functions. As shown in Figure S4 (A), using distinct weights for different interaction blocks would reduce the validation error. With the increasing number of interaction blocks, different ${\mu }_{max}$ and $\text{Δ}\mu$ have been tested. DTNN used 20 Å for ${\mu }_{max}$, which would limit model efficiency and scalability for large molecules. Smaller ${\mu }_{max}$ would be preferred for the sake of potential computational efficiency but would be expected to sacrifice some accuracy. Thus, the result in Figure S4 (B) is quite surprising: a model with 7 for ib and 3 Å for ${\mu }_{max}$ has the lowest validation error among all combinations tested. Meanwhile, models trained with $\text{Δ}\mu$ = 0.1 Å consistently perform better than corresponding ones with $\text{Δ}\mu$ as 0.2 Å (Figure S4(C)). Activation function has been changed into shifted softplus (ssp $\left(x\right)=\text{ln}\left(0.5e^x+0.5\right)$) to alleviate the vanishing-gradient problem, and it performs better than using tanh for deeper models, as shown in Figure S4 (D). Although with different architectures, the optimized hyperparameter set for DTNN_7ib becomes similar to the one in SchNet, including larger number of basis functions in atomic representations (64 in SchNet vs. 256 in DTNN_7ib), deeper interaction blocks (6 in SchNet vs. 7 in DTNN_7ib), distinct weights for different interaction blocks, and shifted softplus activation function.

Training data set has been augmented with 15k distant diatomic systems to further improve atomic vector representations. Comparing the atomization energy distribution for heavy atoms of two models trained with and without distant diatomic systems (Figure S5), we found that the energy ranges for N, O, F become much narrower after training data augmentation. Also, the peak position of C has been moved into lower energy region and can be easily distinguished from N and O. This indicates that model trained with distant diatomic systems can perform better in distinguishing different atom types.

By enhancing the training efficiency, searching hyperparameters and incorporating distant diatomic systems into our training set, as presented above, we have developed our improved model DTNN_7ib. Mean absolute errors (MAE) of QM9 dataset for DTNN_7ib trained with different training set sizes are summarized in Table 3 and compared with the performance of DTNN and SchNet. The learning curves have also been shown in Figure S6. As show in Table 3 and Figure S6(B), DTNN_7ib model can achieve consistently better performance than DTNN and equally good performance as SchNet. DTNN_7ib requires shorter training epochs to achieve 0.34 kcal/mol MAE (around 304 epochs) than original SchNet⁵⁶ (750 – 2400 epochs) and the training process can be finished in 13 hours on an NVIDIA Tesla P40 GPU. It should be noted that the training of SchNet has been sped up a lot (12h, NVIDIA Tesla P100 GPU) in SchNetPack⁵⁷ by using a decay factor in learning rate reducing process if the validation loss doesn’t change in a given number of epochs. Thus, the training efficiency of our DTNN_7ib can be further improved by applying a better training schedule in the future.

Table 3.

QM9 performance (MAE in kcal/mol) for various models with different training set sizes.

# Training Data	DTNN_7iba	TL_QM9Mb	DTNN	SchNet
25k	0.69 ± 0.02	1.49 ± 0.03	1.04 ± 0.02	-
50k	0.46 ± .02	1.01 ± 0.03	0.94 ± 0.02	0.59
100k	0.34 ± 0.01	0.79 ± 0.03	0.84 ± 0.01	0.34c

^aMAE is the average of five models trained with data split by different random seed.

^bTL_QM9_M performance is on QM9_M dataset. The input coordinates are from MMFF optimized geometries.

^cSchNet performance is the one trained with 100k molecules⁷⁰. In recently published paper^56–57, SchNet performance on QM9 with 110k training set is 0.31 kcal/mol and 0.26 kcal/mol, respectively.

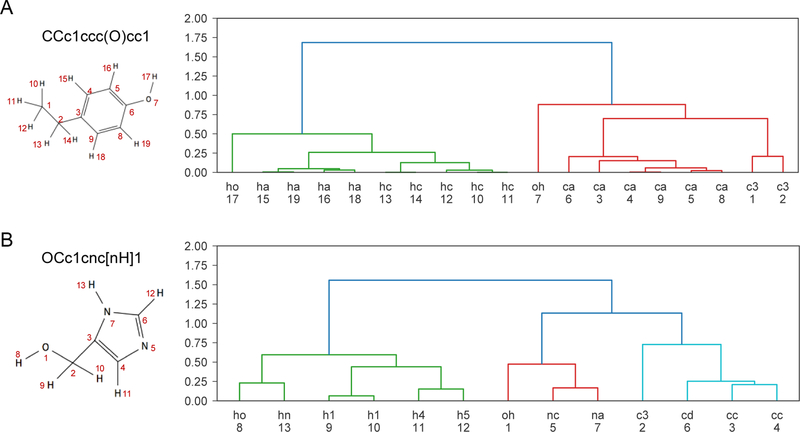
To examine whether final atomic vector representation $c_i^{\left(T\right)}$ learned by DTNN_7ib is chemically meaningful, we used pairwise cosine distance of atomic vector representations as the atomic similarity measure and divided atoms into different categories with hierarchical clustering for two molecules from QM9 dataset: 4-ethylphenol and 4-(hydroxymethyl)imidazole, which mimic amino acid side chains of tyrosine and histidine respectively. Meanwhile, general AMBER force field (gaff)⁷¹ atom types have been assigned for each atom which accounts for its atomic number, hybridization and bonding environment. From Figure 3, we can see that using embedding from DTNN_7ib, atoms in both molecules can be hierarchically clustered into different categories consistent with chemical intuition: heavy atoms and hydrogens immediately divided into two different clusters; different types of heavy atoms have been discriminated by DTNN_7ib and the results are consistent with gaff atom type. It should be noted that this is not a trivial task: we have also trained a DTNN model by using original hyperparameters without distant diatomic molecules and a DTNN_7ib model without distant diatomic molecules. The results in Figure S7 and Figure S8 indicate that clustering from the resulted embedding of these two models is much less chemically meaningful, which confuses among atoms with different atom types and same atom type in different environments. These results demonstrated that improved DTNN_7ib model can yield more chemically meaningful atomic vector representation $c_i^{\left(T\right)}$ which reflects both atom type and bonding environment.

Figure 3.

Atomic vector interpretation. (A) 4-ethylphenol and (B) 4-(hydroxymethyl)imidazole. Left are molecular graphs with SMILES. Right are hierarchical clustering results. The first row of x-axis is gaff atom type and the second row of x-axis is atom indexes numbers which are same as in molecular graph.

B. Transfer Learning Models: TL_QM9_M and TL_eMol9_C_M

Using atomic vector representations in the DTNN_7ib model, we have employed transfer learning strategy and retrained readout layers for a new machine learning model TL_QM9_M with the QM9_M dataset, which has same molecular energies as in the QM9 dataset but with input geometries from the corresponding MMFF minima. The test results are shown in Table 3, in which we also included performance on different training set sizes. It is not surprising that DTNN_7ib leads to a significantly large MAE of 4.55 kcal/mol on QM9_M, which demonstrates the necessity to retrain a model using MMFF optimized geometries. However, for our transfer learning TL_QM9_M, its MAE on QM9_M dataset is 0.79 kcal/mol (100k training references), which is better than 1 kcal/mol (1 kcal/mol is typically considered as chemical accuracy¹¹) and even better than the original model DTNN (0.84 kcal/mol with DFT geometry as input). These results indicate that transfer learning strategy with atomic vector representations in the DTNN_7ib model is a promising direction to develop machine learning models to accurately predict DFT calculated molecular atomization energies using optimized geometries with Merck Molecular Force Field (MMFF).

To identify low-energy conformers for small molecule efficiently is a prerequisite in structure based molecular design, and is typically carried out after the conformation generation process. Accurately molecular energy prediction for diverse conformations of the same molecule is often more difficult since the difference between conformations could be very small. To examine whether machine learning can be used to build an accurate model for conformation analysis, we created the eMol9_C_M dataset and developed TL_eMol9_C_M model using same transfer learning strategy. It should be noted that target molecular energy in eMol9_C_M has been calculated by a different basis set from QM9, which introduces additional difficulty.

Table 5 shows performances of our MMFF-based models on eMol9_C_M dataset. In terms of absolute error, TL_eMol9_C_M can achieve 0.51 kcal/mol MAE, which is close to the performance of our DFT-based model DTNN_7ib on QM9 dataset. On the other hand, MAE and RMSE of TL_QM9_M are much worse than TL_eMol9_C_M model because of the different basis set in energy calculation, which indicates the necessity to retrain the model to adapt to the change of energy calculation method. Meanwhile, in terms of relative error, we can compare the performance of MMFF94, TL_QM9_M and TL_eMol9_C_M together, and our results indicate that both TL_QM9_M and TL_eMol9_C_M can achieve much better performance than MMFF method on MAE, RMSE and success rate, which indicates that it is promising to apply MMFF-based machine learning models to search low-energy conformers and improve conformation stability prediction.

Table 5.

Performance on Plati_C_M dataset^a

		MMFF94c	TL_eMol9_CM
ErrorAb	MAE	None	2.73 ± 0.35
	RMSE	None	4.74 ± 0.39
ErrorRb	MAE	2.65	1.31 ± 0.09
	RMSE	4.40	1.59 ± 0.09
Success Rate		0.49	0.57 ± 0.05

^aBest performances are in bold.

^bUnit is kcal/mol.

^cThere is no standard deviation in MMFF94 method since we used all conformations in Plati_C_M as test set, but for TL_eMol9_C_M we showed performances on five models.

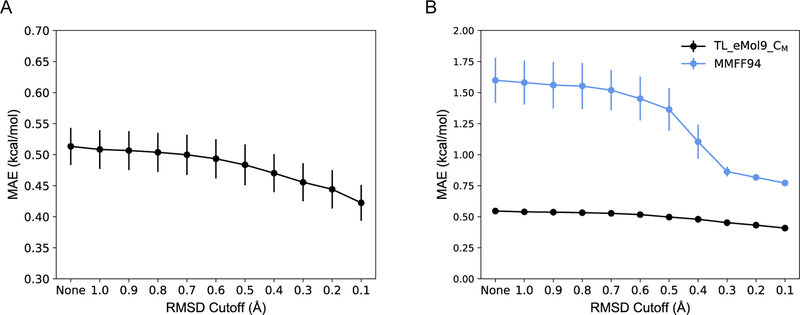
Additionally, to consider the impact of difference between MMFF optimized geometries and DFT optimized geometries on prediction accuracy, the performances on test sets with different RMSD cutoffs have been calculated. As shown in Figure 4 and Figure S9, the performance of TL_eMol9_C_M is quite robust given different RMSD cutoffs while MMFF94 method’s performances deteriorate significantly when RMSD cutoff increases.

Figure 4.

(A) Absolute MAE and (B) relative MAE on test sets with different RMSD cutoffs. “None” means the performance is for total test set, “value” means the performance is for subset, which only includes conformations with RMSD less than “value”. Average and standard deviation of performances from five models trained with random split data have been shown. Performances of TL_eMol9_C_M, MMFF94 are colored as black and blue, respectively.

Besides good performance, to develop MMFF-based models based on transfer learning needs much less training time (TL_QM9_M: 5h, TL_eMol9_C_M: 6h).

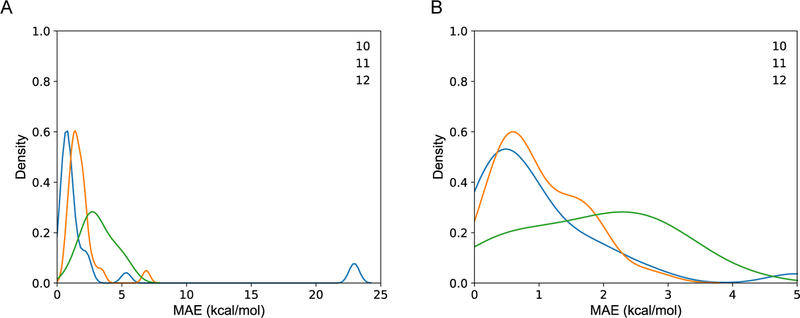
In order to further investigate the applicability and limitation of the TL_eMol9_C_M model, we have built a Plati_C_M dataset, which includes molecules with more heavy atoms (10–12) than molecules in our training set (≤9). Our results show that the overall performance of TL_eMol9_C_M become worse (relative MAE from 0.55 to 1.31 kcal/mol), but it still performs better than MMFF94 (Table 5). To analyze origin of significant performance decreasing of TL_eMol9_C_M, we checked the average error of each molecule and grouped the results based on the number of heavy atoms. Error calculations with consideration of RMSD cutoff have also been conducted (Figure S11). Figure 5 shows the error distribution, and the peaks of two MAE distributions moves from small error region into large error region when the number of heavy atoms increases. It should be noted that there are two molecules with 10 heavy atoms having very large error (> 20 kcal/mol, Figure S10). After computing the cosine similarities between atomic vectors of these two molecules and atomic vectors from our training set, the nitrogen atoms in N(sp3)-N(sp3) group in these two molecules have been identified with lowest similarities. With the help of HasSubstructMatch command in RDKit, we checked the SMILES of whole QM9 dataset, and no similar N-N group has been found. Therefore, our results indicate that the main limitation of the TL_eMol9_C_M model comes from its training data, which needs to be much larger and more diverse for the development of more robust machine learning models in predicting molecular energies and conformation stabilities.

Figure 5.

(A) Absolute MAE and (B) relative MAE distributions for molecules with different number of heavy atoms. Distribution for molecules with 10, 11, 12 heavy atoms is colored as blue, orange, and green, respectively.

V. CONCLUSION

In this work, we demonstrated importance of training efficiency improvement, hyperparameter search and data augmentation in the optimization of machine learning models, and improved DTNN performance from 0.84 kcal/mol to 0.34 kcal/mol on MAE with no change of model architecture. Our newly developed model DTNN_7ib has deeper learning blocks and can generate chemical meaningfully atomic vectors which reflects both atom type and atomic environment. To address the application limitation caused by DFT optimized geometries, three datasets with both DFT calculated properties and MMFF optimized geometries have been created and two MMFF-based models have been developed by implementing transfer learning strategy on atomic vectors learned from DTNN_7ib. TL_QM9_M can achieve better than chemical accuracy performance on QM9_M dataset, and TL_eMol9_C_M can achieve 0.51 kcal/mol MAE on eMol9_C _M dataset. In addition, our work indicates that although the overall presented strategy looks promising, one key challenge is the data set, which needs significantly larger and diverse training set for the development of more robust machine learning models for molecular conformation analysis.

Supplementary Material

SI

Figure S1. Distributions of RMSD between MMFF optimized geometries and DFT optimized geometries.

Figure S2. Efficiency comparison for different training schedule.

Figure S3. MAE of validation set for different atomic vector size.

Figure S4. Hyperparameter search for interaction block.

Figure S5. Atomization energy distribution of model trained with/without distant diatomic systems.

Figure S6. Learning curves for different models.

Figure S7. Atomic vector interpretation for DTNN.

Figure S8. Atomic vector interpretation for DTNN_7ib trained without distant diatomic systems.

Figure S9. Absolute and relative RMSEs on test sets of eMol9_C_M with different RMSD cutoffs.

Figure S10. Two molecules (number of heavy atoms = 10) with large error.

Figure S11. Absolute and relative MAEs on test sets of Plati_C_M with different RMSD cutoffs.

Table 4.

Performance on eMol9_C_M dataset^a

		MMFF94	TL_QM9M	TL_eMol9_CM
ErrorAb	MAE	None	18.30 ± 0.08	0.51 ± 0.03
	RMSE	None	18.66 ± 0.10	1.27 ± 0.28
ErrorRb	MAE	1.60 ± 0.18	1.04 ± 0.18	0.55 ± 0.02
	RMSE	2.70 ± 0.32	1.35 ± 0.18	0.72 ± 0.04
Success Rate		0.59 ± 0.01	0.62 ± 0.00	0.72 ± 0.01

^aBest performances are in bold.

^bUnit is kcal/mol.