Longitudinal Changes in the Cerebral Cortex Functional Organization of Healthy Elderly

Abstract

Healthy aging is accompanied by disruptions in the functional modular organization of the human brain. Cross-sectional studies have shown age-related reductions in the functional segregation and distinctiveness of brain networks. However, less is known about the longitudinal changes in brain functional modular organization and their associations with aging-related cognitive decline. We examined age- and aging-related changes in functional architecture of the cerebral cortex using a dataset comprising a cross-sectional healthy young cohort of 57 individuals (mean ± SD age, 23.71 ± 3.61 years, 22 males) and a longitudinal healthy elderly cohort of 72 individuals (mean ± baseline age, 68.22 ± 5.80 years, 39 males) with 2–3 time points (18–24 months apart) of task-free fMRI data. We found both cross-sectional (elderly vs young) and longitudinal (in elderly) global decreases in network segregation (decreased local efficiency), integration (decreased global efficiency), and module distinctiveness (increased participation coefficient and decreased system segregation). At the modular level, whereas cross-sectional analyses revealed higher participation coefficient across all modules in the elderly compared with young participants, longitudinal analyses revealed focal longitudinal participation coefficient increases in three higher-order cognitive modules: control network, default mode network, and salience/ventral attention network. Cross-sectionally, elderly participants also showed worse attention performance with lower local efficiency and higher mean participation coefficient, and worse global cognitive performance with higher participation coefficient in the dorsal attention/control network. These findings suggest that healthy aging is associated with whole-brain connectome-wide changes in the functional modular organization of the brain, accompanied by loss of functional segregation, particularly in higher-order cognitive networks.

SIGNIFICANCE STATEMENT Cross-sectional studies have demonstrated age-related reductions in the functional segregation and distinctiveness of brain networks. However, longitudinal aging-related changes in brain functional modular architecture and their links to cognitive decline remain relatively understudied. Using graph theoretical and community detection approaches to study task-free functional network changes in a cross-sectional young and longitudinal healthy elderly cohort, we showed that aging was associated with global declines in network segregation, integration, and module distinctiveness, and specific declines in distinctiveness of higher-order cognitive networks. Further, such functional network deterioration was associated with poorer cognitive performance cross-sectionally. Our findings suggest that healthy aging is associated with system-level changes in brain functional modular organization, accompanied by functional segregation loss particularly in higher-order networks specialized for cognition.

Introduction

Healthy aging is accompanied by declines in cognitive function (Schaie, 1996; Hedden and Gabrieli, 2004). Knowledge about brain changes associated with healthy aging and their relationship to cognitive decline can inform efforts to preserve cognitive function. Task-free fMRI, which measures the temporal synchrony of spontaneous low-frequency BOLD signal fluctuations under task-free settings (Biswal et al., 1995; Fox and Raichle, 2007), is particularly promising for studying age-related changes in intrinsic brain functional connectivity networks. Studies using independent component and seed-based analyses have found age-related decreases in intranetwork functional connectivity (Andrews-Hanna et al., 2007; Damoiseaux et al., 2008; Tomasi and Volkow, 2012; Zhang et al., 2014), implying reduced network specialization, as well as increases in positive correlations and decreases in anticorrelations between these networks (Chan et al., 2014; Ferreira et al., 2016), implying age-related reduced network segregation.

Graph theoretical approaches complement seed-based and independent component analysis approaches by providing a system-level quantification of the modular properties of complex networks (Rubinov and Sporns, 2010). The human brain is proposed to have a modular functional network architecture (Ferrarini et al., 2009; He et al., 2009; Meunier et al., 2009b; Power et al., 2011), characterized by segregated brain modules with dense connections within modules and sparse connections between modules (Rubinov and Sporns, 2010). This is thought to confer several organizational advantages, such as adaptability and robustness of network function, minimization of wiring costs, and facilitation of functional specialization (Kashtan and Alon, 2005; Meunier et al., 2010; Bullmore and Sporns, 2012; Sporns and Betzel, 2016). Consistent with the notion that increasing age is associated with reduced functional specialization and segregation of brain networks, studies using graph theoretical approaches have shown disruptions in the brain functional modular organization in healthy elderly persons. Specifically, decreased modularity and increased participation coefficient occur with increased age (Betzel et al., 2014; Chan et al., 2014) and compared with young adults (Song et al., 2014; Geerligs et al., 2015). With both independent component analysis/seed-based and graph theoretical approaches, lower segregation of brain functional networks was also associated with lower cognitive performance (Andrews-Hanna et al., 2007; Damoiseaux et al., 2008; Geerligs et al., 2015).

To date, most of these studies have been cross-sectional, and few studies have examined longitudinal functional connectivity changes in healthy elderly. Compared with cross-sectional studies, longitudinal studies mitigate cohort effects and are hence better suited for tracking the intrasubject, age-related connectivity changes over time (Kraemer et al., 2000). Recently, we reported a link between greater functional connectivity increases between the default mode and control networks and greater declines in processing speed over time (Ng et al., 2016). However, this study was limited in several aspects. First, only three higher-order cognitive networks were examined. Second, we assumed an a priori functional network structure derived from healthy young adults (Yeo et al., 2011). However, there is evidence suggesting that the modular structure of healthy elderly differs from that of young adults (e.g., Meunier et al., 2009a; Geerligs et al., 2015). The use of a group-specific functional network partition rather than an a priori partition could hence allow for a more accurate network structure characterization. Third, segregation in the previous study was narrowly quantified as functional connectivity between two networks (e.g., default mode and control networks). Graph theoretical measures of modular segregation and distinctiveness, such as participation coefficient (which measures the diversity of a region's connections across all modules) and system segregation (which quantifies intermodule connectivity relative to intramodule connectivity), might instead provide a more comprehensive and system-level quantification of network segregation in the brain. Finally, the previous study did not compare connectivity changes in healthy elderly against a reference group of younger adults. As such, it is not known whether the observed connectivity changes with time in the elderly are indeed reflecting the aging process.

To address these gaps, we thus sought to examine both cross-sectional changes (between healthy young and elderly) and longitudinal changes (of healthy elderly) in the functional organization of the cerebral cortex using graph theoretical and community detection approaches. We hypothesized that the healthy elderly would show reduced network segregation and distinctiveness compared with young adults, and such pattern would deteriorate with time. Further, these network deteriorations would be associated with cognitive impairment cross-sectionally and longitudinally.

Materials and Methods

Participants

Longitudinal analyses.

Seventy-two healthy elderly Chinese adults from the Singapore-Longitudinal Aging Brain Study (Chee et al., 2009; Lo et al., 2014; Ng et al., 2016; Leong et al., 2017) were included in the longitudinal analyses (for participant demographic and cognitive characteristics, see Table 1). All participants underwent neuroimaging and neuropsychological assessments at 18 to 24 month intervals within a 5 year period, and had 2 or 3 time points of data (two time points: 39 participants; three time points: 33 participants) with satisfactory quality. Participants met the following criteria at all time points: (1) scored ≥24 in the Mini-Mental State Examination (Folstein et al., 1975); (2) scored <9 in the modified Geriatric Depression Screening Scale (Yesavage and Sheikh, 1986); and (3) did not have the following conditions: (a) history of significant vascular events (i.e., myocardial infarction, stroke, or peripheral vascular disease), (b) history of cardiac, lung, liver, or kidney failure, (c) history of malignant neoplasia of any form, (d) history of head trauma with loss of consciousness, (e) active or inadequately treated thyroid disease, or (f) active neurological or psychiatric conditions. The study was approved by the Institutional Review Board of the National University of Singapore, and written informed consent was obtained from all participants before the start of the study.

Table 1.

Demographic and cognitive characteristics of elderly participants at baseline^a

Characteristic	Elderly (at baseline) n = 72
Age (years)	68.22 (5.80), range = 58.64–84.91
Sex (female/male)	33/39
Handedness (right/left)	68/4
Education (years)	12.32 (3.13), range = 6–20
Hypertension (%)	36.1%
Diabetes (%)	8.3%
MMSE score	28.18 (1.35), range = 24–30
GDS score	1.19 (1.35), range = 0–7
Cognitive domain scores
Attention (n = 71)	50.32 (6.36), range = 34.09–63.32
Processing speed (n = 72)	50.45 (8.72), range = 32.51–73.13
Verbal memory (n = 72)	51.58 (7.85), range = 35.37–64.77
Visuospatial memory (n = 72)	50.83 (7.59), range = 34.36–64.00
Executive function (n = 72)	50.32 (6.29), range = 38.04–65.22

^aMMSE, Mini-Mental State Examination; GDS, Geriatric Depression Screening Scale.

Neuropsychological assessments were performed by trained researchers within 3 months of the neuroimaging scan, and comprised five domains: processing speed, attention, verbal memory, visuospatial memory, and executive functioning (Chee et al., 2009; Lo et al., 2014; Leong et al., 2017). The assessments were administered in English or Mandarin depending on the participant's language proficiency. Details of the neuropsychological test battery are described in our previous study (Leong et al., 2017). Briefly, the five cognitive domains were assessed using the following tests: (1) processing speed: Symbol Digit Modalities Test (Smith, 1991), Symbol Search Task in the Wechsler Memory Scale-Third Edition (Wechsler, 1997), and Trail Making Test A (Reitan and Wolfson, 1985); (2) attention: Digit Span Test and Spatial Span Test in Wechsler Memory Scale-Third Edition; (3) verbal memory: Rey Auditory Verbal Learning Test (Lezak et al., 2004); (4) visuospatial memory: Visual Paired Associates Test; and (5) executive functioning: Categorical Verbal Fluency Test (Lezak et al., 2004), Design Fluency Test in the Delis-Kaplan Executive Function System (Delis Kaplan et al., 2001), and Trail Making Test B (Reitan and Wolfson, 1985). The test scores at each time point were standardized to T scores (mean ± SD, 50 ± 10) with respect to the baseline. For each cognitive domain, we obtained a composite score for each participant at each time point by averaging the standardized T scores across all tests within that domain. Additionally, a measure of global cognitive performance for each participant at each time point was derived by averaging across the T scores of the five cognitive domains.

Cross-sectional analyses.

For the cross-sectional analyses, we examined baseline neuroimaging data from the 72 healthy elderly participants described above, as well as neuroimaging data from a separate dataset comprising 57 healthy young Chinese adults (mean ± SD age, 23.71 ± 3.61 years, range 18.59–34.08 years, 22 males, 55 right-handed). All healthy young participants fulfilled the following criteria: (1) no history of psychiatric or neurologic disorders, (2) no history of severe medical illnesses, (3) not taking any long-term psychoactive medication, (4) nonsmoker, and (5) consume <31 units of alcohol per week. The study on the young participants was approved by the Institutional Review Board of the National University of Singapore, and all participants gave written informed consent before the commencement of the study.

Image acquisition

Both healthy young and elderly participants were scanned at the Centre for Cognitive Neuroscience, Duke-NUS Medical School, on a 3 T Siemens Magnetom Tim Trio System (Siemens, Erlangen, Germany). The scan protocol included a high-resolution T1-weighted structural scan (magnetization-prepared rapid gradient echo (MPRAGE) sequence, repetition time = 2300 ms, echo time = 2.98 ms, inversion time = 900 ms, flip angle = 9°, field of view = 256 × 240 mm², matrix = 256 × 240, 192 continuous sagittal slices, voxel size = 1.0 × 1.0 × 1.0 mm³, bandwidth = 240 Hz/pixel), as well as an 8 min T2*-weighted task-free functional MRI scan where participants were instructed to fixate on a cross in the center of the screen (echo planar sequence, repetition time = 2000 ms, echo time = 30 ms, flip angle = 90°, field of view = 192 × 192, matrix size = 64 × 64, 36 continuous axial slices, voxel size = 3.0 × 3.0 × 3.0 mm³, bandwidth = 2112 Hz/pixel).

Image preprocessing

Functional imaging.

fMRI images were preprocessed using previous protocol (Ng et al., 2016) based on the Analysis of Functional NeuroImages software (Cox, 1996) and the FMRIB (Oxford Centre for Functional MRI of the Brain) Software Library (Jenkinson et al., 2012). Preprocessing steps included the following: (1) removal of first 5 volumes for magnetic field stabilization; (2) slice-time and motion correction; (3) time series despiking and grand mean scaling; (4) spatial smoothing using a 6 mm FWHM Gaussian kernel; (5) bandpass temporal filtering (0.009–0.1 Hz); (6) removal of linear and quadratic trends; (7) structural image coregistration using boundary-based registration, followed by nonlinear registration (FNIRT) of functional images to standard (MNI 152) space; (8) regression of nuisance signals (white matter, CSF, global signal and six motion parameters); and (9) motion scrubbing of volumes with framewise displacement > 0.2 mm and DVARS (root-mean-square intensity difference from one volume to the next) > 0.5% (1 volume before and 2 volumes after these marked volumes were also removed following the scrubbing procedure described in previous studies) (Power et al., 2012, 2014). Before scrubbing, the data had to meet satisfactory motion criteria (maximum absolute displacement ≤ 3 mm); the resultant images were at least 4 min in length (≥120 volumes). Elderly participants had greater mean relative motion (t₍₁₂₆₎ = −5.82, p = 4.56e⁻⁸) and lower number of volumes after scrubbing (t₍₁₂₆₎ = 2.63, p = 9.60e⁻³), but no differences in mean absolute motion compared with young participants (t₍₁₂₆₎ = −0.086, p = 0.931). Additionally, elderly participants did not show significant changes in these motion parameters with time (mean absolute motion: t₍₁₆₇₎ = 1.30, p = 0.194; mean relative motion: t₍₁₆₇₎ = 0.82, p = 0.413; number of volumes: t₍₁₆₇₎ = 1.12, p = 0.261). Motion characteristics of elderly and young participants are given in Table 2.

Table 2.

Motion characteristics of young and elderly participants^a

Characteristic	Young adults	Elderly
		Baseline	Second time point	Third time point
Prescrubbing
Relative motion (mm)	0.050 (0.024)	0.071 (0.028)	0.072 (0.029)	0.067 (0.028)
Absolute motion (mm)	0.261 (0.193)	0.247 (0.146)	0.264 (0.153)	0.279 (0.219)
Postscrubbing
Relative motion (mm)	0.045 (0.016)*	0.063 (0.021)	0.064 (0.022)	0.062 (0.020)
Absolute motion (mm)	0.238 (0.164)	0.232 (0.117)	0.244 (0.140)	0.254 (0.195)
Number of volumes	220.8 (23.3)*	211.0 (25.2)	212.8 (24.7)	220.1 (19.9)

^aData are mean (SD).

*Postscrubbing motion parameters that showed significant differences (p < 0.05) between young and elderly participants. Within the healthy elderly, no postscrubbing motion parameters showed significant changes with time.

Image analyses

Construction of functional connectivity matrices.

Undirected, weighted functional connectivity matrices (“graphs”) were generated for each participant at each time point. Individual preprocessed functional images in standard space were first parcellated into 114 cortical ROIs (“nodes”) defined by a previous functional connectivity-based parcellation scheme (Yeo et al., 2011). Functional graphs for each individual were then computed by calculating the correlation between the mean BOLD time series of each pair of ROIs (“edges”). All diagonal elements and negative connections in the matrices were set to 0.

Derivation of group-level network modular structure.

Group-level network modular structures of young participants as well as elderly participants at each of the three time points were derived using a previously described two-step consensus community detection method (Lancichinetti and Fortunato, 2012; Bertolero et al., 2015). In this method, we first ran community detection on individual functional graphs to generate individual-level modular structures. Then, we summed across the individual modular assignments to produce a group-level allegiance matrix (Braun et al., 2015), and subsequently performed community detection on the allegiance matrix to produce the group-level modular structure. For both steps, community detection was performed across a range of costs (0.10–0.30, in 0.001 steps) using Louvain methods (Blondel et al., 2008) based on maximizing modularity and repeated using a range of gamma values from 1 to 10. The range of costs for the community detection was set to be the same as the range used to compute the graph theoretical measures (determination of network cost thresholds is described in the next section).

To select gamma values at the individual and group level for further analyses, we computed the partition similarity of all possible group-level partitions to the a priori network partition defined by Yeo et al. (2011) using the z score of the Rand coefficient (Traud et al., 2011). The Rand z score (zRand_αβ) denotes the similarity of two partitions α and β beyond chance and is defined as follows:

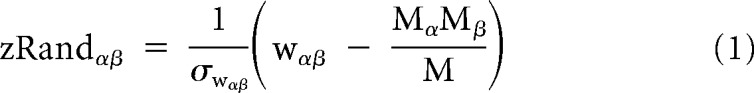where M is the total number of pairs of nodes in the network, M_α is the number of pairs that are assigned to the same module in partition α, M_β is the number of pairs that are assigned to the same module in partition β, w_αβ is the number of pairs that are assigned to the same module both in partition α and partition β, and σ_wαβ is the SD of w_αβ under a hypergeometric distribution with the same number and size of modules. We noted that the optimal group-level partition (i.e., partition with highest similarity to the a priori network partition) (Yeo et al., 2011) differed in terms of the gamma values and number of modules for different subsets of participants. Therefore, to compare across partitions of different groups, we identified a consensus individual and group gamma value that showed (1) the highest average Rand z scores across group partitions derived from young participants, elderly participants at baseline, and young plus elderly participants at baseline, and (2) had six to nine modules across the various group partitions (in line with the eight a priori network partitions) (Yeo et al., 2011). This corresponded to a gamma value of 2 both at the individual and group level (for a comparison of mean Rand z scores across several combinations of gamma parameters, see Table 3).

Table 3.

Mean similarity of group-level partitions to an a priori network parcellation (Yeo et al., 2011)^a

Gamma parameters	Rand z score (number of modules) of group-level partition			Mean Rand z score across the three group-level partitions
	Young adults	Elderly at baseline	Young adults + elderly at baseline
Ind = 1, Grp = 2	32.98 (7)	40.56 (6)	39.48 (6)	37.67
Ind = 2, Grp = 2b	36.13 (7)	43.62 (8)	37.53 (6)	39.09
Ind = 3, Grp = 2	40.22 (8)	40.80 (7)	35.93 (7)	38.98
Ind = 4, Grp = 2	40.46 (10)	39.29 (7)	34.78 (7)	38.18
Ind = 1, Grp = 3	38.04 (7)	41.44 (8)	34.95 (11)	38.14
Ind = 2, Grp = 3	35.26 (7)	39.06 (8)	32.77 (8)	35.69
Ind = 3, Grp = 3	43.94 (10)	37.33 (8)	34.32 (9)	38.53
Ind = 4, Grp = 3	39.63 (10)	30.98 (10)	32.44 (11)	34.35

^aInd, Individual-level gamma; Grp, group-level gamma.

^bBased on the mean Rand z score, the combination of individual gamma = 2 and group gamma = 2 was selected.

To test for group differences (young vs elderly) in similarity of group partitions to the a priori brain network partition (Yeo et al., 2011) (i.e., zRand_young^whole-brain vs zRand_{elderly at baseline}^whole-brain), we calculated 95% CIs for the Rand z scores of young and elderly group partitions, respectively, using subsampling methods. For each group (young or elderly), we first derived 1000 group partitions based on subsamples of 45 participants (constituting at least 80% of participants in the young adults sample). We then calculated Rand z scores (relative to the a priori partition) for each of the 1000 group partitions. To obtain the 95% CIs for the young and elderly group partitions, we calculated the 2.5% (lower bound of the CI) and 97.5% (upper bound of the CI) percentile of the Rand z score distribution from the 1000 group partitions for each group. Differences in Rand z scores between young and elderly group partitions were considered to be significant (α = 0.05) if there were no overlap in CIs of the two groups.

For the cross-sectional analyses, measures of distinctiveness (i.e., participation coefficient, within-module degree, and system segregation) were computed using the group-level modular partition based on the functional graphs of all healthy young participants. For the longitudinal analyses, measures of distinctiveness were computed using the group-level modular structure based on the functional graphs of all elderly participants at their baseline time point.

Graph theoretical analysis.

Following our previous approach (Wang et al., 2018), graph theoretical measures were computed for each participant at each time point using in-house scripts based on the brain connectivity toolbox (Rubinov and Sporns, 2010). Measures were computed over a range of network cost thresholds (0.10 ≤ cost ≤ 0.30, step = 0.01) that met the following criteria: (1) average number of edges per node was larger than the log of the total number of nodes (Watts and Strogatz, 1998; Wang et al., 2009); (2) 80% of the nodes were fully connected (Bassett et al., 2008); and (3) small-worldness of the networks was >1 (Watts and Strogatz, 1998). Composite values for each graph theoretical measure were then obtained by integrating each measure across the entire range of cost thresholds. We computed the following measures of network integration, segregation, and distinctiveness.

Measures of integration.

Global integration in the brain characterizes the ease with which distributed brain regions communicate and integrate information (Rubinov and Sporns, 2010). We calculated as a global measure of integration in brain networks the weighted global efficiency, which is defined as the average of the inverse shortest path length between all pairs of nodes (Latora and Marchiori, 2001; Rubinov and Sporns, 2010).

Measures of segregation.

Local segregation in the brain quantifies the presence of highly connected brain regions (i.e., clusters) within the network and measures the capability for specialized processing to occur within these clusters (Rubinov and Sporns, 2010). We calculated as a global measure of network segregation the weighted local efficiency, which is defined as the average of the inverse shortest path length between all pairs of nodes within the subgraph containing only neighbors of a node (Latora and Marchiori, 2001; Rubinov and Sporns, 2010).

Measures of distinctiveness.

Measures of integration and segregation, such as local and global efficiency, do not take into account the modular structure of the brain. We additionally computed measures that describe the distinctiveness and segregation of functional modules in the brain: participation coefficient, within-module degree, and system segregation. The nodal-weighted participation coefficient is a measure of intermodule connectivity and measures how evenly distributed connections of a node are across modules (Guimerà and Nunes Amaral, 2005). The nodal-weighted within-module degree, on the hand, is a measure of intranetwork connectivity and measures the connectedness of a node to other nodes in the same module (Guimerà and Nunes Amaral, 2005). Finally, based on work by Chan et al. (2014), we computed a global measure of system segregation on the thresholded network matrices, which summarizes values of intramodule correlations relative to intermodule correlations.

We obtained both global-level and modular-level measures of distinctiveness for statistical analyses. To quantify global-level changes in modular segregation and distinctiveness, we examined system segregation as well as a global measure of participation coefficient, which is calculated as the mean composite nodal participation coefficient across all nodes. To quantify changes in the segregation of specific modules (i.e., modular-level changes), we averaged composite nodal participation coefficient values across all nodes in the same module. Additionally, based on the composite nodal participation coefficient and within-module degree values, we can categorize each node into one of four node types (Guimerà and Nunes Amaral, 2005; Power et al., 2013; Bertolero et al., 2015): (1) connector hubs (high participation coefficient and high within-module degree); (2) satellite connectors (high participation coefficient and low within-module degree); (3) provincial hubs (low participation coefficient and high within-module degree); and (4) peripheral nodes (low participation coefficient and low within-module degree). The threshold for a high participation coefficient was determined using a mean-based split of the participation coefficient values across all individuals and all time points, whereas the threshold for a high within-module degree was set at 10⁻⁵ following previous work (Bertolero et al., 2015). To examine age-related changes in the assignment of node types within each module, we then computed the proportion of each node type within each module as follows:

Statistical analyses

Cross-sectional changes in graph theoretical measures between young and elderly participants.

To examine group differences in graph theoretical measures between young and elderly participants, we used linear regression models with the graph theoretical measure as the dependent variable, group as the independent variable of interest, and sex as a nuisance covariate.

Association between cross-sectional changes in graph theoretical measures and cognitive performance.

For those graph theoretical measures that showed differences between young and elderly, we further examined their association with cognitive performance in the elderly participants, of which cognitive information was available. Separate linear regression models for each of the six cognitive measures (i.e., five cognitive domains and global cognitive measure) were performed, with cognitive score as the dependent variable, graph theoretical measure as the independent variable of interest, and sex, education, and age as variables of no interest.

Longitudinal changes in graph theoretical measures of elderly participants.

We examined longitudinal changes in the graph theoretical measures using linear mixed-effects models, which model both fixed and random effects and account for unequal sampling intervals and missing data (Cnaan et al., 1997; Singer and Willett, 2003; Long, 2012). Following previous methods (Ng et al., 2016), random intercepts as well as random slopes for the effect of time (years since baseline) were modeled for each subject, with the effect of time allowed to vary by baseline age (i.e., age × time interaction). We also accounted for the effects of baseline age, sex, and years of education by modeling these variables as fixed effects. The linear mixed-effects model for the changes in graph theoretical measures/cognitive domains is thus as follows:

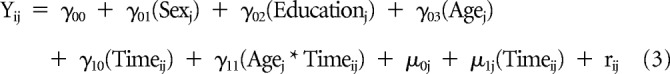where Y_ij denotes the graph theory measure for each participant j at time point i, γ values denote the estimated fixed effect coefficients, μ values denote the estimated random effect coefficients, and r_ij denotes the residual for each participant j at time point i.

Association between longitudinal changes in graph theoretical measures and cognition.

For graph theoretical measures that showed significant longitudinal changes, we examined how longitudinal changes in these graph theoretical measures were associated with longitudinal changes in each of the six cognitive measures. We first obtained the predicted slopes (β_1j.Cognition or β_{1j.Graph theory}) reflecting the effect of time (i.e., γ₁₀(Time_ij) + μ_1j(Time_ij)) for the cognitive measure and the graph theoretical measure of interest based on their respective linear mixed-effects models (i.e., Eq. 3) for each participant j. We then ran multiple regression analyses to evaluate the association between change in cognitive performance (β_1j.Cognition) and change in graph theoretical measure (β_{1j.Graph theory}) as follows:

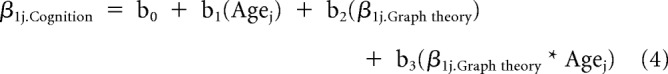where b₂ and b₃ are the estimated brain-cognition coefficients.

Multiple-comparisons correction on the p values of model coefficient estimates was performed for all modular measures (i.e., participation coefficient and proportion of node types) using the false discovery rate (Benjamini and Hochberg, 1995). For analyses examining associations between modular graph theoretical measures and cognitive performance, multiple-comparisons correction was only performed across modules whose measures showed significant age- or aging-related changes.

All statistical analyses were performed using R 3.0.3 (R Core Team, 2015) with Rstudio (RStudio Team, 2015). Linear mixed-effects models were performed using the lme4 (Bates et al., 2015) package. Results were visualized using either R (graphical packages ggplot2) (Wickham, 2009) and ggalluvial (Brunson, 2018) or SPSS version 24.0 (IBM).

Additional validation analyses

Findings from the above analyses could potentially be affected by the presence of other covariates (e.g., motion) or by the choice of methodology (e.g., parcellation scheme). To ensure that our findings were unaffected by these factors, we performed a number of additional analyses as detailed below.

Effects of motion.

Young and elderly participants in this study showed differences in mean relative motion and number of volumes after scrubbing. To ensure that our findings were not affected by motion, we repeated both cross-sectional and longitudinal analyses with mean relative motion and number of volumes added as nuisance covariates. Additionally, studies have suggested that scan length might affect the reliability of functional connectivity estimates (Birn et al., 2013). To ensure that the findings were not affected by scan length, we repeated the analyses: (1) on a subset of participants (cross-sectional: n = 54, young; n = 68, elderly; longitudinal: n = 68, elderly) with at least 5 min of imaging data (≥150 volumes) after scrubbing; and (2) on the original cohort of participants after maintaining equal scan lengths across all participants (i.e., each participant's preprocessed functional image was trimmed to 123 volumes, or 4 min 6 s of data, based on the minimum scan length remaining after scrubbing).

Effects of mean connectivity.

Mean connectivity strength across all edges has been shown to be strongly related to vascular health (Geerligs et al., 2017). Given that age-related differences in mean connectivity strength have also been reported in previous studies (Geerligs et al., 2017), observed age-related differences in functional connectivity-based measures (e.g., graph theoretical measures) may hence be related to these age-related mean connectivity differences and possibly reflect age-related non-neural changes (e.g., changes in vascular factors) rather than neural changes. In our dataset, we similarly observed mean connectivity differences (computed as the mean connectivity strength across all edges in the unthresholded connectivity matrix) between young and elderly participants (elderly > young: t₍₁₂₆₎ = −2.34, p = 0.021), although elderly participants did not show changes in mean connectivity strength with time (t₍₁₆₇₎ = −0.588, p = 0.556). To ensure that our findings were unaffected by age-related mean connectivity differences, we thus repeated the main analyses with mean connectivity included as a nuisance covariate.

Effects of global signal regression.

Global signal regression was included as a preprocessing step in our study as our previous longitudinal aging work has shown that it plays an important factor in revealing aging effects (Ng et al., 2016). However, global signal regression has also been suggested to exert differential effects on groups with different neural network structures (Murphy and Fox, 2017). In view of known differences in brain network architecture between young and older adults (e.g., Meunier et al., 2009a), there is a possibility that global signal regression might impact the observed findings between the young and elderly participants in our study. We thus repeated the cross-sectional analyses without global signal regression.

Choice of parcellation scheme.

To examine whether our findings were affected by the parcellation scheme used, we repeated the analyses using an independent 400-node functional connectivity-based parcellation scheme (Schaefer et al., 2018), whose nodes have been mapped to the network parcellation given by Yeo et al. (2011). Of the 400 nodes, 11 nodes (located primarily in the temporal pole and parietal regions) were removed due to lack of coverage in the functional images of some participants, resulting in 389 nodes used for the connectivity matrix construction and derivation of graph theoretical measures.

Choice of group-level community partition.

In the present study, the cross-sectional analysis was conducted using the group-level modular partition of only the young participants. This might result in a less fitted partition for the elderly participants and potentially influence group differences between young and elderly participants. To ensure that the observed group differences were not the result of an ill-fitted partition, we repeated both cross-sectional and longitudinal analyses using a group-level modular partition based on all young and elderly partitions at baseline.

Results

Group-level modular structures of healthy young and elderly individuals

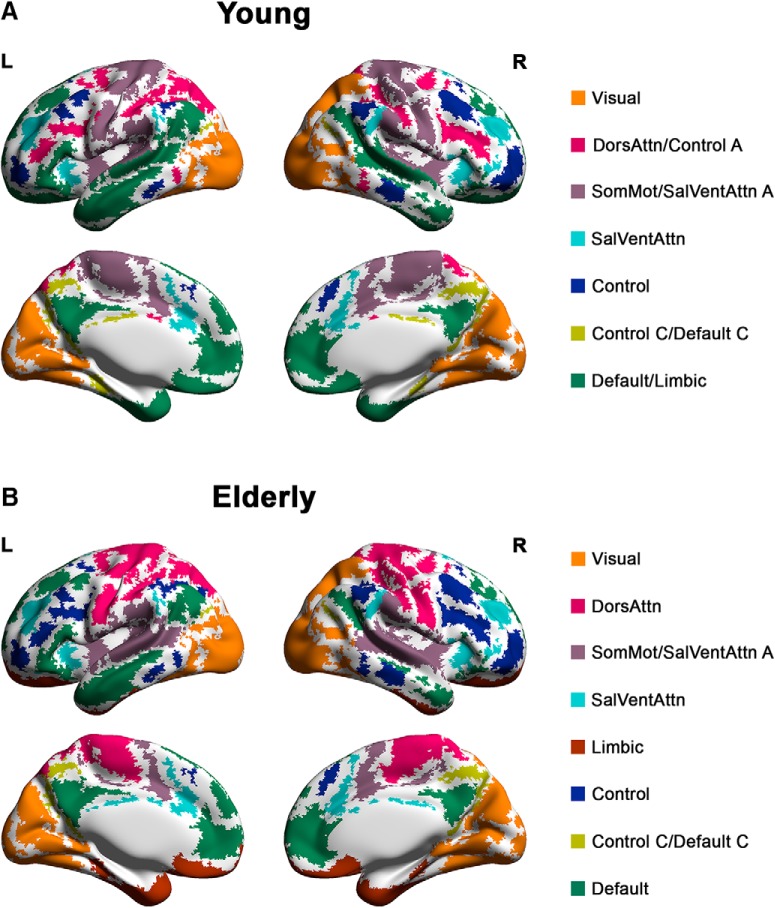
The group-level modular structures of elderly individuals at baseline as well as young individuals are provided in Figure 1 (composition of modules for young and elderly participants at baseline is provided in Fig. 1-1) and Fig. 1-2, respectively). Modules of both structures resembled known intrinsic connectivity networks reported in previous literature (Damoiseaux et al., 2006; Smith et al., 2009; Yeo et al., 2011). To compare the modular structures between the young participants and elderly participants at different time points, we examined how the data-driven modular partitions differed from the subnetwork partition (16 subnetworks) defined by Yeo et al. (2011) using the z score of the Rand index (Fig. 2A). Both group-level modular structures of young and elderly participants at baseline showed significant similarity to the a priori partition beyond chance (zRand_young^whole-brain = 48.73, zRand_{elderly at baseline}^whole-brain = 43.94, p values <1e⁻¹⁰). However, the modular structure of young participants showed significantly higher similarity to the a priori partition than elderly participants at baseline (zRand_young^whole-brain = 48.73, 95% CI of subsamples, 43.65, 49.43) versus zRand_{elderly at baseline}^whole-brain = 43.94 (95% CI of subsamples, 32.26, 43.40). This indicated that the group-level modular structure for healthy elderly at baseline had greater fragmentation of networks compared with young participants, with several brain regions within the same a priori subnetwork being reassigned to different modules (Fig. 2A). Notably, compared with young participants, elderly at baseline had greater fragmentation in higher-order networks (i.e., default mode, salience/ventral attention, and control networks) (zRand_young^{higher-order networks} = 43.37 vs zRand_{elderly at baseline}^{higher-order networks} = 33.11, difference = 10.26) than the other networks (zRand_young^{other networks} = 13.20 vs zRand_{elderly at baseline}^{other networks} = 9.97, difference = 3.23).

Figure 1.

Group-level modular structure of healthy young and elderly participants at baseline. A, The group-level modular structure of young participants comprised seven modules. B, The group-level modular structure of elderly participants at baseline comprised eight modules. Modules of both structures resembled known intrinsic connectivity networks. Module labels were assigned based on the network definition by Yeo et al. (2011). Composition of modules for young and elderly participants at baseline is provided in Figure 1-1 and Figure 1-2, respectively. DorsAttn, Dorsal attention; SomMot, somatomotor; SalVentAttn, salience/ventral attention.

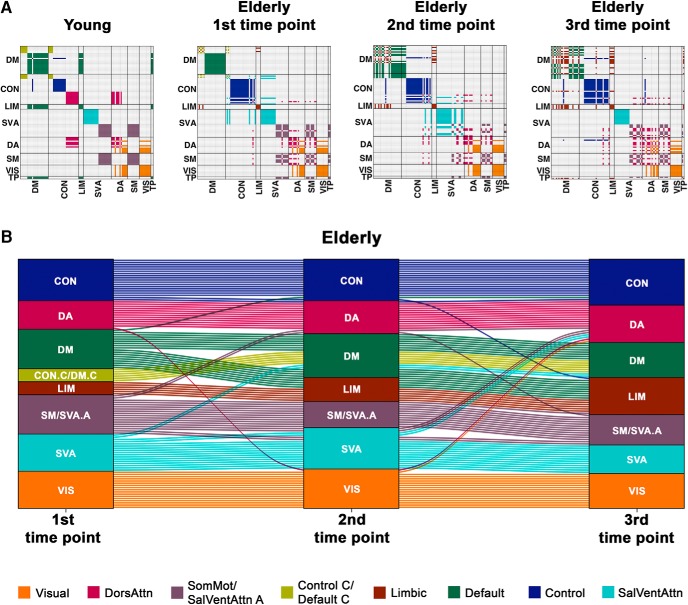
Figure 2.

The modular structure of healthy elderly becomes less distinctive with time. A, Consensus matrices map group-level modular partitions of young participants and elderly participants at each of the three time points to eight networks defined by Yeo et al. (2011). Each module is represented by a single color. With age and time, the modular structure becomes less distinctive, with brain regions within the same a priori subnetwork increasingly getting assigned to different modules. B, The alluvial plot represents changes in group-level modular assignment of brain regions in healthy elderly across three time points. Each block represents a module. Each line indicates a brain region. The color of each line represents the modular assignment of each brain region at the first time point. Among the modules, higher-order networks (e.g., default mode, control, and salience/ventral attention networks) showed the greatest assignment changes in the healthy elderly with time. Similar observations in module fragmentation were made particularly between young and elderly participants at baseline when repeating the analyses with equal scan lengths maintained across participants, where group differences in the modular structure between the two groups remained significant (Figure 2-1; Figure 2-2). DM, Default mode; CON, control; LIM, limbic; SVA, salience/ventral attention; DA, dorsal attention; SM, somatomotor; VIS, visual; TP, temporoparietal; DorsAttn, dorsal attention; SomMot, somatomotor; SalVentAttn, salience/ventral attention.

Figure 1-1

Composition of modules in group-level modular structure of young participants. Download Figure 1-1, DOCX file ^{(80KB, docx)}

Figure 1-2

Composition of modules in baseline group-level modular structure of elderly participants. Download Figure 1-2, DOCX file ^{(132.5KB, docx)}

Figure 2-1

Changes in modular partitions across age groups and with time based on analyses where equal scan lengths were maintained across all participants. (A) Consensus matrices map group-level modular partitions of young participants and elderly participants at each of the three time points to eight networks defined by Yeo et al. (2011), based on the analyses in which equal scan lengths (123 volumes) were maintained across all participants. Each module is represented by a single colour. (B) The alluvial plot illustrates changes in group-level modular assignment of brain regions in healthy elderly across three time points. Each block denotes a module, and each line denotes a brain region. The colour of each line indicates the modular assignment of each brain region at the first time point. In line with the original analyses, the modular structure becomes less distinctive and more fragmented with age (elderly at baseline compared to young) and time (across time points in the elderly), with brain regions within the same a priori subnetwork increasingly getting assigned to different modules. Notably, higher order networks (e.g., default mode, control and salience/ventral attention networks) showed the greatest assignment changes in the healthy elderly compared to young participants and with time. Abbreviations: DM, default mode; CON, control; LIM, limbic; SVA, salience/ventral attention; DA, dorsal attention; SM, somatomotor; VIS, visual; TP, temporoparietal; DorsAttn, dorsal attention; SomMot, somatomotor; SalVentAttn, salience/ventral attention. Download Figure 2-1, DOCX file ^{(126.9KB, docx)}

Figure 2-2

Similarity of group-level modular partitions to a priori network partition (16 subnetworks) (Yeo et al., 2011) based on analyses where equal scan lengths were maintained across all participants. Download Figure 2-2, TIF file ^{(11.4MB, tif)}

This fragmentation of a priori networks in the elderly was also further increased at later time points, with similarity to the a priori partition decreasing with time (zRand_{elderly at baseline}^whole-brain = 43.94, zRand_{elderly at 2nd time point}^whole-brain = 35.22, zRand_{elderly at 3rd time point}^whole-brain = 35.19). Similar to what was observed between young participants and elderly at baseline, higher-order networks showed relatively greater modular assignment changes with time (Fig. 2B) (zRand_{elderly at baseline}^{higher-order networks} = 33.11, zRand_{elderly at 2nd time point}^{higher-order networks} = 23.35, difference from baseline = 9.76, zRand_{elderly at 3rd time point}^{higher-order networks} = 27.65, difference from baseline = 5.46) compared with the other networks (zRand_{elderly at baseline}^{higher-order networks} = 9.97, zRand_{elderly at 2nd time point}^{higher-order networks} = 10.85, difference from baseline = −0.88, zRand_{elderly at 3rd time point}^{higher-order networks} = 8.65, difference from baseline = 1.32). Our observation of increased fragmentation of networks with time in the elderly, with regions within the same subnetwork being assigned to different modules, thus suggests that brain functional networks, particularly the higher-order networks, become less distinct as one ages.

Cross-sectional and longitudinal decreases in global measures of integration, segregation, and distinctiveness in the healthy elderly

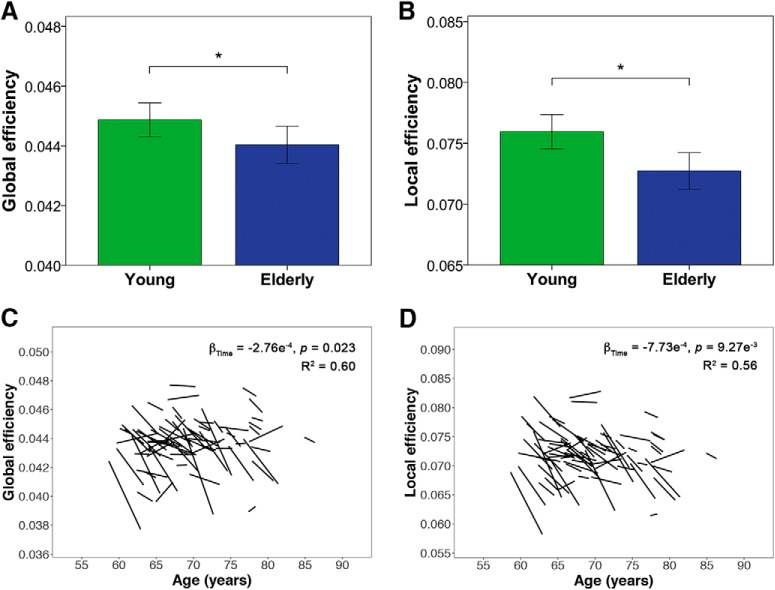
Healthy elderly showed reductions in global measures of integration and segregation, with both lower global efficiency and local efficiency compared with young participants (Fig. 3A,B; Table 4) as well as with time (Fig. 3C,D; Table 5). No age or age × time interaction effects were found for both global and local efficiency in the elderly.

Figure 3.

Healthy elderly show cross-sectional and longitudinal reductions in local and global efficiency. A, B, Bar charts indicate mean (±2 SE) global efficiency and local efficiency of young and elderly participants at baseline. *indicates a statistically significant difference (p < 0.05) between young and elderly participants at baseline. C, D, Spaghetti plots indicate model-fitted longitudinal changes in global and local efficiency for each individual. Results displayed are thresholded at p < 0.05. Healthy elderly showed lower local and global efficiency at the whole-brain level compared with young participants and with time.

Table 4.

Cross-sectional analyses: coefficient estimates for group differences in global measures of integration, segregation, and distinctiveness between young and elderly

Measure	Coefficient	SE	t	p	Validation resultsa
Global efficiency	9.10e−4	4.38e−4	2.08	0.040*	2,3,4
Local efficiency	3.47e−3	1.06e−3	3.29	1.29e−3*	1,2,3,4
Mean participation coefficient	−0.010	1.21e−3	−8.31	1.32e−13*	1,2,3,4
System segregation	9.94e−3	1.28e−3	7.79	2.14e−12*	1,2,3,4

^aValidation results: 1, effect remains significant (p < 0.05) after controlling for mean relative motion and number of volumes; 2, effect remains significant (p < 0.05) after repeating the analyses in a subset of participants (young: n = 54; elderly: n = 68) with at least 150 volumes of good-quality imaging data (i.e., ≥5 min in length) remaining after scrubbing; 3, effect remains significant (p < 0.05) after maintaining equal scan lengths (123 volumes) across all participants; 4, effect remains significant (p < 0.05) after controlling for mean functional connectivity strength across all edges.

*Statistically significant effects (p < 0.05).

Table 5.

Longitudinal analyses: coefficient estimates for time, age, and age × time effects on global measures of integration, segregation, and distinctiveness in elderly

Measure	Predictor	Coefficient	SE	t	p	Validation resultsa
Global efficiency	Time*	−2.76e−4	1.21e−4	−2.28	0.023	2,4
	Age	3.57e−5	5.18e−5	0.69	0.490
	Age × time	1.32e−6	2.26e−5	0.06	0.954
Local efficiency	Time*	−7.73e−4	2.97e−4	−2.60	9.27e−3	1,2,4
	Age	−8.03e−5	1.26e−4	−0.64	0.524
	Age × time	1.76e−5	5.57e−5	0.32	0.752
Mean participation coefficient	Time*	9.55e−4	2.59e−4	3.69	2.24e−4	1,2,3,4
	Age*	3.61e−4	1.20e−4	2.99	2.76e−3	1,2,3,4
	Age × time	−1.76e−5	4.89e−5	−0.36	0.719
System segregation	Time*	−9.59e−4	2.68e−4	−3.58	3.40e−4	1,2,3,4
	Age*	−2.76e−4	1.16e−4	−2.37	0.018	1,3,4
	Age × time	3.63e−6	5.06e−5	0.07	0.943

^aValidation results: 1, effect remains significant (p < 0.05) after controlling for mean relative motion and number of volumes; 2, effect remains significant (p < 0.05) after repeating the analyses in a subset of participants (n = 68) with at least 150 volumes of good-quality imaging data (i.e., ≥5 min in length) remaining after scrubbing; 3, effect remains significant (p < 0.05) after maintaining equal scan lengths (123 volumes) across all participants; 4, effect remains significant (p < 0.05) after controlling for mean functional connectivity strength across all edges.

*Statistically significant effects (p < 0.05).

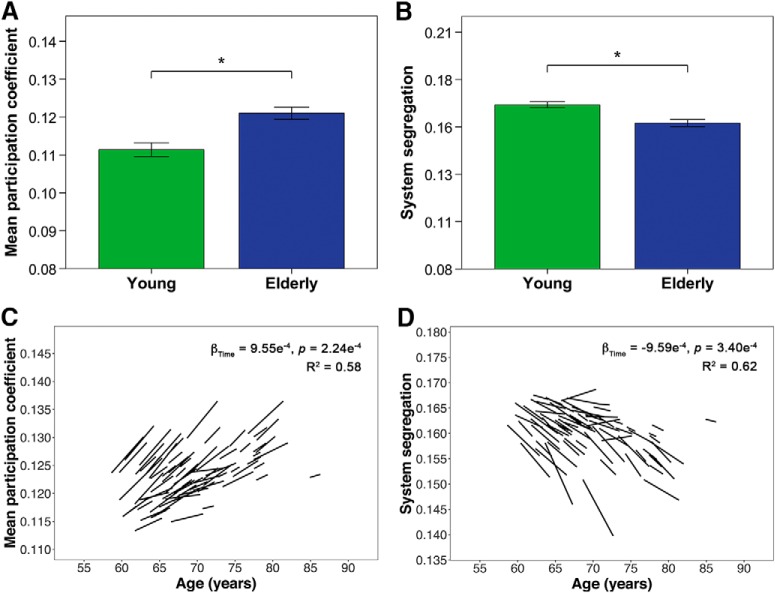
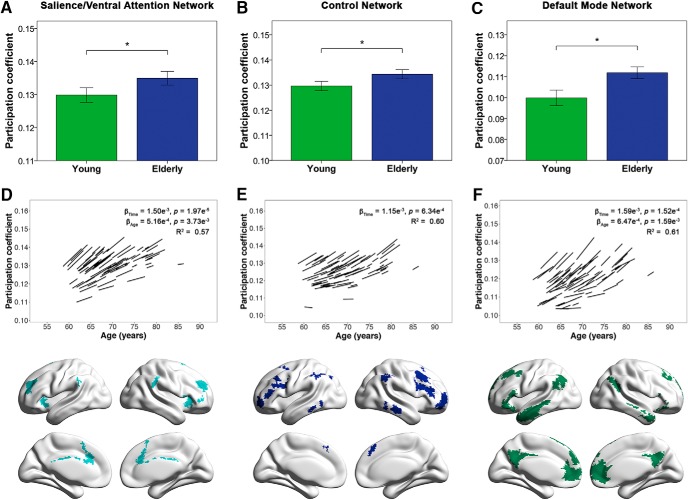
Healthy elderly participants also showed reductions in global measures of distinctiveness, with higher participation coefficient and lower system segregation compared with young participants (Fig. 4A,B; Table 4), as well as with age and time (Fig. 4C,D; Table 5). There were no age × time interaction effects for both mean participation coefficient and system segregation in the elderly.

Figure 4.

Healthy elderly show cross-sectional and longitudinal changes in mean participation coefficient and system segregation. A, B, Bar charts indicate mean (±2 SE) participation coefficient and system segregation of young and elderly participants at baseline. *indicates a statistically significant difference (p < 0.05) between young and elderly participants at baseline. C, D, Spaghetti plots indicate model-fitted longitudinal changes in mean participation coefficient and system segregation for each individual. Results displayed are thresholded at p < 0.05. Healthy elderly showed higher mean participation coefficient across all nodes and lower global system segregation compared with young participants as well as with time.

Cross-sectional and longitudinal decreases in modular measures of distinctiveness in the healthy elderly

Compared with young adults, healthy elderly participants showed higher participation coefficient across all modules (Table 6). Healthy elderly also showed a greater proportion of node types with high participation coefficient (i.e., connector hubs and satellite connectors) and lower proportion of node types with low participation coefficient (i.e., provincial hubs and peripheral nodes) compared with young participants (Table 7). While changes in proportion of node types were strongest for visual, somatomotor/salience ventral attention A and default mode networks, similar trends were also observed for the rest of the modules. Collectively, these findings indicate a general increase in internetwork connectivity and consequently a decrease in segregation across all modules in healthy elderly compared with their younger counterparts.

Table 6.

Cross-sectional analyses: coefficient estimates for group differences in participation coefficient between young and elderly^a

Measure	Coefficient	SE	t	Uncorr p	FDR-adj p	Validation resultsb
Visual*	−0.013	2.29e−3	−5.69	8.54e−8	2.99e−7	1,2,3,4
SomMot/SalVentAttn A*	−0.018	2.28e−3	−7.84	1.69e−12	1.18e−11	1,2,3,4
DorsAttn/Control A*	−4.58e−3	1.21e−3	−3.77	2.50e−4	4.38e−4	1,2,3,4
SalVentAttn*	−5.04e−3	1.54e−3	−3.27	1.39e−3	1.46e−3	2,3,4
Default*	−0.013	2.29e−3	−5.50	2.06e−7	4.81e−7	1,2,3,4
Control*	−4.32e−3	1.33e−3	−3.25	1.46e−3	1.46e−3	1,2,3,4
Control C/Default C*	−5.98e−3	1.82e−3	−3.28	1.33e−3	1.46e−3	2,3,4

^aUncorr, Uncorrected; FDR-adj, false discovery rate-adjusted; DorsAttn, dorsal attention; SomMot, somatomotor; SalVentAttn, salience/ventral attention.

^bValidation results: 1, effect remains significant (FDR-adjusted p < 0.05) after controlling for mean relative motion and number of volumes; 2, effect remains significant (FDR-adjusted p < 0.05) after repeating the analyses in a subset of participants (young: n = 54; elderly: n = 68) with at least 150 volumes of good-quality imaging data (i.e., ≥5 min in length) remaining after scrubbing; 3, effect remains significant (FDR-adjusted p < 0.05) after maintaining equal scan lengths (123 volumes) across all participants; 4, effect remains significant (FDR-adjusted p < 0.05) after controlling for mean functional connectivity strength across all edges.

*Statistically significant effects (FDR-adjusted p < 0.05).

Table 7.

Cross-sectional analyses: coefficient estimates for group differences in proportion of node types between young and elderly^a

Measure	Coefficient	SE	t	Uncorr p	FDR-adj p	Validation resultsb
Proportion of connector hubs
Visual*	−7.21	2.50	−2.88	4.67e−3	0.010	1,2,4
SomMot/SalVentAttn A*	−13.51	2.53	−5.34	4.26e−7	1.19e−5	1,2,3,4
DorsAttn/Control A	−2.00	2.07	−0.97	0.336	0.392
SalVentAttn*	−4.60	2.03	−2.27	0.025	0.039
Default*	−9.10	2.54	−3.59	4.74e−4	1.66e−3	1,2,3,4
Control	−3.15	2.17	−1.45	0.149	0.190
Control C/Default C	−0.25	2.57	−0.10	0.921	0.921
Proportion of satellite connectors
Visual*	−5.51	1.63	−3.37	9.87e−4	3.07e−3	1,2,4
SomMot/SalVentAttn A*	−7.61	1.99	−3.82	2.05e−4	8.20e−4	1,2,3,4
DorsAttn/Control A*	−4.78	1.69	−2.83	5.41e−3	0.011	2,3,4
SalVentAttn	−3.27	2.06	−1.59	0.114	0.152
Default*	−8.12	1.70	−4.77	4.96e−6	3.47e−5	1,2,3,4
Control	−1.55	2.26	−0.68	0.495	0.533
Control C/Default C*	−6.02	2.44	−2.47	0.015	0.024	2,3,4
Proportion of provincial hubs
Visual*	8.17	2.66	3.07	2.64e−3	6.44e−3	1,2,3,4
SomMot/SalVentAttn A*	12.88	2.56	5.03	1.68e−6	2.02e−5	1,2,3,4
DorsAttn/Control A	2.65	1.95	1.36	0.178	0.217
SalVentAttn*	5.04	1.52	3.32	1.17e−3	3.28e−3	1,2,3,4
Default*	11.58	2.81	4.13	6.64e−5	3.72e−4	1,2,3,4
Control*	3.23	1.48	2.18	0.031	0.046
Control C/Default C	0.84	1.98	0.43	0.672	0.696
Proportion of peripheral nodes
Visual*	4.55	1.63	2.80	5.97e−3	0.011	2,4
SomMot/SalVentAttn A*	8.23	1.66	4.97	2.16e−6	2.02e−5	1,2,3,4
DorsAttn/Control A*	4.14	1.35	3.05	2.76e−3	6.44e−3	2,3,4
SalVentAttn	2.84	1.63	1.74	0.084	0.118
Default*	5.65	1.47	3.83	2.00e−4	8.20e−4	1,2,3,4
Control	1.46	1.59	0.92	0.360	0.403
Control C/Default C*	5.44	2.10	2.59	0.011	0.019	2,4

^aUncorr, Uncorrected; FDR-adj, false discovery rate-adjusted; DorsAttn, dorsal attention; SomMot, somatomotor; SalVentAttn, salience/ventral attention.

^bValidation results: 1, effect remains significant (FDR-adjusted p < 0.05) after controlling for mean relative motion and number of volumes; 2, effect remains significant (FDR-adjusted p < 0.05) after repeating the analyses in a subset of participants (young: n = 54; elderly: n = 68) with at least 150 volumes of good-quality imaging data (i.e., ≥5 min in length) remaining after scrubbing; 3, effect remains significant (FDR-adjusted p < 0.05) after maintaining equal scan lengths (123 volumes) across all participants; 4, effect remains significant (FDR-adjusted p < 0.05) after controlling for mean functional connectivity strength across all edges.

*Statistically significant effects (FDR-adjusted p < 0.05).

While the cross-sectional group analyses showed nonspecific age-related decreases in segregation across all modules, longitudinal analyses instead revealed more focal network changes. Specifically, healthy elderly showed increases in the participation coefficient of three higher-order cognitive modules with time and/or with age: the salience/ventral attention network, the default mode network, and the control network (Fig. 5; Table 8). No age × time interaction effects were found. Consistent with our findings of increased participation coefficient in the default mode, salience/ventral attention, and control networks, we also found longitudinal increases in the proportion of node types with high participation coefficient in these three modules. Correspondingly, these modules showed longitudinal decreases in the proportion of node types with low participation coefficient (Table 9).

Figure 5.

Healthy elderly show cross-sectional and longitudinal increases in the participation coefficient of cognitive networks. Bar charts indicate mean (±2 SE) participation coefficient of young and elderly participants at baseline in the (A) salience/ventral attention network, (B) control network, and (C) default mode network. *indicates a statistically significant difference (false discovery rate-corrected p < 0.05) between young and elderly participants at baseline. Spaghetti plots represent model-fitted longitudinal participation coefficient changes for each individual in the respective modules (D–F), whereas brain maps denote brain regions belonging to each module based on the group-level partition of healthy elderly at baseline. Results displayed are thresholded at p < 0.05 (false discovery rate-corrected). Healthy elderly showed higher participation coefficient in these three networks compared with young participants and with time, all of which are key networks involved in higher-order cognitive function.

Table 8.

Longitudinal analyses: coefficient estimates for time, age, and age × time effects on participation coefficient in elderly^a

Measure	Predictor	Coefficient	SE	t	Uncorr p	FDR-adj p	Validation resultsb
Visual	Time	2.57e−4	6.09e−4	0.42	0.673	0.673
	Age	2.00e−4	2.38e−4	0.84	0.401	0.458
	Age × time	−6.05e−5	1.14e−4	−0.53	0.597	0.686
DorsAttn	Time	8.24e−4	4.09e−4	2.01	0.044	0.088
	Age	1.56e−4	1.84e−4	0.85	0.396	0.458
	Age × time	−4.76e−5	7.63e−5	−0.62	0.532	0.686
SomMot/SalVentAttn A	Time	6.11e−4	4.03e−4	1.52	0.129	0.207
	Age	3.50e−4	1.71e−4	2.05	0.040	0.081
	Age × time	−4.34e−5	7.54e−5	−0.57	0.565	0.686
SalVentAttn	Time*	1.50e−3	3.52e−4	4.27	1.97e−5	1.57e−4	1,2,4
	Age*	5.16e−4	1.78e−4	2.90	3.73e−3	0.015	1,2,4
	Age × time	−4.67e−5	6.64e−5	−0.70	0.482	0.686
Limbic	Time	3.50e−4	6.29e−4	0.56	0.579	0.661
	Age	3.42e−4	3.20e−4	1.07	0.285	0.457
	Age × time	−8.75e−5	1.15e−4	−0.76	0.449	0.686
Control	Time*	1.15e−3	3.35e−4	3.42	6.34e−4	1.69e−3	1,2,4
	Age	3.87e−4	1.76e−4	2.19	0.028	0.075
	Age × time	3.32e−5	6.33e−5	0.52	0.600	0.686
Control C/Default C	Time	2.87e−4	4.30e−4	0.67	0.505	0.661
	Age	−2.98e−5	1.84e−4	−0.16	0.871	0.871
	Age × time	7.73e−5	7.94e−5	0.97	0.330	0.686
Default	Time*	1.59e−3	4.20e−4	3.79	1.52e−4	6.08e−4	1,2,3,4
	Age*	6.47e−4	2.05e−4	3.16	1.59e−3	0.013	1,2,3,4
	Age × time	1.72e−5	7.93e−5	0.22	0.829	0.829

^aUncorr, Uncorrected; FDR-adj, false discovery rate-adjusted; DorsAttn, dorsal attention; SomMot, somatomotor; SalVentAttn, salience/ventral attention.

^bValidation results: 1, effect remains significant (FDR-adjusted p < 0.05) after controlling for mean relative motion and number of volumes; 2, effect remains significant (FDR-adjusted p < 0.05) after repeating the analyses in a subset of participants (n = 68) with at least 150 volumes of good-quality imaging data (i.e., ≥5 min in length) remaining after scrubbing; 3, effect remains significant (FDR-adjusted p < 0.05) after maintaining equal scan lengths (123 volumes) across all participants; 4, effect remains significant (FDR-adjusted p < 0.05) after controlling for mean functional connectivity strength across all edges.

*Statistically significant effects (FDR-adjusted p < 0.05).

Table 9.

Longitudinal analyses: coefficient estimates for time, age, and age × time effects on proportion of node types in elderly^a

Measure	Predictor	Coefficient	SE	t	Uncorr p	FDR-adj p	Validation resultsb
Proportion of connector hubs
Visual	Time	0.219	0.577	0.38	0.704	0.835
	Age	−0.170	0.253	−0.67	0.500	0.666
	Age × time	0.135	0.107	1.26	0.206	0.847
DorsAttn	Time	0.640	0.758	0.84	0.398	0.607
	Age	0.034	0.323	0.11	0.916	0.916
	Age × time	−0.140	0.140	−1.00	0.319	0.847
SomMot/SalVentAttn A	Time	0.400	0.709	0.56	0.572	0.796
	Age	0.130	0.315	0.41	0.681	0.778
	Age × time	−0.095	0.132	−0.72	0.471	0.877
SalVentAttn	Time	0.856	0.440	1.94	0.052	0.151
	Age	0.484	0.199	2.43	0.015	0.063
	Age × time	−0.092	0.082	−1.12	0.263	0.847
Limbic	Time	1.058	0.874	1.21	0.226	0.426
	Age	0.379	0.378	1.00	0.317	0.507
	Age × time	−0.197	0.160	−1.23	0.218	0.847
Control	Time*	2.044	0.619	3.30	9.63e−4	7.70e−3	1,2,4
	Age	0.508	0.313	1.62	0.105	0.225
	Age × time	0.110	0.116	0.95	0.344	0.847
Control C/Default C	Time	0.264	0.851	0.31	0.757	0.835
	Age	−0.205	0.333	−0.61	0.539	0.678
	Age × time	0.159	0.155	1.03	0.305	0.847
Default	Time*	1.880	0.650	2.89	3.85e−3	0.021	1,2,3,4
	Age	0.676	0.290	2.34	0.020	0.063
	Age × time	0.126	0.123	1.02	0.306	0.847
Proportion of satellite connectors
Visual	Time	0.075	0.453	0.17	0.869	0.894
	Age	−0.020	0.182	−0.11	0.914	0.916
	Age × time	−0.031	0.085	−0.36	0.716	0.933
DorsAttn	Time	0.677	0.528	1.28	0.200	0.426
	Age	0.084	0.202	0.41	0.679	0.778
	Age × time	0.041	0.099	0.41	0.682	0.933
SomMot/SalVentAttn A	Time*	1.238	0.501	2.47	0.013	0.048	1,4
	Age	0.511	0.196	2.61	9.05e−3	0.058
	Age × time	−0.063	0.093	−0.68	0.494	0.877
SalVentAttn	Time*	1.533	0.513	2.99	2.82e−3	0.018	1,2,4
	Age	0.566	0.239	2.37	0.018	0.063
	Age × time	−0.079	0.096	−0.83	0.409	0.872
Limbic	Time	0.586	0.830	0.71	0.480	0.698
	Age	0.560	0.346	1.62	0.105	0.225
	Age × time	−0.068	0.153	−0.45	0.655	0.933
Control	Time	0.059	0.446	0.13	0.894	0.894
	Age	0.565	0.213	2.66	7.86e−3	0.058
	Age × time	−0.086	0.083	−1.04	0.300	0.847
Control C/Default C	Time	0.277	0.767	0.36	0.718	0.835
	Age	0.312	0.340	0.92	0.359	0.522
	Age × time	−0.032	0.140	−0.23	0.817	0.934
Default	Time*	1.324	0.479	2.76	5.70e−3	0.026	1,2,3,4
	Age	0.512	0.215	2.38	0.017	0.063
	Age × time	0.028	0.089	0.32	0.751	0.933
Proportion of provincial hubs
Visual	Time	−0.321	0.645	−0.50	0.618	0.824
	Age	0.070	0.273	0.26	0.796	0.850
	Age × time	−6.91e−3	0.120	−0.06	0.954	0.967
DorsAttn	Time	−0.631	0.725	−0.87	0.384	0.607
	Age	0.111	0.325	0.34	0.734	0.810
	Age × time	0.042	0.134	0.32	0.751	0.933
SomMot/SalVentAttn A	Time	−1.120	0.740	−1.51	0.130	0.347
	Age	−0.336	0.300	−1.12	0.262	0.465
	Age × time	0.116	0.139	0.84	0.403	0.872
SalVentAttn	Time	−0.751	0.368	−2.04	0.041	0.132
	Age	−0.476	0.168	−2.82	4.77e−3	0.058
	Age × time	7.35e−3	0.068	0.11	0.914	0.967
Limbic	Time	−0.883	0.819	−1.08	0.281	0.500
	Age	−0.345	0.370	−0.93	0.351	0.522
	Age × time	0.079	0.150	0.53	0.596	0.933
Control	Time*	−1.854	0.558	−3.32	8.98e−4	7.70e−3	1,2,4
	Age	−0.893	0.319	−2.80	5.15e−3	0.058
	Age × time	4.32e−3	0.105	0.04	0.967	0.967
Control C/Default C	Time	−0.143	0.698	−0.20	0.838	0.894
	Age	0.202	0.286	0.71	0.479	0.666
	Age × time	−0.164	0.128	−1.28	0.200	0.847
Default	Time*	−1.665	0.652	−2.55	0.011	0.043	1,2,4
	Age	−0.723	0.298	−2.43	0.015	0.063
	Age × time	−0.132	0.123	−1.07	0.284	0.847
Proportion of peripheral nodes
Visual	Time	0.132	0.414	0.32	0.750	0.835
	Age	0.102	0.171	0.60	0.551	0.678
	Age × time	−0.072	0.076	−0.95	0.341	0.847
DorsAttn	Time	−0.665	0.483	−1.38	0.168	0.385
	Age	−0.225	0.187	−1.20	0.230	0.434
	Age × time	0.069	0.090	0.76	0.447	0.877
SomMot/SalVentAttn A	Time	−0.587	0.403	−1.46	0.145	0.356
	Age	−0.277	0.151	−1.83	0.067	0.164
	Age × time	0.020	0.075	0.27	0.787	0.933
SalVentAttn	Time*	−1.698	0.443	−3.83	1.28e−4	0.004	1,2,4
	Age	−0.576	0.215	−2.68	7.27e−3	0.058
	Age × time	0.151	0.083	1.83	0.068	0.847
Limbic	Time	−0.834	0.683	−1.22	0.222	0.426
	Age	−0.588	0.320	−1.84	0.066	0.164
	Age × time	0.166	0.125	1.33	0.183	0.847
Control	Time	−0.175	0.392	−0.45	0.655	0.835
	Age	−0.181	0.181	−1.00	0.317	0.507
	Age × time	−0.021	0.073	−0.29	0.775	0.933
Control C/Default C	Time	−0.487	0.550	−0.89	0.376	0.607
	Age	−0.328	0.253	−1.30	0.194	0.387
	Age × time	0.053	0.100	0.52	0.600	0.933
Default	Time*	−1.483	0.444	−3.34	8.39e−4	0.008	1,2,4
	Age	−0.479	0.209	−2.29	0.022	0.065
	Age × time	−7.88e−3	0.082	−0.10	0.924	0.967

^aUncorr, Uncorrected; FDR-adj, false discovery rate-adjusted; DorsAttn, dorsal attention; SomMot, somatomotor; SalVentAttn, salience/ventral attention.

^bValidation results: 1, effect remains significant (FDR-adjusted p < 0.05) after controlling for mean relative motion and number of volumes; 2, effect remains significant (FDR-adjusted p < 0.05) after repeating the analyses in a subset of participants (n = 68) with at least 150 volumes of good-quality imaging data (i.e., ≥5 min in length) remaining after scrubbing; 3, effect remains significant (FDR-adjusted p < 0.05) after maintaining equal scan lengths (123 volumes) across all participants; 4, effect remains significant (FDR-adjusted p < 0.05) after controlling for mean functional connectivity strength across all edges.

*Statistically significant effects (FDR-adjusted p < 0.05).

Association between cross-sectional and longitudinal changes in graph theoretical measures and cognition of healthy elderly

Among the graph theoretical measures that showed significant group differences between young and elderly, lower local efficiency and higher mean participation coefficient across all nodes were associated with worse attention performance, whereas higher mean participation coefficient in the dorsal attention/control A network was associated with worse global cognitive performance in the healthy elderly after controlling for the effects of age (Table 10). No cross-sectional associations were found for the other cognitive domains.

Table 10.

Cross-sectional analyses: coefficient estimates of multiple regression models showing a significant association between cognition and graph theoretical measures with significant young-elderly group differences^a

Predictor	Coefficient	SE	t	Uncorr p	FDR-adj p	Validation resultsb
Dependent variable: attention
Local efficiency	2.737	1.098	2.49	0.015	—	1,2,3,4
Mean participation coefficient	−2.970	1.139	−2.61	0.011	—	1,2,3,4
Dependent variable: global cognitive performance
DorsAttn/Control A	−2.004	0.669	−3.00	0.004	0.027	1,4

^aUncorr, Uncorrected; FDR-adj, false discovery rate-adjusted; DorsAttn, dorsal attention.

^bValidation results: 1, effect remains significant (global measures: p < 0.05; modular measures: FDR-adjusted p < 0.05) after controlling for mean relative motion and number of volumes; 2, effect remains significant (global measures: p < 0.05; modular measures: FDR-adjusted p < 0.05) after repeating the analyses in a subset of participants (young: n = 54; elderly: n = 68) with at least 150 volumes of good-quality imaging data (i.e., ≥5 min in length) remaining after scrubbing; 3, effect remains significant (global measures: p < 0.05; modular measures: FDR-adjusted p < 0.05) after maintaining equal scan lengths (123 volumes) across all participants; 4, effect remains significant (global measures: p < 0.05; modular measures: FDR-adjusted p < 0.05) after controlling for mean functional connectivity strength across all edges.

For graph theoretical measures that showed significant longitudinal changes in the elderly, no associations between graph theoretical measures and performance in any of the six cognitive measures were found.

Influence of motion, mean connectivity strength, and choice of methodology on findings

The above findings largely remained after accounting for the effects of motion and mean connectivity strength (Tables 4–10). Specifically, similar findings for both cross-sectional and longitudinal analyses were obtained even after: (1) controlling for mean relative motion and number of volumes; (2) repeating the analyses on the subset of participants with at least 5 min of imaging data after scrubbing; (3) repeating the analyses after maintaining equal scan lengths across all participants; and (4) controlling for mean connectivity. In addition, similar observations in module fragmentation were made particularly between young and elderly participants at baseline when repeating the analyses with equal scan lengths maintained across participants, where group differences in the modular structure between the two groups remained significant (Fig. 2-1; Fig. 2-2).

We also obtained largely similar findings after using different methodologies (Table 11): (1) repeating the cross-sectional analyses without performing global signal regression; (2) repeating both cross-sectional and longitudinal analyses using a different parcellation scheme (389 nodes); and (3) repeating both analyses using the group-level modular partition based on all young and elderly participants at baseline.

Table 11.

Comparison of findings using different methodologies^a

Measure	Change in methodology
	Group partition based on young + elderly at baseline, individual gamma = 2, Group gamma = 2	389 nodes, individual gamma = 2, Group gamma = 2	No global regression
Cross-sectional analysis
Global measures
Global efficiency	NA	Young > Elderly (trend; uncorrected p = 0.25)	Young > Elderly
Local efficiency	NA	Young > Elderly (trend; uncorrected p = 0.06)	Young > Elderly
Mean participation coefficient	Elderly > Young	Elderly > Young	Elderly > Young
System segregation	Young > Elderly	Young > Elderly	Young > Elderly
Modular measures
Participation coefficient	Elderly > Young in all modules	Elderly > Young in all modules, except DorsAttn/Control A	Elderly > Young in all modules, except SalVentAttn
Proportion of node types	Elderly > Young in connector hubs and satellite connectors of most modules	Elderly > Young in connector hubs and satellite connectors of most modules	Inconsistent differences in node types; elderly showed both increases and decreases in all node types relative to young adults
	Young > Elderly in provincial hubs and peripheral nodes of most modules	Young > Elderly in provincial hubs and peripheral nodes of most modules
Association with cognition in elderly	Worse attention performance associated with	Worse attention performance associated with	Worse attention performance associated with
	· Lower local efficiency	· Lower local efficiency	· Lower local efficiency (trend; uncorrected p = 0.06)
	· Higher mean participation coefficient	· Higher mean participation coefficient	· Higher mean participation coefficient (trend; uncorrected p = 0.16)
	Worse global cognitive performance associated with higher participation coefficient in Control/DorsAttn B (trend; uncorrected p = 0.08)	Worse global cognitive performance associated with higher participation coefficient in Control (uncorrected p < 0.05)
Longitudinal analysis
Global measures
Global efficiency	NA	Decrease with time	NA
Local efficiency	NA	Decrease with time	NA
Mean participation coefficient	Increase with time	Increase with time	NA
System segregation	Decrease with time	Decrease with time	NA
Modular measures
Participation coefficient	Increase with time in	Increase with time in	NA
	· SalVentAttn	· SalVentAttn
	· Default	· Default
	· Control	· Control (uncorrected p < 0.05)
Proportion of node types	Increased connector hubs and satellite connectors and decreased provincial hubs and peripheral nodes with time in	Increased satellite connectors and decreased provincial hubs with time in	NA
	· Default	· Default (uncorrected p < 0.05)
	· Control	· Control (uncorrected p < 0.05)

^aDorsAttn, Dorsal attention; SomMot, somatomotor; SalVentAttn, salience/ventral attention; TempPar, temporoparietal. The original analyses were performed on functional images with global regression done and using a functional parcellation scheme comprising 114 nodes. For the original cross-sectional analysis, the group-level partition was obtained using individual and group gamma of 2 and was based on all young participants. For the original longitudinal analysis, the group-level partition was obtained using individual and group gamma of 2 and was based on all elderly participants at baseline. Findings described in this table are significant effects (global measures: p < 0.05; modular measures: FDR-adjusted p < 0.05) unless otherwise stated.

Discussion

The present study used graph theory and community detection methods to examine cross-sectional and longitudinal changes in the cortical functional organization of healthy elderly. We found age- and aging-related decreases in the global measures of network integration, segregation, and distinctiveness. At the modular level, healthy elderly showed general loss of distinctiveness and segregation in all modules compared with young participants, but more specific longitudinal declines in the segregation of three higher-order cognitive modules: default mode network, salience/ventral attention network, and control network. Further, in the elderly, worse attention performance was associated cross-sectionally with lower local efficiency and higher mean participation coefficient, whereas worse global cognitive performance was associated with higher participation coefficient in the dorsal attention/control network. Importantly, the results largely remained, even after repeating the analyses controlling for other factors (e.g., motion, global signal, and mean connectivity strength) and using different brain parcellation schemes or modular partitions. Together, our findings from cross-sectional and longitudinal cohorts underscore declines in brain functional network segregation and distinctiveness, particularly within modules supporting higher-order cognitive functions.

Healthy elderly show global decreases in integration and segregation

Healthy elderly showed decreases in global and local efficiency with time and compared with young adults, indicating an overall age- and aging-related reduction in global integration and local segregation. Our findings are consistent with previous cross-sectional studies showing lower local efficiency in elderly compared with young adults (Achard and Bullmore, 2007; Song et al., 2014; Geerligs et al., 2015) and with increasing age (Cao et al., 2014), and suggests that aging is associated with a reduced ability for specialized processing within highly connected clusters (Rubinov and Sporns, 2010). In terms of global efficiency or network integration, whereas some studies have similarly demonstrated lower global efficiency in elderly compared with young adults (Achard and Bullmore, 2007; Gomez-Ramirez et al., 2015), others have reported no age-related changes in global efficiency (Cao et al., 2014; Song et al., 2014; Geerligs et al., 2015) or even age-related increases in global efficiency (Chan et al., 2014). In line with these inconsistencies, age- and aging-related effects on global efficiency were similarly observed to be weaker compared with local efficiency in our study. Nonetheless, given that the cross-sectional and longitudinal changes of global efficiency largely remained after accounting for the effects of other variables (e.g., motion) or changes in methodology, our findings provide limited evidence for global efficiency declines in healthy aging, suggesting deteriorating information integration as one ages (Rubinov and Sporns, 2010). However, while our findings showed some support for aging-related declines in local and global efficiency, it is important to note that the effects of time on global and local efficiency, unlike measures of distinctiveness, were not significant after maintaining equal scan lengths across participants. As such, our findings suggest that aging-related changes in global and local efficiency may not be as robust as aging-related changes in measures of distinctiveness (e.g., participation coefficient and system segregation).

Healthy elderly show decreases in module distinctiveness, especially in higher-order cognitive modules

Our study demonstrated age- and aging-related decreases in functional network distinctiveness at both the global and modular level. One major limitation of cross-sectional studies is that they are confounded by cohort effects and are able to model change with time only under circumstances of a perfectly stable environment and absence of cohort differences (Ryder, 1965; Schaie, 1965, 2005). To this end, longitudinal studies are advantageous because they are able to model intraindividual change as opposed to cross-sectional studies, which are only able to model interindividual differences (Schaie, 2005). Using linear mixed-effects models to model intraindividual changes, we showed that healthy aging was associated with global declines in segregation and distinctiveness, with elderly participants showing increased mean participation coefficient and decreased system segregation with time. In parallel, compared with young participants, we found that healthy elderly showed widespread loss of network segregation and distinctiveness as well as greater proportion of node types with high participation coefficient and lower proportion of node types with low participation coefficient across all modules. These cross-sectional group differences are largely consistent with previous findings (Betzel et al., 2014; Chan et al., 2014; Ferreira et al., 2016; King et al., 2018), although others have also found decreased segregation only in specific networks (Song et al., 2014; Zhang et al., 2014; Geerligs et al., 2015). However, while participation coefficient was increased across all modules in elderly compared with young, we instead found longitudinal increases in the participation coefficient of three higher-order cognitive networks: default mode, salience/ventral attention, and control networks. Similarly, the proportion of node types with high participation coefficient showed longitudinal increases, whereas the proportion of node types with low participation coefficient showed longitudinal declines in these three modules only.

Together, our findings thus indicate both general and network-specific aging-related declines in distinctiveness and segregation of the brain's functional network architecture. While our previous longitudinal study only examined connectivity changes in three networks and reported specific aging-related increases in internetwork connectivity between the default mode and control networks (Ng et al., 2016), our study used a system-level graph theoretical and community detection approach, which allowed us to characterize whole-brain connectome-wide functional network integrity by considering both intranetwork and internetwork connectivity across all modules. Using this approach, we additionally demonstrated aging-related system-level changes in the modular organization of the brain, as evidenced by aging-related increases in mean participation coefficient and decreases in system segregation. In line with this, we similarly showed greater fragmentation of the group-level modular structure, particularly in the higher-order networks, in the elderly with time and compared with young participants (Fig. 2). These whole-brain connectome-wide changes suggest that aging is associated with an overall decline in the distinctiveness and specificity of brain networks, which may in turn relate to reduced processing efficiency in the brain (Rubinov and Sporns, 2010). These findings are also in tandem with the notion that brain regions become functionally dedifferentiated with age, which is supported by numerous reports of over-recruitment and reduced selectivity of brain regions for specific cognitive functions in healthy elderly compared with younger adults (e.g., Park et al., 2004; Dennis et al., 2008; Goh et al., 2010). It has been suggested that less efficient neural processing between brain regions might be the basis for this dedifferentiation process in the elderly (Rypma and D'Esposito, 2000; Morcom et al., 2007; Rypma et al., 2007). The declines in processing efficiency brought about by reduced distinctiveness of brain networks might hence underlie the findings of reduced specificity and over-recruitment of brain regions during tasks in healthy elderly. Supporting this, a recent study (Chan et al., 2017) showed that age-related reductions in intrinsic topological distinction (measured by participation coefficient) between connector and nonconnector nodes were accompanied by age-related reductions in activation selectivity during task performance, most prominently within association and sensory-motor networks.

Additionally, our longitudinal findings revealed that the global changes in the brain's modular organization may in part be driven by specific declines in distinctiveness and segregation of the higher-order networks (default mode, control, and salience/ventral attention networks), with module fragmentation particularly pronounced in these networks (Fig. 2). The default mode, salience/ventral attention, and control networks are core networks thought to be of particular importance in the understanding of higher-order cognitive function and dysfunction (Menon, 2011). These networks are also among the key networks targeted in aging-associated diseases, such as Alzheimer's disease (Greicius et al., 2004; Seeley et al., 2009; Zhou et al., 2010) and cerebrovascular disease (Kim et al., 2016; Chong et al., 2017). Our findings thus highlight aging-related vulnerabilities of these cognitive networks to functional distinctiveness and segregation declines and underscore the importance of these networks in aging and disease.

Finally, while aging is accompanied by declines in functional distinctiveness and segregation of brain networks, the large-scale functional organization of the brain appears to remain relatively intact with age. In the current study, all group-level modular partitions regardless of age group or time point (i.e., young, elderly at baseline and at the second and third time points) showed high similarity to the a priori modular partition (Yeo et al., 2011). Moreover, modules identified in these partitions largely map to the same set of known functional networks (e.g., default mode network). This is consistent with studies reporting comparable network organization across the healthy adult lifespan (Chan et al., 2014, 2017), even when using age cohort-specific parcellations (Han et al., 2018). Nevertheless, we also noted that the magnitude of similarity to the a priori network partition decreased with age (young vs elderly at baseline) and with time (across time points in the elderly), especially for the higher-order networks. These findings therefore suggest that specific aging-related changes in the spatial topology of networks (especially within higher-order networks) exist, despite the qualitatively similar architecture throughout the lifespan.

Relationship between loss of functional segregation and distinctiveness and cognitive impairment

We additionally found some cross-sectional associations between cognitive performance and lower segregation and distinctiveness of healthy elderly. Specifically, elderly participants showed worse attention performance with lower local efficiency and higher mean participation coefficient, and worse global cognitive performance with higher participation coefficient in the dorsal attention/control network. These findings are in line with previous cross-sectional studies linking higher age-related internetwork connectivity and lower functional segregation, particularly in higher-order cognitive networks, to decreases in cognitive functions, such as executive function and memory (Chan et al., 2014; Geerligs et al., 2015). However, we did not find this association in processing speed, executive function, and visuospatial and verbal memory. This lack of association may likely be due to the narrower age range (58–84 years old) of participants with which we conducted our analyses, as opposed to past studies, which had examined brain-cognition associations over a wider age range spanning both young adults and elderly participants. In view of these mixed findings, our results provide some, albeit limited, cross-sectional evidence that loss of segregation and distinctiveness of functional modules might be predictive of age-related cognitive decline.

Moreover, longitudinal changes in measures of segregation and distinctiveness were not found to be associated with longitudinal declines in cognition. These findings differed from our earlier study (Ng et al., 2016), which reported in the same longitudinal elderly cohort a link between faster declines in processing speed and greater functional connectivity increases between the default mode and control networks with time. These discrepant observations suggest that aging-related declines in processing speed may perhaps be a consequence of increased connectivity between specific networks, rather than a general increase in connectivity of one network to all other networks (i.e., increased participation coefficient). However, this postulation remains preliminary and more longitudinal studies are required to shed light on the association between aging-related changes in cognition and aging-related changes in brain functional network architecture. In addition, our current study analyzed functional network changes using a group-level modular partition, which would allow for comparison of these changes in a consistent set of modules across participants. However, many studies have also demonstrated individual differences in the modular partitions of functional networks, particularly that of higher-order networks (Mueller et al., 2013; Gordon et al., 2017; Liao et al., 2017). As such, using group-level partitions may obscure functional network changes and their associations with cognitive decline. Future studies using individualized partitions could account for such individual variability and provide a more accurate characterization of aging-related brain-cognitive associations.

Limitations

Our study has several limitations. First, we probed longitudinal brain functional organization changes in participants aged >55 years. However, cross-sectional studies have shown that loss of functional network segregation and specialization is present at ages as early as 40 years (Betzel et al., 2014; Chan et al., 2014). Second, participants in this study were followed up 2 or 3 times over a relatively short period of 2–5 years, which does not allow reliable examination of nonlinear trends. Future longitudinal studies investigating changes in brain functional organization would benefit from tracking a broader age range of healthy participants over a longer follow-up period. Finally, we used motion scrubbing in this study to reduce the effects of motion. However, this resulted in unequal scan lengths across participants, which may influence the results. Nevertheless, we showed that our main findings of aging-related network segregation and distinctiveness loss remained even after repeating the analyses on images where equal scan lengths were maintained across all participants.

Conclusion

In conclusion, we found that healthy elderly showed cross-sectional and longitudinal reductions in network integration, segregation, and distinctiveness. Notably, healthy elderly showed reduced distinctiveness of all modules compared with young adults but showed only longitudinal declines in distinctiveness of three higher-order cognitive modules: control network, default mode network, and salience/ventral attention network, underscoring the importance of these networks in aging. Further, in the healthy elderly, worse attention performance was cross-sectionally associated with lower module segregation and distinctiveness, whereas worse global cognitive performance was cross-sectionally associated with lower distinctiveness in the dorsal attention/control network. Together, these findings highlight the utility of using longitudinal designs to study brain organization changes in the elderly and suggest that aging is associated with reduced functional segregation and distinctiveness, particularly in higher-order cognitive modules.