Quantitative Systems Pharmacology: An Exemplar Model‐Building Workflow With Applications in Cardiovascular, Metabolic, and Oncology Drug Development

Abstract

Quantitative systems pharmacology (QSP), a mechanistically oriented form of drug and disease modeling, seeks to address a diverse set of problems in the discovery and development of therapies. These problems bring a considerable amount of variability and uncertainty inherent in the nonclinical and clinical data. Likewise, the available modeling techniques and related software tools are manifold. Appropriately, the development, qualification, application, and impact of QSP models have been similarly varied. In this review, we describe the progressive maturation of a QSP modeling workflow: a necessary step for the efficient, reproducible development and qualification of QSP models, which themselves are highly iterative and evolutive. Furthermore, we describe three applications of QSP to impact drug development; one supporting new indications for an approved antidiabetic clinical asset through mechanistic hypothesis generation, one highlighting efficacy and safety differentiation within the sodium‐glucose cotransporter‐2 inhibitor drug class, and one enabling rational selection of immuno‐oncology drug combinations.

In the pharmaceutical industry, the pace of innovation in translational biology, pharmacological modalities, predictive personalized biomarkers, multiomics measurement technologies, and optimal therapeutic drug combinations in nearly all diseases combined with the ever‐present questions on dose posology in patient populations that are increasingly genetically and phenotypically characterized has continued to accelerate. In such a context, quantitative systems pharmacology (QSP), a mechanistically oriented form of drug and disease modeling that integrates data and knowledge, is proving to be increasingly impactful in model‐informed drug discovery and development.1 In this context, the impact of QSP continues to grow and is increasingly recognized within the pharmaceutical industry, from the early stages in drug discovery2, 3 to late‐stage development and life‐cycle management up to support of regulatory submission.4

QSP models integrate features of the drug (dose, dosing regimen, exposure or concentration at target site, potency, or a full pharmacokinetic submodel) with target biology; downstream effectors at the molecular, cellular, and pathophysiological levels; and possibly functional effector(s) of interest, such as a physiologically based pharmacodynamic study end point (Figure  1 a).

Figure 1.

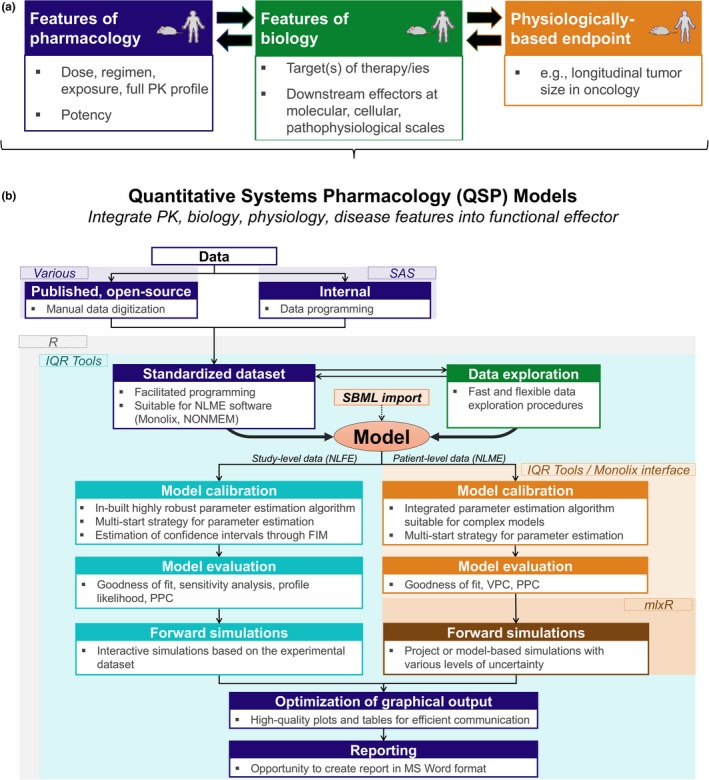
Quantitative systems pharmacology (QSP) model integrated features and development workflow (a) QSP models. (b) QSP model development workflow. NLME, nonlinear mixed‐effects; PK, pharmacokinetics; SBML, systems biology markup language. SAS, Statistical Analysis System; FIM, Fisher Information Matrix; PPC, PPC, Posterior Predictive Checks; VPC, Visual Predictive Check; NLFE, Nonlinear Fixed Effect.

QSP modeling has found multiple domains of use and impact in the industry. QSP models are often used to generate hypotheses and support a quantitative understanding of novel compound mechanism(s) of action, in a specific tissue, disease, or nonclinical experimental or clinical patient population context.1, 2, 4, 5, 6

QSP may further be used in optimizing doses and dosing regimens4, 7, 8 or in support of dose‐sequencing decisions for drug combinations9 given that a QSP model typically contains multiple effectors and at least one pharmacodynamic marker of interest—often the pharmacodynamic endpoint in a given study—downstream of the drug or compound target.

Mechanistically oriented QSP models also prove useful in placing biomarkers of efficacy, safety, or disease pathophysiology and phenotype in the appropriate quantitative and dynamic context for a therapeutic treatment of choice.5, 10, 11, 12, 13 In the course of QSP model development and testing, QSP modeling may help reconcile (or not) what, at a first glance, may appear as discrepancies in data, e.g., as obtained from different animal models or trials or discrepancies between in vitro and in vivo (nonhuman) findings or in vivo and clinical findings.14, 15 Broadly, QSP models may also be used to derive translational significance and to make inferences for compounds within a dynamic pathophysiological context captured in the model, e.g., from in vitro to in vivo (nonhuman) and from in vivo to human.16, 17, 18

QSP models are, arguably, most useful when used in quantitative comparative mode, for they provide a common drug‐exposure and disease “denominator” to perform fair comparisons. These include comparisons, often not mutually exclusive, of (i) a compound of interest in earlier discovery or development vs. forerunner(s) in later phases of development or on the market^19,20 or (ii) multiple choices in therapeutic modalities for a given target, motivated by the challenge of developing the better modality given desired metrics around efficacy, safety, the target patient population, and/or cost of goods, e.g., a small molecule vs. an engineered protein therapy vs. an a ribonucleic acid (RNA)‐based therapy21 or monotherapy vs. drug combination approaches, where the choices of compounds available and corresponding study designs typically grow exponentially, particularly in oncology and immuno‐oncology9, 22, 23, 24, 25 and in many other disease domains as well.26, 27 QSP models have also found use at the early drug‐discovery stage, for example, in optimizing the design of compound pharmacokinetic properties given the desired efficacy and/or safety metrics that can be simulated through the molecular, cellular, or pathophysiological “pharmacodynamic” portion of the QSP model.16, 28

We present several case studies that illustrate (i) the progressive maturation of a QSP modeling workflow focused on a seamless, high‐quality, efficient, multitechnique, semi‐industrialized environment enabling model development through to reporting; and applications ranging from (ii) cardio‐renal drug‐disease QSP‐derived mechanistic insights that corroborated novel clinical renal and cardiovascular outcomes for sodium‐glucose cotransporter (SGLT) inhibitors and subsequent simulations supporting their use in expanded indications such as heart failure; (iii) efficacy and safety differentiation between SGLT inhibitors in the treatment of type 2 diabetes combined with meta‐analyses illustrating the utility of multifactorial modeling approaches to address a drug class question; and (iv) the use of a preclinical, multiscalar molecular and cellular QSP approach tailored to support immuno‐oncology combination treatment decisions based on efficacy projections from the model.

QSP Workflow Description

Methodologically, QSP has not yet reached its full potential; it requires further maturation for definitions7, 10, 14, 16 and standardization and communication of QSP models to provide the timely delivery of high‐quality, reproducible, fit‐for‐purpose results.

To this end, we developed best practices for QSP based on cumulative knowledge and experience in applications,within a single, generalized, seamless, and practical workflow continuum29, 30, 31 (Figure  1 b). This workflow serves as a guide to data programmers and modeling scientists throughout the QSP data structuring and modeling process by providing a recipe with the minimal ingredients needed for a QSP modeling activity to proceed. In addition, each workflow component or tool should have certain features (Figure  1 b, panel‐bulleted lists) to allow a modeler to focus on analysis goals rather than on coding repetitive elements manually.

With such a workflow, we also aspire to progressively bring together QSP and population‐based, mixed‐effect pharmacometrics modeling, two approaches that have more modeling and computational techniques in common than not. For example, the distribution of a certain parameter value (e.g., reflective of interindividual variability) has become an important feature in QSP modeling and may benefit from related parameter estimation techniques borrowed from pharmacometrics modeling. Consequently, hybrid models combining mechanistic and population modeling have emerged and proven necessary for applicability toward practical problems in pharmaceutical research and development. Such models require a workflow and associated tools to enable model development and qualification, with flexible switching from a simplified QSP model without variability, to a QSP model with some variability and uncertainty features included, to possibly a full nonlinear mixed‐effects (NLME) model, depending on the questions to be addressed and the data available. Furthermore, although QSP models are typically assumed to be, as the examples shown here are, composed of ordinary differential equations, the proposed workflow likely has applicability to models with agent‐based32 and partial differential equation (diffusion‐like) components.33 In each case, the crux of the workflow is to enable an efficient means of incorporating information, performing simulations and evolving parameter estimates to best fit the portfolio of source data.

Any modeling task is built around some form of knowledge, including experimental data. Hence, the workflow we developed begins with data programming to convert various types of raw data into a standard format that constitutes the basis for all subsequent data exploration and modeling tasks. Because the data used in QSP and population modeling often share similarities in terms of dosing records, observations, covariates, and multiple individuals or experiments, a key factor in this initial step is to develop a common underlying data format that may be used for QSP and NLME types of models. An important advantage derived from such a master, standardized data set format is that data programming from source data is greatly accelerated, cheaper, and less prone to errors. In addition, it greatly decreases the time required for data exploration, which usually precedes model development per se, making this initial step a highly automated task. By efficiently exploring data, a modeler may assess whether (i) data from different experimental settings indeed differ as expected, (ii) data from a given experimental setting or scenario but described in different records or publications are consistent, and (iii) there would be clear trends in the data that a model would need to account for from the onset of model development. For some of these questions, it might be useful to simulate a model with a priori parameters then interactively visualize the data with model simulations. The manual adjustment of model parameter values may give a first impression of where to expect differences between prior knowledge vs. the information provided within the data.

Although the model together with experimental data form a basis for parameter estimation, QSP modeling is often associated with heterogeneous data sets collected from multiple data sources with differing experimental conditions and designs. One important related feature of a QSP modeling tool is its ability to handle different values of the same model parameter across different experimental conditions—both in estimation and simulation. Once such a multiconditional model is set and linked to the data, it is important to keep track of key characteristics of the data: Is the residual error of the data already known? Which observation and error model should be assumed? Are values below limit of quantification correctly handled by the parameter estimation method that is available in the workflow tool?

The parameter estimation procedure is a cornerstone of model development and presents multiple challenges. Typically, the estimation procedure may yield several solutions that describe the observed data equally well while being different in terms of parameters and the corresponding mechanisms by which the model explains the data. Depending on the estimation problem, it might be highly unlikely to find the best solution after only one fit. Our workflow proposes a multistart strategy for parameter estimation that provides several key insights, for example, in how many ways can the data be explained by the model? Does parameter estimation work reliably and robustly? Furthermore, even if parameter estimation converges reliably, the parameters might not necessarily be identifiable. The Fisher information matrix—which should routinely be evaluated—often provides the necessary information on nonidentifiable parameters. However, there are situations in which the asymptotic standard errors, as provided by the Fisher information matrix, look reasonable, yet not all parameters are identifiable. To address this challenge, we propose to use a profile likelihood method34 to investigate parameter identifiability and to compute confidence intervals.

If parameters turn out to be poorly constrained by the data, the question arises as to whether a new assay or study may provide the missing information to best fill knowledge gaps or identifiability issues. There is, however, no standard procedure to construct such an experiment. Upon consideration of the different solutions found with the multistart optimization approach, the Fisher information matrix35 and the profile likelihood,36 new experimental designs may be evaluated and pursued based on the currently available information.

Each step in the model development and qualification process, from data exploration to forward simulations, should also be supported by companion visualization tools such as high‐quality plots and tables, with goodness‐of‐fit plots being an essential means necessary for model evaluation and tables concisely summarizing modeling results to allow for efficient communication with teams and stakeholders. Finally, to improve transportability and reproducibility, a QSP workflow should enable flexible model export or import, to or from repositories, with systems biology markup language being a commonly used format.37

The conceptual workflow may be established into practice using a variety of model development tools. We evaluated the performance and model development capabilities of multiple packages, mainly focusing on the R software environment and including mrgsolve,38 RxODE39 and IQR tools.40 Each package was tested on three different QSP models developed using study‐level data with substantial mechanistic details and nonlinear features by executing the established workflow step by step for each model, testing for solver speed (for a numerical solution of the Ordinary Differential Equations (ODE) system), quality of visualization, parameter estimation algorithms, model diagnostic options, and compatibility with companion workflows of pharmacometrics.41 We summarize the main findings in Table  1 .

Table 1.

Comparison of R‐based quantitative systems pharmacology modeling workflow features

Functionality	IQRtools	mrgsolve	RxODE
Standardized data set	Yes—flexible data set suitable for heterogeneous data	Yes—flexible data set suitable for heterogeneous data	No—no predefined data set structure
Data exploration	Yes—designated functions available	Yes—designated functions available	No—requires manual implementation
Translation to NLME software	Yes—IQR modeling project can be translated to Monolix, NONMEM, and NLMIXR; projects can be executed and results are postprocessed	No	Yes—works with NLMIXR
Integrated parameter estimation tool	Yes—fully integrated likelihood‐based parameter estimation tool	No—requires additional R packages (e.g., minqa, RcppDE, GenSA, etc.) and manual implementation of objective function	No—requires additional R packages (e.g., minqa, RcppDE, GenSA, etc.) and manual implementation of objective function
Model diagnostics	Yes—automatic simulations vs. the data and goodness of fit plots	Yes—available through model simulations based on data set‐derived event tables	No—requires manual simulations vs. experimental data
Model simulations	Yes	Yes	Yes—the fastest simulation tool
Local sensitivity analysis	Yes—requires additional programming	Yes—fully automated through designated functions	Yes—requires additional programming
Identifiability analysis	Yes—calculation of FIM and evaluation of profile likelihood	No	No
User interface	Yes—available as an add‐on	No	No

NLME, nonlinear mixed‐effects.

When considering all required tool components of a state‐of‐the art QSP workflow, as described previously, mrgsolve and RxODE may be considered primarily as simulation engines, not yet as fully equipped QSP workflow tools. These two packages may certainly be used within a modeling workflow but would require a modeler to provide all other missing pieces on their own. IQR tools proved capable of supporting a flexible and efficient QSP workflow.

Case Study 1: Cardio‐Renal Drug‐Disease QSP Modeling Enabled Mechanistic Insights Into Renal and Cardiovascular Clinical Outcomes for SGLT2 Inhibitors

The scope and application of QSP models range from simpler models (single pathway or mechanism), developed for a specific application, to integrative drug‐disease models of interconnected organ systems developed over time and used repeatedly for multiple applications. An example of the latter is the repeated application of an integrative model of cardiovascular and renal function.12, 42, 43, 44, 45 In brief, this model describes the hemodynamics of blood flow through the kidney, filtration and reabsorption of substances along the nephron, the resulting whole‐body balance of fluid and electrolytes, the distribution of body fluid and sodium between the blood and interstitium, systemic blood pressure, and the neurohormonal systems regulating these processes—including the renin‐angiotensin‐aldosterone system (RAAS).46 The process of QSP drug‐disease model development has been described elsewhere.5, 47 Here we focus on the application of the presented workflow for using an existing QSP drug‐disease model for a new application.

Scoping

Recent cardiovascular outcomes studies, including [Empagliflozin] Cardiovascular outcome event trial in Type 2 diabetes mellitus patients (EMPA‐REG),48 CANagliflozin cardioVascular Assessment Study (CANVAS),49 and Dapagliflozin Effect on CardiovascuLARE EVENTS (DECLARE)50 have shown, unexpectedly, significant improvements in cardio‐renal outcomes with SGLT2 inhibitors. Prior to these trials, Vallon and Thomson51 had proposed SGLT2 as a critical mechanism in initiating diabetic hyperfiltration, which is linked with faster progression of chronic kidney disease. When the first of these trials read out, the Hallow group was in the process of using the cardio‐renal QSP model to understand and explore these hyperfiltration mechanisms; the role of SGLT2 was demonstrated mathematically.44 With the publication of the unexpectedly positive EMPA‐REG results in 2015, the search was on to understand the mechanisms of both cardiovascular (primarily heart failure) and renal benefits with SGLT2 inhibition; numerous mechanisms were proposed,52 with limited experimental or clinical data available to evaluate them.

Fortuitously, a previously conducted drug–drug interaction (DDI) study of dapagliflozin and bumetanide had collected daily urinary excretion data of sodium, glucose, water, and other substrates as well as serum measures of creatinine and sodium concentrations. We sought to couple these data with the existing cardio‐renal QSP model to test various hypothesized renal mechanisms of SGLT2 inhibition and to determine which mechanism or combinations of mechanisms were most consistent with the observed data.53 We expected that this analysis would improve our understanding of the renal benefits of SGLT2 inhibition but did not anticipate, initially, insight into the protective effects in heart failure. However, this analysis provided, ultimately, mechanistic insights into both, as we have described previously.53, 54 We continue to use the model to further explore the cardiac effects of SGLT2 inhibition.

Data standardization and exploration

A DDI study of the urinary biomarker response to dapagliflozin in healthy subjects was the primary data set used in this analysis; it was maintained in the standard NONMEM format to facilitate ease of analysis and visualization with existing codes. However, for QSP models, data for informing the model mechanisms and behavior come not only from clinical or experimental studies of the compound at hand but also from the existing literature, which provides a necessary and valuable source of additional data to constrain or to validate model components and predictions. For the literature studies used, we did not have subject‐level data but, instead, used measures of mean and variance of reported variables. Thus, rather than a single master data set, these literature data were stored in a separate data set, similar to NONMEM in format, but that allowed the tracking of additional important information, including variance measures, experimental design notes, journal, and author, and so on. Data values were obtained either directly from publication tables or by the digitization of publication figures.

An additional aspect of data standardization that must be considered with drug‐disease models is the quality of literature data used. In cardio‐renal pharmacology, as in many fields, there is quite a large body of literature, and studies vary widely in quality. It is important for the modeling scientist to become familiar with the literature body, but it is equally critical to have input from experts in the field who can identify the most important studies, identify groups and labs who produce quality work, provide context, and explain the nuances and limitations of experimental designs and measurement procedures. For instance, tubular micropuncture studies in rodents have provided valuable information for informing tubular reabsorption rate constants and validating model‐predicted changes in tubular pressure in the cardio‐renal model. However, the procedure requires a high degree of experience and expertise, and data should only be used from labs with established expertise in this method.

Describing any one single study can result in bias and overfitting. When multiple high‐quality studies are available, it is best to include each of them in the data set. For example, in Figure  2 a, each observed value represents the mean response from a single drug/dose combination for a particular study of drugs targeting the RAAS pathway. Rather than fitting any one single study and drug/dose combination, parameters are optimized using data from all of the studies together.

Figure 2.

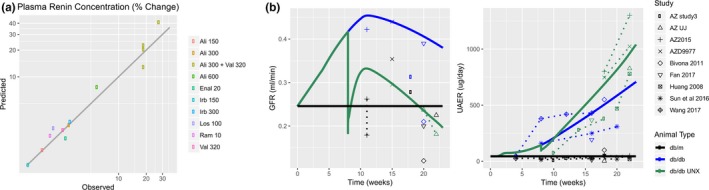
Case study 1. (a) When multiple high‐quality literature studies are available, each study should be included and used in parameter estimation to avoid bias and overfitting to a single study. Each observed value represents the mean plasma renin concentration (PRC) response from a single drug/dose combination for a particular study of drugs targeting the renin‐angiotensin‐aldosterone system (RAAS) pathway. In a model of the RAAS pathway, parameters defining negative feedback on renin secretion were estimated by simultaneously fitting the response to all studies rather than fitting to an individual study. (b) When a single study measuring all timepoints and variables of interest is not available, it is often possible to combine data from multiple studies to generate a composite time course. The time courses of glomerular filtration rate (GFR; left), urinary albumin excretion rate (UAER; right), and other variables (not shown) in db/db and db/db uninephrectomized (UNX) mice were assembled from multiple studies that measured these variables at some but not all times of interest. A quantitative systems pharmacology (QSP) model of diabetic kidney disease progression was calibrated by fitting these composite time courses (points and dashed lines = data; solid lines = model). AZ, AstraZeneca; Ali, aliskiren; Val, valsartan; Irb, irbesartan; Los, losartan; Enal, enalapril; Ram, ramipril db/db; db/m ‐ are not abbreviations. they are standard names for those mouse models

Often, a single study defining the time course of the response may not be available, and all variables of interest may not be measured. For example, we recently used the cardio‐renal model progression of proteinuria in a db/db uninephrectomy mouse model of chronic kidney disease. A single study measuring glomerular filtration rate (GFR) and urinary albumin excretion rate during the full time of interest was not available; however, we were able to piece together the time course by combining internal experimental results with published studies to form db/db mouse models (Figure  2 b).

In the current analysis, in addition to fitting the DDI data in healthy subjects, we used published data to validate the model response by predicting observed changes in urinary glucose excretion (UGE), GFR, and mean arterial pressure in diabetic subjects with moderate renal impairment treated with dapagliflozin.55

Model development/refinement and parameter estimation

In this analysis, our goal was to evaluate the ability of various proposed renal mechanisms of SGLT2 inhibition to explain the observed biomarker response. We were primarily interested in explaining the central tendency in multiple end points simultaneously (glucose, water, and Na⁺ excretion; serum Na⁺; and creatinine) rather than describing the sources of intersubject variability in response to a particular end point. We first estimated the pharmacodynamic parameters for dapagliflozin inhibition of SGLT2 by fitting the UGE response—a direct indicator of SGLT2 inhibition. We then simulated other measured variables, under different hypothesized mechanisms: (i) direct SGLT2 inhibition only, (ii) glucose‐induced osmotic diuresis, and (iii) coupled inhibition of SGLT2 and sodium‐hydrogen antiporter 3 (NHE3). With SGLT2 inhibition alone, all variable responses except UGE were underestimated. Adding osmotic diuresis in the model improved the fit of water and Na⁺ excretion; however, it could not adequately describe the serum creatinine response (osmotic diuresis was modeled from first principles and thus did not require parameter estimation). We thus added an additional effect of SGLT2 inhibition on NHE3—a feature mechanistically supported by preclinical evidence. The model could then appropriately capture the serum creatinine response as well, with only an 8% maximum inhibition of NHE3. This magnitude is consistent with preclinical experimental data.

Overall, the three mechanisms together adequately explained all of the observed data, with one notable exception: plasma sodium concentration. The model predicted a rise in electrolyte‐free water clearance with dapagliflozin (i.e., water cleared in excess of sodium), and this was verified with the experimental data. Conservation of mass indicates that when more water than sodium is removed from the system, sodium concentration should go up; however, no change in sodium concentration was observed. This suggested a missing mechanism for removal of sodium from the circulation. Recent studies have brought to light the role of nonosmotic peripheral sodium storage in regulating sodium balance.56 Thus, we updated the model with a peripheral nonosmotic sodium storage compartment. This allowed the model to capture the flat serum sodium concentration. In addition, we found that the inclusion of this mechanism altered the relative removal of fluid from the blood and interstitium in ways that are likely to be beneficial in volume‐overloaded patients at risk for heart failure. For more details, see the primary publications of these results.53, 54

Seek independent validation of hypothesized mechanisms

Because our understanding of nonosmotic peripheral sodium storage is still emerging, when we added this third compartment there were concerns that we were simply overfitting to the current data set. When adding hypothesized mechanisms to a drug‐disease model, healthy skepticism is warranted, and looking for ways to independently validate the need for that mechanism is highly recommended. To further validate the existence of this compartment, we applied the model to another drug that produces electrolyte‐free water clearance (tolvaptan) using a study in which water and sodium intake and excretion time courses were all measured. We found that this third compartment was necessary to explain the blood Na⁺ concentration in this study as well, providing confidence that this is a genuine, generalizable mechanism.

Use literature values as reality check for estimated parameter values

Another principle of QSP parameter estimation is that, whenever possible, the model fit should be qualified by comparing estimated parameter values with experimentally measured values. As an example, we are currently extending the cardio‐renal model to reproduce states of heart failure in which interstitial edema is an important factor. To achieve this, we are updating the model to more fully describe the mechanical and chemical forces governing fluid movement between the blood and interstitium. We recently found that by fitting the parameters in this updated model, we were able to precisely describe the observed left ventricular pressure‐volume loops in heart failure and the shift in these loops in response to treatment with an ACE inhibitor. However, the estimated value for the capillary ultrafiltration coefficient was two orders of magnitude lower than experimentally measured values—and clearly unreasonable. Further thought and inspection revealed that a parameter we had previously assumed to be constant—because it would change little in normal or hypertensive subjects—was likely to change significantly in heart failure. We were able to identify a published experimental study that could be used to define and constrain a new relationship, which then allowed us to describe the pressure‐volume loops in heart failure using a reasonable estimate for the ultrafiltration coefficient. This type of reality check of parameter values is critical, and the values differing widely from experimental values should not be ignored.

When updating a QSP model, ensure consistency with all previous calibration/validation work

When applying existing drug‐disease QSP models to new problems, it is critical to ensure that the model remains consistent with the body of data used to develop the model. Although we do not have one single master data set, we use a master validation script that steps through each of the critical simulations used to date in developing the model and produces a PDF file of visualizations that can be easily checked to ensure appropriate model behavior. Some examples of checks included in our current validation script for the cardio‐renal model are the following:

• 1
  Baseline “healthy subject” values for all measurable variables fall within the expected normal range (see examples in Figure  3 ). At the same time, all feedback mechanisms are at their set point at baseline, i.e., the “normal” behavior is not being forced by feedback control. This provides confidence that baseline parameters are such that they provide homeostatic baseline behavior. For example, parameter values for each component of the renal vascular resistances (afferent, efferent, etc.) are calculated so that renal blood flow and glomerular hydrostatic pressure fall naturally at their normal value (at normal mean arterial pressure) and are not being forced to their set point by the action of feedbacks such as the tubuloglomerular feedback or RAAS.

  Figure 3.

  

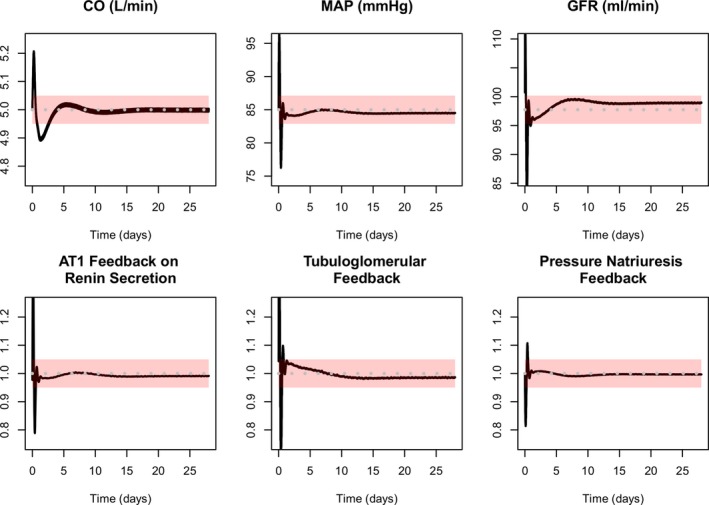  Examples of automated checks of baseline model behavior. Each time the model is updated, a validation script is run and visualizations are produced to facilitate convenient verification of appropriate model behavior. In this example, all variables should settle to values within the pink bands, and a result falling outside these ranges indicate a problem with the model update. Black lines = simulations. Gray dashed line = setpoints. Pink bars = acceptable ranges. Top row shows cardiac output (CO), mean arterial pressure (MAP), and glomerular filtration rate (GFR) all settle near their setpoint, within the acceptable range. Bottom row shows key feedback mechanisms are close to 1 (no effect), confirming that the variables in the top row are not being forced to their setpoints by extreme feedback values. Angiotensin II receptor type 1 (AT1)

• 2The baseline “healthy subject” responds as expected to perturbations. When cardiac demand is increased, the model smoothly and quickly approaches the new set point without oscillations or overshoot. Similarly, when Na⁺ intake is changed, the model smoothly and quickly achieves sodium balance.
• 3. The s

  imulations of the plasma biomarker and mean arterial pressure response to previously calibrated therapies, in hypertensive virtual patients, matches the clinically observed responses (see Figure  2 a).

• 4. The d

  ynamics of renal disease progression remain consistent with previous calibrations using preclinical data (Figure  2 b) and validation with clinical data on rates of GFR progression.

• 5Key clinical trials used to validate portions of the model are still reproduced. For example, the model reproduces the expected change in urinary albumin creatinine ratio and GFR over time, as observed in the reduction of endpoints in NIDDM with the Angiotensin II Antagonist Losartan (RENAAL) study.57

A critical step in the QSP workflow is the documentation of updates and changes to the model. Drug‐disease QSP models are developed iteratively, and each application provides improved constraint and/or extends the applicability of the model. However, this can only occur if the learning from each iteration are retained, the next time the model is used. Thus, data and calibration/validation scripts used should be added to the master validation script as soon as it is complete so that when the next application or iteration of the model takes place, one can ensure that the model remains consistent with the data and behavior determined in the current analysis.

Simulation, visualization, and reporting

After following the aforementioned steps and reaching a final model consistent with the available clinical data, literature data, and our current state of understanding of physiology, the next step consists in generating simulations appropriate for communication of findings on renal mechanisms of SGLT2 inhibition. We used simulations to demonstrate that the combination of SGLT2 inhibition, NHE3 suppression, and osmotic diuresis produced reductions in glomerular hydrostatic pressure that provide an explanation for the observed renal benefits. In addition, prospective simulations with the model indicated that SGLT2 inhibition reduces interstitial fluid volume to a greater extent than blood volume—an experimentally testable hypothesis that may explain the positive effects of these drugs on heart failure hospitalization. These results were communicated through both presentations and peer‐reviewed publications.53, 54 Importantly, this differential volume mechanism lent decision support to development teams weighing the hypothesis that SGLT2 inhibitors would demonstrate clinical benefit in heart failure and slowing renal disease progression, both indications now pursued in several outcomes trials.

Case Study 2: A Renal QSP Framework Enabled Efficacy and Safety Differentiation Among SGLT Inhibitors

Scoping

Type 2 diabetes mellitus (T2DM) is a common metabolic disorder characterized by abnormally high plasma glucose concentration, resulting from resistance to insulin, defects in insulin synthesis, or both.58 T2DM is treated with diet, exercise, and medications that restore sensitivity to insulin, stimulate insulin secretion by pancreatic β‐cells, or decrease glucose absorption from the gastrointestinal tract. Sodium‐glucose cotransporter inhibitors (SGLT inhibitors; gliflozins) are a recently approved class of antidiabetic medications that inhibit glucose reabsorption in the kidney, reduce plasma glucose, and lower hemoglobin glycated hemoglobin (A1c).59 Although different gliflozins were each shown effective and well tolerated in placebo‐controlled, randomized clinical trials, their comparative safety and effectiveness is challenging to determine without a large head‐to‐head clinical study. Having accurate in‐class differentiation is critical to decision making by physicians, payors, formularies, and regulatory agencies but is often studied with meta‐analyses that rarely seek to incorporate mechanistic pharmacological and physiological explanations for the similarities or differences between the class members.

Model development/refinement and parameter estimation

In this case study, we highlight the use of a QSP fit‐for‐purpose model progressively building from first understanding the physiology of the diabetic kidney, then to the mechanistic basis of pharmacological differences in SGLT inhibitors, and finally to demonstrating how such a model can couple to and enhance non‐QSP modeling methodologies (e.g., meta‐analysis).

The development of a quantitative drug‐disease systems model mechanistically describing renal glucose filtration and SGLT‐mediated reabsorption was guided by well‐known physiology and literature on renal glucose excretion.60 The model includes a plasma compartment, renal compartments for proximal convoluted and straight tubule (each characterized by differential expression of SGLT transporters), and a bladder compartment where glucose in urine is collected. The pharmacokinetics and pharmacodynamics (glucosuria) of major SGLT inhibitors were incorporated into the model to reproduce gliflozin mechanism of action and subsequent effects on UGE both in healthy and T2DM subjects (Figure  4 a).

Figure 4.

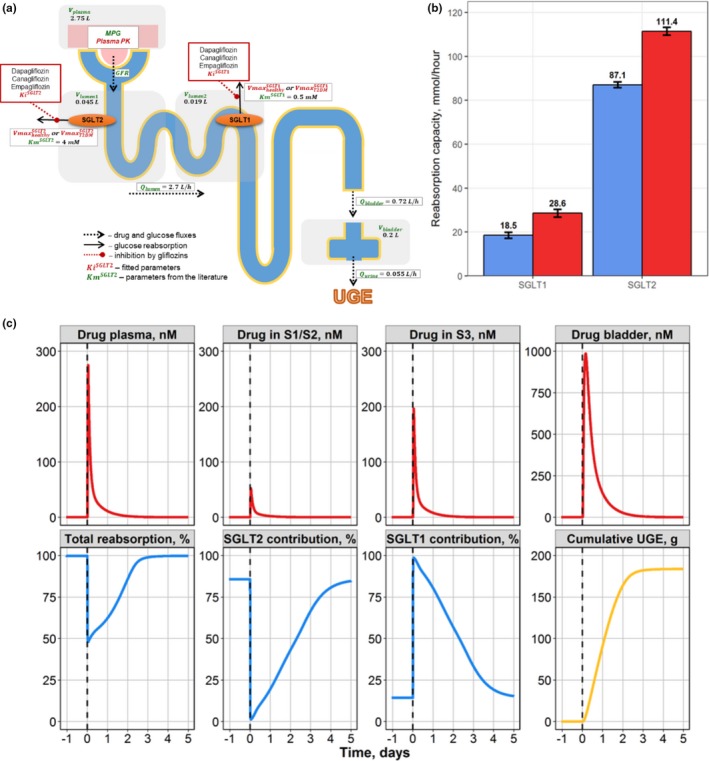
Case study 2. (a) Schematic of drug‐disease quantitative systems pharmacology model for glucose filtration, reabsorption, and excretion. (b) Model‐predicted maximal SGLT1/2 contribution to glucose reabsorption in healthy (blue) and T2DM subjects (red). (c) Compensatory response of the SGLT1 transporter during SGLT2 inhibition by a single 10‐mg dose of dapagliflozin in T2DM subjects. Model simulations of dapagliflozin concentration time profiles in plasma, S1/S2, and S3 proximal tubule segments and bladder, with total reabsorption rate and contributions from each of the SGLT1 and SGLT2 transporters toward renal reabsorption and cumulative urinary glucose. UGE, urinary glucose excretion. T2DM – type 2 diabetes mellitus; S1/S2 denotes 1st and 2nd segments of the proximal tubule respectively; S3 denotes 3rd segment of the proximal tubule; SGLT1 – sodium‐dependent glucose cotransporter 1; SGLT2 – sodium‐dependent glucose cotransporter 2; MPG denotes mean glucose concentration in plasma; GFR – glomerular filtration rate; – urine formation flow; – physiological flux for distal tubules; – physiological flux for proximal tubules; – bladder volume; – plasma volume; – volume of segments of the kidney proximal tubule; reflects the maximum rate of renal glucose reabsorption through an SGLT transporter; Ki are inhibition constants for gliflozins; Km denotes Michaelis constant of glucose affinity

Seek independent validation of hypothesized mechanisms

The predictive power of the model was demonstrated through several benchmarks with experimental data, including showing that simulated UGE and glucose reabsorption align well with the data collected from healthy and T2DM subjects undergoing a stepwise hyperglycemic clamp procedure with and without dapagliflozin treatment (Figure  4 b).61, 62

Simulation, visualization, and reporting

Importantly, using the model to uncover the dynamic shift to SGLT1‐mediated reabsorption resolved an apparent paradox between the large SGLT2‐mediated contribution (~80%) to renal glucose resorption in healthy subjects and only a 30–50% decrease in reabsorption in T2DM patients treated with a SGLT2 inhibitor (Figure  4 c). SGLT2 inhibition upstream dynamically leads to an increased availability of glucose for the SGLT1 transporters located further downstream in the tubule thus changing the effective role of SGLT1 in the development of glucosuria. As a result, less‐selective SGLT2 inhibitors (e.g., canagliflozin) may have clinically important differences arising from SGLT1 inhibition unlike the more selective dapagliflozin and empagliflozin. Although this may be beneficial to maximize UGE and glycemic control, it may also lead to tolerability issues as a result of increased glucosuria and SGLT1 inhibition in nonrenal tissues.

As described previously, SGLT inhibitors improve glycemic control by promoting urinary glucose excretion; therefore, patients taking them may be a greater risk glucosuria‐related adverse events (AEs) such as genital mycotic infections or urinary tract infections.63, 64 Without a head‐to‐head trial, quantitative comparisons of glucosuria‐related AEs between dapagliflozin and canagliflozin have been performed with traditional meta‐analyses65, 66, 67 however, none have considered the dose‐dependent or drug‐to‐drug glucosuria differences as factors in the models. A recent meta‐analysis by our group examined the proportions of patients in the clinical development studies of dapagliflozin and canagliflozin who then experienced glucosuria‐related AEs.68 Large phase 3 clinical trials such as those curated with the meta‐analysis did not broadly record UGE in the patient population, thus it remains challenging to assess the glucosuria–AE response relationship. In a novel approach, glucosuria predicted from the aforementioned QSP model was incorporated in the meta‐analysis as a study arm covariate for normalizing the AE rates to test if glucosuria differences were responsible for the differences in AE rates.

Placebo‐adjusted, but not glucosuria‐normalized, risk differences for mean model estimates of male and female genital mycotic infections incidences showed that patients receiving canagliflozin were 2‐fold to 14‐fold more likely to suffer a genital mycotic infection than patients receiving dapagliflozin. Despite glucosuria normalization, the differences between dapagliflozin and canagliflozin remained, therefore suggesting that factors beyond glucosuria are likely involved in the AE differences between these two drugs.

Case Study 3: QSP Modeling Deepened Mechanistic Understanding and Enabled Rational Selection of Immuno‐Oncology Drug Combinations

Scoping

Modeling in support of preclinical and clinical drug development in oncology has traditionally been focused on the optimization of dose and scheduling using semiempirical, semimechanistic models primarily focused on the characterization of tumor‐size dynamics as an end point.69, 70, 71 Part of the challenge in achieving successful QSP modeling applications in oncology is the weak preclinical‐to‐clinical translatability—or direct scalability—of experimental data, from mouse (the typical preclinical study system of choice for efficacy) to human in particular. This creates a systematic knowledge gap between the detailed mechanistic understanding around an oncology target in a rodent experimental model and its alignment within the proper pathophysiological context in a human cancer indication of interest.72 The rise of immunotherapies supported by regulatory approvals of cytotoxic T‐lymphocyte‐associated protein 4 (CTLA‐4), programmed cell death protein 1 (PD‐1), programmed death‐ligand 1 (PD‐L1) immune checkpoint inhibitors has brought forward additional mechanistic challenges, with the need to consider multiple immune biology events at molecular and cellular levels dynamically interacting, directly or indirectly, with tumor biology and growth, in multiple bodily compartments, including tumor tissue, and with a plethora of “druggable” immune biology targets that may result in antitumor effects.73 These challenges, reflective of a highly dynamic, multicompartment, multiscale, multiplayer environment make immuno‐oncology an attractive “target” for QSP modeling and its applications.74, 75, 76 A systems approach is needed to address the ever‐present questions on dose, scheduling, and sequencing (for combinations),77 now linked to the challenges of predicting antitumor responses through both indirect (immune mediated) and direct (targeted and Standard of care (SoC)) tumor cell kill, while searching for drug combinations that may overcome intrinsic or acquired resistance to existing treatments.78

In the preclinical development of antitumor immuno‐modulatory compounds, knowledge around the mechanism(s) of action is typically derived from syngeneic (immuno‐competent, inbred) mice inoculated with various histocompatible tumor cell lines,79 providing data on tumor‐size responses and the occasionally matched circulatory or tumor tissue biomarker dynamics under various experimental therapies. Despite the relative wealth of such data, quantitative modeling remains challenging given it needs to include a mechanistic description of the cancer immunity cycle, which is characterized by highly dynamic and interactive biological processes, with a vast variety of factors influencing them.80, 81

Model development/refinement and parameter estimation

Capturing most mechanistic details of the cancer immunity cycle while preserving model identifiability, adequate parameter calibration, and predictive power would require an unrealistic amount of detailed molecular‐level and cellular‐level data next to longitudinal tumor‐size profiles. One approach we found actionable to overcome part of this enormous challenge is to use a population QSP modeling strategy, whereby the available mechanistic data, along with longitudinal tumor‐size data, are exploited at the individual animal‐level data in addition to NLME modeling.82, 83, 84 Population QSP modeling thus aims at remaining sufficiently mechanistic (Figure  5 a) while minimizing the number of parameters to be calibrated to preserve model identifiability and predictive power—which can be achieved by taking interindividual variability into account in the model. Longitudinal tumor‐size responses in syngeneic mice, in fact, display large interindividual variability in stark contrast to the tumor‐size data typically seen in immuno‐compromised mouse models. Owing to its mechanistic nature, and upon adequate NLME treatment to adequately describe existing data, the population QSP model may actually point to biological or physical parameters explaining most of the observed variability—these may, in turn, become key parameters to focus on and map to relevant biomarkers when developing a novel therapy.

Figure 5.

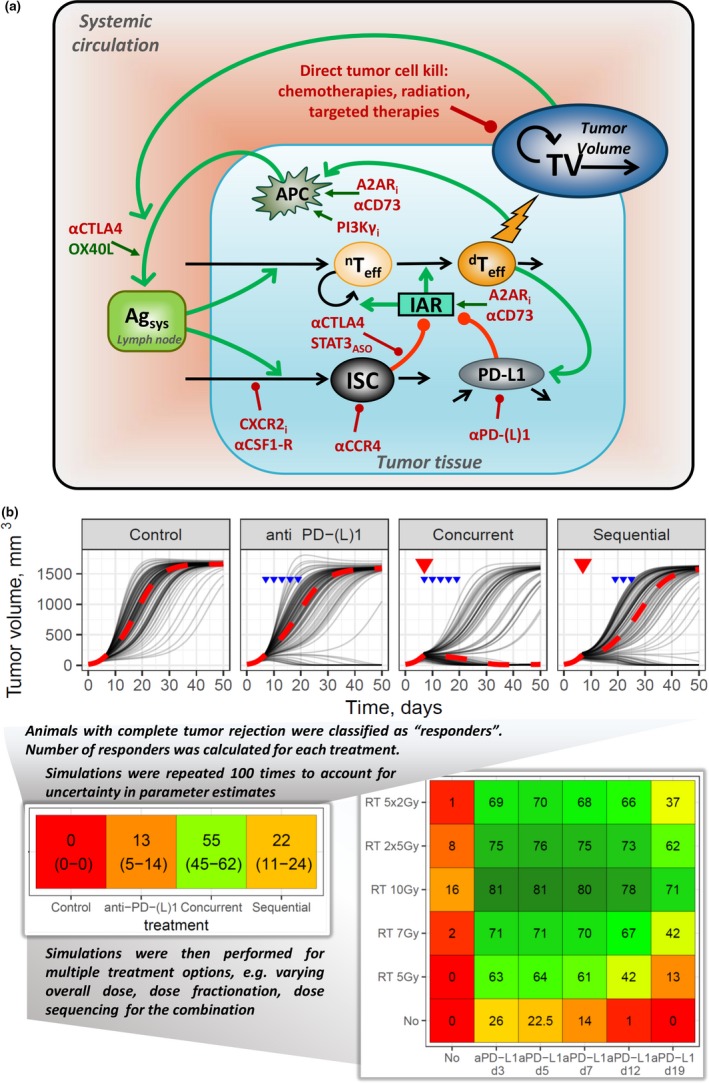
Case study 3. (a) Population quantitative systems pharmacology model of immuno‐oncology. Multiple molecular targets modulating immuno‐suppression and immuno‐activation in the tumor microenvironment are represented as well as direct tumor cell kill mechanisms. Green lines = stimulation; red lines = inhibition, regulation; black lines: variable turnover. (b) Simulations using the quantitative systems pharmacology model. A sample of model simulations is shown, for the following treatment scenarios: (i) control isotype mAb, (ii) anti‐PD‐(L)1 (10 mg/kg 3 q.w., blue arrows) monotherapy treatment, (iii) radiation therapy (RT; 5 Gy, red triangles) + anti‐PD‐(L)1 (10 mg/kg 3 q.w., blue arrows) given concurrently, (iv) RT3 (5 Gy, red triangles) + anti‐PD‐(L)1 (10 mg/kg 3 q.w., blue arrows) given sequentially. Thin gray lines represent individual responses, and dashed red lines represent population median. Per treatment scenario, a total of 2,000 virtual experiments were simulated; each virtual experiment included 100 individual animals. To evaluate an efficacy metric with respect to treatment response, a responder was defined as an individual animal with a tumor volume of ≤10 mm³ at day 50 of treatment; median efficacy for each treatment scenario was estimated with a 90% confidence interval (shown in brackets). Cell colors on the heatmap map to median efficacies: red = no response; orange = 50% responders in the corresponding treatment scenario; green = 100% responders. T _eff, effector T cells; IAR, immune activation rate function; ISC, immune suppressive cells function; APC, antigen‐presenting cells; TV, tumor volume; Ag_sys, systemic antigen level. mAB, monoclonal antibody; anti‐PD‐(L1), anti‐programmed cell death protein 1 or anti‐programmed death ligand 1 antibody; aCTLA4, anti‐cytotoxic T‐lymphocyte‐associated protein 4 antibody; q.w., once weekly; aCD73, Ecto‐5'‐nucleotidase (CD73) inhibitor; A2ARi, Adenosine A2A receptor inhibitor; OX40L, OX40 ligand; CXCR2i, CXCR2 inhibitor; aCSF1‐R, Colony stimulating factor 1 receptor (CSF1‐R) inhibitor; STAT3ASO, Signal transducer and activator of transcription 3 (STAT3) antisense oligonucleotide (ASO); PI3Kgi, phosphoinositide 3‐kinase gamma (PI3Kg) inhibitor

We developed such a population QSP model to characterize synergistic treatment effects when combining radiotherapy (RT) and PD‐(L)1 inhibitors.22 Experimental data on tumor‐size dynamics in CT26 syngeneic mice were used based on the following treatment arms: (i) control isotype mAb, (ii) anti‐PD‐L1 (10 mg/kg 3 q.w.), (iii) fractionated 5 × 2 Gy dose of RT, and (iv) RT and anti‐PD‐(L)1 combination treatment using concurrent and sequenced schedules. In such a setting, we determined that the addition of only one random effect on a parameter quantifying the ability of effector T cells to respond against a systemic antigen level is sufficient to adequately describe the interindividual variability observed in both monotherapy (PD‐(L)1 inhibitor or RT alone) and combination experiments.22

Seek independent validation of hypothesized mechanisms

There are multiple ways to test the predictive power of models, including QSP models. Arguably, an external validation exercise, which makes use of outcome data not used in the calibration phase of model development, is the more robust validation approach. In the present work, we used multiple data sets for external model validation, including (i) a single 7‐Gy dose of RT monotherapy and in combination with anti‐PD‐L1 (10 mg/kg 3 q.w.); (ii) fractionated 3 × 4‐Gy RT monotherapy and in combination with anti‐PD‐L1 (10 mg/kg 3 q.w.); (iii) combination therapy of fractionated 5 × 2‐Gy RT and anti‐PD‐L1 treatment (10 mg/kg 3 q.w.), with and without administration of an anti‐CD8 antibody; and (iv) PD‐L1 expression levels upon RT monotherapy (5 × 2 Gy) and RT + anti‐PD‐1 combination. The QSP model adequately reproduced all of these outcome data (tumor‐size dynamics) for these additional experimental conditions, demonstrating the model's ability to predict individual tumor‐size responses to de novo monotherapy and combination treatment regimens. Simultaneously, the model provided corresponding mechanistic insights of the underlying molecular and cellular dynamical interplays in tumor tissue.22

Predictive simulations for dose and sequencing optimization

The population QSP model, although sufficiently mechanistic (capturing dynamically the beneficial immune‐activating effect of low‐dose fractionated radiation), remained identifiable and was used to perform predictive simulations aimed at identifying optimal treatment sequences and schedules for RT and anti‐PD‐(L)1 agents. Thus, the administration of an anti‐PD‐(L)1 monoclonal antibody concurrently with RT resulted in a rapid increase in the level of mature dendritic cells as well as a gradual activation and accumulation of cytotoxic T lymphocytes in tumor tissue. These cellular biomarker events represent a dynamic, transient window of opportunity for the maximization of therapeutic benefit. Interestingly, such antigen exposure, although certainly necessary, may not be sufficient for generating an effective overall immune response. Hence, tumor microenvironment conditions that prevail immediately following RT intervention combined with a more rapid maturation of dendritic cells appear crucial to achieve an overall antitumor effect.22

In a subsequent step of the analysis, the population QSP model was used to perform predictive simulations aimed at quantifying such a transient window of opportunity to identify an optimal dose and sequencing of RT and anti‐PD‐(L)1 combination treatment. To this end, the availability and functionalities of a semi‐industrialized modeling workflow for trial simulations, with both variability and uncertainty being quantitatively accounted for in the model, are of tremendous help in expanding the number of possible treatment scenarios and their corresponding simulations (Figure  5 a). In the exemplar case featured here, multiple preclinical trial simulations could be performed in silico, strongly supporting concurrent schedule treatment scenarios when RT and anti‐PD‐(L)1 are used in combination.22

Moreover, such a model‐based evaluation of preclinical results may provide a basis for useful inferences in support of early clinical programs. For example, preclinical simulations of various RT and anti‐PD‐(L)1 combination schedules, based on realistic baseline conditions of immune cells and tumor size at start of treatment, point in favor of a concurrent schedule in terms of response optimization, consistent with the results obtained in early clinical trials.85, 86 The value of such a preclinical‐to‐clinical translation is, at most, of a qualitative nature. Building a quantitative inference to the clinic using such a population QSP model would require adjustments of the model in two specific aspects. The first aspect is structural in reducing the overall number of systems parameters so that the model remains identifiable given the parameter estimation procedure to be rerun would rely on clinical output (longitudinal tumor size) data that are typically more sparse than preclinical data. A submodel of tumor‐size dynamics adequately describing the heterogeneity typical found in human tumors—and one that is not overparameterized—is also needed. The second aspect is parametric, to reestimate systems parameter values (including appropriate expression levels of immune checkpoints and turnover rates of specific T cells in human) against the longitudinal tumor‐size data in human.87

Predictive simulations for in silico screening of therapeutic combinations

Another utility of such a systems model is to use it in addressing the “inverse problem”88—in this case, in identifying immuno‐oncology drug combinations with synergistic efficacy effects. With successive updates of the population QSP base model and based on biomarker and longitudinal tumor‐size response data subsequently to modulation of novel immuno‐oncology targets (novel mechanisms of action) mapped to immuno‐suppressive and immuno‐activating cells in the tumor microenvironment, we obtained robust estimates of systems‐related parameters controlling the immune and tumor‐cell dynamical behavior within the cancer immunity cycle.23 These updates resulted in the incorporation of a variety of mechanisms of action into the model (Figure  5 a) mapping to the following: (i) immuno‐suppression and immuno‐activation mechanisms (CTLA‐4, PD‐1/PD‐L1, CC chemokine receptor 4 (CCR4), Colony stimulating factor1 receptor (CSF1‐R), OX40, a member of tumor necrosis factor receptor superfamily; of the effector and regulatory T cell axis, (ii) other mechanisms (C‐X‐C Motif chemokine receptor 2 (CXCR2); Signal transducer and activator of transcription 3(STAT3); Ecto‐5'‐nucleotidase (CD73); phosphoinositide 3‐kinase gamma (PI3Kg); mitogen‐activated extracellular signal‐regulated kinase (MEK)) pertinent to the modulation of other immune cell types in the tumor microenvironment, and (iii) direct tumor cell kill mechanisms (through standard chemo, targeted, or radiation therapies).9, 24, 25

With these robust systems‐related parameter estimates and inherent immune–immune and immune–tumor–cell dynamics captured, we used the population QSP model to predict cellular biomarker and tumor‐size responses following a range of double and triple combination therapies23 (Table  2 ). Importantly, in such a population framework, different sets of baseline immune conditions can be chosen (including with realistic variability at baseline) either to mimic specific syngeneic mouse models or to describe certain immune setpoints within the tumor in a realistic manner, as prevalent in the clinic for specific cancer indications and patients—e.g., immunologically hot vs. cold tumors89—to then predict antitumor response at individual and study levels. This may qualitatively inform the corresponding clinical development strategy, e.g., in supporting the choice of a cancer indication, a phenotype of patients within that indication, a choice of combinations, and/or a concurrent vs. sequenced administration of the combination.

Table 2.

Population quantitative systems pharmacology model simulations of efficacy responses under various drug monotherapy and combination scenarios involving test antibodies against selected targets (PD‐L1, CTLA‐4, OX40, CXCR2) (fifth column) and a range of baseline conditions materialized in the model by different amounts of the different immune cell types (T_eff, T_reg, myeloid‐derived immuno‐suppressive cells, or MDSC) at the start of treatment (second to fourth columns), which are characteristic of the different types of syngeneic tumor models commonly used in IO preclinical research (first column)

Tumor type	Teff	Treg	MDSC	Treatment	Efficacy, %responders
MCA205‐like	+	+/−	++	αPD‐L1	34
				αCXCR2	18
Rhabdomyosarcoma‐like				OX40L	14
				αPD‐L1 + αCXCR2	94
				αPD‐L1 + OX40L	91
CT26‐like	+	++	+/−	αPD‐L1	0
				αCTLA‐4	0
				αPD‐L1 + αCTLA‐4	98
				αCTLA‐4 + OX40L	6
				αPD‐L1 + OX40L	4
				αPD‐L1 + αCXCR2	0
4T1‐like	+	+	++	αCTLA‐4	0
				αPD‐L1 + αCTLA‐4	22
				αPD‐L1 + OX40L	0
				αPD‐L1 + αCXCR2	0
				αCTLA‐4 + αCXCR2	0
				αPD‐L1 + αCTLA‐4 + αCXCR2	99
B16/F10‐like (poorly immunogenic)	+/−	+/−	+	αPD‐L1 + OX40L	1
				αPD‐L1 + αCTLA‐4	9
				αPD‐L1 + αCTLA‐4 + OX40L	74

To derive an efficacy metric at cohort level (sixth column), we computed the percentage of responding animals in the cohort (%responders), “responder” being arbitrarily defined as an animal exhibiting a tumor volume < 100 mm³ at day 50 of the simulated treatment. IO, immuno‐oncology; MDSC, myeloid‐dervied suppressor cell; MCA205, mouse fibrosarcoma cell line; CT26, mouse colerectal carcinoma cell line; 4T1, mammary carcinoma; B16/F10, melonoma cell line

In summary, a mechanistic QSP model of the cancer immunity cycle was developed. A population QSP approach was adopted to capture the inherent variability seen in preclinical in vivo data—the approach also helped in keeping such models sufficiently mechanistic yet identifiable given the typical data encountered in this immuno‐oncology context (tumor‐size dynamics under control and treatment conditions and the occasional molecular and cellular immune biomarker data). Through the successive updates of the population QSP model using data from multiple perturbations of the system materialized by novel therapies directed at specific immuno‐oncology targets, robust estimates of essential systems parameters reflecting immune cell infiltration and immune‐immune and immune‐tumor‐cell interactions were obtained. Subsequently, predictive simulations in the preclinical domain addressing questions around mechanisms of action, sources of interactions leading to efficacy under novel combination treatments, and corresponding dose regimen or dose sequencing optimization could be performed in a quantitative manner. Furthermore, by setting realistic baseline (pretreatment) conditions around the desired immune setpoints, qualitative simulations and inferences could be performed to inform the corresponding early‐stage clinical strategy, including supporting the choice of a cancer indication of a patient phenotype within that indication of a therapeutic combination.

Conclusion

In this review, we presented an exemplar QSP modeling workflow along with a diverse set of case studies showcasing the impact of QSP in tackling the perennial industry challenges of indication expansion, comparative effectiveness, and optimization of combination therapies. In the first example, QSP modeling of the pathophysiology and drug mechanisms identified an unexpected pharmacological difference in how SGLT2 inhibitors act to deplete interstitial, but not plasma fluid, volume. In so doing, this supported investments in trials for SGLT2 inhibitor use in renal and cardiovascular indications. Although this model was not encoded exclusively in IQR tools, it was developed within and over time and served as the prototype analysis that defined the proposed workflow. The other two examples were developed in the workflow with the use of IQR tools. In each example, the detailed information regarding the models developed and implemented in the case studies are available in the primary publications of each analysis.

Furthermore, the examples demonstrate that QSP is not a methodology unto itself but, rather, an approach that can be combined powerfully with other techniques. Across the biopharmaceutical industry, many problems arise that require bespoke modeling; however, efforts such as ours reinforce the potential for semi‐industrialization to enable us to focus increasingly on the science rather than the software.

Funding

The work presented here was funded by AstraZeneca.

Conflict of Interest

G.H., L.C., D.W.B., and R.C.P. are employees of AstraZeneca and may own shares. K.P. and Y.K. are owners, and V.S., V.V., T.Y., I.A., and A.D. are employees of M&S Decisions LLC, a modeling research consultancy contracted by AstraZeneca. H.S. is owner and D.K. is an employee of IntiQuan GmbH, a modeling research consultancy contracted by AstraZeneca. K.M.H. is an associate professor at Georgia State University, Athens, GA, and has received research funds from AstraZeneca.