Using a reaction‐diffusion model to estimate day respiration and reassimilation of (photo)respired CO ₂ in leaves

Summary

• Methods using gas exchange measurements to estimate respiration in the light (day respiration $R_{\mathrm{d}}$) make implicit assumptions about reassimilation of (photo)respired CO ₂; however, this reassimilation depends on the positions of mitochondria.

• We used a reaction‐diffusion model without making these assumptions to analyse datasets on gas exchange, chlorophyll fluorescence and anatomy for tomato leaves. We investigated how $R_{\mathrm{d}}$ values obtained by the Kok and the Yin methods are affected by these assumptions and how those by the Laisk method are affected by the positions of mitochondria.

• The Kok method always underestimated $R_{\mathrm{d}}$. Estimates of $R_{\mathrm{d}}$ by the Yin method and by the reaction‐diffusion model agreed only for nonphotorespiratory conditions. Both the Yin and Kok methods ignore reassimilation of (photo)respired CO ₂, and thus underestimated $R_{\mathrm{d}}$ for photorespiratory conditions, but this was less so in the Yin than in the Kok method. Estimates by the Laisk method were affected by assumed positions of mitochondria. It did not work if mitochondria were in the cytosol between the plasmamembrane and the chloroplast envelope. However, mitochondria were found to be most likely between the tonoplast and chloroplasts.

• Our reaction‐diffusion model effectively estimates $R_{\mathrm{d}}$, enlightens the dependence of $R_{\mathrm{d}}$ estimates on reassimilation and clarifies (dis)advantages of existing methods.

Introduction

Quantifying respiration is important for accurately predicting net ecosystem productivity, as respiratory losses can account for ≤ 40% of gross primary production (Gifford, 2003). At the leaf level, respiration in the light, also called ‘day respiration’ ($R_{\mathrm{d}}$), is an important term in the model of Farquhar, von Caemmerer & Berry (‘FvCB model’; Farquhar et al., 1980), which is used widely as the basic model component for predicting ecosystem productivity. Unlike leaf respiration in the dark ($R_{\mathrm{dk}}$), day respiration occurs simultaneously with photosynthetic CO₂‐assimilation and is difficult to determine by gas‐exchange measuring systems. Uncertainties have arisen over years with regard to, for example, whether $R_{\mathrm{d}}$ differs from $R_{\mathrm{dk}}$ and whether $R_{\mathrm{d}}$ varies with different conditions (Griffin & Turnbull, 2013). Efforts continued recently in updating the biochemical processes underlying $R_{\mathrm{d}}$ (Tcherkez et al., 2017a,2017b;) and in how to better measure or quantify this parameter (Buckley et al., 2017; Farquhar & Busch, 2017; Tcherkez et al., 2017a,2017b; Gong et al., 2018; Way et al., 2019).

Techniques have been developed to measure $R_{\mathrm{d}}$ directly (Loreto et al., 1999, 2001; Pärnik & Keerberg, 2007; Gong et al., 2015; Tcherkez et al., 2017a; Gauthier et al., 2018), but these techniques usually require access to sophisticated and expensive isotope discrimination measuring devices and are often unavailable. Methods exist to indirectly estimate $R_{\mathrm{d}}$ in C₃ leaves from conventional gas‐exchange measurements (Kok, 1948; Laisk, 1977; Brooks & Farquhar, 1985), sometimes combined with chlorophyll fluorescence measurements (Yin et al., 2009). The Laisk method (Laisk, 1977; Brooks & Farquhar, 1985) has become the most common one. It explores the linear part of several $A_{\mathrm{N}}-C_{\mathrm{i}}$ curves at low C _i concentrations ($C_{\mathrm{i}}$ is the intercellular CO₂ partial pressure), measured at difference irradiances. The negative net CO ₂ assimilation rate $A_{\mathrm{N}}$ at the point at which the linear $A_{\mathrm{N}}-C_{\mathrm{i}}$ curves intersect is the estimated $R_{\mathrm{d}}$. $C_{\mathrm{i}}$ at the intersection point ($C_{\mathrm{i}}^{\ast }$) is often used as the CO₂ compensation point ${\mathrm{\Gamma }}^{\ast }$, at which the amount of CO₂ produced by photorespiration equals the amount of CO₂ consumed by ribulose biphosphate (RuBP) carboxylation. The theoretical basis of the Laisk method is the FvCB model:

$$A=\frac{(C_{\mathrm{c}}-{\mathrm{\Gamma }}^{\ast })X_1}{C_{\mathrm{c}}+X_2}-R_{\mathrm{d}},$$ (Eqn 1)

where $C_{\mathrm{c}}$, is the CO₂ partial pressure at the carboxylating sites of Rubisco. The terms $X_1$ and $X_2$ depend on whether carboxylation is limited by Rubisco activity, electron transport (Farquhar et al., 1980), or triose phosphate utilization (Sharkey, 1985). If it is limited by electron transport, $X_1$ is a function of incident irradiance ($I_{\mathrm{inc}}$) and Eqn (Eqn 1) can generate the Laisk plot. However, theoretically, the Laisk method works only if $C_{\mathrm{c}}=C_{\mathrm{i}}$. This was a common assumption at the time when the method was proposed as mesophyll resistance (r _m) was then believed to be negligible compared with stomatal resistance to CO₂ transfer (r _s). Nowadays, r _m (and its inverse, mesophyll conductance g _m) is proven to be relevant under a wide range of conditions and across different species (Evans et al., 1986; Flexas et al., 2008; Niinemets et al., 2009). Consequently, there is a large CO₂ gradient between the intercellular spaces and the chloroplasts (Von Caemmerer & Evans, 1991; Von Caemmerer et al., 1994):

$$C_{\mathrm{c}}=C_{\mathrm{i}}-\frac{A_{\mathrm{N}}}{g_{\mathrm{m}}}.$$ (Eqn 2)

Combining the nonlinear Eqn (Eqn 1) and the linear Eqn (Eqn 2) results in a solution in which $A_{\mathrm{N}}-C_{\mathrm{i}}$ curves at different irradiances will not necessarily intersect at the same value of the $A_{\mathrm{N}}$ axis. Tholen et al. (2012) pointed out that the method of calculating g _m according to Eqn (Eqn 2) implicitly assumes that CO₂ produced by respiration and photorespiration (which will be called ‘(photo)respired CO₂’ hereafter), and the CO₂ molecules from intercellular air‐spaces experience the same mesophyll resistance. However, (photo)respired CO₂, if being reassimilated, probably experiences the chloroplast resistance component (r _ch) only. By contrast, the CO₂ molecules from intercellular air‐spaces experience cell wall and plasma‐membrane resistance (r _wp) as well as r _ch (the sum of r _wp and r _ch makes the total r _m). Therefore, Tholen et al. (2012) concluded that $g_{\mathrm{m}}$ as defined by Eqn (Eqn 2), is an apparent parameter. They demonstrated that if this scheme for r _m resistance components is considered, there is no guarantee that A _N–C _i curves at different $I_{\mathrm{inc}}$ will intersect at the same C _i and at the same $A_{\mathrm{N}}$. This implies that $R_{\mathrm{d}}$ estimated by the Laisk method may depend on the resistance scheme, which, in turn, depends on the cellular position of (photo)respired CO₂ release (see later in this Introduction). Moreover, as pointed out by Yin et al. (2011), the Laisk method has the practical problem that all measurements are at lower than ambient‐air CO₂ concentrations (C _a), requiring the correction of gas exchange data for CO₂ leakage (Flexas et al., 2007).

An alternative method to estimate $R_{\mathrm{d}}$ is the Kok method (Kok, 1948). This method exploits the fact that the response of $A_{\mathrm{N}}$ to irradiance is approximately linear at low irradiances. $R_{\mathrm{d}}$ is calculated as the intercept of this linear relationship. However, at irradiances close to the light compensation point or lower, this slope may become steeper (Kok, 1948; Farquhar & Busch, 2017; Tcherkez et al., 2017a). In order to avoid this so‐called Kok effect, irradiances under which this method is applied should be above this breakpoint (Brooks & Farquhar, 1985). If evaluated from the electron‐transport limited form of Eqn (Eqn 1), the Kok method actually assumes that the quantum yield of Photosystem II electron transport (${\mathrm{\Phi }}_2$) is constant over the same range of irradiances. However, ${\mathrm{\Phi }}_2$ has been observed to decline with increasing irradiances (Genty & Harbinson, 1996) even under low‐irradiance conditions (Yin et al., 2011, 2014). To account for this decline, Yin et al. (2009) proposed a method which also exploits the $A_{\mathrm{N}}-I_{\mathrm{inc}}$ curve at low irradiance, but combines it with simultaneously measured chlorophyll fluorescence to assess ${\mathrm{\Phi }}_2$, and $R_{\mathrm{d}}$ is estimated as the intercept of the linear regression of $A_{\mathrm{N}}$ vs ${\mathrm{\Phi }}_2{I}_{\mathrm{inc}}/4$. To distinguish it from the Kok method, it has been called the Yin method (Tcherkez et al., 2017b). Theoretically, both Kok and Yin methods work only for nonphotorespiratory conditions (Yin et al., 2011), or for photorespiratory conditions if C _c is made to be constant across irradiance intensities. They are sometimes also used for photorespiratory conditions where C _c varies, because usually the plot of measured $A_{\mathrm{N}}$ vs I _inc or vs ${\mathrm{\Phi }}_2{I}_{\mathrm{inc}}/4$ seems linear.

However, when the Yin or Kok methods are applied directly to photorespiratory conditions where only $C_{\mathrm{a}}$ is controlled, the problem associated with the variation of C _i or C _c with $I_{\mathrm{inc}}$ may become relevant. This is because linear regression of $A_{\mathrm{N}}$ against $I_{\mathrm{inc}}$ (Kok method) or against ${\mathrm{\Phi }}_2{I}_{\mathrm{inc}}/4$ (Yin method) implicitly assumes that C _c does not vary with $I_{\mathrm{inc}}$ within the data range used. The present understanding of stomatal conductance (g _s) and g _m shows that g _s and g _m can have very low values at low $I_{\mathrm{inc}}$; when combined with the FvCB model, the low g _s and g _m values predict that C _c decreases sharply with increasing $I_{\mathrm{inc}}$ within the low $I_{\mathrm{inc}}$ range (Farquhar & Busch, 2017). It is known also that a combined FvCB and conductance model can implicitly account for reassimilation of (photo)respired CO₂ (Von Caemmerer, 2013). Therefore, both the Kok and Yin methods, when applied to photorespiratory conditions, may implicitly assume that there is no reassimilation of (photo)respired CO₂ as they assume that C _c remains constant under a range of low light intensities. In fact, there is both experimental (Loreto et al., 1999; Haupt‐Herting et al., 2001; Pärnik & Keerberg, 2007; Busch et al., 2013) and theoretical (Tholen et al., 2012; Ho et al., 2016; Berghuijs et al., 2017; Yin & Struik, 2017) evidence that a substantial fraction of the (photo)respired CO₂ is used for RuBP carboxylation in the chloroplasts before it can escape to the atmosphere. If recycling of CO₂ is not accounted for to determine $R_{\mathrm{d}}$, the true $R_{\mathrm{d}}$ is possibly underestimated (Loreto et al., 1999; Gong et al., 2018). Instead of using simple linear regressions, using the combined FvCB and g _m model to fit types of experimental data (that each method relies on) under photorespiratory conditions would give an estimation of R _d while simultaneously considering reassimilation. However, r _m, let alone its components, r _wp and r _ch, is not known beforehand. In fact, an estimation of r _m or g _m would require an estimate of R _d beforehand (Harley et al., 1992; Yin & Struik, 2009).

According to the resistance model of Tholen et al. (2012), the fraction of reassimilation of (photo)respired CO₂ depends on the relative magnitude of individual resistance components along the path from leaf surface to Rubisco carboxylation sites. These resistances include r _s, r _wp, r _ch and r _cx, where r _cx is carboxylation resistance that can be expressed from Eqn (Eqn 1) as $(C_{\mathrm{c}}+X_2)/X_1$ (Tholen et al., 2012). Because at least r _s and r _cx are known to depend on CO₂ concentration and irradiance, reassimilation also may be affected by environmental variables. A similar statement can be made for any impact of physiological parameters on reassimilation. Yin & Struik (2017) extended the model of Tholen et al. (2012) and pointed out that the fraction of reassimilation of (photo)respired CO₂ not only depends on the relative magnitude of the resistance components but also on intracellular arrangements of chloroplasts and mitochondria. They highlighted that the impact of such intracellular arrangements of organelles is hard to be dealt with by resistance models when the chloroplast coverage of mesophyll areas is low. The resistance model of Tholen et al. (2012) assumes either that there is no CO₂ gradient in the cytosol (Tholen et al., 2014) or that the mitochondria are located in a cytosol layer between the cell wall and the chloroplasts (Berghuijs et al., 2015, 2016). In reality, the mitochondria are mostly located between the chloroplasts and the tonoplasts (Hatakeyama & Ueno, 2016), intimately associated with chloroplasts (Sage & Sage, 2009). Previous studies (Berghuijs et al., 2017; Xiao & Zhu, 2017; Yin & Struik, 2017) showed that the modelled position of mitochondria relative to the chloroplasts can substantially affect $A_{\mathrm{N}}$, reassimilation of photorespired CO₂ and $g_{\mathrm{m}}$.

The CO₂ diffusion pathway between the intercellular airspaces and the chloroplasts is rather complex. Various methods to estimate R _d and other physiological parameters of the FvCB model make simplifying assumptions about this pathway. Such simplification results either in not considering the reassimilation of (photo)respired CO₂ at all or in implicit assumptions about the location of (photo)respired CO₂ release. This problem can be avoided by using reaction‐diffusion models that describe the CO₂ diffusion pathway within mesophyll cells in sufficient detail that they do not have to make these implicit assumptions.

Most reaction‐diffusion models for photosynthesis (Tholen & Zhu, 2011; Ho et al., 2016; Retta et al., 2017; Xiao & Zhu, 2017) are complex and have lengthy computational times. We previously developed a simple reaction‐diffusion model that can be used as an alternative to mesophyll resistance‐based models to estimate photosynthetic parameters (Berghuijs et al., 2017). Here we will use this model as a tool to assess whether the Kok method, the Yin method and the Laisk method underestimate R _d due to their assumptions with regard to reassimilation. Given that reassimilation and mesophyll resistance are affected by the assumed position of the mitochondria relative to the chloroplasts (Berghuijs et al., 2017; Xiao & Zhu, 2017), any assumption about the location of mitochondria in mesophyll cells may affect the estimates of the photosynthetic parameters. Therefore, we will also identify the most likely position of the release of (photo)respired CO₂, relative to the position of the chloroplasts.

Materials and Methods

Experimental data

We used published datasets from two experiments (Berghuijs et al., 2015; Ho et al., 2016), both consisting of simultaneous measurements of gas exchange and chlorophyll fluorescence (Table 1). The Berghuijs et al. (2015) dataset contains measurements taken from the distal leaflet from 15‐ and 25‐d‐old leaves from the tomato (Solanum lycopersicum) cultivars Admiro, Doloress and Growdena. The Ho et al. (2016) dataset contains measurements taken from leaves of the same cultivars as in the experiment of Berghuijs et al. (2015). For each cultivar, two types of leaflets were used for measurements. The first was the distal leaflet of the uppermost fully expanded leaf (the ‘upper leaf’). The second was the most distal leaflet from a leaf four layers below the upper leaf (the ‘lower leaf’). In both experiments, gas exchange measurements were taken under photorespiratory and nonphotorespiratory conditions; but leaf anatomical measurements were taken in the experiment of Berghuijs et al. (2015) only.

Table 1.

Overview of the two experimental datasets used in this study

Source:	Berghuijs et al. (2015)	Ho et al. (2016)
Cultivars:	Admiro, Doloress, Growdena	Admiro, Doloress, Growdena
Leaf types:	15‐d‐old leaves, 25‐d‐old leaves	Upper leaves, lower leaves
Anatomical measurements:	Yes	No
A − C a curves
PR	I inc = 1500 μmol m−2 s−1 O = 21 kPa	I inc = 1000 μmol m−2 s−1 O = 21 kPa
NPR	I inc = 1500 μmol m−2 s−1 O = 2 kPa	I inc = 1000 μmol m−2 s−1 O = 2 kPa
A − I inc curves
PR	C a = 40 Pa O = 21 kPa	C a = 38 Pa O = 21 kPa
NPR	C a = 100 Pa O = 2 kPa	C a = 100 Pa O = 2 kPa

PR, photorespiratory conditions; NPR, nonphotorespiratory conditions.

Mesophyll microstructural model and CO₂ reaction‐diffusion model

We used measured anatomical properties to parameterize the model for the leaf microstructure of each leaf type (three cultivars × two leaf ages/positions × two datasets = 12 leaf types in total). We used measurements of $t_{\mathrm{wall}}$ (cell wall thickness), $t_{\mathrm{cyt}}$ (cytosol thickness), $t_{\mathrm{str}}$ (stroma thickness), $S_{\mathrm{c}}/S_{\mathrm{m}}$ (surface area ratio of exposed chloroplasts to exposed mesophyll) and $S_{\mathrm{m}}/S$ (surface area of exposed mesophyll to leaf) to parameterize the model for leaf types from the Berghuijs et al. (2015) dataset. As the Ho et al. (2016) dataset lacks measurements of these parameters, we assumed for each leaf type in this dataset that $t_{\mathrm{wall}}=120\mathrm{nm}$, $t_{\mathrm{cyt}}=250\mathrm{nm}$, $t_{\mathrm{str}}=2.5\mathrm{\mu }m$, $S_{\mathrm{c}}/S_{\mathrm{m}}=0.90$ and $S_{\mathrm{m}}/S=16$, which are within the same range of the values of Berghuijs et al. (2015). For all types, we assumed that the Michaelis–Menten coefficient for carboxylation by Rubisco, $K_{\mathrm{mC}}$ equals 26.7 Pa (Ho et al., 2016), the Michaelis–Menten coefficient for oxygenation by Rubisco, $K_{\mathrm{mO}}$ equals 16.4 kPa (Ho et al., 2016), and Rubisco specificity S _c/o = 2.6 kPa Pa⁻¹ (Tholen et al., 2012). We ran simulations for three different scenarios. (Photo)respired CO₂ is released either in the inner cytosol (layer between chloroplasts and tonoplast), in cytosol gaps (spaces between two neighbouring chloroplasts) or in the outer cytosol (layer between the chloroplasts and the plasma membrane). Further details on the reconstruction of the leaf geometry, modelling of the scenarios for (photo)respired CO₂ release, the calculation of the fraction of (photo)respired CO₂ that is reassimilated, and the reaction‐diffusion model are provided by Berghuijs et al. (2017).

Parameterization and validation of the reaction‐diffusion model

The linear electron transport rate was calculated as $J=s{I}_{\mathrm{inc}}{\mathrm{\Phi }}_2$, where $I_{\mathrm{inc}}$ is the irradiance for each measurement, ${\mathrm{\Phi }}_2$ is the quantum yield of Photosystem II, and s is a proportionality coefficient, which is calculated as the slope of the linear regression between $A_{\mathrm{N}}$ and $I_{\mathrm{inc}}{\mathrm{\Phi }}_2/4$ under nonphotorespiratory conditions (Yin et al., 2009).

For both datasets, we used only irradiance data ≤ 150 μmol m⁻² s⁻¹, the range usually used for linear regression by the Kok and Yin. We estimated day respiration rate $R_{\mathrm{d}}$ with the reaction‐diffusion model by minimizing the sum of the squared residuals of the measured and the simulated CO₂ assimilation rates. $R_{\mathrm{d}}$ was estimated for each scenario for the location of the release of (photo)respired CO₂. For this optimization, we used the matlab (The Mathwork, Natick, USA) function lsqnonlin(). Supporting Information Notes S1 contains documentation of the source code (Notes S2) for this procedure, with a user guide. The values estimated by the reaction‐diffusion model were compared with the values of $R_{\mathrm{d}}$ estimated by the Yin and Kok methods using linear regression on the same experimental data.

The rate of triose phosphate utilization $T_{\mathrm{p}}$ was determined as $\left(A_{\mathrm{p}}+R_{\mathrm{d}}\right)/3$, where $A_{\mathrm{p}}$ is the mean observed value at the highest $C_{\mathrm{a}}$ of the CO₂ response curve measured under photorespiratory conditions. The reaction‐diffusion model also was used to estimate $V_{\mathrm{cmax}}$ (maximum rate of Rubisco carboxylation) for each scenario, by minimizing the squared difference between the predicted and the measured $A_{\mathrm{N}}$, using only data from the CO₂ response curve measured for O = 21 kPa and C _a < 30 Pa. The remaining gas exchange data for each leaf type were used to validate the model.

Simulations of CO₂ assimilation under conditions of the Laisk method

For using the reaction‐diffusion model to simulate CO₂ assimilation under the conditions only at which the Laisk method is applied, we adjusted the boundary condition at the interface of the intercellular airspace, such that $C_{\mathrm{i}}$ was used as input for the model, rather than g _s and $C_{\mathrm{a}}$. In line with the assumptions of the Laisk method, we assumed that photosynthesis is limited by electron transport. We simulated CO₂ response curves at four intensities of I _inc: 150_, 100, 50 and 25 μmol m⁻² s⁻¹, using a prefixed value for ${\mathrm{\Gamma }}^{\ast }$ and the $R_{\mathrm{d}}$ estimates obtained by the reaction‐diffusion model as input. From measurements of ${\mathrm{\Phi }}_2$ in the light response curve and the estimate of s, we calculated the rate of linear electron transport for these irradiances, according to $J=\mathrm{s}{\mathrm{\Phi }}_2{I}_{\mathrm{inc}},$ as 52.0, 36.3, 19.3 and 9.1 μmol m⁻² s⁻¹, and used these as input for simulation. We ran these simulations for each of the three scenarios with regard to the location of (photo)respired CO₂ release. The results were used to investigate how these scenarios would affect the estimates of R _d if the Laisk method is applied to similar experimental conditions.

Response of $g_{\mathrm{m}}$ and reassimilation to $C_a$ and $I_{\mathrm{inc}}$

We used the reaction‐diffusion model to calculate the apparent $g_{\mathrm{m}}$ for each leaf type and each scenario of (photo)respired CO₂ release. We first used the model to calculate $A_{\mathrm{N}}$, $C_{\mathrm{i}}$ and $C_{\mathrm{c}}$ as described by Berghuijs et al. (2017). Next, we re‐arranged Eqn (Eqn 2) to $g_{\mathrm{m}}=A_{\mathrm{N}}/\left(C_{\mathrm{i}}-C_{\mathrm{c}}\right)$ to calculate $g_{\mathrm{m}}$. We calculated both $g_{\mathrm{m}}$ and the fraction of (photo)respired CO₂ that is reassimilated, $f_{\mathrm{reass}}$, as described by Berghuijs et al. (2017), for various levels of $C_{\mathrm{a}}$, $O$ and $I_{\mathrm{inc}}$.

Method to identify most likely locations of (photo)respired CO₂ release

We calculated the Akaike's Information Criterion (AIC) (Akaike, 1974) for each combination of measured and simulated response curves, for each leaf type and for each scenario. For details, see Methods S1.

Results

Estimation of R _d

We used the reaction‐diffusion model to estimate $R_{\mathrm{d}}$ for the leaf types in the datasets of Berghuijs et al. (2015) (Fig. 1a,b; Table S1) and Ho et al. (2016) (Fig. 1c,d; Table S2). Additionally, we estimated $R_{\mathrm{d}}$ by linear regression for the Yin and Kok methods. In 11 of 12 cases, the $R_{\mathrm{d}}$ values estimated by the reaction‐diffusion model under photorespiratory conditions were higher than the $R_{\mathrm{d}}$ values under nonphotorespiratory conditions.

Figure 1.

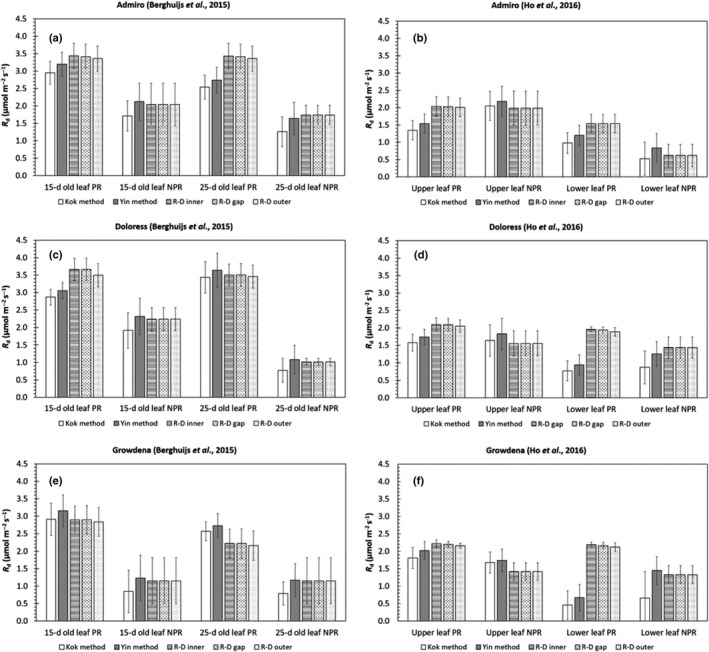
Estimates of day respiration, $R_{\mathrm{d}}$, either estimated by the Kok (1948) method, the Yin et al. (2009) method or by the reaction‐diffusion model (R‐D). Data collected by Berghuijs et al. (2015) (a, c, e) and Ho et al. (2016) (b, d, f) for three cultivars (a,b: Admiro, c,d: Doloress, e,f: Growdena) and two leaf ages (either 15‐ and 25‐d‐old leaves or upper leaves and lower leaves) were used for estimation. Estimates were made both for photorespiratory (PR) and nonphotorespiratory (NPR) conditions. R _d was estimated by the reaction‐diffusion for three diffferent scenarios: (photo)respired CO ₂ was released either in the inner cytosol (RD‐inner), the cytosol gaps (RD‐gaps) or the outer cytosol (RD‐outer). In each panel, the length of the error represents one standard deviation.

The values of $R_{\mathrm{d}}$ estimated by the reaction‐diffusion model did not differ much for the different assumed positions of (photo)respired CO₂ release. In all instances, the values of $R_{\mathrm{d}}$ estimated by the Yin method were higher than the $R_{\mathrm{d}}$ values estimated by the Kok method. In all cases, the values of $R_{\mathrm{d}}$ estimated by the Yin method under nonphotorespiratory conditions were close to the values estimated by the reaction‐diffusion model (Fig. 1b,d). Under photorespiratory conditions, this was not always the case (Fig. 1a,c). The values of $R_{\mathrm{d}}$ estimated by all of the methods did not differ consistently between leaf ages or leaf types.

Determination of $T_p$ and $V_{\mathrm{cmax}}$

Because of the similar estimates for $R_{\mathrm{d}}$, there were also almost no differences for the estimates of $T_{\mathrm{p}}$ for the same leaf types among different assumed locations of (photo)respired CO₂ release (Table S3). The estimate of $V_{\mathrm{cmax}}$ for each leaf type was lower if the (photo)respired CO₂ release was assumed to take place in the inner cytosol than if it was to take place in the cytosol gaps (Table S3). When (photo)respired CO₂ release took place in the outer cytosol, the estimate of $V_{\mathrm{cmax}}$ was always of the same order of magnitude as its standard error.

Model validation

Figs S1 and S2 show a comparison between measured and simulated CO₂ and light response curves, respectively, for each scenario of the location (photo)respired CO₂ release. They display only the part of the curves for which the measured data were not used for parameterization. Under most conditions, there was a good agreement between the measured and simulated net CO₂ assimilation rate for any scenario. However, under photorespiratory conditions the model that assumes (photo)respired CO₂ release in the outer cytosol tended to underestimate the net CO₂ assimilation rate more than the other two scenarios, under low CO₂ concentrations in the CO₂ response curves and high irradiances in the light response curves.

Response of $g_m$, and reassimilation to $C_a$ and I _inc

Figure 2 shows how $g_{\mathrm{m}}$ responded to $C_{\mathrm{a}}$ and to $I_{\mathrm{inc}}$ for the case of 15‐d‐old leaves of cv Admiro. The relationship for other leaf types showed a similar trend, and is therefore not shown here. If (photo)respired CO₂ release took place in the outer cytosol or in the cytosol gap, $g_{\mathrm{m}}$ increased with increasing $C_{\mathrm{a}}$. If (photo)respired CO₂ release took place in the inner cytosol, $g_{\mathrm{m}}$decreased with $C_{\mathrm{a}}$. $g_{\mathrm{m}}$ was always larger if (photo)respiratory CO₂ release took place in the inner cytosol than in the cytosol gaps, and in the cytosol gaps than in the outer cytosol. For each scenario, $g_{\mathrm{m}}$ tended to approach an equilibrium value at a high C _a, and this equilibrium value was the same for 21 and 2 kPa O₂ conditions for the same leaf type. See Methods S2 for further comments.

Figure 2.

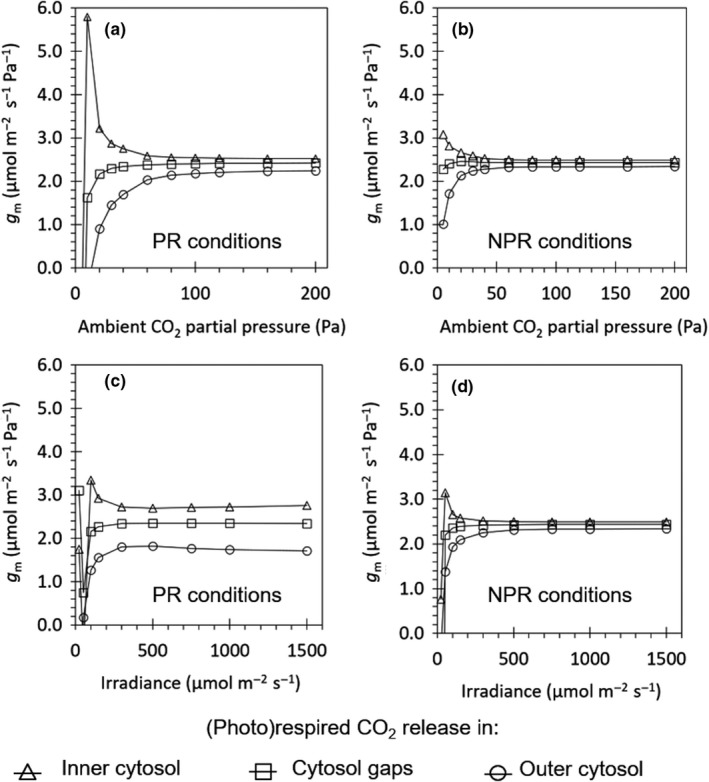
Response of the simulated apparent mesophyll conductance ($g_{\mathrm{m}}$) to increased ambient CO ₂ concentrations (a,b) or light intensities (c,d) under ambient oxygen ($O=21\mathrm{kPa}$) concentrations (a, c) and low oxygen ($O=2\mathrm{kPa}$) concentrations (b, d). The CO ₂ response curves were measured under saturating light (I _inc = 1500 μmol m⁻² s⁻¹) in 15‐d‐old Admiro leaves from the Berghuijs et al. (2015) dataset. The light response curves at low oxygen concentrations were simulated under high CO ₂ concentrations (C _a  = 40 Pa). Light response curves at high oxygen concentrations were measured at ambient CO ₂ concentrations (C _a = 40 Pa). The release of (photo)respiratory CO ₂ is assumed to take place either in the inner cytosol (triangles), the cytosol gaps (squares) or the outer cytosol (circles). The lines connect each of the triangles, squares or circles.

Figure 3 shows the response curves of $f_{\mathrm{reass}}$ to $C_{\mathrm{a}}$ and to $I_{\mathrm{inc}}$, for 15‐d‐old Admiro leaves from Berghuijs et al. (2015), and this relationship are similar for the other leaf types. The relationship with $C_{\mathrm{a}}$ was sigmoidal, and that with $I_{\mathrm{inc}}$ was in a saturation shape, under both oxygen concentrations.

Figure 3.

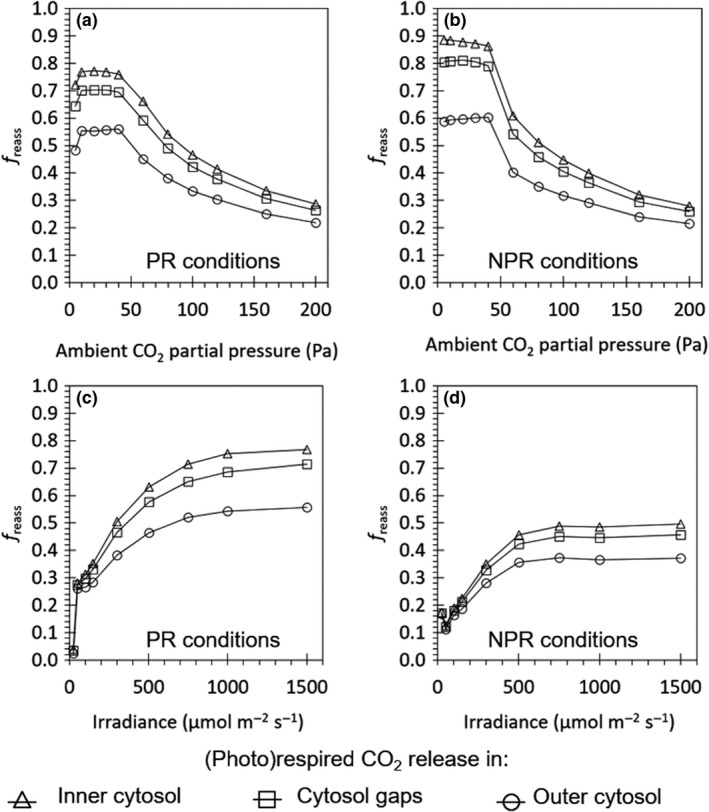
Response of the simulated fraction of reassimilation (photo)respired CO ₂ (f _reass) to increased ambient CO ₂ concentrations (a,b) or light intensities (c,d) under ambient oxygen ($O=21\mathrm{kPa}$) concentrations (a, c) and low oxygen ($O=2\mathrm{kPa}$) concentrations (b, d). The CO ₂ response curves were measured under saturating light (I _inc = 1500 μmol m⁻² s⁻¹) in 15‐d‐old Admiro leaves from the Berghuijs et al. (2015) dataset. The light response curves at low oxygen concentrations were simulated under high CO ₂ concentrations (C _a  = 40 Pa). Light response curves at high oxygen concentrations were measured at ambient CO ₂ concentrations (C _a = 40 Pa). The release of (photo)respiratory CO ₂ is assumed to either take place in the inner cytosol (triangles), the cytosol gaps (squares) or the outer cytosol (circles). The lines connect each of the triangles, squares or circles.

Simulations under conditions of the Laisk method

We simulated $A_{\mathrm{N}}-C_{\mathrm{i}}$ curves under different irradiances, for 15‐d‐old Admiro leaves (Fig. 4) using the $R_{\mathrm{d}}$ values that were previously estimated for each scenario of (photo)respired CO₂ release (Figs S1, S2). If (photo)respired CO₂ release took place in the inner cytosol, the curves had about the same intersection point at $C_{\mathrm{i}}=2.1,\mathrm{Pa}$. If (photo)respired CO₂ release took place in the cytosol gaps, the curves had about the same intersection point in $C_{\mathrm{i}}=3.0,\mathrm{Pa}$. For both scenarios, the common intersection points of the curves also were intersected with the line $A_{\mathrm{N}}=-R_{\mathrm{d}}$. If (photo)respired CO₂ release took place in the outer cytosol, the curves did not intersect at the same value of $C_{\mathrm{i}}$. Instead, individual curves intersected in intercellular CO₂ partial pressures of 4.3, 4.7, 5.1, 5.4 and 5.8 Pa, respectively. The values of $A_{\mathrm{N}}$ in these intersection points were higher than $-R_{\mathrm{d}}$. The intersection points were not obtained by the line $C_{\mathrm{i}}={\mathrm{\Gamma }}^{\ast }$ in any of the three scenarios.

Figure 4.

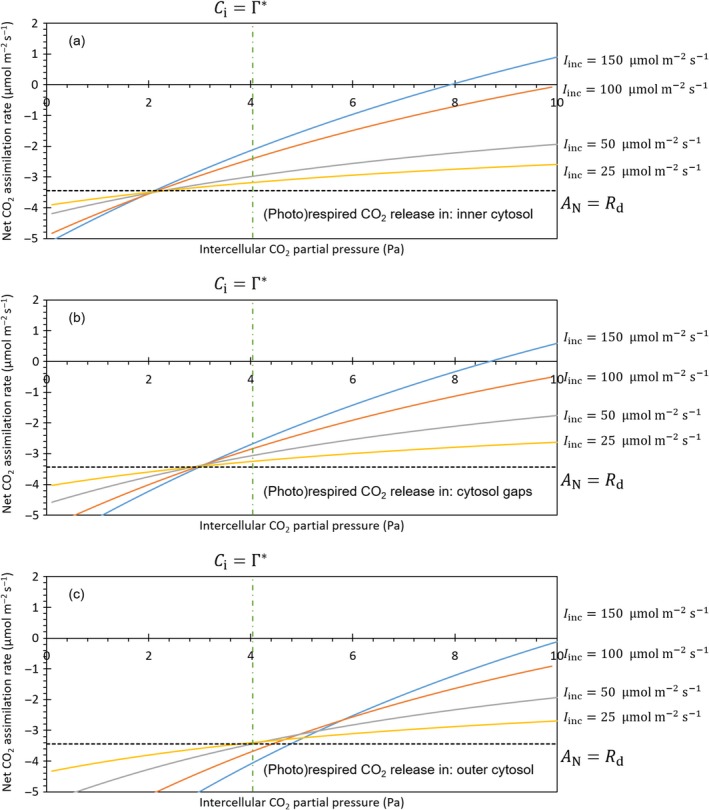
Simulated response curve of the net CO ₂ assimilation rate (A _N) to intercellular CO ₂ partial pressures (C _i) under the conditions of the Laisk method for different scenarios of (photo)respired CO ₂ release. The solid lines represent CO ₂ response curves simulated at different irradiances I _inc (150, 100, 50 and 25 μmol m⁻² s⁻¹). The dashed line represents the net CO ₂ assimilation rate which equals the negative input value of the day respiration rate (R _d). The dashed‐dotted line represents the intercellular partial pressure which equals the CO ₂ compensation point (Γ*). (Photo)respired CO ₂ is released either in the inner cytosol (a), the cytosol gaps (b) or the outer cytosol (c).

Likely locations of (photo)respired CO₂

We calculated $\mathrm{\Delta }AIC$ for each combination of leaf type and scenario for each measured response curve type (Tables S4, S5). The $\mathrm{\Delta }AIC$ values are bold if $\mathrm{\Delta }AIC\le 2$, indicating the corresponding scenario has substantial support (Burnham & Anderson, 2004). There was only one case (Admiro lower leaf CO₂ response curves at ambient O₂; Table S5) in which the scenario that assumed (photo)respired CO₂ release in the outer cytosol had substantially greater support than the scenario that assumed the release in the inner cytosol. There also was only one case in which the scenario that assumed (photo)respired CO₂ release in the cytosol gaps had more support than the other two scenarios. In the other 46 out of 48 cases, the model in which (photo)respired CO₂ release took place in the inner cytosol had either the most support or substantial support relative to the best model. In all cases, all three scenarios had substantial support for the light response curves under nonphotorespiratory conditions.

Discussion

Use of a simple reaction‐diffusion model as a tool to assess $R_d$

Reaction‐diffusion models have been used as powerful tools to investigate mesophyll conductance (g _m) and its response to various environmental and physiological factors (Tholen & Zhu, 2011; Ho et al., 2016). Here, we explored using the simple reaction‐diffusion model of Berghuijs et al. (2017) to investigate the day respiration rate (R _d). Reaction‐diffusion models certainly have limitations. The most relevant one in the context of this study is that these models require prefixed diffusion coefficients as input, whose values are hard to measure. Therefore, we had to adopt these from previous studies (Gutknecht et al., 1977; Evans et al., 2009; Fanta et al., 2012; Ho et al., 2016). Additionally, we simplified the leaf structure to a single rectangular cuboid chloroplast, surrounded by a cytosol layer (Berghuijs et al., 2017). This simplification simulates the leaf tissue as a 2D computational domain, while assuming that the third dimension is homogeneous. These simplifications can potentially affect the simulated results. However, Berghuijs et al. (2017) validated the simple model by comparing the results with those generated by a complex 3D model (Ho et al., 2016). Here, we further validated the model by comparing measured (Berghuijs et al., 2015; Ho et al., 2016) and simulated net CO₂ assimilation rates (Figs S1, S2). Our model had various advantages. First, computational time was greatly reduced, which made it feasible to use the model directly to estimate $R_{\mathrm{d}}$. Second it can be parameterized using a limited number of leaf anatomical parameters. We showed that the model, when combined with anatomical parameters, gas exchange and chlorophyll fluorescence data, adds to the literature by providing an additional method to indirectly estimate R _d under either photorespiratory or nonphotorespiratory conditions. We chose leaf anatomical properties that have been measured in combination with gas exchange in various previous studies (Syvertsen et al., 1995; Tosens et al., 2012; Galmes et al., 2013; Retta et al., 2016b; Ouyang et al., 2017).

Estimation of R _d by the Kok method and the Yin method

Reassimilation and other processes can compromise the indirect estimation of R _d based on gas exchange data. We first examined estimates for nonphotorespiratory conditions where reassimilation is not relevant because then CO₂ released by (photo)respiration does not contribute much to increasing ribulose biphosphate (RuBP) carboxylation (Busch et al., 2013). In most cases, $R_{\mathrm{d}}$values estimated by the Kok method were smaller than estimates by the reaction‐diffusion model, although these differences are sometimes small as the standard deviations overlap. The estimates of $R_{\mathrm{d}}$ obtained from the reaction diffusion model and the ones from the Yin method under nonphotorespiratory conditions are very similar (Figs 1, 2). $R_{\mathrm{d}}$estimates by the Kok method under photorespiratory conditions also were smaller than the estimates by the Yin method (Fig. 1), in line with Yin et al. (2011). Our reaction‐diffusion model, like the Yin method, considers the decrease of ${\mathrm{\Phi }}_2$ with increasing irradiance (Genty & Harbinson, 1996), which occurs even within the low‐irradiance range (Yin et al., 2009, 2011). The Kok method underestimates R _d because it neglects this dependence of ${\mathrm{\Phi }}_2$ on irradiance. Recognizing the decrease of ${\mathrm{\Phi }}_2$ with increasing irradiance also avoids the underestimation of the quantum yield of CO₂‐assimilation (Yin et al., 2014).

For photorespiratory conditions, estimates of R _d by the reaction‐diffusion model were higher than those by the Yin method, let alone by the Kok method, for most leaf types (Fig. 1). The underestimation of R _d by the Yin method relative to the R _d estimated by the reaction‐diffusion was 10.5–13.0%, depending on the scenario that the reaction‐diffusion model assumed with regard to the location of (photo)respired CO₂ release (Fig. S3). Under photorespiratory conditions, chloroplast CO₂ concentration (C _c) decreases significantly with increased light under low light intensities (Farquhar & Busch, 2017). Such variation was generated using the FvCB model coupled with the g _m model of Eqn (Eqn 2), which has a similar form as a stomatal conductance (g _s) model. Therefore, the generated variation of C _c with increasing irradiance is similar to the measured pattern for the decrease of intercellular CO₂ concentration (C _i) with light intensity (Berghuijs et al., 2015). The decrease of C _c with irradiance is a common result when g _m is finite and is greatest when g _m is smallest (Farquhar & Busch, 2017). Similarly, our reaction‐diffusion framework, explicitly modelling CO₂ sources, diffusion and sinks, accounts for the variation of C _c with increasing irradiance. By contrast, the linear regression procedure of the Kok method or the Yin method implicitly assumes that C _c does not vary with irradiance, when applied under photorespiratory conditions. Ignoring this variation of C _i or C _c has been shown by Kirschbaum & Farquhar (1987) and Farquhar & Busch (2017) to lead to an underestimation of R _d (see also Buckley et al., 2017). Therefore, we conclude that the Yin method underestimates R _d for photorespiratory conditions by neglecting the variation of C _c with increasing irradiance.

To what extent is this variation of C _c with increasing irradiance associated with the reassimilation by (photo)respired CO₂? For nonphotorespiratory conditions that are achieved with a very low O₂ concentration, both a g _m model and the reaction‐diffusion model can predict a decline of C _c with increasing irradiance (results not shown), but with a negligible effect on leaf photosynthesis. By contrast, for photorespiratory conditions, this decline is highly relevant as it affects the rate of RuBP carboxylation. The FvCB model, when combined with g _s and g _m, accounts for reassimilation of (photo)respired CO₂ (Tholen et al., 2012; Von Caemmerer, 2013; Yin & Struik, 2017). A high g _m value could predict little drawdown of C _c from C _i with increasing irradiance and a low intracelluar reassimilation. Therefore, for photorespiratory conditions, the modelled variation of C _c with irradiance indirectly reflects the contribution of (photo)respired CO₂ release to C _c, therefore, to reassimilation. This assertion is supported by the similarity between the above‐stated percentages of R _d underestimation by the Yin method (10.5–13.0%) and the values of f _reass we estimated for the low‐irradiance range (Fig. 3). The small difference in f _reass at low light among the three possible positions of mitochondria (Fig. 3) is also in line with the small difference among R _d estimates in different scenarios (Fig. 1). Although the placement of mitochondria is known to affect f _reass (Yin & Struik, 2017), our reaction‐diffusion model predicts that such an effect of the scenario is most expressed under high‐light conditions (Fig. 3).

Because of the above differences in handling the irradiance‐dependence of C _c and reassimilation, the relative value of R _d estimated for the photorespiratory vs nonphotorespiratory conditions by the Yin method and the reaction‐diffusion model differed. The estimates of $R_{\mathrm{d}}$ by the Yin method were either higher or lower in one than in the other conditions, whereas those by the reaction‐diffusion model were always lower for nonphotorespiratory than for photorespiratory conditions (Fig. 1). This is in agreement with results from Buckley et al. (2017), who showed that R _dk was higher at 21% than at 2% O₂ in developing leaves of Vicia faba. Respiration is a process where O₂ is the substrate (Tcherkez et al., 2017b) and respiratory rates measured in terms of O₂ and CO₂ exchange may not be equal (Gauthier et al., 2018). However, the amount of respiratory CO₂ release at the low O₂ concentration, as applied for measurements under nonphotorespiratory conditions, will likely decrease relative to that under ambient O₂ conditions. The Yin method is theoretically valid for nonphotorespiratory conditions only (Yin et al., 2011). However, it is previously unknown to what extent R _d estimated from nonphotorespiratory conditions can be used for photorespiratory conditions. Based on our results and those found in literature (Buckley et al., 2017), we conclude that the R _d estimate obtained under nonphotorespiratory conditions by the Yin method cannot be used as a replacement for R _d under photorespiratory conditions.

This conclusion also applies to the Kok method. One assumption when using the Kok method or the Yin method under photorespiratory conditions is that C _c is constant for different light intensities. However, practically, it is impossible to design an experiment where C _c is maintained constant across various irradiances because g _s, g _m and A _N are not known beforehand (Buckley et al., 2017). Our analysis shows the power of using reaction‐diffusion models parameterized with standard diffusion coefficients (Berghuijs et al., 2017) and leaf anatomical measurements (Berghuijs et al., 2015) to estimate R _d, which can account for the decrease of both ${\mathrm{\Phi }}_2$ and C _c with increasing irradiance.

Estimation of R _d by the Laisk method

The Laisk method relies on measurements at low C _i, the conditions having high photorespiration, but it theoretically has problems if r _m is significant, especially under the framework of multiple components of r _m (Tholen et al., 2012). Yin et al. (2011) stated that R _d estimated by the Laisk method was comparable with the estimates by the Yin method for photorespiratory conditions. Gong et al. (2018) showed that the Laisk method underestimates R _d when compared with their isotopic disequilibrium method that directly estimates R _d.

The results of our simulations of CO₂ response curves under the conditions of the application of the Laisk method (Fig. 4) actually show that assumptions regarding the location of (photo)respired CO₂ release affect the estimates it obtains. If (photo)respired CO₂ is assumed to be released in the outer cytosol, the curves do not intersect in a single point. Moreover, each of the intersection points between two curves has a higher net CO₂ assimilation rate than the prefixed –R _d. Based on their model, which implicitly assumes (photo)respired CO₂ release in the outer cytosol, Tholen et al. (2012) also indicates that the Laisk method will underestimate R _d. Our simulations show that in the other two scenarios, CO₂ response curves actually do intersect in $A_{\mathrm{N}}=-R_{\mathrm{d}}$. This shows that if one of these two scenarios is true, Laisk's method yields a good estimate of $R_{\mathrm{d}}$.

In an application of the Laisk plot, it is still required that all CO₂ response curves share a single intersection point. This issue can be solved by the fitting procedure as described by Yin et al. (2011) for the Laisk method or the slope‐intercept regression analysis as applied by Walker & Ort (2015). However, the Laisk linear plot to estimate R _d should be made as a function of C _c; for that $g_{\mathrm{m}}$ needs to be known. A dilemma is that g _m can be estimated only after R _d is known (Harley et al., 1992). Again, the reaction‐diffusion model does not have this problem as it does not require $g_{\mathrm{m}}$ as an input beforehand. Nevertheless, relying on g _m values indirectly derived from an established relationship between g _m and g _s, Gong et al. (2018) showed that R _d estimated by the Laisk method does not depend on whether it is based on C _i or C _c.

Estimates of photosynthetic parameters and mesophyll conductance in relation to the position of mitochondria

The estimate of $V_{\mathrm{cmax}}$ was always higher if (photo)respiratory CO₂ release took place in the cytosol gap than in the inner cytosol (Table S3). Because the reassimilation of (photo)respiratory CO₂ was higher if (photo)respiratory CO₂ was released in the inner cytosol than in the cytosol gaps (Fig. 3), the model compensated for the lower reassimilation by a higher RuBP carboxylation under Rubisco limited conditions, thereby resulting in a higher estimated $V_{\mathrm{cmax}}$. If (photo)respiratory CO₂ was released in the outer cytosol, the standard error was very high (Table S3), possibly because the model cannot fully compensate for the discrepancy between its prediction of $A_{\mathrm{N}}$ and the measured $A_{\mathrm{N}}$ for this scenario by estimating a high value for $V_{\mathrm{cmax}}$.

For all leaf types, our reaction‐diffusion model generated the same trend in the response of $g_{\mathrm{m}}$ to different values of $C_{\mathrm{a}}$ and $I_{\mathrm{inc}}$ (Fig. 2). If (photo)respired CO₂ release was assumed to take place in the inner cytosol, $g_{\mathrm{m}}$ decreased with an increase in $C_{\mathrm{a}}$. The shape of this response was similar to the response of $g_{\mathrm{m}}$ to $C_{\mathrm{i}}$ (when $C_{\mathrm{i}}$ was above certain values) reported in various studies (Flexas et al., 2007; Yin et al., 2009; Tholen & Zhu, 2011). The apparent g _m model as used in these studies was Eqn (Eqn 2). This model assumes that the mitochondria are located closely behind the chloroplasts as if that (photo)respired CO₂ were released in the same compartment as RuBP carboxylation does (Tholen & Zhu, 2011; Yin & Struik, 2017). If (photo)respired CO₂ was to release in the outer cytosol or in the cytosol gaps, the shape of the response was more similar to the one calculated by Tholen et al. (2012) using a resistance model based on the same assumption. Xiao & Zhu (2017) also found similar differences in the shape of the response curve of $g_{\mathrm{m}}$ to $C_{\mathrm{i}}$ depending on the position of the mitochondria relative to the chloroplasts.

The most likely position of mitochondria relative to the chloroplasts

In a vast majority of cases, the scenario for (photo)respired CO₂ release in the outer cytosol had less support than the scenario that assumed (photo)respired CO₂ release in the inner cytosol (Tables S4 and S5). The consequences of this finding is that, at least in tomato, two‐resistance models (Tholen et al., 2012; Berghuijs et al., 2015) that implicitly assume (photo)respired CO₂ release in the outer cytosol are less likely than the classical single mesophyll resistance models.

This assertion agrees generally with experimental observations like (Hatakeyama & Ueno, 2016), who reported that for 10 C₃ grasses, on average 80% of the mitochondria are located closely on the vacuole side of chloroplasts in mesophyll cells. Sage & Sage (2009) and Busch et al. (2013) had a similar observation for rice and wheat, who even indicated that chloroplast covers > 95% of the mesophyll periphery with a high S _c : S _m ratio that provides an effective mechanism to trap and re‐assimilate (photo)respired CO₂. The classical resistance model, Eqn (Eqn 2), works best if mitochondria are exclusively located closely behind chloroplasts and the S _c : S _m ratio is very close to 1.0, whereas the two‐resistance model of Tholen et al. (2012) works if mitochondria are located predominantly in the outer cytosol combined with a low S _c : S _m and little cytosol resistance (Yin & Struik, 2017). Although the reality may be somewhere between these two extremes, our analysis in Tables S4 and S5 suggests that the classical g _m model, Eqn (Eqn 2), is closer to reality in the two experiments for tomato. It should be noted that the S _c : S_m measurements that were used in this study (between 0.84 and 0.96) (Berghuijs et al., 2015) were all at the higher end of the values mentioned in literature for various species. For instance, considerably lower ranges have been reported for Arabidopsis thaliana (0.43‐0.75) (Tholen et al., 2008). As S _c : S _m decreases with leaf aging and varies with species (Busch et al., 2013) and with environment (Ouyang et al., 2017), it may be hard to ascertain which model of the two is closer to reality.

Concluding remarks

Our reaction‐diffusion model can estimate R _d without making implicit assumptions regarding reassimilation, position of mitochondria, mesophyll conductance and the variability of C _c at low light conditions. In these aspects, our model provides a better tool to estimate R _d than the Laisk, Kok and Yin methods. However, if there are no leaf anatomical data available, it depends on the available data which of the existing models has to be applied. Table 2 shows an overview of the advantages and disadvantages of each method. With leaf anatomical data available, reaction‐diffusion models have previously shown to be useful to study the mechanisms of mesophyll conductance and reassimilation (Tholen & Zhu, 2011; Ho et al., 2016; Retta et al., 2016a, 2017; Berghuijs et al., 2017). We demonstrate here that they also can estimate R _d and photosynthetic parameters. We recommend further research to collect datasets containing leaf anatomical parameters in combination with gas exchange and chlorophyll fluorescence measurements to make the best possible use of our method.

Table 2.

Overview of advantages and disadvantages of estimation methods for R _d

Method	Advantages	Disadvantages
Kok method	Does not require chlorophyll fluorescence measurements	Does not consider the increase of C c with decreased irradiance
	Does not require leaf anatomical measurements	Is theoretically only valid under nonphotorespiratory conditions
		Does not account for the decrease of Φ2 with increased irradiance
Yin method	Does not require leaf anatomical measurements	Requires chlorophyll fluorescence measurements
	Accounts for the decrease of Φ2 with increased irradiance	Does not consider the increase of C c with decreased irradiance
		Is theoretically only valid under nonphotorespiratory conditions
Laisk method	Does not require chlorophyll fluorescence measurements	Requires an assumption of no mesophyll resistance
	Does not require leaf anatomical measurements	Estimate is affected by the position of mitochondria relative to the chloroplasts
	Partly considers the reassimilation of photorespired CO2	Is applied at very low CO2 concentrations and requires gas leakage corrections
	Applies to photorespiratory conditions
Reaction diffusion model	Does not require an estimate of mesophyll conductance	Requires chlorophyll fluorescence measurements
	Accounts for the decrease of Φ2 with increased radiation	Requires leaf anatomical parameters to parameterize the geometry
	The placement of mitochondria relative to the chloroplasts can be defined explicitly	Requires CO2 diffusion coefficients for different mesophyll compartments
	Is theoretically valid under photorespiratory conditions	Has to be solved numerically

Author contributions

HNCB planned the research and wrote the first draft of the manuscript; HNCB and XY ran the simulations; HNCB, XY, QTH, MAR, BMN and PCS interpreted the simulations; and HNCB, XY, QTH, MAR, BMN and PCS wrote the final manuscript.

Supporting information

Please note: Wiley Blackwell are not responsible for the content or functionality of any Supporting Information supplied by the authors. Any queries (other than missing material) should be directed to the New Phytologist Central Office.

Fig. S1 Measured vs simulated CO₂ response curves under photorespiratory and nonphotorespiratory conditions.

Fig. S2 Measured vs simulated light response curves under photorespiratory and nonphotorespiratory conditions.

Fig. S3 Day respiration rate estimates obtained by the reaction diffusion model vs estimates obtained by the Yin method.

Fig. S4 Schematic overview of the flow of the program that was used to estimate parameter values with the reaction diffusion model.

Methods S1 Determination of Akaike's Information Criterion.

Methods S2 Comments on g _m.

Notes S1 Source code to estimate R _d and V _cmax.

Notes S2 Code of M files.

Table S1 Estimates of the lumped calibration factors and the day respiration rates obtained by various methods using data from Berghuijs et al. (2015).

Table S2 Estimates of the lumped calibration factors and the day respiration rates obtained by various methods using data from Ho et al. (2016).

Table S3 Estimates of the maximum RuBP carboxylation rate by Rubisco and the triose phosphate utilization rates obtained by the reaction‐diffusion model for different scenarios of (photo)respired CO₂ release.

Table S4 Akaike's information criteria for different combinations of leaf age, cultivar, photorespiratory conditions and scenarios for the release of (photo)respired CO₂ using the reaction‐diffusion model and data from Berghuijs et al. (2015).

Table S5 Akaike's information criteria for different combinations of leaf age, cultivar, photorespiratory conditions, and scenarios for the release of (photo)respired CO₂ using the reaction‐diffusion model and data from Ho et al. (2016).