Prior Expectations Bias Sensory Representations in Visual Cortex

Abstract

Perception is strongly influenced by expectations. Accordingly, perception has sometimes been cast as a process of inference, whereby sensory inputs are combined with prior knowledge. However, despite a wealth of behavioral literature supporting an account of perception as probabilistic inference, the neural mechanisms underlying this process remain largely unknown. One important question is whether top-down expectation biases stimulus representations in early sensory cortex, i.e., whether the integration of prior knowledge and bottom-up inputs is already observable at the earliest levels of sensory processing. Alternatively, early sensory processing may be unaffected by top-down expectations, and integration of prior knowledge and bottom-up input may take place in downstream association areas that are proposed to be involved in perceptual decision-making. Here, we implicitly manipulated human subjects' prior expectations about visual motion stimuli, and probed the effects on both perception and sensory representations in visual cortex. To this end, we measured neural activity noninvasively using functional magnetic resonance imaging, and applied a forward modeling approach to reconstruct the motion direction of the perceived stimuli from the signal in visual cortex. Our results show that top-down expectations bias representations in visual cortex, demonstrating that the integration of prior information and sensory input is reflected at the earliest stages of sensory processing.

Introduction

Perception is not solely determined by the input from our eyes, but it is strongly influenced by our expectations. In line with this notion, perception has often been cast as a process of inference, whereby sensory inputs are combined with prior knowledge (Helmholtz, 1867). In recent years, this notion has received considerable empirical support (Kersten et al., 2004; Yuille and Kersten, 2006). For example, many perceptual illusions can be explained as the result of prior knowledge about the statistics of the world influencing perceptual inference: we expect light to come from above (Sun and Perona, 1998), faces to be convex and not concave (Gregory, 1997), and objects in the world to move slowly rather than fast (Weiss et al., 2002). Many of these priors are not set in stone, but rather reflect the agent's current model of the world, and can sometimes adjust to (experimentally) altered circumstances on a relatively short timescale (Adams et al., 2004; Chalk et al., 2010; Sotiropoulos et al., 2011).

However, despite a wealth of literature supporting an account of perception as probabilistic inference (Kersten et al., 2004; Yuille and Kersten, 2006), the neural mechanisms underlying this process remain largely unknown. Here, we are particularly concerned with the integration of bottom-up sensory inputs and top-down prior expectations. Specifically, the question we wish to address is whether top-down expectations can bias stimulus representations in early sensory cortex. It is well known that valid prior expectations result in reduced neural activity in sensory cortex (Summerfield et al., 2008; den Ouden et al., 2009; Alink et al., 2010; Todorovic et al., 2011; Kok et al., 2012a; Todorovic and de Lange, 2012), but it is an open question whether expectations are also able to change the contents of the sensory representation. Previous work by Murray et al. (2006) has revealed a neural correlate of an illusion of size as a result of inferred depth in V1, suggesting such modulations are indeed possible. This would reveal the integration of prior knowledge and bottom-up inputs to be a key feature of sensory processing at even the earliest levels, in line with hierarchical inference theories of perception (Lee and Mumford, 2003; Friston, 2005). Alternatively, early sensory processing may be unaffected by top-down expectations, and integration may take place in downstream association areas that are proposed to be involved in perceptual decision-making, such as parietal and prefrontal cortex (Gold and Shadlen, 2007; Heekeren et al., 2008; Rao et al., 2012).

To examine whether priors modify stimulus representations in sensory cortex, we implicitly manipulated human subjects' prior expectations about visual motion stimuli, and probed the effects on both perception and representations in visual cortex. We used functional magnetic resonance imaging (fMRI), in conjunction with a forward modeling approach, to reconstruct the motion direction of the perceived stimuli from signals in visual cortex. To preview, our results show that top-down expectation biases representations in visual cortex, demonstrating that the integration of prior information and sensory input is reflected already at the earliest stages of sensory processing.

Materials and Methods

Subjects.

Twenty-four healthy right-handed individuals (16 female, age 23 ± 3 years, mean ± SD) with normal or corrected-to-normal vision gave written informed consent to participate in this study, in accordance with the institutional guidelines of the local ethics committee (Commissie Mensgebonden Onderzoek region Arnhem-Nijmegen, The Netherlands). Data from one subject were excluded due to excessive head movement (>5 mm).

Stimuli.

Visual stimuli consisted of random dot motion patterns (RDPs), displayed in an annulus (outer diameter, 15° visual angle; inner diameter, 3°) surrounding a white fixation cross (0.3°, 327.0 cd/m²) for a duration of 1 s. The RDPs consisted of 0.1° white (327.0 cd/m²) dots (2.5 dots per square degree) on a dark-gray background (15.5 cd/m²; Weber contrast, 20.1). Within each RDP, there was a proportion of coherently moving dots, while the remaining dots were each assigned a random motion direction. Both coherent and random dots moved at a speed of 6°/s and had a lifetime of 200 ms. The stimuli were generated and presented using Matlab (MathWorks) in conjunction with the Psychophysics Toolbox (Brainard, 1997), and displayed on a rear-projection screen using an EIKI projector (1024 × 768 resolution, 60 Hz refresh rate). Auditory cues consisted of pure tones (450 or 1000 Hz) with a duration of 200 ms, and were presented over MR-compatible earphones. During the behavioral training session, visual stimuli were presented on an LCD monitor (1024 × 768 resolution, 60 Hz refresh rate) and tones were presented over external speakers.

Experimental design.

Each trial started with an auditory cue followed by a visual RDP stimulus [cue-stimulus stimulus-onset asynchrony (SOA), 750 ms]. Subjects were told that they could ignore the auditory tone and that they had to report the predominant motion direction in the subsequent RDP stimulus on a continuous scale by positioning a line segment in a 360° circle (Fig. 1A) using two buttons of an MR-compatible button box to rotate the line clockwise or anticlockwise. The initial direction of the line segment was randomized between −45° and 135°. The stimulus–response interval was jittered between 1000 and 2000 ms, and the intertrial interval was jittered between 2250 and 4250 ms (yielding an RDP SOA of 8–11 s). The jittered intervals were drawn from a uniform distribution. The RDPs always had one of five possible directions of coherent motion: 10, 27.5, 45, 62.5, or 80° (where 0° corresponds to rightward and 90° corresponds to upward motion; Fig. 1B). The discrete nature of the possible motion directions was unknown to the subjects, who were informed that the predominant motion direction would always be in the upper right quadrant, i.e., between 0 and 90°. Prior expectations about the motion direction were implicitly induced by the auditory cue, which had a probabilistic relationship with the distribution from which the stimulus would be drawn. More specifically, there were two tones that each predicted one of the intermediate motion directions (27.5 or 62.5°) with 60% probability. For example, if the auditory cue was a low (high) tone, the RDP was 60% likely to have a 27.5° (62.5°) motion direction (Fig. 1C). The four other (nonpredicted) directions were each 10% likely to occur. The relationship between pitch (low/high) and predicted direction (27.5/62.5°) was counterbalanced across subjects. Subjects were not informed about the relationship between the auditory cue and the visual stimulus. After the experiment, subjects were requested to fill out a questionnaire regarding the relationship between the tones and the moving dots. The exact question posed to them was as follows: “Did you notice any relationship between the tones you heard and the directions of motion you saw? If so, please describe the relationship you observed in the text box below. You can also use the circle to illustrate your answer. You can draw more than one arrow.” Underneath the question, they were given the options “Yes/No,” a text box to describe the relationship they suspected (if any), and a circle into which they could draw arrows indicating the directions of motion related to the tones. Out of 23 included subjects, only one suspected the true relationship between the tones and the moving dots. One other subject suspected the exact opposite of the true relationship, i.e., low tone predicts rightward and high tone predicts upward, whereas the opposite was true. Three subjects suspected a relationship between just one of the two tones and a certain direction of motion, of which only one subject reported the true relationship. The remaining 18 subjects reported suspecting no relationship between the tones and the moving dots. Together, this underlines the implicit nature of the expectation manipulation.

Figure 1.

Experimental paradigm. A, Each trial started with an auditory cue that was followed by a visual RDP stimulus. Subjects were asked to report the predominant motion direction in the subsequent RDP stimulus on a continuous scale, by positioning a line segment in a 360° circle. B, The RDPs had one of five possible directions of coherent motion: 10, 27.5, 45, 62.5, or 80°, with 0° being rightward motion and 90° upward motion. C, The auditory cue had a probabilistic relationship with the distribution from which the stimulus would be drawn. For example, if the auditory cue was a low (high) tone, the RDP was 60% likely to have a 27.5° (62.5°) motion direction. The four other (nonpredicted) directions were each 10% likely to occur. The relationship between pitch (low/high) and predicted direction (27.5/62.5°) was counterbalanced across subjects.

To familiarize subjects with the task and to establish implicit learning of the predictive relationship between the auditory cues and visual stimuli, subjects participated in a behavioral session outside the scanner 1 d before the fMRI session. During this training session, participants performed 12 blocks of 40 trials of the task. The percentage of coherently moving dots was varied pseudorandomly from trial to trial, and could be 10, 20, or 30%.

During the fMRI session, only one coherence level was used, determined on the basis of subjects' performance in the training session. Specifically, we chose the coherence level that resulted in a mean absolute error of ∼15° during the training session. This number was chosen arbitrarily, to approximately equate task difficulty across subjects. In the scanner, each subject performed three runs of the task, with each run containing three blocks of 40 trials, yielding a total of 360 trials. Additionally, all subjects participated in a localizer run, consisting of RDPs with the same overall properties as those presented during the experiment, except that coherence was set to 100%, and seven motion directions were presented in pseudorandom order for a duration of 12 s each. The motion directions were −7.5, 10, 27.5, 45, 62.5, 80, and 97.5°. The localizer consisted of 12 blocks of seven motion directions and one blank fixation screen (12 s) each, resulting in 84 stimulus trials and 12 fixation screens. Throughout the localizer, a (white) fixation cross was presented. This fixation cross dimmed at random moments, and subjects were required to press a button at these events, to ensure central fixation. Finally, subjects engaged in a retinotopic mapping run, in which they viewed a wedge, consisting of a contrast-reversing black-and-white checkerboard pattern (3 Hz), first rotating clockwise for nine cycles and then anticlockwise for another nine cycles (at a rotation speed of 23.4 s/cycle; run duration was ∼8 min). Again, to ensure central fixation, subjects were required to press a button when they detected a dimming of the fixation cross.

Eye-movement recording.

To verify that subjects maintained fixation on the central fixation point throughout the trial, we monitored subjects' eye movements using an infrared eye-tracking system in the scanner (Sensomotoric Instruments). For technical reasons, we did not obtain eye-movement data for all subjects. We obtained eye-movement data of sufficient quality in 12 subjects during the main experiment and for 11 subjects during the localizer run, which we checked for systematic differences in eye movements between conditions. For the localizer run, we compared mean eye position during stimulus presentation to mean eye position during fixation trials (during which no moving dots were presented, but the task at fixation remained the same). This was done separately for vertical and horizontal pupil coordinates, and effects of motion direction on pupil position were tested using a repeated-measures one-way ANOVA at the group level. For the main experiment, we compared mean precue (1000 ms before cue onset) pupil positions with those during the cue–stimulus interval (200–750 ms after cue onset) and the stimulus interval (200–1000 ms after stimulus onset), performing repeated-measures ANOVAs with the factors “prior” and “direction.”

fMRI acquisition parameters.

Functional images were acquired using a 3T Trio MRI system and a 32-channel head coil (Siemens), with a T2*-weighted gradient-echo EPI sequence (TR/TE, 1950/30 ms; 31 slices; voxel size, 3 × 3 × 3 mm; interslice gap, 20%). Anatomical images were acquired with a T1-weighted MP-RAGE sequence, using a generalized autocalibrating partially parallel acquisition acceleration (GRAPPA) factor of 2 (TR/TE, 2300/3.03 ms; voxel size, 1 × 1 × 1 mm).

fMRI data preprocessing.

SPM8 (http://www.fil.ion.ucl.ac.uk/spm, Wellcome Trust Centre for Neuroimaging, London, UK) was used for image preprocessing. The first four volumes of each run were discarded to allow for T1 equilibration. All functional images were spatially realigned to the mean image, yielding head-movement parameters that were used as nuisance regressors in the general linear models, and temporally aligned to the first slice of each volume. The structural image was coregistered with the functional volumes.

fMRI data analysis.

The data of each subject were modeled using an event-related approach, within the framework of the general linear model (GLM), to estimate BOLD response amplitudes of each voxel to each trial type. We specified regressors of interest for each of the 10 conditions (two priors × five motion directions) of the main experiment, by convolving a delta function with a peak at the time of onset of the RDP stimulus with a canonical hemodynamic response function (Friston et al., 1998). Nuisance regressors were constructed for the response periods, instruction screens, and head-movement parameters (Lund et al., 2005). Using these design matrices, we estimated the response amplitudes of each voxel to each trial type using linear regression: multiplying the pseudoinverse of the design matrix with the measured fMRI signal time course. These estimates made up the data for our main analyses.

In a separate analysis, we estimated BOLD amplitudes for each single trial, using the method outlined in Mumford et al. (2012). This consisted of creating as many GLMs as there were trials in a block (n = 40). In each GLM, one trial per block was a trial of interest, yielding as many trials of interest per model as there were blocks in the experiment (m = 9). In this set of models, each trial was a trial of interest exactly once (40 × 9 = 360 trials). These trials of interest were each modeled by a single regressor. In addition, each GLM contained three nuisance regressors, modeling all the other trials in each of the three runs, as well as nuisance regressors modeling the response periods, instruction screens, and head-movement parameters. These design matrices were used to estimate the response amplitude of each voxel to each single trial. These estimates were used to calculate across-trial correlations between the motion directions represented in visual cortex and those reported by subjects (see below).

For the data from the localizer run (collected using a slow event-related design), we created one GLM wherein each trial was modeled by a separate regressor. Since the localizer consisted of a number of blocks of seven consecutive RDPs, separated by empty fixation screens, we expect the largest change in signal recorded from visual cortex to reflect the onset and offset of visual stimulation. This signal is itself not selective to the specific direction of the RDP but does add a source of unexplained variance that makes it difficult to precisely estimate the response to each individual RDP direction. To remove these low-frequency periodical fluctuations, we ran a principal components analysis (PCA) on the localizer parameter estimates, and removed the n components that explained the largest amount of variance from the data. To determine the optimal number of components to remove, while at the same time preventing the removal of informative data, we removed principal components while the mean absolute error (MAE) of motion direction reconstruction decreased. This procedure was run on the localizer data alone (using a leave-one-block-out cross-validation approach), and resulted in four principal components being removed (mean MAE, 6.9°; compared with 7.9° for MAE without principal component removal). As a control, we repeated our analyses after applying a high-pass filter to the parameter estimates, instead of PCA (see Results). Note that this procedure was performed on the data from the independent localizer run alone, while the testing of our hypotheses pertained to reconstructing the motion directions from the main experiment. To compensate for overall amplitude differences between runs, parameter estimates were normalized to z-scores for the localizer run and the experimental runs separately.

Freesurfer (http://surfer.nmr.mgh.harvard.edu/) was used to identify the boundaries of retinotopic areas in early visual cortex, using well established methods (Sereno et al., 1995; DeYoe et al., 1996; Engel et al., 1997). Additionally, we localized area MT+ using the contrast “motion > fixation” from the localizer run. Within each ROI (V1, V2, V3, V4, V3A, and MT+), we identified the 100 most informative voxels according to their response to the RDP stimuli in the independent functional localizer run. Specifically, we computed for each voxel the ANOVA F statistic of parameter estimates from the localizer run across motion directions. Voxels with the highest F statistic (i.e., those voxels that showed the greatest differential responses to the different directions) were selected for further analysis. To increase signal-to-noise ratio, we constructed an ROI that comprised all early visual areas (V1, V2, V3, V4, V3A, and MT+), and selected the 150 most informative voxels from this combined ROI. In a control analysis, we constrained voxel selection so that the combined ROI contained equal numbers of voxels (n = 25) originating from all six visual areas. Our main question was whether perceptual biases as a result of prior expectations affect visual cortex or not (i.e., affect processing in parietal or frontal cortex instead), and combining visual areas enabled us to address this question with maximal sensitivity.

Forward modeling.

To probe stimulus representations in the visual cortex, we used for each trial type a forward modeling approach to reconstruct the motion direction of the RDP stimuli from the BOLD signal (Brouwer and Heeger, 2009, 2011). We characterized the direction selectivity of each voxel as a weighted sum of six hypothetical channels, each with an idealized direction tuning curve (or basis function). Each basis function was a half-wave-rectified sinusoid raised to the fifth power, and the six basis functions were spaced evenly within the 360° direction space, such that a tuning curve with any possible direction preference could be expressed exactly as a weighted sum of the six basis functions. The rectification approximated the effect of the spike threshold for cortical neurons with low spontaneous firing rates, and the squaring made the tuning curves narrower. The shape of the resulting channels was a close approximation of observed tuning curves of neurons in early visual cortex (Heeger, 1992). Although a circular space could have been represented by two channels with sinusoidal tuning curves, the rectification and squaring operations led to the requirement of six channels (Freeman and Adelson, 1991). The half-wave-rectified and squared basis functions were more selective (narrower) than sinusoidal tuning curves, and strictly positive. Had the basis functions been broader, fewer channels would have been needed. If narrower, more channels would have been needed.

Although the actual motion directions used in the current study were taken from a subrange (−7.5–97.5°) of the full span of motion directions (0–360°), the basis functions (channels) in the forward model were not restricted to this subrange. Instead, they were evenly spaced within the full circular space. In this way, the forward model captured the direction selectivity of each voxel in the lower-dimensional space of its basis functions. This maximized the contribution of all voxels to the prediction of motion direction, even though their contribution to the model varied (some voxels could have been tuned to motion directions far away from those used in the current experiment). In addition, to tile the space of motion directions completely (each motion direction is associated with a unique pattern of channel responses), the channels needed to wrap around this circular space. If we would have restricted the channels to span only the subrange of motion directions used in the experiment, the wrapping of the channels would have been discontinuous (the motion direction of −7.5° would wrap around to a motion direction of 97.5°) and therefore unable to fit the continuous tuning curves expected from the fMRI measurements correctly.

In the first stage of the analysis, we used parameter estimates obtained from the localizer run to estimate the weights on the six hypothetical channels separately for each voxel, using linear regression. Specifically, let k be the number of channels, m the number of voxels, and n the number of repeated measurements (motion directions × repeats). The matrix of estimated response amplitudes for the different motion directions during the localizer run (B_loc, m × n) was related to the matrix of hypothetical channel outputs (C_loc, k × n) by a weight matrix (W, m × k) as shown in Equation 1: B = WC_loc.

The least-squares estimate of this weight matrix W was estimated using linear regression shown in Equation 2:

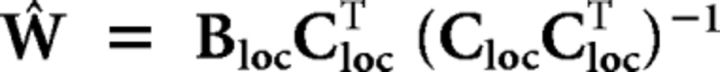These weights reflected the relative contribution of the six hypothetical channels in the forward model (each with their own direction selectivity) to the observed response amplitude of each voxel. Using these weights, the second stage of analysis reconstructed the channel outputs associated with the pattern of activity across voxels evoked by the stimuli in the main experiment (B_exp), again using linear regression. This step transformed each vector of n voxel responses (parameter estimates) to each trial into a vector of six (number of basis functions) channel responses. More specifically, the channel responses (C_exp) associated with the responses in the main experiment (B_exp) were estimated using the estimated weights W as expressed in Equation 3:

These channel outputs were used to compute a weighted average of the six basis functions, and the direction at which the resulting curve reached its maximum value constituted the reconstructed motion direction. Hereby, we obtained a reconstructed direction for each trial type (two priors × five motion directions) of the experiment. We performed the same analysis for the single-trial estimates, enabling us to calculate across-trial correlations between perceived and reconstructed directions.

Given the equal spacing of the hypothetical channels around the full span of 360°, the smaller range of motion directions used in the current study always produced a larger hypothetical response in some channels of the forward model, relative to the other channels. Because of this, the effect of adding increasing levels of noise did not make predictions completely random, but rather resulted in a regression of the predicted motion direction toward the channel with the highest response (the channel centered on the average motion direction). We can explain this by considering the linear regression implemented in the forward model. The forward model consists of two consecutive linear regression fits. To fit the weights, we take our training data B_loc and regress those onto our hypothetical channel responses C_loc, to produce a matrix of weights W (Eq. 2). If we use white noise for B_loc, we can observe the following: since C_loc is not balanced (one regressor or channel has a higher mean response), W too will show this imbalance. Specifically, each voxel in W will have a higher mean weight on the channel with the highest mean response. In the second stage, W is used in combination with the testing data B_exp to produce a reconstructed matrix of channel responses C_exp (Eq. 3). If B_exp also consists of only noise, this projects the imbalance in the weights back onto the reconstructed channel responses, causing them to show the same tendency toward the channel with the highest hypothetical response. In other words, the noise in our measurements will push the reconstructed direction toward the motion direction associated with the peak of the channel showing the highest response (45°). It should be noted that, although this has the effect of narrowing the distribution of reconstructed directions, it does not introduce a bias toward any of the predicted (cued) directions. Rather, this regression to the mean may result in an underestimation of the size of such a bias, and therefore does not taint our comparisons between the reconstructed directions as a function of the different cued directions.

For the behavioral data, we calculated the median perceived direction per condition (prior × direction). We calculated the median rather than the mean since it is more robust to outliers. For the fMRI data, only one estimate of reconstructed direction was obtained per condition. The Pearson correlation between median perceived (reconstructed) and actually presented directions was calculated as a measure of task performance (reconstruction accuracy).

We hypothesized that the auditory cues would result in an attractive bias. In Bayesian models of perceptual inference, the final percept (posterior) is conceptualized as the multiplication of the prior and the stimulus input (likelihood; Kersten et al., 2004). This leads to quite straightforward predictions for three of the motion directions presented in the experiment (27.5, 45, and 62.5°): depending on which cue is presented, the perceived direction should be biased either rightward (27.5°) or upward (62.5°). The direction of the bias for the two outer directions (10 and 80°) is also straightforward: they will be biased in the same direction by both cues: 10° stimuli will always be biased upwards (by both the 27.5 and 62.5° cue), and 80° stimuli will always be biased rightward. Furthermore, we expected a differential effect of the two cues: following Bayes' rule, a prior that is further away from the stimulus input will result in a larger shift than a prior that is closer to the stimulus input. Therefore, a 10° stimulus will be attracted more by a 62.5° cue than by a 27.5° cue, resulting in a relatively larger upward (i.e., toward 90°) bias for the 62.5° cue compared with the 27.5° cue (the same logic applies to the 80° stimulus direction). Empirically, we tested this prediction by computing two-way repeated-measures ANOVAs with the factors “Direction” and “Prior,” and checked for interactions between the two factors. We also assessed the effect of prior expectation on the three middle directions (27.5, 45, and 62.5°) in isolation, since the predicted direction of the effects are potentially more straightforward for these directions than for the outer ones (10 and 80°). All effects of prior expectation on perceived and reconstructed directions were tested for significance using one-tailed tests, since we had clear hypotheses regarding the direction of the effects. All other statistical tests, unless explicitly stated otherwise, were two-tailed. Additionally, we ran repeated-measures ANOVAs with factors “Prior” and “Run” (i.e., first, second, or third run of the experiment) to test for interactions between the effects of the predictive cues and time.

To test whether the representations in visual cortex more closely resembled the perceived or the actually presented directions, we correlated the reconstructed directions on each trial with subjects' perceptual reports and with the presented directions on these same trials, respectively, for each subject. The magnitudes of these two correlations were compared using a paired-sample t test. Additionally, we calculated the partial correlation between perceived and reconstructed directions, regressing out the presented directions.

To test whether there was a relationship between the perceptual bias and the neural bias induced by the predictive cues, we calculated the Pearson correlation between the two measures, across subjects, and performed a one-tailed significance test on the resulting correlation coefficient. Additionally, we performed a median split on the group of subjects on the basis of the size of their perceptual bias, and compared the bias in neural representations between the two subgroups using a two-sample t test. To preclude an explanation of such an effect in terms of differences in signal-to-noise ratios between the groups, we also compared behavioral performance and reconstruction accuracy between the two subgroups.

All statistical tests of correlation coefficients at the group level were preceded by applying Fisher's r-to-Z transform (Fisher, 1915).

Results

Behavioral results

The perceived motion direction largely followed the actual motion direction of the RDP stimuli (correlation between median perceived and presented direction, mean r = 0.93, t₍₂₂₎ = 16.4, p < 0.001; Fig. 2A), indicating that subjects were able to perform the task with high accuracy. Interestingly, the predictive cue induced a bias in perception. When the cue predicted the more rightward (27.5°) motion direction, subjects rated the motion as more rightward than when the cue predicted the more upward (62.5°) motion direction (mean bias, 1.1°; t₍₂₂₎ = 1.81; p = 0.042; Fig. 2A). This effect became stronger over time: a repeated-measures ANOVA showed a significant effect of experimental run on the perceptual bias (F_(2,44) = 4.31, p = 0.020), and a post hoc t test confirmed that the bias was larger in the last run than in the first run (t₍₂₂₎ = 2.52, p = 0.020; Fig. 2B). We return to this point below.

Figure 2.

Effects of expectation on perception and sensory representations. A, Perceived direction as a function of presented direction, separately for the two cue conditions. Inset shows the difference between the two cue conditions, i.e., the bias induced by expectation. B, Perceptual bias induced by expectation per run of the experiment, collapsed over presented directions. C, Direction reconstructed from the BOLD signal in visual cortex (V1, V2, V3, V4, V3A, and MT+), as a function of presented direction, separately for the two cue conditions. Inset shows the difference between the two cue conditions. D, Neural bias induced by expectation per run of the experiment, collapsed over presented directions. All error bars indicate SEM.

Prior expectations bias the neural representation of motion direction

Our main question was whether prior expectations can modify the representations in visual cortex. To answer this question, we used a forward modeling approach to reconstruct the represented motion direction from the BOLD signal in visual cortex for each trial (see Materials and Methods). The motion directions reconstructed from the BOLD signal in visual cortex correlated positively with the actually presented motion directions (mean r = 0.58, t₍₂₂₎ = 4.75, p < 0.001; Fig. 2C), indicating that the model managed to extract direction-specific signals from visual cortex.

More importantly, the prior expectations induced by the auditory cue significantly influenced the sensory representations in visual cortex (Fig. 2C). Notably, the direction reconstructed from visual cortex was more rightward when motion with a predominant rightward component (27.5°) was predicted, compared with when motion with a predominant upward component (62.5°) was predicted (mean bias, 5.9°; t₍₂₂₎ = 2.28; p = 0.017).

Neural representations in visual cortex reflect subjective contents of perception

The results described in the previous paragraph demonstrate that sensory representations in visual cortex are altered by implicit prior expectations. We reasoned that, if representations in visual cortex indeed resemble the (biased) contents of perception, rather than simply reflect bottom-up input, reconstructed directions should correlate more strongly with subjects' perceptual reports than with the actually presented directions, on a trial-by-trial basis. This is indeed what was found: the mean correlation between reconstructed and perceived directions was higher than that between reconstructed and actually presented directions (mean r = 0.25 vs mean r = 0.21, t₍₂₂₎ = 3.13, p = 0.0049; Fig. 3). In line with this, there was a significant partial correlation between reconstructed and perceived directions, regressing out presented directions (mean r = 0.14, t₍₂₂₎ = 7.13, p < 0.001). Furthermore, if the biased representations in visual cortex reflect the biases observed in perception (or vice versa), subjects with a strong perceptual bias should show a stronger bias in their neural representations than subjects with a weak perceptual bias. Indeed, there was a positive correlation between perceptual and neural bias, across subjects (r = 0.40, p = 0.028; Fig. 4A). We also performed a median split on the group of subjects based on the size of their perceptual bias, and found that subjects with a strong perceptual bias (mean bias, 3.2°) had a stronger neural representation bias (mean neural bias, 13.9°, significantly greater than zero; t₍₁₁₎ = 5.84, p < 0.001) than those with a weak perceptual bias (mean perceptual bias, −1.2°; mean neural bias, −2.8°, not significantly different from zero; t₍₁₀₎ = −0.87, p = 0.40; comparison between groups: t₍₂₁₎ = 4.26, p < 0.001; Fig. 4B). There were no significant differences in behavioral task performance (mean r = 0.89 vs 0.98, t₍₂₁₎ = −1.44, p = 0.17) and reconstruction accuracy (mean r = 0.55 vs 0.62, t₍₂₁₎ = −0.04, p = 0.97) between the two subgroups, precluding an explanation in terms of differences in signal-to-noise ratios between the two groups.

Figure 3.

Correlation between perception and neural representations across trials. A, Across-trial correlation between perceived (x-axis) and reconstructed (y-axis) directions for a representative subject. Each dot represents a single trial. B, The mean correlation between perceived (Perc) and reconstructed (Rec) direction (leftmost bar) is significantly higher than the mean correlation between presented (Pres) and reconstructed direction (middle bar). Rightmost bar, Partial correlation of perceived and reconstructed directions, after regressing out presented direction. All correlations are within subjects, across single trials (n = 360, see A); correlation coefficients were averaged over subjects and tested for significance at the group level. Error bars indicate SEM (**p < 0.01, ***p < 0.001).

Figure 4.

Relationship between perceptual and neural bias. A, Correlation between neural bias (x-axis) and perceptual bias (y-axis), across subjects. Each dot represents one subject. B, Subjects were split into two groups on the basis of their perceptual bias toward the cued directions, yielding a group with a strong (dark bars) and one with a weak (light bars) perceptual bias (leftmost bars). The group with the strong perceptual bias also had a strong neural bias, while the group with the weak perceptual bias did not have a significant neural bias (rightmost bars). Error bars indicate SEM (***p < 0.001).

Neural bias in individual regions in visual cortex

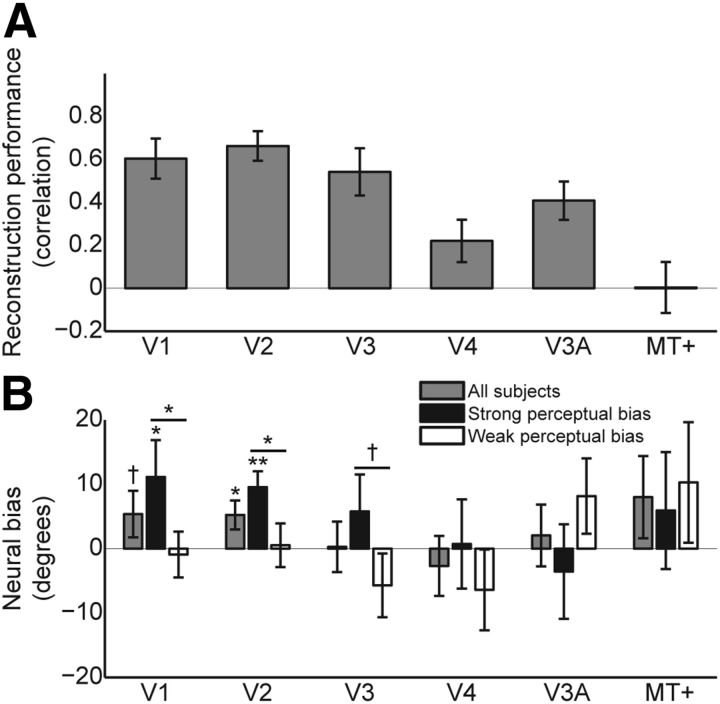
The results above were obtained by collapsing across the different regions within visual cortex (V1, V2, V3, V4, V3A, and MT+) to obtain a maximal signal-to-noise ratio (Kamitani and Tong, 2006). Analysis of the individual regions revealed that reconstruction performance was highest in the early visual regions (V1, V2, and V3; Fig. 5A). Furthermore, neural representations of motion direction were significantly biased toward the cued directions in V2 (t₍₂₂₎ = 2.33, p = 0.015), and a trend toward this effect was observed in V1 (t₍₂₂₎ = 1.49, p = 0.075; Fig. 5B). The neural bias in V1 and V2 was larger for subjects with a strong perceptual bias than those with a weak perceptual bias (V1: t₍₂₁₎ = 1.75, p = 0.048; V2: t₍₂₁₎ = 2.17, p = 0.021), and a trend toward the same effect was present in V3 (t₍₂₁₎ = 1.41, p = 0.074). In fact, in V1 and V2, the neural bias toward the cued directions was significant only for the group of subjects with a strong perceptual bias (strong bias: V1: t₍₁₁₎ = 1.94, p = 0.039; V2: t₍₁₁₎ = 3.86, p = 0.0013; weak bias: V1: t₍₁₁₎ = −0.26, p = 0.40; V2: t₍₁₁₎ = 0.15, p = 0.44). There were no significant effects in the other visual areas (all p > 0.10), possibly due to the fact that reconstruction performance was insufficiently accurate to reveal such biases (Fig. 5A). In other words, signal-to-noise ratio may not have been sufficiently high in these regions when studied separately.

Figure 5.

Reconstruction performance and neural bias per individual ROI. A, The correlation between reconstructed and presented motion directions indicates reconstruction performance. B, Neural bias averaged over all subjects (gray bars), as well as separately for subjects with a strong perceptual bias (black bars) and those with a weak perceptual bias (white bars). Positive neural bias indicates that reconstruction is biased toward the cues. Error bars indicate SEM (†p < 0.10, *p < 0.05, **p < 0.01).

Single-trial reconstructed directions correlated more strongly with perceived than presented motion directions in V1 (mean r = 0.23 vs 0.21, t₍₂₂₎ = 2.18, p = 0.040) and V2 (mean r = 0.27 vs 0.22, t₍₂₂₎ = 3.44, p = 0.0023), while a trend was visible in V3 (mean r = 0.20 vs 0.18, t₍₂₂₎ = 1.77, p = 0.090), but not in the other visual areas (p > 0.10). This suggests that the effect was stronger in early visual cortex (V1, V2, and V3) than in higher-level visual areas (V4, V3A, and MT+). Indeed, there was a significant effect of ROI on the difference between the two correlation measures (F_(5,110) = 4.20, p = 0.0016). As suggested above, the absence of an effect in higher-level areas may be due to the fact that overall reconstruction performance was lower in these regions (Fig. 5A). These results indicate that neural activity in early visual cortex reflects perceptual interpretations over and above the bottom-up input. An additional analysis confirmed this finding, revealing that there was a significant correlation between reconstructed and perceived directions after regressing out the presented directions in all three early visual areas (V1: mean r = 0.11, t₍₂₂₎ = 6.85, p < 0.001; V2: mean r = 0.17, t₍₂₂₎ = 6.78, p < 0.001; V3: mean r = 0.10, t₍₂₂₎ = 4.55, p < 0.001).

Interaction between time (experimental run) and bias

As discussed above, we found that the perceptual bias increased over time, being stronger in the last run of the experiment than in the first. We reasoned that such an increase could be due to either (1) learning of cue-stimulus contingencies over the course of the experiment or (2) noisier task performance in the first part of the fMRI session (perhaps reflecting the novel and unusual environment). To reduce learning during the fMRI session, note that subjects were exposed to the same cue-stimulus contingencies during a behavioral session on the day before. To investigate the possibility of noisier task performance in the first part of the fMRI session, we compared the MAE in task performance between runs. We found that MAE was significantly affected by experimental run (F_(2,44) = 3.38, p = 0.043), being higher in the first run than in the last run (MAE, 14.9 vs 13.1°, t₍₂₂₎ = 2.41, p = 0.025), suggesting that the absence of perceptual bias in the first part of the experiment may be (at least partly) due to noisy task performance.

Unlike for perception, there was no significant effect of experimental run on the neural bias (F_(2,44) = 0.09, p = 0.92; Fig. 2D). Similarly, unlike for behavior, MAE in reconstruction was not significantly modulated by experimental run (F_(2,44) = 0.66, p = 0.52). Thus, whereas noisy behavioral performance may have occluded the perceptual bias in the first part of the experiment, there was no such effect on reconstruction of the neural representations. In other words, the bias may have been present throughout the experiment, but may not have been visible in the behavioral data for the first part of the experiment due to noise in task performance that did not arise from noise in sensory processing.

Interaction between stimulus direction and bias

As outlined in the Materials and Methods section, the hypothesized effects of the predictive cues is potentially more straightforward for the three middle stimulus directions (27.5, 45, and 62.5°) than for the outer directions (10 and 80°). For the middle directions, the stimulus representation is expected to be biased either rightward or upward, depending on which cue is presented, while the direction of the bias is the same for both cues for the outer directions. Based on Bayes' rule, we expected a relative bias in the same direction for the inner directions as for the outer directions (see Materials and Methods). However, the opposite prediction could also be made: priors that are closer to the presented direction might be more compelling than priors that are further away (cf. de Gardelle and Summerfield, 2011). Therefore, we tested whether there was an interaction between stimulus direction and predicted direction. No such interaction was found, either for behavioral (F_(4,88) = 0.41, p = 0.80) or neural (F_(4,88) = 0.21, p = 0.93) data, suggesting that the relative shift induced by the cues is similar for all five stimulus directions. Additionally, we assessed the effect of prior expectation on the three middle directions (27.5, 45, and 62.5°) in isolation. For the behavioral data, the bias was qualitatively similar as when collapsing over all five directions (mean bias, 0.7°, compared with 1.1° for all five directions), but it was no longer statistically significant (t₍₂₂₎ = 0.85, p > 0.10). For the neural data, the effect was both qualitatively similar and statistically significant (mean bias, 7.8°; t₍₂₂₎ = 2.11; p = 0.023), despite the reduction in signal-to-noise ratio resulting from basing subject averages on a subset of trials.

Control analyses

Eye-movement analysis

We took a number of measures to rule out the potential confounding effects of eye movements in our results. First, to minimize potential effects of eye movements on the forward model, the weights of the forward model were estimated based on data from an independent localizer run, during which subjects performed a task at fixation for which the moving dots were irrelevant. Second, we monitored eye movements using an infrared eye tracker, and recorded pupil position for 12 subjects during the main experiment and for 11 subjects during the localizer run (see Materials and Methods). During the localizer, there were no significant effects of presented motion direction on either horizontal (repeated measures one-way ANOVA, F_(6,60) = 0.41, p = 0.87) or vertical (F_(6,60) = 1.3, p = 0.29) pupil position. Similarly, during either the cue-stimulus interval or during stimulus presentation in the main experiment, there were no significant effects of either predicted or presented motion direction on horizontal or vertical pupil position (repeated measures two-way ANOVAs, all p > 0.10). For these 12 subjects, as for the group as a whole, the predictive cue significantly biased motion directions reconstructed from visual cortex (combined ROI: V1, V2, V3, V4, V3A, and MT+; mean neural bias, 8.3°, t₍₁₁₎ = 2.46, p = 0.016), suggesting the reported biases did not arise from systematic differences in eye movements between conditions. Note, however, that the results of these eye-movement analyses should be treated with some caution, given the relatively low sampling rate (50 Hz) and precision of the eye-tracking system used.

Implicit nature of the expectations

Five of 23 subjects indicated that they suspected a relationship between the auditory cues and the RDP stimuli. Though only two of these five subjects suspected the true relationship (one for both tones, the other for just one of the two), one might wonder whether these subjects drove our effects. We compared the perceptual and neural biases in the five subjects that suspected a relationship between the tones and the moving dots (n = 5) to the biases in the subjects that did not (n = 18). There was no significant difference between the two groups of subjects in terms of either perceptual bias (t₍₂₁₎ = 0.82, p = 0.42) or neural bias (t₍₂₁₎ = −0.12, p = 0.91). Furthermore, the neural bias was significant also for subjects that did not suspect a relationship between the tones and the moving dots (t₍₁₇₎ = 2.39, p = 0.014). This shows that the neural bias was present when subjects were unaware of the predictive relationship between the auditory cues and the moving dots.

Analysis parameters

We applied PCA to remove low-frequency fluctuations in the parameter estimates obtained from the localizer data (see Materials and Methods). As a control, we repeated our analyses after applying a high-pass filter, instead of PCA, to the parameter estimates. Reconstruction performance on the localizer data was somewhat worse than when using the PCA approach (MAE, 8.2 vs 6.9°). However, our main result, a bias in the representations reconstructed from visual cortex induced by the predictive cues, remained significant (mean bias, 5.3°; t₍₂₂₎ = 2.34; p = 0.014).

In our main analysis, we used a combined ROI of visual cortex for which the most informative voxels were selected, regardless of which visual area they originated from. We found that the contribution of the individual areas was not equal (V1, 19%; V2, 22%; V3, 19%; V4, 13%; V3A, 12%; MT+, 17%), as shown by a significant effect of ROI on the percentage of selected voxels (repeated-measures ANOVA, F_(5,110) = 7.82, p < 0.001). It seems that the early visual areas contributed slightly more voxels than higher areas, as may be expected from the increased reconstruction performance in early visual areas compared with the late areas (Fig. 5A). However, selecting equal numbers of voxels (n = 25) from each of the six contributing ROIs did not significantly affect our results: the neural bias induced by the predictive cues was still clearly present (mean bias, 7.2°; t₍₂₂₎ = 2.37; p = 0.013).

Finally, the neural bias did not depend on the exact number of voxels selected for our analysis: the effect was robustly present when a sufficient number of voxels was included in the analysis (i.e., when the signal-to-noise ratio was high enough to reconstruct representations accurately), but not when too few voxels were included (Fig. 6).

Figure 6.

Reconstruction performance and neural bias in visual cortex (V1, V2, V3, V4, V3A, and MT+ combined) as a function of the number of voxels selected for analysis. A, Correlation between reconstructed and presented motion directions. B, Neural bias toward the directions predicted by the auditory cues. Error bars indicate SEM.

Discussion

Perception is shaped by both bottom-up inputs and top-down expectations. Here, we observed a direct neural correlate of this integration of inputs and priors in early visual cortex. Previous studies have shown that sensory representations in early visual cortex can be classified (Haynes and Rees, 2005; Kamitani and Tong, 2005, 2006) and reconstructed (Miyawaki et al., 2008; Brouwer and Heeger, 2009, 2011; Naselaris et al., 2009) on the basis of mesoscale fMRI signals during passive viewing of visual stimuli, and that these representations are also present in absence of sensory stimulation, for example during working memory maintenance (Harrison and Tong, 2009; Riggall and Postle, 2012). Additionally, representations in visual cortex have been shown to reflect arbitrary perceptual decisions about randomly moving dot patterns (Serences and Boynton, 2007b). While these previous studies investigated either bottom-up-induced or top-down-induced sensory representations in isolation, here we show that stimulus information and implicit sensory expectations are combined by human observers and that sensory representations reflect an integration of the two. In the present study, both the stimuli and the predictive cues contained information about the (likely) motion direction. This feature of the experiment was crucial to study the integration of bottom-up stimulus information and top-down expectations, instead of either factor in isolation. Subjects' perceptual reports (Fig. 2A) and sensory representations (Fig. 2C) reflected both sources of information. Indeed, sensory representations corresponded more closely to the contents of perception than to the actually presented stimuli (Hsieh et al., 2010). This suggests that prior expectations modify sensory processing at the earliest stages by affecting not only the amplitude of neural responses (Summerfield et al., 2008; den Ouden et al., 2009; Alink et al., 2010; Todorovic et al., 2011; Kok et al., 2012b), or their sharpness (Kok et al., 2012a), but also by changing the contents of sensory representations (Murray et al., 2006). In other words, prior expectations affect what is represented, rather than just how well things are represented.

At first glance, these findings seem at odds with “feedforward” hierarchical models of perceptual decision making, in which sensory areas provide evidence that is integrated in “decision neurons” in parietal and frontal areas (Gold and Shadlen, 2007; Beck et al., 2008). In these models, top-down modulatory factors, such as prior beliefs, modulate (baseline) activity levels in the decision layer, but not in the sensory layer that projects to it. In support of this, a recent study in macaque monkeys showed that a cue predicting the direction of motion of subsequent RDPs affected the neural activity of single cells in the lateral intraparietal area (LIP), but not in MT (Rao et al., 2012). However, in this and many other studies on perceptual decision-making in macaques, it is unclear whether the cue induced a sensory or motor prediction. Namely, the relevant stimulus feature mapped directly onto an overt response, since the monkey was instructed to make a saccade to the target location the dots were moving toward. As LIP is part of an oculomotor network, it is therefore difficult to disambiguate whether the neural activity modulation by the cue in LIP reflects a perceptual or response bias. In the present study, to avoid strategic guessing or response bias, subjects were not informed about the predictive relationship between the cues and the motion direction. Indeed, only one of 23 subjects suspected the true relationship between cues and stimuli, and one subject suspected the exact opposite relationship (see Materials and Methods).

Interestingly, in striking contrast to the findings of Rao et al. (2012), a study that trained monkeys to associate symbolic shapes (arrows) with particular upcoming motion directions observed direction-selective responses to these static stimuli in MT cells after training (Schlack and Albright, 2007), suggesting specific top-down modulations of spiking activity in visual cortex as a result of feature-based expectations.

Area MT+ may be a likely a priori locus for the effects of top-down modulation of motion perception to take place (Serences and Boynton, 2007b). However, the current study reveals no significant bias of representations in area MT+, but rather in earlier visual areas (Fig. 5B). This may be due to the fact that reconstruction was more accurate in lower-order visual areas than in MT+ (Fig. 5A). The lack of reliable motion direction reconstruction in area MT+ is likely due to the relatively small size of this area, compared with V1, V2, and V3 (Kamitani and Tong, 2006; Serences and Boynton, 2007b). Related to this, it may be that direction-selective columns in MT+ are too closely spaced to pick up direction-specific signals in the order of degrees using fMRI, as fMRI multivariate pattern analyses reveal the conjunction of feature specificity and the spatial inhomogeneity of these feature-specific responses, rather than feature specificity per se (Bartels et al., 2008). In other words, the predictive cues may have biased representations throughout visual cortex, but differences in signal-to-noise ratios led to the biases being particularly prominent in early visual areas.

Together, our results support an account of perception as a process of probabilistic inference (Helmholtz, 1867; Yuille and Kersten, 2006), wherein integration of top-down and bottom-up information takes place at every level of the cortical hierarchy (Friston, 2005). One way this may be achieved is through predictive coding (Rao and Ballard, 1999), an information processing framework wherein each cortical area tries to find the hypothesis that best explains the current data, guided by both bottom-up (sensory) and top-down (predictions) inputs, and communicates this hypothesis and the mismatch between the hypothesis and incoming data to the areas immediately below and above it in the hierarchy, respectively.

Mechanistically, the bias we observe may be the result of top-down gain on neurons representing the predicted direction of motion, similar to the mechanism suggested to underlie feature-based attention (Treue and Martínez Trujillo, 1999; Serences and Boynton, 2007a; Jehee et al., 2011). Indeed, studies by Kamitani and Tong (2005, 2006) have shown that voluntary top-down attention to one of two overlapping stimuli allows the attended stimuli to dominate the neural response in early visual cortex. In these studies, a binary classifier was more likely to categorize the neural response evoked by the ambiguous stimulus as having the attended orientation (or motion direction) than the unattended one, in line with theories of attention as biased competition (Desimone and Duncan, 1995). The current study differs from these studies in several respects. First, while Kamitani and Tong studied the effect of voluntary top-down attention, in the current study the prior expectations induced by the auditory cues were fully implicit. Note that it has been shown that attention can be guided by implicit knowledge (Chun and Jiang, 1999), reminiscent of the implicit effects of expectation in the current study. Second, the shift in neural representations we report is directly related to a shift in perception, indicating that the shift we observe is not a binary, “winner-takes-all” type of shift, but may instead reflect an integration of prior expectations and stimulus inputs.

In addition to altering neural representations, attention has also been shown to be capable of altering perception in many diverse ways, such as increasing the perceived contrast of attended stimuli (Carrasco et al., 2004). This makes it likely that the top-down gain mechanisms involved in attention could produce shifts in perception and neural representations similar to those reported here. Crucially, the current study goes beyond these previous studies by reporting a shift in subjective perception, induced by implicit expectations, that is directly correlated to a shift in neural representations in early visual cortex. In fact, neural representations were more closely related to what subjects subjectively perceived than to what was presented on the screen (Fig. 3).

The effect of top-down expectation on sensory cortex may take place already before stimulus onset, allowing prior expectations to bias sensory processing from the outset. Alternatively, sensory representation may be initially unbiased and show a modulation by prior expectation during a later phase of sensory processing. Due to the close temporal proximity of cue and stimuli, as well as the relatively low temporal resolution of fMRI, the current study cannot distinguish between these alternatives. However, recent studies using MEG in humans have shown that expectation can affect sensory responses as early as 100 ms poststimulus (Todorovic et al., 2011; Wacongne et al., 2011; Todorovic and de Lange, 2012), and paired-association studies in monkeys have revealed predictive signals before stimulus onset in the inferotemporal cortex (Sakai and Miyashita, 1991; Erickson and Desimone, 1999; Meyer and Olson, 2011), suggesting that predictive signals may affect sensory processing from the outset (den Ouden et al., 2012).

In sum, our data demonstrate that prior expectations can modify sensory representations in early visual cortex, suggesting that integration of prior and likelihood may not be confined to higher-order neural areas, but is also reflected in early sensory regions.